太原市2014-2015学年高一年级数学第一学段测评解析版

2014-2015学年山西省太原五中高一（下）段考数学试卷一、选择题（每小题3分，共36分，每小题只有一个正确答案）1．若sinα•tanα＞0，则角α的终边在（）A．第一象限B．第四象限C．第一或四象限D．第二或三象限2．cos45°•cos15°+sin45°•sin15°=（）A．B．C．D．3．如图，在正六边形ABCDEF中，点O为其中心，则下列判断错误的是（）A．=B．∥C．D．4．函数y=2cos2（x﹣）﹣1是（）A．最小正周期为π的奇函数B．最小正周期为π的偶函数C．最小正周期为的奇函数D．最小正周期为的偶函数5．下列四式不能化简为的是（）A．B．C．D．6．为了得到函数y=2sin（2x+）的图象，只需把函数y=2sinx的图象（）A．向左平移个单位长度，再把所得各点的横坐标变为原来的2倍（纵坐标不变）B．向左平移个单位长度，再把所得各点的横坐标变为原来的倍（纵坐标不变）C．各点的纵坐标不变、横坐标变为原来的2倍，再把所得图象向左平移个单位长度D．各点的纵坐标不变、横坐标变为原来的倍，再把所得图象向左平移个单位长度7．若P为△ABC所在平面内的一点，满足++=，则点P的位置为（）A．P在△ABC的内部B．P在△ABC的外部C．P在AB边所在的直线上D．P在AC边所在的直线上8．函数y=Asin（ωx+φ）在一个周期内的图象如图，此函数的解析式为（）A．y=2sin（2x+）B．y=2sin（2x+）C．y=2sin（﹣）D．y=2sin （2x﹣）9．设a=cos6°﹣sin6°，b=2sin13°cos13°，c=，则有（）A．a＞b＞c B．a＜b＜c C．b＜c＜a D．a＜c＜b 10．已知，且sinθ+cosθ=a，其中a∈（0，1），则关于tanθ的值，在以下四个答案中，可能正确的是（）A．﹣3 B．3或C．D．﹣3或11．E，F是等腰直角△ABC斜边AB上的三等分点，则tan∠ECF=（）A．B．C．D．12．已知函数f（x）=sinωx+cosωx（ω＞0），如果存在实数x1，使得对任意的实数x，都有f（x1）≤f（x）≤f（x1+2015）成立，则ω的最小值为（）A．B．C．D．二、填空题（每小题4分，共16分）13．在△ABC中，cosA=sinA，则A=．14．若|=||=3，∠AOB=60°，则|+|=．15．=．16．若函数f（x）=2sin（3x﹣），有下列结论：①函数f（x）的图象关于点（，0）对称；②函数f（x）的图象关于直线x=π对称；③在x∈[，π]为单调增函数．则上述结论题正确的是．（填相应结论对应的序号）三、解答题（共48分，每题12分）17．已知，求的值．（2）求的值．1015春•太原校级月考）已知α、β∈（0，π），且tanα、tanβ是方程x2+5x+6=0的两根．（Ⅰ）求α+β的值；（Ⅱ）求cos（α﹣β）的值．1015春•太原校级月考）已知函数，．（I）求函数h（x）=f（x）+g（x）的单调递增区间．（II）设x=x0是函数y=f（x）图象的一条对称轴，求g（x0）的值．2015春•太原校级月考）如图，点A，B是单位圆上的两点，A，B点分别在第一、二象限，点C是圆与x轴正半轴的交点，△AOB是正三角形，记∠COA=α．（1）若点A的坐标为（，），求cos2α的值；（2）分别过A，B作x轴的垂线，垂足为D，E，求当角α为何值时，三角形AED面积最大？并求出这个最大面积．2014-2015学年山西省太原五中高一（下）段考数学试卷参考答案与试题解析一、选择题（每小题3分，共36分，每小题只有一个正确答案）1．若sinα•tanα＞0，则角α的终边在（）A．第一象限B．第四象限C．第一或四象限D．第二或三象限考点：三角函数值的符号；象限角、轴线角．专题：计算题；三角函数的求值．分析：根据同角三角函数的关系化简得sinα•tanα=，结合题意得＞0，所以cosα＞0．由此即可得到角α的终边所在的象限．解答：解：∵tanα=，∴sinα•tanα=sinα•=，∵sinα•tanα＞0，即＞0，可得cosα是正数．∴角α的终边在第一或四象限．故选：C点评：本题给出sinα•tanα＞0，求角α的终边所在的象限．考查了三角函数的定义及其符号判断的知识，属于基础题．2．cos45°•cos15°+sin45°•sin15°=（）A．B．C．D．考点：两角和与差的余弦函数．专题：三角函数的求值．分析：由两角差的余弦公式和题意可得答案．解答：解：由两角差的余弦公式可得cos45°•cos15°+sin45°•sin15°=cos（45°﹣15°）=cos30°=故选：B点评：本题考查两角差的余弦公式，属基础题．3．如图，在正六边形ABCDEF中，点O为其中心，则下列判断错误的是（）A．=B．∥C．D．考点：平行向量与共线向量．专题：平面向量及应用．分析：根据正六边形性质及相等向量的定义可得答案．解答：解：由图可知，，但不共线，故，故选D．点评：本题考查平行向量与共线向量、相等向量的意义，属基础题．4．函数y=2cos2（x﹣）﹣1是（）A．最小正周期为π的奇函数B．最小正周期为π的偶函数C．最小正周期为的奇函数D．最小正周期为的偶函数考点：三角函数的周期性及其求法；函数奇偶性的判断．专题：三角函数的图像与性质．分析：利用二倍角公式化简为一个角的一个三角函数的形式，求出周期，判定奇偶性．解答：解：由y=2cos2（x﹣）﹣1=cos（2x﹣）=sin2x，∴T=π，且y=sin2x奇函数，即函数y=2cos2（x﹣）﹣1是奇函数．故选A．点评：本题考查三角函数的周期性及其求法，函数奇偶性的判断，是基础题．5．下列四式不能化简为的是（）A．B．C．D．考点：向量加减混合运算及其几何意义．专题：证明题．分析：由向量加法的三角形法则和减法的三角形法则，分别将B、C、D三个选项中的向量式化简，利用排除法得正确选项解答：解：由向量加法的三角形法则和减法的三角形法则，===，故排除B==故排除C==，故排除D故选A点评：本题考查了向量加法的三角形法则和减法的三角形法则及其应用，排除法解选择题6．为了得到函数y=2sin（2x+）的图象，只需把函数y=2sinx的图象（）A．向左平移个单位长度，再把所得各点的横坐标变为原来的2倍（纵坐标不变）B．向左平移个单位长度，再把所得各点的横坐标变为原来的倍（纵坐标不变）C．各点的纵坐标不变、横坐标变为原来的2倍，再把所得图象向左平移个单位长度D．各点的纵坐标不变、横坐标变为原来的倍，再把所得图象向左平移个单位长度考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：由条件利用函数y=Asin（ωx+φ）的图象变换规律，可得结论．解答：解：把函数y=2sinx的图象向左平移个单位长度，得到的函数解析式为：y=2sin （x+），再把所得各点的横坐标变为原来的倍（纵坐标不变），得到的函数解析式为：y=2sin（2x+），故选：B．点评：本题考查的知识要点：函数图象的变换问题平移变换和伸缩变换，属于基础题型．7．若P为△ABC所在平面内的一点，满足++=，则点P的位置为（）A．P在△ABC的内部B．P在△ABC的外部C．P在AB边所在的直线上D．P在AC边所在的直线上考点：向量的加法及其几何意义．专题：计算题；平面向量及应用．分析：用向量的运算法则将等式变形，得到=﹣2 ，据三点共线的充要条件得出结论：P在AC边所在的直线上．解答：解：∵++=，∴++=﹣，∴=﹣2 =2，∴P是AC边的一个三等分点．故选：D．点评：本题考查了向量的加法及其几何意义．分析出=﹣2 是解题的难点．8．函数y=Asin（ωx+φ）在一个周期内的图象如图，此函数的解析式为（）A．y=2sin（2x+）B．y=2sin（2x+）C．y=2sin（﹣）D．y=2sin （2x﹣）考点：由y=Asin（ωx+φ）的部分图象确定其解析式．分析：根据已知中函数y=Asin（ωx+ϕ）在一个周期内的图象经过（﹣，2）和（﹣，2），我们易分析出函数的最大值、最小值、周期，然后可以求出A，ω，φ值后，即可得到函数y=Asin（ωx+ϕ）的解析式．解答：解：由已知可得函数y=Asin（ωx+ϕ）的图象经过（﹣，2）点和（﹣，2）则A=2，T=π即ω=2则函数的解析式可化为y=2sin（2x+ϕ），将（﹣，2）代入得﹣+ϕ=+2kπ，k∈Z，即φ=+2kπ，k∈Z，当k=0时，φ=此时故选A点评：本题考查的知识点是由函数y=Asin（ωx+ϕ）的部分图象确定其解析式，其中A=|最大值﹣最小值|，|ω|=，φ=L•ω（L是函数图象在一个周期内的第一点的向左平移量）．9．设a=cos6°﹣sin6°，b=2sin13°cos13°，c=，则有（）A．a＞b＞c B．a＜b＜c C．b＜c＜a D．a＜c＜b考点：两角和与差的正弦函数．专题：三角函数的求值．分析：化简可得a=sin24°，b=sin26°，c=sin25°，由三角函数的单调性可得．解答：解：化简可得a=cos6°﹣sin6°=sin（30°﹣6°）=sin24°；b=2sin13°cos13°=sin26°；c===sin25°，由三角函数的单调性可知a＜c＜b故选：D点评：本题考查三角函数公式的应用，涉及三角函数的单调性，属基础题．10．已知，且sinθ+cosθ=a，其中a∈（0，1），则关于tanθ的值，在以下四个答案中，可能正确的是（）A．﹣3 B．3或C．D．﹣3或考点：同角三角函数间的基本关系．专题：计算题．分析：由θ的范围，得到cosθ大于0，把已知的等式两边平方，利用同角三角函数间的基本关系化简后，由a的范围得到2sinθcosθ的值大于0，进而得到sinθ的值小于0，又根据sinθ+cosθ=a，a大于0，得到cosθ＞﹣sinθ＞0，再利用不等式的基本性质及同角三角函数间的基本关系化简，得到tanθ值的范围，即可判断出符合题意的tanθ值的可能值．解答：解：由，得到cosθ＞0，所以把sinθ+cosθ=a两边平方得：（sinθ+cosθ）2=a2，即sin2θ+cos2θ+2sinθcosθ=1+2sinθcosθ=a2，又a∈（0，1），所以2sinθcosθ=a2﹣1＜0，所以sinθ＜0，又sinθ+cosθ=a＞0，所以cosθ＞﹣sinθ＞0，则﹣1＜tanθ＜0．故选C点评：此题考查了同角三角函数间的基本关系，要求学生掌握余弦函数的图象与性质，不等式的基本性质，以及同角三角函数间的基本关系，解本题的思路是利用同角三角函数间的基本关系及不等式的基本性质求出tanθ的范围．11．E，F是等腰直角△ABC斜边AB上的三等分点，则tan∠ECF=（）A．B．C．D．考点：余弦定理．专题：计算题．分析：约定AB=6，AC=BC=，先在△AEC中用余弦定理求得EC，进而在△ECF中利用余弦定理求得cosECF，进而用同角三角函数基本关系求得答案．解答：解：约定AB=6，AC=BC=，由余弦定理可知cos45°==；解得CE=CF=，再由余弦定理得cos∠ECF==，∴点评：考查三角函数的计算、解析化应用意识．12．已知函数f（x）=sinωx+cosωx（ω＞0），如果存在实数x1，使得对任意的实数x，都有f（x1）≤f（x）≤f（x1+2015）成立，则ω的最小值为（）A．B．C．D．考点：两角和与差的正弦函数；正弦函数的图象．专题：计算题；三角函数的图像与性质．分析：由题意可得区间[x1，x1+2015]能够包含函数的至少一个完整的单调区间，利用两角和的正弦公式求得f（x）=sin（ωx+），由2015≥•求得ω的最小值．解答：解：显然要使结论成立，只需保证区间[x1，x1+2015]能够包含函数的至少一个完整的单调区间即可，又∵f（x）=sinωx+cosωx=sin（ωx+），则2015≥•，∴ω≥，则ω的最小值为：，故选：B．点评：本题主要考查两角和的正弦公式，正弦函数的单调性和周期性，属于中档题．二、填空题（每小题4分，共16分）13．在△ABC中，cosA=sinA，则A=30°．考点：同角三角函数基本关系的运用．专题：三角函数的求值．分析：已知等式变形后，利用同角三角函数间基本关系求出tanA的值，即可确定出A的度数．解答：解：∵在△ABC中，cosA=sinA，即tanA=，∴A=30°，故答案为：30°．点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．14．若|=||=3，∠AOB=60°，则|+|=3．考点：平面向量数量积的运算．专题：平面向量及应用．分析：由已知求出的数量积，然后将所求平方展开，求值．解答：解：由已知得到=32×=，|+|2==32+32+9=27，所以|+|==3；故答案为：3．点评：本题考查了平面向量的数量积公式的运用以及没有坐标表示的向量的模的求法；经常考查，注意掌握．15．=2．考点：两角和与差的正切函数．专题：三角函数的求值．分析：由于原式=1+tan17°+tan28°+tan17°•tan28°，再由tan（17°+28°）==tan45°=1，可得tan17°+tan28°=1﹣tan17°•tan28°，代入原式可得结果．解答：解：原式=1+tan17°+tan28°+tan17°•tan28°，又tan（17°+28°）==tan45°=1，∴tan17°+tan28°=1﹣tan17°•tan28°，故（1+tan17°）（1+tan28°）=2，故答案为2．点评：本题主要考查两角和的正切公式的应用，属于中档题．16．若函数f（x）=2sin（3x﹣），有下列结论：①函数f（x）的图象关于点（，0）对称；②函数f（x）的图象关于直线x=π对称；③在x∈[，π]为单调增函数．则上述结论题正确的是①②③．（填相应结论对应的序号）考点：正弦函数的图象．专题：三角函数的图像与性质．分析：根据三角函数的图象和性质分别进行判断即可得到结论．解答：解：①f（）=2sin（3×﹣）=2sinπ=0，则函数图象关于点（，0）对称，故①正确，②f（π）=2sin（3×π﹣）=2sin=2，则图象关于直线x=π对称，故②正确，③当x∈[，π]，3x﹣∈[]，此时函数单调递增，故③正确，故答案为：①②③．点评：本题主要考查与三角函数命题有关的真假判断，根据三角函数的图象和性质是解决本题的关键．三、解答题（共48分，每题12分）17．已知，求的值．（2）求的值．考点：两角和与差的余弦函数；同角三角函数基本关系的运用．专题：三角函数的求值．分析：（1）由条件利用同角三角函数的基本关系求得cos（α+β）和cos（β﹣）的值，再利用两角和差的三角公式求得=cos[（α+β）﹣（β﹣）]的值．（2）由条件利用同角三角函数的基本关系，二倍角公式、诱导公式求得所给式子的值．解答：解：（1）∵已知，∴α+β∈（，2π），β﹣∈（，），∴cos（α+β）==，cos（β﹣）=﹣=﹣．=cos[（α+β）﹣（β﹣）]=cos（α+β）cos（β﹣）+sin（α+β）sin（β﹣）=+（﹣）•=﹣．（2）=sin50°•=sin50°•=cos40°•==1．点评：本题主要考查同角三角函数的基本关系，二倍角公式，两角和差的三角公式，以及三角函数在各个象限中的符号，属于基础题．1015春•太原校级月考）已知α、β∈（0，π），且tanα、tanβ是方程x2+5x+6=0的两根．（Ⅰ）求α+β的值；（Ⅱ）求cos（α﹣β）的值．考点：两角和与差的正切函数；两角和与差的余弦函数．专题：三角函数的求值．分析：（Ⅰ）由条件利用韦达定理、两角和的正切公式求得tan（α+β）的值，再结合α+β的范围，求得α+β的值．（2）由（1）得cosαcosβ﹣sinαsinβ=﹣，再根据tanα•tanβ==6，求得sinαsinβ和cosαcosβ的值，可得cos（α﹣β）=cosαcosβ+sinαsinβ的值．解答：解：（Ⅰ）由tanα、tanβ是方程x2+5x+6=0的两根，可得tanα+tanβ=﹣5，tanα•tanβ=6，∴tan（α+β）==．再结合α、β∈（0，π），tanα＜0、tanβ＜0，可得α、β∈（，π），∴α+β∈（π，2π），∴α+β=．（Ⅱ）由（1）得cos（α+β）=cosαcosβ﹣sinαsinβ=cos=﹣①，再根据tanα•tanβ==6 ②，由①②求得sinαsinβ=，cosαcosβ=，∴cos（α﹣β）=cosαcosβ+sinαsinβ=．点评：本题主要考查韦达定理、两角和差的三角公式，同角三角函数的基本关系，属于基础题．1015春•太原校级月考）已知函数，．（I）求函数h（x）=f（x）+g（x）的单调递增区间．（II）设x=x0是函数y=f（x）图象的一条对称轴，求g（x0）的值．考点：三角函数中的恒等变换应用；正弦函数的图象．专题：计算题；三角函数的图像与性质．分析：（I）由三角函数中的恒等变换应用化简函数解析式可得h（x）=sin（2x+），令2k≤2x+≤2k，即可解得函数h（x）的单调递增区间．（II）由x=x0是函数y=f（x）图象的一条对称轴，可求2x0+=kπ，解得2x0=k（k∈Z），从而可得g（x0）=1+sin（k），分情况讨论即可得解．解答：解：（I）h（x）=f（x）+g（x）=[1+cos（2x+）]+1+sin2x，…（1分）=[cos（2x+）+sin2x]+=（cos2x+sin2x）+…（2分）=sin（2x+）…（3分）由2k≤2x+≤2k，…（4分）得k≤x≤k（k∈Z）时，…（5分）故函数h（x）的单调递增区间是[k，k]（k∈Z）…（6分）（II）由题设知f（x）=[1+cos（2x+）]．．因为x=x0是函数y=f（x）图象的一条对称轴，所以2x0+=kπ，…（8分）即2x0=k（k∈Z）…（9分）所以g（x0）=1+sin2x0=1+sin（k），…（10分）当k为偶数时，g（x0）=1+sin（﹣）=1﹣=，…（11分）当k为奇数时，g（x0）=1+sin=1+=．…（12分）点评：本题主要考查了三角函数中的恒等变换应用，正弦函数的图象和性质，属于基本知识的考查．2015春•太原校级月考）如图，点A，B是单位圆上的两点，A，B点分别在第一、二象限，点C是圆与x轴正半轴的交点，△AOB是正三角形，记∠COA=α．（1）若点A的坐标为（，），求cos2α的值；（2）分别过A，B作x轴的垂线，垂足为D，E，求当角α为何值时，三角形AED面积最大？并求出这个最大面积．考点：任意角的三角函数的定义．专题：三角函数的求值．分析：（1）由条件利用任意角的三角函数的定义，二倍角的余弦公式，求得cos2α的值．（2）化简S△AED=AD•DE为sin（2α﹣）+，由0＜α＜及＜α+＜π，利用正弦函数的定义域和值域，求得三角形AED面积的最大值．解答：（1）由题意可得sinα=，cosα=，故cos2α=cos2α﹣sin2α=．（2）AD=sinα，OD=cosα，OE=﹣cos（α+），DE=OD+OE=cosα﹣cos（α+），故S△AED=AD•DE=sinα•[cosα﹣cos（α+）]=sinα•（cosα﹣cosα+sinα）=sinα•cosα+sin2α=sin2α﹣cos2α+=sin（2α﹣）+．由0＜α＜及＜α+＜π，可得＜α＜，从而0＜2α﹣＜，故当2α﹣=，即α=时，S△AED取得最大值+．点评：本题主要考查任意角的三角函数的定义，二倍角的余弦公式，三角恒等变换，正弦函数的定义域和值域，属于中档题．。

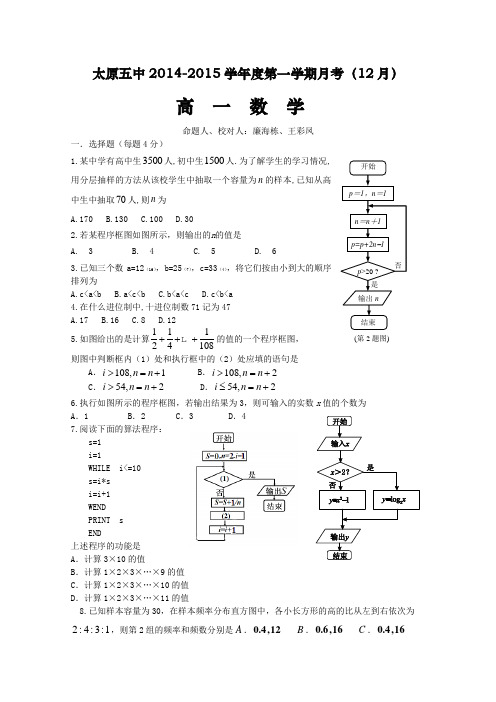
太原五中2014-2015学年度第一学期月考（12月）高 一 数 学命题人、校对人：廉海栋、王彩凤一．选择题（每题4分）1.某中学有高中生3500人,初中生1500人.为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n 的样本,已知从高中生中抽取70人,则n 为 A.170 B.130 C.100 D.302.若某程序框图如图所示，则输出的n 的值是 A. 3 B. 4 C. 5 D. 63.已知三个数a=12（16），b=25（7），c=33（4），将它们按由小到大的顺序排列为A.c<a<bB.a<c<bC.b<a<cD.c<b<a 4.在什么进位制中,十进位制数71记为47 A.17 B.16 C.8 D.12 5.如图给出的是计算11124108+++的值的一个程序框图， 则图中判断框内（1）处和执行框中的（2）处应填的语句是A ．108,1i n n >=+B ．108,2i n n >=+C ．54,2i n n >=+D ．54,2i n n ≤=+6.执行如图所示的程序框图，若输出结果为3，则可输入的实数x 值的个数为 A ．1 B ．2 C ．3 D ．47.阅读下面的算法程序：s=1 i=1WHILE i<=10 s=i*s i=i+1 WEND PRINT s END上述程序的功能是 A ．计算3×10的值B ．计算1×2×3×…×9的值C ．计算1×2×3×…×10的值D ．计算1×2×3×…×11的值8.已知样本容量为30，在样本频率分布直方图中，各小长方形的高的比从左到右依次为1:3:4:2，则第2组的频率和频数分别是A ．0.4,12 B ．0.6,16 C ．0.4,16(第2题图)D ．0.6,129.期中考试后，某校高三(9)班对全班65名学生的成绩进行分析，得到数学成绩y 对总成绩x 的回归直线方程为y ＝6＋0.4x .由此可以估计：若两个同学的总成绩相差50分，则他们的数学成绩大约相差________分． A.20 B.26 C.110 D.12510.已知n 次多项式P n (x)=a 0x n+a 1x n-1+…+a n-1x+a n ，如果在一种算法中，计算kx 0（k=2，3，4，…，n ）的值需要k －1次乘法，计算P 3(x 0)的值共需要9次运算（6次乘法，3次加法），那么计算P 10(x 0)的值共需要__________次运算. A.64 B.19 C.20 D.6511．若当x R ∈时，y =1log ay x=的图像大致是12.已知函数()1f x +是偶函数，当211x x >>时，2121[()()]()0f x f x x x -->恒成立，设1(),(2),(3)2a fb fc f =-==，则,,a b c 的大小关系为A ．b a c <<B ．c b a <<C ．b c a <<D ．a b c <<二．填空题（每题3分）13.两数5280,12155的最大公约数为_________14.下列抽样：①一个总体中共有100个个体，随机编号012399，，，，，，依编号顺序平均分成10个小组，组号依次为12310，，，，．现抽取一个容量为10的样本，规定如果在第1组随机抽取的号码为m ，那么在第k 组中抽取的号码个位数字与m k +的个位数字相同；②厂里生产的产品，用传送带将产品送入包装车间前，检验人员从传送带上每隔5分钟抽一件产品进行检验；③某一市场调查，规定在商场门口随机抽一个人进行询问调查，直到调查到事先规定的人数为止；④影院调查观众的某一指标，通知每排(每排人数相等)座号为12的观众留下来座谈.上述抽样中是系统抽样的是___________.(请把符合条件的序号填到横线上)15. 已知样本9,10,11,,x y 的平均数是10xy =16.已知函数211,0,22()13,,12x x f x x x ⎧⎡⎫+∈⎪⎪⎢⎪⎣⎭=⎨⎡⎤⎪∈⎢⎥⎪⎣⎦⎩，若存在12x x <，使得12()()f x f x =，则12()x f x ⋅的取值范围为三．解答题(每题8分)17.为检测学生的体温状况， 随机抽取甲，乙两个班级各10名同学，测量他们的体温（单位0.1摄氏度）获得体温数据的茎叶图，如图所示.（Ⅰ）根据茎叶图判断哪个班级的平均体温较高； （Ⅱ）计算乙班的样本方差； 18.从100名学生中抽取20名学生某次数学考试成绩(单位:分)的频率分布直方图如下: (1)求频率分布直方图中a 的值;(2)估计总体中成绩落在[50,70)中的学生人数; (3)估计总体的中位数.19.已知关于某设备的使用年限x 与所支出的维修费用y （万元），有如下统计资料： 设y 对x 呈线性相关关系，试求： （1）线性回归方程a bx y +=的回归系数b a ,； （2）估计使用年限为10年时，维修费用是多少？（线性回归方程a bx y += 中的系数b a ,可以用公式⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=∑∑==xb y a x n x y x n y x b n i i i i i 2121）20.某市有甲、乙两家乒乓球俱乐部，两家设备和服务都很好，但收费方式不同，甲家每张球台每小时5元；乙家按月计费，一个月中30小时以内(含30小时)每张球台90元，超过30小时的部分每张球台每小时2元．小张准备下个月从这两家中的一家租一张球台开展活动，其活动时间不少于15小时，也不超过40小时．(1)设在甲家租一张球台开展活动x 小时的收费为f (x )元(15≤x ≤40)，乙家租一张球台开展活动x 小时的收费为g (x )元(15≤x ≤40)．试求f (x )和g (x )；(2)问：小张选择哪家比较合算？为什么？21.已知函数f (x )＝－x 2＋2e x ＋t －1，g (x )＝x ＋e2x(x >0，其中e 表示自然对数的底数)．(1)若g (x )＝m 有零点，求m 的取值范围；(2)确定t 的取值范围，使得g (x )－f (x )＝0有两个相异实根．答案CCABC CCAAD BA 55 124 96[3/16，1/2)17．(1)甲（2）13.4 18.1/200 25 540/7 19. 0.08 1.23 12.38 20.f(x)=5x 15≤x ≤40g(x)=⎩⎨⎧≤<+≤≤40x 30 30,2x 30x 15 ,9015≤x <18 选甲 x=18 甲乙都可 18<x ≤40选乙 21. 2e ≤m t>2e+1-e 2。

山西大学附中2014~2015学年高一第一学期期中考试（总第二次）数学试题考试时间：90分钟 满分：100分一、选择题（本大题共10小题，每小题4分，共40分）1．设全集{}*|6U x N x =∈<，集合{}{}1,3,3,5A B ==，则()U C A B =( )A ．{}2,4B ．{}1,5C ．{}1,4D ．{}2,52． 函数()lg(2)f x x =+的定义域为( ) A ．(2,1)-B ．[2,1)-C ．(2,1]-D ．[]1,2-3．已知0a >且1a ≠，下列四组函数中表示相等函数的是( )A ．log a y x = 与1(log )x y a -=B ．2y x =与2log x a y a =C ．log a xy a=与y x = D ．2log a y x =与2log a y x =4．已知函数21()21x x f x -=+,若()f a b =， 则()f a -=( )A ．bB ．b -C ．1bD ．1b-5．下列函数中值域为()0,+∞的是( )A ．xy -=215 B ．()10y x x x =+> C ．xy -⎪⎭⎫⎝⎛=131D ．()11y x x x=-≥6．已知幂函数()y f x =的图像过点(,则4log (2)f 的值为( )A ．14 B ．14- C ．2 D ．2- 7．在下列区间中，函数()43xf x e x =+-的零点所在的区间为( )A ．1,04⎛⎫- ⎪⎝⎭B ．10,4⎛⎫ ⎪⎝⎭C ．11,42⎛⎫ ⎪⎝⎭D ．13,24⎛⎫ ⎪⎝⎭8．三个数 3.3320.99,log ,log 0.8π的大小关系为( )A ． 3.332log 0.99log 0.8π<<B ． 3.323log 0.8log 0.99π<<C ． 3.3230.99log 0.8l og π<<D ． 3.323log 0.80.99log π<< 9．当(1,2)x ∈，不等式2(1)log a x x -<恒成立，则实数a 的取值范围是（ ）A ．(1,2)B ．(1,2]C ．[)2,+∞ D ．(2,)+∞10．若函数()f x 为定义在R 上的奇函数，且在()0,+∞为增函数，又(2)f 0=，则不等式[]1ln ()0x f x e ⎛⎫⋅⋅< ⎪⎝⎭的解集为( ) A ．()()2,02,-+∞ B ．()(),20,2-∞-C ．()()2,00,2-D ．()(),22,-∞-+∞二、填空题：（本大题共5小题，每小题4分，共20分）11．函数()log 12a y x =++(01)a a >≠且恒过定点，其坐标为 ．12．设1232,2()log (1),2x e x f x x x -⎧<⎪=⎨-≥⎪⎩，则((2))f f 的值为 ．13．已知函数()xf x e x =+，若关于x 的方程()f x k =有两个不同的实根，则实数k 的取值范围是 ．14．已知函数)(x f 满足：)()()(q f p f q p f ⋅=+，2)1(=f ，则：)2013()2014()7()8()5()6()3()4()1()2(f f f f f f f f f f +++++ = ． 15． 给出下列四个命题：①函数2212-+-=x x y 为奇函数；②奇函数的图像一定通过直角坐标系的原点； ③函数xy 12=的值域是()0,+∞；④若函数)2(x f 的定义域为[1,2]，则函数)2(xf 的定义域为[1,2]； ⑤函数()x x y 2lg 2+-=的单调递增区间是(]0,1．其中正确命题的序号是 ．（填上所有正确命题的序号）三、解答题（本大题共5小题，共40分．解答应写出必要的文字说明，证明过程或演算步骤）16．（本小题满分8分）计算：（Ⅰ）()20.532025270.1100964π--⎛⎫⎛⎫++-⋅⎪ ⎪⎝⎭⎝⎭；（Ⅱ）82715lg lg lg12.5log 9log 828-+-⋅+2ln 2e ．17．（本小题满分8分）已知集合{}22|280A x x ax a =--≤． （Ⅰ）当1a =时，求集合R C A ；（Ⅱ）若0a >，且(1,1)A -⊆，求实数a 的取值范围．18．（本小题满分8分）已知二次函数a ax x x f -+-=2)(2在区间[]0,1上有最大值2，求实数a 的值．19．()1,1-上的函数． （Ⅰ）用定义法证明函数()x f 在()1,1-上是增函数； （Ⅱ）解不等式()()01<+-x f x f ．20．（本小题满分8分）已知函数4()log (41)()x f x kx k R =++∈是偶函数． （Ⅰ）求k 的值；（Ⅱ）设44()log (2)3x g x a a =⋅-,若函数()f x 与()g x 的图象有且只有一个公共点，求实数a 的取值范围．山西大学附中2014~2015学年高一第一学期期中考试（总第二次）数学答案二、填空题：（本大题共5小题，每小题4分，共20分）11． ()0,2 12． 2． 13．()1,+∞ 14．2014 15．①④⑤三、解答题（本大题共5小题，共40分．解答应写出必要的文字说明，证明过程或演算步骤）16．（本小题满分8分）计算：（Ⅰ）()20.532025270.1100964π--⎛⎫⎛⎫++-⋅⎪ ⎪⎝⎭⎝⎭； （Ⅱ）82715lg lg lg12.5log 9log 828-+-⋅+2ln 2e ．解：（Ⅰ）319；……………………4分 （Ⅱ）133……………………8分17．（本小题满分8分）已知集合{}22|280A x x ax a =--≤． （Ⅰ）当1a =时，求集合R C A ；（Ⅱ）若0a >，且(1,1)A -⊆，求实数a 的取值范围．解：（Ⅰ）当1=a 时，解不等式0822≤--x x ，得42≤≤-x …………………2分 ∴{}|42R C A x x x =><-或 ………………………………………3分 （Ⅱ）∵22280x ax a --≤，∴0)2)(4(≤+-a x a x又∵0a > ∴24a x a -≤≤ ∴[]2,4A a a =- ……………………5分 又∵()1,1A -⊆ ∴1214aa-≥-⎧⎨≤⎩ …………………………………………7分解得21≥a ，故实数a 的取值范围是1[,)2+∞ …………………………………8分 18．（本小题满分8分）已知二次函数a ax x x f -+-=2)(2在区间[]0,1上有最大值2，求实数a 的值解析：由a a a x x f -+--=22)()(，得函数)(x f 的对称轴为：x a =，……1分 ①当0<a 时，()f x 在]1,0[上递减， 2)0(=∴f ，即2,2-=∴=-a a ； ……………………3分 ②当1>a 时，()f x 在]1,0[上递增， 2)1(=∴f ，即3=a ； ……………………5分③当01a ≤≤时，()f x 在],0[a 递增，在[,1]a 上递减，2)(=∴a f ，即22=-a a ，解得：12-=或a 与01a ≤≤矛盾；……………7分 综上：2a =-或3a = ……………………8分19．（本小题满分8()1,1-上的函数． （Ⅰ）用定义法证明函数()x f 在上是增函数；（Ⅱ）解不等式()()01<+-x f x f ．解：（Ⅰ）证明：对于任意的()1,1,21-∈x x ，且21x x <，则()()()()()()()()()()()()()()22212121222112212122212122212222112111111111111x x x x x x x x x x x x x x x x x x x x x x x x x f x f ++--=++-+-=+++-+=+-+=- 1121<<<-x x ， ()()011,0222121>++<-∴x x x x ，01,12121>-∴<∴x x x x ． ()()021<-∴x f x f ，即()()21x f x f <．∴函数()21xf x x =+在()1,1-上是增函数．…………………… 4分 （Ⅱ）由已知及（Ⅰ）知，()f x 是奇函数且在()1,1-上递增，()()()()()()2102111201111111101<<⇔⎪⎪⎩⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧<<<-<<⇔-<-<<-<-<-⇔-<-⇔-<-⇔<+-x x x x x x x x x f x f x f x f x f x f ∴不等式的解集为10,2⎛⎫⎪⎝⎭．…… 8分．20．（本小题满分8分）已知函数4()log (41)()x f x kx k R =++∈是偶函数． （Ⅰ）求k 的值；（Ⅱ）设44()log (2)3x g x a a =⋅-,若函数()f x 与()g x 的图象有且只有一个公共点，求实数a 的取值范围． 解：（Ⅰ）由函数()f x 是偶函数，可知()().f x f x =-kx kx x x -+=++∴-)14(log )14(log 44,kx x x 21414log 4-=++-即, ,24log 4kx x -= 2x kx ∴=-对一切 x R ∈恒成立21-=∴k ……………3分（Ⅱ）函数()f x 与()g x 的图象有且只有一个公共点,即方程4414log (41)log (2)23x x x a a +-=⋅-有且只有一个实根,化简得: 方程142223x x x a a +=⋅-有且只有一个实根 ……………………4分令20x t =>,则方程24(1)103a t at ---=有且只有一个正根,①314a t =⇒=-,不合题意; ……………………5分②若304a ∆=⇒=或3-；若3,24a t ==-则,不合题意；若132a t =-⇒= ,符合题意③若方程一个正根与一个负根,即1011a a -<⇒>- ……………………7分综上:实数a 的取值范围是{}3(1,)-⋃+∞ ……………………8分。

第1页 共10页 ◎ 第2页 共10页绝密★启用前2014-2015学年度期中卷高一数学考试范围：必修一；考试时间：120分钟；命题人： 注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题（题型注释）1．已知集合{}1,2,3M =，{}2,3,4N =，则 （ ） A ．M N ⊆ B ．N M ⊆ C ．{}1,4MN = D ．{}2,3M N =【答案】D【解析】解：因为根据已知 的集合，可以判定集合间的关系，以及集合的运算，那么显然选项D 成立。

2．设集合}1,0,1{-=M ，},{2a a N =，则使M∩N＝N 成立的a 的值是（ ） A ．1 B ．0 C ．－1 D ．1或－1 【答案】C 【解析】试题分析：由于集合中的元素互不相同，所以20,1a a a a ≠⇒≠≠.又因为M∩N＝N ，所以1a =-. 考点：集合的特征及集合的基本运算. 3．设，则（ ）A ．﹣2＜x ＜﹣1B ．﹣3＜x ＜﹣2C ．﹣1＜x ＜0D ．0＜x ＜1 【答案】A【解析】因为y=3x在R 上单调递增，又，故﹣2＜x ＜﹣1故选A4．若0.90.48 1.54,8,0.5a b c -===则（ ）A .c b a >> B. a c b >> C.b a c >> D.b c a >> 【答案】D【解析】0.9 1.80.48 1.44 1.5 1.542,82.(0.5)2.-===函数2x y =是增函数，1.8 1.5 1.44,>>所以.a c b >>故选D5．函数()f x =的定义域是 A. {x ︱34x >} B. {01x x <≤} C. {1x x ≥} D. {x ︱314x <≤} 【答案】D 【解析】略6．设函数))((R x x f ∈为奇函数，),2()()2(,21)1(f x f xf f +=+=则=)5(f （）A．0B ．1C ．25D ．5【答案】C【解析】令x=-1可得(1)(1)(2)(1)(2),(2)2(1)1,f f f f f f f =-+=-+∴==13(3)(1)(2)122f f f ∴=+=+=,35(5)(3)(2)122f f f =+=+=.7．某同学家门前有一笔直公路直通长城，星期天，他骑自行车匀速前往旅游，他先前进了a km ，觉得有点累，就休息了一段时间，想想路途遥远，有些泄气，就沿原路返回骑了b km(b <a ), 当他记起诗句“不到长城非好汉”，便调转车头继续前进. 则该同学离起点的距离s 与时间t 的函数关系的图象大致为 ( )【答案】C【解析】分析：本题根据运动变化的规律即可选出答案．依据该同学出门后一系列的动作，匀速前往对应的图象是上升的直线，匀速返回对应的图象是下降的直线，等等，从而选出答案． 解答：解：根据他先前进了akm ，得图象是一段上升的直线，DCBA第3页 共10页 ◎ 第4页 共10页由觉得有点累，就休息了一段时间，得图象是一段平行于t 轴的直线，由想想路途遥远，有些泄气，就沿原路返回骑了bkm （b ＜a ），得图象是一段下降的直线， 由记起诗句“不到长城非好汉”，便调转车头继续前进，得图象是一段上升的直线， 综合，得图象是C ， 故选C ．点评：本小题主要考查函数的图象、运动变化的规律等基础知识，考查数形结合思想．属于基础题． 8．函数的单调增区间为（ ）A ．B ．（3，+∞）C ．D ．（﹣∞，2）【答案】D【解析】由题意知，x 2﹣5x+6＞0∴函数定义域为（﹣∞，2）∪（3，+∞），排除A 、C ， 根据复合函数的单调性知的单调增区间为（﹣∞，2），故选D9．若函数()1(0,1)1x mf x a a a =+>≠-是奇函数，则m 为 A.1- B.2 C.1 D.2-【答案】B 【解析】 试题分析：111111x a(),()()xxxm m mf x f x aaa --=+=+-=-+--- 由于函数是奇函数，()(),f x fx ∴-=-即x a (1)1(1)2111x x x x m m m a a a a -+=-+∴=--- 所以2m =，故选：B.考点：函数的奇偶性10． 下列每组中两个函数是同一函数的组数共有（ ） （1）2()1f x x =+和2()1f v v =+(2) y =和y =(3) y=x 和321x xy x +=+ (4) y=和y(A) 1组 (B) 2组 (C) 3组 (D) 4组 【答案】C【解析】根据同意哈函数的定义可知选项A 中定义域和对应关系相同，成立，选项B 中，定义域相同，对应关系相同，选项C 中，相同，选项D 中，定义域不同，故是同一函数的 组数有3组，故选C 11．已知1a >，函数x y a =与log ()a y x =-的图像可能是（ ）【答案】B【解析】试题分析：因为根据1a >,可知指数函数递增函数，排除C ，D 选项，同时在选项A,B 中，由于对数函数log ()a y x =-的图像与log a y x =的图像关于y 轴堆成，那么可知.排除A.正确的选项为B.考点：本题主要是考查同底的指数函数与对数函数图像之间的关系的运用。

2014-2015学年上学期高一期中测试数学试题（含答案） 第I 卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每个小题给出的四个选项中，只有一项是符合要求的）1．下列函数中，既是偶函数又在+∞（0，）单调递增的函数是（ ）A ．3y x =B ． 1y x =+C ．21y x =-+D ． 2x y -=2．在同一坐标系中，表示函数log a y x =与y x a =+的图象正确的是（ ）A B C D3．若1log 12a<，则a 的取值范围是( ) A ．1(0,)(1,)2+∞ B ．1(,1)2 C ．(1,)+∞ D ．1(,1)(1,)2+∞4．已知函数f(x)为定义在R 上的奇函数，当x≥0时， ()22xf x x m =++ (m 为常数)，则(1)f -的值为( )A ．－3B ．－1C ．1D ．35．设全集U =R ，{}|0P x f x x ==∈R （），，{}|0Q x g x x ==∈R （），，{}|0S x x x ϕ==∈R （），，则方程22f x x x ϕ=（）+g （）（）的解集为（ ）A ． P Q SB ．P QC ．P Q S （）D ． P Q S u （C ）5．设9.0log 5.0=a ，9.0log 1.1=b ，9.01.1=c ，则c b a , ,的大小关系为（ ）A ．c b a <<B ．c a b <<C ．a c b <<D ．b c a <<6．设}3 2, ,21 ,31 ,1{-∈α，若函数αx y =是定义域为R 的奇函数，则α的值为（ ）A ．3 ,31B ．3 ,31 ,1- C ．3 ,1- D ．31,1- 7．已知函数)(x f 是奇函数，当0>x 时，)1 ,0( )(≠>=a a a x f x，且3)4(log 5.0-=f ，则a的值为（ ）A ．3B ．3C ．9D ．238．已知函数⎪⎩⎪⎨⎧>-≤=-)1( )23(log )1( 2)(2x x x x f x ，若4)(=a f ，则实数=a （ ） A ．2-或6 B ．2-或310 C ．2-或2 D ．2或3109．方程21231=⎪⎭⎫ ⎝⎛--x x 的解所在的区间为（ ）A ．) 1 ,0 (B ．) 2 ,1 (C ．) 3 ,2 (D ．) 4 ,3 (10．已知函数bx ax y +=2和xb a y =|)| || ,0(b a ab ≠≠在同一直角坐标系中的图象不可能 是（ ）11．已知函数)3(log 221a ax x y +-=在区间) ,2[∞+上是减函数，则a 的取值范围是（ ）A ．)4 ,(-∞B ．]4 ,4[-C ．]4 ,4(-D ．]4 ,(-∞12．若在直角坐标平面内B A ,两点满足条件：①点B A ,都在函数)(x f y =的图象上；②点B A ,关于原点对称，则称B A ,为函数)(x f y =的一个“黄金点对”．那么函数=)(x f ⎪⎩⎪⎨⎧>≤-+)0( 1)0( 222x x x x x 的“黄金点对”的个数是（ ）A ．0个B ．1个C ．2个D ．3个 第Ⅱ卷（非选择题，共90分）二、填空题：本题共4小题，共20分.13．已知集合}06|{2=--=x x x M ，}01|{=+=ax x N ，且M N ⊆，则由a 的取值组成的集合是 ．14．若x x f =)(log 5，则=-)9log 2(log 255f ．15．已知定义在R 上的偶函数)(x f 满足0)1(=-f ，并且)(x f 在)0 ,(-∞上为增函数．若0)( <a f a ，则实数a 的取值范围是 ．16．已知函数()x f 的定义域是}0|{≠∈=x R x D ，对任意D x x ∈21 ,都有：=⋅)(21x x f)()(21x f x f +，且当1>x 时，()0>x f ．给出结论：①()x f 是偶函数；②()x f 在()∞+ ,0上是减函数．则正确结论的序号是 ．三、解答题：本大题共6小题，共70分，解答应写出必要的文字说明、证明过程及演算步骤。

太原市20 1 4 ——20 1 5学年高一年级第二学段测评数学试卷（考试时间：上午8：00——9：30）一、选择题：本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．请将其字母标号填入下表相应位置．1．在简单随机抽样中，某个个体被抽到的可能性A．与第n次有关，第一次可能性最大B．与第n次有关，第一次可能性最小C．与第n次无关，每次可能性不等D．与第n次无关，每次可能性相等答案：D解析：简单随机抽样中，每次可能性都相等，所以选D。

2．某射手在一次射击中，射中10环、9环、8环的概率分别是0.20，0.30，0.20，则此射手在一次射击中不足8环的概率为A．0.40 B．0.30C．0.60 D．0.90答案：B解析：此射手在一次射击中不足8环的对立事件是：一次射击中大于等于8环。

此射手在一次射击中大于等于8环的概率P=0.20+0.30+0.20=0.7，所以答案为1-0.7=0.3.x y（i=1，2，…，10），得散点图(1)；对变量u，v有观测3．对变量x，y有观测数据(,)i iu v（i=1，2，…，10），得散点图(2)．由这两个散点图可以判断数据(,)i iA．变量x与y正相关，u与v正相关B．变量x与y正相关，u与v负相关C．变量x与y负相关，u与v正相关D．变量x与y负相关，u与v负相关答案：C.解析：从图中易看出y随着x增加呈下降趋势，v随着u的增加呈上升趋势，故选C.4．下列各数中，可能是五进制数的是A．55 B．106C．732 D．2134答案：D.解析：由进制的概念可知，进制为五，所有位数上的数5，故选D。

5．读下图程序，当输入的x为60时，输出y的值为A．30 B．31C．36 D．61答案：B.解析：本程序框图是条件结构，分段函数，输入x=60，y=25+0.6*（60-50）=31.6．某班共有52名学生，现根据学生的学号，用系统抽样的方法，抽取一个容量为4的样本，已知3号、29号、42号同学在样本中，那么样本中还有一个同学的学号是A. 10 B．11 C．12 D. 16答案：D.解析：系统抽样中，组距= 524=13，没有剔除数据，所以第一个数为3，第二个数为3+13=16.选D.7．如右图，平面图形中阴影部分面积S 是[]()0,h h H ∈的函数，则该函数的图象大致是答案：D.解析：由图中可知，S 随着h 的增加而减少，并且减小的趋势在减小，当2Hh =时，阴影部分的面积小于整个半圆面积的一半，选D 。

太原市2014～2015学年第二学期高一年级期末测评数学试题参考答案一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项符合题目要求，请将其字母标号填入下表相应位置）二、填空题（本大题共4小题，每小题3分，共12分） 13．814． 1|02x x ⎧⎫<<⎨⎬⎩⎭15． 220 16． 32三、解答题（本大题共5小题，共52分．解答应写出文字说明、证明过程或演算步骤） 17． （本小题满分10分）解：（1） 1cos 601212⋅=︒=⨯⨯=a b a b ， -------------------2分 ()()143-∙+=-=-=-22a b a b a b . ┄┄┄┄┄5分 （2） 222()2-=-=-⋅+a b a b a a b b ---------------------8分1243=-+= ． ┄┄┄┄10分18．（本小题满分10分）解： （1）3()cos sin 22f x x x=+1sin cos 2cos sin 2266x x ππ=++21+------------------------------2分 =1sin(2)26x π=++21+， - ----------------------------- 4分 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案AACDADCBBCAC()f x 的最小正周期为22T ππ==，最大值为23． --------------------------6分（2）当222()262k x k k πππππ-≤+≤+∈Z 时，()f x 的单调递增， -----8分故函数()f x 的单调递增区间是(),36k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z ． ------------------10分19． （本小题满分10分） 解：（1）由正弦定理得：53sin sin ==C B b c ， -----------------------4分 又3=c ，∴b sin 3535sin sin sin 53AC AB AB C AC B C AC B ⨯=⇒==⇒== ． -------------------------5分（2）由余弦定理得：925491cos 22352AB AC BC A AB AC+-+-∠===-⋅⨯⨯bc a c b 2222-+ -------------------------6分=213049925-=-+， -------------------------9分所以120A ∠=︒． ---------------10分20． （本小题满分10分） 解：（1） 池底长方形宽为x1800米， 则S=)180022(2x x ⨯+=)1800(4xx +． --------------------------5分 （2）设总造价为y 元，则⨯+⨯=1301800160y )1800(4xx +≥288000+312002332117≈， --------------------------8分 当且仅当xx 1800=，即230=x 时等号成立，所以230=x 时，总造价最低约为332117元． --------------------------10分21．（本小题满分12分）说明：请考生在（甲）、（乙）两个小题中任选一题作答．（甲）、解：（1）1811-==S a ， -------------------------1分 当1>n 时， 1--=n n n S S a202-=n ， -------------------------5分因为 181-=a 满足上式，所以 220n a n =- ． ------------------------- 6分 （2）由题意可知 202-=n n b ， -------------------------8分 所以123n n T b b b b =++++123(220)(220)(220)(220)n =-+-+-++-123(2222)20n n =++++-1222012n n +-=-- ------------------------ 11分 12202n n +=--． ------------------------- 12分（乙）．解：（1）2232n n S a n n =+--，()()21121312n n S a n n ++∴=++-+-．()11222,212(2)n n n n a a n a n a n ++∴=-+∴-+=-．∴{}n a n 2-是以2为公比的等比数列 ． -------------------------6分 （2） 22,22n n n n a n a n ∴-=∴=+， -------------------------8分∴ n b =121n+ ． -----------------------9分 ∴ 114323221222+-+⋅⋅⋅+++=n n n n b b b b b b b b T=1121+×2121+ + 2×2121+× 3121+ ＋…＋12n -×121n +×1121n ++=12×(1121+－2121+) +12×(2121+－3121+) ＋…＋12×(121n +－1121n ++) =12×(1121+－1121n ++) =16－2122n ++ ． ------------------------12分。

太原五中2014-2015学年度第一学期期中高 一 数 学命题人：王彩凤 校对人：廉海栋一．选择题（每题4分）1.已知全集{}0,1,2,3,4U =，集合{}{}1,2,3,2,4A B ==，则U C A B 为( )A ．{}1,2,4 B.{}2,3,4 C.{}0,2,4 D.{}0,2,3,42. 函数21log (2)y x =-的定义域为（ ） A ．(,2)-∞ B ．(2,)+∞ C ．(2,3)(3,)+∞ D ．(2,4)(4,)+∞3 ．已知y x ,为正实数,则( )A.y x y x lg lg lg lg 222+=+ B.y x y x lg lg )lg(222∙=+ C.y x yx lg lg lg lg 222+=∙ D.y x xy lg lg )lg(222∙= 4. 下列函数中，在区间(0,)+∞为增函数的是（ ）A．y =．2(1)y x =- C ．2x y -= D ．0.5log (1)y x =+5. 在同一直角坐标系中，函数x x g x x x f a a log )(),0()(=≥=的图像可能是（ ）6.要得到12+-=x y 的图像只需要将x y )21(=的图像（ ） A.上移1个单位 B.右移1个单位C.左移1个单位D.先关于y 轴对称再左移1个单位7、设x a )32(=，1)23(-=x b ，x c 32log =，若x>1,则a,b,c 的大小关系是（ ）A 、a<b<cB 、 b<c <aC 、 c <a<bD 、 c<b< a8.设⎪⎩⎪⎨⎧-=-)1(log 2)(231x e x f x )2()2(≥<x x 则[])2(f f =（ ） A .2 B .3 C .9 D .189．如果函数2()2(1)2f x x a x =+-+在区间(],4-∞上单调递减，那么实数a 的取值范围是（ ）A 、3a -≤B 、3a -≥C 、a ≤5D 、a ≥510.函数x x x f 21ln )(+=的零点所在的区间是（ ） A .)1,0(e B .)0,1(- C .)1,1(eD .),1(+∞ 11．已知函数())()11+ln3,.lg 2lg 2f x x f f ⎛⎫=+= ⎪⎝⎭则（ ） A ．1- B ．0C ．1D ．2 12.定义在R 上的偶函数)(x f ，满足0)21(=f ，且在),0(+∞上单调递减，则4(log )0f x <的解集为（ ） A .1-+2∞∞（，）（2，） B .1+2∞（0，）（2，） C .12（，2） D .1+2∞（，） 二．填空题（每题4分）13．方程1313313x x -+=-的实数解为________14.给出以下结论：①11)(--+=x x x f 是奇函数；②221)(2-+-=x x x g 既不是奇函数也不是偶函数；③)()()(x f x f x F -= )(R x ∈是偶函数 ；④x x x h +-=11lg)(是奇函数.其中正确的序号是____________15.函数2()log )f x x =的最小值为_________.16.若函数()(0,1)x f x a a a =>≠在［－1，2］上的最大值为4，最小值为m，且函数()(14g x m =-在[0,)+∞上是增函数，则a ＝_______.三．解答题17.（8分）计算下列各式的值（1）210321(0.1)2()4--++（2）3log lg 25lg 4++18.（8分）函数)1(log )(2-=x x f 的定义域为A,函数)01()21()(≤≤-=x x g x 的值域为B.（1)求B A ⋂(2)若}12|{-≤≤=a x a x C ,且B C ⊆,求实数a 的取值范围.19.（8分）设()f x 是定义在[1,1]-上的奇函数，且当(0,1]x ∈时，)1(log )(+=x x f a ，a>1.（1）求函数()f x 的解析式.（2）解关于x 的不等式)21()(x f x f ->20.（12分）已知函数()22x ax b f x +=+，且417)2(,25)1(==f f . （1）求b a ,；（2）判断函数的单调性，并用定义给出证明；（3）若关于x 的不等式()21x mf x m -≤+-在(0,)+∞上恒成立，求实数m 的取值范围.1-12 CCDAD BCAAC DB 13.4log 314.134 15.41- 16.4117.5 2718.{2} a 23≤19.f(x)=⎩⎨⎧<<---≤≤+01),1(log 10),1(log x x x x a a131≤<x 20.a=-1 b=0 (-∞,0)增 （0，+∞） m 31-≤。

2014-2015学年第一学期高一期末考试数学试题说明：1．本卷共有三个大题，21个小题，全卷满分150分,考试时间120分钟． 2．本卷分为试题卷和答题卷，答案要求写在答题卷上，在试题卷上作答不给分．一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知全集U={1，2，3，4}，集合A={1，2}，B={2，3}，则∁U （A ∪B ）=（ ） A ．{1，3，4}, B ．{3，4}, C ．{3}, D ．{4} 2．一个几何体的三视图形状都相同，大小均相等，那么这个几何体不可以是（ ） A ．球, B ．三棱锥, C ．正方体, D ．圆柱 3．若两个球的表面积之比为1：4，则这两个球的体积之比为（ ） A ．1：2, B ．1：4, C ．1：8, D ．1：164．已知点M （a ，b ）在圆O ：x2+y2=1外，则直线ax+by=1与圆O 的位置关系是（ ） A ．相切, B ．相交, C ．相离, D ．不确定 5．在下列命题中，不是公理的是（ ） A ．平行于同一个平面的两个平面平行B ．过不在同一直线上的三个点，有且只有一个平面C ．如果一条直线上的两点在同一个平面内，那么这条直线上所有点都在此平面内D ．如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线6．由表格中的数据可以判定方程20x e x --=的一个零点所在的区间是(,1)()k k k Z +∈， 则k 的值为A ．-1B ．0C ．1D ．27．若函数11()2xy m -=+的图像与x 轴有公共点，则m 的取值范围是A ．1m ≤-B ．10m -≤<C ．1m ≥D ．01m <≤8．已知函数()f x 是定义在R 上的偶函数, 且在区间[0,)+∞单调递增．若实数a 满足212(log )(log )2(1)f a f f a ≤+, 则a 的取值范围是A ．10,2⎛⎤⎥⎝⎦B ．(0,2]C ．[1,2]D ．1,22⎡⎤⎢⎥⎣⎦9．若定义在区间[-2015，2015]上的函数f （x ）满足：对于任意的x 1，x 2∈[-2015，2015]，都有f （x 1+x 2）=f （x 1）+f （x 2）-2014，且x ＞0时，有f （x ）＞2014，f （x ）的最大值、最小值分别为M ，N ，则M+N 的值为（ ）A ．2014B ．2015C ．4028D ．403010．一个多面体的直观图、主视图、左视图、俯视图如下，M 、N 分别为1A B 、11B C 的中点．下列结论中正确的个数有①直线MN 与1A C 相交． ② MN BC ⊥． ③MN //平面11ACC A ． ④三棱锥1N A BC -的体积为1316N A BC V a -=． A ．4个B ．3个C ．2个D ．1个二、填空题（本大题共5小题，每题5分，共计25分．请将正确答案填在答题卷相应位置．） 11．函数22log (1)y x x =--的定义域为___________．12．在z 轴上与点(4,1,7)A -和点(3,5,2)B -等距离的点C 的坐标为 ．13．已知集合2{(,)49}A x y y x ==-，{(,)}B x y y x m ==+，且A B φ⋂≠，则实数m 的取值范围是_______________．14．已知函数1333,1()log ,01x x f x x x ⎧-≥⎪=⎨<<⎪⎩，则满足不等式1()()9f m f ≤的实数m 的取值范围为 ．15．下列四个命题：其中正确的有________________（写出所有正确命题的序号）．三、解答题：（本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤．） 16．（本小题满分12分）设全集为U R =，集合(,3][6,)A =-∞-⋃+∞，{}2|log (2)4B x x =+<． （1）求如图阴影部分表示的集合；（2）已知{}|21C x x a x a =><+且，若C B ⊆，求实数a 的取值范围．17．（本小题满分12分）已知直线1l ：10ax by ++=，（,a b 不同时为0），2l ：(2)0a x y a -++=， （1）若0b =且12l l ⊥，求实数a 的值；（2）当3b =且12//l l 时，求直线1l 与2l 之间的距离．18．（本小题满分12分）已知幂函数21()(22)m f x m m x +=-++为偶函数．（1）求()f x 的解析式；（2）若函数()2(1)1y f x a x =--+在区间（2，3）上为单调函数，求实数a 的取值范围．19．（本小题满分12分）20．（本小题满分13分）已知圆C 的方程:04222=+--+m y x y x ,其中5m <．（1）若圆C 与直线042:=-+y x l 相交于M ,N 两点，且MN =,求m 的值；（2）在（1）条件下，是否存在直线02:=+-c y x l ，使得圆上有四点到直线l ，若存在，求出c 的范围，若不存在，说明理由．21．（本小题满分14分）定义在D 上的函数()f x ，如果满足：对任意x D ∈，存在常数0M ≥，都有()f x M ≤ 成立，则称()f x 是D 上的有界函数，其中M 称为函数()f x 的一个上界．已知函数11()1()()24x x f x a =++，121()log 1axg x x -=-．（1）若函数()g x 为奇函数，求实数a 的值；（2）在（1）的条件下，求函数()g x 在区间5,33⎡⎤⎢⎥⎣⎦上的所有上界构成的集合；（3）若函数()f x 在[)0,+∞上是以3为上界的有界函数，求实数a 的取值范围．2014-2015学年第一学期高一期末考试数学试题参考答案一、选择题（每小题5分，共50分，在每小题给出的四个选项中只有一个符合要求．）题号 1 2 3 4 5 6 7 8 9 10答案 D D C B A C D D C B2、答案D分析：利用简单几何体的结构特征以及三视图的定义，容易判断圆柱的三视图不可能形状相同，大小均等解答：球的三视图均为圆，且大小均等；正四面体的三视图可以形状都相同，大小均等；正方体的三视图可以是三个大小均等的正方形；圆柱的三视图中必有一个为圆，其他两个为矩形故一个几何体的三视图形状都相同，大小均等，那么这个几何体不可以是圆柱故选D点评：本题主要考查了简单几何体的结构特征，简单几何体的三视图的形状大小，空间想象能力，属基础题3、4、6、7、8、9、10、二、填空题（本大题共5小题，每小题5分，共25分．）11．(]2,1 12．14 (0,0,)913．[7,72]-14．31[,log 5]915．①④⑤三、解答题：（本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．）16．（本小题满分12分）．解：（1）由0216,x <+<得(2,14)B =-， ……………………………2分又(,3][6,)A =-∞-⋃+∞，故阴影部分表示的集合为()(,3][14,)R A C B ⋂=-∞-⋃+∞ ； ……………………5分（2）① 21a a ≥+，即1a ≥时，C =∅，成立； ………………………9分② 21a a <+，即1a <时，(2,1)(2,14)C a a =+⊆-，114,22,a a +≤⎧⎨≥-⎩得11a -≤<， ………………………11分综上所述，a 的取值范围为[1,)-+∞． …………………12分17．（本小题满分12分）解：（1）当0b =时，1l ：10ax +=，由12l l ⊥知(2)0a -=，…………4分解得2a =；……………6分（2）当3b =时，1l ：310ax y ++=，当12//l l 时，有3(2)0,310,a a a --=⎧⎨-≠⎩…………8分解得3a =， …………………9分此时，1l 的方程为：3310x y ++=，2l 的方程为：30x y ++=即3390x y ++=，…………11分则它们之间的距离为229142333d -==+分 18．（本小题满分12分）解：（1）由()f x 为幂函数知2221m m -++=，得 1m =或12m =-……3分 当1m =时，2()f x x =，符合题意；当12m =-时，12()f x x =，不合题意，舍去． ∴2()f x x =． ……………………6分（2）由（1）得22(1)1y x a x =--+，即函数的对称轴为1x a =-， …………8分由题意知22(1)1y x a x =--+在（2，3）上为单调函数，所以12a -≤或13a -≥， ………11分即3a ≤或4a ≥． …………12分19．（本小题满分12分）解：20．（本小题满分13分）．解：（1）圆的方程化为 m y x -=-+-5)2()1(22，圆心 C （1，2），半径 m r -=5，则圆心C （1，2）到直线:240l x y +-=的距离为 5121422122=+-⨯+=d ………3分 由于5MN =125MN =，有2221()2r d MN =+， ,)52()51(522+=-∴m 得4=m ． …………………………6分（2）假设存在直线02:=+-c y x l ，使得圆上有四点到直线l 的距离为55， ……7分 由于圆心 C （1，2），半径1=r ， 则圆心C （1，2）到直线02:=+-c y x l 的距离为 511532122122-<-=++⨯-=c c d ， …………10分 解得5254+<<-c ． …………13分21．（本小题满分14分）解：（1）因为函数)(x g 为奇函数，所以()()g x g x -=-，即11log 11log 2121---=--+x ax x ax ， 即axx x ax --=--+1111，得1±=a ，而当1=a 时不合题意，故1-=a ． ……4分 （2）由（1）得：11log )(21-+=x x x g ， 下面证明函数11log )(21-+=x x x g 在区间(1,)+∞上单调递增， 证明略． ………6分所以函数11log )(21-+=x x x g 在区间]3,35[上单调递增， 所以函数11log )(21-+=x x x g 在区间]3,35[上的值域为]1,2[--， 所以2)(≤x g ，故函数)(x g 在区间]3,35[上的所有上界构成集合为),2[+∞．……8分（3）由题意知，3)(≤x f 在),0[+∞上恒成立．3)(3≤≤-x f ，x x x a ⎪⎭⎫ ⎝⎛-≤⎪⎭⎫ ⎝⎛≤⎪⎭⎫ ⎝⎛--41221414． xx x xa ⎪⎭⎫ ⎝⎛-⋅≤≤⎪⎭⎫ ⎝⎛-⋅-∴21222124在),0[+∞上恒成立． min max 21222124⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⋅≤≤⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⋅-∴x x x x a ……………………10分设t x =2，t t t h 14)(--=，t t t p 12)(-=，由),0[+∞∈x 得1≥t ,设121t t ≤<，21121212()(41)()()0t t t t h t h t t t ---=>， ()()1212121221()()0t t t t p t p t t t -+-=<, 所以)(t h 在),1[+∞上递减，)(t p 在),1[+∞上递增， ………………12分 )(t h 在),1[+∞上的最大值为5)1(-=h ，)(t p 在),1[+∞上的最小值为1)1(=p ．所以实数a 的取值范围为]1,5[-． …………………14分。

山西省太原市2014-2015学年高一上学期期末统考试（考试时间：上午8：00——9：30）一、选择题：本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．请将其字母标号填入下表相应位置．1．在简单随机抽样中，某个个体被抽到的可能性A．与第n次有关，第一次可能性最大B．与第n次有关，第一次可能性最小C．与第n次无关，每次可能性不等D．与第n次无关，每次可能性相等答案：D解析：简单随机抽样中，每次可能性都相等，所以选D。

2．某射手在一次射击中，射中10环、9环、8环的概率分别是0.20，0.30，0.20，则此射手在一次射击中不足8环的概率为A．0.40 B．0.30C．0.60 D．0.90答案：B解析：此射手在一次射击中不足8环的对立事件是：一次射击中大于等于8环。

此射手在一次射击中大于等于8环的概率P=0.20+0.30+0.20=0.7，所以答案为1-0.7=0.3.x y（i=1，2，…，10），得散点图(1)；对变量u，v有观测3．对变量x，y有观测数据(,)i iu v（i=1，2，…，10），得散点图(2)．由这两个散点图可以判断数据(,)i iA．变量x与y正相关，u与v正相关B ．变量x 与y 正相关，u 与v 负相关C ．变量x 与y 负相关，u 与v 正相关D ．变量x 与y 负相关，u 与v 负相关 答案：C.解析：从图中易看出y 随着x 增加呈下降趋势，v 随着u 的增加呈上升趋势，故选C.4．下列各数中，可能是五进制数的是A ．55B ．106C ．732D ．2134 答案：D.解析：由进制的概念可知，进制为五，所有位数上的数5<，故选D 。

5．读右图程序，当输入的x 为60时，输出y 的值为A ．30B ．31C ．36D ．61 答案：B.解析：本程序框图是条件结构，分段函数，输入x=60，y=25+0.6*（60-50）=31.6．某班共有52名学生，现根据学生的学号，用系统抽样的方法，抽取一个容量为4的样本，已知3号、29号、42号同学在样本中，那么样本中还有一个同学的学号是A. 10 B ．11 C ．12 D. 16 答案：D.解析：系统抽样中，组距= 524=13，没有剔除数据，所以第一个数为3，第二个数为3+13=16.选D.7．如右图，平面图形中阴影部分面积S 是[]()0,h h H ∈的函数，则该函数的图象大致是答案：D.解析：由图中可知，S 随着h 的增加而减少，并且减小的趋势在减小，当2Hh =时，阴影部分的面积小于整个半圆面积的一半，选D 。

..太原五中2014-2015学年度第一学期期末高一数学出题人、校对人：张福兰、王芳一、选择题（每小题 3 分 ,共 36 分 ,每小题只有一个正确答案）1.某学校有男、女学生各500 名，为了解男、女学生在学习兴趣与业余爱好方面是否存在显著差异，拟从全体学生中抽取100 名学生进行调查，则宜采用的抽样方法是（） A ．抽签法 B ．随机数法C．系统抽样法D．分层抽样法2.从一批产品中任取 3 件，设 A= “三件全是正品”， B= “三件全是次品”，C= “至少有一件正品”，则下列结论正确的是()A． A 与 C 互斥B．A 与 B 互为对立事件C. B 与 C 互斥D.A 与C 互为对立事件3.为了测算如图阴影部分的面积，作一个边长为 6 的正方形将其包含在内，并向正方形内随机投掷 800 个点，已知恰有200 个点落在阴影部分内，据此，可估计阴影部分的面积是()A．12B．9C．8D． 64.对四组数据进行统计，获得以下散点图，关于其相关系数比较，正确的是()A ． r2<r 4<0< r3<r 1B ．r 4<r2<0<r 1<r3 C． r4<r 2<0< r 3<r1D． r2<r4<0< r1<r 35.集合 M={x |x=k,k∈Z} 与 N={x|x=k)2,k∈ Z} 之间的关系是 ( 2A.M NB.N MC.M=ND.M∩ N=6．将参加数学夏令营的1000 名学生编号如下：0001， 0002，0003 ，⋯， 1000，采用系统抽样方法抽取一个容量为50 的样本，求得间隔数k 1000，即每 20人抽取一个人．在 0001 2050..到 0020 中随机抽得的号码为0015 ，从 0601 到 0785 被抽中的人数为（）A．8 B.9 C.10, D. 117.从甲乙两个城市分别随机抽取16 台自动售货机，对其销售额进行统计，统计数据用茎叶图表示 (如图所示 )，设甲乙两组数据的平均数分别为x 甲， x 乙，中位数分别为m 甲，m 乙，则 ()甲乙8650884001028752202337800312448314238A. x甲 < x乙， m 甲>m 乙 B ．x甲 < x乙，m 甲 <m 乙C．x甲 > x乙，m 甲 >m 乙D．x甲 > x乙， m 甲<m 乙8.已知 A 是⊙Ｏ上一定点 ,在⊙Ｏ上其他位置任取一点B,连接 A 、B 两点 ,所得弦的长度大于等于⊙Ｏ的半径的概率为（）2151A. B. C. D.34629.若运行所给程序输出的值是16，则输入的实数 x 值为 ()A ．32 B.8C．-4或 8D．4 或-4 或 810.执行如图所示的程序框图，若输入m 2010 ， n1541，则输出的m的值为（）A.2010B.1541C.134D.6711.执行如图所示的程序框图，如果输出s＝ 3，那么判断框内应填入的条件是()A ． k ≤ 6B． k ≤7C． k ≤ 8D． k≤9INPUT xIF x<＝0 THENy＝x^ 2 ELSEy＝ 2*x END IF..12.利用随机模拟方法计算y=x 2+1 与 y=5 围成的面积时，先利用计算器产生两组0~1 之间的均匀随机数a1=RAND ， b1=RAND ，然后进行平移与伸缩变换a=4a1- 2， b=4b 1+1，实验进行了1000次，前998 次中落在所求面积区域内的样本点数为624，若最后PRINT y两次实验产生的0~1 之间的均匀随机数为（ 0.3，0.1），（ 0.9，0.7），END则本次模拟得到的面积的估计值是（）A.10251248D.1252 B. C.125 2125二、填空题（每小题 3 分，共 12 分）13.点 P 从 (1，0)出发，沿单位圆x2y 2 1 逆时针方向运动2π弧长到达点 Q，则点 Q 的坐3标为 __________．14.某一总体有 5 位成员，其身高分别为（单位：cm） 172， 174， 175,176，178，今随机抽样 3 人，则抽到平均身高等于总体平均身高的概率为.15.对于n∈N*，将n表示为n＝a0×2k＋a1×2k－1＋a2×2k－2＋⋯＋a k－1×21＋a k×20，当 i ＝0 时，a i＝ 1，当 1≤i≤ k 时，a i为 0 或 1.记 I(n)为上述表示中a i为 0 的个数(例如5＝1× 22＋ 0× 21＋ 1× 20，故 I(5) ＝ 1)，则I (65)=______.16 某班同学利用国庆节进行社会实践，对[25,55]岁的人群随机抽取1000 人进行了一次生活习惯是否符合低碳观念的调查，从年龄段[40 ，55]的人群中采用分层抽样法抽取 6 人参加户外低碳体验活动，其中选取 2 人作为领队，则选取的 2 名领队中至少有 1 人年龄在 [40,45) 岁的概率为三、解答题（共52 分）..17. （本小题满分 10 分）某算法的程序框图如图所示，其中输入的变量x 在 1， 2，3，⋯，24 这 24 个整数中等可能随机产生．(1)分别求出按程序框图正确编程运行时输出y 的值为 i 的概率Pi(i ＝ 1， 2，3)；(2)甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n 次后，统计记录了输出 y 的值为 i(i ＝ 1，2， 3)的频数．以下是甲、乙所作频数统计表的部分数据甲的频数统计表 (部分 )运行输出 y 的值输出 y 的值输出 y 的值次数 n为1的频数为 2的频数为 3的频数3014610⋯⋯⋯⋯2 100 1 027376697乙的频数统计表 (部分 )运行输出 y 的值输出 y 的值输出 y 的值次数 n为1的频数为 2的频数为 3的频数3012117⋯⋯⋯⋯2 100 1 051696353当 n＝ 2 100 时，根据表中的数据，分别写出甲、乙所编程序各自输出y 的值为 i(i ＝ 1， 2， 3)的频率 (用分数表示 )，并判断两位同学中哪一位所编程序符合算法要求的可能性较大；..18.（本小题满分 10 分）某班n位学生一次考试数学成绩的频率分布直方图如图，其中成绩分组区间是 [40,50), [50,60),[60,70) ,[70,80), [80,90), [90,100].若成绩在区间 [70,90) 的人数为 34 人 .(1)求图中 x 的值及 n ;(2)由频率分布直方图，求此次考试成绩平均数的估计值 .19.（本小题满分 10 分）化简：sin 6100tan470sin1101 cos( 1510 )tan470sin110020. （本小题满分10 分）某部门为了了解用电量y (单位：度)与气温x(单位：0C)之间的关系，随机统计了某 4 天的用电量与当天气温，因某天统计的用电量数据丢失，用t表示，如下表：气温（0C ）181310-1用电量 (度 )24t3864(1)由以上数据，求这 4 天气温的方差 .(2)若用电量与气温之间具有较好的线性相关关系，回归直线方程为y2x a ，且由此?预测气温为 4 0C 时，用电量为68度，求t、a的值.21.（本小题满分 12 分）已知二次函数 f(x) ＝ax2bx 1 ， A{ x |1x 3} ，B{ x |1 x4}(1)若a是从集合 A 中任取的一个整数，b是从集合 B 中任取的一个整数，求函数y＝ f(x) 有零点的概率．（Ⅱ）若a是从集合 A 中任取的一个实数， b 是从集合 A 中任取的一个实数，求关于x 的方程 f(x)=0 一根在区间 (0， 1)内，另一根在区间(1， 2)内的概率 .一、选择题：题号123456789101112答案D C B A A B B A C D B A 二、填空题：..13、(1,3)14、115、 5 16、4 225517.解： (1)变量 x 是在 1，2，3，⋯，24 这 24 个整数中随机产生的一个数，共有24 种可能．当 x 从 1， 3，5， 7，9，11，13， 15，17，19，21，23 这 12 个数中产1生时，输出 y 的值为 1，故 P1＝2；当 x 从 2， 4，8，10， 14，16，20， 22 这 8 个1数中产生时，输出y 的值为 2，故 P2＝3；当 x 从 6，12， 18，24 这 4 个数中产生1时，输出 y 的值为 3，故 P3＝6.11所以，输出 y 的值为 1 的概率为2，输出 y 的值为 2的概率为3，输出 y 的值为13 的概率为6.(2)当 n＝ 2 100 时，甲、乙所编程序各自输出y 的值 i(i＝1，2，3)的频率如下：输出 y 的值输出 y 的值输出 y 的值为1的频率为 2的频率为 3的频率甲1 0273766972 100 2 100 2 100乙1 0516963532 100 2 100 2 100比较频率趋势与概率，可得乙同学所编程序符合算法要求的可能性较大．19.sin6100tan 470sin110cos( 1510 ) tan470sin11001sin1100tan110sin1101cos70tan110sin1100..sin 700tan70sin701cos70tan70sin700sin 700tan70sin 701cos70tan70sin700sin 7001cos701cos701cos700sin 7001cos701cos70sin 700= -121.解(1)(a， b)共有 12 种情况．函数 y＝f(x)有零点，＝b2－4a≥ 0，有 (1,2)， (1,3) ， (1,4)， (2,3)， (2,4) ， (3,4)共 6 种情况6 1所以函数 y＝ f(x)有零点的概率为12＝2.(2)设事件 A 为“关于 x 的方程 f(x)=0 一根在区间 (0，1)内，另一根在区间 (1，2)内”．试验的全部结束所构成的区域为(a，b) |1≤ a ≤31，≤ b ≤ 4 ．构成事件 A 的区域为 (a， b) | a b 1 <0，4a -2 b 1 0 ．1331(13)223所以所求的概率为12242．3296..。

太原市2014-2015学年高三第一测评数学试题1．已知集合M={x||x|<2}，N={x|错误！未找到引用源。

}，M∪N=（）A.{错误！未找到引用源。

}B.错误！未找到引用源。

C.{错误！未找到引用源。

}D.错误！未找到引用源。

选D2．函数y=错误！未找到引用源。

的定义域是（）A.(1，+∞)B.(1，2)∪(2，+∞)C.(1，2)D.(2，+错误！未找到引用源。

) 解：错误！未找到引用源。

，错误！未找到引用源。

选B3．已知等差数列{错误！未找到引用源。

}中，错误！未找到引用源。

=1，错误！未找到引用源。

=8，则错误！未找到引用源。

=（）A.7B.8C.13D.15解：错误！未找到引用源。

=错误！未找到引用源。

=8，∴错误！未找到引用源。

=7 选A4．已知实数a，b满足a<b，则下列结论正确的是（）A.错误！未找到引用源。

B.错误！未找到引用源。

C.lna<lnbD.错误！未找到引用源。

解：A中a,b同号不成立；B中错误！未找到引用源。

递增，错；C中无意义错；D中错误！未找到引用源。

递增，正确。

选D5．函数f(x)=lnx错误！未找到引用源。

的零点所在的区间是（）A.(1,2)B.(1,e)C.(e,3)D.(e,+∞)解：f(e)=1错误！未找到引用源。

0，f(3)=ln3错误！未找到引用源。

1>0 选C6．已知等比数列{错误！未找到引用源。

}的公比q>1，且错误！未找到引用源。

，错误！未找到引用源。

，则数列{错误！未找到引用源。

}的前n项和错误！未找到引用源。

=（）A.错误！未找到引用源。

B.错误！未找到引用源。

C.错误！未找到引用源。

D.错误！未找到引用源。

解：错误！未找到引用源。

，错误！未找到引用源。

，又错误！未找到引用源。

，∴错误！未找到引用源。

=2，错误！未找到引用源。

=4，∴q=2。

选C7．函数y=(错误！未找到引用源。

)错误！未找到引用源。

的单调递减区间是（）A.(错误！未找到引用源。

2015年山西省太原市高考数学一模试卷（理科） 参考答案与试题解析 一、选择题1.已知()12i 2i z +=，则复数z =（ ）A.1i +B.1i - C ．1i -+ D.1i -- 答案：A考点：复数代数形式的乘除运算. 专题：数系的扩充和复数．分析：直接利用复数的除法运算法则化简求解即可． 解答：解：()1i 2i z +=， 可得()()()2i 1i 2i 1i 1i 1i 1i z -===+++-． 故选：A ．点评：本题考查复数的基本运算，基本知识的考查． 2.已知全集U =R ，集合()(){}130M x x x =-+<，{}1N x x =≤，则下图阴影部分表示的集合是（ ）A.[)1,1-B.(]3,1-C ．()[),31,--+ ∞∞ D.()3,1--答案：D考点： Venn 图表达集合的关系及运算. 专题：集合．分析：先确定阴影部分对应的集合为()U N M ð，然后利用集合关系确定集合元素即可． 解答：解：阴影部分对应的集合为()U N M ð，{}31M x x =-<< ，{}11N x x =-≤≤， {}11U N x x huox ∴=><-ð， (){}31U N M x x ∴=-<<- ð， 故选：D点评：本题主要考查集合的基本运算，利用Venn 图，确定阴影部分的集合关系是解决本题的关键．3.在单调递减等比数列{}n a 中，若31a =，2452a a +=，则1a =（ ）A.2B.4 D.答案：B考点：等比数列的性质.专题：计算题；等差数列与等比数列．分析：根据等比数列的通项，得到152q q +=，进利用数列{}n a 为递减数列，求出公比q 的值，即可求出1a 的值．解答：解：31a = ，2452a a +=， 152q q ∴+=，数列{}n a 为递减数列，12q ∴=14a ∴=， 故选：B ．点评：此题考查了等比数列的性质，通项公式，考查学生的计算能力，比较基础．．4.已知函数()2log f x x =，若在[]1,8上任取一个实数0x ，则不等式()012f x ≤≤成立的概率是（ ） A.14 B.12 C.27 D.12 答案：C考点：几何概型. 专题：概率与统计．分析：由题意，本题是几何概型的考查，只要求出区间的长度，利用公式解答即可．解答：解：区间[]1,8的长度为7，满足不等式()012f x ≤≤即不等式201log 2x ≤≤，解答024x ≤≤，对应区间[]2,4长度为2，由几何概型公式可得使不等式()012f x ≤≤成立的概率是27； 故选C ．点评：本题考查了几何概型的概率求法；关键是明确结合测度，；本题利用区间长度的比求几何概型的概率．5.执行如图所示程序框图，则输出a =（ ）A.20B.14C.10D.7答案：C考点：程序框图.专题：图表型；算法和程序框图．分析：模拟执行程序框图，依次写出每次循环得到的a ，i 的值，当i=2016时，不满足条件2015i ≤，退出循环，输出a 的值为10．解答：解：模拟执行程序框图，可得10a =，i=1满足条件i 2015≤，不满足条件a 是奇数，5a =，i=2 满足条件i 2015≤，满足条件a 是奇数，14a =，i=3 满足条件i 2015≤，不满足条件a 是奇数，7a =，i=4 满足条件i 2015≤，满足条件a 是奇数，20a =，i=5 满足条件i 2015≤，不满足条件a 是奇数，10a =，i=6满足条件i 2015≤，不满足条件a 是奇数，5a =，i=7 满足条件i 2015≤，满足条件a 是奇数，14a =，i=8≤观察规律可知，a 的取值以5为周期，由20154035=⨯可得 满足条件i 2015≤，不满足条件a 是奇数，10a =，i 2016= 不满足条件i 2015≤，退出循环，输出a 的值为10． 故选：C ．点评：本题主要考查了循环结构的程序框图，观察规律可知a 的取值以5为周期从而解得退出循环时a 的值是解题的关键，属于基本知识的考查．6.已知函数()()πsin 0,2f x x ωφωφ⎛⎫=+>< ⎪⎝⎭的最小正周期是π，若将其图象向右平移π3个单位后得到的图象关于原点对称，则函数()f x 的图象（ ）A.关于直线π12x =对称 B.关于直线5π12x =对称 C.关于点π,012⎛⎫ ⎪⎝⎭对称 D.关于直线5π,012⎛⎫⎪⎝⎭答案：B考点：函数()sin y A x ωφ=+的图象变. 专题：三角函数的图像与性质．分析：根据三角函数的性质求出函数的解析式进行求解即可．解答：解： 函数()()πsin 0,2f x x ωφωφ⎛⎫=+>< ⎪⎝⎭的最小正周期是π，2ππT ω∴==，解得2ω=，即()()sin 2f x x φ=+，将其图象向右平移π3个单位后得到π2πsin 2sin 233y x x φφ⎡⎤⎛⎫⎛⎫=-+=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，若此时函数关于原点对称，则2ππ3k φ-=，即2ππ3k φ=+，k ∈Z ，π2φ< ，∴当1k =-时，π3φ=-．即()πsin 23f x x ⎛⎫=- ⎪⎝⎭．由ππ2π32x k -=+，解得5ππ122k x =+，k ∈Z ，故当0k =时，函数的对称轴为5π12x =，故选：B点评：本题主要考查三角函数解析式的求解以及三角函数的性质的应用，根据条件求出函数的解析式是解决本题的关键．7.已知在圆22420x y x y +-+=内，过点()1,0E 的最长弦和最短弦分别是AC 和BD ，则四边形ABCD的面积为（ ）A. B. C. D.答案：D考点：直线与圆的位置关系. 专题：计算题；直线与圆．分析：圆22420x y x y +-+=即()()22215x y -++=，圆心()2,1M -，半径r =最长弦AC 为圆的直径．BD 为最短弦，AC 与BD 相垂直，求出BD ，由此能求出四边形ABCD 的面积．解答：解：圆22420x y x y +-+=即()()22215x y -++=，圆心()2,1M -，半径r最长弦AC 为圆的直径为， BD 为最短弦AC ∴与BD 相垂直，ME d =，2BD BE ∴==1122ABD BDC ABCD S S S BD EA BD EC =+=⨯+⨯⨯ 四边形△△()111=222BD EA EC BD AC ⨯⨯+=⨯⨯=故选：D点评：本题考查四边形的面积的求法，是中档题，解题时要认真审题，注意圆的性质的合理运用． 8.已知某空间几何体的三视图如右图所示，则该几何体的体积是（ ）A.16B.32C.32D.48 答案：D考点：由三视图求面积、体积.专题：计算题；空间位置关系与距离．分析：根据几何体的三视图，得出该几何体是四棱锥，结合题目中的数据，求出它的体积． 解答：解：根据几何体的三视图，得；该几何体是底面为直角梯形的四棱锥， 如图所示；∴该几何体的体积是()11=2666=4832V ⨯⨯+⨯⨯四棱锥.故选：D ．6266点评：本题考查了利用空间几何体的三视图求体积的应用问题，是基础题目．9.已知实数a ，b 满足23a =，32b =，则函数()x f x a x b =+-的零点所在的区间是（ ） A.()2,1-- B.()1,0-C0()0,1D0()1,2答案：B考点：函数的零点；指数函数的图像与性质. 专题：函数的性质及应用．分析：根据对数，指数的转化得出()()23log 3log 2xf x x =+-单调递增，根据函数的零点判定定理得出()301log 20f =->，()331log 21log 210f -=--=-<，判定即可．解答：解： 实数a ，b 满足23a =，32b =，2log 31a ∴=>，30log 21b <=<，函数()x f x a x b =+-，()()23log 3log 2xf x x ∴=+-单调递增， ()301log 20f =->()331log 21log 210f -=--=-<，∴根据函数的零点判定定理得出函数()x f x a x b =+-的零点所在的区间()1,0-，故选：B ．点评：本题考查了函数的性质，对数，指数的转化，函数的零点的判定定理，属于基础题．10.已知实数x ，y 满足条件2420x x y x y c ⎧⎪+⎨⎪-++⎩≥≤≥若目标函数3z x y =+的最小值为5，其最大值为（ ）A.10B.12C.14D.15 答案：A考点：简单线性规划.专题：不等式的解法及应用． 分析：作出不等式组对应的平面区域，利用目标函数3z x y =+的最小值为5，建立条件关系即可求出k 的值．解答：解：目标函数3z x y =+的最小值为5，3y x z ∴=-+，要使目标函数3z x y =+的最小值为5， 作出不等式组对应的平面区域如图： 则目标函数经过点B 截距最小， 由235x x y =⎧⎨+=⎩，解得21x y =⎧⎨=-⎩，即()2,1B -，同时B 也在直线20x y c -++=，即410c --+=，解得5c =，此时直线方程为250x y -++=，当直线3z x y =+经过点C 时，直线的截距最大，此时z 最大， 由2504x y x y -++=⎧⎨+=⎩，解得31x y =⎧⎨=⎩，即()3,1C ，此时33110z =⨯+=， 故选：A ．点评：本题主要考查线性规划的应用，根据目标函数3z x y =+的最小值为5，确定平面区域的位置，利用数形结合是解决本题的关键．11.已知点O 为双曲线C 的对称中心，过点O 的两条直线1l 与2l 的夹角为60︒，直线1l 与双曲线C 相交于点1A ，1B ，直线2l 与双曲线C 相交于点2A ，2B ，若使1122A B A B =成立的直线1l 与2l 有且只有一对，则双曲线C 离心率的取值范围是（ ）A.,2⎤⎥⎝⎦B.2⎫⎪⎪⎣⎭C.,⎫+⎪⎪⎝⎭∞D.,⎫+⎪⎪⎣⎭∞ 答案：A考点：双曲线的简单性质.专题：圆锥曲线的定义、性质与方程．分析：先设出双曲线的方程，并根据题意画出图象，根据对称性和条件判断出双曲线的渐近线斜率的范围，列出不等式并转化为关于离心率的不等式，再求解即可．解答：解：不妨设双曲线的方程是()222210,0x y a b a b-=>>，由1122A B A B =及双曲线的对称性知1A ，2A ，1B ，2B 关于x 轴对称，如图， 又 满足条件的直线只有一对，当直线与x 轴夹角为30︒时，双曲线的渐近线与x 轴夹角大于30︒， 双曲线与直线才能有交点1A ，2A ，1B ，2B ，若双曲线的渐近线与x 轴夹角等于30︒，则无交点， 且不可能存在1122A B A B =，当直线与x 轴夹角为60︒时，双曲线渐近线与x 轴夹角小于60︒， 双曲线与直线有一对交点1A ，2A ，1B ，2B ，若双曲线的渐近线与x 轴夹角等于60︒，也满足题中有一对直线， 但是如果大于60︒，则有两对直线．不符合题意，tan30tan60b a ∴︒<︒≤b a <≤22133b a <≤， 222b c a =- ，222133c a b -∴<≤，则21e 133<-≤， 解得24e 43<≤e 2<≤， ∴双曲线离心率的范围是2⎤⎥⎝⎦， 故选：A ．点评：本题考查双曲线的简单性质以及应用，考查数形结合思想和分类讨论思想，属于中档题．12.已知数列{}n a 的通项公式为()()()*π121cos 12nn n a n n =--+∈N ，其前n 项和为n S ，则60S =（ ）A.30-B.60-C.90D.120 答案：D考点：数列的求和.专题：计算题；点列、递归数列与数学归纳法．分析：由数列的通项公式求出数列前几项，得到数列的奇数项均为1，每两个偶数项的和为6，由此可以求得60S 的值．解答：解：由()()π121cos12nn n a n =--+，得 1πcos 112a =-+=，23cos π+1=2a =-，33π5cos 112a =-+=，47cos2π+1=8a =，55π9cos 112a =-+=，611cos3π+1=10a =-，77π13cos 112a =-+=，815cos4π+1=16a =，由上可知，数列{}n a 的奇数项为1，每两个偶数项的和为6， ()()60135924586030156120S a a a a a a a ∴=++++++++=+⨯= .故选：D ．点评：本题考查了数列递推式，考查了三角函数的求值，关键是对数列规律的发现，是中档题． 二、填空题13.已知向量a ，b 满足()()26a b a b -+= ，且2a = ，1b =，则a 与b 的夹角为 ．答案：120︒考点：数量积表示两个向量的夹角. 专题：平面向量及应用．分析：将已知等式展开，利用向量的平方与模的平方相等以及向量的数量积公式，得到关于 向量夹角的等式解之．解答：解：由()()26a b a b -+= ，且2a = ，1b = ，得2226a b a b -+⋅= ，即812cos ,6a b -+=，所以1cos ,2a b =- ，所以a 与b的夹角为120︒； 故答案为：120︒．点评：本题考查了向量的数量积的运算以及向量夹角的求法；关键是熟练利用数量积公式． 14.已知2nx⎛⎝展开式的二项式系数之和为64，则其展开式中常数项是 ．答案：60考点：二项式定理.专题：计算题；二项式定理．分析：根据题意，2nx⎛ ⎝的展开式的二项式系数之和为64，由二项式系数的性质，可得264n=，解可得，6n =；进而可得二项展开式，令3602r -=，可得4r =，代入二项展开式，可得答案．解答：解：由二项式系数的性质，可得264n=，解可得，6n =；62x⎛ ⎝的展开式为为()()3666662166C 212C rr r r r r r r T x x -----+⎛=⋅⋅=-⋅⋅⋅ ⎝， 令3602r -=，可得4r =，则展开式中常数项为60． 故答案为：60．点评：本题考查二项式定理的应用，注意系数与二项式系数的区别．15.已知在直角梯形ABCD 中，AB AD ⊥，CD AD ⊥，222AB AD CD ===，将直角梯形ABCD 沿AC 折叠成三棱锥D ABC -，当三棱锥D ABC -的体积取最大值时，其外接球的体积为 ．答案：4π3考点：球的体积和表面积.专题：计算题；空间位置关系与距离． 分析：画出图形，确定三棱锥外接球的半径，然后求解外接球的体积即可．解答：解：已知直角梯形ABCD ，AB AD ⊥，CD AD ⊥，222AB AD CD ===，沿AC 折叠成三棱锥，如图：2AB =，1AD =，1CD =，AC ∴BC ， BC AC ∴⊥，取AC 的中点E ，AB 的中点O ，连结DE ，OE ， 当三棱锥体积最大时， ∴平面DCA ⊥平面ACB ， OB OA OC OD ∴===，1OB ∴=，就是外接球的半径为1，此时三棱锥外接球的体积：34π4π133⨯=．故答案为：4π3．点评：本题考查折叠问题，三棱锥的外接球的体积的求法，考查空间想象能力以及计算能力．16.已知定义在R 上的奇函数()f x 满足()32f x f x ⎛⎫-= ⎪⎝⎭，()23f -=-，数列{}n a 的前n 项和为n S ，且11a =-，()*2n n S a n n =+∈N ，则()()56f a f a += ．答案：3考点：数列与函数的综合. 专题：等差数列与等比数列．分析：先由函数()f x 是奇函数，()32f x f x ⎛⎫-= ⎪⎝⎭，推知()()3f x f x +=，得到()f x 是以3为周期的周期函数．再由11a =-，且2n n S a n =+，推知531a =-，663a =-计算即可．解答：解： 函数()f x 是奇函数 ()()f x f x ∴-=- ()32f x f x ⎛⎫-= ⎪⎝⎭ ，()32f x f x ⎛⎫∴-=-- ⎪⎝⎭()()3f x f x ∴+=()f x ∴是以3为周期的周期函数．数列{}n a 满足11a =-，且2n n S a n =+，1121n n S a n --∴=+-，221n n n a a a ∴=-+， 即121n n a a -=-，()1121n n a a --=-，{}1n a -以2-为首项，2为公比的等比数列． 12n n a =-．531a ∴=-，663a =-()()()()()()()()56316320223f a f a f f f f f f ∴+=-+-=+==--=故答案为：3．点评：本题主要考查函数性质的转化与应用以及数列的通项及求和公式，在函数性质综合应用中相互结合转化中奇偶性，对称性和周期性之间是一个重点． 三、解答题17.已知a ，b ，c 分别是ABC △的角A ，B ，C 所对的边，且2c =，π3C =．（1）若ABC △a ，b ；（2）若()sin sin 2sin2C B A A +-=，求A 的值．考点：余弦定理；正弦定理. 专题：解三角形．分析：（1）2c =，π3C =，由余弦定理可得：2222cos c a b ab C =+-，即224a b ab =+-，利用三角形面积计算公式1πsin 23ab =4ab =．联立解出即可．（2）由()s i n s i n C B A =+，()sin sin 2sin2C B A A +-=，可得2sin cos 4sin cos B A A A =．当c o s 0A =时，解得π2A =；当cos 0A ≠时，sin 2sin B A =，由正弦定理可得：2b a =，联立解得即可． 解答：解：（1）2c = ，π3C =，由余弦定理可得：2222cos c a b ab C =+-，224a b ab ∴=+-， 1πsin 23ab 4ab =． 联立2244a b ab ab ⎧+-=⎨=⎩，解得2a =，2b =．（2）()sin sin C B A =+ ，()sin sin 2sin2C B A A +-=， ()()sin sin 2sin2A B B A A ∴++-=， 2sin cos 4sin cos B A A A =，当cos 0A =时，解得π2A =； 当cos 0A ≠时，sin 2sin B A =， 由正弦定理可得：2b a =，联立2242a b ab b a ⎧+-=⎨=⎩，解得a =，b =，222b a c ∴=+，π2B ∴=，又π3C =，π6A ∴=．综上可得：π2A =或π6A =．点评：本题考查了正弦定理、余弦定理、三角形的面积计算公式、两角和差的正弦公式，考查了分类讨论思想方法，考查了推理能力与计算能力，属于中档题． 18.某工厂为了检查一条流水线的生产情况，从该流水线上随机抽取40件产品，测量这些产品的重量（单位：克），整理后得到如下的频率分布直方图（其中重量的分组区间分别为(]490,495，(]495,500，(]500,505，(]505,510，(]510,515）（I ）若从这40件产品中任取两件，设X 为重量超过505克的产品数量，求随机变量X 的分布列；（Ⅱ）若将该样本分布近似看作总体分布，现从该流水线上任取5件产品，求恰有两件产品的重量超过505克的概率．/克考点：离散型随机变量及其分布列；离散型随机变量的期望与方差. 专题：概率与统计． 分析：（ I ）根据频率分布直方图求出重量超过505克的产品数量，推出随机变量X 的所有可能取值为 0，1，2求出概率，得到随机变量X 的分布列．（Ⅱ）求出该流水线上产品的重量超过505克的概率为0.3，推出()5,0.3Y B ~．然后求解所求概率． 解答：解：（ I ）根据频率分布直方图可知，重量超过505克的产品数量为()0.0010.00554012+⨯⨯=⎡⎤⎣⎦． 由题意得随机变量X 的所有可能取值为0，1，2()228240C 630C 130P X ===，()112812240C C 281C 65P X ===，()212240C 112C 130P X ===．: 505克的概率为0.3设Y 为该流水线上任取5件产品重量超过505克的产品数量，则()5,0.3Y B ~．故所求概率为()22352C 0.30.70.3087P Y ==⨯⨯=．点评：本题考查离散型随机变量的分布列，以及概率的求法，考查计算能力． 19.如图，在斜三棱柱111ABC A B C -中，侧面11AA B B ⊥底面ABC ，侧棱1AA 与底面ABC 的所成角为60︒，12AA =，底面ABC 是边长为2的正三角形，点G 为ABC △的重心，点E 在1BC 上，且113BE BC =．（1）求证：GE ∥平面11AA B B ；（2）求平面1B GE 与底面ABC 所成锐角二面角的余弦值．C 1B 1A 1G ECBA考点：二面角的平面角及求法；直线与平面平行的判定. 专题：空间位置关系与距离；空间角． 分析：（1）连接1B E ，并延长交BC 于点F ，连接1AB ，AF ，证明1GE AB ∥，然后证明GE ∥平面11AA B B ；（2）过点1A 作1AO AB ⊥，垂足为O ，连接OC ，以O 为原点，分别以OC ，OB ，OA 为x ，y ，z 轴建立如图空间直角坐标系O xyz -，求出相关点的坐标，平面1B GE 的一个法向量，平面ABC 的一个法向量，即可求解二面角的余弦函数值． 解答：解：（1）证明：连接1B E ，并延长交BC 于点F ，连接1AB ，AF ， 111ABC A B C - 是三棱柱，11BC B C ∴∥，11EFB EB C ∴△∽△，又113BE BC = ，111112BE EF BF EC EB B C ∴===， 12BF BC ∴=，F ∴是BC 的中点．点G 是ABC △的重心，∴点G 在AF 上，且112GF BF AG EB ==， 1GE AB ∴∥， GE ∴∥平面11AA B B ；（2）证明：过点1A 作1AO AB ⊥，垂足为O ，连接OC ， 侧面11AA B B ⊥底面ABC ，1AO ∴⊥底面ABC ，160A AB ∴∠=︒， 12AA = ，1AO ∴=，2AB = ，∴点O 是AB 的中点，又 点G 是正三角形ABC 的重心∴点G 在OC 上，OC AB ∴⊥，1AO ⊥底面ABC ，1AO OB ∴⊥，1AO OC ⊥，以O 为原点， 分别以OC ，OB ，OA 为x ，y ，z 轴建立如图空间直角坐标系O xyz -，由题意可得：()0,1,0A -，()0,1,0B，)0,0C，(10,0,A，(10,2,B，11,C ，则,0,0G ⎫⎪⎪⎝⎭，110,3BE BC ∴==⎝⎭，,1,E ∴⎝⎭，0,1,GE ⎛∴= ⎝⎭,11,B E =-⎝⎭, 设(),,n x y z = 是平面1B GE 的一个法向量，则1n GE n B E ⎧⎪⎨⎪⎩ ⊥⊥0y y ⎧=⎪⎪∴-=令z =，则x =1y =-，1,n ∴=-，由（1）知(1π0,0,OA ==是平面ABC 的一个法向量，设平面1B GE 与底面ABC 所成锐二面角为θ，则有：cos m n m nθ⋅=⋅ ．FAB CEG A 1B 1C 1点评：本题考查直线与平面平行的判定定理以及二面角的平面角的求法，考查空间想象能力逻辑推理能力以及计算能力．20.已知椭圆()222210x y a b a b+=>>的左右焦点1F ，2F 其离心率为1e=2，点P 为椭圆上的一个动点，12PF F △内切圆面积的最大值为4π3．（1）求a ，b 的值（2）若A 、B 、C 、D 是椭圆上不重合的四个点，且满足11F A FC ∥，11F B F D ∥，0AC BD ⋅= ，求A C B D +的取值范围．考点：直线与圆锥曲线的关系；直线与圆锥曲线的综合问题. 专题：圆锥曲线的定义、性质与方程． 分析：（1）当P 为椭圆上下顶点时，12PF F △内切圆面积取得最大值，设12PF F △内切圆半径为r ，利用()121212121122PF F S F F b bc F F PF PF r =⋅==++△，化为)bc a c +，又12c a =，222a b c =+，联立解得a ，c ，b 即可得出．（2）由满足11F A FC ∥，11F B F D ∥，0AC BD ⋅=，可得直线AC ，BD 垂直相交于点1F ，由（1）椭圆方程2211612x y +=，()12,0F -．①直线AC ，BD 有一条斜率不存在时，14AC BD +=．②当AC 斜率存在且不为0时，设方程()2y k x =+，()11,A x y ，()22,C x y ，与椭圆方程联立化为()2222341616480k xk x k +++-=．利用根与系数的关系可得：()2224134k AC k +=+ ,把1k -代入上述可得：可得()2224143k BD k +=+ ，可得()()()222216814334k AC BD k k ++=++ ，设()210t k k =+≠，1t >．即可得出．解答：解：（1）设12PF F △内切圆半径为r ，由12PF F △的面积为()()1212112222S r PF PF F F r a c =++=+，S 最大，则r 最大，当P 为椭圆上下顶点时，12PF F △的面积最大，其内切圆面积取得最大值，24ππ3r =，r ∴=． ()()1212121211122222PF F S F F b bc F F PF PF r c a =⋅==++=+△，化为)bc a c +，又12c a =，222a b c =+，联立解得4a =，2c =，b = （2） 满足11F A FC ∥，11F B F D ∥，0AC BD ⋅= ， ∴直线AC ，BD 垂直相交于点1F ，由（1）椭圆方程2211612x y +=，()12,0F -．①直线AC ，BD 有一条斜率不存在时，6814AC BD +=+=．②当AC 斜率存在且不为0时，设方程()2y k x =+，()11,A x y ，()22,C x y ， 联立()22211612y k x x y ⎧=+⎪⎨+=⎪⎩，化为()2222341616480k x k x k +++-=．21221634k x x k -∴+=+，2122164834k x x k -=+，()2224134k AC k +∴+ ，把1k -代入上述可得：可得()2224143k BD k +=+ ，()()()222216814334k AC BD k k +∴+=++，设()210t k k =+≠，1t >． 168112AC BD t t∴+=-+ ，1t > ，21104t t -∴<≤，96,147AC BD ⎡⎫∴+∈⎪⎢⎣⎭ ．综上可得：AC BD + 的取值范围是96,147⎡⎤⎢⎥⎣⎦．点评：本题考查了椭圆的标准方程及其性质、直线与椭圆相交转化为方程联立可得根与系数关系、向量垂直与数量积的关系、三角形内切圆的性质、二次函数的性质，考查了“换元法”、推理能力与计算能力，属于难题．21.已知函数()()2ln f x x a x x =++，a ∈R ． （Ⅰ）若当1a =-时，求()f x 的单调区间；（Ⅱ）若()()1e 12f x a >+，求a 的取值范围． 考点：利用导数研究函数的单调性；导数在最大值、最小值问题中的应用. 专题：导数的综合应用． 分析：（Ⅰ）1a =-时，求出()2ln f x x x x =--，通过求导，根据导数符号即可判断出()f x 的单调区间；（Ⅱ）讨论a 的取值：0a =时，容易得出满足题意；0a >时，会发现函数2x ax +在()0,+∞上单调递增，让110e1ax --<<<，便得到()()111ln 110e 12f x a a x a a a a ⎛⎫<++<++--=<+ ⎪⎝⎭，从而这种情况不存在；当0a <时，通过求导，容易判断出，存在()00,x ∈+∞，使()0'0f x =，从而判断出()f x 的最小值()0f x ，再由条件()()1e+12f x a >便可得到()00,e x ∈，并根据()0'0f x =，可求出20021x a x =-+，从而求出a 的取值范围． 解答：解：（Ⅰ）由题意得()0,x ∈+∞； 当1a =-时，()2ln f x x x x =--，()()()212121'x x x x f x x x-+--==；∴x ∈（0，1）时，f ′（x ）＜0，x ∈（1，+∞）时，f ′（x ）＞0； ()f x ∴的单调减区间是()0,1，单调增区间是[)1,+∞；（II ）①当0a =时，()20f x x =>，显然符合题意； ②当0a >时，当110eax --<<时；()()111ln 110e+12f x a a x a a a a ⎛⎫<++<++--=< ⎪⎝⎭,不符合题意；③当0a <时，则()22'x ax af x x++=；对于220x ax a ++=，280a a ∆=->；∴该方程有两个不同实根，且一正一负，即存在()00,x ∈+∞，使得20020x ax a ++=； 即()0'0f x =；00x x ∴<<时，()'0f x <，0x x >时，()'0f x >；()()0min f x f x ∴=()()()220000000001111ln 12ln 12ln 2222x a x x x ax a a x x a x x ⎡⎤⎡⎤=++=+++-+=-+⎣⎦⎣⎦; ()()1e 12f x a >+ ，()002ln e 20x x ∴+-+<；00e x ∴<<；由20020x ax a ++=得，20021x a x =-+；设20021x y x =-+，()2002024'01x x y x +=-<+； ∴函数2021x y x =-+在()0,e 上单调递减； 220022e ,01e+1x x ⎛⎫∴-∈- ⎪+⎝⎭；综上所述，实数a 的取值范围22e ,0e+1⎛⎤-⎥⎝⎦． 点评：考查根据函数导数符号判断函数单调性，求函数单调区间的方法，判别式的取值和一元二次方程根的关系，由韦达定理判断一元二次方程根的符号，以及根据导数求函数最小值的方法与过程，函数单调性定义的运用． 四.选修4-1：几何证明选讲 22.如图，已知点C 是以AB 为直径的半圆O 上一点，过C 的直线交AB 的延长线于E ，交过点A 的圆O 的切线于点D ，BC OD ∥，2AD AB ==． （Ⅰ）求证：直线DC 是圆O 的切线； （Ⅱ）求线段EB 的长．BCADE考点：与圆有关的比例线段；圆的切线的判定定理的证明. 专题：选作题；立体几何．分析：（Ⅰ）要证DE 是圆O 的切线，连接AC ，只需证出90DAO ∠=︒，由B C O D O D A C ⇒∥⊥，则OD是AC 的中垂线．通过AOC △，BOC △均为等腰三角形，即可证得90DAO ∠=︒．（Ⅱ）由BC OD CBA DOA ⇒∠=∠∥，结合BCA DAO ∠=∠，得出ABC AOD △∽△，利用比例线段求出EB ． 解答：（Ⅰ）证明：连接AC ，AB 是直径，则BC AC ⊥， 由BC ∥OD ⇒OD ⊥AC ，则OD 是AC 的中垂线OCA OAC ⇒∠=∠，DCA DAC ∠=∠， 90OCD OCA DCA OAC DAC DAO ⇒∠=∠+∠=∠+∠=∠=︒. OC DE ⇒⊥，所以DE 是圆O 的切线．（Ⅱ）解：BC OD CBA DOA ⇒∠=∠∥，BCA DAO ABC AOD ∠=∠⇒△∽△22225533BC AB OA AB BC BE BE BC BE OA OD OD OD OE OB ⋅⇒=⇒===⇒=⇒=⇒=. EDACB点评：本题考查圆的切线的证明，与圆有关的比例线段．准确掌握与圆有关的线、角的性质是解决此类问题的基础和关键．五.选修4-4：坐标系与参数方程23.直角坐标系xOy 中，曲线1C的参数方程为1x y θθ⎧=⎪⎨=⎪⎩（其中θ为参数），点M 是曲线1C 上的动点，点P 在曲线2C 上，且满足2OP OM =． （Ⅰ）求曲线2C 的普通方程；（Ⅱ）以原点O 为极点，x =轴的正半轴为极轴建立极坐标系，射线π3θ=，与曲线1C ，2C 分别交于A ，B 两点，求AB ．考点：参数方程化成普通方程. 专题：坐标系和参数方程． 分析：（Ⅰ）设(),P x y ，()','M x y ，因为点M 是曲线1C 上的动点，点P 在曲线2C 上，将M 坐标代入，消去θ，得到M 满足的方程，再由向量共线，得到P 满足的方程；（Ⅱ）以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，分别利用极坐标方程表示两个曲线，求出A ，B 的极坐标，得到AB 长度．解答：解：（Ⅰ）因为点M 是曲线1C 上的动点，点P 在曲线2C 上，且满足2OP OM =．设(),P x y ，()','M x y ，则2'x x =，2'y y =，并且'1'x y θθ⎧=⎪⎨⎪⎩，消去θ得，()22'1'3x y -+=，所以曲线2C 的普通方程为：()22212x y -+=；（Ⅱ）以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线1C 的极坐标方程为22cos 20ρρθ--=，将π3θ=代入得2ρ=，A ∴的极坐标为π2,3⎛⎫ ⎪⎝⎭，曲线2C 极坐标方程为24cos 80ρρθ--=，将π3θ=代入得4ρ=，所以B 的极坐标为π4,3⎛⎫ ⎪⎝⎭，所以422AB =-=．点评：本题考查了将参数方程化为普通方程以及利用极坐标方程表示曲线． 五.选修4-5：不等式选讲24.已知函数()21f x x x a =-+-，a ∈R ．（Ⅰ）当3a =时，解不等式()4f x ≤； （Ⅱ）若()1f x x a =-+，求x 的取值范围．考点：绝对值不等式的解法. 专题：不等式的解法及应用． 分析：（Ⅰ）当3a =时，化简函数()f x 的解析式，画出函数()f x 的图象，画出直线4y =，数形结合求得不等式()4f x ≤的解集．（Ⅱ）由条件求得()()210x x a ---≤，分类讨论求得x 的范围． 解答：解：（Ⅰ）当3a =时，函数()34,312132,32143,2x x f x x x x x x x ⎧⎪-⎪⎪=-+-=+<<⎨⎪⎪-⎪⎩≥≤,如图所示：由于直线4y =和函数()f x 的图象交于点()0,4、()2,4，故不等式不等式()4f x ≤的解集为[]0,2．（Ⅱ）由()1f x x a =-+，可得211x x a x a -+-=-+．由于()()21211x x a x x a x a -+----=-+≥，当且仅当()()210x x a -⋅-≤时，取等号． 故有()()210x x a -⋅-≤．当12a =时，可得12x =，故x 的范围为12⎧⎫⎨⎬⎩⎭；当12a >时，可得12x a ≤≤，故x 的范围为1,2a ⎡⎤⎢⎥⎣⎦；当12a <时，可得12a x ≤≤，故x 的范围为1,2a ⎡⎤⎢⎥⎣⎦．点评：本题主要考查带有绝对值的函数，绝对值不等式的解法，体现了转化、数形结合、分类讨论的数学思想，属于中档题．。