计量经济学3.1 矩阵基础及多元线性回归模型
- 格式:ppt
- 大小:364.00 KB
- 文档页数:45


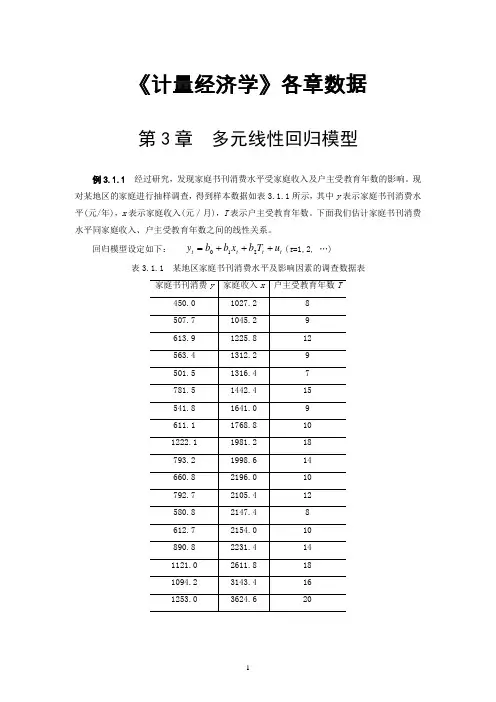
《计量经济学》各章数据第3章 多元线性回归模型例3.1.1 经过研究,发现家庭书刊消费水平受家庭收入及户主受教育年数的影响。
现对某地区的家庭进行抽样调查,得到样本数据如表3.1.1所示,其中y 表示家庭书刊消费水平(元/年),x 表示家庭收入(元/月),T 表示户主受教育年数。
下面我们估计家庭书刊消费水平同家庭收入、户主受教育年数之间的线性关系。
回归模型设定如下: t t t t u T b x b b y +++=210(t =1,2, …)表3.1.1 某地区家庭书刊消费水平及影响因素的调查数据表例3.4.1根据表3.4.1给出的中国1980-2003年间总产出(用国内生产总值GDP度量,单位:亿元),劳动投入L(用从业人员度量,单位为万人),以及资本投入K(用全社会固定投资度量,单位:亿元),试建立我国的柯布——道格拉斯生产函数。
表3.4.1 1980-2003年中国GDP、劳动投入与资本投入数据例3.4.2 某硫酸厂生产的硫酸透明度一直达不到优质要求,经分析透明度低与硫酸中金属杂质的含量太高有关。
影响透明度的主要金属杂质是铁、钙、铅、镁等。
通过正交试验的方法发现铁是影响硫酸透明度的最主要原因。
测量了47组样本值,数据见表3.4.3。
试建立硫酸透明度(y)与铁杂质含量(x)的回归模型。
表3.4.3 硫酸透明度(y)与铁杂质含量(x)数据例3.4.3假设某企业在15年中每年的产量Y(件)和总成本X(元)的统计资料表3.4.7所示,试估计该企业的总成本函数模型。
表3.4.7 某企业15年中每年总产量与总成本统计资料3.6.1 案例1——中国经济增长影响因素分析根据表3.6.1给出的1980-2003年间总产出(用国内生产总值GDP度量,单位:亿元),最终消费CS(单位:亿元),投资总额I(用固定资产投资总额度量,单位:亿元),出口总额(单位:亿元)统计数据,试对中国经济增长影响因素进行回归分析。



第二章经典单方程计量经济学模型:一元线性回归模型一、内容提要本章介绍了回归分析的基本思想与基本方法。
首先,本章从总体回归模型与总体回归函数、样本回归模型与样本回归函数这两组概念开始,建立了回归分析的基本思想。
总体回归函数是对总体变量间关系的定量表述,由总体回归模型在若干基本假设下得到,但它只是建立在理论之上,在现实中只能先从总体中抽取一个样本,获得样本回归函数,并用它对总体回归函数做出统计推断。
本章的一个重点是如何获取线性的样本回归函数,主要涉及到普通最小二乘法(OLS)的学习与掌握。
同时,也介绍了极大似然估计法(ML)以及矩估计法(MM)。
本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断,即进行所谓的统计检验。
统计检验包括两个方面,一是先检验样本回归函数与样本点的“拟合优度”,第二是检验样本回归函数与总体回归函数的“接近”程度。
后者又包括两个层次:第一,检验解释变量对被解释变量是否存在着显著的线性影响关系,通过变量的t检验完成;第二,检验回归函数与总体回归函数的“接近”程度,通过参数估计值的“区间检验”完成。
本章还有三方面的内容不容忽视。
其一,若干基本假设。
样本回归函数参数的估计以及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。
其二,参数估计量统计性质的分析,包括小样本性质与大样本性质,尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则。
Goss-markov定理表明OLS估计量是最佳线性无偏估计量。
其三,运用样本回归函数进行预测,包括被解释变量条件均值与个值的预测,以及预测置信区间的计算及其变化特征。
二、典型例题分析例1、令kids表示一名妇女生育孩子的数目,educ表示该妇女接受过教育的年数。
生育率对教育年数的简单回归模型为β+μβkids=educ+1(1)随机扰动项μ包含什么样的因素?它们可能与教育水平相关吗?(2)上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗?请解释。



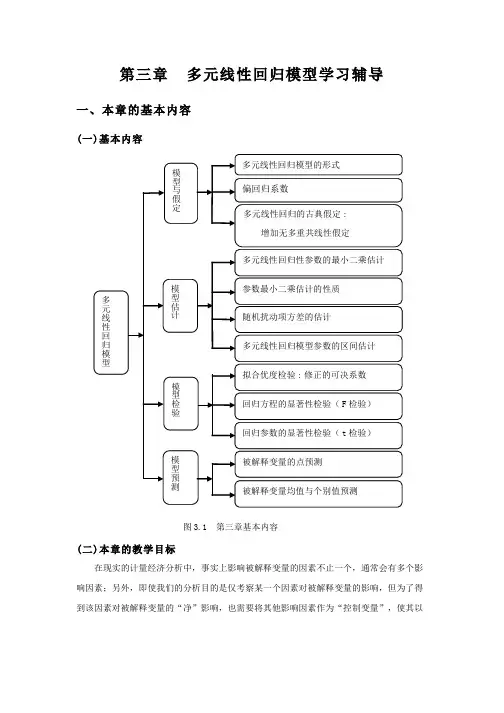
第三章 多元线性回归模型学习辅导一、本章的基本内容(一)基本内容图3.1 第三章基本内容(二)本章的教学目标在现实的计量经济分析中,事实上影响被解释变量的因素不止一个,通常会有多个影响因素;另外,即使我们的分析目的是仅考察某一个因素对被解释变量的影响,但为了得到该因素对被解释变量的“净”影响,也需要将其他影响因素作为“控制变量”,使其以显性形式出现在模型中,以提高模型估计精度。
因此,在对现实经济问题进行计量经济分析时,通常需要建立包含两个及两个以上解释变量的计量模型,此类模型称为多元回归模型。
多元回归模型是在简单回归模型理论基础上的扩展,其建模的理论基础、基本思路、模型估计等与一元回归模型基本一致,只是因解释变量增多,从而带来一些新的内容,比如模型整体显著性检验(F 检验)、修正的可决系数(2R )以及解释变量之间多重共线性等问题。
本章的教学目标是:深刻理解建立多元回归模型的目的;掌握多元线性回归模型估计、检验的理论与方法;熟练掌握多元线性回归EViews 输出结果的解释。
二、重点与难点分析1.对多元线性回归模型参数意义的理解多元线性回归模型的参数与简单线性回归模型的参数有重要区别。
在多元线性回归模型中,解释变量对应的参数是偏回归系数,表达的是控制其他解释变量不变的条件下,该解释变量的单位变动对被解释变量平均值的“净”影响。
为了更深刻理解偏回归系数,可以两个解释变量的多元线性回归模型为例加以说明1。
例如,被解释变量Y 与解释变量2X 和3X 都有关,如果分别建立模型:多元线性回归: 12233i i i i Y X X u b b b =+++简单线性回归 : 1221i i i Y a a X u =++由于Y 与3X 有关,可以作回归:1332i i i Y b b X u =++,若用OLS 估计其参数,并计算残差213333ˆˆˆi i i i i e Y b b X y b x =--=-,这里的2i e 表示除去3i X 影响后的i Y 。

多元线性回归模型多元线性回归模型是一种广泛应用于统计学和机器学习领域的预测模型。
它通过使用多个自变量来建立与因变量之间的线性关系,从而进行预测和分析。
在本文中,我们将介绍多元线性回归模型的基本概念、应用场景以及建模过程。
【第一部分:多元线性回归模型的基本概念】多元线性回归模型是基于自变量与因变量之间的线性关系进行建模和预测的模型。
它假设自变量之间相互独立,并且与因变量之间存在线性关系。
多元线性回归模型的数学表达式如下:Y = β0 + β1X1 + β2X2 + … + βnXn + ε其中,Y表示因变量,X1、X2、…、Xn表示自变量,β0、β1、β2、…、βn表示回归系数,ε表示误差项。
回归系数表示自变量对因变量的影响程度,误差项表示模型无法解释的部分。
【第二部分:多元线性回归模型的应用场景】多元线性回归模型可以应用于各种预测和分析场景。
以下是一些常见的应用场景:1. 经济学:多元线性回归模型可以用于预测GDP增长率、失业率等经济指标,揭示不同自变量对经济变量的影响。
2. 医学研究:多元线性回归模型可以用于预测患者的生存时间、治疗效果等医学相关指标,帮助医生做出决策。
3. 市场研究:多元线性回归模型可以用于预测产品销量、市场份额等市场相关指标,帮助企业制定营销策略。
4. 社会科学:多元线性回归模型可以用于研究教育水平对收入的影响、家庭背景对孩子成绩的影响等社会科学问题。
【第三部分:多元线性回归模型的建模过程】建立多元线性回归模型的过程包括以下几个步骤:1. 数据收集:收集自变量和因变量的数据,确保数据的准确性和完整性。
2. 数据清洗:处理缺失值、异常值和离群点,保证数据的可靠性和一致性。
3. 特征选择:根据自变量与因变量之间的相关性,选择最相关的自变量作为模型的输入特征。
4. 模型训练:使用收集到的数据,利用最小二乘法等统计方法估计回归系数。
5. 模型评估:使用误差指标(如均方误差、决定系数等)评估模型的拟合程度和预测性能。
第五章 多元线性回归模型在第四章中,我们讨论只有一个解释变量影响被解释变量的情况,但在实际生活中,往往是多个解释变量同时影响着被解释变量。
需要我们建立多元线性回归模型。
一、多元线性模型及其假定 多元线性回归模型的一般形式是i iK K i i i x x x y εβββ++++= 2211令列向量x 是变量x k ,k =1,2,的n 个观测值,并用这些数据组成一个n ×K 数据矩阵X ,在多数情况下,X 的第一列假定为一列1,则β1就是模型中的常数项。
最后,令y 是n 个观测值y 1, y 2, …, y n 组成的列向量,现在可将模型写为:εββ++=K K x x y 11构成多元线性回归模型的一组基本假设为 假定1. εβ+=X y我们主要兴趣在于对参数向量β进行估计和推断。
假定2. ,0][][][][21=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n E E E E εεεε 假定3. n I E 2][σεε='假定4. 0]|[=X E ε我们假定X 中不包含ε的任何信息,由于)],|(,[],[X E X Cov X Cov εε= (1)所以假定4暗示着0],[=εX Cov 。
(1)式成立是因为,对于任何的双变量X ,Y ,有E(XY)=E(XE(Y|X)),而且])')|()([(])')((),(EY X Y E EX X E EY Y EX X E Y X Cov --=--=))|(,(X Y E X Cov =这也暗示 βX X y E =]|[假定5 X 是秩为K 的n ×K 随机矩阵 这意味着X 列满秩,X 的各列是线性无关的。
在需要作假设检验和统计推断时,我们总是假定: 假定6 ],0[~2I N σε 二、最小二乘回归 1、最小二乘向量系数采用最小二乘法寻找未知参数β的估计量βˆ,它要求β的估计βˆ满足下面的条件 22min ˆ)ˆ(ββββX y X y S -=-∆ (2)其中()()∑∑==-'-=⎪⎪⎭⎫ ⎝⎛-∆-nj Kj j ij i X y X y x y X y 1212ββββ,min 是对所有的m 维向量β取极小值。
多元线性回归模型引言:多元线性回归模型是一种常用的统计分析方法,用于确定多个自变量与一个连续型因变量之间的线性关系。
它是简单线性回归模型的扩展,可以更准确地预测因变量的值,并分析各个自变量对因变量的影响程度。
本文旨在介绍多元线性回归模型的原理、假设条件和应用。
一、多元线性回归模型的原理多元线性回归模型基于以下假设:1)自变量与因变量之间的关系是线性的;2)自变量之间相互独立;3)残差项服从正态分布。
多元线性回归模型的数学表达式为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中,Y代表因变量,X1,X2,...,Xn代表自变量,β0,β1,β2,...,βn为待估计的回归系数,ε为随机误差项。
二、多元线性回归模型的估计方法为了确定回归系数的最佳估计值,常采用最小二乘法进行估计。
最小二乘法的原理是使残差平方和最小化,从而得到回归系数的估计值。
具体求解过程包括对模型进行估计、解释回归系数、进行显著性检验和评价模型拟合度等步骤。
三、多元线性回归模型的假设条件为了保证多元线性回归模型的准确性和可靠性,需要满足一定的假设条件。
主要包括线性关系、多元正态分布、自变量之间的独立性、无多重共线性、残差项的独立性和同方差性等。
在实际应用中,我们需要对这些假设条件进行检验,并根据检验结果进行相应的修正。
四、多元线性回归模型的应用多元线性回归模型广泛应用于各个领域的研究和实践中。
在经济学中,可以用于预测国内生产总值和通货膨胀率等经济指标;在市场营销中,可以用于预测销售额和用户满意度等关键指标;在医学研究中,可以用于评估疾病风险因素和预测治疗效果等。
多元线性回归模型的应用可以为决策提供科学依据,并帮助解释变量对因变量的影响程度。
五、多元线性回归模型的优缺点多元线性回归模型具有以下优点:1)能够解释各个自变量对因变量的相对影响;2)提供了一种可靠的预测方法;3)可用于控制变量的效果。
然而,多元线性回归模型也存在一些缺点:1)对于非线性关系无法准确预测;2)对异常值和离群点敏感;3)要求满足一定的假设条件。
计量经济学复习笔记(四):多元线性回归⼀元线性回归的解释变量只有⼀个,但是实际的模型往往没有这么简单,影响⼀个变量的因素可能有成百上千个。
我们会希望线性回归模型中能够考虑到这些所有的因素,⾃然就不能再⽤⼀元线性回归,⽽应该将其升级为多元线性回归。
但是,有了⼀元线性回归的基础,讨论多元线性回归可以说是轻⽽易举。
另外我们没必要分别讨论⼆元、三元等具体个数变量的回归问题,因为在线性代数的帮助下,我们能够统⼀讨论对任何解释变量个数的回归问题。
1、多元线性回归模型的系数求解多元线性回归模型是⽤k 个解释变量X 1,⋯,X k 对被解释变量Y 进⾏线性拟合的模型,每⼀个解释变量X i 之前有⼀个回归系数βi ,同时还应具有常数项β0,可以视为与常数X 0=1相乘,所以多元线性回归模型为Y =β0X 0+β1X 1+β2X 2+⋯+βk X k +µ,这⾥的µ依然是随机误差项。
从线性回归模型中抽取n 个样本构成n 个观测,排列起来就是Y 1=β0X 10+β1X 11+β2X 12+⋯+βk X 1k +µ1,Y 2=β0X 20+β1X 21+β2X 22+⋯+βk X 2k +µ2,⋮Y n =β0X n 0+β1X n 1+β2X n 2+⋯+βk X nk +µn .其中X 10=X 20=⋯=X n 0=1。
⼤型⽅程组我们会使⽤矩阵表⽰,所以引⼊如下的矩阵记号。
Y =Y 1Y 2⋮Y n,β=β0β1β2⋮βk,µ=µ1µ2⋮µn.X =X 10X 11X 12⋯X 1k X 20X 21X 22⋯X 2k ⋮⋮⋮⋮X n 0X n 1X n 2⋯X nk.在这些矩阵表⽰中注意⼏点:⾸先,Y 和µ在矩阵表⽰式中都是n 维列向量,与样本容量等长,在线性回归模型中Y ,µ是随机变量,⽽在矩阵表⽰中它们是随机向量,尽管我们不在表⽰形式上加以区分,但我们应该根据上下⽂明确它们到底是什么意义;β是k +1维列向量,其长度与Y ,µ没有关系,这是因为β是依赖于变量个数的,并且加上了对应于常数项的系数(截距项)β0;最后,X 是数据矩阵,且第⼀列都是1。