C.(0,-5),(0,5)
D.(0,- 7),(0, 7)
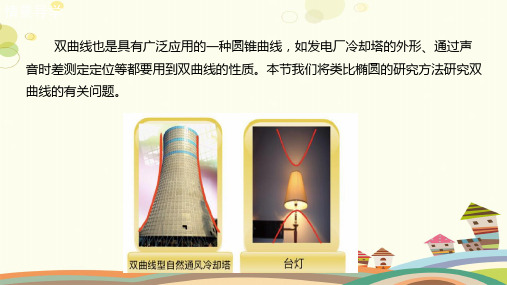
双曲线的定义
2
1.设 F1,F2 分别是双曲线 x2-24=1 的左、右焦点,P 是双曲线上的一点,且 3|PF1|=4|PF2|, 则△PF1F2 的面积等于 ( )
A.4 2
B.8 3
C.24
D.48
2.已知动点 P(x,y)满足 ( + 2)2 + 2- ( -2)2 + 2=2,则动点 P 的轨迹是 ( )
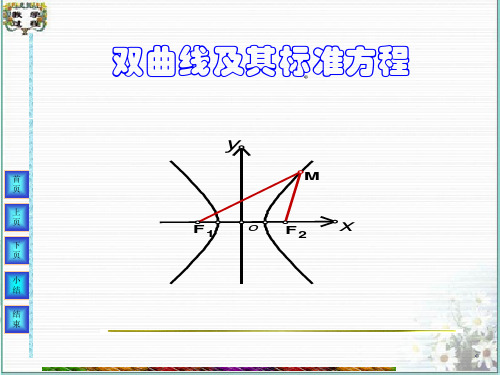
这两个定点叫做双曲线的焦点. 两焦点的距离叫做双曲线的焦距.
y
M
F1 o F2 x
如何理解绝对值?若去掉绝对值则图像有何变化?
03 双曲线的标准方程
1. 建系:如图建立直角坐标系xOy,使x轴经 过点F1,F2,并且点O与线段F1F2中点重合.
y M
F1 O F2
x
2.设点:设M(x , y),双曲线的焦距为2c(c>0),F1(-c,0),F2(c,0) 常数=2a
利用定义求轨迹方程
P P127 习题3.2 第5题
如图,圆O的半径为定长 ,A是圆O外一定点,P是圆上任
意一点,线段AP的垂直平分线l和直线OP相交于点Q,当
O
点P在圆O上运动时,点Q的轨迹是什么?为什么?
A Q
P115 习题3.1 第6题 如图,圆O的半径为定长 ,A是圆O内一定点,P是圆上 任意一点,线段AP的垂直平分线l和半径OP相交于点 Q,当点P在圆O上运动时,点Q的轨迹是什么?为什么?
A.椭圆 C.双曲线的左支
B.双曲线 D.双曲线的右支
双曲线的定义
22
【变式练习】
已知
P
是双曲线