2020年度最新中考~数学分类汇编---相似(超经典)
- 格式:doc
- 大小:1.41 MB
- 文档页数:72


2020相似三角形中考试卷分类汇编篇一:2020初三(九年级)数学相似三角形练习题及答案初三(九年级)数学相似三角形练习题一、填空题: 1、若a?3m,m?2b,则a:b?_____。
2、已知xyz??,且3y?2z?6,则x?____,y?______。
356 _____3、在等腰Rt△ABC中,斜边长为c,斜边上的中线长为m,则m:c?_。
4、反向延长线段AB至C,使AC=1AB,那么BC:AB= ____。
2 5、如果△ABC∽△A′B′C′,相似比为3:2,若它们的周长的差为40厘米,则△A′B′C′的周长为厘米。
6、如图,△AED∽△ABC,其中∠1=∠B,则 ?___???___?。
AD?___BCAB B第6题图第7题图 7、如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=____。
若BC=6,AB=10,则BD= ____,CD= ____。
8、如图,梯形ABCD中,DC∥AB,DC=2cm,AB=3.5cm,且MN∥PQ∥AB, DM=MP=PA,则MN=____,PQ A 第8题图第9题图 9、如图,四边形ADEF为菱形,且AB=14厘米,BC=12厘米,AC=10厘米,那BE=厘米。
10、梯形的上底长1.2厘米,下底长1.8厘米,高1厘米,延长两腰后与下底所成的三角形的高为厘米。
二、选择题: 11、下面四组线段中,不能成比例的是()A、a?3,b?6,c?2,d?4B、a?1,b?,c?,d?C、a?4,b?6,c?5,d?10D、a?2,b?5,c?,d?23 12、等边三角形的中线与中位线长的比值是() 1A、3:1 B、3:2 C、: D、1:3 22 13、已知xyz??,则下列等式成立的是() 457 A、x?y?z7x?y1x?y?z8?? B、? C、z16x?y9x?y?z3 D、y?z?3x ?a?0,b?0?,14、已知直角三角形三边分别为a,a?b,a?2b,则a:b?() A、1:3 B、1:4 C、2:1 D、3:1 15、△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,则最短的一边是()篇二:2020年中考数学试卷分类汇编解析:图形的相似与位似图形的相似与位似一、选择题 1.(2020·湖北十堰)如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为() A.1:3 B.1:4 C.1:5 D.1:9 【考点】位似变换.【分析】先求出位似比,根据位似比等于相似比,再由相似三角形的面积比等于相似比的平方即可.【解答】解:∵OB=3OB′,∴,∵以点O为位似中心,将△ABC缩小后得到△A′B′C′,∴△A′B′C′∽△ABC,∴=.∴ 故选D =,【点评】此题是位似变换,主要考查了位似比等于相似比,相似三角形的面积比等于相似比的平方,解本题的关键是掌握位似的性质. 2.(2020·湖北咸宁)如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①BC=2;②△DOE △COB=2;③=;④△△ADE=. 其中正确的个数有() A. 1个 B. 2个 C.3个D. 4个(第2题)【考点】三角形中位线定理,相似三角形的判定和性质.【分析】①DE是△ABC的中位线,根据三角形的中位线等于第三边长度的一半可判断;②利用相似三角形面积的比等于相似比的平方可判定;③利用相似三角形的性质可判断;④利用相似三角面积的比等于相似比的平方可判定.【解答】解:①∵DE是△ABC的中位线,∴DE=2BC,即BC=2;故①正确;②∵DE是△ABC的中位线,∴DE∥BC ∴△DOE∽△COB △DOE∴△COB ③∵DE∥BC =(BC)=(2)=4, 22故②错误;∴△ADE∽△ABC∴= △DOE∽△COB∴OB=BC ∴AB=OB,故③正确;④∵△ABC的中线BE与CD交于点O。

2019-2020 年中考数学试题分类解析汇编专题38相似一、选择题1.(重庆綦江 4 分)若相似△ ABC 与△ DEF的相似比为 1: 3,则△ ABC 与△ DEF的面积比为A、 1:3B、 1: 9C、3:1D、 1: 3【答案】 B。
【考点】相似三角形的性质。
【分析】由相似△ ABC 与△ DEF 的相似比为1: 3,根据相似三角形面积的比等于相似比的平方,即可求得△ABC与△ DEF的面积比为1:9。
故选 B。
2. (重庆江津 4 分)已知如图:( 1)、( 2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中 AB、 CD交于 0 点,对于各图中的两个三角形而言,下列说法正确的是A、都相似C、只有(1)相似B 、都不相似D、只有( 2)相似【答案】 A。
【考点】相似三角形的判定,三角形内角和定理,对顶角的性质。
【分析】图( 1)根据三角形的内角和定理,即可求得△ABC的第三角,由有两角对应相等的三角形相似,即可判定( 1)中的两个三角形相似;图(2)根据图形中的已知条件,即可证得OA OC,又由对顶角OD OB 相等,即可根据对应边成比例且夹角相等的三角形相似证得相似。
故选A。
3.(重庆潼南 4 分)若△ ABC∽△ DEF,它们的面积比为4: 1,则△ ABC与△ DEF 的相似比为A、 2: 1B、 1: 2C 、 4:1 D、 1: 4【答案】 A。
【考点】相似三角形的性质。
【分析】 由△ ABC ∽△ DEF 与它们的面积比为 4: 1,根据相似三角形面积的比等于相似比的平方,即可求得△ ABC 与△ DEF 的相似比为 2: 1。
故选 A 。
4. (浙江台州4 分) 若两个相似三角形的面积之比为1∶4,则它们的周长之比为A .1∶2B.1∶4C.1∶5D.1∶16【答案】A 。
【考点】 相似三角形的性质。
【分析】 根据相似三角形的面积比等于相似比的平方,即可求得其相似比为1∶2,又由相似三角形的周长的比等于相似比,即可求得它们的周长之比为1∶2。


2020年中考数学试题分类汇编之10相似三角形一、选择题1.(2020成都)(3分)如图,直线123////l l l ,直线AC 和DF 被1l ,2l ,3l 所截,5AB =,6BC =,4EF =,则DE 的长为( )A .2B .3C .4D .1032.(2020哈尔滨)(3分)如图,在ABC ∆中,点D 在BC 边上,连接AD ,点E 在AC 边上,过点E 作//EF BC ,交AD 于点F ,过点E 作//EG AB ,交BC 于点G ,则下列式子一定正确的是( )A .AE EFEC CD= B .EF EGCD AB= C .AF BGFD GC= D .CG AFBC AD= 3.(2020河北)在如图所示的网格中,以点O 为位似中心,四边形ABCD 的位似图形是( )A. 四边形NPMQB. 四边形NPMRC. 四边形NHMQD. 四边形NHMR4.(2020四川绵阳)如图,在四边形ABCD 中,AD ∥BC ,∠ABC =90°,AB =2,AD=2,将△ABC 绕点C 顺时针方向旋转后得△A ′B ′C ,当A ′B ′恰好经过点D 时,△B ′CD 为等腰三角形,若BB ′=2,则AA ′=( )A .B .2C .D .5.(2020无锡)如图,等边ABC ∆的边长为3,点D 在边AC 上,12AD =,线段PQ 在边BA 上运动,12PQ =,有下列结论:①CP 与QD 可能相等;②ΔAQD 与BCP ∆可能相似;③四边形PCDQ 面积的最大值为;④四边形PCDQ 周长的最小值为3+.其中,正确结论的序号为( )A. ①④B. ②④C. ①③D. ②③6.(2020重庆A 卷)如图,在平面直角坐标系中,ABC 的顶点坐标分别是(1,2)A ,(1,1)B ,(3,1)C ,以原点为位似中心,在原点的同侧画DEF ,使DEF 与ABC 成位似图形,且相似比为2:1,则线段DF 的长度为( )B. 2C. 4D.7.(2020重庆B 卷)如图,△ABC 与△DEF 位似,点O 为位似中心.已知OA ∶OD=1∶2, 则△ABC 与△DEF 的面积比为( ) A. 1∶2 B. 1∶3 C. 1∶4 D.1∶58.(2020甘肃定西)生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a 与全身b 的高度比值接近0.618,可以增加视觉美感.若图中b 为2米,则a 约为( )A.1.24米B.1.38米C.1.42米D.1.62米9.(2020四川遂宁)(4分)如图,在平行四边形ABCD 中,∠ABC 的平分线交AC 于点E ,交AD 于点F ,交CD 的延长线于点G ,若AF =2FD ,则BE EG的值为( )A .12B .13C .23D .3410.(2020广西南宁)(3分)如图,在△ABC 中,BC =120,高AD =60,正方形EFGH 一边在BC 上,点E ,F 分别在AB ,AC 上,AD 交EF 于点N ,则AN 的长为( )A .15B .20C .25D .3011.(2020广西玉林)(3分)(2020•玉林)一个三角形木架三边长分别是75cm ,100cm ,120cm ,现要再做一个与其相似的三角形木架,而只有长为60cm 和120cm 的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( ) A .一种B .两种C .三种D .四种12.(2020贵州遵义)(4分)如图,△ABO 的顶点A 在函数y =k x(x >0)的图象上,∠ABO =90°,过AO 边的三等分点M 、N 分别作x 轴的平行线交AB 于点P 、Q .若四边形MNQP 的面积为3,则k 的值为( )A .9B .12C .15D .1813.(3分)(2020•荆门)△ABC 中,AB =AC ,∠BAC =120°,BC =2√3,D 为BC 的中点,AE =14AB ,则△EBD 的面积为( )A .3√34B .3√38C .√34D .√3814.(2020山西)(3分)泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度,金字塔的影长,推算出金字塔的高度,这种测量原理,就是我们所学的( )A .图形的平移B .图形的旋转C .图形的轴对称D .图形的相似15.(2020浙江温州)(4分)如图,在Rt △ABC 中,∠ACB =90°,以其三边为边向外作正方形,过点C 作CR ⊥FG 于点R ,再过点C 作PQ ⊥CR 分别交边DE ,BH 于点P ,Q .若QH =2PE ,PQ =15,则CR 的长为( )A .14B .15C .8√3D .6√516.(2020海南)(3分)如图,在矩形ABCD 中,AB =6,BC =10,点E 、F 在AD 边上,BF 和CE 交于点G ,若EF =AD ,则图中阴影部分的面积为( )A .25B .30C .35D .40二、填空题17.(2020广州)如图7,正方形ABCD 中,△ABC 绕点A 逆时针旋转到△AB C '',AB ',AC '分别交对角线BD 于点E ,F ,若4AE =,则EF ED ⋅的值为 * .图7FB'E C'DCBA18.(2020河南)如图,在边长为的正方形ABCD 中,点,E F 分别是边,AB BC 的中点,连接,,EC FD 点,G H 分别是,EC FD 的中点,连接GH ,则GH 的长度为__________.19.(2020苏州).如图,在平面直角坐标系中,点A 、B 的坐标分别为()4,0-、()0,4,点()3,C n 在第一象限内,连接AC 、BC .已知2BCA CAO ∠=∠,则n =_________.20.(2020乐山)把两个含30角的直角三角板按如图所示拼接在一起,点E 为AD 的中点,连结BE 交AC 于点F .则AFAC=_________.21.(2020无锡)如图,在Rt ABC ∆中,90ACB ∠=︒,4AB =,点D ,E 分别在边AB ,AC 上,且2DB AD =,3AE EC =连接BE ,CD ,相交于点O ,则ABO ∆面积最大值为__________.22.(2020上海)(4分)《九章算术》中记载了一种测量井深的方法.如图所示,在井口B 处立一根垂直于井口的木杆BD ,从木杆的顶端D 观察井水水岸C ,视线DC 与井口的直径AB 交于点E ,如果测得AB =1.6米,BD =1米,BE =0.2米,那么井深AC 为 7 米.23.(2020吉林)(3分)如图,AB ∥CD ∥EF .若=,BD =5,则DF = 10 .24.(2020吉林)(3分)如图,在△ABC 中,D ,E 分别是边AB ,AC 的中点.若△ADE的面积为,则四边形DBCE 的面积为.25.(2020黑龙江牡丹江)(3分)如图,在Rt ABC ∆中,90C ∠=︒,点E 在AC 边上.将A ∠沿直线BE 翻折,点A 落在点A '处,连接A B ',交AC 于点F .若A E AE '⊥,4cos 5A =,则A F BF '= 13.26.(2020黑龙江牡丹江)(3分)如图,在Rt ABC ∆中,CA CB =,M 是AB 的中点,点D 在BM 上,AE CD ⊥,BF CD ⊥,垂足分别为E ,F ,连接EM .则下列结论中:①BF CE =; ②AEM DEM ∠=∠;③AE CE -=; ④2222DE DF DM +=;⑤若AE 平分BAC ∠,则:EF BF ; ⑥CF DM BM DE =,正确的有 ①②③④⑤⑥ .(只填序号)27.(2020山西)(3分)如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =4,CD ⊥AB ,垂足为D ,E 为BC 的中点,AE 与CD 交于点F ,则DF 的长为.解:如图,过点F 作FH ⊥AC 于H .28.(2020四川眉山)(4分)如图,等腰△ABC 中,AB =AC =10,边AC 的垂直平分线交BC 于点D ,交AC 于点E .若△ABD 的周长为26,则DE 的长为.29.(2020浙江温州)(5分)如图,在河对岸有一矩形场地ABCD ,为了估测场地大小,在笔直的河岸l 上依次取点E ,F ,N ,使AE ⊥l ,BF ⊥l ,点N ,A ,B 在同一直线上.在F 点观测A 点后,沿FN 方向走到M 点,观测C 点发现∠1=∠2.测得EF =15米,FM =2米,MN =8米,∠ANE =45°,则场地的边AB 为 15√2 米,BC 为 20√2 米.三、解答题30.(2020杭州)(8分)如图,在△ABC 中,点D ,E ,F 分别在AB ,BC ,AC 边上,DE ∥AC ,EF ∥AB .(1)求证:△BDE ∽△EFC . (2)设AF FC=12,①若BC =12,求线段BE 的长;②若△EFC 的面积是20,求△ABC 的面积.31.(2020安徽)(14分)如图1,已知四边形ABCD是矩形,点E在BA的延长线上,=.EC与BD相交于点G,与AD相交于点F,AF ABAE AD=.⊥;(1)求证:BD EC(2)若1AB=,求AE的长;(3)如图2,连接AG,求证:EG DG-=.32.(2020成都)(4分)如图,在矩形ABCD中,4BC=,E,F分别为AB,AB=,3CD边的中点.动点P从点E出发沿EA向点A运动,同时,动点Q从点F出发沿FC向点C⊥于点H,连接DH.若点P的速度是点Q的速度的2运动,连接PQ,过点B作BH PQ倍,在点P从点E运动至点A的过程中,线段PQ长度的最大值为线段DH长度的最小值为.33.(2020福建)如图,C 为线段AB 外一点.(1)求作四边形ABCD ,使得//CD AB ,且2CD AB =;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的四边形ABCD 中,AC ,BD 相交于点P ,AB ,CD 的中点分别为,M N ,求证:,,M P N 三点在同一条直线上.34.(2020河北)如图1和图2,在ABC ∆中,AB AC =,8BC =,3tan 4C =.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且2AM CN ==.点P 从点M 出发沿折线MB BN -匀速移动,到达点N 时停止;而点Q 在AC 边上随P 移动,且始终保持APQ B ∠=∠.(1)当点P 在BC 上时,求点P 与点A 的最短距离;(2)若点P 在MB 上,且PQ 将ABC ∆面积分成上下4:5两部分时,求MP 的长; (3)设点P 移动的路程为x ,当03x ≤≤及39x ≤≤时,分别求点P 到直线AC 的距离(用含x 的式子表示);(4)在点P 处设计并安装一扫描器,按定角APQ ∠扫描APQ ∆区域(含边界),扫描器随点P 从M 到B 再到N 共用时36秒.若94AK =,请直接..写出点K 被扫描到的总时长.35.(2020江西) 某数学课外活动小组在学习了勾股定理之后,针对图1中所示的“由直角三角形三边向外侧作多边形,它们的面积1S ,2S ,3S 之间的关系问题”进行了以下探究:类比探究(1)如图2,在Rt ABC ∆中,BC 为斜边,分别以,,AB AC BC 为斜边向外侧作Rt ABD ∆,Rt ACE ∆,Rt BCF ∆,若123∠=∠=∠,则面积1S ,2S ,3S 之间的关系式为 ;推广验证(2)如图3,在Rt ABC ∆中,BC 为斜边,分别以,,AB AC BC 为边向外侧作任意ABD ∆,ACE ∆,BCF ∆,满足123∠=∠=∠,D E F ∠=∠=∠,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;拓展应用(3)如图4,在五边形ABCDE 中,105A E C ∠=∠=∠=,90ABC ∠=,AB =2DE =,点P 在AE 上,30ABP ∠=,PE =,求五边形ABCDE 的面积.36.(2020苏州).如图,在矩形ABCD 中,E 是BC 的中点,DF AE ⊥,垂足为F .(1)求证:ABE DFA ∆∆∽;(2)若6AB =,4BC =,求DF 的长.37.(2020南京)(9分)如图,在ABC ∆和△A B C '''中,D 、D '分别是AB 、A B ''上一点,AD A D AB A B ''=''.(1)当CD AC AB C D A C A B ==''''''时,求证ABC ∆∽△A B C ''. 证明的途径可以用下面的框图表示,请填写其中的空格.(2)当CD AC BC C D A C B C ==''''''时,判断ABC ∆与△A B C '''是否相似,并说明理由.38(2020湖北武汉).问题背景:如图(1),已知A ABC DE ∽△△,求证:ABD ACE ∽; 尝试应用:如图(2),在ABC 和ADE 中,90BAC DAE ︒∠=∠=,30ABC ADE ︒∠=∠=,AC 与DE 相交于点F .点D 在BC 边上,AD BD =求DF CF的值;拓展创新:如图(3),D 是ABC 内一点,30BAD CBD ︒∠=∠=,90BDC ︒∠=,4AB =,AC =AD 的长.39.(2020宁夏)(6分)在平面直角坐标系中,△ABC 的三个顶点的坐标分别是A (1,3),B (4,1),C (1,1).(1)画出△ABC 关于x 轴成轴对称的△A 1B 1C 1;(2)画出△ABC 以点O 为位似中心,位似比为1:2的△A 2B 2C 2.40.(2020四川眉山)(10分)如图,△ABC和△CDE都是等边三角形,点B、C、E三点在同一直线上,连接BD,AD,BD交AC于点F.(1)若AD2=DF•DB,求证:AD=BF;(2)若∠BAD=90°,BE=6.①求tan∠DBE的值;②求DF的长.41.(2020山东泰安)(12分)小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形,∠ACB与∠ECD恰好为对顶角,∠ABC=∠CDE=90°,连接BD,AB=BD,点F是线段CE上一点.探究发现:(1)当点F为线段CE的中点时,连接DF(如图(2)),小明经过探究,得到结论:BD⊥DF.你认为此结论是否成立?是.(填“是”或“否”)拓展延伸:(2)将(1)中的条件与结论互换,即:BD⊥DF,则点F为线段CE的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.问题解决:(3)若AB=6,CE=9,求AD的长.42.(2020浙江宁波)(12分)【基础巩固】(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD•AB.【尝试应用】(2)如图2,在▱ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.【拓展提高】(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,∠EDF=12∠BAD,AE=2,DF=5,求菱形ABCD的边长.43.(2020浙江温州)(14分)如图,在四边形ABCD中,∠A=∠C=90°,DE,BF分别平分∠ADC,∠ABC,并交线段AB,CD于点E,F(点E,B不重合).在线段BF 上取点M,N(点M在BN之间),使BM=2FN.当点P从点D匀速运动到点E时,点Q恰好从点M匀速运动到点N.记QN=x,PD=y,已知y=−65x+12,当Q为BF中点时,y=24 5.(1)判断DE与BF的位置关系,并说明理由.(2)求DE,BF的长.(3)若AD=6.①当DP =DF 时,通过计算比较BE 与BQ 的大小关系.②连结PQ ,当PQ 所在直线经过四边形ABCD 的一个顶点时,求所有满足条件的x 的值.2020年中考数学试题分类汇编之10相似三角形四、选择题1.(2020成都)(3分)如图,直线123////l l l ,直线AC 和DF 被1l ,2l ,3l 所截,5AB =,6BC =,4EF =,则DE 的长为( )A .2B .3C .4D .103 解:直线123////l l l ,∴AB DE BC EF=, 5AB =,6BC =,4EF =,∴564DE =, 103DE ∴=, 选:D .2.(2020哈尔滨)(3分)如图,在中,点在边上,连接,点在边上,过点作,交于点,过点作,交于点,则下列式子一定正确的是ABC ∆D BC AD E AC E //EF BC AD F E //EG AB BC G ()A. B . C . D . 解:,, ,, , 故选:.3.(2020河北)在如图所示的网格中,以点O 为位似中心,四边形ABCD 的位似图形是( )A. 四边形NPMQB. 四边形NPMRC. 四边形NHMQD. 四边形NHMR解:如图所示,四边形ABCD 的位似图形是四边形NPMQ .故选:A4.(2020四川绵阳)如图,在四边形ABCD 中,AD ∥BC ,∠ABC =90°,AB =2,AD =2,将△ABC 绕点C 顺时针方向旋转后得△A ′B ′C ,当A ′B ′恰好经过点D 时,△B ′CD 为等腰三角形,若BB ′=2,则AA ′=( )AE EF EC CD =EF EG CD AB =AF BG FD GC =CG AF BC AD =//EF BC ∴AF AE FD EC =//EG AB ∴AE BG EC GC =∴AF BG FD GC=CA.B.2C.D.解:过D作DE⊥BC于E,则∠DEC=∠DEB=90°,∵AD∥BC,∠ABC=90°,∴∠DAB=∠ABC=90°,∴四边形ABED是矩形,∴BE=AD=2,DE=AB=2,∵将△ABC绕点C顺时针方向旋转后得△A′B′C,∴∠DB′C=∠ABC=90°,B′C=BC,A′C=AC,∠A′CA=∠B′CB,∴△A′CA∽△B′CB,∴=,∵△B′CD为等腰三角形,∴△B′CD为等腰直角三角形,∴CD=B′C,设B′C=BC=x,则CD=x,CE=x﹣2,∵CD2=CE2+DE2,∴(x)2=(x﹣2)2+(2)2,∴x=4(负值舍去),∴BC=4,∴AC==2,∴=,∴A′A=,故选:A.5.(2020无锡)如图,等边ABC ∆的边长为3,点D 在边AC 上,12AD =,线段PQ 在边BA 上运动,12PQ =,有下列结论:①CP 与QD 可能相等;②ΔAQD 与BCP ∆可能相似;③四边形PCDQ面积的最大值为16;④四边形PCDQ周长的最小值为32+.其中,正确结论的序号为( ) A. ①④ B. ②④ C. ①③ D. ②③ 解:①∵线段PQ 在边BA 上运动,12PQ =, ∴QD P AP C ≤<,∴CP 与QD 不可能相等,则①错误;②设AQ x =, ∵12PQ =,3AB =, ∴13-=2.52AQ ≤≤0,即 2.5x ≤≤0, 假设ΔAQD 与BCP ∆相似,∵∠A=∠B=60°, ∴AD AQ BP BC =,即121332x x =--, 从而得到22530x x -+=,解得1x =或 1.5x =(经检验是原方程的根),又 2.5x ≤≤0,∴解得的1x =或 1.5x =符合题意,即ΔAQD 与BCP ∆可能相似,则②正确;③如图,过P 作PE ⊥BC 于E ,过F 作DF ⊥AB 于F ,设AQ x =, 由12PQ =,3AB =,得13-=2.52AQ ≤≤0,即 2.5x ≤≤0, ∴132PB x =--,∵∠B=60°,∴132P x E --=⎫⎪⎝⎭,∵12AD =,∠A =60°,∴1224DF =⨯=,则1115332222PBCSBC PE x x ⎫⎫=⨯=⨯--=-⎪⎪⎝⎭⎝⎭,1122DAQSAQ DF x x =⨯=⨯=, ∴四边形PCDQ 面积为:15322ABC PBC DAQSS Sx x x ⎫--=⨯-=⎪⎝⎭, 又∵ 2.5x ≤≤0,∴当 2.5x =时,四边形PCDQ ,即四边形PCDQ , 则③正确;④如图,作点D 关于直线AB 的对称点D 1,连接D D 1,与AB 相交于点Q ,再将D 1Q 沿着AB 向B 端平移PQ 个单位长度,即平移12个单位长度,得到D 2P ,与AB 相交于点P ,连接PC ,∴D 1Q=DQ=D 2P ,11212AD D D AD ===,且∠AD 1D 2=120°,此时四边形PCDQ 的周长为:2CP DQ CD PQ CD CD PQ +++=++,其值最小,∴∠D 1AD 2=30°,∠D 2A D=90°,22AD =,∴根据股股定理可得,22CD =,∴四边形PCDQ 的周长为:2113322CP DQ CD PQ CD CD PQ ⎛⎫+++=++=-+= ⎪⎝⎭则④错误,所以可得②③正确,故选:D .6.(2020重庆A 卷)如图,在平面直角坐标系中,ABC 的顶点坐标分别是(1,2)A ,(1,1)B ,(3,1)C ,以原点为位似中心,在原点的同侧画DEF ,使DEF 与ABC 成位似图形,且相似比为2:1,则线段DF 的长度为( )B. 2C. 4D. 解:∵以原点为位似中心,在原点的同侧画△DEF ,使△DEF 与△ABC 成位似图形,且相似比为2:1,而A (1,2),C (3,1), ∴D (2,4),F (6,2),OFE DCBA∴DF故选:D .7.(2020重庆B 卷)如图,△ABC 与△DEF 位似,点O 为位似中心.已知OA ∶OD=1∶2,则△ABC 与△DEF 的面积比为( ) A. 1∶2 B. 1∶3 C. 1∶4 D.1∶5 .答案C.8.(2020甘肃定西)生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下与全身的高度比值接近0.618,可以增加视觉美感.若图中为2米,则约为( )A.1.24米B.1.38米C.1.42米D.1.62米答案:A9.(2020四川遂宁)(4分)如图,在平行四边形ABCD 中,∠ABC 的平分线交AC 于点E ,交AD 于点F ,交CD 的延长线于点G ,若AF =2FD ,则BE EG的值为( )A .12B .13C .23D .34解:由AF =2DF ,可以假设DF =k ,则AF =2k ,AD =3k , ∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB ∥CD ,AB =CD , ∴∠AFB =∠FBC =∠DFG ,∠ABF =∠G , ∵BE 平分∠ABC ,∴∠ABF =∠CBG , ∴∠ABF =∠AFB =∠DFG=∠G ,a b b a∴AB =CD =2k ,DF =DG =k ,∴CG =CD +DG =3k , ∵AB ∥DG ,∴△ABE ∽△CGE , ∴BE EG=AB CG=2k 3k=23,故选:C .10.(2020广西南宁)(3分)如图,在△ABC 中,BC =120,高AD =60,正方形EFGH 一边在BC 上,点E ,F 分别在AB ,AC 上,AD 交EF 于点N ,则AN 的长为( )A .15B .20C .25D .30解:设正方形EFGH 的边长EF =EH =x ,∵四边EFGH 是正方形,∴∠HEF =∠EHG =90°,EF ∥BC , ∴△AEF ∽△ABC ,∵AD 是△ABC 的高,∴∠HDN =90°, ∴四边形EHDN 是矩形,∴DN =EH =x , ∵△AEF ∽△ABC ,∴=(相似三角形对应边上的高的比等于相似比),∵BC =120,AD =60,∴AN =60﹣x , ∴=,解得:x =40,∴AN =60﹣x =60﹣40=20. 故选:B .11.(2020广西玉林)(3分)(2020•玉林)一个三角形木架三边长分别是75cm ,100cm ,120cm ,现要再做一个与其相似的三角形木架,而只有长为60cm 和120cm 的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( ) A .一种B .两种C .三种D .四种解:长120cm 的木条与三角形木架的最长边相等,则长120cm 的木条不能作为一边, 设从120cm 的木条上截下两段长分别为xcm ,ycm (x +y ≤120), 由于长60cm 的木条不能与75cm 的一边对应,否则x 、y 有大于120cm ,当长60cm的木条与100cm的一边对应,则x75=y120=60100,解得:x=45,y=72;当长60cm的木条与120cm的一边对应,则x75=y100=60120,解得:x=37.5,y=50.答:有两种不同的截法:把120cm的木条截成45cm、72cm两段或把120cm的木条截成37.5cm、50cm两段.故选:B.12.(2020贵州遵义)(4分)如图,△ABO的顶点A在函数y=k x(x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若四边形MNQP的面积为3,则k的值为()A.9B.12C.15D.18解:∵NQ∥MP∥OB,∴△ANQ∽△AMP∽△AOB,∵M、N是OA的三等分点,∴ANAM =12,ANAO=13,∴S△ANQS△AMP =14,∵四边形MNQP的面积为3,∴S△ANQ3+S△ANQ =14,∴S△ANQ=1,∵1S△AOB =(ANAO)2=19,∴S△AOB=9,∴k=2S△AOB=18,故选:D.13.(3分)(2020•荆门)△ABC中,AB=AC,∠BAC=120°,BC=2√3,D为BC的中点,AE=14AB,则△EBD的面积为()A .3√34B .3√38C .√34D .√38解:连接AD ,作EF ⊥BC 于F ,∵AB =AC ,∠BAC =120°,D 为BC 的中点, ∴AD ⊥BC ,AD 平分∠BAC ,∠B =∠C =30° 在Rt △ABD 中,BD =12BC =√3,∠B =30°,∴AB =BDcos30°=√3√32=2,∴AD =12AB =1,∵AE =14AB ,∴BE AB=34,∵EF ⊥BC ,AD ⊥BC ,∴EF ∥AD , ∴△BEF ∽△BAD ,∴EF AD=BE AB,∴EF 1=34∴EF =34, ∴S △BDE =12×BD ×EF =12×√3×34=3√38,选:B .14.(2020山西)(3分)泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度,金字塔的影长,推算出金字塔的高度,这种测量原理,就是我们所学的( )A .图形的平移B .图形的旋转C .图形的轴对称D .图形的相似选:D .15.(2020浙江温州)(4分)如图,在Rt △ABC 中,∠ACB =90°,以其三边为边向外作正方形,过点C 作CR ⊥FG 于点R ,再过点C 作PQ ⊥CR 分别交边DE ,BH 于点P ,Q .若QH =2PE ,PQ =15,则CR 的长为( )A .14B .15C .8√3D .6√5解:如图,连接EC ,CH .设AB 交CR 于J .∵四边形ACDE ,四边形BCJHD 都是正方形, ∴∠ACE =∠BCH =45°, ∵∠ACB =90°,∠BCI =90°,∴∠ACE +∠ACB +∠BCH =180°,∠ACB +∠BCI =90° ∴B ,C ,H 共线,A ,C ,I 共线, ∵DE ∥AI ∥BH ,∴∠CEP =∠CHQ , ∵∠ECP =∠QCH ,∴△ECP ∽△HCQ , ∴PC CQ=CE CH=EP HQ=12,∵PQ =15,∴PC =5,CQ =10, ∵EC :CH =1:2,∴AC :BC =1:2,设AC =a ,BC =2a , ∵PQ ⊥CRCR ⊥AB ,∴CQ ∥AB , ∵AC ∥BQ ,CQ ∥AB ,∴四边形ABQC 是平行四边形,∴AB =CQ =10, ∵AC 2+BC 2=AB 2,∴5a 2=100, ∴a =2√2(负根已经舍弃), ∴AC =2√5,BC =4√5,∵12•AC •BC =12•AB •CJ , ∴CJ =2√5×4√510=4,∵JR =AF =AB =10,∴CR =CJ +JR =14, 故选:A .16.(2020海南)(3分)如图,在矩形ABCD 中,AB =6,BC =10,点E 、F 在AD 边上,BF 和CE 交于点G ,若EF =AD ,则图中阴影部分的面积为( )A .25B .30C .35D .40解:过点G 作GN ⊥AD 于N ,延长NG 交BC 于M , ∵四边形ABCD 是矩形, ∴AD =BC ,AD ∥BC , ∵EF =AD ,∴EF =BC , ∵AD ∥BC ,NG ⊥AD , ∴△EFG ∽△CBG ,GM ⊥BC , ∴GN :GM =EF :BC =1:2, 又∵MN =BC =6, ∴GN =2,GM =4, ∴S △BCG =×10×4=20,∴S △EFG =×5×2=5,S 矩形ABCD =6×10=60, ∴S 阴影=60﹣20﹣5=35. 故选:C .五、填空题17.(2020广州)如图7,正方形ABCD 中,△ABC 绕点A 逆时针旋转到△AB C '',AB ',AC '分别交对角线BD 于点E ,F ,若4AE =,则EF ED ⋅的值为 * .【答案】16. 提示:由△EAF ∽△EDA,得到:EF EAEA ED=,所以:2EA EF ED =,∴EF ED ⋅=1618.(2020河南)如图,在边长为的正方形ABCD 中,点,E F 分别是边,AB BC 的中点,连接,,EC FD 点,G H 分别是,EC FD 的中点,连接GH ,则GH 的长度为__________.【答案】1【详解】过E 作EP DC ⊥,过G 作GQ DC ⊥,过H 作HR BC ⊥,垂足分别为P ,R ,R ,HR 与GQ 相交于I ,如图,∵四边形ABCD 是正方形,∴AB AD DC BC ====图7FB'E C'DCBA90A ADC ∴∠=∠=︒,∴四边形AEPD 是矩形,∴EP AD == ∵点E ,F 分别是AB ,BC 边的中点,∴12PC DC ==12FC BC == EP DC ⊥,GQ DC ⊥,GQ EP ∴//∵点G 是EC 的中点,GQ ∴是EPC ∆的中位线,12GQ EP ∴==,同理可求:HR =,由作图可知四边形HIQP 是矩形, 又HP=12FC ,HI=12HR=12PC , 而FC=PC , ∴ HI HP =,∴四边形HIQP 是正方形,∴2IQ HP ==,∴22GI GQ IQ HI =-=== HIG ∴∆是等腰直角三角形,1GH ∴==故答案为:1.19.(2020苏州).如图,在平面直角坐标系中,点A 、B 的坐标分别为()4,0-、()0,4,点()3,C n 在第一象限内,连接AC 、BC .已知2BCA CAO ∠=∠,则n =_________.【答案】14 5解:如图,过点C作CD⊥y轴,交y轴于点D,则CD∥AO,∴∠DCE=∠CAO,∵∠BCA=2∠CAO,∴∠BCA=2∠DCE,∴∠DCE=∠DCB,∵CD⊥y轴,∴∠CDE=∠CDB=90°,又∵CD=CD,∴△CDE≌△CDB(ASA),∴DE=DB,∵B(0,4),C(3,n),∴CD=3,OD=n,OB=4,∴DE=DB=OB-OD=4-n,∴OE=OD-DE=n-(4-n)=2n-4,∵A(-4,0),∴AO=4,∵CD∥AO,∴AOE∽CDE,∴AO OECD DE=,∴424 34nn-=-,解得:145n=,故答案:145.20.(2020乐山)把两个含30角的直角三角板按如图所示拼接在一起,点E为AD的中点,连结BE 交AC 于点F .则AF AC=_________.解:连接CE ,设CD=2x ,在RtΔACD 和RtΔABC 中,∠BAC=∠CAD=30º,∴∠D=60º,AD=4x ,=, BC=12AC,3=x , ∵点E 为AD 的中点, ∴CE=AE=DE=12AD =2x , ∴ΔCED 为等边三角形,∴∠CED=60º,∵∠BAD=∠BAE+∠CAD=30º+30º=60º,∴∠CED=∠BAD ,∴AB ∥CE ,∴AF BF CF EF=, 在ΔBAE 中,∵∠BAE=∠CAD=30º ∴AF 平分∠BAE ,∴3322AB BF x AE EF x ===, ∴32AF BF CF EF ==, ∴35AF AC =, 故答案为:35.21.(2020无锡)如图,在中,,,点,分别在边,上,且,连接,,相交于点,则面积最大值Rt ABC ∆90ACB ∠=︒4AB =D E AB AC 2DB AD =3AE EC =BE CD O ABO ∆为__________.解:如图1,作DG ∥AC ,交BE 于点G ,∴,∵ , ∴ ∵ ∴∴ ∵AB=4 ∴ ∴若面积最大,则面积最大, 如图2,当点△ABC 为等腰直角三角形时,面积最大,为,∴ 面积最大值为+故答案为:22.(2020上海)(4分)《九章算术》中记载了一种测量井深的方法.如图所示,在井口,BDG BAE ODG OCE △∽△△∽△2,3DG BD AE AB ==∴13CE AE =221DG CE ==ODG OCE △∽△=2DG OD CE OC =23OD CD =23ABO ABC S S =△△ABO ABC ABC 142=42⨯⨯ABO 284=33⨯83B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为7米.解:∵BD⊥AB,AC⊥AB,∴BD∥AC,∴△ACE∽△DBE,∴ACBD =AEBE,∴AC1=1.40.2,∴AC=7(米),答:井深AC为7米.23.(2020吉林)(3分)如图,AB∥CD∥EF.若=,BD=5,则DF=10.解:∵AB∥CD∥EF,∴==,∴DF=2BD=2×5=10.故答案为10.24.(2020吉林)(3分)如图,在△ABC中,D,E分别是边AB,AC的中点.若△ADE 的面积为,则四边形DBCE的面积为.解:∵D,E分别是△ABC的边AB,AC的中点,∴DE是△ABC的中位线,∴DE ∥BC ,DE =BC , ∴△ADE ∽△ABC ,∴=()2=()2=,∵△ADE 的面积为, ∴△ABC 的面积为2,∴四边形DBCE 的面积=2﹣=, 故答案为:.25.(2020黑龙江牡丹江)(3分)如图,在Rt ABC ∆中,90C ∠=︒,点E 在AC 边上.将A ∠沿直线BE 翻折,点A 落在点A '处,连接AB ',交AC 于点F .若A E AE '⊥,4cos 5A =,则A F BF '= 13.【解答】解:90C ∠=︒,4cos 5A =, ∴45AC AB =,设4AC x =,5AB x =,则3BC x =, AE AE ⊥',90AEA ∴∠'=︒,//A E BC ',由于折叠,(36090)2135A EB AEB ∴∠'=∠=-÷=︒,且△A EF BCF '∆∽,45BEC ∴∠=︒,即BCE ∆为等腰直角三角形,3EC x ∴=,AE AC EC x A E ∴=-==', ∴133A E A F x BC BF x ''===, 故答案为:13. 26.(2020黑龙江牡丹江)(3分)如图,在Rt ABC ∆中,CA CB =,M 是AB 的中点,点D 在BM 上,AE CD ⊥,BF CD ⊥,垂足分别为E ,F ,连接EM .则下列结论中: ①BF CE =;②AEM DEM ∠=∠;③AE CE -=;④2222DE DF DM +=;⑤若AE 平分BAC ∠,则:EF BF ;⑥CF DM BM DE =,正确的有 ①②③④⑤⑥ .(只填序号)解:90ACB ∠=︒,90BCF ACE ∴∠+∠=︒,90BCF CBF ∠+∠=︒,ACE CBF ∴∠=∠,又90BFD AEC ∠=︒=∠,AC BC =,()BCF CAE AAS ∴∆≅∆,BF CE ∴=,故①正确;由全等可得:AE CF =,BF CE =,AE CE CF CE EF ∴-===,连接FM ,CM ,点M 是AB 中点,12CM AB BM AM ∴===,CM AB ⊥, 在BDF ∆和CDM ∆中,BFD CMD ∠=∠,BDF CDM ∠=∠,DBF DCM ∴∠=∠,又BM CM =,BF CE =,()BFM CEM SAS ∴∆≅∆,FM EM ∴=,BMF CME ∠=∠,90BMC ∠=︒,90EMF ∴∠=︒,即EMF ∆为等腰直角三角形,EF AE CE ∴=-,故③正确,45MEF MFE ∠=∠=︒,90AEC ∠=︒,45MEF AEM ∴∠=∠=︒,故②正确,设AE 与CM 交于点N ,连接DN ,DMF NME ∠=∠,FM EM =,45DFM DEM AEM ∠=∠=∠=︒,()DFM NEM ASA ∴∆≅∆,DF EN ∴=,DM MN =,DMN ∴∆为等腰直角三角形,2DN DM∴=,而90DEA∠=︒,22222DE DF DN DM∴+==,故④正确;AC BC=,90ACB∠=︒,45CAB∴∠=︒,AE平分BAC∠,22.5DAE CAE∴∠=∠=︒,67.5ADE∠=︒,45DEM∠=︒,67.5EMD∴∠=︒,即DE EM=,AE AE=,AED AEC∠=∠,DAE CAE∠=∠,()ADE ACE ASA∴∆≅∆,DE CE∴=,MEF∆为等腰直角三角形,2EF EM∴=,∴22EF EF EF EMBF CE DE====,故⑤正确;CDM ADE∠=∠,90CMD AED∠=∠=︒,CDM ADE∴∆∽,∴CD CM DMAD AE DE==,BM CM=,AE CF=,∴,,故⑥正确;故答案为:①②③④⑤⑥.27.(2020山西)(3分)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为.解:如图,过点F作FH⊥AC于H.在Rt△ABC中,∵∠ACB=90°,AC=3,BC=4,∴AB===5,BM DMCF DE=CF DM BM DE∴=∵CD⊥AB,∴S△ABC=•AC•BC=•AB•CD,∴CD=,AD===,∵FH∥EC,∴=,∵EC=EB=2,∴=,设FH=2k,AH=3k,CH=3﹣3k,∵tan∠FCH==,∴=,∴k=,∴FH=,CH=3﹣=,∴CF===,∴DF=﹣=,故答案为.28.(2020四川眉山)(4分)如图,等腰△ABC中,AB=AC=10,边AC的垂直平分线交BC于点D,交AC于点E.若△ABD的周长为26,则DE的长为.解:∵边AC的垂直平分线交BC于点D,交AC于点E,∴∠AED=90°,AE=CE=AC==5,AD=CD,∴∠DAC=∠C,∵△ABD的周长为26,∴AB+BD+AD=AB+BD+CD=AB+BC=26,∵AB=AC=10,∴BC=16,∠B=∠C,∴∠B=∠DAC,∴△ABC∽△DAC,∴=,作AM⊥BC于M,∵AB=AC,∴BM=BC=8,∴AM===6,∴=,∴DE=,29.(2020浙江温州)(5分)如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2.测得EF=15米,FM =2米,MN=8米,∠ANE=45°,则场地的边AB为15√2米,BC为20√2米.【解答】解:∵AE⊥l,BF⊥l,∵∠ANE=45°,∴△ANE和△BNF是等腰直角三角形,∴AE=EN,BF=FN,∴EF=15米,FM=2米,MN=8米,∴AE=EN=15+2+8=25(米),BF=FN=2+8=10(米),∴AN=25√2,BN=10√2,∴AB=AN﹣BN=15√2(米);过C作CH⊥l于H,过B作PQ∥l交AE于P,交CH于Q,∴AE∥CH,∴四边形PEHQ和四边形PEFB是矩形,∴PE=BF=QH=10,PB=EF=15,BQ=FH,∵∠1=∠2,∠AEF=∠CHM=90°,∴△AEF ∽△CHM ,∴CH HM =AE EF =2515=53, ∴设MH =3x ,CH =5x ,∴CQ =5x ﹣10,BQ =FH =3x +2,∵∠APB =∠ABC =∠CQB =90°,∴∠ABP +∠PAB =∠ABP +∠CBQ =90°,∴∠PAB =∠CBQ ,∴△APB ∽△BQC ,∴AP BQ =PB CQ , ∴153x+2=155x−10,∴x =6,∴BQ =CQ =20,∴BC =20√2,故答案为:15√2,20√2.六、解答题30.(2020杭州)(8分)如图,在△ABC 中,点D ,E ,F 分别在AB ,BC ,AC 边上,DE ∥AC ,EF ∥AB .(1)求证:△BDE ∽△EFC .(2)设AF FC =12, ①若BC =12,求线段BE 的长;②若△EFC 的面积是20,求△ABC 的面积.【解答】(1)证明:∵DE ∥AC ,∴∠DEB =∠FCE ,∵EF ∥AB ,∴∠DBE =∠FEC ,∴△BDE ∽△EFC ;(2)解:①∵EF ∥AB ,∴BE EC =AF FC =12,∵EC =BC ﹣BE =12﹣BE ,∴BE 12−BE=12,解得:BE =4; ②∵AF FC =12,∴FC AC =23, ∵EF ∥AB ,∴△EFC ∽△BAC ,∴S △EFCS △ABC =(FC AC )2=(23)2=49, ∴S △ABC =94S △EFC =94×20=45. 31.(2020安徽)(14分)如图1,已知四边形是矩形,点在的延长线上,.与相交于点,与相交于点,.(1)求证:;(2)若,求的长;(3)如图2,连接,求证:.(1)证明:四边形是矩形,点在的延长线上,,又,,,,,即,故,(2)解:四边形是矩形,,,,,ABCD E BA AE AD =EC BD G AD F AF AB =BD EC ⊥1AB =AEAG EG DG -=ABCD E BA 90EAF DAB ∴∠=∠=︒AE AD =AF AB =()AEF ADB SAS ∴∆≅∆AEF ADB ∴∠=∠90GEB GBE ADB ABD ∴∠+∠=∠+∠=︒90EGB ∠=︒BD EC ⊥ABCD //AE CD ∴AEF DCF ∴∠=∠EAF CDF ∠=∠AEF DCF ∴∆∆∽, 即,设,则有,化简得,解得(舍去), . (3)如图,在线段上取点,使得,在与中,,,,,,,,为等腰直角三角形,.32.(2020成都)(4分)如图,在矩形中,,,,分别为,边的中点.动点从点出发沿向点运动,同时,动点从点出发沿向点运动,连接,过点作于点,连接.若点的速度是点的速度的2倍,在点从点运动至点的过程中,线段长度的最大值为 ,线段长度的最小值为 .解:连接交于,连接,取的中点,连接,,过点作于.∴AE AF DC DF=AE DF AF DC =(0)AE AD a a ==>(1)1a a -=210a a --=a =AE ∴EG P EP DG =AEP ∆ADG ∆AE AD =AEP ADG ∠=∠EP DG =()AEP ADG SAS ∴∆≅∆AP AG ∴=EAP DAG ∠=∠90PAG PAD DAG PAD EAP DAE ∴∠=∠+∠=∠+∠=∠=︒PAG ∴∆EG DG EG EP PG ∴-=-=ABCD 4AB =3BC =E F AB CD P E EA A Q F FC C PQ B BH PQ ⊥H DH P Q P E A PQ DH EF PQ M BM BM O OH OD O ON CD ⊥N四边形是矩形,,,四边形是矩形,,,,, , ,,,当点与重合时,的值最大,此时,,,,,,,,,,,,,故答案为.33.(2020福建)如图,C为线段AB 外一点.ABCD DF CF =AE EB =∴ADFE 3EF AD ∴==//FQ PE MFQ MEP ∴∆∆∽∴MF FQ ME PE=2PE FQ =2EM MF ∴=2EM ∴=1FM =P A PQ PM ==MQ PQ ∴=////MF ON BC MO OB =1FN CN ∴==3DN DF FN =+=1()22ON FM BC =+=OD ∴==BH PQ ⊥90BHM ∴∠=︒OM OB =1122OH BM ∴==DH OD OH -132DH ∴-DH ∴(1)求作四边形ABCD ,使得//CD AB ,且2CD AB =;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的四边形ABCD 中,AC ,BD 相交于点P ,AB ,CD 的中点分别为,M N ,求证:,,M P N 三点在同一条直线上.解:(1)则四边形ABCD 就是所求作的四边形.(2)∵AB CD ∥,∴ABP CDP ∠=∠,BAP DCP ∠=∠,∴ABP CDP ∆∆∽,∴AB AP CD CP. ∵,M N 分别为AB ,CD 的中点,∴2AB AM =,2CD CN =,∴=AM AP CN CP. 连接MP ,NP ,又∵BAP DCP ∠=∠,∴∽∆∆APM CPN ,∴∠=∠APM CPN ,∵点P 在AC 上∴180∠+∠=︒APM CPM ,∴180∠+∠=︒CPN CPM ,∴,,M P N 三点在同一条直线上.34.(2020河北)如图1和图2,在ABC ∆中,AB AC =,8BC =,3tan 4C =.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且2AM CN ==.点P 从点M 出发沿折线MB BN -匀速移动,到达点N 时停止;而点Q 在AC 边上随P 移动,且始终保持APQ B ∠=∠.(1)当点P 在BC 上时,求点P 与点A 的最短距离;(2)若点P 在MB 上,且PQ 将ABC ∆面积分成上下4:5两部分时,求MP 的长; (3)设点P 移动的路程为x ,当03x ≤≤及39x ≤≤时,分别求点P 到直线AC 的距离(用含x 的式子表示);(4)在点P 处设计并安装一扫描器,按定角APQ ∠扫描APQ ∆区域(含边界),扫描器随点P 从M 到B 再到N 共用时36秒.若94AK =,请直接..写出点K 被扫描到的总时长. (1)当点P 在BC 上时,PA ⊥BC 时PA 最小,∵AB=AC ,△ABC 为等腰三角形,∴PA min =tanC·2BC =34×4=3; (2)过A 点向BC 边作垂线,交BC 于点E ,S 上=S △APQ ,S 下=S 四边形BPQC ,∵APQ B ∠=∠,∴PQ ∥BC ,∴△APQ ∽△ABC , ∴AP AD PQ AB AC BC==,的∴2APQABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭, 当S S 上下=45时,24=9APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭, ∴23AP AB =, AE=2BC ·tan 3C =, 根据勾股定理可得AB=5, ∴2253AP MP AB +==, 解得MP=43; (3)当0≤x≤3时,P 在BM 上运动,P 到AC 的距离:d=PQ·sinC ,由(2)可知sinC=35, ∴d=35PQ , ∵AP=x+2, ∴25AP x PQ AB BC+==, ∴PQ=285x +⨯, ∴d=23855x +⨯⨯=24482525x +, 当3≤x≤9时,P 在BN 上运动,BP=x-3,CP=8-(x-3)=11-x ,d=CP·sinC=35(11-x )=-35x+335, 综上()()24480325253333955x x d x x ⎧+≤≤⎪⎪=⎨⎪-+≤≤⎪⎩;(4)AM=2<AQ=94, 移动的速度=936=14, ①从Q 平移到K ,耗时:92414-=1秒, ②P 在BC 上时,K 与Q 重合时 CQ=CK=5-94=114, ∵∠APQ+∠QPC=∠B+∠BAP ,APQ B ∠=∠∴∠QPC=∠BAP ,又∵∠B=∠C ,∴△ABP ∽△PCQ ,设BP=y ,CP=8-y ,AB BP PC CQ =,即51184y y =-, 整理得y 2-8y=554-, (y-4)2=94, 解得y 1=52,y 2=112, 52÷14=10秒, 112÷14=22秒, ∴点K 被扫描到的总时长36-(22-10)-1=23秒.35.(2020江西) 某数学课外活动小组在学习了勾股定理之后,针对图1中所示的“由直角三角形三边向外侧作多边形,它们的面积,,之间的关系问题”进行了以下探究: 1S 2S 3S类比探究(1)如图2,在中,为斜边,分别以为斜边向外侧作,,,若,则面积,,之间的关系式为 ;推广验证(2)如图3,在中,为斜边,分别以为边向外侧作任意,,,满足,,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;拓展应用(3)如图4,在五边形中,,,,点在上,,,求五边形的面积.【解析】(1) (2)成立;∵∠1=∠2=∠3,∠D=∠E=∠F ,∴△ABD ∽△CAE ∽△BCF. ∴∴∵△ABC 为直角三角形 ∴.∴,∴,∴成立. Rt ABC ∆BC ,,AB AC BC Rt ABD ∆Rt ACE ∆Rt BCF ∆123∠=∠=∠1S 2S 3S Rt ABC ∆BC ,,AB AC BC ABD ∆ACE ∆BCF ∆123∠=∠=∠D E F ∠=∠=∠ABCDE 105A E C ∠=∠=∠=90ABC ∠=AB =2DE =P AE 30ABP ∠=PE =ABCDE 123;S S S +=22122233,.S S AB AC S BC S BC ==221223.S S AB AC S BC ++=222AB AC BC +=1231S S S +=123S S S +=(3)过点A 作⊥BP 于点H.∵∠ABH=30°,AB=∴.∵∠BAP=105°,∴∠HAP=45°.∴∴,BP=BH+PH=∴.连接PD.∵,∴. ∴又∵∠E=∠BAP=105°,△ABP∽△EDP.∴∠EPD=∠APB=45°,.∴∠BPD=90°,∴连接BD.∴.∵tan ∠PBD=,∴∠PBD=30°.∵∠ABC=90°,∠ABC=30°,∴∠DBC=30°∵∠C=105°,∴△ABP ∽△EDP ∽△CBD.∴S △BCD =S △ABP +S△EDP =.∴S 五边形ABCDE =S △ABP +S △EDP +S △BCD +S △BPD36.(2020苏州).如图,在矩形ABCD中,E 是BC 的中点,DFAE ⊥,垂足为F.AH 3,60AH BH BAH ==∠=︒AP =3(33222ABP BP AH S ∆⋅+===2PE ED ==PE ED AP AB ====.PEEDAP AB =BDPEBP AP ==1PD =213BPD ABP S S ∆∆=⋅==32BPD PB PDS ∆⋅===PD BP =31222+=2)3)7++=(1)求证:ABE DFA ∆∆∽;(2)若6AB =,4BC =,求DF 的长.证明:(1)∵四边形ABCD 是矩形,∴90B ∠=︒,AD BC ∥.∴AEB DAF ∠=∠,∵DF AE ⊥,∴90DFA ∠=︒.∴B DFA ∠=∠,∴ABE DFA ∆∆∽.解:(2)∵ABE DFA ∆∆∽, ∴AB AE DF AD=. ∵4BC =,E 是BC 的中点, ∴114222BE BC ==⨯=. ∴在Rt ABE ∆中,AE == 又∵4AD BC ==,∴6DF =∴DF =37.(2020南京)(9分)如图,在和△中,、分别是、上一点,.ABC ∆A B C '''D D 'AB A B ''AD A D AB A B ''=''。

2020-2021全国中考数学相似的综合中考真题汇总及详细答案一、相似1.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴相交于点A(﹣1,0)和点B,与y轴交于点C,对称轴为直线x=1.(1)求点C的坐标(用含a的代数式表示);(2)联结AC、BC,若△ABC的面积为6,求此抛物线的表达式;(3)在第(2)小题的条件下,点Q为x轴正半轴上一点,点G与点C,点F与点A关于点Q成中心对称,当△CGF为直角三角形时,求点Q的坐标.【答案】(1)解:∵抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,而抛物线与x轴的一个交点A的坐标为(﹣1,0)∴抛物线与x轴的另一个交点B的坐标为(3,0)设抛物线解析式为y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,当x=0时,y=﹣3a,∴C(0,﹣3a)(2)解:∵A(﹣1,0),B(3,0),C(0,﹣3a),∴AB=4,OC=3a,∴S△ACB= AB•OC=6,∴6a=6,解得a=1,∴抛物线解析式为y=x2﹣2x﹣3(3)解:设点Q的坐标为(m,0).过点G作GH⊥x轴,垂足为点H,如图,∵点G与点C,点F与点A关于点Q成中心对称,∴QC=QG,QA=QF=m+1,QO=QH=m,OC=GH=3,∴OF=2m+1,HF=1,当∠CGF=90°时,∵∠QGH+∠FGH=90°,∠QGH+∠GQH=90°,∴∠GQH=∠HGF,∴Rt△QGH∽Rt△GFH,∴ = ,即,解得m=9,∴Q的坐标为(9,0);当∠CFG=90°时,∵∠GFH+∠CFO=90°,∠GFH+∠FGH=90°,∴∠CFO=∠FGH,∴Rt△GFH∽Rt△FCO,∴ = ,即 = ,解得m=4,∴Q的坐标为(4,0);∠GCF=90°不存在,综上所述,点Q的坐标为(4,0)或(9,0).【解析】【分析】(1)根据抛物线是轴对称图形和已知条件可求得抛物线与x轴的另一个交点B的坐标,再用交点式可求得抛物线的解析式,然后根据抛物线与y轴交于点C可得x=0,把x=0代入解析式即可求得点C的坐标;(2)由(1)的结论可求得AB=4,OC=3a,根据三角形ABC的面积=AB•OC=6可求得a的值,则解析式可求解;(3)设点Q的坐标为(m,0).过点G作GH⊥x轴,垂足为点H,根据中心对称的性质可得QC=QG,QA=QF=m+1,QO=QH=m,OC=GH=3。

2020-2021全国中考数学相似的综合中考模拟和真题分类汇总含答案解析一、相似1.在矩形ABCD中,BC=6,点E是AD边上一点,∠ABE=30°,BE=DE,连接BD.动点M 从点E出发沿射线ED运动,过点M作MN∥BD交直线BE于点N.(1)如图1,当点M在线段ED上时,求证:MN= EM;(2)设MN长为x,以M、N、D为顶点的三角形面积为y,求y关于x的函数关系式;(3)当点M运动到线段ED的中点时,连接NC,过点M作MF⊥NC于F,MF交对角线BD于点G(如图2),求线段MG的长.【答案】(1)证明::∵ °, ° ,∴ °∵ ,∴∵∥ ,∴∴ °,∴过点作于点 ,则 .在中,∴∴(2)解:在中,,∴∵a.当点在线段上时,过点作于点 ,在中,由(1)可知:,∴∴∴b.当点在线段延长线上时,过点作于点在中, ,在中, ,∴ ,∴(3)解:连接 ,交于点 .∵为的中点∴ ,∴ .∵ ,∴ ,∴ ,∴ ,∴ .∵∥∴ ,∴ ,,∵ ,∴ ,又∵ ,∴∽ ,∴,即 ,∴【解析】【分析】(1)过点E作EH⊥MN于点H ,由已知条件易得EN=EM,解直角三角形EMH易得MH和EM的关系,由等腰三角形的三线合一可得MN=2MH即可求解;(2)在Rt△ABE中,由直角三角形的性质易得DE=BE=2AE,由题意动点M从点E出发沿射线ED运动可知点M可在线段ED上,也可在线段ED外,所以可分两种情况求解:①当点M在线段ED上时,过点N作NI⊥AD于点I ,结合(1)中的结论MN=EM即可求解;②当点M在线段ED延长线上时,过点N作NI'⊥AD于点I ',解RtΔNI′M 和可求得NI'和NE,则DM=NE−DE,所以以M、N、D为顶点的三角形面积y=MD.NI可求解;(3)连接CM,交BD于点N',由(2)中的计算可得MN、CD、MC的长,解直角三角形CDM可得∠DMC的度数,于是由三角形内角和定理可求得∠NMC=,根据平行线的性质可得DMN'是直角三角形,根据直角三角形的性质可得MN′=MD;则NC的长可求,由已知条件易得ΔNMC∽ΔMN′G根据所得的比例式即可求解.,2.如图,抛物线y= x2+bx+c 与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点.(1)求抛物线的解析式及点D的坐标;(2)如图1,抛物线的对称轴与x轴交于点E,连接BD,点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;(3)如图2,若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,求点Q的坐标.【答案】(1)解:把B(6,0),C(0,6)代入y= x2+bx+c,得解得 ,抛物线的解析式是y= x2+2x+6, 顶点D的坐标是(2,8)(2)解:如图1,过F作FG⊥x轴于点G,设F(x, x2+2x+6),则FG= ,∵∠FBA=∠BDE,∠FGB=∠BED=90°,∴△FBG∽△BDE,∴,∵B(6,0),D(2,8),∴E(2,0),BE=4,DE=8,OB=6,∴BG=6-x,∴当点F在x轴上方时,有,∴x=-1或x=6(舍去),此时F1的坐标为(-1,),当点F在x轴下方时,有,∴x=-3或x=6(舍去),此时F2的坐标为(-3,),综上可知F点的坐标为(-1,)或(-3,)(3)解:如图2,不妨M在对称轴的左侧,N在对称轴的左侧,MN和PQ交于点K,由题意得点M,N关于抛物线的对称轴对称,四边形MPNQ为正方形,且点P在x轴上∴点P为抛物线的对称轴与x轴的交点,点Q在抛物线的对称轴上 ,∴KP=KM=k,则Q(2,2k),M坐标为(2-k,k),∵点M在抛物线y= x2+2x+6的图象上,∴k= (2-k)2+2(2-k)+6解得k1= 或k2=∴满足条件的点Q有两个,Q1(2,)或Q2(2,).【解析】【分析】(1)根据点B、C的坐标,利用待定系数法建立关于b、c的方程组,求解就可得出函数解析式,再求出顶点坐标。

2020-2021全国各地中考数学分类:相似综合题汇编及详细答案一、相似1.如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。
(1)求证:DC2=CE·AC;(2)若AE=2EC,求之值;(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH=,求EC之长.【答案】(1)证明:∵CD=BC,∴∠DAC=∠CDB,又∵∠ACD=∠DCE,∴△ACD∽△DCE,∴,∴DC2=CE·AC;(2)解:设EC=k,则AE=2k,∴AC=3k,由(1)DC2=CE·AC=3k2,DC= k,连接OC,OD,∵CD=BC,∴OC平分∠DOB,∴BC=DC= k,∵AB是⊙O的直径,∴在Rt△ACB中,,∴OB=OC=OD= k,∴∠BOD=120°,∴∠DOA=60°,∴AD=AO,∴(3)解:∵CH是⊙O的切线,连接CO,∴OC⊥CH.∵∠COH=60°,∠H=30°,过C作CG⊥AB于G,设EC=k,∵∠CAB=30°,∴,又∵∠H=∠CAB=30°,∴AC=CH=3k,∴AH=,∵S△ACH=,∴,∴k2=4,k=2,即EC=2.【解析】【分析】(1)要证DC2=CE·AC,只需证△ACD∽△DCE即可求解;(2)连接OC,OD,根据已知条件AE=2EC可用含k的代数式表示线段AE、CE、AC,由(1)可将CD用含K的代数式表示,在Rt△ACB中,由勾股定理可将AB用含K的代数式表示,结合已知条件和圆的性质可求解;(3)过C作CG⊥AB于G,设EC=k,由30度角所对的直角边等于斜边的一半可将CG用含K的代数式表示,根据三角形ACH的面积=AH CG=9即可求解。
2.如图,在Rt△ABC中,,角平分线交BC于O,以OB为半径作⊙O.(1)判定直线AC是否是⊙O的切线,并说明理由;(2)连接AO交⊙O于点E,其延长线交⊙O于点D,,求的值;(3)在(2)的条件下,设的半径为3,求AC的长.【答案】(1)解:AC是⊙O的切线理由:,,作于,是的角平分线,,AC是⊙O的切线(2)解:连接,是⊙O的直径,,即 ..又 (同角) ,∽ ,(3)解:设在和中,由三角函数定义有:得:解之得:即的长为【解析】【分析】(1)利用角平分线的性质:角平分线上的点到角两边的距离相等证得点O到AC的距离为半径长,即可证得AC与圆O相切;(2)先连接BE构造一个可以利用正切值的直角三角形,再证得∠1=∠D,从而证得两个三角形ABE与ABD相似,即可求得两个线段长的比值;(3)也可以应用三角形相似的判定与性质解题,其中AB的长度是利用勾股定理与(2)中AE与AB的比值求得的.3.已知如图1,抛物线y=﹣ x2﹣ x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC(1)求出直线AD的解析式;(2)如图2,若在直线AC上方的抛物线上有一点F,当△ADF的面积最大时,有一线段MN= (点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;(3)如图3,将△DBC绕点D逆时针旋转α°(0<α°<180°),记旋转中的△DBC为△DB′C′,若直线B′C′与直线AC交于点P,直线B′C′与直线DC交于点Q,当△CPQ是等腰三角形时,求CP的值.【答案】(1)解:∵抛物线y=﹣ x2﹣ x+3与x轴交于A和B两点,∴0=﹣ x2﹣ x+3,∴x=2或x=﹣4,∴A(﹣4,0),B(2,0),∵D(0,﹣1),∴直线AD解析式为y=﹣ x﹣1(2)解:如图1,过点F作FH⊥x轴,交AD于H,设F(m,﹣ m2﹣ m+3),H(m,﹣ m﹣1),∴FH=﹣ m2﹣ m+3﹣(﹣ m﹣1)=﹣ m2﹣ m+4,∴S△ADF=S△AFH+S△DFH= FH×|x D﹣x A|=2FH=2(﹣ m2﹣ m+4)=﹣m2﹣m+8=﹣(m+ )2+ ,当m=﹣时,S△ADF最大,∴F(﹣,)如图2,作点A关于直线BD的对称点A1,把A1沿平行直线BD方向平移到A2,且A1A2= ,连接A2F,交直线BD于点N,把点N沿直线BD向左平移得点M,此时四边形AMNF 的周长最小..∵OB=2,OD=1,∴tan∠OBD= ,∵AB=6,∴AK= ,∴AA1=2AK= ,在Rt△ABK中,AH= ,A1H= ,∴OH=OA﹣AH= ,∴A1(﹣,﹣),过A2作A2P⊥A2H,∴∠A1A2P=∠ABK,∵A1A2= ,∴A2P=2,A1P=1,∴A2(﹣,﹣)∵F(﹣,)∴A2F的解析式为y=﹣ x﹣①,∵B(2,0),D(0,﹣1),∴直线BD解析式为y=﹣ x﹣1②,联立①②得,x=﹣,∴N点的横坐标为:﹣(3)解:∵C(0,3),B(2,0),D(0,﹣1)∴CD=4,BC= ,OB=2,BC边上的高为DH,根据等面积法得, BC×DH= CD×OB,∴DH= = ,∵A(﹣4,0),C(0,3),∴OA=4,OC=3,∴tan∠ACD= ,①当PC=PQ时,简图如图1,过点P作PG⊥CD,过点D作DH⊥PQ,∵tan∠ACD=∴设CG=3a,则QG=3a,PG=4a,PQ=PC=5a,∴DQ=CD﹣CQ=4﹣6a∵△PGQ∽△DHQ,∴,∴,∴a= ,∴PC=5a= ;②当PC=CQ时,简图如图2,过点P作PG⊥CD,∵tan∠ACD=∴设CG=3a,则PG=4a,∴CQ=PC=5a,∴QG=CQ﹣CG=2a,∴PQ=2 a,∴DQ=CD﹣CQ=4﹣5a∵△PGQ∽△DHQ,同①的方法得出,PC=4﹣,设CG=3a,则PG=4a,从而得出CQ,QG,PQ,DQ的长,由△PGQ∽△DHQ,同①的方法得出,PC的长;③当QC=PQ时,简图如图1过点Q作QG⊥PC,过点C作CN⊥PQ,设CG=3a,则QG=4a,PQ=CQ=5a,∴PG=3a,∴PC=6a∴DQ=CD﹣CQ=4﹣5a,利用等面积法得,CN×PQ=PC×QG,∴CN= a,∵△CQN∽△DQH同①的方法得出PC=④当PC=CQ时,简图如图4,过点P作PG⊥CD,过H作HD⊥PQ,设CG=3a,则PG=4a,CQ=PC=5a,∴QD=4+5a,PQ=4 ,∵△QPG∽△QDH,同①方法得出.CP=综上所述,PC的值为:;4﹣,,=【解析】【分析】(1)根据抛物线与x轴交点的坐标特点,把y=0代入抛物线的解析式,得出一个关于x的一元二次方程,求解得出x的值,进而得出A,B两点的坐标;然后由A,D 两点的坐标利用待定系数法求出直线AD的解析式;(2)过点F作FH⊥x轴,交AD于H,根据函数图像上点的坐标特点,及平行于y轴的直线上的点的坐标特点,设出F,H的坐标,从而得出FH的长度,S△ADF=S△AFH+S△DFH= FH×|x D﹣x A|=2FH,列出关于m的函数解析式,再根据二次函数的性质,由顶点式得出当m=﹣时,S△ADF最大,从而得出F点的坐标;如图2,作点A关于直线BD的对称点A1,把A1沿平行直线BD方向平移到A2,且A1A2= ,连接A2F,交直线BD于点N,把点N沿直线BD向左平移得点M,此时四边形AMNF的周长最小,进而求出点A1,A2坐标,即可确定出A2F的解析式和直线BD解析式联立方程组即可确定出N点的横坐标;(3)根据C,B,D三点的坐标,得出CD,BC,OB的长,BC边上的高为DH,根据等面积法得BC×DH= CD×OB,从而得出DH的长,根据A,C两点的坐标,得出OA,OC的长,根据正切函数的定义得出tan∠ACD= 4∶ 3 ;然后分四种情况讨论:①当PC=PQ时,过点P作PG⊥CD,过点D作DH⊥PQ,由tan∠ACD= 4∶ 3 ,设CG=3a,则QG=3a,PG=4a,PQ=PC=5a,从而由DQ=CD﹣CQ得出DQ的长,根据△PGQ∽△DHQ,得出PG∶DH=PQ∶DQ,从而求出a的值,进而求出PC的值;②当PC=CQ时,简图如图2,过点P作PG⊥CD,tan∠ACD= 4∶3,设CG=3a,则PG=4a,从而得出CQ,QG,PQ,DQ的长,由△PGQ∽△DHQ,同①的方法得出,PC的长;③当QC=PQ时,过点Q作QG⊥PC,过点C作CN⊥PQ,设CG=3a,则QG=4a,PQ=CQ=5a,从而得出PG,PC,DQ的长,利用等面积法得,CN×PQ=PC×QG,从而得出CN,由△CQN∽△DQH同①的方法得出PC的长;④当PC=CQ时,过点P作PG⊥CD,过H作HD⊥PQ,设CG=3a,则PG=4a,CQ=PC=5a,从而得出QD,PQ 的长,由△QPG∽△QDH,同①方法得出.CP的长。

2020-2021全国各地中考数学分类:相似综合题汇编附详细答案一、相似1.如图,在矩形ABCD中,AB=18cm,AD=9cm,点M沿AB边从A点开始向B以2cm/s 的速度移动,点N沿DA边从D点开始向A以1cm/s的速度移动.如果点M、N同时出发,用t(s)表示移动时间(0≤t≤9),求:(1)当t为何值时,∠ANM=45°?(2)计算四边形AMCN的面积,根据计算结果提出一个你认为合理的结论;(3)当t为何值时,以点M、N、A为顶点的三角形与△BCD相似?【答案】(1)解:对于任何时刻t,AM=2t,DN=t,NA=9-t,当AN=AM时,△MAN为等腰直角三角形,即:9-t=2t,解得:t=3(s),所以,当t=3s时,△MAN为等腰直角三角形(2)解:在△NAC中,NA=9-t,NA边上的高DC=12,∴S△NAC= NA•DC= (9-t)•18=81-9t.在△AMC中,AM=2t,BC=9,∴S△AMC= AM•BC= •2t•9=9t.∴S四边形NAMC=S△NAC+S△AMC=81(cm2).由计算结果发现:在M、N两点移动的过程中,四边形NAMC的面积始终保持不变.(也可提出:M、N两点到对角线AC的距离之和保持不变)(3)解:根据题意,可分为两种情况来研究,在矩形ABCD中:①当NA:AB=AM:BC 时,△NAP∽△ABC,那么有:( 9-t):18=2t:9,解得t=1.8(s),即当t=1.8s时,△NAP∽△ABC;②当 NA:BC=AM:AB时,△MAN∽△ABC,那么有:( 9-t):9=2t:18,解得t=4.5(s),即当t=4.5s时,△MAN∽△ABC;所以,当t=1.8s或4.5s时,以点N、A、M为顶点的三角形与△ABC相似【解析】【分析】(1)根据题意可得:因为对于任何时刻t,AM=2t,DN=t,NA=9-t.当NA=AM时,△MAN为等腰直角三角形,可得方程式,解可得答案。

中考专题复习相似1.在的交通旅游图上,南京玄武湖隧道长,则它的实际长度是()A. B. C. D.2.在中,,,是的角平分线,下列结论:①,都是等腰三角形;②;③;④是的黄金分割点其中正确的是()A.个B.个C.个D.个3.有一个多边形的边长分别是 4 cm、5 cm、6 cm、4 cm、5 cm,和它相似的一个多边形最长边为8 cm,那么这个多边形的周长是( )A. 12 cm B. 18 cm C. 32 cm D. 48 cm4.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA∶OA′=2∶3,则四边形ABCD与四边形A′B′C′D′的面积比为( )A.4∶9 B.2∶5 C.2∶3 D.∶5.如图,把△ABC绕点A旋转得到△ADE,当点D刚好落在BC上时,连接CE,设AC、DE相交于点F,则图中相似三角形的对数是( )A. 3 B. 4 C. 5 D. 66.若△ABC∽△A′B′C′,相似比为1∶3,则△ABC与△A′B′C′周长的比为( )A.1∶3B.3∶1C.1∶9D.9∶17.已知△ABC∽△A′B′C′,且=,则S△ABC∶S△A′B′C′为( )A.1∶2B.2∶1C.1∶4D.4∶18.如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论不正确的是( )A.BC=2DEB.△ADE∽△ABCC.=D.S△ABC=3S△ADE9.如图,矩形ABCD∽矩形ADFE,AE=1,AB=4,则AD等于( )A. 2 B. 2.4 C. 2.5 D. 310.如图,圆内接四边形ABCD的BA,CD的延长线交于P,AC,BD交于E,则图中相似三角形有( )A. 2对 B. 3对 C. 4对 D. 5对11.如图,矩形OABC与矩形ODEF是位似图形,点O为位似中心,相似比为1∶1.2,点B的坐标为(-3,2),则点E的坐标是( )A. (3.6,2.4) B. (-3,2.4) C. (-3.6,2) D. (-3.6,2.4) 12.如图,中,,,,,则等于()A. B. C. D.13.如图,,交,,于,,,交,,于,,,以下结论的错误的为()A. B.C. D.14.如图,在中,,,,,则的长为()A. B. C. D.15.如图,在中,是斜边上的高,若,,则的长为()A. B. C. D.16.如图,点是的边的上一点,且;如果,那么________.17.如图,已知,,写出对应边的比例式________.18.如图,中,厘米,厘米,点从出发,以每秒厘米的速度向运动,点从同时出发,以每秒厘米的速度向运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以、、为顶点的三角形与相似时,运动时间为________.19.在阳光下,身高的小林在地面上的影长为,在同一时刻,测得学校的旗杆在地面上的影长为,则旗杆的高度为________.20.如图,,分别在的边,的延长线上,且,若,则的值为________.21.如图,中,,,的垂直平分线交于点,交于点,设的面积为,四边形的面积为,则的值等于________.22.如图,小强和小华共同站在路灯下,小强的身高EF=1.8 m,小华的身高MN=1.5 m,他们的影子恰巧等于自己的身高,即BF=1.8 m,CN=1.5 m,且两人相距4.7 m,则路灯AD 的高度是____________.23.如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=NF;③=;④S四边形CGNF=S四边形ANGD.其中正确的结论的序号是____________.24.如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=的图象上.若点B在反比例函数y=的图象上,则k的值________.25.如图,△ABC与△DOE是位似图形,A(0,3),B(-2,0),C(1,0),E(6,0),△ABC与△DOE 的位似中心为M.(1)写出D点的坐标;(2)在图中画出M点,并求M点的坐标.26.如图:矩形ABCD的长AB=30,宽BC=20.(1)如图(1)若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD与A′B′C′D′相似吗?请说明理由;(2)如图(2),x为多少时,图中的两个矩形ABCD与A′B′C′D′相似?27.如图,已知和是位似图形,,垂直平分,且.求的度数;求的长度.28.如图,已知中于,于,求证:;若时,求与面积之比.29.如图,,,与相交于点,,试说明:;26.如图若,请直接回答中结论是否成立;在中找出、和之间的数量关系,并说明理由.参考答案1-5 BDCAB 6-10 ACDAC 11-15 DCCBB16.或17.,18.或秒19.20.21.22.4 m23.①③24.-425.解(1)过点D作DH⊥OE于点H,∵△ABC与△DOE是位似图形,A(0,3),B(-2,0),C(1,0),E(6,0),∴BC=3,OE=6,△AOB∽△DHO,∴位似比为3∶6=1∶2,∴OH=2OB=4,DH=2OA=6,∴D点的坐标为(4,6);(2)连接DA并延长,交x轴于点M,则点M即为△ABC与△DOE的位似中心;则MO∶MH=1∶2,设MO=x,则MH=x+4,∴x∶(x+4)=1∶2,解得x=4,∴M点的坐标为(-4,0 ).26.解(1)不相似,AB=30,A′B′=28,BC=20,B′C′=18,而≠;(2)矩形ABCD与A′B′C′D′相似,则=,则=,解得x=1.5,或=.解得x=9.27.解:∵垂直平分,∴,∵和是位似图形,∴,∴;证明:∵,∴,∴.或用锐角三角函数求解:(简解如下)由,得到,∴.28.证明:∵,∴∴∴∴解:∵∴29.证明:∵,,∴,∴,∴,同理,∴,即,∴;成立.证明:∵,∴,∵∴,∴,∴;关系式为:.证明如下:分别过作于,过作于,过作交的延长线于由题设可得:,∴,即,又∵,,∴,∴.。

教学资料范本2020中考数学试题分类汇编考点36相似三角形含解析-精装版编辑:__________________时间:__________________【精选】20xx最新20xx中考数学试题分类汇编考点36相似三角形含解析一.选择题(共28小题)1.(20xx•重庆)制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是()A.360元B.720元C.1080元 D.2160元【分析】根据题意求出长方形广告牌每平方米的成本,根据相似多边形的性质求出扩大后长方形广告牌的面积,计算即可.【解答】解:3m×2m=6m2,∴长方形广告牌的成本是120÷6=20元/m2,将此广告牌的四边都扩大为原来的3倍,则面积扩大为原来的9倍,∴扩大后长方形广告牌的面积=9×6=54m2,∴扩大后长方形广告牌的成本是54×20=1080m2,故选:C.2.(20xx•玉林)两三角形的相似比是2:3,则其面积之比是()A.:B.2:3 C.4:9 D.8:27【分析】根据相似三角形的面积比等于相似比的平方计算即可.【解答】解:∵两三角形的相似比是2:3,∴其面积之比是4:9,故选:C.3.(20xx•重庆)要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边为()A.3cm B.4cm C.4.5cm D.5cm【分析】根据相似三角形的对应边成比例求解可得.【解答】解:设另一个三角形的最长边长为xcm,根据题意,得: =,解得:x=4.5,即另一个三角形的最长边长为4.5cm,故选:C.4.(20xx•内江)已知△ABC与△A1B1C1相似,且相似比为1:3,则△ABC与△A1B1C1的面积比为()A.1:1 B.1:3 C.1:6 D.1:9【分析】利用相似三角形面积之比等于相似比的平方,求出即可.【解答】解:已知△ABC与△A1B1C1相似,且相似比为1:3,则△ABC与△A1B1C1的面积比为1:9,故选:D.5.(20xx•××市)已知△ABC∽△DEF,相似比为2,且△ABC的面积为16,则△DEF的面积为()A.32 B.8 C.4 D.16【分析】由△ABC∽△DEF,相似比为2,根据相似三角形的面积的比等于相似比的平方,即可得△ABC与△DEF的面积比为4,又由△ABC的面积为16,即可求得△DEF的面积.【解答】解:∵△ABC∽△DEF,相似比为2,∴△ABC与△DEF的面积比为4,∵△ABC的面积为16,∴△DEF的面积为:16×=4.故选:C.6.(20xx•重庆)已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为()A.1:4 B.4:1 C.1:2 D.2:1【分析】利用相似三角形面积之比等于相似比的平方计算即可.【解答】解:∵△ABC∽△DEF,且相似比为1:2,∴△ABC与△DEF的面积比为1:4,故选:A.7.(20xx•临安区)如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是()A.B.C.D.【分析】根据正方形的性质求出∠ACB,根据相似三角形的判定定理判断即可.【解答】解:由正方形的性质可知,∠ACB=180°﹣45°=135°,A、C、D图形中的钝角都不等于135°,由勾股定理得,BC=,AC=2,对应的图形B中的边长分别为1和,∵=,∴图B中的三角形(阴影部分)与△ABC相似,故选:B.8.(20xx•广东)在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC 的面积之比为()A.B.C.D.【分析】由点D、E分别为边AB、AC的中点,可得出DE为△ABC的中位线,进而可得出DE∥BC及△ADE∽△ABC,再利用相似三角形的性质即可求出△ADE与△ABC 的面积之比.【解答】解:∵点D、E分别为边AB、AC的中点,∴DE为△ABC的中位线,∴DE∥BC,∴△ADE∽△ABC,∴=()2=.故选:C.9.(20xx•自贡)如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积为4,则△ABC的面积为()A.8 B.12 C.14 D.16【分析】直接利用三角形中位线定理得出DE∥BC,DE=BC,再利用相似三角形的判定与性质得出答案.【解答】解:∵在△ABC中,点D、E分别是AB、AC的中点,∴DE∥BC,DE=BC,∴△ADE∽△ABC,∵=,∴=,∵△ADE的面积为4,∴△ABC的面积为:16,故选:D.10.(20xx•××县一模)如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为()A.3:4 B.9:16 C.9:1 D.3:1【分析】可证明△DFE∽△BFA,根据相似三角形的面积之比等于相似比的平方即可得出答案.【解答】解:∵四边形ABCD为平行四边形,∴DC∥AB,∴△DFE∽△BFA,∵DE:EC=3:1,∴DE:DC=3:4,∴DE:AB=3:4,∴S△DFE:S△BFA=9:16.故选:B.11.(20xx•随州)如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为()A.1 B.C. 1 D.【分析】由DE∥BC可得出△ADE∽△ABC,利用相似三角形的性质结合S△ADE=S 四边形BCED,可得出=,结合BD=AB﹣AD即可求出的值,此题得解.【解答】解:∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,∴△ADE∽△ABC,∴()2=.∵S△ADE=S四边形BCED,∴=,∴===﹣1.故选:C.12.(20xx•哈尔滨)如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是()A. = B. = C. = D. =【分析】由GE∥BD、GF∥AC可得出△AEG∽△ABD、△DFG∽△DC A,根据相似三角形的性质即可找出==,此题得解.【解答】解:∵GE∥BD,GF∥AC,∴△AEG∽△ABD,△DFG∽△DCA,∴=, =,∴==.故选:D.13.(20xx•遵义)如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为()A.5 B.4 C.3 D.2【分析】先求出AC,进而判断出△ADF∽△CAB,即可设DF=x,AD=x,利用勾股定理求出BD,再判断出△DEF∽△DBA,得出比例式建立方程即可得出结论.【解答】解:如图,在Rt△ABC中,AB=5,BC=10,∴AC=5过点D作DF⊥AC于F,∴∠AFD=∠CBA,∵AD∥BC,∴∠DAF=∠ACB,∴△ADF∽△CAB,∴,∴,设DF=x,则AD=x,在Rt△ABD中,BD==,∵∠DEF=∠DBA,∠DFE=∠DAB=90°,∴△DEF∽△DBA,∴,∴,∴x=2,∴AD=x=2,故选:D.14.(20xx•扬州)如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE、AE分别交于点P,M.对于下列结论:①△BAE∽△CAD;②MP•MD=MA•ME;③2CB2=CP•CM.其中正确的是()A.①②③B.①C.①②D.②③【分析】(1)由等腰Rt△ABC和等腰Rt△ADE三边份数关系可证;(2)通过等积式倒推可知,证明△PAM∽△EMD即可;(3)2CB2转化为AC2,证明△ACP∽△MCA,问题可证.【解答】解:由已知:AC=AB,AD=AE∴∵∠BAC=∠EAD∴∠BAE=∠CAD∴△BAE∽△CAD所以①正确∵△BAE∽△CAD∴∠BEA=∠CDA∵∠PME=∠AMD∴△PME∽△AMD∴∴MP•MD=MA•ME所以②正确∵∠BEA=∠CDA∠PME=∠AMD∴P、E、D、A四点共圆∴∠APD=∠EAD=90°∵∠CAE=180°﹣∠BAC﹣∠EAD=90°∴△CAP∽△CMA∴AC2=CP•CM∵AC=AB∴2CB2=CP•CM所以③正确故选:A.15.(20xx•贵港)如图,在△ABC中,EF∥BC,AB=3AE,若S四边形BCFE=16,则S△ABC=()A.16 B.18 C.20 D.24【分析】由EF∥BC,可证明△AEF∽△ABC,利用相似三角形的性质即可求出则S△ABC的值.【解答】解:∵EF∥BC,∴△AEF∽△ABC,∵AB=3AE,∴AE:AB=1:3,∴S△AEF:S△ABC=1:9,设S△AEF=x,∵S四边形BCFE=16,∴=,解得:x=2,∴S△ABC=18,故选:B.16.(20xx•孝感)如图,△ABC是等边三角形,△ABD是等腰直角三角形,∠BAD=90°,AE⊥BD于点E,连CD分别交AE,AB于点F,G,过点A作AH⊥CD交BD于点H.则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△AFG∽△CBG;⑤AF=(﹣1)EF.其中正确结论的个数为()A.5 B.4 C.3 D.2【分析】①由等边三角形与等腰直角三角形知△CAD是等腰三角形且顶角∠CAD=150°,据此可判断;②求出∠AFP和∠FAG度数,从而得出∠AGF度数,据此可判断;③证△ADF≌△BAH即可判断;④由∠AFG=∠CBG=60°、∠AGF=∠CGB即可得证;⑤设PF=x,则AF=2x、AP==x,设EF=a,由△ADF≌△BAH 知BH=AF=2x,根据△ABE是等腰直角三角形之BE=AE=a+2x,据此得出EH=a,证△PAF∽△EAH得=,从而得出a与x的关系即可判断.【解答】解:∵△ABC为等边三角形,△ABD为等腰直角三角形,∴∠BAC=60°、∠BAD=90°、AC=AB=AD,∠ADB=∠ABD=45°,∴△CAD是等腰三角形,且顶角∠CAD=150°,∴∠ADC=15°,故①正确;∵AE⊥BD,即∠AED=90°,∴∠DAE=45°,∴∠AFG=∠ADC+∠DAE=60°,∠FAG=45°,∴∠AGF=75°,由∠AFG≠∠AGF知AF≠AG,故②错误;记AH与CD的交点为P,由AH⊥CD且∠AFG=60°知∠FAP=30°,则∠BAH=∠ADC=15°,在△ADF和△BAH中,∵,∴△ADF≌△BAH(ASA),∴DF=AH,故③正确;∵∠AFG=∠CBG=60°,∠AGF=∠CGB,∴△AFG∽△CBG,故④正确;在Rt△APF中,设PF=x,则AF=2x、AP==x,设EF=a,∵△ADF≌△BAH,∴BH=AF=2x,△ABE中,∵∠AEB=90°、∠ABE=45°,∴BE=AE=AF+EF=a+2x,∴EH=BE﹣BH=a+2x﹣2x=a,∵∠APF=∠AEH=90°,∠FAP=∠HAE,∴△PAF∽△EAH,∴=,即=,整理,得:2x2=(﹣1)ax,由x≠0得2x=(﹣1)a,即AF=(﹣1)EF,故⑤正确;故选:B.17.(20xx•泸州)如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则的值是()A.B.C.D.【分析】如图作,FN∥AD,交AB于N,交BE于M.设DE=a,则AE=3a,利用平行线分线段成比例定理解决问题即可;【解答】解:如图作,FN∥AD,交AB于N,交BE于M.∵四边形ABCD是正方形,∴AB∥CD,∵FN∥AD,∴四边形ANFD是平行四边形,∵∠D=90°,∴四边形ANFD是解析式,∵AE=3DE,设DE=a,则AE=3a,AD=AB=CD=FN=4a,AN=DF=2a,∵AN=BN,MN∥AE,∴BM=ME,∴MN=a,∴FM=a,∵AE∥FM,∴===,故选:C.18.(20xx•临安区)如图,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,若AD=4,DB=2,则DE:BC的值为()A.B.C.D.【分析】根据平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似,再根据相似三角形的对应边成比例解则可.【解答】解:∵DE∥BC,∴△ADE∽△ABC,∴===.故选:A.19.(20xx•恩施州)如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为()A.6 B.8 C.10 D.12【分析】根据正方形的性质可得出AB∥CD,进而可得出△ABF∽△GDF,根据相似三角形的性质可得出==2,结合FG=2可求出AF、AG的长度,由CG∥AB、AB=2CG可得出CG为△EAB的中位线,再利用三角形中位线的性质可求出AE的长度,此题得解.【解答】解:∵四边形ABCD为正方形,∴AB=CD,AB∥CD,∴∠ABF=∠GDF,∠BAF=∠DGF,∴△ABF∽△GDF,∴==2,∴AF=2GF=4,∴AG=6.∵CG∥AB,AB=2CG,∴CG为△EAB的中位线,∴AE=2AG=12.故选:D.20.(20xx•杭州)如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE.记△ADE,△BCE的面积分别为S1,S2()A.若2AD>AB,则3S1>2S2 B.若2AD>AB,则3S1<2S2C.若2AD<AB,则3S1>2S2 D.若2AD<AB,则3S1<2S2【分析】根据题意判定△ADE∽△ABC,由相似三角形的面积之比等于相似比的平方解答.【解答】解:∵如图,在△ABC中,DE∥BC,∴△ADE∽△ABC,∴=()2,∴若2AD>AB,即>时,>,此时3S1>S2+S△BDE,而S2+S△BDE<2S2.但是不能确定3S1与2S2的大小,故选项A不符合题意,选项B不符合题意.若2AD<AB,即<时,<,此时3S1<S2+S△BDE<2S2,故选项C不符合题意,选项D符合题意.故选:D.21.(20xx•永州)如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为()A.2 B.4 C.6 D.8【分析】只要证明△ADC∽△ACB,可得=,即AC2=AD•AB,由此即可解决问题;【解答】解:∵∠A=∠A,∠ADC=∠ACB,∴△ADC∽△ACB,∴=,∴AC2=AD•AB=2×8=16,∵AC>0,∴AC=4,故选:B.22.(20xx•××区)如图,点D、E、F分别是△ABC的边AB、AC、BC上的点,若DE∥BC,EF∥AB,则下列比例式一定成立的是()A. = B. = C. = D. =【分析】用平行线分线段成比例定理和相似三角形的判定即可得出结论.【解答】解:∵DE∥BC,∴,∵DE∥BC,∴△ADE∽△ABC,∴,∵EF∥AB,∴,∵EF∥AB,∴△CEF∽△CAB,∴,∵DE∥BC,EF∥AB,∴四边形BDEF是平行四边形,∴DE=BF,EF=BD,∴,,,,∴正确,故选:C.23.(20xx•荆门)如图,四边形ABCD为平行四边形,E、F为CD边的两个三等分点,连接AF、BE交于点G,则S△EFG:S△ABG=()A.1:3 B.3:1 C.1:9 D.9:1【分析】利用相似三角形的性质面积比等于相似比的平方即可解决问题;【解答】解:∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB,∵DE=EF=FC,∴EF:AB=1:3,∴△EFG∽△BAG,∴=()2=,故选:C.24.(20xx•达州)如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则的值为()A.B.C.D.1【分析】首先证明AG:AB=CH:BC=1:3,推出GH∥AC,推出△BGH∽△BAC,可得==()2=()2=, =,由此即可解决问题.【解答】解:∵四边形ABCD是平行四边形∴AD=BC,DC=AB,∵AC=CA,∴△ADC≌△CBA,∴S△ADC=S△ABC,∵AE=CF=AC,AG∥CD,CH∥AD,∴AG:DC=AE:CE=1:3,CH:AD=CF:AF=1:3,∴AG:AB=CH:BC=1:3,∴GH∥AC,∴△BGH∽△BAC,∴==()2=()2=,∵=,∴=×=,故选:C.25.(20xx•南充)如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF.下列结论正确的是()A.CE= B.EF= C.cos∠CEP=D.HF2=EF•CF【分析】首先证明BH=AH,推出EG=BG,推出CE=CB,再证明△CEH≌△CBH,Rt△HFE≌Rt△HFA,利用全等三角形的性质即可一一判断.【解答】解:连接EH.∵四边形ABCD是正方形,∴CD=AB═BC=AD=2,CD∥AB,∵BE⊥AP,CH⊥BE,∴CH∥PA,∴四边形CPAH是平行四边形,∴CP=AH,∵CP=PD=1,∴AH=PC=1,∴AH=BH,在Rt△ABE中,∵AH=HB,∴EH=HB,∵HC⊥BE,∴BG=EG,∴CB=CE=2,故选项A错误,∵CH=CH,CB=CE,HB=HE,∴△ABC≌△CEH,∴∠CBH=∠CEH=90°,∵HF=HF,HE=HA,∴Rt△HFE≌Rt△HFA,∴AF=EF,设EF=AF=x,在Rt△CDF中,有22+(2﹣x)2=(2+x)2,∴x=,∴EF=,故B错误,∵PA∥CH,∴∠CEP=∠ECH=∠BCH,∴cos∠CEP=cos∠BCH==,故C错误.∵HF=,EF=,FC=∴HF2=EF•FC,故D正确,故选:D.26.(20xx•临沂)如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是()A.9.3m B.10.5m C.12.4m D.14m【分析】先证明∴△ABE∽△ACD,则利用相似三角形的性质得=,然后利用比例性质求出CD即可.【解答】解:∵EB∥CD,∴△ABE∽△ACD,∴=,即=,∴CD=10.5(米).故选:B.27.(20xx•长春)《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为()A.五丈B.四丈五尺C.一丈D.五尺【分析】根据同一时刻物高与影长成正比可得出结论.【解答】解:设竹竿的长度为x尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,∴,解得x=45(尺).故选:B.28.(20xx•绍兴)学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为()A.0.2m B.0.3m C.0.4m D.0.5m【分析】由∠ABO=∠CDO=90°、∠AOB=∠COD知△ABO∽△CDO,据此得=,将已知数据代入即可得.【解答】解:∵AB⊥BD,CD⊥BD,∴∠ABO=∠CDO=90°,又∵∠AOB=∠COD,∴△ABO∽△CDO,则=,∵AO=4m,AB=1.6m,CO=1m,∴=,解得:CD=0.4,故选:C.二.填空题(共7小题)29.(20xx•邵阳)如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形:△ADF∽△ECF.【分析】利用平行四边形的性质得到AD∥CE,则根据相似三角形的判定方法可判断△ADF∽△ECF.【解答】解:∵四边形ABCD为平行四边形,∴AD∥CE,∴△ADF∽△ECF.故答案为△ADF∽△ECF.30.(20xx•北京)如图,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,若AB=4,AD=3,则CF的长为.【分析】根据矩形的性质可得出AB∥CD,进而可得出∠FAE=∠FCD,结合∠AFE=∠CFD(对顶角相等)可得出△AFE∽△CFD,利用相似三角形的性质可得出==2,利用勾股定理可求出AC的长度,再结合CF=•AC,即可求出CF的长.【解答】解:∵四边形ABCD为矩形,∴AB=CD,AD=BC,AB∥CD,∴∠FAE=∠FCD,又∵∠AFE=∠CFD,∴△AFE∽△CFD,∴==2.∵AC==5,∴CF=•AC=×5=.故答案为:.31.(20xx•包头)如图,在▱ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相交于点F,3AE=2EB,连接DF.若S△AEF=1,则S△ADF的值为.【分析】由3AE=2EB可设AE=2a、BE=3a,根据EF∥BC得=()2=,结合S△AEF=1知S△ADC=S△ABC=,再由==知=,继而根据S△ADF=S△ADC可得答案.【解答】解:∵3AE=2EB,∴可设AE=2a、BE=3a,∵EF∥BC,∴△AEF∽△ABC,∴=()2=()2=,∵S△AEF=1,∴S△ABC=,∵四边形ABCD是平行四边形,∴S△ADC=S△ABC=,∵EF∥BC,∴===,∴==,∴S△ADF=S△ADC=×=,故答案为:.32.(20xx•资阳)已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为9 .【分析】设四边形BCED的面积为x,则S△ADE=12﹣x,由题意知DE∥BC且DE=BC,从而得=()2,据此建立关于x的方程,解之可得.【解答】解:设四边形BCED的面积为x,则S△ADE=12﹣x,∵点D、E分别是边AB、AC的中点,∴DE是△ABC的中位线,∴DE∥BC,且DE=BC,∴△ADE∽△ABC,则=()2,即=,解得:x=9,即四边形BCED的面积为9,故答案为:9.33.(20xx•泰安)《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步面见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC 上)?请你计算KC的长为步.【分析】证明△CDK∽△DAH,利用相似三角形的性质得=,然后利用比例性质可求出CK的长.【解答】解:DH=100,DK=100,AH=15,∵AH∥DK,∴∠CDK=∠A,而∠CKD=∠AHD,∴△CDK∽△DAH,∴=,即=,∴CK=.答:KC的长为步.故答案为.。
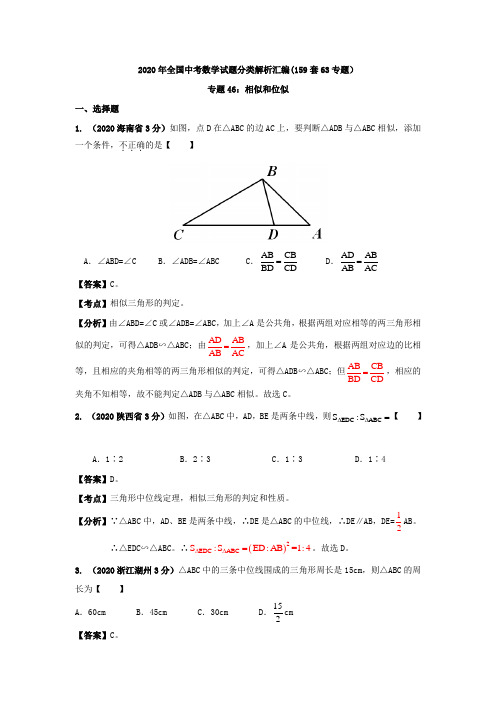
2020年全国中考数学试题分类解析汇编(159套63专题)专题46:相似和位似一、选择题1. (2020海南省3分)如图,点D 在△ABC 的边AC 上,要判断△ADB 与△ABC 相似,添加一个条件,不正确...的是【 】A .∠ABD=∠C B.∠ADB=∠ABC C.AB CB BD CD = D .AD AB AB AC= 【答案】C 。
【考点】相似三角形的判定。
【分析】由∠ABD=∠C 或∠ADB=∠ABC,加上∠A 是公共角,根据两组对应相等的两三角形相似的判定,可得△ADB∽△ABC;由AD AB AB AC=,加上∠A 是公共角,根据两组对应边的比相等,且相应的夹角相等的两三角形相似的判定,可得△ADB∽△ABC;但AB CB BD CD =,相应的夹角不知相等,故不能判定△ADB 与△ABC 相似。
故选C 。
2. (2020陕西省3分)如图,在△ABC 中,AD ,BE 是两条中线,则EDC ABC S S :∆∆=【 】A .1∶2B .2∶3C .1∶3D .1∶4【答案】D 。
【考点】三角形中位线定理,相似三角形的判定和性质。
【分析】∵△ABC 中,AD 、BE 是两条中线,∴DE 是△ABC 的中位线,∴DE∥AB,DE=12AB 。
∴△EDC∽△ABC。
∴()2EDC ABC S :S ED:AB =1:4∆∆=。
故选D 。
3. (2020浙江湖州3分)△ABC 中的三条中位线围成的三角形周长是15cm ,则△ABC 的周长为【 】A .60cmB .45cmC .30cmD .152cm 【答案】C 。
【考点】三角形中位线定理,相似三角形的性质。
【分析】∵三角形的中位线平行且等于底边的一半,∴△ABC 三条中位线围成的三角形与△ABC 相似,且相似比是12。
∵△ABC 中的三条中位线围成的三角形周长是15cm ,∴△ABC 的周长为30cm 。
故选C 。
4. (2020湖北咸宁3分)如图,正方形OABC 与正方形ODEF 是位似图形,O 为位似中心,相似比为1∶2,点A 的坐标为(1,0),则E 点的坐标为【 】.A .(2,0)B .(23,23)C .(2,2)D .(2,2)【答案】C 。

2020年全国中考数学试题分类(14)——图形的相似一.黄金分割(共1小题) 1.(2020•泸州)古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G 将一线段MN 分为两线段MG ,GN ,使得其中较长的一段MG 是全长MN 与较短的一段GN 的比例中项,即满足MM MM=MM MM=√5−12,后人把√5−12这个数称为“黄金分割”数,把点G 称为线段MN 的“黄金分割”点.如图,在△ABC 中,已知AB =AC =3,BC =4,若D ,E 是边BC 的两个“黄金分割”点,则△ADE 的面积为( )A .10﹣4√5B .3√5−5C .5−2√52D .20﹣8√5 二.平行线分线段成比例(共4小题)2.(2020•营口)如图,在△ABC 中,DE ∥AB ,且MM MM=32,则MM MM的值为( )A .35B .23C .45D .323.(2020•成都)如图,直线l 1∥l 2∥l 3,直线AC 和DF 被l 1,l 2,l 3所截,AB =5,BC =6,EF =4,则DE的长为( )A .2B .3C .4D .1034.(2020•宜宾)在Rt △ABC 中,∠ACB =90°,D 是AB 的中点,BE 平分∠ABC 交AC 于点E ,连结CD 交BE 于点O .若AC =8,BC =6,则OE 的长是 .5.(2020•无锡)如图,在Rt △ABC 中,∠ACB =90°,AB =4,点D ,E 分别在边AB ,AC 上,且DB =2AD ,AE =3EC ,连接BE ,CD ,相交于点O ,则△ABO 面积最大值为 .三.相似三角形的判定(共3小题)6.(2020•昆明)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有()A.4个B.5个C.6个D.7个7.(2020•攀枝花)如图,在边长为4的正方形ABCD中,点E、F分别是BC、CD的中点,DE、AF交于点G,AF的中点为H,连接BG、DH.给出下列结论:①AF⊥DE;②DG=85;③HD∥BG;④△ABG∽△DHF.其中正确的结论有.(请填上所有正确结论的序号)8.(2020•南京)如图,在△ABC和△A'B'C'中,D、D'分别是AB、A'B'上一点,MMMM=M′M′M′M′.(1)当MMM′M′=MMM′M′=MMM′M′时,求证△ABC∽△A'B'C'.证明的途径可以用下面的框图表示,请填写其中的空格.(2)当MMM′M′=MM M′M′=MMM′M′时,判断△ABC 与△A 'B 'C ′是否相似,并说明理由.四.相似三角形的判定与性质(共29小题) 9.(2020•贵港)如图,在△ABC 中,点D 在AB 边上,若BC =3,BD =2,且∠BCD =∠A ,则线段AD 的长为( )A .2B .52C .3D .9210.(2020•海南)如图,在▱ABCD 中,AB =10,AD =15,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F ,BG ⊥AE 于点G ,若BG =8,则△CEF 的周长为( )A .16B .17C .24D .25 11.(2020•牡丹江)如图,在矩形ABCD 中,AB =3,BC =10,点E 在BC 边上,DF ⊥AE ,垂足为F .若DF =6,则线段EF 的长为( )A .2B .3C .4D .5 12.(2020•遂宁)如图,在正方形ABCD 中,点E 是边BC 的中点,连接AE 、DE ,分别交BD 、AC 于点P 、Q ,过点P 作PF ⊥AE 交CB 的延长线于F ,下列结论: ①∠AED +∠EAC +∠EDB =90°, ②AP =FP , ③AE =√102AO ,④若四边形OPEQ 的面积为4,则该正方形ABCD 的面积为36, ⑤CE •EF =EQ •DE .其中正确的结论有( )A .5个B .4个C .3个D .2个13.(2020•遵义)如图,△ABO的顶点A在函数y=MM(x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若四边形MNQP的面积为3,则k的值为()A.9 B.12 C.15 D.1814.(2020•眉山)如图,正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.以下四个结论:①∠EAB=∠GAD;②△AFC∽△AGD;③2AE2=AH•AC;④DG⊥AC.其中正确的个数为()A.1个B.2个C.3个D.4个15.(2020•海南)如图,在矩形ABCD中,AB=6,BC=10,点E、F在AD边上,BF和CE交于点G,若EF=12AD,则图中阴影部分的面积为()A.25 B.30 C.35 D.4016.(2020•益阳)如图,在矩形ABCD中,E是DC上的一点,△ABE是等边三角形,AC交BE于点F,则下列结论不成立的是()A .∠DAE =30°B .∠BAC =45° C .MM MM=12D .MM MM=√3217.(2020•云南)如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,E 是CD 的中点.则△DEO 与△BCD 的面积的比等于( )A .12B .14C .16D .1818.(2020•潍坊)如图,点E 是▱ABCD 的边AD 上的一点,且MM MM=12,连接BE 并延长交CD 的延长线于点F ,若DE =3,DF =4,则▱ABCD 的周长为( )A .21B .28C .34D .42 19.(2020•哈尔滨)如图,在△ABC 中,点D 在BC 边上,连接AD ,点E 在AC 边上,过点E 作EF ∥BC ,交AD 于点F ,过点E 作EG ∥AB ,交BC 于点G ,则下列式子一定正确的是( )A .MM MM=MM MMB .MM MM=MM MMC .MM MM=MM MMD .MM MM=MM MM20.(2020•柳州)如图,在矩形纸片ABCD 中,AB =6,BC =10,点E 在CD 上,将△BCE 沿BE 折叠,点C 恰好落在边AD 上的点F 处,点G 在AF 上,将△ABG 沿BG 折叠,点A 恰好落在线段BF 上的H 处,有下列结论:①∠EBG =45°;②2S △BFG =5S △FGH ;③△DEF ∽△ABG ;④4CE =5ED .其中正确的是 .(填写所有正确结论的序号)21.(2020•锦州)如图,在△ABC 中,D 是AB 中点,DE ∥BC ,若△ADE 的周长为6,则△ABC 的周长为 .22.(2020•鞍山)如图,在菱形ABCD 中,∠ADC =60°,点E ,F 分别在AD ,CD 上,且AE =DF ,AF 与CE 相交于点G ,BG 与AC 相交于点H .下列结论:①△ACF ≌△CDE ;②CG 2=GH •BG ;③若DF =2CF ,则CE=7GF;④S四边形ABCG=√34BG2.其中正确的结论有.(只填序号即可)23.(2020•东营)如图,P为平行四边形ABCD边BC上一点,E、F分别为P A、PD上的点,且P A=3PE,PD=3PF,△PEF、△PDC、△P AB的面积分别记为S、S1、S2.若S=2,则S1+S2=.24.(2020•随州)如图,已知矩形ABCD中,AB=3,BC=4,点M,N分别在边AD,BC上,沿着MN折叠矩形ABCD,使点A,B分别落在E,F处,且点F在线段CD上(不与两端点重合),过点M作MH⊥BC于点H,连接BF,给出下列判断:①△MHN∽△BCF;②折痕MN的长度的取值范围为3<MN<15 4;③当四边形CDMH为正方形时,N为HC的中点;④若DF=13DC,则折叠后重叠部分的面积为5512.其中正确的是.(写出所有正确判断的序号)25.(2020•牡丹江)如图,在Rt△ABC中,CA=CB,M是AB的中点,点D在BM上,AE⊥CD,BF⊥CD,垂足分别为E,F,连接EM.则下列结论中:①BF=CE;②∠AEM=∠DEM;③AE﹣CE=√2ME;④DE2+DF2=2DM2;⑤若AE平分∠BAC,则EF:BF=√2:1;⑥CF•DM=BM•DE,正确的有.(只填序号)26.(2020•黑龙江)如图,直线AM 的解析式为y =x +1与x 轴交于点M ,与y 轴交于点A ,以OA 为边作正方形ABCO ,点B 坐标为(1,1).过点B 作EO 1⊥MA 交MA 于点E ,交x 轴于点O 1,过点O 1作x 轴的垂线交MA 于点A 1,以O 1A 1为边作正方形O 1A 1B 1C 1,点B 1的坐标为(5,3).过点B 1作E 1O 2⊥MA 交MA 于E 1,交x 轴于点O 2,过点O 2作x 轴的垂线交MA 于点A 2.以O 2A 2为边作正方形O 2A 2B 2C 2.….则点B 2020的坐标 .27.(2020•长沙)如图,点P 在以MN 为直径的半圆上运动(点P 不与M ,N 重合),PQ ⊥MN ,NE 平分∠MNP ,交PM 于点E ,交PQ 于点F . (1)MM MM+MM MM= .(2)若PN 2=PM •MN ,则MM MM= .28.(2020•临沂)如图,在△ABC 中,D 、E 为边AB 的三等分点,EF ∥DG ∥AC ,H 为AF 与DG 的交点.若AC =6,则DH = .29.(2020•咸宁)如图,四边形ABCD 是边长为2的正方形,点E 是边BC 上一动点(不与点B ,C 重合),∠AEF =90°,且EF 交正方形外角的平分线CF 于点F ,交CD 于点G ,连接AF ,有下列结论: ①△ABE ∽△ECG ; ②AE =EF ;③∠DAF =∠CFE ;④△CEF 的面积的最大值为1. 其中正确结论的序号是 .(把正确结论的序号都填上)30.(2020•泸州)如图,在矩形ABCD中,E,F分别为边AB,AD的中点,BF与EC、ED分别交于点M,N.已知AB=4,BC=6,则MN的长为.31.(2020•黑龙江)如图,直线AM的解析式为y=x+1与x轴交于点M,与y轴交于点A,以OA为边作正方形ABCO,点B坐标为(1,1).过B点作直线EO1⊥MA交MA于点E,交x轴于点O1,过点O1作x 轴的垂线交MA于点A1.以O1A1为边作正方形O1A1B1C1,点B1的坐标为(5,3).过点B1作直线E1O2⊥MA交MA于E1,交x轴于点O2,过点O2作x轴的垂线交MA于点A2.以O2A2为边作正方形O2A2B2C2,…,则点B2020的坐标.32.(2020•兰州)如图,在正方形ABCD中,对角线AC与BD相交于点O,AB=2,点E在AB的延长线上,且AE=AC,EF⊥AC于点F,连接BF并延长交CD于点G,则DG=.33.(2020•西宁)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC和DE.(1)求证:四边形ABFC是菱形;(2)若CD=1,BE=2,求⊙O的半径.34.(2020•朝阳)如图,以AB为直径的⊙O经过△ABC的顶点C,过点O作OD∥BC交⊙O于点D,交AC于点F,连接BD交AC于点G,连接CD,在OD的延长线上取一点E,连接CE,使∠DEC=∠BDC.(1)求证:EC 是⊙O 的切线;(2)若⊙O 的半径是3,DG •DB =9,求CE 的长.35.(2020•黄冈)已知:如图,AB 是⊙O 的直径,点E 为⊙O 上一点,点D 是MM̂上一点,连接AE 并延长至点C ,使∠CBE =∠BDE ,BD 与AE 交于点F . (1)求证:BC 是⊙O 的切线;(2)若BD 平分∠ABE ,求证:AD 2=DF •DB .36.(2020•杭州)如图,在△ABC 中,点D ,E ,F 分别在AB ,BC ,AC 边上,DE ∥AC ,EF ∥AB . (1)求证:△BDE ∽△EFC . (2)设MM MM=12,①若BC =12,求线段BE 的长;②若△EFC 的面积是20,求△ABC 的面积.37.(2020•杭州)如图,在正方形ABCD 中,点E 在BC 边上,连接AE ,∠DAE 的平分线AG 与CD 边交于点G ,与BC 的延长线交于点F .设MM MM=λ(λ>0).(1)若AB =2,λ=1,求线段CF 的长. (2)连接EG ,若EG ⊥AF , ①求证:点G 为CD 边的中点. ②求λ的值.五.相似三角形的应用(共4小题) 38.(2020•玉林)一个三角形木架三边长分别是75cm ,100cm ,120cm ,现要再做一个与其相似的三角形木架,而只有长为60cm 和120cm 的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有()A.一种B.两种C.三种D.四种39.(2020•山西)泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度,金字塔的影长,推算出金字塔的高度,这种测量原理,就是我们所学的()A.图形的平移B.图形的旋转C.图形的轴对称D.图形的相似40.(2020•绍兴)如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2:5,且三角板的一边长为8cm.则投影三角板的对应边长为()A.20cm B.10cm C.8cm D.3.2cm41.(2020•温州)如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C 点发现∠1=∠2.测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为米,BC为米.六.作图-相似变换(共1小题)42.(2020•济宁)如图,在△ABC中,AB=AC,点P在BC上.(1)求作:△PCD,使点D在AC上,且△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)(2)在(1)的条件下,若∠APC=2∠ABC.求证:PD∥AB.七.位似变换(共4小题)43.(2020•重庆)如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为()A .1:2B .1:3C .1:4D .1:544.(2020•重庆)如图,在平面直角坐标系中,△ABC 的顶点坐标分别是A (1,2),B (1,1),C (3,1),以原点为位似中心,在原点的同侧画△DEF ,使△DEF 与△ABC 成位似图形,且相似比为2:1,则线段DF 的长度为( )A .√5B .2C .4D .2√545.(2020•兰州)如图,四边形ABCD 与四边形A ′B ′C ′D ′位似,位似中心为点O ,OC =6,CC ′=4,AB =3,则A ′B ′= .46.(2020•盘锦)如图,△AOB 三个顶点的坐标分别为A (5,0),O (0,0),B (3,6),以点O 为位似中心,相似比为23,将△AOB 缩小,则点B 的对应点B '的坐标是 . 八.作图-位似变换(共2小题)47.(2020•朝阳)如图所示的平面直角坐标系中,△ABC 的三个顶点坐标分别为A (﹣3,2),B (﹣1,3),C (﹣1,1),请按如下要求画图:(1)以坐标原点O 为旋转中心,将△ABC 顺时针旋转90°,得到△A 1B 1C 1,请画出△A 1B 1C 1;(2)以坐标原点O 为位似中心,在x 轴下方,画出△ABC 的位似图形△A 2B 2C 2,使它与△ABC 的位似比为2:1.48.(2020•宁夏)在平面直角坐标系中,△ABC 的三个顶点的坐标分别是A (1,3),B (4,1),C (1,1).(1)画出△ABC 关于x 轴成轴对称的△A 1B 1C 1;(2)画出△ABC 以点O 为位似中心,位似比为1:2的△A 2B 2C 2.九.相似形综合题(共2小题)49.(2020•荆州)如图,在矩形ABCD 中,AB =20,点E 是BC 边上的一点,将△ABE 沿着AE 折叠,点B 刚好落在CD 边上点G 处;点F 在DG 上,将△ADF 沿着AF 折叠,点D 刚好落在AG 上点H 处,此时S △GFH :S △AFH =2:3,(1)求证:△EGC ∽△GFH ;(2)求AD 的长;(3)求tan ∠GFH 的值.50.(2020•福建)如图,△ADE 由△ABC 绕点A 按逆时针方向旋转90°得到,且点B 的对应点D 恰好落在BC 的延长线上,AD ,EC 相交于点P .(1)求∠BDE 的度数;(2)F 是EC 延长线上的点,且∠CDF =∠DAC .①判断DF 和PF 的数量关系,并证明;②求证:MM MM =MM MM .2020年全国中考数学试题分类(14)——图形的相似参考答案与试题解析一.黄金分割(共1小题)1.【解答】解:作AH ⊥BC 于H ,如图,∵AB =AC ,∴BH =CH =12BC =2,在Rt △ABH 中,AH =√32−22=√5,∵D ,E 是边BC 的两个“黄金分割”点,∴BE =√5−12BC =2(√5−1)=2√5−2,∴HE =BE ﹣BH =2√5−2﹣2=2√5−4,∴DE =2HE =4√5−8∴S △ADE =12×(4√5−8)×√5=10﹣4√5.故选:A .二.平行线分线段成比例(共4小题)2.【解答】解:∵DE ∥AB ,∴MM MM =MM MM =32, ∴MM MM 的值为35,故选:A .3.【解答】解:∵直线l 1∥l 2∥l 3,∴MM MM=MM MM , ∵AB =5,BC =6,EF =4, ∴56=MM 4,∴DE =103, 故选:D .4.【解答】解:在Rt △ACB 中,∠ACB =90°,AC =8,BC =6,由勾股定理得:AB =10, 过A 作AF ∥BC ,交BE 延长线于F ,∵AF ∥BC ,∴∠F =∠CBE ,∵BE 平分∠ABC ,∴∠ABE =∠CBE ,∴∠F =∠ABE ,∴AB =AF =10,∵AF ∥BC ,∴△AEF ∽△CEB ,∴MM MM =MM MM , ∴106=MM 8−MM,解得:AE =5,CE =8﹣5=3,在Rt △ECB 中,由勾股定理得:BE =√62+32=3√5,过D 作DM ∥AC ,交BC 于M ,交BE 于N ,∵D 为AB 的中点,DM ∥AC ,∴M 为BC 的中点,N 为BE 的中点,∴DN =12AE =12×5=2.5,BN =NE =12BE =3√52,∵DM ∥AC ,∴△DNO ∽△CEO ,∴MM MM =MM MM , ∴2.53=3√52−MM MM , 解得:OE =9√511, 故答案为:9√511.5.【解答】解:如图,过点D 作DF ∥AE , 则MM MM =MM MM =23, ∵MM MM =13,∴DF =2EC ,∴DO =2OC ,∴DO =23DC ,∴S △ADO =23S △ADC ,S △BDO =23S △BDC ,∴S △ABO =23S △ABC , ∵∠ACB =90°,∴C 在以AB 为直径的圆上,设圆心为G ,当CG ⊥AB 时,△ABC 的面积最大为:12×4×2=4,此时△ABO 的面积最大为:23×4=83.故答案为:83.三.相似三角形的判定(共3小题)6.【解答】解:如图,所以使得△ADE ∽△ABC 的格点三角形一共有6个.故选:C .7.【解答】解:∵四边形ABCD 为正方形,∴∠ADC =∠BCD =90°,AD =CD ,∵E 和F 分别为BC 和CD 中点,∴DF =EC =2,∴△ADF ≌△DCE (SAS ),∴∠AFD =∠DEC ,∠F AD =∠EDC ,∵∠EDC +∠DEC =90°,∴∠EDC +∠AFD =90°,∴∠DGF =90°,即DE ⊥AF ,故①正确;∵AD =4,DF =12CD =2,∴AF =√42+22=2√5,∴DG =AD ×DF ÷AF =4√55,故②错误;∵H 为AF 中点,∴HD =HF =12AF =√5, ∴∠HDF =∠HFD ,∵AB ∥DC ,∴∠HDF =∠HFD =∠BAG ,∵AG =√MM 2−MM 2=8√55,AB =4, ∴MM MM =MM MM =4√55=MM MM ,∴△ABG ~△DHF ,故④正确;∴∠ABG =∠DHF ,而AB ≠AG ,则∠ABG 和∠AGB 不相等,故∠AGB ≠∠DHF ,故HD 与BG 不平行,故③错误;故答案为:①④.8.【解答】(1)证明:∵MM MM =M′M′M′M′, ∴MM M′M′=MM M′M′, ∵MM M′M′=MM M′M′=MM M′M′, ∴MM M′M′=MM M′M′=MM M′M′, ∴△ADC ∽△A ′D ′C ', ∴∠A =∠A ′, ∵MM M′M′=MM M′M′,∴△ABC ∽△A ′B ′C ′. 故答案为:MM M′M′=MM M′M′=MM M′M′,∠A =∠A ′.(2)如图,过点D ,D ′分别作DE ∥BC ,D ′E ′∥B ′C ′,DE 交AC 于E ,D ′E ′交A ′C ′于E ′.∵DE ∥BC ,∴△ADE ∽△ABC ,∴MM MM =MM MM =MM MM , 同理,M′M′M′M′=M′M′M′M′=M′M′M′M′, ∵MM MM =M′M′M′M′, ∴MM MM =M′M′M′M′,∴MM M′M′=MM M′M′, 同理,MM MM =M′M′M′M′, ∴MM −MM MM =M′M′−M′M′M′M′,即MM MM =M′M′M′M′, ∴MM M′M′=MM M′M′, ∵MM M′M′=MM M′M′=MM M′M′, ∴MM M′M′=MM M′M′=MM M′M′,∴△DCE ∽△D ′C ′E ′,∴∠CED =∠C ′E ′D ′,∴∠CED +∠ACB =180°,同理,∠C ′E ′D ′+∠A ′C ′B ′=180°,∴∠ACB =∠A ′C ′B ′,∵MM M′M′=MM M′M′, ∴△ABC ∽△A ′B ′C ′.四.相似三角形的判定与性质(共29小题)9.【解答】解:∵∠BCD =∠A ,∠B =∠B ,∴△BCD ∽△BAC ,∴MM MM=MM MM , ∵BC =3,BD =2, ∴3MM =23, ∴BA =92, ∴AD =BA ﹣BD =92−2=52.故选:B .10.【解答】解:∵在▱ABCD 中,CD =AB =10,BC =AD =15,∠BAD 的平分线交BC 于点E , ∴AB ∥DC ,∠BAF =∠DAF ,∴∠BAF =∠F ,∴∠DAF =∠F ,∴DF =AD =15,同理BE =AB =10,∴CF =DF ﹣CD =15﹣10=5;∴在△ABG 中,BG ⊥AE ,AB =10,BG =8,在Rt △ABG 中,AG =√MM 2−MM 2=√102−82=6,∴AE =2AG =12,∴△ABE 的周长等于10+10+12=32,∵四边形ABCD 是平行四边形,∴AB ∥CF ,∴△CEF ∽△BEA ,相似比为5:10=1:2,∴△CEF 的周长为16.故选:A .11.【解答】解:∵四边形ABCD 为矩形,∴AB =CD =3,BC =AD =10,AD ∥BC ,∴∠AEB =∠DAF ,∴△AFD ∽△EBA ,∴MM MM =MM MM =MM MM ,∵DF =6,∴AF =√MM 2−MM 2=√102−62=8,∴8MM =10MM =63,∴EF =AF ﹣AE =8﹣5=3.故选:B .12.【解答】解:如图,连接OE .∵四边形ABCD 是正方形,∴AC ⊥BD ,OA =OC =OB =OD ,∴∠BOC =90°,∵BE =EC ,∴∠EOB =∠EOC =45°,∵∠EOB =∠EDB +∠OED ,∠EOC =∠EAC +∠AEO ,∴∠AED +∠EAC +∠EDO =∠EAC +∠AEO +∠OED +∠EDB =90°,故①正确, 连接AF .∵PF ⊥AE ,∴∠APF =∠ABF =90°,∴A ,P ,B ,F 四点共圆,∴∠AFP =∠ABP =45°,∴∠P AF =∠PF A =45°,∴P A =PF ,故②正确,设BE =EC =a ,则AE =√5a ,OA =OC =OB =OD =√2a ,∴MM MM =√5M √2M =√102,即AE =√102AO ,故③正确, 根据对称性可知,△OPE ≌△OQE ,∴S △OEQ =12S 四边形OPEQ =2,∵OB =OD ,BE =EC ,∴CD =2OE ,OE ∥CD ,∴MMMM =MMMM =12,△OEQ ∽△CDQ , ∴S △ODQ =4,S △CDQ =8,∴S △CDO =12,∴S 正方形ABCD =48,故④错误,∵∠EPF =∠DCE =90°,∠PEF =∠DEC ,∴△EPF ∽△ECD ,∴MMMM =MMMM ,∵EQ =PE ,∴CE •EF =EQ •DE ,故⑤正确,故选:B .13.【解答】解:∵NQ ∥MP ∥OB ,∴△ANQ ∽△AMP ∽△AOB ,∵M 、N 是OA 的三等分点,∴MM MM =12,MM MM =13, ∴M △MMMM △MMM =14,∵四边形MNQP 的面积为3, ∴M △MMM3+M △MMM=14, ∴S △ANQ =1, ∵1M △MMM =(MM MM )2=19,∴S △AOB =9,∴k =2S △AOB =18,故选:D .14.【解答】解:∵四边形ABCD ,四边形AEFG 都是正方形,∴∠EAG =∠BAD =90°,∠F AG =∠AFG =∠DAC =∠ACB =45°,AF =√2AG ,AC =√2AD , ∴∠EAG ﹣∠BAG =∠BAD ﹣∠BAG ,∴∠EAB =∠DAG ,故①正确;∵AF =√2AG ,AC =√2AD ,∴MM MM =√2=MM MM , ∵∠F AG =∠CAD =45°,∴∠F AC =∠DAG ,∴△F AC ∽△DAG ,故②正确,∴∠ADG =∠ACB =45°,延长DG 交AC 于N ,∵∠CAD =45°,∠ADG =45°,∴∠AND =90°,∴DG ⊥AC ,故④正确,∵∠F AC =∠F AH ,∠AFG =∠ACF =45°,∴△AFH ∽△ACF ,∴MM MM =MM MM ,∴AF 2=AH •AC ,∴2AE 2=AH •AC ,故③正确,故选:D .15.【解答】解:过点G 作GN ⊥AD 于N ,延长NG 交BC 于M ,∵四边形ABCD 是矩形,∴AD =BC ,AD ∥BC ,∵EF =12AD , ∴EF =12BC ,∵AD ∥BC ,NG ⊥AD ,∴△EFG ∽△CBG ,GM ⊥BC ,∴GN :GM =EF :BC =1:2,又∵MN =AB =6,∴GN =2,GM =4,∴S △BCG =12×10×4=20,∴S △EFG =12×5×2=5,S 矩形ABCD =6×10=60,∴S 阴影=60﹣20﹣5=35.故选:C .16.【解答】解:∵四边形ABCD 是矩形,△ABE 是等边三角形,∴AB =AE =BE ,∠EAB =∠EBA =60°,AD =BC ,∠DAB =∠CBA =90°,AB ∥CD ,AB =CD , ∴∠DAE =∠CBE =30°,故选项A 不合题意,∴cos ∠DAE =√32=MM MM =MM MM ,故选项D 不合题意,在△ADE 和△BCE 中,{MM =MM MMMM =MMMM MM =MM ,∴△ADE ≌△BCE (SAS ),∴DE =CE =12CD =12AB ,∵AB ∥CD ,∴△ABF ∽△CEF ,∴MM MM =MM MM =12,故选项C 不合题意, 故选:B .17.【解答】解:∵平行四边形ABCD 的对角线AC ,BD 相交于点O ,∴点O 为线段BD 的中点.又∵点E 是CD 的中点,∴线段OE 为△DBC 的中位线,∴OE ∥BC ,OE =12BC , ∴△DOE ∽△DBC ,∴M △MMMM △MMM =(MM MM )2=14. 故选:B .18.【解答】解:∵四边形ABCD 是平行四边形,∴AB ∥CF ,AB =CD ,∴△ABE ∽△DFE ,∴MM MM =MM MM =12,∵DE =3,DF =4,∴AE =6,AB =8,∴AD =AE +DE =6+3=9,∴平行四边形ABCD 的周长为:(8+9)×2=34.故选:C .19.【解答】解:∵EF ∥BC ,∴MM MM=MM MM , ∵EG ∥AB , ∴MM MM =MM MM , ∴MM MM =MM MM ,故选:C .20.【解答】解:①由折叠的性质可知:∠CBE =∠FBE ,∠ABG =∠FBG , ∵四边形ABCD 是矩形,∴∠ABC =90°,∴∠EBG =∠GBH +∠EBF =12∠CBF +12∠ABF =12∠ABC =45°. 故①正确;②由折叠的性质可知:BF =BC =10,BH =AB =6,∴HF =BF ﹣BH =4,∴M △MMMM △MMM =MM MM =104=52, ∴2S △BFG =5S △FGH ;故②正确;③∵四边形ABCD 是矩形,∴∠A =∠D =90°,在Rt △ABF 中,AF =√MM 2−MM 2=8,设GF =x ,即HG =AG =8﹣x ,在Rt △HGF 中,HG 2+HF 2=GF 2,即(8﹣x )2+42=x 2,解得x =5,∴AG =3,∴FD =2;同理可得ED =83,∴MM MM =63=2, MM MM =832=43, ∴MM MM ≠MM MM , ∴△ABG 与△DEF 不相似,故③错误;④∵CD =AB =6,ED =83,∴CE =CD ﹣ED =103,∴MM MM =54,∴4CE =5ED .故④正确.综上所述,正确的结论的序号为①②④.21.【解答】解:∵DE ∥BC ,∴△ADE ∽△ABC ,∵D 是AB 的中点,∴MM MM =12, ∴△MMM 的周长△MMM 的周长=12 ∵△ADE 的周长为6,∴△ABC 的周长为12,故答案为:12.22.【解答】解:∵ABCD 为菱形,∴AD =CD ,∵AE =DF ,∴DE =CF ,∵∠ADC =60°,∴△ACD 为等边三角形,∴∠D =∠ACD =60°,AC =CD ,∴△ACF ≌△CDE (SAS ),故①正确;过点F 作FP ∥AD ,交CE 于P 点.∵DF =2CF ,∴FP :DE =CF :CD =1:3,∵DE =CF ,AD =CD ,∴AE =2DE ,∴FP :AE =1:6=FG :AG ,∴AG =6FG ,∴CE =AF =7GF ,故③正确;过点B 作BM ⊥AG 于M ,BN ⊥GC 于N ,∵∠AGE =∠ACG +∠CAF =∠ACG +∠GCF =60°=∠ABC , 即∠AGC +∠ABC =180°,∴点A 、B 、C 、G 四点共圆,∴∠AGB =∠ACB =60°,∠CGB =∠CAB =60°,∴∠AGB =∠CGB =60°,∴BM =BN ,又AB =BC ,∴△ABM ≌△CBN (HL ),∴S 四边形ABCG =S 四边形BMGN ,∵∠BGM =60°,∴GM =12BG ,BM =√32BG ,∴S 四边形BMGN =2S △BMG =2×12×12MM ×√32MM =√34BG 2,故④正确; ∵∠CGB =∠ACB =60°,∠CBG =∠HBC ,∴△BCH ∽△BGC ,∴MM MM =MM MM =MM MM ,则BG •BH =BC 2,则BG •(BG ﹣GH )=BC 2,则BG 2﹣BG •GH =BC 2,则GH •BG =BG 2﹣BC 2,当∠BCG =90°时,BG 2﹣BC 2=CG 2,此时GH •BG =CG 2, 而题中∠BCG 未必等于90°,故②不成立,故正确的结论有①③④,故答案为:①③④.23.【解答】解:∵P A =3PE ,PD =3PF ,∴MM MM =MM MM =13, ∴EF ∥AD ,∴△PEF ∽△P AD ,∴M △MMMM △MMM =(13)2, ∵S △PEF =2,∴S △P AD =18,∵四边形ABCD是平行四边形, ∴S △P AD =12S 平行四边形ABCD ,∴S 1+S 2=S △P AD =18,故答案为18.24.【解答】解:①如图1,由折叠可知BF ⊥MN ,∴∠BOM =90°,∵MH ⊥BC ,∴∠BHP =90°=∠BOM ,∵∠BPH =∠OPM ,∴∠CBF =∠NMH ,∵∠MHN =∠C =90°,∴△MHN ∽△BCF ,故①正确;②当F 与C 重合时,MN =3,此时MN 最小,当F 与D 重合时,如图2,此时MN 最大,由勾股定理得:BD =5,∵OB =OD =52,∵tan ∠DBC =MM MM =MM MM ,即MM 52=34, ∴ON =158, ∵AD ∥BC ,∴∠MDO =∠OBN ,在△MOD 和△NOB 中,∵{∠MMM =∠MMMMM =MM MMMM =MMMM,∴△DOM ≌△BON (ASA ),∴OM =ON ,∴MN =2ON =154,∵点F 在线段CD 上(不与两端点重合),∴折痕MN 的长度的取值范围为3<MN <154; 故②正确;③如图3,连接BM ,FM ,当四边形CDMH 为正方形时,MH =CH =CD =DM =3,∵AD =BC =4,∴AM =BH =1,由勾股定理得:BM =√32+12=√10,∴FM =√10,∴DF =√MM 2−MM 2=√(√10)2−32=1,∴CF =3﹣1=2,设HN =x ,则BN =FN =x +1,在Rt △CNF 中,CN 2+CF 2=FN 2,∴(3﹣x )2+22=(x +1)2,解得:x =32,∴HN =32,∵CH =3,∴CN =HN =32,∴N 为HC 的中点;故③正确;④如图4,连接FM ,∵DF =13DC ,CD =3,∴DF =1,CF =2, ∴BF =√22+42=2√5,∴OF =√5,设FN =a ,则BN =a ,CN =4﹣a ,由勾股定理得:FN 2=CN 2+CF 2,∴a 2=(4﹣a )2+22,∴a =52,∴BN =FN =52,CN =32,∵∠NFE =∠CFN +∠DFQ =90°,∠CFN +∠CNF =90°,∴∠DFQ =∠CNF ,∵∠D =∠C =90°,∴△QDF ∽△FCN ,∴MM MM =MM MM ,即MM 2=132,∴QD =43,∵tan ∠HMN =tan ∠CBF =MM MM =MM MM ,∴MM 3=24,∴HN =32,∴MN =√32+(32)2=3√52,∵CH =MD =HN +CN =32+32=3,∴MQ =3−43=53,∴折叠后重叠部分的面积为:S△MNF+S△MQF=12⋅MM⋅MM+12⋅MM⋅MM=12×3√52×√5+12×53×1=5512;法二:折叠后重叠部分的面积为:S△MNF+S△MQF=S正方形CDMH﹣S△QDF﹣S△NFC﹣S△MNH=3×3−12×43×1−12×32×2−12×32×3=5512;故④正确;所以本题正确的结论有:①②③④;故答案为:①②③④.25.【解答】解:∵∠ACB=90°,∴∠BCF+∠ACE=90°,∵∠BCF+∠CBF=90°,∴∠ACE=∠CBF,又∵∠BFD=90°=∠AEC,AC=BC,∴△BCF≌△CAE(AAS),∴BF=CE,故①正确;由全等可得:AE=CF,BF=CE,∴AE﹣CE=CF﹣CE=EF,连接FM,CM,∵点M是AB中点,∴CM=12AB=BM=AM,CM⊥AB,在△BDF和△CDM中,∠BFD=∠CMD,∠BDF=∠CDM,∴∠DBF=∠DCM,又BM=CM,BF=CE,∴△BFM≌△CEM(SAS),∴FM=EM,∠BMF=∠CME,∵∠BMC=90°,∴∠EMF=90°,即△EMF为等腰直角三角形,∴EF=√2EM=AE﹣CE,故③正确,∠MEF=∠MFE=45°,∵∠AEC=90°,∴∠MEF=∠AEM=45°,故②正确,设AE与CM交于点N,连接DN,∵∠DMF=∠NME,FM=EM,∠DFM=∠DEM=∠AEM=45°,∴△DFM≌△NEM(ASA),∴DF=EN,DM=MN,∴△DMN为等腰直角三角形,∴DN=√2DM,而∠DEA=90°,∴DE2+DF2=DN2=2DM2,故④正确;∵AC=BC,∠ACB=90°,∴∠CAB=45°,∵AE平分∠BAC,∴∠DAE=∠CAE=22.5°,∠ADE=67.5°,∵∠DEM=45°,∴∠EMD=67.5°,即DE=EM,∵AE=AE,∠AED=∠AEC,∠DAE=∠CAE,∴△ADE≌△ACE(ASA),∴DE=CE,∵△MEF 为等腰直角三角形,∴EF =√2EM ,∴MM MM=MM MM =MM MM =√2MM MM =√2,故⑤正确; ∵∠CDM =∠ADE ,∠CMD =∠AED =90°, ∴△CDM ∽△ADE , ∴MM MM=MM MM =MM MM , ∵BM =CM ,AE =CF , ∴MM MM =MM MM ,∴CF •DM =BM •DE ,故⑥正确;故答案为:①②③④⑤⑥.26.【解答】解:∵点B 坐标为(1,1),∴OA =AB =BC =CO =CO 1=1,∵A 1(2,3),∴A 1O 1=A 1B 1=B 1C 1=C 1O 2=3,∴B 1(5,3),∴A 2(8,9),∴A 2O 2=A 2B 2=B 2C 2=C 2O 3=9,∴B 2(17,9),同理可得B 3(53,27),B 4(161,81),…由上可知,B n (2×3n ﹣1,3n ),∴当n =2020时,B n (2×32020﹣1,32020).故答案为:(2×32020﹣1,32020).27.【解答】解:(1)∵MN 为⊙O 的直径,∴∠MPN =90°,∵PQ ⊥MN ,∴∠PQN =∠MPN =90°,∵NE 平分∠PNM ,∴∠MNE =∠PNE ,∴△PEN ∽△QFN ,∴MM MM =MM MM ,即MM MM =MM MM ①,∵∠PNQ +∠NPQ =∠PNQ +∠PMQ =90°,∴∠NPQ =∠PMQ ,∵∠PQN =∠PQM =90°,∴△NPQ ∽△PMQ ,∴MM MM =MM MM ②, ∴①×②得MM MM =MM MM , ∵QF =PQ ﹣PF , ∴MM MM =MM MM =1−MM MM , ∴MM MM +MM MM =1,故答案为:1;(2)∵∠PNQ =∠MNP ,∠NQP =∠NPM ,∴△NPQ ∽△NMP ,∴MM MM =MM MM ,∴PN 2=QN •MN ,∵PN 2=PM •MN ,∴PM =QN ,∴MM MM =MM MM , ∵cos ∠M =MM MM =MM MM , ∴MM MM =MM MM , ∴MM MM=MM MM +MM , ∴NQ 2=MQ 2+MQ •NQ ,即1=MM 2MM 2+MM MM , 设MM MM=M ,则x 2+x ﹣1=0, 解得,x =√5−12,或x =−√5+12<0(舍去), ∴MM MM =√5−12, 故答案为:√5−12.28.【解答】解:∵D 、E 为边AB 的三等分点,EF ∥DG ∥AC , ∴BE =DE =AD ,BF =GF =CG ,AH =HF ,∴AB =3BE ,DH 是△AEF 的中位线,∴DH =12EF ,∵EF ∥AC , ∴△BEF ∽△BAC , ∴MM MM =MM MM ,即MM 6=MM 3MM ,解得:EF =2, ∴DH =12EF =12×2=1,故答案为:1.29.【解答】解:①∵四边形ABCD 是正方形,∴∠B =∠ECG =90°,∵∠AEF =90°,∴∠AEB +∠CEG =∠AEB +∠BAE ,∴∠BAE =∠CEG ,∴△ABE ∽△ECG ,故①正确;②在BA 上截取BM =BE ,如图1,∵四边形ABCD 为正方形,∴∠B =90°,BA =BC ,∴△BEM 为等腰直角三角形,∴∠BME =45°,∴∠AME =135°,∵BA ﹣BM =BC ﹣BE ,∴AM =CE ,∵CF 为正方形外角平分线,∴∠DCF =45°,∴∠ECF =135°,∵∠AEF =90°,∴∠AEB +∠FEC =90°,而∠AEB +∠BAE =90°,∴∠BAE =∠FEC ,在△AME 和△ECF 中{∠MMM =∠MMM MM =MM MMMM =MMMM,∴△AME ≌△ECF (ASA ),∴AE =EF ,故②正确;③∵AE =EF ,∠AEF =90°,∴∠EAF =45°,∴∠BAE +∠DAF =45°,∵∠BAE +∠CFE =∠CEF +∠CFE =45°, ∴∠DAF =∠CFE ,故③正确;④设BE =x ,则BM =x ,AM =AB ﹣BM =2﹣x , S △ECF =S △AME =12•x •(2﹣x )=−12(x ﹣1)2+12, 当x =1时,S △ECF 有最大值12,故④错误.故答案为:①②③. 30.【解答】解:延长CE 、DA 交于Q ,如图1, ∵四边形ABCD 是矩形,BC =6,∴∠BAD =90°,AD =BC =6,AD ∥BC , ∵F 为AD 中点,∴AF =DF =3,在Rt △BAF 中,由勾股定理得:BF =√MM 2+MM 2=√42+32=5,∵AD ∥BC ,∴∠Q =∠ECB ,∵E 为AB 的中点,AB =4,∴AE =BE =2,在△QAE 和△CBE 中{∠MMM =∠MMM MM =MMMMMM =MM∴△QAE ≌△CBE (AAS ),∴AQ =BC =6,即QF =6+3=9,∵AD ∥BC ,∴△QMF ∽△CMB ,∴MM MM =MM MM =96, ∵BF =5,∴BM =2,FM =3,延长BF 和CD ,交于W ,如图2,同理AB =DW =4,CW =8,BF =FW =5,∵AB ∥CD ,∴△BNE ∽△WND ,∴MM MM =MM MM , ∴MM 5−MM +5=24, 解得:BN =103, ∴MN =BN ﹣BM =103−2=43, 故答案为:43.31.【解答】解:∵点B 坐标为(1,1),∴OA =AB =BC =CO =CO 1=1,∵A 1(2,3),∴A 1O 1=A 1B 1=B 1C 1=C 1O 2=3,∴B 1(5,3),∴A 2(8,9),∴A 2O 2=A 2B 2=B 2C 2=C 2O 3=9,∴B 2(17,9),同理可得B 3(53,27),B 4(161,81),…由上可知,M M (2×3M −1,3M ),∴当n =2020时,M M (2×32020−1,32020).故答案为:(2×32020﹣1,32020).32.【解答】解:∵四边形ABCD 是正方形,∴AB =BC =CD =AD =2,∠BDC =∠EAF =45°,AC ⊥BD ,BD =AC =2√2,∵AE =AC =2√2,∠EF A =∠CBA ,∠EAF =∠BAC =45°,∴△AEF ≌△ACB (AAS ),∴∠E =∠ACB =45°,EF =BC =2,AF =AB =2,∴∠E =∠BDG ,∵EF ⊥AC ,AC ⊥BD ,∴EF ∥BD ,∴∠EFB =∠DBG ,∴△EBF ∽△DGB ,∴MM MM =MM MM , ∴2√2−2MM =2√2, ∴DG =4﹣2√2,故答案为:4﹣2√2,33.【解答】(1)证明:∵AB 为⊙O 的直径,∴∠AEB =90°(直径所对的圆周角是直角),∴AF ⊥BC .∵在△ABC 中 AB =AC ∴CE =BE (等腰三角形三线合一),∵AE =EF .∴四边形ABFC 是平行四边形(对角线互相平分的四边形是平行四边形).又∵AF ⊥BC ,∴▱ABFC 是菱形(对角线互相垂直的平行四边形是菱形).(2)解:∵圆内接四边形ABED ,∴∠ADE +∠ABC =180°(圆内接四边形的对角互补).∵∠ADE +∠CDE =180°,∴∠ABC =∠CDE .∵∠ACB =∠ECD (公共角).∴△ECD ∽△ACB (两角分别对应相等的两个三角形相似).∴MM MM =MMMM (相似三角形的对应边成比例).∵四边形ABFC 是菱形,∴MM =MM =12MM =2.∴CE =2BC =4.∴2MM =14. ∴AC =8.∴AB =AC =8.∴⊙O 的半径为4.34.【解答】解:(1)证明:如图,连接OC ,∵AB 是直径,∴∠ACB =90°,∵OD ∥BC ,∴∠CFE =∠ACB =90°,∴∠DEC +∠FCE =90°,∵∠DEC =∠BDC ,∠BDC =∠A ,∴∠DEC =∠A ,∵OA =OC ,∴∠OCA =∠A ,∴∠OCA =∠DEC ,∵∠DEC +∠FCE =90°,∴∠OCA +∠FCE =90°,即∠OCE =90°,∴OC ⊥CE ,又∵OC 是⊙O 的半径,∴CE 是⊙O 切线.(2)由(1)得∠CFE =90°,∴OF ⊥AC ,∵OA =OC ,∴∠COF =∠AOF ,∴MM̂=MM ̂, ∴∠ACD =∠DBC ,又∵∠BDC =∠BDC ,∴△DCG ∽△DBC ,∴MM MM =MM MM ,∴DC 2=DG •DB =9,∴DC =3,∵OC =OD =3,∴△OCD 是等边三角形,∴∠DOC =60°,在Rt △OCE 中MMM60°=MM MM, ∴√3=MM 3, ∴MM =3√3.35.【解答】证明:(1)∵AB 是⊙O 的直径,∴∠AEB =90°,∴∠EAB +∠EBA =90°,∵∠CBE =∠BDE ,∠BDE =∠EAB ,∴∠EAB =∠CBE ,∴∠EBA +∠CBE =90°,即∠ABC =90°,∴CB ⊥AB ,∵AB 是⊙O 的直径,∴BC 是⊙O 的切线;(2)证明:∵BD 平分∠ABE ,∴∠ABD =∠DBE ,∵∠DAF =∠DBE ,∴∠DAF =∠ABD ,∵∠ADB =∠ADF ,∴△ADF ∽△BDA ,∴MM MM =MM MM ,∴AD 2=DF •DB .36.【解答】(1)证明:∵DE ∥AC ,∴∠DEB =∠FCE ,∵EF ∥AB ,∴∠DBE =∠FEC ,∴△BDE ∽△EFC ;(2)解:①∵EF ∥AB ,∴MM MM =MM MM =12, ∵EC =BC ﹣BE =12﹣BE , ∴MM12−MM=12, 解得:BE =4; ②∵MM MM =12, ∴MM MM =23,∵EF ∥AB ,∴△EFC ∽△BAC ,∴M △MMMM △MMM =(MM MM )2=(23)2=49, ∴S △ABC =94S △EFC =94×20=45. 37.【解答】解:(1)∵在正方形ABCD 中,AD ∥BC ,∴∠DAG =∠F ,又∵AG 平分∠DAE ,∴∠DAG =∠EAG ,∴∠EAG =∠F ,∴EA =EF ,∵AB =2,∠B =90°,点E 为BC 的中点,∴BE =EC =1,∴AE =√MM 2+MM 2=√5,∴EF =√5,∴CF =EF ﹣EC =√5−1;(2)①证明:∵EA =EF ,EG ⊥AF ,∴AG =FG ,在△ADG 和△FCG 中{∠M =∠MMM MMMM =MMMM MM =MM,∴△ADG ≌△FCG (AAS ),∴DG =CG ,即点G 为CD 的中点;②设CD =2a ,则CG =a ,由①知,CF =DA =2a ,∵EG ⊥AF ,∠GCF =90°,∴∠EGC +∠CGF =90°,∠F +∠CGF =90°,∠ECG =∠GCF =90°,∴∠EGC =∠F ,∴△EGC ∽△GFC ,∴MM MM=MM MM , ∵GC =a ,FC =2a , ∴MM MM =12, ∴MM MM =12, ∴EC =12a ,BE =BC ﹣EC =2a −12a =32a ,∴λ=MM MM =12M 32M=13.五.相似三角形的应用(共4小题)38.【解答】解:长120cm 的木条与三角形木架的最长边相等,要满足两边之和大于第三边,则长120cm 的木条不能作为一边,设从120cm 的木条上截下两段长分别为xcm ,ycm (x +y ≤120),由于长60cm 的木条不能与75cm 的一边对应,否则x +y >120cm ,当长60cm 的木条与100cm 的一边对应,则M 75=M 120=60100, 解得:x =45,y =72; 当长60cm 的木条与120cm 的一边对应,则M 75=M 100=60120,解得:x =37.5,y =50.∴有两种不同的截法:把120cm 的木条截成45cm 、72cm 两段或把120cm 的木条截成37.5cm 、50cm 两段.故选:B .39.【解答】解:泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度,金字塔的影长,推算出金字塔的高度,这种测量原理,就是我们所学的图形的相似,故选:D .40.【解答】解:设投影三角尺的对应边长为xcm ,∵三角尺与投影三角尺相似,∴8:x =2:5,解得x =20.故选:A .41.【解答】解:∵AE ⊥l ,BF ⊥l ,∵∠ANE =45°,∴△ANE 和△BNF 是等腰直角三角形,∴AE =EN ,BF =FN ,∴EF =15米,FM =2米,MN =8米,∴AE =EN =15+2+8=25(米),BF =FN =2+8=10(米),∴AN =25√2(米),BN =10√2(米),∴AB =AN ﹣BN =15√2(米);过C 作CH ⊥l 于H ,过B 作PQ ∥l 交AE 于P ,交CH 于Q ,∴AE ∥CH ,∴四边形PEHQ 和四边形PEFB 是矩形,∴PE =BF =QH =10,PB =EF =15,BQ =FH ,∵∠1=∠2,∠AEF =∠CHM =90°,∴△AEF ∽△CHM ,∴MM MM =MM MM =2515=53, ∴设MH =3x ,CH =5x ,∵CQ =5x ﹣10,BQ =FH =3x +2,∵∠APB =∠ABC =∠CQB =90°,∴∠ABP +∠P AB =∠ABP +∠CBQ =90°,∴∠P AB =∠CBQ ,∴△APB ∽△BQC ,∴MM MM =MM MM ,∴153M +2=155M −10,∴x =6,∴BQ =CQ =20,∴BC =20√2(米),方法二:∵∠ANE =45°,∴∠ABP =45°,∴∠CBQ =45°,∴CQ =BQ ,∵CQ =5x ﹣10,BQ =FH =3x +2,∴5x ﹣10=3x +2,∴x =6,∴BQ =CQ =20,∴BC =20√2(米),故答案为:15√2,20√2.六.作图-相似变换(共1小题)42.【解答】解:(1)如图:作出∠APD=∠ABP,即可得到△PCD∽△ABP;(2)证明:如图,∵∠APC=2∠ABC,∠APD=∠ABC,∴∠DPC=∠ABC∴PD∥AB.七.位似变换(共4小题)43.【解答】解:∵△ABC与△DEF是位似图形,OA:OD=1:2,∴△ABC与△DEF的位似比是1:2.∴△ABC与△DEF的相似比为1:2,∴△ABC与△DEF的面积比为1:4,故选:C.44.【解答】解:∵以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,而A(1,2),C(3,1),∴D(2,4),F(6,2),∴DF=√(2−6)2+(4−2)2=2√5.故选:D.45.【解答】解:∵四边形ABCD与四边形A′B′C′D′位似,其位似中心为点O,OC=6,CC′=4,∴MMMM′=610=35,∴MMM′M′=35,∵AB=3,∴A′B′=5.故答案为:5.46.【解答】解:如图,∵△OAB∽△OA′B′,相似比为3:2,B(3.6),∴B′(2,4),根据对称性可知,△OA″B″在第三象限时,B″(﹣2,﹣4),∴满足条件的点B′的坐标为(2,4)或(﹣2,﹣4).故答案为(2,4)或(﹣2,﹣4).八.作图-位似变换(共2小题)47.【解答】解:(1)如图,△A1B1C1即为所求.(2)如图,△A2B2C2即为所求.48.【解答】解:(1)由题意知:△ABC的三个顶点的坐标分别是A(1,3),B(4,1),C(1,1),则△ABC关于x轴成轴对称的△A1B1C1的坐标为A1(1,﹣3),B1(4,﹣1),C1(1,﹣1),连接A1C1,A1B1,B1C1得到△A1B1C1.如图所示△A1B1C1为所求;(2)由题意知:位似中心是原点,则分两种情况:第一种,△A2B2C2和△ABC在同一侧则A2(2,6),B2(8,2),C2(2,2),连接各点,得△A2B2C2.第二种,△A2B2C2在△ABC的对侧A2(﹣2,﹣6),B2(﹣8,﹣2),C2(﹣2,﹣2),连接各点,得△A2B2C2.因为在网格中作图,图中网格是有范围的,只能在网格中作图,所以位似放大只能画一个.综上所述:如图所示△A2B2C2为所求.九.相似形综合题(共2小题)49.【解答】(1)证明:∵四边形ABCD是矩形,∴∠B=∠D=∠C=90°,由折叠对称知:∠AGE=∠B=90°,∠AHF=∠D=90°,∴∠GHF=∠C=90°,∠EGC+∠HGF=90°,∠GFH+∠HGF=90°,∴∠EGC=∠GFH,∴△EGC∽△GFH.(2)解:∵S△GFH:S△AFH=2:3,且△GFH和△AFH等高,∴GH:AH=2:3,∵将△ABE沿着AE折叠,点B刚好落在CD边上点G处,∴AG=AB=GH+AH=20,∴GH=8,AH=12,∴AD=AH=12.(3)解:在Rt△ADG中,DG=√MM2−MM2=√202−122=16,由折叠的对称性可设DF=FH=x,则GF=16﹣x,∵GH2+HF2=GF2,∴82+x2=(16﹣x)2,解得:x=6,∴HF=6,在Rt△GFH中,tan∠GFH=MMMM=86=43.50.【解答】解:(1)∵△ADE由△ABC绕点A按逆时针方向旋转90°得到,∴AB=AD,∠BAD=90°,△ABC≌△ADE,在Rt△ABD中,∠B=∠ADB=45°,∴∠ADE=∠B=45°,∴∠BDE=∠ADB+∠ADE=90°.(2)①DF=PF.证明:由旋转的性质可知,AC=AE,∠CAE=90°,在Rt△ACE中,∠ACE=∠AEC=45°,∵∠CDF=∠CAD,∠ACE=∠ADB=45°,∴∠ADB+∠CDF=∠ACE+∠CAD,即∠FPD=∠FDP,∴DF=PF.②证明:过点P作PH∥ED交DF于点H,。

2020-2021全国各地中考数学分类:相似综合题汇编含详细答案一、相似1.如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣ x﹣1交于点C.(1)求抛物线解析式及对称轴;(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.【答案】(1)解:把A(-2,0),B(4,0)代入抛物线y=ax2+bx-1,得解得∴抛物线解析式为:y= x2−x−1∴抛物线对称轴为直线x=- =1(2)解:存在使四边形ACPO的周长最小,只需PC+PO最小∴取点C(0,-1)关于直线x=1的对称点C′(2,-1),连C′O与直线x=1的交点即为P 点.设过点C′、O直线解析式为:y=kx∴k=-∴y=- x则P点坐标为(1,- )(3)解:当△AOC∽△MNC时,如图,延长MN交y轴于点D,过点N作NE⊥y轴于点E∵∠ACO=∠NCD,∠AOC=∠CND=90°∴∠CDN=∠CAO由相似,∠CAO=∠CMN∴∠CDN=∠CMN∵MN⊥AC∴M、D关于AN对称,则N为DM中点设点N坐标为(a,- a-1)由△EDN∽△OAC∴ED=2a∴点D坐标为(0,- a−1)∵N为DM中点∴点M坐标为(2a,a−1)把M代入y= x2−x−1,解得a=4则N点坐标为(4,-3)当△AOC∽△CNM时,∠CAO=∠NCM∴CM∥AB则点C关于直线x=1的对称点C′即为点N由(2)N(2,-1)∴N点坐标为(4,-3)或(2,-1)【解析】【分析】(1)根据点A、B的坐标,可求出抛物线的解析式,再求出它的对称轴即可解答。
(2)使四边形ACPO的周长最小,只需PC+PO最小,取点C(0,-1)关于直线x=1的对称点C′(2,-1),连C′O与直线x=1的交点即为P点,利用待定系数法求出直线C′O的解析式,再求出点P的坐标。

2020-2021全国各地中考数学分类:相似综合题汇编附答案一、相似1.定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4求BN的长;(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D 是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可);(3)如图3,正方形ABCD中,M,N分别在BC,DC上,且BM≠DN,∠MAN=45°,AM,AN分别交BD于E,F.求证:①E、F是线段BD的勾股分割点;②△AMN的面积是△AEF面积的两倍.【答案】(1)解:(1)①当MN为最大线段时,∵点M,N是线段AB的勾股分割点,∴BM= = = ,②当BN为最大线段时,∵点M,N是线段AB的勾股分割点,∴BN= = =5,综上,BN= 或5;(2)解:作法:①在AB上截取CE=CA;②作AE的垂直平分线,并截取CF=CA;③连接BF,并作BF的垂直平分线,交AB于D;点D即为所求;如图2所示.(3)解:①如图3中,将△ADF绕点A顺时针性质90°得到△ABH,连接HE.∵∠DAF+∠BAE=90°﹣∠EAF=45°,∠DAF=∠BAH,∴∠EAH=∠EAF=45°,∵EA=EA,AH=AF,∴△EAH≌△EAF,∴EF=HE,∵∠ABH=∠ADF=45°=∠ABD,∴∠HBE=90°,在Rt△BHE中,HE2=BH2+BE2,∵BH=DF,EF=HE,∵EF2=BE2+DF2,∴E、F是线段BD的勾股分割点.②证明:如图4中,连接FM,EN.∵四边形ABCD是正方形,∴∠ADC=90°,∠BDC=∠ADB=45°,∵∠MAN=45°,∴∠EAN=∠EDN,∵∠AFE=∠FDN,∴△AFE∽△DFN,∴∠AEF=∠DNF,,∴,∵∠AFD=∠EFN,∴△AFD∽△EFN,∴∠DAF=∠FEN,∵∠DAF+∠DNF=90°,∴∠AEF+∠FEN=90°,∴∠AEN=90°∴△AEN是等腰直角三角形,同理△AFM是等腰直角三角形;∵△AEN是等腰直角三角形,同理△AFM是等腰直角三角形,∴AM= AF,AN= AE,∵S△AMN= AM•AN•sin45°,S△AEF= AE•AF•sin45°,∴ =2,∴S△AMN=2S△AEF.【解析】【分析】(1)此题分两种情况:①当MN为最大线段时,②当BN为最大线段时,根据线段的勾股分割点的定义,利用勾股定理分别得出BM的长;(2)利用尺规作图,将线段AC,CD,DB转化到同一个直角三角形中,①在AB上截取CE=CA;②作AE的垂直平分线,并截取CF=CA;这样的作图可以保证直角的出现,及AC 是一条直角边,③连接BF,并作BF的垂直平分线,交AB于D;这样的作图意图利用垂直平分线上的点到线段两个端点的距离相等,即BD=DF,从而实现将三条线段转化到同一直角三角形的目的;(3)①如图3中,将△ADF绕点A顺时针性质90°得到△ABH,连接HE.根据正方形的性质及旋转的性质得出∠EAH=∠EAF=45°,AH=AF,利用SAS判断出△EAH≌△EAF,根据全等三角形对应边相等得出EF=HE,根据正方形的每条对角线平分一组对角,及旋转的性质得出∠ABH=∠ADF=45°=∠ABD,故∠HBE=90°,在Rt△BHE中,HE2=BH2+BE2,根据等量代换得出结论;②证明:如图4中,连接FM,EN.根据正方形的性质及对顶角相等判断出△AFE∽△DFN,根据相似三角形对应角相等,对应边成比例得出∠AEF=∠DNF, AF∶DF =EF∶FN ,根据比例的性质进而得出AF∶EF =DF∶FN,再判断出△AFD∽△EFN,根据相似三角形对应角相等得出∠DAF=∠FEN,根据直角三角形两锐角互余,及等量代换由∠DAF+∠DNF=90°,得出∠AEF+∠FEN=90°,即∠AEN=90°,从而判断出△AEN是等腰直角三角形,同理△AFM是等腰直角三角形;根据等腰直角三角形的边之间的关系AM= AF,AN= AE,从而分别表示出S△AMN与S△AEF,求出它们的比值即可得出答案。

2020年中考数学试题《相似》试题精编含答案1.(2020•朝阳)如图,以AB为直径的⊙O经过△ABC的顶点C,过点O作OD∥BC交⊙O 于点D,交AC于点F,连接BD交AC于点G,连接CD,在OD的延长线上取一点E,连接CE,使∠DEC=∠BDC.(1)求证:EC是⊙O的切线;(2)若⊙O的半径是3,DG•DB=9,求CE的长.2.(2020•兰州)如图,在▱ABCD中,DE⊥AC于点O,交BC于点E,EG=EC,GF∥AD 交DE于点F,连接FC,点H为线段AO上一点,连接HD,HF.(1)判断四边形GECF的形状,并说明理由;(2)当∠DHF=∠HAD时,求证:AH•CH=EC•AD.3.(2020•呼伦贝尔)如图,⊙O是△ABC的外接圆,直线EG与⊙O相切于点E,EG∥BC,连接AE交BC于点D.(1)求证:AE平分∠BAC;(2)若∠ABC的平分线BF交AD于点F,且DE=3,DF=2,求AF的长.4.(2020•朝阳)如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,2),B(﹣1,3),C(﹣1,1),请按如下要求画图:(1)以坐标原点O为旋转中心,将△ABC顺时针旋转90°,得到△A1B1C1,请画出△A1B1C1;(2)以坐标原点O为位似中心,在x轴下方,画出△ABC的位似图形△A2B2C2,使它与△ABC的位似比为2:1.5.(2020•永州)如图,△ABC内接于⊙O,AB是⊙O的直径,BD与⊙O相切于点B,BD 交AC的延长线于点D,E为BD的中点,连接CE.(1)求证:CE是⊙O的切线.(2)已知BD=3,CD=5,求O,E两点之间的距离.6.(2020•宁夏)在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(1,3),B(4,1),C(1,1).(1)画出△ABC关于x轴成轴对称的△A1B1C1;(2)画出△ABC以点O为位似中心,位似比为1:2的△A2B2C2.7.(2020•湖北)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D 的直线EF交AC于点F,交AB的延长线于点E,且∠BAC=2∠BDE.(1)求证:DF是⊙O的切线;(2)当CF=2,BE=3时,求AF的长.8.(2020•通辽)如图,⊙O的直径AB交弦(不是直径)CD于点P,且PC2=PB•P A,求证:AB⊥CD.9.(2020•宜宾)如图,已知AB是⊙O的直径,点C是圆上异于A、B的一点,连结BC并延长至点D,使CD=BC,连结AD交⊙O于点E,连结BE.(1)求证:△ABD是等腰三角形;(2)连结OC并延长,与以B为切点的切线交于点F,若AB=4,CF=1,求DE的长.10.(2020•黄冈)已知:如图,AB是⊙O的直径,点E为⊙O上一点,点D是上一点,连接AE并延长至点C,使∠CBE=∠BDE,BD与AE交于点F.(1)求证:BC是⊙O的切线;(2)若BD平分∠ABE,求证:AD2=DF•DB.11.(2020•怀化)如图,在⊙O中,AB为直径,点C为圆上一点,延长AB到点D,使CD =CA,且∠D=30°.(1)求证:CD是⊙O的切线.(2)分别过A、B两点作直线CD的垂线,垂足分别为E、F两点,过C点作AB的垂线,垂足为点G.求证:CG2=AE•BF.12.(2020•南京)如图,在△ABC和△A'B'C'中,D、D'分别是AB、A'B'上一点,=.(1)当==时,求证△ABC∽△A'B'C'.证明的途径可以用下面的框图表示,请填写其中的空格.(2)当==时,判断△ABC与△A'B'C′是否相似,并说明理由.13.(2020•乐山)如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD =2,CE=1.求DF的长度.14.(2020•凉山州)如图,一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?15.(2020•泰州)如图,在△ABC中,∠C=90°,AC=3,BC=4,P为BC边上的动点(与B、C不重合),PD∥AB,交AC于点D,连接AP,设CP=x,△ADP的面积为S.(1)用含x的代数式表示AD的长;(2)求S与x的函数表达式,并求当S随x增大而减小时x的取值范围.16.(2020•绥化)如图,△ABC内接于⊙O,CD是直径,∠CBG=∠BAC,CD与AB相交于点E,过点E作EF⊥BC,垂足为F,过点O作OH⊥AC,垂足为H,连接BD、OA.(1)求证:直线BG与⊙O相切;(2)若=,求的值.17.(2020•安顺)如图,四边形ABCD是矩形,E是BC边上一点,点F在BC的延长线上,且CF=BE.(1)求证:四边形AEFD是平行四边形;(2)连接ED,若∠AED=90°,AB=4,BE=2,求四边形AEFD的面积.18.(2020•苏州)如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.(1)求证:△ABE∽△DF A;(2)若AB=6,BC=4,求DF的长.19.(2020•滨州)如图,AB是⊙O的直径,AM和BN是它的两条切线,过⊙O上一点E 作直线DC,分别交AM、BN于点D、C,且DA=DE.(1)求证:直线CD是⊙O的切线;(2)求证:OA2=DE•CE.20.(2020•济宁)如图,在△ABC中,AB=AC,点P在BC上.(1)求作:△PCD,使点D在AC上,且△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)(2)在(1)的条件下,若∠APC=2∠ABC.求证:PD∥AB.21.(2020•无锡)如图,DB过⊙O的圆心,交⊙O于点A、B,DC是⊙O的切线,点C是切点,已知∠D=30°,DC=.(1)求证:△BOC∽△BCD;(2)求△BCD的周长.22.(2020•上海)已知:如图,在菱形ABCD中,点E、F分别在边BC、CD上,BE=FD,AF的延长线交BC的延长线于点H,AE的延长线交DC的延长线于点G.(1)求证:△AFD∽△GAD;(2)如果DF2=CF•CD,求证:BE=CH.23.(2020•衢州)如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.(1)求证:∠CAD=∠CBA.(2)求OE的长.24.(2020•杭州)如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.(1)求证:△BDE∽△EFC.(2)设,①若BC=12,求线段BE的长;②若△EFC的面积是20,求△ABC的面积.25.(2020•杭州)如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设=λ(λ>0).(1)若AB=2,λ=1,求线段CF的长.(2)连接EG,若EG⊥AF,①求证:点G为CD边的中点.②求λ的值.26.(2020•黔西南州)古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.(1)求证:CD是⊙O的切线;(2)小明在研究的过程中发现是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.27.(2019•恩施州)如图,在⊙O中,AB是直径,BC是弦,BC=BD,连接CD交⊙O于点E,∠BCD=∠DBE.(1)求证:BD是⊙O的切线.(2)过点E作EF⊥AB于F,交BC于G,已知DE=2,EG=3,求BG的长.28.(2019•铁岭)如图,在▱ABCD中,AD=2AB,以点A为圆心、AB的长为半径的⊙A 恰好经过BC的中点E,连接DE,AE,BD,AE与BD交于点F.(1)求证:DE与⊙A相切.(2)若AB=6,求BF的长.29.(2019•莱芜区)如图,已知AB是⊙O的直径,CB⊥AB,D为圆上一点,且AD∥OC,连接CD,AC,BD,AC与BD交于点M.(1)求证:CD为⊙O的切线;(2)若CD=AD,求的值.30.(2019•上海)已知:如图,AB、AC是⊙O的两条弦,且AB=AC,D是AO延长线上一点,联结BD并延长交⊙O于点E,联结CD并延长交⊙O于点F.(1)求证:BD=CD;(2)如果AB2=AO•AD,求证:四边形ABDC是菱形.31.(2019•雅安)如图,▱ABCD的对角线AC、BD相交于点O,EF经过O,分别交AB、CD于点E、F,EF的延长线交CB的延长线于M.(1)求证:OE=OF;(2)若AD=4,AB=6,BM=1,求BE的长.32.(2019•娄底)如图,点D在以AB为直径的⊙O上,AD平分∠BAC,DC⊥AC,过点B 作⊙O的切线交AD的延长线于点E.(1)求证:直线CD是⊙O的切线.(2)求证:CD•BE=AD•DE.33.(2019•宁夏)如图在△ABC中,AB=BC,以AB为直径作⊙O交AC于点D,连接OD.(1)求证:OD∥BC;(2)过点D作⊙O的切线,交BC于点E,若∠A=30°,求的值.34.(2019•百色)如图,已知AC、AD是⊙O的两条割线,AC与⊙O交于B、C两点,AD 过圆心O且与⊙O交于E、D两点,OB平分∠AOC.(1)求证:△ACD∽△ABO;(2)过点E的切线交AC于F,若EF∥OC,OC=3,求EF的值.[提示:(+1)(﹣1)=1]35.(2019•梧州)如图,在矩形ABCD中,AB=4,BC=3,AF平分∠DAC,分别交DC,BC的延长线于点E,F;连接DF,过点A作AH∥DF,分别交BD,BF于点G,H.(1)求DE的长;(2)求证:∠1=∠DFC.36.(2019•张家界)如图,在平行四边形ABCD中,连接对角线AC,延长AB至点E,使BE=AB,连接DE,分别交BC,AC交于点F,G.(1)求证:BF=CF;(2)若BC=6,DG=4,求FG的长.37.(2019•湘西州)如图,△ABC内接于⊙O,AC=BC,CD是⊙O的直径,与AB相交于点G,过点D作EF∥AB,分别交CA、CB的延长线于点E、F,连接BD.(1)求证:EF是⊙O的切线;(2)求证:BD2=AC•BF.38.(2019•泸州)如图,AB为⊙O的直径,点P在AB的延长线上,点C在⊙O上,且PC2=PB•P A.(1)求证:PC是⊙O的切线;(2)已知PC=20,PB=10,点D是的中点,DE⊥AC,垂足为E,DE交AB于点F,求EF的长.39.(2019•荆门)如图,为了测量一栋楼的高度OE,小明同学先在操场上A处放一面镜子,向后退到B处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E(O,A,B,C,D在同一条直线上),测得AC=2m,BD=2.1m,如果小明眼睛距地面髙度BF,DG为1.6m,试确定楼的高度OE.40.(2019•黄冈)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE.(1)求证:△DBE是等腰三角形;(2)求证:△COE∽△CAB.1.【解答】解:(1)证明:如图,连接OC,∵AB是直径,∴∠ACB=90°,∵OD∥BC,∴∠CFE=∠ACB=90°,∴∠DEC+∠FCE=90°,∵∠DEC=∠BDC,∠BDC=∠A,∴∠DEC=∠A,∵OA=OC,∴∠OCA=∠A,∴∠OCA=∠DEC,∵∠DEC+∠FCE=90°,∴∠OCA+∠FCE=90°,即∠OCE=90°,∴OC⊥CE,又∵OC是⊙O的半径,∴CE是⊙O切线.(2)由(1)得∠CFE=90°,∴OF⊥AC,∵OA=OC,∴∠COF=∠AOF,∴,∴∠ACD=∠DBC,又∵∠BDC=∠BDC,∴△DCG∽△DBC,∴DC2=DG•DB=9,∴DC=3,∵OC=OD=3,∴△OCD是等边三角形,∴∠DOC=60°,在Rt△OCE中,∴,∴.2.【解答】解:(1)四边形GECF是菱形,∵EG=EC,DE⊥AC,∴GO=CO,∵GF∥AD,AD∥BC,∴GF∥BC,∴∠FGO=∠ECO,∠GFO=∠CEO,∴△GFO≌△CEO(AAS),∴GF=EC,∴四边形GFCE是平行四边形,又∵EG=EC,∴平行四边形GFCE是菱形;(2)∵∠DHC=∠DAH+∠ADH=∠DHF+∠FHC,∠DHF=∠HAD,∴∠ADH=∠FHC,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAH=∠ACB,∵四边形GFCE是菱形,∴CE=CF,∠HCF=∠ACB,∴∠HCF=∠DAH,∴△ADH∽△CHF,∴AH•CH=AD•EC.3.【解答】解:(1)连接OE.∵直线EG与⊙O相切于E,∴OE⊥EG,∵EG∥BC,∴OE⊥BC,∴,∴∠BAE=∠CAE.∴AE平分∠BAC;(2)如图,∵AE平分∠BAC,∴∠1=∠4,∵∠1=∠5,∴∠4=∠5,∵BF平分∠ABC,∴∠2=∠3,∵∠6=∠3+∠4=∠2+∠5,即∠6=∠EBF,∴EB=EF,∵DE=3,DF=2,∴BE=EF=DE+DF=5,∵∠5=∠4,∠BED=∠AEB,∴△EBD∽△EAB,∴,即,∴AF=AE﹣EF=.4.【解答】解:(1)如图,△A1B1C1即为所求.(2)如图,△A2B2C2即为所求.5.【解答】证明:(1)如图,连接OC,∵OB=OC,∴∠OBC=∠OCB,∵AB是直径,∴∠ACB=90°,∵E为BD的中点,∴BE=CE=DE,∴∠ECB=∠EBC,∵BD与⊙O相切于点B,∴∠ABD=90°,∴∠OBC+∠EBC=90°,∴∠OCB+∠ECB=90°,∴∠OCE=90°∴OC⊥CE,又∵OC为半径,∴CE是⊙O的切线;(2)连接OE,∵∠D=∠D,∠BCD=∠ABD,∴△BCD∽△ABD,∴,∴BD2=AD•CD,∴(3)2=5AD,∴AD=9,∵E为BD的中点,AO=BO,∴OE=AD=,∴O,E两点之间的距离为.6.【解答】解:(1)由题意知:△ABC的三个顶点的坐标分别是A(1,3),B(4,1),C (1,1),则△ABC关于x轴成轴对称的△A1B1C1的坐标为A1(1,﹣3),B1(4,﹣1),C1(1,﹣1),连接A1C1,A1B1,B1C1得到△A1B1C1.如图所示△A1B1C1为所求;(2)由题意知:位似中心是原点,则分两种情况:第一种,△A2B2C2和△ABC在同一侧则A2(2,6),B2(8,2),C2(2,2),连接各点,得△A2B2C2.第二种,△A2B2C2在△ABC的对侧A2(﹣2,﹣6),B2(﹣8,﹣2),C2(﹣2,﹣2),连接各点,得△A2B2C2.因为在网格中作图,图中网格是有范围的,只能在网格中作图,所以位似放大只能能画一个.综上所述:如图所示△A2B2C2为所求.7.【解答】(1)证明:连接OD,AD,∵AB是直径,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴∠BAC=2∠BAD,∵∠BAC=2∠BDE,∴∠BDE=∠BAD,∵OA=OD,∴∠BAD=∠ADO,∵∠ADO+∠ODB=90°,∴∠BDE+∠ODB=90°,即DF⊥OD,∵OD是⊙O的半径,∴DF是⊙O的切线.(2)解:∵AB=AC,AD⊥BC,∴BD=CD,∵BO=AO,∴OD∥AC,∴△EOD∽△EAF,∴,设OD=x,∵CF=2,BE=3,∴OA=OB=x,AF=AC﹣CF=2x﹣2,EO=x+3,EA=2x+3,∴=,解得x=6,经检验,x=6是分式方程的解,∴AF=2x﹣2=10.8.【解答】证明:连接AC、BD,如图,∵∠A=∠D,∠C=∠B,∴△APC∽△BPD,∴PC:PB=P A:PD,∵PC2=PB•P A,∴PC=PD,∵AB为直径,∴AB⊥CD.9.【解答】证明:(1)∵AB是⊙O的直径,∴∠ACB=90°,∴AC⊥BD,又∵CD=BC,∴AB=AD,∴△ABD是等腰三角形;(2)∵△ABD是等腰三角形,∴∠BAC=∠BAD,AB=AD,BC=BD,又∵∠BAC=∠BOC,∴∠BOC=∠BAD,∵BF是⊙O的切线,∴∠FBO=90°,∵AB是⊙O的直径,∴∠AEB=90°=∠OBF,∴△OBF∽△AEB,∴,∵AB=4,CF=1,∴OB=2,OF=OC+CF=3,∴,∴AE=,∴DE=AD﹣AE=.10.【解答】证明:(1)∵AB是⊙O的直径,∴∠AEB=90°,∴∠EAB+∠EBA=90°,∵∠CBE=∠BDE,∠BDE=∠EAB,∴∠EAB=∠CBE,∴∠EBA+∠CBE=90°,即∠ABC=90°,∴CB⊥AB,∵AB是⊙O的直径,∴BC是⊙O的切线;(2)证明:∵BD平分∠ABE,∴∠ABD=∠DBE,∵∠DAF=∠DBE,∴∠DAF=∠ABD,∵∠ADB=∠ADF,∴△ADF∽△BDA,∴,∴AD2=DF•DB.11.【解答】(1)证明:连接OC,如图所示,∵CA=CD,且∠D=30°,∴∠CAD=∠D=30°,∵OA=OC,∴∠CAD=∠ACO=30°,∴∠COD=∠CAD+∠ACO=30°+30°=60°,∴∠OCD=180°﹣∠D﹣∠COD=180°﹣30°﹣60°=90°,∴OC⊥CD,∴CD是⊙O的切线;(2)∵∠COB=60°,且OC=OB,∴△OCB为等边三角形,∴∠CBG=60°,又∵CG⊥AD,∴∠CGB=90°,∴∠GCB=∠CGB﹣∠CBG=30°,又∵∠GCD=60°,∴CB是∠GCD的角平分线,∵BF⊥CD,BG⊥CG,∴BF=BG,又∵BC=BC,∴Rt△BCG≌Rt△BCF(HL),∴CF=CG.∵∠D=30°,AE⊥ED,∠AED=90°,∴∠EAD=60°,又∵∠CAD=30°,∴AC是∠EAG的角平分线,∵CE⊥AE,CG⊥AB,∴CE=CG,∵∠AEC=∠BFC=90°,∠EAC=30°=∠BCF,∴△AEC∽△CFB,∴,即AE•BF=CF•CE,又CE=CG,CF=CG,∴AE•BF=CG2.12.【解答】(1)证明:∵=,∴=,∵==,∴==,∴△ADC∽△A′D′C',∴∠A=∠A′,∵=,∴△ABC∽△A′B′C′.故答案为:==,∠A=∠A′.(2)如图,过点D,D′分别作DE∥BC,D′E′∥B′C′,DE交AC于E,D′E′交A′C′于E′.∵DE∥BC,∴△ADE∽△ABC,∴==,同理,==,∵=,∴=,∴=,同理,=,∴=,即=,∴=,∵==,∴==,∴△DCE∽△D′C′E′,∴∠CED=∠C′E′D′,∵DE∥BC,∴∠CED+∠ACB=180°,同理,∠C′E′D′+∠A′C′B′=180°,∴∠ACB=∠A′C′B′,∵=,∴△ABC∽△A′B′C′.13.【解答】解:∵四边形ABCD是矩形,∴DC=AB=3,∠ADC=∠C=90°.∵CE=1,∴DE==.∵AF⊥DE,∴∠AFD=90°=∠C,∠ADF+∠DAF=90°.又∵∠ADF+∠EDC=90°,∴∠EDC=∠DAF,∴△EDC∽△DAF,∴=,即=,∴FD=,即DF的长度为.14.【解答】解:∵四边形EGHF为正方形,∴BC∥EF,∴△AEF∽△ABC;设正方形零件的边长为x mm,则KD=EF=xmm,AK=(80﹣x)mm,∵AD⊥BC,∴=,∴=,解得:x=48.答:正方形零件的边长为48mm.15.【解答】解:(1)∵PD∥AB,∴,∵AC=3,BC=4,CP=x,∴,∴CD=,∴AD=AC﹣CD=3﹣,即AD=;(2)根据题意得,S=,∴当x≥2时,S随x的增大而减小,∵0<x<4,∴当S随x增大而减小时x的取值范围为2≤x<4.16.【解答】解:(1)连接OB,如图,∵CD是⊙O的直径,∴∠DBC=90°,∴∠D+∠BCD=90°,∵OB=OC,∴∠OCB=∠OBC,∴∠D+∠OBC=90°,∵∠D=∠BAC,∠BAC=∠CBG,∴∠CBG+∠OBC=90°,即∠OBG=90°,∴直线BG与⊙O相切;(2)∵OA=OC,OH⊥AC,∴∠COH=∠COA,CH=,∵∠ABC=∠AOC,∴∠EBF=∠COH,∵EF⊥BC,OH⊥AC,∴∠BEF=∠OHC=90°,∴△BEF∽△COH,∴,∵=,OC=OD,∴,∵CH=AC,∴,17.【解答】(1)证明:∵∠四边形ABCD是矩形,∴AD∥BC,AD=BC,∵BE=CF,∴BE+EC=EC+CF,即BC=EF,∴AD=EF,∴四边形AEFD是平行四边形;(2)解:连接DE,如图,∵四边形ABCD是矩形,∴∠B=90°,在Rt△ABE中,AE==2,∵AD∥BC,∴∠AEB=∠EAD,∵∠B=∠AED=90°,∴△ABE∽△DEA,∴AE:AD=BE:AE,∴AD==10,∵AB=4,∴四边形AEFD的面积=AB×AD=4×10=40.18.【解答】解:(1)∵四边形ABCD是矩形,∴AD∥BC,∠B=90°,∴∠DAF=∠AEB,∵DF⊥AE,∴∠AFD=∠B=90°,∴△ABE∽△DF A;(2)∵E是BC的中点,BC=4,∴BE=2,∵AB=6,∴AE=,∵四边形ABCD是矩形,∴AD=BC=4,∵△ABE∽△DF A,∴,∴.19.【解答】解:(1)连接OD,OE,如图1,在△OAD和△OED中,,∴△OAD≌△OED(SSS),∴∠OAD=∠OED,∵AM是⊙O的切线,∴∠OAD=90°,∴∠OED=90°,∴直线CD是⊙O的切线;(2)过D作DF⊥BC于点F,如图2,则∠DFB=∠DFC=90°,∵AM、BN都是⊙O的切线,∴∠ABF=∠BAD=90°,∴四边形ABFD是矩形,∴DF=AB=2OA,AD=BF,∵CD是⊙O的切线,∴DE=DA,CE=CB,∴CF=CB﹣BF=CE﹣DE,∵DF2=CD2﹣CF2,∴4OA2=(CE+DE)2﹣(CE﹣DE)2,即4OA2=4DE•CE,∴OA2=DE•CE.20.【解答】解:(1)如图:作出∠APD=∠ABP,即可得到△PCD∽△ABP;(2)证明:如图,∵∠APC=2∠ABC,∠APD=∠ABC,∴∠DPC=∠ABC∴PD∥AB.21.【解答】证明:(1)∵DC是⊙O的切线,∴∠OCD=90°,∵∠D=30°,∴∠BOC=∠D+∠OCD=30°+90°=120°,∵OB=OC,∴∠B=∠OCB=30°,∴∠DCB=120°=∠BOC,又∵∠B=∠B=30°,∴△BOC∽△BCD;(2)∵∠D=30°,DC=,∠OCD=90°,∴DC=OC=,DO=2OC,∴OC=1=OB,DO=2,∵∠B=∠D=30°,∴DC=BC=,∴△BCD的周长=CD+BC+DB=++2+1=3+2.22.【解答】(1)证明:∵四边形ABCD是菱形,∴AB=AD,∠B=∠D,又∵BE=DF,∴△ABE≌△ADF(SAS),∴∠BAE=∠DAF.∵AB∥CD,∴∠G=∠BAE=∠DAF,又∵∠D=∠D,∴△AFD∽△GAD.(2)证明:∵DF2=CF•CD,∴=,∵AD∥BH,∴=,∴=,∵AD=CD,∴CH=DF,∵△ABE≌△ADF,∴BE=DF,∴BE=CH.23.【解答】(1)证明:∵AE=DE,OC是半径,∴=,∴∠CAD=∠CBA.(2)解:∵AB是直径,∴∠ACB=90°,∵AE=DE,∴OC⊥AD,∴∠AEC=90°,∴∠AEC=∠ACB,∴△AEC∽△BCA,∴=,∴=,∴CE=3.6,∵OC=AB=5,∴OE=OC﹣EC=5﹣3.6=1.4.24.【解答】(1)证明:∵DE∥AC,∴∠DEB=∠FCE,∵EF∥AB,∴∠DBE=∠FEC,∴△BDE∽△EFC;(2)解:①∵EF∥AB,∴==,∵EC=BC﹣BE=12﹣BE,∴=,解得:BE=4;②∵=,∴=,∵EF∥AB,∴△EFC∽△BAC,∴=()2=()2=,∴S△ABC=S△EFC=×20=45.25.【解答】解:(1)∵在正方形ABCD中,AD∥BC,∴∠DAG=∠F,又∵AG平分∠DAE,∴∠DAG=∠EAG,∴∠EAG=∠F,∴EA=EF,∵AB=2,∠B=90°,点E为BC的中点,∴BE=EC=1,∴AE==,∴EF=,∴CF=EF﹣EC=﹣1;(2)①证明:∵EA=EF,EG⊥AF,∴AG=FG,在△ADG和△FCG中,∴△ADG≌△FCG(AAS),∴DG=CG,即点G为CD的中点;②设CD=2a,则CG=a,由①知,CF=DA=2a,∵EG⊥AF,∠GCF=90°,∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,∠ECG=∠GCF=90°,∴∠EGC=∠F,∴△EGC∽△GFC,∴,∵GC=a,FC=2a,∴,∴,∴EC=a,BE=BC﹣EC=2a﹣a=a,∴λ=.26.【解答】解:(1)如图1中,连接OD、DB,∵点E是线段OB的中点,DE⊥AB交⊙O于点D,∴DE垂直平分OB,∴DB=DO,OE=BE.解法一:∵在⊙O中,DO=OB,∴DB=DO=OB,∴△ODB是等边三角形,∴∠BDO=∠DBO=60°,∵BC=OB=BD,且∠DBE为△BDC的外角,∴∠BCD=∠BDC=∠DBO.∵∠DBO=60°,∴∠CDB=30°.∴∠ODC=∠BDO+∠BDC=60°+30°=90°,∴CD是⊙O的切线;解法二:∵BC=OB,OB=OD,∴===,又∵∠DOE=∠COD,∴△EOD∽△DOC,∴∠CDO=∠DEO=90°,∴CD为圆O的切线;(2)答:这个确定的值是.连接OP,如图2中:由已知可得:OP=OB=BC=2OE.∴==,又∵∠COP=∠POE,∴△OEP∽△OPC,∴==.27.【解答】(1)证明:如图1,连接AE,则∠A=∠C,∵AB是直径,∴∠AEB=90°,∴∠A+∠ABE=90°,∵∠C=∠DBE,∴∠ABE+∠DBE=90°,即∠ABD=90°,∴BD是⊙O的切线(2)解:如图2,延长EF交⊙O于H,∵EF⊥AB,AB是直径,∴,∴∠ECB=∠BEH,∵∠EBC=∠GBE,∴△EBC∽△GBE,∴,∵BC=BD,∴∠D=∠C,∵∠C=∠DBE,∴∠D=∠DBE,∴BE=DE=2,又∠AFE=∠ABD=90°,∴BD∥EF,∴∠D=∠CEF,∴∠C=∠CEF,∴CG=GE=3,∴BC=BG+CG=BG+3,∴,∴BG=﹣8(舍)或BG=5,即BG的长为5.28.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AB=CD,∵EC=EB,∴BC=2BE=2CE,∵AD=2AB,∴AB=BE,∴AB=BE=AE,∴△ABE是等边三角形,∴∠ABE=∠AEB=60°,∵AB∥CD,∴∠C=180°﹣∠ABE=120°,∵CD=AB,AB=BE=CE,∴CD=CE,∴∠CED=(180°﹣∠C)=30°,∴∠AED=180°﹣∠AEB﹣∠CED=90°,∴DE⊥AE,∵AE是⊙A的半径,∴DE与⊙A相切.(2)如图,作BM⊥AE于M.∵△AEB是等边三角形,∴AE=AB=6,∵AD∥BC,∴△ADF∽△EBF,∴==2,∴AF=2EF,∴AF=AE=4,∵BM⊥AE,BA=BE,∴AM=ME=AE=3,∴FM=1,BM===3,在Rt△BFM中,BF==2.29.【解答】(1)证明:连接OD,设OC交BD于K.∵AB是直径,∴∠ADB=90°,∴AD⊥BD,∵OC∥AD,∴OC⊥BD,∴DK=KB,∴CD=CB,∵OD=OB,OC=OC,CD=CB,∴△ODC≌△OBC(SSS),∴∠ODC=∠OBC,∵CB⊥AB,∴∠OBC=90°,∴∠ODC=90°,∴OD⊥CD,∴CD是⊙O的切线.(2)解:∵CD=AD,∴可以假设AD=a,CD=a,设KC=b.∵DK=KB,AO=OB,∴OK=AD=a,∵∠DCK=∠DCO,∠CKD=∠CDO=90°,∴△CDK∽△COD,∴=,∴=整理得:2()2+()﹣4=0,解得=或(舍弃),∵CK∥AD,∴===.30.【解答】证明:(1)如图1,连接BC,OB,OC,∵AB、AC是⊙O的两条弦,且AB=AC,∴A在BC的垂直平分线上,∵OB=OA=OC,∴O在BC的垂直平分线上,∴AO垂直平分BC,∴BD=CD;(2)如图2,连接OB,∵AB2=AO•AD,∴=,∵∠BAO=∠DAB,∴△ABO∽△ADB,∴∠OBA=∠ADB,∵OA=OB,∴∠OBA=∠OAB,∴∠OAB=∠BDA,∴AB=BD,∵AB=AC,BD=CD,∴AB=AC=BD=CD,∴四边形ABDC是菱形.31.【解答】(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD,BC=AD,∴∠OAE=∠OCF,在△AOE和△COF中,,∴△AOE≌△COF(ASA),∴OE=OF;(2)解:过点O作ON∥BC交AB于N,则△AON∽△ACB,∵OA=OC,∴ON=BC=2,BN=AB=3,∵ON∥BC,∴△ONE∽△MBE,∴=,即=,解得,BE=1.32.【解答】证明:(1)连接OD,∵AD平分∠BAC,∴∠CAD=∠BAD,∵OA=OD,∴∠BAD=∠ADO,∴∠CAD=∠ADO,∴AC∥OD,∵CD⊥AC,∴CD⊥OD,∴直线CD是⊙O的切线;(2)连接BD,∵BE是⊙O的切线,AB为⊙O的直径,∴∠ABE=∠BDE=90°,∵CD⊥AC,∴∠C=∠BDE=90°,∵∠CAD=∠BAE=∠DBE,∴△ACD∽△BDE,∴CD•BE=AD•DE.33.【解答】解:(1)证明∵AB=BC ∴∠A=∠C∵OD=OA∴∠A=∠ADO∴∠C=∠ADO∴OD∥BC(2)如图,连接BD,∵∠A=30°,∠A=∠C∴∠C=30°∵DE为⊙O的切线,∴DE⊥OD∵OD∥BC∴DE⊥BC∴∠BED=90°∵AB为⊙O的直径∴∠BDA=90°,∠CBD=60°∴=tan∠C=tan30°=∴=cos∠CBD=cos60°=∴BE=BD=CD∴=34.【解答】证明:(1)∵OB平分∠AOC ∴∠BOE=∠AOC∵OC=OD∴∠D=∠OCD∵∠AOC=∠D+∠OCD∴∠D=∠AOC∴∠D=∠BOE,且∠A=∠A∴△ACD∽△ABO(2)∵EF切⊙O于E∴∠OEF=90°∵EF∥OC∴∠DOC=∠OEF=90°∵OC=OD=3∴CD==3∵△ACD∽△ABO∴∴∴AE=3∵EF∥OC∴∴∴EF=6﹣335.【解答】(1)解:∵矩形ABCD中,AD∥CF,∴∠DAF=∠ACF,∵AF平分∠DAC,∴∠DAF=∠CAF,∴∠F AC=∠AFC,∴AC=CF,∵AB=4,BC=3,∴==5,∴CF=5,∵AD∥CF,∴△ADE∽△FCE,∴,设DE=x,则,解得x=∴;(2)∵AD∥FH,AF∥DH,∴四边形ADFH是平行四边形,∴AD=FH=3,∴CH=2,BH=5,∵AD∥BH,∴△ADG∽△HBG,∴,∴,∴DG=,∵DE=,∴=,∴EG∥BC,∴∠1=∠AHC,又∵DF∥AH,∴∠AHC=∠DFC,∠1=∠DFC.36.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴△EBF∽△EAD,∴==,∴BF=AD=BC,∴BF=CF;(2)解:∵四边形ABCD是平行四边形,∴AD∥CF,∴△FGC∽△DGA,∴=,即=,解得,FG=2.37.【解答】证明:(1)∵AC=BC,CD是圆的直径,∴由圆的对称性可知:∠ACD=∠BCD,∴CD⊥AB,∵AB∥EF,∴∠CDF=∠CGB=90°,∵OD是圆的半径,∴EF是⊙O的切线;(2)∵CD是圆的直径,∴∠CBD=90°,∵∠BDF+∠CDB=∠CDB+∠BCD=90°,∴∠BDF=∠BCD,∴△BCD∽△BDF,∴,∴BD2=BC•BF,∵BC=AC,∴BD2=AC•BF.38.【解答】(1)证明:连接OC,如图1所示:∵PC2=PB•P A,即=,∵∠P=∠P,∴△PBC∽△PCA,∴∠PCB=∠P AC,∵AB为⊙O的直径,∴∠ACB=90°,∴∠A+∠ABC=90°,∵OC=OB,∴∠OBC=∠OCB,∴∠PCB+∠OCB=90°,即OC⊥PC,∴PC是⊙O的切线;(2)解:连接OD,如图2所示:∵PC=20,PB=10,PC2=PB•P A,∴P A===40,∴AB=P A﹣PB=30,∵△PBC∽△PCA,∴==2,设BC=x,则AC=2x,在Rt△ABC中,x2+(2x)2=302,解得:x=6,即BC=6,∵点D是的中点,AB为⊙O的直径,∴∠AOD=90°,∵DE⊥AC,∴∠AEF=90°,∵∠ACB=90°,∴DE∥BC,∴∠DFO=∠ABC,∴△DOF∽△ACB,∴==,∴OF=OD=,即AF=,∵EF∥BC,∴==,∴EF=BC=.39.【解答】解:令OE=a,AO=b,CB=x,则由△GDC∽△EOC得,即,整理得:3.2+1.6b=2.1a﹣ax①,由△FBA∽△EOA得,即,整理得:1.6b=2a﹣ax②,将②代入①得:3.2+2a﹣ax=2.1a﹣ax,∴a=32,即OE=32,答:楼的高度OE为32米.40.【解答】证明:(1)连接OD,如图所示:∵DE是⊙O的切线,∴∠ODE=90°,∴∠ADO+∠BDE=90°,∵∠ACB=90°,∴∠CAB+∠CBA=90°,∵OA=OD,∴∠CAB=∠ADO,∴∠BDE=∠CBA,∴EB=ED,∴△DBE是等腰三角形;(2)∵∠ACB=90°,AC是⊙O的直径,∴CB是⊙O的切线,∵DE是⊙O的切线,∴DE=EC,∵EB=ED,∴EC=EB,∵OA=OC,∴OE∥AB,。

中考数学真题汇编:图形的相似一、选择题1.已知,下列变形错误的是()A. B.C.D.【答案】B2.已知与相似,且相似比为,则与的面积比()A. B.C.D.【答案】D3.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为,和,另一个三角形的最短边长为2.5 cm,则它的最长边为()A. 3cmB. 4cmC. 4.5cmD. 5cm【答案】C4.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为()A. (5,1)B. (4,3) C. (3,4) D. (1,5)【答案】C5.如图,△ACB 和△ECD 都是等腰直角三角形,CA=CB ,CE=CD ,△ACB 的顶点A 在△ECD 的斜边DE 上,若AE=,AD=,则两个三角形重叠部分的面积为( )A. B. C. D.【答案】D6.在平面直角坐标系中,点是线段上一点,以原点 为位似中心把放大到原来的两倍,则点 的对应点的坐标为( )A.B. 或C.D.或【答案】B 7.如图,点 在线段 上,在的同侧作等腰和等腰, 与、分别交于点 、.对于下列结论:①;②;③.其中正确的是( )∵∠BEA=∠CDA ∠PME=∠AMD∴P 、E 、D 、A 四点共圆 ∴∠APD=AED=90°∵∠CAE=180°-∠BAC-∠EAD=90° ∴△CAP ∽△CMA ∴AC 2=CP•CM ∵AC=AB∴2CB 2=CP•CM所以③正确A. ①②③B. ①C. ①②D. ②③【答案】A8.如图,将沿边上的中线平移到的位置,已知的面积为9,阴影部分三角形的面积为4.若,则等于()A. 2B. 3C.D.【答案】A9.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,,垂足分别为,,,,,则栏杆端应下降的垂直距离为( )A. B.C.D.【答案】C10.如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1, S2,()A. 若,则B. 若,则C. 若,则D. 若,则【答案】D11.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD =60°,则△OCE的面积是()。

2020-2021全国中考数学相似的综合中考真题分类汇总及详细答案一、相似1.如图所示,将二次函数y=x2+2x+1的图象沿x轴翻折,然后向右平移1个单位,再向上平移4个单位,得到二次函数y=ax2+bx+c的图象.函数y=x2+2x+1的图象的顶点为点A.函数y=ax2+bx+c的图象的顶点为点B,和x轴的交点为点C,D(点D位于点C的左侧).(1)求函数y=ax2+bx+c的解析式;(2)从点A,C,D三个点中任取两个点和点B构造三角形,求构造的三角形是等腰三角形的概率;(3)若点M是线段BC上的动点,点N是△ABC三边上的动点,是否存在以AM为斜边的Rt△AMN,使△AMN的面积为△ABC面积的?若存在,求tan∠MAN的值;若不存在,请说明理由.【答案】(1)解:y=x2+2x+1=(x+1)2的图象沿x轴翻折,得y=﹣(x+1)2,把y=﹣(x+1)2向右平移1个单位,再向上平移4个单位,得y=﹣x2+4,∴所求的函数y=ax2+bx+c的解析式为y=﹣x2+4(2)解:∵y=x2+2x+1=(x+1)2,∴A(﹣1,0),当y=0时,﹣x2+4=0,解得x=±2,则D(﹣2,0),C(2,0);当x=0时,y=﹣x2+4=4,则B(0,4),从点A,C,D三个点中任取两个点和点B构造三角形的有:△ACB,△ADB,△CDB,∵AC=3,AD=1,CD=4,AB= ,BC=2 ,BD=2 ,∴△BCD为等腰三角形,∴构造的三角形是等腰三角形的概率=(3)解:存在,易得BC的解析是为y=﹣2x+4,S△ABC= AC•OB= ×3×4=6,M点的坐标为(m,﹣2m+4)(0≤m≤2),①当N点在AC上,如图1,∴△AMN的面积为△ABC面积的,∴(m+1)(﹣2m+4)=2,解得m1=0,m2=1,当m=0时,M点的坐标为(0,4),N(0,0),则AN=1,MN=4,∴tan∠MAC= =4;当m=1时,M点的坐标为(1,2),N(1,0),则AN=2,MN=2,∴tan∠MAC= =1;②当N点在BC上,如图2,BC= =2 ,∵BC•AN= AC•BC,解得AN= ,∵S△AMN= AN•MN=2,∴MN= = ,∴∠MAC= ;③当N点在AB上,如图3,作AH⊥BC于H,设AN=t,则BN= ﹣t,由②得AH= ,则BH= ,∵∠NBG=∠HBA,∴△BNM∽△BHA,∴,即,∴MN= ,∵AN•MN=2,即•(﹣t)• =2,整理得3t2﹣3 t+14=0,△=(﹣3 )2﹣4×3×14=﹣15<0,方程没有实数解,∴点N在AB上不符合条件,综上所述,tan∠MAN的值为1或4或【解析】【分析】(1)将y=x2+2x+1配方成顶点式,根据轴对称的性质,可得出翻折后的函数解析式,再根据函数图像平移的规律:上加下减,左加右减,可得出答案。
相似一.选择题1.如图,在四边形ABCD 中,DC ∥AB ,CB ⊥AB ,AB=AD ,CD=AB ,点E 、F 分别为AB 、AD 的中点,则△AEF 与多边形BCDFE 的面积之比为( )A .B .C .D .2.如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O 为位似中心,相似比为31,在第一象限内把线段AB 缩小后得到线段CD ,则点C 的坐标为( )A .(2,1)B .(2,0)C .(3,3)D .(3,1)3.如图,已知AB 、CD 、EF 都与BD 垂直,垂足分别是B 、D 、F ,且AB =1,CD =3,那么EF 的长是 ( )A .13 B .23 C .34 D .454.如图所示,△ABC 中,DE ∥BC ,若,则下列结论中正确的是( )A .B .C .D .5.(2015•甘肃武威,第9题3分)如图,D 、E 分别是△ABC 的边AB 、BC 上的点,DE ∥AC ,若S △BDE :S △CDE =1:3,则S △DOE :S △AOC 的值为( )A .B .C .D .6.如图,在△ABC 中,AB=CB ,以AB 为直径的⊙O 交AC 于点D .过点C 作CF ∥AB ,在CF 上取一点E ,使DE=CD ,连接AE .对于下列结论:①AD=DC ;②△CBA ∽△CDE ;③=;④AE 为⊙O 的切线,一定正确的结论全部包含其中的选项是( )A . ①②B . ①②③C . ①④D . ①②④7.如图,点P 在△ABC 的边AC 上,要判断△ABP ∽△ACB ,添加一个条件,不正确的是( )A . ∠ABP=∠CB .∠APB=∠ABC C .=D .=10. 如图,△OAB 与△OCD 是以点O 为位似中心的位似图形,相似比为l :2,∠OCD=90°,CO=CD.若B(1,0),则点C[中国^的坐标为( )A.(1,2)B.(1,1)C.(2, 2)D.(2,1)11.如图,在ABC ∆中,BC DE //,6=AD ,3=DB ,4=AE ,则EC 的长为(A )1 (B )2 (C )3 (D )412.如图,∥∥,两条直线与这三条平行线分别交于点A 、B 、C 和D 、E 、F .已知,则的值为( )A .B .C .D .13.如图,AD ∥BE ∥CF ,直线l 1、l 2这与三条平行线分别交于点A 、B 、C 和点D 、E 、F .已知AB=1,BC=3,DE=2,则EF 的长为( )A. 4 B. 5 C. 6 D. 814.如图,在矩形ABCD中,AB=10 , BC=5 .若点M、N分别是线段AC AB上的两个动点,则BM+MN的最小值为()A. 10 B. 8 C. 53 D. 615.若,则的值为()A.1 B. C. D.16.如图,在Rt△ABC中,∠ABC=90°,AB=BC.点D是线段AB上的一点,连结CD,过点B 作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①;②若点D是AB的中点,则AF=AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若,则.其中正确的结论序号是()A.①② B.③④ C.①②③ D.①②③④17.如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF.若BD=6,AF=4,CD=3,则BE的长是()A. 2 B. 4 C. 6 D. 8考点:平行线分线段成比例;菱形的判定与性质;作图—基本作图..分析:根据已知得出MN是线段AD的垂直平分线,推出AE=DE,AF=DF,求出DE∥AC,DF ∥AE,得出四边形AEDF是菱形,根据菱形的性质得出AE=DE=DF=AF,根据平行线分线段成比例定理得出=,代入求出即可.解答:解:∵根据作法可知:MN是线段AD的垂直平分线,∴AE=DE,AF=DF,∴∠EAD=∠EDA,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠EDA=∠CAD,∴DE∥AC,同理DF∥AE,∴四边形AEDF是菱形,∴AE=DE=DF=AF,∵AF=4,∴AE=DE=DF=AF=4,∵DE∥AC,∴=,∵BD=6,AE=4,CD=3,∴=,∴BE=8,故选D.点评:本题考查了平行线分线段成比例定理,菱形的性质和判定,线段垂直平分线性质,等腰三角形的性质的应用,能根据定理四边形AEDF是菱形是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例.……依次顺延18.(2015•甘肃兰州,第5题,4分)如图,线段CD两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(5,0),则点A的坐标为A.(2,5)B.(2.5,5)C. (3,5)D.(3,6)【答案】B【考点解剖】本题考查了坐标和相似的有关知识【思路点拔】根据题意:AO:CO=BO:DO=5:2,而位似中心恰好是坐标原点O,所以点A的横、纵坐标都是点C横、纵坐标的2.5倍,因此选B。
【题目星级】★★★19.(2015•安徽省,第9题,4分)如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是[()]A.2 5 B.3 5 C.5 D.6考点:菱形的性质;矩形的性质..分析:连接EF交AC于O,由四边形EGFH是菱形,得到EF⊥AC,OE=OF,由于四边形ABCD 是矩形,得到∠B=∠D=90°,AB∥CD,通过△CFO≌△AOE,得到AO=CO,求出AO=AC=2,根据△AOE∽△ABC,即可得到结果.解答:解;连接EF交AC于O,∵四边形EGFH是菱形,∴EF⊥AC,OE=OF,∵四边形ABCD是矩形,∴∠B=∠D=90°,AB∥CD,∴∠ACD=∠CAB,在△CFO与△AOE中,,∴△CFO≌△AOE,∴AO=CO,∵AC==4,∴AO=AC=2,∵∠CAB=∠CAB,∠AOE=∠B=90°,∴△AOE∽△ABC,∴,∴,∴AE=5.故选C.点评:本题考查了菱形的性质,全等三角形的判定和性质,相似三角形的判定和性质,熟练运用定理是解题的关键.20. (2015山东济宁,10,3分)将一副三角尺(在中,∠ACB=,∠B=;在中,∠EDF=,∠E=)如图摆放,点D 为AB 的中点,DE 交AC 于点P ,DF 经过点C.将绕点D 顺时针方向旋转角,交AC 于点M ,交BC 于点N ,则的值为( )A. B. C. D.【答案】C 【解析】试题分析:由题意知D 为Rt △ABC 的斜边上的中点,根据直角三角形斜边上的中线等于斜边的一半,可得CD=AD=BD=AB ,再由∠B=60°可知△BCD 是等边三角形,因此可得∠DCP=30°,且可求∠DPC=60°,因此tan30°=.根据旋转变换的性质,可知∠PDM=∠CDN ,因此可知△PDM ∽△CDN ,再由相似三角形的性质可得,因此是一个定值.故选C考点:直角三角形斜边上的中线,相似三角形,旋转变换二.填空题1.(2015·贵州六盘水,第14题4分)已知0654≠==ab c ,则a c b +的值为 .考点:比例的性质..分析:根据比例的性质,可用a 表示b 、c ,根据分式的性质,可得答案.解答:解:由比例的性质,得c=a ,b=A .===.故答案为:.点评:本题考查了比例的性质,利用比例的性质得出a 表示b 、c 是解题关键,又利用了分式的性质.2. (2015·河南,第10题3分)如图,△ABC 中,点D 、E 分别在边AB ,BC 上,DE//AC ,若DB=4,DA=2,BE=3,则EC= .23【解析】本题考查平行线分线段成比例定理.∵DE ∥AC ,∴ECBEDA BD =,∴EC=23432BD BE DA =⨯=⋅.3.(2015•广东梅州,第14题5分)已知:△ABC 中,点E 是AB 边的中点,点F 在AC 边上,若以A ,E ,F 为顶点的三角形与△ABC 相似,则需要增加的一个条件是 AF=AC 或∠AFE=∠ABC .(写出一个即可)考点: 相似三角形的判定. 专题:开放型.E C DBA第10题分析:根据相似三角形对应边成比例或相似三角形的对应角相等进行解答;由于没有确定三角形相似的对应角,故应分类讨论.解答:解:分两种情况:①∵△AEF∽△ABC,∴AE:AB=AF:AC,即1:2=AF:AC,∴AF=AC;②∵△AFE∽△ACB,∴∠AFE=∠ABC.∴要使以A、E、F为顶点的三角形与△ABC相似,则AF=AC或∠AFE=∠ABC.故答案为:AF=AC或∠AFE=∠ABC.点评:本题很简单,考查了相似三角形的性质,在解答此类题目时要找出对应的角和边.4.(2015•广东佛山,第13题3分)如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是 25 .考点:相似三角形的判定与性质;正方形的性质.分析:由已知可得到△AFE∽△ABC,根据相似三角形的边对应成比例即可求得EF的长,进而根据正方形的面积公式即可求得.解答:解:∵在Rt△ABC中,AB2+BC2=AC2,∵AB=BC,AC=10.∴2AB2=200,∴AB=BC=10,设EF=x,则AF=10﹣x∵EF∥BC,∴△AFE∽△ABC∴=,即=,∴x=5,∴EF=5,∴此正方形的面积为5×5=25. 故答案为25. 点评:主要考查了正方形基本性质和比例线段的运用.解题的关键是准确的找到相似三角形并根据其相似比列方程求解.5. (2015·河南,第22题10分)如图1,在Rt △ABC 中,∠B=90°,BC=2AB=8,点D ,E 分别是边BC ,AC 的中点,连接DE. 将△EDC 绕点C 按顺时针方向旋转,记旋转角为α.(1)问题发现① 当︒=0α时,_____________=BDAE;② 当︒=180α时,.__________=BDAE(2)拓展探究试判断:当0°≤α<360°时,DBAE的大小有无变化?请仅就图2的情况给出证明.(3)问题解决当△EDC 旋转至A 、D 、E 三点共线时,直接写出线段BD 的长.(1)【分析】①根据题意可得DE 是三角形ABC 的中位线和BD 的长,根据中位线的性质和勾股定理求得AE 的长即可求解;②根据旋转180°的特性,结合①,分别得到AC 、CE 、BC 和CD 的长即可求解.1分)ECDBA (图1) E DBA C(图2)(备用图)CBA②2.……………………………………………………(2分)【解法提示】①当α=0°,如解图①,∵BC=2AB=8,∴AB=4,∵点D ,E 分别是边BC ,AC的中点,∴DE=121=AB ,AE=EC,,∵∠B=90°,∴AC ==,∴AE=CE=∴AE BD ==;②当α=180度,如解图②,由旋转性质可得CE=5,CD=2,∵AC=BC=8,∴25485254=++=++=CD BC CE AC BD AE .(2)【分析】在由解图①中,由平行线分线段成比例得到CBCDCA CE =,再观察图②中△EDC 绕点C 的旋转过程,结合旋转的性质得到CBCDCA CE =任然成立,从而求得△ACE ∽△BCD ,利用其性质,结合题干求得AC 的长即可得到结论.第22题解图③(3) 【分析】解:5………………………………………………………………………(10分)【解法提示】当△EDC 在BC 上方,且A ,D ,E 三点共线时,四边形ABCD 为矩形,∴BD=AC=EDC 在BC 下方,且A ,E ,D 三点共线时,△ADC 为直角三角形,由勾股定理可求得AD=8,∴AE=6,根据AE BD =2可求得BD =5.图④图⑤第22题解图6.(2015·黑龙江绥化,第21题分)在矩形ABCD中,AB=4 , BC=3 , 点P在AB上。