2020届赢在微点大一轮总复习数学理 (47)
- 格式:ppt
- 大小:3.25 MB
- 文档页数:40


必/考/部/分第一章集合与常用逻辑用语第一节集合2019考纲考题考情1.集合的含义与表示方法(1)集合的含义:研究对象叫做元素,一些元素组成的总体叫做集合。
集合中元素的性质:确定性、无序性、互异性。
(2)元素与集合的关系:①属于,记为∈;②不属于,记为∉。
(3)集合的表示方法:列举法、描述法和图示法。
(4)常用数集的记法:自然数集N,正整数集N*或N+,整数集Z,有理数集Q,实数集R。
2.集合间的基本关系3.集合的基本运算1.集合元素的三个特性确定性、无序性、互异性。
2.集合的子集个数若有限集A中有n个元素,则A的子集有2n个,非空子集有2n-1个,真子集有2n-1个。
3.注意空集空集是任何集合的子集,是任何非空集合的真子集,应时刻关注对空集的讨论,防止漏解。
4.集合的运算性质(1)并集的性质:A∪∅=A;A∪A=A;A∪B=B∪A;A∪B =A⇔B⊆A。
(2)交集的性质:A∩∅=∅;A∩A=A;A∩B=B∩A;A∩B =A⇔A⊆B。
(3)补集的性质:A∪(∁U A)=U;A∩(∁U A)=∅;∁U(∁U A)=A。
∁U(A∩B)=(∁U A)∪(∁U B);∁U(A∪B)=(∁U A)∩(∁U B)。
一、走进教材1.(必修1P12A组T5改编)若集合P={x∈N|x≤ 2 018},a =22,则()A.a∈P B.{a}∈PC.{a}⊆P D.a∉P解析因为a=22不是自然数,而集合P是不大于 2 018的自然数构成的集合,所以a∉P。
故选D。
答案 D2.(必修1P12B组T1改编)已知集合M={0,1,2,3,4},N={1,3,5},则集合M∪N的子集的个数为________。
解析由已知得M∪N={0,1,2,3,4,5},所以M∪N的子集有26=64(个)。
答案64二、走近高考3.(2018·全国卷Ⅰ)已知集合A={x|x2-x-2>0},则∁R A=()A.{x|-1<x<2}B.{x|-1≤x≤2}C.{x|x<-1}∪{x|x>2}D.{x|x≤-1}∪{x|x≥2}解析解不等式x2-x-2>0得x<-1或x>2,所以A={x|x<-1或x>2},所以∁R A={x|-1≤x≤2}。

必/考/部/分第一章集合与常用逻辑用语第一节集合2019考纲考题考情1.集合的含义与表示方法(1)集合的含义:研究对象叫做元素,一些元素组成的总体叫做集合。
集合中元素的性质:确定性、无序性、互异性。
(2)元素与集合的关系:①属于,记为∈;②不属于,记为∉。
(3)集合的表示方法:列举法、描述法和图示法。
(4)常用数集的记法:自然数集N,正整数集N*或N+,整数集Z,有理数集Q,实数集R。
2.集合间的基本关系3.集合的基本运算1.集合元素的三个特性确定性、无序性、互异性。
2.集合的子集个数若有限集A中有n个元素,则A的子集有2n个,非空子集有2n-1个,真子集有2n-1个。
3.注意空集空集是任何集合的子集,是任何非空集合的真子集,应时刻关注对空集的讨论,防止漏解。
4.集合的运算性质(1)并集的性质:A∪∅=A;A∪A=A;A∪B=B∪A;A∪B =A⇔B⊆A。
(2)交集的性质:A∩∅=∅;A∩A=A;A∩B=B∩A;A∩B =A⇔A⊆B。
(3)补集的性质:A∪(∁U A)=U;A∩(∁U A)=∅;∁U(∁U A)=A。
∁U(A∩B)=(∁U A)∪(∁U B);∁U(A∪B)=(∁U A)∩(∁U B)。
一、走进教材1.(必修1P12A组T5改编)若集合P={x∈N|x≤ 2 018},a =22,则()A.a∈P B.{a}∈PC.{a}⊆P D.a∉P解析因为a=22不是自然数,而集合P是不大于 2 018的自然数构成的集合,所以a∉P。
故选D。
答案 D2.(必修1P12B组T1改编)已知集合M={0,1,2,3,4},N={1,3,5},则集合M∪N的子集的个数为________。
解析由已知得M∪N={0,1,2,3,4,5},所以M∪N的子集有26=64(个)。
答案64二、走近高考3.(2018·全国卷Ⅰ)已知集合A={x|x2-x-2>0},则∁R A=()A.{x|-1<x<2}B.{x|-1≤x≤2}C.{x|x<-1}∪{x|x>2}D.{x|x≤-1}∪{x|x≥2}解析解不等式x2-x-2>0得x<-1或x>2,所以A={x|x<-1或x>2},所以∁R A={x|-1≤x≤2}。


高三数学一轮总结复习目录理科数学 -模拟试题分类目录1第一章会合与常用逻辑用语1.1 会合的观点与运算专题 1 会合的含义与表示、会合间的基本关系专题 2 会合的基本运算专题 3 与会合有关的新观点问题1.2 命题及其关系、充要条件专题 1 四种命题及其关系、命题真假的判断专题 2 充足条件和必需条件专题 3 充足、必需条件的应用与研究(利用关系或条件求解参数范围问题)1.3 简单的逻辑联络词、全称量词与存在量词专题 1 含有简单逻辑联络词的命题的真假专题 2 全称命题、特称命题的真假判断专题 3 含有一个量词的命题的否认专题 4 利用逻辑联络词求参数范围第二章函数2.1 函数及其表示专题 1 函数的定义域专题 2 函数的值域专题 3 函数的分析式专题 4 分段函数2.2 函数的单一性与最值专题 1 确立函数的单一性(或单一区间)专题 2 函数的最值专题 3 单一性的应用2.3 函数的奇偶性与周期性专题 1 奇偶性的判断专题 2 奇偶性的应用专题 3 周期性及其应用2.4 指数与指数函数专题 1 指数幂的运算专题 2 指数函数的图象及应用专题 3 指数函数的性质及应用2.5 对数与对数函数专题 1 对数的运算专题 2 对数函数的图象及应用专题 3 对数函数的性质及应用2.6 幂函数与二次函数专题 1 幂函数的图象与性质专题 2 二次函数的图象与性质2.7 函数的图像专题 1 函数图象的辨别专题 2 函数图象的变换专题 3 函数图象的应用2.8 函数与方程专题 1 函数零点所在区间的判断专题 2 函数零点、方程根的个数专题 3 函数零点的综合应用2.9 函数的应用专题 1 一次函数与二次函数模型专题 2 分段函数模型2专题 3 指数型、对数型函数模型第三章导数及其应用3.1 导数的观点及运算专题 1 导数的观点与几何意义专题 2 导数的运算3.2 导数与函数的单一性、极值、最值专题 1 导数与函数的单一性专题 2 导数与函数的极值专题 3 导数与函数的最值3.3 导数的综合应用专题 1 利用导数解决生活中的优化问题专题 2 利用导数研究函数的零点或方程的根专题 3 利用导数解决不等式的有关问题3.4 定积分与微积分基本定理专题 1 定积分的计算专题 2 利用定积分求平面图形的面积专题 4 定积分在物理中的应用第四章三角函数、解三角形4.1 三角函数的观点、同角三角函数的基本关系及引诱公式专题 1 三角函数的观点专题 2 同角三角函数的基本关系专题 3 引诱公式4.2 三角函数的图像与性质专题 1 三角函数的定义域、值域、最值专题 2 三角函数的单一性专题 3 三角函数的奇偶性、周期性和对称性4.3 函数 y = A sin(wx +j ) 的图像及应用专题 1 三角函数的图象与变换专题 2 函数 y=Asin( ωx+φ ) 图象及性质的应用4.4 两角和与差的正弦、余弦与正切公式专题 1 非特别角的三角函数式的化简、求值专题 2 含条件的求值、求角问题专题 3 两角和与差公式的应用4.5 三角恒等变换专题 1 三角函数式的化简、求值专题 2 给角求值与给值求角专题 3 三角变换的综合问题4.6 解三角形专题 1 利用正弦定理、余弦定理解三角形专题 2 判断三角形的形状专题 3 丈量距离、高度及角度问题专题 4 与平面向量、不等式等综合的三角形问题第五章平面向量5.1 平面向量的观点及线性运算专题 1 平面向量的线性运算及几何意义专题 2 向量共线定理及应用专题 3 平面向量基本定理的应用5.2 平面向量基本定理及向量的坐标表示专题 1 平面向量基本定理的应用3专题 2 平面向量的坐标运算专题 3 平面向量共线的坐标表示5.3 平面向量的数目积专题 1 平面向量数目积的运算专题 2 平面向量数目积的性质专题 3 平面向量数目积的应用5.4 平面向量的应用专题 1 平面向量在几何中的应用专题 2 平面向量在物理中的应用专题 3 平面向量在三角函数中的应用专题 4 平面向量在分析几何中的应用第六章数列6.1 数列的观点与表示专题 1 数列的观点专题 2 数列的通项公式6.2 等差数列及其前 n 项和专题 1 等差数列的观点与运算专题 2 等差数列的性质专题 3 等差数列前 n 项和公式与最值6.3 等比数列及其前 n 项和专题 1 等比数列的观点与运算专题 2 等比数列的性质专题 3 等比数列前 n 项和公式6.4 数列乞降专题 1 分组乞降与并项乞降专题 2 错位相减乞降专题 3 裂项相消乞降6.5 数列的综合应用专题 1 数列与不等式相联合问题专题 2 数列与函数相联合问题专题 3 数列中的研究性问题第七章不等式推理与证明7.1 不等关系与一元二次不等式专题 1 不等式的性质及应用专题 2 一元二次不等式的解法专题 3 一元二次不等式恒建立问题7.2 二元一次不等式(组)与简单的线性规划问题专题 1 二元一次不等式(组)表示的平面地区问题专题 2 与目标函数有关的最值问题专题 3 线性规划的实质应用7.3 基本不等式及其应用专题 1 利用基本不等式求最值专题 2 利用基本不等式证明不等式专题 3 基本不等式的实质应用7.4 合情推理与演绎推理专题 1 概括推理专题 2 类比推理专题 3 演绎推理7.5 直接证明与间接证明专题 1 综合法4专题 2 剖析法专题 3 反证法7.6 数学概括法专题 1 用数学概括法证明等式专题 2 用数学概括法证明不等式专题 3 概括-猜想-证明第八章立体几何8.1 空间几何体的构造及其三视图和直观图专题 1 空间几何体的构造专题 2 三视图与直观图8.2 空间几何体的表面积与体积专题 1 空间几何体的表面积专题 2 空间几何体的体积专题 3 组合体的“接”“切”综合问题8.3 空间点、直线、平面之间的地点关系专题 1 平面的基天性质及应用专题 2 空间两条直线的地点关系专题 3 异面直线所成的角8.4 直线、平面平行的判断与性质专题 1 线面平行、面面平行基本问题专题 2 直线与平面平行的判断与性质专题 3 平面与平面平行的判断与性质8.5 直线、平面垂直的判断与性质专题 1 垂直关系的基本问题专题 2 直线与平面垂直的判断与性质专题 3 平面与平面垂直的判断与性质专题 4 空间中的距离问题专题 5 平行与垂直的综合问题(折叠、研究类)8.6 空间向量及其运算专题 1 空间向量的线性运算专题 2 共线定理、共面定理的应用专题 3 空间向量的数目积及其应用8.7 空间几何中的向量方法专题 1 利用空间向量证明平行、垂直专题 2 利用空间向量解决研究性问题专题 3 利用空间向量求空间角第九章分析几何9.1 直线的倾斜角、斜率与直线的方程专题 1 直线的倾斜角与斜率专题 2 直线的方程9.2 点与直线、两条直线的地点关系专题 1 两条直线的平行与垂直专题 2 直线的交点问题专题 3 距离公式专题 4 对称问题9.3 圆的方程专题 1 求圆的方程专题 2 与圆有关的轨迹问题专题 3 与圆有关的最值问题59.4 直线与圆、圆与圆的地点关系专题 1 直线与圆的地点关系专题 2 圆与圆的地点关系专题 3 圆的切线与弦长问题专题 4 空间直角坐标系9.5 椭圆专题 1 椭圆的定义及标准方程专题 2 椭圆的几何性质专题 3 直线与椭圆的地点关系9.6 双曲线专题 1 双曲线的定义与标准方程专题 2 双曲线的几何性质9.7 抛物线专题 1 抛物线的定义与标准方程专题 2 抛物线的几何性质专题 3 直线与抛物线的地点关系9.8 直线与圆锥曲线专题 1 轨迹与轨迹方程专题 2 圆锥曲线中的范围、最值问题专题 3 圆锥曲线中的定值、定点问题专题 4 圆锥曲线中的存在、研究性问题第十章统计与统计事例10.1 随机抽样专题 1 简单随机抽样专题 2 系统抽样专题 3 分层抽样10.2 用样本预计整体专题 1 频次散布直方图专题 2 茎叶图专题 3 样本的数字特点专题 4 用样本预计整体10.3 变量间的有关关系、统计事例专题 1 有关关系的判断专题 2 回归方程的求法及回归剖析专题 3 独立性查验第十一章计数原理11.1 分类加法计数原理与分步乘法计数原理专题 1 分类加法计数原理专题 2 分步乘法计数原理专题 3 两个计数原理的综合应用11.2 摆列与组合专题 1 摆列问题专题 2 组合问题专题 3 摆列、组合的综合应用11.3 二项式定理专题 1 通项及其应用专题 2 二项式系数的性质与各项系数和专题 3 二项式定理的应用第十二章概率与统计612.1 随机事件的概率专题 1 事件的关系专题 2 随机事件的频次与概率专题 3 互斥事件、对峙事件12.2 古典概型与几何概型专题 1 古典概型的概率专题 2 古典概型与其余知识的交汇(平面向量、直线、圆、函数等)专题 3 几何概型在不一样测度中的概率专题 4 生活中的几何概型问题12.3 失散型随机变量及其散布列专题 1 失散型随机变量的散布列的性质专题 2 求失散型随机变量的散布列专题 3 超几何散布12.4 失散型随机变量的均值与方差专题 1 简单的均值、方差问题专题 2 失散型随机变量的均值与方差专题 3 均值与方差在决议中的应用12.5 二项散布与正态散布专题 1 条件概率专题 2 互相独立事件同时发生的概率专题 3 独立重复试验与二项散布专题 4 正态散布下的概率第十三章算法初步、复数13.1 算法与程序框图专题 1 次序构造专题 2 条件构造专题 3 循环构造13.2 基本算法语句专题 1 输入、输出和赋值语句专题 2 条件语句专题 3 循环语句13.3 复数专题 1 复数的有关观点专题 2 复数的几何意义专题 3 复数的代数运算第十四章选修模块14.1 几何证明选讲专题 1 平行线分线段成比率定理专题 2 相像三角形的判断与性质专题 3 直角三角形的射影定理专题 4 圆周角、弦切角及圆的切线专题 5 圆内接四边形的判断及性质专题 6 圆的切线的性质与判断专题 7 与圆有关的比率线段14.2 坐标系与参数方程专题 1 极坐标与直角坐标的互化专题 2 直角坐标方程与极坐标方程的互化专题 3 曲线的极坐标方程的求解专题 4 曲线的参数方程的求解专题 5 参数方程与一般方程的互化7专题 6 极坐标方程与参数方程的应用14.3 不等式选讲专题 1 含绝对值不等式的解法专题 2 绝对值三角不等式的应用专题 3 含绝对值不等式的问题专题 4 不等式的证明8。

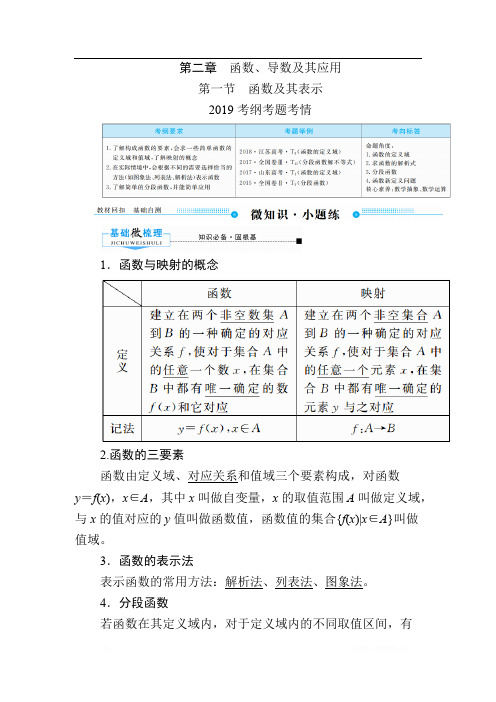
第二章函数、导数及其应用第一节 函数及其表示2019考纲考题考情1.函数与映射的概念2.函数的三要素函数由定义域、对应关系和值域三个要素构成,对函数y=f(x),x∈A,其中x叫做自变量,x的取值范围A叫做定义域,与x的值对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做值域。
3.函数的表示法表示函数的常用方法:解析法、列表法、图象法。
4.分段函数若函数在其定义域内,对于定义域内的不同取值区间,有着不同的对应关系,这样的函数通常叫做分段函数。
分段函数虽然由几部分组成,但它表示的是一个函数。
1.一种优先意识函数定义域是研究函数的基础依据,对函数的研究,必须坚持定义域优先的原则。
2.两个关注点(1)分段函数是一个函数。
(2)分段函数的定义域、值域是各段定义域、值域的并集。
3.直线x =a (a 是常数)与函数y =f (x )的图象有0个或1个交点。
一、走进教材1.(必修1P 18例2改编)下列函数中,与函数y =x +1是相等函数的是( )A .y =()2B .y =+1x +13x 3C .y =+1 D .y =+1x 2x x 2解析 对于A ,函数y =()2的定义域为{x |x ≥-1},x +1与函数y =x +1的定义域不同,不是相等函数;对于B ,定义域和对应法则都相同,是相等函数;对于C ,函数y =+1的x 2x 定义域为{x |x ≠0},与函数y =x +1的定义域不同,不是相等函数;对于D ,定义域相同,但对应法则不同,不是相等函数。
故选B 。
答案 B2.(必修1P 25B 组T 1改编)函数y =f (x )的图象如图所示,那么,f (x )的定义域是________;值域是________;其中只有唯一的x 值与之对应的y 值的范围是________。
答案 [-3,0]∪[2,3] [1,5] [1,2)∪(4,5]二、走近高考3.(2018·江苏高考)函数f (x )=的定义域为log2x -1________。



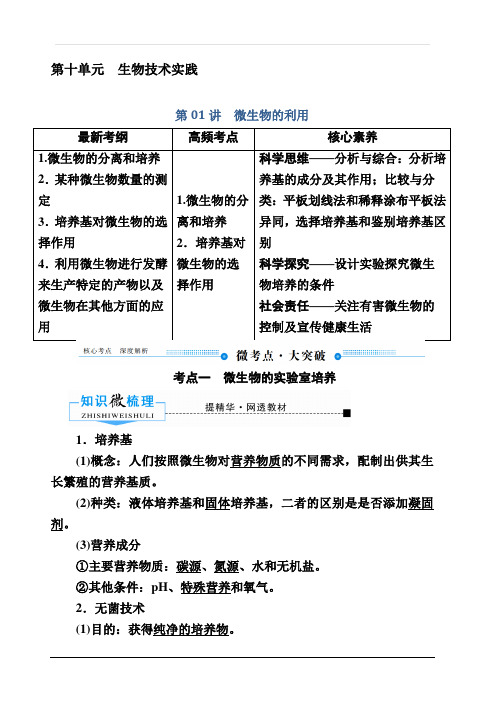
第十单元 生物技术实践第01讲 微生物的利用考点一 微生物的实验室培养1.培养基(1)概念:人们按照微生物对营养物质的不同需求,配制出供其生长繁殖的营养基质。
(2)种类:液体培养基和固体培养基,二者的区别是是否添加凝固剂。
(3)营养成分①主要营养物质:碳源、氮源、水和无机盐。
②其他条件:pH 、特殊营养和氧气。
2.无菌技术(1)目的:获得纯净的培养物。
(2)关键:防止外来杂菌的入侵。
(3)常用方法:灭菌和消毒。
(4)无菌技术的主要方法及适用对象(连一连)答案 a —Ⅲ—⑤ a —V —④ a —Ⅵ—③ b —Ⅰ—⑥ b —Ⅱ—① b —Ⅳ—②3.制备牛肉膏蛋白胨固体培养基(1)计算:依据配方比例,计算配制100 mL 的培养基时,各种成分的用量。
(2)称量:准确地称取各种成分。
(3)溶化⎩⎪⎪⎨⎪⎪⎧①牛肉膏连同称量纸一同放入烧杯②加入少量水,加热③牛肉膏溶化后取出称量纸④加入称量好的蛋白胨和氯化钠,搅拌⑤加入琼脂,加热使其熔化,并不断搅拌⑥补加蒸馏水定容(5)倒平板:待培养基冷却至50 ℃左右时,在酒精灯火焰附近倒平板。
4.纯化大肠杆菌(1)菌落:由一个细胞繁殖而来的肉眼可见的子细胞群体。
(2)主要方法及纯化原理(选修1 P 18旁栏小资料改编)微生物的接种方法只有平板划线法和稀释涂布平板法吗?微生物接种的核心是什么?答案 不是。
微生物的接种方法还包括斜面接种、穿刺接种等,其核心是防止杂菌污染,保证培养物的纯度。
诊断辨析(1)培养基一般都含有水、碳源、氮源和无机盐,有时还需要加入一些特殊的物质。
(√)(2)倒平板时,应将打开的皿盖放到一边,以免培养基溅到皿盖上。
(×)(3)消毒的原则是既杀死材料表面的微生物,又减少消毒剂对细胞的伤害。
(√)(4)为了防止污染,接种环经火焰灭菌后应趁热快速挑取菌落。
(×)(5)用稀释涂布平板法纯化大肠杆菌时,只要稀释度足够高,就能在培养基表面形成单个菌落。

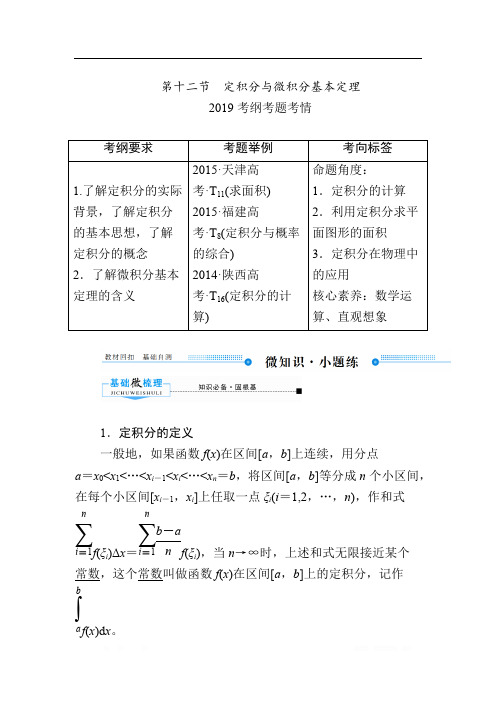


选修4-4 坐标系与参数方程第一节 坐 标 系2019考纲考题考情1.平面直角坐标系中的伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换φ:Error!的作用下,点P(x,y)对应点P′(x′,y′),称φ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换。
2.极坐标的概念(1)极坐标系:如图所示,在平面内取一个定点O,叫做极点,从O点引一条射线Ox,叫做极轴,选定一个单位长度和角及其正方向(通常取逆时针方向),这样就确定了一个平面极坐标系,简称为极坐标系。
(2)极坐标:对于平面内任意一点M,用ρ表示线段OM的长,θ表示以Ox 为始边、OM为终边的角度,ρ叫做点M的极径,θ叫做点M的极角,有序实数对(ρ,θ)叫做点M的极坐标,记作M(ρ,θ)。
当点M在极点时,它的极径ρ=0,极角θ可以取任意值。
(3)点与极坐标的关系:平面内一点的极坐标可以有无数对,当k∈Z时,(ρ,θ),(ρ,θ+2kπ),(-ρ,θ+(2k+1)π)表示同一个点,而用平面直角坐标表示点时,每一个点的坐标是唯一的。
如果规定ρ>0,0≤θ<2π,或者-π<θ≤π,那么,除极点外,平面内的点和极坐标就一一对应了。
3.极坐标和直角坐标的互化(1)互化背景:把平面直角坐标系的原点作为极点,x轴的正半轴作为极轴,建立极坐标系,并在两种坐标系中取相同的单位长度,如图所示。
(2)互化公式:设M是坐标平面内任意一点,它的直角坐标是(x,y),极坐标是(ρ,θ)(ρ>0,θ∈[0,2π)),于是极坐标与直角坐标的互化公式如表:点M直角坐标(x,y)极坐标(ρ,θ)互化公式Error!ρ2=x 2+y 2tan θ=(x≠0)y x在一般情况下,由tan θ确定角时,可根据点M 所在的象限取最小正角。
4.常见曲线的极坐标方程曲线图形极坐标方程圆心在极点,半径为r 的圆ρ=r (0≤θ<2π)圆心为(r,0),半径为r 的圆ρ=2r cos θ(-π2≤θ<π2)圆心为,(r ,π2)半径为r 的圆ρ=2r sin θ(0≤θ<π)过极点,倾斜角为α的直线①θ=α(ρ∈R )或θ=π+α(ρ∈R )②θ=α(ρ≥0)和θ=π+α(ρ≥0)过点(a,0),与极轴垂直的直线ρcos θ=a (-π2<θ<π2)过点,与(a ,π2)极轴平行的直线ρsin θ=a (0<θ<π)过点(a,0),倾斜角为α的直线ρsin(α-θ)=a sin α1.明辨两个坐标伸缩变换关系式Error!点(x ,y )在原曲线上,点(x ′,y ′)在变换后的曲线上,因此点(x ,y )的坐标满足原来的曲线方程,点(x ′,y ′)的坐标满足变换后的曲线方程。