主成分分析计算方法和步骤

主成分分析法的步骤和原理
1.数据标准化：针对原始数据集，对每个变量进行标准化处理，使得
每个变量的均值为0，方差为1、这样做的目的是确保每个变量都具有相
同的重要性。

2.计算协方差矩阵：协方差矩阵是一个对称的矩阵，它描述了变量之
间的线性关系。

通过计算原始数据的协方差矩阵，可以得到变量之间的相
关程度。

3.计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征
值和特征向量。

特征值表示了每个主成分所解释的方差的大小，而特征向
量表示了每个主成分的方向。

4.选择主成分：根据特征值的大小，选择解释方差较大的前k个主成分，通常只选取特征值大于1的主成分。

这些主成分可以解释原始数据中
大部分的方差。

5.构建特征向量矩阵：将选取的k个特征向量按照特征值从大到小的
顺序排列，构成一个特征向量矩阵。

6.数据转换：将原始数据与特征向量矩阵相乘，得到降维后的数据集。

每个样本由k个主成分组成，而不再包含原始数据中的所有变量。

主成分分析的原理是基于最大方差的思想。

在原始数据中，方差较大
的变量携带了较多的信息，而方差较小的变量携带了较少的信息。

主成分
分析的目标是将原始数据投影到方差较大的方向上，以便在保留较多信息
的同时降低数据的维度。

通过特征值分解协方差矩阵，可以得到原始数据的主成分。

特征向量代表了每个主成分的方向，而特征值则表示了每个主成分所解释的方差大小。

通常，选择特征值较大的前几个主成分，可以达到保留较多信息的目的。

同时，主成分之间是正交的，即它们之间没有相关性，这样可以进一步减少数据冗余。

主成分分析法的步骤和原理[技巧](一)主成分分析法的基本思想主成分分析(Principal Component Analysis)是利用降维的思想，将多个变量转化为少数几个综合变量(即主成分)，其中每个主成分都是原始变量的线性组合，各主成分之间互不相关，从而这些主成分能够反映始变量的绝大部分信息，[2]且所含的信息互不重叠。

采用这种方法可以克服单一的财务指标不能真实反映公司的财务情况的缺点，引进多方面的财务指标，但又将复杂因素归结为几个主成分，使得复杂问题得以简化，同时得到更为科学、准确的财务信息。

(二)主成分分析法代数模型假设用p个变量来描述研究对象，分别用X，X…X来表示，这p个变量12p t构成的p维随机向量为X=(X，X…X)。

设随机向量X的均值为μ，协方差矩12p阵为Σ。

假设 X 是以 n 个标量随机变量组成的列向量，并且μk 是其第k个元素的期望值，即，μk= E(xk)，协方差矩阵然后被定义为:Σ=E{(X-E[X])(X-E[X])}=(如图对X进行线性变化，考虑原始变量的线性组合:Z1=μ11X1+μ12X2+…μ1pXpZ2=μ21X1+μ22X2+…μ2pXp…… …… ……Zp=μp1X1+μp2X2+…μppXp主成分是不相关的线性组合Z，Z……Z，并且Z是X1，X2…Xp的线性组12p1 合中方差最大者，Z是与Z不相关的线性组合中方差最大者，…，Zp是与Z，211Z ……Z都不相关的线性组合中方差最大者。

2p-1(三)主成分分析法基本步骤第一步:设估计样本数为n，选取的财务指标数为p，则由估计样本的原始数据可得矩阵X=(x)，其中x表示第i家上市公司的第j项财务指标数据。

ijm×pij 第二步:为了消除各项财务指标之间在量纲化和数量级上的差别，对指标数据进行标准化，得到标准化矩阵(系统自动生成)。

第三步:根据标准化数据矩阵建立协方差矩阵R，是反映标准化后的数据之间相关关系密切程度的统计指标，值越大，说明有必要对数据进行主成分分析。

主成分分析法pca的流程
主成分分析（PCA）是一种常见的数据降维方法，其主要流程如下：
1. 数据预处理：先对原始数据进行标准化（均值中心化和方差缩放），保证各个维度数据具有可比性。

2. 计算协方差矩阵：通过样本数据求解协方差矩阵，反映各个变量间的线性相关性。

3. 特征值与特征向量计算：对协方差矩阵进行特征值分解或奇异值分解，得到对应的特征值和特征向量。

4. 选择主成分：按照特征值大小排序，选择前k个最大特征值对应的特征向量作为新的坐标轴（主成分）。

5. 数据转换：将原始数据投影到选定的主成分上，实现降维，新坐标系下的数据称为主成分得分。

6. 解释主成分：根据特征向量的结构理解主成分代表的含义，并可能通过累计贡献率评估降维效果。

总之，PCA通过挖掘数据内在结构，将高维数据转换为低维表示，同时保留主要变异信息。

（一）主成分分析法的基本思想主成分分析（Principal Component Analysis ）是利用降维的思想，将多个变量转化为少数几个综合变量（即主成分），其中每个主成分都是原始变量的线性组合，各主成分之间互不相关，从而这些主成分能够反映始变量的绝大部分信息，且所含的信息互不重叠。

[2]采用这种方法可以克服单一的财务指标不能真实反映公司的财务情况的缺点，引进多方面的财务指标，但又将复杂因素归结为几个主成分，使得复杂问题得以简化，同时得到更为科学、准确的财务信息。

（二）主成分分析法代数模型假设用p 个变量来描述研究对象，分别用X 1，X 2…X p 来表示，这p 个变量构成的p 维随机向量为X=(X 1，X 2…X p )t 。

设随机向量X 的均值为μ，协方差矩阵为Σ。

对X 进行线性变化，考虑原始变量的线性组合： Z 1=μ11X 1+μ12X 2+…μ1p X pZ 2=μ21X 1+μ22X 2+…μ2p X p…… …… ……Z p =μp1X 1+μp2X 2+…μpp X p主成分是不相关的线性组合Z 1，Z 2……Z p ，并且Z 1是X 1，X 2…X p 的线性组合中方差最大者，Z 2是与Z 1不相关的线性组合中方差最大者，…，Z p 是与Z 1，Z 2 ……Z p-1都不相关的线性组合中方差最大者。

（三）主成分分析法基本步骤第一步：设估计样本数为n ，选取的财务指标数为p ，则由估计样本的原始数据可得矩阵X=(x ij )m ×p ，其中x ij 表示第i 家上市公司的第j 项财务指标数据。

第二步：为了消除各项财务指标之间在量纲化和数量级上的差别，对指标数据进行标准化，得到标准化矩阵（系统自动生成）。

第三步：根据标准化数据矩阵建立协方差矩阵R ，是反映标准化后的数据之间相关关系密切程度的统计指标，值越大，说明有必要对数据进行主成分分析。

其中，R ij （i ，j=1，2，…，p ）为原始变量X i 与X j 的相关系数。

主成分分析法的原理应用及计算步骤1.计算协方差矩阵：首先，我们需要将原始数据进行标准化处理，即使每个特征都有零均值和单位方差。

假设我们有m个n维样本，数据集为X，标准化后的数据集为Z。

那么，计算协方差矩阵的公式如下：Cov(Z) = (1/m) * Z^T * Z其中，Z^T为Z的转置。

2.计算特征向量：通过对协方差矩阵进行特征值分解，可以得到特征值和特征向量。

特征值表示了新坐标系中每个特征的重要性程度，特征向量则表示了数据在新坐标系中的方向。

将协方差矩阵记为C，特征值记为λ1, λ2, ..., λn，特征向量记为v1, v2, ..., vn，那么特征值分解的公式如下：C*v=λ*v计算得到的特征向量按特征值的大小进行排序，从大到小排列。

3.选择主成分：从特征向量中选择与前k个最大特征值对应的特征向量作为主成分，即新坐标系的基向量。

这些主成分可以解释原始数据中大部分的方差。

我们可以通过设定一个阈值或者看特征值与总特征值之和的比例来确定保留的主成分个数。

4.映射数据：对于一个n维的原始数据样本x，通过将其投影到前k个主成分上，可以得到一个k维的新样本，使得新样本的方差最大化。

新样本的计算公式如下：y=W*x其中，y为新样本，W为特征向量矩阵，x为原始数据样本。

PCA的应用：1.数据降维：PCA可以通过主成分的选择，将高维数据降低到低维空间中，减少数据的复杂性和冗余性，提高计算效率。

2.特征提取：PCA可以通过寻找数据中的最相关的特征，提取出主要的信息，从而减小噪声的影响。

3.数据可视化：通过将数据映射到二维或三维空间中，PCA可以帮助我们更好地理解和解释数据。

总结：主成分分析是一种常用的数据降维方法，它通过投影数据到一个新的坐标系中，使得投影后的数据具有最大的方差。

通过计算协方差矩阵和特征向量，我们可以得到主成分，并将原始数据映射到新的坐标系中。

PCA 在数据降维、特征提取和数据可视化等方面有着广泛的应用。

一、概述 在处理信息时，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此课题的信息有一定的重叠，例如，高校科研状况评价中的立项课题数与项目经费、经费支出等之间会存在较高的相关性；学生综合评价研究中的专业基础课成绩与专业课成绩、获奖学金次数等之间也会存在较高的相关性。

而变量之间信息的高度重叠和高度相关会给统计方法的应用带来许多障碍。

为了解决这些问题，最简单和最直接的解决方案是削减变量的个数，但这必然又会导致信息丢失和信息不完整等问题的产生。

为此，人们希望探索一种更为有效的解决方法，它既能大大减少参与数据建模的变量个数，同时也不会造成信息的大量丢失。

主成分分析正是这样一种能够有效降低变量维数，并已得到广泛应用的分析方法。

主成分分析以最少的信息丢失为前提，将众多的原有变量综合6210x 较少几个综合指标，通常综合指标（主成分）有以下几个特点：✍主成分个数远远少于原有变量的个数原有变量综合成少数几个因子之后，因子将可以替代原有变量参与数据建模，这将大大减少分析过程中的计算工作量。

✍主成分能够反映原有变量的绝大部分信息因子并不是原有变量的简单取舍，而是原有变量重组后的结果，因此不会造成原有变量信息的大量丢失，并能够代表原有变量的绝大部分信息。

✍主成分之间应该互不相关通过主成分分析得出的新的综合指标（主成分）之间互不相关，因子参与数据建模能够有效地解决变量信息重叠、多重共线性等给分析应用带来的诸多问题。

✍主成分具有命名解释性总之，主成分分析法是研究如何以最少的信息丢失将众多原有变量浓缩成少数几个因子，如何使因子具有一定的命名解释性的多元统计分析方法。

二、基本原理主成分分析是数学上对数据降维的一种方法。

其基本思想是设法将原来众多的具有一定相关性的指标X1，X2，…，XP （比如p 个指标），重新组合成一组较少个数的互不相关的综合指标Fm 来代替原来指标。

那么综合指标应该如何去提取，使其既能最大程度的反映原变量Xp 所代表的信息，又能保证新指标之间保持相互无关（信息不重叠）。

主成分分析法的原理应用及计算步骤主成分分析的目标是通过线性变换找到一组新的变量，使得原始数据在这组新变量上的投影具有最大方差。

假设有m个观测样本和n个变量，我们的目标是找到n个线性无关的主成分变量Z1,Z2,...,Zn。

首先，我们选择第一个主成分变量Z1，使得数据在Z1上的投影具有最大的方差。

然后，我们选择第二个主成分Z2，使得Z1和Z2的协方差尽可能小，即Z2与Z1无关。

依此类推，我们依次选择第三、第四...第n个主成分变量，一直到第n个主成分Zn，使得Z1、Z2...Zn两两不相关。

通过这种方式，我们实现了对数据的降维，将原始的高维数据使用较低维的主成分表示。

1.标准化数据：将原始数据按列进行标准化处理，即将每一列的数据减去该列的均值，然后再除以该列的标准差。

这样做的目的是使得相对较大方差的变量与相对较小方差的变量处于同一个尺度上。

2.计算协方差矩阵：通过计算标准化后的数据的协方差矩阵，来描述各个变量之间的线性关系。

协方差矩阵的元素C[i][j]表示第i个变量与第j个变量的协方差。

3.计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征值和特征向量。

特征值表示数据在对应特征向量方向上的方差，特征向量表示数据在对应特征向量方向上的投影。

4.选择主成分：根据特征值的大小，选择前k个特征值对应的特征向量作为前k个主成分。

通常选择的主成分数目k是根据方差解释率来确定的。

5.数据降维：将原始数据通过选取的主成分线性变换到低维空间中。

只选择部分主成分（前k个），可以减小数据的维度。

6.可视化与解释：通过可视化的方式展示主成分之间的关系，解释主成分所代表的意义，从而达到对数据的理解和分析。

总结：主成分分析方法通过线性变换将高维数据转化为低维数据，保留了原始数据中最大方差的性质。

它的计算步骤包括数据标准化、计算协方差矩阵、计算特征值和特征向量、选择主成分、数据降维和可视化与解释。

主成分分析方法在数据分析和特征提取中有广泛的应用，能够帮助我们更好地理解和处理高维数据。

主成分分析的原理与方法主成分分析（Principal Component Analysis, PCA）是一种常用的数据降维和特征提取方法。

它通过提取数据中的主要特征，将高维数据转化为低维表示，从而简化数据分析和可视化过程。

本文将介绍主成分分析的原理与方法，并对其在实际应用中的一些注意事项进行探讨。

一、主成分分析的原理主成分分析的基本原理是通过线性变换将原始数据映射到一组新的正交变量上，这些新的变量被称为主成分。

主成分的生成过程为以下几个步骤：1. 数据标准化在进行主成分分析之前，首先要对原始数据进行标准化处理，确保数据在不同维度上具有相同的尺度，避免因为尺度不同而影响主成分的提取。

2. 计算协方差矩阵计算标准化后的数据的协方差矩阵，协方差矩阵反映了不同维度之间的相关性。

通过协方差矩阵，可以确定数据中的主要方向和相关性强弱。

3. 特征值分解对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。

特征值表示了每个主成分所解释的方差比例，而特征向量则是对应于特征值的主成分。

4. 选择主成分根据特征值的大小，选择前k个最大的特征值对应的特征向量作为主成分，其中k是用户预设的维度。

二、主成分分析的方法主成分分析一般可以通过以下几个步骤来完成：1. 数据准备首先，需要准备原始数据集，并对数据进行标准化处理，使得数据在不同维度上具有相同的尺度。

2. 计算协方差矩阵根据标准化后的数据，计算协方差矩阵，可以使用公式进行计算，也可以使用相关的库函数进行计算。

3. 特征值分解对协方差矩阵进行特征值分解，可以得到特征值和对应的特征向量。

4. 选择主成分根据特征值的大小，选择前k个最大的特征值对应的特征向量作为主成分。

5. 数据转换将原始数据通过选取的主成分进行线性变换，得到在主成分上的投影值，即将高维数据转化为低维表示。

三、注意事项与应用场景在进行主成分分析时，需要注意以下几个事项：1. 数据的线性关系主成分分析假设数据具有线性关系，如果数据之间的关系是非线性的，主成分分析可能无法提取到有效的信息。

（完整版）主成分分析法的原理应⽤及计算步骤..⼀、概述在处理信息时，当两个变量之间有⼀定相关关系时，可以解释为这两个变量反映此课题的信息有⼀定的重叠，例如，⾼校科研状况评价中的⽴项课题数与项⽬经费、经费⽀出等之间会存在较⾼的相关性；学⽣综合评价研究中的专业基础课成绩与专业课成绩、获奖学⾦次数等之间也会存在较⾼的相关性。

⽽变量之间信息的⾼度重叠和⾼度相关会给统计⽅法的应⽤带来许多障碍。

为了解决这些问题，最简单和最直接的解决⽅案是削减变量的个数，但这必然⼜会导致信息丢失和信息不完整等问题的产⽣。

为此，⼈们希望探索⼀种更为有效的解决⽅法，它既能⼤⼤减少参与数据建模的变量个数，同时也不会造成信息的⼤量丢失。

主成分分析正式这样⼀种能够有效降低变量维数，并已得到⼴泛应⽤的分析⽅法。

主成分分析以最少的信息丢失为前提，将众多的原有变量综合成较少⼏个综合指标，通常综合指标（主成分）有以下⼏个特点：↓主成分个数远远少于原有变量的个数原有变量综合成少数⼏个因⼦之后，因⼦将可以替代原有变量参与数据建模，这将⼤⼤减少分析过程中的计算⼯作量。

↓主成分能够反映原有变量的绝⼤部分信息因⼦并不是原有变量的简单取舍，⽽是原有变量重组后的结果，因此不会造成原有变量信息的⼤量丢失，并能够代表原有变量的绝⼤部分信息。

↓主成分之间应该互不相关通过主成分分析得出的新的综合指标（主成分）之间互不相关，因⼦参与数据建模能够有效地解决变量信息重叠、多重共线性等给分析应⽤带来的诸多问题。

↓主成分具有命名解释性总之，主成分分析法是研究如何以最少的信息丢失将众多原有变量浓缩成少数⼏个因⼦，如何使因⼦具有⼀定的命名解释性的多元统计分析⽅法。

⼆、基本原理主成分分析是数学上对数据降维的⼀种⽅法。

其基本思想是设法将原来众多的具有⼀定相关性的指标X1，X2，…，XP （⽐如p 个指标），重新组合成⼀组较少个数的互不相关的综合指标Fm 来代替原来指标。

那么综合指标应该如何去提取，使其既能最⼤程度的反映原变量Xp 所代表的信息，⼜能保证新指标之间保持相互⽆关（信息不重叠）。

主成分分析法的原理应用及计算步骤Σ的前m 个较大的特征值λ1≥λ2≥…λm>0,就是前m 个主成分对应的方差，i λ对应的单位特征向量i a 就是主成分Fi 的关于原变量的系数，则原变量的第i 个主成分Fi 为：Fi ='i a X主成分的方差（信息）贡献率用来反映信息量的大小，i α为：1/mi i ii αλλ==∑（3）选择主成分最终要选择几个主成分，即F1,F2,……,Fm 中m 的确定是通过方差（信息）累计贡献率G(m)来确定11()/pmi ki k G m λλ===∑∑当累积贡献率大于85%时，就认为能足够反映原来变量的信息了，对应的m 就是抽取的前m 个主成分。

（4）计算主成分载荷主成分载荷是反映主成分Fi 与原变量Xj 之间的相互关联程度，原来变量Xj （j=1，2 ，…， p ）在诸主成分Fi （i=1，2，…，m ）上的荷载 lij （ i=1，2，…，m ； j=1，2 ，…，p ）。

：(,)(1,2,,;1,2,,)i j i ij l Z X a i m j p λ===在SPSS 软件中主成分分析后的分析结果中，“成分矩阵”反应的就是主成分载荷矩阵。

（5）计算主成分得分计算样品在m 个主成分上的得分：1122...i i i pi p F a X a X a X =+++ i = 1，2，…，m实际应用时，指标的量纲往往不同，所以在主成分计算之前应先消除量纲的影响。

消除数据的量纲有很多方法，常用方法是将原始数据标准化，即做如下数据变换：*1,2,...,;1,2,...,ij jijjx x x i n j ps -===其中：11n j ij i x x n ==∑，2211()1n j ij j i s x x n ==--∑ 根据数学公式知道，①任何随机变量对其作标准化变换后，其协方差与其相关系数是一回事，即标准化后的变量协方差矩阵就是其相关系数矩阵。

主成分分析计算方法与步骤：在对某一事物或现象进行实证研究时,为了充分反映被研究对象个体之间得差异, 研究者往往要考虑增加测量指标,这样就会增加研究问题得负载程度。

但由于各指标都就是对同一问题得反映,会造成信息得重叠,引起变量之间得共线性,因此,在多指标得数据分析中,如何压缩指标个数、压缩后得指标能否充分反映个体之间得差异,成为研究者关心得问题。

而主成分分析法可以很好地解决这一问题。

主成分分析得应用目得可以简单地归结为: 数据得压缩、数据得解释。

它常被用来寻找与判断某种事物或现象得综合指标,并且对综合指标所包含得信息给予适当得解释, 从而更加深刻地揭示事物得内在规律。

主成分分析得基本步骤分为: ①对原始指标进行标准化,以消除变量在数量极或量纲上得影响;②根据标准化后得数据矩阵求出相关系数矩阵 R; ③求出 R 矩阵得特征根与特征向量; ④确定主成分,结合专业知识对各主成分所蕴含得信息给予适当得解释;⑤合成主成分,得到综合评价值。

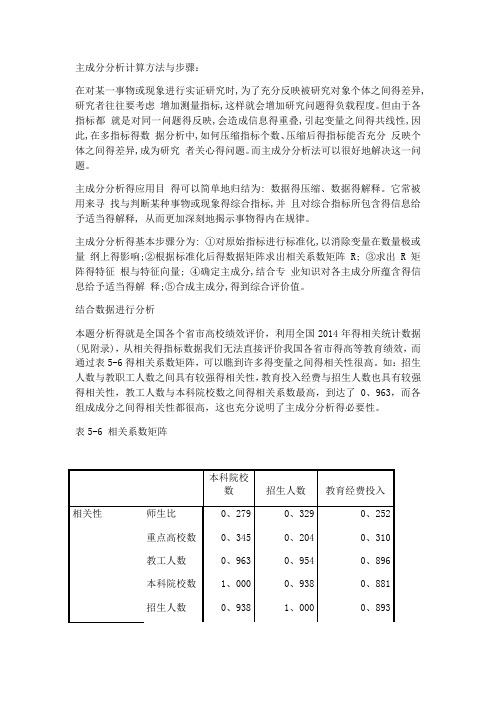
结合数据进行分析本题分析得就是全国各个省市高校绩效评价，利用全国2014年得相关统计数据(见附录)，从相关得指标数据我们无法直接评价我国各省市得高等教育绩效，而通过表5-6得相关系数矩阵，可以瞧到许多得变量之间得相关性很高。

如：招生人数与教职工人数之间具有较强得相关性，教育投入经费与招生人数也具有较强得相关性，教工人数与本科院校数之间得相关系数最高，到达了0、963，而各组成成分之间得相关性都很高，这也充分说明了主成分分析得必要性。

表5-6 相关系数矩阵本科院校数招生人数教育经费投入相关性师生比0、279 0、329 0、252重点高校数0、345 0、204 0、310教工人数0、963 0、954 0、896本科院校数1、000 0、938 0、881招生人数0、938 1、000 0、893表5-7给出得就是各主成分得方差贡献率与累计贡献率，我们选取主成分得标准有两个：第一，特征根大于1，因为，如果特征根小于1，说明该主成分得解释力度太弱，还比不上直接引入一个原始变量得平均解释力度大；第二，方差贡献率大于85%，如果这两个标准不能同时符合要求,则往往就是因为选择得指标不合理或者样本容量太小,应继续调整。

主成分分析计算方法和步骤：在对某一事物或现象进行实证研究时,为了充分反映被研究对象个体之间的差异, 研究者往往要考虑增加测量指标,这样就会增加研究问题的负载程度。

但由于各指标都是对同一问题的反映,会造成信息的重叠,引起变量之间的共线性,因此,在多指标的数据分析中,如何压缩指标个数、压缩后的指标能否充分反映个体之间的差异,成为研究者关心的问题。

而主成分分析法可以很好地解决这一问题。

主成分分析的应用目的可以简单地归结为: 数据的压缩、数据的解释。

它常被用来寻找和判断某种事物或现象的综合指标,并且对综合指标所包含的信息给予适当的解释, 从而更加深刻地揭示事物的内在规律。

主成分分析的基本步骤分为: ①对原始指标进行标准化,以消除变量在数量极或量纲上的影响;②根据标准化后的数据矩阵求出相关系数矩阵 R; ③求出 R 矩阵的特征根和特征向量; ④确定主成分,结合专业知识对各主成分所蕴含的信息给予适当的解释;⑤合成主成分,得到综合评价值。

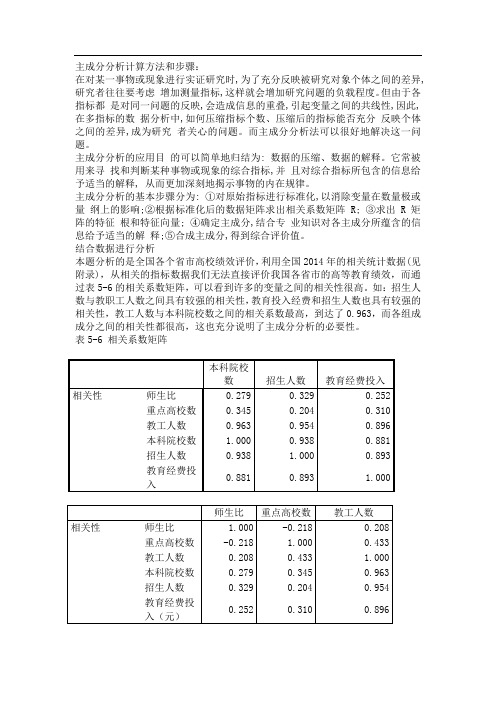
结合数据进行分析本题分析的是全国各个省市高校绩效评价，利用全国2014年的相关统计数据(见附录)，从相关的指标数据我们无法直接评价我国各省市的高等教育绩效，而通过表5-6的相关系数矩阵，可以看到许多的变量之间的相关性很高。

如：招生人数与教职工人数之间具有较强的相关性，教育投入经费和招生人数也具有较强的相关性，教工人数与本科院校数之间的相关系数最高，到达了0.963，而各组成成分之间的相关性都很高，这也充分说明了主成分分析的必要性。

表5-6 相关系数矩阵本科院校数招生人数教育经费投入相关性师生比0.279 0.329 0.252重点高校数0.345 0.204 0.310教工人数0.963 0.954 0.896本科院校数 1.000 0.938 0.881招生人数0.938 1.000 0.893教育经费投0.881 0.893 1.000入师生比重点高校数教工人数相关性师生比 1.000 -0.218 0.208重点高校数-0.218 1.000 0.433教工人数0.208 0.433 1.000本科院校数0.279 0.345 0.963招生人数0.329 0.204 0.954教育经费投0.252 0.310 0.896入（元）表5-7给出的是各主成分的方差贡献率和累计贡献率，我们选取主成分的标准有两个：第一，特征根大于1，因为，如果特征根小于1，说明该主成分的解释力度太弱，还比不上直接引入一个原始变量的平均解释力度大；第二，方差贡献率大于85%，如果这两个标准不能同时符合要求,则往往是因为选择的指标不合理或者样本容量太小,应继续调整。

主成分分析的步骤与实施方法主成分分析（Principal Component Analysis，PCA）是一种常用的降维技术，用于将高维数据转化为低维数据，并提取数据中最重要的特征。

本文将介绍主成分分析的步骤和实施方法。

一、主成分分析的步骤主成分分析的步骤通常包括以下几个部分：1. 数据准备首先，需要对数据进行准备工作。

这包括数据清洗、缺失值处理和数据标准化等。

数据清洗是指检查数据中是否存在异常值或者不一致的数据，并进行相应的处理。

缺失值处理是指对数据中的缺失值进行填充或删除，以确保数据的完整性。

数据标准化是指对数据进行归一化处理，消除不同变量之间的量纲差异。

2. 计算协方差矩阵在进行主成分分析之前，需要计算原始数据的协方差矩阵。

协方差矩阵反映了不同变量之间的相关性。

对于给定的数据集，假设有n个变量，那么协方差矩阵的维度为n×n。

3. 特征值分解接下来，对协方差矩阵进行特征值分解。

特征值分解可以得到协方差矩阵的特征值和特征向量。

特征值表示对应特征向量的重要程度，特征向量表示原始变量在新的主成分空间中的权重。

4. 选择主成分在进行主成分分析时，需要选择保留多少个主成分。

一般来说，我们选择特征值较大的前k个主成分，并将其对应的特征向量作为主成分。

选择主成分的主要标准是保留足够的信息量，即尽可能多地保留原始数据的方差。

5. 构建主成分根据所选择的主成分的特征向量，将原始数据转化为新的主成分空间。

这相当于将原始数据投影到主成分所张成的空间中。

二、主成分分析的实施方法主成分分析可以通过各种软件和编程语言来实施。

下面介绍两种常用的实施方法：1. 使用Python实施Python是一种简单易用且功能强大的编程语言，在进行主成分分析时非常方便。

可以使用Python中的科学计算库NumPy和数据分析库pandas来进行主成分分析。

具体步骤如下：(1) 导入所需的库```import numpy as npimport pandas as pdfrom sklearn.decomposition import PCA```(2) 读取数据```data = pd.read_csv('data.csv')```(3) 数据预处理对数据进行清洗、缺失值处理和数据标准化等预处理操作。

主成分分析计算方法与步骤:在对某一事物或现象进行实证研究时,为了充分反映被研究对象个体之间的差异, 研究者往往要考虑增加测量指标,这样就会增加研究问题的负载程度。

但由于各指标都就是对同一问题的反映,会造成信息的重叠,引起变量之间的共线性,因此,在多指标的数据分析中,如何压缩指标个数、压缩后的指标能否充分反映个体之间的差异,成为研究者关心的问题。

而主成分分析法可以很好地解决这一问题。

主成分分析的应用目的可以简单地归结为: 数据的压缩、数据的解释。

它常被用来寻找与判断某种事物或现象的综合指标,并且对综合指标所包含的信息给予适当的解释, 从而更加深刻地揭示事物的内在规律。

主成分分析的基本步骤分为: ①对原始指标进行标准化,以消除变量在数量极或量纲上的影响;②根据标准化后的数据矩阵求出相关系数矩阵 R; ③求出 R 矩阵的特征根与特征向量; ④确定主成分,结合专业知识对各主成分所蕴含的信息给予适当的解释;⑤合成主成分,得到综合评价值。

结合数据进行分析本题分析的就是全国各个省市高校绩效评价,利用全国2014年的相关统计数据(见附录),从相关的指标数据我们无法直接评价我国各省市的高等教育绩效,而通过表5-6的相关系数矩阵,可以瞧到许多的变量之间的相关性很高。

如:招生人数与教职工人数之间具有较强的相关性,教育投入经费与招生人数也具有较强的相关性,教工人数与本科院校数之间的相关系数最高,到达了0、963,而各组成成分之间的相关性都很高,这也充分说明了主成分分析的必要性。

表5-6 相关系数矩阵本科院校数招生人数教育经费投入相关性师生比0、279 0、329 0、252重点高校数0、345 0、204 0、310教工人数0、963 0、954 0、896本科院校数1、000 0、938 0、881招生人数0、938 1、000 0、893教育经费投0、881 0、893 1、000入师生比重点高校数教工人数相关性师生比1、000 -0、218 0、208重点高校数-0、218 1、000 0、433教工人数0、208 0、433 1、000本科院校数0、279 0、345 0、963招生人数0、329 0、204 0、954教育经费投0、252 0、310 0、896入(元)表5-7给出的就是各主成分的方差贡献率与累计贡献率,我们选取主成分的标准有两个:第一,特征根大于1,因为,如果特征根小于1,说明该主成分的解释力度太弱,还比不上直接引入一个原始变量的平均解释力度大;第二,方差贡献率大于85%,如果这两个标准不能同时符合要求,则往往就是因为选择的指标不合理或者样本容量太小,应继续调整。

主成分分析计算方法和步骤：在对某一事物或现象进行实证研究时,为了充分反映被研究对象个体之间的差异, 研究者往往要考虑增加测量指标,这样就会增加研究问题的负载程度。

但由于各指标都是对同一问题的反映,会造成信息的重叠,引起变量之间的共线性,因此,在多指标的数据分析中,如何压缩指标个数、压缩后的指标能否充分反映个体之间的差异,成为研究者关心的问题。

而主成分分析法可以很好地解决这一问题。

主成分分析的应用目的可以简单地归结为: 数据的压缩、数据的解释。

它常被用来寻找和判断某种事物或现象的综合指标,并且对综合指标所包含的信息给予适当的解释, 从而更加深刻地揭示事物的内在规律。

主成分分析的基本步骤分为: ①对原始指标进行标准化,以消除变量在数量极或量纲上的影响;②根据标准化后的数据矩阵求出相关系数矩阵 R; ③求出 R 矩阵的特征根和特征向量; ④确定主成分,结合专业知识对各主成分所蕴含的信息给予适当的解释;⑤合成主成分,得到综合评价值。

结合数据进行分析本题分析的是全国各个省市高校绩效评价，利用全国2014年的相关统计数据(见附录)，从相关的指标数据我们无法直接评价我国各省市的高等教育绩效，而通过表5-6的相关系数矩阵，可以看到许多的变量之间的相关性很高。

如：招生人数与教职工人数之间具有较强的相关性，教育投入经费和招生人数也具有较强的相关性，教工人数与本科院校数之间的相关系数最高，到达了0.963，而各组成成分之间的相关性都很高，这也充分说明了主成分分析的必要性。

表5-6 相关系数矩阵本科院校数招生人数教育经费投入相关性师生比0.279 0.329 0.252重点高校数0.345 0.204 0.310教工人数0.963 0.954 0.896本科院校数 1.000 0.938 0.881招生人数0.938 1.000 0.893教育经费投0.881 0.893 1.000入师生比重点高校数教工人数相关性师生比 1.000 -0.218 0.208重点高校数-0.218 1.000 0.433教工人数0.208 0.433 1.000本科院校数0.279 0.345 0.963招生人数0.329 0.204 0.954教育经费投0.252 0.310 0.896入（元）表5-7给出的是各主成分的方差贡献率和累计贡献率，我们选取主成分的标准有两个：第一，特征根大于1，因为，如果特征根小于1，说明该主成分的解释力度太弱，还比不上直接引入一个原始变量的平均解释力度大；第二，方差贡献率大于85%，如果这两个标准不能同时符合要求,则往往是因为选择的指标不合理或者样本容量太小,应继续调整。

（一）主成分分析法的基本思想主成分分析（Principal Component Analysis）是利用降维的思想，将多个变量转化为少数几个综合变量（即主成分），其中每个主成分都是原始变量的线性组合，各主成分之间互不相关，从而这些主成分能够反映始变量的绝大部分信息，且所含的信息互不重叠。

[2]采用这种方法可以克服单一的财务指标不能真实反映公司的财务情况的缺点，引进多方面的财务指标，但又将复杂因素归结为几个主成分，使得复杂问题得以简化，同时得到更为科学、准确的财务信息。

（二）主成分分析法代数模型假设用p个变量来描述研究对象，分别用X1，X2…X p来表示，这p个变量构成的p维随机向量为X=(X1，X2…X p)t。

设随机向量X的均值为μ，协方差矩阵为Σ。

对X进行线性变化，考虑原始变量的线性组合：Z1=μ11X1+μ12X2+…μ1p X pZ2=μ21X1+μ22X2+…μ2p X p………………Z p=μp1X1+μp2X2+…μpp X p主成分是不相关的线性组合Z1，Z2……Z p，并且Z1是X1，X2…X p的线性组合中方差最大者，Z2是与Z1不相关的线性组合中方差最大者，…，Z p是与Z1，Z2……Z p-1都不相关的线性组合中方差最大者。

（三）主成分分析法基本步骤第一步：设估计样本数为n，选取的财务指标数为p，则由估计样本的原始数据可得矩阵X=(x ij)m×p，其中x ij表示第i家上市公司的第j项财务指标数据。

第二步：为了消除各项财务指标之间在量纲化和数量级上的差别，对指标数据进行标准化，得到标准化矩阵（系统自动生成）。

第三步：根据标准化数据矩阵建立协方差矩阵R ，是反映标准化后的数据之间相关关系密切程度的统计指标，值越大，说明有必要对数据进行主成分分析。

其中，R ij （i ，j=1，2，…，p ）为原始变量X i 与X j 的相关系数。

R 为实对称矩阵（即R ij =R ji ），只需计算其上三角元素或下三角元素即可，其计算公式为：2211)()()()(j kj nk i kj j kj n k i kj ij X X X X X X X X R -=--=-=∑∑ 第四步：根据协方差矩阵R 求出特征值、主成分贡献率和累计方差贡献率，确定主成分个数。

主成分分析的方法
主成分分析（Principal Component Analysis，PCA）是一种常用的降维方法，通过线性变换将原始数据投影到一个新的空间中，使得数据在新的空间中的最大方差出现在第一个主成分上，第二大方差出现在第二个主成分上，以此类推。

这样可以保留较多的原始数据信息，同时减少数据的维度。

主成分分析的方法可以简洁地总结为以下几个步骤：
1. 标准化数据：将原始数据进行标准化处理，使得各个特征具有相同的尺度。

2. 计算协方差矩阵：计算标准化后的数据各个特征之间的协方差矩阵。

3. 计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。

4. 选择主成分数量：根据特征值的大小选择主成分的数量，通常选择特征值大于某个阈值的主成分。

5. 构造变换矩阵：将特征值较大的特征向量作为基向量构造出变换矩阵，以实现数据的降维。

6. 数据投影：将原始数据通过变换矩阵进行投影，得到降维后的数据。

主成分分析的目标是选择能够最大程度保留原始数据信息的主成分，这可以通过保留最大方差或者最小重构误差来衡量。

主成分分析在数据预处理、特征提取和可视化等领域有广泛的应用。