流体力学第五章习题答案学习资料

第五章 层流、紊流及其能量损失5—1 (1)某水管的直径d ＝100 mm ，通过流量Q ＝4 L/s ，水温T ＝20℃；(2)条件与以上相同，但管道中流过的是重燃油，其运动粘度6215010m /s ν-=⨯。

试判别以上两种情况下的流态。

解：(1) 200C 时，水的运动粘性系数ν=1.007×10-6m 2/s ，24Q u d π=水的雷诺数Re 为：-3-6244 4 L/s 10Re 5060020001.00710m /s 3.140.1mud Q v v d π⨯⨯====>⨯⨯⨯，紊流 (2) 石油：-3-6244 4 L/s 10Re 339.7200015010m /s 3.140.1m ud Q v v d π⨯⨯====<⨯⨯⨯，层流 5—2 温度为0℃的空气，以4 m/s 的速度在直径为l00 mm 的圆管中流动，试确定其流态(空气的运动粘度为521.3710m /s ν-=⨯)。

若管中的流体换成运动粘度为621.79210m /s ν-=⨯的水，问水在管中呈何流态?解：空气的雷诺数Re 为：-524 m/s 0.1m Re 2919720001.3710m /sud v ⨯===>⨯，紊流 水的雷诺数Re 为：-624 m/s 0.1m Re 223 21420001.79210m /sud v ⨯===>⨯，紊流 5—3 (1)一梯形断面排水沟，底宽0.5m ，边坡系数cot θ＝1.5(θ为坡角)，水温为20℃，水深0.4m ，流速为0.1m ／s ，试判别其流态；(2)如果水温保持不变，流速减小到多大时变为层流?解：200C 时，水的运动粘性系数ν=1.007×10-6m 2/s 水力直径为(0.520.60.5)0.4/20.23m 0.50.722AR χ+⨯+⨯===+⨯ 4-620.1m/s 0.23m Re 2.24101.00710m /sR uR ν⨯===⨯⨯，42.24102000⨯>，湍流 水流为层流时Re 500uR ν≤=(明渠流)，故 63Re 500 1.00710 2.210m/s 0.23u R ν--⨯⨯≤==⨯ 5—4 由若干水管组装成的冷凝器，利用水流经过水管不断散热而起到冷凝作用。

⼯程流体⼒学（⽔⼒学）闻德第五章-实际流体动⼒学基础课后答案⼯程流体⼒学闻德课后习题答案第五章实际流体动⼒学基础5—1设在流场中的速度分布为u x =2ax ，u y =-2ay ，a 为实数，且a >0。

试求切应⼒τxy 、τyx 和附加压应⼒p ′x 、p ′y 以及压应⼒p x 、p y 。

解：0y x xy yx u u x y ττµ==+=24xxu p a xµµ?'=-=-?，24y y u p a y µµ?'=-=?， 4x x p p p p a µ'=+=-，4y y p p p p a µ'=+=+5－2 设例５－1中的下平板固定不动，上平板以速度v 沿x 轴⽅向作等速运动（如图所⽰），由于上平板运动⽽引起的这种流动，称柯埃梯（Couette ）流动。

试求在这种流动情况下，两平板间的速度分布。

（请将d 0d px=时的这⼀流动与在第⼀章中讨论流体粘性时的流动相⽐较）解：将坐标系ox 轴移⾄下平板，则边界条件为 y ＝０，0X u u ==；y h =，u v =。

由例５－1中的（11）式可得2d (1)2d h y p y yu v h x h h µ=-- （１）当d 0d p x =时，y u v h=，速度ｕ为直线分布，这种特殊情况的流动称简单柯埃梯流动或简单剪切流动。

它只是由于平板运动，由于流体的粘滞性带动流体发⽣的流动。

当d 0d px≠时，即为⼀般的柯埃梯流动，它是由简单柯埃梯流动和泊萧叶流动叠加⽽成，速度分布为(1)u y y yp v h h h=-- （２）式中2d ()2d h pp v xµ=- （３）当p ＞０时，沿着流动⽅向压强减⼩，速度在整个断⾯上的分布均为正值；当p ＜０时，沿流动⽅向压强增加，则可能在静⽌壁⾯附近产⽣倒流，这主要发⽣p ＜－１的情况．5－3 设明渠⼆维均匀（层流）流动，如图所⽰。

第五章习题简答5-１有一薄壁圆形孔口，直径d= １0ｍm ，水头H 为2m 。

现测得射流收缩断面的直径d c 为8m ｍ,在３2.8s 时间内，经孔口流出的水量为0.０1ｍ3，试求该孔口的收缩系数ε，流量系数μ,流速系数φ及孔口局部损失系数ζ。

解: 64.010822=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛==d d A A c c εs m d Q v /06.6008.08.32/01.04422=⨯⨯==ππ 62.097.064.006.0197.011197.028.9206.62222=⨯===-=-==⨯⨯==⇒=εϕμϕζϕϕgHvgH v5-2薄壁孔口出流,直径ｄ=2cm,水箱水位恒定H ＝2ｍ，试求:(1)孔口流量Q ；(2）此孔口外接圆柱形管嘴的流量Ｑn ；(3)管嘴收缩断面的真空高度。

题5-２图解:(1）孔口出流流量为s L s m gH A Q /219.1/10219.128.9202.0462.02332=⨯=⨯⨯⨯⨯⨯==πϕ（2)s L gH A Q n /612.128.9202.0482.022=⨯⨯⨯⨯⨯==πμ(３)真空高度：m H gpg p C Cv 48.1274.074.0=⨯==-=ρρ ５-3 水箱用隔板分为A 、B 两室,隔板上开一孔口,其直径ｄ1=４cm ，在B 室底部装有圆柱形外管嘴,其直径d 2=3cm 。

已知Ｈ=３m ，ｈ3＝0.5m 试求:(1）ｈ 1,h 2;(2)流出水箱的流量Q 。

题５-3图解:隔板孔口的流量 112gh A Q μ=圆柱形外管嘴的流量()()132222h H g A h h g A Q -=+=μμ由题意可得Q 1=Q ２,则()()1212122212111211303.082.004.062.022h h h H d h d h H g A gh A -⨯⨯=⨯⨯-=-=μμμμ解得m h 07.11=sL s m gh A Q mh h H h /56.3/1056.307.18.9204.0462.0243.15.007.1333211312=⨯=⨯⨯⨯⨯⨯==∴=--=--=∴-πμ5－4 有一平底空船，其船底面积Ω为8m ２,船舷高ｈ为０.5m ，船自重G 为9．8kN 。

第5章 压力管路的水力计算
5-1．某水罐1液面高度位于地平面以上z 1＝60m ，通过分支管把水引向高于地
平面z 2＝30m 和z 3＝15m 的水罐2和水罐3，假设l 1=l 2=l 3=2500m, d 1=d 2=d 3=0.5m, 各管的沿程阻力系数均为λ＝0.04。

试求引入每一水罐的流量。

解：取1-1、2-2两液面列伯努利方程：
2121f f h h z z ++=
g
V d L h g
V
d L h f f 222
22222
2
1
1111
λλ==
所以，41.42221=+V V （1） 取1-1、3-3两液面列伯努利方程：
3131f f h h z z ++=
所以，94.22321=+V V （2）
又 ⎩⎨⎧==+=321
321d d d Q Q Q Ö 321V V V += （3）
得 ⎪⎩⎪
⎨⎧===s m V s m V s m V /39.0/28.1/67.13
21 Ö
⎩⎨⎧==s
m Q s
m Q /0765.0/251.03
332
5-2．
水从封闭水箱上部直径d 1=30mm 的孔口流至下部，然后经d 2=20mm 的圆柱行管嘴排向大气中，流动恒定后，水深h 1=2m ，h 2=3m ，水箱上的压力计读数为4.9MPa ，
求流量Q 和下水箱水面上的压强p 2，设为稳定流。

6.01=μ，82.02=μ。

解：经过孔口的流量Q 1
经过管嘴的流量Q 2
因为稳定流，所以Q 1＝Q 2 整理得：Pa p 421034.4×=。

第五章 层流、紊流及其能量损失5—1 (1)某水管的直径d ＝100 mm ，通过流量Q ＝4 L/s ，水温T ＝20℃；(2)条件与以上相同，但管道中流过的是重燃油，其运动粘度6215010m /s ν-=⨯。

试判别以上两种情况下的流态。

解：(1) 200C 时，水的运动粘性系数ν=×10-6m 2/s ，24Qu d π= 水的雷诺数Re 为：-3-6244 4 L/s 10Re 5060020001.00710m /s 3.140.1mud Q v v d π⨯⨯====>⨯⨯⨯，紊流(2) 石油：-3-6244 4 L/s 10Re 339.7200015010m /s 3.140.1mud Q v v d π⨯⨯====<⨯⨯⨯，层流 5—2 温度为0℃的空气，以4 m/s 的速度在直径为l00 mm 的圆管中流动，试确定其流态(空气的运动粘度为521.3710m /s ν-=⨯)。

若管中的流体换成运动粘度为621.79210m /s ν-=⨯的水，问水在管中呈何流态解：空气的雷诺数Re 为：-524 m/s 0.1mRe 2919720001.3710m /sud v ⨯===>⨯，紊流 水的雷诺数Re 为：-624 m/s 0.1mRe 223 21420001.79210m /sud v ⨯===>⨯，紊流 5—3 (1)一梯形断面排水沟，底宽0.5m ，边坡系数cot θ＝(θ为坡角)，水温为20℃，水深0.4m ，流速为0.1m ／s ，试判别其流态；(2)如果水温保持不变，流速减小到多大时变为层流解：200C 时，水的运动粘性系数ν=×10-6m 2/s水力直径为(0.520.60.5)0.4/20.23m 0.50.722AR χ+⨯+⨯===+⨯4-620.1m/s 0.23m Re 2.24101.00710m /sR uRν⨯===⨯⨯，42.24102000⨯>，湍流 水流为层流时Re 500uRν≤=(明渠流)，故63Re 500 1.00710 2.210m/s 0.23u R ν--⨯⨯≤==⨯5—4 由若干水管组装成的冷凝器，利用水流经过水管不断散热而起到冷凝作用。

第五章习题简答5-1有一薄壁圆形孔口，直径d= 10mm ，水头H 为2m 。

现测得射流收缩断面的直径d c为8mm ，在32.8s 时间内，经孔口流出的水量为0.01m 3，试求该孔口的收缩系数ε，流量系数μ，流速系数φ及孔口局部损失系数ζ。

解: 64.010822=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛==d d A A c c εs m d Q v /06.6008.08.32/01.04422=⨯⨯==ππ 62.097.064.006.0197.011197.028.9206.62222=⨯===-=-==⨯⨯==⇒=εϕμϕζϕϕgHvgH v5-2薄壁孔口出流，直径d=2cm ，水箱水位恒定H=2m ，试求：（1）孔口流量Q ；（2）此孔口外接圆柱形管嘴的流量Q n ；（3）管嘴收缩断面的真空高度。

题5-2图解：（1）孔口出流流量为s L s m gH A Q /219.1/10219.128.9202.0462.02332=⨯=⨯⨯⨯⨯⨯==πϕ（2）s L gH A Q n /612.128.9202.0482.022=⨯⨯⨯⨯⨯==πμ（3）真空高度：m H gpg p C Cv 48.1274.074.0=⨯==-=ρρ 5-3 水箱用隔板分为A 、B 两室，隔板上开一孔口，其直径d 1=4cm ，在B 室底部装有圆柱形外管嘴，其直径d 2=3cm 。

已知H=3m ，h 3=0.5m 试求：（1）h 1，h 2；（2）流出水箱的流量Q 。

题5-3图解：隔板孔口的流量 112gh A Q μ=圆柱形外管嘴的流量 ()()132222h H g A h h g A Q +=+=μμ由题意可得Q1=Q2，则()()1212122212111211303.082.004.062.022h h h H d h d h H g A gh A -⨯⨯=⨯⨯+=+=μμμμ解得m h 07.11=sL s m gh A Q mh h H h /56.3/1056.307.18.9204.0462.0243.15.007.1333211312=⨯=⨯⨯⨯⨯⨯==∴=--=--=∴-πμ5-4 有一平底空船，其船底面积Ω为8m 2，船舷高h 为0.5m ，船自重G 为9.8kN。

第五章 势流理论5-1流速为u 0=10m/s 沿正向的均匀流与位于原点的点涡叠加。

已知驻点位于(0，-5)，试求： (1)点涡的强度；(2) (0,5)点的流速以及通过驻点的流线方程。

答：（1）求点涡的强度Γ：设点涡的强度为Γ，则均匀流的速度势和流函数分别为：x u 01=ϕ，y u 01=ψ；点涡的速度势和流函数为：xy arctg πϕ22Γ-=，r y x ln 2)ln(221222ππψΓ=+Γ=； 因此，流动的速度势和流函数为：θπθπϕϕϕ2cos 20021Γ-=Γ-=+=r u x y arctg x u ， r y u y x y u ln 2sin )ln(202122021πθπψψψΓ+=+Γ+=+=；则速度分布为：2202y x yu y x u +⋅Γ+=∂∂=∂∂=πψϕ， 222yx x x y v +⋅Γ=∂∂-=∂∂=πψϕ； 由于)5,0(-为驻点，代入上式第一式中则得到：0)5(052220=-+-⋅Γ+πu ， 整理得到：ππ100100==Γu 。

（2）求)5,0(点的速度：将π100=Γ代入到速度分布中，得到：222222050102100102y x y y x y y x y u u ++=+⋅+=+⋅Γ+=πππ，2222225021002y x x y x x y x x v +=+⋅=+⋅Γ=πππ； 将0=x 、5=y 代入上述速度分布函数，得到：201010505501022=+=+⨯+=u （m/s ），05005022=+⨯=v （m/s ）；（3）求通过)5,0(点的流线方程：由流函数的性质可知，流函数为常数时表示流线方程C =ψ，则流线方程为：C y x y u =+Γ+21220)ln(2π；将0=x 、5=y 代入，得到：5ln 5050)50ln(21005102122+=+⨯+⨯=ππC ；则过该点的流线方程为：5ln 5050)ln(2100102122+=++y x y ππ，整理得到：5ln 55)ln(52122+=++y x y5-2 平面势流由点源和点汇叠加而成，点源位于（-1，0），其流量为θ1=20m 3/s ，点汇位于（2,0）点，其流量为θ2=40m 3/s ，已知流体密度为ρ=1.8kg/m 3，流场中（0，0）点的压力为0，试求点（0,1）和（1,1）的流速和压力。

第五章习题答案选择题（单选题）5.1 速度v ，长度l ，重力加速度g 的无量纲集合是：（b ）（a ）lv g ；（b ）v gl ；（c ）l gv ；（d ）2v gl。

5.2 速度v ，密度ρ，压强p 的无量纲集合是：（d ）（a ）p v ρ；（b ）v p ρ；（c ）2pv ρ；（d ）2p v ρ。

5.3 速度v ，长度l ，时间t 的无量纲集合是：（d ）（a ）v lt ；（b ）t vl ；（c ）2l vt ；（d ）lvt。

5.4 压强差p ，密度ρ，长度l ，流量Q 的无量纲集合是：（d ）（a ）2Qpl ρ；（b ）2lpQ ρ；（c ）plQρ；（d 。

5.5 进行水力模型实验，要实现明渠水流的动力相似，应选的相似准则是：（b ）（a ）雷诺准则；（b ）弗劳德准则；（c ）欧拉准则；（d ）其他。

5.6 进行水力模型实验，要实现有压管流的动力相似，应选的相似准则是：（a ）（a ）雷诺准则；（b ）弗劳德准则；（c ）欧拉准则；（d ）其他。

5.7 雷诺数的物理意义表示：（c ）（a ）粘滞力与重力之比；（b ）重力与惯性力之比；（c ）惯性力与粘滞力之比；（d ）压力与粘滞力之比。

5.8 明渠水流模型实验，长度比尺为4，模型流量应为原型流量的：（c ）（a ）1/2；（b ）1/4；（c ）1/8；（d ）1/32。

5.9 压力输水管模型实验，长度比尺为8，模型水管的流量应为原型输水管流量的：（c ）（a ）1/2；（b ）1/4；（c ）1/8；（d ）1/16。

5.10 假设自由落体的下落距离s 与落体的质量m 、重力加速度g 及下落时间t 有关，试用瑞利法导出自由落体下落距离的关系式。

解： ∵s Km g t αβγ=[]s L =；[]m M =；[]2g T L -=；[]t T =∴有量纲关系：2L M TL T αββγ-=可得：0α=；1β=；2γ= ∴2s Kgt =答：自由落体下落距离的关系式为2s Kgt =。

第五章 不可压缩流体一维层流流动思考题建立流体流动微分方程依据的是什么基本原理?有哪几个基本步骤导致流体流动的常见因素有哪些?流体流动有哪几种常见的边界条件?如何确定这些边界条件? 对缝隙流动、管内流动或降膜流动，关于切应力和速度的微分方程对牛顿流体和非牛顿流体均适用吗？为什么一、选择题1、圆管层流过流断面的流速分布为A 均匀分布；B 对数曲线分布；C 二次抛物线分布；D 三次抛物线分布。

2、两根相同直径的圆管，以同样的速度输送水和空气，不会出现____情况。

A 水管内为层流状态，气管内为湍流状态；B 水管、气管内都为层流状态；C 水管内为湍流状态，气管内为层流状态；D 水管、气管内都为湍流状态。

3、变直径管流，细断面直径为d 1，粗断面直径为d 2，122d d 粗断面雷诺数Re 2与细断面雷诺数Re 1的关系是：A Re 1=0.5Re 2B Re 1=Re 2C Re 1=1.5Re 2D Re 1=2Re 24、圆管层流，实测管轴线上的流速为4m/s,则断面平均流速为：A 4m/sB 3.2m/sC 2m/sD 2.5m/s5 圆管流动中过流断面上的切应力分布如图 中的哪一种？A 在过流断面上是常数B 管轴处是零，且与半径成正比C 管壁处为零 ，向管轴线性增大D 抛物线分布9．下列压强分布图中哪个是错误的？B10．粘性流体总水头线沿程的变化是( A ) 。

A. 沿程下降B. 沿程上升C. 保持水平D. 前三种情况都有可能。

1．液体粘度随温度的升高而___，气体粘度随温度的升高而___( A )。

A.减小，增大；B.增大，减小；C.减小，不变；D.减小，减小四、计算题(50分)30.(6分)飞机在10000m 高空(T=223.15K,p=0.264bar)以速度800km/h 飞行，燃烧室的进口扩压通道朝向前方，设空气在扩压通道中可逆压缩，试确定相对于扩压通道的来流马赫数和出口压力。

(空气的比热容为C p =1006J/(kg ·K)，等熵指数为k=1.4，空气的气体常数R 为287J/(kg ·K))T 0=T ∞+v C p ∞=+⨯⨯23222231580010360021006/.()/() =247.69K M ∞=v a ∞∞=⨯⨯⨯=(/)...80010360014287223150743 P 0=p ∞11221+-⎡⎣⎢⎤⎦⎥∞-k M kk =0.26411412074038214141+-⨯⎡⎣⎢⎤⎦⎥=-.....bar31.(6分)一截面为圆形风道，风量为10000m 3/h ，最大允许平均流速为20m/s ，求：(1)此时风道内径为多少?(2)若设计内径应取50mm 的整倍数，这时设计内径为多少?(3)核算在设计内径时平均风速为多少?依连续方程（ρ=C ）v 1A 1=v 2A 2=q v(1)v 1π412d q v = d 1=100004360020⨯⨯π=0.42m=420mm (2)设计内径应取450mm 为50mm 的9倍，且风速低于允许的20m/s(3) 在设计内径450mm 时，风速为 v q d m s v 2222441000036000451746==⨯⨯=ππ../ 32.(7分)离心式风机可采用如图所示的集流器来测量流量，已知风机入口侧管道直径d=400mm,U 形管读数h=100mmH 2O ，水与空气的密度分别为ρ水=1000kg/m 3，ρ空=1.2kg/m 3，忽略流动的能量损失，求空气的体积流量q v 。

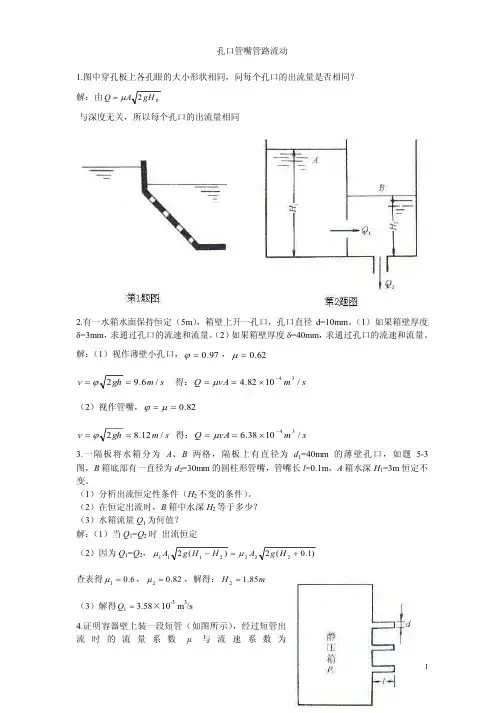
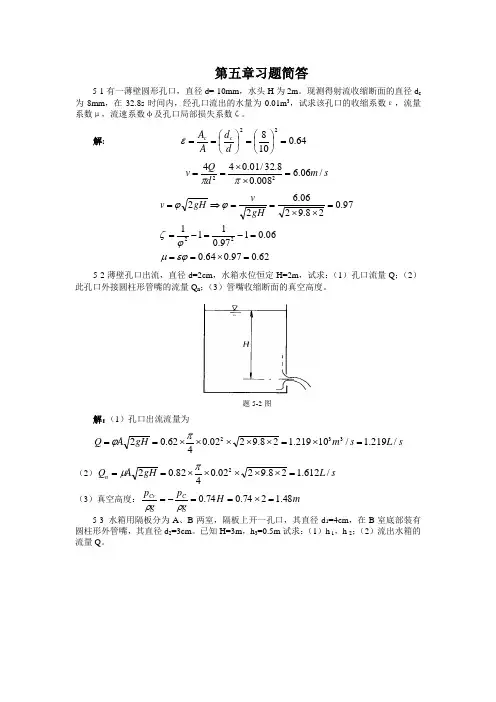
第五章孔口管嘴管路流动1.图中穿孔板上各孔眼的大小形状相同，问每个孔口的出流量是否相同？ 解：由02gH A Q μ=与深度无关，所以每个孔口的出流量相同2.有一水箱水面保持恒定（5m ），箱壁上开一孔口，孔口直径d=10mm 。

（1）如果箱壁厚度δ=3mm ，求通过孔口的流速和流量。

（2）如果箱壁厚度δ=40mm ，求通过孔口的流速和流量。

解：（1）视作薄壁小孔口，97.0=ϕ，62.0=μs m gh v /6.92==ϕ 得：s m vA Q /1082.434-⨯==μ（2）视作管嘴，82.0==μϕs m gh v /12.82==ϕ 得：s m vA Q /1038.634-⨯==μ3.一隔板将水箱分为A 、B 两格，隔板上有直径为d 1=40mm 的薄壁孔口，如题5-3 图，B 箱底部有一直径为d 2=30mm 的圆柱形管嘴，管嘴长l =0.1m ，A 箱水深H 1=3m 恒定不变。

（1）分析出流恒定性条件（H 2不变的条件）。

（2）在恒定出流时，B 箱中水深H 2等于多少？ （3）水箱流量Q 1为何值？ 解：（1）当Q 1=Q 2时 出流恒定 （2）因为Q 1=Q 2，=-)(22111H H g A μ)1.0(2222+H g A μ查表得6.01=μ，82.02=μ，解得：m H 85.12=（3）解得=1Q 3.58×10-3 m 3/s4.证明容器壁上装一段短管（如图所示），经过短管出流时的流量系数μ与流速系数为∑++==11ζλμϕdl证：∵∑++=gv d l g v g v H 2222220λζ ∴02gH v ϕ= 其中=ϕ∑++11ζλdl5.某诱导器的静压箱上装有圆柱形管嘴，管径为4mm ，长度l =100mm ，λ=0.02，从管嘴入口到出口的局部阻力系数5.0=ζ∑，求管嘴的流速系数和流量系数（见上题图）。

解：由题得707.011=++==∑ζλμϕdl6.如上题，当管嘴外空气压强为当地大气压强时，要求管嘴出流流速为30m/s 。

第五章 层流、紊流及其能量损失5—1 (1)某水管的直径d ＝100 mm ，通过流量Q ＝4 L/s ，水温T ＝20℃；(2)条件与以上相同，但管道中流过的是重燃油，其运动粘度6215010m /s ν-=⨯。

试判别以上两种情况下的流态。

解：(1) 200C 时，水的运动粘性系数ν=×10-6m 2/s ，24Qu d π= 水的雷诺数Re 为：-3-6244 4 L/s 10Re 5060020001.00710m /s 3.140.1m ud Q v v d π⨯⨯====>⨯⨯⨯，紊流(2) 石油：-3-6244 4 L/s 10Re 339.7200015010m /s 3.140.1mud Q v v d π⨯⨯====<⨯⨯⨯，层流 5—2 温度为0℃的空气，以4 m/s 的速度在直径为l00 mm 的圆管中流动，试确定其流态(空气的运动粘度为521.3710m /s ν-=⨯)。

若管中的流体换成运动粘度为621.79210m /s ν-=⨯的水，问水在管中呈何流态解：空气的雷诺数Re 为：-524 m/s 0.1m Re 2919720001.3710m /sud v ⨯===>⨯，紊流 水的雷诺数Re 为：-624 m/s 0.1mRe 223 21420001.79210m /sud v ⨯===>⨯，紊流 5—3 (1)一梯形断面排水沟，底宽0.5m ，边坡系数cot θ＝(θ为坡角)，水温为20℃，水深0.4m ，流速为0.1m ／s ，试判别其流态；(2)如果水温保持不变，流速减小到多大时变为层流 ，解：200C 时，水的运动粘性系数ν=×10-6m 2/s 水力直径为(0.520.60.5)0.4/20.23m 0.50.722AR χ+⨯+⨯===+⨯4-620.1m/s 0.23mRe 2.24101.00710m /sR uRν⨯===⨯⨯，42.24102000⨯>，湍流 水流为层流时Re 500uRν≤=(明渠流)，故63Re 500 1.00710 2.210m/s 0.23u R ν--⨯⨯≤==⨯5—4 由若干水管组装成的冷凝器，利用水流经过水管不断散热而起到冷凝作用。

第五章压力管路的水力计算主要内容长管水力计算短管水力计算串并联管路和分支管路孔口和管嘴出流基本概念：1、压力管路：在一定压差下，液流充满全管的流动管路。

（管路中的压强可以大于大气压，也可以小于大气压）注：输送气体的管路都是压力管路。

2、分类：按管路的结构特点，分为简单管路：等径无分支复杂管路：串联、并联、分支按能量比例大小，分为长管：和沿程水头损失相比，流速水头和局部水头损失可以忽略的流动管路。

短管：流速水头和局部水头损失不能忽略的流动管路。

第一节管路的特性曲线一、定义：水头损失与流量的关系曲线称为管路的特性曲线。

二、特性曲线（1）把225222284212QQdgLdQgdLgVdLhwαπλπλλ==⎪⎭⎫⎝⎛==（2）把上式绘成曲线得图。

第二节 长管的水力计算一、简单长管1、 定义：由许多管径相同的管子组成的长输管路，且沿程损失较大、局部损失较小，计算时可忽略局部损失和流速水头。

2、计算公式：简单长管一般计算涉及公式2211A V A V = （3） fh p z p z +++γγ2211＝ （4）g VD L h f 22λ= （5）说明： 有时为了计算方便，h f 的计算采用如下形式：mmmf dLQh --=52νβ（6）其中，β因为g VD L h f 22λ= 且所以 （7）a. 层流时，Re 64=λ 代入（7）式得：15112415.415.4--==dLQdL Q h f νν即：β＝ 4.15，m ＝1 b. 水力光滑区，25.0Re3164.0=λ代入（7）式得：25.0525.025.0175.425.075.10246.00246.0--==dLQdLQh f νν即：β＝ 0.0246，m ＝1c. 由大庆设计院推得经验公式，在混合区：877.4123.0877.10802.0dLQAh f ν=即：β＝ 0.0802A ，m ＝0.123其中，()0627.0lg 127.0,10r A ∆==-εεd. 粗糙区5225220826.082dL Q Q dg L gVd L h f λπλλ===即：β＝ 0.0826λ，m ＝03、简单长管的三类计算问题 （1）第一类：已知：输送流体的性质 μ，γ管道尺寸 d ，L ，Δ 地形 Δz流量 Q ， ， 求：h f ，Δp ，i解：Q →V确定流态 → β， m ，λ → h f → 伯努利方程求Δp（2） 第二类：已知：μ，γ，d ，L ，Δ，Δz ，Δp 求：Q解：Q 未知→流态也未知→ β， m ，λ 无法确定 → 试算法或绘图法A. 试算法a 、先假设一流态，取β， m 值，算出Q ’f pz h ∆+∆=γb 、Q ’ →m ’ ，校核流态如由 Q ’ →Re ’ 和假设一致， Q ’ 即为所求Q c 、如由 Q ’ →定出的流态和假设不一致，重复a 。

流体力学泵与风机第五版答案第五章一、单选题（每题3分，共10道小题，总分值30分）1.某给定的开敞式（进、出水池水面为一个大气压）离心泵系统中，当进水池的水面升高时，水泵的工作扬程将减小，而其轴功率将（）。

（3分）A不变B增大C减小正确答案B您的答案是 B回答正确展开2.离心式水泵叶轮的叶片形状一般采用（）。

（3分）A向前弯曲B径向延伸C向后弯曲正确答案C您的答案是未作答回答错误展开3.两台风机并联运行的主要目的是（）（3分）A增加流量B增加扬程C增加全压D既增加扬程也增加全压正确答案A您的答案是未作答回答错误展开4.立式混流水轮机的安装高程是指（）的高程。

（3分）A其固定底座平面；B其基准面；C其进口导叶水平中心平面。

正确答案C您的答案是未作答回答错误展开5.离心式泵的主要部件不包括（）（3分）A叶轮B汽缸C机壳D吸入室正确答案B您的答案是未作答回答错误展开6.某台水泵在转速不变时，当输送的水温度增加时，其轴功率（）（3分）A增加B降低C不变D先降低，后增加正确答案B您的答案是未作答回答错误展开7.当流体以的方向进入叶轮时，离心式泵的无限多叶片的理论扬程为（）（3分）8.下列各项中与有效汽蚀余量NPSHa值无关的是（）（3分）A吸入管路参数B管路中流量C泵的结构D泵入口压力正确答案C您的答案是未作答回答错误展开9.水轮机的轴功率N（）（3分）A是发电机的输出功率B是水轮机的输出功率C等于正确答案B您的答案是未作答回答错误展开10.对于某叶片式流体机械，当流过它的流量偏离设计值时，冲角会发生变化，正冲角将导致在叶片的（）产生旋涡。

（3分）A工作面B背面C工作面和背面正确答案B您的答案是未作答回答错误展开二、判断题（每题3分，共10道小题，总分值30分）1.给定流量等其他参数不变，控制在一定的限制范围内提高叶轮的转速，其叶片进口的冲角将加大。

（）（3分）正确答案正确您的答案是未作答回答错误展开2.有限多叶片叶槽内轴向旋涡的旋向与叶轮转动的方向相同。