圆的面积公式推导过程

圆形面积的推导过程1. 圆形面积的定义圆是一个平面上的几何图形，由与一个固定点的距离相等的所有点组成。

圆内部的区域称为圆的内部，圆外部的区域称为圆的外部。

圆上的任意两点都可以确定一条弧，而圆心到弧上任意一点所对应的弧长称为弧度。

2. 圆周率π在推导圆形面积之前，我们需要引入一个重要的数学常数——圆周率π。

π是一个无理数，其近似值约为3.14159。

它是一个十分特殊且重要的数，与圆相关性极高。

3. 圆形面积公式根据几何学知识，我们知道圆形面积可以通过半径r来计算。

下面我们来推导出这个公式。

首先，我们将一个半径为r的圆分成许多个扇形，每个扇形都是由半径和相邻两条弧所围成。

如果我们将所有这些扇形按照一定方式排列，并且让它们尽可能靠拢地拼接起来，那么最终就会得到一个近似于矩形（长方形）的形状。

这个近似的矩形的宽度约等于扇形的弧长，而高度则等于圆的半径。

我们可以看到，这个近似的矩形与真正的矩形有一定的差距，即多出了一些面积。

但是，如果我们将圆分得足够细致，并且将所有扇形拼接起来，那么这个差距就会越来越小。

现在，我们来计算这个近似矩形的面积。

设扇形弧长为s，圆的半径为r，则近似矩形的宽度为s，高度为r。

根据矩形面积公式：面积 = 宽度× 高度，我们可以得到：近似矩形面积= s × r接下来，我们考虑如何计算扇形弧长s。

由于一个完整圆周上有360°（角度）或2π（弧度），而一个扇形所对应的角度可以表示为θ（角度）或θ（弧度），那么扇形弧长与圆周长之间存在以下关系：s / 圆周长= θ / 360° 或 s / 圆周长= θ / 2π由于圆周长等于2πr（其中r为半径），所以可以得到：s = 圆周长× θ / 2π将此式代入近似矩形面积的公式中，可以得到：近似矩形面积 = (圆周长× θ / 2π) × r进一步化简，可以得到：近似矩形面积= r × 圆周长× θ / 2π由于圆周长等于2πr，所以可以继续化简为：近似矩形面积= r × 2πr × θ / 2π最终化简为：近似矩形面积= r² × θ由于我们是以扇形作为基本单位进行拼接的，而一个完整的圆共有360°或2π弧度，因此θ等于360°或2π弧度。

微积分圆面积的推导过程
微积分中推导圆的面积是一个经典的问题，我们可以通过多种方法来推导圆的面积，其中最常见的方法是使用定积分。

下面我将从多个角度来解释这个问题。

首先，我们知道圆的面积公式是πr^2，其中r是圆的半径。

要推导这个公式，我们可以从圆的定义出发，假设我们要计算半径为r的圆的面积。

我们可以将圆分成许多细小的扇形，然后将这些扇形拼接成一个近似于圆的形状。

接着，我们可以计算每个扇形的面积，然后将这些面积相加，最后取极限得到圆的面积。

另一种方法是利用积分的概念。

我们可以将圆分成许多细小的扇形，每个扇形的面积可以近似为一个矩形的面积，然后我们可以对所有这些矩形的面积进行累加，最后取极限得到圆的面积。

具体来说，我们可以将圆分成许多扇形，每个扇形的面积可以表示为r 乘以扇形的弧长，然后对所有的扇形面积进行积分，即可得到圆的面积公式πr^2。

另外，我们还可以利用极坐标系来推导圆的面积公式。

在极坐标系中，圆的方程可以表示为r=cos(theta)，其中r是到原点的距
离，theta是与x轴的夹角。

我们可以利用极坐标系下的面积元素公式来推导圆的面积，然后对整个圆的面积元素进行积分，最终也可以得到圆的面积公式πr^2。

总之，推导圆的面积是微积分中的经典问题，可以通过分割成扇形、利用积分的概念以及极坐标系等多种方法来完成。

以上是我对微积分圆面积推导过程的多角度解释，希望能够帮助到你。

圆的面积推导过程微积分圆环圆的面积推导过程是微积分中的一个经典问题，下面我将用简体中文写出推导过程，并保持条理清晰。

1.首先，我们先来回顾一下圆的定义。

圆是指平面内的一组点，这些点到圆心的距离都相等。

圆心到圆上一点的距离称为半径，常用字母r表示。

2.我们先将圆分成无穷多个小的扇形。

我们知道，扇形的面积与其对应的圆心角有关。

设扇形的圆心角为θ。

3.一个扇形的面积可以表示为A = 1/2 * r^2 * θ，其中r为圆的半径。

这个公式可以用几何方法来证明，但在这里我们将使用微积分的方法进行推导。

4.现在我们将圆分成无穷多个无限小的扇形，每个扇形的圆心角可以表示为dθ。

由于dθ是一个无限小的量，我们可以将其视为一个无穷小的直角三角形的弧度量。

5.扇形的面积dA可以表示为dA = 1/2 * r^2 * dθ。

这个公式是根据前面的一个扇形面积公式进行推导得到的。

对于每个扇形，这个公式都成立。

6.现在我们要计算整个圆的面积，即将所有扇形的面积加起来。

由于圆是连续、无穷的，我们需要对所有扇形的面积求和。

7.我们可以将所有扇形的面积相加的表达式写成积分形式，即A = ∫dA = ∫(1/2 * r^2 * dθ)。

8.根据微积分的基本性质，我们可以对积分进行计算，得到A = 1/2 * r^2 * ∫dθ。

9.上述积分中，我们对dθ进行积分，即对圆心角进行积分。

在整个圆周上，圆心角的取值范围是从0到2π。

10.对于∫dθ这个积分，由于θ是无穷小的，积分结果是θ在0到2π上的取值范围。

即∫dθ = θ|0到2π = 2π - 0 = 2π。

11.将积分结果代入到之前的表达式中，得到A = 1/2 * r^2 *2π = π * r^2。

12.综上所述，我们推导出了圆的面积公式A = π * r^2。

这个公式是高中数学中常用的一个结论。

通过以上推导过程，我们可以看到，圆的面积公式的推导利用了微积分的方法，特别是积分的概念和计算方法。

圆面积推导公式的五种方法
1、直接公式法：这是最常用的一种方法，即利用圆面积公式
A=πr2，只要知道半径r，就可以求出该圆的面积A。

2、三角函数法：对于圆周上的一个点P，把其它点P1、P2…依次从这点出发经过一定的角度旋转，构成多边形，当回到P点时，多边形就会变成圆形，则圆面积A等于多边形的面积。

3、积分法：设圆的半径是r，将水平实际轴和垂直虚轴分别等分成N份，每份大小为：Δx=2πr/N；遍历每条水平小线段，求出每条小线段上宽Δx所围出来区域面积S=2πryΔx，然后将所有小线段上的区域加总，最终可得出圆的面积A。

4、极坐标法：用极坐标表示圆的面积的时候，可以看成一堆正方形的面积一起组成，而用它们的和来表示圆面积。

这个方法在计算机环境下使用比较多，但具体用法有很多。

5、三角测量法：采用三角测量法，可以把圆分为多个三角形，每个三角形的面积都可以求出来，再将所有三角形的面积加起来，就可以得出圆的面积。

圆形面积的计算公式圆形面积的计算公式是数学中常见的一个公式，用于计算圆的面积。

圆形面积的计算公式是πr²，其中π是一个无理数，近似值为3.14159，r是圆的半径。

圆形面积的计算公式可以通过以下步骤进行推导。

首先，我们知道圆是由无数个点组成的，这些点到圆心的距离都相等。

我们可以将圆划分为无数个同心圆环，每个圆环的宽度都非常小，可以近似为0。

假设我们要计算的圆的半径为r，我们可以将圆环的宽度设为Δr。

我们可以用这个圆环近似代表整个圆，计算圆环的面积，然后将所有圆环的面积累加起来，就可以得到整个圆的面积。

圆环的面积可以通过矩形面积的计算公式来计算。

假设矩形的宽度为Δr，高度为2πr，其中2πr是矩形的周长。

矩形的面积为宽度乘以高度，即Δr * 2πr = 2πr²Δr。

由于圆环的宽度Δr非常小，可以近似为0，所以我们可以将圆环的面积近似为0 * 2πr² = 0。

但是当我们将所有圆环的面积累加起来时，就可以得到整个圆的面积。

我们将所有圆环的面积累加起来，可以得到以下等式：圆的面积= 0 + 0 + 0 + ... = ∑(2πr²Δr) = 2πr²∑(Δr)其中∑(Δr)表示将所有圆环的宽度累加起来。

由于圆环的宽度Δr非常小，可以近似为0，所以∑(Δr)可以近似为圆的周长2πr。

所以，圆的面积可以近似为2πr² * 2πr = 4π²r³。

但是我们知道，圆的面积应该是πr²，而不是4π²r³。

为了解决这个问题，我们需要将圆环的宽度Δr逐渐缩小，使得Δr趋近于0。

当Δr趋近于0时，2πr²∑(Δr)趋近于πr²。

所以，当Δr趋近于0时，圆的面积可以近似为πr²。

圆形面积的计算公式是πr²。

这个公式可以用于计算任意圆的面积，无论圆的半径大小如何。

通过这个公式，我们可以计算出许多圆的面积。

圆面积的推导过程
将一个圆形平均分成若干份，拼成一个近似的平行四边形，平均分成的份数越多，越近似一个长方形。

长方形的长是圆形周长的一半，长方形的宽是圆形的半径，圆周长的一半乘圆的半径就等于圆形的面积。

长方形的宽就等于圆的半径（r），长方形的长就是圆周长（C）的一半。

长方形的面积是ab，那圆的面积就是：圆的半径（r）乘以二分之一周长C，
S=r*C/2=r*πr。

扩展资料：
与圆相关的公式：
1、圆面积：S=πr²，S=π(d/2)²。

（d为直径，r为半径）。

2、半圆的面积：S半圆=(πr^2)/2。

（r为半径）。

3、圆环面积：S大圆-S小圆=π(R^2-r^2)(R为大圆半径，r为小圆半径)。

4、圆的周长：C=2πr或c=πd。

（d为直径，r为半径）。

5、半圆的周长：d+(πd)/2或者d+πr。

（d为直径，r为半径）。

圆的性质
1、圆是轴对称图形，其对称轴是任意一条通过圆心的直线。

圆也是中心对称图形，其对称中心是圆心。

2、垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的2条弧。

3、垂径定理的逆定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的2条弧。

4、在同圆或等圆中，如果两个圆心角，两个圆周角，两组弧，两条弦，两条弦心距中有一组量相等，那么他们所对应的其余各组量都分别相等。

5、在同圆或等圆中，相等的弧所对的圆周角等于它所对的圆心角的一半（圆周角与圆心角在弦的同侧）。

圆面积的计算公式表
一、圆面积计算公式推导。

1. 将圆转化为近似图形。

- 把一个圆平均分成若干个相等的小扇形（分的份数越多，拼成的图形就越接近长方形）。

- 然后把这些小扇形拼接起来，可以拼成一个近似的长方形。

2. 推导过程。

- 这个近似长方形的长相当于圆周长的一半，因为圆的周长C = 2π r，所以圆周长的一半就是π r。

- 这个近似长方形的宽相当于圆的半径r。

- 根据长方形的面积公式S =长×宽，所以圆的面积S=π r× r=π r^2。

二、圆面积计算公式相关示例。

1. 已知半径求面积。

- 例：一个圆的半径r = 3厘米，求它的面积。

- 解：根据圆面积公式S=π r^2，π取3.14，则S = 3.14×3^2=3.14×9 = 28.26（平方厘米）。

2. 已知直径求面积。

- 例：一个圆的直径d = 8厘米，求它的面积。

- 解：先求出半径r=(d)/(2)=(8)/(2) = 4厘米，再根据面积公式S=π r^2，π取3.14，则S = 3.14×4^2=3.14×16 = 50.24（平方厘米）。

3. 已知周长求面积。

- 例：一个圆的周长C = 18.84厘米，求它的面积。

- 解：先根据周长公式C = 2π r求出半径r，r=(C)/(2π)=(18.84)/(2×3.14)=3厘米，然后根据面积公式S=π r^2，π取3.14，则S = 3.14×3^2=28.26（平方厘米）。

圆面积的公式推导过程要推导圆的面积公式，我们首先需要了解一些基本概念和前提条件。

一个圆由半径r定义，半径是圆心到圆周上任意一点的距离。

我们可以选择以圆心O为原点，将圆周上一点A的坐标表示为(x,y)。

在这个坐标系中，圆的方程为x^2+y^2=r^2、这个方程描述了所有满足半径为r的圆上点的位置。

我们可以利用这个方程来推导圆的面积公式。

.....**********************在这个图中，我们选择一个扇形的顶角θ（在弧度制度量）作为单位扇形。

单位扇形的面积可以表示为A=1/2*r*r*θ，其中1/2*r*r是扇形的底边长度，θ是扇形的角度。

现在我们需要找出单位扇形的角度θ与半径r之间的关系。

我们可以将单位扇形完全展开，形成一个很小的弧长。

这个弧长等于扇形的半径乘以单位扇形的角度（θ）：s=r*θ我们知道一个完整的圆的弧长是2πr（圆的周长）。

所以我们可以得到：s=2πr将上面两个方程相等，我们可以得到：2πr=r*θ将两边都除以r，我们得到：2π=θ根据这个关系，我们可以把单位扇形的面积公式A=1/2*r*r*θ重写为：A=1/2*r*r*2π化简得：A=πr^2所以，圆的面积等于半径的平方乘以π。

这个结果被称为圆的面积公式。

它可以用来计算任何半径为r的圆的面积。

在这个推导过程中，我们使用了几何和代数的原理，包括圆的定义、直角三角形的面积公式和三角函数。

总结起来，圆的面积公式推导的基本思路是将圆分成无限多的扇形，然后将扇形的面积相加。

通过对单位扇形进行分析，我们得到了单位扇形的面积公式，并通过几何和代数的原理，将单位扇形的面积转化为整个圆的面积公式。

圆的面积的推导过程
圆的面积公式为$S=\pi r^2$，其中$S$表示圆的面积，$r$表示圆的半径，$\pi$为圆周率，约等于$3.14$。

推导圆的面积公式的过程如下：
1. 我们将圆分成很多很多小块，每一块都是一个近似的三角形。

2. 我们将这些小块拼成一个近似的长方形。

3. 长方形的长等于圆周长的一半，即$\pi r$。

4. 长方形的宽等于圆的半径，即$r$。

5. 由于长方形的面积等于长乘以宽，所以圆的面积就等于$\pi r \times r$，即$S=\pi r^2$。

通过这个推导过程，我们得到了圆的面积公式$S=\pi r^2$。

需要注意的是，这个推导过程是一种近似方法，实际上圆是一个曲线图形，无法真正被分成无数个小块。

但通过这种方法，我们可以得到一个非常接近真实值的圆的面积公式。

希望这个推导过程能帮助你更好地理解圆的面积公式的来源和意义。

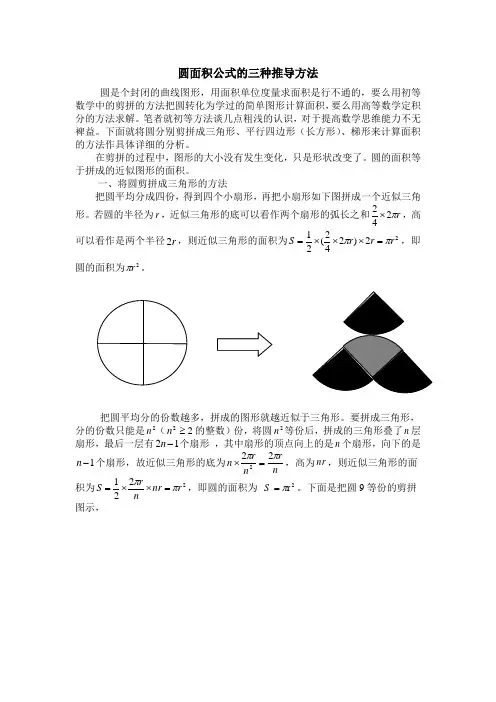
圆面积公式的三种推导方法圆是个封闭的曲线图形，用面积单位度量求面积是行不通的，要么用初等数学中的剪拼的方法把圆转化为学过的简单图形计算面积，要么用高等数学定积分的方法求解。

笔者就初等方法谈几点粗浅的认识，对于提高数学思维能力不无裨益。

下面就将圆分别剪拼成三角形、平行四边形（长方形）、梯形来计算面积的方法作具体详细的分析。

在剪拼的过程中，图形的大小没有发生变化，只是形状改变了。

圆的面积等于拼成的近似图形的面积。

一、将圆剪拼成三角形的方法把圆平均分成四份，得到四个小扇形，再把小扇形如下图拼成一个近似三角形。

若圆的半径为r ，近似三角形的底可以看作两个扇形的弧长之和r π242⨯，高可以看作是两个半径r 2，则近似三角形的面积为22)242(21r r r S ππ=⨯⨯⨯=，即圆的面积为2r π。

把圆平均分的份数越多，拼成的图形就越近似于三角形。

要拼成三角形，分的份数只能是2n （22≥n 的整数）份，将圆2n 等份后，拼成的三角形叠了n 层扇形，最后一层有12-n 个扇形 ，其中扇形的顶点向上的是n 个扇形，向下的是1-n 个扇形，故近似三角形的底为n r nr n ππ222=⨯，高为nr ，则近似三角形的面积为2221r nr nr S ππ=⨯⨯=，即圆的面积为 2r π= S 。

下面是把圆9等份的剪拼图示，二、将圆剪拼成平行四边形的方法把圆平均分成四份，得到四个小扇形，再把小扇形如图拼成一个近似平行四边形。

同样，圆的半径为r ，近似平行四边形的底可以看作2个扇形并成的为r π242⨯，高可以看作是小扇形的半径r ，则近似平行四边形的面积为222r r r S ππ=⨯⨯=，即圆的面积为2r π= S 。

同样的把圆平均分的份数越多，拼出来的图形越接近平行四边形，当分的份数无限大时，拼出的图形也可以看作是长方形。

要拼成平行四边形，分的份数只能是n 2（2≥n 的自然数）份，将圆n 2等份后，拼成的平行四边形（叠了一层）的底为n r n 22π⨯，高为半径r ，则平行四边形的面积为222r r nr n S ππ=⨯⨯=，即圆的面积2r π= S 。

圆的面积是怎么推导出来的
圆的面积公式是S=π×(r^2)
1圆的面积公式是如何推导出来
圆的面积s=π×r×r。

其中，π是周围率，等于3.14，r是圆的半径。

把圆平均分成若干份，可以拼成一个近似的长方形。

长方形的宽就等于圆的半径(r)，长方形的长就是圆周长(C)的一半。

长方形的面积是ab，那圆的面积就是:圆的半径(r)乘以二分之一周长C，S=r*C/2=r*πr。

2关于圆还有什么公式
圆的半径:r
直径:d
圆周率:π(数值为3.1415926至3.1415927之间……无限不循环小数)，通常采用3.14作为π的数值
圆面积:S=πr²;S=π(d/2)²
半圆的面积:S半圆=(πr^2;)/2
圆环面积:S大圆-S小圆=π(R^2-r^2)(R为大圆半径，r为小圆半径)
圆的周长:C=2πr或c=πd
半圆的周长:d+(πd)/2或者d+πr
圆的周长计算公式为：C=2πR。

C代表圆的周长，r代表圆的半径。

圆的面积公式为：S=πR2（R的平方）。

S代表圆的面积，r为圆的半径。

3椭圆的公式有什么
椭圆周长计算公式：
椭圆周长公式：L=2πb+4(a-b)
椭圆周长定理：椭圆的周长等于该椭圆短半轴长为半径的圆周长（2πb）加上四倍的该椭圆长半轴长（a）与短半轴长（b）的差。

椭圆面积计算公式：
椭圆面积公式：S=πab
椭圆面积定理：椭圆的面积等于圆周率（π）乘该椭圆长半轴长（a）与短半轴长（b）的乘积。

圆的面积公式的推导和计算圆是由平面上距离一个固定点（圆心）等于一个常数（半径）的点组成的集合。

面积是一个平面图形所占据的二维空间的大小。

我们的目标是求解圆的面积公式。

首先，我们考虑圆通过旋转一条线段而形成的图形，称为圆锥。

如果我们旋转一个半径为r的线段360度，我们会得到一个圆锥，其底面的周长是2πr。

现在，考虑一个半径为r的圆。

我们可以将这个圆分成无限多个非常小的扇形区域。

每个扇形的弧长可以近似看作一个三角形的周长。

根据三角形的周长公式，我们可以得到每个扇形的面积为0.5r*r。

由于圆有无限多个扇形，我们只需要将每个扇形的面积相加，我们就可以得到整个圆的面积。

但是，由于扇形的数量是无穷的，这个方法并不可行。

为了解决这个问题，我们将半径为r的圆分成n个相等的扇形。

每个扇形的弧长为2πr/n，面积为0.5r*r*2πr/n=πr^2/n。

现在，让n趋近于无穷大，即n→∞。

随着n的增大，每个扇形的面积趋近于0，但是扇形的总数无限大，所以整个圆的面积可以表示为无限求和的形式：A = lim(n→∞) Σ(πr^2 / n)我们可以将求和公式转化为积分形式：A = ∫(0→r) πr^2 dx通过对积分公式的求解，我们可以得到圆的面积公式：A=πr^2这就是圆的面积公式的推导过程。

现在我们来使用这个公式来计算一些例子。

1. 一个半径为5cm的圆的面积：A=π*5^2=π*25≈78.54平方厘米2.一个半径为10m的圆的面积：A=π*10^2=π*100≈314.16平方米3.一个半径为2.5英寸的圆的面积：A=π*(2.5)^2=π*6.25≈19.63平方英寸通过圆的面积公式，我们可以轻松计算出任意圆的面积。

圆面积推导过程一、基本概念圆是指平面上的所有点，到圆心处的距离都相等，这个距离叫做半径，用r表示。

圆周长是指圆上全部点的集合所构成的曲线的长度，用C表示。

圆的面积是指圆内部的所有点所构成的区域的大小，用πr²表示。

二、圆的周长圆周长的公式是C = 2πr，其中π约等于3.14。

这个公式的意思是，圆周长等于圆的直径乘以π。

因为圆的直径等于半径的2倍，所以也可以写成C = πd。

三、圆的面积圆的面积的公式是 S = πr²。

这个公式的意思是，圆的面积等于半径的平方乘以π。

这个公式的推导过程可以分成以下几步：1. 构造圆的近似正多边形可以从一个n边形开始，将其边数n逐渐增大，直至趋于无限。

这么做的目的是将圆的面积划分为n个近似面积相等的小扇形，然后将它们按照顺序排列起来，形成一个近似的正多边形。

2. 计算正多边形的面积由于正多边形的面积公式早已得到（即面积等于n个小三角形的面积之和），所以可以通过求出每个小扇形的面积，再将它们加起来，得到完整正多边形的面积。

3. 取极限当n趋于无限大时，由于扇形趋近于小区间，可以得到圆的面积公式：S = πr²。

四、圆面积公式的证明为了证明圆的面积公式S = πr²，需要进行一些比较复杂的数学推导。

此处仅列出大致过程：1. 画出一个半径为r的圆，再在圆内划一扇形。

2. 把这个扇形的弧和弧心的连线上垂直于圆周的线段分别称为弦和弦上的线段，同时将扇形划分成多个小的三角形。

3. 根据勾股定理，可以得到每个小三角形的面积公式，从而得到扇形的面积公式。

4. 将圆沿半径线切割成多个小扇形，并将它们排列起来，得到一个近似的正多边形。

5. 通过增加正多边形的边数，可以逐渐逼近一个完整的圆。

6. 利用前面推导出的扇形面积公式，将每个小扇形的面积求和，得到圆的面积公式S = πr²。

五、结论综合以上推导过程可知，圆的周长公式是C = 2πr，圆的面积公式是 S = πr²。

圆的周长面积公式推导过程圆的周长公式推导：我们知道圆是一个几何图形，由一个中心点和一条半径组成。

圆是没有角度和边的，因此无法使用传统的角度和边的方式对其进行计算。

因此，我们需要使用圆的半径或直径来计算其周长。

假设圆的半径为r，根据定义，我们可以知道圆的周长等于它的边界的长度。

首先，我们可以以圆心为起点，沿着圆的边界沿着任意方向绕一圈，然后返回到起点。

这条边界的长度就是圆的周长。

想象我们在圆周上切割出一个等腰三角形，其中圆心是它的顶点。

我们可以看到这个三角形的底边正好是圆的周长。

现在我们来计算这个等腰三角形的底边。

根据三角形的性质，它的底边等于两个相邻边的和。

由于这是一个等腰三角形，所以两个相邻边的长度都等于r，因此底边的长度就是2r。

所以，圆的周长等于等腰三角形的底边长度，即C=2r。

这就是圆的周长公式，也被称为圆周长的最简形式。

圆的面积公式推导：要计算圆的面积，我们可以使用半径或直径的长度来计算。

假设圆的半径为r，我们可以使用以下的步骤来计算圆的面积。

首先，我们可以在圆内画一个正多边形，这个正多边形的边数非常多，而且趋近于无穷大。

这是因为当我们增加正多边形的边数时，这个多边形的形状就越接近圆。

当边数无限增加时，这个正多边形的形状就完全与圆重合了。

现在，我们将这个正多边形分成许多小的扇形，其中每个扇形都是由圆心和相邻两个顶点所形成的三角形。

每个小扇形的面积我们可以计算出来，然后将它们全部加起来就可以得到整个正多边形的面积。

现在，我们要计算每个小扇形的面积。

每个小扇形的底边就是正多边形的边长，为s。

而扇形的底边是正多边形的一小部分，在增加正多边形的边数时趋近于0。

因此，当正多边形的边数趋近于无穷大时，每个小扇形的底边就趋近于圆的一半，也就是s/2扇形的高就是圆的半径r。

因此，每个小扇形的面积可以通过扇形面积公式计算出来，即A=(1/2)*r*(s/2)=(1/4)*r*s。

现在我们可以将所有小扇形的面积加起来，得到正多边形的面积。