(完整版)高中数学必修一第二章测试题(含答案).docx

高中数学必修一第二章一、单选题1．已知a≥0，b≥0，且a+b=2，则（ ）A．ab≤12B．ab≥12C．a2+b2≥2D．a2+b2≤32．已知正数x，y满足x+1y=1，则1x+4y的最小值为（ ）A．9B．10C．6D．83．在实数集上定义运算⊗：x⊗y=x（1﹣y），若不等式（x﹣a）⊗（x+a）＜1对任意实数x都成立，则实数a的取值范围是（ ）A．（﹣1，1）B．（0，2）C．(―12，32)D．(―32，12)4．已知1≤a+b≤5，―1≤a―b≤3，则3a―2b的取值范围是（ ）A．[―6，14]B．[―2，14]C．[―2，10]D．[―6，10] 5．若关于x的不等式x2―4x―2―a>0在区间(1，4)内有解，则实数a的取值范围是（ ）A．a<―2B．a>―2C．a>―6D．a<―6 6．若x=5―2，y=2―3，则x，y满足（ ）A．x＞y B．x≥y C．x＜y D．x=y7．正数a,b满足9a +1b=2，若a+b≥x2+2x对任意正数a,b恒成立，则实数x的取值范围是（ ）A．[―4,2]B．[―2,4]C．(―∞,―4]∪[2,+∞)D．(―∞,―2]∪[4,+∞)8．设正数a，b满足b―a<2，若关于x的不等式(a2―4)x2+4bx―b2<0的解集中的整数解恰有4个，则a的取值范围是（ ）A．(2，3)B．(3，4)C．(2，4)D．(4，5)二、多选题9．下列函数最小值为2的是（ ）A．y=x2+1x2B．y=x2+3+1x2+3C．y=2x+12x D．y=x2+1x，x>010．已知a>0，b>0.若4a+b=1，则（ ）A．14a +1b的最小值为9B．1a+1b的最小值为9C．(4a+1)(b+1)的最大值为94D．(a+1)(b+1)的最大值为9411．已知a>0，b>0，则下列式子一定成立的有（ ）A．2aba+b ≤ab B．a2+b22≤a+b2C．1a +1b≤4a+bD．a2+b22≤a2+b2a+b12．已知正数a，b满足a(a+b)=1，下列结论中正确的是（ ）A．a2+b2的最小值为22―2B．2a+b的最小值为2C．1a +1b的最小值为332D．a―b的最大值为1三、填空题13．设一元二次不等式ax2+bx+1＞0的解集为{x|―1<x<13}，则ab的值是 ．14．已知x,y为正实数，且x+4y=1x+1y=m，则m的最小值为 .15．已知实数a,b满足ab>0，则aa+b―aa+2b的最大值为 16．已知实数x，y，z满足：{x+y+z=3x2+y2+z2=36，则|x|+|y|+|z|的最大值为 .四、解答题17．已知集合A={x|―2<x<5}，B={x|m+1≤x≤2m―1}．（1）当m=3时，求（∁R A）∩B；（2）若A∪B=A，求实数m的取值范围．18．求证下列问题：（1）已知a，b，c均为正数，求证：bca +acb+abc≥a+b+c.（2）已知xy>0，求证：1x>1y的充要条件是x<y.19．已知不等式组{―x<2，x2+7x―8<0的解集为A，集合B={x|a―5<x<3a―5}．（1）求A；（2）若A∪B=B，求a的取值范围．20．已知函数g(x)=k2x+k，ℎ(x)=x2―2(k2―k+1)x+4．（1）当k=1时，求函数y=ℎ(x)g(x)，x∈(―∞,―1)的最大值；（2）令f(x)={g(x),x>0ℎ(x),x<0，求证：对任意给定的非零实数x1，存在惟一的实数x2(x1≠x2)使得f(x1)=f(x2)成立的充要条件是k=4．21．若函数f(x)=a x2―(2a+1)x+2.（1）讨论f(x)>0的解集；（2）若a=1时，总∃x∈[13，1]，对∀m∈[1，4]，使得f(1x)+3―2mx≤b2―2b―2恒成立，求实数b的取值范围.22．已知函数f(x)=2|x+1|―|x―a|(a∈R)．（Ⅰ）当a=2时，求不等式f(x)⩾x+2的解集；（Ⅱ）设函数g(x)=f(x)+3|x―a|，当a=1时，函数g(x)的最小值为t，且2m +12n=t(m>0,n>0)，求m+n的最小值．答案解析部分1．【答案】C 2．【答案】A 3．【答案】C 4．【答案】C 5．【答案】A 6．【答案】C 7．【答案】A 8．【答案】C 9．【答案】A,C 10．【答案】B,C 11．【答案】A,D 13．【答案】614．【答案】315．【答案】3―2216．【答案】1+22217．【答案】（1）解：∵集合A ={x|―2<x <5}，B ={x|m +1≤x ≤2m ―1}．∴∁R A ={x|x ≤―2或x ≥5}，m =3时，B ={x|4≤x ≤5}，∴（∁R A ）∩B ={5}（2）解：若A ∪B =A ，则B ⊆A ，当B =∅时，m +1>2m ―1，解得m <2，成立；当B ≠∅时，{m +1≤2m ―1m +1>―22m ―1<5，解得2≤m <3，综上实数m 的取值范围为（―∞，3）18．【答案】（1）证明：bc a +ac b +ab c =2bc a +2ac b +2ab c 2=bc a +ac b +bc a +ab c +ac b +ab c 2≥2bc a ⋅ac b+2bc a ⋅ab c+2ac b ⋅ab c=a +b +c ，当且仅当bc a =ac b ，bc a=ab c ，acb =abc ，即a =b =c 时等号成立.（2）证明：依题意xy >0，则{x >0y >0或{x <0y <0，所以：1x >1y ⇔1x ―1y =y ―x xy >0⇔y ―x >0⇔x <y ，所以：1x>1y 的充要条件是x <y .19．【答案】（1）解：由{―x <2x 2+7x ―8<0，得{x >―2―8<x <1，得―2<x <1，所以A ={x |―2<x <1}．（2）解：由A ∪B =B ，得A ⊆B ，所以{a ―5≤―23a ―5≥1，得2≤a ≤3，故a 的取值范围为[2，3]．20．【答案】（1）解：当 k =1 时，函数 y =x 2―2x +4x +1， x ∈(―∞,―1) ，令 t =x +1<0 ，则 y =t +7t―4 ，此时 ―t >0 ，由 (―t )+(―7t )≥2(―t )×7―t =27 ，即 t +7t≤―27 ，当且仅当 t =―7 ，即 x =―7―1 时取等号，综上，当 x =―7―1 时， y 最大值是 ―27―4 ．（2）解：充分性：当 k =4 时， f (x )={16x +4,x >0x 2―26x +4,x <0 ， 当 x >0 时， y =16x +4 在 (0,+∞) 单调递增，且 y >4 ，当 x <0 时， y =x 2―26x +4 在 (―∞,0) 单调递减，且 y >4 ，若 x 1>0 ，则存在惟一的 x 2<0 ，使得 f (x 1)=f (x 2) ，同理 x 1<0 时也成立，必要性：当 x >0 时， y =k 2x +k ，当 k =0 时， f (x ) 在 (0,+∞) 上的值域为 {0} ，显然不符合题意，因此 k ≠0 ，当 x >0 时， f (x ) 在 f (x ) 的取值集合 A =(k ,+∞) ，x <0 ， f (x )=x 2―2(k 2―k +1)x +4 的对称轴 x =k 2―k +1>0 ， f (x ) 在 (―∞,0) 上递减， f (x )>f (0)=4 ，所以 f (x ) 的取值集合 B =(4,+∞) ，①若 x 1>0 ， f (x ) 且在 (0,+∞) 上单调递增，要使 f (x 1)=f (x 2) ，则 x 2<0 ，且 A ⊆B ，有 k ≥4 ．②若 x 1<0 ， f (x ) 且在 (―∞,0) 上单调递减，要使 f (x 1)=f (x 2) ，则 x 2>0 ，且 B ⊆A ，有 k ≤4 ．综上： k =4 ．21．【答案】（1）已知f (x )=a x 2―(2a +1)x +2，①当a =0时，f (x )=―x +2>0时，即x <2；②当a ≠0时，f (x )=a (x ―1a )(x ―2)，若a <0，f (x )>0，解得 1a <x <2，若0<a <12，f (x )>0，解得x <2或x >1a ，若a =12，f (x )>0，解得x ≠2，若a >12时，f (x )>0，解得x <1a 或x >2，综上所述：当a <0时，f (x )>0的解集为(1a ，2)；当a =0时，f (x )>0的解集为(―∞，2)；当0<a <12时，f (x )>0的解集为(―∞，2)∪(1a ，+∞)；当a =12时，f (x )>0的解集为(―∞，2)∪(2，+∞)；当a >12时，f (x )>0的解集为(―∞，1a )∪(2，+∞).（2）若a =1，则f (x )=x 2―3x +2，∴f (1x )+3―2m x =1x 2―2m x +2，令t =1x ，原题等价于∃t ∈[1，3]，对∀m ∈[1，4]使得t 2―2mt +2≤b 2―2b ―2恒成立，令g (m )=―2tm +t 2+2，∴g (m )是关于m 的减函数，∴对∀m ∈[1，4]，g (m )≤b 2―2b ―2恒成立，即b 2―2b ―2≥g (m )max =g (1)=t 2―2t +2，又∃t ∈[1，3]，b 2―2b ―2≥t 2―2t +2，即b 2―2b ―2≥(t 2―2t +2)min =12―2×1+2=1，故b 2―2b ―3=(b ―3)(b +1)≥0，解得b ≤―1或b ≥3.22．【答案】解：（Ⅰ）当 a =2 时， f (x )⩾x +2 化为 2|x +1|―|x ―2|≥x +2 ，当 x⩽―1 时，不等式化为 ―x ―4⩾x +2 ，解得 x⩽―3 ；当 ―1<x <2 时，不等式化为 3x⩾x +2 ，解得 1⩽x <2 ；当 x⩾2 时，不等式化为 x +4⩾x +2 ，解得 x⩾2 ，综上不等式 f (x )⩾x +2 的解集是 {x |x⩽―3或x⩾1}（Ⅱ）当 a =1 时， g (x )=2|x +1|+2|x ―1|⩾2|x +1+1―x |=4 ，当且仅当 (x +1)(x ―1)⩽0 ，即 ―1⩽x⩽1 时，等号成立．所以，函数 g (x ) 的最小值 t =4 ，所以 2m +12n =4 ， 12m +18n=1 ．m +n =(m +n )(12m +18n )=n 2m +m 8n +58⩾2n 2m ⋅m 8n +58=98 ，当且仅当 {12m +18n =1，n 2m =m 8n 即 {m =34，n =38时等号成立，所以 m +n 的最小值为 98．。

高一数学必修一第二章试卷及答案一、选择题1.(20 13年高考四川卷)设集合a={1,2,3},集合b={ -2,2},则a∩b等于( b )(a) (b){2}(c){-2,2} (d){-2,1,2,3}解析:a∩b={2},故挑选b.(a){2} (b){0,2}(c){-1,2} (d){-1,0,2}解析:依题意得集合p={-1,0,1},(a)1个 (b)2个 (c)4个 (d)8个4.(年高考全国新课标卷ⅰ)已知集合a={x|x2-2x>0},b={x|-(a)a∩b= (b)a∪b=r解析:a={x|x>2或x<0},∴a∪b=r,故挑选b.5.已知集合m={x ≥0,x∈r},n={y|y=3x2+1,x∈r},则m∩n等于( c )(a) (b){x|x≥1}(c){x|x>1} (d){x|x≥1或x<0}解析:m={x|x≤0或x>1},n={y|y≥1}={x|x≥1}.∴m∩n={x|x>1},故选c.6.设子集a={x + =1},子集b={y - =1},则a∩b等同于( c )(a)[-2,- ] (b)[ ,2](c)[-2,- ]∪[ ,2] (d)[-2,2]解析:集合a表示椭圆上的点的横坐标的取值范围a=[-2,2],集合b表示双曲线上的点的纵坐标的取值范围b=(-∞,- ]∪[ ,+∞),所以a∩b=[-2,- ]∪[ ,2].故选c.二、填空题7.( 年高考上海卷)若集合a={x|2x+1>0},b={x||x-1|<2},则a∩b=.解析:a={x x>- },b={x|-1所以a∩b={x -答案:{x -解析:因为2∈a,所以 <0,即(2a-1)(a- 2)>0,Champsaura>2或a< .①若3∈a,则 <0,即为( 3a-1)(a-3)>0,解得a>3或a< ,①②挑关连得实数a的值域范围就是∪(2,3].答案: ∪(2,3]若a≠0,b=(- ),∴- =-1或- =1,∴a=1或a=-1.所以a=0或a=1或a=-1组成的集合为{-1,0,1}.答案:{-1,0,1}10.已知集合a={x|x2+ x+1=0},若a∩r= ,则实数m的取值范围是.解析:∵a∩r= ,∴a= ,∴δ=( )2-4<0,∴0≤m<4.答案:[0,4)11.已知集合a={x|x2-2x-3>0},b={x|x2+ax+b≤0},若a∪b=r,a∩b={x| 3解析:a={x|x<-1或x>3},∵a∪b=r,a∩b={x|3∴b={x|-1≤x≤4},即方程x2+ax+b=0的两根为x1=-1,x2=4.∴a=-3,b=-4,∴a+b=-7.答案:-7三、解答题12.未知子集a={-4,2a-1,a2},b={a-5,1-a,9},分别谋适宜以下条件的a的值.(1)9∈(a∩b);(2){9}=a∩b.解:(1) ∵9∈(a∩b),∴2a-1= 9或a2=9,∴a=5或a=3或a=-3.当a=5时,a={-4,9,25},b={0,-4,9};当a=3时,a-5=1-a=-2,不满足集合元素的互异性;当a=-3时,a={-4,-7,9},b={-8,4,9},所以a=5或a=-3.(2)由(1)所述,当a=5时,a∩b={-4,9},相左题意,当a=-3时,a∩b={9}.所以a=- 3.13.已知集合a={x|x2-2x-3≤0};b={x|x2-2mx+m2-4≤0,x∈r,m∈r}.(1)若a∩b=[0,3],谋实数m的值;解:由已知得a={x|-1≤x≤3},b={x|m-2≤x≤m+2}.(1)∵a∩b=[0,3],∴∴m=2.∴m-2>3或m+2<-1,即m>5或m<-3.14.设u=r,子集a={x |x2+3x+2=0},b={x|x2+(m+1)x+m=0},若解:a={x|x=-1或x=-2},方程x2+(m+1)x+m=0的根是x1=-1,x2=-m,当-m=-1,即m=1时,b={-1},当-m≠-1,即m≠1时,b={-1,-m},∴-m=-2,即m=2.所以m=1或m=2.集合的三个特性(1)无序性指集合中的元素排列没有顺序，如集合a={1,2}，集合b={2,1}，则集合a=b。

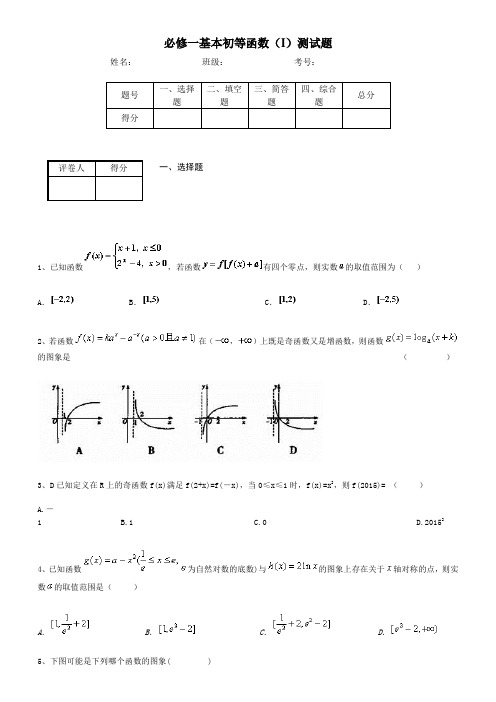
必修一基本初等函数（I）测试题姓名：_______________班级：_______________考号：_______________题号一、选择题二、填空题三、简答题四、综合题总分得分一、选择题1、已知函数，若函数有四个零点，则实数的取值范围为（）A． B． C． D．2、若函数在（，）上既是奇函数又是增函数，则函数的图象是（）3、D已知定义在R上的奇函数f(x)满足f(2+x)=f(－x)，当0≤x≤1时，f(x)=x2，则f(2015)= （）A.－1 B.1 C.0 D.201524、已知函数为自然对数的底数)与的图象上存在关于轴对称的点，则实数的取值范围是（）A．B．C．D．5、下图可能是下列哪个函数的图象( )评卷人得分. .. .6、已知，，，则的大小关系是（）A ．B ．C ．D ．7、设，，，则的大小关系是A. B. C. D.8、下列函数中值域为（0，）的是（）A. B. C. D.9、已知函数为自然对数的底数)与的图象上存在关于轴对称的点，则实数的取值范围是（）A ．B ．C ．D ．10、已知函数，若，则的取值范围是（）A． B． C． D．11、已知函数的最小值为（）A．6 B．8 C．9D．1212、已知f（x）是定义在R上的奇函数，当x<0时，f(x)=那么的值是( )A． B．－ C． D．－13、下列函数中，反函数是其自身的函数为A． B．C． D．14、对于函数，令集合，则集合M为A．空集 B．实数集 C．单元素集 D．二元素集15、函数y=定义域是A ．B ．C ．D ．二、填空题评卷人得分16、函数为奇函数，则实数 .17、设函数，给出下列四个命题：①函数为偶函数；②若其中，则；③函数在上为单调增函数；④若，则。

则正确命题的序号是．.18、若,则定义域为 .19、若方程有两个不相等的实数根，则的取值范围是20、定义函数，若存在常数，对于任意，存在唯一的，使得，则称函数在上的“均值”为，已知，则函数在上的“均值”为．21、在R+上定义一种运算“*”：对于、R+，有*=，则方程*=的解是= 。

2018-2019学年必修一第二章训练卷基本初等函数（一）注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1．函数ln 11x y x+=-定义域为（ ） A ．()4,1--B ．()4,1-C ．()1,1-D ．(]1,1-2．已知log 92a ＝-，则a 的值为（ ） A ．3-B ．13-C ．3D ．133．3662log 2+3log 3=（ ） A ．0B ．1C ．6D ．62log 34．已知函数()e 11ln 1x x f x xx ⎧-≤=⎨>⎩，那么()ln2f 的值是（ ）A ．0B ．1C ．()ln ln 2D ．25．已知集合2log |1{}A y y x x >＝＝，，1|,>1}2xB y y x ⎛⎫={= ⎪⎝⎭，则A B I ＝（ ） A ．1{|0}2y y <<B ．{}1|0y y <<C ．1{|1}2y y << D ．∅6．设05log 06a ．＝．，11log 06b ．＝．，0611c ．＝．，则（ ） A ．a b c << B ．b c a <<C ．b a c <<D ．c a b <<7．函数2xy -＝的单调递增区间是（ ）A ．()-∞∞，+B ．()0-∞，C ．(0)∞，+D ．不存在8．函数41()2x x f x +=的图象（ ）A ．关于原点对称B ．关于直线y x ＝对称C ．关于x 轴对称D ．关于y 轴对称9．函数2log ||||xy x x =的大致图象是（ ）10．定义运算aa ba b ba b≤⎧⊕=⎨>⎩则函数()12x f x ⊕＝的图象是（ ） 此卷只装订不密封班级 姓名 准考证号 考场号 座位号11．函数()log (1)xa f x a x ＝＋＋在[]0,1上的最大值与最小值和为a ，则a 的值为（ ）A ．14B ．12C ．2D ．412．已知函数()f x 满足：当4x ≥时，1()2xf x ⎛⎫= ⎪⎝⎭；当4x <时，()()1f x f x ＝＋，则22lo )g 3(f ＋＝（ ） A ．124B ．112 C ．18D ．38二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）13．幂函数()f x 的图象过点14,2⎛⎫⎪⎝⎭，那么()8f ＝________．14．若01a <<，1b <-，则函数()x f x a b ＝＋的图象不经过第________象限． 15．已知m 为非零实数，若函数ln 11m y x ⎛⎫=-⎪-⎝⎭的图象关于原点中心对称，则m ＝________．16．对于下列结论：①函数2()R x y a x ∈＋＝的图象可以由函数01()x y a a a >≠＝，且的图象平移得到；②函数2x y ＝与函数2log y x ＝的图象关于y 轴对称； ③方程255()log 21log 2()x x ＋＝－的解集为{}1,3-； ④函数()(n )l 1ln 1y x x -=+-为奇函数．其中正确的结论是________．(把你认为正确结论的序号都填上)三、解答题（本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．(10分)计算下列各式： （1）1220.5312+22 (0.01)54--⎛⎫⎛⎫⋅- ⎪ ⎪⎝⎭⎝⎭．（2）2 30.5207103720.12 392748--⎛⎫⎛⎫+++π+⎪⎪⎝⎭⎝⎭18．(12分)求值：（1）112 23312+2|.064| 2 54-⎛⎫⎛⎫⋅0- ⎪ ⎪⎝⎭⎝⎭；（2）21 239483(log 2log 2)(log 3log 3)log 3lg1⎛⎫+⋅+++ ⎪⎝⎭．19．(12分)已知,2[]3x∈-，求11()142x xf x=-+的最小值与最大值．20．(12分)已知函数22x xy b a+＋＝（a，b是常数，且0a>，1a≠）在区间3,02⎡⎤-⎢⎥⎣⎦上有max3y＝，min52y=，试求a和b的值．21．(12分)设a ，R b ∈，且2a ≠，定义在区间()b b -，内的函数1()lg 12axf x x +=+是奇函数．（1）求b 的取值范围； （2）讨论函数()f x 的单调性．22．(12分)设()()1 2log 10f x ax -＝，a 为常数．若()32f ＝-．（1）求a 的值；（2）求使()0f x ≥的x 的取值范围；（3）若对于区间[]3,4上的每一个x 的值，不等式1()2xf x m ⎛⎫>+ ⎪⎝⎭恒成立，求实数m 的取值范围．2018-2019学年必修一第二章训练卷基本初等函数（一）答 案一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1．【答案】C【解析】∵10x +>，10x ->，∴11x -<<．故选C ． 2．【答案】D【解析】∵log 92a ＝-，∴22193a --⎛⎫== ⎪⎝⎭，且0a >，∴13a =．故选D ．3．【答案】B【解析】原式666log 2log 3log 61＝＋＝＝．故选B ． 4．【答案】B【解析】∵0ln21<<，∴()ln 2ln 2e 1211f =-=-=．故选B ． 5．【答案】A【解析】∵1x >，∴2log 0y x >＝，即{}|0A y y >＝．又1x >，∴1122xy ⎛⎫=< ⎪⎝⎭，即1{|0}2B y y =<<．∴1{|0}2A B y y =<<I ．故选A ．6．【答案】C【解析】∵050505log 1log 06log 05<<．．．．．，∴01a <<．1111log 06log 10<．．．＝， 即0b <．061.11>．．011＝，即1c >．∴b a c <<．故选C ．7．【答案】B 【解析】函数122x xy -⎛⎫== ⎪⎝⎭，当0x <时为2x y ＝，递增，当0x >时为12xy ⎛⎫= ⎪⎝⎭，递减．故2xy -＝的单调增区间为()0-∞，．故选B ．8．【答案】D【解析】函数()f x 的定义域是R ，4144414()()2242x x x x xx x x x f x f x ----+⨯++-====⨯，则函数()f x 是偶函数，其图象关于y 轴对称．故选D ． 9．【答案】D【解析】当0x >时，22log log xy x x x ==，当0x <时，22log ()l ()og xy x xx =---＝-，分别作图象可知选D ． 10．【答案】A【解析】据题意20()121x xx f x x ⎧≤=⊕=⎨>⎩，故选A ．11．【答案】B【解析】∵函数x y a ＝与()log 1a y x ＝＋在[]0,1上具有相同的单调性，∴函数()f x 的最大值、最小值应在[]0,1的端点处取得，由01log 1log 2a a a a a ＋＋＋＝，得12a =． 故选B ． 12．【答案】A【解析】222222log 3log 4log 3log 12log 164<＋＝＋＝＝，22log 24log 164>＝， 由于当4x <时，()()1f x f x ＝＋， 则()()22222log 3log 121log 12log 2()4()f f f f ＋＝＝＋＝， 又当4x ≥时，1()2xf x ⎛⎫= ⎪⎝⎭，所以22log 241log 24211(log 24)2=224f ⎛⎫== ⎪⎝⎭， 所以21(2log 3)24f +=．故选A ．二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上） 13．【解析】设()f x x α＝，将14,2⎛⎫⎪⎝⎭代入，求得12α=-．则12() f x x =，所以12(8)8f =． 14．【答案】一【解析】定义域是R ，函数()f x 的大致图象如图1所示，当0x <时，1x a >，则1x a b b >＋＋，由于1b <-，则10b <＋，则函数()f x 的图象经过第二、三象限；当0x ≥时，01x a <≤，则10x b a b b <≤<＋＋，则函数()f x 的图象经过第四象限，不经过第一象限．图115．【答案】2-【解析】由图象关于原点中心对称可知函数ln 11m y x ⎛⎫=-⎪-⎝⎭为奇函数， 即有ln 1ln 111m m x x ⎛⎫⎛⎫-=--⎪ ⎪---⎝⎭⎝⎭对于定义域内任意x 恒成立， 化简并整理得()20m m ＋＝，因为m 为非零实数，因此解得2m ＝-． 16．【答案】①④【解析】2x y a ＋＝的图象可由x y a ＝的图象向左平移2个单位得到，①正确； 2x y ＝与2log y x ＝的图象关于直线y x ＝对称，②错误；由255()log 21log 2()x x ＋＝－得2221221020x x x x ⎧+=-⎪->⎨⎪->⎩∴1,312x x x x ⎧=-⎪⎪>-⎨⎪⎪><⎩或∴3x ＝．③错误；设()()()ln 1ln 1f x x x -+-＝，定义域为()1,1-，关于原点对称，()()()()[ln 1ln 1ln 1()l 1()]n f x x x x x f x -++----＝＝-＝-．∴()f x 是奇函数，④正确．故正确的结论是①④．三、解答题（本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．【答案】（1）1615；（2）100． 【解析】（1）原式1211116114310061015⎛⎫⎛⎫+⋅ ⎪ ⎪⎝⎭⎝⎭＝-＝＋－＝． （2）原式122322564375937 +10 3+1003+=1009274831648⎛⎫⎛⎫+-=++- ⎪ ⎪⎝⎭⎝⎭．18．【答案】（1）25-；（2）2．【解析】（1）原式1232=1+4525⨯-=-．（2）原式lg3lg3113lg 25lg3353·022lg 23lg 2422lg36lg 24lg 2lg 2lg3234g 4l ⎛⎫⎛⎫+-⋅ ⎪ ⎪⎝⎭⎝+⎭＝＋＋＝＋＝＋＝． 19．【答案】34，57． 【解析】设12x t =，即12xt ⎛⎫= ⎪⎝⎭，∵,2[]3x ∈-，∴184t ≤≤．∴2213()124f t t t t ⎛⎫=-+=-+ ⎪⎝⎭．又∵184t ≤≤，∴当12t =，即1x =时，()f x 有最小值34；当8t =，即3x ＝-时，()f x 有最大值57． 20．【答案】2a =，2b =．【解析】令22(211)u x x x ++-＝＝，3,02x ⎡⎤∈-⎢⎥⎣⎦，所以，当1x ＝-时，min 1u ＝-；当0x ＝时，max 0u ＝．当01a <<时，满足10352a b a b -⎧+=⎪⎨+=⎪⎩，即2332a b ⎧=⎪⎪⎨⎪=⎪⎩， 当1a >时，满足10523a b a b -⎧+=⎪⎨⎪+=⎩，即22a b =⎧⎨=⎩， 综上：23a =，32b =，或2a =，2b =． 21．【答案】（1）10,2⎛⎤⎥⎝⎦；（2）见解析．【解析】（1）1()lg()12axf x b x b x+=-<<+是奇函数等价于：对任意()x b b ∈-，都有()()1012f x f x axx ⎧-=-⎪⎨+>⎪+⎩①②①式即为112lg=lg 121ax x x ax -+-+，由此可得112=121ax x x ax-+-+，也即2224a x x ＝， 此式对任意()x b b ∈-，都成立相当于24a ＝，因为2a ≠，所以2a ＝-， 代入②式，得12>012x x -+，即1122x -<<，此式对任意()x b b ∈-，都成立相当于 1122b b -≤-<≤，所以b 的取值范围是10,2⎛⎤⎥⎝⎦． （2）设任意的1x ，2()x b b -∈，，且12x x <，由10,2b ⎛⎤∈ ⎥⎝⎦，得121122b x x b -≤-<<<≤，所以2101212x x <-<-，1201212x x <+<+．从而()()()()()()212121221112121212lglg lg lg1012121212x x x x x x x x f x f x -+----=<=+++-＝．因此()f x 在()b b -，内是减函数，具有单调性．22．【答案】（1）2；（2）9,52x ⎡⎫∈⎪⎢⎣⎭；（3）178m <-．【解析】（1）∵()32f ＝-，∴()1 2log 102ax -＝-．即211032a -⎛⎫-= ⎪⎝⎭，∴2a =．（2）∵()()1 2log 100x f x a -≥＝，∴1021x -≤．又1020x ->，∴9,52x ⎡⎫∈⎪⎢⎣⎭．（3）设()()1 21=log 102xax g x ⎛⎫-- ⎪⎝⎭．由题意知()g x m >在[]3,4x ∈上恒成立，∵()g x 在[]3,4上为增函数，∴17(3)8m g <=-．。

高中数学必修一第二 1D . y = X +函 数 的 是A . (2 ,+OO) ()B . (— 0,2)A. y =In (x+2) C[4+O )B . y =—-,x+ 1D . [3,+o )Cy=1x11.函数xy = a-1 十0, 且a 工1）的图象( )A、 y 3 y 1 y 2B 、牡 * wc 、y 1 y 3 y 2 D 、％ y ?出6. F 列函数中，在区间 （0, ）上为增 ( ) 章14 —7.若a<2则化简 2的结果是的是A . a p a qB . a p a qC . a 』a 乂D -a p -a q2、 已知f( 1x0二 x ,则 f( 5=)( )A 、 105B 、 510C 、 Ig10D 、Ig52a — 13 .函数y = log a x 当x>2时恒有y >1, 则a的取值范围是1口A.' a < 2 且 a = 121B . 0 ::: a 或 1 ：： a 乞2C . 1 ：： a乞 2 21D. a _1或0 ：： a _ —24.当 a = 0 时，函数 y = ax b 和 y = b ax& 函数y = . Ig x + lg(5 — 3x)的定义域是 [05B . [0,耳C .[15、设 * =40.9,y 2 =80.48,y 3 = 1 ，则12丿A A1 r4丿它的单间是工J ■+ 00 )Doo, 0)10.函数 y = 2+ Iog 2(x 2 + 3)(x > 1)的值域、选择1 .已知p>q>1,0<a<1,则下列各式中正确 ( )A. B . - 2a — 1C. D . — 1 — 2aA C . (—3y v 3xIog4x v Iog4y+ 3的图象一定过定点15.设函数f(x)是定义在R上的奇函数，若当x€ (0, )时,f(x)= lg x,则满足f(x) > 0的x的取值范围是13.将函数y=2x的图象向左平移一个单位，得到图象C1，再将G向上平移一个单位得到图象C2,作出C2关于直线y=x对称的图象C3,贝V C3的解析式为.三、解答题17. 化简下列各式：(2)2|g 2+ |g 3(2) 1 1 .1 +2 lg 0.36 + 砂16 18. 已知f(x)为定义在［—1,1］上的奇函数，1 a 当x€ ［—1,0］时，函数解析式f(x)=才—(a€ R).(1) 写出f(x)在［0,1］上的解析式；(2) 求f(x)在［0,1］上的最大值.419. 已知x> 1 且x工3，f(x) = 1 + log x3,g(x) = 2log x2，试比较f(x)与g(x)的大小.x120. 已知函数f(x)= 2 —尹|.(1) 若f(x) = 2,求x 的值；(2) 若2t f(2t)+ mf(t) > 0 对于t€［1,2］恒成立，求实数m的取值范围.21 .已知函数f(x)= a x T(a>0 且a工1).(1) 若函数y = f(x)的图象经过P(3,4) 点，求a的值；(2) 若f(lg a) = 100,求a 的值；(3) 比较f lg 盘与f( —2.1)的大小，并写出比较过程.10x—10—x22•已矢口f(x)= 10X十10-X.(1) 求证f(x)是定义域内的增函数；(2) 求f(x)的值域.答案.选择题1 —5.BDAAC 6—10.ACCCC 11 —12.DC二.填空题13 . (1,4) 14. — ^,+m15 .(—1,0) U (1 ,+^ )16. y=log2(xT)-1( )AB. Iog x3v log y3C1 1D.(4)x<(4)y二、填空题13. 函数f(x)= a x「1P,则P点的坐标是__________ .14. 函数f(x) = Iog5(2x+ 1)的单调增区间是(1)[(0.064 5厂2.5]3-17. 解2lg 2 + lg 31 + 2lg 0.62+ 4|g 242lg 2 + lg 32lg 2 + lg 31 + lg2 + lg3 —lg 10 + lg 2=2lg 2 + lg 3 = 1—2lg 2 + lg 3 —.18. 解(1) •/ f(x)为定义在[—1,1]上的奇函数，且f(x)在x= 0处有意义，•-f(0) = 0,1 a即f(0) = 40—尹=1 —a= O..・.a = 1.4 4即当 1 v x v-时,f(x) v g(x);当x>4时，3 3f(x) > g(x).20. 解(1)当x v 0 时，f(x)= 0;当x>0 时，f(x) = 2x—*.1由条件可知2x— /= 2,即22x— 2 -2x—1 =0,解得2x= 1± 2.••• 2x> 0, • x= log2(1 + 2)./ 2t 1、f t 1(2)当t € [1,2]时,2 2 —尹 + m 2—2> 0,即m©—1) > —(24t—1).•/ 22—1> 0, • m> —(22t+ 1).•-1 € [1,2], • —(1 + 221) € [ —17 ,—5],故m的取值范围是[—5, + ).• lg a lg a—1= 2(或lg a —1= log a100).设x€ [0,1],则一x€ [ —1,0].21 .解(1) •••函数y = f(x)的图象经过又f( —x) = —f(x),—f(x)= 4x—2x.••• f(x) = 2x—4x.(2)当x€ [0,1] , f(x) = 2x—4x= 2x—(2x)2,•••设t= 2x(t> 0)，则f(t)=t —『.••• x€ [0,1] , • t€ [1,2] •当t= 1 时，取最大值，最大值为 1 — 1 = 0.19. 解f(x) —g(x) = 1 + Iog x3 —2log x2 = 1 +log x4= log x4x,4 3 3当 1 v x v §时，4X V 1, • log^x v 0; P(3,4),• a31= 4, 即卩a2= 4.又a>0 ,所以a = 2.(2)原式=1 + lg2 X 310+ lg 2--f(— x)=⑴原式竝蟲升5卜眾(2)由f(lg a) = 100 知，a lg a」100. • (lg a—1) lg a = 2.• lg a—lg a — 2 = 0,• lg a=— 1 或lg a= 2,1 • a=或a= 100.10⑶当a>1 时，fig 盘>f(— 2.1);当x>4时，4x> 1, 3•- log x4x>0. 因为，f lg =f(—2)=a 3,当0<a<1 时，f lg f( —2.1).—3.1f( —2.1) = a ,当a>1时，y= a x在(—^, + )上为增函数，•/ —3>— 3.1 , ••• a—3>a—3.1.即f g疵>f(—巾；当0<a<1时，y= a x在(—m，+ m)上为减函数，•/ —3>— 3.1 , • a—3<a—3.1,即f g盅<f(—巾-22. (1)证明因为f(x)的定义域为R,口10—X—10x且f( —x) = —x x =—f(x),10 x+ 10x所以f(x)为奇函数.10x—10—x 102x— 1 2 f(x)= 10x+ 10-x- 1o2x+ 1= 1 —102x+ 1. 令X2> X1，则2f(X2)—f(x1)= (1 —102x2+ 1 ) —(1 —2102X1 + 1)- 102x2—102xi—2 • 102x2 + 1 102xi+ 1 .因为y= 10x为R上的增函数，所以当X2> X1 时，102x2 —102x1 > 0.又因为102x1+ 1 > 0,102X2+ 1> 0.故当X2> X1 时,f(X2)—f(X1)> 0,即f(X2)> f(X1).所以f(x)是增函数.102x— 1 “⑵解令y= f(x).由y=岳TR，解得102x-严.1 —y因为102x> 0，所以一1 v y v 1.即f(x)的值域为(一1,1).。

高中数学必修一第二章一、单选题1．已知a>b>0,c>d，下列不等式中必成立的一个是（ ）A．a c>bdB．ad<bc C．a+c>b+d D．a―c>b―d2．已知x，y均为正实数，且1x+2+4y+3=12，则x+y的最小值为( )A．10B．11C．12D．133．若两个正实数x,y满足2x+1y=1,且x+2y>m2+2m恒成立，则实数m的取值范围是（ ）A．(―∞,―2)∪[4,+∞)B．(―∞,―4)∪[2,+∞)C．(―2,4)D．(―4,2)4．若x，y∈R+，且x+3y=5xy，则3x+4y的最小值是（ ）A．5B．245C．235D．1955．小明从甲地到乙地往返的时速分别为a和b（a＜b），其全程的平均时速为v，则（ ）A．a＜v＜ab B．v＝ab C．ab＜v＜a+b2D．v＝a+b26．已知a＞0，b＞0，若不等式m3a+b ―3a―1b≤0恒成立，则m的最大值为（ ）A．4B．16C．9D．37．已知x，y∈（―2，2），且xy＝1，则22―x2+44―y2的最小值是（ ）A．207B．127C．16+427D．16―4278．已知函数f(x)=2x|2x―a|，若0≤x≤1时f(x)≤1，则实数a的取值范围为（ ）A．[74，2]B．[53，2]C．[32，2]D．[32，53]二、多选题9．已知a>b>c>0，则（ ）A．a+c>b+c B．ac>bc C．aa+c>bb+cD．a x<b c10．已知a>0，b>0，且a+b=ab，则（ ）A．(a―1)(b―1)=1B．ab的最大值为4C．a+4b的最小值为9D．1a2+2b2的最小值为2311．已知a，b∈R∗，a+2b=1，则b2a +12b+12ab的值可能为（ ）A．6B．315C．132D．5212． 现有图形如图所示，C 为线段AB 上的点，且AC ＝a ，BC ＝b ，O 为AB 的中点，以AB 为直径作半圆.过点.C 作AB 的垂线交半圆于点D ，连结OD ，AD ，BD ，过点C 作OD 的垂线，垂足为E.则该图形可以完成的无字证明有（ ）A ．a +b 2≥ab (a >0,b >0)B ．a 2+b 2≥2ab (a >0,b >0)C ．a 2+b 22≥a +b2(a ≥0,b >0)D ．ab ≥21a+1b(a >0,b >0)三、填空题13．已知不等式|x ―1|+|x +2|≥5的解集为　　．14． 已知实数x ，y 满足―1≤x +y ≤4且2≤x ―y ≤3，则x +3y 的取值范围是　　.15．若关于x 的不等式x 2+mx ―2<0在区间[1，2]上有解，则实数m 的取值范围为　　.16．设正实数x ，y ，z 满足x 2―3xy +4y 2―z =0，则当xyZ 取得最大值时，2x+1y ―2z的最大值为 .四、解答题17．U =R ，非空集合 A ={x |x 2―5x +6<0} ，集合 B ={x |(x ―a )(x ―a 2―2)<0} ．（1）a =12时，求 (∁ U B )∩A ；（2）若 x ∈B 是 x ∈A 的必要条件，求实数 a 的取值范围．18．已知 p :|1―x ―13|≤2 ， q :x 2―2x +1―m 2≤0(m >0) ，若 ¬p 是 ¬q 的充分而不必要条件，求实数m 的取值范围.19.求解不等式x 2―a ≥|x ―1|―120.已知a ，b ，c 都为正实数，满足abc （a ＋b ＋c ）＝1（1）求S ＝（a ＋c ）（b ＋c ）的最小值（2）当S 取最小值时，求c 的最大值.21.某项研究表明；在考虑行车安全的情况下，某路段车流量F （单位时间内经过测量点的车辆数，单位；辆∕时）与车流速度v （假设车辆以相同速度v 行驶，单位米∕秒）、平均车长l （单位:米）的值有关，其公式为F =76000νv 2+18v +20l（1）如果不限定车型，l ＝6.05，则最大车流量为多少.（2）如果限定车型，l ＝5，则最大车流量比（1）中的最大车流量增加多少.22．已知a ，b ，c 为实数且a +2b +5c =10.（1）若a ，b ，c 均为正数，当2ab +5ac +10bc =10时，求a +b +c 的值；（2）证明：(2b +5c )2+(a +b +5c )2+(a +2b +4c )2≥4903.答案解析部分1．C已知a>b>0,c>d,由不等式的同向相加的性质得到a+c>b+d正确；当a=2,b=1,c=-1,d=-2时，a c<bd, ，a―c=b―d A，D不正确；c=2，d=1时，ad=bc,B不正确. 2．D解：因为x,y>0，且1x+2+4y+3=12，则x+y=(x+2)+(y+3)―5=2(1x+2+4y+3)[(x+2)+(y+3)]―5=2(5+y+3x+2+4(x+2)y+3)―5≥2(5+2y+3x+2⋅4(x+2)y+3―5=13，当且仅当y+3x+2=4(x+2)y+3，即x=4,y=9时等号成立，则x+y的最小值为13.3．D由基本不等式得x+2y=(x+2y)(2x +1y)=4yx+xy+4≥24yx⋅xy+4=8，当且仅当4yx=xy，由于x>0，y>0，即当x=2y时，等号成立，所以，x+2y的最小值为8，由题意可得m2+2m<8，即m2+2m―8<0，解得―4<m<2，因此，实数m的取值范围是(―4,2)，4．A从题设可得15y+35x=1，则3x+4y=15(3x+4y)(1y+3x)=15(3x y+12yx+13)≥15(12+13)=5，5．A6．B7．C8．C不等式f(x)≤1可化为|2x―a|≤2―x，有―2―x≤a―2x≤2―x，有2x―2―x≤a≤2x+2―x，当0≤x≤1时，2x+2―x≥22x×2―x=2（当且仅当x=0时取等号），2x―2―x≤2―12=32，故有32≤a≤2。

第二章综合测试一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.下列结论正确的是（ ）A .若ac bc ＞，则a b＞B .若22a b ＞，则a b ＞C .若a b ＞，0c ＜，则a c b c++＜D .a b＜2.若++，则a ，b 必须满足的条件是（ ）A .0a b ＞＞B .0a b ＜＜C .a b＞D .0a ≥，0b ≥，且a b≠3.已知关于x 的不等式2680kx kx k -++≥对任意x ÎR 恒成立，则k 的取值范围是（ ）A .01k ≤≤B .01k ＜≤C .0k ＜或1k ＞D .0k ≤或1k ≥4.已知“x k ＞”是“311x +”的充分不必要条件，则k 的取值范围是（ ）A .2k ≥B .1k ≥C .2k ＞D .1k -≤5.如果关于x 的不等式2x ax b +＜的解集是{}|13x x ＜＜，那么a b 等于（ ）A .81-B .81C .64-D .646.若a ，b ，c 为实数，且0a b ＜＜，则下列命题正确的是（ ）A .22ac bc ＜B .11a b＜C .baab＞D .22a ab b ＞＞7.关于x 的不等式210x a x a -++（）＜的解集中恰有3个整数，则a 的取值范围是（ ）A .45a ＜＜B .32a --＜＜或45a ＜＜C .45a ＜≤D .32a --≤＜或45a ＜≤8.若不等式210x ax ++≥对一切02x ＜＜恒成立，则实数a 的最小值是（ ）A .0B .2-C .52-D .3-9.已知全集=U R ，则下列能正确表示集合{}=012M ，，和{}2=|+2=0N x x x 关系的Venn 图是（ ）A BCD10.若函数1=22y x x x +-（＞）在=x a 处取最小值，则a 等于（ ）A .1+B .1或3C .3D .411.已知ABC △的三边长分别为a ，b ，c ，且满足3b c a +≤，则ca 的取值范围为（ ）A .1c a＞B .02c a＜C .13c a ＜＜D .03c a＜12.已知a b ＞，二次三项式220ax x b ++≥对一切实数x 恒成立，又0x $ÎR ，使202=0ax x b ++成立，则22a b a b+-的最小值为（ ）A .1B C .2D .二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中横线上）13.已经1a ＜，则11a+与1a -的大小关系为________.14.若不等式22210x ax -+≥对一切实数x 都成立，则实数a 的取值范围是________.15.已知三个不等式：①0ab ＞，②c da b--＜，③bc ad ＞.以其中两个作为条件，余下一个作为结论，则可以组成________个正确命题.16.若不等式2162a bx x b a++＜的对任意0a ＞，0b ＞恒成立，则实数x 的取值范围是________.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤）17.（本小题满分10分）已知集合{2=|31=0A x ax x ++，}x ÎR ，（1）若A 中只有一个元素，求实数a 的值；（2）若A 中至多有一个元素，求实数a 的取值范围.18.（本小题满分12分）解下列不等式.（1）2560x x --+＜；（2）20a x a x --()()＞.19.（本小题满分12分）已知集合23=|=12A y y x x ì-+íî，324x üýþ≤≤，{}2=|1B x x m +≥.p x A Î:，q x B Î:，并且p 是q 的充分条件，求实数m 的取值范围.20.（本小题满分12分）已知集合{}2=|30A x x x -≤，{=|23B x a x a +≤≤，}a ÎR .（1）当=1a 时，求A B I ；（2）若=A B A U ，求实数a 的取值范围.21.（本小题满分12分）设a 、b 为正实数，且11a b+.（1）求22a b +的最小值；（2）若234a b ab -（）≥（），求ab 的值.22.（本小题满分12分）已知函数=1y ax a -+（）.（1）求关于x 的不等式0y ＜的解集；（2）若当0x ＞时，2y x x a --≤恒成立，求a 的取值范围.第二章综合测试答案解析一、1.【答案】D【解析】当0c ＜时，A 选项不正确；当0a ＜时，B 选项不正确；两边同时加上一个数，不等号方向不改变，故C 选项错误.故选D .2.【答案】D【解析】2=()=a b +-+-（(.++Q a \，b 必须满足的条件是0a ≥，0b ≥，且a b ≠.故选D .3.【答案】A【解析】当=0k 时，不等式2680kx kx k -++≥化为80≥，恒成立，当0k ＜时，不等式2680kx kx k -++≥不能恒成立，当0k ＞时，要使不等式2680kx kx k -++≥对任意x ÎR 恒成立，需22=36480k k k D -+（）≤，解得01k ≤≤，故01k ＜≤.综上，k 的取值范围是01k ≤≤.故选A .4.【答案】A【解析】由311x +＜，得3101x -+＜，201x x -++＜，解得1x -＜或2x ＞.因为“x k ＞”是“311x +”的充分不必要条件，所以2k ≥.5.【答案】B【解析】不等式2x ax b +＜可化为20x ax b --＜，其解集是{}|13x x ＜＜，那么由根与系数的关系得13=13=a b +ìí-î´，，解得=4=3a b ìí-î，，所以4=3=81a b -（）.故选B .6.【答案】D【解析】选项A ，c Q 为实数，\取=0c ，此时22=ac bc ，故选项A 不成立；选项B ，11=b aa b ab--，0a b Q ＜＜，0b a \-＞，0ab ＞，0b a ab -\，即11a b＞，故选项B 不成立；选项C ，0a b Q ＜＜，\取=2a -，=1b -，则11==22b a --，2==21a b --，\此时b aa b＜，故选项C 不成立；选项D ，0a b Q ＜＜，2=0a ab a a b \--（）＞，2=0ab b b a b --（）＞，22a ab b \＞＞，故选项D 正确.7.【答案】D【解析】210x a x a -++Q （）＜，10x x a \--（）（）＜，当1a ＞时，1x a ＜＜，此时解集中的整数为2，3，4，故45a ＜≤.当1a ＜时，1a x ＜＜，此时解集中的整数为2-，1-，0，故32a --≤＜.故a 的取值范围是32a --≤＜或45a ＜≤.故选D .8.【答案】B【解析】不等式210x ax ++≥对一切02x ＜＜恒成立，1a x x\--≥在02x ＜＜时恒成立.11=2x x x x ---+--Q （）≤（当且仅当=1x 时取等号），2a \-≥，\实数a 的最小值是2-.故选B .9.【答案】A【解析】由题知{}=20N -，，则{}=0M N I .故选A .10.【答案】C【解析】2x Q ＞，20x \-＞.11==222=422y x x x x \+-+++--（）≥，当且仅当12=2x x --，即=3x 时等号成立.=3a \.11.【答案】B【解析】由已知及三角形三边关系得3a b c a a b c a c b +ìï+íï+î＜≤，＞，＞，即1311b ca abc a a c b a aì+ïïï+íïï+ïî＜≤，＞，＞，1311b c a ac b a a ì+ïï\íï--ïî＜≤，＜＜，两式相加得024c a ´＜.c a \的取值范围为02ca＜.12.【答案】D【解析】Q 二次三项式220ax x b ++≥对一切实数x 恒成立，0a \＞，且=440ab D -≤，1ab \≥.又0x $ÎR ，使2002=0ax x b ++成立，则=0D ，=1ab \，又a b ＞，0a b \-＞.22222==a b a b ab a b a b a b a b +-+\-+---（）（）当且仅当a b -时等号成立.22a b a b+\-的最小值为故选D .二、13.【答案】111a a-+【解析】由1a ＜，得11a -＜＜.10a \+＞，10a -＞.2111=11a a a +--.2011a -Q ＜≤，2111a \-，111a a\-+≥.14.【答案】a【解析】不等式22210x ax -+≥对一切实数x 都成立，则2=44210a D -´´≤，解得a ，\实数a 的取值范围是a .15.【答案】3【解析】若①②成立，则c dab ab a b--（）＜（），即bc ad --＜，bc ad \＞，即③成立；若①③成立，则bc ad ab ab ，即c d a b ＞，c d a b \--＜，即②成立；若②③成立，则由②得c d a b ＞，即0bc ad ab -，Q ③成立，0bc ad \-＞，0ab \＞，即①成立.故可组成3个正确命题.16.【答案】42x -＜＜【解析】不等式2162a b x x ba ++＜对任意0a ＞，0b ＞恒成立，等价于2162a bx x b a++m i n ＜（）.因为16a b b a +≥（当且仅当=4a b 时等号成立）.所以228x x +＜，解得42x -＜＜.三、17.【答案】（1）当=0a 时，31=0x +只有一解，满足题意；当0a ≠时，=94=0a D -，9=4a .所以满足题意的实数a 的值为0或94.（5分）（2）若A 中只有一个元素，则由（1）知实数a 的值为0或94.若=A Æ，则=940a D -＜，解得94a ＞.所以满足题意的实数a 的取值范围为=0a 或94a ≥.（10分）18.【答案】（1）2560x x --+Q ＜，2560x x \+-＞，160x x \-+()()＞，解得6x -＜或1x ＞，\不等式2560x x --+＜的解集是{|6x x -＜或}1x ＞.（4分）（2）当0a ＜时，=2y a x a x --()()的图象开口向下，与x 轴的交点的横坐标为1=x a ，2=2x ，且2a ＜，20a x a x \--()()＞的解集为{}|2x a x ＜＜.（6分）当=0a 时，2=0a x a x --()()，20a x a x \--()()＞无解.（8分）当0a ＞时，抛物线=2y a x a x --()()的图象开口向上，与x 轴的交点的横坐标为=x a ，=2x .当=2a 时，原不等式化为2220x -（）＞，解得2x ≠.当2a ＞时，解得2x ＜或x a ＞.当2a ＜时，解得x a ＜或2x ＞.（10分）综上，当0a ＜时，原不等式的解集是{}|2x a x ＜＜；当=0a 时，原不等式的解集是Æ；当02a ＜＜时，原不等式的解集是{|x x a ＜或}2x ＞；当=2a 时，原不等式的解集是{}|2x x ≠；当2a ＞时，原不等式的解集是{|2x x ＜或}x a ＞.（12分）19.【答案】23=12y x x -+，配方得237=416y x -+（）.因为324x ≤≤，所以min 7=16y ，max =2y .所以7216y ≤.所以7=|216A y y ìüíýîþ≤≤.（6分）由21x m +≥，得21x m -≥，所以{}2=|1B x x m -≥.（8分）因为p 是q 的充分条件，所以A B Í.所以27116m -≤，（10分）解得实数m 的取值范围是34m ≥或34m -≤.（12分）20.【答案】（1）由题意知{}=|03A x x ≤≤，{}=|24B x x ≤≤，则{}=|23A B x x I ≤≤.（3分）（2）因为=A B A U ，所以B A Í.①当=B Æ，即23a a +＞，3a ＞时，B A Í成立，符合题意.（8分）②当=B Æ，即23a a +≤，3a ≤时，由B A Í，有0233a a ìí+î≤，≤，解得=0a .综上，实数a 的取值范围为=0a 或3a ＞.（12分）21.【答案】（1）a Q 、b 为正实数，且11a b+.11a b \+=a b 时等号成立），即12ab ≥.（3分）2221122=a b ab +´Q ≥≥（当且仅当=a b 时等号成立），22a b \+的最小值为1.（6分）（2）11a b+Q，a b \+.234a b ab -Q （）≥（），2344a b ab ab \+-（）≥（），即2344ab ab -（）≥（），2210ab ab -+（）≤，210ab -（）≤，a Q 、b 为正实数，=1ab \.（12分）22.【答案】（1）当=0a 时，原不等式可化为10-＜，所以x ÎR .当0a ＜时，解得1a x a +＞.当0a ＞时，解得1a x a+＜.综上，当=0a 时，原不等式的解集为R ；当0a ＜时，原不等式的解集为1|a x x a +ìüíýîþ＞；当0a ＞时，原不等式的解集为1|a x x a +ìüíýîþ＜.（6分）（2）由21ax a x x a -+--（）≤，得21ax x x -+≤.因为0x ＞，所以211=1x x a x x x-++-≤，因为2y x x a --≤在0+¥（，）上恒成立，所以11a x x+-≤在0+¥（，）上恒成立.令1=1t x x+-，只需min a t ≤，因为0x ＞，所以1=11=1t x x +-≥，当且仅当=1x 时等式成立.所以a 的取值范围是1a ≤.（12分）。

加油！有志者事竟成答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！第二章综合测试一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.下列结论正确的是（ ） A .若ac bc ＞，则a b ＞B .若22a b ＞，则a b ＞C .若a b ＞，0c ＜，则a c b c ++＜D ，则a b ＜2.若++，则a ，b 必须满足的条件是（ ） A .0a b ＞＞ B .0a b ＜＜C .a b ＞D .0a ≥，0b ≥，且a b ≠3.已知关于x 的不等式2680kx kx k -++≥对任意x ∈R 恒成立，则k 的取值范围是（ ） A .01k ≤≤ B .01k ＜≤ C .0k ＜或1k ＞D .0k ≤或1k ≥4.已知“x k ＞”是“311x +＜”的充分不必要条件，则k 的取值范围是（ ） A .2k ≥B .1k ≥C .2k ＞D .1k -≤5.如果关于x 的不等式2x ax b +＜的解集是{}|13x x ＜＜，那么a b 等于（ ） A .81-B .81C .64-D .646.若a ，b ，c 为实数，且0a b ＜＜，则下列命题正确的是（ ） A .22ac bc ＜B .11a b＜C .b aab＞D .22a ab b ＞＞ 7.关于x 的不等式210x a x a -++（）＜的解集中恰有3个整数，则a 的取值范围是（ ）A .45a ＜＜B .32a --＜＜或45a ＜＜C .45a ＜≤D .32a --≤＜或45a ＜≤8.若不等式210x ax ++≥对一切02x ＜＜恒成立，则实数a 的最小值是（ ） A .0B .2-C .52-D .3-9.已知全集=U R ，则下列能正确表示集合{}=012M ，，和{}2=|+2=0N x x x 关系的Venn 图是（ ）A BCD10.若函数1=22y x x x +-（＞）在=x a 处取最小值，则a 等于（ ）A .1+B .1或3C .3D .411.已知ABC △的三边长分别为a ，b ，c ，且满足3b c a +≤，则ca 的取值范围为（ ） A .1c a＞B .02c a＜＜C .13c a ＜＜D .03c a＜＜12.已知a b ＞，二次三项式220ax x b ++≥对一切实数x 恒成立，又0x ∃∈R ，使202=0ax x b ++成立，则22a b a b+-的最小值为（ ）A .1BC .2D .二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中横线上）13.已经1a ＜，则11a+与1a -的大小关系为________. 14.若不等式22210x ax -+≥对一切实数x 都成立，则实数a 的取值范围是________.15.已知三个不等式：①0ab ＞，②c da b--＜，③bc ad ＞.以其中两个作为条件，余下一个作为结论，则可以组成________个正确命题. 16.若不等式2162a bx x b a++＜的对任意0a ＞，0b ＞恒成立，则实数x 的取值范围是________. 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤）17.（本小题满分10分）已知集合{2=|31=0A x ax x ++，}x ∈R ，（1）若A 中只有一个元素，求实数a 的值；（2）若A 中至多有一个元素，求实数a 的取值范围.18.（本小题满分12分）解下列不等式. （1）2560x x --+＜；（2）20a x a x --()()＞.19.（本小题满分12分）已知集合23=|=12A y y x x ⎧-+⎨⎩，324x ⎫⎬⎭≤≤，{}2=|1B x x m +≥.p x A ∈:，q x B ∈:，并且p 是q 的充分条件，求实数m 的取值范围.20.（本小题满分12分）已知集合{}2=|30A x x x -≤，{=|23B x a x a +≤≤，}a ∈R .（1）当=1a 时，求A B ；（2）若=A B A ，求实数a 的取值范围.21.（本小题满分12分）设a 、b 为正实数，且11a b+. （1）求22a b +的最小值；（2）若234a b ab -（）≥（），求ab 的值.22.（本小题满分12分）已知函数=1y ax a -+（）.（1）求关于x 的不等式0y ＜的解集；（2）若当0x ＞时，2y x x a --≤恒成立，求a 的取值范围.第二章综合测试答案解析一、 1.【答案】D【解析】当0c ＜时，A 选项不正确；当0a ＜时，B 选项不正确；两边同时加上一个数，不等号方向不改变，故C 选项错误.故选D . 2.【答案】D【解析】2=()=a b +-+-+（.+ ，a ∴，b 必须满足的条件是0a ≥，0b ≥，且a b ≠.故选D .3.【答案】A【解析】当=0k 时，不等式2680kx kx k -++≥化为80≥，恒成立，当0k ＜时，不等式2680kx kx k -++≥不能恒成立，当0k ＞时，要使不等式2680kx kx k -++≥对任意x ∈R 恒成立，需22=36480k k k ∆-+（）≤，解得01k ≤≤，故01k ＜≤.综上，k 的取值范围是01k ≤≤.故选A . 4.【答案】A【解析】由311x +＜，得3101x -+＜，201x x -++，解得1x -＜或2x ＞.因为“x k ＞”是“311x +”的充分不必要条件，所以2k ≥.5.【答案】B【解析】不等式2x ax b +＜可化为20x ax b --＜，其解集是{}|13x x ＜＜，那么由根与系数的关系得13=13=a b +⎧⎨-⎩⨯，，解得=4=3a b ⎧⎨-⎩，，所以4=3=81a b -（）.故选B . 6.【答案】D【解析】选项A ，c 为实数，∴取=0c ，此时22=ac bc ，故选项A 不成立；选项B ，11=b a a b ab--，0a b ＜＜，0b a ∴-＞，0ab ＞，0b a ab -∴，即11a b＞，故选项B 不成立；选项C ，0a b ＜＜，∴取=2a -，=1b -，则11==22b a --，2==21a b --，∴此时b aa b ，故选项C 不成立；选项D ，0a b ＜＜，2=0a ab a a b ∴--（）＞，2=0ab b b a b --（）＞，22a ab b ∴＞＞，故选项D 正确.7.【答案】D【解析】210x a x a -++ （）＜，10x x a ∴--（）（）＜，当1a ＞时，1x a ＜＜，此时解集中的整数为2，3，4，故45a ＜≤.当1a ＜时，1a x ＜＜，此时解集中的整数为2-，1-，0，故32a --≤＜.故a 的取值范围是32a --≤＜或45a ＜≤.故选D . 8.【答案】B【解析】不等式210x ax ++≥对一切02x ＜＜恒成立，1a x x∴--≥在02x ＜＜时恒成立.11=2x x x x ---+-- （（当且仅当=1x 时取等号），2a ∴-≥，∴实数a 的最小值是2-.故选B . 9.【答案】A【解析】由题知{}=20N -，，则{}=0M N .故选A . 10.【答案】C【解析】2x ＞，20x ∴-＞.11==222=422y x x x x ∴+-+++--（）≥，当且仅当12=2x x --，即=3x 时等号成立.=3a ∴. 11.【答案】B【解析】由已知及三角形三边关系得3a b c a a b c a c b +⎧⎪+⎨⎪+⎩＜≤，＞，＞，即1311b ca abc a a c b a a⎧+⎪⎪⎪+⎨⎪⎪+⎪⎩＜，＞＞1311b c a ac b a a ⎧+⎪⎪∴⎨⎪--⎪⎩＜≤，＜，两式相加得024c a ⨯＜＜.c a ∴的取值范围为02ca＜＜.12.【答案】D【解析】 二次三项式220ax x b ++≥对一切实数x 恒成立，0a ∴＞，且=440ab ∆-≤，1ab ∴≥.又0x ∃∈R ，使2002=0ax x b ++成立，则=0∆，=1ab ∴，又a b ＞，0a b ∴-＞.22222==a b a b ab a b a b a b a b +-+∴-+---（）（），当且仅当a b -时等号成立.22a b a b+∴-的最小值为D .二、 13.【答案】111a a-+ 【解析】由1a ＜，得11a -＜＜.10a ∴+＞，10a -＞.2111=11a a a +--.2011a - ＜≤，2111a∴-，111a a∴-+≥.14.【答案】a【解析】不等式22210x ax -+≥对一切实数x 都成立，则2=44210a ∆-⨯⨯≤，解得a ，∴实数a 的取值范围是a .15.【答案】3【解析】若①②成立，则cd ab ab a b --（（），即bc ad --＜，bc ad ∴＞，即③成立；若①③成立，则bc ad ab ab＞，即c d a b ＞，c d a b ∴--＜，即②成立；若②③成立，则由②得c d a b ＞，即0bc adab-＞， ③成立，0bc ad ∴-＞，0ab ∴＞，即①成立.故可组成3个正确命题.16.【答案】42x -＜＜ 【解析】不等式2162ab x x b a ++＜对任意0a ＞，0b ＞恒成立，等价于2162a bx x b a++min ＜（）.因为16a b b a +≥（当且仅当=4a b 时等号成立）.所以228x x +＜，解得42x -＜＜. 三、17.【答案】（1）当=0a 时，31=0x +只有一解，满足题意；当0a ≠时，=94=0a ∆-，9=4a . 所以满足题意的实数a 的值为0或94.（5分）（2）若A 中只有一个元素，则由（1）知实数a 的值为0或94. 若=A ∅，则=940a ∆-＜，解得94a ＞.所以满足题意的实数a 的取值范围为=0a 或94a ≥.（10分） 18.【答案】（1）2560x x --+ ＜，2560x x ∴+-＞，160x x ∴-+()()＞，解得6x -＜或1x ＞，∴不等式2560x x --+＜的解集是{|6x x -＜或}1x ＞.（4分）（2）当0a ＜时，=2y a x a x --()()的图象开口向下，与x 轴的交点的横坐标为1=x a ，2=2x ，且2a ＜，20a x a x ∴--()()＞的解集为{}|2x a x ＜＜.（6分）当=0a 时，2=0a x a x --()()，20a x a x ∴--()()＞无解.（8分）当0a ＞时，抛物线=2y a x a x --()()的图象开口向上，与x 轴的交点的横坐标为=x a ，=2x .当=2a 时，原不等式化为2220x -（）＞，解得2x ≠.当2a ＞时，解得2x ＜或x a ＞. 当2a ＜时，解得x a ＜或2x ＞.（10分）综上，当0a ＜时，原不等式的解集是{}|2x a x ＜＜； 当=0a 时，原不等式的解集是∅；当02a ＜＜时，原不等式的解集是{|x x a ＜或}2x ＞； 当=2a 时，原不等式的解集是{}|2x x ≠；当2a ＞时，原不等式的解集是{|2x x ＜或}x a ＞.（12分）19.【答案】23=12y x x -+， 配方得237=416y x -+（）. 因为324x ≤≤，所以min 7=16y ，max =2y .所以7216y ≤.所以7=|216A y y ⎧⎫⎨⎬⎩⎭≤≤.（6分） 由21x m +≥，得21x m -≥， 所以{}2=|1B x x m -≥.（8分） 因为p 是q 的充分条件， 所以A B ⊆. 所以27116m -≤，（10分） 解得实数m 的取值范围是34m ≥或34m -≤.（12分） 20.【答案】（1）由题意知{}=|03A x x ≤≤，{}=|24B x x ≤≤， 则{}=|23A B x x ≤≤.（3分） （2）因为=A B A ，所以B A ⊆.①当=B ∅，即23a a +＞，3a ＞时，B A ⊆成立，符合题意.（8分）②当=B ∅，即23a a +≤，3a ≤时， 由B A ⊆，有0233a a ⎧⎨+⎩≤，≤，解得=0a .综上，实数a 的取值范围为=0a 或3a ＞.（12分）21.【答案】（1）a 、b 为正实数，且11a b+.11a b ∴+（当且仅当=a b 时等号成立）， 即12ab ≥.（3分）2221122=a b ab +⨯ ≥≥（当且仅当=a b 时等号成立），22a b ∴+的最小值为1.（6分）（2）11a b+，a b ∴+.234a b ab - （）≥（）， 2344a b ab ab ∴+-（）≥（），即2344ab ab -（）≥（）， 2210ab ab -+（）≤， 210ab -（）≤，a 、b 为正实数，=1ab ∴.（12分）22.【答案】（1）当=0a 时，原不等式可化为10-＜，所以x ∈R .当0a ＜时，解得1a x a +＞. 当0a ＞时，解得1a x a+＜.综上，当=0a 时，原不等式的解集为R ； 当0a ＜时，原不等式的解集为1|a x x a +⎧⎫⎨⎬⎩⎭＞； 当0a ＞时，原不等式的解集为1|a x x a +⎧⎫⎨⎬⎩⎭＜.（6分） （2）由21ax a x x a -+--（）≤，得21ax x x -+≤.高中数学 必修第一册 6 / 6 因为0x ＞，所以211=1x x a x x x-++-≤， 因为2y x x a --≤在0+∞（，）上恒成立， 所以11a x x +-≤在0+∞（，）上恒成立. 令1=1t x x+-，只需min a t ≤， 因为0x ＞，所以1=11=1t x x +-≥，当且仅当=1x 时等式成立. 所以a 的取值范围是1a ≤.（12分）。

第二章综合测试一、单选题（每小题5分，共40分）， 1.函数()f x =） A .[]12−，B .(]12−，C .[)2+∞，D .[)1+∞，2.设函数()221121x x f x x x x ⎧−⎪=⎨+−⎪⎩，≤，，＞，则()12f f ⎫⎛⎪ ⎪⎝⎭的值为（ ） A .1− B .34C .1516D .43.已知()32f x x x =+，则()()f a f a +−=（ ） A .0B .1−C .1D .24.幂函数223a a y x −−=是偶函数，且在()0+∞，上单调递减，则整数a 的值是（ ） A .0或1B .1或2C .1D .25.函数()34f x ax bx =++（a b ，不为零），且()510f =，则()5f −等于（ ） A .10−B .2−C .6−D .146.已知函数22113f x x x x ⎫⎛+=++ ⎪⎝⎭，则()3f =（ ）A .8B .9C .10D .117.如果函数()2f x x bx c =++对于任意实数t 都有()()22f t f t +=−，那么（ ） A .()()()214f f f ＜＜ B .()()()124f f f ＜＜ C .()()()421f f f ＜＜D .()()()241f f f ＜＜8.定义在R 上的偶函数()f x 满足对任意的[)()12120x x x x ∈+∞≠，，，有()()21210f x f x x x −−＜，且()20f =，则不等式()0xf x ＜的解集是（ ）A .()22−，B .()()202−+∞，，C .()()8202−−，，D .()()22−∞−+∞，，二、多选题（每小题5分，共20分，全部选对得5分，选对但不全的得3分，有选错的得0分）9.定义运算()()a ab a b b a b ⎧⎪=⎨⎪⎩≥□＜，设函数()12x f x −=□，则下列命题正确的有（ ）A .()f x 的值域为[)1+∞，B .()f x 的值域为(]01，C .不等式()()12f x f x +＜成立的范围是()0−∞，D .不等式()()12f x f x +＜成立的范围是()0+∞，10.关于函数()f x = ）A .定义域、值域分别是[]13−，，[)0+∞，B .单调增区间是(]1−∞，C .定义域、值域分别是[]13−，，[]02，D .单调增区间是[]11−，11.函数()f x 是定义在R 上的奇函数，下列命题中是正确命题的是（ ） A .()00f =B .若()f x 在[)0+∞，上有最小值1−，则()f x 在(]0−∞，上有最大值1 C .若()f x 在[)1+∞，上为增函数，则()f x 在(]1−∞−，上为减函数 D .若0x ＞时，()22f x x x =−，则0x ＜时，()22f x x x =−−12.关于函数()1f x =，有下列结论，正确的结论是（ ）A .函数是偶函数B .函数在()1−∞−，）上递减 C .函数在()01，上递增D .函数在()33−，上的最大值为1 三、填空题（每小题5分，共20分）13.已知函数()()f x g x ，分别由表给出，则()()2g f =________.14.已知()f x 为R 上的减函数，则满足()11f f x ⎫⎛ ⎪⎝⎭＞的实数x 的取值范围为________.15.已知函数()f x 是奇函数，当()0x ∈−∞，时，()2f x x mx =+，若()23f =−，则m 的值为________.16.符号[]x 表示不超过x 的最大整数，如[][]3.143 1.62=−=−，，定义函数：()[]f x x x =−，则下列说法正确的是________. ①()0.80.2f −=；②当12x ≤＜时，()1f x x −；③函数()f x 的定义域为R ，值域为[)01，； ④函数()f x 是增函数，奇函数. 四、解答题（共70分）17.（10分）已知一次函数()f x 是R 上的增函数，()()()g x f x x m =+，且()()165f f x x =+. （1）求()f x 的解析式.（2）若()g x 在()1+∞，上单调递增，求实数m 的取值范围.18.（12分）已知()()212021021 2.f x x f x x x x x +−⎧⎪=+⎨⎪−⎩，＜＜，，≤＜，，≥ （1）若()4f a =，且0a ＞，求实数a 的值.（2）求32f ⎫⎛− ⎪⎝⎭的值.19.（12分）已知奇函数()q f x px r x =++（p q r ，，为常数），且满足()()5171224f f ==，. （1）求函数()f x 的解析式.（2）试判断函数()f x 在区间102⎛⎤⎥⎝⎦，上的单调性，并用函数单调性的定义进行证明.（3）当102x ⎛⎤∈ ⎥⎝⎦，时，()2f x m −≥恒成立，求实数m 的取值范围.20.（12分）大气中的温度随着高度的上升而降低，根据实测的结果，上升到12km 为止，温度的降低大体上与升高的距离成正比，在12km 以上温度一定，保持在55−℃.（1）当地球表面大气的温度是a ℃时，在km x 的上空为y ℃，求a x y 、、间的函数关系式.（2）问当地表的温度是29℃时，3km 上空的温度是多少?21.（12分）已知函数()f x 是定义在[]11−，上的奇函数，且()11f =，对任意[]110a b a b ∈−+≠，，，时有()()0f a f b a b++＞成立.（1）解不等式()1122f x f x ⎫⎛+− ⎪⎝⎭＜.（2）若()221f x m am −+≤对任意[]11a ∈−，恒成立，求实数m 的取值范围.22.（12分）已知函数()[](]2312324.x x f x x x ⎧−∈−⎪=⎨−∈⎪⎩，，，，，（1）画出()f x 的图象.（2）写出()f x 的单调区间，并指出单调性（不要求证明）.（3）若函数()y a f x =−有两个不同的零点，求实数a 的取值范围.第二章综合测试 答案解析一、 1.【答案】B 【解析】选B .由10420x x +⎧⎨−⎩＞，≥，得12x −＜≤.2.【答案】C【解析】选C .因为()222224f =+−=，所以()211115124416f f f ⎫⎛⎫⎫⎛⎛==−=⎪ ⎪ ⎪ ⎪⎝⎝⎭⎭⎝⎭. 3.【答案】A【解析】选A .()32f x x x =+是R 上的奇函数，故()()f a f a −=−，所以()()0f a f a +−=. 4.【答案】C【解析】选C .因为幂函数223aa y x −−=是偶函数，且在()0+∞，上单调递减， 所以2223023a a a z a a ⎧−−⎪∈⎨⎪−−⎩＜，，是偶数.解得1a =. 5.【答案】B【解析】选B .因为()51255410f a b =++=， 所以12556a b +=，所以()()51255412554642f a b a b −=−−+=−++=−+=−. 6.【答案】C【解析】选C .因为22211131f x x x x x x ⎫⎫⎛⎛+=++=++ ⎪ ⎪⎝⎝⎭⎭，所以()21f x x =+（2x −≤或2x ≥），所以()233110f =+=. 7.【答案】A【解析】选A .由()()22f t f t +=−，可知抛物线的对称轴是直线2x =，再由二次函数的单调性，可得()()()214f f f ＜＜.8.【答案】B 【解析】选B .因为()()21210f x f x x x −−＜对任意的[)()12120x x x x ∈+∞≠，，恒成立，所以()f x 在[)0+∞，上单调递减，又()20f =， 所以当2x ＞时，()0f x ＜；当02x ≤＜时，()0f x ＞， 又()f x 是偶函数，所以当2x −＜时，()0f x ＜； 当20x −＜＜时，()0f x ＞，所以()0xf x ＜的解集为()()202−+∞，，. 二、9.【答案】AC【解析】选AC .根据题意知()10210xx f x x ⎧⎫⎛⎪ ⎪=⎨⎝⎭⎪⎩，≤，，＞， ()f x 的图象为所以()f x 的值域为[)1+∞，，A 对； 因为()()12f x f x +＜，所以1210x x x +⎧⎨+⎩＞≤，或2010x x ⎧⎨+⎩＜＞，所以11x x ⎧⎨−⎩＜≤，或01x x ⎧⎨−⎩＜＞，所以1x −≤或10x −＜＜， 所以0x ＜，C 对. 10.【答案】CD【解析】选CD .由2230x x −++≥可得，2230x x −−≤，解可得，13x −≤≤，即函数的定义域为[]13−，，由二次函数的性质可知，()[]22231404y x x x =−++=−−+∈，，所以函数的值域为[]02，，结合二次函数的性质可知，函数在[]11−，上单调递增，在[]13，上单调递减. 11.【答案】ABD【解析】选ABD .()f x 为R 上的奇函数，则()00f =，A 正确；其图象关于原点对称，且在对称区间上具有相同的单调性，最值相反且互为相反数，所以B 正确，C 不正确；对于D ，0x ＜时，()()()22022x f x x x x x −−=−−−=+＞，，又()()f x f x −=−，所以()22f x x x =−−，即D 正确.12.【答案】ABD【解析】选ABD .函数满足()()f x f x −=，是偶函数；作出函数图象，可知在()1−∞−，，()01，上递减， ()10−，，()1+∞，上递增， 当()33x ∈−，时，()()max 01f x f ==.三、13.【答案】1【解析】由题表可得()()2331f g ==，， 故()()21g f =.14.【答案】()()01−∞+∞，，【解析】因为()f x 在R 上是减函数， 所以11x＜，解得1x ＞或0x ＜. 15.【答案】12【解析】因为()f x 是奇函数， 所以()()223f f −=−=， 所以()2223m −−=，解得12m =. 16.【答案】①②③【解析】()[]f x x x =−，则()()0.80.810.2f −=−−−=，①正确， 当12x ≤＜时，()[]1f x x x x =−=−，②正确，函数()f x 的定义域为R ，值域为[)01，，③正确， 当01x ≤＜时，()[]f x x x x =−=； 当12x ≤＜时，()1f x x =−， 当0.5x =时，()0.50.5f =； 当 1.5x =时，()1.50.5f =，则()()0.5 1.5f f =，即有()f x 不为增函数，由()()1.50.5 1.50.5f f −==，，可得()()1.5 1.5f f −=，即有()f x 不为奇函数，④错误. 四、17.【答案】（1）由题意设()()0f x ax b a =+＞.从而()()()2165f f x a ax b b a x ab b x =++=++=+，所以21655a ab ⎧=⎨+=⎩，，解得41a b =⎧⎨=⎩，或453a b =−⎧⎪⎨=−⎪⎩，（不合题意，舍去）. 所以()f x 的解析式为()41f x x =+.（2）()()()()()()()414241g x f x x m x x m x m x m g x =+=++=+++，图象的对称轴为直线418m x +=−. 若()g x 在()1+∞，上单调递增，则4118m +−≤，解得94m −≥，所以实数m 的取值范围为94⎫⎡−+∞⎪⎢⎣⎭，. 18.【答案】（1）若02a ＜＜，则()214f a a =+=， 解得32a =，满足02a ＜＜； 若2a ≥，则()214f a a =−=，解得a =或a =， 所以32a =或a =.（2）由题意，3311222f f f ⎫⎫⎫⎛⎛⎛−=−+=− ⎪ ⎪ ⎪⎝⎝⎝⎭⎭⎭1111212222f f ⎫⎫⎛⎛=−+==⨯+= ⎪ ⎪⎝⎝⎭⎭.19.【答案】（1）因为()f x 为奇函数，所以()()f x f x −=−，所以0r =.又()()5121724f f ⎧=⎪⎪⎨⎪=⎪⎩，即52172.24p q q p ⎧+=⎪⎪⎨⎪+=⎪⎩，解得212p q =⎧⎪⎨=⎪⎩，，所以()122f x x x =+. （2）()122f x x x =+在区间102⎛⎤⎥⎝⎦，上单调递减. 证明如下：设任意的两个实数12x x ，，且满足12102x x ＜＜≤，则()()()12121211222f x f x x x x x −=−+− ()()()()21211212121214222x x x x x x x x x x x x −−−=−+=.因为12102x x ＜＜≤，所以2112121001404x x x x x x −−＞，＜＜，＞， 所以()()120f x f x −＞， 所以()122f x x x =+在区间102⎛⎤⎥⎝⎦，上单调递减. （3）由（2）知()122f x x x =+在区间102⎛⎤⎥⎝⎦，上的最小值是122f ⎫⎛= ⎪⎝⎭. 要使当102x ⎛⎤∈ ⎥⎝⎦，时，()2f x m −≥恒成立，只需当102x ⎛⎤∈ ⎥⎝⎦，时，()min 2f x m −≥，即22m −≥，解得0m ≥即实数m 的取值范围为[)0+∞，.20.【答案】（1）由题意知，可设()0120y a kx x k −=≤≤，＜，即y a kx =+.依题意，当12x =时，55y =−， 所以5512a k −=+，解得5512a k +=−. 所以当012x ≤≤时，()()5501212x y a a x =−+≤≤. 又当12x ＞时，55y =−.所以所求的函数关系式为 ()55012125512.x a a x y x ⎧−+⎪=⎨⎪−⎩，≤≤，，＞ （2）当293a x ==，时，()3295529812y =−+=， 即3km 上空的温度为8℃. 21.【答案】（1）任取[]121211x x x x ∈−，，，＜，()()()()()()()()1212121212f x f x f x f x f x f x x x x x +−−=+−=−+−由已知得()()()12120f x f x x x +−+−＞， 所以()()120f x f x −＜，所以()f x 在[]11−，上单调递增， 原不等式等价于112211121121x x x x ⎧+−⎪⎪⎪−+⎨⎪−−⎪⎪⎩＜，≤≤≤≤， 所以106x ≤＜，原不等式的解集为106⎫⎡⎪⎢⎣⎭，. （2）由（1）知()()11f x f =≤，即2211m am −+≥，即220m am −≥，对[]11a ∈−，恒成立.设()22g a ma m =−+，若0m =，显然成立；若0m ≠，则()()1010g g −⎧⎪⎨⎪⎩≥≥，即2m −≤或2m ≥，故2m −≤或2m ≥或0m =.22.【答案】（1）由分段函数的画法可得()f x 的图象.（2）单调区间：[]10−，，[]02，，[]24，，()f x 在[]10−，，[]24，上递增，在[]02，上递减. （3）函数()y a f x =−有两个不同的零点， 即为()f x a =有两个实根，由图象可得，当11a −＜≤或23a ≤＜时，()y f x =与y a =有两个交点，则a 的范围是(][)1123−，，.。

必修一第二章姓名：___________班级：___________考号：___________一、单选题1．已知13log 4a =，2log 3b =，0.32c -=，则a ，b ，c 的大小关系是（ ）A ．a b c >>B ．b a c >>C ．c a b >>D ．b c a >>2．已知函数()112x f x b -⎛⎫=+ ⎪⎝⎭，且函数图像不经过第一象限，则b 的取值范围是（ ） A ．(),1-∞-B ．(],1-∞-C ．(],2-∞-D ．(),2-∞-3．下列各式正确的是（ ）A 3=-B a =C ．32=-D 2=40)a >可化为（ ）A ．25aB ．52aC ．25a-D ．－52a5．函数2x y －＝ 的单调递增区间是( ) A ．(－∞，＋∞) B ．(－∞，0] C ．[0，＋∞)D ．(0，＋∞)6．已知函数()lg 030x x x f x x >⎧=⎨≤⎩，则1100f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦（ ） A ．-2B ．9C ．19D ．lg 27．已知函数()f x 为定义在R 上的奇函数，且当0x ≥时，()()31f x log x a =++，则()8f -等于（ ） A ．3a --B ．3a +C ．2-D ．28．函数x y a =与log (0,1)a y x a a =->≠且在同一坐标系中的图像只可能是（ ）A ．B ．C ．D ．9．若函数()y f x =是函数3x y =的反函数，则12f ⎛⎫⎪⎝⎭的值为（ ） A ．2log 3-B ．3log 2-C ．19D10．已知(32)4,1()log ,1a a x a x f x x x -+<⎧=⎨≥⎩, 对任意1212,(,),x x x x ∈-∞+∞≠,都有1212()()0f x f x x x -<-，那么实数a 的取值范围是 （ ）A ．()0,1B ．2(0,)3C ．1173⎡⎫⎪⎢⎣⎭, D ．22,73⎡⎫⎪⎢⎣⎭11．函数3()log (1)f x x =+的定义域为（ ） A ．[1,1]-B ．[1,1)-C ．(]1,1-D ．(1,1)-12．当1a >时，x y a -=的图象与log ay x =的图象是（ ）A ．B ．C ．D ．二、填空题13．函数231(0x y a a -=⋅+>且1)a ≠的图象必经过点______． 14．已知log 2,log 3a a m n ==，则2m n a -=__________．15．函数y =log a (x −2)+3(a >0且a ≠1)恒过定点为 _________16．函数()212log 32y x x =-+的单调递增区间为__________． 三、解答题 17．（1（2）已知13x x -+=，求22x x -+的值.18．计算：（1）2lg 2lg3111lg 0.36lg823+++；（2）19．（1）已知53a =，54b =，用a ，b 表示25log 36． （2）求值)7112log 422116log 744π⎛⎫-++ ⎪⎝⎭．20．（121032128log 16()25e π-++-++； （2）若3log 14a >（0a >且1a ≠），求a 的取值范围.21．已知幂函数()()2157m f x m m x-=-+为偶函数.（1）求()f x 的解析式；（2）若()()3g x f x ax =--在[]1,3上不是单调函数，求实数a 的取值范围.22．已知幂函数()f x 的图象经过点13,3⎛⎫⎪⎝⎭．（1）求函数()f x 的解析式；（2）设函数()()()2g x x f x =-⋅，试判断函数()g x 在区间1,12⎡⎤⎢⎥⎣⎦上的单调性，并求函数()g x 在区间1,12⎡⎤⎢⎥⎣⎦上的值域．参考答案1．D 【解析】 【分析】先由对数函数，以及指数函数的性质，确定a ，b ，c 的范围，进而可得出结果. 【详解】 因为1133log 4log 10a =<=，22log 321log b =>=，0.300221c -<=<=， 所以b c a >>. 故选：D. 【点睛】本题主要考查比较指数幂，以及对数的大小，熟记对数函数以及指数函数的性质即可，属于基础题型. 2．C 【解析】 【分析】利用指数函数的图像即可求解。

新版高一数学必修第一册第二章全部配套练习题（含答案和解析）2.1 等式性质与不等式性质基 础 练巩固新知 夯实基础1．若1a <1b <0，则下列结论中不正确的是( )A ．a 2<b 2B ．ab <b 2C ．a ＋b <0D ．|a |＋|b |>|a ＋b |2．已知a >b >0，则下列不等式一定成立的是( ) A ．a ＋1b >b ＋1aB ．a ＋1a ≥b ＋1bC ．b a >b ＋1a ＋1D ．b －1b >a －1a3．下列说法正确的是( )A ．若a >b ，c >d ，则ac >bdB ．若1a >1b，则a <bC ．若b >c ，则|a |b ≥|a |cD ．若a >b ，c >d ，则a －c >b －d 4．若y 1＝3x 2－x ＋1，y 2＝2x 2＋x －1，则y 1与y 2的大小关系是( ) A ．y 1<y 2 B ．y 1＝y 2C ．y 1>y 2D ．随x 值变化而变化 5．一辆汽车原来每天行驶x km ，如果这辆汽车每天行驶的路程比原来多19 km ，那么在8天内它的行程就超过2 200 km ，写成不等式为________；如果它每天行驶的路程比原来少12 km ，那么它原来行驶8天的路程就得花9天多的时间，用不等式表示为________．6．已知三个不等式①ab >0；①c a >db ；①bc >ad .若以其中的两个作为条件，余下的一个作为结论，则可以组成________个正确命题．7．若x ①R ，则x 1＋x2与12的大小关系为________． 8．已知1<α<3，－4< β <2，若z ＝12α－β，则z 的取值范围是________．9.已知a >b ，1a <1b ，求证：ab >0.10．已知－2<a ≤3，1≤b <2，试求下列代数式的取值范围．(1)|a |； (2)a ＋b ； (3)a －b ； (4)2a －3b .能 力 练综合应用 核心素养11．设a >b >c ，且a ＋b ＋c ＝0，则下列不等式恒成立的是( ) A ．ab >bc B ．ac >bc C ．ab >acD ．a |b |>c |b |12．若abcd ＜0，且a ＞0，b ＞c ，d ＜0，则( ) A ．b ＜0，c ＜0 B ．b ＞0，c ＞0 C ．b ＞0，c ＜0D ．0＜c ＜b 或c ＜b ＜013．实数a ，b ，c ，d 满足下列三个条件：①d >c ；①a ＋b ＝c ＋d ；①a ＋d <b ＋c .则将a ，b ，c ，d 按照从小到大的次序排列为________． 14．已知|a |<1，则11＋a 与1－a 的大小关系为________．15．已知a ，b ①R ，a ＋b >0，试比较a 3＋b 3与ab 2＋a 2b 的大小．16．已知0<a <b 且a ＋b ＝1，试比较： (1)a 2＋b 2与b 的大小； (2)2ab 与12的大小．17．已知1≤a －b ≤2,2≤a ＋b ≤4，求4a －2b 的取值范围．18．建筑设计规定，民用住宅的窗户面积必须小于地板面积．但按采光标准，窗户面积与地板面积的比值应不小于10%，且这个比值越大，住宅的采光条件就越好，试问：同时增加相等的窗户面积和地板面积，住宅的采光条件是变好了，还是变坏了？请说明理由．【参考答案】1. D 解析： ①1a <1b <0，①b <a <0，①b 2>a 2，ab <b 2，a ＋b <0，①A 、B 、C 均正确，①b <a <0，①|a |＋|b |＝|a ＋b |，故D 错误．2. A 解析：因为a >b >0，所以1b >1a >0，所以a ＋1b >b ＋1a，故选A.3. C 解析 A 项：a ，b ，c ，d 的符号不确定，故无法判断；B 项：不知道ab 的符号，无法确定a ，b 的大小；C 项：|a |≥0，所以|a |b ≥|a |c 成立；D 项：同向不等式不能相减．4. C 解析y 1－y 2＝(3x 2－x ＋1)－(2x 2＋x －1)＝x 2－2x ＋2＝(x －1)2＋1>0， 所以y 1>y 2.故选C.5. 8(x ＋19)>2 200 8x >9(x －12) 解析：①原来每天行驶x km ，现在每天行驶(x ＋19)km.则不等关系“在8天内的行程超过2 200 km”，写成不等式为8(x ＋19)>2 200.①若每天行驶(x －12)km ，则不等关系“原来行驶8天的路程现在花9天多时间”， 写成不等式为8x >9(x －12)． 6. 3 解析：①①①①，①①①①.(证明略)由①得bc －ad ab >0，又由①得bc －ad >0.所以ab >0①①.所以可以组成3个正确命题．7. x 1＋x 2≤12 解析：①x 1＋x 2－12＝2x －1－x 22(1＋x 2)＝－(x －1)22(1＋x 2)≤0，①x 1＋x 2≤12. 8. ⎩⎨⎧⎭⎬⎫z ⎪⎪－32<z <112 解析：①1<α<3，①12<12α<32，又－4<β<2，①－2<－β<4.①－32<12α－β<112，即－32<z <112. 9.证明：①1a <1b ，①1a －1b <0，即b －a ab<0，而a >b ，①b －a <0，①ab >0. 10. 解：(1)|a |①[0，3]．(2)－1<a ＋b <5.(3)依题意得－2<a ≤3，－2<－b ≤－1，相加得－4<a －b ≤2；(4)由－2<a ≤3得－4<2a ≤6，①由1≤b <2得－6<－3b ≤－3，①由①＋①得，－10<2a －3b ≤3. 11. C 解析：选C.因为a >b >c ，且a ＋b ＋c ＝0，所以a >0，c <0，b 可正、可负、可为零． 由b >c ，a >0知，ab >ac .12. D 解析： 由a ＞0，d ＜0，且abcd ＜0，知bc ＞0，又①b ＞c ，①0＜c ＜b 或c ＜b ＜0. 13. a <c <d <b 解析：由①得a ＝c ＋d －b 代入①得c ＋d －b ＋d <b ＋c ，①c <d <b .由①得b ＝c ＋d －a 代入①得a ＋d <c ＋d －a ＋c ，①a <c .①a <c <d <b . 14.11＋a≥1－a 解析：由|a |<1，得－1<a <1. ①1＋a >0,1－a >0.即11＋a 1－a ＝11－a 2①0<1－a 2≤1，①11－a 2≥1，①11＋a≥1－a . 15.解：因为a ＋b >0，(a －b )2≥0，所以a 3＋b 3－ab 2－a 2b ＝a 3－a 2b ＋b 3－ab 2＝a 2(a －b )＋b 2(b －a )＝(a －b )(a 2－b 2)＝(a －b )(a －b )(a ＋b )＝(a －b )2(a ＋b )≥0，所以a 3＋b 3≥ab 2＋a 2b .16.解：(1)因为0<a <b 且a ＋b ＝1，所以0<a <12<b ，则a 2＋b 2－b ＝a 2＋b (b －1)＝a 2－ab ＝a (a －b )<0，所以a 2＋b 2<b .(2)因为2ab －12＝2a (1－a )－12＝－2a 2＋2a －12＝－2⎝⎛⎭⎫a 2－a ＋14＝－2⎝⎛⎭⎫a －122<0，所以2ab <12.17.解：令4a －2b ＝m (a －b )＋n (a ＋b )，①⎩⎪⎨⎪⎧ m ＋n ＝4，－m ＋n ＝－2，解得⎩⎪⎨⎪⎧m ＝3，n ＝1.又①1≤a －b ≤2，①3≤3(a －b )≤6，又①2≤a ＋b ≤4，①5≤3(a －b )＋(a ＋b )≤10，即5≤4a －2b ≤10. 故4a －2b 的取值范围为5≤4a －2b ≤10.18.解：设住宅窗户面积、地板面积分别为a ，b ，同时增加的面积为m ，根据问题的要求a <b ，且ab ≥10%.由于a ＋mb ＋m －a b ＝m (b －a )b (b ＋m )>0，于是a ＋m b ＋m >a b .又a b ≥10%，因此a ＋m b ＋m >ab≥10%.所以同时增加相等的窗户面积和地板面积后，住宅的采光条件变好了．2.2 第1课时 基本不等式的证明基 础 练巩固新知 夯实基础1．已知a ，b ①R ，且ab >0，则下列结论恒成立的是( )A ．a 2＋b 2>2abB ．a ＋b ≥2ab C.1a ＋1b >2ab D.b a ＋a b ≥2 2．不等式a 2＋1≥2a 中等号成立的条件是( )A ．a ＝±1B ．a ＝1C ．a ＝－1D ．a ＝03．对x ①R 且x ≠0都成立的不等式是( )A ．x ＋1x ≥2B ．x ＋1x ≤－2C.|x |x 2＋1≥12D.⎪⎪⎪⎪x ＋1x ≥2 4．已知x >0，y >0，x ≠y ，则下列四个式子中值最小的是( )A.1x ＋yB.14⎝⎛⎭⎫1x ＋1yC. 12(x 2＋y 2)D.12xy5．给出下列不等式：①x ＋1x ≥2； ①⎪⎪⎪⎪x ＋1x ≥2； ①x 2＋y 2xy ≥2； ①x 2＋y 22>xy ； ①|x ＋y |2≥|xy |.其中正确的是________(写出序号即可)．6．若a >0，b >0，a ＋b ＝2，则下列不等式对一切满足条件的a ，b 恒成立的是________(填序号)．①ab ≤1； ①a ＋b ≤2； ①a 2＋b 2≥2； ①a 3＋b 3≥3； ①1a ＋1b≥2.7．设a ，b ，c 都是正数，求证：bc a ＋ac b ＋abc≥a ＋b ＋c .能 力 练综合应用 核心素养8．若0<a <b ，a ＋b ＝1，则a ，12，2ab 中最大的数为( )A ．aB ．2ab C.12D ．无法确定9．已知a >0，b >0，则a ＋b2，ab ，a 2＋b 22，2aba ＋b中最小的是( ) A.a ＋b 2B.abC.a 2＋b 22D.2aba ＋b10．设a >0，b >0，则下列不等式中不一定成立的是( )A ．a ＋b ＋1ab≥22 B.2ab a ＋b ≥abC.a 2＋b 2ab ≥a ＋b D ．(a ＋b )⎝⎛⎭⎫1a ＋1b ≥4 11．已知a ，b ①(0，＋∞)，且a ＋b ＝1，则下列各式恒成立的是( )A.1ab≥8 B.1a ＋1b≥4C.ab ≥12D.1a 2＋b2≤12 12．若a ＜1，则a ＋1a －1与－1的大小关系是________．13．给出下列结论：①若a >0，则a 2＋1>a .①若a >0，b >0，则⎝⎛⎭⎫1a ＋a ⎝⎛⎭⎫b ＋1b ≥4. ①若a >0，b >0，则(a ＋b )⎝⎛⎭⎫1a ＋1b ≥4. ①若a ①R 且a ≠0，则9a ＋a ≥6.其中恒成立的是________．14．已知x ＞0，y ＞0，z ＞0.求证：⎝⎛⎭⎫y x ＋z x ⎝⎛⎭⎫x y ＋z y ⎝⎛⎭⎫x z ＋y z ≥8.15．已知a >0，b >0，a ＋b ＝1，求证⎝⎛⎭⎫1＋1a ⎝⎛⎭⎫1＋1b ≥9.【参考答案】1. D 解析：选D.对于A ，当a ＝b 时，a 2＋b 2＝2ab ，所以A 错误；对于B ，C ，虽然ab >0，只能说明a ，b 同号，当a ，b 都小于0时，B ，C 错误；对于D ，因为ab >0，所以b a >0，a b >0，所以b a ＋ab ≥2b a ·a b ，即b a ＋a b≥2成立．2. B [解析] a 2＋1－2a ＝(a －1)2≥0，①a ＝1时，等号成立．3. D [解析] 因为x ①R 且x ≠0，所以当x >0时，x ＋1x ≥2；当x <0时，－x >0，所以x ＋1x ＝－⎝⎛⎭⎫－x ＋1－x ≤－2，所以A 、B 都错误；又因为x 2＋1≥2|x |，所以|x |x 2＋1≤12，所以C 错误，故选D. 4. C [解析] 解法一：①x ＋y >2xy ，①1x ＋y <12xy，排除D ；①14⎝⎛⎭⎫1x ＋1y ＝x ＋y 4xy ＝14xy x ＋y >1(x ＋y )2x ＋y ＝1x ＋y ，①排除B ；①(x ＋y )2＝x 2＋y 2＋2xy <2(x 2＋y 2)，①1x ＋y>12(x 2＋y 2)，排除A.解法二：取x ＝1，y ＝2.则1x ＋y ＝13；14⎝⎛⎭⎫1x ＋1y ＝38；12(x 2＋y 2)＝110；12xy ＝122＝18.其中110最小． 5. ① 解析：当x >0时，x ＋1x ≥2；当x <0时，x ＋1x≤－2，①不正确；因为x 与1x 同号，所以⎪⎪⎪⎪x ＋1x ＝|x |＋1|x |≥2，①正确； 当x ，y 异号时，①不正确； 当x ＝y 时，x 2＋y 22＝xy ，①不正确；当x ＝1，y ＝－1时，①不正确．6. ①①① [解析] 令a ＝b ＝1，排除①①；由2＝a ＋b ≥2ab ①ab ≤1，①正确；a 2＋b 2＝(a ＋b )2－2ab ＝4－2ab ≥2，①正确；1a ＋1b ＝a ＋b ab ＝2ab≥2，①正确．7.[证明] 因为a ，b ，c 都是正数，所以bc a ，ac b ，ab c 也都是正数．所以bc a ＋ac b ≥2c ，ac b ＋ab c ≥2a ，bc a ＋abc≥2b ，三式相加得2⎝⎛⎭⎫bc a ＋ac b ＋ab c ≥2(a ＋b ＋c )，即bc a ＋ac b ＋abc ≥a ＋b ＋c ，当且仅当a ＝b ＝c 时取等号． 8. C 解析：选C.因为0<a <b ，a ＋b ＝1，所以a <12，因为ab <⎝⎛⎭⎫a ＋b 22＝14，所以2ab <12，则a ，12，2ab 中最大的数为12，故选C.9. D [解析] 因为a >0，b >0，所以2ab a ＋b ≤2ab2ab ＝ab ，a ＋b 2≥ab ，a 2＋b 22＝2(a 2＋b 2)4≥(a ＋b )24＝a ＋b2(当且仅当a ＝b >0时，等号成立)．所以a ＋b2，ab ，a 2＋b 22，2ab a ＋b 中最小的是2aba ＋b，故选D. 10. B 解析：选B.因为a >0，b >0，所以a ＋b ＋1ab ≥2ab ＋1ab ≥22，当且仅当a ＝b 且2ab ＝1ab即a ＝b ＝22时取等号，故A 一定成立．因为a ＋b ≥2ab >0，所以2ab a ＋b ≤2ab2ab ＝ab ，当且仅当a ＝b 时取等号，所以2ab a ＋b ≥ab 不一定成立，故B 不成立．因为2ab a ＋b ≤2ab 2ab＝ab ，当且仅当a ＝b 时取等号，所以a 2＋b 2a ＋b ＝（a ＋b ）2－2ab a ＋b ＝a ＋b －2ab a ＋b ≥2ab －ab ，当且仅当a ＝b 时取等号，所以a 2＋b 2a ＋b ≥ab ，所以a 2＋b 2ab≥a ＋b ，故C 一定成立．因为(a ＋b )⎝⎛⎭⎫1a ＋1b ＝2＋b a ＋ab≥4，当且仅当a ＝b 时取等号，故D 一定成立，故选B. 11. B [解析] ①当a ，b ①(0，＋∞)时，a ＋b ≥2ab ，又a ＋b ＝1，①2ab ≤1，即ab ≤12.①ab ≤14.①1ab ≥4.故选项A 不正确，选项C 也不正确．对于选项D ，①a 2＋b 2＝(a ＋b )2－2ab ＝1－2ab ，当a ，b ①(0，＋∞)时，由ab ≤14可得a 2＋b 2＝1－2ab ≥12.所以1a 2＋b 2≤2，故选项D 不正确．对于选项B ，①a >0，b >0，a ＋b ＝1，①1a ＋1b ＝⎝⎛⎭⎫1a ＋1b (a ＋b )＝1＋b a ＋ab＋1≥4，当且仅当a ＝b 时，等号成立．故选B.12. a ＋1a －1≤－1 解析:因为a ＜1，即1－a >0,所以－⎝⎛⎭⎫a －1＋1a －1＝(1－a )＋11－a≥2（1－a ）·11－a＝2.即a ＋1a －1≤－1.13.①①① [解析] 因为(a 2＋1)－a ＝⎝⎛⎭⎫a －122＋34>0，所以a 2＋1>a ，故①恒成立． 因为a >0，所以a ＋1a ≥2，因为b >0，所以b ＋1b ≥2，所以当a >0，b >0时，⎝⎛⎭⎫a ＋1a ⎝⎛⎭⎫b ＋1b ≥4，故①恒成立． 因为(a ＋b )⎝⎛⎭⎫1a ＋1b ＝2＋b a ＋a b ，又因为a ，b ①(0，＋∞)，所以b a ＋ab ≥2，所以(a ＋b )⎝⎛⎭⎫1a ＋1b ≥4，故①恒成立． 因为a ①R 且a ≠0，不符合基本不等式的条件，故9a＋a ≥6是错误的．14.证明：因为x ＞0，y ＞0，z ＞0，所以y x ＋z x ≥2yz x ＞0，x y ＋z y ≥2xz y ＞0，x z ＋y z ≥2xyz ＞0，所以⎝⎛⎭⎫y x ＋z x ⎝⎛⎭⎫x y ＋z y ⎝⎛⎭⎫x z ＋y z ≥8yz ·xz ·xyxyz＝8，当且仅当x ＝y ＝z 时等号成立． 15.[证明] 证法一：因为a >0，b >0，a ＋b ＝1，所以1＋1a ＝1＋a ＋b a ＝2＋b a ，同理1＋1b ＝2＋a b，故⎝⎛⎭⎫1＋1a ⎝⎛⎭⎫1＋1b ＝⎝⎛⎭⎫2＋b a ⎝⎛⎭⎫2＋a b ＝5＋2⎝⎛⎭⎫b a ＋a b ≥5＋4＝9.所以⎝⎛⎭⎫1＋1a ⎝⎛⎭⎫1＋1b ≥9(当且仅当a ＝b ＝12时取等号)．证法二：因为a ，b 为正数，a ＋b ＝1.所以⎝⎛⎭⎫1＋1a ⎝⎛⎭⎫1＋1b ＝1＋1a ＋1b ＋1ab ＝1＋a ＋b ab ＋1ab ＝1＋2ab ， ab ≤⎝⎛⎭⎫a ＋b 22＝14，于是1ab ≥4，2ab ≥8，因此⎝⎛⎭⎫1＋1a ⎝⎛⎭⎫1＋1b ≥1＋8＝9⎝⎛⎭⎫当且仅当a ＝b ＝12时等号成立.2.2 第2课时 基本不等式的综合应用基 础 练巩固新知 夯实基础1.（3－a ）（a ＋6）(－6≤a ≤3)的最大值为( )A ．9 B.92 C ．3 D.3222．设x >0，则y ＝3－3x －1x的最大值是( )A ．3B ．3－22C ．3－2 3D ．－1 3．若0＜x ＜12，则函数y ＝x 1－4x 2的最大值为( )A ．1 B.12 C.14D.184．某车间分批生产某种产品，每批的生产准备费用为800元．若每批生产x 件，则平均仓储时间为x8天，且每件产品每天的仓储费用为1元．为使平均到每件产品的生产准备费用与仓储费用之和最小，每批应生产产品( )A ．60件B ．80件C ．100件D ．120件5．已知a >0，b >0，2a ＋1b ＝16，若不等式2a ＋b ≥9m 恒成立，则m 的最大值为( )A ．8B ．7C ．6D ．56．已知y ＝4x ＋ax (x >0，a >0)在x ＝3时取得最小值，则a ＝________．7．已知y ＝x ＋1x.(1)已知x ＞0，求y 的最小值；(2)已知x ＜0，求y 的最大值．8．已知a >0，b >0，且2a ＋b ＝ab .(1)求ab 的最小值； (2)求a ＋2b 的最小值．能 力 练综合应用 核心素养9．已知a <b ，则b －a ＋1b －a＋b －a 的最小值为( )A ．3B ．2C ．4D ．110．已知实数x ，y 满足x >0，y >0，且2x ＋1y＝1，则x ＋2y 的最小值为( )A ．2B ．4C ．6D ．811．设x ＞0，则函数y ＝x ＋22x ＋1－32的最小值为( ) A ．0 B.12C ．1D.3212．已知x ≥52，则y ＝x 2－4x ＋52x －4有( )A ．最大值54B ．最小值54za C ．最大值1D ．最小值113．已知不等式(x ＋y )⎝ ⎛⎭⎪⎫1x ＋a y ≥9对任意正实数x ，y 恒成立，则正实数a 的最小值为( )A ．2B ．4C ．6D ．814．已知x ＞0，y ＞0，2x ＋3y ＝6，则xy 的最大值为________．15．若点A (－2，－1)在直线mx ＋ny ＋1＝0上，其中mn >0，则1m ＋2n的最小值为________．16．设a>b>c，且1a－b＋1b－c≥ma－c恒成立，求m的取值范围．17．(1)若x＜3，求y＝2x＋1＋1x－3的最大值；(2)已知x＞0，求y＝2xx2＋1的最大值．【参考答案】1. B 解析：选B.因为－6≤a ≤3，所以3－a ≥0，a ＋6≥0，所以（3－a ）（a ＋6）≤（3－a ）＋（a ＋6）2＝92.即（3－a ）（a ＋6）(－6≤a ≤3)的最大值为92.2. C 解析：y ＝3－3x －1x＝3－⎝⎛⎭⎫3x ＋1x ≤3－2 3x ·1x ＝3－23，当且仅当3x ＝1x ，即x ＝33时取等号． 3. C 解析：因为0＜x ＜12，所以1－4x 2＞0，所以x 1－4x 2＝12×2x 1－4x 2≤12×4x 2＋1－4x 22＝14，当且仅当2x＝1－4x 2，即x ＝24时等号成立，故选C. 4. B 解析：设每件产品的平均费用为y 元，由题意得y ＝800x ＋x 8≥2800x ·x8＝20. 当且仅当800x ＝x8(x >0)，即x ＝80时“＝”成立，故选B.5. C 解析：可得6⎝⎛⎭⎫2a ＋1b ＝1，所以2a ＋b ＝6⎝⎛⎭⎫2a ＋1b ·(2a ＋b )＝6⎝⎛⎭⎫5＋2a b ＋2b a ≥6×(5＋4)＝54，当且仅当2ab ＝2ba时等号成立，所以9m ≤54，即m ≤6，故选C. 6. 36 解析：y ＝4x ＋ax≥24x ·a x ＝4a (x >0，a >0)，当且仅当4x ＝a x ，即x ＝a2时等号成立，此时y 取得最小值4a . 又由已知x ＝3时，y 的最小值为4a ，所以a2＝3，即a ＝36. 7. 解：(1)因为x ＞0，所以x ＋1x≥2x ·1x ＝2，当且仅当x ＝1x，即x ＝1时等号成立．所以y 的最小值为2. (2)因为x ＜0，所以－x ＞0.所以f (x )＝－⎣⎡⎦⎤（－x ）＋1－x ≤－2（－x ）·1－x ＝－2，当且仅当－x ＝1－x，即x ＝－1时等号成立．所以y 的最大值为－2. 8. 解：因为2a ＋b ＝ab ，所以1a ＋2b＝1；(1)因为a >0，b >0， 所以1＝1a ＋2b≥22ab ，当且仅当1a ＝2b ＝12，即a ＝2，b ＝4时取等号，所以ab ≥8，即ab 的最小值为8；(2)a ＋2b ＝(a ＋2b )⎝⎛⎭⎫1a ＋2b ＝5＋2b a ＋2ab ≥5＋22b a ·2ab＝9， 当且仅当2b a ＝2ab ，即a ＝b ＝3时取等号，所以a ＋2b 的最小值为9.9. A 解析：因为a <b ，所以b －a >0，由基本不等式可得b －a ＋1b －a ＋b －a ＝1＋1b －a＋(b －a )≥1＋21b －a·（b －a ）＝3， 当且仅当1b －a ＝b －a (b >a )，即当b －a ＝1时，等号成立，因此，b －a ＋1b －a ＋b －a 的最小值为3,故选A.10. D 解析：因为x >0，y >0，且2x ＋1y ＝1，所以x ＋2y ＝(x ＋2y )⎝⎛⎭⎫2x ＋1y ＝4＋4y x ＋xy≥4＋24y x ·xy＝8， 当且仅当4y x ＝xy时等号成立．故选D.11. A 解析：选A.因为x ＞0，所以x ＋12＞0，所以y ＝x ＋22x ＋1－32＝⎝⎛⎭⎫x ＋12＋1x ＋12－2≥2⎝⎛⎭⎫x ＋12·1x ＋12－2＝0，当且仅当x ＋12＝1x ＋12，即x ＝12时等号成立，所以函数的最小值为0. 12. D 解析：y ＝x 2－4x ＋52x －4＝（x －2）2＋12（x －2）＝12⎣⎡⎦⎤（x －2）＋1x －2，因为x ≥52，所以x －2＞0，所以12⎣⎡⎦⎤（x －2）＋1x －2≥12·2（x －2）·1x －2＝1，当且仅当x －2＝1x －2，即x ＝3时取等号．故y 的最小值为1.13. B 解析 (x ＋y )⎝⎛⎭⎫1x ＋a y ＝1＋a ＋ax y ＋y x ≥1＋a ＋2a ＝(a ＋1)2⎝⎛⎭⎫当且仅当y x ＝a 时取等号 .①(x ＋y )⎝⎛⎭⎫1x ＋a y ≥9对任意正实数x ，y 恒成立，①(a ＋1)2≥9.①a ≥4.14. 32 解析：因为x ＞0，y ＞0，2x ＋3y ＝6，所以xy ＝16(2x ·3y )≤16·⎝⎛⎭⎫2x ＋3y 22＝16·⎝⎛⎭⎫622＝32.当且仅当2x ＝3y ，即x ＝32，y ＝1时，xy 取到最大值32.15. 8 解析：因为点A (－2，－1)在直线mx ＋ny ＋1＝0上，所以2m ＋n ＝1， 所以1m ＋2n ＝2m ＋n m ＋2（2m ＋n ）n＝4＋⎝⎛⎭⎫n m ＋4m n ≥8. 16.解 由a >b >c ，知a －b >0，b －c >0，a －c >0.因此，原不等式等价于a －c a －b ＋a －c b －c≥m .要使原不等式恒成立，只需a －c a －b ＋a －cb －c的最小值不小于m 即可． 因为a －c a －b ＋a －c b －c ＝(a －b )＋(b －c )a －b ＋(a －b )＋(b －c )b －c ＝2＋b －c a －b ＋a －b b －c≥2＋2b －c a －b ×a －bb －c＝4， 当且仅当b －c a －b ＝a －b b －c，即2b ＝a ＋c 时，等号成立．所以m ≤4，即m ①{m |m ≤4}.17.解：(1)因为x ＜3，所以3－x ＞0.又因为y ＝2(x －3)＋1x －3＋7＝－⎣⎡⎦⎤2（3－x ）＋13－x ＋7，由基本不等式可得2(3－x )＋13－x≥22（3－x ）·13－x ＝22，当且仅当2(3－x )＝13－x，即x ＝3－22时，等号成立，于是－⎣⎡⎦⎤2（3－x ）＋13－x ≤－22，－⎣⎡⎦⎤2（3－x ）＋13－x ＋7≤7－22，故y 的最大值是7－2 2.(2)y ＝2x x 2＋1＝2x ＋1x .因为x ＞0，所以x ＋1x ≥2x ·1x ＝2，所以0＜y ≤22＝1，当且仅当x ＝1x，即x ＝1时，等号成立．故y 的最大值为1.2.3 第1课时 二次函数与一元二次方程、不等式基 础 练巩固新知 夯实基础1．已知集合M＝{x|x2－3x－28≤0}，N＝{x|x2－x－6>0}，则M∩N为()A．{x|－4≤x<－2或3<x≤7} B．{x|－4<x≤－2或3≤x<7}C．{x|x≤－2或x>3} D．{x|x<－2或x≥3}2．一元二次方程ax2＋bx＋c＝0的根为2，－1，则当a<0时，不等式ax2＋bx＋c≥0的解集为() A．{x|x<－1或x>2} B．{x|x≤－1或x≥2}C．{x|－1<x<2} D．{x|－1≤x≤2}3．一元二次方程ax2＋bx＋c＝0的根为2，－1，则当a<0时，不等式ax2＋bx＋c≥0的解() A．{x|x<－1或x>2} B．{x|x≤－1或x≥2}C．{x|－1<x<2} D．{x|－1≤x≤2}4．关于x的不等式ax－b>0的解集是(1，＋∞)，则关于x的不等式(ax＋b)(x－3)>0的解集是() x|x<－1或x>3B．{x|－1<x<3}A.{}C．{x|1<x<3} D．{x|x<1或x>3}5．若不等式ax2－x－c>0的解集为{x|－2<x<1}，则函数y＝ax2－x－c的图象为()6．设集合A＝{x|(x－1)2<3x＋7，x①R}，则集合A∩Z中有________个元素．7．不等式－1<x2＋2x－1≤2的解集是________．8．解关于x的不等式：x2＋(1－a)x－a<0.9． 解不等式：x 2－3|x |＋2≤0.能 力 练综合应用 核心素养10． 若0<t <1，则关于x 的不等式(t －x )(x －1t)>0的解集是( )A.⎩⎨⎧⎭⎬⎫x |1t <x <tB.⎩⎨⎧⎭⎬⎫x |x >1t 或x <tC.⎩⎨⎧⎭⎬⎫x |x <1t 或x >tD.⎩⎨⎧⎭⎬⎫x |t <x <1t11．设函数f (x )＝⎩⎪⎨⎪⎧x 2－4x ＋6，x ≥0，x ＋6， x <0，则不等式f (x )>f (1)的解集是( )A ．(－3,1)①(3，＋∞)B ．(－3,1)①(2，＋∞)C ．(－1,1)①(3，＋∞)D ．(－∞，－3)①(1,3)12．不等式x 2－px －q <0的解集是{x |2<x <3}，则不等式qx 2－px －1>0的解是( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪ x <－12或x >－13 B.⎩⎨⎧⎭⎬⎫x ⎪⎪－12<x <－13 C.⎩⎨⎧⎭⎬⎫x ⎪⎪13<x <12 D.{}x | x <2或x >3 13．已知x ＝1是不等式k 2x 2－6kx ＋8≥0的解，则k 的取值范围是______________．14．方程x 2＋(m －3)x ＋m ＝0的两根都是负数，则m 的取值范围为________．15．若关于x 的不等式ax 2－6x ＋a 2>0的解集为{x |1<x <m }，则a ＝________，m ＝________. 16．若不等式ax 2＋bx ＋c ≥0的解集为⎩⎨⎧⎭⎬⎫x |－13≤x ≤2，求关于x 的不等式cx 2－bx ＋a <0的解集．17．解关于x 的不等式ax 2－2(a ＋1)x ＋4>0.【参考答案】1. A 解析 ①M ＝{x |x 2－3x －28≤0}＝{x |－4≤x ≤7}，N ＝{x |x 2－x －6>0}＝{x |x <－2或x >3}，①M ∩N ＝{x |－4≤x <－2或3<x ≤7}．2. D 解析 由题意知，－b a ＝1，ca ＝－2，①b ＝－a ，c ＝－2a ，又①a <0，①x 2－x －2≤0，①－1≤x ≤2.3. D 解析 由方程ax 2＋bx ＋c ＝0的根为2，－1，知函数y ＝ax 2＋bx ＋c 的零点为2，－1，又①a <0，①函数y ＝ax 2＋bx ＋c 的图象是开口向下的抛物线，①不等式ax 2＋bx ＋c ≥0的解集为{x |－1≤x ≤2}．4. A 解析 由题意，知a >0，且1是ax －b ＝0的根，所以a ＝b >0，所以(ax ＋b )(x －3)＝a (x ＋1)(x －3)>0，所以x <－1或x >3，因此原不等式的解集为{x |x <－1或x >3}．5. B 解析 因为不等式的解集为{x |－2<x <1}，所以a <0，排除C 、D ；又与坐标轴交点的横坐标为－2,1，故选B.6. 6 解析 由(x －1)2<3x ＋7，解得－1<x <6，即A ＝{x |－1<x <6}，则A ∩Z ＝{0,1,2,3,4,5}，故A ∩Z 共有6个元素．7. {x |－3≤x <－2或0<x ≤1} 解析 ①⎩⎪⎨⎪⎧x 2＋2x －3≤0，x 2＋2x >0，①－3≤x <－2或0<x ≤1.8. 解 方程x 2＋(1－a )x －a ＝0的解为x 1＝－1，x 2＝a .函数y ＝x 2＋(1－a )x －a 的图象开口向上，所以(1)当a <－1时，原不等式解集为{x |a <x <－1}； (2)当a ＝－1时，原不等式解集为①； (3)当a >－1时，原不等式解集为{x |－1<x <a }． 9. 解 原不等式等价于|x |2－3|x |＋2≤0，即1≤|x |≤2.当x ≥0时，1≤x ≤2；当x <0时，－2≤x ≤－1. ①原不等式的解集为{x |－2≤x ≤－1或1≤x ≤2}．10. D 解析 ①0<t <1，①1t >1，①1t >t .①(t －x )(x －1t )>0①(x －t )(x －1t )<0①t <x <1t .11. A 解析 f (1)＝12－4×1＋6＝3，当x ≥0时，x 2－4x ＋6>3，解得x >3或0≤x <1；当x <0时，x ＋6>3，解得－3<x <0. 所以f (x )>f (1)的解集是(－3,1)①(3，＋∞)．12. B [解析] 易知方程x 2－px －q ＝0的两个根是2,3.由根与系数的关系得⎩⎪⎨⎪⎧ 2＋3＝p ，2×3＝－q ，解得⎩⎪⎨⎪⎧p ＝5，q ＝－6，不等式qx 2－px －1>0为－6x 2－5x －1>0，解得－12<x <－13.13. k ≤2或k ≥4 解析 x ＝1是不等式k 2x 2－6kx ＋8≥0的解，把x ＝1代入不等式得k 2－6k ＋8≥0，解得k ≥4或k ≤2.14. {m |m ≥9} 解析 ①⎩⎪⎨⎪⎧Δ＝(m －3)2－4m ≥0，x 1＋x 2＝3－m <0，x 1x 2＝m >0，①m ≥9.15. －3 －3 解析 可知1，m 是方程ax 2－6x ＋a 2＝0的两个根，且a <0， ①⎩⎪⎨⎪⎧1＋m ＝6a 1×m ＝a解得⎩⎪⎨⎪⎧ a ＝－3m ＝－3或⎩⎪⎨⎪⎧a ＝2m ＝2(舍去)． 16.解 由ax 2＋bx ＋c ≥0的解集为⎩⎨⎧⎭⎬⎫x |－13≤x ≤2，知a <0，且关于x 的方程ax 2＋bx ＋c ＝0的两个根分别为－13，2，①⎩⎨⎧－13＋2＝－b a－13×2＝c a，①b ＝－53a ，c ＝－23a .所以不等式cx 2－bx ＋a <0可变形为⎝⎛⎭⎫－23a x 2－⎝⎛⎭⎫－53a x ＋a <0，即2ax 2－5ax －3a >0. 又因为a <0，所以2x 2－5x －3<0，所以所求不等式的解集为⎩⎨⎧⎭⎬⎫x |－12<x <3.17.解 (1)当a ＝0时，原不等式可化为－2x ＋4>0，解得x <2，所以原不等式的解集为{x |x <2}．(2)当a >0时，原不等式可化为(ax －2)(x －2)>0，对应方程的两个根为x 1＝2a，x 2＝2.①当0<a <1时，2a >2，所以原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x >2a ，或x <2；①当a ＝1时，2a＝2，所以原不等式的解集为{x |x ≠2}；①当a >1时，2a <2，所以原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x >2，或x <2a . (3)当a <0时，原不等式可化为(－ax ＋2)(x －2)<0，对应方程的两个根为x 1＝2a ，x 2＝2，则2a<2，所以原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪2a<x <2. 综上，a <0时，原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪2a<x <2； a ＝0时，原不等式的解集为{x |x <2}；0<a ≤1时，原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x >2a，或x <2； 当a >1时，原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x >2，或x <2a2.3 第2课时 一元二次不等式的应用基 础 练巩固新知 夯实基础1．不等式x ＋5(x －1)2≥2的解集是( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪ －3≤x ≤12 B.⎩⎨⎧⎭⎬⎫x ⎪⎪－12≤x ≤3C.⎩⎨⎧⎭⎬⎫x ⎪⎪ 12≤x <1或1<x ≤3 D.⎩⎨⎧⎭⎬⎫x ⎪⎪－12≤x ≤3且x ≠1 2．不等式4x ＋23x －1>0的解集是( )A.⎩⎨⎧⎭⎬⎫x | x >13或x <－12 B.⎩⎨⎧⎭⎬⎫x | －12<x <13C.⎩⎨⎧⎭⎬⎫x | x >13 D.⎩⎨⎧⎭⎬⎫x | x <－123．不等式2－xx ＋1<1的解集是( )A ．{x |x >1}B ．{x |－1<x <2} C.⎩⎨⎧⎭⎬⎫x | x <－1或x >12 D.⎩⎨⎧⎭⎬⎫x | －1<x <124． 若集合A ＝{x |ax 2－ax ＋1<0}＝①，则实数a 的值的集合是( )A ．{a |0<a <4}B ．{a |0≤a <4}C ．{a |0<a ≤4}D ．{a |0≤a ≤4}5． 若关于x 的不等式x 2－4x －m ≥0对任意x ①(0,1]恒成立，则m 的最大值为 ( )A ．1B ．－1C ．－3D ．36．在如图所示的锐角三角形空地中，欲建一个面积不小于300 m 2的内接矩形花园(阴影部分)，则其边长x (单位：m)的取值范围是( )A ．15≤x ≤30B ．12≤x ≤25C ．10≤x ≤30D ．20≤x ≤307． 若关于x 的不等式x －a x ＋1>0的解集为(－∞，－1)①(4，＋∞)，则实数a ＝________.8.若不等式x 2＋mx ＋1>0的解集为R ，则m 的取值范围是__________．9．解下列分式不等式：(1)x ＋12x －3≤1； (2)2x ＋11－x <0.10. 当a 为何值时，不等式(a 2－1)x 2－(a －1)x －1<0的解集为R?能 力 练综合应用 核心素养11． 不等式x 2－2x －2x 2＋x ＋1<2的解集为( )A ．{x |x ≠－2}B ．RC ．①D ．{x |x <－2或x >2}12．若不等式mx2＋2mx－4<2x2＋4x的解集为R，则实数m的取值范围是()A．(－2,2) B．(－2,2]C．(－∞，－2)①[2，＋∞) D．(－∞，2)13．对任意a①[－1,1]，函数f(x)＝x2＋(a－4)x＋4－2a的值恒大于零，则x的取值范围是() A．1<x<3 B．x<1或x>3C．1<x<2 D．x<1或x>214．在R上定义运算①：x①y＝x(1－y)．若不等式(x－a)①(x＋a)<1对任意的实数x都成立，则a的取值范围是________.15．已知2≤x≤3时，不等式2x2－9x＋a<0恒成立，则a的取值范围为________．16．方程x2＋(m－3)x＋m＝0有两个正实根，则m的取值范围是________．17．已知关于x的一元二次方程x2＋2mx＋2m＋1＝0.若方程有两根，其中一根在区间(－1,0)内，另一根在区间(1,2)内，求m的取值范围．18．某地区上年度电价为0.8元/kW·h，年用电量为a kW·h，本年度计划将电价降低到0.55元/kW·h至0.75元/kW·h之间，而用户期望电价为0.4元/kW·h.经测算，下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为k)．该地区电力的成本价为0.3元/kW·h.(1)写出本年度电价下调后，电力部门的收益y与实际电价x的函数关系式；(2)设k＝0.2a，当电价最低定为多少时仍可保证电力部门的收益比上年度至少增长20%?注：收益＝实际用电量×(实际电价－成本价)．【参考答案】1. D 解析①原不等式等价于⎩⎪⎨⎪⎧ x ＋5≥2(x －1)2，x ≠1，①⎩⎪⎨⎪⎧2x 2－5x －3≤0，x ≠1，①⎩⎪⎨⎪⎧－12≤x ≤3，x ≠1，即⎩⎨⎧⎭⎬⎫x ⎪⎪－12≤x ≤3且x ≠1. 2. A 解析4x ＋23x －1>0①(4x ＋2)(3x －1)>0①x >13或x <－12，此不等式的解集为⎩⎨⎧⎭⎬⎫x | x >13或x <－12.3. C 解析原不等式等价于2－x x ＋1－1<0①1－2x x ＋1<0①(x ＋1)·(1－2x )<0①(2x －1)(x ＋1)>0，解得x <－1或x >12.4. D 解析 a ＝0时符合题意，a >0时，相应二次方程中的Δ＝a 2－4a ≤0，得{a |0<a ≤4}，综上得{a |0≤a ≤4}.5. C 解析 由已知可得m ≤x 2－4x 对一切x ①(0,1]恒成立，又f (x )＝x 2－4x 在(0,1]上为减函数，①f (x )min ＝f (1)＝－3，①m ≤－3.6. C 解析 设矩形的另一边长为y m ，则由三角形相似知，x 40＝40－y40，①y ＝40－x ，①xy ≥300，①x (40－x )≥300，①x 2－40x ＋300≤0，①10≤x ≤30. 7. 4 解析x －ax ＋1>0①(x ＋1)(x －a )>0 ①(x ＋1)(x －4)>0，①a ＝4. 8. －2<m <2 解析 由题意知，不等式x 2＋mx ＋1>0对应的函数的图象在x 轴的上方，所以Δ＝(m )2－4×1×1<0，所以－2<m <2.9. 解 (1)①x ＋12x －3≤1，①x ＋12x －3－1≤0，①－x ＋42x －3≤0，即x －4x －32≥0.此不等式等价于(x －4)⎝⎛⎭⎫x －32≥0且x －32≠0，解得x <32或x ≥4.①原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x <32或x ≥4. (2)由2x ＋11－x <0得x ＋12x －1>0，此不等式等价于⎝⎛⎭⎫x ＋12(x －1)>0，解得x <－12或x >1， ①原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x <－12或x >1.10.解 ①当a 2－1＝0时，a ＝1或－1.若a ＝1，则原不等式为－1<0，恒成立．若a ＝－1，则原不等式为2x －1<0即x <12，不合题意，舍去．①当a 2－1≠0时，即a ≠±1时，原不等式的解集为R 的条件是⎩⎪⎨⎪⎧a 2－1<0，Δ＝[－a －1]2＋4a 2－1<0.解得－35<a <1.综上a 的取值范围是⎝⎛⎦⎤－35，1. 11. A 解析①x 2＋x ＋1>0恒成立，①原不等式①x 2－2x －2<2x 2＋2x ＋2①x 2＋4x ＋4>0①(x ＋2)2>0，①x ≠－2. ①不等式的解集为{x |x ≠－2}．12. B 解析 ①mx 2＋2mx －4<2x 2＋4x ， ①(2－m )x 2＋(4－2m )x ＋4>0.当m ＝2时，4>0，x ①R ；当m <2时，Δ＝(4－2m )2－16(2－m )<0，解得－2<m <2.此时，x ①R . 综上所述，－2<m ≤2.13. B 解析 设g (a )＝(x －2)a ＋(x 2－4x ＋4)，g (a )>0恒成立且a ①[－1,1]①⎩⎪⎨⎪⎧ g1＝x 2－3x ＋2>0g－1＝x 2－5x ＋6>0①⎩⎪⎨⎪⎧x <1或x >2x <2或x >3①x <1或x >3. 14. －12 <a <32 解析 根据定义得(x －a )①(x ＋a )＝(x －a )[1－(x ＋a )]＝－x 2＋x ＋a 2－a ，又(x －a )①(x ＋a )<1对任意的实数x 都成立，所以x 2－x ＋a ＋1－a 2>0对任意的实数x 都成立，所以Δ<0，即1－4(a ＋1－a 2)<0，解得－12<a <32.15. a <9 解析 ①当2≤x ≤3时，2x 2－9x ＋a <0恒成立，①当2≤x ≤3时，a <－2x 2＋9x 恒成立．令y ＝－2x 2＋9x .①2≤x ≤3，且对称轴方程为x ＝94，①y min ＝9，①a <9.①a 的取值范围为a <9.16. (0,1] 解析 由题意得⎩⎪⎨⎪⎧Δ＝m －32－4m ≥0x 1＋x 2＝3－m ＞0x 1x 2＝m ＞0， 解得0＜m ≤1.17. 解 设f (x )＝x 2＋2mx ＋2m ＋1，根据题意，画出示意图由图分析可得，m 满足不等式组⎩⎪⎨⎪⎧ f 0＝2m ＋1<0f －1＝2>0f 1＝4m ＋2<0f 2＝6m ＋5>0解得－56<m <－12. 18. 解(1)设下调后的电价为x 元/kW·h ，依题意知，用电量增至k x －0.4＋a ，电力部门的收益为y ＝⎝⎛⎭⎫k x －0.4＋a (x －0.3)(0.55≤x ≤0.75)．(2)依题意，有⎩⎪⎨⎪⎧⎝⎛⎭⎫0.2ax －0.4＋a (x －0.3)≥[a ×(0.8－0.3)](1＋20%)，0.55≤x ≤0.75.整理，得⎩⎪⎨⎪⎧ x 2－1.1x ＋0.3≥0，0.55≤x ≤0.75.解此不等式，得0.60≤x ≤0.75.①当电价最低定为0.60元/kW·h 时，仍可保证电力部门的收益比上年度至少增长20%.。

一、选择题1．已知函数()f x =的定义域为R ，则实数m 的取值范围是（ ）A ．04m ≤≤B ．04m <≤C ．04m ≤<D ．04m <<2．函数25,1(),1x ax x f x a x x⎧---≤⎪=⎨>⎪⎩满足对任意12x x ≠都有()()12120f x f x x x ->-，则a 的取值范围是（ ） A ．30a -≤<B ．32a --≤≤C ．2a ≤-D ．0a <3．已知函数22()2(2)f x x a x a =-++，23()2(2)8g x x a x a =-+--+．设()(){1max ,H x f x =}()g x ．()()(){}2min ,H x f x g x =（其中{}max ,p q 表示p ，q中较大值，{}min ,p q 表示p ，q 中较小值），记()1H x 的最小值为A ，()2H x 的最大值为B ，则A B -=（ ） A ．16-B ．16C ．8aD ．816a -4．已知函数()y f x =是定义在R 上的单调函数，()0,2A ，()2,2B -是其函数图像上的两点，则不等式()12f x ->的解集为（ ） A ．()1,3 B ．()(),31,-∞-⋃+∞ C ．()1,1-D ．()(),13,-∞+∞5．函数()()1ln 24f x x x =-+-的定义域是（ ） A ．[)2,4B ．()2,+∞C ．()()2,44,⋃+∞D ．[)()2,44,+∞6．对于每个实数x ，设()f x 取24y x =-+，41y x =+，2y x =+三个函数值中的最小值，则()f x （ ） A ．无最大值，无最小值 B ．有最大值83，最小值1 C ．有最大值3，无最小值D ．有最大值83，无最小值 7．已知函数2()(3)1f x mx m x =--+，()g x mx =，若对于任意实数x ，()f x 与()g x 的值至少有一个为正数，则实数m 的取值范围是（ ） A ．(1,9)B ．(3,+)∞C ．(,9)-∞D ．(0,9)8．已知2()2af x x ax =-+在区间[0，1]上的最大值为g (a )，则g (a )的最小值为（ ） A ．0B ．12C ．1D ．29．对x R ∀∈，用()M x 表示()f x ，()g x 中较大者，记为()()()max{,}M x f x g x =，若()()2{3,1}M x x x =-+-，则()M x 的最小值为（ ）A ．-1B ．0C ．1D ．410．如果()()211f x mx m x =+-+在区间(]1-∞，上为减函数，则m 的取值范围（ ） A ．103⎛⎤ ⎥⎝⎦， B ．103⎡⎤⎢⎥⎣⎦，C ．103⎡⎫⎪⎢⎣⎭，D ．103⎛⎫ ⎪⎝⎭，11．函数sin sin 122xxy =+的部分图象大致是（ ）A ．B ．C ．D ．12．已知函数()113sin 22f x x x ⎛⎫=+-+ ⎪⎝⎭，则122018201920192019f f f ⎛⎫⎛⎫⎛⎫++⋅⋅⋅+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭（ ） A ．2018 B ．2019 C ．4036D ．4038二、填空题13．函数()()2325f x kx k x =+--在[)1+∞，上单调递增，则k 的取值范围是________. 14．已知函数()2f x x =，()1g x a x =-，a 为常数，若对于任意1x ，[]20,2x ∈，且12x x <，都有()()()()1212f x f x g x g x -<-则实数a 的取值范围为________.15．已知函数f (x )满足2f (x )＋f (－x )＝3x ，则f (x )＝________．16．已知函数()225f x x ax =-+在(],2-∞上是减函数，且对任意的1x 、[]21,1x a ∈+，总有()()124f x f x -≤，则实数a 的取值范围是________.17．已知函数()f x 的定义域为(1,1)-，则函数()()(1)2xg x f f x =+-的定义域是________.18．已知()()21353m f x m m x+=++是幂函数，对12,(0,)x x ∈+∞且12x x ≠有()()12120f x f x x x ->-，若,a b ∈R ，0a b +<，0ab <，则()()f a f b +________0（填>，<）.19．已知函数()f x 是R 上的奇函数，()()2g x af x bx =++，若(2)16g =，则(2)g -=______．20．已知函数2262()2x ax x f x a x x⎧-+⎪=⎨>⎪⎩，≤，，是R 上的减函数，则a 的取值范围为______．三、解答题21．定义：满足()f x x =的实数x 为函数()f x 的“不动点”，已知二次函数()()20f x ax bx a =+≠，()1f x +为偶函数，且()f x 有且仅有一个“不动点”．（1）求()f x 的解析式；（2）若函数()()2g x f x kx =+在()0,4上单调递增，求实数k 的取值范围；（3）是否存在区间[](),m n m n <，使得()f x 在区间[],m n 上的值域为[]3,3m n ？若存在，请求出m ，n 的值；若不存在，请说明理由．22．已知函数()f x 为二次函数，满足()()139f f -==，且()03f =．（1）求函数()f x 的解析式；（2）设()()g x f x mx =-在[]1,3上是单调函数，求实数m 的取值范围． 23．定义在()0,∞+的函数()f x ，满足()()()f mn f m f n =+，且当1x >时，()0f x >.（1）求证：()()m f f m f n n ⎛⎫=- ⎪⎝⎭（2）讨论函数()f x 的单调性，并说明理由； （3）若()21f =，解不等式()()333f x f x +->. 24．已知函数()x af x x+=（a 为常数），其中()0f x <的解集为()4,0-. （1）求实数a 的值；（2）设()()g x x f x =+，当()0x x >为何值时，()g x 取得最小值，并求出其最小值. 25．已知二次函数()2()f x ax bx a b R =+∈、满足：①()()11f x f x +=-；②对一切x ∈R ，都有()f x x ≤.（1）求()f x ；（2）是否存在实数(),m n m n <使得()f x 的定义域为[],m n 、值域为[]3,3m n ，如果存在，求出m ，n 的值；如果不存在，说明理由. 26．已知11012x f x x x ⎛⎫⎛⎫=<≤⎪ ⎪-⎝⎭⎝⎭. （1）求()f x 的表达式；（2）判断()f x 在其定义域内的单调性，并证明.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】由题意可知，对任意的x ∈R ，210mx mx ++>恒成立，然后分0m =和0m ≠，结合题意可得出关于实数m 的不等式组，由此可解得实数m 的取值范围. 【详解】由题意可知，对任意的x ∈R ，210mx mx ++>恒成立. 当0m =时，则有10>，合乎题意；当0m ≠时，则有240m m m >⎧⎨∆=-<⎩，解得04m <<. 综上所述，04m ≤<. 故选：C. 【点睛】结论点睛：利用二次不等式在实数集上恒成立，可以利用以下结论来求解： 设()()20f x ax bx c a =++≠①()0f x >在R 上恒成立，则00a >⎧⎨∆<⎩；②()0f x <在R 上恒成立，则00a <⎧⎨∆<⎩；③()0f x ≥在R 上恒成立，则00a >⎧⎨∆≤⎩；④()0f x ≤在R 上恒成立，则00a <⎧⎨∆≤⎩.2．B解析：B 【分析】由题得函数在定义域上单增，列出不等式组得解. 【详解】因为对任意12x x ≠都有()()12120f x f x x x ->-，所以函数在定义域R 上单增，01215a a a a <⎧⎪⎪-≥⎨⎪≥---⎪⎩ 解得32a --≤≤ 故选：B 【点睛】分段函数在R 上单增，关键抓住函数在端点处右侧的函数值大于等于左侧的函数值是解题关键.3．A解析：A 【分析】根据()()22()244,()2412f x x a a g x x a a =----=-+-+，由()(){1max ,H x f x =}()g x ．()()(){}2min ,H x f x g x =，得到max ()412B g x a ==-+，min ()44A f x a ==--求解.【详解】因为函数22()2(2)f x x a x a =-++，23()2(2)8g x x a x a =-+--+， 所以()()22()244,()2412f x x a a g x x a a =----=-+-+， 如图所示：当2x a =+时，()()44f x g x a ==--， 当2=-x a 时，()()412f x g x a ==-+， 因为max ()412g x a =-+，所以()()2max ()412H x g x g x a ≤≤=-+， 因为min ()44f x a =--，所以()()1min ()44H x f x f x a ≥≥=--， 所以44,412A a B a =--=-+， 所以16A B -=-， 故选：A 【点睛】方法点睛：(1)识别二次函数的图象主要从开口方向、对称轴、特殊点对应的函数值这几个方面入手．(2)用数形结合法解决与二次函数图象有关的问题时，要尽量规范作图，尤其是图象的开口方向、顶点、对称轴及与两坐标的交点要标清楚，这样在解题时才不易出错．4．D解析：D 【分析】根据题意可得出(0)2,(2)2f f ==-，从而得出()f x 在R 上为减函数，从而根据不等式()12f x ->得，(1)(2)f x f -<或(1)(0)f x f ->，从而得出12x ->或10x -<，解出x 的范围 【详解】解：由题意得(0)2,(2)2f f ==-， 因为函数()y f x =是定义在R 上的单调函数， 所以()f x 在R 上为减函数，由()12f x ->，得(1)2f x ->或(1)2f x -<-， 所以(1)(0)f x f ->或(1)(2)f x f -<， 所以10x -<或12x ->， 解得1x <或3x >，所以不等式()12f x ->的解集为()(),13,-∞+∞，故选：D 【点睛】关键点点睛：此题考查函数单调性的应用，考查绝对值不等式的解法，解题的关键是把()12f x ->转化为(1)(0)f x f ->或(1)(2)f x f -<，再利用()f x 在R 上为减函数，得10x -<或12x ->，考查数学转化思想，属于中档题5．C解析：C 【分析】先根据函数的解析式建立不等式组，再解不等式组求定义域即可. 【详解】解：因为函数的解析式：()()1ln 24f x x x =-+- 所以2040x x ->⎧⎨-≠⎩，解得24x x >⎧⎨≠⎩故函数的定义域为：()(2,4)4,+∞故选：C 【点睛】数学常见基本初等函数定义域是解题关键.6．D解析：D 【分析】作出函数()f x 的图象，结合图象可得出结论. 【详解】由已知可得(){}min 24,41,2f x x x x =-+++，作出函数()f x 的图象如下图所示：函数()f x 的图象如上图中的实线部分，联立224y x y x =+⎧⎨=-+⎩，解得2383x y ⎧=⎪⎪⎨⎪=⎪⎩，由图象可知，函数()f x 有最大值83，无最小值. 故选：D. 【点睛】关键点点睛：本题考查函数最值的求解，解题的关键就是结合函数()f x 的定义，进而作出函数()f x 的图象，利用图象得出结论.7．D解析：D 【分析】根据所给条件，结合二次函数的图像与性质，分类讨论，即可得解. 【详解】当0m <时，二次函数2()(3)1f x mx m x =--+的图像开口向下，()g x mx =单调递减，故存在x 使得()f x 与()g x 同时为负，不符题意； 当0m =时，()31f x x =-+，()0g x =显然不成立； 当0m >时，2109m m ∆=-+， 若∆<0，即19m <<时，显然成立，0∆=，1m =或9m =，则1m =时成立，9m =时，13x =-时不成立，若0∆>，即01m <<或9m >，由(0)1f =可得：若要()f x 与()g x 的值至少有一个为正数，如图，则必须有302mm->，解得01m <<， 综上可得：09m <<， 故答案为：D. 【点睛】本题考查了二次函数和一次函数的图像与性质，考查了分类讨论思想和计算能力，属于中档题.解决此类问题的关键主要是讨论，涉及二次函数的讨论有： （1）如果平方项有参数，则先讨论； （2）再讨论根的判别式； （3）最后讨论根的分布.8．B解析：B 【分析】由已知结合对称轴与区间端点的远近可判断二次函数取得最值的位置，从而可求．【详解】解：因为2()2af x x ax =-+的开口向上，对称轴2a x =， ①122a即1a 时，此时函数取得最大值()()112a g a f ==-，②当122a >即1a >时，此时函数取得最大值()()02ag a f ==，故()1,12,12aa g a a a ⎧-⎪⎪=⎨⎪>⎪⎩，故当1a =时，()g a 取得最小值12． 故选：B ． 【点睛】本题主要考查了二次函数闭区间上最值的求解，体现了分类讨论思想的应用，属于中档题．9．C解析：C 【分析】根据定义求出()M x 的表达式，然后根据单调性确定最小值． 【详解】由23(1)x x -+=-解得：1x =-或2x =，2(1)3x x -≥-+的解集为1x ≤-或2x ≥，2(1)3x x -<-+的解为12x -<<，∴2(1),12()3,12x x x M x x x ⎧-≤-≥=⎨-+-<<⎩或，∴2x ≤时，()M x 是减函数，2x >时，()M x 是增函数，∴min ()(2)1M x M ==． 故选：C ． 【点睛】关键点点睛：本题考查新定义函数，解题关键是确定新定义函数的解析式，根据新定义通过求最大值得出新函数的解析式，然后根据分段函数研究新函数的性质．10．B解析：B 【分析】当m =0时，()f x =1x -，符合题意.当0m ≠时，由题意可得0112m m m>⎧⎪-⎨≥⎪⎩，求得m 的范围.综合可得m 的取值范围. 【详解】当0m =时，()1f x x =-+，满足在区间(]1-∞，上为减函数； 当0m ≠时，由于()()211f x mx m x =+-+的对称轴为12mx m-=，且函数在区间(]1-∞，上为减函数， 则0112m m m>⎧⎪-⎨≥⎪⎩，解得103m <≤.综上可得，103m ≤≤. 故选：B 【点睛】要研究二次型函数单调区间有关问题，首先要注意二次项系数是否为零.当二次项系数不为零时，利用二次函数的对称轴来研究单调区间.11．D解析：D 【解析】因为()sin()sin sin()sin 11()2222x x x xf x y f x ---=+==+=，所以函数sin sin 122xxy =+是定义在R 上的偶函数，排除A 、B 项；又sin2sin2115()222222f πππ=+=+=，排除C ，综上，函数sin sin 122xxy =+大致的图象应为D 项，故选D.12．A解析：A 【分析】根据函数解析式可验证出()()12f x f x +-=，采用倒序相加法可求得结果. 【详解】()11113sin 22f x x x ⎛⎫-=-+-+ ⎪⎝⎭，()()12f x f x ∴+-=，令122018201920192019S f f f ⎛⎫⎛⎫⎛⎫=++⋅⋅⋅+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 则201712019201922018019S f f f ⎛⎫⎛⎫⎛⎫=++⋅⋅⋅+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，两式相加得：222018S =⨯，2018S ∴=. 故选：A . 【点睛】本题考查倒序相加法求和的问题，解题关键是能够根据函数解析式确定()()1f x f x +-为常数.二、填空题13．【分析】根据函数的解析式分和两种情况讨论利用一次二次函数的性质即可求解【详解】由已知函数在上单调递增可得当时函数在上单调递减不满足题意；当时则满足解得综上所述实数的取值范围是故答案为：【点睛】本题主解析：25⎡⎫+∞⎪⎢⎣⎭， 【分析】根据函数的解析式，分0k =和0k ≠两种情况讨论，利用一次、二次函数的性质，即可求解. 【详解】由已知函数()()2325f x kx k x =+--在[)1+∞，上单调递增可得， 当0k =时，函数()25f x x =--在[)1+∞，上单调递减，不满足题意； 当0k ≠时，则满足03212k k k >⎧⎪-⎨-≤⎪⎩，解得25k ≥，综上所述，实数k 的取值范围是25⎡⎫+∞⎪⎢⎣⎭，. 故答案为：25⎡⎫+∞⎪⎢⎣⎭，. 【点睛】本题主要考查了函数单调性的应用，其中解答中熟记一次函数、二次函数的图象与性质是解答的关键，着重考查了分类讨论思想，以及推理与计算能力，属于基础题.14．02【分析】构造函数F （x ）＝f （x ）﹣g （x ）利用F （x ）的单调性求出a 【详解】解：对于任意x1x2∈02且x1＜x2都有f （x1）﹣f （x2）＜g （x1）﹣g （x2）即f （x1）﹣g （x1）＜f解析：[0，2] 【分析】构造函数F （x ）＝f （x ）﹣g （x ），利用F （x ）的单调性求出a 【详解】解：对于任意x 1，x 2∈[0，2]，且x 1＜x 2，都有f （x 1）﹣f （x 2）＜g （x 1）﹣g （x 2），即f（x 1）﹣g （x 1）＜f （x 2）﹣g （x 2），令F （x ）＝f （x ）﹣g （x ）＝x 2﹣a |x ﹣1|，即F （x 1）＜F （x 2），只需F （x ）在[0，2]单调递增即可，当x ＝1时，F （x ）＝0，图象恒过（1，0）点， 当x ＞1时，F （x ）＝x 2﹣ax +a ， 当x ＜1时，F （x ）＝x 2+ax ﹣a ， 要使F （x ）在[0，2]递增，则当1＜x ≤2时，F （x ）＝x 2﹣ax +a 的对称轴x ＝12a≤，即a ≤2， 当0≤x ＜1时，F （x ）＝x 2+ax ﹣a 的对称轴x ＝02a-≤，即a ≥0， 故a ∈[0，2]， 故答案为：[0，2] 【点睛】考查恒成立问题，函数的单调性问题，利用了构造函数法，属于中档题．15．【分析】因为2f(x)＋f(－x)＝3x①所以将x 用－x 替换得2f(－x)＋f(x)＝－3x②解上面两个方程即得解【详解】因为2f(x)＋f(－x)＝3x①所以将x 用－x 替换得2f(－x)＋f(x) 解析：3x【分析】因为2f (x )＋f (－x )＝3x ，①,所以将x 用－x 替换，得2f (－x )＋f (x )＝－3x ，②,解上面两个方程即得解. 【详解】因为2f (x )＋f (－x )＝3x ，①所以将x 用－x 替换，得2f (－x )＋f (x )＝－3x ，② 解由①②组成的方程组得f (x )＝3x . 故答案为3x 【点睛】本题主要考查函数的解析式的求法，意在考查学生对该知识的理解掌握水平，属于基础题.16．【分析】根据二次函数的单调性求得求得函数在区间上的最大值和最小值由题意可得出可得出关于实数的不等式进而可求得实数的取值范围【详解】二次函数的图象开口向上对称轴为直线由于函数在上是减函数则则所以函数在 解析：[]2,3【分析】根据二次函数()y f x =的单调性求得2a ≥，求得函数()y f x =在区间[]1,1a +上的最大值和最小值，由题意可得出()()max min 4f x f x -≤，可得出关于实数a 的不等式，进而可求得实数a 的取值范围.【详解】二次函数()225f x x ax =-+的图象开口向上，对称轴为直线x a =，由于函数()225f x x ax =-+在(],2-∞上是减函数，则2a ≥，则()1,1a a ∈+， 所以，函数()y f x =在区间[)1,a 上单调递减，在区间(],1a a +上单调递增， 所以，()()2min 5f x f a a ==-，又()162f a =-，()216f a a +=-，则()()()211220f f a a a a a -+=-=-≥，()()max 162f x f a ∴==-，对任意的1x 、[]21,1x a ∈+，总有()()124f x f x -≤，则()()()()22max min 625214f x f x a a a a -=---=-+≤，即2230a a --≤，解得13a -≤≤， 又2a ≥，则23a ≤≤，因此，实数a 的取值范围是[]2,3.故答案为：[]2,3. 【点睛】本题考查利用不等式恒成立求参数值，同时也考查了利用二次函数在区间上的单调性求参数，考查计算能力，属于中等题.17．【分析】根据题意得到函数满足即可求解【详解】由题意函数的定义域为则函数满足即解得即函数的定义域为故答案为：【点睛】本题主要考查了抽象函数的定义域的求解其中解答中熟记抽象函数的定义域的求解方法是解答的 解析：()0,2【分析】根据题意，得到函数()g x 满足112111x x ⎧-<<⎪⎨⎪-<-<⎩，即可求解. 【详解】由题意，函数()f x 的定义域为(1,1)-，则函数()()(1)2x g x f f x =+-满足112111x x ⎧-<<⎪⎨⎪-<-<⎩，即2202x x -<<⎧⎨<<⎩，解得02x <<， 即函数()g x 的定义域为()0,2. 故答案为：()0,2. 【点睛】本题主要考查了抽象函数的定义域的求解，其中解答中熟记抽象函数的定义域的求解方法是解答的关键，着重考查推理与运算能力，属于基础题.18．【分析】先根据是幂函数求出的值再根据且有得出为增函数进而得到函数解析式再根据函数的奇偶性即可求解【详解】解：是幂函数解得：或当时当时又对且时都有在上单调递增易知的定义域为且为上的奇函数且在上单调递增 解析：<【分析】先根据()()21353m f x m m x+=++是幂函数，求出m 的值，再根据12,(0,)x x ∈+∞且12x x ≠有()()12120f x f x x x ->-，得出()f x 为增函数，进而得到函数解析式，再根据函数的奇偶性即可求解. 【详解】 解：()()21353m f x m m x +=++是幂函数，23531m m +∴+=，解得：23m =-或1m =-， 当23m =-时，()13f x x =，当1m =-时，()01f x x ==，又对12,(0,)x x ∈+∞且12x x ≠时，都有()()12120f x f x x x ->-，()f x ∴在(0,)+∞上单调递增， ()13f x x∴=，易知()f x 的定义域为R ，且()()()1133f x x x f x -=-=-=-，()f x ∴为R 上的奇函数，且在R 上单调递增，0a b <+，a b ∴<-，()()()f a f b f b ∴<-=-，()()0f a f b ∴+<.故答案为：<. 【点睛】关键点点睛：本题解题的关键是利用幂函数以及单调性得出函数的解析式.19．【分析】分析的奇偶性根据的结果求解出的值【详解】令因为为上的奇函数且也为上的奇函数所以为上的奇函数所以所以且所以故答案为：【点睛】结论点睛：已知（1）当为奇数时且此时为奇函数；（2）当为偶数时为偶函数 解析：12-【分析】分析()()2h x g x =-的奇偶性，根据()()22h h +-的结果求解出()2g -的值. 【详解】令()()()2h x g x af x bx =-=+，因为()f x 为R 上的奇函数，且y bx =也为R 上的奇函数，所以()()2h x g x =-为R 上的奇函数，所以()()220h h +-=， 所以()()22220g g -+--=，且()216g =，所以()212g -=-， 故答案为：12-. 【点睛】结论点睛：已知()(),0nf x x a n Z n =+∈≠，（1）当n 为奇数时，且0a =，此时()f x 为奇函数； （2）当n 为偶数时，()f x 为偶函数.20．2【分析】由已知利用分段函数的性质及二次函数与反比例函数的单调性可求【详解】解；是上的减函数解可得故答案为：【点睛】本题主要考查了分段函数的单调性的应用二次函数及反比例函数性质的应用是求解问题的关键解析：[2，209] 【分析】由已知利用分段函数的性质及二次函数与反比例函数的单调性可求． 【详解】 解；226,2(),2x ax x f x a x x⎧-+⎪=⎨>⎪⎩是R 上的减函数，∴204462a a a a ⎧⎪⎪>⎨⎪⎪-+⎩， 解可得，2029a． 故答案为：202,9⎡⎤⎢⎥⎣⎦【点睛】本题主要考查了分段函数的单调性的应用，二次函数及反比例函数性质的应用是求解问题的关键，属于中档题．三、解答题21．（1）21()2f x x x =-+（2）3,8⎡⎫+∞⎪⎢⎣⎭（3）4,0m n =-=，证明见解析 【分析】（1）根据二次函数的对称性求出2b a =-，再将()f x 有且仅有一个“不动点转化为方程()f x x =有且仅有一个解，从而得出()f x 的解析式；（2）当102k -=时，由一次含函数的性质得出12k =满足题意，当102k -≠时，讨论二次函数()g x 的开口方向，根据单调性确定112x k=-与区间()0,4端点的大小关系得出实数k 的取值范围； （3）由2111()(1)222f x x =--+得出16m n <，结合二次函数的单调性确定()f x 在区间[],m n 上是增函数，从而得出()3()3f m m f n n=⎧⎨=⎩，再解方程2132x x x -+=得出m ，n 的值.【详解】（1）22(1)(1)(1)(2)f x a x b x ax a b x a b +=+++=++++为偶函数20,22a bb a a+∴=∴=-- 2()2f x ax ax ∴=-f x 有且仅有一个“不动点”∴方程()f x x =有且仅有一个解，即[](21)0ax x a -+=有且仅有一个解211210,,()22a a f x x x ∴+==-=-+（2）221()()2g x f x kx k x x ⎛⎫=+=-+ ⎪⎝⎭，其对称轴为112x k=- 函数()()2g x f x kx =+在()0,4上单调递增∴当12k <时，1412k -，解得3182k < 当12k =时，()g x x =符合题意 当12k >时，1012k<-恒成立综上，3,8k ⎡⎫∈+∞⎪⎢⎣⎭（3）221111()(1)2222f x x x x =-+=--+ f x 在区间[],m n 上的值域为[]3,3m n ，113,26nn ∴，故16m n < ()f x ∴在区间[],m n 上是增函数()3()3f m m f n n =⎧∴⎨=⎩，即22132132m m m n n n ⎧-+=⎪⎪⎨⎪-+=⎪⎩∴,m n 是方程2132x x x -+=的两根，解得0x =或4x =-4,0m n ∴=-=【点睛】关键点睛：已知函数21()2g x k x x ⎛⎫=-+ ⎪⎝⎭在具体区间上的单调性求参数k 的范围时，关键是讨论二次项系数的值，结合二次函数的单调性确定参数k 的范围. 22．（1）()2243f x x x =-+；（2）8m ≥或0m ≤．【分析】（1）设函数()2f x ax bx c =++（0a ≠），代入已知条件解得,,a b c ，得解析式；（2）由对称轴不在区间内可得． 【详解】（1）设函数()2f x ax bx c =++（0a ≠）∵()()139f f -==，且()03f = ∴99313a b c a b c c -+=⎧⎪++=⎨⎪=⎩，解得243a b c =⎧⎪=-⎨⎪=⎩∴()2243f x x x =-+．（2）由（1）()()2243g x x m x =-++，其对称轴为4144m mx +==+ ∵()()g x f x mx =-在[]1,3上单调函数，∴134m +≥，或114m+≤，解得：8m ≥或0m ≤． 【点睛】方法点睛：本题考查求二次函数的解析式，二次函数的单调性．二次函数解析式有三种形式：（1）一般式：2()f x ax bx c =++；（2）顶点式：2()()f x a x h m =-+；（3）交点式（两根式）：12()()()f x a x x x x =--． 23．（1）见解析；（2）见解析；（3）3023x x ⎧⎫<<⎨⎬⎩⎭【分析】（1）由()m f m f n n ⎛⎫=⋅⎪⎝⎭，结合题意即可得结果； （2）利用函数单调性的定义证明即可；（3）将原不等式等价转化为()()324f x f x +>，结合定义域和单调性即可得结果. 【详解】解：（1）由题可得()()m m f m f n f f n n n ⎛⎫⎛⎫=⋅=+ ⎪ ⎪⎝⎭⎝⎭， 即()()m f f m f n n ⎛⎫=- ⎪⎝⎭；（2）任取1x ，()20,x ∈+∞，且12x x <，则211x x >， 由（1）得：()()22110x f x f x f x ⎛⎫-=>⎪⎝⎭，即()()21f x f x >， ()f x ∴在()0,∞+上是增函数；（3）()21f =，()()()2224f f f ∴=+=，()()()3428f f f =+=，()()333f x f x +->， ()()()338f x f x f +>+，()()324f x f x +>，又()f x 在()0,∞+上为增函数，30,240,324,x x x x +>⎧⎪∴>⎨⎪+>⎩， 解得：0323x <<， 故不等式()()333f x f x +->的解集为3023x x ⎧⎫<<⎨⎬⎩⎭. 【点睛】关键点点睛：本题解题的关键是利用()m f m f n n ⎛⎫=⋅ ⎪⎝⎭，再结合题意，即可判断函数单调性和解不等式.24．（1）4a =；（2）当2x =时，()g x 取得最小值为5. 【分析】（1）利用不等式的解集，推出对应方程的根，然后求解a ． （2）化简函数的解析式，利用基本不等式转化求解函数的最值即可． 【详解】（1）因为()00x af x x+<⇔<的解集为()4,0-， 故()0x af x x+==一个根为-4， 404a-+=- 得4a =（2）()()441x g x x f x x x x x+=+=+=++因为0x >，所以4115x x ++≥=， 当且仅当4x x=，即2x =时取等号； 所以当2x =时，()g x 取得最小值为5. 【点睛】在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”（即条件要求中字母为正数）、“定”（不等式的另一边必须为定值）、“等”（等号取得的条件）的条件才能应用，否则会出现错误.25．（1）21()2f x x x =-+；（2）存在，40m n =-⎧⎨=⎩.【分析】（1）由(1)(1)f x f x +=-，得到20b a +=，再由()f x x ≤恒成立，列出方程组，求得,a b 的值，得到函数的解析式；（2）假设存在()m n m n <、，根据题意得到[],m n 必在对称轴的左侧，且()f x 在[],m n 单调递增，列出方程组，即可求解. 【详解】（1）因为22(1)(1)(1)(2)f x a x b x ax a b x a b +=+++=++++，22(1)(1)(1)(2)f x a x b x ax a b x a b -=-+-=-+++，由()()11f x f x +=-可知，20a b +=，由于对一切x ∈R ，都有()f x x ≤即2()(1)0f x x ax b x -=+-≤，于是由二次函数的性质可得()()21400*a b a <⎧⎪⎨∆=--⨯≤⎪⎩由()*知()210b -≤，而()210b -≥，所以()210b -=即1b =，将1b =代入20a b +=得12a =-， 所以21()2f x x x =-+； （2）因为221111()(1)2222f x x x x =-+=--+≤， 若存在满足条件的实数(),m n m n <则必有132n ≤，解得16n ≤， 又因为()f x 在(],1-∞上单调递增，所以()f x 在[],m n 上单调递增.所以()()33fm m fn n ⎧=⎪⎨=⎪⎩，22132132m m mn n n ⎧-+=⎪⎪⎨⎪-+=⎪⎩,解得40m n =-⎧⎨=⎩或04m n =⎧⎨=-⎩，因为m n <，所以40m n =-⎧⎨=⎩，故存在40m n =-⎧⎨=⎩满足条件.【点睛】关键点点睛：本题主要考查了二次函数的图象与性质的应用，其中解答中熟记二次函数的图象与性质，以及根据函数的值域判断出函数在[,]m n 上的单调性是解答的关键，着重考查了分析问题和解答问题的能力，属于中档试题. 26．（1）()1(2)1f x x x =≥-；（2）()f x 在[)2,+∞上递减，证明见解析. 【分析】 （1）令1(2)t t x =≥，则1x t=，求得()1(2)1f t t t =≥-，从而可得答案. （2）()f x 在[)2,+∞上递减，证任取122x x >≥，则210x x -<，1110x ->>，2110x -≥>，可证明()()120f x f x -<，从而可得结论.【详解】 （1）令1(2)t t x =≥，则1x t= 因为11012x f x x x ⎛⎫⎛⎫=<≤⎪ ⎪-⎝⎭⎝⎭所以()111(2)11t tf t t t ==≥--， 所以()1(2)1f x x x =≥-； （2）()f x 在[)2,+∞上递减，证明如下：任取122x x >≥，则210x x -<，1110x ->>，2110x -≥>，因为()()12121111f x f x x x -=--- ()()()()21121111x x x x ---=-- ()()2112011x x x x -=<--所以()()12f x f x <，则()f x 在[)2,+∞上递减.【点睛】方法点睛：利用定义法判断函数的单调性的一般步骤是：（1）在已知区间上任取21x x >；（2）作差()()21f x f x -；（3）判断()()21f x f x -的符号（往往先分解因式，再判断各因式的符号），()()210f x f x -> 可得()f x 在已知区间上是增函数，()()210f x f x -< 可得()f x 在已知区间上是减函数.。

第二章综合测试一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.下列等式一定正确的是（ ）A .()lg lg lg xy x y=+B .222m n m n++=C .222m n m n+×=D .2ln 2ln x x=2.若函数()12122m y m m x -=+-是幂函数，则m =（）A .1B .3-C .3-或1D .23.下列函数既是增函数，图像又关于原点对称的是（ ）A .y x x=B .xy e =C .1y x=-D .2log y x=4.函数()ln 3y x =- ）A .[)23，B .[)2+¥，C .()3-¥，D .()23，5.下列各函数中，值域为()0¥，+的是（ ）A .22xy -=B.y =C .21y x x =++D .113x y +=6.已知()x f x a =，()()log 01a g x x a a =＞，且≠，若()()330f g ＜，那么()f x 与()g x 在同一坐标系内的图像可能是（）A BC D7.已知0.2log 2.1a =， 2.10.2b =，0.22.1c =则（ ）A .c b a＜＜B .c a b＜＜C .a b c＜＜D .a c b＜＜8.已知()()221122x a x x f x x ì-ï=íæö-ïç÷èøî，≥，，＜是R 上的减函数，则实数a 的取值范围是（ ）A .()2-¥，B .138æù-¥çúèû，C .()02，D .1328éö÷êëø，9.已知函数()y f x =是定义在R 上的偶函数，当0x ≥时，()2x f x e x =+，则()ln 2f -=（ ）A .12ln 22-B .12ln 22+C .22ln 2-D .22ln 2+10.已知函数()()()x xf x x e ae x -=+ÎR ，若()f x 是偶函数，记a m =；若()f x 是奇函数，记a n =.则2m n +的值为（ ）A .0B .1C .2D .1-11.已知实数a ，b 满足等式20172018a b =，则下列关系式不可能成立的是（ ）A .0a b ＜＜B .0a b ＜＜C .0b a＜＜D .a b=12.已知函数()221222log x mx m x m f x x x m ì-++ï=íïî，≤，，＞，其中01m ＜＜，若存在实数a ，使得关于x 的方程()f x a=恰有三个互异的实数解，则实数m 的取值范围是（）A .104æöç÷èø，B .102æöç÷èø，C .114æöç÷èøD .112æöç÷èø，二、填空题：本大题共4小题，每小题5分，共20分.13.满足31164x -æöç÷èø＞的x 的取值范围是________.14.若函数()212log 35y x ax =-+在[)1-+¥，上是减函数，则实数a 的取值范围是________.15.如图，矩形ABCD 的三个顶点A ，B ，C分别在函数y x =，12y x =，xy =的图像上，且矩形的边分别平行于两坐标轴.若点A 的纵坐标为2，则点D 的坐标为________.16.定义新运算Ä：当m n ≥时，m n m Ä=；当m n ＜时，m n n Ä=.设函数()()()2221log 2xx f x x éùÄ-Ä×ëû，则函数()f x 在()02，上的值域为________.三、解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.17.（本小题满分10分）计算下列各式的值：（1）7015log 243210.06470.250.58--æö--++´ç÷èø；（2）()2235lg5lg 2lg5lg 20log 25log 4log 9+´++´´.18.（本小题满分12分）已知定义域为R 的单调函数()f x 是奇函数，当0x ＞时，()23x xf x =-.（1）求()f x 的解析式；（2）若对任意的t ÎR ，不等式()()22220f t t f t k -+-＜恒成立，求实数k 的取值范围.19.（本小题满分12分）已知实数x 满足9123270x x -×+≤，函数()2log 2xf x =×（1）求实数x 的取值范围；（2）求函数()f x 的最值，并求此时x 的值.20.（本小题满分12分）已知函数()x f x a =，()2x g x a m =+，其中0m ＞，0a ＞且1a ≠.当[]11x Î-，时，()y f x =的最大值与最小值之和为52.（1）求a 的值；（2）若1a ＞，记函数()()()2h x g x mf x =-，求当[]0x Î，1时，()h x 的最小值()H m .21.（本小题满分12分）以德国数学家狄利克雷（l805-1859）命名的狄利克雷函数定义如下：对任意的x ÎR ，()10.x D x x ì=íî，为有理数，，为无理数研究这个函数，并回答如下问题：（1）写出函数()D x 的值域；（2）讨论函数()D x 的奇偶性；（3）若()()()212x x D x x f x D x x ì-ï=íïî+，为有理数，+，为无理数，，求()f x 的值域.22.（本小题满分12分）若函数()f x 满足()()21log 011a a f x x a a a x æö=×-ç÷-èø＞，且≠.（1）求函数()f x 的解析式，并判断其奇偶性和单调性；（2）当()2x Î-¥，时，()4f x -的值恒为负数，求a 的取值范围.第二章综合测试答案解析一、1.【答案】C【解析】对于A ，D ，若x ，y 为非正数，则不正确；对于B ，C ，根据指数幂的运算性质知C 正确，B 错误.故选C .2.【答案】B【解析】因为函数()12122m y m n x -=+-是幂函数，所以22211m m m +-=且≠，解得3m =-.3.【答案】A【解析】2200x x y x x x x ìï==í-ïî，≥，，＜为奇函数且是R 上的增函数，图像关于原点对称；x y e =是R 上的增函数，无奇偶性；1y x=-为奇函数且在()0-¥，和()0+¥，上单调递增，图像关于原点对称，但是函数在整个定义域上不是增函数；2log y x =在()0+¥，上为增函数，无奇偶性.故选A .4.【答案】A【解析】函数()ln 3y x =-+x 满足条件30240xx -ìí-î＞，≥，解得32x x ìíî＜，≥，即23x ≤＜，所以函数的定义域为[)23，，故选A .5.【答案】A【解析】对于A，22xxy -==的值域为()0+¥，；对于B ，因为120x -≥，所以21x ≤，0x ≤，y =(]0-¥，，所以021x ＜≤，所以0121x -≤＜，所以y =[)01，；对于C ，2213124y x x x æö=++=++ç÷èø的值域是34éö+¥÷êëø，；对于D ，因为()()1001x Î-¥+¥+，∪，，所以113x y +=的值域是()()011+¥，∪，.6.【答案】C【解析】由指数函数和对数函数的单调性知，函数()x f x a =与()()log 01a g x x a a =＞，且≠在()0+¥，上的单调性相同，可排除B ，D .再由关系式()()330f g ×＜可排除A ，故选C .7.【答案】C【解析】 2.100.200.20.2log 2.1log 1000.20.21 2.1 2.1 1.a b c a b c ======\Q ＜，＜＜，＞＜＜.故选C .8.【答案】B【解析】由题意得，函数()()221122x a x x f x x ì-ï=íæö-ïç÷èøî，≥，，＜是R 上的减函数，则()2201122,2a a -ìïíæö--´ïç÷èøî＜，≥解得138a ≤，故选B .9.【答案】D【解析】Q 函数()y f x =是定义在R 上的偶函数，且当0x ≥时，()2x f x e x =+，()()ln 2ln 2ln 22ln 222ln 2f f e \-==+=+.故选D .10.【答案】B【解析】当()f x 是偶函数时，()()f x f x =-，即()()x x x x x e ae x e ae --+=-×+，即()()10x x a e e x -++=.因为上式对任意实数x 都成立，所以1a =-，即1m =-.当()f x 是奇函数时，()()f x f x =--，即()()x x x x x e ae x e ae --+=+，即()()10x x a e e x ---=.因为上式对任意实数x 都成立，所以1a =，即1n =.所以21m n +=.11.【答案】A【解析】分别画出2017x y =，2018x y =的图像如图所示，实数a ，b 满足等式20172018a b =，由图可得0a b ＞＞或0a b ＜＜或0a b ==，而0a b ＜＜不成立.故选A .12.【答案】A【解析】当01m ＜＜时，函数()221222log x mx m x m f x x x m ì-++ï=£íïî，≤，，＞，的大致图像如图所示.Q 当x m ≤时，()()2222222f x x mx m x m =-++=-+≥，\要使得关于x 的方程()f x a =有三个不同的根，则12log 2m ＞.又01m ＜＜，解得104m ＜＜.故选A .二、13.【答案】()1-¥，【解析】由题可得，321144x --æöæöç÷ç÷èøèø＞，则32x --＜，解得1x ＜.14.【答案】(]86--，【解析】令()235g x x ax =-+，其图像的对称轴为直线6a x =.依题意，有()1610ag ì-ïíï-î，＞，即68.a a -ìí-î≤，＞故(]86a Î--，.15.【答案】1124æöç÷èø，【解析】由图像可知，点()2A A x ，在函数y x =的图像上，所以2A x =，212A x ==.点()2B B x ，在函数12y x =的图像上，所以122B x =，4x =.点()4,C C y 在函数x y =的图像上，所以414C y ==.又因为12D A xx ==，14D C y y ==，所以点D 的坐标为1124æöç÷èø，.16.【答案】()112，【解析】根据题意，当22x ≥，即1x ≥时，222x x Ä=；当22x ＜，即1x ＜时，222x Ä=.当2log 1x ≤，即02x ＜≤时，21log 1x Ä=；当21log x ＜，即2x ＞时，221log log x x Ä=.()()2220122122log 2 2.x x x x xx f x x x x ìïï\=-íï-×ïî，＜＜，，≤≤，，＞\①当01x ＜＜时，()2x f x =是增函数，()12f x \＜＜；②当12x ≤＜，()221122224xxx f x æö=-=--ç÷èø，1222 4.x x \Q ≤＜，≤＜()221111242424f x æöæö\----ç÷ç÷èøèø＜，即()212f x ≤＜.综上，()f x 在()02，上的值域为()112，.三、17.【答案】解（1）70515log 244321510.06470.250.51224822--æöæö--++´=-++´=ç÷ç÷èøèø.（2）()()22352lg52lg 22lg3lg5lg 2lg5lg 20log 25log 4log 9lg5lg5lg 2lg 21lg 2lg3lg5+´++´´=++++´´11810=++=.18.【答案】解（1）Q 定义域为R 的函数()f x 是奇函数，()00f \=.Q 当0x ＜时，0x -＞，()23x xf x --\-=-.又Q 函数()f x 是奇函数，()()f x f x \-=-，()23x xf x -\=+.综上所述，()2030020.3xx x x f x x xx -ì-ïï==íïï+î，＞，，，，＜（2）()()51003f f -==Q ＞，且()f x 为R 上的单调函数，()f x \在R 上单调递减.由()()22220f t t f t k -+-＜得()()2222f t t f t k ---＜.()f x Q 是奇函数，()()2222f t t f k t \--＜.又()f x Q 是减函数，2222t t k t \--＞，即2320t t k --＞对任意t ÎR 恒成立，4120k \D =+＜，解得13k -＜，即实数k 的取值范围为13æö-¥-ç÷èø，.19.【答案】解（1）由9123270x x -×+≤，得()23123270xx -×+≤，即()()33390x x --≤，所以339x ≤≤，所以12x ≤≤，满足02x 0.所以实数x 的取值范围为[]12，.（2）()()()()2222222231log log 1log 2log 3log 2log 224xf x x x x x x æö=×=--=-+=--ç÷èø.因为12x ≤≤，所以20log 1x ≤≤.所以2log 1x =，即2x =时，()min 0f x =；当2log 0x =，即1x =时，()max 2f x =.故函数()f x 的最小值为0，此时2x =，最大值为2，此时1x =.20.【答案】解（1）()f x Q 在[]11-，上为单调函数，()f x \的最大值与最小值之和为152a a -+=，2a \=或12a =.（2）1a Q ＞，2a \=.()2222x x h x m m =+-×，即()()2222xx h x m m =-×+.令2x t =，则()h x 可转化为()22k t t mt m =-+，其图像对称轴为直线t m =.[]01x ÎQ ，，[]12t \Î，，\当01m ＜＜时，()()11H m k m ==-+；当12m ≤≤时，()()2H m k m m m ==-+；当2m ＞时，()()234H m k m ==-+.综上所述，()21011234 2.m m H m m m m m m -+ìï=-+íï-+î，＜＜，，≤≤，，＞21.【答案】解（1）函数()D x 的值域为{}01，.（2）当x 为有理数时，则x -为无理数，则()()1D x D x -==；当x 为无理数时，则为x -为无理数，则()()0D x D x -==.故当x ÎR 时，()()D x D x -=，所以函数()D x 为偶函数.（3）由()D x 的定义知，()22x x x f x x ìï=íïî，为有理数，，为无理数.即当x ÎR 时，()2x f x =.故()f x 的值域为()0+¥，.22.【答案】解（1）令log a x t =，则t x a =，()()21t t a f t a a a -\=--.()()()21x x a f x a a x a -\=-Î-R .()()()()2211x x x x a a f x a a a a f x a a ---=-=--=---Q ，()f x \为奇函数.当1a ＞时，x y a =为增函数，xy a -=-为增函数，且2201a a -，()f x \为增函数.当01a ＜＜时，x y a =为减函数，x y a -=-为减函数，且2201a a -＜，()f x \为增函数.()f x \在R 上为增函数.（2）()f x Q 是R 上的增函数，()4y f x \=-也是R 上的增函数.由2x ＜，得()()2f x f ＜，要使()4f x -在()2-¥，上恒为负数，只需()240f -≤，即()22241a a a a ---≤.422141a a a a-\×-≤，214a a \+≤，2410a a \-+≤，22a \-+≤.又1a Q ≠，a \的取值范围为)(21,2éë.。

人教版高中数学必修一第二章 《一元二次函数、方程和不等式》测试题及答案解析(时间：120分钟 满分：150分)一、单项选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．不等式x 2≥2x 的解集是( ) A ．{x |x ≥2} B ．{x |x ≤2} C ．{x |0≤x ≤2}D ．{x |x ≤0或x ≥2}解析：选D 由x 2≥2x 得x (x －2)≥0，解得x ≤0或x ≥2，故选D. 2．若A ＝a 2＋3ab ，B ＝4ab －b 2，则A ，B 的大小关系是( ) A ．A ≤B B ．A ≥B C ．A <B 或A >BD ．A >B解析：选B ∵A－B ＝a 2＋3ab －(4ab －b 2)＝⎝ ⎛⎭⎪⎫a －b 22＋34b 2≥0，∴A ≥B.3．不等式组⎩⎨⎧x 2－1<0，x 2－3x <0的解集为( )A ．{x |－1<x <1}B ．{x |0<x <3}C ．{x |0<x <1}D ．{x |－1<x <3}解析：选C 由⎩⎨⎧x2－1<0，x2－3x<0，得⎩⎨⎧－1<x<1，0<x<3，所以0<x<1，即不等式组的解集为{x|0<x<1}，故选C.4．已知2a ＋1<0，则关于x 的不等式x 2－4ax －5a 2>0的解集是( ) A ．{x |x <5a 或x >－a } B ．{x |x >5a 或x <－a } C ．{x |－a <x <5a }D ．{x |5a <x <－a }解析：选A 方程x 2－4ax －5a 2＝0的两根为－a ，5a.因为2a ＋1<0，所以a<－12，所以－a>5a.结合二次函数y ＝x 2－4ax －5a 2的图象，得原不等式的解集为{x|x<5a 或x>－a}，故选A.5．已知a ，b ，c ∈R ，则下列说法中错误的是( ) A ．a >b ⇒ac 2≥bc 2 B.a c >b c，c <0⇒a <b C ．a 3>b 3，ab >0⇒1a <1bD ．a 2>b 2，ab >0⇒1a <1b解析：选D 对于A ，c 2≥0，则由a>b 可得ac 2≥bc 2，故A 中说法正确； 对于B ，由a c >b c ，得a c －b c ＝a －bc >0，当c<0时，有a －b<0，则a<b ，故B 中说法正确；对于C ，∵a 3>b 3，ab>0，∴a 3>b 3两边同乘1a3b3，得到1b3>1a3，∴1a <1b，故C 中说法正确；对于D ，∵a 2>b 2，ab>0，∴a 2>b 2两边同乘1a2b2， 得到1b2>1a2，不一定有1a <1b，故D 中说法错误．故选D.6．若关于x 的一元二次不等式x 2＋mx ＋1≥0的解集为R ，则实数m 的取值范围是( )A ．m ≤－2或m ≥2B ．－2≤m ≤2C ．m <－2或m >2D ．－2<m <2解析：选B 因为不等式x 2＋mx ＋1≥0的解集为R ，所以Δ＝m 2－4≤0，解得－2≤m≤2.7．某地为了加快推进垃圾分类工作，新建了一个垃圾处理厂，每月最少要处理300吨垃圾，最多要处理600吨垃圾，月处理成本y (元)与月处理量x (吨)之间的函数关系可近似地表示为y ＝12x 2－300x ＋80 000，为使平均处理成本最低，该厂每月处理量应为( )A ．300吨B ．400吨C ．500吨D ．600吨解析：选B 由题意，月处理成本y(元)与月处理量x(吨)的函数关系为y＝12x 2－300x ＋80 000，所以平均处理成本为s ＝y x ＝12x2－300x ＋80 000x ＝x 2＋80 000x －300，其中300≤x≤600，又x 2＋80 000x－300≥2x 2·80 000x－300＝400－300＝100，当且仅当x 2＝80 000x 时等号成立，所以x ＝400时，平均处理成本最低．故选B.8．设正数x ，y ，z 满足x 2－3xy ＋4y 2－z ＝0，则当xy z 取得最大值时，2x ＋1y－2z的最大值是( ) A ．0 B ．1 C.94D ．3解析：选B 由题意得xy z ＝xy x2－3xy ＋4y2＝1x y ＋4y x －3≤14－3＝1，当且仅当x＝2y 时，等号成立，此时z ＝2y 2.故2x ＋1y －2z ＝－1y2＋2y ＝－⎝ ⎛⎭⎪⎫1y －12＋1≤1，当且仅当y ＝1时，等号成立，故所求的最大值为1.二、多项选择题(本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多个选项是符合题目要求的，全部选对的得5分，选对但不全的得3分，有选错的得0分)9．已知不等式ax 2＋bx ＋c >0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12<x <2，则下列结论正确的是( )A ．a >0B ．b >0C ．c >0D ．a ＋b ＋c >0解析：选BCD 因为不等式ax 2＋bx ＋c>0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12<x<2，故相应的二次函数y ＝ax 2＋bx ＋c 的图象开口向下，所以a<0，故A 错误；易知2和－12是关于x 的方程ax 2＋bx ＋c ＝0的两个根，则有c a ＝2×⎝ ⎛⎭⎪⎫－12＝－1<0，－b a ＝2＋⎝ ⎛⎭⎪⎫－12＝32>0，又a<0，故b>0，c>0，故B 、C 正确；因为ca ＝－1，所以a ＋c ＝0，又b>0，所以a ＋b ＋c>0，故D 正确．故选B 、C 、D.10．下列结论中正确的有( )A ．若a ，b 为正实数，a ≠b ，则a 3＋b 3>a 2b ＋ab 2B ．若a ，b ，m 为正实数，a <b ，则a ＋m b ＋m <a bC ．若a c 2>bc2，则a >bD ．当x >0时，x ＋2x的最小值为2 2解析：选ACD 对于A ，∵a ，b 为正实数，a ≠b ，∴a 3＋b 3－(a 2b ＋ab 2)＝(a －b)2(a ＋b)>0，∴a 3＋b 3>a 2b ＋ab 2，故A 正确；对于B ，若a ，b ，m 为正实数，a<b ，则a ＋m b ＋m －a b ＝m （b －a ）b （b ＋m ）>0，则a ＋m b ＋m >ab，故B 错误；对于C ，若a c2>bc2，则a>b ，故C 正确； 对于D ，当x>0时，x ＋2x 的最小值为22，当且仅当x ＝2时取等号，故D正确．故选A 、C 、D.11．下列各式中，最大值是12的是( )A ．y ＝x 2＋116x 2B ．y ＝x 1－x 2(0≤x ≤1)C ．y ＝x 2x 4＋1D ．y ＝x ＋4x ＋2(x >－2) 解析：选BCA中，y ＝x 2＋116x2≥2x2·116x2＝12⎝ ⎛⎭⎪⎫当且仅当x ＝±12时取等号，因此式子无最大值；B 中，y 2＝x 2(1－x2)≤⎝⎛⎭⎪⎫x2＋1－x222＝14，y ≥0， ∴0≤y ≤12，当且仅当x ＝22时y 取到最大值12； C 中，当x ＝0时，y ＝0，当x≠0时，y ＝1x2＋1x2≤12x2·1x2＝12，当且仅当x ＝±1时y 取到最大值12；D 中，y ＝x ＋4x ＋2＝x ＋2＋4x ＋2－2≥2（x ＋2）·4x ＋2－2＝2(x>－2)(当且仅当x ＝0时取等号)，无最大值，故选B 、C.12．某文具店购进一批新型台灯，若按每盏台灯15元的价格销售，每天能卖出30盏，若售价每提高1元，则日销售量将减少2盏．为了使这批台灯每天获得400元以上(不含400)的销售收入，则这批台灯的售价x (元)的取值可以是( )A ．10B ．15C ．16D ．20解析：选BC 设这批台灯的售价定为x 元，x ≥15，则[30－(x －15)×2]·x>400，即x 2－30x ＋200<0，因为方程 x 2－30x ＋200＝0的两根分别为x 1＝10，x 2＝20，所以x 2－30x ＋200<0的解集为{x|10<x<20}，又因为x≥15，所以15≤x<20.故选B 、C.三、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上)13．已知a >b ，a －1a >b －1b同时成立，则ab 应满足的条件是________．解析：因为a －1a >b －1b ，所以⎝ ⎛⎭⎪⎫a －1a －⎝ ⎛⎭⎪⎫b －1b ＝（a －b ）（ab ＋1）ab >0.又a>b ，即a －b>0，所以ab ＋1ab>0，从而ab(ab ＋1)>0，所以ab<－1或ab>0.答案：ab<－1或ab>014．一个大于50小于60的两位数，其个位数字b 比十位数字a 大2.则这个两位数为________．解析：由题意知⎩⎨⎧50<10a ＋b<60，b －a ＝2，0<a ≤9，0≤b ≤9，解得4411<a<5311. 又a∈N*，∴a ＝5.∴b ＝7，∴所求的两位数为57. 答案：5715．一元二次不等式x 2＋ax ＋b >0的解集为{x |x <－3或x >1}，则a ＋b ＝________，一元一次不等式ax ＋b <0的解集为________．解析：由题意知，－3和1是方程x 2＋ax ＋b ＝0的两根， 所以⎩⎨⎧－3＋1＝－a ，－3×1＝b ，解得⎩⎨⎧a ＝2，b ＝－3， 故a ＋b ＝－1.不等式ax ＋b<0即为2x －3<0， 所以x<32.答案：－1⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x<32 16．已知正数x ，y 满足x ＋2y ＝2，则x ＋8yxy的最小值为________． 解析：因为x ，y 为正数，且x ＋2y ＝2，所以x 2＋y ＝1，所以x ＋8yxy ＝⎝ ⎛⎭⎪⎫1y ＋8x ·⎝ ⎛⎭⎪⎫x 2＋y ＝x 2y ＋8yx ＋5≥2x 2y ·8y x ＋5＝9，当且仅当x ＝4y ＝43时，等号成立，所以x ＋8yxy的最小值为9. 答案：9四、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)解下列不等式： (1)2＋3x －2x 2>0； (2)x (3－x )≤x (x ＋2)－1.解：(1)原不等式可化为2x 2－3x －2<0，所以(2x ＋1)(x －2)<0，故原不等式的解集是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－12<x<2. (2)原不等式可化为2x 2－x －1≥0. 所以(2x ＋1)(x －1)≥0，故原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x≤－12或x≥1.18．(本小题满分12分)当p ，q 都为正数且p ＋q ＝1时，试比较代数式(px ＋qy )2与px 2＋qy 2的大小．解：(px ＋qy)2－(px 2＋qy 2)＝p(p －1)x 2＋q(q －1)y 2＋2pqxy. 因为p ＋q ＝1，所以p －1＝－q ，q －1＝－p ，所以(px ＋qy)2－(px 2＋qy 2)＝－pq(x 2＋y 2－2xy)＝－pq(x －y)2. 因为p ，q 都为正数，所以－pq(x －y)2≤0，因此(px ＋qy)2≤px 2＋qy 2，当且仅当x ＝y 时等号成立．19．(本小题满分12分)已知关于x 的方程x 2－2x ＋a ＝0.当a 为何值时， (1)方程的一个根大于1，另一个根小于1?(2)方程的一个根大于－1且小于1，另一个根大于2且小于3?解：(1)已知方程的一个根大于1，另一个根小于1，结合二次函数y ＝x 2－2x ＋a 的图象(如图所示)知，当x ＝1时，函数值小于0，即12－2＋a<0，所以a<1.因此a 的取值范围是{a|a<1}．(2)由方程的一个根大于－1且小于1，另一个根大于2且小于3，结合二次函数y ＝x 2－2x ＋a 的图象(如图所示)知，x 取－1，3时函数值为正，x 取1，2时函数值为负，即⎩⎨⎧1＋2＋a>0，1－2＋a<0，4－4＋a<0，9－6＋a>0，解得－3<a<0.因此a 的取值范围是{a|－3<a<0}．20．(本小题满分12分)已知a >0，b >0且1a ＋2b＝1.(1)求ab 的最小值； (2)求a ＋b 的最小值．解：(1)因为a>0，b>0且1a ＋2b ＝1，所以1a ＋2b≥21a ·2b＝22ab，则22ab≤1， 即ab≥8，当且仅当⎩⎪⎨⎪⎧1a ＋2b ＝1，1a ＝2b ，即⎩⎨⎧a ＝2，b ＝4时取等号，所以ab 的最小值是8. (2)因为a>0，b>0且1a ＋2b ＝1，所以a ＋b ＝⎝ ⎛⎭⎪⎫1a ＋2b (a ＋b)＝3＋b a ＋2ab≥3＋2b a ·2ab＝3＋22， 当且仅当⎩⎪⎨⎪⎧1a ＋2b ＝1，b a ＝2a b ，即⎩⎪⎨⎪⎧a ＝1＋2，b ＝2＋2时取等号，所以a ＋b 的最小值是3＋2 2.21．(本小题满分12分)设y ＝ax 2＋(1－a )x ＋a －2.(1)若不等式y ≥－2对一切实数x 恒成立，求实数a 的取值范围； (2)解关于x 的不等式ax 2＋(1－a )x ＋a －2<a －1(a ∈R)．解：(1)ax 2＋(1－a)x ＋a －2≥－2对于一切实数x 恒成立等价于ax 2＋(1－a)x ＋a≥0对于一切实数x 恒成立．当a ＝0时，不等式可化为x≥0，不满足题意； 当a≠0时，由题意得⎩⎨⎧a>0，（1－a ）2－4a2≤0，解得a≥13.所以实数a的取值范围是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ⎪⎪⎪a ≥13.(2)不等式ax 2＋(1－a)x ＋a －2<a －1等价于ax 2＋(1－a)x －1<0. 当a ＝0时，不等式可化为x<1，所以不等式的解集为{x|x<1}； 当a>0时，不等式可化为(ax ＋1)(x －1)<0，此时－1a<1，所以不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－1a <x<1； 当a<0时，不等式可化为(ax ＋1)(x －1)<0，①当a ＝－1时，－1a＝1，不等式的解集为{x|x≠1}；②当－1<a<0时，－1a >1，不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x<1或x>－1a ；③当a<－1时，－1a <1，不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x<－1a 或x>1. 综上所述，当a<－1时，不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x<－1a 或x>1；当a ＝－1时，不等式的解集为{x|x≠1}；当－1<a<0时，不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x<1或x>－1a ；当a ＝0时，不等式的解集为{x|x<1}；当a>0时，不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－1a <x<1. 22．(本小题满分12分)某企业准备投入适当的广告费对某产品进行促销，在一年内预计销售量Q (万件)与广告费x (万元)之间的关系式为Q ＝3x ＋1x ＋1(x ≥0)．已知生产此产品的年固定投入为3万元，每生产1万件此产品仍需再投入32万元，若该企业产能足够，生产的产品均能售出，且每件销售价为“年平均每件生产成本的150%”与“年平均每件所占广告费的50%”之和．(1)试写出年利润W (万元)与年广告费x (万元)的关系式；(2)当年广告费投入多少万元时，企业年利润最大？最大年利润为多少？ 解：(1)由题意可得，每年产品的生产成本为(32Q ＋3)万元，每万件销售价为⎝⎛⎭⎪⎫32Q ＋3Q ×150%＋x Q ×50%万元， ∴年销售收入为⎝⎛⎭⎪⎫32Q ＋3Q ×150%＋x Q ×50%·Q ＝32(32Q ＋3)＋12x ， ∴W ＝32(32Q ＋3)＋12x －(32Q ＋3)－x＝12(32Q ＋3)－12x ＝12(32Q ＋3－x) ＝－x2＋98x ＋352（x ＋1）(x≥0)．(2)由(1)得，W ＝－x2＋98x ＋352（x ＋1）＝－（x ＋1）2＋100（x ＋1）－642（x ＋1）＝－x ＋12－32x ＋1＋50.∵x ＋1≥1，∴x ＋12＋32x ＋1≥2x ＋12·32x ＋1＝8， ∴W ≤42，当且仅当x ＋12＝32x ＋1，即x ＝7时，W 有最大值42，即当年广告费投入7万元时，企业年利润最大，最大年利润为42万元．。

第二章综合测试一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.若23A a ab =+，24B ab b =-，则A ，B 的大小关系是（ ）A .AB B .A BC .A B ＜或A B ＞D .A B ＞2.下列结论正确的是（ ）A .若ac bc ＞，则a b ＞B .若22a b ＞，则a b ＞C .若a b ＞，0c ＜，则a c b c ++＜D ，则a b ＜3.下列变形是根据等式的性质的是（ ）A .由213x -=得24x =B .由2x x =得1x =C .由29x =得x=3D .由213x x -=得51x =-4.实数a ，b 在数轴上的位置如图所示，以下说法正确的是（ ）A .0a b +=B .b a ＜C .0ab ＞D .||||b a ＜5.已知||a b a ＜＜，则（ ）A .11a b ＞B .1ab ＜C .1a bD .22a b ＞6.若41x -＜＜，则222()1x x f x x -+=-（ ） A .有最小值2B .有最大值2C .有最小值2-D .有最大值2-7.已知0a ＞，0b ＞，2a b +=，则14y a b =+的最小值是（ ） A .72 B .4 C .92 D .58.已知1x ，2x 是关于x 的方程230x bx +-=的两根，且满足121234x x x x +-=，那么b 的值为（ ）A .5B .5-C .4D .4-9.不等式22120x ax a --＜（其中0a ＜）的解集为（ ） A .(3,4)a a - B .(4,3)a a - C .(3,4)-D .(2,6)a a 10.某汽车运输公司购买了一批豪华大客车投入运营.据市场分析，每辆客车营运的总利润y （单位：10万元）与营运年数()*x x ∈N 为二次函数的关系（如图），则每辆客车营运_____年，营运的年平均利润最大（ ）A .3B .4C .5D .611.若正数x ，y 满足35x y xy +=，则34x y +的最小值是（ ）A .245B .285C .5D .612.已知a b ＞，二次三项式220ax x b ++ 对于一切实数x 恒成立，又0x ∃∈R ，使20020ax x b ++=成立，则22a b a b+-的最小值为（ ）A .1BC .2D .二、填空题（本大题共4小题，每小题5分，共20分.请把正确答案填在题中的横线上）13.当1x ＞时，不等式11x a x +-≥恒成立，则实数a 的取值范围为__________. 14.若0a b ＜＜，则1a b -与1a 的大小关系为__________. 15.若正数a ，b 满足3ab a b =++，则ab 的取值范围是__________.16.已知关于x 的一元二次方程2320x x m -+=有两个不相等的实数根1x 、2x .若1226x x -=，则实数m 的值为__________.三、解答题（本大题共6小题，共70分，解答时写出必要的文字说明、证明过程或演算步骤）17.（本小题满分10分）解下列不等式（组）：（1）2(2)01x x x +⎧⎨⎩＞，＜； （2）262318x x x --＜ .18.（本小题满分12分）已知a ，b ，c 为不全相等的正实数，且1abc =.111a b c++＜.19.（本小题满分12分）已知21()1f x x a x a ⎛⎫=-++ ⎪⎝⎭. （1）当12a =时，解不等式()0f x ； （2）若0a ＞，解关于x 的不等式()0f x .20.（本小题满分12分）某镇计划建造一个室内面积为2800 m 的矩形蔬菜温室.在温室内，沿左、右两侧与后侧内墙各保留1 m 宽的通道，沿前侧内墙保留3 m 宽的空地.当矩形温室的边长各为多少时，蔬菜的种植面积最大？最大种植面积是多少？21.（未小题满分12分）设函数2()3(0)f x ax bx a =++≠.（1）若不等式()0f x ＞的解集为(1,3)-，求a ，b 的值；（2）若(1)4f =，0a ＞，0b ＞，求14a b+的最小值.22.（本小题满分12分）解下列不等式.（1）2560x x --+＜；（2）()(2)0a x a x --＞.第二章综合测试答案解析一、1.【答案】B【解析】()2222334240b A B a ab ab b a b ⎛⎫-=+--=-+ ⎪⎝⎭∵ ，A B ∴ . 2.【答案】D【解析】当0c ＜时，A 选项不正确；当0a ＜时，B 选项不正确；两边同时加上一个数，不等号方向不改变，故C 选项错误.3.【答案】A【解析】A .根据等式的性质1，在等式213x -=的左右两边同时加上1，可得24x =，故本选项正确；B .在等式2x x =的左右两边同时除以x ，可得1x =，但是当0x =时，不成立，故本选项错误；C .将等式29x =的左右两边开平方，可得3x =±，故本选项错误；D .根据等式的性质1，在等式213x x -=的左右两边同时加上(31)x +，可得561x x =+，故本选项错误.4.【答案】D【解析】根据题图可知，21a --＜＜，01b ＜＜，所以||||b a ＜.5.【答案】D【解析】由||a b a ＜＜，可知0||||b a ＜ ，由不等式的性质可知22||||b a ＜，所以22a b ＞.6.【答案】D 【解析】2221()(1)11x x f x x x x -+==-+--. 又41x -∴＜＜，10x -∴＜，(1)0x --∴＞1()(1)2(1)f x x x ⎡⎤=---+-⎢⎥--⎣⎦∴ 当且仅当111x x -=-，即0x =时等号成立. 7.【答案】C【解析】2a b +=∵，12a b +=∴ ∴14142a b a b a b +⎛⎫+=+⋅ ⎪⎝⎭52592222a b b a ⎛⎫=+++= ⎪⎝⎭（当且仅当22a b b a =，即423b a ==时，等号成立） 故14y a b =+的最小值为92. 8.【答案】A【解析】12,x x ∵是关于x 的方程230x bx +-=的两根，12x x b +=-∴，123x x =-，121234x x x x +-=∵，94b -+=∴，解得5b =.9.【答案】B【解析】方程22120x ax a --=的两根为4a ，3a -，且43a a -＜，43a x a <<-∴.10.【答案】C【解析】求得函数式为2(6)11y x =--+，则营运的年平均利润2512122y x x x ⎛⎫=-+-= ⎪⎝⎭ ， 当且仅当25x x=时，取“=”号，解得5x =. 11.【答案】C【解析】35x y xy +=∵，13155y x+=∴ 1334(34)1(34)55x y x y x y y x ⎛⎫+=+⨯=++ ⎪⎝⎭∴3941213555555x y y x =++++= 当且仅当31255x y y x =，即1x =，12y =时等号成立. 12.【答案】D【解析】a b ∵＞，二次三项式220ax x b ++≥对于一切实数x 恒成立，0a ∴＞，且440ab ∆=- ，1ab ≥∴.再由0x ∃∈R ，使20020ax x b ++=成立，可得0∆ ，1ab ∴ ，又a b ＞，1a ＞.2224231101a a b a a a b a a a a +++==---∴ 2242484243624222211211211222a a a a a a a a a a a a a a a a ⎛⎫+++ ⎪⎛⎫+++⎝⎭=== ⎪-+-⎛⎫⎝⎭+-+- ⎪⎝⎭ 22222221124412a a a a a a ⎛⎫⎛⎫+-++- ⎪ ⎪⎝⎭⎝⎭=⎛⎫+- ⎪⎝⎭ 令22112a a +=＞，则24231(2)4(2)44(2)444822a t t t a a t t ⎛⎫+-+-+==-+++= ⎪---⎝⎭， 当且仅当4t =，即a =时取等. 故2431a a a ⎛⎫+ ⎪-⎝⎭的最小值为8，故22a b a b +-=. 二、13.【答案】(,3]-∞【解析】1x ∵＞，11(1)11311x x x x +=-+++=--∴ .3a ∴ . 14.【答案】11a b a -＜ 【解析】110()()a ab b a b a a a b a a b -+-==---∵＜. 11a b a-∴＜ 15.【答案】[9,)+∞【解析】33ab a b =+++ ，所以1)0-+ ，3，所以9ab .16.【答案】2-【解析】由题意知123x x +=，1226x x -=∵，即12236x x x +-=，2336x -=∴，解得21x =-，代入到方程中，得1320m ++=，解得2m =-.三、17.【答案】（1）原不等式组可化为 2 0,11,x x x -⎧⎨-⎩＜或＞＜＜ 即01x ＜＜，所以原不等式组的解集为{|01}x x ＜＜.（2）原不等式等价于22623,318,x x x x x ⎧--⎨-⎩≤＜即2260,3180,x x x x ⎧--⎨--⎩＜ 因式分解，得(3)(2)0,(6)(3)0,x x x x -+⎧⎨-+⎩＜ 所以 2 3,36,x x -⎧⎨-⎩或＜＜ 所以132x --＜≤或36x ＜ .所以不等式的解集为{|3236}x x x --＜≤或≤＜.18.【答案】证明：因为a ，b ，c 都是正实数，且1abc =，所以112a b +=11b c +=11a c +=以上三个不等式相加，得1112a b c ⎛⎫++ ⎪⎝⎭，即111a b c+++ 因为a ，b ，c 不全相等，所以上述三个不等式中的“=”不同时成立.111a b c++++＜. 19.【答案】（1）当12a =时，有不等式25()102f x x x =-+≤， 1(2)02x x ⎛⎫-- ⎪⎝⎭∴ ，122x ∴ ，即所求不等式的解集为1,22⎡⎤⎢⎥⎣⎦. （2）1()()0f x x x a a ⎛⎫=-- ⎪⎝⎭∵ ，0a ＞ 且方程1()0x x a a ⎛⎫--= ⎪⎝⎭的两根为1x a =，21x a =， ∴当1a a ＞，即011a ＜＜，不等式的解集为1,a a ⎡⎤⎢⎥⎣⎦； 当1a a ＜，即1a ＞，不等式的解集为1,a a ⎡⎤⎢⎥⎣⎦； 当1a a=，即1a =，不等式的解集为{1}. 20.【答案】设矩形温室的左侧边长为 m a ，后侧边长为 m b ，蔬菜的种植面积为2 m S ，则800ab =.所以(4)(2)4288082(2)808648S a b ab b a a b =--=--+=-+-=当且仅当2a b =，即40a =，20b =时等号成立，则648S =最大值.故当矩形温室的左侧边长为40 m ，后侧边长为20 m 时，蔬菜的种植面积最大，最大种植面积为2648 m .21.【答案】（1）因为不等式()0f x ＞的解集为(1,3)-，所以1-和3是方程()0f x =的两个实根，从而有(1)30,(3)9330,f a b f a b -=-+=⎧⎨=++=⎩解得1,2,a b =-⎧⎨=⎩（2）由(1)4f =，得1a b +=，又0a ＞，0b ＞， 所以1414()a b a b a b ⎛⎫+=++ ⎪⎝⎭4559b a a b =+++= 当且仅当4b a a b =即1,32,3a b ⎧=⎪⎪⎨⎪=⎪⎩时等号成立， 所以14a b+的最小值为9.22.【答案】（1）2560x x --+<∵，2560x x +->∴，(1)(6)0x x -+∴＞，解得6x -＜或1x ＞，∴不等式2560x x --+＜的解集是{| 6 1}x x x -＜或＞.（2）当0a ＜时，()(2)y a x a x =--的图象开口向下，与x 轴交点的横坐标为x a =，2x =，且2a <， ()(2)0a x a a --∴＞的解集为{|2}x a x ＜＜.当0a =时，()(2)0a x a x --=，()(2)0a x a x --∴＞无解.当0a ＞时，抛物线()(2)y a x a x =--的图像开口向上，与x 轴交点的横坐标为x a =，2x =.当2a =时，不等式可化为22(2)0x -＞，解得2x ≠.当2a ＞时，解得2x ＜或x a ＞.当2a ＜时，解得x a ＜或2x ＞.综上，当0a ＜时，不等式的解集是{|2}x a x ＜＜；当0a =时，不等式的解集是∅；当02a ＜＜时，不等式的解集是{| 2}x x a x ＜或＞；当2a =时，不等式的解集是{|2}x x ≠；当2a ＞时，不等式的解集是{|2}x x x a ＜或＞.。

高中数学必修一第二章一、单选题1．已知集合A ={x‖x ―2|<1}， B ={x |x 2―2x ―3<0}.则A ∩B =A ．{x |1<x <3}B ．{x |―1<x <3}C ．{x |―1<x <2}D ．{x |x >3}2．下列结论成立的是（ ）A ．若ac ＞bc ，则a ＞bB ．若a ＞b ，则a 2＞b 2C ．若a ＞b ，c ＜d ，则a+c ＞b+dD ．若a ＞b ，c ＞d ，则a ﹣d ＞b ﹣c3．已知关于 x 的不等式 a x 2―2x +3a <0 在 (0,2] 上有解，则实数 a 的取值范围是（ ）A ．(―∞,33)B ．(―∞,47)C ．(33,+∞)D ．(47,+∞)4．当x ＞3时，不等式x+1x ―1≥a 恒成立，则实数a 的取值范围是（ ） A ．（﹣∞，3]B ．[3，+∞）C ．[ 72，+∞）D ．（﹣∞， 72]5．下列不等式恒成立的是（ ）A ．a 2+b 2≤2abB ．a +b ≥―2|ab |C ．a 2+b 2≥―2abD ．a +b ≤2|ab |6．已知 x >2 ，函数 y =4x ―2+x 的最小值是（ ） A ．5B ．4C ．8D ．67．设正实数x ，y ，z 满足x 2―3xy +4y 2―z =0，则当xy z取得最大值时，2x +1y ―2z 的最大值是（ ）A ．0B ．1C ．94D ．38．已知正数x ，y 满足x+y ＝1，且 x 2y +1+y 2x +1≥m ，则m 的最大值为（ ） A ．163B ．13C ．2D ．4二、多选题9．设正实数a ，b 满足a +b =1，则（ ）A ．a 2b +b 2a ≥14B ．1a +2b +12a +b ≥43C ．a 2+b 2≥12D ．a 3+b 3≥1410．若a ，b ∈(0，+∞)，a +b =1，则下列说法正确的有（ ）A ．(a +1a)(b +1b )的最小值为4B ．1+a +1+b 的最大值为6C．1a +2b的最小值为3+22D．2aa2+b+ba+b2的最大值是3+23311．已知a，b是正实数，若2a+b=2，则（ ）A．ab的最大值是12B．12a+1b的最小值是2C．a2+b2的最小值是54D．14a+b+2a+b的最小值是3212．已知a，b，c为实数，则下列命题中正确的是（ ）A．若a c2<bc2，则a<b B．若ac>bc，则a>bC．若a>b，c>d，则a+c>b+d D．若a<b<0，则1a >1 b三、填空题13．不等式﹣2x（x﹣3）（3x+1）＞0的解集为 ．14．已知正实数x，y满足xy―x―2y=0，则x+y的最小值是 . 15．已知a，b均为正数，且ab―a―2b=0，则a24+b2的最小值为 ．16．以max A表示数集A中最大的数．已知a>0，b>0，c>0，则M=max{1c +ba,1ac+b,ab+c}的最小值为 四、解答题17．已知U=R且A={x∣x2―5x―6<0}，B={x∣―4≤x≤4}，求：（1）A∪B；（2）(C U A)∩(C U B)．18．解下列关于x的不等式:（1）x2―2x―3≤0;（2）―x2+4x―5>0;（3）x2―ax+a―1≤019．已知关于x的不等式2x2+x>2ax+a(a∈R)．（1）若a=1，求不等式的解集;（2）解关于x的不等式．20．某县一中计划把一块边长为20米的等边三角形ABC的边角地辟为植物新品种实验基地，图中DE 需把基地分成面积相等的两部分，D在AB上，E在AC上．（1）设AD=x（x≥10），ED=y，试用x表示y的函数关系式；（2）如果DE是灌溉输水管道的位置，为了节约，则希望它最短，DE的位置应该在哪里？如果DE 是参观线路，则希望它最长，DE的位置又应该在哪里？说明理由．答案解析部分1．【答案】A2．【答案】D3．【答案】A4．【答案】D5．【答案】C6．【答案】D7．【答案】B8．【答案】B9．【答案】B,C,D10．【答案】B,C,D11．【答案】A,B12．【答案】A,C,D13．【答案】（﹣∞，﹣1）∪（0，3）314．【答案】3+2215．【答案】816．【答案】217．【答案】（1）解：因为A={x∣x2―5x―6<0}=(―1，6)，且B={x∣―4≤x≤4}=[―4，4]，则A ∪B=[―4，6)．（2）解：由（1）可知，A=(―1，6)，B=[―4，4]，则C U A=(―∞，―1]∪[6，+∞)，C U B=(―∞，―4)∪(4，+∞)，所以(C U A)∩(C U B)=(―∞，―4)∪[6，+∞)．18．【答案】（1）解：x2―2x―3≤0,(x―3)(x+1)≤0⇒x≤―1或x≥3,故解集为: (―∞,―1]∪[3,+∞).（2）解：―x2+4x―5>0,∴x2―4x+5<0⇒(x―2)2+1<0⇒x无解,故解集为: ∅（3）解：x2―ax+a―1≤0,∴[x―(a―1)](x―1)≤0,当a―1<1,即a<2时,解集为[a―1,1],当a―1=1,即a=2时,解集为x=1,当 a ―1>1 ,即 a >2 时,解集为 [1,a ―1] .所以:当 a <2 时,解集为 [a ―1,1] ,当 a =2 时,解集为 x =1 ,当 a >2 时,解集为 [1,a ―1] .19．【答案】（1）解：2x 2+x >2ax +a ，∴x (2x +1)>a (2x +1)，∴(x ―a )(2x +1)>0，当a =1时，可得解集为{x |x >1或x <―12}.（2）对应方程的两个根为a ，―12，当a =―12时，原不等式的解集为{x |x ≠―12}，当a >―12时，原不等式的解集为{x |x >a 或x <―12}，当a <―12时，原不等式的解集为{x |x <a 或x >―12}.20．【答案】（1）解：∵△ABC 的边长是20米，D 在AB 上，则10≤x≤20，S △ADE = 12S △ABC ，∴12 x•AEsin60°= 12 • 34 •（20）2，故AE= 200x，在三角形ADE 中，由余弦定理得：y= x 2+4⋅104x 2―200 ，（10≤x≤20）；（2）解：若DE 作为输水管道，则需求y 的最小值， ∴y= x 2+4⋅104x 2―200 ≥ 400―200 =10 2 ，当且仅当x 2= 4⋅104x 2即x=10 2 时“=”成立．。

完整版)高中数学必修一第二章测试题(含答案)1.已知p>q>1,0<a<1，则下列各式中正确的是：A。

ap>aq B。

pa>qa C。

a-p>a-q D。

p-a>q-a正确答案：A解析：因为p>q>1，所以p-q>0，又因为0<a<1，所以a 的p-q次方小于1，即a^p-q<1，所以ap<aq，即选项A正确。

2.已知f(10x)=x，则f(5)=？A。

105 B。

510 C。

lg10 D。

lg5正确答案：B解析：将f(10x)=x代入x=5/10=1/2中，得到f(1/2)=5，又因为f(5)=f(1/2)/10=5/10=1/2，所以选项B正确。

3.当a≠0时，函数y=ax+b和y=ba^x的图象只可能是？正确答案：直线和指数函数曲线解析：当a=1时，y=x+b和y=be^x，即两个函数都是直线；当a>1时，y=ax+b的图象是一条上升的直线，y=ba^x的图象是一条上升的指数函数曲线；当0<a<1时，y=ax+b的图象是一条下降的直线，y=ba^x的图象是一条下降的指数函数曲线。

4.当a≠1时，函数y=a^(x+b)和y=b^(ax)的图象只可能是？正确答案：指数函数曲线解析：y=a^(x+b)可以化为y=a^b*a^x，因此是一条上升的指数函数曲线；y=b^(ax)可以化为y=(b^a)^x，因此也是一条上升的指数函数曲线。

5.设y1=4,y2=80.90.48，y3=1/2，则递增区间是？正确答案：(0，+∞)解析：因为y1<y3<y2，所以递增区间是(0，+∞)。

6.下列函数中，在区间(0，+∞)上为增函数的是？A。

y=ln(x+2) B。

y=-x+1 C。

y=1/(1+x) D。

y=sin(x)正确答案：A解析：求导可得y'=(1/(x+2))>0，所以y在区间(0，+∞)上为增函数，因此选项A正确。

一、选择题1．已知a >0，b >0，a +b =1，则下列等式可能成立的是（ ） A ．221a b += B ．1ab = C ．212a b +=D ．2212a b -=2．已知函数22(0)y ax bx c a =+->的图象与x 轴交于()2,0A 、()6,0B 两点，则不等式220cx bx a +-< 的解集为（ ） A ．(6,2)-- B ．11,,62⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭C ．11,26--⎛⎫⎪⎝⎭D ．11,,26⎛⎫⎛⎫-∞--+∞ ⎪ ⎪⎝⎭⎝⎭3．若,a b ∈R ，且0ab >，则下列不等式中恒成立的是（ ）A ．222a b ab +>B ．a b +≥C ．11a b +>D ．2b aa b+≥ 4．下列函数中，最大值为12的是（ ）A ．22116y x x=+B ．yC ．241x y x =+D ．()422y x x x =+>-+ 5．函数2()f x x bx c =++对任意实数t 满足()(4)f t f t =-，则(1),(2),(4)f f f 的大小关系是（ ） A ．(1)(2)(4)f f f << B ．(2)(1)(4)f f f << C ．(4)(2)(1)f f f <<D ．(4)(1)(2)f f f <<6．已知不等式20ax bx c ++>的解集是{}41x x -<<，则不等式2(1)(3)0b x a x c -+++>的解集为（ ）A ．{}14x x -<< B ．413x x ⎧⎫-<<⎨⎬⎩⎭C ．413x x x⎧⎫⎨⎬⎩⎭或 D ．{}21x x x -或7．已知2x >，那么函数42y x x =+-的最小值是（ ） A ．5B ．6C ．4D ．88．若对于任意的x ＞0，不等式231xa x x ≤++恒成立，则实数a 的取值范围是( )A ．a ≥15B ．a ＞15C ．a ＜15D ．a ≤159．两个正实数a ，b 满足3a ，12，b 成等差数列，则不等式2134m m a b+≥+恒成立时实数m 的取值范围是（ ） A ．[]4,3- B ．[]2,6- C ．[]6,2- D ．[]3,4-10．若不等式2210ax ax ++>对任意的x ∈R 恒成立，则实数a 的取值范围是（ ）A ．[)0,1B ．[)0,+∞C ．(](),01,-∞+∞ D ．()0,111．下列命题正确的是（ ） A ．若a bc c>，则a b > B ．若22a b >，则a b >C ．若2211a b>，则a b < D <a b <12．若a ＞b ，则下列不等式一定成立的是（ ）. A ．11a b< B ．55a b > C ．22ac bc >D ．a b >二、填空题13．已知函数2()22b a f x ax x =+-，当[1,1]x ∈-时，1()2f x ≥-恒成立，则+a b 的最大值为________.14．定义,,a a ba b b a b ≥⎧⊗=⎨<⎩，若,0x y >，则222241616xy y x xy x y μ⎛⎫⎛⎫++=⊗ ⎪ ⎪⎝⎭⎝⎭的最小值____________.15．已知函数2()21f x x ax =-+，若对∀(]0,2x ∈，恒有()0f x ≥，则实数a 的取值范围是___________．16．已知正实数m ，n 满足119222m n m n +++=，则2m n +的最小值是_______． 17．已知向量()2,1a y =-，(),3b x =，且a b ⊥，若x ，y 均为正数，则32x y+的最小值是______．18．若命题“对任意实数0a >，0b >且4a b +=，不等式41m a b+>恒成立”为假命题，则m 的取值范围为_______.19．一批救灾物资随51辆汽车从某市以/vkm h 的速度匀速直达灾区，已知两地公路线长400km ，为了安全起见，两辆汽车的间距不得小于2800v km ，那么这批物资全部到达灾区，最少需要______.h20．已知函数3()3f x x x =-，若对任意的实数x ，不等式()()(0)f x t f x t t +>+≠恒成立，则实数t 的取值范围__________．三、解答题21．近年来，某西部乡村农产品加工合作社每年消耗电费24万元.为了节能环保，决定修建一个可使用16年的沼气发电池，并入该合作社的电网.修建沼气发电池的费用（单位：万元）与沼气发电池的容积x （单位：米3）成正比，比例系数为0.12.为了保证正常用电，修建后采用沼气能和电能互补的供电模式用电.设在此模式下，修建后该合作社每年消耗的电费C （单位：万元）与修建的沼气发电池的容积x （单位：米3）之间的函数关系为()50kC x x =+（0x ≥，k 为常数）.记该合作社修建此沼气发电池的费用与16年所消耗的电费之和为F （单位：万元）.（1）解释()0C 的实际意义，并写出F 关于x 的函数关系；（2）该合作社应修建多大容积的沼气发电池，可使F 最小，并求出最小值.（3）要使F 不超过140万元，求x 的取值范围.22．对于四个正数x y z w ，，，，如果xw yz <，那么称()x y ，是()z w ，的“下位序对”． （1）对于23711，，，，试求()27，的“下位序对”； （2）设a b c d ，，，均为正数，且()a b ，是()c d ，的“下位序对”，试判断c a a cd b b d++，，之间的大小关系.23．已知关于x 的不等式2120x mx +-<的解集为(6,)n -. （1）求实数m ，n 的值；（2）正实数a ，b 满足22na mb +=. ①求11a b+的最小值； ②若2160a b t +-≥恒成立，求实数t 的取值范围.24．已知不等式()21460a x x --+>的解集为{}31x x -<<．（1）解不等式()2220x a x a +-->；（2）b 为何值时，230ax bx ++≥的解集为R ？25．已知二次函数()f x 满足()01f =，()()125f x f x x +-=+. （1）求()f x 的解析式；（2）若[]3,1x ∈-，若()25f x m m ≤-恒成立，求实数m 的取值范围.26．已知0a b c d >>>>，ad bc =． （Ⅰ）证明：a d b c +>+； （Ⅱ）证明：a b c b c a a b c a b c >．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】根据已知条件由2()2a b ab +≤可求出2212a b +≥，又由完全平方公式可得221a b +<，即可判断A 、B ；由已知条件可知01b <<，则2b b >，因此22212a b a b +>+≥，可判断C ；由平方差公式可得12a b -=，与1a b +=联立可求出满足条件的a 、b ，故D 可能成立. 【详解】001a b a b >>+=，，2222211()21212()12()222a b a b a b ab ab +∴+=+-=-≥-⋅=-⨯=， 当且仅当12a b ==时等号成立， 又0ab >，222()2121b a b a ab a b +=+-=-<∴，22112a b ≤+<∴，则221a b +=不可能成立； 2211()()224a b ab ≤==+，当且仅当12a b ==时等号成立，故1ab =不可能成立；001a b a b >>+=，，，01b ∴<<，2b b ∴>，22212b a b a +>+≥∴（由A 可知），则212a b +=不可能成立； ()()2212a b a b a b a b -=+-=-=，联立112a b a b +=⎧⎪⎨-=⎪⎩，解得31,44a b ==，满足条件，D 成立. 故选：D2．D解析：D 【分析】利用函数图象与x 的交点，可知()2200ax bx c a +-=>的两个根分别为12x =或26x =，再利用根与系数的关系，转化为4b a =-，12c a =-，最后代入不等式220cx bx a +-<，求解集.【详解】由条件可知()2200ax bx c a +-=>的两个根分别为12x =或26x =，则226b a +=-，26ca⨯=-，得4b a =-，12c a =-， 22201280cx bx a ax ax a ∴+-<⇔---<，整理为：()()21281021610x x x x ++>⇔++>， 解得：16x >-或12x <-， 所以不等式的解集是11,,26⎛⎫⎛⎫-∞--+∞ ⎪ ⎪⎝⎭⎝⎭. 故选：D 【点睛】思路点睛：本题的关键是利用根与系数的关系表示4b a =-，12c a =-，再代入不等式220cx bx a +-<化简后就容易求解.3．D解析：D 【分析】利用基本不等式的性质来逐一判断正误即可. 【详解】对于A ，222a b ab +≥，当且仅当a b =时，等号成立，故A 错误；对于B 、C ，虽然0ab >，只能说明,a b 同号，若,a b 都小于0时，则不等式不成立，故B ，C 错误；对于D ，0ab >，,0b aa b∴>，2b a a b ∴+≥，当且仅当a b =时，等号成立，故D 正确； 故选：D. 【点睛】易错点睛：本题考查基本不等式的相关性质，利用基本不等式求最值时，要注意其必须满足的三个条件：一正、二定、三相等，考查学生的逻辑推理能力，属于基础题.4．C解析：C 【分析】 用排除法求解． 【详解】由于20x >，因此22116y x x=+无最大值，A 错；[0,1]y =，最小值为0，最大值为1，B 错； 2x >-，20x +>，42y x x =++无最大值，D 错， 只有C 正确、 故选：C ． 【点睛】关键点点睛：本题考查求函数的最大值．对于单选题可以从简单入手，利用排除法确定正确选项．实际上C 可以用基本不等式求解：24()1x f x x =+，0x =时，(0)0f =，0x ≠时，221()1f x x x =+， 而2212x x +≥，当且仅当1x =±时等号成立，∴10()2f x <≤， 综上有()f x 的值域是1[0,]2，最大值为12． 5．B解析：B 【分析】由题意知()f x 关于2x =对称，结合函数解析式即可判断(1),(2),(4)f f f 的大小. 【详解】由对任意实数t 满足()(4)f t f t =-，知：()f x 关于2x =对称， 由函数2()f x x bx c =++知：图象开口向上，对称轴为22bx =-=， ∴()f x 在[2,)+∞上单调递增，而(1)(41)(3)f f f =-=，∴(2)(1)(4)f f f <<. 故选：B 【点睛】本题考查了二次函数的性质，根据对称性，结合二次函数的性质比较函数值的大小，属于基础题.6．B解析：B 【分析】根据不等式的解集与对应的方程根的关系的关系求得3,4b a c a ==-且0a <，化简不等式为2340x x +-<，结合一元二次不等式的解法，即可求解. 【详解】由题意，不等式20ax bx c ++>的解集是{}41x x -<<， 可得4x =-和1x =是方程20ax bx c ++=的两根，且0a <，所以4141b a c a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩，可得3,4b a c a ==-，所以不等式2(1)(3)0b x a x c -+++>可化为23(1)(3)40a x a x a -++->， 因为0a <，所以不等式等价于23(1)(3)40x x -++-<， 即234(1)(34)0x x x x +-=-+<，解得413x -<<， 即不等式2(1)(3)0b x a x c -+++>的解集为413x x ⎧⎫-<<⎨⎬⎩⎭. 故选：B. 【点睛】解答中注意解一元二次不等式的步骤：（1）变：把不等式变形为二次项系数大于零的标准形式； （2）判：计算对应方程的判别式；（3）求出对应的一元二次方程的根，或根据判别式说明方程有没有实根； （4）利用“大于取两边，小于取中间”写出不等式的解集.7．B解析：B 【分析】根据基本不等式可求得最小值． 【详解】 ∵2x >，∴442+24+2622y x x x x =+=+-≥==--，当且仅当422x x =--，即4x =时等号成立．∴y 的最小值是6． 故选：B ． 【点睛】本题考查用基本不等式求最值，利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.8．A解析：A 【分析】由于x ＞0，对不等式左侧分子分母同时除以x ，再求出左侧最大值即可求解. 【详解】由题：对于任意的x ＞0，不等式231xa x x ≤++恒成立，即对于任意的x ＞0，不等式113ax x≤++恒成立，根据基本不等式：10,335x x x >++≥+=，当且仅当1x =时，取得等号， 所以113x x++的最大值为15， 所以15a ≥. 故选：A【点睛】此题考查不等式恒成立求参数范围，通过转化成求解函数的最值问题，结合已学过的函数模型进行求解，平常学习中积累常见函数处理办法可以事半功倍.9．C解析：C 【分析】由题意利用等差数列的定义和性质求得13a b =+，再利用基本不等式求得112ab，根据题意，2412m m +，由此求得m 的范围． 【详解】解：两个正实数a ，b 满足3a ，12，b 成等差数列， 13a b ∴=+，123ab ∴，112ab∴，∴112ab． ∴不等式2134m m a b ++恒成立，即234a b m m ab++恒成立， 即214m m ab+恒成立． 2412m m ∴+，求得62m -，故选：C ． 【点睛】本题主要考查等差数列的定义和性质，不等式的恒成立问题，基本不等式的应用，属于基础题．10．A解析：A 【分析】设函数()221f x ax ax =++，把不等式2210ax ax ++>在x ∈R 上恒成立，转化为()0f x >对于x R ∀∈恒成立，结合函数的性质，即可求解.【详解】解：设函数()221f x ax ax =++，则不等式2210ax ax ++>在x ∈R 上恒成立，即()0f x >对于x R ∀∈恒成立， 当0a =时，()10f x =>，显然成立； 当0a ≠时，要使()0f x >在x ∈R 上恒成立，需函数()221f x ax ax =++开口向上，且与x 轴没有交点，即20(2)410a a a >⎧⎨∆=-⨯⨯<⎩，解得01a <<， 综上知，实数a 的取值范围为[0,1).故选：A. 【点睛】本题主要考查了不等式的恒成立问题，以及二次函数的图象与性质的应用，其中解答中把不等式的恒成立问题转化为利用二次函数的性质求解是解答的关键，着重考查转化思想，以及推理与计算能力.11．D解析：D 【分析】A 项中，需要看分母的正负；B 项和C 项中，已知两个数平方的大小只能比较出两个数绝对值的大小.【详解】A 项中，若0c <，则有a b <，故A 项错误；B 项中，若22a b >，则a b >，故B 项错误；C 项中，若2211a b>则22a b <即a b <，故C 项错误；D <定有a b <，故D 项正确. 故选：D 【点睛】本题主要考查不等关系与不等式，属于基础题.12．B解析：B 【分析】利用函数的单调性、不等式的基本性质即可判断出结论． 【详解】 a ＞b ，则1a 与1b的大小关系不确定；由函数y =x 5在R 上单调递增，∴a 5＞b 5； c =0时，ac 2=bc 2；取a =-1，b =-2，|a |＞|b |不成立．因此只有B 成立． 故选B ． 【点睛】本题考查了函数的单调性、不等式的基本性质，考查了推理能力与计算能力，属于基础题．二、填空题13．2【分析】由时恒成立转化为恒成立根据中ab 系数相等令求解【详解】因为时恒成立所以恒成立令则或当时即当时即要使时的等号成立则即解得函数图象开口向上对称轴为所以则的最大值为2故答案为：2【点睛】关键点点解析：2 【分析】由[1,1]x ∈-时，1()2f x ≥-恒成立，转化为211222xa xb ⎛⎫-+≥- ⎪⎝⎭恒成立，根据+a b中，a ，b 系数相等，令2122xx -=求解. 【详解】因为[1,1]x ∈-时，1()2f x ≥-恒成立， 所以2211()22222b a x f x ax x a x b ⎛⎫=+-=-+≥- ⎪⎝⎭恒成立， 令2122x x -=，则12x =-或1x =，当1x =时，()21122a b f =+≥- ，即1a b +≥-， 当12x =-时，112442a b f ⎛⎫-=--≥- ⎪⎝⎭，即2a b +≤， 要使12x =-时，1()2f x ≥-的等号成立， 则min 11()22f x f ⎛⎫=-=- ⎪⎝⎭，即14211114422b a a b a ⎧-=-⎪⎪⎨⎪--=-⎪⎩， 解得2343a b ⎧=⎪⎪⎨⎪=⎪⎩，203a =>，函数图象开口向上，对称轴为12x =-， 所以则+a b 的最大值为2，故答案为：2【点睛】关键点点睛：由+a b 中，a ，b 系数相等，令2122x x -=是本题求解的关键.. 14．【分析】换元判定单调性利用基本不等式求解【详解】令则在为增函数在在为减函数从而当且仅当时取等号故答案为：【点睛】易错点睛：利用基本不等式求最值时要注意其必须满足的三个条件：（1）一正二定三相等一正就 解析：94【分析】换元判定单调性，利用基本不等式求解【详解】 令y t x =，则 22244xy y t t x+=+在()0,∞+为增函数， 22216111616x xy y t t+=+在在()0,∞+为减函数， 从而22111942164t t t t μ⎛⎫≥+++≥ ⎪⎝⎭， 当且仅当12t =时取等号. 故答案为：94【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方15．【分析】利用参变分离得在上恒成立结合双勾函数性质求出的最小值即可【详解】解：由题意知：在上恒成立所以在上恒成立又因为函数在上单调递减在上单调递增所以当时最小为2所以即故答案为：【点睛】方法点睛：在解 解析：1a ≤【分析】 利用参变分离得2112x a x x x+≤=+在(]02x ∈，上恒成立，结合双勾函数性质求出1y x x=+的最小值即可． 【详解】 解：由题意知：()2210f x x ax =-+≥在(]02x ∈，上恒成立，所以2112x a x x x +≤=+在(]02x ∈，上恒成立， 又因为函数1y x x=+在()01x ∈，上单调递减，在()12x ∈，上单调递增，所以当1x =时，1x x+最小为2， 所以2a ≤2，即1a ≤，故答案为：1a ≤．【点睛】方法点睛：在解决二次函数的恒成立问题，常常采用参变分离法，如此可以避免对参数进行分类讨论．16．【分析】利用基本不等式可求得再结合可得从而可求出的取值范围即可得到的最小值【详解】由题意当且仅当时等号成立又所以令则解得所以即的最小值是故答案为：【点睛】关键点点睛：本题考查求代数式的最值解题关键是 解析：32【分析】()1112222n m m n m n m n ⎛⎫++=+++ ⎪⎝⎭，利用基本不等式，可求得()119222m n m n ⎛⎫++≥ ⎪⎝⎭，再结合()119222m n m n +=-+，可得()()992222m n m n ⎡⎤+-+≥⎢⎥⎣⎦，从而可求出2m n +的取值范围，即可得到2m n +的最小值.【详解】由题意，()11155922222222n m m n m n m n ⎛⎫++=+++≥+=+= ⎪⎝⎭，当且仅当n m m n=时，等号成立， 又()119222m n m n +=-+，所以()()()1199222222m n m n m n m n ⎛⎫⎡⎤++=+-+≥ ⎪⎢⎥⎝⎭⎣⎦， 令2m n t +=，则9922t t ⎛⎫-≥ ⎪⎝⎭，解得332t ≤≤， 所以32,32m n ⎡⎤+∈⎢⎥⎣⎦，即2m n +的最小值是32. 故答案为：32. 【点睛】关键点点睛：本题考查求代数式的最值，解题关键是利用基本不等式求出()119222m n m n ⎛⎫++≥ ⎪⎝⎭，再根据()119222m n m n ⎛⎫+++= ⎪⎝⎭，可得到只包含2m n +的关系式()()992222m n m n ⎡⎤+-+≥⎢⎥⎣⎦，从而可求出2m n +的范围.考查学生的逻辑推理能力，计算求解能力，属于中档题.17．8【分析】由题意利用两个向量垂直的性质基本不等式求得的最大值可得要求式子的最小值【详解】解：向量且若均为正数则当且仅当时取等号则故答案为：8【点睛】本题主要考查两个向量垂直的性质基本不等式的应用属于 解析：8【分析】由题意利用两个向量垂直的性质，基本不等式，求得xy 的最大值，可得要求式子的最小值．【详解】 解：向量(2,1)a y =-，(,3)b x =，且a b ⊥，∴23(1)0a b x y =+-=．若x ，y 均为正数，则23326x y xy +=，38xy∴，当且仅当3232x y ==时，取等号．则32233838y x x y xy ++==，故答案为：8． 【点睛】本题主要考查两个向量垂直的性质，基本不等式的应用，属于中档题．18．【分析】利用基本不等式求出的最小值可得不等式恒成立时的取值范围再取其补集即可【详解】若不等式对任意实数且恒成立则当且仅当且即时等号成立所以故命题为假命题时的取值范围为故答案为:【点睛】本题主要考查命 解析：94m ≥ 【分析】 利用基本不等式求出41a b +的最小值，可得不等式41m a b+>恒成立时，m 的取值范围，再取其补集即可.【详解】若不等式41m a b+>对任意实数0a >，0b >且4a b +=恒成立，则411411419()()(5)5)4444b a a b a b a b a b +=++=++≥=， 当且仅当4b a a b =且4a b +=，即83a =，43b =时等号成立. 所以94m <，故命题为假命题时，m 的取值范围为94m ≥. 故答案为: 94m ≥【点睛】本题主要考查命题的真假，基本不等式的应用，属于中档题.19．10【分析】用速度v 表示时间结合基本不等式计算最小值即可【详解】当最后一辆车子出发第一辆车子走了小时最后一辆车走完全程共需要小时所以一共需要小时结合基本不等式计算最值可得故最小值为10小时【点睛】考 解析：10【分析】用速度v 表示时间，结合基本不等式，计算最小值，即可．【详解】当最后一辆车子出发，第一辆车子走了25080016v v v ⋅=小时，最后一辆车走完全程共需要400v 小时，所以一共需要40016v v +小时，结合基本不等式，计算最值，可得4001016v v +≥=，故最小值为10小时 【点睛】考查了基本不等式计算函数最值问题，关键利用a b +≥中等．20．【分析】代入函数解析式可得不等式等价于任意的实数恒成立利用判别式小于0即可求解【详解】不等式恒成立即恒成立整理得恒成立可知则任意的实数恒成立解得（舍去）或实数的取值范围是故答案为：【点睛】本题考查一 解析：()4,+∞【分析】代入函数解析式可得不等式等价于223340x tx t 任意的实数x 恒成立，利用判别式小于0即可求解.【详解】 3()3f x x x =-，不等式()()(0)f x t f x t t +>+≠恒成立，即()()3333x t x t x x t +-+>-+恒成立，整理得2233340tx t x t t 恒成立，可知0t >，则223340x tx t 任意的实数x 恒成立，2234340t t ，解得4t <-（舍去）或4t >， ∴实数t 的取值范围是()4,+∞.故答案为：()4,+∞.【点睛】本题考查一元二次不等式的恒成立，属于基础题.三、解答题21．（1）()0C 的实际意义是未修建沼气发电池时，该合作社每年消耗的电费；192000.1250F x x =++，0x ≥；（2）该合作社应修建容积为350立方米的沼气发电池时，可使F 最小，且最小值为90万元；（3）3050100,3⎡⎤⎢⎥⎣⎦. 【分析】（1）根据题中函数关系式，可直接得到()0C 的实际意义；求出k ，进而可得F 关于x 的函数关系；（2）根据（1）中F 的函数关系，利用基本不等式，即可求出最小值；（3）将140F ≤，转化为关于x 的不等式，求解即可.【详解】（1）()0C 的实际意义是修建这种沼气发电池的面积为0时的用电费用，即未修建沼气发电池时，该合作社每年消耗的电费；由题意可得，()02450k C ==，则1200k =； 所以该合作社修建此沼气发电池的费用与16年所消耗的电费之和为120019200160.120.125050F x x x x =⨯+=+++，0x ≥； （2）由（1）()19200192000.120.125065050F x x x x =+=++-++690≥=， 当且仅当()192000.125050x x =++，即350x =时，等号成立, 即该合作社应修建容积为350立方米的沼气发电池时， 可使F 最小，且最小值为90万元；（3）为使F 不超过140万元，只需192000.1214050F x x =+≤+， 整理得2333503050000x x -+≤，则()()330501000x x --≤，解得30501003x ≤≤， 即x 的取值范围是3050100,3⎡⎤⎢⎥⎣⎦【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.22．无23．无24．无25．无26．无。