八年级数学《几何证明初步》练习题

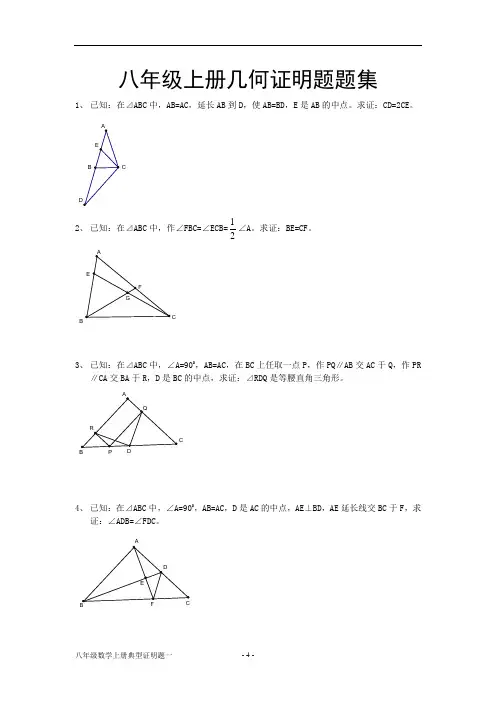
C八年级上册几何证明题题集1、 已知：在⊿ABC 中，AB=AC ，延长AB 到D ，使AB=BD ，E 是AB 的中点。

求证：CD=2CE 。

2、 已知：在⊿ABC 中，作∠FBC=∠ECB=21∠A 。

求证：BE=CF 。

B3、 已知：在⊿ABC 中，∠A=900，AB=AC ，在BC 上任取一点P ，作PQ ∥AB 交AC 于Q ，作PR∥CA 交BA 于R ，D 是BC 的中点，求证：⊿RDQ 是等腰直角三角形。

CB4、 已知：在⊿ABC 中，∠A=900，AB=AC ，D 是AC 的中点，AE ⊥BD ，AE 延长线交BC 于F ，求证：∠ADB=∠FDC 。

ABB DCA B C DE P 图 ⑴5、如图甲，Rt ∆ABC 中，AB=AC ，点D 、E 是线段AC 上两动点，且AD=EC ，AM ⊥BD ，垂足为M ，AM 的延长线交BC 于点N ，直线BD 与直线NE 相交于点F 。

（1）试判断∆DEF 的形状，并加以证明。

（2）如图乙，若点D 、E 是直线AC 上两动点，其他条件不变，试判断∆DEF 的形状，并加以证明。

6、已知：在⊿ABC 中BD 、CE 是高，在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ，求证：MA ⊥NA 。

7、已知：如图(1)，在△ABC 中，BP 、CP 分别平分∠ABC 和∠ACB ，DE 过点P 交AB 于D ，交AC 于E ，且DE ∥BC ．求证：DE －DB=EC ．①②③图88、△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM=CN，直线BN与AM相交于Q点，就下面给出的三种情况，如图8中的①②③，先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度．并利用图③证明你的结论．9、在Rt△ABC中，AB＝AC，∠BAC=90°，O为BC的中点。

(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明)；(2)如果点M、N分别在线段AB、AC上移动，在移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。

几何证明初步练习题1、三角形的内角和定理：三角形的内角和等于180°．推理过程：○1 作CM ∥AB ，则∠A= ，∠B= ，∵∠ACB +∠1+∠2=1800（ ，∴∠A+∠B+∠ACB=1800． ○2 作MN ∥BC ，则∠2= ，∠3= ，∵∠1+∠2+∠3=1800，∴∠BAC+∠B+∠C=1800． 2．求证：在一个三角形中，至少有一个内角大于或者等于60°。

3、.如图，在△ABC 中，∠C ＞∠B,求证：AB ＞AC 。

4. 已知，如图，AE5. 已知：如图，EF ∥AD ，∠1 =∠2. 求证：∠AGD ＋∠BAC = 180°.反证法经典例题6.求证:两条直线相交有且只有一个交点.7.如图，在平面内，AB 是L 的斜线，CD 是L 的垂线。

求证：AB 与CD 必定相交。

8.2一．角平分线－－轴对称9、已知在ΔABC 中，Ｅ为ＢＣ的中点，AD 平分BAC ∠，BD ⊥AD 于D ．AB ＝9，ＡＣ＝13求ＤＥ的长第9题图 第10题图 第11题图分析：延长ＢＤ交ＡＣ于Ｆ．可得ΔABD ≌ΔAFD ．则BD ＝DF ．又BE ＝EC ，即D Ｅ为ΔBCF 的中位线．∴DE=12FC=12(AC-AB)=2． 10、已知在ΔABC 中，108A ∠=，AB ＝AC ，BD 平分ABC ∠．求证：BC ＝AB ＋CD ． 分析：在ＢＣ上截取ＢＥ＝ＢＡ，连接ＤＥ．可得ΔBAD ≌ΔBED ．由已知可得：18ABD DBE ∠=∠=，108A BED ∠=∠=，36C ABC ∠=∠=．∴72DEC EDC ∠=∠=，∴CD＝CE ，∴BC ＝AB ＋CD ．11、如图，ΔABC 中，Ｅ是BC 边上的中点，DE ⊥BC 于E ，交BAC ∠的平分线AD 于D ，过D 作DM ⊥AB 于Ｍ，作DN ⊥ＡC 于N ．求证：BM ＝CN ．分析：连接DB 与DC ．∵DE 垂直平分BC ，∴DB ＝DC ．易证ΔAMD ≌ΔAND ．∴有DM ＝DN ．∴ΔBMD ≌ΔCND （ＨＬ）．∴BM ＝CN ．二、旋转12、如图，已知在正方形ABCD 中，Ｅ在BC 上，Ｆ在DC 上，BE ＋DF＝EF ．求证：45EAF ∠=． C B ADE F D A B C B A E D NM B D A C分析：将ΔADF 绕Ａ顺时针旋转90得ABG ．∴GAB FAD ∠=∠．易证ΔAGE ≌ΔAFE ．∴ 1452FAE GAE FAG ∠=∠=∠= 13、如图，点E 在ΔABC 外部，D 在边BC 上，DE 交AC 于F ．若123∠=∠=∠，ＡＣ＝ＡＥ．求证：ΔABC ≌ΔADE ．分析：若ΔABC ≌ΔADE ，则ΔADE 可视为ΔABC 绕Ａ逆时针旋转1∠所得．则有B ADE ∠=∠．∵12B ADE ∠+∠=∠+∠，且12∠=∠．∴B ADE ∠=∠．又∵13∠=∠．∴BAC DAE ∠=∠．再∵ＡＣ＝ＡＥ．∴ΔABC ≌ΔADE ．14、如图，点Ｅ为正方形ＡＢＣＤ的边ＣＤ上一点，点Ｆ为ＣＢ的延长线上的一点，且ＥＡ⊥ＡＦ．求证：ＤＥ＝ＢＦ．分析：将ΔABF 视为ΔADE 绕Ａ顺时针旋转90即可．∵90FAB BAE EAD BAE ∠+∠=∠+∠=．∴FBA EDA ∠=∠． 又∵90FBA EDA ∠=∠=，ＡＢ＝ＡＤ．∴ΔABF ≌ΔADE ．（ＡＳＡ）∴ＤＥ＝ＤＦ． 平移第14题图 第15题图 第16题图 第17题图三、平移15、如图，在梯形ABCD 中，BD ⊥AC ，AC ＝８，BD ＝１５．求梯形ABCD 的中位线长． 分析：延长ＤＣ到Ｅ使得ＣＥ＝ＡＢ．连接ＢＥ．可得ACEB ．可视为将ＡＣ平移到ＢＥ．ＡＢ平移到ＣＥ．由勾股定理可得ＤＥ＝１７．∴梯形ＡＢＣＤ中位线长为８．５．16、已知在ΔABC 中，AB ＝AC ，D 为AB 上一点，Ｅ为AC 延长线一点，且BD ＝CE ．求证：DM ＝EM 分析：作ＤＦ∥ＡＣ交ＢＣ于Ｆ．易证ＤＦ＝ＢＤ＝ＣＥ．则ＤＦ可视为ＣＥ平移所得．∴四边形ＤＣＥＦ为DCEF ．∴ＤＭ＝ＥＭ．线段中点的常见技巧 --倍长四、倍长17、已知，ＡＤ为ABC 的中线．求证：ＡＢ＋ＡＣ>２ＡＤ．分析：延长ＡＤ到Ｅ使得ＡＥ＝２ＡＤ．连接ＢＥ易证ΔBDE ≌ΔCDA ．∴ＢＥ＝ＡＣ．∴ＡＢ＋ＡＣ>２ＡＤ．18、如图，AD 为ΔABC 的角平分线且BD ＝CD ．求证：AB ＝AC ． 分析：延长ＡＤ到Ｅ使得ＡＤ＝ＥＤ．易证ΔABD ≌ΔECD ．∴ＥＣ＝ＡＢ． ∵BAD CAD ∠=∠．∴E CAD ∠=∠．∴ＡＣ＝ＥＣ＝ＡＢ． 19、已知在等边三角形ＡＢＣ中，Ｄ和Ｅ分别为ＢＣ与ＡＣ上的点，且ＡＥ＝ＣＤ．连接ＡＤ与ＢＥ交于点Ｐ，作ＢＱ⊥ＡＤ于Ｑ．求证：ＢＰ＝２ＰＱ．分析：延长ＰＤ到Ｆ使得ＦＱ＝ＰＱ．在等边三角形ＡＢＣ中ＡＢ＝ＢＣ＝ＡＣ，60ABD C ∠=∠=．又∵ＡＥ＝ＣＤ，∴ＢＤ＝ＣＥ．∴ΔABD ≌ΔBCE ．∴CBE BAD ∠=∠．∴60BPQ PBA PAB PBA DBP ∠=∠+∠=∠+∠=．易证ΔBPQ ≌ΔBFQ ．得ＢＰ＝ＢＦ，又60BPD ∠=．∴ΔBPF 为等边三角形．∴ＢＰ＝２ＰＱ．中位线五、中位线、中线：20、已知在梯形ABCD 中，AD ∥BC ，Ｅ和Ｆ分别为BD 与AC 的中点, 求证：1()2EF BC AD =-． 分析：取ＤＣ中点Ｇ，连接ＥＧ与ＦＧ．则ＥＧ为ΔBCD 中位线，ＦＧ为ΔACD 的中位线． ∴ＥＧ∥＝12BC ，FG ∥＝12AD ．∵AD ∥BC ．∴过一点Ｇ有且只有一条直线平行于已知直线ＢＣ，即Ｅ、Ｆ、Ｇ共线．∴1()2EF BC AD =-． 直角三角形斜边上的中线等于斜边的一半21、已知，在ABCD 中BD AB 21=．Ｅ为ＯＡ的中点，Ｆ为ＯＤ中点，Ｇ为ＢＣ中点． 求证：ＥＦ＝ＥＧ．分析：连接ＢE ．∵BD AB 21=，ＡＥ＝O Ｅ．∴ＢＥ⊥ＣＥ，∵ＢＧ＝ＣＧ． ∴BD EG 21=．又ＥＦ为ΔAOD 的中位线．∴AD EF 21=．∴ＥＦ＝ＥＧ． 22、在ΔABC 中，ＡＤ是高，ＣＥ是中线，ＤＣ＝ＢＥ，ＤＧ⊥ＣＥ于Ｇ．求证：（１）ＣＧ＝ＥＧ．（２）2B BCE ∠=∠．分析：（１）连接ＤＥ．则有ＤＥ＝ＢＥ＝ＤＣ．∴Rt ΔCDG ≌Rt ΔEDG （ＨＬ）．∴ＥＧ＝ＣＧ．∵ＤＥ＝ＢＥ．∴B BDE DEC BCE ∠=∠=∠+∠．∵ＤＥ＝ＣＤ．∴DEC BCE ∠=∠．∴2B BCE ∠=∠．几何证明初步测验题（1）一、选择题（每空3 分，共36 分）1、使两个直角三角形全等的条件是（ ）A 、一组锐角对应相等B 、两组锐角分别对应相等C 、一组直角边对应相等D 、两组直角边分别对应相等2、如图，已知AB ∥CD ，∠A ＝50°，∠C ＝∠E ．则∠C ＝（ ）A ．20°B ．25°C ．30°D ．40°第2题图 第4题图 第6题图 第7题图3、用反证法证明命题“一个三角形中不能有两个角是直角”，应先假设这个三角形中（ ）A ．有两个角是直角B ．有两个角是钝角C ．有两个角是锐角D ．一个角是钝角，一个角是直角4、如图，直线AB 、CD 相交于点O ，∠BOE=90°，OF 平分∠AOE ，∠1=15°30’，则下列结论不正确的是( ) A D B E F OC B E F ED G AA．∠2=45° B．∠1=∠3 C．∠AOD+∠1=180° D．∠EOD=75°30’5、下列说法中，正确的个数为（）①三角形的三条高都在三角形内，且都相交于一点②三角形的中线都是过三角形的某一个顶点，且平分对边的直线③在△ABC中，若∠A=12∠B=13∠C，则△ABC是直角三角形④一个三角形的两边长分别是8和10，那么它的最短边的取值范围是2<b<18A．1个 B．2个 C．3个 D．4个6、如图，在AB=AC的△ABC中，D是BC边上任意一点，DF⊥AC于F，E在AB边上，使ED⊥BC于D，∠AED=155°，则∠EDF等于（）A、50°B、65°C、70°D、75°7、如图，已知△ABC是等腰直角三角形，∠A=90°，BD是∠ABC的平分线，DE⊥BC于E，若BC=10cm，则△DEC的周长为（）A．8cm B．10cm C．12cm D．14cm8、如图，已知△ABC中，∠ABC=45°，AC=4，H是高AD和BE的交点，则线段BH的长度为（）A. B.9、如图，正方形ABCD内有两条相交线段MN、EF，M、N、E、F分别在边AB、CD、AD、BC上．小明认为：若MN = EF，则MN⊥EF；小亮认为: 若MN⊥EF，则MN = EF．你认为（）A．仅小明对 B．仅小亮对 C．两人都对 D．两人都对第9题图第10题图第11题图第12题图10、如图，△ABC为等边三角形，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，•则四个结论正确的是（）．①点P在∠A的平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.A．全部正确; B．仅①和②正确; C．仅②③正确; D．仅①和③正确11、如图，△ABC中，CD⊥AB于D，一定能确定△ABC为直角三角形的条件的个数是（）①∠1=∠②③∠+∠2=90°④=3:4:5 ⑤A．1 B．2 C．3 D．412、如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA＝CQ时，连PQ交AC边于D，则DE的长为（）A．13B．12C．23D．不能确定二、填空题（每空3 分，共15 分）13、命题“对顶角相等”中的题设是_________ ,结论是___________ 。

初二数学几何证明题（5篇可选）第一篇：初二数学几何证明题1.在△ABC中，AB=AC，D在AB上，E在AC的延长线上，且BD=CE，线段DE交BC于点F，说明：DF=EF。

2.已知：在正方形ABCD中，M是AB的中点，E是AB延长线上的一点，MN垂直DM于点M，且交∠CBE的平分线于点N.（1）求证：MD＝MN.（2）若将上述条件中的“M是AB的中点”改为“M 是AB上任意一点”其余条件不变，则（1）的结论还成立吗？如果成立，请证明，如果不成立，请说明理由。

3.。

如图，点E,F分别是菱形ABCD的边CD和CB延长线上的点，且DE=BF，求证∠E=∠F。

4，如图，在△ABC中，D,E,F,分别为边AB,BC,CA,的中点，求证四边形DECF为平行四边形。

5.如图，在菱形ABCD中，∠DAB=60度，过点C作CE垂直AC 且与AB的延长线交与点E，求证四边形AECD是等腰梯形？6.如图，已知平行四边形ABCD中，对角线AC,BD，相交与点0，E是BD延长线上的点，且三角形ACE是等边三角形。

1.求证四边形ABCD是菱形。

2.若∠AED=2∠EAD，求证四边形ABCD是正方形。

7.已知正方形ABCD中，角EAF=45度，F点在CD边上，E点在BC边上。

求证：EF=BE+DF第二篇：初二几何证明题1如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=DCCF．（1）求证：D是BC的中点；（2）如果AB=ACADCF的形状，并证明你的结论AEB第三篇：初二几何证明题初二几何证明题1.已知：如图，在△ABC中，AD⊥BC，垂足为D，BE⊥AC，垂足为E。

M为AB中点，联结ME,MD、ED求证：角EMD=2角DAC证明：∵M为AB边的中点，AD⊥BC，BE⊥AC，∴MD=ME=MA=MB(斜边上的中线=斜边的一半)∴△MED为等腰三角形∵ME=MA∴∠MAE=∠MEA∴∠BME=2∠MAE∵MD=MA∴∠MAD=∠MDA,∴∠BMD=2∠MAD,∵∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC2.如图，已知四边形ABCD中，AD=BC,E、F分别是AB、CD中点，AD、BC的延长线与EF的延长线交于点H、D求证：∠AHE=∠BGE证明：连接AC，作EM‖AD交AC于M，连接MF.如下图：∵E是CD的中点，且EM‖AD，∴EM=1/2AD，M是AC的中点，又因为F是AB的中点∴MF‖BC，且MF=1/2BC.∵AD=BC，∴EM=MF，三角形MEF为等腰三角形，即∠MEF=∠MFE.∵EM‖AH，∴∠MEF=∠AHF ∵FM‖BG，∴∠MFE=∠BGF∴∠AHF=∠BGF.3.写出“等腰三角形两底角的平分线相等”的逆命题，并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知BD平分∠ABC,CE平分∠ACB,BD=CE,求证:AB=AC证明:BD平分∠ABC==>BE/AE=BC/AC==>BE/AB=BC/(BC+AC)==>BE=AB*BC/(BC+AC)同理:CD=AC*BC/(BC+AB)假设AB≠AC,不妨设AB>AC.....(*)AB>AC==>BC+ACAC*BC==>AB*AB/(BC+AC)>AC*BC/(BC+AB)==>BE>CDAB>AC==>∠ACB>∠ABC∠BEC=∠A+∠ACB/2,∠BDC=∠A+∠ABC/2==>∠BEC>∠BDC过B作CE平行线,过C作AB平行线,交于F,连DF则BECF为平行四边形==>∠BFC=∠BEC>∠BDC (1)BF=CE=BD==>∠BDF=∠BFDCF=BE>CD==>∠CDF>∠CFD==>∠BDF+∠CDF>∠BFD+∠CFD==>∠BDC>∠BFC (2)(1)(2)矛盾,从而假设(*)不成立所以AB=AC。

第5章几何证明初步检测题（时间：90分钟，满分：100分）一、选择题（每小题3分，共30分）1. 下列语句中，不是命题的是（）A．若两角之和为90°，则这两个角互补B．同角的余角相等C．作线段的垂直平分线D．相等的角是对顶角2. 下列语句中属于定义的是（）A．直角都相等B．作已知角的平分线C．连接两点的线段的长度，叫做这两点间的距离D．两点之间，线段最短3. 下面关于定理的说法不正确的是（）A．定理是真命题B．定理的正确性不需要证明C．定理可以作为推理论证的依据D．定理的正确性需证明4. 如图，在等边△中，，则等于（）A. B. C. D.5.如图，已知，，，结论：①；②；③；④△≌△．其中正确的有（）A.1个B.2个C.3个D.4个6. 对于图中标记的各角，下列条件能够推理得到∥的是（）A．∠1=∠2 B. ∠2=∠4C. ∠3=∠4 D．∠1+∠4=180°7.如图，∥，，若，则等于（）A. B. C. D.8.如图,在四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是（）A.AB=ADB.CA平分∠BCDC.AB=BDD.△BEC≌△DEC9.如图，直线AB、CD交于点O，OT⊥AB于O，CE∥AB交CD于点C，若∠ECO=30°，则∠DOT等于（）第6题图A ．30°B ．45°C ．60°D ．120°10. 图中有四条互相不平行的直线L 1、L 2、L 3、L 4所截出的七个角，关于这七个角的度数关系，下列选项正确的是（ ）A ．∠2=∠4+∠7B ．∠3=∠1+∠6C ．∠1+∠4+∠6=180°D ．∠2+∠3+∠5=360° 二、填空题（每小题3分，共24分）11. 写一个与直角三角形有关的定理 .12. 如图，一个直角三角形纸片，剪去直角后，得到一个四边形， 则∠1+∠2= 度．13. 如图所示，将△ABC 沿着DE 翻折，若∠1+∠2=80°，则∠B = 度．14. 若一个三角形的三个内角之比为4∶3∶2，则这个三角形的最大内角为 度. 15. 如图，在△ABC 中，AB =AC ，∠BAC =54°，∠BAC 的平分线与AB 的垂直平分线交于点O ，将∠C 沿EF （E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合，则∠OEC = . 16. 如图，将三角形的直角顶点放在直尺的一边上，∠1=30°，∠3=20°，则∠2= .17. 请写出一个原命题是真命题，逆命题是假命题的命题： . 18. 如图，AB ∥CD ，∠ABE =66°，∠D =54°，则∠E = 度． 三、解答题（共46分）19.（6分） 下列句子是命题吗？若是，把它改写成“如果……那么……” 的形式，并判断是否正确．（1）一个角的补角比这个角的余角大多少度？ （2）垂线段最短，对吗？（3）等角的补角相等．（4）两条直线相交只有一个交点． （5）同旁内角互补．（6）邻补角的角平分线互相垂直.20.（8分）如图，在四边形ABCD 中，点E 在边CD 上，连接AE 、BE ，给出下列五个关系式：①AD ∥BC ；②DE =CE ；③∠1=∠2；④∠3=∠4；⑤AD +BC =AB .将其中的三个关系式作为题设，另外两个作为结论，便构成一个命题．第10题图第12题图第13题图第9题图第16题图第18题图（1）用序号写出一个真命题（书写形式：如果×××，那么×××），并给出证明． （2）用序号再写出三个真命题（不要求证明）.21.（8分）如图，CD =CA ，∠1=∠2，EC =BC ，求证：DE =AB ． 22.（8分）如图，是∠内的一点，，，垂足分别为，． 求证：（1）； （2）点在∠的平分线上．23.（8分）如图，点B ，F ，C ，E 在一条直线上，∠A =∠D ，AC =DF ，且AC ∥DF ．求证：△ABC ≌△DEF ．24.（8分）如图，已知DG ⊥BC ，AC ⊥BC ，EF ⊥AB ，∠1=∠2，求证：CD ⊥AB第24题图 第20题图 第23题图 第21题图第5章几何证明初步检测题参考答案1. C 解析：根据命题的定义，可知A、B、D都是命题，而C属于作图语言，不是命题．故选C．2. C 解析：A是直角的性质，不是定义；B是作图语言，不是定义；C是定义；D是公理，不是定义．故选C．3. B 解析：根据定理的定义，可知A，C，D是正确的，B是错误的．故选B．4.C 解析：在等边△中，有，.又因为，所以△≌△，所以．所以．故选C．5. C 解析：因为，，，所以△≌△（AAS），所以，所以，即故③正确.又因为，，所以△≌△（ASA）.所以.故①正确. 由△≌△，知，又因为，，所以△≌△，故④正确.由于条件不足，无法证得②故正确的结论有：①③④.6. D 解析：A.∠1与∠2是邻角，不是被第三条直线所截得的同位角或内错角，不能推出平行；B.∠2+∠3与∠4是被截得的同位角，而∠2与∠4不是，不能推出平行；C.∠3与∠4，不是被截得的同位角，不能推出平行；D.∠1+∠4=180°，∠1的对顶角与∠4是被截得的同旁内角，能推出平行．故选D．7. C 解析：因为∥，所以.因为，所以.如图，过点作∠∠交于点，则△≌△，所以，因为，所以．8.C 解析：∵AC垂直平分BD，∴AB=AD,BC=DC,∠BCE=∠DCE,∴CA平分∠BCD.AB与BD不一定相等，故选C.9.C 解析：∵CE∥AB，∴∠DOB=∠ECO=30°.∵OT⊥AB，∴∠BOT=90°，∴∠DOT=∠BOT-∠DOB=90°-30°=60°．故选C．10.C 解析：根据四条互相不平行的直线L1、L2、L3、L4所截出的七个角，可知∠1+∠4+∠6=180°．故选C．11.直角三角形两直角边的平方和等于斜边的平方解析：本题是一道开放型题目，只要保证命题是真命题即可.12.270 解析：如图，根据题意可知∠5=90°，∴∠3+∠4=90°，∴∠1+∠2=180°+180°-（∠3+∠4）=360°-90°=270°.13.40 解析：∵△ABC沿着DE翻折，∴∠1+2∠BED=180°，∠2+2∠BDE=180°，∴∠1+∠2+2（∠BED+∠BDE）=360°，而∠1+∠2=80°，∠B+∠BED+∠BDE=180°，∴ 80°+2（180°-∠B）=360°，第12题答图∴ ∠B =40°．14.80 解析：这个三角形的最大内角为180°×49=80°． 15. 108° 解析：如图，连接OB ，OC . ∵ ∠BAC =54°，AO 为∠BAC 的平分线， ∴又∵ AB =AC ， ∴.∵ DO 是AB 的垂直平分线， ∴ OA =OB ，∴ ∠ABO =∠BAO =27°，∴ ∠OBC=∠ABC-∠ABO =63°-27°=36°.∵ DO 是AB 的垂直平分线，AO 为∠BAC 的平分线， ∴ 点O 是△ABC 的外心， ∴ OB=OC ，∴ ∠OCB =∠OBC =36°，∵ 将∠C 沿EF （E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合， ∴ OE=CE ， ∴ ∠COE =∠OCB =36°. 在△OCE 中，∠OEC =180°-∠COE -∠OCB =180°-36°-36°=108°． 16. 50° 解析：如图，由三角形的外角性质可得∠4=∠1+∠3=50°，∵ ∠2和∠4是两平行线间的内错角，∴ ∠2=∠4=50°．17. 对顶角相等（答案不唯一） 解析：本题是一道开放性题目，答案不唯一，只要符合条件即可．把一个命题的条件和结论互换就得到它的逆命题．正确的命题叫真命题，错误的命题叫假命题．18. 12 解析：∵ AB ∥CD ，∴ ∠BFC =∠ABE =66°. 在△EFD 中，利用三角形的外角等于与它不相邻的两个内角的和，得到∠BFC =∠E +∠D , ∴ ∠E =∠BFC -∠D =12°．19.分析：根据命题的定义先判断出哪些是命题，再把命题的题设写在“如果”后面，结论放在“那么”后面．解：对一件事情做出判断的句子是命题，因为（1）（2）是问句，所以（1）（2）不是命题，其余4个都是命题．（3）如果两个角相等，那么它们的补角相等，正确； （4）如果两条直线相交，那么它们只有一个交点，正确； （5）如果两个角是同旁内角，那么它们互补，错误；（6）如果两条射线是邻补角的角平分线，那么它们互相垂直，正确. 20.分析：（1）如果①②③，那么④⑤．过E 点作EF ∥AD ，与AB 交于点F ，根据平行线的性质推出EF 为梯形ABCD 的中位线，根据平行线的性质和等量代换，即可推出∠4=∠3，AB =2EF ，通过2EF =AD +BC ，即可推出AB =AD +BC .（2）根据真命题的定义，写出命题即可． 解：（1）如果①②③，那么④⑤．证明如下：如图，过E 点作EF ∥AD ，与AB 交于点F . ∵ AD ∥BC ，∴ EF ∥BC .∵ DE =CE ，∴ AF =BF .即EF为梯形ABCD 的中位线，∴ 2EF =AD +BC ，第20题答图 第16题答图∴∠1=∠AEF，∠4=∠FEB.∵∠1=∠2，∴∠2=∠AEF，∴AF=EF.∵AF=BF，∴BF=EF，∴∠3=∠FEB，∴∠4=∠3.∵AB=AF+BF，∴AB=2EF.∵ 2EF=AD+BC，∴AB=AD+BC．（2）如果①②④，那么③⑤；如果①③④，那么②⑤；如果①②⑤，那么③④．21.分析：根据三角形全等的判定，由已知先证∠ACB=∠DCE，再根据SAS可证△ABC≌△DEC，继而可得出结论．证明：∵∠1=∠2，∴∠1+∠ECA=∠2+∠ACE，即∠ACB=∠DCE.在△ABC和△DEC中，∵CA＝CD，∠ACB＝∠DCE，BC＝EC，∴△ABC≌△DEC（SAS）．∴DE=AB．22.分析：（1）连接AP，根据HL证明△APF≌△APE，可得到PE=PF；（2）利用（1）中的全等，可得出∠F AP=∠EAP，那么点P在∠BAC的平分线上．证明：（1）如图，连接AP并延长，∵ PE⊥AB，PF⊥AC，∴∠AEP=∠AFP=90°.在Rt△AEP和Rt△AFP中，AE=AF，AP=AP，∴ Rt△AEP≌Rt△AFP（HL），∴PE=PF．（2）∵ Rt△AEP≌Rt△AFP，∴∠EAP=∠FAP，∴ AP是∠BAC的角平分线，故点P在∠BAC的角平分线上．23.分析：利用ASA证明两个三角形全等即可．证明：∵AC∥DF，∴∠ACB=∠DFE．在△ABC和△DEF中，∠A＝∠D，AC＝DF，∠ACB＝∠DFE，∴△ABC≌△DEF．24.分析：灵活运用垂直的定义，注意由垂直可得90°角，由90°角可得垂直，结合平行线的判定和性质，只要证得∠ADC=90°，即可得CD⊥AB．证明：∵DG⊥BC，AC⊥BC（已知），∴∠DGB=∠ACB=90°（垂直的定义），∴DG∥AC（同位角相等，两直线平行）.∴∠2=∠ACD（两直线平行，内错角相等）.∵∠1=∠2（已知），∴∠1=∠ACD（等量代换），∴EF∥CD（同位角相等，两直线平行）.∴∠AEF=∠ADC（两直线平行，同位角相等）.∵EF⊥AB（已知），∴∠AEF=90°（垂直的定义），∴∠ADC=90°（等量代换）.∴CD⊥AB（垂直的定义）．。

初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．（初二）.如下图做GH ⊥AB,连接EO 。

由于GOFE 四点共圆，所以∠GFH ＝∠OEG ,即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ，所以CD=GF 得证。

APDAFGCEBOD2、已知：如图，P是正方形ABCD内点，∠PAD＝∠PDA＝150．求证：△PBC是正三角形．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF =GOGH=COCD,又CO=EO，所以CD=GF得证。

.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF =GOGH=COCD,又CO=EO，所以CD=GF得证。

3、如图，已知四边形ABCD、A1B1C1D1都是正方形，A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点．求证：四边形A2B2C2D2是正方形．（初二）4、已知：如图，在四边形ABCD中，AD＝、CD的中点，AD、BC的延长线交求证：∠DEN＝∠F．D2C2B2A2D1C1B1C BD AA1经典题（二）1、已知：△ABC中，H为垂心（各边高线的交点），O为外心，且OM⊥BC于M．（2）若∠BAC＝600，求证：AH＝AO．F2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于条直线，交圆于B 、C 及D 、E ，直线EB 及Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点． 求证：点P 到边AB 的距离等于AB经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ． 求证：AE ＝AF ．3、设P是正方形ABCD一边BC上的任一点，PF⊥AP，CF平分∠DCE．求证：PA＝PF．（初二）4、如图，PC切圆O于C，ACAF与直线PO相交于B、D经典题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PC ＝5．求：∠APB的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA． 求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD中，设E、F分别是BC、AB上的一点，AE与CF相交于P，且AE＝CF．求证：∠DPA＝∠DPC．（初二）经典难题（五）1、设P是边长为1的正△ABC内任一点，L求证：≤L＜2．2、已知：P 是边长为1的正方形ABCD的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

青岛版八年级上册数学第5章几何证明初步含答案一、单选题(共15题，共计45分)1、为了从500只外形相同的鸡蛋中找到唯一的一只双黄蛋，检查员将这些鸡蛋按1－500的顺序排成一列，第一次先从中取出序号为单数的蛋，发现其中没有双黄蛋，他将剩下的蛋的原来位置上又按1－250编号（即原来的2号变为1号，原来的4号变成2号，…，原来的500号变成250号）。

又从中取出新序号为单数的蛋进行检查，任没有发现双黄蛋，……，如此下去，检查到最后的一个是双黄蛋，问这只双黄蛋最初的序号是（）A.48B.250C.256D.5002、已知三角形ABC的三个内角满足关系∠B＋∠C=3∠A，则此三角形( ).A.一定有一个内角为45°B.一定有一个内角为60°C.一定是直角三角形D.一定是钝角三角形3、如图，在四边形ABCD中，∠DAB的角平分线与∠ABC的外角平分线相交于点P，且∠D+∠C=200°，则∠P=（）A.10°B.20°C.30°D.40°4、如图，把一块含45°角的三角板的直角顶点靠在长尺（两边a∥b）的一边b上，若∠1=30°，则三角板的斜边与长尺的另一边a的夹角∠2的度数为（）A.10°B.15°C.30°D.35°5、如图所示，点E在AC的延长线上，下列条件中不能判断BD∥AE的是（）A.∠D＝∠DCEB.∠D＋∠ACD＝180°C.∠1＝∠2D.∠3＝∠46、在△ABC中，∠A，∠B，∠C的对边分别是a，b，c，满足下列条件的△ABC 不是直角三角形的是（）A.∠A∶∠B∶∠C = 1∶1∶2B.a∶b∶c =1∶1∶C.D.∠A+∠B=2∠C7、如图，把一个三角形纸片ABC的三个顶角向内折叠之后（3个顶点不重合），那么图中的度数和是（）A. B. C. D.8、如图，将矩形纸带ABCD，沿EF折叠后，C、D两点分别落在C′、D′的位置，经测量得∠EFB=65°，则∠AED′的度数是（）A.65°B.55°C.50°D.25°9、如图，点D在BA的延长线上，AE∥BC.若∠DAC=100°，∠B=65°，则∠ACB 的度数为（）A.65°B.35°C.30°D.40°10、如图，在△ABC中，过顶点A的直线DE∥BC，∠ABC、∠ACB的平分线分别交DE于点E、D，若AC=3，AB=4，则DE的长为（）A.6B.7C.8D.911、如图，BE，CF是△ABC的角平分线，∠ABC=80°，∠ACB=60°，EB，CF相交于D，则∠CDE的度数是（）A.130°B.70°C.80°D.75°12、如图，在中，，的外角，则的度数是（）A.30°B.45°C.60°D.75°13、如图，已知∠1＝∠2＝∠3＝55º，则∠4＝（）A.135ºB.125ºC.110ºD.无法确定14、如图，直线a、b被直线c所截，现给出下列四个条件：（1）∠1=∠5；（2）∠4=∠7，（3）∠2+∠3=180°；（4）∠1=∠7；其中能判定a∥b的条件的序号是（）A.（1），（2）B.（2），（3）C.（1），（4）D.（3），（4）15、小颖在做下面的数学作业时，因钢笔漏墨水，不小心将部分字迹污损了，作业过程如下(涂黑部分即为污损部分)：如图，OP平分∠AOB，MN∥OB，试说明：OM=MN.理由：因为OP平分∠AOB，所以■，又因为MN∥OB，所以■，故∠1=∠3，所以OM=MN.小颖思考：污损部分应分别是以下四项中的两项：①∠1=∠2；②∠2=∠3；③∠3=∠4；④∠1=∠4.那么她补出来的部分应是( )A.①④B.②③C.①②D.③④二、填空题(共10题，共计30分)16、如图，若，，则________．17、将一张矩行纸片按图中方式折叠,若∠1 =50°，则∠2为________度.18、如图，AD是△ABC的高，BE是△ABC的内角平分线，BE、AD相交于点F，已知∠BAD=40°，则∠BFD=________°．19、在△ABC中，∠A﹣∠B=10°，，则∠C=________20、如图，EF⊥AB于点F，CD⊥AB于点D，E是AC上一点，∠1=∠2，则图中互相平行的直线有________ 对．21、按要求完成下列证明如图，AB∥CD，CB∥DE，求证：∠B+∠D=180°．证明：∵AB∥CD，∴∠B=________（________）．∵CB∥DE，∴∠C+________=180°（________）．∴∠B+∠D=180°．22、完成推理过程如图，AB∥DC，AE⊥BD，CF⊥BD，BF=DE．求证：AE=CF．证明∵AB∥DC，∴∠1=________．∵AE⊥BD，CF⊥BD，∴∠AEB=________∵BF=DE，∴BF﹣EF=DE﹣EF∴________=________．∴△ABE≌△CDF________．∴AE=CF________23、阅读下面解答过程，并填空或填理由．已知如下图，点E、F分别是AB和CD上的点，DE、AF分别交BC于点G、H，∠A=∠D，∠1=∠2．试说明：∠B=∠C．解：∵∠1=∠2（已知）∠2=∠3（________）∴∠3=∠1（等量代换）∴AF∥DE（________）∴∠4=∠D（________）又∵∠A=∠D（已知）∴∠A=∠4（等量代换）∴AB∥CD（________）∴∠B=∠C（________）．24、如图，一个正方形和两个等边三角形的位置如图所示，若∠2=52°，则∠1+∠3=________°.25、平行四边形ABCD中，∠ABC的平分线将AD边分成的两部分的长分别为2和3，则平行四边形ABCD的周长是________．三、解答题(共5题，共计25分)26、如图，，，，求、的度数．27、如图，已知在△ABC中，BD平分∠ABC，CD平分△ABC的外角∠ACE，BD、CD相交于D，试说明∠A=2∠D的理由.28、如图，已知∠A＝∠F，∠C＝∠E，求证：BE∥CD．29、已知，如图，MN⊥AB，垂足为G，MN⊥CD，垂足为H，直线EF分别交AB、CD于G、Q，∠GQC＝120°，求∠EGB和∠HGQ的度数．30、在平面上有三条直线a，b，c，它们之间有哪几种可能的位置关系？你能画出来吗？参考答案一、单选题(共15题，共计45分)1、C2、A3、A4、B5、C6、D7、C8、C9、B10、B11、B12、A13、B14、C15、C二、填空题(共10题，共计30分)17、18、19、20、21、22、23、24、三、解答题(共5题，共计25分)26、27、29、。

证明题
1、一个零件的形状如图，按规定∠A=90°，∠B=32°，∠C=21°，求∠BDC 的度数？
2.如图,已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证:(2)CF=DF.
3、如图所示,BC=DE,BE=DC,求证:(1)BC//DE；（2）∠A=∠ADE.
4、如图，在四边形ABCD中，AB=AD，CB=CD．求证：∠B=∠D．
5、已知AB=CD,AD=BC
，点O为BD的中点，过点O的直线分别与AD,BC交于点E F，求证：DE=BF
6、P是∠BAC内的一点，PE⊥AB，PF⊥AC,垂足分别为点E,F,AE=AF
求证：（1）PE=PF （2）点P在∠BAC的角平分线上
7、已知AB=DC,AE=DF,CE=BF,证明：AF=DE
9、如图所示，在△ABC中，AB=AC，在AB上取一点E，在AC延长线上取一点F，使BE=CF，EF交BC于G.求证：EG=FG。

10、如图，在△ABC中，∠ACB=90°，∠A=30°，BD平分∠ABC．求证：AD=2CD．
11、E为等边三角形ABC的边AC上一点，∠1=∠2，CD=BE，判断△ADE的形状
12、如下图，己知等边三角形ABC，D是AC的中点，E为BC延长线上一点，且
∠E＝30°，DM⊥BC垂足为M .（1）若DM＝2，求DE的长；（2）求证：M是BE的中点。

13、如图,在△ABC中,已知AB=AC,∠A=120°,AB的垂直平分线交BC于点D,交AB于点E.求BC的长。

14、在△ABC中BD=DC,AD⊥ AC,∠BAD=30°,求证AC= 1
2
AB。

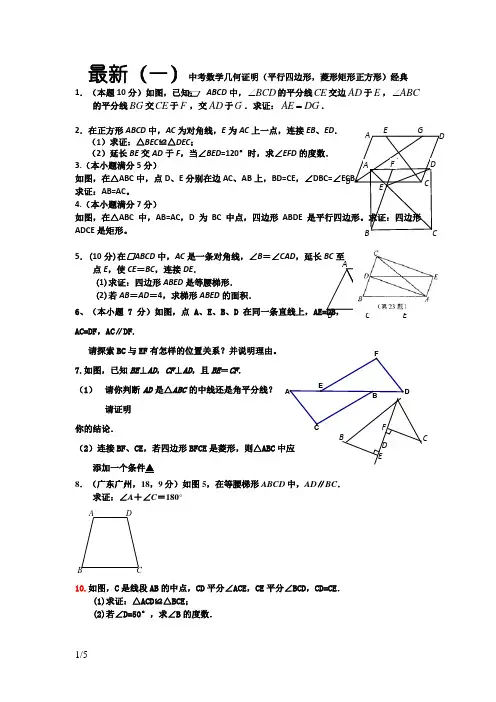
A DB C EBCD FEFEBAC D最新（一）中考数学几何证明（平行四边形，菱形矩形正方形）经典1．（本题10分）如图，已知： ABCD 中，BCD ∠的平分线CE 交边AD 于E ，ABC∠的平分线BG 交CE 于F ，交AD 于G ．求证：AE DG =．2．在正方形ABCD 中，AC 为对角线，E 为AC 上一点，连接EB 、ED ． （1）求证：△BEC ≌△DEC ；（2）延长BE 交AD 于F ，当∠BED =120°时，求∠EFD 的度数．3.（本小题满分5分）如图，在△ABC 中，点D 、E 分别在边AC 、AB 上，BD=CE ，∠DBC=∠ECB 。

求证：AB=AC 。

4.（本小题满分7分）如图，在△ABC 中，AB=AC ，D 为BC 中点，四边形ABDE 是平行四边形。

求证：四边形ADCE 是矩形。

5．(10分)在□ABCD 中，AC 是一条对角线，∠B ＝∠CAD ，延长BC 至点E ，使CE ＝BC ，连接DE ．(1)求证：四边形ABED 是等腰梯形．(2)若AB ＝AD ＝4，求梯形ABED 的面积． 6、（本小题7分）如图，点A 、E 、B 、D 在同一条直线上，AE=DB ，AC=DF ，AC ∥DF.请探索BC 与EF 有怎样的位置关系？并说明理由。

7.如图，已知BE ⊥AD ，CF ⊥AD ，且BE ＝CF ．（1） 请你判断AD 是△ABC 的中线还是角平分线？请证明你的结论．（2）连接BF 、CE ，若四边形BFCE 是菱形，则△ABC 中应添加一个条件▲8．（广东广州，18，9分）如图5，在等腰梯形ABCD 中，AD ∥BC ．求证：∠A ＋∠C ＝180°AB CD10.如图，C 是线段AB 的中点，CD 平分∠ACE ，CE 平分∠BCD ，CD=CE ．(1)求证：△ACD≌△BCE；(2)若∠D=50°，求∠B 的度数．A B C E F GEB D AC F A FDE B C11．(本题6分)如图，在△ABC 中，D 是BC 边上的点（不与B ，C 重合），F ，E 分别是AD 及其延长线上的点，CF ∥BE. 请你添加一个条件，使△BDE ≌△CDF (不再添加其它线段，不再标注或使用其他字母)，并给出证明．（1）你添加的条件是： ▲ ；（2）证明：.12.（8分）如图，请在下列四个关系中，选出两个恰当．．．．的关系作为条件，推出四边形ABCD 是平行四边形，并予以证明．（写出一种即可）关系：①AD ∥BC ，②CD AB =，③C A ∠=∠，④︒=∠+∠180C B ．已知：在四边形ABCD 中，，； 求证：四边形ABCD 是平行四边形． 13．(本题满分9分)将三角形纸片ABC (AB ＞AC )沿过点A 的直线折叠，使得AC 落在AB 边上，折痕为AD ，展平纸片，如图(1)；再次折叠该三角形纸片，使得点A 与点D 重合，折痕为EF ，再次展平后连接DE 、DF ，如图2，证明：四边形AEDF 是菱形．14．如图10，已知ABC ADE Rt △≌Rt △，90ABC ADE ∠=∠=°，BC 与DE 相交于点F ，连接CD ，EB ．（1）图中还有几对全等三角形，请你一一列举. （2）求证：.CF EF = 15．（本小题满分8分）如图，已知：点B 、F 、C 、E 在一条直线上，FB =CE ，AC =DF ． A CBDFE (第11题)AB C(1) (2) 第13题图 ABDCCDBF AEABDFB CDE FAA EB FC DA GEB CF D 能否由上面的已知条件证明AB ∥ED ？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件．．．．．．．，添加到已知条件中，使AB ∥ED 成立，并给出证明． 供选择的三个条件（请从其中选择一个）： ①AB =ED ； ②BC =EF ； ③∠ACB =∠DFE ． 16．(6分)已知：正方形ABCD 中，E 、F 分别是边CD 、DA 上的点，且CE =DF ，AE 与BF 交于点M ． （1）求证：△ABF ≌△DAE ；（2）找出图中与△ABM 相似的所有三角形（不添加任何辅助线）．17．(6分)如图，在△ABC 中，BC ＞AC ，点D 在BC 上，且DC ＝AC ，∠ACB 的平分线CF 交AD 于点F ．点E 是AB 的中点，连接EF ．(1)求证：EF ∥BC ；(2)若△ABD 的面积是6，求四边形BDFE 的面积．18．（本小题满分8分） 如图，四边形ABCD 的对角线AC 、DB 相交于点O ，现给出如下三个条件：AB DC AC DB OBC OCB ==∠=∠①②③.（1）请你再增加一个．．条件：________，使得四边形ABCD 为矩形（不添加其它字母和辅助线，只填一个即可，不必证明）；（2）请你从①②③中选择两个条件________（用序号表示，只填一种情况），使得AOB DOC △≌△，并加以证明.19．如图，在直角梯形ABCD 中，AD ∥BC ，∠A ＝90º，AB ＝AD ＝6，DE ⊥CD交AB 于E ，DF 平分∠CDE 交BC 于F ，连接EF ． (1)证明：CF ＝EF ； (2)当tan ∠ADE ＝ 13时，求EF 的长．20．(10分)如图，在□ABCD 中，E 、F 分别是边AB 、CD的中点，AG ∥BD 交CB 的延长线于点G ．(1)求证：△ADE ∽≌△CBF ；(2)若四边形BEDF 是菱形，则四边形AGBD 是什么特殊四边形？请说明你的理由． 21．（本题满分8分）如图，在ABCD 中，点E 、F 是对角线AC 上两点，且CF AE =．求证：FDE EBF =∠．22.（8分）如图，四边形ABCD 是矩形，∠EDC=∠CAB ， ∠DEC=90°。