课前复习
已知函数f (x),对任意的x, y恒有 f (x y) f (x) f (y) (1)求证f (x)是奇函数 （2）若x 0时，f (x) 0,且f (1) 2，求f ( 在[3,3]的最值
知 识 改 变 命 运,勤 奋 创 造 奇 迹.
2020年11月2日星期一
复习:对数的概念
求下列函数的反函数：
（1） y 3x ；（2） y log 6 x
函数y f (x)是函数y 1 log2 x的反函数，求 f (3)
对数函数及性质
练习
1.函数 y loga (2x 1) 1(a＞0且a≠1)图象
恒过定点 （0，－1) .
1
lg 2
2、已知函数f (x5) lg x，则f (2)=___5______；
01
y=log b x
x
y=log c x y=log d x
答：b>a>1>d>c
2、底数不同，真数相同
(4) log35 和 log45 (5) log23 和 log43
（二）同真数, 常借助图象比较，也可 用换底公式转化为同底数的对数后比较。
3、底数不同，真数不同
（6）log 6 7 与 log 7 6 （7） log 3π 与 log 20.8
定义：一般地，如果 a a 0, a 1 的b次幂等于N,
就是 ab N 那么数 b叫做 以a为底 N的对数，记作:
loga N b a叫做对数的底数，N叫做真数。
例5 生物机体内碳14的“半衰期” 为5730年，湖南长沙马王堆汉墓女尸 出土时碳14的残余量约占原始含量的 76.7％，试推算马王堆古墓的年代.
图象向上、向下无限延伸 值 域 : R
自左向右看图象逐渐下降 在(0,+∞)上是：减函数
对数函数及性质
对数函数y=log a x (a>0, a≠1)
a>1 图y
0<a<1
y
象 o (1, 0) x
（1, 0)
o
x
0
(1) 定义域： (0,+∞lo)ga N 0
性 (2) 值域：R
0
a, N (0,1)或a, N (1,) N 1 a, N中一个在(0,1),另一个在
练习：判断下列对数 式的符号 log2.5 4 log0.7 5 log30.2 log0.1 0.2 log2.71
+
-
-
+
0
例1:求下列函数的定义域:
(1) y=logax2 (2) y=loga(4-x)
(3) y=log(x-1)(3-x) (4) y=log2(2x-3)
(5) y 1 log 2 x
3
y 2
1 11 42
0 1 23 4 -1 -2
y log 2 x
x
y log 1 x
2
探究：对数函数:y = loga x (a＞0,且a≠ 1) 图象与性质
y
探索发现:认
2
真观察函数
1 11
42
y=log2x 的图象填写
0 123 4 -1
x
下表
-2
图象特征
图象位于y轴右方
代数表述
定义域 : ( 0,+∞)
2
真观察函数
1 11
42
y=log2x 的图象填写
0 123 4 -1
x
下表
-2
图象特征
图象位于y轴右方
代数表述
定义域 : ( 0,+∞)
图象向上、向下无限延伸 值 域 : R
自左向右看图象逐渐上升 在(0,+∞)上是：增函数
探究：对数函数:y = loga x (a＞0,且a≠ 1) 图象与性质
画出下列函数的图象，说出由 y lg的x 图象 经过怎样的变化得到
(1).y lg(x 1) (2).y lg x 1 (3).y lg(x 1) 1 (4).y lg x
(5).y lg x
一般地，对数函数y=logax在a>1及0<a<1这两种情况 下的图象和性质如下表所示：
a＞1
(3) 过点(1,0), 即x=1 时, y=0
(4) 在(0,+∞)上是增函数 (4) 在(0,+∞)上是减函数
质 (5) 0<x<1时, y<0; (5) 0<x<1时, y>0;
x>1时, y>0
x>1时, y<0
探究：对数函数:y = loga x (a＞0,且a≠ 1) 图象与性质
y
探索发现:认
y 说出这两个图象的y 2特x 点y=？x
y log2 x
x
反函数：
对数函数y＝loga x就是指数函数y＝ax的反函数。 即它们互为反函数。
对数函数y=log x的图象
y (1)x
y
2
y=x
先画 y (1 )x 的图象
2
x
y=log x
y=ax (a>1)
图象
y
1
定义域
0
x
R
值域 (0, )
研究方法： 具体到一般；画出函数图象，结合图象 研究函数的性质； 研究内容： 定义域、值域、定点 、单调性、奇偶 性．
探究：对数函数:y = loga x (a＞0,且a≠ 1) 图象与
性质
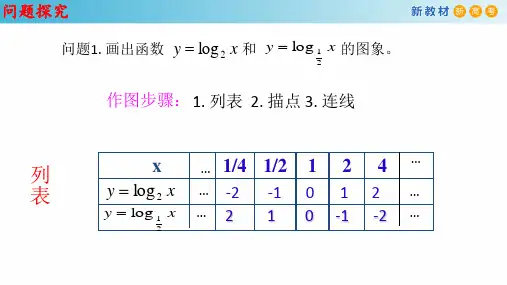
在同一坐标系中用描点法画出对数函数
y log 2 x和y log 1 x 的图象。
2
作图步骤: ①列表,
（三）若底数、真数都不相同, 则常借助1、0等中间量进 行比较,也可借助图象进行比较
练习：
(1) log 1 3与log 1 3
2
5
23log 4 5与2 log 2 3
3log 1 0.3与log 2 0.8
3
二、利用对数函数单调性解不等式
变式1：、log 1 (2x 1) log 1 2
2
0.001 57104
考古学家通过提取附着在出土文物,古迹址生物体
的残留物,利用 t log
P 估算出出土文物
1
或古遗址的年代.
5730
2
对于任意个碳14的含量P,利用上式都有唯一确定
的年代t与之对应,所以,t是P的函数.
对数函数
定义：函数 y log a x(a 0，且 a 1)
叫做对数函数，其中x是自变量，函数的定 义域是（0，+∞）。
3、方程log2 (x 3) 3x的实根的个数为 ___2___;
4.已知函数 y
log 2
x，若x
(1 ，8]， 2
则y __（__－_1_，__３_］_
例3、已知函数 f (x) log1 (3 2x x2 ).
2
（1）求函数 f (x) 的定义域； （2）求函数 f (x) 的单调区间； （3）求函数 f (x) 的值域。
，
判断：以下函数是否是对数函数
1. y=log2(3x-2) 3. y=log1/3x2
5. y log x 6
2. y=log(x-1)x
4.y=lnx
6. y 3 log2x 5
思考1:函数 y log3 x2 与 y 2 log3 x 相同吗？ 为什么？
思考2：你能类比前面探讨指数函数性质的思 路，提出研究对数函数的性质的方法和步骤吗?
②描点, ③用平滑曲线连接。
探究：对数函数:y = loga x (a＞0,且a≠ 1) 图象与
性质
作y=log2x图象
列 X 1/4 表 y=log2x -2
y
描2 点
1 11 42
0 12
连 -1 线 -2
1/2 1 -1 0
34
2 4… 1 2…
x
探究：对数函数:y = loga x (a＞0,且a≠ 1) 图象与
变式1：求函数 y=log0.5 (x-1) (1 <x≤3) 的值 域.
变式2：y log 4 16 4x
变式3：求函数f (x) log 2 (x2 2x 3) 的值 域
变式4
2
：求函数y log 1 x 2
1 2
log 1
2
x
5
在区间2，4的值域
四、对数函数单调性的判断
2、求（f x）＝log0.（2 2x－1）的单区间。
探索发现:认
y
真观察函数
2
y log1 x
2
的图象填写
1 11
42
0 1 23 4
x
-1
下表
-2
图象特征
函数性质
图象位于y轴右方
定义域 : ( 0,+∞)
图象向上、向下无限延伸 值 域 : R
自左向右看图象逐渐下降 在(0,+∞)上是：减函数
结合对数函数的性质思考： a和 x为何值时，y loga x 是一个正数？是一个负数？
当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约经过5730年 衰减为原来的一半,这个时间称为”半衰期”.根据此规律,人们获得了生物 体内碳14含量P与死亡年数t之间的关系:
t
P
1 2
5730
碳14的含量P 0.5 0.3 0.1 0.01
生物死亡年
数t
5730 9953 19035 38069
0＜a＜1
图
象
当0＜x＜1时，y＜0 当x=1时，y=0 当x＞1时，y＞0
当0＜x＜1时，y＞0 当x=1时，y=0 当x＞1时，y＜0
性
定义域：（0，+∞） 值域： R
质 过特殊点： 过点（1，0），即x=1时y=0 单调性 ：在（0，+∞）上是增函数 单调性：在（0，+∞）上是减函数
