物理学常数表

kb玻尔兹曼常数玻尔兹曼常数（Boltzmann constant）是物理学中的一个基本常数，用符号k表示，通常在SI单位制中的数值为1.380649 ×10^(-23) J/K。

这个常数在统计物理学、热力学和量子力学中具有重要的意义。

玻尔兹曼常数最早由维尔纳·海森伯在1884年提出，并由马克斯·普朗克在1900年命名为玻尔兹曼常数，以纪念他在统计热力学中的贡献。

玻尔兹曼常数与其他基本常数（如普朗克常数和光速）一起，构成了物理学中的基本定值。

玻尔兹曼常数的物理含义是衡量了热力学温度和能量之间的关系。

它的值是能量单位与温度单位之间的比例关系。

具体而言，玻尔兹曼常数是将能量的单位（焦耳）转换为温度的单位（开尔文）时所需的比例系数。

根据玻尔兹曼常数的定义，如果一个系统的温度为1K，则其内能等于玻尔兹曼常数乘以1.380649 × 10^(-23)焦耳。

玻尔兹曼常数还与熵的概念密切相关。

熵是热力学中的一个重要量，用来描述一个系统的无序程度。

根据统计物理学，系统的熵等于玻尔兹曼常数乘以自然对数的倒数，并乘以可能的微观状态的数量。

这个关系表明，熵的量级与微观粒子数之间存在着关联，玻尔兹曼常数是将两者联系起来的关键因素。

在量子力学中，玻尔兹曼常数也扮演着重要的角色。

根据波尔兹曼-统计物理学，玻尔兹曼常数与量子力学中的普朗克常数之间存在一定的关系。

具体而言，将普朗克常数的平方除以玻尔兹曼常数，得到了一个称为波尔兹曼常数P的值，约为6.62607015 × 10^(-34) J·s / (1.380649 × 10^(-23) J/K)。

这个比值在量子力学中具有重要意义，帮助人们理解粒子的量子行为和统计特性。

综上所述，玻尔兹曼常数是物理学中非常重要的一个常数，它关系着热力学、统计物理学和量子力学等多个领域。

通过玻尔兹曼常数，我们可以将能量和温度联系起来，理解系统的熵以及量子粒子的统计特性。

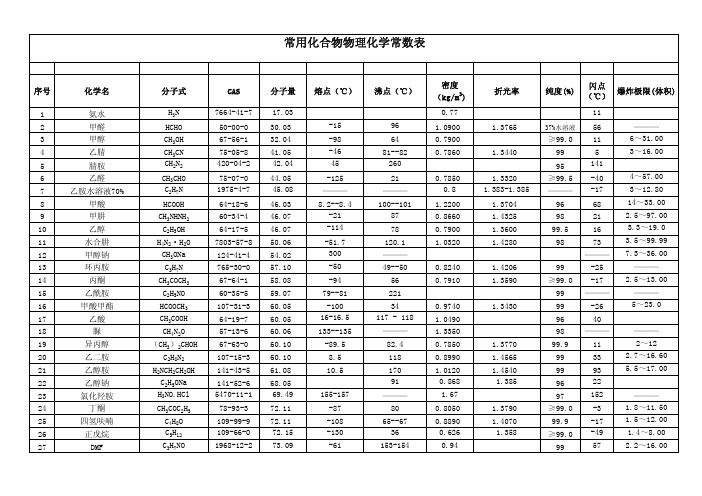
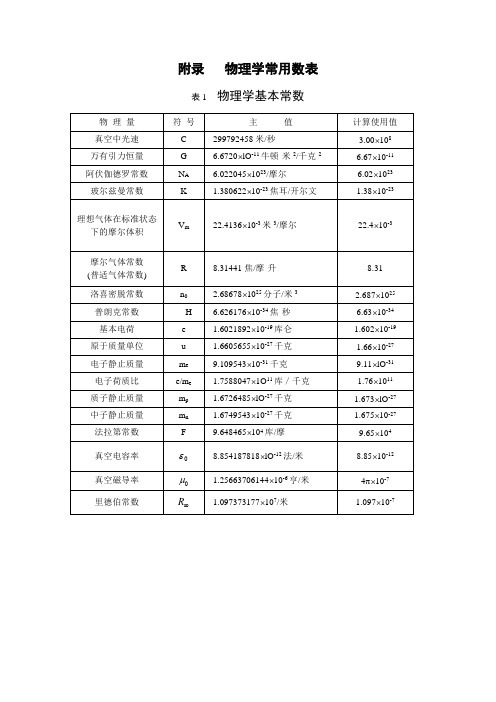
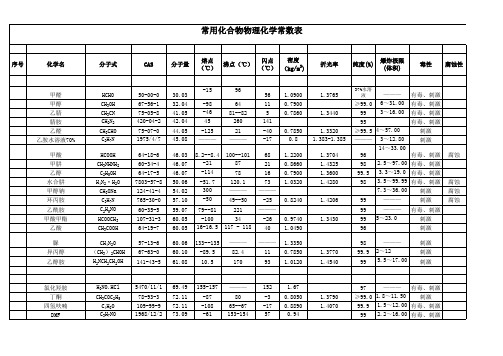
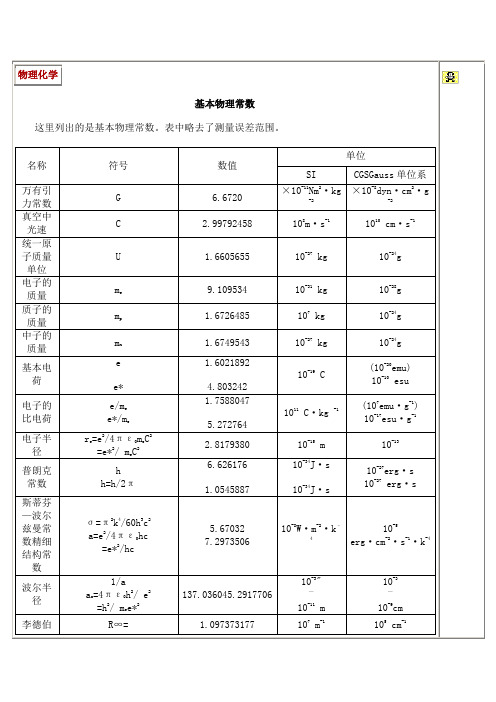
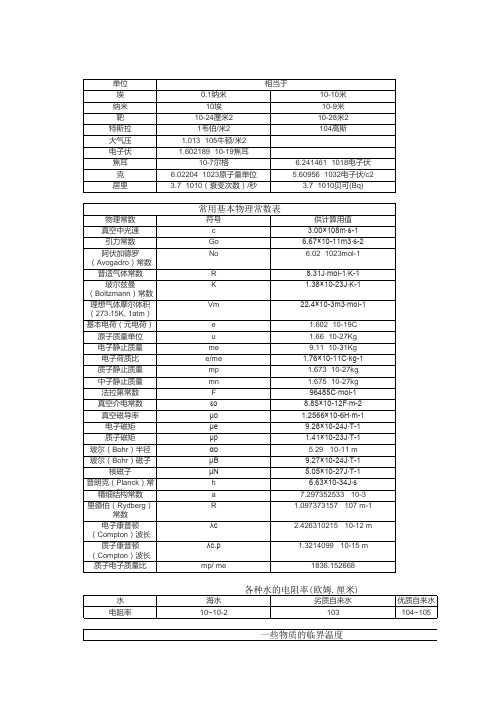
附录物理学常用数表表1 物理学基本常数
表2 我国某些城市的重力加速度（单位：米/秒2）
表3 一般固态物质的密度（克/厘米3）
表4 液体密度(克/厘米3)
表5 水的表面张力系数α随温度t的变化
表6 几种物质的绝对折射率和临界角
表7 常用光谱灯的可见谱线波长(nm)
表8 常用仪器量具的主要技术指标和极限误差
注：一般而言，有刻度的仪器、量具的最大允差大约对应于其最小分度值所代表的物理量；对于数学式仪表，测量值的误差往往在于所显示的能稳定不变的数字中最末一位的半个单位所代表的物理量。

应当说明，“最大允差”是指所制造的同型号同规格的所有仪器中有可能产生的最大误差，并不表明每一台仪器的每个测量值都有如此之大的误差，它既包括仪器在设计、加工、装配过程中乃至材料选择中的缺欠所造成的系统误差，也包括正常使用过程中测量环境和仪器性能随机涨落的影响。

表9 常用电气仪表面板上的标记符号。

25个物理常数篇一：标题: 25个物理常数(创建与标题相符的正文并拓展)正文:物理学是研究自然现象的科学,其基础是一些基本常数。

这些常数是通过对自然界的观察和实验得出的,它们对物理学的理论和实践具有至关重要的影响。

本文将介绍25个基本的物理学常数,包括它们的值、定义和意义。

1. 开尔文(k)开尔文(k)是一个常量,它的值为1.19264×10-19J/(K·K)。

它是电离常数,用于描述电解质的电离程度。

2. 普朗克常数(h)普朗克常数(h)是一个基本的物理学常数,它的值为6.626176×10-35J/(K·s)。

它是热力学中的基本常数,用于描述能量和热量之间的关系。

3. 光速(c)光速(c)是一个基本的物理学常数,它的值为299,792,458米/秒。

它是真空中光的速度,也是宇宙中最基本的速度。

4. 磁感应强度(B)磁感应强度(B)是一个物理学常数,用于描述磁场的强度。

它的值通常在0到1000特斯拉之间,磁感应强度越大,磁场越强。

5. 电容(C)电容(C)是一个物理学常数,用于描述电容器的电容值。

它的值通常在0到1特斯拉之间,电容器的电容值越大,电容器的储存电能的能力越强。

6. 电阻(R)电阻(R)是一个物理学常数,用于描述导体的电阻值。

它的值通常在0到无穷大之间,电阻值越大,导体的电阻能力越强。

7. 温度(T)温度(T)是物理学中的基本常数,用于描述物体的状态。

它的值通常在0到开尔文之间,温度越高,物体的状态越热。

8. 引力(G)引力(G)是物理学中的基本常数,用于描述物体之间的引力大小。

它的值通常在6.6743×10-11N·(m/kg)^2。

9. 电磁场频率(E)电磁场频率(E)是物理学常数,用于描述电磁场的传播速度。

它的值通常在真空中约为3×10^10米/秒。

10. 质能关系(E=mc2)质能关系(E=mc2)是物理学中的一个重要公式,用于描述质量和能量之间的关系。

PrefaceFundamental Physical Constants: 1998Peter J. Mohr and Barry N. TaylorNational Institute of standards and Technology, Gaithersburg, MD 20899-8401This table gives the 1998 self-consistent set of values of the basic constants and conversion factors of physics and chemistry recommended by the Committee on Data for Science and Technology (CODATA) for international use. Further, it describes in detail the adjustment of the values of the subset of constants on which the complete 1998 set of recommended values is based. The 1998 set replaces its immediate predecessor recommended by CODATA in 1986. The new adjustment, which takes into account all of the data available through 31 December 1998, is a significant advance over its 1986 counterpart. The 1998 adjustment was carried out by P. J. Mohr and B. N. Taylor of the National Institute of Standards and Technology (NIST) under the auspices of the CODATA Task Group on Fundamental Constants. The standard uncertainties (i.e., estimated standard deviations) of the new recommended values are in most cases about 1/5 to 1/12 and in some cases 1/160 times the standard uncertainties of the corresponding 1986 values. Moreover, in almost all cases the absolute values of the differences between the 1998 values and the corresponding 1986 values are less than twice the standard uncertainties of the 1986 values.The Task Group was established in 1969 with the aim of periodically providing the scientific and technological communities with a self-consistent set of internationally recommended values of the fundamental physical constants based on all applicable information available at a given point in time. The first set was published in 1973 and was followed by a revised set first published in 1986; the current 1998 set first appeared in 1999. In the future, the CODATA Task Group plans to take advantage of the high level of automation developed for the current set in order to issue a new set of recommended values at least every four years.Relative std. Quantity Symbol Value Unit uncert.u ra Value recommended by the Particle Data Group,Caso et al.,Eur.Phys.J.C3(1-4),1-794(1998).b Based on the ratio of the masses of the W and Z bosons mW/m Z recommended by the Particle Data Group(Caso et al.,1998).The value for sin2θW they recommend,which is based on a particular variant of the modified minimal subtraction(。

普朗克常数和玻尔兹曼常数是描述微观世界物理现象的两个重要常数。

它们在量子力学和统计物理中有着重要的作用，是研究微观粒子运动和能量转换的基本参量。

由于量子力学和统计物理中常常涉及到单位的换算，因此掌握普朗克常数和玻尔兹曼常数的单位换算表可以帮助我们更好地理解和应用这两个常数。

下面是普朗克常数和玻尔兹曼常数的单位换算表：普朗克常数：1. 普朗克常数的国际单位制（SI单位制）表示为 h，其数值为6.xxx × 10^-34 J·s。

2. 普朗克常数的厘米-克-秒单位制（cgs单位制）表示为 h，其数值为6.xxx × 10^-27 erg·s。

3. 普朗克常数的电子伏特单位制（eV单位制）表示为ℏ，其数值为4.xxx × 10^-15 eV·s。

玻尔兹曼常数：1. 玻尔兹曼常数的国际单位制（SI单位制）表示为 k，其数值为 1.xxx × 10^-23 J/K。

2. 玻尔兹曼常数的厘米-克-秒单位制（cgs单位制）表示为 k，其数值为1.xxx × 10^-16 erg/K。

3. 玻尔兹曼常数的电子伏特单位制（eV单位制）表示为 k，其数值为8.xxx × 10^-5 eV/K。

通过以上的单位换算表，我们可以看出普朗克常数和玻尔兹曼常数在不同的单位制下的具体数值，这有助于我们在实际计算和研究中的应用。

在量子力学和统计物理的研究中，常常需要根据实际问题的不同，选择合适的单位进行计算和描述，因此熟练掌握常数的单位换算表是非常重要的。

普朗克常数和玻尔兹曼常数在科学研究和工程技术领域中有着广泛的应用。

比如在半导体物理中，玻尔兹曼常数常常用于描述半导体中电子的能级分布；在纳米材料的研究中，普朗克常数常常用于描述纳米材料的量子效应。

掌握好普朗克常数和玻尔兹曼常数的单位换算表，对于开展相关领域的研究工作具有重要的指导意义。

普朗克常数和玻尔兹曼常数作为描述微观世界物理现象的重要常数，其在量子力学和统计物理中有着重要的作用。

物理常数引力常数G= 6.672×10-11牛顿·米2/千克2单元电荷e= 1.602189×10-19库仑阿伏加德罗常数N0= 6.02204×1023个粒子数/摩尔法拉第常数F= 96484.6库仑/摩尔斯忒藩―玻尔兹曼常数σ= 5.6703×10-8瓦·米2/K4气体常数R=8.3144焦耳/摩尔·K真空的电容率库仑/焦耳·米光速c= 2.99792458 ×108米/秒真空的磁导率牛顿/安2精细结构常数α=7.297351×10-3=1/137电子康普顿波长米里德伯常数R∞=1.096737318×107米-1质子康普顿波长米里德伯频率cR∞=3.2898420×1015赫兹质子电子质量比值里德伯能量hcR∞=13.60580电子伏玻尔兹曼常数k= 1.38066×10-23焦耳/K = 8.6174×10-5电子伏/K库仑常数k = 1/ (4πε0) = 8.98755179×109牛顿·米2/库仑2电子静质量m e=9.10953×10-31千克=5.485802×10-4u（原子单位）=0.511003兆电子伏/c2质子静质量m p=1.672648×10-27千克= 1.00727674u = 938.280兆电子伏/c2中子静质量m n=1.674954×10-27千克= 1.00866501u = 939.573兆电子伏/c2统一质量单位（原子单位）u =1.660566×10-27千克=931.502兆电子伏/c2玻尔半径a0=5.291771×10-11米玻尔磁子焦耳/特斯拉 = 5.788378×10-9电子伏/高斯核磁子焦耳/特斯拉= 3.152452×10-12电子伏/高斯普朗克常数h= 6.62818×10-34 焦耳·秒= 4.13570×10-15 电子伏·秒焦耳·秒= 6.58217×10-16 电子伏·秒。

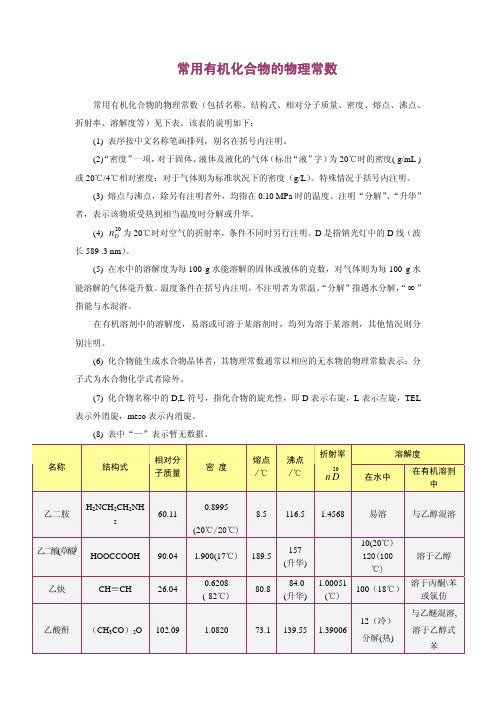
市制暂时允许使用的市制单位列于下表，其它市制单位不准使用。

一般不要将市制单位与国际单位制单位或任何其它单位构成组合单位。

市制单位单位换算以下各表列出各种单位换算关系。

各表中SI单位均印制粗体。

长度1埃（Å）=10-10米1光年=9.4600×1012千米1码=3尺1x单位=10-13米1秒差距=3.084×1013千米1竿（rod）=16.5尺1噚=6尺1密耳（mil）=10-3寸1海里=1852米=1.151哩=6076尺标准波长计量学上第一次定义的标准波长是一定条件下的氪__86（86Kr）放电管发出的2P10—5d5间跃迁谱线在真空中的波长λKr,其值为：λKr=109nm/1650763.73=605.78021059……nm计量学上第二次定义的标准波长是一定条件下的氪__86（86Kr）,汞__198（198Hg）,镉__114（114Cd）放电管发出的如下谱线在真空中的波长（单位nm）：86Kr（645.80720，642.28006，565.11286，450.36162）198Hg（579.22683，577.11983，546.22705，435.95624）114Cd（644.02480，508.72379，480.12521，467.94581）为了能方便地用内插法求出未知波长，需要精密测定从铁、氖和氪发出的波长为240nm到70nm的340条左右谱线在光谱学标准空气中的波长。

以这些为标准规定了计量学上的第三次标准波长。

主要的音响单位声强：某点在特定方向的声强是每秒钟穿过垂直于传播方向的单位面积的声能通量。

单位为瓦特每平方米（Watt/m2）。

声压：单位为微巴（μb）,达因每平方厘米（dyn/cm2）或牛顿每平方米（N/m2）。

1N/ m2=10μb,声强级：以声强I和标准声强I。

之比的常数对数的十倍表示（即10log10(I/Io)，其中Io=10- 12Watt/m2），单位为分贝（dB）。

介电常数表Markdown是一种轻量级的标记语言，可以用于文档的编写和格式化。

在本文档中，我们将介绍关于介电常数的表格。

介电常数是一种物质的特性，它描述了该物质在电场中的电极化程度。

在电磁学和材料科学中，介电常数经常被用于描述电磁波在不同物质中传播的速度和吸收的能力。

以下是一份介电常数表格，它列出了一些常见物质的介电常数。

物质介电常数真空 1.0000空气 1.0006水80.4冰 3.18玻璃7.5 - 10.3陶瓷 6.2 - 16.0金属 1.0 - 100二氧化硅 3.9 - 4.5盐水 4.0 - 81.0聚乙烯 2.2 - 2.4聚氯乙烯 3.1 - 6.7聚苯乙烯 2.5 - 2.7天然橡胶 2.5 - 3.0硅胶 2.5 - 3.5聚偏氟乙烯8.0 - 8.4聚醚砜 3.0 - 3.5聚丙烯 2.1 - 2.4聚四氟乙烯 2.0 - 2.1以上是只列出了一部分物质的介电常数。

可以看出，不同物质的介电常数存在很大的差异。

介电常数越高，物质在电场中的电极化效果越强。

一些物质，如金属，具有非常低的介电常数，几乎不会被电场极化。

而其他物质，如水和玻璃，具有较高的介电常数，容易被电场极化。

介电常数的值可以通过实验测量得到，也可以通过理论计算来预测。

它们在工程和科学领域中有着广泛的应用。

例如，在电子器件的设计中，介电常数的值对于材料的选择和性能的预测至关重要。

另外，在电磁学中，介电常数的值对于预测电磁波在不同介质中的传播速度和衰减情况也非常重要。

需要注意的是，介电常数的值通常是频率依赖的。

因此，在使用介电常数时，需要明确是在哪个频率范围内进行测量或计算，并参考相应的数据。

总结起来，介电常数是描述物质在电场中电极化程度的物理量。

它的值对于电子器件设计和电磁波传播的研究非常重要。

通过合适的测量和计算方法，我们可以获取不同物质的介电常数值。

希望这份介电常数表格能为你的工作和研究提供参考。

h常数的值
h常数是物理学中的一个重要概念，它是一个常数，用来表示光的波长和能量
之间的关系。

它的符号是h，它的值是6.626 070 15 × 10-34 J·s，它是由德国物理学家爱因斯坦在1905年发现的。

h常数是物理学中最重要的常数之一，它是物理学家们研究物质的基础。

它表
明了光的波长和能量之间的关系，即能量E和波长λ之间的关系：E=hc/λ，其中c是光速。

这个公式表明，当波长变短时，能量就会增加，反之亦然。

h常数也可以用来计算物质的热力学性质，它可以用来计算物质的熵和热容量。

它还可以用来计算物质的热力学性质，如熵和热容量。

h常数在物理学中有着重要的作用，它是物理学家们研究物质的基础。

它可以
用来计算物质的熵和热容量，也可以用来计算光的波长和能量之间的关系。

它的值是6.626 070 15 × 10-34 J·s，是由德国物理学家爱因斯坦在1905年发现的。