聚类分析例题及解答
- 格式：doc
- 大小：76.01 KB
- 文档页数：2
下载文档原格式
合集下载
聚类分析实例分析题(推荐文档)
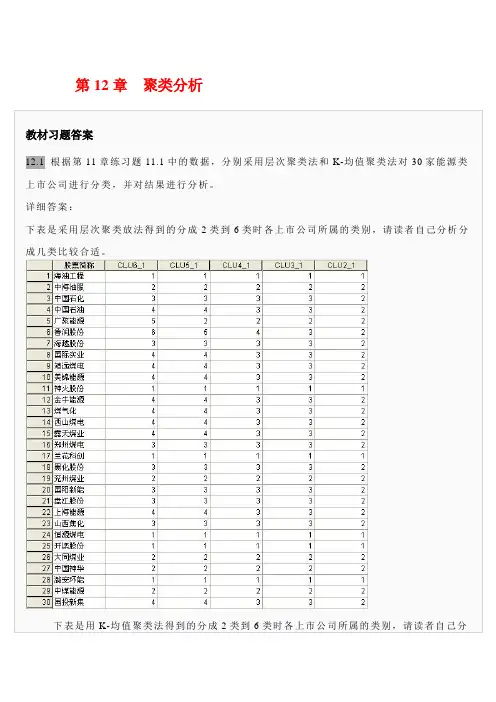
5.2酿酒葡萄的等级划分5.2.1葡萄酒的质量分类由问题1中我们得知，第二组评酒员的的评价结果更为可信，所以我们通过第二组评酒员对于酒的评分做出处理。
我们通过excel计算出每位评酒员对每支酒的总分，然后计算出每支酒的10个分数的平均值，作为总的对于这支酒的等级评价。
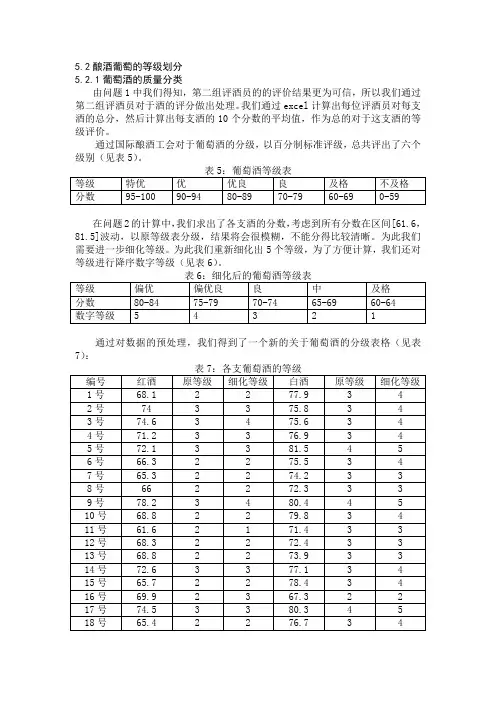
通过国际酿酒工会对于葡萄酒的分级，以百分制标准评级，总共评出了六个级别（见表5）。
在问题2的计算中，我们求出了各支酒的分数，考虑到所有分数在区间[61.6，81.5]波动，以原等级表分级，结果将会很模糊，不能分得比较清晰。
为此我们需要进一步细化等级。
为此我们重新细化出5个等级，为了方便计算，我们还对等级进行降序数字等级（见表6）。
通过对数据的预处理，我们得到了一个新的关于葡萄酒的分级表格（见表7）：考虑到葡萄酒的质量与酿酒葡萄间有比较之间的关系，我们将保留葡萄酒质量对于酿酒葡萄的影响，先单纯从酿酒葡萄的理化指标对酿酒葡萄进行分类，然后在通过葡萄酒质量对酿酒葡萄质量的优劣进一步进行划分。
5.2.2建立模型在通过酿酒葡萄的理化指标对酿酒葡萄分类的过程，我们用到了聚类分析方法中的ward 最小方差法，又叫做离差平方和法。
聚类分析是研究分类问题的一种多元统计方法。
所谓类，通俗地说，就是指相似元素的集合。
为了将样品进行分类，就需要研究样品之间关系。
这里的最小方差法的基本思想就是将一个样品看作P 维空间的一个点，并在空间的定义距离，距离较近的点归为一类；距离较远的点归为不同的类。
面对现在的问题，我们不知道元素的分类，连要分成几类都不知道。
现在我们将用SAS 系统里面的stepdisc 和cluster 过程完成判别分析和聚类分析，最终确定元素对象的分类问题。
建立数据阵，具体数学表示为：1111...............m n nm X X X X X ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦（5.2.1） 式中，行向量1(,...,)i i im X x x =表示第i 个样品；列向量1(,...,)'j j nj X x x =’，表示第j 项指标。
08聚类分析与判别分析的例题
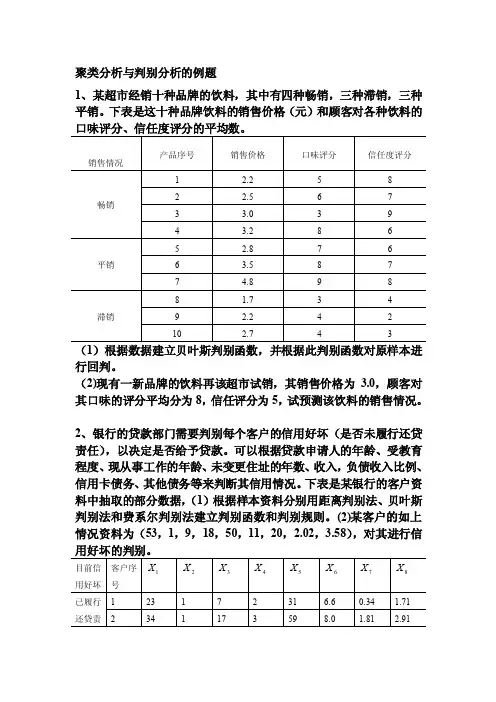
聚类分析与判别分析的例题1、某超市经销十种品牌的饮料，其中有四种畅销，三种滞销，三种平销。
下表是这十种品牌饮料的销售价格（元）和顾客对各种饮料的口味评分、信任度评分的平均数。
（1）根据数据建立贝叶斯判别函数，并根据此判别函数对原样本进行回判。
（2)现有一新品牌的饮料再该超市试销，其销售价格为3.0，顾客对其口味的评分平均分为8，信任评分为5，试预测该饮料的销售情况。
2、银行的贷款部门需要判别每个客户的信用好坏（是否未履行还贷责任），以决定是否给予贷款。
可以根据贷款申请人的年龄、受教育程度、现从事工作的年龄、未变更住址的年数、收入，负债收入比例、信用卡债务、其他债务等来判断其信用情况。
下表是某银行的客户资料中抽取的部分数据，（1）根据样本资料分别用距离判别法、贝叶斯判别法和费系尔判别法建立判别函数和判别规则。
(2)某客户的如上情况资料为（53，1，9，18，50，11，20，2.02，3.58），对其进行信3、从胃癌患者、萎缩性胃炎患者和非胃炎患者中分别抽取五个病人进行思想生化指标的化验：血清铜蛋白、蓝色反应、尿吲哚乙酸和中性硫化物，数据见下表。
试用距离判别法建立判别函数，并根据此判4、为了了解儿童的生长发育规律，今随机抽取了男孩从出生到11岁每年平均增长的重量数据表，试问男孩发育可分为几个阶段？表1~11岁儿童每年平均增长的重量5、下表是15个上市公司2001年的一些主要财务指标，使用系统聚类法和K均值法分别对这些公司进行聚类，并对结果进行分析。
6、下表是某年我国16个地区农民支出情况的抽样调查数据，每个地区调查了反映每人平均生活消费支出情况的六个经济指标。
试通过统计分析软件用不同的方法进行系统聚类分析，并比较何种方法与人们观察到的实际情况较接近。
7、下表是2003年我国省会城市和计划单列市的主要经济指标：人均GDP元、人均工业产值元、客运总量万人、货运总量万人、地方财政预算内收入亿元、固定资产投资总额亿元、在岗职工人数占总人口的比例%、在岗职工人均工资额元、城乡居民年底储蓄余额亿元。
聚类分析实例分析题(推荐文档)
5.2酿酒葡萄的等级划分5.2.1葡萄酒的质量分类由问题1中我们得知，第二组评酒员的的评价结果更为可信，所以我们通过第二组评酒员对于酒的评分做出处理。
我们通过excel计算出每位评酒员对每支酒的总分，然后计算出每支酒的10个分数的平均值，作为总的对于这支酒的等级评价。
通过国际酿酒工会对于葡萄酒的分级，以百分制标准评级，总共评出了六个级别（见表5）。
在问题2的计算中，我们求出了各支酒的分数，考虑到所有分数在区间[61.6，81.5]波动，以原等级表分级，结果将会很模糊，不能分得比较清晰。
为此我们需要进一步细化等级。
为此我们重新细化出5个等级，为了方便计算，我们还对等级进行降序数字等级（见表6）。
通过对数据的预处理，我们得到了一个新的关于葡萄酒的分级表格（见表7）：考虑到葡萄酒的质量与酿酒葡萄间有比较之间的关系，我们将保留葡萄酒质量对于酿酒葡萄的影响，先单纯从酿酒葡萄的理化指标对酿酒葡萄进行分类，然后在通过葡萄酒质量对酿酒葡萄质量的优劣进一步进行划分。
5.2.2建立模型在通过酿酒葡萄的理化指标对酿酒葡萄分类的过程，我们用到了聚类分析方法中的ward 最小方差法，又叫做离差平方和法。
聚类分析是研究分类问题的一种多元统计方法。
所谓类，通俗地说，就是指相似元素的集合。
为了将样品进行分类，就需要研究样品之间关系。
这里的最小方差法的基本思想就是将一个样品看作P 维空间的一个点，并在空间的定义距离，距离较近的点归为一类；距离较远的点归为不同的类。
面对现在的问题，我们不知道元素的分类，连要分成几类都不知道。
现在我们将用SAS 系统里面的stepdisc 和cluster 过程完成判别分析和聚类分析，最终确定元素对象的分类问题。
建立数据阵，具体数学表示为：1111...............m n nm X X X X X ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦（5.2.1） 式中，行向量1(,...,)i i im X x x =表示第i 个样品；列向量1(,...,)'j j nj X x x =’，表示第j 项指标。
统计问题 5 聚类分析
上表为聚类的步骤。
由上图可知易分为两类，X与Z一类，Y一类。1234 Nhomakorabea5
6
7
8
X
1.8
2.1
3.2
2.2
2.5
2.8
1.9
2.0
Y
95
99
101
103
98
102
120
130
Z
0.15
0.21
0.18
0.17
0.16
0.20
0.09
0.11
解答：
题目要求对8各企业技术密集水平聚类，即R聚类（变量聚类）
上表为Proximity相关系数。由上表知X和Z的正相关性较大，Y与Z的负相关性较大，Y与X也程现负相关性。
生产工人劳动生产率x每百万元固定资产所容纳的职工人数y和技术管理人员在职工中的比重z
5、聚类分析现有8个企业，对每个企业用3个指标来刻画企业的技术密集水平：生产工人劳动生产率（x）、每百万元固定资产所容纳的职工人数（y）和技术管理人员在职工中的比重(z)。具体数据如下表，试对这8个企业的技术密集水平作聚类分析。
由上图可知易分为两类，X与Z一类，Y一类。1234 Nhomakorabea5
6
7
8
X
1.8
2.1
3.2
2.2
2.5
2.8
1.9
2.0
Y
95
99
101
103
98
102
120
130
Z
0.15
0.21
0.18
0.17
0.16
0.20
0.09
0.11
解答：
题目要求对8各企业技术密集水平聚类，即R聚类（变量聚类）
上表为Proximity相关系数。由上表知X和Z的正相关性较大，Y与Z的负相关性较大，Y与X也程现负相关性。
生产工人劳动生产率x每百万元固定资产所容纳的职工人数y和技术管理人员在职工中的比重z
5、聚类分析现有8个企业，对每个企业用3个指标来刻画企业的技术密集水平：生产工人劳动生产率（x）、每百万元固定资产所容纳的职工人数（y）和技术管理人员在职工中的比重(z)。具体数据如下表，试对这8个企业的技术密集水平作聚类分析。
聚类分析实验报告例题
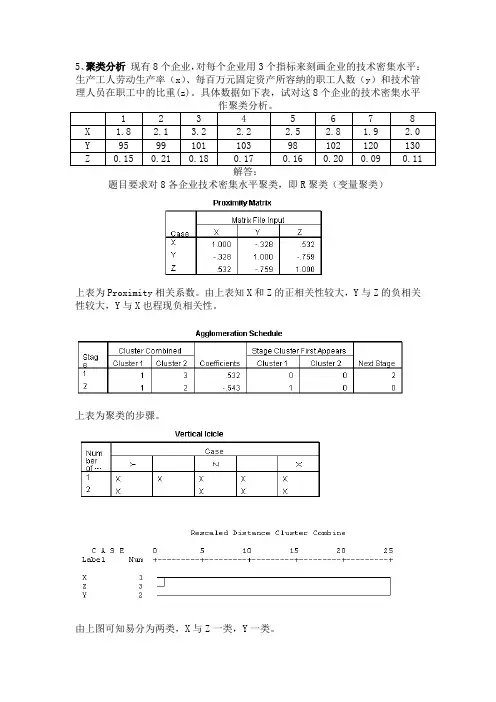
一、实验目的1. 理解聚类分析的基本原理和方法。
2. 掌握K-means、层次聚类等常用聚类算法。
3. 学习如何使用Python进行聚类分析，并理解算法的运行机制。
4. 分析实验结果，并评估聚类效果。
二、实验环境1. 操作系统：Windows 102. 编程语言：Python3.83. 库：NumPy、Matplotlib、Scikit-learn三、实验数据本次实验使用的数据集为Iris数据集，包含150个样本，每个样本有4个特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度），属于3个不同的类别。
四、实验步骤1. 导入Iris数据集，并进行数据预处理。
2. 使用K-means算法进行聚类分析，选择合适的K值。
3. 使用层次聚类算法进行聚类分析，观察聚类结果。
4. 分析两种算法的聚类效果，并进行比较。
5. 使用Matplotlib绘制聚类结果的可视化图形。
五、实验过程1. 数据预处理```pythonfrom sklearn import datasetsimport numpy as np# 加载Iris数据集iris = datasets.load_iris()X = iris.datay = iris.target# 数据标准化X = (X - np.mean(X, axis=0)) / np.std(X, axis=0) ```2. K-means聚类分析```pythonfrom sklearn.cluster import KMeans# 选择K值k_values = range(2, 10)inertia_values = []for k in k_values:kmeans = KMeans(n_clusters=k, random_state=42) kmeans.fit(X)inertia_values.append(kmeans.inertia_)# 绘制肘部图import matplotlib.pyplot as pltplt.plot(k_values, inertia_values, marker='o') plt.xlabel('Number of clusters')plt.ylabel('Inertia')plt.title('Elbow Method')plt.show()```3. 层次聚类分析```pythonfrom sklearn.cluster import AgglomerativeClustering# 选择层次聚类方法agglo = AgglomerativeClustering(n_clusters=3)y_agglo = agglo.fit_predict(X)```4. 聚类效果分析通过观察肘部图，可以发现当K=3时，K-means算法的聚类效果最好。
聚类分析习题
聚类分析习题
一、填空题
1、系统聚类法是在聚类分析的开始，每个样本自成________；然后，按照某种方法度量所有样本之间的亲疏程度，并把最相似的样本首先聚成一小类；接下来，度量剩余的样本和小类间的___________，并将当前最接近的样本或小类再聚成一类；如此反复，直到所有样本聚成一类为止。
2、常见的两类聚类法分别为：__________________和________________。
二、判断题
1、快速（动态）聚类分析中，分类的个数是确定的，不可改变。
（）
2、K均值聚类分析中，样品一旦划入某一类就不可改变。
（）
3、系统聚类可以对不同的类数产生一系列的聚类结果。
（）
4、K均值聚类和系统聚类一样，可以用不同的方法定义点点间的距离。
（）
5、K均值聚类和系统聚类一样，都是以距离的远近亲疏为标准进行聚类的。
（）
三、计算题
设有六个样品，每个样品只测量一个指标，分别是1，2，5，7，9，10。
（1）试用最短距离法、最长距离法、中间距离法、类平均法、重心法和离差平方和法将它们分类，并画出聚类谱系图。
（2）自己设置一个距离阈值d，写出最终的聚类结果。
聚类分析例题及解答
聚类分析作业之青柳念文创作
例题：
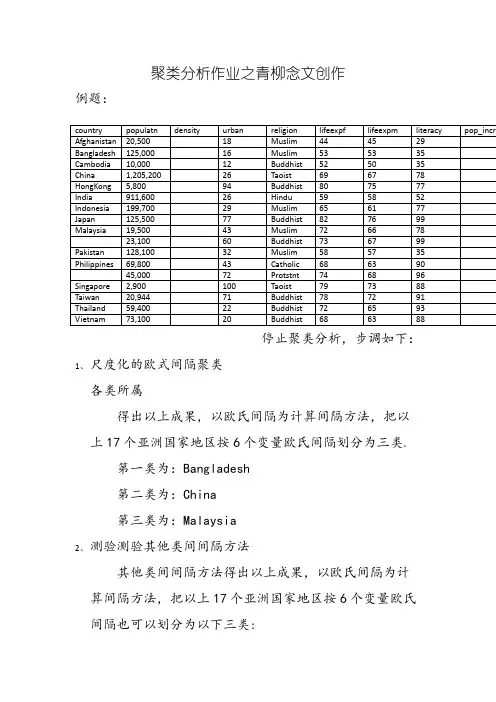
停止聚类分析，步调如下：
1、尺度化的欧式间隔聚类
各类所属
得出以上成果，以欧氏间隔为计算间隔方法，把以
上17个亚洲国家地区按6个变量欧氏间隔划分为三类.
第一类为：Bangladesh
第二类为：China
第三类为：Malaysia
2、测验测验其他类间间隔方法
其他类间间隔方法得出以上成果，以欧氏间隔为计
算间隔方法，把以上17个亚洲国家地区按6个变量欧氏
间隔也可以划分为以下三类:
第一类为：Bangladesh
第二类为：China
第三类为：Malaysia
3、用样本主成分画图
由图可知，所聚成的3类中:
第1类有5个样本，类间间隔较接近，效果较好；第2类有6个样本，类间间隔较接近，效果次之；第3类有6个样本.类间间隔较团圆，效果最差.。
第12章聚类分析习题答案
1
兰花科创
2
1
1
2
4
黑化股份
1
2
3
3
1
兖州煤业
2
22Leabharlann 14国阳新能
2
2
3
3
1
盘江股份
1
2
3
5
1
上海能源
2
2
3
1
1
山西焦化
1
2
3
3
1
恒源煤电
2
1
1
2
3
开滦股份
2
1
1
2
2
大同煤业
2
2
2
1
4
中国神华
2
2
2
1
4
潞安环能
2
1
1
2
2
中煤能源
2
2
2
1
4
国投新集
2
2
3
1
1
12.2下表是摘自《世界竞争力报告——1997》关于20个国家和地区的信息基础设施发展状况数据，各变量的含义为：call——每千人拥有电话线数，movecall——每千户居民蜂窝移动电话数，fee——高峰时期每三分钟国际电话的成本，computer——每千人拥有的计算机数，mips——每千人中计算机功率，net——每千人互联网络户主数。试根据该数据对这些国家和地区进行分层聚类分析，比较不同距离定义下的聚类结果，你会选择分几类？
Cluster6
海油工程
2
1
1
2
2
中海油服
1
2
2
5
5
中国石化
1
3
3
3
兰花科创
2
1
1
2
4
黑化股份
1
2
3
3
1
兖州煤业
2
22Leabharlann 14国阳新能
2
2
3
3
1
盘江股份
1
2
3
5
1
上海能源
2
2
3
1
1
山西焦化
1
2
3
3
1
恒源煤电
2
1
1
2
3
开滦股份
2
1
1
2
2
大同煤业
2
2
2
1
4
中国神华
2
2
2
1
4
潞安环能
2
1
1
2
2
中煤能源
2
2
2
1
4
国投新集
2
2
3
1
1
12.2下表是摘自《世界竞争力报告——1997》关于20个国家和地区的信息基础设施发展状况数据，各变量的含义为：call——每千人拥有电话线数，movecall——每千户居民蜂窝移动电话数，fee——高峰时期每三分钟国际电话的成本，computer——每千人拥有的计算机数，mips——每千人中计算机功率，net——每千人互联网络户主数。试根据该数据对这些国家和地区进行分层聚类分析，比较不同距离定义下的聚类结果，你会选择分几类？
Cluster6
海油工程
2
1
1
2
2
中海油服
1
2
2
5
5
中国石化
1
3
3
3
机器学习与人工智能(聚类分析)习题与答案
一、填空题1.EM算法中，E代表期望，M代表（）。
正确答案：最大化2.无监督学习中除了聚类，另一种是（）。
正确答案：建模3.我们将一个数据可以属于多个类（概率）的聚类称作（）。
正确答案：软聚类二、判断题1.聚类算法中的谱聚类算法是一种分层算法。
正确答案：×解析：聚类算法中的谱聚类算法是一种扁平算法。
2.两个向量之间的余弦距离等于1减这两个向量的余弦相似度。
正确答案：√3.K-均值++算法能够克服最远点不能处理离群值的问题。
正确答案：√4.K-means和EM聚类之间的主要区别之一是EM聚类是一种“软”聚类算法。
正确答案：√5.监督学习的训练集时有标签的数据。
正确答案：√6.在文本聚类中，欧氏距离是比较适合的。
正确答案：×三、单选题1.以下哪些方法可以确定K-均值算法已经收敛？（）A.划分不再改变B.聚类中心不再改变C.固定次数的迭代D.以上三种均是正确答案：D2.以下哪些算法可以处理非高斯数据？（）A.K-means算法B.EM算法C.谱聚类算法D.以上三种算法都可以正确答案：C四、多选题1、无监督学习可以应用于哪些方面？（）A.图像压缩B.生物信息学：学习基因组C.客户细分（即分组）D.学习没有任何标签的聚类/群组正确答案：A、B、C、D2、以下哪些选项是K-均值聚类面临的问题？（）A.K的选择具有挑战性B.硬聚类并不总是正确的C.贪婪算法存在的问题D.关于数据的球形假设（到聚类中心的距离）正确答案：A、B、C、D3、聚类可以应用于哪些方面？（）A.基因表达数据的研究B.面部聚类C.搜索结果聚类D.新闻搜索正确答案：A、B、C、D4、在K-均值算法中，以下哪些方法可以用于随机种子的选择？（）A.随机选择数据作为中心B.空间中的随机位置作为中心C.尝试多个初始起点D.使用另一个聚类方法的结果进行初始化正确答案：A、B、C、D5、EM算法可以应用于以下哪些方面？（）A.学习贝叶斯网络的概率B.EM-聚类C.训练HMMD.学习微信好友网络正确答案：A、B、C、D。
(6)聚类分析例子
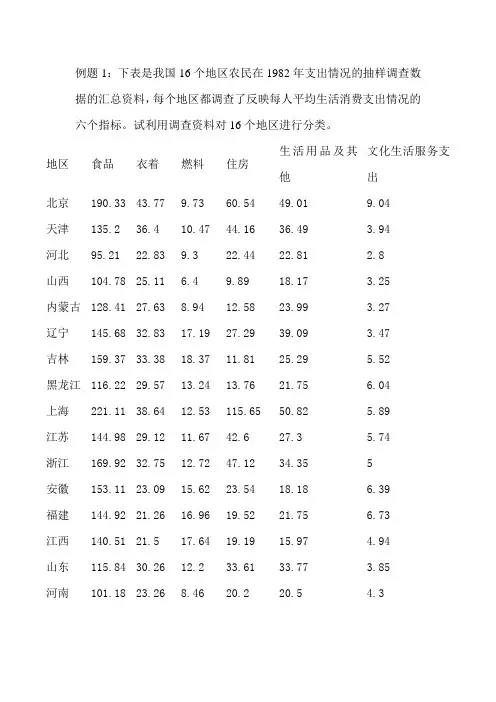
例题1：下表是我国16个地区农民在1982年支出情况的抽样调查数据的汇总资料，每个地区都调查了反映每人平均生活消费支出情况的六个指标。
试利用调查资料对16个地区进行分类。
地区食品衣着燃料住房生活用品及其他文化生活服务支出北京190.33 43.77 9.73 60.54 49.01 9.04 天津135.2 36.4 10.47 44.16 36.49 3.94 河北95.21 22.83 9.3 22.44 22.81 2.8 山西104.78 25.11 6.4 9.89 18.17 3.25 内蒙古128.41 27.63 8.94 12.58 23.99 3.27 辽宁145.68 32.83 17.19 27.29 39.09 3.47 吉林159.37 33.38 18.37 11.81 25.29 5.52 黑龙江116.22 29.57 13.24 13.76 21.75 6.04 上海221.11 38.64 12.53 115.65 50.82 5.89 江苏144.98 29.12 11.67 42.6 27.3 5.74 浙江169.92 32.75 12.72 47.12 34.35 5安徽153.11 23.09 15.62 23.54 18.18 6.39 福建144.92 21.26 16.96 19.52 21.75 6.73 江西140.51 21.5 17.64 19.19 15.97 4.94 山东115.84 30.26 12.2 33.61 33.77 3.85 河南101.18 23.26 8.46 20.2 20.5 4.3下面用统计学软件 SAS(Statistical Analysis System) data dfdf;input city $ x1 x2 x3 x4 x5 x6;cards;beijing 190.33 43.77 9.73 60.54 49.01 9.04tianjing 135.20 36.40 10.47 44.16 36.49 3.94hebei 95.21 22.83 9.30 22.44 22.81 2.80shanxi 104.78 25.11 6.40 9.89 18.17 3.25 neimenggu 128.41 27.63 8.94 12.58 23.99 3.27 liaoning 145.68 32.83 17.19 27.29 39.09 3.47jilin 159.37 33.38 18.37 11.81 25.29 5.22 heilongjiang 116.22 29.57 13.24 13.76 21.75 6.04 shanghai 221.11 38.64 12.53 115.65 50.82 5.89 jiangsu 144.98 29.12 11.67 42.60 27.30 5.74 zhejiang 169.92 32.75 12.72 47.12 34.35 5.00anhui 153.11 23.09 15.62 23.54 18.18 6.39fujian 144.92 21.26 16.96 19.52 21.75 6.73jiangxi 140.54 21.50 17.64 19.19 15.97 4.94 shandong 115.84 30.26 12.20 33.61 33.77 3.85henan 101.18 23.26 8.46 20.20 20.50 4.30;run;proc cluster data=dfdf std outtree=tree method=ave pesudo rsq;id city;run; /*ward离差平方和法 war; 类平均法 ave; 重心法 cen;最长距离法 com;中间距离法 med; 最短距离法 sin;密度估计法 den;极大似然法 eml; 可变类平均 fle;相似分析法 mcq; 两阶段密度估计 two; */proc tree data=tree out=new graphics horizontal；id city;run;Cluster HistoryNormRMS NCL Clusters Joined--- FREQ SPRSQ RSQ PSF PST2 Dist 15 anhui fujian 2 0.0025 0.998 28.7 . 0.193 14 hebei henan 2 0.0055 0.992 19.1 . 0.2869 13 CL14 shanxi 3 0.0068 0.985 16.7 1.2 0.3116 12 CL15 jiangxi 3 0.0099 0.975 14.4 4 0.3481 11 jiangsu zhejiang 2 0.0089 0.966 14.4 . 0.366 10 CL13 neimengg 4 0.0106 0.956 14.4 1.7 0.3692 9 tianjing shandong 2 0.0092 0.947 15.5 . 0.3711 8 CL9 CL11 4 0.0237 0.923 13.7 2.6 0.4957 7 liaoning jilin 2 0.0189 0.904 14.1 . 0.5329 6 heilongj CL12 4 0.0267 0.877 14.3 4.3 0.5463 5 CL8 CL7 6 0.0528 0.824 12.9 3.5 0.6681 4 CL5 CL6 10 0.1269 0.698 9.2 6.6 0.7823 3 CL4 CL10 14 0.1955 0.502 6.6 7.8 0.8751 2 beijing shanghai 2 0.0562 0.446 11.3 . 0.91841CL2 CL3 16 0.4458 0 . 11.3 1.5454（1）2R 统计量（列标题为RSQ ）用于评价每次合并成NCL 个类时的聚类效果。
聚类分析例题
聚类分析例题聚类分析例题5.2酿酒葡萄的等级划分5.2.1葡萄酒的质量分类由问题1中我们得知，第二组评酒员的的评价结果更为可信，所以我们通过第二组评酒员对于酒的评分做出处理。
我们通过excel计算出每位评酒员对每支酒的总分，然后计算出每支酒的10个分数的平均值，作为总的对于这支酒的等级评价。
通过国际酿酒工会对于葡萄酒的分级，以百分制标准评级，总共评出了六个级别（见表5）。
等级特优优优良良及格不及格分数95-100 90-94 80-89 70-79 60-69 0-59在问题2的计算中，我们求出了各支酒的分数，考虑到所有分数在区间[61.6，81.5]波动，以原等级表分级，结果将会很模糊，不能分得比较清晰。
为此我们需要进一步细化等级。
为此我们重新细化出5个等级，为了方便计算，我们还对等级进行降序数字等级（见表6）。
等级偏优偏优良良中及格分数80-84 75-79 70-74 65-69 60-64数字等级 5 4 3 2 1通过对数据的预处理，我们得到了一个新的关于葡萄酒的分级表格（见表7）：编号红酒原等级细化等级白酒原等级细化等级1号68.1 2 2 77.9 3 4 2号74 3 3 75.8 3 4 3号74.6 3 4 75.6 3 4 4号71.2 3 3 76.9 3 4 5号72.1 3 3 81.5 4 5 6号66.3 2 2 75.5 3 4 7号65.3 2 2 74.2 3 3 8号66 2 2 72.3 3 3 9号78.2 3 4 80.4 4 510号68.8 2 2 79.8 3 411号61.6 2 1 71.4 3 312号68.3 2 2 72.4 3 313号68.8 2 2 73.9 3 314号72.6 3 3 77.1 3 415号65.7 2 2 78.4 3 416号69.9 2 3 67.3 2 217号74.5 3 3 80.3 4 518号65.4 2 2 76.7 3 419号 72.6 3 3 76.4 3 4 20号 75.8 3 4 76.6 3 4 21号 72.2 3 2 79.2 3 4 22号 71.6 3 3 79.4 3 4 23号 77.1 3 4 77.4 3 4 24号 71.5 3 3 76.1 3 4 25号 68.2 2 2 79.5 3 4 26号 72 3 3 74.3 3 3 27号 71.5 3 3 77 3 4 28号 79.6 3 4 考虑到葡萄酒的质量与酿酒葡萄间有比较之间的关系，我们将保留葡萄酒质量对于酿酒葡萄的影响，先单纯从酿酒葡萄的理化指标对酿酒葡萄进行分类，然后在通过葡萄酒质量对酿酒葡萄质量的优劣进一步进行划分。
练习聚类分析
练习：今有6个铅弹头，用“中子活化”方法测得7种微量元素的含量数据，如下表：⑴试用多种系统聚类法对6个弹头进行分类，并比较分类结果；⑵试用多种方法对7种微量元素进行分类.第一问：解：此题可用多种系统聚类法进行分析，共采用五种聚类方法：类平均法、重心法、密度估计法、最小距离法和Ward法。
（1）类平均法可采用以下SAS程序．该程序第一步建立名为bom的数据集，此数据集包括1-6个弹头的资料。
紧接着的proc cluster 语句调用cluster过程用来对数据集bom进行聚类,method=average表示采用类平均法,其中语句var x1 x2 x3 x4 x5 x6 x7表明对x1 x2 x3 x4 x5 x6 x7这7种元素进行聚类分析。
Id number；表明用弹头样品号区分聚类的观测．类平均法的输出如下由上图（Cluster History）给出了用类平均法聚类的结过程，每行指出新聚类的弹头样品号．各行为：1）分成五类{2 6}，{1}，{3}，{4}，{5}．2）分成四类{1 2 6}，{3}，{4}，{5}．3）分成三类{1 2 6 }，{3 5}，{4}．4）分成二类{1 2 4 6}，{3 5}．5）分成一类{1 2 3 4 5 6 }(2)使用重心法，重心法得出的输出结果如下：上图中（Cluster History）给出了用重心法聚类的过程，每行指出新聚类的弹头样品号．各行为：各行为：1）分成五类{2 6}，{1}，{3}，{4}，{5}．2）分成四类{1 2 6}，{3}，{4}，{5}．3）分成三类{1 2 6 }，{3 5}，{4}．4）分成二类{1 2 4 6}，{3 5}．5）分成一类{1 2 3 4 5 6 }⑶使用密度法使用密度法得到的输出结果如下：上图中（Cluster History）给出了用密度法聚类的过程，每行指出新聚类的弹头样品号．各行为：1）分成五类{2 6}，{1}，{3}，{4}，{5}．2）分成四类{1 2 6}，{3}，{4}，{5}．3）分成三类{1 2 6 4}，{3}，{5}．4）分成二类{1 2 34 6}，{5}．5）分成一类{1 2 3 4 5 6 }（4）使用最短距离法：使用最短距离法得到的输出结果如下：上图中（Cluster History）给出了用最短距离法聚类的过程，每行指出新聚类的弹头样品号．各行为：1）分成五类{2 6}，{1}，{3}，{4}，{5}．2）分成四类{1 2 6}，{3}，{4}，{5}．3）分成三类{1 2 6 4}，{3}，{5}．4）分成二类{1 2 4 6}，{3 5}．5）分成一类{1 2 3 4 5 6 }（5）使用ward法使用ward法得到的输出结果如下上图中（Cluster History）给出了用最短距离法聚类的过程，每行指出新聚类的弹头样品号．各行为：1）分成五类{2 6}，{1}，{3}，{4}，{5}．2）分成四类{1 2 6}，{3}，{4}，{5}．3）分成三类{1 2 6 }，{4}，{3 5}．4）分成二类{1 2 4 6}，{3 5}．5）分成一类{1 2 3 4 5 6 }对上述五种方法的结果进行分析:我们看一下分成三类，则上述方法的分析结果为：类平均法：{1 2 6 }，{3 5}，{4}．重心法{1 2 6 }，{3 5}，{4}．密度法．{1 2 6 4}，{3}，{5}．最小距离法{1 2 6 4}，{3}，{5}．Ward法{1 2 6 }，{4}，{3 5}．由以上结果可见用不同的方法进行聚类其结果是有差异的。
应用多元统计分析第六章习题解答
证明：设第L次合并Gp和Gq为新类Gr后,并类距离DL ＝ Dpq,且必有Dpq2≤Dij2 . 新类Gr与其它类Gk的距离平方的 递推公式 ,当γ＝0,αp≥0,αq≥0, αp+αq+ β ≥1 时
2 2 2 2 2 2 Dkr p Dpk q Dqk Dpq ( p q )Dpq Dpq
rij
(x
t 1 n t 1
n
ti
xi )(xtj x j )
2 ( x x ) tj j t 1
7
2 ( x x ) ti i
n
ab ac ( xti xi )(xtj x j ) xti xtj nxi x j a n n n t 1 t 1 1 1 [an (a b)(a c)] [a (a b c d ) (a b)(a c)] n n ad bc n
证明 : (1)设d 和d 为距离, 令d d
(1) ( 2)
(1)
d .
( 2)
2
以下来验证d满足作为距离所要求的3个条件.
第六章 聚类分析
① ② ③
(2) 设d是距离,a >0为正常数.令d*=ad,显然有
① ②
d cd ij 0, 且仅当X (i ) X ( j )时d 0;
X ( 2) X ( 3) 3 5 0 X (5) 7 10 8 0 CL 4
11
第六章 聚类分析
② 合并{X(2),X(5)}=CL3,并类距离 D2=3.
D
( 3)
0 X ( 3) 10 0 CL 4 CL3 9 8 0
③ 合并{CL3,CL4}=CL2,并类距离 D3=8.
应用多元统计分析第六章习题解答
D2 0.85 0.922 1 D1 A
故重心法法不具有单调性。
并类过程如下：
B
C
D (1)
0
1.1 0
110..01
A B C
D(2)
0
D(3) 0
0.85 0
A Gr
24
第六章 聚类分析
6-7 试推导重心法的距离递推公式(6.3.2);
来证明当γ＝0,αp≥0,αq≥0,αp+αq+β≥1时,系统聚类中的类平均法、可变类平 均法、可变法、Ward法的单调性.
证明：设第L次合并Gp和Gq为新类Gr后,并类距离DL ＝Dpq,且必有Dpq2≤Dij2 . 新类Gr与其它类Gk的距离平方的递推公式 ,当γ＝0,αp≥0,αq≥0, αp+αq+ β ≥1 时
Dr2k
np nr
Dp2k
nq nr
Dq2k
n p nq nr2
Dp2q
解一: 利用
X (r) 1 nr
n p X ( p) nq X (q)
如果样品间的距离定义为欧氏距离,则有
Dr2k ( X (k ) X (r ) )'( X (k ) X (r ) )
0
X (5) CL4
11
第六章 聚类分析
② 合并{X(2),X(5)}=CL3,并类距离 D2=3.
D(3) 100 9
0 8
0
X (3)
CL4 CL3
③ 合并{CL3,CL4}=CL2,并类距离 D3=8.
D(4) 100
故重心法法不具有单调性。
并类过程如下：
B
C
D (1)
0
1.1 0
110..01
A B C
D(2)
0
D(3) 0
0.85 0
A Gr
24
第六章 聚类分析
6-7 试推导重心法的距离递推公式(6.3.2);
来证明当γ＝0,αp≥0,αq≥0,αp+αq+β≥1时,系统聚类中的类平均法、可变类平 均法、可变法、Ward法的单调性.
证明：设第L次合并Gp和Gq为新类Gr后,并类距离DL ＝Dpq,且必有Dpq2≤Dij2 . 新类Gr与其它类Gk的距离平方的递推公式 ,当γ＝0,αp≥0,αq≥0, αp+αq+ β ≥1 时
Dr2k
np nr
Dp2k
nq nr
Dq2k
n p nq nr2
Dp2q
解一: 利用
X (r) 1 nr
n p X ( p) nq X (q)
如果样品间的距离定义为欧氏距离,则有
Dr2k ( X (k ) X (r ) )'( X (k ) X (r ) )
0
X (5) CL4
11
第六章 聚类分析
② 合并{X(2),X(5)}=CL3,并类距离 D2=3.
D(3) 100 9
0 8
0
X (3)
CL4 CL3
③ 合并{CL3,CL4}=CL2,并类距离 D3=8.
D(4) 100
聚类分析实例
聚类分析实例一、聚类分析例1、为深入了解我国人口的文化程度状况，现利用1990年全国人口普查数据对全国30个省市自治区进行聚类分析。
分析选用了三个指标：（1）大学以上文化程度的人口占全部人口的比例（DXBZ）；（2）初中文化程度的人口占全部人口的比例（CZBZ）；（3）文盲半文盲人口占全部人口的比例（WMBZ），分别用来反映较高、中等、较低文化程度人口的状况，原始数据如下表：（%）例2、根据信息基础设施的发展状况，对世界20个国家和地区进行分类。
这里选取了发达国家、新兴工业化国家、拉美国家、亚洲发展中国家、转型国家等不同类型的20个国家作聚类分析。
描述信息基础设施的变量主要的有六个：call——千人拥有电话号码，movecall——每千户居民蜂窝移动电话，fee——高峰时期每三分钟国际电话成本，computer——每千人拥有的计算机数，mips——每千人中计算机功率，net——每千人互联网例3、为了研究1982年全国各地区农民家庭收支的分布规律，根据抽样调查资料进行分类处理，共抽取28个省、市、自治区的样本，每个样本有六个指标，这六个指标反映了平均每人生活消费的支出情况，其原始数据见表3。
例4为了研究世界各国森林、草原资源的分布规律，共抽取了21个国家的数据，每个国家例5 若要从沪市的蒲发银行、齐鲁石化、东北高速、武钢股份、东风汽车等53家上市公司中优选适合开放式基金组合投资的10只股票，我们以总股本和流通股本为分类标志，根据这53家公司的总股本和A股流通股本数据（见表5.3），用聚类分析法将它们分成若干类，再从各类公司中选出比较活跃的股票建立股票池。
表5.3 53家上市公司股本资料单位：十万股例6沪市上市公司2001年末总股本在10000—12000万股、流通股本在3600—5050万股之间共有23家（对于股本结构在其它范围内的上市公司，用雷同的方法，可以建立相应的每股收益预测模型），各公司2000年及2001年有关的财务数据见表。
聚类分析期末试题题库及答案
聚类分析期末试题题库及答案一、选择题1. 聚类分析属于以下哪一类学习方式？A. 监督学习B. 无监督学习C. 增强学习D. 半监督学习答案：B2. 聚类分析的目标是什么？A. 对样本进行分类B. 预测样本的输出C. 减少数据的维度D. 发现数据中的固有结构答案：D3. 下面哪种方法不适用于聚类分析？A. K-means算法B. 层次聚类C. 支持向量机D. DBSCAN算法答案：C4. 当聚类分析中的聚类数目不事先给定时，以下哪个指标可以帮助我们选择合适的聚类数目？A. 轮廓系数B. 均方误差C. 方差解释比例D. 马氏距离答案：A5. 在使用K-means算法进行聚类分析时，初始聚类中心的选择对结果有何影响？A. 不影响结果B. 会导致陷入局部最优解C. 会导致算法收敛速度变慢D. 使得聚类数目增加答案：B二、填空题1. 聚类分析是一种_____________学习方式。
答案：无监督2. 聚类分析的目标是发现数据中的_____________结构。
答案：固有3. 聚类分析中最常用的算法之一是_____________算法。
答案：K-means4. 聚类分析中的聚类数目可以通过_____________系数来选择。
答案：轮廓5. 初始聚类中心的选择会对K-means算法的结果产生_____________。
答案：影响三、简答题1. 简述聚类分析的步骤及流程。
答：聚类分析的一般步骤包括：数据预处理、选择聚类算法、确定聚类数目、计算聚类中心、分配样本到聚类、评估聚类结果。
首先，需要对数据进行预处理，包括数据清洗、特征选择、数据标准化等。
然后，选择合适的聚类算法，如K-means、层次聚类、DBSCAN等。
接下来，通过轮廓系数等指标选择合适的聚类数目。
然后，计算聚类中心，即确定每个聚类的重心或代表性样本。
再次，将样本分配到各个聚类中心，形成聚类结果。
最后，评估聚类结果的质量，如通过轮廓系数、均方误差等指标进行评价。
聚类分析例子
案例数据源：有20种12盎司啤酒成分和价格的数据，变量包括啤酒名称、热量、钠含量、酒精含量、价格。
【一】问题一：选择那些变量进行聚类？——采用“R型聚类”1、现在我们有4个变量用来对啤酒分类2、先确定用相似性来测度，度量标准选用pearson系数，聚类方法选最远元素，将来的相似性矩阵里的数字为相关系数。
若果有某两个变量的相关系数接近1或-1，说明两个变量可互相替代。
3、只输出“树状图”就可以了，从proximity matrix表中可以看出热量和酒精含量两个变量相关系数0.903，最大，二者选其一即可，没有必要都作为聚类变量，导致成本增加。
至于热量和酒精含量选择哪一个作为典型指标来代替原来的两个变量，可以根据专业知识或测定的难易程度决定。
（与因子分析不同，是完全踢掉其中一个变量以达到降维的目的。
）这里选用酒精含量，至此，确定出用于聚类的变量为：酒精含量，钠含量，价格。
【二】问题二：20中啤酒能分为几类？——采用“Q型聚类”1、现在开始对20中啤酒进行聚类。
开始不确定应该分为几类，暂时用一个3-5类范围来试探，这一回用欧式距离平方进行测度。
2、主要通过树状图和冰柱图来理解类别。
最终是分为4类还是3类，这是个复杂的过程，需要专业知识和最初的目的来识别。
我这里试着确定分为4类。
选择“保存”，则在数据区域内会自动生成聚类结果。
【三】问题三：用于聚类的变量对聚类过程、结果又贡献么，有用么？——采用“单因素方差分析”1、聚类分析除了对类别的确定需讨论外，还有一个比较关键的问题就是分类变量到底对聚类有没有作用有没有贡献，如果有个别变量对分类没有作用的话，应该剔除。
2、这个过程一般用单因素方差分析来判断。
注意此时，因子变量选择聚为4类的结果，而将三个聚类变量作为因变量处理。
方差分析结果显示，三个聚类变量sig值均极显著，我们用于分类的3个变量对分类有作用，可以使用，作为聚类变量是比较合理的。
【四】问题四：聚类结果的解释？——采用”均值比较描述统计“1、聚类分析最后一步，也是最为困难的就是对分出的各类进行定义解释，描述各类的特征，即各类别特征描述。
最新聚类分析例题及解答
聚类分析作业例题：country populatn density urban religion lifeexpf lifeexpm literacy pop_incr Afghanistan 20,500 25.0 18 Muslim 44 45 29 2.8 Bangladesh 125,000 800.0 16 Muslim 53 53 35 2.4 Cambodia 10,000 55.0 12 Buddhist 52 50 35 2.9 China 1,205,200 124.0 26 Taoist 69 67 78 1.1 HongKong 5,800 5,494.0 94 Buddhist 80 75 77 -0.1 India 911,600 283.0 26 Hindu 59 58 52 1.9 Indonesia 199,700 102.0 29 Muslim 65 61 77 1.6 Japan 125,500 330.0 77 Buddhist 82 76 99 0.3 Malaysia 19,500 58.0 43 Muslim 72 66 78 2.3N.Korea 23,100 189.0 60 Buddhist 73 67 99 1.8 Pakistan 128,100 143.0 32 Muslim 58 57 35 2.8 Philippines 69,800 221.0 43 Catholic 68 63 90 1.9S.Korea 45,000 447.0 72 Protstnt 74 68 96 1.0 Singapore 2,900 4,456.0 100 Taoist 79 73 88 1.2 Taiwan 20,944 582.0 71 Buddhist 78 72 91 0.9 Thailand 59,400 115.0 22 Buddhist 72 65 93 1.4 Vietnam 73,100 218.0 20 Buddhist 68 63 88 1.8进行聚类分析，步骤如下：1、标准化的欧式距离聚类各类所属得出以上结果，以欧氏距离为计算距离方法，把以上17个亚洲国家地区按6个变量欧氏距离划分为三类。
聚类分析习题及答案
第三章 聚类分析一、填空题1.在进行聚类分析时，根据变量取值的不同，变量特性的测量尺度有以下三种类型： 间隔尺度 、 顺序尺度 和 名义尺度 。
2．Q 型聚类法是按___样品___进行聚类，R 型聚类法是按_变量___进行聚类。
3．Q 型聚类统计量是____距离_，而R 型聚类统计量通常采用_相似系数____。
4．在聚类分析中，为了使不同量纲、不同取值范围的数据能够放在一起进行比较，通常需要对原始数据进行变换处理。
常用的变换方法有以下几种：__中心化变换_____、__标准化变换____、____规格化变换__、__ 对数变换 _。
5．距离ij d 一般应满足以下四个条件：对于一切的i,j ，有0≥ij d 、 j i =时，有0=ij d 、对于一切的i,j ，有ji ij d d =、对于一切的i,j,k ，有kj ik ij d d d +≤。
6.相似系数一般应满足的条件为： 若变量i x 与 j x 成比例，则1±=ij C 、 对一1≤ij 和 对一切的i,j ，有ji ij C C =。
7.常用的相似系数有 夹角余弦 和 相关系数 两种。
8.常用的系统聚类方法主要有以下八种： 最短距离法 、最长距离法、中间距离法、重心法、类平均法、可变类平均法、可变法、离差平方和法。
9．快速聚类在SPSS 中由__K-mean_____________过程实现。
10.常用的明氏距离公式为：()pk q jk ik ij x x q d 11⎥⎦⎤⎢⎣⎡-=∑=，当1=q 时，它表示 绝对距离 ；当2=q 时，它表示 欧氏距离 ；当q 趋于无穷时，它表示 切比雪夫距离 。
11．聚类分析是将一批 样品 或 变量 ，按照它们在性质上 的 亲疏、相似程度 进行分类。
12．明氏距离的缺点主要表现在两个方面：第一 明氏距离的值与各指标的量纲有关 ，第二 明氏距离没有考虑到各个指标（变量）之间的相关性 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
聚类分析作业
令狐采学
例题：
进行聚类分析，步骤如下：
1、标准化的欧式距离聚类
各类所属
得出以上结果，以欧氏距离为计算距离方法，把以上
17个亚洲国家地区按6个变量欧氏距离划分为三类。
第一类为：Bangladesh
第二类为：China
第三类为：Malaysia
2、尝试其他类间距离方法
其他类间距离方法得出以上结果，以欧氏距离为计算距
离方法，把以上17个亚洲国家地区按6个变量欧氏距离也可以划分为以下三类:
第一类为：Bangladesh
第二类为：China
第三类为：Malaysia
3、用样本主成分画图
由图可知，所聚成的3类中:
第1类有5个样本，类间距离较接近，效果较好；
第2类有6个样本，类间距离较接近，效果次之；
第3类有6个样本。
类间距离较离散，效果最差。