2017年高考数学空间几何高考真题

2017年浙江省高考数学试卷(真题详细解析)1.已知集合P={x|-1<x<1}，Q={x|1<x<2}，则P∪Q=(-1,2)。

2.椭圆+1的离心率是1/2.3.几何体的三视图无法确定，无法计算体积。

4.若x、y满足约束条件z=x+2y，则z的取值范围是[4.+∞)。

5.函数f(x)=x^2+ax+b在区间[0,1]上的最大值是M，最小值是m，则M-m与a有关，但与b无关。

6.已知等差数列{an}的公差为d，前n项和为Sn，则d>0是S4+S6>2S5的必要不充分条件。

7.函数y=f(x)的图象可能是B。

8.已知随机变量ξi满足P(ξi=1)=pi，P(ξi=0)=1-pi，i=1，2.若0<p1<p2<1，则E(ξ1)<E(ξ2)，D(ξ1)<D(ξ2)。

9.正四面体D-ABC，P、Q、R分别为AB、BC、CA上的点，AP=PB=√2，记二面角D-PR-Q，D-PQ-R，D-QR-P的平面角为α、β、γ，则α<β<γ。

10.平面四边形ABCD，AB⊥BC，AB=BC=AD=2，CD=3，AC与BD交于点O，记I1=OI2/OC，I2=OI3/OD，I3=OI1/OA，则I3<I1<I2.二、填空题：11．XXX创立的“割圆术”可以估算圆周率π，理论上能把π的值计算到任意精度，祖冲之继承并发展了“割圆术”，将π的值精确到小数点后七位。

割圆术的第一步是计算单位圆内接正六边形的面积S6，S6=3√3/2.12．已知a、b∈R，（a+bi）2=3+4i（i是虚数单位），则a2+b2=5，ab=2.13．已知多项式（x+1）（x+2）=x2+3x+2，则a4=34，a5=123.14．已知△ABC，AB=AC=4，BC=2，点D为AB延长线上一点，BD=2，连结CD，则△BDC的面积是2√3，cos∠BDC=1/2.15．已知向量a、b满足||a||=1，||b||=2，则|a+b|+|a-b|-|a|-|b|的最小值是0，最大值是4.16．从6男2女共8名学生中选出队长1人，副队长1人，普通队员2人组成4人服务队，要求服务队中至少有1名女生，共有56种不同的选法。

2017年浙江省高考数学试卷一、选择题（共10小题，每小题4分，满分40分）1．（4分）已知集合P={x|﹣1＜x＜1}，Q={x|0＜x＜2}，那么P∪Q=（）A．（﹣1，2）B．（0，1）C．（﹣1，0）D．（1，2）2．（4分）椭圆+=1的离心率是（）A．B．C．D．3．（4分）某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）A．+1B．+3C．+1D．+34．（4分）若x、y满足约束条件，则z=x+2y的取值范围是（）A．[0，6]B．[0，4]C．[6，+∞）D．[4，+∞）5．（4分）若函数f（x）=x2+ax+b在区间[0，1]上的最大值是M，最小值是m，则M﹣m（）A．与a有关，且与b有关B．与a有关，但与b无关C．与a无关，且与b无关D．与a无关，但与b有关6．（4分）已知等差数列{an }的公差为d，前n项和为Sn，则“d＞0”是“S4+S6＞2S5”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件7．（4分）函数y=f（x）的导函数y=f′（x）的图象如图所示，则函数y=f（x）的图象可能是（）A．B．C．D．8．（4分）已知随机变量ξi 满足P（ξi=1）=pi，P（ξi=0）=1﹣pi，i=1，2．若0＜p1＜p2＜，则（）A．E（ξ1）＜E（ξ2），D（ξ1）＜D（ξ2）B．E（ξ1）＜E（ξ2），D（ξ1）＞D（ξ2）C．E（ξ1）＞E（ξ2），D（ξ1）＜D（ξ2）D．E（ξ1）＞E（ξ2），D（ξ1）＞D（ξ2）9．（4分）如图，已知正四面体D﹣ABC（所有棱长均相等的三棱锥），P、Q、R 分别为AB、BC、CA上的点，AP=PB，==2，分别记二面角D﹣PR﹣Q，D ﹣PQ﹣R，D﹣QR﹣P的平面角为α、β、γ，则（）A．γ＜α＜βB．α＜γ＜βC．α＜β＜γD．β＜γ＜α10．（4分）如图，已知平面四边形ABCD，AB⊥BC，AB=BC=AD=2，CD=3，AC与BD交于点O，记I1=•，I2=•，I3=•，则（）A．I1＜I2＜I3B．I1＜I3＜I2C．I3＜I1＜I2D．I2＜I1＜I3二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分11．（4分）我国古代数学家刘徽创立的“割圆术”可以估算圆周率π，理论上能把π的值计算到任意精度，祖冲之继承并发展了“割圆术”，将π的值精确到小数点后七位，其结果领先世界一千多年，“割圆术”的第一步是计算单位圆内接正六边形的面积S6，S6= ．12．（6分）已知a、b∈R，（a+bi）2=3+4i（i是虚数单位），则a2+b2= ，ab= ．13．（6分）已知多项式（x+1）3（x+2）2=x5+a1x4+a2x3+a3x2+a4x+a5，则a4= ，a5= ．14．（6分）已知△ABC，AB=AC=4，BC=2，点D为AB延长线上一点，BD=2，连结CD，则△BDC的面积是，cos∠BDC= ．15．（6分）已知向量、满足||=1，||=2，则|+|+|﹣|的最小值是，最大值是．16．（4分）从6男2女共8名学生中选出队长1人，副队长1人，普通队员2人组成4人服务队，要求服务队中至少有1名女生，共有种不同的选法．（用数字作答）17．（4分）已知a∈R，函数f（x）=|x+﹣a|+a在区间[1，4]上的最大值是5，则a的取值范围是．三、解答题（共5小题，满分74分）18．（14分）已知函数f（x）=sin2x﹣cos2x﹣2sinx cosx（x∈R）．（Ⅰ）求f（）的值．（Ⅱ）求f（x）的最小正周期及单调递增区间．19．（15分）如图，已知四棱锥P﹣ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．20．（15分）已知函数f（x）=（x﹣）e﹣x（x≥）．（1）求f（x）的导函数；（2）求f（x）在区间[，+∞）上的取值范围．21．（15分）如图，已知抛物线x2=y，点A（﹣，），B（，），抛物线上的点P（x，y）（﹣＜x＜），过点B作直线AP的垂线，垂足为Q．（Ⅰ）求直线AP斜率的取值范围；（Ⅱ）求|PA|•|PQ|的最大值．22．（15分）已知数列{xn }满足：x1=1，xn=xn+1+ln（1+xn+1）（n∈N*），证明：当n∈N*时，（Ⅰ）0＜xn+1＜xn；（Ⅱ）2xn+1﹣xn≤；（Ⅲ）≤xn≤．2017年浙江省高考数学试卷参考答案与试题解析一、选择题（共10小题，每小题4分，满分40分）1．（4分）已知集合P={x|﹣1＜x＜1}，Q={x|0＜x＜2}，那么P∪Q=（）A．（﹣1，2）B．（0，1）C．（﹣1，0）D．（1，2）【考点】1D：并集及其运算．【专题】11：计算题；37：集合思想；5J：集合．【分析】直接利用并集的运算法则化简求解即可．【解答】解：集合P={x|﹣1＜x＜1}，Q={x|0＜x＜2}，那么P∪Q={x|﹣1＜x＜2}=（﹣1，2）．故选：A．【点评】本题考查集合的基本运算，并集的求法，考查计算能力．2．（4分）椭圆+=1的离心率是（）A．B．C．D．【考点】K4：椭圆的性质．【专题】11：计算题；35：转化思想；5D：圆锥曲线的定义、性质与方程．【分析】直接利用椭圆的简单性质求解即可．【解答】解：椭圆+=1，可得a=3，b=2，则c==，所以椭圆的离心率为：=．故选：B．【点评】本题考查椭圆的简单性质的应用，考查计算能力．3．（4分）某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）A．+1B．+3C．+1D．+3【考点】L!：由三视图求面积、体积．【专题】11：计算题；31：数形结合；44：数形结合法；5Q：立体几何．【分析】根据几何体的三视图，该几何体是圆锥的一半和一个三棱锥组成，画出图形，结合图中数据即可求出它的体积．【解答】解：由几何的三视图可知，该几何体是圆锥的一半和一个三棱锥组成，圆锥的底面圆的半径为1，三棱锥的底面是底边长2的等腰直角三角形，圆锥的高和棱锥的高相等均为3，故该几何体的体积为××π×12×3+××××3=+1，故选：A．【点评】本题考查了空间几何体三视图的应用问题，解题的关键是根据三视图得出原几何体的结构特征，是基础题目．4．（4分）若x、y满足约束条件，则z=x+2y的取值范围是（）A．[0，6]B．[0，4]C．[6，+∞）D．[4，+∞）【考点】7C：简单线性规划．【专题】11：计算题；31：数形结合；35：转化思想；5T：不等式．【分析】画出约束条件的可行域，利用目标函数的最优解求解即可．【解答】解：x、y满足约束条件，表示的可行域如图：目标函数z=x+2y经过C点时，函数取得最小值，由解得C（2，1），目标函数的最小值为：4目标函数的范围是[4，+∞）．故选：D．【点评】本题考查线性规划的简单应用，画出可行域判断目标函数的最优解是解题的关键．5．（4分）若函数f（x）=x2+ax+b在区间[0，1]上的最大值是M，最小值是m，则M﹣m（）A．与a有关，且与b有关B．与a有关，但与b无关C．与a无关，且与b无关D．与a无关，但与b有关【考点】3V：二次函数的性质与图象．【专题】32：分类讨论；4C：分类法；51：函数的性质及应用．【分析】结合二次函数的图象和性质，分类讨论不同情况下M﹣m的取值与a，b 的关系，综合可得答案．【解答】解：函数f（x）=x2+ax+b的图象是开口朝上且以直线x=﹣为对称轴的抛物线，①当﹣＞1或﹣＜0，即a＜﹣2，或a＞0时，函数f（x）在区间[0，1]上单调，此时M﹣m=|f（1）﹣f（0）|=|a+1|，故M﹣m的值与a有关，与b无关②当≤﹣≤1，即﹣2≤a≤﹣1时，函数f（x）在区间[0，﹣]上递减，在[﹣，1]上递增，且f（0）＞f（1），此时M﹣m=f（0）﹣f（﹣）=，故M﹣m的值与a有关，与b无关③当0≤﹣＜，即﹣1＜a≤0时，函数f（x）在区间[0，﹣]上递减，在[﹣，1]上递增，且f（0）＜f（1），此时M﹣m=f（1）﹣f（﹣）=1+a+，故M﹣m的值与a有关，与b无关综上可得：M﹣m的值与a有关，与b无关故选：B．【点评】本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．6．（4分）已知等差数列{an }的公差为d，前n项和为Sn，则“d＞0”是“S4+S6＞2S5”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【考点】29：充分条件、必要条件、充要条件．【专题】11：计算题；35：转化思想；4R：转化法；54：等差数列与等比数列；5L：简易逻辑．【分析】根据等差数列的求和公式和S4+S6＞2S5，可以得到d＞0，根据充分必要条件的定义即可判断．【解答】解：∵S4+S6＞2S5，∴4a1+6d+6a1+15d＞2（5a1+10d），∴21d＞20d，∴d＞0，故“d＞0”是“S4+S6＞2S5”充分必要条件，故选：C．【点评】本题借助等差数列的求和公式考查了充分必要条件，属于基础题7．（4分）函数y=f（x）的导函数y=f′（x）的图象如图所示，则函数y=f（x）的图象可能是（）A．B．C．D．【考点】3A：函数的图象与图象的变换．【专题】31：数形结合；44：数形结合法；52：导数的概念及应用．【分析】根据导数与函数单调性的关系，当f′（x）＜0时，函数f（x）单调递减，当f′（x）＞0时，函数f（x）单调递增，根据函数图象，即可判断函数的单调性，然后根据函数极值的判断，即可判断函数极值的位置，即可求得函数y=f（x）的图象可能【解答】解：由当f′（x）＜0时，函数f（x）单调递减，当f′（x）＞0时，函数f（x）单调递增，则由导函数y=f′（x）的图象可知：f（x）先单调递减，再单调递增，然后单调递减，最后单调递增，排除A，C，且第二个拐点（即函数的极大值点）在x轴上的右侧，排除B，故选：D．【点评】本题考查导数的应用，考查导数与函数单调性的关系，考查函数极值的判断，考查数形结合思想，属于基础题．8．（4分）已知随机变量ξi 满足P（ξi=1）=pi，P（ξi=0）=1﹣pi，i=1，2．若0＜p1＜p2＜，则（）A．E（ξ1）＜E（ξ2），D（ξ1）＜D（ξ2）B．E（ξ1）＜E（ξ2），D（ξ1）＞D（ξ2）C．E（ξ1）＞E（ξ2），D（ξ1）＜D（ξ2）D．E（ξ1）＞E（ξ2），D（ξ1）＞D（ξ2）【考点】CH：离散型随机变量的期望与方差．【专题】11：计算题；34：方程思想；49：综合法；5I：概率与统计．【分析】由已知得0＜p1＜p2＜，＜1﹣p2＜1﹣p1＜1，求出E（ξ1）=p1，E（ξ2）=p2，从而求出D（ξ1），D（ξ2），由此能求出结果．【解答】解：∵随机变量ξi 满足P（ξi=1）=pi，P（ξi=0）=1﹣pi，i=1，2，…，0＜p1＜p2＜，∴＜1﹣p2＜1﹣p1＜1，E（ξ1）=1×p1+0×（1﹣p1）=p1，E（ξ2）=1×p2+0×（1﹣p2）=p2，D（ξ1）=（1﹣p1）2p1+（0﹣p1）2（1﹣p1）=，D（ξ2）=（1﹣p2）2p2+（0﹣p2）2（1﹣p2）=，D（ξ1）﹣D（ξ2）=p1﹣p12﹣（）=（p2﹣p1）（p1+p2﹣1）＜0，∴E（ξ1）＜E（ξ2），D（ξ1）＜D（ξ2）．故选：A．【点评】本题考查离散型随机变量的数学期望和方差等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，是中档题．9．（4分）如图，已知正四面体D﹣ABC（所有棱长均相等的三棱锥），P、Q、R 分别为AB、BC、CA上的点，AP=PB，==2，分别记二面角D﹣PR﹣Q，D ﹣PQ﹣R，D﹣QR﹣P的平面角为α、β、γ，则（）A．γ＜α＜βB．α＜γ＜βC．α＜β＜γD．β＜γ＜α【考点】MJ：二面角的平面角及求法．【专题】5F：空间位置关系与距离；5G：空间角；5H：空间向量及应用．【分析】解法一：如图所示，建立空间直角坐标系．设底面△ABC的中心为O．不妨设OP=3．则O（0，0，0），P（0，﹣3，0），C（0，6，0），D（0，0，6），Q，R，利用法向量的夹角公式即可得出二面角．解法二：如图所示，连接OP，OQ，OR，过点O分别作垂线：OE⊥PR，OF⊥PQ，OG⊥QR，垂足分别为E，F，G，连接DE，DF，DG．．可得tanα=．tanβ=，tanγ=．由已知可得：OE＞OG＞OF．即可得出．【解答】解法一：如图所示，建立空间直角坐标系．设底面△ABC的中心为O．不妨设OP=3．则O（0，0，0），P（0，﹣3，0），C（0，6，0），D（0，0，6），B（3，﹣3，0）．Q，R，=，=（0，3，6），=（，6，0），=，=．设平面PDR的法向量为=（x，y，z），则，可得，可得=，取平面ABC的法向量=（0，0，1）．则cos==，取α=arccos．同理可得：β=arccos．γ=arccos．∵＞＞．∴α＜γ＜β．解法二：如图所示，连接OP，OQ，OR，过点O分别作垂线：OE⊥PR，OF⊥PQ，OG⊥QR，垂足分别为E，F，G，连接DE，DF，DG．设OD=h．则tanα=．同理可得：tanβ=，tanγ=．由已知可得：OE＞OG＞OF．∴tanα＜tanγ＜tanβ，α，β，γ为锐角．∴α＜γ＜β．故选：B．【点评】本题考查了空间角、空间位置关系、正四面体的性质、法向量的夹角公式，考查了推理能力与计算能力，属于难题．10．（4分）如图，已知平面四边形ABCD，AB⊥BC，AB=BC=AD=2，CD=3，AC与BD交于点O，记I1=•，I2=•，I3=•，则（）A．I1＜I2＜I3B．I1＜I3＜I2C．I3＜I1＜I2D．I2＜I1＜I3【考点】9O：平面向量数量积的性质及其运算．【专题】31：数形结合；48：分析法；5A：平面向量及应用．【分析】根据向量数量积的定义结合图象边角关系进行判断即可．【解答】解：∵AB⊥BC，AB=BC=AD=2，CD=3，∴AC=2，∴∠AOB=∠COD＞90°，由图象知OA＜OC，OB＜OD，∴0＞•＞•，•＞0，即I3＜I1＜I2，故选：C．【点评】本题主要考查平面向量数量积的应用，根据图象结合平面向量数量积的定义是解决本题的关键．二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分11．（4分）我国古代数学家刘徽创立的“割圆术”可以估算圆周率π，理论上能把π的值计算到任意精度，祖冲之继承并发展了“割圆术”，将π的值精确到小数点后七位，其结果领先世界一千多年，“割圆术”的第一步是计算单位圆内接正六边形的面积S6，S6= ．【考点】CE：模拟方法估计概率．【专题】31：数形结合；4O：定义法；5B：直线与圆．【分析】根据题意画出图形，结合图形求出单位圆的内接正六边形的面积．【解答】解：如图所示，单位圆的半径为1，则其内接正六边形ABCDEF中，△AOB是边长为1的正三角形，所以正六边形ABCDEF的面积为S6=6××1×1×sin60°=．故答案为：．【点评】本题考查了已知圆的半径求其内接正六边形面积的应用问题，是基础题．12．（6分）已知a、b∈R，（a+bi）2=3+4i（i是虚数单位），则a2+b2= 5 ，ab=2 ．【考点】A5：复数的运算．【专题】34：方程思想；35：转化思想；5N：数系的扩充和复数．【分析】a、b∈R，（a+bi）2=3+4i（i是虚数单位），可得3+4i=a2﹣b2+2abi，可得3=a2﹣b2，2ab=4，解出即可得出．【解答】解：a、b∈R，（a+bi）2=3+4i（i是虚数单位），∴3+4i=a2﹣b2+2abi，∴3=a2﹣b2，2ab=4，解得ab=2，，．则a2+b2=5，故答案为：5，2．【点评】本题考查了复数的运算法则、复数的相等、方程的解法，考查了推理能力与计算能力，属于基础题．13．（6分）已知多项式（x+1）3（x+2）2=x5+a1x4+a2x3+a3x2+a4x+a5，则a4= 16 ，a5= 4 ．【考点】DA：二项式定理．【专题】11：计算题；35：转化思想；5P：二项式定理．【分析】利用二项式定理的展开式，求解x的系数就是两个多项式的展开式中x与常数乘积之和，a5就是常数的乘积．【解答】解：多项式（x+1）3（x+2）2=x5+a1x4+a2x3+a3x2+a4x+a5，（x+1）3中，x的系数是：3，常数是1；（x+2）2中x的系数是4，常数是4，a4=3×4+1×4=16；a5=1×4=4．故答案为：16；4．【点评】本题考查二项式定理的应用，考查计算能力，是基础题．14．（6分）已知△ABC，AB=AC=4，BC=2，点D为AB延长线上一点，BD=2，连结CD，则△BDC的面积是，cos∠BDC= ．【考点】HT：三角形中的几何计算．【专题】11：计算题；35：转化思想；44：数形结合法；58：解三角形．【分析】如图，取BC得中点E，根据勾股定理求出AE，再求出S△ABC ，再根据S△BDC =S△ABC即可求出，根据等腰三角形的性质和二倍角公式即可求出【解答】解：如图，取BC得中点E，∵AB=AC=4，BC=2，∴BE=BC=1，AE⊥BC，∴AE==，∴S△ABC=BC•AE=×2×=，∵BD=2，∴S△BDC =S△ABC=，∵BC=BD=2，∴∠BDC=∠BCD，∴∠ABE=2∠BDC在Rt△ABE中，∵cos∠ABE==，∴cos∠ABE=2cos2∠BDC﹣1=，∴cos∠BDC=，故答案为：，【点评】本题考查了解三角形的有关知识，关键是转化，属于基础题15．（6分）已知向量、满足||=1，||=2，则|+|+|﹣|的最小值是 4 ，最大值是．【考点】3H：函数的最值及其几何意义；91：向量的概念与向量的模．【专题】11：计算题；31：数形结合；44：数形结合法；51：函数的性质及应用．【分析】通过记∠AOB=α（0≤α≤π），利用余弦定理可可知|+|=、|﹣|=，进而换元，转化为线性规划问题，计算即得结论．【解答】解：记∠AOB=α，则0≤α≤π，如图，由余弦定理可得：|+|=，|﹣|=，令x=，y=，则x2+y2=10（x、y≥1），其图象为一段圆弧MN，如图，令z=x+y，则y=﹣x+z，=1+3=3+1=4，则直线y=﹣x+z过M、N时z最小为zmin当直线y=﹣x+z与圆弧MN相切时z最大，由平面几何知识易知zmax即为原点到切线的距离的倍，也就是圆弧MN所在圆的半径的倍，所以zmax=×=．综上所述，|+|+|﹣|的最小值是4，最大值是．故答案为：4、．【点评】本题考查函数的最值及其几何意义，考查数形结合能力，考查运算求解能力，涉及余弦定理、线性规划等基础知识，注意解题方法的积累，属于中档题．16．（4分）从6男2女共8名学生中选出队长1人，副队长1人，普通队员2人组成4人服务队，要求服务队中至少有1名女生，共有660 种不同的选法．（用数字作答）【考点】D9：排列、组合及简单计数问题．【专题】11：计算题；32：分类讨论；4O：定义法；5O：排列组合．【分析】由题意分两类选1女3男或选2女2男，再计算即可【解答】解：第一类，先选1女3男，有C63C21=40种，这4人选2人作为队长和副队有A42=12种，故有40×12=480种，第二类，先选2女2男，有C62C22=15种，这4人选2人作为队长和副队有A42=12种，故有15×12=180种，根据分类计数原理共有480+180=660种，故答案为：660【点评】本题考查了分类计数原理和分步计数原理，属于中档题17．（4分）已知a∈R，函数f（x）=|x+﹣a|+a在区间[1，4]上的最大值是5，则a的取值范围是（﹣∞，] ．【考点】3H：函数的最值及其几何意义．【专题】11：计算题；35：转化思想；49：综合法；51：函数的性质及应用．【分析】通过转化可知|x+﹣a|+a≤5且a≤5，进而解绝对值不等式可知2a﹣5≤x+≤5，进而计算可得结论．【解答】解：由题可知|x+﹣a|+a≤5，即|x+﹣a|≤5﹣a，所以a≤5，又因为|x+﹣a|≤5﹣a，所以a﹣5≤x+﹣a≤5﹣a，所以2a﹣5≤x+≤5，又因为1≤x≤4，4≤x+≤5，所以2a﹣5≤4，解得a≤，故答案为：（﹣∞，]．【点评】本题考查函数的最值，考查绝对值函数，考查转化与化归思想，注意解题方法的积累，属于中档题．三、解答题（共5小题，满分74分）18．（14分）已知函数f（x）=sin2x﹣cos2x﹣2sinx cosx（x∈R）．（Ⅰ）求f（）的值．（Ⅱ）求f（x）的最小正周期及单调递增区间．【考点】3G：复合函数的单调性；GF：三角函数的恒等变换及化简求值；H1：三角函数的周期性；H5：正弦函数的单调性．【专题】35：转化思想；4R：转化法；57：三角函数的图像与性质．【分析】利用二倍角公式及辅助角公式化简函数的解析式，（Ⅰ）代入可得：f（）的值．（Ⅱ）根据正弦型函数的图象和性质，可得f（x）的最小正周期及单调递增区间【解答】解：∵函数f（x）=sin2x﹣cos2x﹣2sinx cosx=﹣sin2x﹣cos2x=2sin （2x+）（Ⅰ）f（）=2sin（2×+）=2sin=2，（Ⅱ）∵ω=2，故T=π，即f（x）的最小正周期为π，由2x+∈[﹣+2kπ，+2kπ]，k∈Z得：x∈[﹣+kπ，﹣+kπ]，k∈Z，故f（x）的单调递增区间为[﹣+kπ，﹣+kπ]或写成[kπ+，kπ+]，k∈Z．【点评】本题考查的知识点是三角函数的化简求值，三角函数的周期性，三角函数的单调区间，难度中档．19．（15分）如图，已知四棱锥P﹣ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．【考点】LS：直线与平面平行；MI：直线与平面所成的角．【专题】14：证明题；31：数形结合；41：向量法；5F：空间位置关系与距离；5G：空间角．【分析】（Ⅰ）取AD的中点F，连结EF，CF，推导出EF∥PA，CF∥AB，从而平面EFC∥平面ABP，由此能证明EC∥平面PAB．（Ⅱ）连结BF，过F作FM⊥PB于M，连结PF，推导出四边形BCDF为矩形，从而BF⊥AD，进而AD⊥平面PBF，由AD∥BC，得BC⊥PB，再求出BC⊥MF，由此能求出sinθ．【解答】证明：（Ⅰ）取AD的中点F，连结EF，CF，∵E为PD的中点，∴EF∥PA，在四边形ABCD中，BC∥AD，AD=2DC=2CB，F为中点，∴CF∥AB，∴平面EFC∥平面ABP，∵EC⊂平面EFC，∴EC∥平面PAB．解：（Ⅱ）连结BF，过F作FM⊥PB于M，连结PF，∵PA=PD，∴PF⊥AD，推导出四边形BCDF为矩形，∴BF⊥AD，∴AD⊥平面PBF，又AD∥BC，∴BC⊥平面PBF，∴BC⊥PB，设DC=CB=1，由PC=AD=2DC=2CB，得AD=PC=2，∴PB===，BF=PF=1，∴MF=，又BC⊥平面PBF，∴BC⊥MF，∴MF⊥平面PBC，即点F到平面PBC的距离为，∵MF=，D到平面PBC的距离应该和MF平行且相等，为，E为PD中点，E到平面PBC的垂足也为垂足所在线段的中点，即中位线，∴E到平面PBC的距离为，在，由余弦定理得CE=，设直线CE与平面PBC所成角为θ，则sinθ==．【点评】本题考查线面平行的证明，考查线面角的正弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，是中档题．20．（15分）已知函数f（x）=（x﹣）e﹣x（x≥）．（1）求f（x）的导函数；（2）求f（x）在区间[，+∞）上的取值范围．【考点】6B：利用导数研究函数的单调性；6E：利用导数研究函数的最值．【专题】35：转化思想；48：分析法；53：导数的综合应用．【分析】（1）求出f（x）的导数，注意运用复合函数的求导法则，即可得到所求；（2）求出f（x）的导数，求得极值点，讨论当＜x＜1时，当1＜x＜时，当x＞时，f（x）的单调性，判断f（x）≥0，计算f（），f（1），f（），即可得到所求取值范围．【解答】解：（1）函数f（x）=（x﹣）e﹣x（x≥），导数f′（x）=（1﹣••2）e﹣x﹣（x﹣）e﹣x=（1﹣x+）e﹣x=（1﹣x）（1﹣）e﹣x；（2）由f（x）的导数f′（x）=（1﹣x）（1﹣）e﹣x，可得f′（x）=0时，x=1或，当＜x＜1时，f′（x）＜0，f（x）递减；当1＜x＜时，f′（x）＞0，f（x）递增；当x＞时，f′（x）＜0，f（x）递减，且x≥⇔x2≥2x﹣1⇔（x﹣1）2≥0，则f（x）≥0．由f（）=e，f（1）=0，f（）=e，即有f（x）的最大值为e，最小值为f（1）=0．则f（x）在区间[，+∞）上的取值范围是[0，e]．【点评】本题考查导数的运用：求单调区间和极值、最值，考查化简整理的运算能力，正确求导是解题的关键，属于中档题．21．（15分）如图，已知抛物线x2=y，点A（﹣，），B（，），抛物线上的点P（x，y）（﹣＜x＜），过点B作直线AP的垂线，垂足为Q．（Ⅰ）求直线AP斜率的取值范围；（Ⅱ）求|PA|•|PQ|的最大值．【考点】KI：圆锥曲线的综合；KN：直线与抛物线的综合．【专题】11：计算题；33：函数思想；49：综合法；5E：圆锥曲线中的最值与范围问题．【分析】（Ⅰ）通过点P在抛物线上可设P（x，x2），利用斜率公式结合﹣＜x ＜可得结论；（Ⅱ）通过（I）知P（x，x2）、﹣＜x＜，设直线AP的斜率为k，联立直线AP、BQ方程可知Q点坐标，进而可用k表示出、，计算可知|PA|•|PQ|=（1+k）3（1﹣k），通过令f（x）=（1+x）3（1﹣x），﹣1＜x＜1，求导结合单调性可得结论．【解答】解：（Ⅰ）由题可知P（x，x2），﹣＜x＜，所以k==x﹣∈（﹣1，1），AP故直线AP斜率的取值范围是：（﹣1，1）；（Ⅱ）由（I）知P（x，x2），﹣＜x＜，所以=（﹣﹣x，﹣x2），设直线AP的斜率为k，则k==x﹣，即x=k+，则AP：y=kx+k+，BQ：y=﹣x++，联立直线AP、BQ方程可知Q（，），故=（，），又因为=（﹣1﹣k，﹣k2﹣k），故﹣|PA|•|PQ|=•=+=（1+k）3（k﹣1），所以|PA|•|PQ|=（1+k）3（1﹣k），令f（x）=（1+x）3（1﹣x），﹣1＜x＜1，则f′（x）=（1+x）2（2﹣4x）=﹣2（1+x）2（2x﹣1），由于当﹣1＜x＜时f′（x）＞0，当＜x＜1时f′（x）＜0，故f（x）max=f（）=，即|PA|•|PQ|的最大值为．【点评】本题考查圆锥曲线的最值问题，考查运算求解能力，考查函数思想，注意解题方法的积累，属于中档题．22．（15分）已知数列{xn }满足：x1=1，xn=xn+1+ln（1+xn+1）（n∈N*），证明：当n∈N*时，（Ⅰ）0＜xn+1＜xn；（Ⅱ）2xn+1﹣xn≤；（Ⅲ）≤xn≤．【考点】8H：数列递推式；8K：数列与不等式的综合．【专题】15：综合题；33：函数思想；35：转化思想；49：综合法；4M：构造法；53：导数的综合应用；54：等差数列与等比数列；55：点列、递归数列与数学归纳法；5T：不等式．【分析】（Ⅰ）用数学归纳法即可证明，（Ⅱ）构造函数，利用导数判断函数的单调性，把数列问题转化为函数问题，即可证明，（Ⅲ）由≥2xn+1﹣xn得﹣≥2（﹣）＞0，继续放缩即可证明【解答】解：（Ⅰ）用数学归纳法证明：x n ＞0， 当n=1时，x 1=1＞0，成立， 假设当n=k 时成立，则x k ＞0，那么n=k+1时，若x k+1＜0，则0＜x k =x k+1+ln （1+x k+1）＜0，矛盾， 故x n+1＞0，因此x n ＞0，（n ∈N*） ∴x n =x n+1+ln （1+x n+1）＞x n+1， 因此0＜x n+1＜x n （n ∈N *），（Ⅱ）由x n =x n+1+ln （1+x n+1）得x n x n+1﹣4x n+1+2x n =x n+12﹣2x n+1+（x n+1+2）ln （1+x n+1）， 记函数f （x ）=x 2﹣2x+（x+2）ln （1+x ），x ≥0 ∴f′（x ）=+ln （1+x ）＞0，∴f （x ）在（0，+∞）上单调递增， ∴f （x ）≥f （0）=0，因此x n+12﹣2x n+1+（x n+1+2）ln （1+x n+1）≥0， 故2x n+1﹣x n ≤；（Ⅲ）∵x n =x n+1+ln （1+x n+1）≤x n+1+x n+1=2x n+1， ∴x n ≥，由≥2x n+1﹣x n 得﹣≥2（﹣）＞0， ∴﹣≥2（﹣）≥…≥2n ﹣1（﹣）=2n ﹣2，∴x n ≤， 综上所述≤x n ≤．【点评】本题考查了数列的概念，递推关系，数列的函数的特征，导数和函数的单调性的关系，不等式的证明，考查了推理论证能力，分析解决问题的能力，运算能力，放缩能力，运算能力，属于难题。

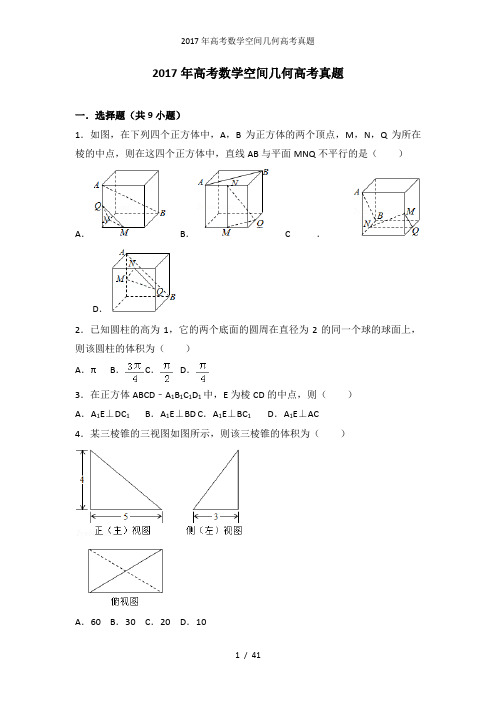
2017年高考数学空间几何高考真题一．选择题（共9小题）1．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（）A．B．C．D．2．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB． C．D．3．在正方体ABCD﹣A1B1C1D1中，E为棱CD的中点，则（）A．A1E⊥DC1B．A1E⊥BD C．A1E⊥BC1D．A1E⊥AC4．某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．60 B．30 C．20 D．105．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm2）是（）A．+1 B．+3 C．+1 D．+36．如图，已知正四面体D﹣ABC（所有棱长均相等的三棱锥），P、Q、R分别为AB、BC、CA上的点，AP=PB，==2，分别记二面角D﹣PR﹣Q，D﹣PQ﹣R，D﹣QR﹣P的平面角为α、β、γ，则（）A．γ＜α＜β B．α＜γ＜β C．α＜β＜γ D．β＜γ＜α7．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）A．90πB．63πC．42πD．36π1．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（）A．10 B．12 C．14 D．162．已知直三棱柱ABC﹣A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，则异面直线AB1与BC1所成角的余弦值为（）A．B．C．D．二．填空题（共5小题）8．已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S﹣ABC的体积为9，则球O的表面积为．9．长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为．10．已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为．11．由一个长方体和两个圆柱体构成的几何体的三视图如图，则该几何体的体积为．12．如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则的值是．三．解答题（共9小题）13．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，且四棱锥P﹣ABCD的体积为，求该四棱锥的侧面积．14．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．15．如图四面体ABCD中，△ABC是正三角形，AD=CD．（1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB=BD，若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．16．如图，直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．（1）求三棱柱ABC﹣A1B1C1的体积；（2）设M是BC中点，求直线A1M与平面ABC所成角的大小．17．如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D 为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．18．如图，在四棱锥P﹣ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD=1，BC=3，CD=4，PD=2．（Ⅰ）求异面直线AP与BC所成角的余弦值；（Ⅱ）求证：PD⊥平面PBC；（Ⅲ）求直线AB与平面PBC所成角的正弦值．19．如图，已知四棱锥P﹣ABCD，△PAD是以AD为斜边的等腰直角三角形，BC ∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．20．由四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后得到的几何体如图所示，四边形ABCD为正方形，O为AC与BD 的交点，E为AD的中点，A1E⊥平面ABCD，（Ⅰ）证明：A1O∥平面B1CD1；（Ⅱ）设M是OD的中点，证明：平面A1EM⊥平面B1CD1．21．如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．3．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C的余弦值．4．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°，E是PD的中点．（1）证明：直线CE∥平面PAB；（2）点M在棱PC 上，且直线BM与底面ABCD所成角为45°，求二面角M﹣AB﹣D的余弦值．5．如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（1）证明：平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D﹣AE﹣C的余弦值．6．如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，PA=PD=，AB=4．（1）求证：M为PB的中点；（2）求二面角B﹣PD﹣A的大小；（3）求直线MC与平面BDP所成角的正弦值．7．如图，在三棱锥P﹣ABC中，PA⊥底面ABC，∠BAC=90°．点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2．（Ⅰ）求证：MN∥平面BDE；（Ⅱ）求二面角C﹣EM﹣N的正弦值；（Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为，求线段AH的长．8．如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是的中点．（Ⅰ）设P是上的一点，且AP⊥BE，求∠CBP的大小；（Ⅱ）当AB=3，AD=2时，求二面角E﹣AG﹣C的大小．2017年高考数学空间几何高考真题参考答案与试题解析一．选择题（共7小题）1．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（）A．B．C．D．【解答】解：对于选项B，由于AB∥MQ，结合线面平行判定定理可知B不满足题意；对于选项C，由于AB∥MQ，结合线面平行判定定理可知C不满足题意；对于选项D，由于AB∥NQ，结合线面平行判定定理可知D不满足题意；所以选项A满足题意，故选：A．2．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB． C．D．【解答】解：∵圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，∴该圆柱底面圆周半径r==，∴该圆柱的体积：V=Sh==．故选：B．3．在正方体ABCD﹣A1B1C1D1中，E为棱CD的中点，则（）A．A1E⊥DC1B．A1E⊥BD C．A1E⊥BC1D．A1E⊥AC【解答】解：法一：连B1C，由题意得BC1⊥B1C，∵A1B1⊥平面B1BCC1，且BC1⊂平面B1BCC1，∴A1B1⊥BC1，∵A1B1∩B1C=B1，∴BC1⊥平面A1ECB1，∵A1E⊂平面A1ECB1，∴A1E⊥BC1．故选：C．法二：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，设正方体ABCD﹣A1B1C1D1中棱长为2，则A1（2，0，2），E（0，1，0），B（2，2，0），D（0，0，0），C1（0，2，2），A（2，0，0），C（0，2，0），=（﹣2，1，﹣2），=（0，2，2），=（﹣2，﹣2，0），=（﹣2，0，2），=（﹣2，2，0），∵•=﹣2，=2，=0，=6，∴A1E⊥BC1．故选：C．4．某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．60 B．30 C．20 D．10【解答】解：由三视图可知：该几何体为三棱锥，该三棱锥的体积==10．故选：D．5．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm2）是（）A．+1 B．+3 C．+1 D．+3【解答】解：由几何的三视图可知，该几何体是圆锥的一半和一个三棱锥组成，圆锥的底面圆的半径为1，三棱锥的底面是底边长2的等腰直角三角形，圆锥的高和棱锥的高相等均为3，故该几何体的体积为××π×12×3+××××3=+1，故选：A6．如图，已知正四面体D﹣ABC（所有棱长均相等的三棱锥），P、Q、R分别为AB、BC、CA上的点，AP=PB，==2，分别记二面角D﹣PR﹣Q，D﹣PQ﹣R，D﹣QR﹣P的平面角为α、β、γ，则（）A．γ＜α＜β B．α＜γ＜β C．α＜β＜γ D．β＜γ＜α【解答】解法一：如图所示，建立空间直角坐标系．设底面△ABC的中心为O．不妨设OP=3．则O（0，0，0），P（0，﹣3，0），C（0，﹣6，0），D（0，0，6），Q，R，=，=（0，3，6），=（，5，0），=，=．设平面PDR的法向量为=（x，y，z），则，可得，可得=，取平面ABC的法向量=（0，0，1）．则cos==，取α=arccos．同理可得：β=arccos．γ=arccos．∵＞＞．∴α＜γ＜β．解法二：如图所示，连接OP，OQ，OR，过点O分别作垂线：OE⊥PR，OF⊥PQ，OG⊥QR，垂足分别为E，F，G，连接DE，DF，DG．设OD=h．则tanα=．同理可得：tanβ=，tanγ=．由已知可得：OE＞OG＞OF．∴tanα＜tanγ＜tanβ，α，β，γ为锐角．∴α＜γ＜β．故选：B．7．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）A．90πB．63πC．42πD．36π【解答】解：由三视图可得，直观图为一个完整的圆柱减去一个高为6的圆柱的一半，V=π•32×10﹣•π•32×6=63π，故选：B．1．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（）A．10 B．12 C．14 D．16【解答】解：由三视图可画出直观图，该立体图中只有两个相同的梯形的面，S梯形=×2×（2+4）=6，∴这些梯形的面积之和为6×2=12，故选：B2．已知直三棱柱ABC﹣A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，则异面直线AB1与BC1所成角的余弦值为（）A．B．C．D．【解答】解：【解法一】如图所示，设M、N、P分别为AB，BB1和B1C1的中点，则AB1、BC1夹角为MN和NP夹角或其补角（因异面直线所成角为（0，]），可知MN=AB1=，NP=BC1=；作BC中点Q，则△PQM为直角三角形；∵PQ=1，MQ=AC，△ABC中，由余弦定理得AC2=AB2+BC2﹣2AB•BC•cos∠ABC=4+1﹣2×2×1×（﹣）=7，∴AC=，∴MQ=；在△MQP中，MP==；在△PMN中，由余弦定理得cos∠MNP===﹣；又异面直线所成角的范围是（0，]，∴AB1与BC1所成角的余弦值为．【解法二】如图所示，补成四棱柱ABCD﹣A1B1C1D1，求∠BC1D即可；BC1=，BD==，C1D=，∴+BD2=，∴∠DBC1=90°，∴cos∠BC1D==．二．填空题（共5小题）8．已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S﹣ABC的体积为9，则球O的表面积为36π．【解答】解：三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径，若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S﹣ABC的体积为9，可知三角形SBC与三角形SAC都是等腰直角三角形，设球的半径为r，可得，解得r=3．球O的表面积为：4πr2=36π．故答案为：36π．9．长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为14π．【解答】解：长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，可知长方体的对角线的长就是球的直径，所以球的半径为：=．则球O的表面积为：4×=14π．故答案为：14π．10．已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为．【解答】解：设正方体的棱长为a，∵这个正方体的表面积为18，∴6a2=18，则a2=3，即a=，∵一个正方体的所有顶点在一个球面上，∴正方体的体对角线等于球的直径，即a=2R，即R=，则球的体积V=π•（）3=；故答案为：．11．由一个长方体和两个圆柱体构成的几何体的三视图如图，则该几何体的体积为2+．【解答】解：由长方体长为2，宽为1，高为1，则长方体的体积V1=2×1×1=2，圆柱的底面半径为1，高为1，则圆柱的体积V2=×π×12×1=，则该几何体的体积V=V1+2V1=2+，故答案为：2+．12．如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则的值是．【解答】解：设球的半径为R，则球的体积为：R3，圆柱的体积为：πR2•2R=2πR3．则==．故答案为：．三．解答题（共9小题）13．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，且四棱锥P﹣ABCD的体积为，求该四棱锥的侧面积．【解答】证明：（1）∵在四棱锥P﹣ABCD中，∠BAP=∠CDP=90°，∴AB⊥PA，CD⊥PD，又AB∥CD，∴AB⊥PD，∵PA∩PD=P，∴AB⊥平面PAD，∵AB⊂平面PAB，∴平面PAB⊥平面PAD．解：（2）设PA=PD=AB=DC=a，取AD中点O，连结PO，∵PA=PD=AB=DC，∠APD=90°，平面PAB⊥平面PAD，∴PO⊥底面ABCD，且AD==，PO=，∵四棱锥P﹣ABCD的体积为，∴V P=﹣ABCD====，解得a=2，∴PA=PD=AB=DC=2，AD=BC=2，PO=，∴PB=PC==2，∴该四棱锥的侧面积：S侧=S△PAD+S△PAB+S△PDC+S△PBC=+++==6+2．14．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．【解答】（1）证明：四棱锥P﹣ABCD中，∵∠BAD=∠ABC=90°．∴BC∥AD，∵AD⊂平面PAD，BC⊄平面PAD，∴直线BC∥平面PAD；（2）解：四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．设AD=2x，则AB=BC=x，CD=，O是AD的中点，连接PO，OC，CD的中点为：E，连接OE，则OE=，PO=，PE==，△PCD面积为2，可得：=2，即：，解得x=2，PE=2．=×（BC+AD）×AB×PO==4．则V P﹣ABCD15．如图四面体ABCD中，△ABC是正三角形，AD=CD．（1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB=BD，若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．【解答】证明：（1）取AC中点O，连结DO、BO，∵△ABC是正三角形，AD=CD，∴DO⊥AC，BO⊥AC，∵DO∩BO=O，∴AC⊥平面BDO，∵BD⊂平面BDO，∴AC⊥BD．解：（2）法一：连结OE，由（1）知AC⊥平面OBD，∵OE⊂平面OBD，∴OE⊥AC，设AD=CD=，则OC=OA=1，∴E是线段AC垂直平分线上的点，∴EC=EA=CD=，由余弦定理得：cos∠CBD==，即，解得BE=1或BE=2，∵BE＜＜BD=2，∴BE=1，∴BE=ED，∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h，∵BE=ED ，∴S △DCE =S △BCE ，∴四面体ABCE 与四面体ACDE 的体积比为1． 法二：设AD=CD=，则AC=AB=BC=BD=2，AO=CO=DO=1，∴BO==，∴BO 2+DO 2=BD 2，∴BO ⊥DO ，以O 为原点，OA 为x 轴，OB 为y 轴，OD 为z 轴，建立空间直角坐标系， 则C （﹣1，0，0），D （0，0，1），B （0，，0），A （1，0，0），设E （a ，b ，c ），，（0≤λ≤1），则（a ，b ，c ﹣1）=λ（0，，﹣1），解得E （0，，1﹣λ），∴=（1，），=（﹣1，），∵AE ⊥EC ，∴=﹣1+3λ2+（1﹣λ）2=0，由λ∈[0，1]，解得，∴DE=BE ，∵四面体ABCE 与四面体ACDE 的高都是点A 到平面BCD 的高h ， ∵DE=BE ，∴S △DCE =S △BCE ，∴四面体ABCE 与四面体ACDE 的体积比为1．16．如图，直三棱柱ABC ﹣A 1B 1C 1的底面为直角三角形，两直角边AB 和AC 的长分别为4和2，侧棱AA 1的长为5． （1）求三棱柱ABC ﹣A 1B 1C 1的体积；（2）设M 是BC 中点，求直线A 1M 与平面ABC 所成角的大小．【解答】解：（1）∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．∴三棱柱ABC﹣A1B1C1的体积：V=S△ABC×AA1===20．（2）连结AM，∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5，M是BC中点，∴AA1⊥底面ABC，AM==，∴∠A1MA是直线A1M与平面ABC所成角，tan∠A1MA===，∴直线A1M与平面ABC所成角的大小为arctan．17．如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D 为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．【解答】解：（1）证明：由PA⊥AB，PA⊥BC，AB⊂平面ABC，BC⊂平面ABC，且AB∩BC=B，可得PA⊥平面ABC，由BD⊂平面ABC，可得PA⊥BD；（2）证明：由AB=BC，D为线段AC的中点，可得BD⊥AC，由PA⊥平面ABC，PA⊂平面PAC，可得平面PAC⊥平面ABC，又平面ABC∩平面ABC=AC，BD⊂平面ABC，且BD⊥AC，即有BD⊥平面PAC，BD⊂平面BDE，可得平面BDE⊥平面PAC；（3）PA∥平面BDE，PA⊂平面PAC，且平面PAC∩平面BDE=DE，可得PA∥DE，又D为AC的中点，可得E为PC的中点，且DE=PA=1，由PA⊥平面ABC，可得DE⊥平面ABC，可得S△BDC =S△ABC=××2×2=1，则三棱锥E﹣BCD的体积为DE•S=×1×1=．△BDC18．如图，在四棱锥P﹣ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD=1，BC=3，CD=4，PD=2．（Ⅰ）求异面直线AP与BC所成角的余弦值；（Ⅱ）求证：PD⊥平面PBC；（Ⅲ）求直线AB与平面PBC所成角的正弦值．【解答】解：（Ⅰ）如图，由已知AD∥BC，故∠DAP或其补角即为异面直线AP与BC所成的角．因为AD⊥平面PDC，所以AD⊥PD．在Rt△PDA中，由已知，得，故．所以，异面直线AP与BC所成角的余弦值为．证明：（Ⅱ）因为AD⊥平面PDC，直线PD⊂平面PDC，所以AD⊥PD．又因为BC∥AD，所以PD⊥BC，又PD⊥PB，所以PD⊥平面PBC．解：（Ⅲ）过点D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角．因为PD⊥平面PBC，故PF为DF在平面PBC上的射影，所以∠DFP为直线DF和平面PBC所成的角．由于AD∥BC，DF∥AB，故BF=AD=1，由已知，得CF=BC﹣BF=2．又AD⊥DC，故BC⊥DC，在Rt△DCF中，可得．所以，直线AB与平面PBC所成角的正弦值为．19．如图，已知四棱锥P﹣ABCD，△PAD是以AD为斜边的等腰直角三角形，BC ∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．【解答】证明：（Ⅰ）取AD的中点F，连结EF，CF，∵E为PD的中点，∴EF∥PA，在四边形ABCD中，BC∥AD，AD=2DC=2CB，F为中点，∴CF∥AB，∴平面EFC∥平面ABP，∵EC⊂平面EFC，∴EC∥平面PAB．解：（Ⅱ）连结BF，过F作FM⊥PB于M，连结PF，∵PA=PD，∴PF⊥AD，推导出四边形BCDF为矩形，∴BF⊥AD，∴AD⊥平面PBF，又AD∥BC，∴BC⊥平面PBF，∴BC⊥PB，设DC=CB=1，则AD=PC=2，∴PB=，BF=PF=1，∴MF=，又BC⊥平面PBF，∴BC⊥MF，∴MF⊥平面PBC，即点F到平面PBC的距离为，∵MF=，D到平面PBC的距离应该和MF平行且相等，为，E为PD中点，E到平面PBC的垂足也为垂足所在线段的中点，即中位线，∴E到平面PBC的距离为，在，由余弦定理得CE=，设直线CE与平面PBC所成角为θ，则sinθ==．20．由四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后得到的几何体如图所示，四边形ABCD为正方形，O为AC与BD 的交点，E为AD的中点，A1E⊥平面ABCD，（Ⅰ）证明：A1O∥平面B1CD1；（Ⅱ）设M是OD的中点，证明：平面A1EM⊥平面B1CD1．【解答】证明：（Ⅰ）取B1D1中点G，连结A1G、CG，∵四边形ABCD为正方形，O为AC与BD 的交点，∴四棱柱ABCD﹣A 1B1C1D1截去三棱锥C1﹣B1CD1后，A1G OC，∴四边形OCGA1是平行四边形，∴A1O∥CG，∵A1O⊄平面B1CD1，CG⊂平面B1CD1，∴A1O∥平面B1CD1．（Ⅱ）四棱柱ABCD﹣A 1B1C1D1截去三棱锥C1﹣B1CD1后，BD B1D1，∵M是OD的中点，O为AC与BD 的交点，E为AD的中点，A1E⊥平面ABCD，又BD⊂平面ABCD，∴BD⊥A1E，∵四边形ABCD为正方形，O为AC与BD 的交点，∴AO⊥BD，∵M是OD的中点，E为AD的中点，∴EM⊥BD，∵A1E∩EM=E，∴BD⊥平面A1EM，∵BD∥B1D1，∴B1D1⊥平面A1EM，∵B1D1⊂平面B1CD1，∴平面A1EM⊥平面B1CD1．21．如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．【解答】证明：（1）因为AB⊥AD，EF⊥AD，且A、B、E、F四点共面，所以AB∥EF，又因为EF⊊平面ABC，AB⊆平面ABC，所以由线面平行判定定理可知：EF∥平面ABC；（2）在线段CD上取点G，连结FG、EG使得FG∥BC，则EG∥AC，因为BC⊥BD，FG∥BC，所以FG⊥BD，又因为平面ABD⊥平面BCD，所以FG⊥平面ABD，所以FG⊥AD，又因为AD⊥EF，且EF∩FG=F，所以AD⊥平面EFG，所以AD⊥EG，故AD⊥AC．3．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C的余弦值．【解答】（1）证明：∵∠BAP=∠CDP=90°，∴PA⊥AB，PD⊥CD，∵AB∥CD，∴AB⊥PD，又∵PA∩PD=P，且PA⊂平面PAD，PD⊂平面PAD，∴AB⊥平面PAD，又AB⊂平面PAB，∴平面PAB⊥平面PAD；（2）解：∵AB∥CD，AB=CD，∴四边形ABCD为平行四边形，由（1）知AB⊥平面PAD，∴AB⊥AD，则四边形ABCD为矩形，在△APD中，由PA=PD，∠APD=90°，可得△PAD为等腰直角三角形，设PA=AB=2a，则AD=．取AD中点O，BC中点E，连接PO、OE，以O为坐标原点，分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系，则：D（），B（），P（0，0，），C（）．，，．设平面PBC的一个法向量为，由，得，取y=1，得．∵AB⊥平面PAD，AD⊂平面PAD，∴AB⊥PD，又PD⊥PA，PA∩AB=A，∴PD⊥平面PAB，则为平面PAB的一个法向量，．∴cos＜＞==．由图可知，二面角A﹣PB﹣C为钝角，∴二面角A﹣PB﹣C的余弦值为．4．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°，E是PD的中点．（1）证明：直线CE∥平面PAB；（2）点M在棱PC 上，且直线BM与底面ABCD所成角为45°，求二面角M﹣AB﹣D的余弦值．【解答】（1）证明：取PA的中点F，连接EF，BF，因为E是PD的中点，所以EF AD，AB=BC=AD，∠BAD=∠ABC=90°，∴BC∥AD，∴BCEF是平行四边形，可得CE∥BF，BF⊂平面PAB，CE⊄平面PAB，∴直线CE∥平面PAB；（2）解：四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°，E是PD的中点．取AD的中点O，M在底面ABCD上的射影N在OC上，设AD=2，则AB=BC=1，OP=，∴∠PCO=60°，直线BM与底面ABCD所成角为45°，可得：BN=MN，CN=MN，BC=1，可得：1+BN2=BN2，BN=，MN=，作NQ⊥AB于Q，连接MQ，所以∠MQN就是二面角M﹣AB﹣D的平面角，MQ==，二面角M﹣AB﹣D的余弦值为：=．5．如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（1）证明：平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D﹣AE﹣C的余弦值．【解答】（1）证明：如图所示，取AC的中点O，连接BO，OD．∵△ABC是等边三角形，∴OB⊥AC．△ABD与△CBD中，AB=BD=BC，∠ABD=∠CBD，∴△ABD≌△CBD，∴AD=CD．∵△ACD是直角三角形，∴AC是斜边，∴∠ADC=90°．∴DO=AC．∴DO2+BO2=AB2=BD2．∴∠BOD=90°．∴OB⊥OD．又DO∩AC=O，∴OB⊥平面ACD．又OB⊂平面ABC，∴平面ACD⊥平面ABC．（2）解：设点D，B到平面ACE的距离分别为h D，h E．则=．∵平面AEC把四面体ABCD分成体积相等的两部分，∴===1．∴点E是BD的中点．建立如图所示的空间直角坐标系．不妨取AB=2．则O（0，0，0），A（1，0，0），C（﹣1，0，0），D（0，0，1），B（0，，0），E．=（﹣1，0，1），=，=（﹣2，0，0）．设平面ADE的法向量为=（x，y，z），则，即，取=．同理可得：平面ACE的法向量为=（0，1，）．∴cos===﹣．∴二面角D﹣AE﹣C的余弦值为．6．如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，PA=PD=，AB=4．（1）求证：M为PB的中点；（2）求二面角B﹣PD﹣A的大小；（3）求直线MC与平面BDP所成角的正弦值．【解答】（1）证明：如图，设AC∩BD=O，∵ABCD为正方形，∴O为BD的中点，连接OM，∵PD∥平面MAC，PD⊂平面PBD，平面PBD∩平面AMC=OM，∴PD∥OM，则，即M为PB的中点；（2）解：取AD中点G，∵PA=PD，∴PG⊥AD，∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，∴PG⊥平面ABCD，则PG⊥AD，连接OG，则PG⊥OG，由G是AD的中点，O是AC的中点，可得OG∥DC，则OG⊥AD．以G为坐标原点，分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系，由PA=PD=，AB=4，得D（2，0，0），A（﹣2，0，0），P（0，0，），C（2，4，0），B（﹣2，4，0），M（﹣1，2，），，．设平面PBD的一个法向量为，则由，得，取z=，得．取平面PAD的一个法向量为．∴cos＜＞==．∴二面角B﹣PD﹣A的大小为60°；（3）解：，平面BDP的一个法向量为．∴直线MC与平面BDP所成角的正弦值为|cos＜＞|=||=||=．7．如图，在三棱锥P﹣ABC中，PA⊥底面ABC，∠BAC=90°．点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2．（Ⅰ）求证：MN∥平面BDE；（Ⅱ）求二面角C﹣EM﹣N的正弦值；（Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为，求线段AH的长．【解答】（Ⅰ）证明：取AB中点F，连接MF、NF，∵M为AD中点，∴MF∥BD，∵BD⊂平面BDE，MF⊄平面BDE，∴MF∥平面BDE．∵N为BC中点，∴NF∥AC，又D、E分别为AP、PC的中点，∴DE∥AC，则NF∥DE．∵DE⊂平面BDE，NF⊄平面BDE，∴NF∥平面BDE．又MF∩NF=F．∴平面MFN∥平面BDE，则MN∥平面BDE；（Ⅱ）解：∵PA⊥底面ABC，∠BAC=90°．∴以A为原点，分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系．∵PA=AC=4，AB=2，∴A（0，0，0），B（2，0，0），C（0，4，0），M（0，0，1），N（1，2，0），E （0，2，2），则，，设平面MEN的一个法向量为，由，得，取z=2，得．由图可得平面CME的一个法向量为．∴cos＜＞=．∴二面角C﹣EM﹣N的余弦值为，则正弦值为；（Ⅲ）解：设AH=t，则H（0，0，t），，．∵直线NH与直线BE所成角的余弦值为，∴|cos＜＞|=||=||=．解得：t=或t=．∴当H与P重合时直线NH与直线BE所成角的余弦值为，此时线段AH的长为或．8．如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是的中点．（Ⅰ）设P是上的一点，且AP⊥BE，求∠CBP的大小；（Ⅱ）当AB=3，AD=2时，求二面角E﹣AG﹣C的大小．【解答】解：（Ⅰ）∵AP⊥BE，AB⊥BE，且AB，AP⊂平面ABP，AB∩AP=A，∴BE⊥平面ABP，又BP⊂平面ABP，∴BE⊥BP，又∠EBC=120°，因此∠CBP=30°；（Ⅱ）解法一、取的中点H，连接EH，GH，CH，∵∠EBC=120°，∴四边形BECH为菱形，∴AE=GE=AC=GC=．取AG中点M，连接EM，CM，EC，则EM⊥AG，CM⊥AG，∴∠EMC为所求二面角的平面角．又AM=1，∴EM=CM=．在△BEC中，由于∠EBC=120°，由余弦定理得：EC2=22+22﹣2×2×2×cos120°=12，∴，因此△EMC为等边三角形，故所求的角为60°．解法二、以B为坐标原点，分别以BE，BP，BA所在直线为x，y，z轴建立空间直角坐标系．由题意得：A（0，0，3），E（2，0，0），G（1，，3），C（﹣1，，0），故，，．设为平面AEG的一个法向量，由，得，取z1=2，得；设为平面ACG的一个法向量，由，可得，取z2=﹣2，得．∴cos＜＞=．∴二面角E﹣AG﹣C的大小为60°．2017年高考数学空间几何高考真题 41 /41。

2017年高考数学空间几何高考真题一．选择题（共9小题）1．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（）A．B．C．D．2．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB．C．D．3．在正方体ABCD﹣A1B1C1D1中，E为棱CD的中点，则（）A．A1E⊥DC1B．A1E⊥BD C．A1E⊥BC1D．A1E⊥AC4．某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．60 B．30 C．20 D．105．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm2）是（）A．+1 B．+3 C．+1 D．+36．如图，已知正四面体D﹣ABC（所有棱长均相等的三棱锥），P、Q、R分别为AB、BC、CA上的点，AP=PB，==2，分别记二面角D﹣PR﹣Q，D﹣PQ﹣R，D ﹣QR﹣P的平面角为α、β、γ，则（）A．γ＜α＜β B．α＜γ＜β C．α＜β＜γ D．β＜γ＜α7．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）A．90πB．63πC．42πD．36π1．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（）A．10 B．12 C．14 D．162．已知直三棱柱ABC﹣A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，则异面直线AB1与BC1所成角的余弦值为（）A． B．C．D．二．填空题（共5小题）8．已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S﹣ABC的体积为9，则球O的表面积为．9．长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为．10．已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为．11．由一个长方体和两个圆柱体构成的几何体的三视图如图，则该几何体的体积为．12．如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则的值是．三．解答题（共9小题）13．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，且四棱锥P﹣ABCD的体积为，求该四棱锥的侧面积．14．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．15．如图四面体ABCD中，△ABC是正三角形，AD=CD．（1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB=BD，若E为棱BD上与D不重合的点，且AE ⊥EC，求四面体ABCE与四面体ACDE的体积比．16．如图，直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．（1）求三棱柱ABC﹣A1B1C1的体积；（2）设M是BC中点，求直线A1M与平面ABC所成角的大小．17．如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．18．如图，在四棱锥P﹣ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD=1，BC=3，CD=4，PD=2．（Ⅰ）求异面直线AP与BC所成角的余弦值；（Ⅱ）求证：PD⊥平面PBC；（Ⅲ）求直线AB与平面PBC所成角的正弦值．19．如图，已知四棱锥P﹣ABCD，△PAD是以AD为斜边的等腰直角三角形，BC ∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．20．由四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后得到的几何体如图所示，四边形ABCD为正方形，O为AC与BD 的交点，E为AD的中点，A1E⊥平面ABCD，（Ⅰ）证明：A1O∥平面B1CD1；（Ⅱ）设M是OD的中点，证明：平面A1EM⊥平面B1CD1．21．如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．3．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C的余弦值．4．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°，E是PD的中点．（1）证明：直线CE∥平面PAB；（2）点M在棱PC 上，且直线BM与底面ABCD所成角为45°，求二面角M﹣AB ﹣D的余弦值．5．如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（1）证明：平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D﹣AE﹣C的余弦值．6．如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，PA=PD=，AB=4．（1）求证：M为PB的中点；（2）求二面角B﹣PD﹣A的大小；（3）求直线MC与平面BDP所成角的正弦值．7．如图，在三棱锥P﹣ABC中，PA⊥底面ABC，∠BAC=90°．点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2．（Ⅰ）求证：MN∥平面BDE；（Ⅱ）求二面角C﹣EM﹣N的正弦值；（Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为，求线段AH的长．8．如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是的中点．（Ⅰ）设P是上的一点，且AP⊥BE，求∠CBP的大小；（Ⅱ）当AB=3，AD=2时，求二面角E﹣AG﹣C的大小．2017年高考数学空间几何高考真题参考答案与试题解析一．选择题（共7小题）1．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（）A．B．C．D．【解答】解：对于选项B，由于AB∥MQ，结合线面平行判定定理可知B不满足题意；对于选项C，由于AB∥MQ，结合线面平行判定定理可知C不满足题意；对于选项D，由于AB∥NQ，结合线面平行判定定理可知D不满足题意；所以选项A满足题意，故选：A．2．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB．C．D．【解答】解：∵圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，∴该圆柱底面圆周半径r==，∴该圆柱的体积：V=Sh==．故选：B ．3．在正方体ABCD ﹣A 1B 1C 1D 1中，E 为棱CD 的中点，则（ ） A ．A 1E ⊥DC 1 B ．A 1E ⊥BD C ．A 1E ⊥BC 1 D ．A 1E ⊥AC 【解答】解：法一：连B 1C ，由题意得BC 1⊥B 1C ， ∵A 1B 1⊥平面B 1BCC 1，且BC 1⊂平面B 1BCC 1， ∴A 1B 1⊥BC 1， ∵A 1B 1∩B 1C=B 1， ∴BC 1⊥平面A 1ECB 1， ∵A 1E ⊂平面A 1ECB 1， ∴A 1E ⊥BC 1． 故选：C ．法二：以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系， 设正方体ABCD ﹣A 1B 1C 1D 1中棱长为2，则A 1（2，0，2），E （0，1，0），B （2，2，0），D （0，0，0），C 1（0，2，2），A （2，0，0），C （0，2，0），=（﹣2，1，﹣2），=（0，2，2），=（﹣2，﹣2，0），=（﹣2，0，2），=（﹣2，2，0），∵•=﹣2，=2，=0，=6，∴A 1E ⊥BC 1． 故选：C ．4．某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．60 B．30 C．20 D．10【解答】解：由三视图可知：该几何体为三棱锥，该三棱锥的体积==10．故选：D．5．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm2）是（）A．+1 B．+3 C．+1 D．+3【解答】解：由几何的三视图可知，该几何体是圆锥的一半和一个三棱锥组成，圆锥的底面圆的半径为1，三棱锥的底面是底边长2的等腰直角三角形，圆锥的高和棱锥的高相等均为3，故该几何体的体积为××π×12×3+××××3=+1，故选：A6．如图，已知正四面体D﹣ABC（所有棱长均相等的三棱锥），P、Q、R分别为AB、BC、CA上的点，AP=PB，==2，分别记二面角D﹣PR﹣Q，D﹣PQ﹣R，D ﹣QR﹣P的平面角为α、β、γ，则（）A．γ＜α＜β B．α＜γ＜β C．α＜β＜γ D．β＜γ＜α【解答】解法一：如图所示，建立空间直角坐标系．设底面△ABC的中心为O．不妨设OP=3．则O（0，0，0），P（0，﹣3，0），C（0，﹣6，0），D（0，0，6），Q，R，=，=（0，3，6），=（，5，0），=，=．设平面PDR的法向量为=（x，y，z），则，可得，可得=，取平面ABC的法向量=（0，0，1）．则cos==，取α=arccos．同理可得：β=arccos．γ=arccos．∵＞＞．∴α＜γ＜β．解法二：如图所示，连接OP，OQ，OR，过点O分别作垂线：OE⊥PR，OF⊥PQ，OG⊥QR，垂足分别为E，F，G，连接DE，DF，DG．设OD=h．则tanα=．同理可得：tanβ=，tanγ=．由已知可得：OE＞OG＞OF．∴tanα＜tanγ＜tanβ，α，β，γ为锐角．∴α＜γ＜β．故选：B．7．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）A．90πB．63πC．42πD．36π【解答】解：由三视图可得，直观图为一个完整的圆柱减去一个高为6的圆柱的一半，V=π•32×10﹣•π•32×6=63π，故选：B．1．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（）A．10 B．12 C．14 D．16【解答】解：由三视图可画出直观图，该立体图中只有两个相同的梯形的面，S梯形=×2×（2+4）=6，∴这些梯形的面积之和为6×2=12，故选：B2．已知直三棱柱ABC﹣A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，则异面直线AB1与BC1所成角的余弦值为（）A． B．C．D．【解答】解：【解法一】如图所示，设M、N、P分别为AB，BB1和B1C1的中点，则AB1、BC1夹角为MN和NP夹角或其补角（因异面直线所成角为（0，]），可知MN=AB1=，NP=BC1=；作BC中点Q，则△PQM为直角三角形；∵PQ=1，MQ=AC，△ABC中，由余弦定理得AC2=AB2+BC2﹣2AB•BC•cos∠ABC=4+1﹣2×2×1×（﹣）=7，∴AC=，∴MQ=；在△MQP中，MP==；在△PMN中，由余弦定理得cos∠MNP===﹣；又异面直线所成角的范围是（0，]，∴AB1与BC1所成角的余弦值为．【解法二】如图所示，补成四棱柱ABCD﹣A1B1C1D1，求∠BC1D即可；BC1=，BD==，C1D=，∴+BD2=，∴∠DBC1=90°，∴cos∠BC1D==．二．填空题（共5小题）8．已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S﹣ABC的体积为9，则球O的表面积为36π．【解答】解：三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径，若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S﹣ABC的体积为9，可知三角形SBC与三角形SAC都是等腰直角三角形，设球的半径为r，可得，解得r=3．球O的表面积为：4πr2=36π．故答案为：36π．9．长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为14π．【解答】解：长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，可知长方体的对角线的长就是球的直径，所以球的半径为：=．则球O的表面积为：4×=14π．故答案为：14π．10．已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为．【解答】解：设正方体的棱长为a，∵这个正方体的表面积为18，∴6a2=18，则a2=3，即a=，∵一个正方体的所有顶点在一个球面上，∴正方体的体对角线等于球的直径，即a=2R，即R=，则球的体积V=π•（）3=；故答案为：．11．由一个长方体和两个圆柱体构成的几何体的三视图如图，则该几何体的体积为2+．【解答】解：由长方体长为2，宽为1，高为1，则长方体的体积V1=2×1×1=2，圆柱的底面半径为1，高为1，则圆柱的体积V2=×π×12×1=，则该几何体的体积V=V1+2V1=2+，故答案为：2+．12．如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则的值是．【解答】解：设球的半径为R，则球的体积为：R3，圆柱的体积为：πR2•2R=2πR3．则==．故答案为：．三．解答题（共9小题）13．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB ⊥平面PAD ；（2）若PA=PD=AB=DC ，∠APD=90°，且四棱锥P ﹣ABCD 的体积为，求该四棱锥的侧面积．【解答】证明：（1）∵在四棱锥P ﹣ABCD 中，∠BAP=∠CDP=90°， ∴AB ⊥PA ，CD ⊥PD ， 又AB ∥CD ，∴AB ⊥PD ， ∵PA ∩PD=P ，∴AB ⊥平面PAD ，∵AB ⊂平面PAB ，∴平面PAB ⊥平面PAD ．解：（2）设PA=PD=AB=DC=a ，取AD 中点O ，连结PO ， ∵PA=PD=AB=DC ，∠APD=90°，平面PAB ⊥平面PAD ， ∴PO ⊥底面ABCD ，且AD==，PO=，∵四棱锥P ﹣ABCD 的体积为， ∴V P ﹣ABCD =====， 解得a=2，∴PA=PD=AB=DC=2，AD=BC=2，PO=，∴PB=PC==2，∴该四棱锥的侧面积： S 侧=S △PAD +S △PAB +S △PDC +S △PBC =+++==6+2．14．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．【解答】（1）证明：四棱锥P﹣ABCD中，∵∠BAD=∠ABC=90°．∴BC∥AD，∵AD ⊂平面PAD，BC⊄平面PAD，∴直线BC∥平面PAD；（2）解：四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．设AD=2x，则AB=BC=x，CD=，O是AD的中点，连接PO，OC，CD的中点为：E，连接OE，则OE=，PO=，PE==，△PCD面积为2，可得：=2，即：，解得x=2，PE=2．=×（BC+AD）×AB×PO==4．则VP﹣ABCD15．如图四面体ABCD中，△ABC是正三角形，AD=CD．（1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB=BD，若E为棱BD上与D不重合的点，且AE ⊥EC，求四面体ABCE与四面体ACDE的体积比．【解答】证明：（1）取AC中点O，连结DO、BO，∵△ABC是正三角形，AD=CD，∴DO⊥AC，BO⊥AC，∵DO∩BO=O，∴AC⊥平面BDO，∵BD⊂平面BDO，∴AC⊥BD．解：（2）法一：连结OE，由（1）知AC⊥平面OBD，∵OE⊂平面OBD，∴OE⊥AC，设AD=CD=，则OC=OA=1，∴E是线段AC垂直平分线上的点，∴EC=EA=CD=，由余弦定理得：cos∠CBD==，即，解得BE=1或BE=2，∵BE＜＜BD=2，∴BE=1，∴BE=ED，∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h，∵BE=ED，∴S△DCE =S△BCE，∴四面体ABCE与四面体ACDE的体积比为1．法二：设AD=CD=，则AC=AB=BC=BD=2，AO=CO=DO=1，∴BO==，∴BO2+DO2=BD2，∴BO⊥DO，以O为原点，OA为x轴，OB为y轴，OD为z轴，建立空间直角坐标系，则C（﹣1，0，0），D（0，0，1），B（0，，0），A（1，0，0），设E（a，b，c），，（0≤λ≤1），则（a，b，c﹣1）=λ（0，，﹣1），解得E（0，，1﹣λ），∴=（1，），=（﹣1，），∵AE⊥EC，∴=﹣1+3λ2+（1﹣λ）2=0，由λ∈[0，1]，解得，∴DE=BE，∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h，∵DE=BE，∴S△DCE =S△BCE，∴四面体ABCE与四面体ACDE的体积比为1．16．如图，直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．（1）求三棱柱ABC﹣A1B1C1的体积；（2）设M是BC中点，求直线A1M与平面ABC所成角的大小．【解答】解：（1）∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．∴三棱柱ABC﹣A1B1C1的体积：V=S△ABC ×AA1===20．（2）连结AM，∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5，M是BC中点，∴AA1⊥底面ABC，AM==，∴∠A1MA是直线A1M与平面ABC所成角，tan∠A1MA===，∴直线A1M与平面ABC所成角的大小为arctan．17．如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．【解答】解：（1）证明：由PA⊥AB，PA⊥BC，AB⊂平面ABC，BC⊂平面ABC，且AB∩BC=B，可得PA⊥平面ABC，由BD⊂平面ABC，可得PA⊥BD；（2）证明：由AB=BC，D为线段AC的中点，可得BD⊥AC，由PA⊥平面ABC，PA⊂平面PAC，可得平面PAC⊥平面ABC，又平面ABC∩平面ABC=AC，BD⊂平面ABC，且BD⊥AC，即有BD⊥平面PAC，BD⊂平面BDE，可得平面BDE⊥平面PAC；（3）PA∥平面BDE，PA⊂平面PAC，且平面PAC∩平面BDE=DE，可得PA∥DE，又D为AC的中点，可得E为PC的中点，且DE=PA=1，由PA⊥平面ABC，可得DE⊥平面ABC，可得S△BDC =S△ABC=××2×2=1，则三棱锥E﹣BCD的体积为DE•S=×1×1=．△BDC18．如图，在四棱锥P﹣ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD=1，BC=3，CD=4，PD=2．（Ⅰ）求异面直线AP与BC所成角的余弦值；（Ⅱ）求证：PD⊥平面PBC；（Ⅲ）求直线AB与平面PBC所成角的正弦值．【解答】解：（Ⅰ）如图，由已知AD∥BC，故∠DAP或其补角即为异面直线AP与BC所成的角．因为AD⊥平面PDC，所以AD⊥PD．在Rt△PDA中，由已知，得，故．所以，异面直线AP与BC所成角的余弦值为．证明：（Ⅱ）因为AD⊥平面PDC，直线PD⊂平面PDC，所以AD⊥PD．又因为BC∥AD，所以PD⊥BC，又PD⊥PB，所以PD⊥平面PBC．解：（Ⅲ）过点D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角．因为PD⊥平面PBC，故PF为DF在平面PBC上的射影，所以∠DFP为直线DF和平面PBC所成的角．由于AD∥BC，DF∥AB，故BF=AD=1，由已知，得CF=BC﹣BF=2．又AD⊥DC，故BC⊥DC，在Rt△DCF中，可得．所以，直线AB与平面PBC所成角的正弦值为．19．如图，已知四棱锥P﹣ABCD，△PAD是以AD为斜边的等腰直角三角形，BC ∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．【解答】证明：（Ⅰ）取AD的中点F，连结EF，CF，∵E为PD的中点，∴EF∥PA，在四边形ABCD中，BC∥AD，AD=2DC=2CB，F为中点，∴CF∥AB，∴平面EFC∥平面ABP，∵EC⊂平面EFC，∴EC∥平面PAB．解：（Ⅱ）连结BF，过F作FM⊥PB于M，连结PF，∵PA=PD，∴PF⊥AD，推导出四边形BCDF为矩形，∴BF⊥AD，∴AD⊥平面PBF，又AD∥BC，∴BC⊥平面PBF，∴BC⊥PB，设DC=CB=1，则AD=PC=2，∴PB=，BF=PF=1，∴MF=，又BC⊥平面PBF，∴BC⊥MF，∴MF⊥平面PBC，即点F到平面PBC的距离为，∵MF=，D到平面PBC的距离应该和MF平行且相等，为，E为PD中点，E到平面PBC的垂足也为垂足所在线段的中点，即中位线，∴E到平面PBC的距离为，在，由余弦定理得CE=，设直线CE与平面PBC所成角为θ，则sinθ==．20．由四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后得到的几何体如图所示，四边形ABCD为正方形，O为AC与BD 的交点，E为AD的中点，A1E⊥平面ABCD，（Ⅰ）证明：A1O∥平面B1CD1；（Ⅱ）设M是OD的中点，证明：平面A1EM⊥平面B1CD1．【解答】证明：（Ⅰ）取B1D1中点G，连结A1G、CG，∵四边形ABCD为正方形，O为AC与BD 的交点，∴四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后，A1G OC，∴四边形OCGA1是平行四边形，∴A1O∥CG，∵A1O⊄平面B1CD1，CG⊂平面B1CD1，∴A1O∥平面B1CD1．（Ⅱ）四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后，BD B1D1，∵M是OD的中点，O为AC与BD 的交点，E为AD的中点，A1E⊥平面ABCD，又BD⊂平面ABCD，∴BD⊥A1E，∵四边形ABCD为正方形，O为AC与BD 的交点，∴AO⊥BD，∵M是OD的中点，E为AD的中点，∴EM⊥BD，∵A1E∩EM=E，∴BD⊥平面A1EM，∵BD∥B1D1，∴B1D1⊥平面A1EM，∵B1D1⊂平面B1CD1，∴平面A1EM⊥平面B1CD1．21．如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．【解答】证明：（1）因为AB⊥AD，EF⊥AD，且A、B、E、F四点共面，所以AB∥EF，又因为EF⊊平面ABC，AB⊆平面ABC，所以由线面平行判定定理可知：EF∥平面ABC；（2）在线段CD上取点G，连结FG、EG使得FG∥BC，则EG∥AC，因为BC⊥BD，FG∥BC，所以FG⊥BD，又因为平面ABD⊥平面BCD，所以FG⊥平面ABD，所以FG⊥AD，又因为AD⊥EF，且EF∩FG=F，所以AD⊥平面EFG，所以AD⊥EG，故AD⊥AC．3．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C的余弦值．【解答】（1）证明：∵∠BAP=∠CDP=90°，∴PA⊥AB，PD⊥CD，∵AB∥CD，∴AB⊥PD，又∵PA∩PD=P，且PA⊂平面PAD，PD⊂平面PAD，∴AB⊥平面PAD，又AB⊂平面PAB，∴平面PAB⊥平面PAD；（2）解：∵AB∥CD，AB=CD，∴四边形ABCD为平行四边形，由（1）知AB⊥平面PAD，∴AB⊥AD，则四边形ABCD为矩形，在△APD中，由PA=PD，∠APD=90°，可得△PAD为等腰直角三角形，设PA=AB=2a，则AD=．取AD中点O，BC中点E，连接PO、OE，以O为坐标原点，分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系，则：D（），B（），P（0，0，），C（）．，，．设平面PBC的一个法向量为，由，得，取y=1，得．∵AB⊥平面PAD，AD⊂平面PAD，∴AB⊥PD，又PD⊥PA，PA∩AB=A，∴PD⊥平面PAB，则为平面PAB的一个法向量，．∴cos＜＞==．由图可知，二面角A﹣PB﹣C为钝角，∴二面角A﹣PB﹣C的余弦值为．4．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°，E是PD的中点．（1）证明：直线CE∥平面PAB；（2）点M在棱PC 上，且直线BM与底面ABCD所成角为45°，求二面角M﹣AB ﹣D的余弦值．【解答】（1）证明：取PA的中点F，连接EF，BF，因为E是PD的中点，所以EF AD，AB=BC=AD，∠BAD=∠ABC=90°，∴BC∥AD，∴BCEF是平行四边形，可得CE∥BF，BF⊂平面PAB，CE⊄平面PAB，∴直线CE∥平面PAB；（2）解：四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°，E是PD的中点．取AD的中点O，M在底面ABCD上的射影N在OC上，设AD=2，则AB=BC=1，OP=，∴∠PCO=60°，直线BM与底面ABCD所成角为45°，可得：BN=MN，CN=MN，BC=1，可得：1+BN2=BN2，BN=，MN=，作NQ⊥AB于Q，连接MQ，所以∠MQN就是二面角M﹣AB﹣D的平面角，MQ==，二面角M﹣AB﹣D的余弦值为：=．5．如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（1）证明：平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D﹣AE﹣C的余弦值．【解答】（1）证明：如图所示，取AC的中点O，连接BO，OD．∵△ABC是等边三角形，∴OB⊥AC．△ABD与△CBD中，AB=BD=BC，∠ABD=∠CBD，∴△ABD≌△CBD，∴AD=CD．∵△ACD是直角三角形，∴AC是斜边，∴∠ADC=90°．∴DO=AC．∴DO2+BO2=AB2=BD2．∴∠BOD=90°．∴OB⊥OD．又DO∩AC=O，∴OB⊥平面ACD．又OB⊂平面ABC，∴平面ACD⊥平面ABC．（2）解：设点D，B到平面ACE的距离分别为hD ，hE．则=．∵平面AEC把四面体ABCD分成体积相等的两部分，∴===1．∴点E是BD的中点．建立如图所示的空间直角坐标系．不妨取AB=2．则O（0，0，0），A（1，0，0），C（﹣1，0，0），D（0，0，1），B（0，，0），E．=（﹣1，0，1），=，=（﹣2，0，0）．设平面ADE的法向量为=（x，y，z），则，即，取=．同理可得：平面ACE的法向量为=（0，1，）．∴cos===﹣．∴二面角D﹣AE﹣C的余弦值为．6．如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，PA=PD=，AB=4．（1）求证：M为PB的中点；（2）求二面角B﹣PD﹣A的大小；（3）求直线MC与平面BDP所成角的正弦值．【解答】（1）证明：如图，设AC∩BD=O，∵ABCD为正方形，∴O为BD的中点，连接OM，∵PD∥平面MAC，PD⊂平面PBD，平面PBD∩平面AMC=OM，∴PD∥OM，则，即M为PB的中点；（2）解：取AD中点G，∵PA=PD，∴PG⊥AD，∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，∴PG⊥平面ABCD，则PG⊥AD，连接OG，则PG⊥OG，由G是AD的中点，O是AC的中点，可得OG∥DC，则OG⊥AD．以G为坐标原点，分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系，由PA=PD=，AB=4，得D（2，0，0），A（﹣2，0，0），P（0，0，），C（2，4，0），B（﹣2，4，0），M（﹣1，2，），，．设平面PBD的一个法向量为，则由，得，取z=，得．取平面PAD的一个法向量为．∴cos＜＞==．∴二面角B﹣PD﹣A的大小为60°；（3）解：，平面BDP的一个法向量为．∴直线MC与平面BDP所成角的正弦值为|cos＜＞|=||=||=．7．如图，在三棱锥P﹣ABC中，PA⊥底面ABC，∠BAC=90°．点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2．（Ⅰ）求证：MN∥平面BDE；（Ⅱ）求二面角C﹣EM﹣N的正弦值；（Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为，求线段AH的长．【解答】（Ⅰ）证明：取AB中点F，连接MF、NF，∵M为AD中点，∴MF∥BD，∵BD⊂平面BDE，MF⊄平面BDE，∴MF∥平面BDE．∵N为BC中点，∴NF∥AC，又D、E分别为AP、PC的中点，∴DE∥AC，则NF∥DE．∵DE⊂平面BDE，NF⊄平面BDE，∴NF∥平面BDE．又MF∩NF=F．∴平面MFN∥平面BDE，则MN∥平面BDE；（Ⅱ）解：∵PA⊥底面ABC，∠BAC=90°．∴以A为原点，分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系．∵PA=AC=4，AB=2，∴A（0，0，0），B（2，0，0），C（0，4，0），M（0，0，1），N（1，2，0），E （0，2，2），则，，设平面MEN的一个法向量为，由，得，取z=2，得．由图可得平面CME的一个法向量为．∴cos＜＞=．∴二面角C﹣EM﹣N的余弦值为，则正弦值为；（Ⅲ）解：设AH=t，则H（0，0，t），，．∵直线NH与直线BE所成角的余弦值为，∴|cos＜＞|=||=||=．解得：t=或t=．∴当H与P重合时直线NH与直线BE所成角的余弦值为，此时线段AH的长为或．8．如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是的中点．（Ⅰ）设P是上的一点，且AP⊥BE，求∠CBP的大小；（Ⅱ）当AB=3，AD=2时，求二面角E﹣AG﹣C的大小．【解答】解：（Ⅰ）∵AP⊥BE，AB⊥BE，且AB，AP⊂平面ABP，AB∩AP=A，∴BE⊥平面ABP，又BP⊂平面ABP，∴BE⊥BP，又∠EBC=120°，因此∠CBP=30°；（Ⅱ）解法一、取的中点H，连接EH，GH，CH，∵∠EBC=120°，∴四边形BECH为菱形，∴AE=GE=AC=GC=．取AG中点M，连接EM，CM，EC，则EM⊥AG，CM⊥AG，∴∠EMC为所求二面角的平面角．又AM=1，∴EM=CM=．在△BEC中，由于∠EBC=120°，由余弦定理得：EC2=22+22﹣2×2×2×cos120°=12，∴，因此△EMC为等边三角形，故所求的角为60°．解法二、以B为坐标原点，分别以BE，BP，BA所在直线为x，y，z轴建立空间直角坐标系．由题意得：A（0，0，3），E（2，0，0），G（1，，3），C（﹣1，，0），故，，．设为平面AEG的一个法向量，=2，得；由，得，取z1设为平面ACG的一个法向量，=﹣2，得．由，可得，取z2∴cos＜＞=．∴二面角E﹣AG﹣C的大小为60°．WORD格式-可编辑专业知识--整理分享。

山东省2017年高考数学（理科）专题练习空间几何体表面积或体积的求解答 案[A 组高考达标] 一、选择题 1~5．DBDBA 二、填空题6．3+7．148．(16π三、解答题9．解：(1)证明：取PA 的中点F ，连接EF ，BF ，则EF AD BC ，即EF ，BC共面．∵PB ⊥平面ABCD ，∴PB BC ⊥，又BC AB ⊥且PB AB B =，∴BC ⊥平面PAB ，∴.BC PA ⊥ ∵PB AB =，∴BF PA ⊥，又BC BF B =，∴PA ⊥平面EFBC ，∴PA CE ⊥． (2)设四棱锥P ABCD -的表面积为S ，∵PB ABCD ⊥平面，∴PB CD ⊥，又CD BC ⊥，PBBC B =，∴CD PBC ⊥平面，∴CD PC ⊥，即△PCD 为直角三角形， 由(1)知BC PAB ⊥平面，而AD BC ，∴AD PAB ⊥平面， 故AD PA ⊥，即△P AD 也为直角三角形．224ABCD S ==⨯=，12222PBC PAB PDA S S S ===⨯⨯=△△△，122PCDS=⨯= ∴ABCD PBC PDA PAB PCD S S S S S S ==++++△△△△表10=+10．解：．(1)证明：因为D ，E 分别为棱AC ，BC 的中点，所以DE 是△ABC 的中位线，所以DEAB又11DE ABB A ⊄平面，AB ⊂平面11ABB A ，所以DE 平面11ABB A ．同理DG 平面11ABB A ，又DE DG D =，所以平面DEFG 平面11ABB A ．(2)当直三棱柱111ABC A B C -容器的侧面11AA B B 水平放置时，由(1)可知，液体部分是直四棱柱，其高即为原直三棱柱111ABC A B C -容器的高，即侧棱长l ，当底面ABC 水平放置时，设液面的高为h ，ABC △的面积为S ，则由已知条件可知，CDE ABC △∽△，且14CDE S S =△，所以34ABED S S =四边形． 由于两种状态下液体体积相等，所以34ABED V Sh S l Sl ===液体四边形，即34h l =．因此，当底面ABC 水平放置时，液面的高为34l ． [B 组名校冲刺] 一、选择题 1~4．ABDC 二、填空题5 6．83π2三、解答题7．解：(1)证明：设EC 与DF 交于点N ，连接MN ，在矩形CDEF 中，点N 为EC 中点， 因为M 为EA 中点，所以MNAC ．又因为AC MDF ⊄平面，MN MDF ⊂平面， 所以AC MDF 平面．(2)取CD 中点为G ，连接1A BG ，EG ，CDEF ABCD ⊥平面平面，CDEF ABCD CD =平面平面，AD ABCD ⊂平面，AD CD ⊥，所以AD CDEF ⊥平面，同理ED ABCD ⊥平面， 所以ED 的长即为四棱锥E-ABCD 的高. 在梯形ABCD 中，12AB CD DG ==，AB DG ， 所以四边形ABGD 是平行四边形，BG AD ，所以BG CDEF ⊥平面．又DF ⊂平面CDEF ，所以BG DF ⊥，又BE DF ⊥，BE BG B =，所以DF BEG ⊥平面，DF EG ⊥．注意到Rt DEG Rt EFD △∽△，所以28DE DG EF ==，DE = 所以1423E ABCD ABCDV S ED -==梯形． 8．解：(1)证明：∵△CMD 是等腰直角三角形，90CMD ∠=︒，点O 为CD 的中点，∴OM CD ⊥．∵CMD BCD ⊥平面平面，CMD BCD CD =平面平面，OM CMD ⊂平面，∴OM BCD ⊥平面． ∵AB ⊥平面BCD ，∴OMAB .∵AB ABD ⊂平面，OM ABD ⊄平面，∴OM ABD 平面．(2)法一：由(1)知OMABD 平面，∴点M 到平面ABD 的距离等于点O 到平面ABD 的距离． 过点O 作OH BD ⊥，垂足为点H ．∵AB BCD ⊥平面，OH BCD ⊂平面，∴OH AB ⊥． ∵AB ABD ⊂平面，BD ABD ⊂平面，AB BD B =，∴OH ABD ⊥平面．∵2AB BC ==，△BCD 是等边三角形，∴2BD =，1OD =，sin60=2OH OD =︒． ∴A BDM M ABD V V --=三棱锥三棱锥1132AB BD OH =⨯⨯11223223=⨯⨯⨯⨯=．∴三棱锥A -BDM ． 法二：由(1)知OMABD 平面，∴点M 到平面ABD 的距离等于点O 到平面ABD 的距离. ∵2AB BC ==，△BCD 是等边三角形，∴21BD OD ==，． 连接OB ，则OB CD ⊥，sin60=3OB BD =︒ ∴A BDM M ABD O ABD A BDO V V V V ----===三棱锥三棱锥三棱锥三棱锥1132OD OB AB =⨯⨯111232=⨯⨯=．∴三棱锥A -BDM 的体积为3．山东省2017年高考数学（理科）专题练习空间几何体表面积或体积的求解解 析[建议A 、B 组各用时：45分钟] [A 组高考达标] 一、选择题 1.D[分析三视图可知，该几何体为如图所示的三棱锥，其中平面ACD ⊥平面BCD ，故选D.] 2．B[由三视图可知该几何体由半球内挖去一个同底的圆锥得到，所以该几何体的体积为V ＝12×43π×13－13π×12×1＝π3.]3．D[由三视图可知，几何体是一个三棱柱，体积V 1＝12×2×2×2＝4，设外接球的半径为R ，则4R 2＝22＋22＋22＝12，所以R ＝3.所以球的体积V 2＝43πR 3＝43π，体积比V 1∶V 2＝4∶43π＝1∶3π.] 4．B[分析题意可知，该几何体是由如图所示的三棱柱ABC -A 1B 1C 1截去四棱锥A -BEDC 得到的，故其体积V ＝34×22×3－13×1＋22×2×3＝23，故选B.] 5．A[在正方体中还原出该四面体C -A 1EC 1如图所示，可求得该四面体的表面积为8＋82＋4 6.] 二、填空题6．3＋2 2[依题意，边长是3的等边△ABC 的外接圆半径r ＝12·3sin 60°＝1.∵球O 的表面积为36π＝4πR 2，∴球O 的半径R ＝3，∴球心O 到平面ABC 的距离d ＝R 2－r 2＝22，∴球面上的点P 到平面ABC 距离的最大值为R ＋d ＝3＋2 2.] 7．14[如图，设S △ABD ＝S 1，S △PAB ＝S 2，E 到平面ABD 的距离为h 1，C 到平面PAB 的距离为h 2，则S 2＝2S 1，h 2＝2h 1，V 1＝13S 1h 1，V 2＝13S 2h 2，所以V 1V 2＝S 1h 1S 2h 2＝14．] 8．16(π－2)[设内接正四棱柱底边长为a ，高为h ，那么16＝2a 2＋h 2≥22ah ，正四棱柱的侧面积S ＝4ah ≤162，球的表面积与该正四棱柱的侧面积之差是16(π－2)．] 三、解答题9． 解：(1)证明：取P A 的中点F ，连接EF ，BF ，则EF ∥AD ∥BC ，即EF ，BC 共面．∵PB ⊥平面ABCD ，∴PB ⊥BC ，又BC ⊥AB 且PB ∩AB ＝B ， ∴BC ⊥平面P AB ，∴BC ⊥P A ．3分 ∵PB ＝AB ，∴BF ⊥P A ，又BC ∩BF ＝B ， ∴P A ⊥平面EFBC ，∴P A ⊥CE ．6分 (2)设四棱锥P -ABCD 的表面积为S ，∵PB ⊥平面ABCD ，∴PB ⊥CD ，又CD ⊥BC ，PB ∩BC ＝B ， ∴CD ⊥平面PBC ，∴CD ⊥PC ，即△PCD 为直角三角形，8分 由(1)知BC ⊥平面P AB ，而AD ∥BC ，∴AD ⊥平面P AB ， 故AD ⊥P A ，即△P AD 也为直角三角形． S ▱ABCD ＝2×2＝4，S △PBC ＝S △P AB ＝S △PDA ＝12×2×2＝2，S △PCD ＝12×2×22＋22＝22，10分∴S 表＝S ▱ABCD ＋S △PBC ＋S △PDA ＋S △P AB ＋S △PCD ＝10＋22．12分10．解：(1)证明：因为D ，E 分别为棱AC ，BC 的中点，所以DE 是△ABC 的中位线，所以DE ∥AB .又DE ⊄平面ABB 1A 1，AB ⊂平面ABB 1A 1，所以DE ∥平面ABB 1A 1.同理DG ∥平面ABB 1A 1，又DE ∩DG ＝D ，所以平面DEFG ∥平面ABB 1A 1．6分(2)当直三棱柱ABC -A 1B 1C 1容器的侧面AA 1B 1B 水平放置时，由(1)可知，液体部分是直四棱柱，其高即为原直三棱柱ABC -A 1B 1C 1容器的高，即侧棱长l ，当底面ABC 水平放置时，设液面的高为h ，△ABC 的面积为S ，则由已知条件可知，△CDE ∽△ABC ，且S △CDE ＝14S ，所以S 四边形ABED ＝34S ．9分由于两种状态下液体体积相等，所以V 液体＝Sh ＝S 四边形ABED l ＝34Sl ，即h ＝34l .因此，当底面ABC 水平放置时，液面的高为34l ．12分[B 组名校冲刺] 一、选择题1．A[过点D 在平面PCD 内作DN ⊥PM 于点N ，又平面PMB ⊥平面PCD ，平面PMB ∩平面PCD ＝PM ，所以DN ⊥平面PMB ，所以DN ⊥BM .又由PD ⊥平面ABCD ，得PD ⊥BM ，又PD 与DN 是平面PDC 内的两条相交直线，所以BM ⊥平面PDC ，则BM ⊥CD .又点M 是CD 的中点，BC ＝CD ，所以∠BCD ＝60°，所以底面菱形ABCD 的面积为2×2×sin 60°＝23，故该四棱锥的体积为13×23×2＝433．]2．B[根据三视图可知，几何体是由一个直三棱柱与一个三棱锥所组成的，其中该直三棱柱的底面是一个直角三角形(直角边长分别为1,2，高为1)；该三棱锥的底面是一个直角三角形(腰长分别为1,2，高为1)，因此该几何体的体积为12×2×1×1＋13×12×2×1×1＝43，选B ．] 3．D[由三视图知，该几何体为一个底面半径为1，高为1的圆柱体，与底面半径为1，高为2的半圆柱体构成，所以该三视图的体积为π×12×1＋12π×12×2＝2π，故选D ．] 4．C[设OP 交平面ABC 于O ′，由题得△ABC 和△P AB 为正三角形，所以O ′A ＝33AB ＝33AP .因为AO ′⊥PO ，OA ⊥P A ，所以OP OA ＝AP AO ′，AO ′AB＝33，AO ′AP ＝33，所以OA ＝OP ·O ′A AP ＝3×33＝1，即球的半径为1，所以其体积为43π×13＝43π．选C ．]二、填空题 5．55π6[由题意知六棱柱的底面正六边形的外接圆半径r ＝1, 其高h ＝1，∴球半径为R ＝r 2＋⎝⎛⎭⎫h 22＝1＋14＝54，∴该球的体积V ＝43πR 3＝43×⎝⎛⎭⎫543π＝55π6．]6．832π[由题可知，△ABC 中AC 边上的高为15－32＝6，球心O 在底面ABC 的投影即为△ABC 的外心D ，设DA ＝DB ＝DC ＝x ，∴x 2＝32＋(6－x )2，解得x ＝546，∴R 2＝x 2＋⎝⎛⎭⎫PC 22＝758＋1＝838(其中R 为三棱锥外接球的半径)，∴外接球的表面积S ＝4πR 2＝832π．]三、解答题7．解：(1)证明：设EC 与DF 交于点N ，连接MN ，在矩形CDEF 中，点N 为EC 中点， 因为M 为EA 中点，所以MN ∥AC ．2分 又因为AC ⊄平面MDF ，MN ⊂平面MDF ， 所以AC ∥平面MDF ．4分(2)取CD 中点为G ，连接BG ，EG ，平面CDEF ⊥平面ABCD ，平面CDEF ∩平面ABCD ＝CD ， AD ⊂平面ABCD ，AD ⊥CD ，所以AD ⊥平面CDEF ，同理ED ⊥平面ABCD ，7分 所以ED 的长即为四棱锥E -ABCD 的高．8分 在梯形ABCD 中，AB ＝12CD ＝DG ，AB ∥DG ，所以四边形ABGD 是平行四边形，BG ∥AD ，所以BG ⊥平面CDEF . 又DF ⊂平面CDEF ，所以BG ⊥DF ，又BE ⊥DF ，BE ∩BG ＝B ， 所以DF ⊥平面BEG ，DF ⊥EG ．10分注意到Rt △DEG ∽Rt △EFD ，所以DE 2＝DG ·EF ＝8，DE ＝22， 所以V E -ABCD ＝13S 梯形ABCD ·ED ＝42．12分 8．解：(1)证明：∵△CMD 是等腰直角三角形，∠CMD ＝90°，点O 为CD 的中点，∴OM ⊥CD ．1分∵平面CMD ⊥平面BCD ，平面CMD ∩平面BCD ＝CD ，OM ⊂平面CMD ， ∴OM ⊥平面BCD ．2分∵AB⊥平面BCD，∴OM∥AB．3分∵AB⊂平面ABD，OM⊄平面ABD，∴OM∥平面ABD．4分(2)法一：由(1)知OM∥平面ABD，∴点M到平面ABD的距离等于点O到平面ABD的距离．5分过点O作OH⊥BD，垂足为点H.∵AB⊥平面BCD，OH⊂平面BCD，∴OH⊥AB．6分∵AB⊂平面ABD，BD⊂平面ABD，AB∩BD＝B，∴OH⊥平面ABD．7分∵AB＝BC＝2，△BCD是等边三角形，∴BD＝2，OD＝1，OH＝OD·sin 60°＝32．9分∴V三棱锥A-BDM＝V三棱锥M-ABD＝13×12×AB·BD·OH＝13×12×2×2×32＝33．11分∴三棱锥A-BDM的体积为33．12分法二：由(1)知OM∥平面ABD，∴点M到平面ABD的距离等于点O到平面ABD的距离．5分∵AB＝BC＝2，△BCD是等边三角形，∴BD＝2，OD＝1．6分连接OB，则OB⊥CD，OB＝BD·sin 60°＝3．7分∴V三棱锥A-BDM＝V三棱锥M-ABD＝V三棱锥O-ABD＝V三棱锥A-BDO＝13×12×OD·OB·AB＝13×12×1×3×2＝33．11分∴三棱锥A-BDM的体积为33．12分。

高考数学空间几何高考真题HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】2017年高考数学空间几何高考真题一．选择题（共9小题）1．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（）A．B．C．D．2．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB．C．D．3．在正方体ABCD﹣A1B1C1D1中，E为棱CD的中点，则（）A．A1E⊥DC1B．A1E⊥BD C．A1E⊥BC1D．A1E⊥AC4．某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．60 B．30 C．20 D．105．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm2）是（）A．+1 B．+3 C．+1 D．+36．如图，已知正四面体D﹣ABC（所有棱长均相等的三棱锥），P、Q、R分别为AB、BC、CA上的点，AP=PB，==2，分别记二面角D﹣PR﹣Q，D﹣PQ﹣R，D﹣QR﹣P的平面角为α、β、γ，则（）A．γ＜α＜βB．α＜γ＜βC．α＜β＜γD．β＜γ＜α7．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）A．90πB．63πC．42πD．36π1．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（）A．10 B．12 C．14 D．162．已知直三棱柱ABC﹣A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，则异面直线AB1与BC1所成角的余弦值为（）A．B．C．D．二．填空题（共5小题）8．已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S﹣ABC的体积为9，则球O的表面积为．9．长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为．10．已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为．11．由一个长方体和两个圆柱体构成的几何体的三视图如图，则该几何体的体积为．12．如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则的值是．三．解答题（共9小题）13．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，且四棱锥P﹣ABCD的体积为，求该四棱锥的侧面积．14．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．15．如图四面体ABCD中，△ABC是正三角形，AD=CD．（1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB=BD，若E为棱BD上与D不重合的点，且AE ⊥EC，求四面体ABCE与四面体ACDE的体积比．16．如图，直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．（1）求三棱柱ABC﹣A1B1C1的体积；（2）设M是BC中点，求直线A1M与平面ABC所成角的大小．17．如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D 为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．18．如图，在四棱锥P﹣ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD=1，BC=3，CD=4，PD=2．（Ⅰ）求异面直线AP与BC所成角的余弦值；（Ⅱ）求证：PD⊥平面PBC；（Ⅲ）求直线AB与平面PBC所成角的正弦值．19．如图，已知四棱锥P﹣ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．20．由四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后得到的几何体如图所示，四边形ABCD为正方形，O为AC与BD 的交点，E为AD的中点，A1E⊥平面ABCD，（Ⅰ）证明：A1O∥平面B1CD1；（Ⅱ）设M是OD的中点，证明：平面A1EM⊥平面B1CD1．21．如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．3．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C的余弦值．4．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°，E是PD的中点．（1）证明：直线CE∥平面PAB；（2）点M在棱PC 上，且直线BM与底面ABCD所成角为45°，求二面角M﹣AB﹣D的余弦值．5．如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（1）证明：平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D﹣AE﹣C的余弦值．6．如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，PA=PD=，AB=4．（1）求证：M为PB的中点；（2）求二面角B﹣PD﹣A的大小；（3）求直线MC与平面BDP所成角的正弦值．7．如图，在三棱锥P﹣ABC中，PA⊥底面ABC，∠BAC=90°．点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2．（Ⅰ）求证：MN∥平面BDE；（Ⅱ）求二面角C﹣EM﹣N的正弦值；（Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为，求线段AH的长．8．如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是的中点．（Ⅰ）设P是上的一点，且AP⊥BE，求∠CBP的大小；（Ⅱ）当AB=3，AD=2时，求二面角E﹣AG﹣C的大小．2017年高考数学空间几何高考真题参考答案与试题解析一．选择题（共7小题）1．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（）A．B．C．D．【解答】解：对于选项B，由于AB∥MQ，结合线面平行判定定理可知B不满足题意；对于选项C，由于AB∥MQ，结合线面平行判定定理可知C不满足题意；对于选项D，由于AB∥NQ，结合线面平行判定定理可知D不满足题意；所以选项A满足题意，故选：A．2．已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB．C．D．【解答】解：∵圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，∴该圆柱底面圆周半径r==，∴该圆柱的体积：V=Sh==．故选：B．3．在正方体ABCD﹣A1B1C1D1中，E为棱CD的中点，则（）A．A1E⊥DC1B．A1E⊥BD C．A1E⊥BC1D．A1E⊥AC【解答】解：法一：连B1C，由题意得BC1⊥B1C，∵A1B1⊥平面B1BCC1，且BC1⊂平面B1BCC1，∴A1B1⊥BC1，∵A1B1∩B1C=B1，∴BC1⊥平面A1ECB1，∵A1E⊂平面A1ECB1，∴A1E⊥BC1．故选：C．法二：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，设正方体ABCD﹣A1B1C1D1中棱长为2，则A1（2，0，2），E（0，1，0），B（2，2，0），D（0，0，0），C1（0，2，2），A（2，0，0），C（0，2，0），=（﹣2，1，﹣2），=（0，2，2），=（﹣2，﹣2，0），=（﹣2，0，2），=（﹣2，2，0），∵•=﹣2，=2，=0，=6，∴A1E⊥BC1．故选：C．4．某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．60 B．30 C．20 D．10【解答】解：由三视图可知：该几何体为三棱锥，该三棱锥的体积==10．故选：D．5．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm2）是（）A．+1 B．+3 C．+1 D．+3【解答】解：由几何的三视图可知，该几何体是圆锥的一半和一个三棱锥组成，圆锥的底面圆的半径为1，三棱锥的底面是底边长2的等腰直角三角形，圆锥的高和棱锥的高相等均为3，故该几何体的体积为××π×12×3+××××3=+1，故选：A6．如图，已知正四面体D﹣ABC（所有棱长均相等的三棱锥），P、Q、R分别为AB、BC、CA上的点，AP=PB，==2，分别记二面角D﹣PR﹣Q，D﹣PQ﹣R，D﹣QR﹣P的平面角为α、β、γ，则（）A．γ＜α＜βB．α＜γ＜βC．α＜β＜γD．β＜γ＜α【解答】解法一：如图所示，建立空间直角坐标系．设底面△ABC的中心为O．不妨设OP=3．则O（0，0，0），P（0，﹣3，0），C（0，﹣6，0），D（0，0，6），Q，R，=，=（0，3，6），=（，5，0），=，=．设平面PDR的法向量为=（x，y，z），则，可得，可得=，取平面ABC的法向量=（0，0，1）．则cos==，取α=arccos．同理可得：β=arccos．γ=arccos．∵＞＞．∴α＜γ＜β．解法二：如图所示，连接OP，OQ，OR，过点O分别作垂线：OE⊥PR，OF⊥PQ，OG⊥QR，垂足分别为E，F，G，连接DE，DF，DG．设OD=h．则tanα=．同理可得：tanβ=，tanγ=．由已知可得：OE＞OG＞OF．∴tanα＜tanγ＜tanβ，α，β，γ为锐角．∴α＜γ＜β．故选：B．7．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）A．90πB．63πC．42πD．36π【解答】解：由三视图可得，直观图为一个完整的圆柱减去一个高为6的圆柱的一半，V=π•32×10﹣•π•32×6=63π，故选：B．1．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（）A．10 B．12 C．14 D．16【解答】解：由三视图可画出直观图，该立体图中只有两个相同的梯形的面，S梯形=×2×（2+4）=6，∴这些梯形的面积之和为6×2=12，故选：B2．已知直三棱柱ABC﹣A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，则异面直线AB1与BC1所成角的余弦值为（）A．B．C．D．【解答】解：【解法一】如图所示，设M、N、P分别为AB，BB1和B1C1的中点，则AB1、BC1夹角为MN和NP夹角或其补角（因异面直线所成角为（0，]），可知MN=AB1=，NP=BC1=；作BC中点Q，则△PQM为直角三角形；∵PQ=1，MQ=AC，△ABC中，由余弦定理得AC2=AB2+BC2﹣2AB•BC•cos∠ABC=4+1﹣2×2×1×（﹣）=7，∴AC=，∴MQ=；在△MQP中，MP==；在△PMN中，由余弦定理得cos∠MNP===﹣；又异面直线所成角的范围是（0，]，∴AB1与BC1所成角的余弦值为．【解法二】如图所示，补成四棱柱ABCD﹣A1B1C1D1，求∠BC1D即可；BC1=，BD==，C1D=，∴+BD2=，∴∠DBC1=90°，∴cos∠BC1D==．二．填空题（共5小题）8．已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S﹣ABC的体积为9，则球O的表面积为36π．【解答】解：三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径，若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S﹣ABC的体积为9，可知三角形SBC与三角形SAC都是等腰直角三角形，设球的半径为r，可得，解得r=3．球O的表面积为：4πr2=36π．故答案为：36π．9．长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为14π．【解答】解：长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，可知长方体的对角线的长就是球的直径，所以球的半径为：=．则球O的表面积为：4×=14π．故答案为：14π．10．已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为．【解答】解：设正方体的棱长为a，∵这个正方体的表面积为18，∴6a2=18，则a2=3，即a=，∵一个正方体的所有顶点在一个球面上，∴正方体的体对角线等于球的直径，即a=2R，即R=，则球的体积V=π•（）3=；故答案为：．11．由一个长方体和两个圆柱体构成的几何体的三视图如图，则该几何体的体积为2+．【解答】解：由长方体长为2，宽为1，高为1，则长方体的体积V1=2×1×1=2，圆柱的底面半径为1，高为1，则圆柱的体积V2=×π×12×1=，则该几何体的体积V=V1+2V1=2+，故答案为：2+．12．如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则的值是．【解答】解：设球的半径为R，则球的体积为：R3，圆柱的体积为：πR2•2R=2πR3．则==．故答案为：．三．解答题（共9小题）13．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，且四棱锥P﹣ABCD的体积为，求该四棱锥的侧面积．【解答】证明：（1）∵在四棱锥P﹣ABCD中，∠BAP=∠CDP=90°，∴AB⊥PA，CD⊥PD，又AB∥CD，∴AB⊥PD，∵PA∩PD=P，∴AB⊥平面PAD，∵AB⊂平面PAB，∴平面PAB⊥平面PAD．解：（2）设PA=PD=AB=DC=a，取AD中点O，连结PO，∵PA=PD=AB=DC，∠APD=90°，平面PAB⊥平面PAD，∴PO⊥底面ABCD，且AD==，PO=，∵四棱锥P﹣ABCD的体积为，∴V P﹣ABCD=====，解得a=2，∴PA=PD=AB=DC=2，AD=BC=2，PO=，∴PB=PC==2，∴该四棱锥的侧面积：S侧=S△PAD+S△PAB+S△PDC+S△PBC=+++==6+2．14．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．【解答】（1）证明：四棱锥P﹣ABCD中，∵∠BAD=∠ABC=90°．∴BC∥AD，∵AD⊂平面PAD，BC⊄平面PAD，∴直线BC∥平面PAD；（2）解：四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°．设AD=2x，则AB=BC=x，CD=，O是AD的中点，连接PO，OC，CD的中点为：E，连接OE，则OE=，PO=，PE==，△PCD面积为2，可得：=2，即：，解得x=2，PE=2．则V P﹣ABCD=×（BC+AD）×AB×PO==4．15．如图四面体ABCD中，△ABC是正三角形，AD=CD．（1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB=BD，若E为棱BD上与D不重合的点，且AE ⊥EC，求四面体ABCE与四面体ACDE的体积比．【解答】证明：（1）取AC中点O，连结DO、BO，∵△ABC是正三角形，AD=CD，∴DO⊥AC，BO⊥AC，∵DO∩BO=O，∴AC⊥平面BDO，∵BD⊂平面BDO，∴AC⊥BD．解：（2）法一：连结OE，由（1）知AC⊥平面OBD，∵OE⊂平面OBD，∴OE⊥AC，设AD=CD=，则OC=OA=1，∴E是线段AC垂直平分线上的点，∴EC=EA=CD=，由余弦定理得：cos∠CBD==，即，解得BE=1或BE=2，∵BE＜＜BD=2，∴BE=1，∴BE=ED，∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h，∵BE=ED，∴S△DCE=S△BCE，∴四面体ABCE与四面体ACDE的体积比为1．法二：设AD=CD=，则AC=AB=BC=BD=2，AO=CO=DO=1，∴BO==，∴BO2+DO2=BD2，∴BO⊥DO，以O为原点，OA为x轴，OB为y轴，OD为z轴，建立空间直角坐标系，则C（﹣1，0，0），D（0，0，1），B（0，，0），A（1，0，0），设E（a，b，c），，（0≤λ≤1），则（a，b，c﹣1）=λ（0，，﹣1），解得E（0，，1﹣λ），∴=（1，），=（﹣1，），∵AE⊥EC，∴=﹣1+3λ2+（1﹣λ）2=0，由λ∈[0，1]，解得，∴DE=BE，∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h，∵DE=BE，∴S△DCE=S△BCE，∴四面体ABCE与四面体ACDE的体积比为1．16．如图，直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．（1）求三棱柱ABC﹣A1B1C1的体积；（2）设M是BC中点，求直线A1M与平面ABC所成角的大小．【解答】解：（1）∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．∴三棱柱ABC﹣A1B1C1的体积：V=S△ABC×AA1===20．（2）连结AM，∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5，M是BC中点，∴AA1⊥底面ABC，AM==，∴∠A1MA是直线A1M与平面ABC所成角，tan∠A1MA===，∴直线A1M与平面ABC所成角的大小为arctan．17．如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D 为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．【解答】解：（1）证明：由PA⊥AB，PA⊥BC，AB⊂平面ABC，BC⊂平面ABC，且AB∩BC=B，可得PA⊥平面ABC，由BD⊂平面ABC，可得PA⊥BD；（2）证明：由AB=BC，D为线段AC的中点，可得BD⊥AC，由PA⊥平面ABC，PA⊂平面PAC，可得平面PAC⊥平面ABC，又平面ABC∩平面ABC=AC，BD⊂平面ABC，且BD⊥AC，即有BD⊥平面PAC，BD⊂平面BDE，可得平面BDE⊥平面PAC；（3）PA∥平面BDE，PA⊂平面PAC，且平面PAC∩平面BDE=DE，可得PA∥DE，又D为AC的中点，可得E为PC的中点，且DE=PA=1，由PA⊥平面ABC，可得DE⊥平面ABC，可得S△BDC=S△ABC=××2×2=1，则三棱锥E﹣BCD的体积为DE•S△BDC=×1×1=．18．如图，在四棱锥P﹣ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD=1，BC=3，CD=4，PD=2．（Ⅰ）求异面直线AP与BC所成角的余弦值；（Ⅱ）求证：PD⊥平面PBC；（Ⅲ）求直线AB与平面PBC所成角的正弦值．【解答】解：（Ⅰ）如图，由已知AD∥BC，故∠DAP或其补角即为异面直线AP与BC所成的角．因为AD⊥平面PDC，所以AD⊥PD．在Rt△PDA中，由已知，得，故．所以，异面直线AP与BC所成角的余弦值为．证明：（Ⅱ）因为AD⊥平面PDC，直线PD⊂平面PDC，所以AD⊥PD．又因为BC∥AD，所以PD⊥BC，又PD⊥PB，所以PD⊥平面PBC．解：（Ⅲ）过点D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角．因为PD⊥平面PBC，故PF为DF在平面PBC上的射影，所以∠DFP为直线DF和平面PBC所成的角．由于AD∥BC，DF∥AB，故BF=AD=1，由已知，得CF=BC﹣BF=2．又AD⊥DC，故BC⊥DC，在Rt△DCF中，可得．所以，直线AB与平面PBC所成角的正弦值为．19．如图，已知四棱锥P﹣ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值．【解答】证明：（Ⅰ）取AD的中点F，连结EF，CF，∵E为PD的中点，∴EF∥PA，在四边形ABCD中，BC∥AD，AD=2DC=2CB，F为中点，∴CF∥AB，∴平面EFC∥平面ABP，∵EC⊂平面EFC，∴EC∥平面PAB．解：（Ⅱ）连结BF，过F作FM⊥PB于M，连结PF，∵PA=PD，∴PF⊥AD，推导出四边形BCDF为矩形，∴BF⊥AD，∴AD⊥平面PBF，又AD∥BC，∴BC⊥平面PBF，∴BC⊥PB，设DC=CB=1，则AD=PC=2，∴PB=，BF=PF=1，∴MF=，又BC⊥平面PBF，∴BC⊥MF，∴MF⊥平面PBC，即点F到平面PBC的距离为，∵MF=，D到平面PBC的距离应该和MF平行且相等，为，E为PD中点，E到平面PBC的垂足也为垂足所在线段的中点，即中位线，∴E到平面PBC的距离为，在，由余弦定理得CE=，设直线CE与平面PBC所成角为θ，则sinθ==．20．由四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后得到的几何体如图所示，四边形ABCD为正方形，O为AC与BD 的交点，E为AD的中点，A1E⊥平面ABCD，（Ⅰ）证明：A1O∥平面B1CD1；（Ⅱ）设M是OD的中点，证明：平面A1EM⊥平面B1CD1．【解答】证明：（Ⅰ）取B1D1中点G，连结A1G、CG，∵四边形ABCD为正方形，O为AC与BD 的交点，∴四棱柱ABCD﹣A 1B1C1D1截去三棱锥C1﹣B1CD1后，A1G OC，∴四边形OCGA1是平行四边形，∴A1O∥CG，∵A1O⊄平面B1CD1，CG⊂平面B1CD1，∴A1O∥平面B1CD1．（Ⅱ）四棱柱ABCD﹣A 1B1C1D1截去三棱锥C1﹣B1CD1后，BD B1D1，∵M是OD的中点，O为AC与BD 的交点，E为AD的中点，A1E⊥平面ABCD，又BD⊂平面ABCD，∴BD⊥A1E，∵四边形ABCD为正方形，O为AC与BD 的交点，∴AO⊥BD，∵M是OD的中点，E为AD的中点，∴EM⊥BD，∵A1E∩EM=E，∴BD⊥平面A1EM，∵BD∥B1D1，∴B1D1⊥平面A1EM，∵B1D1⊂平面B1CD1，∴平面A1EM⊥平面B1CD1．21．如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．【解答】证明：（1）因为AB⊥AD，EF⊥AD，且A、B、E、F四点共面，所以AB∥EF，又因为EF⊊平面ABC，AB⊆平面ABC，所以由线面平行判定定理可知：EF∥平面ABC；（2）在线段CD上取点G，连结FG、EG使得FG∥BC，则EG∥AC，因为BC⊥BD，FG∥BC，所以FG⊥BD，又因为平面ABD⊥平面BCD，所以FG⊥平面ABD，所以FG⊥AD，又因为AD⊥EF，且EF∩FG=F，所以AD⊥平面EFG，所以AD⊥EG，故AD⊥AC．3．如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）证明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C的余弦值．【解答】（1）证明：∵∠BAP=∠CDP=90°，∴PA⊥AB，PD⊥CD，∵AB∥CD，∴AB⊥PD，又∵PA∩PD=P，且PA⊂平面PAD，PD⊂平面PAD，∴AB⊥平面PAD，又AB⊂平面PAB，∴平面PAB⊥平面PAD；（2）解：∵AB∥CD，AB=CD，∴四边形ABCD为平行四边形，由（1）知AB⊥平面PAD，∴AB⊥AD，则四边形ABCD为矩形，在△APD中，由PA=PD，∠APD=90°，可得△PAD为等腰直角三角形，设PA=AB=2a，则AD=．取AD中点O，BC中点E，连接PO、OE，以O为坐标原点，分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系，则：D（），B（），P（0，0，），C（）．，，．设平面PBC的一个法向量为，由，得，取y=1，得．∵AB⊥平面PAD，AD⊂平面PAD，∴AB⊥PD，又PD⊥PA，PA∩AB=A，∴PD⊥平面PAB，则为平面PAB的一个法向量，．∴cos＜＞==．由图可知，二面角A﹣PB﹣C为钝角，∴二面角A﹣PB﹣C的余弦值为．4．如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°，E是PD的中点．（1）证明：直线CE∥平面PAB；（2）点M在棱PC 上，且直线BM与底面ABCD所成角为45°，求二面角M﹣AB﹣D的余弦值．【解答】（1）证明：取PA的中点F，连接EF，BF，因为E是PD的中点，所以EF AD，AB=BC=AD，∠BAD=∠ABC=90°，∴BC∥AD，∴BCEF是平行四边形，可得CE∥BF，BF⊂平面PAB，CE⊄平面PAB，∴直线CE∥平面PAB；（2）解：四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD，∠BAD=∠ABC=90°，E是PD的中点．取AD的中点O，M在底面ABCD上的射影N在OC上，设AD=2，则AB=BC=1，OP=，∴∠PCO=60°，直线BM与底面ABCD所成角为45°，可得：BN=MN，CN=MN，BC=1，可得：1+BN2=BN2，BN=，MN=，作NQ⊥AB于Q，连接MQ，所以∠MQN就是二面角M﹣AB﹣D的平面角，MQ==，二面角M﹣AB﹣D的余弦值为：=．5．如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．（1）证明：平面ACD⊥平面ABC；（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D﹣AE﹣C的余弦值．【解答】（1）证明：如图所示，取AC的中点O，连接BO，OD．∵△ABC是等边三角形，∴OB⊥AC．△ABD与△CBD中，AB=BD=BC，∠ABD=∠CBD，∴△ABD≌△CBD，∴AD=CD．∵△ACD是直角三角形，∴AC是斜边，∴∠ADC=90°．∴DO=AC．∴DO2+BO2=AB2=BD2．∴∠BOD=90°．∴OB⊥OD．又DO∩AC=O，∴OB⊥平面ACD．又OB⊂平面ABC，∴平面ACD⊥平面ABC．（2）解：设点D，B到平面ACE的距离分别为h D，h E．则=．∵平面AEC把四面体ABCD分成体积相等的两部分，∴===1．∴点E是BD的中点．建立如图所示的空间直角坐标系．不妨取AB=2．则O（0，0，0），A（1，0，0），C（﹣1，0，0），D（0，0，1），B（0，，0），E．=（﹣1，0，1），=，=（﹣2，0，0）．设平面ADE的法向量为=（x，y，z），则，即，取=．同理可得：平面ACE的法向量为=（0，1，）．∴cos===﹣．∴二面角D﹣AE﹣C的余弦值为．6．如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD∥平面MAC，PA=PD=，AB=4．（1）求证：M为PB的中点；（2）求二面角B﹣PD﹣A的大小；（3）求直线MC与平面BDP所成角的正弦值．【解答】（1）证明：如图，设AC∩BD=O，∵ABCD为正方形，∴O为BD的中点，连接OM，∵PD∥平面MAC，PD⊂平面PBD，平面PBD∩平面AMC=OM，∴PD∥OM，则，即M为PB的中点；（2）解：取AD中点G，∵PA=PD，∴PG⊥AD，∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，∴PG⊥平面ABCD，则PG⊥AD，连接OG，则PG⊥OG，由G是AD的中点，O是AC的中点，可得OG∥DC，则OG⊥AD．以G为坐标原点，分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系，由PA=PD=，AB=4，得D（2，0，0），A（﹣2，0，0），P（0，0，），C （2，4，0），B（﹣2，4，0），M（﹣1，2，），，．设平面PBD的一个法向量为，则由，得，取z=，得．取平面PAD的一个法向量为．∴cos＜＞==．∴二面角B﹣PD﹣A的大小为60°；（3）解：，平面BDP的一个法向量为．∴直线MC与平面BDP所成角的正弦值为|cos＜＞|=||=||=．7．如图，在三棱锥P﹣ABC中，PA⊥底面ABC，∠BAC=90°．点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2．（Ⅰ）求证：MN∥平面BDE；（Ⅱ）求二面角C﹣EM﹣N的正弦值；（Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为，求线段AH的长．【解答】（Ⅰ）证明：取AB中点F，连接MF、NF，∵M为AD中点，∴MF∥BD，∵BD⊂平面BDE，MF⊄平面BDE，∴MF∥平面BDE．∵N为BC中点，∴NF∥AC，又D、E分别为AP、PC的中点，∴DE∥AC，则NF∥DE．∵DE⊂平面BDE，NF⊄平面BDE，∴NF∥平面BDE．又MF∩NF=F．∴平面MFN∥平面BDE，则MN∥平面BDE；（Ⅱ）解：∵PA⊥底面ABC，∠BAC=90°．∴以A为原点，分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系．∵PA=AC=4，AB=2，∴A（0，0，0），B（2，0，0），C（0，4，0），M（0，0，1），N（1，2，0），E（0，2，2），则，，设平面MEN的一个法向量为，由，得，取z=2，得．由图可得平面CME的一个法向量为．∴cos＜＞=．∴二面角C﹣EM﹣N的余弦值为，则正弦值为；（Ⅲ）解：设AH=t，则H（0，0，t），，．∵直线NH与直线BE所成角的余弦值为，∴|cos＜＞|=||=||=．解得：t=或t=．∴当H与P重合时直线NH与直线BE所成角的余弦值为，此时线段AH的长为或．8．如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是的中点．（Ⅰ）设P是上的一点，且AP⊥BE，求∠CBP的大小；（Ⅱ）当AB=3，AD=2时，求二面角E﹣AG﹣C的大小．【解答】解：（Ⅰ）∵AP⊥BE，AB⊥BE，且AB，AP⊂平面ABP，AB∩AP=A，∴BE⊥平面ABP，又BP⊂平面ABP，∴BE⊥BP，又∠EBC=120°，因此∠CBP=30°；（Ⅱ）解法一、取的中点H，连接EH，GH，CH，∵∠EBC=120°，∴四边形BECH为菱形，∴AE=GE=AC=GC=．取AG中点M，连接EM，CM，EC，则EM⊥AG，CM⊥AG，∴∠EMC为所求二面角的平面角．又AM=1，∴EM=CM=．在△BEC中，由于∠EBC=120°，由余弦定理得：EC2=22+22﹣2×2×2×cos120°=12，∴，因此△EMC为等边三角形，故所求的角为60°．解法二、以B为坐标原点，分别以BE，BP，BA所在直线为x，y，z轴建立空间直角坐标系．由题意得：A（0，0，3），E（2，0，0），G（1，，3），C（﹣1，，0），故，，．设为平面AEG的一个法向量，由，得，取z1=2，得；设为平面ACG的一个法向量，由，可得，取z2=﹣2，得．∴cos＜＞=．∴二面角E﹣AG﹣C的大小为60°．。

绝密★启用前2017年普通高等学校招生全国统一考试（江苏卷）数学I注意事项考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷共4页，包含非选择题（第1题 ~ 第20题，共20题）.本卷满分为160分，考试时间为120分钟。

考试结束后，请将本试卷和答题卡一并交回。

2. 答题前，请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。

3.请认真核对监考员在答题上所粘贴的条形码上的姓名、准考证号与本人是否相符。

4.作答试题，必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效。

5.如需改动，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗一、填空题：本大题共14小题，每小题5分，共计70分，请把答案填写在答题卡相应位置上 1.已知集合{}=1,2A ，{}=+2,3B a a，若AB ={1}则实数a 的值为________2.已知复数z=（1+i ）（1+2i ）,其中i 是虚数单位，则z 的模是__________3.某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200,400,300,100件，为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取 件.4.右图是一个算法流程图，若输入x 的值为116，则输出的y 的值是 .5.若tan 1-=46πα⎛⎫ ⎪⎝⎭,则tan α= .6.如图，在圆柱O 1 O 2 内有一个球O ，该球与圆柱的上、下底面及母线均相切。

记圆柱O 1 O 2 的体积为V 1 ,球O 的体积为V 2 ，则12V V 的值是7.记函数()f x =的定义域为D.在区间[-4,5]上随机取一个数x ，则x ∈ D 的概率是8.在平面直角坐标系xoy 中 ,双曲线2213x y -= 的右准线与它的两条渐近线分别交于点P,Q ，其焦点是F 1 , F 2 ,则四边形F 1 P F 2 Q 的面积是9.等比数列{}na 的各项均为实数，其前n 项的和为S n，已知36763，44SS ==， 则8a =10.某公司一年购买某种货物600吨，每次购买x 吨，运费为6万元/次，一年的总存储费用为4x 万元，要使一年的总运费与总存储费之和最小，则x 的值是11.已知函数()3xx12x+e -e-f x =x ，其中e 是自然数对数的底数，若()()2a-1+2a ≤f f 0，则实数a 的取值范围是 。

绝密★启用前2017年普通高等学校招生全国统一考试（浙江卷）数学【试卷点评】 选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合{|11}P x x =-<<，{02}Q x =<<，那么P Q =A ．(1,2)-B ．(0,1)C ．(1,0)-D ．(1,2)【答案】A【考点】集合运算【名师点睛】对于集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图处理．2．椭圆22194x y +=的离心率是A 13B 5C ．23D ．59【答案】B 【解析】 试题分析：945e -B ． 【考点】 椭圆的简单几何性质【名师点睛】解决椭圆和双曲线的离心率的求值及范围问题，其关键就是确立一个关于,,a b c 的方程或不等式，再根据,,a b c 的关系消掉b 得到,a c 的关系式，建立关于,,a b c 的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等．3．某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是（第3题图）A ．12π+ B ．32π+ C ．312π+ D ．332π+ 【答案】A【考点】 三视图【名师点睛】思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽．由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整． 4．若x ，y 满足约束条件03020x x y x y ≥⎧⎪+-≥⎨⎪-≤⎩，则2z x y =+的取值范围是A ．[0，6]B ．[0，4]C ．[6，)+∞D ．[4，)+∞【答案】D 【解析】试题分析：如图，可行域为一开放区域，所以直线过点(2,1)时取最小值4，无最大值，选D ．【考点】 简单线性规划【名师点睛】本题主要考查线性规划问题，首先由不等式组作出相应的可行域，作图时，可将不等式0Ax By C ++≥转化为y kx b ≤+（或y kx b ≥+），“≤”取下方，“≥”取上方，并明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线，其次确定目标函数的几何意义，是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等，最后结合图形确定目标函数最值取法、值域范围．5．若函数f (x )=x 2+ ax +b 在区间[0，1]上的最大值是M ，最小值是m ，则M – mA ．与a 有关，且与b 有关B ．与a 有关，但与b 无关C ．与a 无关，且与b 无关D ．与a 无关，但与b 有关【答案】B【考点】二次函数的最值【名师点睛】对于二次函数的最值或值域问题，通常先判断函数图象对称轴与所给自变量闭区间的关系，结合图象，当函数图象开口向上时，若对称轴在区间的左边，则函数在所给区间内单调递增；若对称轴在区间的右边，则函数在所给区间内单调递减；若对称轴在区间内，则函数图象顶点的纵坐标为最小值，区间端点距离对称轴较远的一端取得函数的最大值．6．已知等差数列{a n }的公差为d ，前n 项和为S n ，则“d >0”是“S 4 + S 6>2S 5”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】C 【解析】试题分析：由46511210212(510)S S S a d a d d +-=+-+=，可知当0d >时，有46520S S S +->，即4652S S S +>，反之，若4652S S S +>，则0d >，所以“d >0”是“S 4 + S 6>2S 5”的充要条件，选C ．【考点】 等差数列、充分必要性【名师点睛】本题考查等差数列的前n 项和公式，通过套入公式与简单运算，可知4652S S S d +-=， 结合充分必要性的判断，若p q ⇒，则p 是q 的充分条件，若p q ⇐，则p 是q 的必要条件，该题“0d >”⇔“46520S S S +->”，故互为充要条件．7．函数y=f (x )的导函数()y f x '=的图象如图所示，则函数y=f (x )的图象可能是（第7题图）【答案】D【考点】 导函数的图象【名师点睛】本题主要考查导数图象与原函数图象的关系：若导函数图象与x 轴的交点为0x ，且图象在0x 两侧附近连续分布于x 轴上下方，则0x 为原函数单调性的拐点，运用导数知识来讨论函数单调性时，由导函数()f'x 的正负，得出原函数()f x 的单调区间．8．已知随机变量i ξ满足P （i ξ=1）=p i ，P （i ξ=0）=1–p i ，i =1，2． 若0<p 1<p 2<12，则 A ．1()E ξ<2()E ξ，1()D ξ<2()D ξ B ．1()E ξ<2()E ξ，1()D ξ>2()D ξ C ．1()E ξ>2()E ξ，1()D ξ<2()D ξD ．1()E ξ>2()E ξ，1()D ξ>2()D ξ【答案】A 【解析】试题分析：∵1122(),()E p E p ξξ==，∴12()()E E ξξ<，∵111222()(1),()(1)D p p D p p ξξ=-=-，∴121212()()()(1)0D D p p p p ξξ-=---<，故选A ．【考点】 两点分布【名师点睛】求离散型随机变量的分布列，首先要根据具体情况确定X 的取值情况，然后利用排列，组合与概率知识求出X 取各个值时的概率．对于服从某些特殊分布的随机变量，其分布列可以直接应用公式给出，其中超几何分布描述的是不放回抽样问题，随机变量为抽到的某类个体的个数．由已知本题随机变量iξ服从两点分布，由两点分布数学期望与方差的公式可得A 正确．9．如图，已知正四面体D –ABC （所有棱长均相等的三棱锥），P ，Q ，R 分别为AB ，BC ，CA 上的点，AP=PB ，2BQ CRQC RA==，分别记二面角D –PR –Q ，D –PQ –R ，D –QR –P 的平面角为α，β，γ，则（第9题图）A ．γ<α<βB ．α<γ<βC ．α<β<γD ．β<γ<α【答案】B【考点】 空间角（二面角）【名师点睛】立体几何是高中数学中的重要内容，也是高考重点考查的考点与热点．这类问题的设置一般有线面位置关系的证明与角度距离的计算等两类问题．解答第一类问题时一般要借助线面平行与垂直的判定定理进行；解答第二类问题时先建立空间直角坐标系，运用空间向量的坐标形式及数量积公式进行求解．10．如图，已知平面四边形ABCD ，AB ⊥BC ，AB ＝BC ＝AD ＝2，CD ＝3，AC 与BD 交于点O ，记1·I OA OB ＝，2·I OB OC ＝，3·I OC OD ＝，则（第10题图）A ．123I I I <<B ．132I I I <<C ．312I I I <<D ．213I I I <<【答案】C【考点】 平面向量的数量积运算【名师点睛】平面向量的计算问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式，涉及几何图形的问题，先建立适当的平面直角坐标系，可起到化繁为简的妙用．利用向量夹角公式、模公式及向量垂直的充要条件，可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决．列出方程组求解未知数．本题通过所给条件结合数量积运算，易得90AOB COD ∠=∠>，由AB ＝BC ＝AD ＝2，CD ＝3，可求得OA OC <，OB OD <，进而得到312I I I <<． 非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

2017年高考数学试题分项版—立体几何（解析版）一、选择题1．(2017·全国Ⅰ文，6)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q 为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是()1．【答案】A【解析】A项，作如图①所示的辅助线，其中D为BC的中点，则QD∥AB.∵QD∩平面MNQ＝Q，∴QD与平面MNQ相交，∴直线AB与平面MNQ相交；B项，作如图②所示的辅助线，则AB∥CD，CD∥MQ，∴AB∥MQ，又AB⊄平面MNQ，MQ⊂平面MNQ，∴AB∥平面MNQ；C项，作如图③所示的辅助线，则AB∥CD，CD∥MQ，∴AB∥MQ，又AB⊄平面MNQ，MQ⊂平面MNQ，∴AB∥平面MNQ；D项，作如图④所示的辅助线，则AB∥CD，CD∥NQ，∴AB∥NQ，又AB ⊄平面MNQ ，NQ ⊂平面MNQ ，∴AB ∥平面MNQ .故选A.2．(2017·全国Ⅱ文，6)如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为( )A ．90πB ．63πC ．42πD ．36π2．【答案】B【解析】方法一 (割补法)如图所示，由几何体的三视图，可知该几何体是一个圆柱被截去上面虚线部分所得．将圆柱补全，并将圆柱体从点A 处水平分成上下两部分．由图可知，该几何体的体积等于下部分圆柱的体积加上上部分圆柱体积的12，所以该几何体的体积V ＝π×32×4＋π×32×6×12＝63π.故选B.方法二 (估值法)由题意，知12V 圆柱＜V 几何体＜V 圆柱． 又V 圆柱＝π×32×10＝90π，∴45π＜V 几何体＜90π.观察选项可知只有63π符合．故选B.3．(2017·全国Ⅲ文，9)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A ．πB ．3π4C ．π2D ．π43．【答案】B【解析】设圆柱的底面半径为r ，球的半径为R ，且R ＝1，由圆柱两个底面的圆周在同一个球的球面上可知，r ，R 及圆柱的高的一半构成直角三角形．∴r ＝ 1－⎝⎛⎭⎫122＝32.∴圆柱的体积为V ＝πr 2h ＝34π×1＝3π4. 故选B.4．(2017·全国Ⅲ文，10)在正方体ABCDA 1B 1C 1D 1中，E 为棱CD 的中点，则( )A ．A 1E ⊥DC 1B ．A 1E ⊥BDC ．A 1E ⊥BC 1D ．A 1E ⊥AC4．【答案】C【解析】方法一 如图，∵A 1E 在平面ABCD 上的投影为AE ，而AE 不与AC ，BD 垂直，∴B ，D 错；∵A 1E 在平面BCC 1B 1上的投影为B 1C ，且B 1C ⊥BC 1，∴A 1E ⊥BC 1，故C 正确；(证明：由条件易知，BC 1⊥B 1C ，BC 1⊥CE ，又CE ∩B 1C ＝C ，∴BC 1⊥平面CEA 1B 1. 又A 1E ⊂平面CEA 1B 1，∴A 1E ⊥BC 1)∵A 1E 在平面DCC 1D 1上的投影为D 1E ，而D 1E 不与DC 1垂直，故A 错．故选C.方法二 (空间向量法)建立如图所示的空间直角坐标系，设正方体的棱长为1，则A (1,0,0)，B (1,1,0)，C (0,1,0)，D (0,0,0)，A 1(1,0,1)，C 1(0,1,1)，E ⎝⎛⎭⎫0，12，0，∴A 1E →＝⎝⎛⎭⎫－1，12，－1，DC 1→＝(0,1,1)，BD →＝(－1，－1，0)，BC 1→＝(－1,0,1)，AC →＝(－1,1,0)，∴A 1E →·DC 1→≠0，A 1E →·BD →≠0，A 1E →·BC 1→＝0，A 1E →·AC →≠0，∴A 1E ⊥BC 1.故选C.5．(2017·北京文，6)某三棱锥的三视图如图所示，则该三棱锥的体积为( )A ．60B ．30C ．20D ．105．【答案】D【解析】由三视图画出如图所示的三棱锥P －ACD ，过点P 作PB ⊥平面ACD 于点B ，连接BA ，BD ，BC ，根据三视图可知，底面ABCD 是矩形，AD ＝5，CD ＝3，PB ＝4，所以V 三棱锥P ACD ＝13×12×3×5×4＝10. 故选D.6.(2017·浙江，3)某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm 3)是( )A ．π2＋1 B ．π2＋3 C ．3π2＋1 D ．3π2＋3 6.【答案】A【解析】由几何体的三视图可知，该几何体是一个底面半径为1，高为3的圆锥的一半与一个底面为直角边长是2的等腰直角三角形，高为3的三棱锥的组合体，∴该几何体体积为V ＝13×12π×12×3＋13×12×2×2×3＝π2＋1. 故选A.7．(2017·浙江，9)如图，已知正四面体DABC (所有棱长均相等的三棱锥)，P ，Q ，R 分别为AB ，BC ，CA 上的点，AP ＝PB ，BQ QC ＝CR RA＝2，分别记二面角DPRQ ，DPQR ，DQRP 的平面角为α，β，γ，则( )A ．γ＜α＜βB ．α＜γ＜βC ．α＜β＜γD ．β＜γ＜α7．【答案】B【解析】如图①，作出点D 在底面ABC 上的射影O ，过点O 分别作PR ，PQ ，QR 的垂线OE ，OF ，OG ，连接DE ，DF ，DG ，则α＝∠DEO ，β＝∠DFO ，γ＝∠DGO .由图可知它们的对边都是DO ，∴只需比较EO ，FO ，GO 的大小即可．如图②，在AB 边上取点P ′，使AP ′＝2P ′B ，连接OQ ，OR ，则O 为△QRP ′的中心． 设点O 到△QRP ′三边的距离为a ，则OG ＝a ，OF ＝OQ ·sin ∠OQF ＜OQ ·sin ∠OQP ′＝a ，OE ＝OR ·sin ∠ORE ＞OR ·sin ∠ORP ′＝a ，∴OF ＜OG ＜OE ，∴OD tan β＜OD tan γ＜OD tan α， ∴α＜γ＜β.故选B.8．(2017·全国Ⅰ理，7)某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为( )A ．10B ．12C ．14D ．168．【答案】B【解析】观察三视图可知，该多面体是由直三棱柱和三棱锥组合而成的，且直三棱柱的底面是直角边长为2的等腰直角三角形，侧棱长为2.三棱锥的底面是直角边长为2的等腰直角三角形，高为2，如图所示．因此该多面体各个面中有两个梯形，且这两个梯形全等，梯形的上底长为2，下底长为4，高为2，故这两个梯形的面积之和为2×12×(2＋4)×2＝12.故选B.9．(2017·全国Ⅱ理，4)如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为( )A ．90πB ．63πC ．42πD ．36π9．【答案】B【解析】方法一 (割补法)由几何体的三视图可知，该几何体是一个圆柱截去上面虚线部分所得，如图所示．将圆柱补全，并将圆柱从点A 处水平分成上下两部分．由图可知，该几何体的体积等于下部分圆柱的体积加上上部分圆柱体积的12，所以该几何体的体积V ＝π×32×4＋π×32×6×12＝63π.故选B.方法二 (估值法)由题意知，12V 圆柱<V 几何体<V 圆柱，又V 圆柱＝π×32×10＝90π，∴45π<V 几何体<90π.观察选项可知只有63π符合．故选B.10．(2017·全国Ⅱ理，10)已知直三棱柱ABCA 1B 1C 1中，∠ABC ＝120°，AB ＝2，BC ＝CC 1＝1，则异面直线AB 1与BC 1所成角的余弦值为( ) A.32 B.155 C.105 D.3310．【答案】C【解析】方法一 将直三棱柱ABC －A 1B 1C 1补形为直四棱柱ABCD －A 1B 1C 1D 1，如图①所示，连接AD 1，B 1D 1，BD .由题意知∠ABC ＝120°，AB ＝2，BC ＝CC 1＝1， 所以AD 1＝BC 1＝2，AB 1＝5，∠DAB ＝60°.在△ABD 中，由余弦定理知BD 2＝22＋12－2×2×1×cos 60°＝3，所以BD ＝3，所以B 1D 1＝ 3. 又AB 1与AD 1所成的角即为AB 1与BC 1所成的角θ，所以cos θ＝AB 21＋AD 21－B 1D 212×AB 1×AD 1＝5＋2－32×5×2＝105. 故选C.方法二 以B 1为坐标原点，B 1C 1所在的直线为x 轴，垂直于B 1C 1的直线为y 轴，BB 1所在的直线为z 轴建立空间直角坐标系，如图②所示．由已知条件知B 1(0,0,0)，B (0,0,1)，C 1(1,0,0)，A (－1，3，1)，则BC 1→＝(1,0，－1)，AB 1→＝(1，－3，－1)．所以cos 〈AB 1→，BC 1→〉＝AB 1→·BC 1→|AB 1→||BC 1→|＝25×2＝105. 所以异面直线AB 1与BC 1所成的角的余弦值为105. 故选C.11．(2017·全国Ⅲ理，8)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( ) A ．πB.3π4C.π2D.π4 11．【答案】B【解析】设圆柱的底面半径为r ，球的半径为R ，且R ＝1，由圆柱两个底面的圆周在同一个球的球面上可知，r ，R 及圆柱的高的一半构成直角三角形．∴r ＝12－⎝⎛⎭⎫122＝32.∴圆柱的体积为V ＝πr 2h ＝π×⎝⎛⎭⎫322×1＝3π4. 故选B.12．(2017·北京理，7)某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为( )A ．3 2B ．2 3C ．2 2D ．212．【答案】B 【解析】在正方体中还原该四棱锥，如图所示，可知SD 为该四棱锥的最长棱．由三视图可知正方体的棱长为2，故SD ＝22＋22＋22＝2 3.故选B.二、填空题1．(2017·全国Ⅰ文，16)已知三棱锥SABC 的所有顶点都在球O 的球面上，SC 是球O 的直径．若平面SCA ⊥平面SCB ，SA ＝AC ，SB ＝BC ，三棱锥SABC 的体积为9，则球O 的表面积为________．1．【答案】36π【解析】如图，连接OA ，OB .由SA ＝AC ，SB ＝BC ，SC 为球O 的直径知，OA ⊥SC ，OB ⊥SC .由平面SCA ⊥平面SCB ，平面SCA ∩平面SCB ＝SC ，OA ⊥SC 知，OA ⊥平面SCB . 设球O 的半径为r ，则OA ＝OB ＝r ，SC ＝2r ，∴三棱锥S －ABC 的体积V ＝13×(12SC ·OB )·OA ＝r 33， 即r 33＝9，∴r ＝3，∴S 球表＝4πr 2＝36π. 2．(2017·全国Ⅱ文，15)长方体的长、宽、高分别为3,2,1，其顶点都在球O 的球面上，则球O 的表面积为________．2．【答案】14π【解析】∵长方体的顶点都在球O 的球面上，∴长方体的体对角线的长度就是其外接球的直径．设球的半径为R ，则2R ＝32＋22＋12＝14.∴球O 的表面积为S ＝4πR 2＝4π×⎝⎛⎭⎫1422＝14π. 3．(2017·天津文，11)已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为________．3．【答案】9π2【解析】设正方体的棱长为a ，则6a 2＝18，∴a ＝ 3.设球的半径为R ，则由题意知2R ＝a 2＋a 2＋a 2＝3，∴R ＝32. 故球的体积V ＝43πR 3＝43π×⎝⎛⎭⎫323＝9π2. 4．(2017·山东文，13)由一个长方体和两个14圆柱构成的几何体的三视图如图，则该几何体的体积为________．4．【答案】2＋π2【解析】该几何体由一个长、宽、高分别为2,1,1的长方体和两个半径为1，高为1的14圆柱体构成，∴V ＝2×1×1＋2×14×π×12×1＝2＋π2. 5.(2017·浙江，11)我国古代数学家刘徽创立的“割圆术”可以估算圆周率π，理论上能把π的值计算到任意精度．祖冲之继承并发展了“割圆术”，将π的值精确到小数点后七位，其结果领先世界一千多年，“割圆术”的第一步是计算单位圆内接正六边形的面积S 6，S 6＝________. 5．【答案】332【解析】作出单位圆的内接正六边形，如图，则OA ＝OB ＝AB ＝1，S 6＝6S △OAB ＝6×12×1×32＝332.6．(2017·江苏，6)如图，在圆柱O 1O 2内有一个球O ，该球与圆柱的上、下面及母线均相切．记圆柱O 1O 2的体积为V 1，球O 的体积为V 2，则V 1V 2的值是________．6．【答案】32【解析】设球O 的半径为R ，∵球O 与圆柱O 1O 2的上、下底面及母线均相切， ∴圆柱O 1O 2的高为2R ，底面半径为R . ∴V 1V 2＝πR 2·2R 43πR 3＝32. 7．(2017·全国Ⅰ理，16)如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O .D ，E ，F 为圆O 上的点，△DBC ，△ECA ，△F AB 分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ，CA ，AB 为折痕折起△DBC ，△ECA ，△F AB ，使得D ，E ，F 重合，得到三棱锥．当△ABC 的边长变化时，所得三棱锥体积(单位：cm 3)的最大值为________．7．【答案】415【解析】如图，连接OD ，交BC 于点G ，由题意知，OD ⊥BC ，OG ＝36BC . 设OG ＝x ，x ∈⎝⎛⎭⎫0，52， 则BC ＝23x ，DG ＝5－x ， 三棱锥的高h ＝DG 2－OG 2 ＝25－10x ＋x 2－x 2＝25－10x ，S △ABC ＝12×23x ×3x ＝33x 2，则三棱锥的体积V ＝13S △ABC ·h ＝3x 2·25－10x ＝3·25x 4－10x 5.令f (x )＝25x 4－10x 5，x ∈⎝⎛⎭⎫0，52，则f ′(x )＝100x 3－50x 4. 令f ′(x )＝0，得x ＝2.当x ∈(0,2)时，f ′(x )>0，f (x )单调递增，当x ∈⎝⎛⎭⎫2，52时，f ′(x )<0，f (x )单调递减，故当x ＝2时，f (x )取得最大值80，则V ≤3×80＝415. 所以三棱锥体积的最大值为415 cm 3.8．(2017·全国Ⅲ理，16)a ，b 为空间中两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以直线AC 为旋转轴旋转，有下列结论： ①当直线AB 与a 成60°角时，AB 与b 成30°角； ②当直线AB 与a 成60°角时，AB 与b 成60°角； ③直线AB 与a 所成角的最小值为45°； ④直线AB 与a 所成角的最大值为60°.其中正确的是________．(填写所有正确结论的编号) 8．【答案】②③【解析】依题意建立如图所示的空间直角坐标系，设等腰直角三角形ABC 的直角边长为1.由题意知，点B 在平面xOy 中形成的轨迹是以C 为圆心，1为半径的圆．设直线a 的方向向量为a ＝(0,1,0)，直线b 的方向向量为b ＝(1,0,0)，CB →以Ox 轴为始边沿逆时针方向旋转的旋转角为θ，θ∈[)0，2π，则B (cos θ，sin θ，0)， ∴AB →＝(cos θ，sin θ，－1)，|AB →|＝ 2. 设直线AB 与a 所成的夹角为α， 则cos α＝|AB →·a ||a ||AB →|＝22|sin θ|∈⎣⎡⎦⎤0，22，∴45°≤α≤90°，∴③正确，④错误； 设直线AB 与b 所成的夹角为β， 则cos β＝|AB →·b ||b ||AB →|＝22|cos θ|.当直线AB 与a 的夹角为60°，即α＝60°时， 则|sin θ|＝2cos α＝2cos 60°＝22， ∴|cos θ|＝22，∴cos β＝22|cos θ|＝12. ∵45°≤β≤90°，∴β＝60°，即直线AB 与b 的夹角为60°. ∴②正确，①错误．9．(2017·天津理，10)已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为________． 9．【答案】92π【解析】设正方体棱长为a ，则6a 2＝18，∴a ＝ 3.设球的半径为R ，则由题意知2R ＝a 2＋a 2＋a 2＝3，∴R ＝32.故球的体积V ＝43πR 3＝43π×⎝⎛⎭⎫323＝92π.10．(2017·山东理，13)由一个长方体和两个14圆柱体构成的几何体的三视图如下，则该几何体的体积为________．10．【答案】2＋π2【解析】该几何体由一个长、宽、高分别为2,1,1的长方体和两个底面半径为1，高为1的四分之一圆柱体构成，∴V ＝2×1×1＋2×14×π×12×1＝2＋π2.三、解答题1．(2017·全国Ⅰ文，18)如图，在四棱锥P ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°.(1)证明：平面P AB ⊥平面P AD ；(2)若P A ＝PD ＝AB ＝DC ，∠APD ＝90°，且四棱锥P ABCD 的体积为83，求该四棱锥的侧面积．1．(1)证明 由已知∠BAP ＝∠CDP ＝90°， 得AB ⊥P A ，CD ⊥PD .由于AB ∥CD ，故AB ⊥PD ，从而AB ⊥平面P AD . 又AB ⊂平面P AB ， 所以平面P AB ⊥平面P AD .(2)解 如图，在平面P AD 内作PE ⊥AD ，垂足为E .由(1)知，AB ⊥平面P AD ，故AB ⊥PE ，AB ⊥AD ， 所以PE ⊥平面ABCD .设AB ＝x ，则由已知可得AD ＝2x ，PE ＝22x ， 故四棱锥P ABCD 的体积V P ABCD ＝13AB ·AD ·PE ＝13x 3.由题设得13x 3＝83，故x ＝2.从而结合已知可得P A ＝PD ＝AB ＝DC ＝2，AD ＝BC ＝22，PB ＝PC ＝22， 可得四棱锥P ABCD 的侧面积为12P A ·PD ＋12P A ·AB ＋12PD ·DC ＋12BC 2sin 60°＝6＋2 3. 2．(2017·全国Ⅱ文，18)如图，四棱锥P ABCD 中，侧面P AD 为等边三角形且垂直于底面ABCD ，AB ＝BC ＝12AD ，∠BAD ＝∠ABC ＝90°.(1)证明：直线BC ∥平面P AD ；(2)若△PCD 的面积为27，求四棱锥P ABCD 的体积．2．(1)证明 在平面ABCD 内，因为∠BAD ＝∠ABC ＝90°，所以BC ∥AD . 又BC ⊄平面P AD ，AD ⊂平面P AD ， 故BC ∥平面P AD .(2)解 如图，取AD 的中点M ，连接PM ，CM .由AB ＝BC ＝12AD 及BC ∥AD ，∠ABC ＝90°得四边形ABCM 为正方形，则CM ⊥AD .因为侧面P AD 为等边三角形且垂直于底面ABCD ，平面P AD ∩平面ABCD ＝AD ，所以PM ⊥AD ，PM ⊥底面ABCD .因为CM ⊂底面ABCD ，所以PM ⊥CM . 设BC ＝x ，则CM ＝x ，CD ＝2x ，PM ＝3x ，PC ＝PD ＝2x . 取CD 的中点N ，连接PN ，则PN ⊥CD ， 所以PN ＝142x . 因为△PCD 的面积为27， 所以12×2x ×142x ＝27，解得x ＝－2(舍去)或x ＝2.于是AB ＝BC ＝2，AD ＝4，PM ＝2 3.所以四棱锥P ABCD 的体积V ＝13×2(2＋4)2×23＝4 3.3．(2017·全国Ⅲ文，19)如图，四面体ABCD 中，△ABC 是正三角形，AD ＝CD .(1)证明：AC ⊥BD ；(2)已知△ACD 是直角三角形，AB ＝BD .若E 为棱BD 上与D 不重合的点，且AE ⊥EC ，求四面体ABCE 与四面体ACDE 的体积比．3．(1)证明 如图，取AC 的中点O ，连接DO ，BO . 因为AD ＝CD ，所以AC ⊥DO . 又由于△ABC 是正三角形， 所以AC ⊥BO . 又DO ∩OB ＝O ，所以AC ⊥平面DOB ，故AC ⊥BD . (2)解 连接EO .由(1)及题设知∠ADC ＝90°，所以DO ＝AO . 在Rt △AOB 中，BO 2＋AO 2＝AB 2.又AB ＝BD ，所以BO 2＋DO 2＝BO 2＋AO 2＝AB 2＝BD 2，故∠DOB ＝90°. 由题设知△AEC 为直角三角形，所以EO ＝12AC .又△ABC 是正三角形，且AB ＝BD ，所以EO ＝12BD .故E 为BD 的中点，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，四面体ABCE的体积为四面体ABCD 的体积的12，即四面体ABCE 与四面体ACDE 的体积之比为1∶1.4．(2017·北京文，18)如图，在三棱锥P －ABC 中，P A ⊥AB ，P A ⊥BC ，AB ⊥BC ，P A ＝AB ＝BC ＝2，D 为线段AC 的中点，E 为线段PC 上一点．(1)求证：P A ⊥BD ；(2)求证：平面BDE ⊥平面P AC ；(3)当P A ∥平面BDE 时，求三棱锥E －BCD 的体积． 4．(1)证明 因为P A ⊥AB ，P A ⊥BC ，AB ∩BC ＝B ， 所以P A ⊥平面ABC .又因为BD ⊂平面ABC ，所以P A ⊥BD .(2)证明 因为AB ＝BC ，D 是AC 的中点，所以BD ⊥AC . 由(1)知，P A ⊥BD ， 又P A ∩AC ＝A ， 所以BD ⊥平面P AC . 所以平面BDE ⊥平面P AC .(3)解 因为P A ∥平面BDE ，平面P AC ∩平面BDE ＝DE ，所以P A ∥DE . 因为D 为AC 的中点，所以DE ＝12P A ＝1，BD ＝DC ＝ 2.由(1)知，P A ⊥平面ABC ，所以DE ⊥平面ABC ， 所以三棱锥E －BCD 的体积V ＝16BD ·DC ·DE ＝13.5．(2017·天津文，17)如图，在四棱锥P ABCD 中，AD ⊥平面PDC ，AD ∥BC ，PD ⊥PB ，AD ＝1，BC ＝3，CD ＝4，PD ＝2.(1)求异面直线AP 与BC 所成角的余弦值； (2)求证：PD ⊥平面PBC ；(3)求直线AB 与平面PBC 所成角的正弦值．5．(1)解 由已知AD ∥BC ，故∠DAP 或其补角即为异面直线AP 与BC 所成的角． 因为AD ⊥平面PDC ，直线PD ⊂平面PDC ，所以AD ⊥PD . 在Rt △PDA 中，由已知，得AP ＝AD 2＋PD 2＝5， 故cos ∠DAP ＝AD AP ＝55.所以异面直线AP 与BC 所成角的余弦值为55. (2)证明 由(1)知AD ⊥PD . 又因为BC ∥AD ，所以PD ⊥BC .又PD ⊥PB ，PB ∩BC ＝B ，所以PD ⊥平面PBC .(3)解 如图，过点D 作DF ∥AB ，交BC 于点F ，连接PF ，则DF 与平面PBC 所成的角等于AB 与平面PBC 所成的角．因为PD ⊥平面PBC ，所以PF 为DF 在平面PBC 上的射影，所以∠DFP 为直线DF 和平面PBC 所成的角．由于AD ∥BC ，DF ∥AB ，故BF ＝AD ＝1. 由已知，得CF ＝BC －BF ＝2. 又AD ⊥DC ，所以BC ⊥DC .在Rt △DCF 中，可得DF ＝CD 2＋CF 2＝25， 在Rt △DPF 中，可得sin ∠DFP ＝PD DF ＝55.所以直线AB 与平面PBC 所成角的正弦值为55. 6．(2017·山东文，18)由四棱柱ABCD －A 1B 1C 1D 1截去三棱锥C 1－B 1CD 1后得到的几何体如图所示．四边形ABCD 为正方形，O 为AC 与BD 的交点，E 为AD 的中点，A 1E ⊥平面ABCD .(1)证明：A 1O ∥平面B 1CD 1；(2)设M 是OD 的中点，证明：平面A 1EM ⊥平面B 1CD 1. 6．证明 (1)取B 1D 1的中点O 1，连接CO 1，A 1O 1， 由于ABCD －A 1B 1C 1D 1是四棱柱， 所以A 1O 1∥OC ，A 1O 1＝OC ，因此四边形A 1OCO 1为平行四边形，所以A 1O ∥O 1C . 又O 1C ⊂平面B 1CD 1，A 1O ⊄平面B 1CD 1， 所以A 1O ∥平面B 1CD 1.(2)因为AC ⊥BD ，E ，M 分别为AD 和OD 的中点， 所以EM ⊥BD .又A 1E ⊥平面ABCD ，BD ⊂平面ABCD ， 所以A 1E ⊥BD .因为B 1D 1∥BD ，所以EM ⊥B 1D 1，A 1E ⊥B 1D 1. 又A 1E ，EM ⊂平面A 1EM ，A 1E ∩EM ＝E ，所以B 1D 1⊥平面A 1EM . 又B 1D 1⊂平面B 1CD 1， 所以平面A 1EM ⊥平面B 1CD 1.7．(2017·浙江，19)如图，已知四棱锥P ABCD ，△P AD 是以AD 为斜边的等腰直角三角形，BC ∥AD ，CD ⊥AD ，PC ＝AD ＝2DC ＝2CB ，E 为PD 的中点．(1)证明：CE ∥平面P AB ；(2)求直线CE 与平面PBC 所成角的正弦值． 7．(1)证明 如图，设P A 中点为F ，连接EF ，FB .因为E ，F 分别为PD ，P A 中点， 所以EF ∥AD 且EF ＝12AD ，又因为BC ∥AD ，BC ＝12AD ，所以EF ∥BC 且EF ＝BC ，所以四边形BCEF 为平行四边形，所以CE ∥BF . 因为BF ⊂平面P AB ，CE ⊄平面P AB ， 因此CE ∥平面P AB .(2)解 分别取BC ，AD 的中点为M ，N ， 连接PN 交EF 于点Q ，连接MQ .因为E ，F ，N 分别是PD ，P A ，AD 的中点， 所以Q 为EF 中点，在平行四边形BCEF 中，MQ ∥CE . 由△P AD 为等腰直角三角形得PN ⊥AD .由DC ⊥AD ，BC ∥AD ，BC ＝12AD ，N 是AD 的中点得BN ⊥AD .所以AD ⊥平面PBN .由BC ∥AD 得BC ⊥平面PBN ， 那么平面PBC ⊥平面PBN .过点Q 作PB 的垂线，垂足为H ，连接MH .MH 是MQ 在平面PBC 上的射影，所以∠QMH 是直线CE 与平面PBC 所成的角． 设CD ＝1.在△PCD 中，由PC ＝2，CD ＝1，PD ＝2得CE ＝2， 在△PBN 中，由PN ＝BN ＝1，PB ＝3得QH ＝14，在Rt △MQH 中，QH ＝14，MQ ＝2，所以sin ∠QMH ＝28， 所以直线CE 与平面PBC 所成角的正弦值是28. 8．(2017·江苏，15)如图，在三棱锥ABCD 中，AB ⊥AD ，BC ⊥BD ，平面ABD ⊥平面BCD ，点E ，F (E 与A ，D 不重合)分别在棱AD ，BD 上，且EF ⊥AD .求证：(1)EF ∥平面ABC ； (2)AD ⊥AC .8．证明 (1)在平面ABD 内，因为AB ⊥AD ，EF ⊥AD ， 则AB ∥EF .又因为EF ⊄平面ABC ，AB ⊂平面ABC ， 所以EF ∥平面ABC .(2)因为平面ABD ⊥平面BCD ，平面ABD ∩平面BCD ＝BD ，BC ⊂平面BCD ，BC ⊥BD ， 所以BC ⊥平面ABD .因为AD ⊂平面ABD ，所以BC ⊥AD .又AB ⊥AD ，BC ∩AB ＝B ，AB ⊂平面ABC ，BC ⊂平面ABC ， 所以AD ⊥平面ABC .又因为AC ⊂平面ABC ，所以AD ⊥AC .9．(2017·江苏，18)如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32 cm ，容器Ⅰ的底面对角线AC 的长为107 cm ，容器Ⅱ的两底面对角线EG ，E 1G 1的长分别为14 cm 和62 cm.分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12 cm.现有一根玻璃棒l ，其长度为40 cm.(容器厚度、玻璃棒粗细均忽略不计)．(1)将l 放在容器Ⅰ中，l 的一端置于点A 处，另一端置于侧棱CC 1上，求l 没入水中部分的长度；(2)将l 放在容器Ⅱ中，l 的一端置于点E 处，另一端置于侧棱GG 1上，求l 没入水中部分的长度． 9．解 (1)由正棱柱的定义，CC 1⊥平面ABCD ，所以平面A 1ACC 1⊥平面ABCD ，CC 1⊥AC ，如图①，记玻璃棒的另一端落在CC 1上点M 处．①因为AC ＝107，AM ＝40，所以MC ＝402－1072＝30，从而sin ∠MAC ＝34. 记AM 与水面的交点为P 1，过P 1作P 1Q 1⊥AC ，Q 1为垂足，则P 1Q 1⊥平面ABCD ，故P 1Q 1＝12，从而AP 1＝P 1Q 1sin ∠MAC＝16. 答 玻璃棒l 没入水中的部分的长度为16 cm.(如果将“没入水中部分”理解为“水面以上部分”，则结果为24 cm)(2)如图②，O ，O 1是正棱台的两底面中心．②由正棱台的定义，OO 1⊥平面EFGH ，所以平面E 1EGG 1⊥平面EFGH ，O 1O ⊥EG .同理，平面E 1EGG 1⊥平面E 1F 1G 1H 1，O 1O ⊥E 1G 1.记玻璃棒的另一端落在GG 1上点N 处．过G 作GK ⊥E 1G 1，K 为垂足，则GK ＝OO 1＝32.因为EG ＝14，E 1G 1＝62，所以KG 1＝62－142＝24， 从而GG 1＝KG 21＋GK 2＝242＋322＝40. 设∠EGG 1＝α，∠ENG ＝β，则sin α＝sin ⎝⎛⎭⎫π2＋∠KGG 1＝cos ∠KGG 1＝45. 因为π2<α<π，所以cos α＝－35. 在△ENG 中，由正弦定理可得40sin α＝14sin β， 解得sin β＝725. 因为0<β<π2，所以cos β＝2425. 于是sin ∠NEG ＝sin(π－α－β)＝sin(α＋β)＝sin αcos β＋cos αsin β＝45×2425＋⎝⎛⎭⎫－35×725＝35. 记EN 与水面的交点为P 2，过P 2作P 2Q 2⊥EG ，Q 2为垂足，则P 2Q 2⊥平面EFGH ，故P 2Q 2＝12，从而EP 2＝P 2Q 2sin ∠NEG＝20. 答 玻璃棒l 没入水中部分的长度为20 cm.(如果将“没入水中部分”理解为“水面以上部分”，则结果为20 cm)10．(2017·江苏，22)如图，在平行六面体ABCDA 1B 1C 1D 1中，AA 1⊥平面ABCD ，且AB ＝AD ＝2，AA 1＝3，∠BAD ＝120°.(1)求异面直线A 1B 与AC 1所成角的余弦值；(2)求二面角BA 1DA 的正弦值．10．解 在平面ABCD 内，过点A 作AE ⊥AD ，交BC 于点E .因为AA 1⊥平面ABCD ，所以AA 1⊥AE ，AA 1⊥AD .如图，以{AE →，AD →，AA 1→}为正交基底，建立空间直角坐标系Axyz .因为AB ＝AD ＝2，AA 1＝3，∠BAD ＝120°，则A (0,0,0)，B (3，－1,0)，D (0,2,0)，E (3，0,0)，A 1(0,0，3)，C 1(3，1，3)． (1)A 1B →＝(3，－1，－3)，AC 1→＝(3，1，3)，则cos 〈A 1B →，AC 1→〉＝A 1B →·AC 1→|A 1B →||AC 1→|＝(3，－1，－3)·(3，1，3)7＝－17， 因此异面直线A 1B 与AC 1所成角的余弦值为17. (2)平面A 1DA 的一个法向量为AE →＝(3，0,0)．设m ＝(x ，y ，z )为平面BA 1D 的一个法向量，又A 1B →＝(3，－1，－3)，BD →＝(－3，3,0)，则⎩⎪⎨⎪⎧ m ·A 1B →＝0，m ·BD →＝0，即⎩⎨⎧3x －y －3z ＝0，－3x ＋3y ＝0. 不妨取x ＝3，则y ＝3，z ＝2，所以m ＝(3，3，2)为平面BA 1D 的一个法向量，从而cos 〈AE →，m 〉＝AE →·m |AE →||m |＝(3，0，0)·(3，3，2)3×4＝34. 设二面角BA 1DA 的大小为θ，则|cos θ|＝34. 因为θ∈[0，π]，所以sin θ＝1－cos 2θ＝74. 因此二面角BA 1DA 的正弦值为74. 11．(2017·全国Ⅰ理，18)如图，在四棱锥P ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°.(1)证明：平面P AB ⊥平面P AD ；(2)若P A ＝PD ＝AB ＝DC ，∠APD ＝90°，求二面角APBC 的余弦值．11．(1)证明 由已知∠BAP ＝∠CDP ＝90°，得AB ⊥AP ，CD ⊥PD ，因为AB ∥CD ，所以AB ⊥PD .又AP ∩DP ＝P ，所以AB ⊥平面P AD .因为AB ⊂平面P AB ，所以平面P AB ⊥平面P AD .(2)解 在平面P AD 内作PF ⊥AD ，垂足为点F .由(1)可知，AB ⊥平面P AD ，故AB ⊥PF ，可得PF ⊥平面ABCD .以点F 为坐标原点，的方向为x 轴正方向，||为单位长度建立如图所示的空间直角坐标系F －xyz .由(1)及已知可得A ⎝⎛⎭⎫22，0，0，P ⎝⎛⎭⎫0，0，22，B ⎝⎛⎭⎫22，1，0，C ⎝⎛⎭⎫－22，1，0， 所以＝⎝⎛⎭⎫－22，1，－22，＝(2，0,0)，＝⎝⎛⎭⎫22，0，－22，＝(0,1,0)． 设n ＝(x 1，y 1，z 1)是平面PCB 的一个法向量，则即⎩⎪⎨⎪⎧－22x 1＋y 1－22z 1＝0，2x 1＝0.所以可取n ＝(0，－1，－2)． 设m ＝(x 2，y 2，z 2)是平面P AB 的一个法向量，则 即⎩⎪⎨⎪⎧22x 2－22z 2＝0，y 2＝0.所以可取m ＝(1,0,1)，则cos 〈n ，m 〉＝n ·m |n ||m |＝－23×2＝－33. 所以二面角A －PB －C 的余弦值为－33. 12．(2017·全国Ⅱ理，19)如图，四棱锥P ABCD 中，侧面P AD 为等边三角形且垂直于底面ABCD ，AB ＝BC ＝12AD ，∠BAD ＝∠ABC ＝90°，E 是PD 的中点．(1)证明：直线CE ∥平面P AB ；(2)点M 在棱PC 上，且直线BM 与底面ABCD 所成角为45°，求二面角MABD 的余弦值．12．(1)证明 取P A 的中点F ，连接EF ，BF .因为E 是PD 的中点，所以EF ∥AD ，EF ＝12AD . 由∠BAD ＝∠ABC ＝90°，得BC ∥AD ，又BC ＝12AD ， 所以EF BC ，四边形BCEF 是平行四边形，CE ∥BF ，又BF ⊂平面P AB ，CE ⊄平面P AB ，故CE ∥平面P AB .(2)解 由已知得BA ⊥AD ，以A 为坐标原点，AB →的方向为x 轴正方向，|AB →|为单位长度，建立如图所示的空间直角坐标系Axyz ，则A (0,0,0)，B (1,0,0)，C (1,1,0)，P (0,1，3)，PC →＝(1,0，－3)，AB →＝(1,0,0)．设M (x ，y ，z )(0<x <1)，则BM →＝(x －1，y ，z )，PM →＝(x ，y －1，z －3)．因为BM 与底面ABCD 所成的角为45°，而n ＝(0,0,1)是底面ABCD 的法向量，所以|cos 〈BM →，n 〉|＝sin 45°， |z |(x －1)2＋y 2＋z 2＝22， 即(x －1)2＋y 2－z 2＝0.①又M 在棱PC 上，设PM →＝λPC →，则x ＝λ，y ＝1，z ＝3－3λ.②由①②解得⎩⎨⎧x ＝1＋22，y ＝1，z ＝－62(舍去)或⎩⎨⎧ x ＝1－22，y ＝1，z ＝62， 所以M ⎝⎛⎭⎫1－22，1，62，从而AM →＝⎝⎛⎭⎫1－22，1，62. 设m ＝(x 0，y 0，z 0)是平面ABM 的法向量，则⎩⎪⎨⎪⎧ m ·AM →＝0，m ·AB →＝0，即⎩⎨⎧(2－2)x 0＋2y 0＋6z 0＝0，x 0＝0， 所以可取m ＝(0，－6，2)．于是cos 〈m ，n 〉＝m ·n |m ||n|＝105. 所以二面角MABD 的余弦值为105.13．(2017·全国Ⅲ理，19)如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形，∠ABD ＝∠CBD ，AB ＝BD .(1)证明：平面ACD ⊥平面ABC ；(2)过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角DAEC 的余弦值．13．(1)证明 由题设可得△ABD ≌△CBD .从而AD ＝CD ，又△ACD 为直角三角形，所以∠ADC ＝90°，取AC 的中点O ，连接DO ，BO ，则DO ⊥AC ，DO ＝AO .又因为△ABC 是正三角形，故BO ⊥AC ，所以∠DOB 为二面角DACB 的平面角，在Rt △AOB 中，BO 2＋OA 2＝AB 2，又AB ＝BD ，所以BO 2＋DO 2＝BO 2＋AO 2＝AB 2＝BD 2，故∠DOB ＝90°，所以平面ACD ⊥平面ABC .(2)解 由题设及(1)知，OA ，OB ，OD 两两垂直，以O 为坐标原点，OA →为x 轴正方向，OB →为y 轴正方向，OD →为z 轴正方向，|OA →|为单位长度，建立如图所示的空间直角坐标系O －xyz ，则O (0,0,0)，A ()1，0，0，D ()0，0，1，B ()0，3，0，C (－1，0,0)，由题设知，四面体ABCE的体积为四面体ABCD 的体积的12，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，即E 为DB 的中点，得E ⎝⎛⎭⎫0，32，12，故AE →＝⎝⎛⎭⎫－1，32，12，AD →＝()－1，0，1，OA →＝()1，0，0. 设平面AED 的法向量为n 1＝(x 1，y 1，z 1)，平面AEC 的法向量为n 2＝(x 2，y 2，z 2)，则⎩⎪⎨⎪⎧ AE →·n 1＝0，AD →·n 1＝0，即⎩⎪⎨⎪⎧－x 1＋32y 1＋12z 1＝0，－x 1＋z ＝0，令x 1＝1，则n 1＝(1，33，1)． ⎩⎪⎨⎪⎧ AE →·n 2＝0，OA →·n 2＝0，即⎩⎪⎨⎪⎧－x 2＋32y 2＋12z 1＝0，x 2＝0，令y 2＝－1，则n 2＝(0，－1，3)，设二面角DAEC 的平面角为θ，易知θ为锐角，则cos θ＝|n 1·n 2||n 1||n 2|＝77. 14．(2017·北京理，16)如图，在四棱锥P ABCD 中，底面ABCD 为正方形，平面P AD ⊥平面ABCD ，点M 在线段PB 上，PD ∥平面MAC ，P A ＝PD ＝6，AB ＝4.(1)求证：M 为PB 的中点；(2)求二面角BPDA 的大小；(3)求直线MC 与平面BDP 所成角的正弦值．14．(1)证明：设AC ，BD 交于点E ，连接ME ，如图．因为PD ∥平面MAC ，平面MAC ∩平面PDB ＝ME ，所以PD ∥ME .因为四边形ABCD 是正方形，所以E 为BD 的中点，所以M 为PB 的中点．(2)解：取AD 的中点O ，连接OP ，OE .因为P A ＝PD ，所以OP ⊥AD ，又因为平面P AD ⊥平面ABCD ，且OP ⊂平面P AD ，所以OP ⊥平面ABCD .因为OE ⊂平面ABCD ，所以OP ⊥OE .因为四边形ABCD 是正方形，所以OE ⊥AD ，如图，建立空间直角坐标系O －xyz ，则P (0,0，2)，D (2,0,0)，B (－2,4,0)，BD →＝(4，－4,0)，PD →＝(2,0，－2)．设平面BDP 的法向量n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ·BD →＝0，n ·PD →＝0，即⎩⎨⎧4x －4y ＝0，2x －2z ＝0. 令x ＝1，则y ＝1，z ＝ 2.于是n ＝(1,1，2)．平面P AD 的法向量为p ＝(0,1,0)，所以cos 〈n ，p 〉＝n ·p |n ||p |＝12. 由题意知二面角B －PD －A 为锐角，所以它的大小为π3. (3)解：由题意知M ⎝⎛⎭⎫－1，2，22，C (2,4,0)，MC →＝⎝⎛⎭⎫3，2，－22. 设直线MC 与平面BDP 所成的角为α，则sin α＝|cos 〈n ，MC →〉|＝|n ·MC →||n ||MC →|＝269. 所以直线MC 与平面BDP 所成角的正弦值为269. 15．(2017·天津理，17)如图，在三棱锥P ABC 中，P A ⊥底面ABC ，∠BAC ＝90°.点D ，E ，N 分别为棱P A ，PC ，BC 的中点，M 是线段AD 的中点，P A ＝AC ＝4，AB ＝2.(1)求证：MN ∥平面BDE ；(2)求二面角CEMN 的正弦值；(3)已知点H 在棱P A 上，且直线NH 与直线BE 所成角的余弦值为721，求线段AH 的长． 15．解 如图，以A 为原点，分别以AB →，AC →，AP →方向为x 轴、y 轴、z 轴正方向建立空间直角坐标系．依题意，可得A (0,0,0)，B (2,0,0)，C (0,4,0)，P (0,0,4)，D (0,0,2)，E (0,2,2)，M (0,0,1)，N (1,2,0)．(1)证明 DE →＝(0,2,0)，DB →＝(2,0，－2)．设n ＝(x ，y ，z )为平面BDE 的一个法向量，则⎩⎪⎨⎪⎧ n ·DE →＝0，n ·DB →＝0，即⎩⎪⎨⎪⎧2y ＝0，2x －2z ＝0.不妨设z ＝1， 可得n ＝(1,0,1)．又MN →＝(1,2，－1)，可得MN →·n ＝0.因为MN ⊄平面BDE ，所以MN ∥平面BDE .(2)易知n 1＝(1,0,0)为平面CEM 的一个法向量．设n 2＝(x 1，y 1，z 1)为平面EMN 的一个法向量，则⎩⎪⎨⎪⎧ n 2·EM →＝0，n 2·MN →＝0， 因为EM →＝(0，－2，－1)，MN →＝(1,2，－1)，所以⎩⎪⎨⎪⎧－2y 1－z 1＝0，x 1＋2y 1－z 1＝0. 不妨设y 1＝1，可得n 2＝(－4,1，－2)．因此cos 〈n 1，n 2〉＝n 1·n 2|n 1||n 2|＝－421， 于是sin 〈n 1，n 2〉＝10521.所以，二面角CEMN 的正弦值为10521. (3)解 依题意，设AH ＝h (0≤h ≤4)，则H (0,0，h )，进而可得NH →＝(－1，－2，h )， BE →＝(－2,2,2)．由已知，得|cos 〈NH →，BE →〉|＝|NH →·BE →||NH →||BE →|＝|2h －2|h 2＋5×23＝721， 整理得10h 2－21h ＋8＝0，解得h ＝85或h ＝12. 所以，线段AH 的长为85或12. 16．(2017·山东理，17)如图，几何体是圆柱的一部分，它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120°得到的，G 是DF 的中点．(1)设P 是CE 上的一点，且AP ⊥BE ，求∠CBP 的大小；(2)当AB ＝3，AD ＝2时，求二面角E —AG —C 的大小．16．解 (1)因为AP ⊥BE ，AB ⊥BE ，AB ，AP ⊂平面ABP ，AB ∩AP ＝A ，所以BE ⊥平面ABP .又BP ⊂平面ABP ，所以BE ⊥BP ，又∠EBC ＝120°，所以∠CBP ＝30°.(2)方法一 取EC 的中点H ，连接EH ，GH ，CH .因为∠EBC ＝120°，所以四边形BEHC 为菱形，所以AE ＝GE ＝AC ＝GC ＝32＋22＝13.取AG 的中点M ，连接EM ，CM ，EC ，则EM ⊥AG ，CM ⊥AG ，所以∠EMC 为所求二面角的平面角．又AM ＝1，所以EM ＝CM ＝13－1＝2 3.在△BEC 中，由于∠EBC ＝120°，由余弦定理得EC 2＝22＋22－2×2×2×cos 120°＝12，所以EC ＝23，因此△EMC 为等边三角形，故所求的角为60°.方法二 在平面EBC 内，作EB ⊥BP 交CE 于点P .以B 为坐标原点，分别以BE ，BP ，BA 所在的直线为x ，y ，z 轴，建立如图所示的空间直角坐标系．由题意得A (0,0,3)，E (2,0,0)，G (1，3，3)，C (－1，3，0)，故AE →＝(2,0，－3)，AG →＝(1，3，0)，CG →＝(2,0,3)，设m ＝(x 1，y 1，z 1)是平面AEG 的一个法向量．由⎩⎪⎨⎪⎧ m · AE →＝0，m ·AG →＝0，可得⎩⎨⎧2x 1－3z 1＝0，x 1＋3y 1＝0. 取z 1＝2，可得平面AEG 的一个法向量m ＝(3，－3，2)．设n ＝(x 2，y 2，z 2)是平面ACG 的一个法向量．由⎩⎪⎨⎪⎧ n ·AG →＝0，n ·CG →＝0，可得⎩⎨⎧x 2＋3y 2＝0，2x 2＋3z 2＝0. 取z 2＝－2，可得平面ACG 的一个法向量n ＝(3，－3，－2)．所以cos 〈m ，n 〉＝m ·n |m ||n |＝12.因此所求的角为60°.。

.专业.专注.数学（理科）第I 卷（选择题共40分）、选择题：本大题共10小题，每小题4分，共40分，在每小题给出的四个选项中三棱锥的底面是底边长 2的等腰直角三角形，圆锥的高和棱锥的高相等均为3，故该几何体2 的体积为V 二1 3「 — 1 2 1^n1 ,故选A .3 2 2 2 点评】本题考查了空间几何体三视图的应用问题 ，解题的关键是根据三视图得出原几何体的结构特征，是基础题目.x _0(4 )12017年浙江，4 , 4分】若x , y 满足约束条件 x ，y-3_0,则z=x'2y 的取值范围是x -2y 空0( )(A ) 0,6 丨 (B ) b,4 1 (C ) 6,=丨 (D ) !4, :: 1答案】D,所以直线过点 2,1时取最小值4,无最大值，故选D .2017年普通高等学校招生全国统一考试（浙江卷）点评】本题考查线性规划的简单应用 ,画出可行域判断目标函数的最优解是解题的关键,只有一项符合题目要(1 )匸017年浙江，1 , 4 分】已知 P ={x| -1 ：：:x ：：:1}, Q 二{ —2 ：：: x ：：:0},贝V P^Q 二( (A ) (-2,1)( B ) (-1,0)(C ) (0,1)答案】A解析】取P,Q 所有元素，得P j Q =(21),故选A .(D) (-2,-1)点评】本题考查集合的基本运算，并集的求法，考查计算能力9 | 4(A ) 13(B ) 丄33答案】B解析】e = .^45 -,故选B .3 3点评】本题考查椭圆的简单性质的应用,考查计算能力.(3 )12017年浙江 ,3 , 4分】某几何体的三视图如图所示位：cm 3) 是（)JI313兀, (A ) -1(B ) — 3(C ) — 1222答案】A，该几何体是圆锥的一半和一个三棱锥组成解军析】如图，可行域为一开放区域 （2）12017年浙江，2, 4分】椭圆— 11的离心率是(C )解析】由几何的三视图可知 （单,圆锥的底面圆的半径为1 ,.专业.专注.(5) [2017年浙江，5, 4分】若函数f x =x2 - ax b在区间10,1 ]上的最大值是M ,最小值是m ,则M -m ()(A)与a有关，且与b有关(B)与a有关，但与b无关(C)与a无关，且与b无关(D)与a无关，但与b有关答案】Ba a2解析】解法一：因为最值在f (0) =b, f(1) =1 • a • b, f (―?) =b —匸中取，所以最值之差一定与b无关，故选B.解法二：函数f x =x2 ax b的图象是开口朝上且以直线为对称轴的抛物线，①当-空1或」 2 2a0 ,即a ::：-2 ,或a ■ 0时，函数f x在区间0,1 ]上单调，此时M —m =M - m的值与a有关，与b无关，故选B.点评】本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键.(6)12017年浙江，6, 4分】已知等差数列Ia n 1的公差为d ,前n项和为§，则’d 0堤’S4 S6 2S5”的()(A)充分不必要条件(B)必要不充分条件(C)充分必要条件(D)既不充分也不必要条件答案】C解析】由S4 S6 -2S5 =10a1 21^2 5a1 10d =d ,可知当d 0 时，有Q •足-2S5 0 ,即S4S6 2Ss ,反之，若S4 Ss 2S S ,则d・0,所以d 0堤S4 S6 .2S5 ”的充要条件，故选C.点评】本题借助等差数列的求和公式考查了充分必要条件，属于基础题答案】D 瞰军析】解法一：由当f x <0时，函数f( x)单调递减，当「X 0时，函数f(x)单调递增，则由导函数y二「x的图象可知：f x先单调递减，再单调递增，然后单调递减，最后单调递增，排除A, C, 且第二个拐点(即函数的极大值点)在x轴上的右侧，排除B,,故选D.解法二：原函数先减再增，再减再增，且x=0位于增区间内，故选D .点评】本题考查导数的应用，考查导数与函数单调性的关系，考查函数极值的判断，考查数形结合思想，属于基础题.(8 )【2017年浙江，8 , 4分】已知随机变量1满足P \ =1 [=P i , P \ =0[=1 - P i , i =1,2 .若.word可编辑.f 1 - f 0|; |a ,故1 aM -m的值与a有关，与b无关；②当 1 ,即_2辽a辽-1时，函数f x在区间0,a=—，故M - m的值与a有关，与b无.2 4a 1 a I关；③当0 ,即-1 ：：：a乞0时，函数f X在区间0,-2 2 1! 2 一=a -,故M ~^m的值与a有关，与b无关.综上可得：.2 4，且 f 0 . f 1 ,此时M -m = f 0：：-ff 0 :：: f 1 ，此时M —m 二f 0 —f上递减，上递减，在-旦,1上递增，且2(7)y = f (x)的图像如图所示在-?1匸017年浙江，7 , 4分】函数y=f x的导函数,则函数y = f x的.专业.专注.1…0 ：：： pi ::: P 2 ＜2，则((A ) E(J ：：：E ( 2),(C ) E( J .E( 2), 答案】A 解析】E( J = p,E( 2) *2,. E( J ：：：E( 2) ： D( J 二 口(1一 pJ,D( 2) = P 2(1-P 2),■ D( 1) -D( 2)=(P 1 -P 2)(1-P 1 -P 2)O 故选 A •点评】本题考查离散型随机变量的数学期望和方差等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，是中档题•9 , 4分】如图，已知正四面体 D -ABC (所有棱长均相等的三棱锥 PQRD -PQ -R , D(A) l ：,答案】B懈析】解法一：如图所示，建立空间直角坐标系.设底面- ABC 的中心为O •不妨设 OP =3•贝 UO 0,0,0 , P 0, -3,0 , C 0,-6,0 , D 0,0,6 .2 , Q 3,2,0 , R -2 3,0,0 , PR =[「2 .3,3,0 , PD = 0,3,6 . 2 , PQ = 3,5,0 , QR =[—3 一 3, 一2,0 ,QD - - .3, -2,6 . 2 •设平面PDR 的法向量为n = x,y,z ,贝卩. [n PD =0-2 3x 3y =0 { _ ,可得n =(用,2 72, 7 \,取平面ABC 的法向量m =(0,0,1 ). 3y 6 2z =0 m n1卄1 「 一 ,口则 cos m,n,取〉二arccos^= •同理可得：* 2 123= arccos .T.••.「：：：：:：-.V 95 V 15 V 95 V681解法二：如图所示,连接OD , OQ , OR , OG _QR ,垂足分别为E , F , cos ：二汪=OE S 卸R PE=—OE •同理可得:cos ： =OFOE 2 h 2PF由已知可得：OE OG OF .二 cos 、； n cos • cos ：,:-,-, 为锐角.•••％＜丫＜3 故选 B .点评】本题考查了空间角、空间位置关系、正四面体的性质、法向量的夹角公式，考查了推理能力与计算能力 属于难题•(10 )12017年浙江，10, 4分】如图，已知平面四边形 ABCD , AB — BC , AB = BC = AD =2 , CD =3，AC 与 BD 交于点 O ,记 h=OAOB , 12= OB OC , J=OCOD ,贝U ()(B ) E( \) :::E( ；) , D( \) D( 2) (D ) E( J .E( ；) , D( J ：：：D(；)D( J ：：：D( 2)D( J ：：：(9 )12017年浙江， BQ CR,CA 上的点，AP=PB , 竺=竺=2 ,分别记二面角 D -PR -Q ,QC RA-QR -P 的平面较为:,'■,,贝卩( ) (B ) 「：：：：：： - (C ):-:::::::分别为AB , BC 0E _ DR , OF _ DQ ,过点0发布作垂线 3 =arccos^^V681P 设 OP=h •, 连接P E 0G OFc , OF 2 h 2cos cos ：,:-,期 OG cos PGOG 2 h 2(D )1,可得 则.专业.专注.(A ) I 1：： I 2：：I 3( B ) I 1 ：：： I 3 ：：： I 2( C ) I 3 ：：： h ：：： I 2 ( D ) I 2 ：：： I 2 ：：：爲答案】c解析】・・AB_BC , AB =BC =AD =2 , CD =3，二 AC =2* 2，「上AOB /COD 90 ,由图象知 OA :：: OC , OB ：：OD ，二 0 OA OB O C OD , OB O C .0,即 l 3 ：： h ：： l 2 ,故选 C . 点评】本题主要考查平面向量数量积的应用，根据图象结合平面向量数量积的定义是解决本题的关键.第口卷(非选择题共110分)二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分. (11 )2017年浙江，算到任意精度。

2017年高考数学试题分项版—解析几何（解析版）一、选择题1．(2017·全国Ⅰ文，5)已知F 是双曲线C ：x 2－y 23＝1的右焦点，P 是C 上一点，且PF 与x轴垂直，点A 的坐标是(1,3)，则△APF 的面积为( ) A ．13 B ．12 C ．23 D ．321．【答案】D【解析】因为F 是双曲线C ：x 2－y 23＝1的右焦点，所以F (2,0)．因为PF ⊥x 轴，所以可设P 的坐标为(2，y P )． 因为P 是C 上一点，所以4－y 2P3＝1，解得y P ＝±3，所以P (2，±3)，|PF |＝3.又因为A (1,3)，所以点A 到直线PF 的距离为1， 所以S △APF ＝12×|PF |×1＝12×3×1＝32.故选D.2．(2017·全国Ⅰ文，12)设A ，B 是椭圆C ：x 23＋y 2m ＝1长轴的两个端点．若C 上存在点M 满足∠AMB ＝120°，则m 的取值范围是( ) A ．(0,1]∪[9，＋∞) B ．(0，3]∪[9，＋∞) C ．(0,1]∪[4，＋∞) D ．(0，3]∪[4，＋∞)2．【答案】A【解析】方法一 设焦点在x 轴上，点M (x ，y )． 过点M 作x 轴的垂线，交x 轴于点N ， 则N (x,0)．故tan ∠AMB ＝tan(∠AMN ＋∠BMN ) ＝3＋x |y |＋3－x|y |1－3＋x |y |·3－x |y |＝23|y |x 2＋y 2－3.又tan ∠AMB ＝tan 120°＝－3， 且由x 23＋y 2m ＝1，可得x 2＝3－3y 2m ，则23|y |3－3y 2m ＋y 2－3＝23|y |(1－3m)y2＝－ 3.解得|y |＝2m3－m.又0＜|y |≤m ，即0＜2m3－m ≤m ，结合0＜m ＜3解得0＜m ≤1.对于焦点在y 轴上的情况，同理亦可得m ≥9. 则m 的取值范围是(0,1]∪[9，＋∞)． 故选A.方法二 当0＜m ＜3时，焦点在x 轴上， 要使C 上存在点M 满足∠AMB ＝120°， 则a b ≥tan 60°＝3，即3m ≥3， 解得0＜m ≤1.当m ＞3时，焦点在y 轴上，要使C 上存在点M 满足∠AMB ＝120°， 则a b ≥tan 60°＝3，即m3≥3，解得m ≥9. 故m 的取值范围为(0,1]∪[9，＋∞)． 故选A.3．(2017·全国Ⅱ文，5)若a >1，则双曲线x 2a 2－y 2＝1的离心率的取值范围是( )A ．(2，＋∞)B ．(2，2)C ．(1，2)D ．(1,2)3．【答案】C【解析】由题意得双曲线的离心率e ＝a 2＋1a .∴e 2＝a 2＋1a 2＝1＋1a2.∵a ＞1，∴0＜1a 2＜1，∴1＜1＋1a 2＜2，∴1＜e ＜ 2. 故选C.4．(2017·全国Ⅱ文，12)过抛物线C ：y 2＝4x 的焦点F ，且斜率为3的直线交C 于点M (M 在x 轴上方)，l 为C 的准线，点N 在l 上且MN ⊥l ，则M 到直线NF 的距离为( )A.5B ．22C ．23D ．3 3 4．【答案】C【解析】抛物线y 2＝4x 的焦点为F (1,0)，准线方程为x ＝－1.由直线方程的点斜式可得直线MF 的方程为y ＝3(x －1)．联立得方程组⎩⎨⎧y ＝3(x －1)，y 2＝4x ，解得⎩⎨⎧x ＝13，y ＝－233或⎩⎨⎧x ＝3，y ＝2 3.∵点M 在x 轴的上方，∴M (3,23)． ∵MN ⊥l ，∴N (－1,23)．∴|NF |＝(1＋1)2＋(0－23)2＝4， |MF |＝|MN |＝3－(－1)＝4.∴△MNF 是边长为4的等边三角形． ∴点M 到直线NF 的距离为2 3. 故选C.5．(2017·全国Ⅲ文，11)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线bx －ay ＋2ab ＝0相切，则椭圆C 的离心率为( ) A ．63 B ．33 C ．23 D ．135．【答案】A【解析】由题意知以A 1A 2为直径的圆的圆心坐标为(0,0)，半径为a . 又直线bx －ay ＋2ab ＝0与圆相切， ∴圆心到直线的距离d ＝2aba 2＋b 2＝a ，解得a ＝3b， ∴b a ＝13，∴e ＝ca ＝a 2－b 2a＝1－⎝⎛⎭⎫b a 2＝1－⎝⎛⎭⎫132＝63. 6．(2017·天津文，5)已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的右焦点为F ，点A 在双曲线的渐近线上，△OAF 是边长为2的等边三角形(O 为原点)，则双曲线的方程为( ) A ．x 24－y 212＝1B ．x 212－y 24＝1C ．x 23－y 2＝1D ．x 2－y 23＝16．【答案】D【解析】根据题意画出草图如图所示⎝⎛⎭⎫不妨设点A 在渐近线y ＝ba x 上.由△AOF 是边长为2的等边三角形得到∠AOF ＝60°，c ＝|OF |＝2. 又点A 在双曲线的渐近线y ＝b a x 上，∴ba ＝tan 60°＝ 3.又a 2＋b 2＝4，∴a ＝1，b ＝3， ∴双曲线的方程为x 2－y 23＝1.故选D.7．(2017·浙江，2)椭圆x 29＋y 24＝1的离心率是( )A ．133B ．53C ．23D ．597．【答案】B【解析】∵椭圆方程为x 29＋y 24＝1，∴a ＝3，c ＝a 2－b 2＝9－4＝ 5. ∴e ＝c a ＝53.故选B.8．(2017·全国Ⅰ理，10)已知F 为抛物线C ：y 2＝4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A ，B 两点，直线l 2与C 交于D ，E 两点，则|AB |＋|DE |的最小值为( )A ．16B ．14C ．12D ．10 8．【答案】A【解析】因为F 为y 2＝4x 的焦点，所以F (1,0)．由题意知直线l 1，l 2的斜率均存在，且不为0，设l 1的斜率为k ，则l 2的斜率为－1k ，故直线l 1，l 2的方程分别为y ＝k (x －1)，y ＝－1k(x －1)．由⎩⎪⎨⎪⎧y ＝k (x －1)，y 2＝4x ，得k 2x 2－(2k 2＋4)x ＋k 2＝0. 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝2k 2＋4k 2，x 1x 2＝1，所以|AB |＝1＋k 2·|x 1－x 2| ＝1＋k 2·(x 1＋x 2)2－4x 1x 2 ＝1＋k 2·⎝⎛⎭⎫2k 2＋4k 22－4＝4(1＋k 2)k 2.同理可得|DE |＝4(1＋k 2)．所以|AB |＋|DE |＝4(1＋k 2)k 2＋4(1＋k 2) ＝4⎝⎛⎭⎫1k 2＋1＋1＋k 2 ＝8＋4⎝⎛⎭⎫k 2＋1k 2≥8＋4×2＝16， 当且仅当k 2＝1k 2，即k ＝±1时，取得等号．故选A.9．(2017·全国Ⅱ理，9)若双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的一条渐近线被圆(x －2)2＋y 2＝4所截得的弦长为2，则C 的离心率为( ) A ．2 B ． 3 C ． 2D ．2339．【答案】A【解析】设双曲线的一条渐近线方程为y ＝b a x ，圆的圆心为(2,0)，半径为2，由弦长为2得出圆心到渐近线的距离为22－12＝ 3. 根据点到直线的距离公式，得|2b |a 2＋b 2＝3，解得b 2＝3a 2. 所以C 的离心率e ＝ca ＝c 2a 2＝1＋b 2a2＝2. 故选A.10．(2017·全国Ⅲ理，5)已知双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的一条渐近线方程为y ＝52x ，且与椭圆x 212＋y 23＝1有公共焦点，则C 的方程为( )A ．x 28－y 210＝1B ．x 24－y 25＝1C ．x 25－y 24＝1D ．x 24－y 23＝110．【答案】B 【解析】由y ＝52x ，可得b a ＝52.① 由椭圆x 212＋y 23＝1的焦点为(3,0)，(－3,0)，可得a 2＋b 2＝9.② 由①②可得a 2＝4，b 2＝5. 所以C 的方程为x 24－y 25＝1.故选B.11．(2017·全国Ⅲ理，10)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线bx －ay ＋2ab ＝0相切，则C 的离心率为( ) A ．63B ．33C ．23D ．1311．【答案】A【解析】由题意知，以A 1A 2为直径的圆的圆心为(0,0)，半径为a .又直线bx －ay ＋2ab ＝0与圆相切，∴圆心到直线的距离d ＝2aba 2＋b 2＝a ，解得a ＝3b ，∴b a ＝13， ∴e ＝c a ＝a 2－b 2a ＝1－⎝⎛⎭⎫b a 2＝1－⎝⎛⎭⎫132＝63.故选A.12．(2017·天津理，5)已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左焦点为F ，离心率为 2.若经过F和P (0,4)两点的直线平行于双曲线的一条渐近线，则双曲线的方程为( ) A ．x 24－y 24＝1B ．x 28－y 28＝1C ．x 24－y 28＝1D ．x 28－y 24＝112．【答案】B【解析】由题意可得ca ＝2，即c ＝2a .又左焦点F (－c,0)，P (0,4)，则直线PF 的方程为y －04－0＝x ＋c 0＋c，化简即得y ＝4c x ＋4.结合已知条件和图象易知直线PF 与y ＝b a x 平行，则4c ＝ba，即4a ＝bc .由⎩⎪⎨⎪⎧c ＝2a ，4a ＝bc ，a 2＋b 2＝c 2，解得⎩⎪⎨⎪⎧a 2＝8，b 2＝8，故双曲线方程为x 28－y 28＝1.故选B. 二、填空题1．(2017·全国Ⅲ文，14)双曲线x 2a 2－y 29＝1(a >0)的一条渐近线方程为y ＝35x ，则a ＝________.1．【答案】5【解析】∵双曲线的标准方程为x 2a 2－y 29＝1(a ＞0)，∴双曲线的渐近线方程为y ＝±3ax .又双曲线的一条渐近线方程为y ＝35x ，∴a ＝5.2．(2017·北京文，10)若双曲线x 2－y 2m＝1的离心率为3，则实数m ＝________.2．【答案】2【解析】由双曲线的标准方程知a ＝1，b 2＝m ，c ＝1＋m ， 故双曲线的离心率e ＝ca ＝1＋m ＝3，∴1＋m ＝3，∴m ＝2.3.(2017·北京文，12)已知点P 在圆x 2＋y 2＝1上，点A 的坐标为(－2,0)，O 为原点，则AO →·AP →的最大值为________． 3．【答案】6【解析】方法一 根据题意作出图象，如图所示，A (－2,0)，P (x ，y )．由点P 向x 轴作垂线交x 轴于点Q ，则点Q 的坐标为(x,0)． AO →·AP →＝|AO →|·|AP →|cos θ， |AO →|＝2，|AP →|＝(x ＋2)2＋y 2， cos θ＝AQAP ＝x ＋2(x ＋2)2＋y 2，所以AO →·AP →＝2(x ＋2)＝2x ＋4.点P 在圆x 2＋y 2＝1上，所以x ∈[－1,1]． 所以AO →·AP →的最大值为2＋4＝6.方法二 如图所示，因为点P 在圆x 2＋y 2＝1上， 所以可设P (cos α，sin α)(0≤α＜2π)， 所以AO →＝(2,0)，AP →＝(cos α＋2，sin α)， AO →·AP →＝2cos α＋4≤2＋4＝6，当且仅当cos α＝1，即α＝0，P (1,0)时“＝”号成立．4．(2017·天津文，12)设抛物线y 2＝4x 的焦点为F ，准线为l .已知点C 在l 上，以C 为圆心的圆与y 轴的正半轴相切于点A .若∠F AC ＝120°，则圆的方程为________．4．【答案】(x ＋1)2＋(y －3)2＝1【解析】由y 2＝4x 可得点F 的坐标为(1,0)，准线l 的方程为x ＝－1.由圆心C 在l 上，且圆C 与y 轴正半轴相切(如图)，可得点C 的横坐标为－1，圆的半径为1，∠CAO ＝90°.又因为∠F AC ＝120°， 所以∠OAF ＝30°，所以|OA |＝3， 所以点C 的纵坐标为 3.所以圆的方程为(x ＋1)2＋(y －3)2＝1.5.(2017·山东文，15)在平面直角坐标系xOy 中，双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的右支与焦点为F 的抛物线x 2＝2py (p >0)交于A ，B 两点，若|AF |＋|BF |＝4|OF |，则该双曲线的渐近线方程为________． 5．【答案】y ＝±22x【解析】设A (x 1，y 1)，B (x 2，y 2)．由⎩⎪⎨⎪⎧x 2a 2－y 2b 2＝1，x 2＝2py ，得a 2y 2－2pb 2y ＋a 2b 2＝0， ∴y 1＋y 2＝2pb 2a 2.又∵|AF |＋|BF |＝4|OF |，∴y 1＋p 2＋y 2＋p 2＝4×p2，∴y 1＋y 2＝p ，∴2pb 2a 2＝p ，即b 2a 2＝12，∴b a ＝22， ∴双曲线的渐近线方程为y ＝±22x .6.(2017·江苏，8)在平面直角坐标系xOy 中，双曲线x 23－y 2＝1的右准线与它的两条渐近线分别交于点P ，Q ，其焦点是F 1，F 2，则四边形F 1PF 2Q 的面积是________．6．【答案】2 3【解析】如图所示，双曲线x 23－y 2＝1的焦点为F 1(－2,0)，F 2(2,0)，所以|F 1F 2|＝4.双曲线x 23－y 2＝1的右准线方程为x ＝a 2c ＝32，渐近线方程为y ＝±33x .由⎩⎨⎧x ＝32，y ＝33x得P ⎝⎛⎭⎫32，32.同理可得Q ⎝⎛⎭⎫32，－32.∴|PQ |＝3，∴S 四边形12F PF Q ＝12·|F 1F 2|·|PQ |＝12×4×3＝2 3.7．(2017·江苏，13)在平面直角坐标系xOy 中，A (－12,0)，B (0,6)，点P 在圆O ：x 2＋y 2＝50上，若P A →·PB →≤20，则点P 的横坐标的取值范围是________． 7．【答案】[－52，1]【解析】方法一 因为点P 在圆O ：x 2＋y 2＝50上， 所以设P 点坐标为(x ，±50－x 2)(－52≤x ≤52)． 因为A (－12,0)，B (0,6)，所以P A →＝(－12－x ，－50－x 2)或P A →＝(－12－x ，50－x 2)， PB →＝(－x,6－50－x 2)或PB →＝(－x,6＋50－x 2)． 因为P A →·PB →≤20，先取P (x ，50－x 2)进行计算， 所以(－12－x )·(－x )＋(－50－x 2)(6－50－x 2)≤20， 即2x ＋5≤50－x 2.当2x ＋5＜0，即x ＜－52时，上式恒成立．当2x ＋5≥0，即x ≥－52时，(2x ＋5)2≤50－x 2，解得－52≤x ≤1，故x ≤1.同理可得P (x ，－50－x 2)时，x ≤－5. 又－52≤x ≤52，所以－52≤x ≤1. 故点P 的横坐标的取值范围为[－52，1]． 方法二 设P (x ，y )，则P A →＝(－12－x ，－y )，PB →＝(－x,6－y )． ∵P A →·PB →≤20，∴(－12－x )·(－x )＋(－y )·(6－y )≤20， 即2x －y ＋5≤0.如图，作圆O ：x 2＋y 2＝50，直线2x －y ＋5＝0与⊙O 交于E ，F 两点，∵P 在圆O 上且满足2x －y ＋5≤0，∴点P 在 EDF 上．由⎩⎪⎨⎪⎧x 2＋y 2＝50，2x －y ＋5＝0得F 点的横坐标为1， 又D 点的横坐标为－52，∴P 点的横坐标的取值范围为[－52，1]．8．(2017·全国Ⅰ理，15)已知双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的右顶点为A ，以A 为圆心，b为半径作圆A ，圆A 与双曲线C 的一条渐近线交于M ，N 两点．若∠MAN ＝60°，则C 的离心率为________． 8．【答案】233【解析】如图，由题意知点A (a,0)，双曲线的一条渐近线l 的方程为y ＝ba x ，即bx －ay ＝0，∴点A 到l 的距离d ＝aba 2＋b 2. 又∠MAN ＝60°，MA ＝NA ＝b ，∴△MAN 为等边三角形， ∴d ＝32MA ＝32b ，即ab a 2＋b2＝32b ，∴a 2＝3b 2， ∴e ＝ca＝a 2＋b 2a 2＝233.9．(2017·全国Ⅱ理，16)已知F 是抛物线C ：y 2＝8x 的焦点，M 是C 上一点，FM 的延长线交y 轴于点N .若M 为FN 的中点，则|FN |＝________. 9．【答案】6【解析】如图，不妨设点M 位于第一象限内，抛物线C 的准线交x 轴于点A ，过点M 作准线的垂线，垂足为点B ，交y 轴于点P ，∴PM ∥OF .由题意知，F (2,0)，|FO |＝|AO |＝2. ∵点M 为FN 的中点，PM ∥OF ， ∴|MP |＝12|FO |＝1.又|BP |＝|AO |＝2， ∴|MB |＝|MP |＋|BP |＝3.由抛物线的定义知|MF |＝|MB |＝3，故|FN |＝2|MF |＝6.10．(2017·北京理，9)若双曲线x 2－y 2m＝1的离心率为3，则实数m ＝________.10．【答案】2【解析】由双曲线的标准方程知a ＝1，b 2＝m ，c ＝1＋m ， 故双曲线的离心率e ＝ca＝1＋m ＝3，∴1＋m ＝3，解得m ＝2.11．(2017·北京理，14)三名工人加工同一种零件，他们在一天中的工作情况如图所示，其中点A i 的横、纵坐标分别为第i 名工人上午的工作时间和加工的零件数，点B i 的横、纵坐标分别为第i 名工人下午的工作时间和加工的零件数，i ＝1,2,3.①记Q i 为第i 名工人在这一天中加工的零件总数，则Q 1，Q 2，Q 3中最大的是________． ②记p i 为第i 名工人在这一天中平均每小时加工的零件数，则p 1，p 2，p 3中最大的是________．11．【答案】Q 1 p 2【解析】设A 1(xA 1，yA 1)，B 1(xB 1，yB 1)，线段A 1B 1的中点为E 1(x 1，y 1)，则Q 1＝yA 1＋yB 1＝2y 1.因此，要比较Q 1，Q 2，Q 3的大小，只需比较线段A 1B 1，A 2B 2，A 3B 3中点纵坐标的大小，作图比较知Q 1最大．又p 1＝yA 1＋yB 1xA 1＋xB 1＝2y 12x 1＝y 1x 1＝y 1－0x 1－0，其几何意义为线段A 1B 1的中点E 1与坐标原点连线的斜率，因此，要比较p 1，p 2，p 3的大小，只需比较线段A 1B 1，A 2B 2，A 3B 3中点与坐标原点连线的斜率，作图比较知p 2最大．12．(2017·山东理，14)在平面直角坐标系xOy 中，双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的右支与焦点为F 的抛物线x 2＝2py (p ＞0)交于A ，B 两点，若|AF |＋|BF |＝4|OF |，则该双曲线的渐近线方程为________． 12．【答案】y ＝±22x【解析】设A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧x 2a 2－y 2b 2＝1，x 2＝2py ，得a 2y 2－2pb 2y ＋a 2b 2＝0， ∴y 1＋y 2＝2pb 2a 2.又∵|AF |＋|BF |＝4|OF |，∴y 1＋p 2＋y 2＋p 2＝4×p2，即y 1＋y 2＝p ，∴2pb 2a 2＝p ，即b 2a 2＝12，∴b a ＝22， ∴双曲线的渐近线方程为y ＝±22x .三、解答题1．(2017·全国Ⅰ文，20)设A ，B 为曲线C ：y ＝x 24上两点，A 与B 的横坐标之和为4.(1)求直线AB 的斜率；(2)设M 为曲线C 上一点，C 在M 处的切线与直线AB 平行，且AM ⊥BM ，求直线AB 的方程．1．解 (1)设A (x 1，y 1)，B (x 2，y 2)， 则x 1≠x 2，y 1＝x 214，y 2＝x 224，x 1＋x 2＝4，于是直线AB 的斜率k ＝y 1－y 2x 1－x 2＝x 1＋x 24＝1.(2)由y ＝x 24，得y ′＝x2.设M (x 3，y 3)，由题设知x 32＝1，解得x 3＝2，于是M (2,1)．设直线AB 的方程为y ＝x ＋m ，故线段AB 的中点为N (2,2＋m )，|MN |＝|m ＋1|. 将y ＝x ＋m 代入y ＝x 24，得x 2－4x －4m ＝0.当Δ＝16(m ＋1)>0，即m >－1时，x 1,2＝2±2m ＋1. 从而|AB |＝2|x 1－x 2|＝42(m ＋1).由题设知|AB |＝2|MN |，即42(m ＋1)＝2(m ＋1)，解得m ＝7. 所以直线AB 的方程为y ＝x ＋7.2．(2017·全国Ⅱ文，20)设O 为坐标原点，动点M 在椭圆C ：x 22＋y 2＝1上，过M 作x 轴的垂线，垂足为N ，点P 满足NP →＝2NM →. (1)求点P 的轨迹方程；(2)设点Q 在直线x ＝－3上，且OP →·PQ →＝1.证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F .2．(1)解 设P (x ，y )，M (x 0，y 0)，则N (x 0,0)，NP →＝(x －x 0，y )，NM →＝(0，y 0)．由NP →＝2NM →得x 0＝x ，y 0＝22y .因为M (x 0，y 0)在C 上，所以x 22＋y 22＝1.因此点P 的轨迹方程为x 2＋y 2＝2. (2)证明 由题意知F (－1,0)．设Q (－3，t )，P (m ，n )，则OQ →＝(－3，t )， PF →＝(－1－m ，－n )，OQ →·PF →＝3＋3m －tn ， OP →＝(m ，n )，PQ →＝(－3－m ，t －n )． 由OP →·PQ →＝1，得－3m －m 2＋tn －n 2＝1. 又由(1)知m 2＋n 2＝2，故3＋3m －tn ＝0. 所以OQ →·PF →＝0，即OQ →⊥PF →. 又过点P 存在唯一直线垂直于OQ ，所以过点P 且垂直于OQ 的直线l 过C 的左焦点F .3．(2017·全国Ⅲ文，20)在直角坐标系xOy 中，曲线y ＝x 2＋mx －2与x 轴交于A ，B 两点，点C 的坐标为(0,1)．当m 变化时，解答下列问题： (1)能否出现AC ⊥BC 的情况？说明理由；(2)证明过A ，B ，C 三点的圆在y 轴上截得的弦长为定值． 3．(1)解 不能出现AC ⊥BC 的情况．理由如下： 设A (x 1,0)，B (x 2,0)，则x 1，x 2满足x 2＋mx －2＝0， 所以x 1x 2＝－2. 又点C 的坐标为(0,1)，故AC 的斜率与BC 的斜率之积为－1x 1·－1x 2＝－12，所以不能出现AC ⊥BC 的情况．(2)证明 BC 的中点坐标为⎝⎛⎭⎫x 22，12，可得BC 的中垂线方程为y －12＝x 2⎝⎛⎭⎫x －x 22. 由(1)可得x 1＋x 2＝－m ， 所以AB 的中垂线方程为x ＝－m2.联立⎩⎨⎧x ＝－m2，y －12＝x 2⎝⎛⎭⎫x －x 22，又x 22＋mx 2－2＝0，可得⎩⎨⎧x ＝－m 2，y ＝－12.所以过A ，B ，C 三点的圆的圆心坐标为⎝⎛⎭⎫－m 2，－12，半径r ＝m 2＋92. 故圆在y 轴上截得的弦长为2r 2－⎝⎛⎭⎫m 22＝3，即过A ，B ，C 三点的圆在y 轴上截得的弦长为定值．4．(2017·北京文，19)已知椭圆C 的两个顶点分别为A (－2,0)，B (2,0)，焦点在x 轴上，离心率为32. (1)求椭圆C 的方程；(2)点D 为x 轴上一点，过D 作x 轴的垂线交椭圆C 于不同的两点M ，N ，过D 作AM 的垂线交BN 于点E .求证：△BDE 与△BDN 的面积之比为4∶5. 4．(1)解 设椭圆C 的方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)，由题意得⎩⎪⎨⎪⎧a ＝2，c a ＝32，解得c ＝3，所以b 2＝a 2－c 2＝1， 所以椭圆C 的方程为x 24＋y 2＝1.(2)证明 设M (m ，n )，则D (m,0)，N (m ，－n )， 由题设知m ≠±2，且n ≠0. 直线AM 的斜率k AM ＝nm ＋2， 故直线DE 的斜率k DE ＝－m ＋2n ，所以直线DE 的方程为y ＝－m ＋2n(x －m )， 直线BN 的方程为y ＝n2－m(x －2)．联立⎩⎨⎧y ＝－m ＋2n(x －m )，y ＝n2－m (x －2)，解得点E 的纵坐标y E ＝－n (4－m 2)4－m 2＋n 2.由点M 在椭圆C 上，得4－m 2＝4n 2，所以y E ＝－45n .又S △BDE ＝12|BD |·|y E |＝25|BD |·|n |，S △BDN ＝12|BD |·|n |，所以△BDE 与△BDN 的面积之比为4∶5.5．(2017·天津文，20)已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左焦点为F (－c,0)，右顶点为A ，点E 的坐标为(0，c )，△EF A 的面积为b 22.(1)求椭圆的离心率；(2)设点Q 在线段AE 上，|FQ |＝3c2，延长线段FQ 与椭圆交于点P ，点M ，N 在x 轴上，PM∥QN ，且直线PM 与直线QN 间的距离为c ，四边形PQNM 的面积为3c . ①求直线FP 的斜率； ②求椭圆的方程．5．解 (1)设椭圆的离心率为e . 由已知可得12(c ＋a )c ＝b 22.又由b 2＝a 2－c 2，可得2c 2＋ac －a 2＝0， 即2e 2＋e －1＝0，解得e ＝－1或e ＝12.又因为0<e <1，所以e ＝12.所以椭圆的离心率为12.(2)①依题意，设直线FP 的方程为x ＝my －c (m >0)，则直线FP 的斜率为1m.由(1)知a ＝2c ，可得直线AE 的方程为x 2c ＋yc ＝1，即x ＋2y －2c ＝0，与直线FP 的方程联立，可解得x ＝(2m －2)c m ＋2，y ＝3cm ＋2，即点Q 的坐标为⎝⎛⎭⎪⎫(2m －2)c m ＋2，3c m ＋2.由已知|FQ |＝3c 2，有⎣⎢⎡⎦⎥⎤(2m －2)c m ＋2＋c 2＋⎝⎛⎭⎫3c m ＋22＝⎝⎛⎭⎫3c 22，整理得3m 2－4m ＝0，所以m ＝43(m ＝0舍去)，即直线FP 的斜率为34.②由a ＝2c ，可得b ＝3c ， 故椭圆方程可以表示为x 24c 2＋y 23c2＝1.由①得直线FP 的方程为3x －4y ＋3c ＝0，与椭圆方程联立⎩⎪⎨⎪⎧3x －4y ＋3c ＝0，x 24c 2＋y 23c 2＝1，消去y ，整理得7x 2＋6cx －13c 2＝0，解得x ＝－13c7(舍去)或x ＝c .因此可得点P ⎝⎛⎭⎫c ，3c 2， 进而可得|FP |＝(c ＋c )2＋⎝⎛⎭⎫3c 22＝5c2，所以|PQ |＝|FP |－|FQ |＝5c 2－3c2＝c .由已知，线段PQ 的长即为PM 与QN 这两条平行直线间的距离，故直线PM 和QN 都垂直于直线FP .因为QN ⊥FP ，所以|QN |＝|FQ |·tan ∠QFN ＝3c 2×34＝9c 8，所以△FQN 的面积为12|FQ ||QN |＝27c 232.同理△FPM 的面积等于75c 232.由四边形PQNM 的面积为3c ，得75c 232－27c 232＝3c ，整理得c 2＝2c ，又由c >0，得c ＝2. 所以椭圆的方程为x 216＋y 212＝1.6．(2017·山东文，21)在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，椭圆C 截直线y ＝1所得线段的长度为2 2. (1)求椭圆C 的方程；(2)动直线l ：y ＝kx ＋m (m ≠0)交椭圆C 于A ，B 两点，交y 轴于点M .点N 是M 关于O 的对称点，⊙N 的半径为|NO |.设D 为AB 的中点，DE ，DF 与⊙N 分别相切于点E ，F ，求∠EDF 的最小值．6．解 (1)由椭圆的离心率为22，得a 2＝2(a 2－b 2)， 又当y ＝1时，x 2＝a 2－a 2b 2，得a 2－a 2b2＝2， 所以a 2＝4，b 2＝2.因此椭圆方程为x 24＋y 22＝1.(2)设A (x 1，y 1)，B (x 2，y 2)． 联立方程，得⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y 22＝1，得(2k 2＋1)x 2＋4kmx ＋2m 2－4＝0. 由Δ>0，得m 2<4k 2＋2，(*) 且x 1＋x 2＝－4km2k 2＋1，因此y 1＋y 2＝2m2k 2＋1，所以D ⎝⎛⎭⎫－2km 2k 2＋1，m2k 2＋1.又N (0，－m )，所以|ND |2＝⎝⎛⎭⎫－2km 2k 2＋12＋⎝⎛⎭⎫m2k 2＋1＋m 2，整理得|ND |2＝4m 2(1＋3k 2＋k 4)(2k 2＋1)2.因为|NF |＝|m |，所以|ND |2|NF |2＝4(k 4＋3k 2＋1)(2k 2＋1)2＝1＋8k 2＋3(2k 2＋1)2.令t ＝8k 2＋3，t ≥3， 故2k 2＋1＝t ＋14.所以|ND |2|NF |2＝1＋16t (1＋t )2＝1＋16t ＋1t ＋2. 令y ＝t ＋1t ，所以y ′＝1－1t 2.当t ≥3时，y ′>0，从而y ＝t ＋1t 在[3，＋∞)上单调递增，因此t ＋1t ≥103，当且仅当t ＝3时等号成立，此时k ＝0， 所以|ND |2|NF |2≤1＋3＝4.由(*)得－2<m <2且m ≠0，故|NF ||ND |≥12. 设∠EDF ＝2θ，则sin θ＝|NF ||ND |≥12，所以θ的最小值为π6，从而∠EDF 的最小值为π3，此时直线l 的斜率是0.综上所述，当k ＝0，m ∈(－2，0)∪(0，2)时，∠EDF 取到最小值π3.7．(2017·浙江，21)如图，已知抛物线x 2＝y ，点A ⎝⎛⎭⎫－12，14，B ⎝⎛⎭⎫32，94，抛物线上的点P (x ，y )⎝⎛⎭⎫－12＜x ＜32，过点B 作直线AP 的垂线，垂足为Q .(1)求直线AP 斜率的取值范围； (2)求|P A |·|PQ |的最大值．7．解 (1)设直线AP 的斜率为k ，k ＝x 2－14x ＋12＝x －12，因为－12＜x ＜32.所以直线AP 斜率的取值范围为(－1,1)．(2)联立直线AP 与BQ 的方程⎩⎨⎧kx －y ＋12k ＋14＝0，x ＋ky －94k －32＝0，解得点Q 的横坐标是x Q ＝－k 2＋4k ＋32 k 2＋1.因为|P A |＝1＋k 2⎝⎛⎭⎫x ＋12＝1＋k 2(k ＋1)，|PQ |＝1＋k 2(x Q －x )＝－(k －1)(k ＋1)2k 2＋1， 所以|P A |·|PQ |＝－(k －1)(k ＋1)3， 令f (k )＝－(k －1)(k ＋1)3， 因为f ′(k )＝－(4k －2)(k ＋1)2，所以f (k )在区间⎝⎛⎭⎫－1，12上单调递增，⎝⎛⎭⎫12，1上单调递减． 因此当k ＝12时，|P A |·|PQ |取得最大值2716.8．(2017·江苏，17)如图，在平面直角坐标系xOy 中，椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，离心率为12，两准线之间的距离为8.点P 在椭圆E 上，且位于第一象限，过点F 1作直线PF 1的垂线l 1，过点F 2作直线PF 2的垂线l 2.(1)求椭圆E 的标准方程；(2)若直线l 1，l 2的交点Q 在椭圆E 上，求点P 的坐标． 8．解 (1)设椭圆的半焦距为c .因为椭圆E 的离心率为12，两准线之间的距离为8，所以c a ＝12，2a 2c ＝8，解得a ＝2，c ＝1，于是b ＝a 2－c 2＝3， 因此椭圆E 的标准方程是x 24＋y 23＝1.(2)由(1)知，F 1(－1,0)，F 2(1,0)．设P (x 0，y 0)，因为P 为第一象限的点，故x 0>0，y 0>0. 当x 0＝1时，l 2与l 1相交于F 1，与题设不符．当x 0≠1时，直线PF 1的斜率为y 0x 0＋1，直线PF 2的斜率为y 0x 0－1.因为l 1⊥PF 1，l 2⊥PF 2， 所以直线l 1的斜率为－x 0＋1y 0，直线l 2的斜率为－x 0－1y 0，从而直线l 1的方程为y ＝－x 0＋1y 0(x ＋1)，① 直线l 2的方程为y ＝－x 0－1y 0(x －1)．②由①②，解得x ＝－x 0，y ＝x 20－1y 0，所以Q ⎝⎛⎭⎫－x 0，x 20－1y 0.因为点Q 在椭圆E 上，由对称性，得x 20－1y 0＝±y 0，即x 20－y 20＝1或x 20＋y 20＝1.又点P 在椭圆E 上，故x 204＋y 203＝1.由⎩⎪⎨⎪⎧ x 20－y 20＝1，x 204＋y 203＝1，解得x 0＝477，y 0＝377； ⎩⎪⎨⎪⎧x 20＋y 20＝1，x 204＋y 203＝1无解． 因此点P 的坐标为⎝⎛⎭⎫477，377.9．(2017·全国Ⅰ理，20)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)，四点P 1(1,1)，P 2(0,1)，P 3⎝⎛⎭⎫－1，32，P 4⎝⎛⎭⎫1，32中恰有三点在椭圆C 上． (1)求C 的方程；(2)设直线l 不经过P 2点且与C 相交于A ，B 两点．若直线P 2A 与直线P 2B 的斜率的和为－1，证明：l 过定点．9．(1)解 由于P 3，P 4两点关于y 轴对称，故由题设知椭圆C 经过P 3，P 4两点． 又由1a 2＋1b 2>1a 2＋34b 2知，椭圆C 不经过点P 1，所以点P 2在椭圆C 上．因此⎩⎨⎧1b 2＝1，1a 2＋34b 2＝1，解得⎩⎪⎨⎪⎧a 2＝4，b 2＝1.故椭圆C 的方程为x 24＋y 2＝1.(2)证明 设直线P 2A 与直线P 2B 的斜率分别为k 1，k 2.如果l 与x 轴垂直，设l ：x ＝t ，由题设知t ≠0，且|t |<2，可得A ，B 的坐标分别为⎝ ⎛⎭⎪⎫t ，4－t 22，⎝⎛⎭⎪⎫t ，－4－t 22，则k 1＋k 2＝4－t 2－22t －4－t 2＋22t ＝－1，得t ＝2，不符合题设． 从而可设l ：y ＝kx ＋m (m ≠1)． 将y ＝kx ＋m 代入x 24＋y 2＝1，得(4k 2＋1)x 2＋8kmx ＋4m 2－4＝0. 由题设可知Δ＝16(4k 2－m 2＋1)>0.设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－8km4k 2＋1，x 1x 2＝4m 2－44k 2＋1.而k 1＋k 2＝y 1－1x 1＋y 2－1x 2＝kx 1＋m －1x 1＋kx 2＋m －1x 2＝2kx 1x 2＋(m －1)(x 1＋x 2)x 1x 2.由题设k 1＋k 2＝－1，故(2k ＋1)x 1x 2＋(m －1)(x 1＋x 2)＝0. 即(2k ＋1)·4m 2－44k 2＋1＋(m －1)·－8km4k 2＋1＝0，解得k ＝－m ＋12.当且仅当m >－1时，Δ>0， 于是l ：y ＝－m ＋12x ＋m ，即y ＋1＝－m ＋12(x －2)，所以l 过定点(2，－1)．10．(2017·全国Ⅱ理，20)设O 为坐标原点，动点M 在椭圆C ：x 22＋y 2＝1上，过M 作x 轴的垂线，垂足为N ，点P 满足NP →＝2NM →. (1)求点P 的轨迹方程；(2)设点Q 在直线x ＝－3上，且OP →·PQ →＝1.证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F .10．解 (1)设P (x ，y )，M (x 0，y 0)，则N (x 0,0)， NP →＝(x －x 0，y )，NM →＝(0，y 0)． 由NP →＝2NM →，得x 0＝x ，y 0＝22y ，因为M (x 0，y 0)在C 上，所以x 22＋y 22＝1.因此点P 的轨迹方程为x 2＋y 2＝2.(2)由题意知F (－1,0)．设Q (－3，t )，P (m ，n )，则OQ →＝(－3，t )，PF →＝(－1－m ，－n )， OQ →·PF →＝3＋3m －tn ，OP →＝(m ，n )，PQ →＝(－3－m ，t －n )， 由OP →·PQ →＝1，得－3m －m 2＋tn －n 2＝1， 又由(1)知m 2＋n 2＝2，故3＋3m －tn ＝0，所以OQ →·PF →＝0，即OQ →⊥PF →，又过点P 存在唯一直线垂直于OQ ，所以过点P 且垂直于OQ 的直线l 过C 的左焦点F .11．(2017·全国Ⅲ理，20)已知抛物线C ：y 2＝2x ，过点(2,0)的直线l 交C 与A ，B 两点，圆M 是以线段AB 为直径的圆． (1)证明：坐标原点O 在圆M 上；(2)设圆M 过点P (4，－2)，求直线l 与圆M 的方程． 11．(1)证明 设A (x 1，y 1)，B (x 2，y 2)，l ：x ＝my ＋2.由⎩⎪⎨⎪⎧x ＝my ＋2，y 2＝2x ，可得y 2－2my －4＝0，则y 1y 2＝－4. 又x 1＝y 212，x 2＝y 222，故x 1x 2＝(y 1y 2)24＝4.因此OA 的斜率与OB 的斜率之积为y 1x 1·y 2x 2＝－44＝－1，所以OA ⊥OB ，故坐标原点O 在圆M 上． (2)解 由(1)可得y 1＋y 2＝2m ， x 1＋x 2＝m (y 1＋y 2)＋4＝2m 2＋4， 故圆心M 的坐标为(m 2＋2，m )， 圆M 的半径r ＝(m 2＋2)2＋m 2.由于圆M 过点P (4，－2)，因此AP →·BP →＝0， 故(x 1－4)(x 2－4)＋(y 1＋2)(y 2＋2)＝0， 即x 1x 2－4(x 1＋x 2)＋y 1y 2＋2(y 1＋y 2)＋20＝0. 由(1)可知y 1y 2＝－4，x 1x 2＝4，所以2m 2－m －1＝0，解得m ＝1或m ＝－12.当m ＝1时，直线l 的方程为x －y －2＝0，圆心M 的坐标为(3,1)，圆M 的半径为10， 圆M 的方程为(x －3)2＋(y －1)2＝10.当m ＝－12时，直线l 的方程为2x ＋y －4＝0，圆心M 的坐标为⎝⎛⎭⎫94，－12，圆M 的半径为854， 圆M 的方程为⎝⎛⎭⎫x －942＋⎝⎛⎭⎫y ＋122＝8516. 12．(2017·北京理，18)已知抛物线C ：y 2＝2px 过点P (1,1)，过点⎝⎛⎭⎫0，12作直线l 与抛物线C 交于不同的两点M ，N ，过点M 作x 轴的垂线分别与直线OP ，ON 交于点A ，B ，其中O 为原点．(1)求抛物线C 的方程，并求其焦点坐标和准线方程； (2)求证：A 为线段BM 的中点．12．(1)解：由抛物线C ∶y 2＝2px 过点P (1,1)，得p ＝12，所以抛物线C 的方程为y 2＝x ，抛物线C 的焦点坐标为⎝⎛⎭⎫14，0，准线方程为x ＝－14. (2)证明：由题意，设直线l 的方程为y ＝kx ＋12(k ≠0)，l 与抛物线C 的交点为M (x 1，y 1)，N (x 2，y 2)．由⎩⎪⎨⎪⎧y ＝kx ＋12，y 2＝x ，得4k 2x 2＋(4k －4)x ＋1＝0，则x 1＋x 2＝1－k k 2，x 1x 2＝14k 2.因为点P 的坐标为(1,1)，所以直线OP 的方程为y ＝x ，点A 的坐标为(x 1，x 1)． 直线ON 的方程为y ＝y 2x 2x ，点B 的坐标为⎝⎛⎭⎫x 1，y 2x 1x 2. 因为y 1＋y 2x 1x 2－2x 1＝y 1x 2＋y 2x 1－2x 1x 2x 2＝⎝⎛⎭⎫kx 1＋12x 2＋⎝⎛⎭⎫kx 2＋12x 1－2x 1x 2x 2＝(2k －2)x 1x 2＋12(x 2＋x 1)x 2＝(2k －2)×14k 2＋1－k2k2x 2＝0，所以y 1＋y 2x 1x 2＝2x 1，故A 为线段BM 的中点．13．(2017·天津理，19)设椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左焦点为F ，右顶点为A ，离心率为12.已知A 是抛物线y 2＝2px (p >0)的焦点，F 到抛物线的准线l 的距离为12.(1)求椭圆的方程和抛物线的方程；(2)设l 上两点P ，Q 关于x 轴对称，直线AP 与椭圆相交于点B (B 异于点A )，直线BQ 与x 轴相交于点D .若△APD 的面积为62，求直线AP 的方程． 13．解 (1)设点F 的坐标为(－c,0)，依题意，得c a ＝12，p 2＝a ，a －c ＝12，解得a ＝1，c ＝12，p ＝2，于是b 2＝a 2－c 2＝34.所以，椭圆的方程为x 2＋4y 23＝1，抛物线的方程为y 2＝4x .(2)设直线AP 的方程为x ＝my ＋1(m ≠0)，与直线l 的方程x ＝－1联立， 可得点P ⎝⎛⎭⎫－1，－2m ， 故点Q ⎝⎛⎭⎫－1，2m . 将x ＝my ＋1与x 2＋4y 23＝1联立，消去x ，整理得(3m 2＋4)y 2＋6my ＝0，解得y ＝0或y ＝－6m3m 2＋4.由点B 异于点A ，可得点B ⎝ ⎛⎭⎪⎫－3m 2＋43m 2＋4，－6m 3m 2＋4， 由Q ⎝⎛⎭⎫－1，2m ，可得直线BQ 的方程为 ⎝ ⎛⎭⎪⎫－6m 3m 2＋4－2m (x ＋1)－⎝ ⎛⎭⎪⎫－3m 2＋43m 2＋4＋1⎝⎛⎭⎫y －2m ＝0， 令y ＝0，解得x ＝2－3m 23m 2＋2，故点D ⎝ ⎛⎭⎪⎫2－3m 23m 2＋2，0. 所以|AD |＝1－2－3m 23m 2＋2＝6m 23m 2＋2.又因为△APD 的面积为62， 故12×6m 23m 2＋2×2|m |＝62， 整理得3m 2－26|m |＋2＝0， 解得|m |＝63，所以m ＝±63. 所以，直线AP 的方程为3x ＋6y －3＝0或3x －6y －3＝0.14．(2017·山东理，21)在平面直角坐标系xOy 中，椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为22，焦距为2.(1)求椭圆E 的方程； (2)如图，动直线l ：y ＝k 1x －32交椭圆E 于A ，B 两点，C 是椭圆E 上一点，直线OC 的斜率为k 2，且k 1k 2＝24.M 是线段OC 延长线上一点，且|MC |∶|AB |＝2∶3，⊙M 的半径为|MC |，OS ，OT 是⊙M 的两条切线，切点分别为S ，T .求∠SOT 的最大值，并求取得最大值时直线l 的斜率．14．解 (1)由题意知e ＝c a ＝22，2c ＝2，所以c ＝1，所以a ＝2，b ＝1，所以椭圆E 的方程为x 22＋y 2＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，联立方程⎩⎨⎧x 22＋y 2＝1，y ＝k 1x －32，得(4k 21＋2)x 2－43k 1x －1＝0.由题意知Δ＞0，且x 1＋x 2＝23k 12k 21＋1，x 1x 2＝－12(2k 21＋1)， 所以|AB |＝1＋k 21|x 1－x 2|＝21＋k 211＋8k 211＋2k 21.由题意可知，圆M 的半径r 为r ＝23|AB |＝223·1＋k 211＋8k 212k 21＋1， 由题设知k 1k 2＝24， 所以k 2＝24k 1，因此直线OC 的方程为y ＝24k 1x . 联立方程⎩⎨⎧x 22＋y 2＝1，y ＝24k 1x ，得x 2＝8k 211＋4k 21，y 2＝11＋4k 21， 因此|OC |＝x 2＋y 2＝1＋8k 211＋4k 21. 由题意可知，sin ∠SOT 2＝r r ＋|OC |＝11＋|OC |r .而|OC |r ＝1＋8k 211＋4k 21223·1＋k 211＋8k 211＋2k 21 ＝324·1＋2k 211＋4k 211＋k 21， 令t ＝1＋2k 21，则t ＞1，1t ∈(0,1)， 因此|OC |r ＝32·t 2t 2＋t －1＝32·12＋1t －1t 2＝32·1－⎝⎛⎭⎫1t －122＋94≥1， 当且仅当1t ＝12，即t ＝2时等号成立，此时k 1＝±22，所以sin∠SOT 2≤12，因此∠SOT 2≤π6， 所以∠SOT 的最大值为π3.综上所述，∠SOT 的最大值为π3，取得最大值时直线l 的斜率为k 1＝±22.。

2017年高考真题--立体几何部分2017年高考真题--立体几何部分学校: ___________ 姓名： ____________ 级:___________ 号： _______________一、解答题1 • (12 分)如图，四棱锥P-ABCD 中，侧面PAD 为等比三 角形且垂直于底面 ABCD ,(1)证明：直线CE//平面PAB(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成锐角为45。

，求二面角MABD 的余弦值 2( 12分)如图，在四棱锥P-ABCD 中AB//CD 且 BAP CDP 90。

90o ,E 是PD 的中点.AB BC 1 AD, BAD ABC⑴证明：平面PABL平面PAD(2)若PA=PDAB=DC APD 900,求二面角APBC 的余弦值.3. (12分)如图，四面体ABCD中, △ ABC是正三角形，△ ACD是直角三角形，/ ABD M CBD(1)证明：平面ACDL平面ABC(2)过AC的平面交BD于点E,若平面AEC 把四面体ABCD分成体积相等的两部分，求二面角D- AE- C的余弦值.4.如图，在四棱锥P-ABCD中，底面ABC助正方形，平面PAD L平面ABCD点M在线段PB 上, PD// 平面MAC PA=PD=76，AB=4.(I )求证：M为PB的中点；(II )求二面角BPDA的大小；(Ill )求直线MC与平面BDP所成角的正弦值.5 .如图，在三棱锥P- ABC中, P从底面ABC BAC90 .点D, E, N分别为棱PA P C, BC的中点，M是线段AD的中点，PAAC=4, AB=2. (l)求证：MN/平面BDE(U)求二面角GEMN的正弦值；(m) 已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为^7，求线段AH的长.6 . 17.如图，几何体是圆柱的一部分，它是由矩形肋切(及其内部)以班边所在直线为旋转轴旋转咗疔得到的，”是亦的中点.(I)设尸是在上的一点，且黠-施，求如尸的大小；(H)当肺^,皿"，求二面角£-^-c的大小.7 •(本题满分15分)如图，已知四棱锥P -ABCD，APAD是以AD为斜边的等腰直角三角形，BC II AD , CD 丄AD ,PC=AD=2DC=2CB, E 为PD 的中点.I平面PAB;(H)求直线CE与平面PBC所成角的正弦1.(1 )详见解析连接 EF 、BF 、EC・• E、F 分别为PD 、PA 中点 •••已 2AD，又•••叱 0・•・EF £BC,•四边形BCEF 为平行四边形 •・CE //平面PAD(2 )取AD 中点O ，连PO ,由于△ PAD 为正三角形 •・ PO AD又I 平面 PAD 平面ABCD ，平面PAD 平面ABCD AD参考答案(2 ) cos【解析】 (1)取PA 中点F ,・•・PO平面ABCD，连OC，四边形ABCD为正方形。

2021年高考数学空间几何高考真题一．选择题〔共9小题〕1．如图，在以下四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，那么在这四个正方体中，直线与平面不平行的是〔〕A．B．C．D．2．圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，那么该圆柱的体积为〔〕A．πB．C．D．3．在正方体﹣A1B1C1D1中，E为棱的中点，那么〔〕A．A1E⊥1B．A1E⊥ C．A1E⊥1D．A1E⊥4．某三棱锥的三视图如下图，那么该三棱锥的体积为〔〕A．60 B．30 C．20 D．105．某几何体的三视图如下图〔单位：〕，那么该几何体的体积〔单位：2〕是〔〕A．+1 B．+3 C．+1 D．+36．如图，正四面体D﹣〔所有棱长均相等的三棱锥〕，P、Q、R 分别为、、上的点，，2，分别记二面角D﹣﹣Q，D﹣﹣R，D ﹣﹣P的平面角为α、β、γ，那么〔〕A．γ＜α＜β B．α＜γ＜β C．α＜β＜γ D．β＜γ＜α7．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一局部后所得，那么该几何体的体积为〔〕A．90πB．63πC．42πD．36π1．某多面体的三视图如下图，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有假设干个是梯形，这些梯形的面积之和为〔〕A．10 B．12 C．14 D．162．直三棱柱﹣A1B1C1中，∠120°，2，1=1，那么异面直线1与1所成角的余弦值为〔〕A．B．C．D．二．填空题〔共5小题〕8．三棱锥S﹣的所有顶点都在球O的球面上，是球O的直径．假设平面⊥平面，，，三棱锥S﹣的体积为9，那么球O的外表积为．9．长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，那么球O的外表积为．10．一个正方体的所有顶点在一个球面上，假设这个正方体的外表积为18，那么这个球的体积为．11．由一个长方体和两个圆柱体构成的几何体的三视图如图，那么该几何体的体积为．12．如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，那么的值是．三．解答题〔共9小题〕13．如图，在四棱锥P﹣中，∥，且∠∠90°．〔1〕证明：平面⊥平面；〔2〕假设，∠90°，且四棱锥P﹣的体积为，求该四棱锥的侧面积．14．如图，四棱锥P﹣中，侧面为等边三角形且垂直于底面，，∠∠90°．〔1〕证明：直线∥平面；〔2〕假设△面积为2，求四棱锥P﹣的体积．15．如图四面体中，△是正三角形，．〔1〕证明：⊥；〔2〕△是直角三角形，，假设E为棱上与D不重合的点，且⊥，求四面体与四面体的体积比．16．如图，直三棱柱﹣A1B1C1的底面为直角三角形，两直角边和的长分别为4和2，侧棱1的长为5．〔1〕求三棱柱﹣A1B1C1的体积；〔2〕设M是中点，求直线A1M与平面所成角的大小．17．如图，在三棱锥P﹣中，⊥，⊥，⊥，2，D为线段的中点，E为线段上一点．〔1〕求证：⊥；〔2〕求证：平面⊥平面；〔3〕当∥平面时，求三棱锥E﹣的体积．18．如图，在四棱锥P﹣中，⊥平面，∥，⊥，1，3，4，2．〔Ⅰ〕求异面直线与所成角的余弦值；〔Ⅱ〕求证：⊥平面；〔Ⅲ〕求直线与平面所成角的正弦值．19．如图，四棱锥P﹣，△是以为斜边的等腰直角三角形，∥，⊥，22，E为的中点．〔Ⅰ〕证明：∥平面；〔Ⅱ〕求直线与平面所成角的正弦值．20．由四棱柱﹣A1B1C1D1截去三棱锥C1﹣B11后得到的几何体如下图，四边形为正方形，O为与的交点，E为的中点，A1E⊥平面，〔Ⅰ〕证明：A1O∥平面B11；〔Ⅱ〕设M是的中点，证明：平面A1⊥平面B11．21．如图，在三棱锥A﹣中，⊥，⊥，平面⊥平面，点E、F〔E 与A、D不重合〕分别在棱，上，且⊥．求证：〔1〕∥平面；〔2〕⊥．3．如图，在四棱锥P﹣中，∥，且∠∠90°．〔1〕证明：平面⊥平面；〔2〕假设，∠90°，求二面角A﹣﹣C的余弦值．4．如图，四棱锥P﹣中，侧面为等边三角形且垂直于底面，，∠∠90°，E是的中点．〔1〕证明：直线∥平面；〔2〕点M在棱上，且直线与底面所成角为45°，求二面角M ﹣﹣D的余弦值．5．如图，四面体中，△是正三角形，△是直角三角形，∠∠，．〔1〕证明：平面⊥平面；〔2〕过的平面交于点E，假设平面把四面体分成体积相等的两局部，求二面角D﹣﹣C的余弦值．6．如图，在四棱锥P﹣中，底面为正方形，平面⊥平面，点M 在线段上，∥平面，，4．〔1〕求证：M为的中点；〔2〕求二面角B﹣﹣A的大小；〔3〕求直线与平面所成角的正弦值．7．如图，在三棱锥P﹣中，⊥底面，∠90°．点D，E，N分别为棱，，的中点，M是线段的中点，4，2．〔Ⅰ〕求证：∥平面；〔Ⅱ〕求二面角C﹣﹣N的正弦值；〔Ⅲ〕点H在棱上，且直线与直线所成角的余弦值为，求线段的长．8．如图，几何体是圆柱的一局部，它是由矩形〔及其内部〕以边所在直线为旋转轴旋转120°得到的，G是的中点．〔Ⅰ〕设P是上的一点，且⊥，求∠的大小；〔Ⅱ〕当3，2时，求二面角E﹣﹣C的大小．2021年高考数学空间几何高考真题参考答案与试题解析一．选择题〔共7小题〕1．如图，在以下四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，那么在这四个正方体中，直线与平面不平行的是〔〕A．B．C．D．【解答】解：对于选项B，由于∥，结合线面平行判定定理可知B不满足题意；对于选项C，由于∥，结合线面平行判定定理可知C不满足题意；对于选项D，由于∥，结合线面平行判定定理可知D不满足题意；所以选项A满足题意，应选：A．2．圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，那么该圆柱的体积为〔〕A．πB．C．D．【解答】解：∵圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，∴该圆柱底面圆周半径，∴该圆柱的体积：．应选：B．3．在正方体﹣A1B1C1D1中，E为棱的中点，那么〔〕A．A1E⊥1B．A1E⊥ C．A1E⊥1D．A1E⊥【解答】解：法一：连B1C，由题意得1⊥B1C，∵A1B1⊥平面B11，且1⊂平面B11，∴A1B1⊥1，∵A1B1∩B11，∴1⊥平面A11，∵A1E⊂平面A11，∴A1E⊥1．应选：C．法二：以D为原点，为x轴，为y轴，1为z轴，建立空间直角坐标系，设正方体﹣A1B1C1D1中棱长为2，那么A1〔2，0，2〕，E〔0，1，0〕，B〔2，2，0〕，D〔0，0，0〕，C1〔0，2，2〕，A〔2，0，0〕，C〔0，2，0〕，=〔﹣2，1，﹣2〕，=〔0，2，2〕，=〔﹣2，﹣2，0〕，=〔﹣2，0，2〕，=〔﹣2，2，0〕，∵•=﹣2，=2，=0，=6，∴A1E⊥1．应选：C．4．某三棱锥的三视图如下图，那么该三棱锥的体积为〔〕A．60 B．30 C．20 D．10【解答】解：由三视图可知：该几何体为三棱锥，该三棱锥的体积10．应选：D．5．某几何体的三视图如下图〔单位：〕，那么该几何体的体积〔单位：2〕是〔〕A．+1 B．+3 C．+1 D．+3【解答】解：由几何的三视图可知，该几何体是圆锥的一半和一个三棱锥组成，圆锥的底面圆的半径为1，三棱锥的底面是底边长2的等腰直角三角形，圆锥的高和棱锥的高相等均为3，故该几何体的体积为××π×12×3+××××31，应选：A6．如图，正四面体D﹣〔所有棱长均相等的三棱锥〕，P、Q、R 分别为、、上的点，，2，分别记二面角D﹣﹣Q，D﹣﹣R，D ﹣﹣P的平面角为α、β、γ，那么〔〕A．γ＜α＜β B．α＜γ＜β C．α＜β＜γ D．β＜γ＜α【解答】解法一：如下图，建立空间直角坐标系．设底面△的中心为O．不妨设3．那么O〔0，0，0〕，P〔0，﹣3，0〕，C〔0，﹣6，0〕，D〔0，0，6〕，Q，R，=，=〔0，3，6〕，=〔，5，0〕，=，=．设平面的法向量为=〔x，y，z〕，那么，可得，可得=，取平面的法向量=〔0，0，1〕．那么，取α．同理可得：β．γ．∵＞＞．∴α＜γ＜β．解法二：如下图，连接，，，过点O分别作垂线：⊥，⊥，⊥，垂足分别为E，F，G，连接，，．设．那么α=．同理可得：β=，γ=．由可得：＞＞．∴α＜γ＜β，α，β，γ为锐角．∴α＜γ＜β．应选：B．7．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一局部后所得，那么该几何体的体积为〔〕A．90πB．63πC．42πD．36π【解答】解：由三视图可得，直观图为一个完整的圆柱减去一个高为6的圆柱的一半，π•32×10﹣•π•32×6=63π，应选：B．1．某多面体的三视图如下图，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有假设干个是梯形，这些梯形的面积之和为〔〕A．10 B．12 C．14 D．16【解答】解：由三视图可画出直观图，该立体图中只有两个一样的梯形的面，S梯形=×2×〔2+4〕=6，∴这些梯形的面积之和为6×2=12，应选：B2．直三棱柱﹣A1B1C1中，∠120°，2，1=1，那么异面直线1与1所成角的余弦值为〔〕A．B．C．D．【解答】解：【解法一】如下图，设M、N、P分别为，1和B1C1的中点，那么1、1夹角为和夹角或其补角〔因异面直线所成角为〔0，]〕，可知1=，1=；作中点Q，那么△为直角三角形；∵1，，△中，由余弦定理得222﹣2••∠=4+1﹣2×2×1×〔﹣〕=7，∴，∴；在△中，；在△中，由余弦定理得∠﹣；又异面直线所成角的范围是〔0，]，∴1与1所成角的余弦值为．【解法二】如下图，补成四棱柱﹣A1B1C1D1，求∠1D即可；1=，，C1，∴2=，∴∠1=90°，∴∠1．二．填空题〔共5小题〕8．三棱锥S﹣的所有顶点都在球O的球面上，是球O的直径．假设平面⊥平面，，，三棱锥S﹣的体积为9，那么球O的外表积为36π．【解答】解：三棱锥S﹣的所有顶点都在球O的球面上，是球O 的直径，假设平面⊥平面，，，三棱锥S﹣的体积为9，可知三角形与三角形都是等腰直角三角形，设球的半径为r，可得，解得3．球O的外表积为：4πr2=36π．故答案为：36π．9．长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，那么球O的外表积为14π．【解答】解：长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，可知长方体的对角线的长就是球的直径，所以球的半径为：=．那么球O的外表积为：4×=14π．故答案为：14π．10．一个正方体的所有顶点在一个球面上，假设这个正方体的外表积为18，那么这个球的体积为．【解答】解：设正方体的棱长为a，∵这个正方体的外表积为18，∴6a2=18，那么a2=3，即，∵一个正方体的所有顶点在一个球面上，∴正方体的体对角线等于球的直径，即2R，即，那么球的体积π•〔〕3=；故答案为：．11．由一个长方体和两个圆柱体构成的几何体的三视图如图，那么该几何体的体积为2+．【解答】解：由长方体长为2，宽为1，高为1，那么长方体的体积V1=2×1×1=2，圆柱的底面半径为1，高为1，那么圆柱的体积V2=×π×12×1=，那么该几何体的体积1+2V1=2+，故答案为：2+．12．如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，那么的值是．【解答】解：设球的半径为R，那么球的体积为：R3，圆柱的体积为：πR2•22πR3．那么．故答案为：．三．解答题〔共9小题〕13．如图，在四棱锥P﹣中，∥，且∠∠90°．〔1〕证明：平面⊥平面；〔2〕假设，∠90°，且四棱锥P﹣的体积为，求该四棱锥的侧面积．【解答】证明：〔1〕∵在四棱锥P﹣中，∠∠90°，∴⊥，⊥，又∥，∴⊥，∵∩，∴⊥平面，∵⊂平面，∴平面⊥平面．解：〔2〕设，取中点O，连结，∵，∠90°，平面⊥平面，∴⊥底面，且，，∵四棱锥P﹣的体积为，∴﹣，解得2，∴2，2，，∴2，∴该四棱锥的侧面积：S侧△△△△==6+2．14．如图，四棱锥P﹣中，侧面为等边三角形且垂直于底面，，∠∠90°．〔1〕证明：直线∥平面；〔2〕假设△面积为2，求四棱锥P﹣的体积．【解答】〔1〕证明：四棱锥P﹣中，∵∠∠90°．∴∥，∵⊂平面，⊄平面，∴直线∥平面；〔2〕解：四棱锥P﹣中，侧面为等边三角形且垂直于底面，，∠∠90°．设2x，那么，，O是的中点，连接，，的中点为：E，连接，那么，，，△面积为2，可得：=2，即：，解得2，2．那么V P﹣×〔〕××4．15．如图四面体中，△是正三角形，．〔1〕证明：⊥；〔2〕△是直角三角形，，假设E为棱上与D不重合的点，且⊥，求四面体与四面体的体积比．【解答】证明：〔1〕取中点O，连结、，∵△是正三角形，，∴⊥，⊥，∵∩，∴⊥平面，∵⊂平面，∴⊥．解：〔2〕法一：连结，由〔1〕知⊥平面，∵⊂平面，∴⊥，设，那么1，∴E是线段垂直平分线上的点，∴，由余弦定理得：∠，即，解得1或2，∵＜＜2，∴1，∴，∵四面体与四面体的高都是点A到平面的高h，∵，∴S△△，∴四面体与四面体的体积比为1．法二：设，那么2，1，∴，∴222，∴⊥，以O为原点，为x轴，为y轴，为z轴，建立空间直角坐标系，那么C〔﹣1，0，0〕，D〔0，0，1〕，B〔0，，0〕，A〔1，0，0〕，设E〔a，b，c〕，，〔0≤λ≤1〕，那么〔a，b，c﹣1〕=λ〔0，，﹣1〕，解得E〔0，，1﹣λ〕，∴=〔1，〕，=〔﹣1，〕，∵⊥，∴=﹣1+3λ2+〔1﹣λ〕2=0，由λ∈[0，1]，解得，∴，∵四面体与四面体的高都是点A到平面的高h，∵，∴S△△，∴四面体与四面体的体积比为1．16．如图，直三棱柱﹣A1B1C1的底面为直角三角形，两直角边和的长分别为4和2，侧棱1的长为5．〔1〕求三棱柱﹣A1B1C1的体积；〔2〕设M是中点，求直线A1M与平面所成角的大小．【解答】解：〔1〕∵直三棱柱﹣A1B1C1的底面为直角三角形，两直角边和的长分别为4和2，侧棱1的长为5．∴三棱柱﹣A1B1C1的体积：△×1=20．〔2〕连结，∵直三棱柱﹣A1B1C1的底面为直角三角形，两直角边和的长分别为4和2，侧棱1的长为5，M是中点，∴1⊥底面，，∴∠A1是直线A1M与平面所成角，∠A1，∴直线A1M与平面所成角的大小为．17．如图，在三棱锥P﹣中，⊥，⊥，⊥，2，D为线段的中点，E为线段上一点．〔1〕求证：⊥；〔2〕求证：平面⊥平面；〔3〕当∥平面时，求三棱锥E﹣的体积．【解答】解：〔1〕证明：由⊥，⊥，⊂平面，⊂平面，且∩，可得⊥平面，由⊂平面，可得⊥；〔2〕证明：由，D为线段的中点，可得⊥，由⊥平面，⊂平面，可得平面⊥平面，又平面∩平面，⊂平面，且⊥，即有⊥平面，⊂平面，可得平面⊥平面；〔3〕∥平面，⊂平面，且平面∩平面，可得∥，又D为的中点，可得E为的中点，且1，由⊥平面，可得⊥平面，可得S△△××2×2=1，那么三棱锥E﹣的体积为•S△×1×1=．18．如图，在四棱锥P﹣中，⊥平面，∥，⊥，1，3，4，2．〔Ⅰ〕求异面直线与所成角的余弦值；〔Ⅱ〕求证：⊥平面；〔Ⅲ〕求直线与平面所成角的正弦值．【解答】解：〔Ⅰ〕如图，由∥，故∠或其补角即为异面直线与所成的角．因为⊥平面，所以⊥．在△中，由，得，故．所以，异面直线与所成角的余弦值为．证明：〔Ⅱ〕因为⊥平面，直线⊂平面，所以⊥．又因为∥，所以⊥，又⊥，所以⊥平面．解：〔Ⅲ〕过点D作的平行线交于点F，连结，那么与平面所成的角等于与平面所成的角．因为⊥平面，故为在平面上的射影，所以∠为直线和平面所成的角．由于∥，∥，故1，由，得﹣2．又⊥，故⊥，在△中，可得．所以，直线与平面所成角的正弦值为．19．如图，四棱锥P﹣，△是以为斜边的等腰直角三角形，∥，⊥，22，E为的中点．〔Ⅰ〕证明：∥平面；〔Ⅱ〕求直线与平面所成角的正弦值．【解答】证明：〔Ⅰ〕取的中点F，连结，，∵E为的中点，∴∥，在四边形中，∥，22，F为中点，∴∥，∴平面∥平面，∵⊂平面，∴∥平面．解：〔Ⅱ〕连结，过F作⊥于M，连结，∵，∴⊥，推导出四边形为矩形，∴⊥，∴⊥平面，又∥，∴⊥平面，∴⊥，设1，那么2，∴，1，∴，又⊥平面，∴⊥，∴⊥平面，即点F到平面的距离为，∵，D到平面的距离应该和平行且相等，为，E为中点，E到平面的垂足也为垂足所在线段的中点，即中位线，∴E到平面的距离为，在，由余弦定理得，设直线与平面所成角为θ，那么θ．20．由四棱柱﹣A1B1C1D1截去三棱锥C1﹣B11后得到的几何体如下图，四边形为正方形，O为与的交点，E为的中点，A1E⊥平面，〔Ⅰ〕证明：A1O∥平面B11；〔Ⅱ〕设M是的中点，证明：平面A1⊥平面B11．【解答】证明：〔Ⅰ〕取B1D1中点G，连结A1G、，∵四边形为正方形，O为与的交点，∴四棱柱﹣A1B1C1D1截去三棱锥C1﹣B11后，A1，∴四边形1是平行四边形，∴A1O∥，∵A1O⊄平面B11，⊂平面B11，∴A1O∥平面B11．〔Ⅱ〕四棱柱﹣A1B1C1D1截去三棱锥C1﹣B11后，1D1，∵M是的中点，O为与的交点，E为的中点，A1E⊥平面，又⊂平面，∴⊥A1E，∵四边形为正方形，O为与的交点，∴⊥，∵M是的中点，E为的中点，∴⊥，∵A1E∩，∴⊥平面A1，∵∥B1D1，∴B1D1⊥平面A1，∵B1D1⊂平面B11，∴平面A1⊥平面B11．21．如图，在三棱锥A﹣中，⊥，⊥，平面⊥平面，点E、F〔E 与A、D不重合〕分别在棱，上，且⊥．求证：〔1〕∥平面；〔2〕⊥．【解答】证明：〔1〕因为⊥，⊥，且A、B、E、F四点共面，所以∥，又因为⊊平面，⊆平面，所以由线面平行判定定理可知：∥平面；〔2〕在线段上取点G，连结、使得∥，那么∥，因为⊥，∥，所以⊥，又因为平面⊥平面，所以⊥平面，所以⊥，又因为⊥，且∩，所以⊥平面，所以⊥，故⊥．3．如图，在四棱锥P﹣中，∥，且∠∠90°．〔1〕证明：平面⊥平面；〔2〕假设，∠90°，求二面角A﹣﹣C的余弦值．【解答】〔1〕证明：∵∠∠90°，∴⊥，⊥，∵∥，∴⊥，又∵∩，且⊂平面，⊂平面，∴⊥平面，又⊂平面，∴平面⊥平面；〔2〕解：∵∥，，∴四边形为平行四边形，由〔1〕知⊥平面，∴⊥，那么四边形为矩形，在△中，由，∠90°，可得△为等腰直角三角形，设2a，那么．取中点O，中点E，连接、，以O为坐标原点，分别以、、所在直线为x、y、z轴建立空间直角坐标系，那么：D〔〕，B〔〕，P〔0，0，〕，C〔〕．，，．设平面的一个法向量为，由，得，取1，得．∵⊥平面，⊂平面，∴⊥，又⊥，∩，∴⊥平面，那么为平面的一个法向量，．∴＜＞．由图可知，二面角A﹣﹣C为钝角，∴二面角A﹣﹣C的余弦值为．4．如图，四棱锥P﹣中，侧面为等边三角形且垂直于底面，，∠∠90°，E是的中点．〔1〕证明：直线∥平面；〔2〕点M在棱上，且直线与底面所成角为45°，求二面角M ﹣﹣D的余弦值．【解答】〔1〕证明：取的中点F，连接，，因为E是的中点，所以，，∠∠90°，∴∥，∴是平行四边形，可得∥，⊂平面，⊄平面，∴直线∥平面；〔2〕解：四棱锥P﹣中，侧面为等边三角形且垂直于底面，，∠∠90°，E是的中点．取的中点O，M在底面上的射影N在上，设2，那么1，，∴∠60°，直线与底面所成角为45°，可得：，，1，可得：122，，，作⊥于Q，连接，所以∠就是二面角M﹣﹣D的平面角，=，二面角M﹣﹣D的余弦值为：=．5．如图，四面体中，△是正三角形，△是直角三角形，∠∠，．〔1〕证明：平面⊥平面；〔2〕过的平面交于点E，假设平面把四面体分成体积相等的两局部，求二面角D﹣﹣C的余弦值．【解答】〔1〕证明：如下图，取的中点O，连接，．∵△是等边三角形，∴⊥．△与△中，，∠∠，∴△≌△，∴．∵△是直角三角形，∴是斜边，∴∠90°．∴．∴2222．∴∠90°．∴⊥．又∩，∴⊥平面．又⊂平面，∴平面⊥平面．〔2〕解：设点D，B到平面的距离分别为，．那么=．∵平面把四面体分成体积相等的两局部，∴1．∴点E是的中点．建立如下图的空间直角坐标系．不妨取2．那么O〔0，0，0〕，A〔1，0，0〕，C〔﹣1，0，0〕，D〔0，0，1〕，B〔0，，0〕，E．=〔﹣1，0，1〕，=，=〔﹣2，0，0〕．设平面的法向量为=〔x，y，z〕，那么，即，取=．同理可得：平面的法向量为=〔0，1，〕．∴﹣．∴二面角D﹣﹣C的余弦值为．6．如图，在四棱锥P﹣中，底面为正方形，平面⊥平面，点M 在线段上，∥平面，，4．〔1〕求证：M为的中点；〔2〕求二面角B﹣﹣A的大小；〔3〕求直线与平面所成角的正弦值．【解答】〔1〕证明：如图，设∩，∵为正方形，∴O为的中点，连接，∵∥平面，⊂平面，平面∩平面，∴∥，那么，即M为的中点；〔2〕解：取中点G，∵，∴⊥，∵平面⊥平面，且平面∩平面，∴⊥平面，那么⊥，连接，那么⊥，由G是的中点，O是的中点，可得∥，那么⊥．以G为坐标原点，分别以、、所在直线为x、y、z轴距离空间直角坐标系，由，4，得D〔2，0，0〕，A〔﹣2，0，0〕，P〔0，0，〕，C 〔2，4，0〕，B〔﹣2，4，0〕，M〔﹣1，2，〕，，．设平面的一个法向量为，那么由，得，取，得．取平面的一个法向量为．∴＜＞．∴二面角B﹣﹣A的大小为60°；〔3〕解：，平面的一个法向量为．∴直线与平面所成角的正弦值为＜＞．7．如图，在三棱锥P﹣中，⊥底面，∠90°．点D，E，N分别为棱，，的中点，M是线段的中点，4，2．〔Ⅰ〕求证：∥平面；〔Ⅱ〕求二面角C﹣﹣N的正弦值；〔Ⅲ〕点H在棱上，且直线与直线所成角的余弦值为，求线段的长．【解答】〔Ⅰ〕证明：取中点F，连接、，∵M为中点，∴∥，∵⊂平面，⊄平面，∴∥平面．∵N为中点，∴∥，又D、E分别为、的中点，∴∥，那么∥．∵⊂平面，⊄平面，∴∥平面．又∩．∴平面∥平面，那么∥平面；〔Ⅱ〕解：∵⊥底面，∠90°．∴以A为原点，分别以、、所在直线为x、y、z轴建立空间直角坐标系．∵4，2，∴A〔0，0，0〕，B〔2，0，0〕，C〔0，4，0〕，M〔0，0，1〕，N 〔1，2，0〕，E〔0，2，2〕，那么，，设平面的一个法向量为，由，得，取2，得．由图可得平面的一个法向量为．∴＜＞=．∴二面角C﹣﹣N的余弦值为，那么正弦值为；〔Ⅲ〕解：设，那么H〔0，0，t〕，，．∵直线与直线所成角的余弦值为，∴＜＞．解得：或．∴当H与P重合时直线与直线所成角的余弦值为，此时线段的长为或．8．如图，几何体是圆柱的一局部，它是由矩形〔及其内部〕以边所在直线为旋转轴旋转120°得到的，G是的中点．〔Ⅰ〕设P是上的一点，且⊥，求∠的大小；〔Ⅱ〕当3，2时，求二面角E﹣﹣C的大小．【解答】解：〔Ⅰ〕∵⊥，⊥，且，⊂平面，∩，∴⊥平面，又⊂平面，∴⊥，又∠120°，因此∠30°；〔Ⅱ〕解法一、取的中点H，连接，，，∵∠120°，∴四边形为菱形，∴．取中点M，连接，，，那么⊥，⊥，∴∠为所求二面角的平面角．又1，∴．在△中，由于∠120°，由余弦定理得：2=22+22﹣2×2×2×120°=12，∴，因此△为等边三角形，故所求的角为60°．解法二、以B为坐标原点，分别以，，所在直线为x，y，z轴建立空间直角坐标系．由题意得：A〔0，0，3〕，E〔2，0，0〕，G〔1，，3〕，C〔﹣1，，0〕，故，，．设为平面的一个法向量，由，得，取z1=2，得；设为平面的一个法向量，由，可得，取z2=﹣2，得．∴＜＞=．∴二面角E﹣﹣C的大小为60°．。