2-2泵与风机的性能曲线

2.5离心式泵与风机的理论性能曲线本节研究泵或风机所具备的技术性能的表达方式。

泵与风机的扬程、流量、功率、效率和转速等性能是互相影响的，当一个参数变化时，其他的都随之变化，这种函数关系用曲线表示，就是泵与风机的性能曲线。

通常用以下三种形式来表示这些性能之间的关系：(1)泵或风机所提供的流量和扬程之间的关系，用）（Q H 1f =来表示：(2)泵或风机所提供的流量和所需外加轴功率之间的关系，用）（Q N 2f =来表示；(3)泵或风机所提供的流量与设备本身效率之间的关系，用）（T T Q H 1f =及）（T T Q N 2f =来表示。

理论性能曲线是从欧拉方程出发，研究无损失流动这一理想条件下及的关系。

如叶轮出口前盘与后盘之间的轮宽为b 2,则叶轮在工作时所排出的理论流量应为：222r T v b D Q επ=(2-15)式中符号同前。

将式(2-15)变换后代入(2-13)可得：对于大小一定的泵或风机来说，转速不变时，上式中u 2，g ，ε，D 2及B 2均为定值，故上式可改写为：(2-16)式中gu 22=A ，222b επD 1g u B ∙=均为常数，而cot β2代表叶型种类，也是常量。

此时说明在固定转速下，不论叶型如何，泵或风机理论上的流量与扬程关系是线形的。

同时还可以看出，当Q T ＝0时，H T ＝gu 22=A 。

图2-8为3种不同叶型的泵和风机理论上的流量-扬程曲线。

显然由所代表的曲线斜率是不同的，因而3种叶型具有各自的曲线倾向。

下面研究理论上的流量与外加功率的关系。

在无损失流动条件下，理论上的有效功率就是轴功率，可按式(1-4)计算，即：当输送某种流体时=常数。

用式(2-16)代人此式可得：(2-17)可见对于不同的值具有不同形状的曲线。

但当Q T =0时，3种叶型的理论轴功率都等于零，3条曲线同相交于原点(见图2-9)。

图2-83种不同叶型的泵图2-93种不同叶型的泵和风机理论上的流量-扬程曲线和风机理论上的流量-功率曲线对于具有径向叶型的叶轮来说=90°，，功率曲线为一条直线。

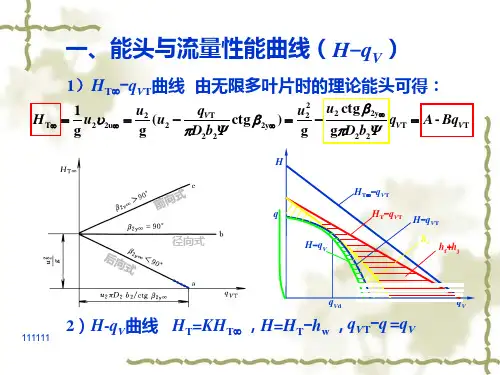
泵的工作曲线1、水泵的性能曲线主要有流量-扬程曲线(Q-H)，流量-功率曲线(Q-P)，流量-效率曲线(Q-η)。

2、首先看曲线是否平坦，有无驼峰。

泵曲线越平越好，当然驼峰是不允许的。

其次看它的效率哪个高。

然后比较他们的范围哪个更宽广，范围越广阔，调整、使用越好。

3、在生产实践中，必须参照泵的性能曲线来选择泵的运行工况点，这样才能使泵经常保持在率区间运行。

4、在性能曲线上，对于一个任意的流量点，都可以找出一组与其相对应的扬程、功率和效率值。

通常，把一组相对应的参数称为工况点称为最好工况点。

5、泵在最率点运行是最理想的。

但用户的要求是千差万别的，不一定和最率点下的性能相一致。

为此，规定了一个范围(效率下降5%~8%为界)，泵在此范围内运行，效率下降不算太大，这个范围就是泵的工作范围(也称范围)。

超出此范围时，效率低，不经济。

扩展资料：常见的性能曲线有三种：1、平坦的性能曲线这种性能曲线适用于流量调节范围较大，而压力变化较小的系统，也就是对扬程要求变化较小、流量变化要求相对较低的系统中。

大多数泵如IS单级离心泵、D型泵、双吸泵、IH化工离心泵等曲线的都是比较平坦的。

2、陡降的性能曲线这种性能曲线适用于对流量的要求较高而压力的要求不高的系统中。

一般像螺杆泵等都具有这种特性。

3、有驼峰的性能曲线有驼峰的性能曲线的泵在运行中可能会出现不稳定工况，泵出现噪音、震动等，一般是不允许出现的。

水泵的性能参数，标志着水泵的性能。

但各性能参数不是孤立的、静止的，而是相互联系和相互制约的。

对于特定的水泵，这种联系和制约具有一定的规律性。

充分了解水泵的性能，熟悉性能曲线的特点，掌握其变化规律，对合理选型配套、正确确定水泵的安装高度、调节水泵运行工况、加强泵站的科学管理等极为重要。

离心风机性能曲线离心风机性能曲线，即压力p 、效率η、功率N 与流量Q 的关系曲线，与离心泵性能曲线的理论定性分析和实测性能曲线的讨论是完全类似的。

但是，由于流体的物理性质的差异，使得在实际应用中，离心风机的性能曲线与水泵有所不同。

如离心风机的静压、静压效率曲线，离心风机的无量纲性能曲线，都在风机中有重要的应用。

一、风机的全压与静压性能曲线1、风机的全压、静压和动压水泵扬程计算式是根据水泵进出口的能量关系，对单位重量液体所获得的能量建立的关系式，即H =（Z 2-Z 1）+g p p ρ12-+gv v 22122-（m ）对于水泵，（Z 2-Z 1）+gv v 22122-<<g p p ρ12-。

故在应用中，水泵的扬程即全压等于静压，也就是水泵单位重量液体获得的总能量可用压能表示。

建立风机进出口的能量关系式，同气体的位能g ρ(Z 2-Z 1)可以忽略，得到单位容积气体所获能量的表达式，即=-=12p p p （2222v p st ρ+）-（2121v p st ρ+） (N/㎡) (4—1)即风机全压p 等于风机出口全压2p 与进口全压1p 之差。

风机进出口全压分别等于各自的静压1st p 、2st p 与动压212v ρ、222v ρ之和。

式（1）适用于风机进出口不直接通大气（即配置有吸风管和压风管）的情况下，风机性能试验的全压计算公式。

该系统称为风机的进出口联合实验装置，是风机性能试验所采用的三种不同实验装置之一。

风机的全压p 是由静压st p 和动压d p 两部分组成。

离心风机全压值上限仅为1500mm （14710Pa ），而出口流速可达30m/s 左右；且流量Q （即出口流速2v ）越大，全压p 就越小。

因此，风机出口动压不能忽略，即全压不等于静压。

例如，当送风管路动压全部损失（即出口损失）的情况下，管路只能依靠静压工作。

为此，离心风机引入了全压、静压和动压的概念。