一次函数图象的平移及解析式的变化规律

一次函数图象的平移及解析式的变化规律我们在研究两个一次函数的图象平行的条件时,曾得出“其中一条直线可以由另外一条直线通过平移得到”的结论,这就涉及到一次函数图象平移的问题. 函数的图象及其解析式,是从“形”和“数”两个方面反映函数的性质,也是初中数学中数形结合思想的重要体现.在平面直角坐标系中,当一次函数的图象发生平移（平行移动）时,与之对应的函数解析式也随之发生改变,并且函数解析式的变化呈现出如下的变化规律:一次函数()0≠+=k b kx y 的图象平移后其解析式的变化遵循“上加下减，左加右减”的规律:（1）上下平移,k 值不变,b 值“上加下减”:将一次函数()0≠+=k b kx y 的图象向上平移m 个单位长度,解析式变为()0≠++=k m b kx y ;将一次函数()0≠+=k b kx y 的图象向下平移m 个单位长度,解析式变为()0≠-+=k m b kx y .（2）左右平移,k 值不变,自变量x “左加右减”:将一次函数()0≠+=k b kx y 的图象向左平移n 个单位长度,解析式变为()()0≠++=k b n x k y ,展开得()0≠++=k b kn kx y ;将一次函数()0≠+=k b kx y 的图象向右平移n 个单位长度,解析式变为()()0≠+-=k b n x k y ,展开得()0≠+-=k b kn kx y .注意:（1）无论一次函数的图象作何种平移,平移前后,k 值不变,b 值改变.设上下平移的单位长度为m ,则b 值变为m b ±;设左右平移的单位长度为n ,则b 值变为kn b ±.（2）上面的规律如下页图（51）所示.图（51）一次函数图象的平移及其解析式的变化规律1. 将直线x y 3=向下平移2个单位,得到直线________________.2. 将直线5--=x y 向上平移5个单位,得到直线________________.3. 将直线32+=x y 向下平移5个单位,得到直线________________.4. 将直线23-=x y 向左平移1个单位,得到直线________________.5. 将直线12--=x y 向上平移3个单位,得到的直线是________________.6. 将一次函数32-=x y 的图象沿y 轴向上平移8个单位长度,所得直线的函数表达式为 【 】（A ）52-=x y （B ）52+=x y（C ）82+=x y （D ）82-=x y7. 将直线x y 2=向右平移2个单位所得的直线是 【 】（A ）22+=x y （B ）22-=x y（C ）()22-=x y （D ）()22+=x y8. 将函数x y 3-=的图象沿y 轴向上平移2个单位后,所得图象对应的函数表达式为 【 】（A ）23+-=x y （B ）23--=x y（C ）()23+-=x y （D ）()23--=x y9. 直线43+=x y 向下平移4个单位,得到直线________________.10. 函数32-=x y 的图象可以看作由函数72+=x y 的图象向_________平移_________个单位得到.11. 把函数32+-=x y 的图象向下平移4个单位后的函数图象的表达式为 【 】 （A ）72+-=x y （B ）36+-=x y（C ）12--=x y （D ）52--=x y12. 将直线42-=x y 向上平移5个单位后,所得直线的表达式是_____________. 13. 直线23+=x y 沿y 轴向下平移5个单位,则平移后直线与y 轴的交点坐标为_________.14. 若直线b kx y +=平行于直线43-=x y ,且过点()2,1-,则该直线对应的函数表达式是 【 】（A ）23-=x y （B ）63--=x y（C ）53-=x y （D ）53+=x y15. 将直线x y 2=先向右平移2个单位长度,再向下平移2个单位长度,所得直线的表达式是________________.16. 直线12-=x y 向上平移3个单位长度后,所得直线与y 轴的交点坐标为_________.17. 已知直线()3252-+-=k x k y ,若该直线经过原点,则=k _________;若该直线与直线53--=x y 平行,则=k _________.18. 若把直线32-=x y 向上平移3个单位长度,得到的图象的表达式是 【 】 （A ）x y 2= （B ）62-=x y（C ）35-=x y （D ）3--=x y19. 要从直线x y 34=的图象得到直线324-=x y ,就要将直线x y 34= 【 】 （A ）向上平移32个单位 （B ）向下平移32个单位 （C ）向上平移2个单位 （D ）向下平移2个单位20. 函数4-=kx y 的图象平行于直线x y 2-=,求函数的表达式.21. 已知一次函数4-=kx y ,当2=x 时,3-=y .（1）求一次函数的关系式;（2）将该函数的图象向上平移6个单位,求平移后的图象与x 轴的交点的坐标.22. 一次函数b kx y +=的图象与y 轴交于点)2,0(-,且与直线213-=x y 平行,求它的函数关系式.23. 在直线321+-=x y 上分别找出满足下列条件的点,并写出它的坐标: （1）横坐标是4-;（2）和x 轴的距离是2个单位.图（52）分析:若不借助于图象,只通过计算,你能确定上面问题的答案吗?。

五种类型一次函数解析式的确定确定一次函数的解析式，是一次函数学习的重要内容。

下面就确定一次函数的解析式的题型作如下的归纳，供同学们学习时参考。

一、根据直线的解析式和图像上一个点的坐标，确定函数的解析式例1、若函数y=3x+b经过点（2，-6），求函数的解析式。

分析：因为，函数y=3x+b经过点（2，-6），所以，点的坐标一定满足函数的关系式，所以，只需把x=2，y=-6代入解析式中，就可以求出b的值。

函数的解析式就确定出来了。

解：因为，函数y=3x+b经过点（2，-6），所以，把x=2，y=-6代入解析式中，得：-6=3×2+b，解得：b=-12，所以，函数的解析式是：y=3x-12.二、根据直线经过两个点的坐标，确定函数的解析式例2、直线y=kx+b的图像经过A（3，4）和点B（2，7），求函数的表达式。

分析：把点的坐标分别代入函数的表达式，用含k的代数式分别表示b，因为b是同一个，这样建立起一个关于k的一元一次方程，这样就可以把k的值求出来，然后，就转化成例1的问题了。

解：因为，直线y=kx+b的图像经过A（3，4）和点B（2，7），所以，4=3k+b，7=2k+b，所以，b=4-3k，b=7-2k，所以，4-3k=7-2k，解得：k=-3，所以，函数变为：y=-3x+b，把x=3，y=4代入上式中，得：4=-3×3+b，解得：b=13，所以，一次函数的解析式为：y=-3x+13。

三、根据函数的图像，确定函数的解析式例3、如图1表示一辆汽车油箱里剩余油量y（升）与行驶时间x（小时）之间的关系．求油箱里所剩油y（升）与行驶时间x（小时）之间的函数关系式，并且确定自变量x的取值范围。

分析：根据图形是线段，是直线上的一部分，所以，我们可以确定油箱里所剩油y（升）是行驶时间x（小时）的一次函数，明白这些后，就可以利用设函数解析式的方法去求函数的解析式。

解：因为，函数的图像是直线，所以，油箱里所剩油y（升）是行驶时间x（小时）的一次函数，设：一次函数的表达式为：y=kx+b，因为，图像经过点A（0，40），B（8，0），所以，把x=0，y=40，x=8，y=0，分别代入y=kx+b中，得：40=k×0+b，0=8k+b解得：k=-5，b=40，所以，一次函数的表达式为：y=-5x+40。

一次函数图象的变换（一）——平移求一次函数图像平移后的解析式是一类重要题型，同学们在做时经常做错，下面我介绍一种简便的方法：抓住点的坐标变化解决问题。

知识点：“已知一个点的坐标和直线的斜率 k，我们就可以写出这条直线的解析式”。

我们知道：y =kx+b经过点（0，b)，而（0，b)向上平移m个单位得到点（0，b+m)，向下平移m个单位得到点（0，b－m)，向左平移m个单位得到点（0－m，b)，向右平移m个单位得到点（0+m，b )，直线y =kx+b平移后斜率不变仍然是k，设出平移后的解析式为y =kx+ h,把平移后得到的点的坐标带入这个解析式求出h，就可以求出平移后直线的解析式。

下面我们通过例题的讲解来反馈知识的应用：例1：把直线y=2x-1向右平移1个单位，求平移后直线的解析式。

分析:y=2x-1经过点（0，-1），向右平移1个单位得到（1，-1）。

平移后斜率不变，即k=2，所以可以设出平移后的解析式为y =2x+ h，再将点（1，-1）代入求出解析式中的h，就可以求出平移后直线的解析式。

解：设平移后的直线解析式为y=2x+h点（0，-1）在y=2x-1上，向右平移1个单位得到（1，-1），将点（1，-1）代入y=2x+h中得：-1=2×1+hh=-3所以平移后直线的解析式为y=2x-3例2：把直线y=2x-1向上平移3个单位，再向右平移1个单位，求平移后直线的解析式。

分析：点（0，-1）在直线y=2x-1上，当直线向上平移3个单位，点变为（0，-1+3），即为（0,2）；再向右平移1个单位后，点（0，2）变为点（0+1，2），即点变为（1,2）。

设出平移后的解析式为y =kx+h，根据斜率k =2不变，以及点（1,2）就可以求出h,从而就可以求出平移后直线的解析式。

解：设平移后的直线解析式为y=2x+h.易知点（0，-1）在直线y=2x-1上，则此点按要求平移后的点为：平移后得到的点（1,2）在直线y=2x+h 上则：2=2×1+hh=0所以平移后的直线解析式为y=2x总结：求直线平移后的解析式时，只要找出一个点坐标，求出按要求平移后此点的坐标变为多少，再根据斜率不变和变化后的点来求解析式。

函数图像的移动规律: 若把一次函数解析式写成y=k（x+0）+b、二次函数的解析式写成y=a（x+h）2+k的形式，则用下面后的口诀“左右平移在括号,上下平移在末稍,左正右负须牢记,上正下负错不了”。

一次函数图像与性质口诀:一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远。

??二次函数图像与性质口诀:二次函数抛物线，图象对称是关键；开口、顶点和交点, 它们确定图象现；开口、大小由a断,c与Y 轴来相见,b的符号较特别，符号与a相关联；顶点位置先找见，Y轴作为参考线，左同右异中为0，牢记心中莫混乱；顶点坐标最重要,一般式配方它就现，横标即为对称轴,纵标函数最值见。

若求对称轴位置, 符号反,一般、顶点、交点式，不同表达能互换。

反比例函数图像与性质口诀:反比例函数有特点,双曲线相背离的远;k为正,图在一、三(象)限,k为负,图在二、四(象)限;图在一、三函数减,两个分支分别减。

图在二、四正相反,两个分支分别添;线越长越近轴,永远与轴不沾边。

函数学习口决：正比例函数是直线，图象一定过圆点，k的正负是关键，决定直线的象限，负k经过二四限，x增大y在减，上下平移k不变，由引得到一次线，向上加b向下减，图象经过三个限，两点决定一条线，选定系数是关键。

反比例函数双曲线，待定只需一个点，正k落在一三限，x增大y在减，图象上面任意点，矩形面积都不变，对称轴是角分线x、y的顺序可交换。

二次函数抛物线，选定需要三个点，a的正负开口判，c的大小y轴看，△的符号最简便，x轴上数交点，a、b同号轴左边抛物线平移a不变，顶点牵着图象转，三种形式可变换，配方法作用最关键。

圆的证明歌：圆的证明不算难，常把半径直径连；有弦可作弦心距，它定垂直平分弦；直径是圆最大弦，直圆周角立上边，它若垂直平分弦，垂径、射影响耳边；还有与圆有关角，勿忘相互有关联，圆周、圆心、弦切角，细找关系把线连。

适用八年级一次函数图象“平移”规律函数的图象及其解析式，是从“形”与“数”两个方面反映函数的性质，也是初中数学中数形结合思想方法的重要体现．在平面直角坐标系内，当一次函数图象发生平移（平行移动）时与之相对应的解析式也随之会改变，本文就其变化规律归纳如下，仅供同学们学习时参考．直线的平移与其解析式y kx b k =+≠()0的关系：① 直线y kx b k =+≠()0平移时，系数k 的值保持不变．② 直线y kx b k =+≠()0向上或向下平移m （m >0）个单位时，解析式变为y kx b m =++或y kx b m =+-，这时可简记为“上加（＋），下减（－）”． ③ 直线y kx b k =+≠()0向左或向右平移m （m >0）个单位时，解析式变为y k x m b =++()或y k x m b =-+()，这时可简记为“左加（＋），右减（－）”． 例1．（2008年上海市）在图1，将直线OA 向上平移1个单位，得到一个一次函数的图像，那么这个一次函数的解析式是 ．【分析】通过观察图象可求出直线OA 的解析式，再根据上面平移与解析式之间的关系进行解答．解：设OA 的解析式为：y kx =，因OA 过A （2，4），所以4＝2k ,解得k ＝2，所以OA 的解析式为：2y x =，上移一个单位后，解析式为：21y x =+．例2．把直线y x =-+21平行移动后过点A ()-42，，求平移后的直线解析式，并说明是向上还是向下平移几个单位得到的．【分析】因知道直线平移过点A ()-42，，而平移系数k 不改变．所以可设解析式为：y x b =-+2，进而求b ．解析：根据题意可设所求的直线为：y x b =-+2；由A ()-42，在此直线上，得 2＝－2×(－4)＋b ，解得b ＝－6．故所求直线为y x =--26，由y x =-+21得y x =-+-217知可将原直线向下平移7个单位得到．请同学们再思考一下：若直线y x =-+21左右平行移动后能否过点A ()-42，呢？请说明理由．参考答案：设y x m =-++21()，由A ()-42，，求得m ＝72．所以由y x =-+21得26y x =--知可将原直线向左平移72个单位．。

一次函数左右平移规律推导过程在平面直角坐标系中，将二次函数图象进行平移，求平移以后的二次函数的解析式，或者已知平移之后的二次函数解析式求平移之前的二次函数解析式，是学生学习中的一个难点，但也是一个充满乐趣，值得探究的知识点．二次函数图象的平移包括上下平移和左右平移．图象的上下平移符合学生直觉，而图象的左右平移恰巧是反直觉的，图象上下平移和左右平移之间的不一致，往往是造成学生理解平移的困难，研究表明，学生理解二次函数左右平移的困难要大于上下平移，上下平移的动作是直接操作在函数上，而左右平移包含的动作首先操作在自变量上，进而再操作到函数上，这是产生困难的原因．无论是哪种平移，都可以用求解析式的方式来解，而且二次函数的平移是可逆的，解题时主要是要理解二次函数平移的整个过程和思路现分类举例说明如下：一、三点法从最直观的角度——三点可以确定一条抛物线，那么就找一条抛物线上的任三点，再找这三点平移之后的对应点坐标，根据待定系数法求解二次函数的解析式．例1 将抛物线y＝－x2－2x＋4向右平移3个单位，求平移后的函数解析式．解在抛物线y＝x2－2x＋4上任取三个点a(1，1)，b（2，－4），c(－1，5)，把点a、b、c分别向右平移3个单位后得a'(4，1)，b'(5，－4)，c'(2，5)设所求的二次函数解析式为y＝ax2＋bx＋c，∵a'(4，1)，b'（5，－4），c'(2，5)在y＝ax2＋bx＋c上．∴∴平移后的函数解析式为y＝－x2＋4x＋1．二、顶点法抛物线平移前后形状相同，位置不同，那么它们的二次项系数是相等的，即知道二次函数解析式中的a，再求出原抛物线的顶点，找出平移以后的顶点，根据待定系数法求解二次函数的解析式．例2 将抛物线y＝－x2－2x＋4向左平移2个单位，求平移后的函数解析式．解设平移后的函数解析式为y＝－（x－h）2＋k．∵ y＝－x2－2x＋4＝－（x＋1）2＋5，∴y＝－x2－2x＋4的顶点坐标是a（－1，5)．∴a（－1，5）向左平移2个单位后得到a'(－3，5)，∴h＝－3，k＝5．∴平移后的函数解析式为y＝－（x＋3）2＋5，即y＝－x2－6x－4三、交点法图象分析也是一种颇有意思的解题过程，学生觉得函数图象的平移就要巧妙地利用图象上的一些特殊点，只要找到函数与坐标轴的交点，把合适的坐标轴上点进行平移，通过左右平移找x轴上的点，上下平移找y轴上的点，将x轴上的点左右平移后，或将y轴上的点上下平移后，代入a相同的二次函数解析式求解即可．例3 将抛物线y＝－x2－2x＋3向右平移4个单位，求平移后的函数解析式．解设平移后的函数解析式为y＝－（x－x1）（x－x2）．抛物线y＝－x2－2x＋3与x轴的交点为a(－3，0)，b(1，0)．∵a（－3，0），b(1，0)向右平移4个单位后得到a'(1，0)，b'(5，0)，∴x1＝1，x2＝5，∴y＝－(x－1)(x－5)，即y＝－x2＋6x－5例4 将抛物线y＝－x2－2x＋3向下平移4个单位，求平移后的函数解析式．解设平移后的函数解析式为y＝ax2＋bx＋c．将抛物线y＝－x2－2x＋3向下平移，则其形状大小，对称轴不变，故平移后的函数解析式的a和b值不变，∴a＝－1，b＝－2．又抛物线y＝－x2－2x＋3与y轴交点为a(0，3)，而a(0，3)向下平移4个单位后得到a'（0，－1），∴c＝－1．∴平移后的函数解折式为y＝－x2－2x－1．四、图象法从函数图象平移前后点的变化特征出发，可理解为：将函数向右平移时，函数中的x值会变大，而相应的y值不变，那么就要把因为移动而多的单位数减去（向左平移x值减少就要把少的单位数加上），函数值不变例5 将抛物线y＝－x2－2x＋4向右平移3个单位，求平移后的函数解析式．解抛物线向右平移3个单位时，函数中的x值会增大3个单位，而相应的y值不变，那么就要把x的值减去因为移动而多的3个单位数．故平移后的函数解析式为y＝－（x－3）2－2（x－3）＋4，即y＝－x2＋4x＋1．对于将二次函数向上平移的情况就是函数的y值会增加，而自变量x值不变，那么就要将函数值y减去移动的单位数（向下平移y值减少就要把少的单位数加上），而等式右边不变．例6 将抛物线y＝－x2－2x＋4向上平移3个单位，求平移后的函数解析式．解抛物线向上平移3个单位时，函数的y值会增加3个单位，而自变量x值不变，那么就要将函数值y减去因为移动而多的3个单位数，故平移后的函数解析式为y－3＝－x2－2x＋4，即y＝－x2－2x＋7．将平移前后的二次函数解析式进行比较，可以得到常用的函数平移口诀：“左加右减，上加下减；左右平移在括号内，上下平移在括号外．”例7 将抛物线y＝0.5x2－4x＋3先向左平移5个单位，再向上平移6个单位，求平移后函数解析式．解抛物线向左平移5个单位时，函数中的x值会减少5个单位，而相应的y值不变，那么就要把x的值加上因为移动而少的5个单位数．抛物线向上平移6个单位时，函数的y值会增加6个单位，而自变量x值不变，那么就要将函数值y减去因为移动而多的6个单位数．y－6＝0.5(x＋5)2－4(x＋5)＋3，化简得y＝0.5x2＋x＋1.5例8 抛物线向右平移3个单位，向下平移2个单位得到y＝－2x2＋20x－52，求平移前函数解析式．解根据二次函数的平移是可逆的，则平移前函数解析式是y－2＝－2(x＋3)2＋20(x＋3)－52，化简得y＝－2x2＋8x－8．数学学习需要在知识获取的过程中有完整的体验，这样才能很好的理解每个知识点。

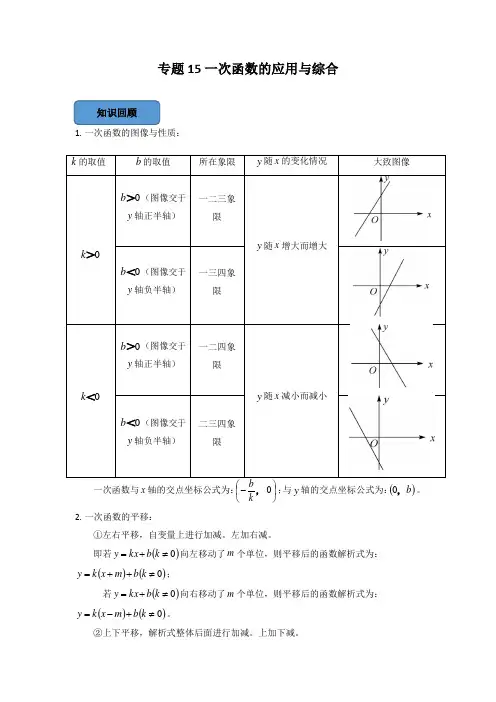
知识回顾专题15一次函数的应用与综合1. 一次函数的图像与性质：一次函数与x 轴的交点坐标公式为：⎪⎭⎫ ⎝⎛-0 ，k；与y轴的交点坐标公式为：()b ，0。

2. 一次函数的平移：①左右平移，自变量上进行加减。

左加右减。

即若()0≠+=k b kx y 向左移动了m 个单位，则平移后的函数解析式为：()()0≠++=k b m x k y ；若()0≠+=k b kx y 向右移动了m 个单位，则平移后的函数解析式为：()()0≠+-=k b m x k y 。

②上下平移，解析式整体后面进行加减。

上加下减。

k 的取值 b 的取值 所在象限y 随x 的变化情况大致图像0＞k0＞b （图像交于y 轴正半轴）一二三象限y 随x 增大而增大0＜b （图像交于y 轴负半轴）一三四象限0＜k0＞b （图像交于y 轴正半轴）一二四象限y 随x 减小而减小0＜b （图像交于y 轴负半轴）二三四象限即若()0≠+=k b kx y 向上移动了m 个单位，则平移后的函数解析式为：()0≠++=k m b kx y ；若()0≠+=k b kx y 向下移动了m 个单位，则平移后的函数解析式为：()0≠-+=k m b kx y 。

3. 一次函数的对称变换：①若一次函数关于x 轴对称，则自变量不变，函数值变为相反数。

即()0≠+=k b kx y 关于x 轴的函数解析式为：()0≠+=-k b kx y ，即()0≠--=k b kx y 。

②若一次函数关于y 轴对称，则函数值不变，自变量变成相反数。

即()0≠+=k b kx y 关于y 轴的函数解析式为：()()0≠+-=k b x k y ，即()0≠+-=k b kx y 。

③若一次函数关于原点对称，则自变量与函数值均变成相反数。

即()0≠+=k b kx y 关于原点的函数解析式为：()()0≠+-=-k b x k y ，即()0≠-=k b kx y 。

一次函数【一次函数图象的平移规律】一个点作上下平移时，横坐标不变，纵坐标发生变化（向上平移,纵坐标变大；向下平移,纵坐标变小）。

同理，一个点作左右平移时，纵坐标不变，横坐标发生变化（向右平移,横坐标变大，向左平移，横坐标变小）。

由于图形在平移时，图形上的每一个点都作了相同的平移，所以在理解一次函数平移时，只须抓住一个点的变化去理解就行了。

直线y=kx+b上下平移m个单位时，每个对应点的x取值不变，但对应的函数值y增加或减少m个单位，故解析式变为y=kx+b±m。

直线y=kx+b左右平移时，我们不防将函数解析式变一下形，得到 x = yk－bk当直线y=kx+b，即x = yk－bk左右平移m个单位时，每个对应点的y取值不变，但对应的函数值x减少或增加m个单位，故解析式变为 x = yk－bk-m或 x =yk－bk+m 化成一般式就得到 y=kx+b±km 即y=k(x±m)+b观察得出规律：直线y=kx+b平移时，“上加下减只变b,左加右减括号里”【例谈求一次函数解析式的常见题型】一. 定义型例1. 已知函数是一次函数，求其解析式。

注意：利用定义求一次函数解析式时，要保证。

如本例中应保证二. 点斜型例2. 已知一次函数的图像过点（2，－1），求这个函数的解析式。

三. 两点型已知某个一次函数的图像与x轴、y轴的交点坐标分别是（－2，0）、（0，4），则这个函数的解析式为_____________。

五. 斜截型例5. 已知直线与直线平行，且在y轴上的截距为2，则直线的解析式为___________。

六. 平移型例6. 把直线向下平移2个单位得到的图像解析式为___________。

七. 实际应用型例7. 某油箱中存油20升，油从管道中匀速流出，流速为0.2升/分钟，则油箱中剩油量Q（升）与流出时间t（分钟）的函数关系式为___________。

注意：求实际应用型问题的函数关系式要写出自变量的取值范围。

）左右平移过程中，纵坐标不变，改变的是横坐标也就是自变量，向左平移自变量变小，因此要加上平移的变大，因此要减去平移的量，简述为“左加右减”．
“左加右减，上加下减；左右平移在括号，上下平移在末稍”．
（）关于轴对称（翻折）后，纵坐标不变，横坐标变为相反数．
即关于轴对称后的解析式为18/06/12
x x 2y y =kx +b y
（）关于原点对称（绕原点旋转即关于原点对称后的解析式为【方法】口诀：“关于谁，谁不变；另一个，变相反；关于原点都要变”．
（）关于直线对称（翻折）
【方法】
①根据两点确定一条直线，结合图形求出对称后直线上两个点的坐标，再用待定系数法求出解析式即可．3y =kx +b 已知直线与直线1y =kx +b 2y =n
【方法】根据两点确定一条直线，结合图形求出对称后直线上两个点的坐标，再用待定系数法求出解析式即可．
直线绕原点逆时针旋转后的解析式为（ ）．
A. B. C. D. y =3x O 90∘y =− x 13
y =3x
y = x 13
y =−3x。

一次函数图象平移规律教学目标：1、了解一次函数图象的平移规律，加深对函数图象的理解2、体会一次函数的平移过程，能根据已知条件确定平移后的表达式重点：了解一次函数图象的平移规律难点：函数图象的左右平移规律用待定系数法求一次函数解析式教学过程一、上下平移规律在同一坐标系内画出y=x 和y=x+1 以及y=x-1的图象，比较它们的相同点和不同点，填出你的观察结果。

如图一图一图二图三1、三个函数的图象形状，并且倾斜程度。

2、函数y=x的图象经过原点，3、函数y=x+1的图象与y轴交于点，它可以看做由直线y=x向平移个单位长度而得到的。

4、函数y=x+1的图象与y轴交于点，它可以看做由直线y=x向平移个单位长度而得到的。

二、上下平移规律函数y=2x的图象如图二；1.将y=2x向右平移4个单位；2.将y=2x向左平移4个单位；图三（直线的平移就是点的平移，写出y=2x平移后对应的点的坐标，再利用待定系数法求平移后的函数解析式，根据解析式与y=2x的关系，找出一次函数左右平移的规律）三、课堂练习1.请将对应的项目匹配（连线）y=3x向下平移2个单位长度；y=3x+2y=3x向上平移2个单位长度；y=3x-2y=3x向左平移2个单位长度；y=3x-6y=3x向右平移2个单位长度；y=3x+6；3.不画图象，仅从函数解析式说出直线y=3x+4 与y=3x-4 具有什么样的位置关系3.一次函数y=(m-2)x-1 与y=3x的图象平行，则m的值是4. 3.将直线y=2x向上平移两个单位长度，再向右平移三个单位长度，得到的解析式是5..一次函数向下平移5 个单位后得到y=-3x+12，则原来的函数解析式为四、判断正误1.y=2x+3是正比例函数2.y=0.3x的图象过一三象限3.y=2x的图象向上平移3个单位后得到y=2x+34.y=2x的图象向右平移3个单位后得到y=2x-35.y=2x-5是由y=5x向下平移5个单位得到的6.y=-3x+4和y=3x-5的图象平行7.y=2x-5与y轴交点坐标为（0，-5）8.y=2x-5与x轴交点坐标为（0，-5）五、总结一次函数图象平移规律1.k相同，两直线平行2.上加下减常数项3.左加右减自变量。

一次函数图象的平移变换问题的探究求一次函数图象平移后的解析式是一类重要题型，在各省市中考试题频繁亮相.在一次函数y kx b =+中常数k 决定着直线的倾斜程度：直线111y k x b =+与直线222y k x b =+平行⇔12k k =.一、一次函数平移的三种方式：⑴上下平移：在这种平移中，横坐标不变，改变的是纵坐标也就是函数值y .平移规律是上加下减.⑵左右平移：在这种平移中，纵坐标不变，改变的是横坐标也就是自变量x .平移规律是左加右减.⑶沿某条直线平移：这类题目稍有难度.“沿”的含义是一次函数图象在平移的过程中与沿着的那条直线的夹角不变.解题时抓住平移前后关键点坐标的变化. 二、典型例题：（1）点(0,1)向下平移2个单位后的坐标是 ___，直线21y x =+向下平移2个单位后的解析式是所谓平移变换就是在平面内，.经过平移后的图形与原来的图形相比大小、形状不变，只是位置发生了变化.简单的点P （x ，y ）平移规律如下：（1）将点P （x ，y ）向左平移a 个单位，得到P 1（x －a ，y ） （2）将点P （x ，y ）向右平移a 个单位，得到P 2（x+a ，y ） （3）将点P （x ，y ）向下平移a 个单位，得到P 3（x ，y －a ）（4）将点P （x ，y ）向上平移a 个单位，得到P 4（x ，y+a ）反之也成立.下面我们来探索直线的平移问题.【引例1】探究一次函数l ：y=32x 与1l ：y=32x+2，2l ：y=32x －2的关系. .【拓广】：一般地，一次函数y=kx+b 的图象是由正比例函数y=kx 的图象沿y 轴向上（b>0）或向下（b<0）平移b 个单位长度得到的一条直线.【应用】：例1、（08上海市）在图2中，将直线OA 向上平移1个单位，得到一个一次函数的图像，那么这个一次函数的解析式是 ．2lx练习1. 直线y=2x+1向上平移4个单位得到直线 2. 直线y=-3x+5向下平移6个单位得到直线 3. 过点（2，-3）且平行于直线y=2x 的直线是____ _____。

一次函数图像的平移集团文件发布号：（9816-UATWW-MWUB-WUNN-INNUL-DQQTY-一次函数图像的平移函数y＝kx＋b上的每个点（x,y）一、向左移动m个单位后,y不变,而x变成了x＋m，函数就变成了y＝k（x+m）＋b二、向右移动m个单位后,y不变,而x变成了x－m，函数就变成了y＝k（x-m）＋b三、向上移动n个单位后,x不变, y＝kx＋b在b后面加上n，函数就变成了y＝kx＋b+n四、向下移动n个单位后,x不变, y＝kx＋b在b后面减去n，函数就变成了y＝kx＋b-n一次函数y=kx+b的规律：“上加下减，左加右减”，上下平移时在整体后面进行加减，左右平移时针对的是x进行加减。

例如：y=2x+1向上平移2个单位，向左平移3个单位，可得y=2（x+3）+1+2，最后函数为y=2x+9．一次函数y=kx+b的图象是一条直线，它可以看作由直线y=kx平移∣b∣个单位长度得到(当b＞0时，向上平移；当b＜0时，向上平移)．或者说，直线y=kx平移∣b∣个单位长度得到直线y=kx+b (当b＞0时，向上平移；当b＜0时，向下平移)．例如，将直线y=-x向上平移3个单位长度就得到直线y=-x+3，将直线y=-x向下平移1个单位长度就可以得到直线y=-x-1．需要注意的是，函数图象的平移，既可以上下平移，也可以左右平移．这里所说的平移，是指函数图象的上下平移，而非左右平移．以上平移比较简单，因为它是对最简单的一次函数即正比例函数进行平移．对于一个一般形式的一次函数图象又该怎样进行平移呢问题1已知直线l1：y=2x-3，将直线l1向上平移2个单位得到直线l2，求直线l2的解析式分析：根据“两直线平行，对应函数的一次项系数相等”，可设直线l2的解析式为y=2x+ b，由于直线l2的解析式中只有一个未知数，因此再需一个条件即可．怎样得到这个条件呢注意到直线l1与两条坐标轴分别交于两点，而直线l1与y轴的交点易求，这样就得到一个条件，于是直线l2的解析式可求．解：设直线l2的解析式为y=2x+b，直线l1交y轴于点(0，-3)，向上平移2个单位长度后变为(0，-1)．把(0，-1)坐标代入y=2x+b，得b=-1，从而直线l2的解析式为y=2x-1．问题2 已知直线l1：y=2x-3，将直线l1向下平移2个单位得到直线l2，求直线l2的解析式答案：直线l2的解析式为y=2x-5．(解答过程请同学们自己完成)对比直线l1和直线直线l2的解析式可以发现：将直线l1：y=2x-3向上平移2个单位长度得到直线l2的解析式为：y=2x-3+2；将直线l1：y=2x-3向下平移2个单位长度得到直线l2的解析式为：y=2x-3-2．(此时你有什么新发现)问题3 已知直线l1：y=kx+b，将直线l1向上平移m个单位得到直线l2，求直线l2的解析式解：设直线l 2的解析式为y=kx+n ，直线l 1交y 轴于点(0，b)，向上平移m 个单位长度后变为(0，b+m)，把(0，b+m)坐标代入l 2的解析式可得，n=b+m ．从而直线l 2的解析式为y=kx+b+m ．问题4已知直线l 1：y=kx+b ，将直线l 1向下平移m 个单位得到直线l 2，求直线l 2的解析式答案：直线l 2的解析式为y=kx+b-m由此我们得到：直线y=kx+b 向上平移m （m 为正）个单位长度得到直线y=kx+b+m ，直线y=kx+b 向下平移m （m 为正）个单位长度得到直线y=kx+b-m ，这是直线直线y=kx+b 上下(或沿y 轴)平移的规律这个规律可以简记为：以上我们探究了直线y=kx+b 的上下 (或沿y 轴)的平移，如果直线y=kx+b 不是上下(或沿y 轴)平移，而是左右(或沿x 轴)平移，又该怎样进行平移呢问题5已知直线l 1：y=3x-12，将直线l 1向左平移5个单位得到直线l 2，求直线l 2的解析式解：根据“两直线平行，对应函数的一次项系数相等”，可设直线l 2的解析式为y=3x+b ，直线l 1交x 轴于点(4，0)，向左平移5个单位长度后变为(-1，0)．把(-1，0)坐标代入y=3x+b ，得b=3，从而直线l 2的解析式为y=3x+3问题6 已知直线l 1：y=3x-12，将直线l 1向右平移5个单位得到直线l 2，求直线l 2的解析式．答案：直线l 2的解析式为y=3x-27对比直线l 1和直线直线l 2的解析式可以发现：将直线l 1：y=3x-12向左平移5个单位长度得到直线l 2的解析式为：y=3(x+5)-12；将直线l 1：y=3x-12向右平移5个单位长度得到直线l 2的解析式为：y=3(x-5)-12问题7已知直线l 1：y=kx+b ，将直线l 1向左平移m 个单位长度得到直线l 2，求直线l 2的解析式解：设直线l 2的解析式为y=kx+n ，直线l 1交x 轴于点(-b ／k ，0)，向左平移m 个单位长度后变为(0，-b ／k -m)，把(0，-b ／k -m)坐标代入l 2的解析式可得，n=km+b ．从而直线l 2的解析式为y=kx+km+b ，即y=k(x+m)+b ．问题8已知直线l 1：y=kx+b ，将直线l 1向右平移m 个单位长度得到直线l 2，求直线l 2的解析式答案：直线l 2的解析式为y=k(x-m)+b由此我们得到：直线y=kx+b 向左平移m （m 为正）个单位长度得到直线y=k(x+m)+b ，直线y=kx+b 向右平移m （m 为正）个单位长度得到直线y=k(x-m)+b ，这是直线y=kx+b 左右(或沿x 轴)平移的规律这个规律可以简记为：例1:将直线l 1：y=kx+b （k≠0）向上平移5个单位长度后，得到直线l 2，l 2经过点（1，2）和坐标原点，求直线l 1的解析式解：直线y=kx+b （k≠0）的图象向上平移5个单位长度后的解析式为：y=kx+b+5，将点（1，2），（0，0）代入y=kx+b+5，得k+b+5=2，b+5=0，解得：k=2，b=-5，即平移后直线的解析式为y=2x-5例2:一次函数y=kx+b 的图象经过点（-1，1）和点（1，-5），求①函数的解析式；②将该一次函数的图象向上平移3个单位，直接写出平移后的函数解析式解：①根据题意，得1=-k+b,-5=k+b，解得k=-3,b=-2，则一次函数的解析式为y=-3x-2②将一次函数y=﹣3x﹣2的图象向上平移3个单位后的解析式为y=-3x-2+3，即y=-3x+1练习：1.直线y=-x-3向上平移2个单位长度后得到的直线解析式是＿＿＿；直线y=x／3 -2向下平移3个单位长度后得到的直线解析式是＿＿＿2.直线y=-5x-12向左平移2个单位长度后得到的直线解析式是＿＿＿；直线y=(x+1)／6向右平移3个单位长度后得到的直线解析式是＿＿＿3.直线y=8x+13既可以看作直线y=8x-3向＿＿＿平移(填“上”或“下”)＿＿＿单位长度得到；也可以看作直线y=8x-3向＿＿＿平移(填“左”或“右”)＿＿＿单位长度得到?4．要由直线y=2x+12得到直线y=2x-6，可以通过平移得到：先将直线y=2x+12向＿＿＿平移(填“上”或“下”)＿＿＿单位长度得到直线y=2x，再将直线y=2x向＿＿＿平移(填“上”或“下”)得到直线y=2x-6；当然也可以这样平移：先将直线y=2x+12向＿＿＿平移(填“左”或“右”)＿＿＿单位长度得到直线y=2x，再将直线y=2x向＿＿＿平移(填“左”或“右”)得到直线y=2x-6；以上这两种方法是分步平移．也可以一次直接平移得到，即将直线y=2x+12向＿＿＿平移(填“上”或“下”)直接得到直线y=2x-6，或者将直线y=2x+12向＿＿＿平移(填“左”或“右”)直接得到直线y=2x-6。

一次函数图像平移的探究Revised on November 25, 2020一次函数图像平移的探究我们知道，一次函数y=kx+b 的图像是一条直线，我们称它为直线y=kx+b ，它可以看作由直线y=kx 平移∣b ∣个单位长度得到(当b ＞0时，向上平移；当b ＜0时，向上平移)．或者说，直线y=kx 平移∣b ∣个单位长度得到直线y=kx+b (当b ＞0时，向上平移；当b ＜0时，向下平移)．例如，将直线y=-x 向上平移3个单位长度就得到直线y=-x+3，将直线y=-x 向下平移1个单位长度就可以得到直线y=-x -1．需要注意的是，函数图像的平移，既可以上下平移，也可以左右平移．这里所说的平移，是指函数图像的上下平移，而非左右平移．以上平移比较简单，因为它是对最简单的一次函数即反比例函数进行平移．对于一个一般形式的一次函数图像又该怎样进行平移呢让我们一起进行探究：问题1 已知直线1l ：y=2x -3，将直线1l 向上平移2个单位长度得到直线2l ，求直线2l 的解析式．分析：根据“两直线平行，对应函数的一次项系数相等”，可设直线2l 的解析式为y=2x+ b ，由于直线2l 的解析式中只有一个未知数，因此再需一个条件即可．怎样得到这个条件呢注意到直线1l 与两条坐标轴分别交于两点，而直线1l 与y 轴的交点易求，这样就得到一个条件，于是直线2l 的解析式可求． 解：设直线2l 的解析式为y=2x+b ，直线1l 交y 轴于点(0，-3)，向上平移2个单位长度后变为(0，-1)．把(0，-1)坐标代入y=2x+b ，得b =-1，从而直线2l 的解析式为y=2x -1．问题2 已知直线1l ：y=2x -3，将直线1l 向下平移2个单位长度得到直线2l ，求直线2l 的解析式．答案：直线2l 的解析式为y=2x -5．(解答过程请同学们自己完成)对比直线1l 和直线直线2l 的解析式可以发现：将直线1l ：y=2x -3向上平移2个单位长度得到直线2l 的解析式为：y=2x -3+2；将直线1l ：y=2x -3向下平移2个单位长度得到直线2l 的解析式为：y=2x -3-2．(此时你有什么新发现)问题3 已知直线1l ：y=kx+b ，将直线1l 向上平移m 个单位长度得到直线2l ，求直线2l 的解析式．简解：设直线2l 的解析式为y=kx+n ，直线1l 交y 轴于点(0，b )，向上平移m 个单位长度后变为(0，b+m )，把(0，b+m )坐标代入2l 的解析式可得，n=b+m ．从而直线2l 的解析式为y=kx+b+m ．问题4 已知直线1l ：y=kx+b ，将直线1l 向下平移m 个单位长度得到直线2l ，求直线2l 的解析式．答案：直线2l 的解析式为y=kx+b -m ．(解答过程请同学们自己完成) 由此我们得到：直线y=kx+b 向上平移∣m ∣个单位长度得到直线y=kx+b +m ，直线y=kx+b 向下平移∣m ∣个单位长度得到直线y=kx+b -m ，即直线y=kx+b 平移∣m ∣个单位长度得到直线y=kx+b +m (当m ＞0时，向上平移；当m ＜0时，向下平移)，这是直线直线y=kx+b 上下(或沿y 轴)平移的规律．这个规律可以简记为：⎪⎩⎪⎨⎧++=−−−−−−−−→−+=++=−−−−−−−−→−+=>>m b kx y b kx y m b kx y b kx y m m m m 直线直线直线直线）个单位长度（向下平移）个单位长度（向上平移00．以上我们探究了直线y=kx+b 的上下 (或沿y 轴)的平移，如果直线y=kx+b 不是上下(或沿y 轴)平移，而是左右(或沿x 轴)平移，又该怎样进行平移呢Let ,s go ，让我们一起继续探究！问题5 已知直线1l ：y=3x -12，将直线1l 向左平移5个单位长度得到直线2l ，求直线2l 的解析式．简解：根据“两直线平行，对应函数的一次项系数相等”，可设直线2l 的解析式为y=3x+b ，直线1l 交x 轴于点(4，0)，向左平移5个单位长度后变为(-1，0)．把(-1，0)坐标代入y=3x+b ，得b =3，从而直线2l 的解析式为y=3x +3．问题6 已知直线1l ：y=3x -12，将直线1l 向右平移5个单位长度得到直线2l ，求直线2l 的解析式．答案：直线2l 的解析式为y=3x -27．(解答过程请同学们自己完成)对比直线1l 和直线直线2l 的解析式可以发现：将直线1l ：y=3x -12向左平移5个单位长度得到直线2l 的解析式为：y=3(x +5)-12；将直线1l ：y=3x -12向右平移5个单位长度得到直线2l 的解析式为：y=3(x -5)-12．(此时你有什么新发现)问题7 已知直线1l ：y=kx+b ，将直线1l 向左平移m 个单位长度得到直线2l ，求直线2l 的解析式．简解：设直线2l 的解析式为y=kx+n ，直线1l 交x 轴于点(k b -，0)，向左平移m 个单位长度后变为(0，k b --m )，把(0，kb --m )坐标代入2l 的解析式可得，n=km+b ．从而直线2l 的解析式为y=kx+km+b ，即y=k (x+m )+b ．问题8 已知直线1l ：y=kx+b ，将直线1l 向右平移m 个单位长度得到直线2l ，求直线2l 的解析式．答案：直线2l 的解析式为y=k (x -m )+b ．(解答过程请同学们自己完成) 由此我们得到：直线y=kx+b 向左平移∣m ∣个单位长度得到直线y=k (x+m )+b ，直线y=kx+b 向右平移m 个单位长度得到直线y=k (x -m )+b ，即直线y=kx+b 平移∣m ∣个单位长度得到直线y=k (x+m )+b (当m ＞0时，向左平移；当m ＜0时，向右平移)，这是直线y=kx+b 左右(或沿x 轴)平移的规律．这个规律可以简记为：⎪⎩⎪⎨⎧+-=−−−−−−−−→−+=++=−−−−−−−−→−+=>>b m x k y b kx y b m x k y b kx y m m m m )()(00直线直线直线直线）个单位长度（向右平移）个单位长度（向左平移．。