计量经济学答案部分Word版

计量经济学（第四版）习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。

一般说来，计量经济分析按照以下步骤进行：（1）陈述理论（或假说） （2）建立计量经济模型 （3）收集数据 （4）估计参数 （5）假设检验 （6）预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实，我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素，这些因素包括相对而言不重要因而未被引入模型的变量，以及纯粹的随机因素。

1.3什么是时间序列和横截面数据? 试举例说明二者的区别。

时间序列数据是按时间周期（即按固定的时间间隔）收集的数据，如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。

横截面数据是在同一时点收集的不同个体（如个人、公司、国家等）的数据。

如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。

1.4估计量和估计值有何区别？估计量是指一个公式或方法，它告诉人们怎样用手中样本所提供的信息去估计总体参数。

在一项应用中，依据估计量算出的一个具体的数值，称为估计值。

如Y就是一个估计量，1nii YY n==∑。

现有一样本，共4个数，100，104，96，130，则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。

第二章 计量经济分析的统计学基础2.1 略，参考教材。

2.2请用例2.2中的数据求北京男生平均身高的99％置信区间NSS x ==45=1.25 用α=0.05，N-1=15个自由度查表得005.0t =2.947，故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说，根据样本，我们有99%的把握说，北京男高中生的平均身高在170.316至177.684厘米之间。

（完整word版）计量经济学基本点练习题及答案Chap1—31、在同⼀时间不同统计单位的相同统计指标组成的数据组合，是（）A、原始数据B、时点数据C、时间序列数据D、截⾯数据2、回归分析中定义的( )A、解释变量和被解释变量都是随机变量B、解释变量为⾮随机变量，被解释变量为随机变量C、解释变量和被解释变量都为⾮随机变量D、解释变量为随机变量，被解释变量为⾮随机变量3、在⼀元线性回归模型中，样本回归⽅程可表⽰为：（）4、⽤模型描述现实经济系统的原则是( )A、以理论分析作先导，解释变量应包括所有解释变量B、以理论分析作先导，模型规模⼤⼩要适度C、模型规模越⼤越好；这样更切合实际情况D、模型规模⼤⼩要适度，结构尽可能复杂5、回归分析中使⽤的距离是点到直线的垂直坐标距离。

最⼩⼆乘准则是指（）6、设OLS法得到的样本回归直线为A、⼀定不在回归直线上B、⼀定在回归直线上C、不⼀定在回归直线上D、在回归直线上⽅7、下图中“{”所指的距离是A.随机误差项B.残差C.因变量观测值的离差D.因变量估计值的离差8、下⾯哪⼀个必定是错误的9、线性回归模型的OLS估计量是随机变量Y的函数，所以OLS估计量是（）。

A.随机变量B.⾮随机变量C.确定性变量D.常量10、为了对回归模型中的参数进⾏假设检验，必须在古典线性回归模型基本假定之外，再增加以下哪⼀个假定：A.解释变量与随机误差项不相关B.随机误差项服从正态分布C.随机误差项的⽅差为常数D.两个误差项之间不相关D B C B D B B C A BChap41、⽤OLS估计总体回归模型，以下说法不正确的是：2、包含有截距项的⼆元线性回归模型中的回归平⽅和ESS的⾃由度是（）A、nB、n-2C、n-3D、23、对多元线性回归⽅程的显著性检验，，k代表回归模型中待估参数的个数，所⽤的F统计量可表⽰为：4、已知三元线性回归模型估计的残差平⽅和为800，样本容量为24，则随机误差项的⽅差估计量为( )A 、33.33B 、 40C 、 38.09D 、36.365、在多元回归中，调整后的判定系数与判定系数的关系为6、下⾯哪⼀表述是正确的：A.线性回归模型的零均值假设是指B.对模型进⾏⽅程总体显著性检验（即F 检验），检验的零假设是C.相关系数较⼤意味着两个变量存在较强的因果关系D.当随机误差项的⽅差估计量等于零时，说明被解释变量与解释变量之间为函数关系7、在模型的回归分析结果报告中，有F=263489，p=0.000，则表明（）A 、解释变量X1对Y 的影响是显著的B 、解释变量X2对Y 的影响是显著的C 、解释变量X1, X2对的Y 联合影响是显著的D 、解释变量X1, X2对的Y 的影响是均不显著8、关于判定系数，以下说法中错误的是（）A 、判定系数是因变量的总变异中能由回归⽅程解释的⽐例；B 、判定系数的取值范围为0到1；C 、判定系数反映了样本回归线对样本观测值拟合优劣程度的⼀种描述；D 、判定系数的⼤⼩不受到回归模型中所包含的解释变量个数的影响。

第一章判断题1、在经济计量分析中，模型参数一旦被估计出来，就可将估计模型直接运用于实际的计量经济分析。

错。

参数一经估计，建立了样本回归模型，还需要对模型进行检验，包括经济意义检验、统计检验、计量经济专门检验等。

4.一元线性回归模型中，对样本回归函数整体的显著性检验与斜率系数的显著性检验是一致的；正确最好能够写出一元线性回归模型；F 统计量与t统计量的关系，即F= t2的来历；或者说明一元线性回归仅有一个解释变量，因此对斜率系数的t 检验等价于对方程的整体性检验。

6、在对参数进行最小二乘估计之前，没有必要对模型提出经典假定。

错误在经典假定条件下，OLS 估计得到的参数估计量是该参数的最佳线性无偏估计（具有线性、无偏性、有效性）。

总之，提出古典假定是为了使所作出的估计量具有较好的统计性质和方便地进行统计推断。

简答题1．在确定了被解释变量之后，怎样才能正确地选择解释变量？（1）需要正确理解和把握所研究的经济现象中暗含的经济学理论和经济行为规律。

（2）要考虑数据的可得性。

（3）要考虑所以入选变量之间的关系，使得每一个解释变量都是独立的。

2．时间序列数据和横截面数据有何不同？时间序列数据是一批按照时间先后排列的统计数据。

截面数据是一批发生在同一时间截面上的调查数据。

3．相关关系与因果关系的区别与联系。

相关关系是指两个以上的变量的样本观测值序列之间表现出来的随机数学关系，用相关系数来衡量。

因果关系是指两个或两个以上变量在行为机制上的依赖性，作为结果的变量是由作为原因的变量所决定的，原因变量的变化引起结果变量的变化。

因果关系有单向因果关系和互为因果关系之分。

具有因果关系的变量之间一定具有数学上的相关关系。

而具有相关关系的变量之间并不一定具有因果关系。

4．回归分析与相关分析的区别与联系。

相关分析是判断变量之间是否具有相关关系的数学分析方法，通过计算变量之间的相关系数来实现。

回归分析也是判断变量之间是否具有相关关系的一种数学分析方法，它着重判断一个随机变量与一个或几个可控变量之间是否具有相关关系。

（完整word版）计量经济学期末复习资料及答案（word文档良心出品）一、单项选择题：1．下面哪个假定保证了线性模型y = Xβ + μ的OLS估计量的无偏性。

（ A ）A．X与μ不相关。

B．μ是同方差的。

C．μ无序列相关。

D．矩阵X是满秩的。

2．下列对于自相关问题的表述，哪个是不正确的。

（ B ）A．Durbin-Watson检验只用于检验一阶自相关。

B．BG（Breusch-Godfrey）统计量只用于检验高阶自相关。

C．一阶自相关系数可以通过ρ=1-DW/2进行估计。

D．DW检验不适用于模型中存在被解释变量的滞后项作解释变量的情形。

3．下列关于时间序列的论述哪个是不正确的。

（C ）A．AR过程的自相关函数呈拖尾特征。

B．MA过程的偏自相关函数呈拖尾特征。

C．对于一个时间序列，其自相关函数和偏自相关函数必定有一个是截尾的。

D．在MA(q)过程中，白噪声项对该随机过程的影响只会持续q 期。

4.对于ARMA（1，1）过程（x t = ?1 x t-1 + u t + θ1 u t-1）,其相关图(上)与偏相关图（下）如下:则可以确定（ C ）是正确的。

A. ?1>0；θ1<0B. ?1<0；θ1<0C. ?1>0；θ1>0D. ?1<0；θ1>0()()11212120.3.0.70.1.0.60.1.0.70.6t t t tt t t t t t t tt t t tx x B x x x C x x x D x x x μμμμμ-------=+=-+=-+=++5.下列不平稳的时间序列为白噪声过程有A.(D){}()(){}{}{}(){}01..t t t t t t t t t t X X t X B X t X D X E X δδμμμ=++---6.设时间序列是由是一白噪声过程生成,下列陈述正确的是A.是平稳时间序列是平稳时间序列C.是平稳时间序列是平稳时间序列(D){}()()()()()()()()()()()120,11,22....t t t t t t t t t t t t t t t X E X Var X A E X Var X B E X Var X C E X Va r X D E X Var X μμμμ--=-+7.设是一个期望为方差为1的独立同分布随机时间序列,定义如下随机过程:则对与的描述,下列正确的是与均与时间t 有关与时间t 有关,而与时间t 无关与均与时间t 无关与时间t 无关,而与时间t 有关(C)二、判断并说明理由（四个全对） ()()()()011221011221.1;2,,.1045i i i i i i i i i i i i i Y X X Y X X X i P αααμβββνμνμν=+++-=+++=-有两个模型:为白噪声过程则对相同的样本,两个模型的最小二乘法残差相等,即对任何有教材22.,,YX XY YX XY Y X X Y r r X Y ββββ=令和分别为对的回归方程及对回归方程中的斜率则有其中为与之间的线性相关系数.10112231121210112231,,t t t t t t t t t t t t t t t t t tt t Y X X Y Y X X Y X X Y Y X X Y Y ββββμμββββμμ----=++++=++++3.对模型假设与相关,而与,无关,为了消除相关性,先作关于与回归,得到再作如下回归:这一方法可以消除原模型中与的相关性.()0101,,,t t t t t t t t t t t t t t t t t t Y X X X X X e e X X X e Y X ββμμββνν*****=++=-=-=++4.对于一元线性回归模型假设解释变量的实测值与之有偏误:其中是具有零均值,不序列相关,且与及不相关的随机变量.我们可直接将代入原模型使之变换成为变换后模型的随机干扰项进行OLS 估计,依然能够实现BLUE 性质.综合题：1.1;1/20.55t t t u u DW ρνρ-=+=-=2.()()()()11221212()::11t t t p t pt t pt p AR p Y Y Y Y CE DY C E DY C E DY φφφφφφφφφ---=++ +=----?=----注:中与漂移项之间的关系是教材P290()()()12011101220112231112,,:123,i i i i i i i i i i Y X X Y X Y X Y X X ααμββμγγγμαγβγ=++=++=+++==3.对于涉及三个变量的数据做以下回归问在什么条件下才能有及即多元回归与各自的一元回归所得的参数估计相同.()()12222,,11t t t t st t t sCov μμμρμμμσσμμμρρρ--=+==--4.试证明对于具有形如的一阶自相关随机干扰项的方差与协方差为:Var。

第一章绪论1-14．计量经济模型中为何要包括随机误差项？简述随机误差项形成的原因。

答：由于客观经济现象的复杂性，以至于人们目前仍难以完全地透彻地了解它的全貌。

对于某一种经济现象而言，往往受到很多因素的影响，而人们在认识这种经济现象的时候，只能从影响它的很多因素中选择一种或若干种来说明。

这样就会有许多因素未被选上，这些未被选上的因素必然也会影响所研究的经济现象。

因此，由被选因素构成的数学模型与由全部因素构成的数学模型去描述同一经济现象，必然会有出入。

为使模型更加确切地说明客观经济现象，所以有必要引入随机误差项。

随机误差项形成的原因：①在解释变量中被忽略的因素；②变量观测值的观测误差；③模型的关系误差或设定误差；④其他随机因素的影响。

第二章 一元线性回归模型例1、令kids 表示一名妇女生育孩子的数目，educ 表示该妇女接受过教育的年数。

生育率对教育年数的简单回归模型为μββ++=educ kids 10（1）随机扰动项μ包含什么样的因素？它们可能与教育水平相关吗？（2）上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗？请解释。

解答：（1）收入、年龄、家庭状况、政府的相关政策等也是影响生育率的重要的因素，在上述简单回归模型中，它们被包含在了随机扰动项之中。

有些因素可能与增长率水平相关，如收入水平与教育水平往往呈正相关、年龄大小与教育水平呈负相关等。

（2）当归结在随机扰动项中的重要影响因素与模型中的教育水平educ 相关时，上述回归模型不能够揭示教育对生育率在其他条件不变下的影响，因为这时出现解释变量与随机扰动项相关的情形，基本假设4不满足。

例2．已知回归模型μβα++=N E ，式中E 为某类公司一名新员工的起始薪金（元），N 为所受教育水平（年）。

随机扰动项μ的分布未知，其他所有假设都满足。

（1）从直观及经济角度解释α和β。

（2）OLS 估计量αˆ和βˆ满足线性性、无偏性及有效性吗？简单陈述理由。

计量经济学题库计算与分析题（每小题10分）1X:年均汇率（日元/美元） Y:汽车出口数量（万辆）问题：（1）画出X 与Y 关系的散点图。

（2）计算X 与Y 的相关系数。

其中X 129.3＝，Y 554.2＝，2X X 4432.1∑（－）＝，2Y Y 68113.6∑（－）＝，()()X X Y Y ∑－－＝16195.4 （3）采用直线回归方程拟和出的模型为 ˆ81.72 3.65YX =+ t 值 1.2427 7.2797 R 2=0.8688 F=52.99解释参数的经济意义。

2．已知一模型的最小二乘的回归结果如下：i iˆY =101.4-4.78X 标准差 （45.2） （1.53） n=30 R 2=0.31 其中，Y ：政府债券价格（百美元），X ：利率（%）。

回答以下问题：（1）系数的符号是否正确，并说明理由；（2）为什么左边是iˆY 而不是i Y ； （3）在此模型中是否漏了误差项i u ；（4）该模型参数的经济意义是什么。

3．估计消费函数模型i i i C =Y u αβ++得i i ˆC =150.81Y + t 值 （13.1）（18.7） n=19 R 2=0.81其中，C ：消费（元） Y ：收入（元）已知0.025(19) 2.0930t =，0.05(19) 1.729t =，0.025(17) 2.1098t =，0.05(17) 1.7396t =。

问：（1）利用t 值检验参数β的显著性（α＝0.05）；（2）确定参数β的标准差；（3）判断一下该模型的拟合情况。

4．已知估计回归模型得i i ˆY =81.7230 3.6541X + 且2X X 4432.1∑（－）＝，2Y Y 68113.6∑（－）＝， 求判定系数和相关系数。

5．有如下表数据（1拟合什么样的模型比较合适？ （2）根据以上数据，分别拟合了以下两个模型：模型一：16.3219.14P U=-+ 模型二：8.64 2.87P U =- 分别求两个模型的样本决定系数。

各位同学：请大家按照这个复习重点进行认真复习，考试时请大家带上计算器，平时成绩占30%，期末占70%。

考试题型：一、名词解释题(每小题4分，共20分)计量经济学：一门由经济学、统计学和数学结合而成的交叉学科. 经济学提供理论基础,统计学提供资料依据,数学提供研究方法总体回归函数：被解释变量的均值同一个或者多个解释变量之间的关系样本回归函数：是总体回归函数的近似OLS 估计量 ：以残差平方和最小的原则对回归模型中的系数进行估计的方法。

普通最小二乘法估计量OLS 估计量可以由观测值计算OLS 估计量是点估计量一旦从样本数据取得OLS 估计值，就可以画出样本回归线BLUE 估计量、BLUE ：最优线性无偏估计量, 其估计量是无偏估计量，且在所有的无偏估计量中其方差最小。

拟合优度、衡量了解释变量能解释的离差占被解释变量的百分比。

拟合优度R 2(被解释部分在总平方和(SST)中所占的比例)虚拟变量陷阱、 带有截距项的回归模型，如果有m 个定性变量，只能引入m-1个虚拟变量。

如果引入了m 个，就将陷入虚拟变量陷阱。

既模型中存在完全共线性，使得模型无法估计方差分析模型、解释变量仅包含定性变量或虚拟变量的模型。

协方差分析模型、回归模型中的解释变量有些是定性的有些是定量的。

多重共线性 多重共线性是指解释变量之间存在完全的线性关系或近似的线性关系.分为完全多重共线性和不完全多重共线性ˆˆ)X |E(Y ˆ) )X |E(Y ( ˆˆˆ :SRF 2211i 21i 21的估计量。

是的估计量；是的估计量；是其中相对于ββββββββi i ii Y X X Y +=+=∑∑==222ˆi i y y TSS ESS R自相关： 随机误差项当期值和滞后期相关。

在古典线性回归模型中，我们假定随机扰动项序列的各项之间，如果这一假定不满足，则称之为自相关。

即用符号表示为：自相关常见于时间序列数据。

异方差、 是指模型误差项的方差随着变量的改变而不同随机误差项：模型中没有包含的所有因素的代表例：Y — 消费支出 X —收入、— —参数 u —随机误差项 显著性检验 ：显著性检验时利用样本结果，来证实一个零假设的真伪的一种检验程序。

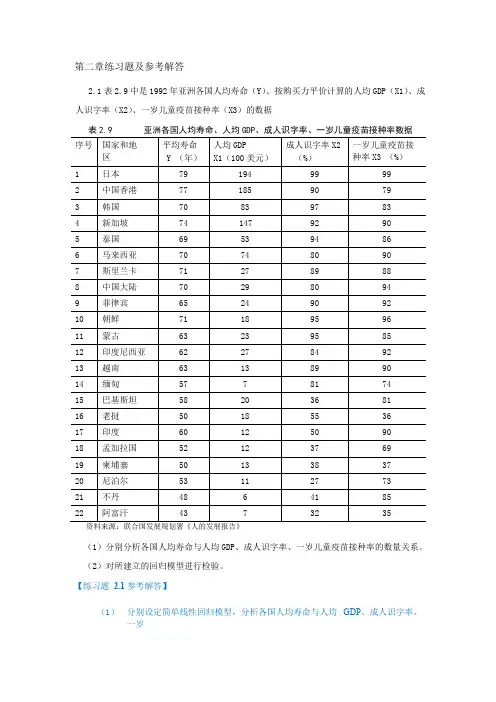
第二章练习题及参考解答2.1表2.9中是1992年亚洲各国人均寿命（Y）、按购买力平价计算的人均GDP（X1）、成人识字率（X2）、一岁儿童疫苗接种率（X3）的数据（1）分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。

（2）对所建立的回归模型进行检验。

【练习题2.1 参考解答】（1）分别设定简单线性回归模型，分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系（2）对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于0.05,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显著影响.（3）分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为0.5261 人均寿命与成人识字率回归的可决系数为0.7168 人均寿命与一岁儿童疫苗接种率的可决系数为0.5379相对说来,人均寿命由成人识字率作出解释的比重更大一些2.2为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:的显著性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年，全省生产总值为32000 亿元，比上年增长9.0%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显著性,并解释所估计参数的经济意义【练习题2.2 参考解答】建议学生独立完成2.3 由12对观测值估计得消费函数为：（1）消费支出C的点预测值；（2）在95%的置信概率下消费支出C平均值的预测区间。

（整理）计量经济学-参考答案⼀、解释概念：1、多重共线性：是指在多元线性回归模型中，解释变量之间存在的线性关系。

2、SRF：就是样本回归函数。

即是将样本应变量的条件均值表⽰为解释变量的某种函数。

3、解释变量的边际贡献：在回归模型中新加⼊⼀个解释变量所引起的回归平⽅和或者拟合优度的增加值。

4、⼀阶偏相关系数：反映⼀个经济变量与某个经济变量的线性相关程度时，剔除另⼀个变量对它们的影响的真实相关程度的指标。

5、最⼩⽅差准则：在模型参数估计时，应当选择其抽样分布具有最⼩⽅差的估计式，该原则就是最佳性准则，或者称为最⼩⽅差准则。

6、OLS：普通最⼩⼆乘估计。

是利⽤残差平⽅和为最⼩来求解回归模型参数的参数估计⽅法。

7、偏相关系数：反映⼀个经济变量与某个经济变量的线性相关程度时，剔除其它变量（部分或者全部变量）对它们的影响的真实相关程度的指标。

8、WLS：加权最⼩⼆乘法。

是指估计回归⽅程参数时，按照残差平⽅加权求和最⼩的原则进⾏的估计⽅法。

9、U t⾃相关：即回归模型中随机误差项逐项值之间的相关。

即Cov（U t，U s）≠0 t ≠s。

10、⼆阶偏相关系数：反映⼀个经济变量与某个经济变量的线性相关程度时，剔除另两个变量对它们的影响的真实相关程度的指标。

11、技术⽅程式：根据⽣产技术关系建⽴的计量经济模型。

13、零阶偏相关系数：反映⼀个经济变量与某个经济变量的线性相关程度时，不剔除任何变量对它们的影响的相关程度的指标。

也就是简单相关系数。

14、经验加权法：是根据实际经济问题的特点及经验判断，对滞后经济变量赋予⼀定的权数，利⽤这些权数构成各滞后变量的线性组合，以形成新的变量，再⽤最⼩⼆乘法进⾏参数估计的有限分布滞后模型的修正估计⽅法。

15、虚拟变量：在计量经济学中，我们把取值为0和1 的⼈⼯变量称为虚拟变量，⽤字母D表⽰。

（或称为属性变量、双值变量、类型变量、定性变量、⼆元型变量）16、不完全多重共线性：是指在多元线性回归模型中，解释变量之间存在的近似的线性关系。

计量经济学导论一、单项选择题1、计量经济学是__________的一个分支学科。

CA统计学B数学C经济学D数理统计学2、计量经济学成为一门独立学科的标志是__________.BA 1930年世界计量经济学会成立B 1933年《计量经济学》会刊出版C 1969年诺贝尔经济学奖设立D 1926年计量经济学（Economics）一词构造出来3、外生变量和滞后变量统称为__________。

DA控制变量B解释变量C被解释变量D前定变量4、横截面数据是指__________。

AA 同一时点上不同统计单位相同统计指标组成的数据B 同一时点上相同统计单位相同统计指标组成的数据C 同一时点上相同统计单位不同统计指标组成的数据D 同一时点上不同统计单位不同统计指标组成的数据5、同一统计指标,同一统计单位按时间顺序记录形成的数据列是__________.CA时期数据B混合数据C时间序列数据D横截面数据6、在计量经济模型中，由模型系统内部因素决定，表现为具有一定的概率分布的随机变量，其数值受模型中其他变量影响的变量是__________。

BA 内生变量B 外生变量C 滞后变量D 前定变量7、描述微观主体经济活动中的变量关系的计量经济模型是__________.AA 微观计量经济模型B 宏观计量经济模型C 理论计量经济模型D 应用计量经济模型8、经济计量模型的被解释变量一定是__________。

CA 控制变量B 政策变量C 内生变量D 外生变量9、下面属于横截面数据的是__________.DA 1991－2003年各年某地区20个乡镇企业的平均工业产值B 1991－2003年各年某地区20个乡镇企业各镇的工业产值C 某年某地区20个乡镇工业产值的合计数D 某年某地区20个乡镇各镇的工业产值10、经济计量分析工作的基本步骤是__________。

AA 建立模型、收集样本数据、估计参数、检验模型、应用模型B 设定模型、估计参数、检验模型、应用模型、模型评价C 个体设计、总体设计、估计模型、应用模型、检验模型D 确定模型导向、确定变量及方程式、估计模型、检验模型、应用模型11、将内生变量的前期值作解释变量，这样的变量称为__________。

计量经济学答案部分Word版第一章导论一、单项选择题1-6: CCCBCAC二、多项选择题ABCD;ACD;ABCD三.问答题什么是计量经济学？答案见教材第3页四、案例分析题假定让你对中国家庭用汽车市场发展情况进行研究，应该分哪些步骤，分别如何分析？（参考计量经济学研究的步骤）第一步：选取被研究对象的变量：汽车销售量第二步：根据理论及经验分析，寻找影响汽车销售量的因素，如汽车价格，汽油价格，收入水平等第三步：建立反映汽车销售量及其影响因素的计量经济学模型第四步：估计模型中的参数；第五步：对模型进行计量经济学检验、统计检验以及经济意义检验；第六步：进行结构分析及在给定解释变量的情况下预测中国汽车销售量的未来值为汽车业的发展提供政策实施依据。

第二章简单线性回归模型一、填空题1、线性、无偏、最小方差性（有效性），BLUE。

2、解释变量；参数；参数。

3、随机误差项；随机误差项。

二、单项选择题1-4：BBDA;6-11：CDCBCA三、多项选择题1.ABC;2.ABC;3.BC;4.ABE;5.AD;6.BC四、判断正误：1. 错；2. 错；3. 对；4.错；5. 错；6. 对；7. 对；8.错五、简答题：1.为什么模型中要引入随机扰动项？答：模型是对经济问题的一种数学模型，在模型中，被解释变量是研究的对象，解释变量是其确定的解释因素，但由于实际问题的错综复杂，影响被解释变量的因素中，除了包括在模型中的解释变量以外，还有其他一些因素未能包括在模型中，但却影响被解释变量，我们把这类变量统一用随机误差项表示。

随机误差项包含的因素有：第一，未知影响因素的代表；第二，无法取得数据的已知因素的代表；第三，众多细小影响因素的综合代表；第四，模型的设定误差；第五，变量的观测误差；第六，经济现象的内在随机性。

由此可见，随机误差项有十分丰富的内容，在计量经济研究中起着重要的作用，一定程度上，随机误差项的性质决定着计量经济方法的选择和使用。

2011年各地区的百户拥有家用汽车■等效据第三章习题 3.1地区 百户拥有家用汽车量Y/辆人均GDPX2/万元城慎人口比复X3/*交通工具消费价格指数X4 （上年=100）北京 37.71 8.05 S6. 20 95. 92 天津 20. 62 & 31 80. 50 103. 57 河北 23. 32 3. 39 15. 60 99. 03 山西 18. 60 3.13 19. 68 98. 96 内蒙 古 19. 625. 7956. 6299.11辽宁 11.15 5.07 64.05 100. 12 吉林 11. 24 3.81 53.40 97.15 黑龙 江 5.293.2856. 50100. 54上海 18. 15 8・18 S9. 30 101.58 江苏 23. 92 6.22 61.90 9& 95 浙江 33. 85 5.92 62. 30 96. 69 安徽 9. 20 2.56 44.80 100. 25 福建 17. 83 1. 72 5& 10 100. 75 江西 8.88 2.61 45.70 100. 91 山东28.12 1. 71 50. 95 98. 501-1. 062.87 10. 57 100. 59 湖北 9. 693. 41 51.83 101.15 湖南 12. 82 2.98 15.10 100. 02 广东 30.71 5.07 66. 50 97. 55 广西 17. 24 2. 52 41.80 102.28 海南15. 82 2.88 50. 50 102.0610. 143. 43 55.02 99.12 四川 12. 25 2.61 41. 83 99. 76 贵州 10. 18 1・64 34.96 100. 71 云南 23. 32 1.92 36. 80 96. 25 西藏 25. 302.00 22.71 99. 95 陕西19 9?3. 31 17. 30 101. 597. 331.96 37.15 100. 51 青海 6. 082.94 16. 22 100. 16 宁夏12. 40 3.29 49.82 100. 99 新9112. 322.9943. 51100. 97一、 研究的目的和要求经济增长，公共服务、市场价格、交通状况，社会环境、政策因素都会影响中国汽车拥有量。

思考题答案第一章绪论思考题1。

1怎样理解产生于西方国家的计量经济学能够在中国的经济理论研究和现代化建设中发挥重要作用？答：计量经济学的产生源于对经济问题的定量研究，这是社会经济发展到一定阶段的客观需要。

计量经济学的发展是与现代科学技术成就结合在一起的，它反映了社会化大生产对各种经济因素和经济活动进行数量分析的客观要求。

经济学从定性研究向定量分析的发展，是经济学逐步向更加精密、更加科学发展的表现。

我们只要坚持以科学的经济理论为指导，紧密结合中国经济的实际，就能够使计量经济学的理论与方法在中国的经济理论研究和现代化建设中发挥重要作用。

1。

2理论计量经济学和应用计量经济学的区别和联系是什么？答：计量经济学不仅要寻求经济计量分析的方法，而且要对实际经济问题加以研究，分为理论计量经济学和应用计量经济学两个方面。

理论计量经济学是以计量经济学理论与方法技术为研究内容，目的在于为应用计量经济学提供方法论。

所谓计量经济学理论与方法技术的研究，实质上是指研究如何运用、改造和发展数理统计方法，使之成为适合测定随机经济关系的特殊方法。

应用计量经济学是在一定的经济理论的指导下，以反映经济事实的统计数据为依据，用计量经济方法技术研究计量经济模型的实用化或探索实证经济规律、分析经济现象和预测经济行为以及对经济政策作定量评价。

1.3怎样理解计量经济学与理论经济学、经济统计学的关系?答：1、计量经济学与经济学的关系。

联系：计量经济学研究的主体—经济现象和经济关系的数量规律;计量经济学必须以经济学提供的理论原则和经济运行规律为依据；经济计量分析的结果：对经济理论确定的原则加以验证、充实、完善.区别:经济理论重在定性分析，并不对经济关系提供数量上的具体度量；计量经济学对经济关系要作出定量的估计，对经济理论提出经验的内容.2、计量经济学与经济统计学的关系。

联系：经济统计侧重于对社会经济现象的描述性计量；经济统计提供的数据是计量经济学据以估计参数、验证经济理论的基本依据；经济现象不能作实验，只能被动地观测客观经济现象变动的既成事实，只能依赖于经济统计数据。

欢迎共阅计量经济学练习题第一章导论一、单项选择题⒈计量经济研究中常用的数据主要有两类：一类是时间序列数据，另一类是【B】A总量数据B横截面数据CABCDCDAABCD解释变量为随机变量，被解释变量为非随机变量二、填空题⒈计量经济学是经济学的一个分支学科，是对经济问题进行定量实证研究的技术、方法和相关理论，可以理解为数学、统计学和_经济学_三者的结合。

⒉现代计量经济学已经形成了包括单方程回归分析，联立方程组模型，时间序列分析三大支柱。

⒊经典计量经济学的最基本方法是回归分析。

计量经济分析的基本步骤是：理论（或假说）陈述、建立计量经济模型、收集数据、计量经济模型参数的估计、检验和模型修正、预测和政策分析。

⒋常用的三类样本数据是截面数据、时间序列数据和面板数据。

⒌经济变量间的关系有不相关关系、相关关系、因果关系、相互影响关系和恒等关系。

三、简答题⒈什么是计量经济学？它与统计学的关系是怎样的？计量经济学就是对经济规律进行数量实证研究，包括预测、检验等多方面的工作。

计量经济学估计值、而统计先能够对分析、研究和预测更广泛的经济问题起重要作用。

计量经济学从经济理论和经济模型出发进行计量经济分析的过程，也是对经济理论证实或证伪的过程。

这些是以处理数据为主，与经济理论关系比较松散统计学研究不能比拟的功能，也是计量经济学与统计学的区别。

⒉经济数据在计量经济分析中的作用是什么？经济数据是计量经济分析的材料。

经济数据是通过对经济变量进行观测和统计，从现实经济和经济历史中得到的，反映经济活动水平的数字特征。

从本质上说，经济数据都是由相关的经济规律生成的，因此是反映经济规律的信息载体，确定经济规律的基本材料。

经济数据的数量和质量，对计量经济分析的有效性和价值有举足轻重轻重的影响。

⒊试分别举出时间序列数据、横截面数据、面板数据的实例。

时间序列数据指对同一个观测单位，在不同时点的多个观测值构成的观测值序列，或者以时间为序收集统计和排列的数据，如浙江某省从1980年到2007年各年的GDP ；横截面数据是指在现一时点上，对不同观测单位观测得到的多个数据构成的数据集，如2007年全国31个省自治区直辖市的GDP ；面板数据就是由对许多个体组成的同一个横截面，在不同时点的观测值构成的数据，如从1980⒈表示x A t y ˆˆβ=C t y β=⒉参数?AVar(βˆC(βˆ－?⒊产量（】 A B C D ⒋对回归模型t t t x y εββ++=10进行统计检验时，通常假定t ε服从【C 】AN （0，2i σ）Bt(n-2)CN （0，2σ）Dt(n)⒌以y 表示实际观测值，yˆ表示回归估计值，则普通最小二乘法估计参数的准则是使【D 】 A )ˆ(i i yy -∑＝0B 2)ˆ(i i y y -∑＝0C )ˆ(i i yy -∑为最小D 2)ˆ(i i y y -∑为最小 ⒍以X 为解释变量，Y 为被解释变量，将X 、Y 的观测值分别取对数，如果这些对数值描成的散点图近似形成为一条直线，则适宜配合下面哪一模型形式?(D)A.Y i =β0+β1X i +μiB.lnY i =β0+β1X i +μiC.Y i =β0+β1lnX i +μiD.lnY i =β0+β1lnX i +μi ⒎下列各回归方程中，哪一个必定是错误的?(C) A.Y i =50+0.6X i r XY =0.8B.Y i =-14+0.8X i r XY =0.87C.Y i =15-1.2X i r XY =0.89D.Y i =-18-5.3X i r XY =-0.96(B) A.0.81C.0.66(A)A.E(μi C.Cov(μi ,作t A 05.0t （A C i i i A ．随机误差项的均值为零 B ．所有随机误差都有相同的方差C ．两个随机误差互不相关D ．误差项服从正态分布二、判断题⒈随机误差项εi 与残差项e i 是一回事。