2019年管理类MBA综合考试数学真题及详细答案解析(word版)

2019年管理类联考综合能力真题一、问题求解：第1-15小题,每小题3分,共45分. 下列每题给出的A、B、C、D、E五个选项中, 只有一项是符合试题要求的. 请在答题卡上将所选项的字母涂黑.1. 某家庭在一年总支出中，子女教育支出与生活资料支出的比为，文化娱乐支出与子女教育支出为 . 已知文化娱乐支出占家庭总支出的，则生活资料支出占家庭总支出的（A）40% （B）42% （C）48% （D）56% （E）64%【参考答案】D2. 有一批同规格的正方形瓷砖，用它们铺满整个正方形区域时剩余块，将此正方形区域的边长增加一块瓷砖的长度时，还需要增加块瓷砖才能铺满，该批瓷砖共有（A）块（B）块（C）块（D）块（E）块【参考答案】C3. 上午9时一辆货车从甲地出发前往乙地，同时一辆客车从乙地出发前往甲地，中午12时两车相遇，当客车到达甲地时货车距离乙地的距离是（A）30千米（B）43千米（C）45千米（D）50千米（E）57千米【参考答案】E4. 在分别标记了数字1、2、3、4、5、6的6张卡片中随机选取3张，其上数字和等于10的概率（）（A）0.05 （B）0.1 （C）0.15 （D）0.2 （E）0.25【参考答案】C5. 某商场将每台进价为2000元的冰箱以2400元销售时，每天销售8台，调研表明这种冰箱的售价每降低50元，每天就能销售4台。

若要每天销售利润最大，则该冰箱的定价应为（）（A） 2200 （B）2250 （C）2300 （D）2350 （E）2400【参考答案】B6. 某委员会由三个不同专业的人员组成，三个专业的人数分别是2，3, 4，从中选派2位不同专业的委员外出调研，则不同的选派方式有（）（A） 36种（B）26种（C）12种（D）8种（E）6种【参考答案】B7. 从1到100的整数中任取一个数，则该数能被5或7整除的概率为（）（A）0.02 （B）0.14 （C）0.2 （D）0.32 （E）0.34【参考答案】D8.如图1，在四边形ABCD中，AB//CD，AB与CD的边长分别为4和8，若 ABE的面积为4，则四边形ABCD 的面积为（）(A)24. (B)30. (C)32. (D)36. (E)40.【参考答案】D9. 现有长方形木板340张，正方形木板160张（图2），这些木板加好可以装配若干竖式和横式的天盖箱子（图3），装配成的竖式和横式箱子的个数为（）（A）25, 80 （B）60, 50 （C）20, 70 （D）60, 40 （E）40, 60【参考答案】E10. 圆上到原点距离最远的点是（）（A）（B）（C）（D）（E）【参考答案】E11. 如图4，点A,B,O,的坐标分别为(4,0), (0,3),(0,0),若(x,y)是中的点，则的最大值为（）（A）6 （B）7 （C）8 （D）9 （E）12【参考答案】D12. 设抛物线与轴相交于A,B两点，点C坐标为(0,2),若的面积等于6，则（）（A）（B）（C）（D）（E）【参考答案】A13. 某公司以分期付款方式购买一套定价为1100万元的设备，首期付款100万元后，之后每月付款50万元，并支付上期余款的利息，月利率1%，该公司共为此设备支付了（）（A）1195万元（B）1200万元（C）1205万元（D）1215万元（E）1300万元【参考答案】C14. 某学生要在4门不同的课程中选修2门课程，这4门课程中的2门个开设一个班，另外2门各开设2个班，该学生不同的选课方式共有（）（A）6种（B）8种（C）10种（D）13种（E）15种【参考答案】D15. 如图5，在半径为10厘米的球体上开一个底面半径是6厘米的圆柱形洞，则洞的内壁面积为（单位：平方厘米）（）（A）48 （B）288 （C）96 （D）576 （E）192二、条件充分性判断：第16-25小题,每小题3分,共30分.要求判断每题给出得条件（1）和（2）能否充分支持题干所陈述的结论. A、B、C、D、E五个选项为判断结果, 请选择一项符合试题要求得判断, 在答题卡上将所选项得字母涂黑.16. 已知某公司男员工的平均年龄和女员工的平均年龄，则能确定该公司员工的平均年龄（1）已知该公司员工的人数（2）已知该公司男女员工的人数之比【参考答案】B17. 如图6，正方形由四个相同的长方形和一个小正方形拼成，则能确定小正方形的面积（1）已知正方形的面积（2）已知长方形的长宽之比【参考答案】C18. 利用长度为和的两种管材能连接成长度为37的管道（单位：米）【参考答案】A19. 设x,y是实数，则，【参考答案】C20. 将2升甲酒精和1升乙酒精混合到得到丙酒精，则能确定甲、乙两种酒精的浓度（1）1升甲酒精和5升乙酒精混合后的浓度是丙酒精浓度的1/2倍（2）1升甲酒精和5升乙酒精混合后的浓度是丙酒精浓度的2/3倍【参考答案】E21. 设有两组数据,则能确定a的值（1）与的均值相等（2）与的方差相等【参考答案】A【参考答案】D24. 已知M是一个平面有限点集。

2019年1月份管综初数真题一、问题求解（本大题共5小题，每小题3分，共45分）下列每题给出5个选项中，只有一个是符合要求的，请在答题卡上将所选择的字母涂黑。

1、某车间计划10天完成一项任务，工作3天后因故停工2天。

若要按原计划完成任务，则工作效率需要提高 （ ）A. 20%B.30%C.40%D.50%E.60% 【答案】C【详解】整个工程看做单位“1”，原计划的工作效率为110，实际的工作效率为113710103250-⨯=--，，因此工作效率提高了71501040%110-=，选C 。

2、设函数()()220af x x a x =+>在()0,+∞内的最小值为()012f x =，则0x =（ ）A.5B.4C.3D.2E.1 【答案】B【详解】利用三个数的均值定理求最值：33a b c abc ++≥。

()322223a a a f x x x x x x x x x=+=++≥⋅⋅，因此最小值为331264a a =→=，因此2644x x x x ==→=，选B 。

3、某影城统计了一季度的观众人数，如图，则一季度的男士观众人数之比为（） A.3:4 B.5：6 C.12：13 D.13:12 E.4：3男女123451234561月份2月份3月份单位（万人）O【答案】C【详解】如图可得:一季度男女观众人数分别为： 男：54312w w w w ++= 女：63413w w w w ++=故一季度男女人数比为：12:13,选C 。

4、设实数b a ,满足6=ab ，6=-++b a b a ，则=+22b aA.10B.11C.12D.13E.14 【答案】D【详解】观察选项，所求的值必然是唯一的，因此为了去掉已知等式的绝对值，可以设定a 、b 的正负性和大小关系。

由6ab =可知a 、b 同号，故设0,0,a b a b >>>，因此去掉绝对值可得：63a b a b a ++-=→=，又已知6ab =，得2b =，所求2213a b +=，选D 。

2019年全国硕士研究生入学统一考试管理类专业学位联考综合能力试题说明：由于2019年试题为一题多卷，因此现场试卷中的选择题部分，不同考生有不同顺序。

请在核对答案时注意题目和选项的具体内容。

一、问题求解（第1～15小题，每小题3分，共45分，下列每题给出的A 、B 、C 、D 、E 五个选项中，只有一个是符合试题要求的，请在答题卡上将所选项的字母涂黑）。

1.某工厂生产一批零件，计划10天完成任务，实际提前两天完成，则每天的产量比计划平均提高了（ ）。

A.15%B.20%C.25%D.30%E.35%2.甲乙两人同时从A 地出发，沿400米跑道同向匀速行走，25分钟后乙比甲少走了一圈。

若乙行走一圈需要8分钟，则甲的速度是（ ）米/分钟A.62B.65C.66D.67E.693.甲班共有30名学生，在一次满分为100分的考试中，全班平均成绩为90分，则成绩低于60分的学生至多有（ ）个。

A.8B.7C.6D.5E.44.某工程由甲公司承包需60天完成，由甲、乙两公司共同承包需28天完成，由乙、丙两公司共同承包需35天完成，则由丙公司承包并完成该工程需要的天数是（ ）A.85B.90C.95D.100E.105 5.已知)10)(9(1)3)(2(1)2)(1(1)(+++⋅⋅⋅++++++=x x x x x x x f ，则=)8(f （ ） A.91 B.101 C.161 D.171 E.181 6.甲乙两商店同时购进了某品牌电视机，当甲商店售出了15台时乙商店售出了10台，此时两店的库存比为8:7，库存差为5，则甲乙两店总进货量为（ ）A.75B.80C.85D.100E.1257.如图，在直角三角形ABC 中，4=AC ，3=BC ，BC DE //，已知梯形BCDE 的面积为3，则=DE （ ） A.3 B.13+ C.434- D.223 E.12+8.点)4,0(关于关于直线012=++y x 的对称点为（ ）A.)0,2(B.)0,3(-C.)1,6(-D.)2,4(E.)2,4(- 9.在52)53(++x x 的展开式中，2x 的系数为（ ）A.5B.10C.45D.90E.9510.有一批水果要装箱，一名熟练工单独装箱需要10天，每天报酬为200元；一名普通工单独装箱需要15天，每天报酬为120元。

2019年管理类MBA 综合考试数学真题及详细答案解析一、问题求解：第1～15小题，每小题3分，共45分。

下列每题给出的A 、B 、C 、D 、E五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项的字母涂黑。

1. 某车间计划10天完成一项任务，工作了3天后因故停工2天，若要按原计划完成任务，则工作效率需要提高（ ）.A ．20% B. 30% C. 40% D. 50% E. 60%解析：（C ）解法1：将整个任务的工作量看作单位“1”，则原计划的工作效率为110.工作3天后因故停工2天，余下的工作量为17131010-⨯=，需要5天完成，则工作效率为7751050÷=，工作效率提高了71501040%10-=.解法2：工作3天后因故停工2天,若要按原计划完成任务，就要在剩余的5天内完成原计划7天的工作量，则工作效率需要提高11757100%1100%40%157⎛⎫- ⎪⎛⎫⨯=-⨯= ⎪ ⎪⎝⎭ ⎪⎝⎭。

2. 设函数2()2(0)af x x a x=+>在(0,)+∞内的最小值为0()12f x =，则0x =( ).A. 5B. 4C. 3D. 2E. 1解析：（B ）利用三个数的均值定理求最值：a b c ++≥，且“=”只在a b c ==时取到。

322()231264a a f x x x x x x a a x x =+=++≥==⇒=， 此时有2644x x x x==⇒= 注：本解法中2x 一定要拆成两个相等的数相加，即x x +，如果拆成其它形式(如0.5 1.5x x +)，则不等式取等号的条件就不满足了。

3. 某影城统计了一季度的观众人数，如图，则一季度的男性观众人数与女性观众之比为( ) A. 3:4 B. 5:6 C. 12:13 D. 13:12 E. 4:3 解析：（C ）由图可得一季度男女观众人数分别为：男：54312++=万人； 女：63413++=万人因此一季度男女人数比为：12:134. 设实数,a b 满足6,6ab a b a b =++-=，则22a b +=( ). A. 10 B. 11 C. 12 D. 13 E. 14解析：（D ）解法1：想办法去掉绝对值，由60ab =>知,a b 同号，若同正，不妨设0a b >>，此时263a b a b a b a b a a ++-=++-==⇒=，进而62b a==，代入得2213a b +=；若同负，不妨设0a b <<，此时263a b a b a b a b a a ++-=---+=-=⇒=-，进而62b a==-，代入得2213a b +=。

1、某车间计划10天完成一项任务，工作3天后事故停工2天，若仍要按原计划完成任务，则工作效率要提高( )% % % % E. 60%[参考答案]C[详解]整个工程看做单位"1"，原计划的工作效率为1/10，实际的工作效率为(1-1/10x3)/( 10-3-2) =7/50，因此工作效率提高了(7/50-1/10)/(1/10)=40%，选C。

2、函数f(x)=2x+a/π²(a﹥0)，在(0，+∞)内最小值为f(x0)=12，则x0=[参考答案]B[详解]利用三个数的均值定理求最值：a+b+c≥33√abc。

f(x)=2x+a/x2=x+x+a/x2≥33√x*x*a/x2，因此最小值为33√a=12→a=64，因此x=x=64/x2→x=4，选B。

（3、某影城统计了一季度的观众人数，如图，则一季度的男、女观众人数为（）:4 :6 :13 :12 :3[参考答案]C[详解]如图可得：一季度男女观众人数分別为:男: 5w+ 4w+ 3w= 12w女: 6w+ 3w+ 4w= l3w故一季度男女人数比的: 12:13，选C。

4、;2+b2=( )5、没实数a,b満足ab=6，|a+b| +|a-b|=6，则aE. 14[参考答案]D[解析] : ab=6,特值法a=2，b=3満足条件，a2+b2=4+9=13，选D。

6、设圆C与圆(x-5)2+y2=2，关于y=2x时称，则圆C方程为( )A.(x-3)2+(y-4)2=2B.(x+4)2+(y-3)2=2B.(x-3)2+(y+4)2=2 D.(x+3)2+(y+4)2=2E.(x+3)2+(y-4)2= 2…[参考答案]E7、将一批树苗种在应该正方形花园边上，四角都种，如果每隔3米种一棵，那么剩下10课树苗,如果每隔2米种一棵那么种满正方形的3条边,则这批树苗有( ) 棵A、54B、60C、70D、82E、94[参考答案]D[详解]设正方形的边长为x，由已知可得方程4x/3+10=3x/2+1，求解得x=54故树苗有(54x4)/3+10=82，选D。

2019年管理类联考数学真题一、问题求解（本大题共5小题，每小题3分，共45分）下列每题给出5个选项中，只有一个是符合要求的，请在答题卡上讲所选择的的字母涂黑。

1、某车间计划10天完成一项任务，工作3天后因故停工2天。

若要按原计划完成任务，则工作效率需要提高（）【答案】C解析：男观众：3+4+5=12女观众：3+4+6=13；男：女=12:134、设实数a,b 满足ab =6,|a+b|+|a-b|=6,则a 2+b 2=()A.10B.11C.12D.13E.14【答案】DA.B.C.D.E.棵树苗；如果每隔2米种一颗，那么恰好种满正方形的3条边，则这批树苗有（）棵A.54B.60C.70D.82E.94【答案】D解析：设正方形边长为m，则有1321043+⋅=+⋅mm ，解得54=m ；则树苗共有：82104354=+⋅，故选D.7、在分别标记1、2、3、4、5、6的6张卡片，甲抽取1张，乙从余下的卡片中再抽取2张，乙的卡片数字之和大于甲的卡片数字的概率为（）A.11/60 B.13/60 C.43/60 D.47/60 E.49/60【答案】D解析：总数：602516=C C ，不符合条件的：甲取3，乙取12；甲取4，乙取12,13；甲取5，乙取12,13,14,23；甲取6，乙取12,13,14,15,23,24,；6047601360=-=p【答案】E解析：正方体表面积最大，则说明正方体上面四个顶点都在圆上，如图作辅助线，设正方体棱长为m。

则勾股定理方程：222322=⎪⎪⎭⎫ ⎝⎛+m m ，可得62=m ，则正方体表面积为3662=m ，故选B。

10、在三角形ABC 中，AB=4,AC=6，BC=8，D 为BC 的中点，则AD =A.B.C.3D.22E.【答案】B解析：如图，作辅助线AE⊥BC 于E，故选B。

ABCED设BE=m,则CE=8-m勾股定理列方程：2222)8(6-4m m --=，得m=BE=411，则4153)411(422=-=AE ,45=DE ，勾股定理：AD=1011、某单位要铺设草坪，若甲、乙两公司合作需6天，工时费共2.4万元。

2019管综数学题2019年全国硕士研究生招生考试管理类联考综合能力试题（数学部分）一、问题求解：1. 某单位组织出游，36人排成两行，每行相邻两员工的距离相等，第一个员工在队头，从第二个员工起到队尾，每个员工所占的距离是前一个员工的倍。

求第一个员工所占的距离。

2. 甲、乙、丙三人进行象棋比赛，每两人赛一盘，规定：赢一盘得2分，输得0分，打平各得1分。

全部比赛的三盘棋下完后，甲得3分，乙得1分，那么丙得多少分。

3. 某项密码破译工作需甲、乙、丙、丁四人完成，已知每人独立译出密码的概率为，若二人合为一组则该组破译的概率为，若三人合为一组则该组破译的概率为，若四人合作则破译的概率提升到。

为完成此项工作，现有四种方案，方案1：四人独立翻译；方案2：分为两组每组两人，两组独立翻译；方案3：分为两组，一组三人、一组一人，两组独立翻译；方案4：四人一组合作翻译。

则密码能被译出的概率最大的是（）。

A.方案1B.方案2C.方案3D.方案44. 甲、乙、丙三人按任意次序站成一排，对于任何一种站法，甲都不站在两端的概率是（）A. 1/4B. 1/3C. 1/2D. 2/35. 小张用40元钱去买5元一张的电影票和2元一张的小食品，要求小食品的数量不少于电影票数量的2倍，且电影票数量不少于两张。

则不同的购买方式有（）种。

A. 3B. 4C. 5D. 6二、条件充分性判断：1. 在三角形ABC中，AB = AC，∠BAC = 120°，若AC为直径的圆O与AB相切于点D，问切线长AD与半径OC的比值是多少？（1）作过点A与BC平行的直线AM与直线BC相交于点M，且与半径OC相交于点D。

（2）连接BD、CD、AO。

A. 仅条件（1）充分B. 仅条件（2）充分C. 条件（1）（2）单独都不充分D. 条件（1）（2）联合起来充分2. 一个盒子中装有大小相同的红球、黄球和蓝球共100个，已知从盒中任意摸出n个球时，摸到红球的概率为(n-2)/3n(n∈N)。

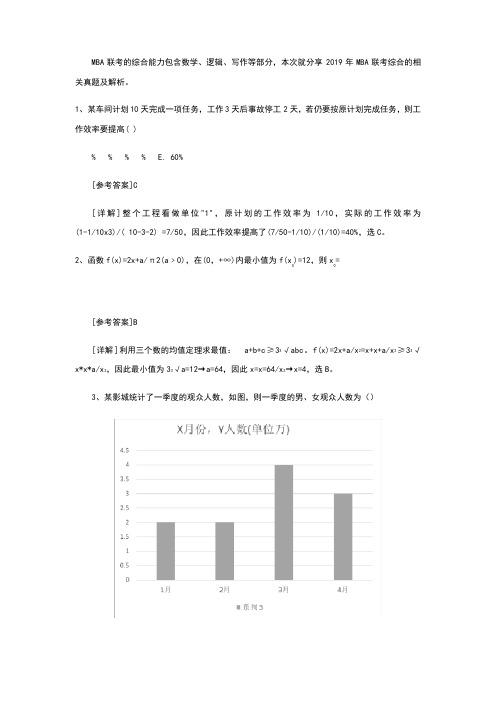
MBA联考综合能力真题2019年2. 设函数在(0，+∞)内的最小值为f(x0)=12，则x0=______ •B[解析] 本题考查均值不等式。

由于x＞0，a＞0，则f(x)的表达式各项均大于0，考虑运用均值不等式分析其最小值。

则a=64，当且仅当，即x=4时取等号。

故本题选B。

•方法二(计算法)：两圆圆心关于直线y=2x 对称，即两点连线的中点在y=2x 上，两点连线与y=2x垂直。

设圆C 的圆心为(a ，b)，则满足方程组解得即圆C 的圆心为(-3，4)，半径与已知圆半径相等，所以圆C 的方程为(x+3)2+(y-4)=2。

故本题选E 。

6. 将一批树苗种在一个正方形花园的边上，四角都种。

如果每隔3米种一棵，那么剩余10棵树苗；如果每隔2米种一棵，那么恰好种满整个正方形的3条边，则这批树苗有______D[解析] 本题考查植树问题。

设正方形边长为x，四个角都种树且每隔3米种一棵树，四边种满，则所种树总数为；四个角都种树且每隔2米种一棵树，种满三边，则所种树总数为。

根据题意有，得x=54。

这批树苗共有棵。

故本题选D。

注：在封闭路线上植树，植树总棵数=距离÷间距。

在非封闭路线上植树，若两端都植树，植树总棵数=距离÷间距+1。

7. 在分别标记了数字1，2，3，4，5，6的6张卡片中，甲随机抽取1张后，乙从余下的卡片中再随机抽取2张，乙的卡片数字之和大于甲的卡片数字的概率为______A．B．C．D．E．D[解析] 本题考查古典概型。

甲先抽取到每一个数字的概率均为。

乙从剩下的卡片中抽取两张，不同的情况总数均为，其中有一些情况不满足大于甲所抽取的卡片数字。

如下表：所求事件概率为。

故本题选D。

B[解析] 本题考查均值与方差。

语文成绩从小到大排序，86，87，88，89，90，91，92，93，94，95，为连续自然数，均值；数学成绩从小到大排序，80，82，84，85，88，90，93，94，96，98，前后对应位置两个数之和都相等，均值。

2019年管理类综合能力真题E.22(3)(4)2x y ++-=【答案】E【解析】看图，不需要计算，直接观察坐标位置即可。

Pyxy=2x11223456643-1-2-1-2-3-4(5,0)6、在分别记了数字1、2、3、4、5、6的6张卡片中，甲随机抽取1张后，乙从余下的卡片中再随机抽取2张，乙的卡片数字之和大于甲的卡片数字的概率为（）。

A.1160B.1360C.4360D.4760E.4960【答案】D【解析】一共有种选取方法1265C C =60种，作为分母。

分子有以下几种情形。

甲取1，乙有25C =10种，甲取2；乙有25C =10种；甲取3，乙有25C -1=9种；甲取4，乙有25C -2=8种；甲取5，乙有25C -4=6种；甲取6，乙有2+5、3+4、3+5、4+5=4种，一种有47种。

7、将一批树苗种在一个正方形花园的边上，四角都种，如果每隔3米种一颗，那么剩余10颗树苗，如果每隔2米种一颗那么恰好种满正方形的3边，则这批树苗有（）。

A.54颗B.60颗C.70颗D.82颗E.94颗 【答案】D【解析】设正方形周长为S ，则根据树的总数相等列方程0.7510=132S S ++=21610823S S ⇒+=树有8、10名同学的语文和数学的成绩如表：语文成绩 90 92 94 88 86 95 87 89 91 93 数学成绩94 88 96 93 90 85 84 80 82 98语文和数学成绩的均值分别为E 1和E 2，标准差分别为σ1和σ2，则（）。

A. E 1＞E 2，σ1＞σ2B. E 1＞E 2，σ1＜σ2C. E1＞E2，σ1=σ2D.E1＜E2，σ1＞σ2E. E1＜E2，σ1＜σ2【答案】B【解析】可根据数据范围来估算平均值跟标准差。

语文成绩范围是[86，95]，数学成绩范围是[80，98]，语文分数范围更集中，且整体略高于数学，故可判断问平均分更高，方差更小。

2017年管理类专业联考综合能力数学试题及解析一、问题求解：第1~15小题，每小题3分，共45分。

下列每题给出的A ．B ．C ．D ．E 五个选项中，只有一项是符合试题要求的，请在答题卡上将所选项的字母涂黑。

1、某品牌的电冰箱连续两次降价10%后的售价是降价前的（） %%%%%2、甲、乙、丙三种货车的载重量成等差数列，2辆甲种车和1辆乙种车满载量为95吨，1辆甲种车和3辆丙种车满载量为150吨。

则用甲、乙、丙各1辆车一次最多运送货物（）吨3、张老师到一所中学进行招生咨询，上午接受了45名同学的咨询，其中的9名同学下午又咨询了张老师，占张老师下午咨询学生的10%。

一天中向张老师咨询的学生人数为（）4、某种机器人可搜索到的区域是半径为1米的圆，若该机器人沿直线行走10米。

其搜索过的区域的面积（单位：平方米）为（） A.102π+B.10π+C.202π+D.20π+E.10π5、不等式12x x -+≤的解集为（） A.(],1-∞B.3,2⎛⎤-∞ ⎥⎝⎦C.31,2⎡⎤⎢⎥⎣⎦D.[)1,+∞E.3,2⎡⎫+∞⎪⎢⎣⎭6、在1与100之间，能被9整除的整数的平均值为（）7、某试卷由15道选择题组成，每道题有4个选项，只有一项是符合试题要求的，甲有6道题能确定正确选项，有5道题能排除2个错误选项，有4道题能排除1个错误选项。

若从每题排除后剩余的选项中选1个作为答案，则甲能得满分的概率为（）A.451123⋅B.541123⋅C.541123+D.541324⎛⎫⋅ ⎪⎝⎭E.541324⎛⎫+ ⎪⎝⎭8、某公司用1万元购买了价格分别是1750元和950元的甲、乙两种办公设备，则购买的甲、乙办公设备的件数分别为（） ,5,3,4,6,29、如图1，在扇形AOB 中，,1,4AOB OA AC OB π∠==⊥，则阴影部分的面积为（）A.184π- B.188π- C.142π-图1D.144π- E.148π- 10、老师问班上50名同学周末复习的情况，结果有20人复习过数学，30人复习过语文，6人复习过英语，且同时复习了数学和语文的有10人，语文和英语的有2人，英语和数学的有3人。

2019年管理类MBA综合考试数学真题及详细答案解析一、问题求解：第1～15小题，每小题3分，共45分。

下列每题给出A、B、C、D、E五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项字母涂黑。

1. 学科竞赛设一等奖、二等奖和三等奖，比例为1：3：8，获奖率为30%，已知10人获得一等奖，则参加竞赛的人数为（）A．300 B. 400 C. 500 D. 550 E. 600解析：（B）解法1：由一等奖：二等奖：三等奖=1：3：8，且一等奖10人，可推出二等奖、三等奖分别为30人和80人，所以获奖人数为10+30+80=120人，所以参加竞赛人数为12030%=400÷人。

解法2：设参加竞赛的人数为x，根据题意有130%10400138x x=⇒=++。

2. 为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：A. 32, 30B. 32, 29.5C. 32, 27D. 30, 27E. 29.5, 27解析：（A）23+26+28+30+32+34+36+38+41==329x男23+25+27+27+29+31==276x 女329+276==3015x⨯⨯总3. 某单位采取分段收费的方式收取网络流量(单位: GB)费用，每月流量20(含)以内免费，流量20到30(含)的每GB收费1元，流量30到40(含)的每GB收费3元，流量40以上的每GB收费5元，小王这个月用了45GB的流量，则他应该交费（）A. 45元B. 65元C. 75元D. 85元E. 135元解析：（B）各个流量段所需缴费数额见下表：所以小王应该缴费0+10+30+25=65元。

4. 如图，圆O 是三角形ABC 的内切圆，若三角形ABC 的面积与周长的大小之比为1:2，则圆O 的面积为( ) A. π B.2π C. 3π D. 4π E. 5π解析：（A ）解法1：设三角形边长分别为,,a b c ，内切圆O 的半径为r ，则三角形周长L a b c =++，三角形面积12S Lr =(最好记住该结论)。

2019全国M B A联考综合能力真题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN1、某车间计划10天完成一项任务，工作3天后事故停工2天，若仍要按原计划完成任务，则工作效率要提高( )A.20%B.30%C.40%D.50%E. 60%[参考答案]C[详解]整个工程看做单位"1"，原计划的工作效率为1/10，实际的工作效率为(1-1/10x3)/( 10-3-2) =7/50，因此工作效率提高了(7/50-1/10)/(1/10)=40%，选C。

2、函数f(x)=2x+a/π²(a﹥0)，在(0，+∞)内最小值为f(x0)=12，则x=A.5B.4C.3D.2E.1[参考答案]B[详解]利用三个数的均值定理求最值：a+b+c≥33√abc。

f(x)=2x+a/x2=x+x+a/x2≥33√x*x*a/x2，因此最小值为33√a=12→a=64，因此x=x=64/x2→x=4，选B。

3、某影城统计了一季度的观众人数，如图，则一季度的男、女观众人数为（）A.3:4B.5:6C.12:13D.13:12E.4:3[参考答案]C[详解]如图可得：一季度男女观众人数分別为:男: 5w+ 4w+ 3w= 12w女: 6w+ 3w+ 4w= l3w故一季度男女人数比的: 12:13，选C。

4、没实数a,b満足ab=6，|a+b| +|a-b|=6，则a2+b2=( )A.10B.11C.12D.13E. 14[参考答案]D[解析] : ab=6,特值法a=2，b=3満足条件，a2+b2=4+9=13，选D。

5、设圆C与圆(x-5)2+y2=2，关于y=2x时称，则圆C方程为( )A.(x-3)2+(y-4)2=2B.(x+4)2+(y-3)2=2B.(x-3)2+(y+4)2=2 D.(x+3)2+(y+4)2=2E.(x+3)2+(y-4)2= 2[参考答案]E6、将一批树苗种在应该正方形花园边上，四角都种，如果每隔3米种一棵，那么剩下10课树苗,如果每隔2米种一棵那么种满正方形的3条边,则这批树苗有( ) 棵A、54B、60C、70D、82E、94[参考答案]D[详解]设正方形的边长为x，由已知可得方程4x/3+10=3x/2+1，求解得x=54故树苗有(54x4)/3+10=82，选D。

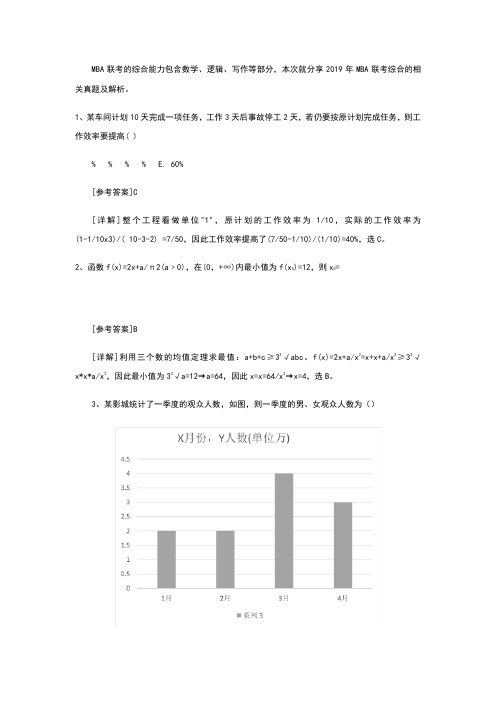
MBA联考的综合能力包含数学、逻辑、写作等部分，本次就分享2019年MBA联考综合的相关真题及解析。

1、某车间计划10天完成一项任务，工作3天后事故停工2天，若仍要按原计划完成任务，则工作效率要提高( )% % % % E. 60%[参考答案]C[详解]整个工程看做单位"1"，原计划的工作效率为1/10，实际的工作效率为(1-1/10x3)/( 10-3-2) =7/50，因此工作效率提高了(7/50-1/10)/(1/10)=40%，选C。

2、函数f(x)=2x+a/π2(a﹥0)，在(0，+∞)内最小值为f(x0)=12，则x0=[参考答案]B[详解]利用三个数的均值定理求最值：a+b+c≥33√abc。

f(x)=2x+a/x2=x+x+a/x2≥33√x*x*a/x2，因此最小值为33√a=12→a=64，因此x=x=64/x2→x=4，选B。

3、某影城统计了一季度的观众人数，如图，则一季度的男、女观众人数为（）:4 :6 :13 :12 :3[参考答案]C[详解]如图可得：一季度男女观众人数分别为:男: 5w+ 4w+ 3w= 12w女: 6w+ 3w+ 4w= l3w故一季度男女人数比的: 12:13，选C。

4、没实数a,b満足ab=6，|a+b| +|a-b|=6，则a2+b2=( )E. 14[参考答案]D[解析] : ab=6,特值法a=2，b=3満足条件，a2+b2=4+9=13，选D。

5、设圆C与圆(x-5)2+y2=2，关于y=2x时称，则圆C方程为( )A.(x-3)2+(y-4)2=2B.(x+4)2+(y-3)2=2B.(x-3)2+(y+4)2=2 D.(x+3)2+(y+4)2=2E.(x+3)2+(y-4)2= 2[参考答案]E6、将一批树苗种在应该正方形花园边上，四角都种，如果每隔3米种一棵，那么剩下10课树苗,如果每隔2米种一棵那么种满正方形的3条边,则这批树苗有( ) 棵A、54B、60C、70D、82E、94[参考答案]D[详解]设正方形的边长为x，由已知可得方程4x/3+10=3x/2+1，求解得x=54故树苗有(54x4)/3+10=82，选D。