尼曼 半导体物理与器件第七章

半导体物理与器件(尼曼第四版)答案第一章：半导体材料与晶体1.1 半导体材料的基本特性半导体材料是一种介于导体和绝缘体之间的材料。

它的基本特性包括：1.带隙：半导体材料的价带与导带之间存在一个禁带或带隙，是电子在能量上所能占据的禁止区域。

2.拉伸系统：半导体材料的结构是由原子或分子构成的晶格结构，其中的原子或分子以确定的方式排列。

3.载流子：在半导体中，存在两种载流子，即自由电子和空穴。

自由电子是在导带上的，在外加电场存在的情况下能够自由移动的电子。

空穴是在价带上的，当一个价带上的电子从该位置离开时，会留下一个类似电子的空位，空穴可以看作电子离开后的痕迹。

4.掺杂：为了改变半导体材料的导电性能，通常会对其进行掺杂。

掺杂是将少量元素添加到半导体材料中，以改变载流子浓度和导电性质。

1.2 半导体材料的结构与晶体缺陷半导体材料的结构包括晶体结构和非晶态结构。

晶体结构是指材料具有有序的周期性排列的结构，而非晶态结构是指无序排列的结构。

晶体结构的特点包括：1.晶体结构的基本单位是晶胞，晶胞在三维空间中重复排列。

2.晶格常数是晶胞边长的倍数，用于描述晶格的大小。

3.晶体结构可分为离子晶体、共价晶体和金属晶体等不同类型。

晶体结构中可能存在各种晶体缺陷，包括：1.点缺陷：晶体中原子位置的缺陷，主要包括实际缺陷和自间隙缺陷两种类型。

2.线缺陷：晶体中存在的晶面上或晶内的线状缺陷，主要包括位错和脆性断裂两种类型。

3.面缺陷：晶体中存在的晶面上的缺陷，主要包括晶面位错和穿孔两种类型。

1.3 半导体制备与加工半导体制备与加工是指将半导体材料制备成具有特定电性能的器件的过程。

它包括晶体生长、掺杂、薄膜制备和微电子加工等步骤。

晶体生长是将半导体材料从溶液或气相中生长出来的过程。

常用的晶体生长方法包括液相外延法、分子束外延法和气相外延法等。

掺杂是为了改变半导体材料的导电性能，通常会对其进行掺杂。

常用的掺杂方法包括扩散法、离子注入和分子束外延法等。

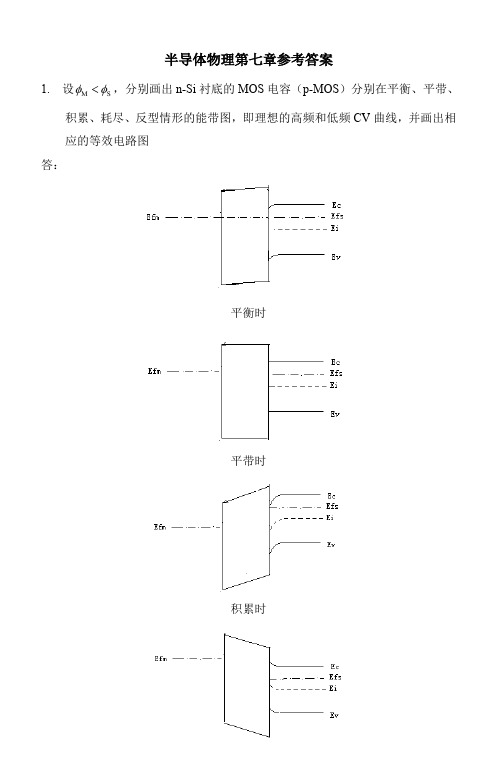
半导体物理第七章参考答案1. 设M S φφ<，分别画出n-Si 衬底的MOS 电容（p-MOS ）分别在平衡、平带、积累、耗尽、反型情形的能带图，即理想的高频和低频CV 曲线，并画出相应的等效电路图 答：平衡时平带时积累时耗尽时弱反时强反时理想的高频和低频CV曲线等效电路图2. 设氧化层厚度为1μm 的Si MOS 结构的p 型衬底的掺杂浓度分别为N ＝1015/cm 3和1016/cm 3，比较这两种结构的耗尽层电容和MOS 电容的极小值。

答：1) 耗尽层电容由耗尽层厚度决定，而耗尽层厚度与Si 表面势有关，根据耗尽层厚度、表面势，可求得耗尽层电容为：()d Sid sdd Q C d W εψ-==又由MOS 电容为氧化层电容与耗尽层电容串联而成：dox C C C 111+= 以及栅压方程：g fb s oxV V ψ-=消去表面势s ψ，可得：C =显然，相同氧化层厚度，即相同氧化层电容，相同栅压下，衬底掺杂浓度高的MOS 结构耗尽层电容大。

2) 由C =MOS 电容的极小值出现在强反型时，此时耗尽层厚度最大，表面势为2B φ：max d W ==min maxSid d C W ε==则：1minmin 11ox d C C C -⎛⎫=+ ⎪⎝⎭当N ＝1015/cm 3时，12min min 1126.7ox d C F m C C μ-⎛⎫=+= ⎪⎝⎭当N ＝1016/cm 3时，12min min 1131.3ox d C F m C C μ-⎛⎫=+= ⎪⎝⎭3. 从物理上说明F B i C C 随氧化层厚度及掺杂浓度的变化趋势，并计算315/10cm N =，nm t ox 10=的Si MOS 结构的FB i C C 值和德拜长度。

答：由公式：11ox D FB i Si ox t L C C εε=+=+有：11FB D i iSi C L C C ε==+ 其中oxi oxC t ε=。

半导体物理学第七版完整答案修订版IBMT standardization office【IBMT5AB-IBMT08-IBMT2C-ZZT18】第一章习题1．设晶格常数为a 的一维晶格，导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为：E C （K ）=0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ （1）禁带宽度;（2）导带底电子有效质量;（3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化解：（1）2. 晶格常数为0.25nm 的一维晶格，当外加102V/m ，107 V/m 的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：tkhqE f ∆∆== 得qE k t -∆=∆补充题1分别计算Si （100），（110），（111）面每平方厘米内的原子个数，即原子面密度（提示：先画出各晶面内原子的位置和分布图）Si 在（100），（110）和（111）面上的原子分布如图1所示：（a ）(100)晶面 （b ）(110)晶面（c ）(111)晶面补充题2一维晶体的电子能带可写为)2cos 81cos 87()22ka ka ma k E +-=（， 式中a 为 晶格常数，试求（1）布里渊区边界；（2）能带宽度；（3）电子在波矢k 状态时的速度；（4）能带底部电子的有效质量*n m ；（5）能带顶部空穴的有效质量*p m解：（1）由0)(=dk k dE 得 an k π= （n=0，?1，?2…）进一步分析an k π)12(+= ，E （k ）有极大值，ank π2=时，E （k ）有极小值所以布里渊区边界为an k π)12(+=(2)能带宽度为222)()mak E k E MINMAX =-（ (3）电子在波矢k 状态的速度)2sin 41(sin 1ka ka ma dk dE v -==（4）电子的有效质量能带底部 an k π2=所以m m n2*= (5)能带顶部 an k π)12(+=， 且**n p m m -=，所以能带顶部空穴的有效质量32*mm p =半导体物理第2章习题1. 实际半导体与理想半导体间的主要区别是什么答：（1）理想半导体：假设晶格原子严格按周期性排列并静止在格点位置上，实际半导体中原子不是静止的，而是在其平衡位置附近振动。

第 1 页第一章 半导体中的电子状态1. 设晶格常数为 a 的一维晶格，导带极小值附近能量 E c （k ）和价带极大值附近 能量 E v （k ）分别为：E c (k)=2 2h k + 3m 02h (k − m 0k1) 2和 E v (k)= 2 2h k － 6m 0322h k ； m 0m 0为电子惯性质量，k 1＝1/2a ；a ＝0.314nm 。

试求： ①禁带宽度；②导带底电子有效质量； ③价带顶电子有效质量；④价带顶电子跃迁到导带底时准动量的变化。

[解] ①禁带宽度 Eg22h k − k ＝0；可求出对应导带能量极小值 E min的 k 值：根据 dEc (k ) ＝2h k ＋2( dk 3m 0m 03 ，1 )k min＝ k 14由题中 E C式可得：E min＝E C(K)|k=k min=h k 2；m 401 由题中 E V式可看出，对应价带能量极大值 Emax 的 k 值为：k max＝0；2 2 2h 2并且 E min＝E V(k)|k=k max＝k ；∴Eg ＝E min－E max＝hk 1＝ h 21 6m 12m48m a 20 −27 20 0＝×−28× (6.62 ×10) −8 2 ×× −11＝0.64eV48 × 9.1 10(3.14 ×10 1.6 10②导带底电子有效质量 m n22 2 22d E C= 2h + 2h = 8h ；∴ m n＝ h2 / d E C =3 m 0dk 23m 0 m 0 3m 0dk 28 ③价带顶电子有效质量 m ’222d E V= −6h'=，∴ mh2/ d E V= − 1 mdk 2m 0ndk 2 6 0④准动量的改变量h△k ＝ h (k min-k max)=3 4h k1=3h 8a2. 晶格常数为 0.25nm 的一维晶格，当外加 102V/m ，107V/m 的电场时，试分别 计算电子自能带底运动到能带顶所需的时间。

饱和蒸汽密度表表中压力为绝对压力，密度单位为kg/m3温度(t)℃压力(P)MPa 密度(ρ)温度(t)℃压力(P)MPa 密度(ρ)1000.10130.59771280.2543 1.4151010.10500.61801290.2621 1.4551020.10880.63881300.2701 1.4971030.11270.66011310.2783 1.5391040.11670.68211320.2867 1.5831050.12080.70461330.2953 1.6271060.12500.72771340.3041 1.6721070.12940.75151350.3130 1.7191080.13390.77581360.3222 1.7661090.13850.80081370.3317 1.8151100.14330.82651380.3414 1.8641110.14810.85281390.3513 1.9151120.15320.87981400.3614 1.9671130.15830.90751410.3718 2.0191140.16360.93591420.3823 2.0731150.16910.96501430.3931 2.1291160.17460.99481440.4042 2.1851170.1804 1.0251450.4155 2.2421180.1863 1.0571460.4271 2.3011190.1923 1.0891470.4389 2.3611200.1985 1.1221480.4510 2.4221210.2049 1.1551490.4633 2.4841220.2114 1.1901500.4760 2.5481230.2182 1.2251510.4888 2.6131240.2250 1.2611520.5021 2.6791250.2321 1.2981530.5155 2.7471260.2393 1.3361540.5292 2.8161270.2467 1.3751550.5433 2.8861560.5577 2.958184 1.0983 5.6291570.5723 3.032185 1.1233 5.7521580.5872 3.106186 1.1487 5.8771590.6025 3.182187 1.1746 6.0031600.6181 3.260188 1.2010 6.1311610.6339 3.339189 1.2278 6.2641620.6502 3.420190 1.2551 6.3971630.6666 3.502191 1.2829 6.5531640.68353.586192 1.3111 6.6711650.7008 3.671193 1.33976.8121660.7183 3.758194 1.3690 6.955 1670.7362 3.847195 1.39877.100 1680.7544 3.937196 1.42897.248 1690.7730 4.029197 1.45967.398 1700.7920 4.123198 1.49097.551 1710.8114 4.218199 1.52257.706 1720.8310 4.316200 1.55487.864 1730.8511 4.415201 1.58768.025 1740.8716 4.515202 1.62108.188 1750.8924 4.618203 1.65488.354 1760.9137 4.723204 1.68928.522 1770.9353 4.829205 1.72428.694 1780.9573 4.937206 1.75978.868 1790.9797 5.048207 1.79599.045 180 1.0197 5.160208 1.83269.225 181 1.0259 5.274209 1.86999.408 182 1.0496 5.391210 1.90779.593 183 1.0737 5.509211 1.94629.782 212 1.98529.974231 2.849114.25 213 2.024810.17232 2.901014.52 214 2.065010.37233 2.954614.78 215 2.105910.57234 3.008515.05 216 2.147410.77235 3.063115.33 217 2.189610.98236 3.118515.61 218 2.232311.19237 3.174615.89 219 2.275711.41238 3.231616.18 220 2.319811.62239 3.289216.47 221 2.364511.84240 3.347716.76 222 2.409812.07241 3.407017.06 223 2.455912.30242 3.467017.37 224 2.502612.53243 3.527917.68 225 2.550012.76244 3.589717.99 226 2.598113.00245 3.652218.31 227 2.646913.24246 3.715518.64 228 2.696313.49247 3.779718.97 229 2.746613.74248 3.844819.30 230 2.797514.00249 3.910719.64过热蒸汽密度表过热蒸汽是对应于当时压力下的饱和温度而言的，同样压力下的蒸汽，在饱和点的温度就是饱和温度。

【半导体物理与器件】【尼曼】【课后小结与重要术语解释】汇总第一章固体晶体结构小结1.硅是最普遍的半导体材料2.半导体和其他材料的属性很大程度上由其单晶的晶格结构决定。

晶胞是晶体中的一小块体积，用它可以重构出整个晶体。

三种基本的晶胞是简立方、体心立方和面心立方。

3.硅具有金刚石晶体结构。

原子都被由4个紧邻原子构成的四面体包在中间。

二元半导体具有闪锌矿结构，它与金刚石晶格基本相同。

4.引用米勒系数来描述晶面。

这些晶面可以用于描述半导体材料的表面。

密勒系数也可以用来描述晶向。

5.半导体材料中存在缺陷，如空位、替位杂质和填隙杂质。

少量可控的替位杂质有益于改变半导体的特性。

6.给出了一些半导体生长技术的简单描述。

体生长生成了基础半导体材料，即衬底。

外延生长可以用来控制半导体的表面特性。

大多数半导体器件是在外延层上制作的。

重要术语解释1.二元半导体：两元素化合物半导体，如GaAs。

2.共价键：共享价电子的原子间键合。

3.金刚石晶格：硅的院子晶体结构，亦即每个原子有四个紧邻原子，形成一个四面体组态。

4.掺杂：为了有效地改变电学特性，往半导体中加入特定类型的原子的工艺。

5.元素半导体：单一元素构成的半导体，比如硅、锗。

6.外延层：在衬底表面形成的一薄层单晶材料。

7.离子注入：一种半导体掺杂工艺。

8.晶格：晶体中原子的周期性排列9.密勒系数：用以描述晶面的一组整数。

10.原胞：可复制以得到整个晶格的最小单元。

11.衬底：用于更多半导体工艺比如外延或扩散的基础材料，半导体硅片或其他原材料。

12.三元半导体：三元素化合物半导体，如AlGaAs。

13.晶胞：可以重构出整个晶体的一小部分晶体。

14.铅锌矿晶格：与金刚石晶格相同的一种晶格，但它有两种类型的原子而非一种。

第二章量子力学初步小结1.我们讨论了一些量子力学的概念，这些概念可以用于描述不同势场中的电子状态。

了解电子的运动状态对于研究半导体物理是非常重要的。

2.波粒二象性原理是量子力学的重要部分。

半导体物理与器件（教学大纲）Semiconductor Physics and Devices课程编码：12330540学分：课程类别：专业基础课计划学时： 48 其中讲课： 48 实验或实践： 0 上机：0适用专业：IC设计、电信推荐教材：尼曼（Donald H.Neamen）著，赵毅强，姚素英。

解晓东译，《半导体物理与器件》（第3版），电子工业出版社，2010参考书目：D. A. Neamen，《Semiconductor Physics and Devices: Basic Principles》，清华出版社，2003R. T. Pierret著，黄如等译，《半导体器件基础》，电子工业出版社，2004刘恩科、朱秉升、罗晋生等，《半导体物理学》，西安交通大学出版社，2004黄昆、谢希德，《半导体物理学》，科学出版社，1958曾谨言，《量子力学》，科学出版社，1981谢希德、方俊鑫，《固体物理学》,上海科学技术出版社，1961课程的教学目的与任务本课程是集成电路专业的重要选修课之一。

本课程较全面地论述了半导体的一些基本物理概念、现象、物理过程及其规律，并在此基础上选择目前集成电路与系统的核心组成部分，如双极型晶体管（BJT）、金属－半导体场效应晶体管（MESFET）和ＭOS场效应晶体管（MOSFET）等，作为分析讨论的主要对象来介绍半导体器件基础。

学习和掌握这些半导体物理和半导体器件的基本理论和分析方法，为学习诸如《集成电路工艺》、《集成电路设计》等后续课程打下基础，也为将来从事微电子学的研究以及现代VLSI与系统设计和制造工作打下坚实的理论基础。

课程的基本要求本课程要求学生掌握半导体物理和半导体器件的基本概念和基本规律，对于基础理论，要求应用简单的模型定性说明，并能作简单的数学处理。

学习过程中，注意提高分析和解决实际问题的能力，并重视理论与实践的结合。

本课程涉及的物理概念和基本原理较多，为了加深对它们的理解，在各章节里都给学生留有一些习题或思考题，这些题目有的还是基本内容的补充。

第一章习题1．设晶格常数为a 的一维晶格，导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为：E C （K ）=0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。

试求：为电子惯性质量，nm a ak 314.0,1==π（1）禁带宽度;（2）导带底电子有效质量; （3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化 解：（1）eVm k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ 因此：取极大值处，所以又因为得价带：取极小值处，所以：在又因为：得：由导带：043222*83)2(1m dk E d mk k C nC===sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===⨯=-=-=∆=-== 所以：准动量的定义：2. 晶格常数为0.25nm 的一维晶格，当外加102V/m ，107 V/m 的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：t k hqE f ∆∆== 得qEk t -∆=∆ sat sat 137192821911027.810106.1)0(1027.810106.1)0(----⨯=⨯⨯--=∆⨯=⨯⨯--=∆ππ补充题1分别计算Si （100），（110），（111）面每平方厘米内的原子个数，即原子面密度（提示：先画出各晶面内原子的位置和分布图）Si 在（100），（110）和（111）面上的原子分布如图1所示：（a ）(100)晶面 （b ）(110)晶面（c ）(111)晶面补充题2一维晶体的电子能带可写为)2cos 81cos 87()22ka ka ma k E +-=（， 式中a 为 晶格常数，试求（1）布里渊区边界；（2）能带宽度；（3）电子在波矢k 状态时的速度；（4）能带底部电子的有效质量*n m ；（5）能带顶部空穴的有效质量*p m解：（1）由0)(=dk k dE 得 an k π= （n=0，1，2…）进一步分析an k π)12(+= ，E （k ）有极大值，222)mak E MAX =（ ank π2=时，E （k ）有极小值所以布里渊区边界为an k π)12(+=(2)能带宽度为222)()ma k E k E MIN MAX =-（ (3）电子在波矢k 状态的速度)2sin 41(sin 1ka ka ma dk dE v -== （4）电子的有效质量)2cos 21(cos 222*ka ka mdkEd m n-== 能带底部 an k π2=所以m m n 2*= (5)能带顶部 an k π)12(+=， 且**n p m m -=，所以能带顶部空穴的有效质量32*mm p =半导体物理第2章习题1. 实际半导体与理想半导体间的主要区别是什么？答：（1）理想半导体：假设晶格原子严格按周期性排列并静止在格点位置上，实际半导体中原子不是静止的，而是在其平衡位置附近振动。

半导体物理与器件第四版答案半导体物理与器件第四版答案【篇一：半导体物理第五章习题答案】>1. 一个n型半导体样品的额外空穴密度为1013cm-3，已知空穴寿命为100?s，计算空穴的复合率。

解：复合率为单位时间单位体积内因复合而消失的电子-空穴对数，因此1013u1017cm?3?s ?6100?102. 用强光照射n型样品，假定光被均匀吸收，产生额外载流子，产生率为gp，空穴寿命为?，请①写出光照开始阶段额外载流子密度随时间变化所满足的方程；②求出光照下达到稳定状态时的额外载流子密度。

解：⑴光照下，额外载流子密度?n=?p，其值在光照的开始阶段随时间的变化决定于产生和复合两种过程，因此，额外载流子密度随时间变化所满足的方程由产生率gp和复合率u的代数和构成，即 d(?p)?p gp? dt?d(?p)0，于是由上式得⑵稳定时额外载流子密度不再随时间变化，即dtp?p?p0?gp?3. 有一块n型硅样品，额外载流子寿命是1?s，无光照时的电阻率是10??cm。

今用光照射该样品，光被半导体均匀吸收，电子-空穴对的产生率是1022/cm3?s，试计算光照下样品的电阻率，并求电导中少数载流子的贡献占多大比例？解：光照被均匀吸收后产生的稳定额外载流子密度p??n?gp??1022?10?6?1016 cm－3取?n?1350cm2/(v?s)，?p?500cm/(v?s)，则额外载流子对电导率的贡献2pq(?n??p)?1016?1.6?10?19?(1350?500)?2.96 s/cm无光照时?0?10.1s/cm，因而光照下的电导率02.96?0.1?3.06s/cm相应的电阻率 ??110.33??cm 3.06少数载流子对电导的贡献为：?p?pq?p??pq?p?gp?q?p代入数据：?p?(p0??p)q?p??pq?p?1016?1.6?10?19?500?0.8s/cm∴p?00.80.26?26﹪ 3.06即光电导中少数载流子的贡献为26﹪4.一块半导体样品的额外载流子寿命? =10?s，今用光照在其中产生非平衡载流子，问光照突然停止后的20?s时刻其额外载流子密度衰减到原来的百分之几？解：已知光照停止后额外载流子密度的衰减规律为p(t)??p0e?因此光照停止后任意时刻额外载流子密度与光照停止时的初始密度之比即为t??p(t)e? ?p0t当t?20?s?2?10?5s时20??p(20)e10?e?2?0.135?13.5﹪ ?p05. 光照在掺杂浓度为1016cm-3的n型硅中产生的额外载流子密度为?n=?p= 1016cm-3。

半导体物理知识点及重点习题总结Document number：NOCG-YUNOO-BUYTT-UU986-1986UT基本概念题：第一章半导体电子状态半导体通常是指导电能力介于导体和绝缘体之间的材料，其导带在绝对零度时全空，价带全满，禁带宽度较绝缘体的小许多。

能带晶体中，电子的能量是不连续的，在某些能量区间能级分布是准连续的，在某些区间没有能及分布。

这些区间在能级图中表现为带状，称之为能带。

能带论是半导体物理的理论基础，试简要说明能带论所采用的理论方法。

答：能带论在以下两个重要近似基础上，给出晶体的势场分布，进而给出电子的薛定鄂方程。

通过该方程和周期性边界条件最终给出E-k关系，从而系统地建立起该理论。

单电子近似：将晶体中其它电子对某一电子的库仑作用按几率分布平均地加以考虑，这样就可把求解晶体中电子波函数的复杂的多体问题简化为单体问题。

绝热近似：近似认为晶格系统与电子系统之间没有能量交换，而将实际存在的这种交换当作微扰来处理。

克龙尼克—潘纳模型解释能带现象的理论方法答案：克龙尼克—潘纳模型是为分析晶体中电子运动状态和E-k关系而提出的一利用该势场模型就可给出一维晶体中电子所遵守的薛定谔方程的具体表达式，进而确定波函数并给出E-k关系。

由此得到的能量分布在k空间上是周期函数，而且某些能量区间能级是准连续的（被称为允带），另一些区间没有电子能级（被称为禁带）。

从而利用量子力学的方法解释了能带现象，因此该模型具有重要的物理意义。

导带与价带有效质量有效质量是在描述晶体中载流子运动时引进的物理量。

它概括了周期性势场对载流子运动的影响，从而使外场力与加速度的关系具有牛顿定律的形式。

其大小由晶体自身的E-k 关系决定。

本征半导体既无杂质有无缺陷的理想半导体材料。

空穴空穴是为处理价带电子导电问题而引进的概念。

设想价带中的每个空电子状态带有一个正的基本电荷，并赋予其与电子符号相反、大小相等的有效质量，这样就引进了一个假想的粒子，称其为空穴。

第一章习题1．设晶格常数为a 的一维晶格，导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为：E C （K ）=0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。

试求：为电子惯性质量，nm a ak 314.0,1==π（1）禁带宽度;（2）导带底电子有效质量; （3）价带顶电子有效质量;（4）价带顶电子跃迁到导带底时准动量的变化 解：（1）eVm k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ 因此：取极大值处，所以又因为得价带：取极小值处，所以：在又因为：得：由导带：043222*83)2(1m dk E d mk k C nC=== sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===⨯=-=-=∆=-== 所以：准动量的定义：2. 晶格常数为0.25nm 的一维晶格，当外加102V/m ，107 V/m 的电场时，试分别计算电子自能带底运动到能带顶所需的时间。

解：根据：tkhqE f ∆∆== 得qE k t -∆=∆sat sat 137192821911027.810106.1)0(1027.810106.1)0(----⨯=⨯⨯--=∆⨯=⨯⨯--=∆ππ补充题1分别计算Si （100），（110），（111）面每平方厘米内的原子个数，即原子面密度（提示：先画出各晶面内原子的位置和分布图）Si 在（100），（110）和（111）面上的原子分布如图1所示：（a）(100)晶面（b）(110)晶面（c）(111)晶面214221422142822/1083.7342232212414111/1059.92422124142110/1078.6)1043.5(224141100cmatomaaacmatomaaacmatomaa⨯==⨯+⨯+⨯⨯==⨯⨯+⨯+⨯=⨯==⨯+-）：（）：（）：（补充题2一维晶体的电子能带可写为)2cos 81cos 87()22ka ka ma k E +-=（， 式中a 为 晶格常数，试求（1）布里渊区边界； （2）能带宽度；（3）电子在波矢k 状态时的速度；（4）能带底部电子的有效质量*n m ；（5）能带顶部空穴的有效质量*p m解：（1）由0)(=dk k dE 得 an k π=（n=0，±1，±2…） 进一步分析an k π)12(+= ，E （k ）有极大值，222)mak E MAX=（ ank π2=时，E （k ）有极小值所以布里渊区边界为an k π)12(+=(2)能带宽度为222)()mak E k E MIN MAX =-（ (3）电子在波矢k 状态的速度)2sin 41(sin 1ka ka ma dk dE v -== （4）电子的有效质量)2cos 21(cos 222*ka ka mdkEd m n-==能带底部 an k π2=所以m m n 2*= (5)能带顶部 an k π)12(+=， 且**n p m m -=，所以能带顶部空穴的有效质量32*mm p =半导体物理第2章习题1. 实际半导体与理想半导体间的主要区别是什么？答：（1）理想半导体：假设晶格原子严格按周期性排列并静止在格点位置上，实际半导体中原子不是静止的，而是在其平衡位置附近振动。