华工电信信号与系统实验报告一(杨萃老师)

信号与系统测试报告(一)信号与系统测试报告引言•介绍信号与系统的基本概念和重要性。

测试目的•解释测试信号与系统的目的和意义。

测试方法1.选择合适的测试信号：–正弦信号–方波信号–脉冲信号2.测试系统的响应：–离散时间系统–连续时间系统3.分析信号与系统间的关系：–线性与非线性系统–时不变与时变系统测试结果•列出使用不同测试信号对系统进行测试的结果。

结论•总结测试的结果并对信号与系统的性能进行评估。

结果分析•对测试结果进行更深入的分析，比较不同测试信号的效果。

推荐改进措施•提出改进系统性能的建议和方案。

测试总结•总结整个测试过程和测试的收获。

参考文献•列出引用的相关资料、图书和论文等。

注意事项： - 文章中不可出现HTML字符。

- 文章中不可出现网址、图片及电话号码等内容。

信号与系统测试报告引言信号与系统是电子工程、通信工程等学科中的重要基础知识，对于系统分析和信号处理具有重要意义。

本测试报告旨在对信号与系统进行测试，并评估其在不同条件下的性能。

测试目的通过对信号与系统的测试，旨在探究系统对不同类型信号的响应特性，了解信号与系统之间的关系，并通过测试结果评估系统的性能。

测试方法1.选择合适的测试信号：–正弦信号：用于测试系统的频率响应。

–方波信号：用于测试系统的阶跃响应和频率特性。

–脉冲信号：用于测试系统的冲击响应和频率特性。

2.测试系统的响应：–离散时间系统：用离散信号输入离散系统进行测试。

–连续时间系统：用连续信号输入连续系统进行测试。

3.分析信号与系统间的关系：–线性与非线性系统：比较线性系统和非线性系统对不同信号的响应差异。

–时不变与时变系统：测试系统对于不同时间偏移的信号的响应。

测试结果•对于正弦信号输入，不同频率下系统的响应特性进行记录。

•对于方波信号输入，观察系统的阶跃响应和频率特性。

•对于脉冲信号输入，测试系统的冲击响应和频率特性。

结论根据测试结果的分析，得出以下结论： - 系统对不同频率的正弦信号具有不同的响应特性。

信号与系统实验报告实验一：常用信号分类与观察一、实验目的：1、观察常用信号的波形，了解其特点及产生方法。

2、学会用示波器测量常用波形的基本参数，了解信号及信号的特性。

二、实验内容：1、了解几种常用典型信号的解析式及时域波形。

2、观察这些信号的波形，思考可以从那几个角度观察分析这些信号的参数。

三、实验仪器：1、数字信号处理模块 S4 1 块2、20MHz 双踪示波器 1 台四、实验数据及分析： 1、指数信号波形：S3=10000000 S4=01000000 分析：指数信号()tf t Ke α=（K>0）开关S3第一位拨为1，其余为0，使得0α>，因此是一个增长的指数信号。

开关S3第二位拨为1，其余为0，使得0α<，因此是一个衰减的指数信号。

2、指数正弦信号波形：S3=00100000 S3=00010000分析：指数正弦信号()sin()tf t Ke t αω=（K>0）开关S3第三位拨为1，其余为0，使得0α<，因此是一个衰减的指数正弦信号。

开关S3第四位拨为1，其余为0，使得0α>，因此是一个增长的指数正弦信号。

3、抽样信号的波形：S3=00001000分析：抽样信号sin ()a tS t t=，该函数是一个偶函数，(0)t n n π=±≠时，函数值等于零。

4、钟形信号的波形：S3=00000100 分析：钟形信号（高斯函数）2()()t f t Eeτ-=0t =时函数值最大等于E,向两边递减。

五、实验总结：观察了一些常用信号的波形，了解了它们的一些特性以及产生方法。

实验二：阶跃响应与冲激响应一、实验目的1、观察和测量 RLC 串联电路的阶跃响应与冲激响应的波形和有关参数，并研究其电路元件参数变化对响应状态的影响；2、掌握有关信号时域的测量分析方法。

二、实验仪器1、信号源及频率计模块 S2 1 块2、模块一 S5 1 块3、数字万用表 1 台4、双踪示波器 1 台三、实验内容、数据、分析 （1）阶跃响应实验激励波形为方波，振幅0.7V ，周期T=1.8ms ，占空比=0.5，波形如下欠阻尼电路下的响应波形如下：经测量P12与P13之间的实际电阻 3.742632LR C =Ω<=Ω临界阻尼电路下的响应波形如下：经测量P12与P13之间的实际电阻726.52632LR C =Ω≈=Ω过阻尼电路下的响应波形如下：经测量P12与P13之间的实际电阻38682632LR C =Ω>=Ω（2）冲激响应波形观察： 激励波形如下：欠阻尼下电路下的响应波形：临界阻尼电路下的响应波形：过阻尼下的响应波形：四、实验总结：观察了不同阻尼下的各类响应波形，对冲激响应和阶跃响应有了更深入的了解。

目录实验一信号的时域基本运算 (2)实验二连续信号卷积与系统的时域分析 (7)实验三离散信号卷积与系统的时域分析 (11)实验四信号的频域分析 (14)实验五连续时间信号的采样与恢复 (18)实验六系统的频域分析 (23)实验一 信号的时域基本运算一.实验目的1.掌握时域内信号的四则运算基本方法；2.掌握时域内信号的平移、反转、倒相、尺度变换等基本变换；3.注意连续信号与离散信号在尺度变换运算上区别。

二.实验原理信号的时域基本运算包括信号的相加（减）和相乘（除）。

信号的时域基本变换包括信号的平移（移位）、反转、倒相以及尺度变换。

(1) 相加（减）: ()()()t x t x t x 21±= [][][]n x n x n x 21±= (2) 相乘: ()()()t x t x t x 21•= [][][]n x n x n x 21•=(3) 平移（移位）: ()()0t t x t x -→ 00>t 时右移，00<t 时左移[][]N n x n x -→ 0>N 时右移，0<N 时左移(4) 反转：()()t x t x -→ [][]n x n x -→ (5) 倒相：()()t x t x -→ [][]n x n x -→ (6) 尺度变换: ()()at x t x →1>a 时尺度压缩，1<a 时尺度拉伸，0<a 时还包含反转[][]mn x n x → m 取整数1>m 时只保留m 整数倍位置处的样值，1<m 时相邻两个样值间插入1-m 个0，0<m 时还包含反转三．实验结果与理论计算比较 1.连续时间信号的加法运算 （1）实验图形（2）理论计算1sin x t t ⎡⎤=⎣⎦ 22cos x t t ⎡⎤=⎣⎦ 则12sin )2cos 5sin(63.4x t x t t t t ⎡⎤⎡⎤+=+=+⎦⎣⎦︒⎣通过计算几个零点的值可以看出实际值与图形比较符合。

电气学科大类级《信号与控制综合实验》课程实验报告(基本实验一:信号与系统基本实验)姓名学号专业班号同组者1 学号专业班号同组者2 学号专业班号指导教师日期实验成绩评阅人实验评分表基本实验实验编号名称/内容（此列由学生自己填写）实验分值评分实验一常用信号的观察 5实验二零输入,零状态及完全响应 5实验五无源与有源滤波器10实验六低通高通带通带阻滤波器的转换10实验七信号的采样与恢复15实验八调制与解调15设计性实验实验名称/内容实验分值评分创新性实验实验名称/内容实验分值评分教师评价意见总分目录一、实验内容（一）实验一常用信号的观察实验任务与目的总体方案设计方案实现和具体设计实验设计与实验结果结果分析、讨论与思考题（二）实验二零输入。

零状态及完全响应实验任务与目的总体方案设计方案实现和具体设计实验设计与实验结果结果分析、讨论与思考题（三）实验五无源与有源滤波器实验任务与目的总体方案设计方案实现和具体设计实验设计与实验结果结果分析、讨论与思考题（四）实验六低通、高通、带通、带阻滤波器间的变换实验任务与目的总体方案设计方案实现和具体设计实验设计与实验结果结果分析、讨论与思考题（五）实验七信号的采样与恢复实验实验任务与目的总体方案设计方案实现和具体设计实验设计与实验结果结果分析、讨论与思考题（六）实验八调制与解调实验实验任务与目的总体方案设计方案实现和具体设计实验设计与实验结果结果分析、讨论与思考题二、实验总结三、实验心得与体会四、参考文献实验一常用信号的观察一、实验任务与目的1.了解常用的信号的波形和特点；2.理解相应信号的参数。

3.学习函数发生器和示波器的使用。

4.学习示波器波形采样软件Wavestar的使用二、实验内容1．观察常用的信号，如：正弦波，三角波，锯齿波及一些组合函数的波形2．用示波器测量信号，读取信号的幅度和频率三、实验结果正弦波(sin)直流波(DC)脉冲波方波（puls）锯齿波（RAMP）三角波(TRIA)振荡波四实验心得通过此次实验,让我看到了常用的信号的波形及其产生过程,加深了对该信号的理解,平时应用时更加了解其特性.实验二零输入零状态及完全响应一.实验任务与目的1.通过实验，进一步了解系统的零输入相应，零状态相应和完全响应的原理。

华南理⼯⼤学信号与系统实验报告Experiment ExportName:Student No:Institute:Dec 26, 2011Experiment Purposes1. Be familiar with the software Environment and Programming flow in MATLAB5.3.2. Learn how to draw the signal waveform and determine the signal properties.3. Calculate the convolution, frequency response and system output by using the functions: conv, freqz, freqs and filter. Experiment Contents实验项⽬⼀：MATLAB编程基础及典型实例①画出离散时间正弦信号并确定基波周期(注：pi 表⽰圆周率)1 x1[n]=sin(pi*4/4)*cos(pi*n/4)2 x2[n]=cos(pi*n/4)*cos(pi*n/4)3 x3[n]=sin(pi*n/4)*cos(pi*n/8)program for matlabn=0:31;x1=sin(pi*n/4).*cos(pi*n/4);x2=cos(pi*n/4).*cos(pi*n/4);x3=sin(pi*n/4).*cos(pi*n/8);subplot(3,1,1);stem(n,x1);title('x1');subplot(3,1,2);stem(n,x2);title('x2');subplot(3,1,3);stem(n,x3);title('x3');grid on;Conclusion: These signals is periodic, the first and second signal’s per iod are 4. The third signal’s period is 16.②离散时间系统性质：离散时间系统往往是⽤⼏个性质来表征，如线性、时不变性、稳定性、因果性及可逆性等。

信号与系统实验报告.实验名称：滤波器设计及信号频谱分析实验目的：1、了解滤波器的基本概念及分类。

2、了解滤波器的频率响应及其特性。

3、设计低通滤波器和高通滤波器。

4、利用频谱分析软件对信号进行频谱分析。

实验原理：滤波器是信号处理中非常常用的一种器件。

根据滤波器能够通过的信号频率范围不同，可以将滤波器分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器四类。

1、低通滤波器：只允许低于截止频率的信号通过。

在信号处理的过程中，经常需要对信号进行滤波处理。

信号通常由不同频率分量的波形组成，如果采用合适的滤波器将特定频率范围内的信号提取出来并进行处理，可以得到对应的有效信息。

滤波器的特性可以通过频率响应来描述。

滤波器的频率响应具有若干几何特性，例如：2、截止频率：指的是滤波器特定类型的过渡点频率。

在低通滤波器中，截止频率为允许通过信号的最高频率。

3、带宽：指的是在带通滤波器中通过的频率范围。

4、阻抗耦合：指的是输入和输出端口之间的阻抗匹配。

实验装置：1、信号发生器。

2、测量电压的万用表。

3、示波器。

4、计算机。

5、信号分析软件MATLAB。

实验步骤：2、将信号发生器输出的信号输入到低通滤波器和高通滤波器的输入端口。

4、通过MATLAB软件对所得到的信号波形和频谱进行分析和处理。

实验结果：本实验中选用的信号发生器的频率范围在200 Hz-1000 Hz之间。

故设计低通滤波器的截止频率取200 Hz，设计高通滤波器的截止频率取1000 Hz。

图一为经过低通滤波器的信号波形和频谱图。

可以看出，低通滤波器只保留了低于200 Hz的信号分量，而高于200 Hz的分量被过滤掉了。

频谱图的通带增益为1，即在200 Hz的频率范围内信号的增益不受影响。

通过MATLAB软件对滤波器的频谱进行分析，可以得到图三和图四。

图三表示低通滤波器的频率响应，可以看出，当频率小于截止频率200 Hz时，滤波器的增益随频率增大而逐渐下降；当频率大于200 Hz时，滤波器的增益为零。

信号与系统分析实验报告信号与系统分析实验报告引言：信号与系统分析是电子工程领域中的重要课程之一，通过实验可以更好地理解信号与系统的基本概念和原理。

本实验报告将对信号与系统分析实验进行详细的描述和分析。

实验一：信号的采集与重构在这个实验中，我们学习了信号的采集与重构。

首先，我们使用示波器采集了一个正弦信号，并通过数学方法计算出了信号的频率和幅值。

然后，我们使用数字信号处理器对采集到的信号进行重构，并与原始信号进行比较。

实验结果表明，重构后的信号与原始信号非常接近，证明了信号的采集与重构的有效性。

实验二：线性系统的时域响应本实验旨在研究线性系统的时域响应。

我们使用了一个线性系统，通过输入不同的信号，观察输出信号的变化。

实验结果显示，线性系统对于不同的输入信号有不同的响应，但都遵循线性叠加的原则。

通过分析输出信号与输入信号的关系，我们可以得出线性系统的传递函数，并进一步研究系统的稳定性和频率响应。

实验三：频域特性分析在这个实验中，我们研究了信号的频域特性。

通过使用傅里叶变换，我们将时域信号转换为频域信号，并观察信号的频谱。

实验结果显示，不同频率的信号在频域上有不同的分布特性。

我们还学习了滤波器的设计和应用，通过设计一个低通滤波器，我们成功地去除了高频噪声，并得到了干净的信号。

实验四：系统辨识本实验旨在研究系统的辨识方法。

我们使用了一组输入信号和对应的输出信号，通过数学建模的方法，推导出了系统的传递函数。

实验结果表明，通过系统辨识可以准确地描述系统的特性，并为系统的控制和优化提供了基础。

结论：通过本次实验，我们深入学习了信号与系统分析的基本概念和原理。

实验结果证明了信号的采集与重构的有效性，线性系统的时域响应的线性叠加原则，信号的频域特性和滤波器的设计方法，以及系统辨识的重要性。

这些知识和技能对于我们理解和应用信号与系统分析具有重要的意义。

通过实验的实际操作和分析，我们对信号与系统的理论有了更深入的理解，为我们今后的学习和研究打下了坚实的基础。

华南理⼯⼤学信号与系统实验,电信学院实验三利⽤DFT 分析连续信号频谱⼀、实验⽬的应⽤离散傅⾥叶变换(DFT)，分析模拟信号x (t )的频谱。

深刻理解利⽤DFT 分析模拟信号频谱的原理，分析过程中出现的现象及解决⽅法。

⼆、实验原理连续周期信号相对于离散周期信号，连续⾮周期信号相对于离散⾮周期信号，都可以通过时域抽样定理建⽴相互关系。

因此，在离散信号的DFT 分析⽅法基础上，增加时域抽样的步骤，就可以实现连续信号的DFT 分析。

三、实验内容1. 利⽤FFT 分析信号)(e )(2t u t x t -=的频谱。

(1) 确定DFT 计算的各参数（抽样间隔，截短长度，频谱分辨率等）；答：选取fm=25Hz 为近似的最⾼频率，则抽样间隔T=)2/(1m f =0.02s选取6=p T s 进⾏分析，则截短点数为N==T T p /300采⽤矩形窗，确定频域抽样点数为512点。

Matlab 函数如下：%对连续信号x=e(-2t)分析fsam=50;Tp=6; N=512; T=1/fsam;t=0:T:Tp;x=exp(-2*t);X=T*fft(x,N);subplot(2,1,1);plot(t,x);xlabel('t');title('时域波形 N=512');legend('理论值');w=(-N/2:N/2-1)*(2*pi/N)*fsam;y=1./(j*w+2);subplot(2,1,2);plot(w,abs(fftshift(X)),w,abs(y),'r-.');title('幅度谱 N=512');xlabel('w');legend('理论值','计算值',0);axis([-10,10,0,1.4])结果：(2) ⽐较理论值与计算值，分析误差原因，提出改善误差的措施。

信号与系统的实验报告信号与系统的实验报告引言：信号与系统是电子工程、通信工程等领域中的重要基础学科，它研究的是信号的传输、处理和变换过程，以及系统对信号的响应和特性。

在本次实验中，我们将通过实际操作和数据分析，深入了解信号与系统的相关概念和实际应用。

实验一：信号的采集与重构在这个实验中，我们使用了示波器和函数发生器来采集和重构信号。

首先，我们通过函数发生器产生了一个正弦信号，并将其连接到示波器上进行观测。

通过调整函数发生器的频率和幅度，我们可以观察到信号的不同特性，比如频率、振幅和相位等。

然后，我们将示波器上的信号通过数据采集卡进行采集，并使用计算机软件对采集到的数据进行处理和重构。

通过对比原始信号和重构信号，我们可以验证信号的采集和重构过程是否准确。

实验二：信号的时域分析在这个实验中，我们使用了示波器和频谱分析仪来对信号进行时域分析。

首先，我们通过函数发生器产生了一个方波信号，并将其连接到示波器上进行观测。

通过调整函数发生器的频率和占空比，我们可以观察到方波信号的周期和占空比等特性。

然后，我们使用频谱分析仪对方波信号进行频谱分析，得到信号的频谱图。

通过分析频谱图，我们可以了解信号的频率成分和能量分布情况，进而对信号的特性进行深入研究。

实验三：系统的时域响应在这个实验中，我们使用了函数发生器、示波器和滤波器来研究系统的时域响应。

首先，我们通过函数发生器产生了一个正弦信号，并将其连接到滤波器上进行输入。

然后，我们通过示波器观测滤波器的输出信号，并记录下其时域波形。

通过改变滤波器的参数，比如截止频率和增益等，我们可以观察到系统对信号的响应和滤波效果。

通过对比输入信号和输出信号的波形，我们可以分析系统的时域特性和频率响应。

实验四：系统的频域响应在这个实验中，我们使用了函数发生器、示波器和频谱分析仪来研究系统的频域响应。

首先，我们通过函数发生器产生了一个正弦信号，并将其连接到系统中进行输入。

然后，我们通过示波器观测系统的输出信号，并记录下其时域波形。

电气学科大类10 级《信号与控制综合实验》课程实验报告(基本实验一:信号与系统基本实验)姓名学号专业班号同组者学号专业班号指导教师何俊佳日期2012年12月7日实验成绩评阅人实验评分表目录一、实验内容 (4)（一）实验三非正弦信号的分解与合成 (4)（二）实验五无源与有源滤波器 (12)（三）实验六低通高通带通带阻滤波器之间的变换 (20)（四）实验七信号的采样与恢复实验 (26)（五）实验八调制与解调实验 (37)（六）实验九不同阶数相同类型滤波器的滤波效果 (40)二、实验总结 (52)三、实验心得与体会 (53)四、参考文献 (54)实验内容 实验三一、实验原理对于一个非正弦的周期性信号，都可以利用傅里叶分解将其分解为频率、幅值、相位各不相同的个个正弦信号的叠加。

本次实验通过对其中一些特殊的非正弦周期信号的研究来认识傅里叶变换的作用。

二、实验电路分析图 3-1对于如上图形，我们对于任意一个周期信号，将其分别利用低通滤波器和相应的带通滤波器，分解为各个频率的谐波分量。

然后通过加法器，选择某些频率的谐波进行叠加，观察波形，并分析所得波形的性质。

三、实验仿真在实验之前，先利用Matlab 对于实验中所要分解的波形进行仿真，并对于理想情况下的分解和实际情况下的分解作比较，分析实验结果。

方波分解的代码如下：t=-3*pi:pi/100000:3*pi;y=square(2*pi*50*t,50);f1=4*sin(2*pi*50*t)/pi;f2=4*sin(6*pi*50*t)/(pi*3);f3=4*sin(10*pi*50*t)/(pi*5);f4=4*sin(14*pi*50*t)/(pi*7);subplot(321),plot(t,y);grid onaxis([-0.05 0.05 -1.5 1.5]);subplot(322),plot(t,f1);grid onaxis([-0.05 0.05 -1.5 1.5]);subplot(323),plot(t,f2);grid onaxis([-0.05 0.05 -1.5 1.5]);subplot(324),plot(t,f3);grid onaxis([-0.05 0.05 -1.5 1.5]);subplot(325),plot(t,f4);grid onaxis([-0.05 0.05 -1.5 1.5]);仿真的结果如下图：图3-2我们可以发现基波的幅值甚至超过了原方波，而且高次谐波随着次数的增高幅值减少。

信号与系统实验报告一、实验目的信号与系统是电子信息类专业的一门重要基础课程，通过实验可以更深入地理解信号与系统的基本概念和原理，掌握信号的分析与处理方法，提高实践动手能力和解决实际问题的能力。

本次实验的目的主要包括以下几个方面：1、熟悉信号的表示与运算，包括连续时间信号和离散时间信号。

2、掌握线性时不变系统的特性和分析方法。

3、学会使用实验设备和软件工具进行信号的产生、采集、分析和处理。

4、培养观察、分析和总结实验结果的能力，以及撰写实验报告的规范和能力。

二、实验设备与软件本次实验使用的设备和软件主要有：1、计算机一台2、 MATLAB 软件三、实验内容与步骤（一）连续时间信号的表示与运算1、生成常见的连续时间信号，如正弦信号、余弦信号、方波信号、三角波信号等。

在MATLAB 中，使用`sin`、｀cos`函数可以生成正弦和余弦信号，例如：｀t ＝ 0:001:10; y ＝ sin(2pit)； plot(t,y)；｀可以生成一个频率为 1Hz 的正弦信号。

使用`square`函数可以生成方波信号，｀sawtooth`函数可以生成三角波信号。

2、对连续时间信号进行基本运算，如加法、减法、乘法和微分、积分等。

信号的加法和减法可以直接将对应的函数相加或相减，例如：｀y1 ＝ sin(2pit)； y2 ＝ cos(2pit)； y ＝ y1 ＋ y2; plot(t,y)；｀实现了正弦信号和余弦信号的加法。

乘法运算可以通过相应的函数相乘实现。

微分和积分可以使用`diff`和`cumtrapz`函数来完成。

（二）离散时间信号的表示与运算1、生成常见的离散时间信号，如单位脉冲序列、单位阶跃序列、正弦序列等。

单位脉冲序列可以通过数组的定义来实现，例如：｀n ＝ 0:10; x ＝1,zeros(1,10)； stem(n,x)；｀单位阶跃序列可以通过逻辑判断来生成。

正弦序列使用`sin`函数结合离散时间变量生成。

华工电信学院信号与系统实验信号与系统实验报告（一）实验项目名称：MATLAB 编程基础及典型实例 上机实验题目：信号的时域运算及MA TLAB 实现 一、实验目的学习并掌握使用MATLAB 产生基本信号、绘制信号波形、实现信号的可视化表示，为信号分析和系统设计奠定基础。

二、实验内容1. 利用Matlab 产生下列连续信号并作图。

(1) 51),1(2)(<<---=t t u t x(2) 2000,)8.0cos()1.0cos()(<<=t t t t x ππ 2. 利用Matlab 产生下列离散序列并作图。

(1) ⎩⎨⎧≤≤-=其他,055,1][k k x , 设1515-≤<k 。

(2) )]25.0cos()25.0[sin()9.0(][k k k x k ππ+=,设2020-≤<k 。

3. 已知序列]3,2,1,0,1,2;2,3,1,0,2,1[][--=-=k k x ， ]21,0,1,1,1[][=-=k k h 。

(1) 计算离散序列的卷积和][][][k h k x k y *=，并绘出其波形。

(2) 计算离散序列的相关函数][][][n k y k x k R k xy +=∑∞-∞=，并绘出其波形。

(3) 序列相关与序列卷积有何关系？三、实验细节1. 利用Matlab 产生下列连续信号并作图。

(1) 51),1(2)(<<---=t t u t xt=-1:0.01:5;x=-2.*((t-1)>=0); plot(t,x);axis([-1,5,-2.2,0.2])-112345-2-1.5-1-0.5(2) 2000,)8.0cos()1.0cos()(<<=t t t t x ππ t=0:2:200;x=cos(0.1*pi*t).*cos(0.8*pi*t); plot(t,x);20406080100120140160180200-1-0.8-0.6-0.4-0.200.20.40.60.812. 利用Matlab 产生下列离散序列并作图。

信号与系统实验报告信号与系统实验报告一、引言信号与系统是电子信息工程领域中的重要基础课程，通过实验可以加深对于信号与系统理论的理解和掌握。

本次实验旨在通过实际操作，验证信号与系统的基本原理和性质，并对实验结果进行分析和解释。

二、实验目的本次实验的主要目的是：1. 了解信号与系统的基本概念和性质；2. 掌握信号与系统的采样、重建、滤波等基本操作；3. 验证信号与系统的时域和频域特性。

三、实验仪器与原理1. 实验仪器本次实验所需的主要仪器有：信号发生器、示波器、计算机等。

其中，信号发生器用于产生不同类型的信号，示波器用于观测信号波形，计算机用于数据处理和分析。

2. 实验原理信号与系统的基本原理包括采样定理、重建定理、线性时不变系统等。

采样定理指出，对于带限信号，为了能够完全恢复原始信号，采样频率必须大于信号最高频率的两倍。

重建定理则是指出，通过理想低通滤波器可以将采样得到的离散信号重建为连续信号。

四、实验步骤与结果1. 采样与重建实验首先，将信号发生器输出的正弦信号连接到示波器上，观察信号的波形。

然后，将示波器的输出信号连接到计算机上，进行采样，并通过计算机对采样信号进行重建。

最后，将重建得到的信号与原始信号进行对比，分析重建误差。

实验结果显示，当采样频率满足采样定理时，重建误差较小，重建信号与原始信号基本一致。

而当采样频率不满足采样定理时，重建信号存在失真和混叠现象。

2. 系统特性实验接下来，通过调节示波器和信号发生器的参数，观察不同系统对信号的影响。

例如，将示波器设置为高通滤波器，通过改变截止频率，观察信号的低频衰减情况。

同样地，将示波器设置为低通滤波器，观察信号的高频衰减情况。

实验结果表明，不同系统对信号的频率特性有着明显的影响。

高通滤波器会使低频信号衰减，而低通滤波器则会使高频信号衰减。

通过调节滤波器的参数，可以实现对信号频率的选择性衰减。

五、实验分析与讨论通过本次实验，我们对信号与系统的基本原理和性质有了更深入的理解。

信号与系统实验报告信号与系统实验报告引言信号与系统是电子与通信工程领域中的重要基础课程，通过实验可以更好地理解信号与系统的概念、特性和应用。

本实验报告旨在总结和分析在信号与系统实验中所获得的经验和结果，并对实验进行评估和展望。

实验一：信号的采集与重构本实验旨在通过采集模拟信号并进行数字化处理，了解信号采集与重构的原理和方法。

首先，我们使用示波器采集了一个正弦信号，并通过模数转换器将其转化为数字信号。

然后，我们利用数字信号处理软件对采集到的信号进行重构和分析。

实验结果表明，数字化处理使得信号的重构更加准确，同时也提供了更多的信号处理手段。

实验二：滤波器的设计与实现在本实验中，我们学习了滤波器的基本原理和设计方法。

通过使用滤波器，我们可以对信号进行频率选择性处理，滤除不需要的频率分量。

在实验中，我们设计了一个低通滤波器，并通过数字滤波器实现了对信号的滤波。

实验结果表明，滤波器能够有效地滤除高频噪声，提高信号的质量和可靠性。

实验三：系统的时域和频域响应本实验旨在研究系统的时域和频域响应特性。

我们通过输入不同频率和幅度的信号，观察系统的输出响应。

实验结果表明，系统的时域响应可以反映系统对输入信号的时域处理能力，而频域响应则可以反映系统对输入信号频率成分的处理能力。

通过分析系统的时域和频域响应，我们可以更好地理解系统的特性和性能。

实验四：信号的调制与解调在本实验中，我们学习了信号的调制与解调技术。

通过将低频信号调制到高频载波上，我们可以实现信号的传输和远距离通信。

实验中，我们使用调制器将音频信号调制到无线电频率上，并通过解调器将其解调回原始信号。

实验结果表明，调制与解调技术可以有效地实现信号的传输和处理，为通信系统的设计和实现提供了基础。

结论通过本次信号与系统实验，我们深入了解了信号的采集与重构、滤波器的设计与实现、系统的时域和频域响应以及信号的调制与解调等基本概念和方法。

实验结果表明，信号与系统理论与实践相结合，可以更好地理解和应用相关知识。

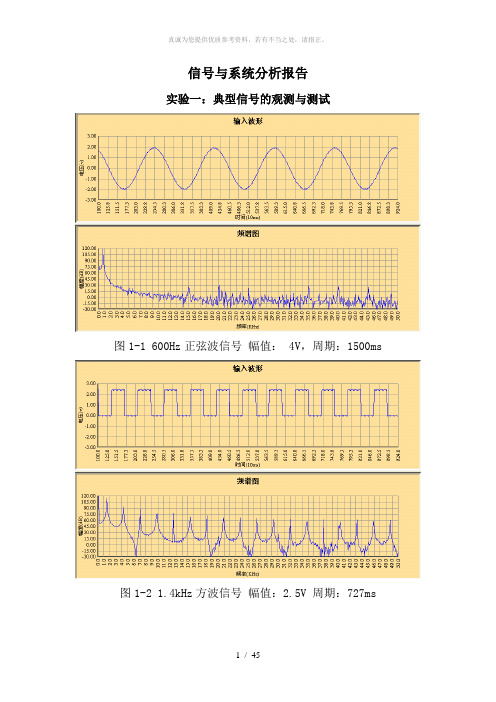
信号与系统分析报告实验一：典型信号的观测与测试图1-1 600Hz正弦波信号幅值： 4V，周期：1500ms 图1-2 1.4kHz方波信号幅值：2.5V 周期：727ms图1-3 2.2kHz三角波信号幅值：2.2V 周期：512ms 图1-4 1000Hz冲击串信号幅值：2.5V 周期：1003ms实验二：线性时不变系统的冲激响应和阶跃响应1.有源低通滤波器的单位冲击和阶跃响应图2-1 1000Hz冲激串为输入信号的输出波形图2-2 500Hz冲激串为输入信号的输出波形图2-3 333Hz冲激串为输入信号的输出波形图2-4 250Hz冲激串为输入信号的输出波形图2-5 200Hz冲激串为输入信号的输出波形图2-6 200Hz方波作为输入信号的输出波形图2-7 1000Hz方波作为输入信号的输出波形图2-8 5kHz方波作为输入信号的输出波形2.无源低通滤波器的单位冲激和阶跃响应图2-9 1000Hz冲激串作为输入信号的输出波形图2-10 500Hz冲激串作为输入信号的输出波形图2-11 333Hz冲激串作为输入信号的输出波形图2-12 250Hz冲激串作为输入信号的输出波形图2-13 200Hz冲激串作为输入信号的输出波形图2-14 5kHz方波作为输入信号的输出波形图2-15 2.2kHz方波作为输入信号的输出波形图2-16 600Hz方波作为输入信号的响应的输出波形实验三：连续信号的分解及频谱图3-1 未被分解的输入1kHz方波信号分析：可以看到该输入方波幅度为2.5V，周期为1030ms，占空比为50%，包含众多奇次频率分量。

由频谱图可以看出，当频率为1kHz时幅度最大。

由傅立叶级数的知识可以知道，方波的傅立叶级数为：a k=sin（πk/2）/kπ，k≠0；当k为偶数（不为零），a k=0。

也就是说，方波的频谱图应只含有奇次分量，对应偶次分量的幅度为零。

实验结果存在较少偶次分量的也正说明了这一点。