下载文档原格式
习题9－2图习题20-3图习题20-3解图OxF Oy F gm Ddα第9章 动量矩定理及其应用9－1 计算下列情形下系统的动量矩。
1. 圆盘以ω的角速度绕O 轴转动，质量为m 的小球M 可沿圆盘的径向凹槽运动，图示瞬时小球以相对于圆盘的速度v r 运动到OM = s 处（图a ）；求小球对O 点的动量矩。
2. 图示质量为m 的偏心轮在水平面上作平面运动。
轮心为A ，质心为C ，且AC = e ；轮子半径为R ，对轮心A 的转动惯量为J A ；C 、A 、B 三点在同一铅垂线上（图b ）。
（1）当轮子只滚不滑时，若v A 已知，求轮子的动量和对B 点的动量矩；（2）当轮子又滚又滑时，若v A 、ω已知，求轮子的动量和对B 点的动量矩。
解：1、2s m L O ω=（逆）2、（1）)1()(Remv e v m mv p A A C +=+==ωRv me J R e R mv J e R mv L A A A C C B)()()(22-++=++=ω（2）)(e v m mv p A C ω+==ωωωω)()()())(()(2meR J v e R m me J e R e v m J e R mv L A A A A C C B +++=-+++=++=9－2 图示系统中，已知鼓轮以ω的角速度绕O 轴转动，其大、小半径分别为R 、r ，对O 轴的转动惯量为J O ；物块A 、B 的质量分别为m A 和m B ；试求系统对O 轴的动量矩。
解：ω)(22r m R m J L B A O O ++=9－3 图示匀质细杆OA 和EC 的质量分别为50kg 和100kg ，并在点A 焊成一体。
若此结构在图示位置由静止状态释放，计算刚释放时，杆的角加速度及铰链O 处的约束力。
不计铰链摩擦。
解：令m = m OA = 50 kg ，则m EC = 2m 质心D 位置：（设l = 1 m) m 6565===l OD d 刚体作定轴转动，初瞬时ω=0l mg lmg J O ⋅+⋅=22α222232)2(212131ml ml l m ml J O =+⋅⋅+=即mgl ml 2532=α2rad/s 17.865==g l α gl a D 362565t =⋅=α 由质心运动定理： Oy D F mg a m -=⋅33t4491211362533==-=mg g mmg F Oy N （↑） 0=ω，0n=D a ， 0=Ox F习题9－1图(a)v (b)（b ） 习题9－5解图习题9－5图J 9－4 卷扬机机构如图所示。
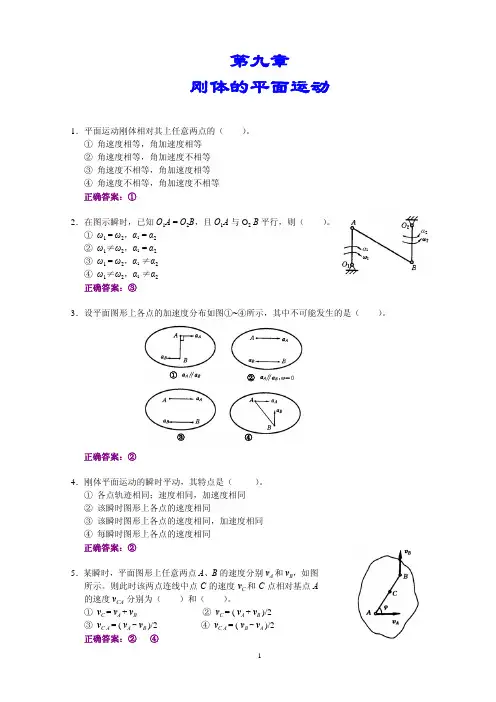
第九章刚体的平面运动1．平面运动刚体相对其上任意两点的（ ）。
① 角速度相等，角加速度相等② 角速度相等，角加速度不相等③ 角速度不相等，角加速度相等④ 角速度不相等，角加速度不相等正确答案：①2．在图示瞬时，已知O 1A = O 2B ，且O 1A 与O 2 B 平行，则（ ）。
① ω1 = ω2，α1 = α2② ω1≠ω2，α1 = α2③ ω1 = ω2，α1 ≠α2④ ω1≠ω2，α1 ≠α2正确答案：③3．设平面图形上各点的加速度分布如图①~④所示，其中不可能发生的是（ ）。
正确答案：②4．刚体平面运动的瞬时平动，其特点是（ ）。
① 各点轨迹相同；速度相同，加速度相同② 该瞬时图形上各点的速度相同③ 该瞬时图形上各点的速度相同，加速度相同④ 每瞬时图形上各点的速度相同正确答案：②5．某瞬时，平面图形上任意两点A 、B 的速度分别v A 和v B ，如图所示。
则此时该两点连线中点C 的速度v C 和C 点相对基点A的速度v CA 分别为（ ）和（ ）。
① v C = v A + v B ② v C = ( v A + v B )/2③ v C A = ( v A - v B )/2 ④ v C A = ( v B - v A )/2正确答案：② ④α1α2 ①②③④6．平面图形上任意两点A 、B 的加速度a A 、a B 与连线AB 垂直，且a A ≠ a B ，则该瞬时，平面图形的角速度ω和角加速度α应为（ ）。
① ω≠0，α ≠0② ω≠0，α = 0③ ω = 0，α ≠0④ ω = 0，α = 0正确答案：③7．平面机构在图示位置时，AB 杆水平，OA 杆鉛直。
若B 点的速度v B ≠0，加速度τB a = 0，则此瞬时OA 杆的角速度ω和角加速度α为（ ）。
① ω = 0，α ≠0② ω≠0，α = 0③ ω = 0，α = 0④ ω≠0，α ≠0正确答案：②8．在图示三种运动情况下，平面运动刚体的速度瞬心：（a ）为（ ）；（b ）为（ ）；（c ）为（ ）。
理论力学中的动力学分析在理论力学中，动力学是研究物体受力作用下的运动规律和力的作用关系的学科。
它是力学的一个重要分支，与静力学相对应。
动力学分析通过运用物理学理论和数学方法，揭示了物体运动的规律和力的作用方式。
本文将就理论力学中的动力学分析进行探讨。
动力学分析的基本原理在于牛顿运动定律。
牛顿第一定律指出：任何物体都具有惯性，即物体在没有外力作用时将保持静止或作匀速直线运动。
该定律为动力学分析提供了基础。
其次，牛顿第二定律指出：物体的运动状态随受力而改变，物体所受合力等于物体质量乘以加速度。
这一定律在动力学分析中起着至关重要的作用。
最后，牛顿第三定律表明：力的作用总是成对出现，且大小相等、方向相反，这被称为作用-反作用定律。
动力学分析中，必须考虑到这个定律以正确分析物体间的相互作用。
动力学分析主要关注以下几个方面：质点的运动、刚体的运动、动力学方程的建立和解法以及力的分析。
首先，在质点的运动中，动力学分析需要确定质点所受的合力，以及由此产生的加速度和运动规律。
对于匀加速运动、自由落体等常见情况，可以通过简单的公式进行分析；而对于复杂的情况，例如曲线运动或非匀加速运动，则需要运用微积分和矢量分析等数学工具进行求解。
其次，在刚体的运动中，动力学分析需要考虑刚体的平动和转动。
对于平动，需要计算刚体所受的合力和合力矩，以及由此产生的加速度和角加速度。
对于转动，需要考虑刚体的转动惯量和角速度，以及刚体所受的力矩。
然后，在动力学分析中，建立和解动力学方程是至关重要的。
根据牛顿第二定律，通过建立物体所受力的合力和合力矩与物体质量、加速度以及惯性矩之间的关系，可以得到动力学方程。
解动力学方程可以推导出物体的运动规律和力的作用方式，进一步分析物体的运动状态。
最后，在力的分析中，动力学分析需要考虑力的种类、力的大小和方向以及力的作用点。
常见的力包括重力、摩擦力、弹力等。
力的分析可以揭示物体间相互作用的规律，为动力学分析提供了重要的依据。
刚体动力学的基本概念第二篇动力学第五章刚体动力学的基本概念一、目的要求 1．深入地理解力、刚体、平衡和约束等重要概念。
2．静力学公理（或力的基本性质）是静力学的理论基础，要求深入理解。
3. 能正确地将力沿坐标轴分解和求力在坐标轴上的投影，对合力投影定理有清晰的理解。
4. 理解力对点之矩的概念，并能熟练地计算。
5．深入理解力偶和力偶矩的概念，明确力偶的性质和力偶的等效条件。
6．明确和掌握约束的基本特征及约束反力的画法。
7．熟练而正确地对单个物体与物体系统进行受力分析，画出受力图。
二、基本内容 1．重要概念 1）平衡：物体机械运动的一种特殊状态。
在静力学中，若物体相对于地面保持静止或作匀速直线平动，则称物体处于平衡。
2）刚体：在力作用下不变形的物体。
刚体是静力学中的理想化力学模型。
3）约束：1/ 11对非自由体的运动所加的限制条件。
在刚体静力学中指限制研究对象运动的物体。
约束对非自由体施加的力称为约束反力。
约束反力的方向总是与约束所能阻碍的物体的运动或运动趋势的方向相反。
4）力：物体之间的相互机械作用。
其作用效果可使物体的运动状态发生改变和使物体产生变形。
前者称为力的运动效应或外效应，后者称为力的变形效应或内效应，理论力学只研究力的外效应。
力对物体作用的效应取决于力的大小、方向、作用点这三个要素，且满足平行四边形法则，故力是定位矢量。
5）力的分类：集中力、分布力；主动力、约束反力 6）力系：同时作用于物体上的一群力称为力系。
按其作用线所在的位置，力系可以分为平面力系和空间力系，按其作用线的相互关系，力系分为共线力系、平行力系、汇交力系和任意力系等等。
7）等效力系：分别作用于同一刚体上的两组力系，如果它们对该刚体的作用效果完全相同，则此两组力系互为等效力系。
8）平衡力系：若物体在某力系作用下保持平衡，则称此力系为平衡力系。
9）力的合成与分解：若力系与一个力FR等效，则力FR称为力系的合力，而力系中的各力称为合力FR的分力。
