桥梁荷载横向分布系数的各种计算方法综述.
- 格式:pdf
- 大小:317.52 KB
- 文档页数:8

探讨横向分配系数计算方法桥梁荷载横向分配系数的计算主要有铰接板(梁)法、刚接板(梁)法、偏心压力法、修正偏压法、比拟正交异性板法(G-M法)、弹性支承连续梁法、考虑抗扭的弹性支承连续梁法等[1]。
如何正确选择适用方法是广大设计人员面对的一个重要问题。
1、荷载横向分配系数计算理论在荷载横向分配计算中,结构的横向连接刚度起着至关重要的作用。
横向连接刚度越大,荷载横向分布作用越显著,各主梁所分配的荷载也越趋均匀。
因此需要根据实际的横向结构拟定出较为合理的简化计算模型,从而确定相应的计算方法。
对于城市宽桥,需要用梁格法,通过有限元计算来得到桥梁的横向分配系数[2]。
梁格系理论是将桥梁上部结构用一个等效梁格来代替分析,等效梁格后再将其结果还原到结构中就可得到所需的计算结果。
此法易于理解,便于使用,而且比较精确。
一般说来等效梁格的网格越密,计算结果的精确度就越高。
梁格法主要应用简支梁桥挠度参数跟横向分配系数的关系来求得横向分配系数。
通过最不利荷载的布置求得各片主梁的挠度,再由在单片主梁上跨中加载所得的挠度,从而得出各片主梁的荷载横向分配系数[2]。
2、应用梁格法的实例橄榄河桥位于省道S214线上,原桥为5-15m双曲拱桥,由于该桥病害严重,相关单位对该桥进行了重建。
2014年重建桥梁为4跨预应力混凝土连续梁桥,主梁结构为4片预应力混凝土连续小箱梁。
桥跨布置为19.92m+20m+20m+19.92m。
梁格法采用Midas/civil结构分析软件进行计算,图1为计算模型。
全桥模型在横向最不利汽车荷载布置下各片梁所承受内力值与跨中各片梁内力值之和的比值即为该片梁的横向分配系数。
同时采用刚性梁法计算该桥在最不利汽车荷载作用下的横向分配系数。
主梁从左往右编号为1-4号见图2。
表1为两种方法计算出的1-4号梁的荷载横向分配系数。
3、结语采用刚接梁法及梁格法对一座4片小箱梁构成的主梁的横向分配系数进行了计算。
经过对计算结果比较,可以得到如下结论:1)因刚接梁法主要考虑箱梁翼缘及各片箱梁之间湿接缝的刚接,横隔板的刚度平均分配到梁的纵向,故其横向分配系数计算结果偏大。

桥梁荷载横向分布系数的各种计算方法综述姓名:XXX 学号:50XXXXXXX3摘要:公路桥梁荷载横向分布有多种计算模型,其中比较实用的有:1)杠杆原理法;2)偏心压力法、修正偏心压力法;3)铰接板(梁)法;4)刚接板(梁)法等。
这些理论方法有各自的适用范围,应按具体情况选用适当的方法来运用。
关键词:混凝土简支梁桥;荷载横向分布系数;影响线;影响因素1 引言随着国民经济的发展,对交通的需求日益提高,众多的高速公路及城市快速干道相继修建。
公路桥梁上行驶车辆的轴重加重、速度提高,车流密度也相应提高。
使之在设计过程中如何确保桥梁结构在使用寿命期限内的安全性,准确计算各片梁所需承担的最大活载弯矩就显得尤为重要。
特别是对于中小跨多片梁型的桥梁,当跨数较多时,用测试横向分布状态的方法对桥梁运营状态进行评价,具有简洁、实用、可靠等优点,具有较高的推广价值。
所谓荷载横向分布系数(Lateral Distribution Factor of Live Load)是指公路车辆荷载在桥梁横向各主梁间分配的百分数。
普通简支桥梁中它和各主梁间的联结方式(铰接或刚接),有无内横梁及其数目,断面的抗弯刚度和抗扭刚度,以及车辆荷载在桥上的位置等有关。
它是一个复杂的空间结构问题,在桥梁设计中常简化为平面问题而引用荷载横向分布系数。
[1]目前广泛采用的是利用主梁的纵向影响线和它的荷载横向分布影响线相结合的方法,荷载横向分布系数是在荷载横向分布影响线的基础上按荷载的最不利位置布载,并将荷载位置相应的影响线竖标值求和得到的最后数值结果。
对于混凝土简支梁桥,荷载横向分布系数的影响因素主要有桥粱跨度(Z)、主梁间距(S)、桥面板的厚度(t0)、主梁刚度(K0)、横隔梁(板)的数量及位置、车载类型及布栽位置、车辆间距、栏杆及横跨比等。
[2][3][4][9]2 计算方法及其适用范围荷载横向分布理论在桥梁设计中占有重要地位。
目前桥梁荷载横向分布系数常用的计算方法主要有杠杆原理法、偏心压力法(修正偏心压力法)、铰接板(梁)法、刚接梁法和比拟正交异性板法(G-M法)等。

梁式桥荷载横向分布计算方法概要湾区(广东)建筑装配科技有限公司广东东莞 523000摘要:对于桥梁这种空间体系的结构,设计者想要了解某根主梁所分担的最不利荷载,是一个比较重要和复杂的问题,一直以来都受到各学者的研究,荷载横向分布计算成为桥梁学科百花齐放的局面,采用空间立体计算还是简化成平面杆系来分析,是各理论的两个基本点。
本文介绍了荷载横向分布系数的定义,然后选取了几种荷载横向分布计算方法做了概述,介绍了其基本原理和适用条件。
关键词:梁氏桥;横向分布系数;横向分布影响线;荷载横向分布计算1、引言我们若想要知道桥梁某个截面的最大内力时,先要确定某个截面的纵向影响线,把纵向影响线确定之后,荷载在截面横向哪个位置时最大的,在各梁的分配占比问题需要横向分布影响线来分析确定[1]。
a)在梁式桥上 b)在单梁上图1 荷载作用下的内力计算由于梁式桥的构造设计、施工工艺、截面类型等不同,使得梁式桥的横向联结方式大不相同,选择相对应的荷载横向分布计算方法,才能使荷载横向分布计算方法能更准确[2]。
以下介绍梁式桥几种常用的横向分布影响线的计算方法。
2、简支梁荷载横向分布计算方法概要2.1杠杆原理法(1)计算原理把端横隔梁视作在主梁上断开而简支在其上的简支梁或者悬臂梁,简化了实际设计中的计算,以支反力作为分析的依据[3]。
(2)适用条件1)分析支点附近截面处的荷载横向分布问题;2)计算双主梁的横向分布系数;3)适用于横向联系较弱的多梁式桥梁。
2.2偏心压力法(1)计算原理把横隔梁视作刚性极大的梁,通过力的平衡关系导出的偏压法的普遍公式,其基本假定为:1)在汽车荷载这个因各种体系不同而变化的变量,横隔梁仅发生刚体位移;2)忽略主梁的抗扭刚度,不计入扭矩抵抗汽车荷载的影响。
以下介绍在单位荷载作用下,各主梁所承担的力的简要推导。
单位荷载桥梁上呈偏载作用时,可将荷载进行分解,以此来分开分析。
分解为中心荷载和偏心力矩(e为偏心距),不考虑截面因扭转产生的抗扭矩。

关于DB纵向计算和横向计算中汽车荷载加载的总结在DB的纵向计算和横向计算中,都是将空间问题简化为平面问题进行处理的,这样必然涉及到活载加载在程序中的实现问题,下面对汽车荷载的加载方式总结如下:一、纵向计算纵向计算针对全桥结构验算,在纵向计算中,是灰色的,不需要填写,是因为车道数已经反映在了中。
关于如何取值,分下面两种结构形式的桥梁进行讨论:预制梁(板梁、T梁、小箱梁)。
此时的即“横向分布系数1.m”。
m=车辆在横向影响线最不利布置值×横向折减×纵向折减,取m最大的那片梁进行计算。
可见,多片梁中一片梁的横向分布系数即每一片梁承担了多少车道。
2.整体箱梁。
此时的已经失去了横向分布的意义,这里所说的横向分布调整系数=偏载系数(一般取1.15)×车道数×横向折减×纵向折减。
可见,整体箱梁的横向分布调整系数即整片梁承担所有车道后,考虑剪力滞(截面应力在横向分布不均匀)后的一个系数,其中偏载系数反映了剪力滞作用。
在程序计算时,乘以车道荷载在DB中的平面单梁模型中进行纵向影响线的最不利加载,即得汽车效应。
二、横向计算横向计算针对横梁、盖梁等的计算,下面就横梁和盖梁计算分别讨论:1.横梁计算(整体箱梁)横梁按照一次落架的施工方法采用平面杆系理论进行计算。
荷载按恒载和活载分别输入。
(1)恒载恒载分两部分:a.横梁的自重由桥博自动计入,二恒按均布力施加;b.此外还有两边梁体靠腹板传给横梁的恒载剪力。
将桥梁纵向计算得到的一、二期恒载),扣除横梁模型中自重与施加的二期恒载,然后总和(即纵向计算中的V自重+二恒分成三个集中力加在三道腹板中间。
(2)活载将纵向一列车的支反力作为汽车横向分布调整系数,即通过纵向计算得到的活载效应(该值为纵向计算时,使用阶段支撑反力汇总输出结果里面,汽车MaxQ 对应下的最大值),除以纵向计算时汽车的横向分布调整系数求得的一列车的活载效应,填到中,然后在桥梁博士中进行横向加载。

桥梁上部计算教程--横向力分布系数计算(转)总的来说,横向力分布系数计算归结为两大类(对于新手能够遇到的):1、预制梁(板梁、T梁、箱梁)这一类也可分为简支梁和简支转连续2、现浇梁(主要是箱梁)首先我们来讲一下现浇箱梁(上次lee_2007兄弟问了,所以先讲这个吧)在计算之前,请大家先看一下截面这是一个单箱三室跨径27+34+27米的连续梁,梁高1.55米,桥宽12.95米!!支点采用计算方法为为偏压法(刚性横梁法)mi=P/n±P×e×ai/(∑ai x ai)跨中采用计算方法为修正偏压法(大家注意两者的公式,只不过多了一个β)mi=P/n±P×e×ai×β/(∑ai x ai)β---抗扭修正系数β=1/(1+L^2×G×∑It/(12×E×∑ai^2 Ii)其中:∑It---全截面抗扭惯距Ii ---主梁抗弯惯距 Ii=K Ii` K为抗弯刚度修正系数,见后L---计算跨径G---剪切模量 G=0.4E 旧规范为0.43EP---外荷载之合力e---P对桥轴线的偏心距ai--主梁I至桥轴线的距离在计算β值的时候,用到了上次课程/thread-54712-1-1.html我们讲到的计算截面几何性质中的抗弯惯矩和抗扭惯矩,可以采用midas计算抗弯和抗扭,也可以采用桥博计算抗弯,或者采用简化截面计算界面的抗扭,下面就介绍一下这种大箱梁是如何简化截面的:简化后箱梁高度按边肋中线处截面高度(1.55m)计算,悬臂比拟为等厚度板。
①矩形部分(不计中肋):计算公式:It1=4×b^2×h1^2/(2×h/t+b/t1+b/t2)其中:t,t1,t2为各板厚度h,b为板沿中心线长度h为上下板中心线距离It1=4×((8.096+7.281)/2)^2×1.34^2/(2×1.401/0.603+8.097/0 .22+7.281/0.2)=5.454 m4②悬臂部分计算公式: It2=∑Cibiti3其中:ti,bi为单个矩形截面宽度、厚度Ci为矩形截面抗扭刚度系数,按下式计算:Ci=1/3×(1-0.63×ti/bi + 0.052×(ti/bi)^5)=1/3×(1-0.63×0.26/2.2+0.052×(0.26/2.2)^5)=0.309It2=2×0.309×2.2×0.26^3=0.0239 m4③截面总的抗扭惯距It= It1+ It2=5.454+0.0239=5.4779 m4大家可以用midas计算对比一下看看简化计算和实际能差多少??先计算一下全截面的抗弯和中性轴,下面拆分主梁需要用的到采用<<桥梁博士>>V2.9版中的截面设计模块计算全截面抗弯惯距,输出结果如下:<<桥梁博士>>---截面设计系统输出文档文件: D: \27+34+27.sds文档描述: 桥梁博士截面设计调试任务标识: 组合截面几何特征任务类型: 截面几何特征计算------------------------------------------------------------截面高度: 1.55 m------------------------------------------------------------计算结果:基准材料: JTJ023-85: 50号混凝土基准弹性模量: 3.5e+04 MPa换算面积: 7.37 m2换算惯矩: 2.24 m4中性轴高度: 0.913 m沿截面高度方向 5 点换算静矩(自上而下):主截面:点号: 高度(m): 静矩(m××3):1 1.55 0.02 1.16 1.773 0.775 1.834 0.388 1.585 0.0 0.0------------------------------------------------------------计算成功完成结果:I全= 2.24 m4 中性轴高度H=0.913m下面来讲一下主梁拆分的原则:将截面划分为τ梁和I梁,保持将两截面中性轴与全截面中性轴位置一致。

桥梁荷载横向分布系数计算方法桥梁是交通系统中重要的基础设施,承载着大量的车辆和行人荷载。
桥梁荷载横向分布系数的计算对于桥梁设计和施工具有重要意义。
本文将详细介绍桥梁荷载横向分布系数的计算方法,包括计算原理、步骤和注意事项,并通过具体算例进行分析和说明。
桥梁荷载是指作用在桥梁上的各种力量,包括车辆荷载、人群荷载、风荷载等。
横向分布系数是用来描述桥梁荷载在桥面横向分布的系数,其大小与桥梁的形状、结构形式等因素有关。
桥梁荷载横向分布系数的计算是桥梁设计的重要环节,也是施工过程中的关键步骤。
计算桥梁荷载横向分布系数的方法可以分为理论计算和数值模拟两种。
理论计算方法包括集中力作用下的横向分布系数计算和均布力作用下的横向分布系数计算。
数值模拟方法则是利用计算机进行模拟分析,得到更精确的横向分布系数。
根据集中荷载作用下的弯矩和剪力,计算横向分布系数。
根据车道均布荷载的弯矩和剪力,计算横向分布系数。
数值模拟方法可以利用有限元软件进行模拟分析,得到更精确的横向分布系数。
具体步骤如下:通过对模型的应力、应变等进行分析,得出横向分布系数。
下面通过一个简单的算例来说明桥梁荷载横向分布系数的计算方法。
该桥梁为简支梁结构,跨度为20米,桥面宽度为10米。
车辆荷载为50吨的重车,速度为20公里/小时,作用在桥上长度为10米。
通过集中力作用下的横向分布系数计算方法,来计算该桥梁的横向分布系数。
计算桥梁单位长度的自重为5吨/米。
然后,确定车辆荷载的大小为50吨,位置为桥面中心线偏左1米处。
根据车辆荷载作用下的弯矩和剪力,可以得出横向分布系数为67。
根据横向分布系数的定义可知,该桥梁在车辆荷载作用下的横向分布系数为67。
桥梁荷载横向分布系数的计算是桥梁设计和施工中的重要环节,对于保证桥梁的安全性和正常使用具有重要意义。
本文详细介绍了桥梁荷载横向分布系数的计算方法,包括计算原理、步骤和注意事项,并通过具体算例进行了分析和说明。
随着计算机技术和数值模拟方法的发展,未来的研究方向将更加倾向于开发更加精确、便捷的计算方法和模型,以便更好地应用于实际工程中。


公路桥梁荷载横向分布系数的计算问题作者:叶思凯来源:《卷宗》2012年第01期摘要:在公路桥梁的设计中,荷载横向分布系数的计算问题是设计的核心内容。
虽然公路桥梁荷载横向分布系数的计算方式有多种,但是在实质上它们之间是有差异的。
为了改进计算方式,使计算过程更加简化和精确。
本文阐述了常用的公路桥梁荷载横向分布系数的计算方法及公路桥梁荷载横向分布系数对比,对影响计算问题的主要参数进行了分析。
关键词:公路桥梁;荷载横向分布系数;计算Roads and bridges lateral load distribution factor calculation problemAbstract: In the highway bridge design, the lateral load distribution factor calculation is the core of the design. Although roads and bridges lateral load distribution factor is calculated in different ways, but in essence there is a difference between them. To improve the method of calculation, the computation process more streamlined and accurate. This paper describes commonly used roads and bridges lateral load distribution factor in the calculation and distribution of highway bridges lateral load factor comparison, the main problem affecting the calculation of parameters analyzed.Keyword: roads and bridges; lateral load distribution factors; calculation自从国内外的学者对公路桥梁结构的计算进行大量的研究开始,荷载横向分布系数计算就被广泛应用。

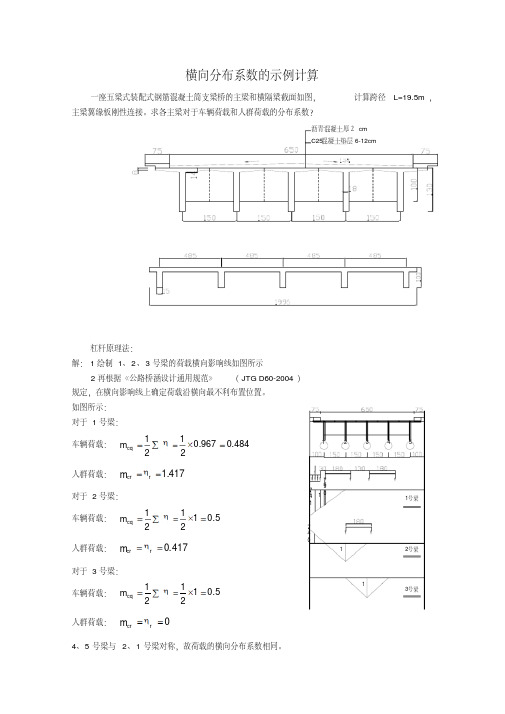
实用文档标准文案横向分布系数的示例计算一座五梁式装配式钢筋混凝土简支梁桥的主梁和横隔梁截面如图,计算跨径L=19.5m ,主梁翼缘板刚性连接。
求各主梁对于车辆荷载和人群荷载的分布系数?杠杆原理法:解:1绘制1、2、3号梁的荷载横向影响线如图所示2再根据《公路桥涵设计通用规范》(JTG D60-2004) 规定,在横向影响线上确定荷载沿横向最不利布置位置。
如图所示: 对于1号梁: 车辆荷载:484.0967.02121=⨯==∑ηcq m 人群荷载:417.1==r cr m η 对于2号梁: 车辆荷载:5.012121=⨯==∑ηcq m 人群荷载:417.0==r cr m η 对于3号梁: 车辆荷载:5.012121=⨯==∑ηcq m 人群荷载:0==r cr m η4、5号梁与2、1号梁对称,故荷载的横向分布系数相同。
偏心压力法(一)假设:荷载位于1号梁 1长宽比为26.25.155.19>=⨯=b l ,故可按偏心压力法来绘制横向影响线并计算横向分布系数c m 。
本桥的各根主梁的横截面积均相等,梁数为5,梁的间距为1.5m ,则:5.220)5.11(2)5.12(2222524232221512=+⨯+⨯=++++=∑=a a a a a ai i2所以1号5号梁的影响线竖标值为:6.0122111=+=∑i a a n η 2.0122115-=-=∑i a a n η由11η和15η绘制荷载作用在1号梁上的影响线如上图所示,图中根据《公路桥涵设计通用规范》(JTG D60-2004)规定,在横向影响线上确定荷载沿横向最不利布置位置。
进而由11η和15η绘制的影响线计算0点得位置,设0点距离1号梁的距离为x ,则:4502.015046.0=⇒-⨯=x xx 0点已知,可求各类荷载相应于各个荷载位置的横向影响线竖标值3计算荷载的横向分布系数 车辆荷载:()533.0060.0180.0353.0593.02121=-++⨯==∑ηcq m 人群荷载:683.0==r cr m η (二)当荷载位于2号梁时 与荷载作用在1号梁的区别以下:4.0122112=+=∑i a a a n η实用文档标准文案0122552=-=∑ia a a n η 其他步骤同荷载作用在1号梁时的计算修正偏心压力法(一)假设:荷载位于1号梁 1计算I 和T I :2.3813018)2814(150)18150()2814(1301821)(2122221=⨯++⨯-+++⨯⨯=+-++⨯=ch bd c b d ch y8.912.3813012=-=-=y y y[][]43333313132106543)112.38)(18150(2.381508.911831))((31cm d y c b by cy I ⨯=---⨯+⨯⨯=---+⨯=对于翼板1.0073.01501111<==b t ,对于梁肋151.01191822==b t 查下表得所以:311=c ,301.02=c 433331027518119301.01115031cm t b c I i i i T ⨯=⨯⨯+⨯⨯==∑2计算抗扭修正系数β 与主梁根数有关的系数ε则n=5,ε=1.042 G=0.425E875.055.15.1910654310275425.0042.111)(112332=⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯+=+=E E B l EI GI T εβ 3计算荷载横向影响线竖标值11η和15η55.0122111=+=∑i a a n βη 15.0122115-=-=∑ia a n βη 由11η和15η绘制荷载作用在1号梁上的影响线如上图所示,图中根据《公路桥涵设计通用规范》(JTG D60-2004)规定,在横向影响线上确定荷载沿横向最不利布置位置。


荷载横向分布综述载荷载横向分布综述[荷载横向分布计算综述]桥梁结构分析大致分为两大类:一:直接釆用三维有限元通用分析软件对结构作空间整体分析,以得到结构的内力(更多的是应力分析),即纯数值法;-:将空间结构简化为平面结构用平面杆系程序分析,而空间效应通过荷载横向分布系数考虑,即所谓半解析数值法。
由于三维有限元程序分析使用中的各种限制条件(如应力分析对实际配筋设计指导性较差、模型建立的困难等等),往往不如单纯的平面分析考虑横向分布系数的方法简便、实用(有时精度也差不多,特别是大跨径结构恒、活载比例的增大,两者差别更小),同时更有益于培养一个桥梁设计者对结构的定性分析、结构受力估算及有限元分析结果的正确判断等方面的能力。
因此桥梁结构简化分析荷载横向分布计算是必要的,并将与有限元分析互相补遗、长期并存!实际的工作中主要也是简化分析(即荷载横向分布系数计算与平面杆系电算相结合)的多,而有限元用的少!结构简化分析通常按以下步骤进行(结构尺寸已经初步拟定好):1.计算桥跨结构荷载横向分布系数;2.以荷载横向分布系数为乘积因子,按平面杆系结构进行桥跨结构的内力分析;3.按建筑结构设计原理作构件的配筋设计。
对于荷载横向分布系数计算大致有以下一些方法:1.杠杆法;2.梁格法,包括刚性横梁法(也称偏压法)以及修正刚性横梁法(修正偏压法)、弹性支承连续梁法;3.梁系法,包括狡接板法、刚接板法、较接梁法、刚接梁法;4.板系法,如比拟正交异性板法(G-M法);5.增大系数法(弯矩增大15%,剪力增大5%)等。
不同截面类型、不同的横向连接方式、桥跨结构的不同位置通常具有不同的荷载横向分布系数计算方法。
上述梁格法、梁系法及板系法等都是建立在等截面简支体系结构上的荷载横向分布计算方法。
增大系数法一般用于箱形截面梁设计,其主导思想来自杆件弯扭相互独立理论,即认为杆件的中心荷载由梁的弯曲内力承担,而扭转荷载由杆件的自由与约束扭转内力承担,因截面翘曲约束正应力w 一般为纵向正应力M的15%左右,故弯矩增大系数取1.15;而翘曲扭转剪应力w 约为弯曲剪应力M的5%左右,故剪力增大系数取1.05;而实际上箱梁是弯扭共同作用,所以是不合理的,它与箱梁的综合抗扭刚度2H值有关,计算结果可能过安全也可能不安全,强烈建议慎用!有关横向分布系数计算的详细分析参见李国豪、石洞《公路桥梁荷载横向分布计算》、胡肇滋《桥跨结构结构简化分析荷载横向分布》等文献。


摘要:在公路桥梁的设计中,荷载横向分布系数的计算问题是设计的核心内容。
虽然公路桥梁荷载横向分布系数的计算方式有多种,但是在实质上它们之间是有差异的。
为了改进计算方式,使计算过程更加简化和精确。
本文阐述了常用的公路桥梁荷载横向分布系数的计算方法及公路桥梁荷载横向分布系数对比,对影响计算问题的主要参数进行了分析。
关键词:公路桥梁;荷载横向分布系数;计算roads and bridges lateral load distribution factor calculation problem自从国内外的学者对公路桥梁结构的计算进行大量的研究开始,荷载横向分布系数计算就被广泛应用。
采用荷载横向分布系数计算对公路桥梁进行分析,是为了能够使精确的影响面被近似的影响面所取代。
此计算主要是将空间问题转变为平面问题进行解决,也就是借助荷载横向分布系数计算出公路桥梁的梁间内力的分布状况。
在荷载横向分布系数的计算中,常用的方法有横向铰接板梁法和横向刚接板梁法、偏心压力法和杠杆原理法、比拟正交异性板法和简化计算法,以及修正偏心压力法和弹性支承连续法等。
一、常用的公路桥梁荷载横向分布系数的计算方法1、横向铰接板梁法和横向刚接板梁法横向铰接板梁法适应于在无中间横隔梁的装配式桥与无横隔梁的组合式梁桥中。
由于正弦荷载取代集中荷载可以减小计算中的误差,所以在假定竖向荷载作用时,可以忽略计算g (x)竖向剪力与m(x)横向弯矩,以及t(x)纵向剪力与n(x)法向力。
用半波正弦荷载p(x)=psin 代替集中荷载p,所以正弦分布的竖向剪力为:。
横向刚接板梁法适应于翼缘板刚性连接的肋梁桥中。
按照理论基础进行计算,将赘余弯矩mi引入到铰接的地方,就能够建立赘余力正则方程。
由于相邻的主梁接合的地方可以承受弯矩,设定平p(x)=isin,因此正弦分布的赘余力素为:,其中是峰值,所以可以计算出刚接梁桥系。
如:30米小箱梁计算。
跨径30米,横向6片,桥面宽14米,4车道,公路1级荷载。



横向分布系数取值详细介绍(桥博)(2008-03-18 21:39:19)标签:杂谈分类:桥梁技术关于横向分布调整系数:一、进行桥梁的纵向计算时:a)汽车荷载1对于整体箱梁、整体板梁等整体结构其分布调整系数就是其所承受的汽车总列数,考虑纵横向折减、偏载后的修正值。
例如,对于一个跨度为230米的桥面4车道的整体箱梁验算时,其横向分布系数应为4 x 0.67(四车道的横向折减系数)x 1.15(经计算而得的偏载系数)x0.97(大跨径的纵向折减系数)= 2.990。
汽车的横向分布系数已经包含了汽车车道数的影响。
2多片梁取一片梁计算时按桥工书中的几种算法计算即可,也可用程序自带的横向分布计算工具来算。
计算时中梁边梁分别建模计算,中梁取横向分布系数最大的那片中梁来建模计算。
b)人群荷载1对于整体箱梁、整体板梁等整体结构人群集度,人行道宽度,公路荷载填所建模型的人行道总宽度,横向分布系数填1即可。
因为在桥博中人群效应=人群集度x人行道宽度x人群横向分布调整系数。
城市荷载填所建模型的单侧人行道宽度,若为双侧人行道且宽度相等,横向分布系数填2,因为城市荷载的人群集度要根据人行道宽度计算。
2多片梁取一片梁计算时人群集度按实际的填写,横向分布调整系数按求得的横向分布系数填写,一般算横向分布时,人行道宽度已经考虑了,所以人行道宽度填1。
c)满人荷载1对于整体箱梁、整体板梁等整体结构满人宽度填所建模型扣除所有护栏的宽度,横向分布调整系数填1。
与人群荷载不同,城市荷载不对满人的人群集度折减。
2多片梁取一片梁计算时满人宽度填1,横向分布调整系数填求得的。
注:1、由于最终效应:人群效应=人群集度x人行道宽度x人群横向分布调整系数。
满人效应=人群集度x满人总宽度x满人横向分布调整系数。
所以,关于两项的一些参数,也并非一定按上述要求填写,只要保证几项参数乘积不变,也可按其他方式填写。
2、新规范对满人、特载、特列没作要求。
所以程序对满人工况没做任何设计验算的处理,用户若需要对满人荷载进行验算的话,可以自定义组合。
桥梁荷载横向分布系数的各种计算方法综述姓名:XXX学号:50XXXXXXX3摘要:公路桥梁荷载横向分布有多种计算模型,其中比较实用的有:1)杠杆原理法;2)偏心压力法、修正偏心压力法;3)铰接板(梁)法;4)刚接板(梁)法等。
这些理论方法有各自的适用范围,应按具体情况选用适当的方法来运用。
关键词:混凝土简支梁桥;荷载横向分布系数;影响线;影响因素1引言随着国民经济的发展,对交通的需求日益提高,众多的高速公路及城市快速干道相继修建。
公路桥梁上行驶车辆的轴重加重、速度提高,车流密度也相应提高。
使之在设计过程中如何确保桥梁结构在使用寿命期限内的安全性,准确计算各片梁所需承担的最大活载弯矩就显得尤为重要。
特别是对于中小跨多片梁型的桥梁,当跨数较多时,用测试横向分布状态的方法对桥梁运营状态进行评价,具有简洁、实用、可靠等优点,具有较高的推广价值。
所谓荷载横向分布系数(Lateral Distribution Factor of Live Load)是指公路车辆荷载在桥梁横向各主梁间分配的百分数。
普通简支桥梁中它和各主梁间的联结方式(铰接或刚接),有无内横梁及其数目,断面的抗弯刚度和抗扭刚度,以及车辆荷载在桥上的位置等有关。
它是一个复杂的空间结构问题,在桥梁设计中常简化为平面问题而引用荷载横向分布系数。
[1]目前广泛采用的是利用主梁的纵向影响线和它的荷载横向分布影响线相结合的方法,荷载横向分布系数是在荷载横向分布影响线的基础上按荷载的最不利位置布载,并将荷载位置相应的影响线竖标值求和得到的最后数值结果。
对于混凝土简支梁桥,荷载横向分布系数的影响因素主要有桥粱跨度(Z)、主梁间距(S)、桥面板的厚度(t0)、主梁刚度(K0)、横隔梁(板)的数量及位置、车载类型及布栽位置、车辆间距、栏杆及横跨比等。
[2][3][4][9]2计算方法及其适用范围荷载横向分布理论在桥梁设计中占有重要地位。
目前桥梁荷载横向分布系数常用的计算方法主要有杠杆原理法、偏心压力法(修正偏心压力法)、铰接板(梁)法、刚接梁法和比拟正交异性板法(G-M法)等。
下面对这些方法逐一进行介绍和分析。
1)杠杆原理法忽略主梁之间横向结构的联系作用,即假设桥面板在主梁梁肋处断开,而当作沿横向支承在主梁上的简支梁或悬臂梁来考虑。
图一杠杆法计算实例假定荷载横向分布影响线的坐标为η,车辆荷载轴重为P,轮重为P/2,将车辆荷载按最不利情况加载,则分布到某主梁的最大荷载为P’max=Σ(P/2)·η=(1/2×∑η)·P(1)根据荷载横向分布系数的定义可知,式(1)的1/2∑η即为车辆荷载的横向分布系数。
《桥规》(JTG D60)中规定,车道荷载横向分布系数按车辆荷载横向分布系数计,因此,因此,两者可统称为汽车荷载横向分布系数,其值为m oq=1/2∑ηq(2)同理可得人群荷载横向分布系数为m or=ηr(3)式(2)(3)中:m o——按杠杆原理法计算的荷载横向分布系数;脚标q和r——分别指汽车和人群荷载;ηq和ηr——汽车车轮和每延米人群荷载集度对应的荷载横向分布影响线坐标。
杠杆原理法适用于荷载位于靠近主梁支点时的荷载横向分布计算。
此时,主梁的支承刚度远大于主梁间横向联系的刚度,荷载作用于某处时,基本上由相邻的两根梁承担,并传递给支座,受力特性与杠杆原理法接近。
此外,该法也可以用于双主梁桥,或者横向联系很弱的无中间横格梁的桥梁。
2)偏心压力法基本假定是:一,在车辆荷载作用下,中间横隔梁可近似地看作一根刚度无穷大的刚性梁,横梁全长呈直线变形;二,忽略主梁的抗扭刚度,即不计入主梁对横隔梁的抵抗扭矩。
计算原理:设单位竖向集中荷载P=1作用在离截面扭转中心O的距离为e处,各片主梁的抗弯刚度I i、主梁间距a i都各不相等。
下面分析荷载在各片主梁上的横向分布情况。
由于假定横梁是刚体,所以可以按刚体力学关于力的平移原理,将荷载P移到中间主梁上,用一个作用在扭转中心(中心主梁)上的竖向力P和一个作用于刚体上的偏心力矩M=P·e=1·e代替。
偏心荷载的作用应为P和M作用的叠加。
①中心荷载P=1的作用。
R‘i=I i/(∑I i)(4)②偏心力矩M=P·e=1·e的作用。
R”i=ea i I i/(∑a i2I i)(5)③偏心荷载P=1产生的总作用力。
偏心荷载P作用于k号梁时,在i号梁上产生的总作用力,即i号主梁所分配到的荷载,等于上诉两种情况的叠加,即R ik=R‘ik+R”ik=I i/(∑I i)±a i a k I i/(∑a i2I i)(6)④求荷载横向分布系数m。
ηki=R ki=1/n±a k a i/(∑a i2)(7)式(6)(7)中,当e和a i位于同一侧时,第二项取正号,反之则取负号。
用偏心压力法计算荷载横向分布适用于桥上具有可靠的横向连接,且桥的宽跨比B/L 小于或接近0.5的情况时(一般称为窄桥)的跨中区域的荷载横向分布影响线。
偏心压力法具有概念清楚、公式简明和计算方便等优点。
3)修正偏心压力法在偏心压力法的推导中由于作了横隔梁近似绝对刚性和忽略主梁抗扭刚度的两项假定,这就导致了边梁受力偏大的计算结果。
因此,在实用计算中有按偏心压力法求得的边梁最大横向分布系数乘以0.9加以折减的方法。
为了弥补偏心压力的不足,国内外也广泛地采用考虑主梁抗扭刚度的修正偏心压力法,引入一个抗扭修正系数β。
这一方法既不失偏心压力的优点,又避免了结构偏大的缺陷,因此修正偏心压力法是一个具有较高实用价值的近似方法。
【5】对于简支梁桥,若主梁截面均相同,即I i=I,I Ti=I T,则ηki=R ki=1/n±β·a k a i/(∑a i2)(8)其中β=1/[1+nl2G c I T/﹙12E c I∑a i2﹚](9)由式(9)可以看出,当桥梁宽度一定时,随着跨度增大,β减小。
即抗扭刚度对横向分布系数的影响增大。
根据《桥规》(JTG D62),式(9)中混凝土的剪变模量G c可取0.4E c;对于由矩形组合而成的梁截面,如T型或I字形梁,其抗扭惯矩I T近似等于各个矩形截面的抗扭惯矩之和,即I T=∑c i b i t i3(10)式(10)中:b i,t i——相应为单个矩形截面的宽度和厚度;c i——矩形截面抗扭刚度系数(根据t/b比值查表可知);m——梁截面划分成单个矩形截面的块数。
修正偏心压力法的适用范围与偏心压力法相同,这一方法既不失偏心压力的优点,又避免了结构偏大的缺陷,因此修正偏心压力法是一个具有较高实用价值的近似方法。
[1][5] 4)弹性支承连续梁法弹性支承连续梁法主要是根据桥梁结构纵横梁刚度(抗弯及抗扭)的比例不同,通过假设横梁为弹性支撑在各纵梁位置的弹性支承连续梁(该弹性支撑的刚度即纵梁抗弯刚度),按弹性支承连续梁计算出各支撑处的反力即可得到荷载的横向分布。
此法不仅适用于宽跨比小于0.5的窄桥,也适用宽跨比大于0.5的宽桥[5]。
弹性支承连续梁的解法很多,比较简便的是初参数法。
1954年,中国学者翻译了原苏联奥西波夫所著的《弹性支承连续梁》,给出了初参数法导出的2-8跨弹性支承连续梁支点反力的公式和数值表。
后来,中国学者又补充了关于9跨、10跨的公式和表,并在引用、开发和推广方面做了大量工作,使这一方法在桥梁设计上得到广泛应用,且此方法常用于计算平面曲线桥的横向分布系数[6]。
5)铰接板(梁)法对于用现浇混凝土纵向企口缝连接的装配式板桥以及仅在翼板间用焊接钢板或伸出交叉钢筋连接的无中间横隔梁的装配式桥,由于快件间横向具有一定的连接构造,但其连接刚性又很薄弱。
这类结构的受力状态实际接近于数根并列而相互间横向铰接的狭长板(梁),以此为基础发展了横向铰接板(梁)理论来计算荷载的横向分布。
图二铰接梁法计算实例基本假定有:在竖向荷载作用下,接缝内只传递竖向剪力g(x);采用半波正弦荷载来分析跨中荷载横向分布的规律,g i(x)=g i·sin(π·x/l);每块板梁在偏心荷载下只产生垂直位移ω和转角φ,而不发生横向弯曲。
计算原理:应用结构力学的方法列出正则方程组,整理并引入刚度系数γ=bφ/(2ω),则得到一个只含γ和g i的新方程组。
由此只要确定了刚度参数γ、板块数量n和荷载作用位置,就可以解出所有(n-1)个未知铰力的幅值,从而绘制出各梁的横向影响线。
γ=0.5bφ/ω=0.5·[pbl2/(2π2GI T)]/[pl4/(π4EI)](11)式(11)中对于混凝土,取E=E c,G=G c=0.4E c。
6)刚接板梁法在铰接板(梁)桥计算理论的基础上,在铰接处补充引入赘余弯矩M i,可建立计横向刚性连接特点的赘余力正则方程。
用这一方法来求解各梁荷载横向分布的问题,就称为刚接梁法。
对于相邻二片主梁的接合处可以承受弯矩的,或虽然桥面系没有经过构造处理,但没有多片内横箱梁的,或桥面浇筑成一快整体板的桥跨结构,可以看作是刚接梁系,都适用刚接板梁法来计算荷载横向分布系数。
7)比拟正交异性板法对于由主梁、连续的桥面板和多横隔梁所组成的梁桥,当其宽度与跨度之比值较大时,可将其简化比拟为一块矩形的平板作为弹性薄板,按古典弹性理论来进行分析,即所谓“比拟正交异性板法”或称“G-M法”。
一些学者研究认为使用“G-M法”计算的荷载横向分布系数比实际测量的值偏大一些。
因此,在新桥设计阶段我们按照“G-M法”计算的数据来计算结构的内力是偏于安全的,是可行的;而在旧桥加固的计算时,如仍然采用“G-M法”计算荷载横向分布系数,会导致加固工程量偏大,不仅会造成经济上的浪费,而且有可能在实际的加固设计中不可能实现。
[7]8)广义梁格分析法实际上是推广直梁桥中的梁格理论,但广义梁格分析法不同于刚性横梁法,刚性横梁法是梁格理论在桥梁上运用的特例。
广义梁格法也不同于正桥中的弹性支承连续梁法,广义梁格法不仅考虑主梁的抗扭惯矩,而且充分考虑由于弯扭耦合作用而产生的主梁的实际挠曲变形和扭转变形,同时在计算中也充分地考虑了横梁本身的弯曲变形。
因而,广义梁格分析法是一种可通用于直、斜、弯梁桥跨的横梁内力计算和主梁内力横向分布计算的方法,它既是一种实用简便的计算方法,又是一种比较精确的计算方法。
实质上,这是一个用结构力学位移法简化分析杆系空间结构的方法,由于它从横梁结构的分析入手,所以又可以叫做横梁分析法[8]。
3结语本文就混凝土简支梁桥荷载横向分布系数的各种计算方法进行了系统的总结和分析,得出计算桥梁荷载横向分布系数的结论如下。
(1)以上各种理论方法计算荷载横向分布系数具有一定的局限性,不同的计算方法有各自的适用范围,不可盲目使用。