2019-2020年高二数学上册 9.4《三阶行列式》教案(1) 沪教版
- 格式:doc
- 大小:126.50 KB
- 文档页数:6



三阶行列式【学习目标】1.通过类比理解三阶行列式的符号特征。
2.掌握三阶行列式的对角线展开法则和按某一行(列)展开的方法。
3.理解余子式和代数余子式的概念,感悟类比思想方法在数学研究中的应用。
【学习重难点】1.三阶行列式的展开。
2.三阶行列式按某一行(列)展开。
【学习过程】一、知识点1.三阶行列式:__________________________________。
2.三阶行列式对角线展开法则:__________________________________。
3.余子式:__________________________________。
代数余子式:__________________________________。
4.三阶行列式按某一行(列)展开:__________________________________。
5.三角形的面积公式:__________________________________。
二、典型例题例1.用对角线法则展开行列式:(1)302213231--;(2)213302231--;(3)232103321--。
例2.如图,在平面直角坐标系中,点A 、B 、C 的坐标分别为12(,)x y 、22(,)x y 、33(,)x y ,求ABC ∆的面积。
例3.按下列要求计算行列式302213231D -=-。
(1)按第一行展开;(2)按第一列展开。
练习:用对角线法则展开下列行列式,并化简。
(1)234521123--;(2)010111111aa+-; (3)000a b cd e f 。
2.(1)在三阶行列式351236724---中,元素6-的余子式为_____________,6-的代数余子式为_____________。
(2)在三阶行列式240521143---中,哪几个元素的余子式和它的代数余子式相同?3.分别用按第一行展开和第一列展开的方式计算下列三阶行列式。

行列式【教学目标】1、理解行列式的概念和意义,理解行列式对角线方程的意义;2、掌握二阶行列式和三阶行列式展开的对角线法则;3、理解余之式和代数余之式的概念,掌握三阶行列式按某一行(列)展开的方法【教学重点】对角线法则【教学难点】用三阶行列式解三元线性方程组,会对含字母系数的三元一次房产证的解的情况进行讨论【教学方法】讲练结合 【教学过程】 一、主要知识:1.二阶行列式的定义及其展开方法——对角线法则。
2.利用二阶行列式解二元一次方程组。
设二元一次方程组111222(1)(2)a xb yc a x b y c +=⎧⎨+=⎩(1a 、2a 、1b 、2b 不全为零)()()2112b b ⨯-⨯,得()12211221a b a b x c b c b -=-;()()1221a a ⨯-⨯,得()12211221a b a b y a c a c -=-;当12210a b a b -≠时,方程组有唯一解:1221122112211221c b c b x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩设111111222222;,x y a b c b a c D D D a b c b a c ===,那么(1)当0D ≠时,方程组有唯一解 ;(2)当0D =,若,x y D D 中至少有一个不为零,即0x x D ⋅=或0y x D ⋅=中至少有一个无解,所以方程组无解;(3)当0x y D D D ===时,即12210a b a b -=,且12210a c a c -=不妨设10a ≠,则2121a b b a =,2121a c c a =,于是方程(2)为2121211a b a ca x y a a +=,即()21121a a xb y ac +=,即方程(1)的解都是方程(2)的解,而方程(1)有无数组解,所以方程组有无数组解。
3.三阶行列式的定义及其展开方法——对角线法则4.按一行(或一列)展开求三阶行列式的方法:111222111111 333a b ca b c a A b B c C a b c=++5.利用三阶行列式解三元一次方程组111122223333 a x b y c z d a x b y c z d a x b y c z d++=⎧⎪++=⎨⎪++=⎩设行列式111111111111 222222222222 333333333333 ,,,x y za b c d b c a d c a b d D a b c D d b c D a d c D a b da b c d b c a d c a b d ====当0D≠时,方程组有唯一解当0D=时,方程组无解或有无穷多解。

三阶行列式【教学目标】1.掌握余子式、代数余子式的概念;2.经历实验、分析的数学探究,逐步归纳和掌握代数余子式的符号的确定方法和三阶行列式按一行(或一列)展开方法,体验研究数学的一般方法;3.体会用简单(二阶行列式)刻画复杂(三阶行列式)、将复杂问题简单化的数学思想。
【教学重难点】三阶行列式按一行(或一列)展开、代数余子式的符号的确定。
【教学过程】 一、情景引入(1)将下列行列式按对角线展开:2233b c b c =_______________;2233a b a b =_______________;2233a c a c =_______________;111222333a b c a b c a b c =_______________。
(2)对比、分析以上几个行列式的展开式,你能将三阶行列式111222333a b c a b c a b c 表示成含有几个二阶行列式运算的式子吗?说明:(1)请学生展开几个行列式的主要目的是:巩固复习前面学习的知识;同时,有意识地设计这几个行列式的展开,有助于学生发现三阶行列式111222333a b c a b c a b c 与相应的二阶行列式间的关系。
(2)将三阶行列式111222333a b c a b c a b c 表示成几个含有二阶行列式运算的式子,结果可能不唯一,可以有111222222222111333333333a b c b c a c ab a bc a b c b c a c a b a b c =-+等等。
二、学习新课1.知识解析。
在刚才的实验中,将三阶行列式111222333a b c a b c a b c 表示成了含有三个二阶行列式运算的式子,主要有:111222222222111333333333a b c b c a c ab a bc a b c b c a c a b a b c =-+; 111221111222123333322333a b c b c b c bc a b c a a a b c a c b c a b c =-+;111221111222123333322333a b c a c a c ac a b c b b b a c a c a c a b c =-+-等等。

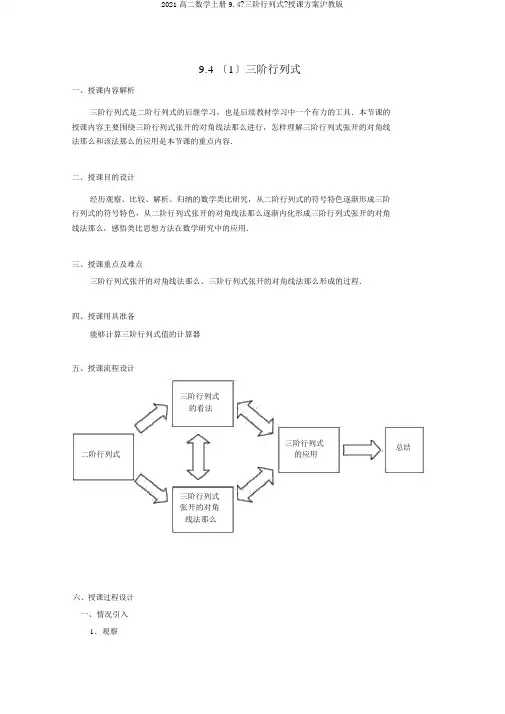
9.4 〔1〕三阶行列式一、授课内容解析三阶行列式是二阶行列式的后继学习,也是后续教材学习中一个有力的工具.本节课的授课内容主要围绕三阶行列式张开的对角线法那么进行,怎样理解三阶行列式张开的对角线法那么和该法那么的应用是本节课的重点内容.二、授课目的设计经历观察、比较、解析、归纳的数学类比研究,从二阶行列式的符号特色逐渐形成三阶行列式的符号特色,从二阶行列式张开的对角线法那么逐渐内化形成三阶行列式张开的对角线法那么,感悟类比思想方法在数学研究中的应用.三、授课重点及难点三阶行列式张开的对角线法那么、三阶行列式张开的对角线法那么形成的过程.四、授课用具准备能够计算三阶行列式值的计算器五、授课流程设计三阶行列式的看法三阶行列式总结二阶行列式的应用三阶行列式张开的对角线法那么六、授课过程设计一、情况引入1.观察(1) 观察二阶行列式的符号特色:1 3 02 6 12 a b 2 531711c d(2) 观察二阶行列式的张开式特色:1 3 02 13 ( 2)2 112330 1 1612 a b d c b76(11)712c a11d2.思虑(1) 二阶行列式算式的符号有哪些特色?(2) 你能总结一下二阶行列式的张开式有哪些特色吗?[说明](1) 请学生观察二阶行列式的符号特色,主若是观察二阶行列式有几个元素,这几个元素怎么分布?从而能够类比获取三阶行列式的符号特色.(2) 请学生观察和总结二阶行列式的张开式特色,能够提示学生主要着力于以下几个方 面:① 观察二阶行列式的张开式有几项?② 二阶行列式的张开式中每一项有几个元素相乘;这几个元素在行列式中的地址有什么要求吗?③ 二阶行列式的元素在其张开式中出现了几次?每个元素出现的次数相同吗?二、学习新课1.新课解析【问题商议】结合情况引入的两个思虑问题,教师能够设计一些更加细化的问题引导学生发现二阶行列式的符号特色以及二阶行列式的张开式特色,从而类比获取三阶行列式相应特色.比方教师能够设计以下几个问题:问题一, 经过学习和观察,我们发现二阶行列式就是表示四个数四个数分布成两行两列的方阵,那么三阶行列式符号应该有怎么样的特色呢?( 或式 ) 的特定算式,这问题二, 说出二阶行列式的张开式有哪些特色?( ① 二阶行列式的张开式共有两项;②二阶行列式的张开式中每一项有两个元素相乘;③ 相乘的两个元素在行列式位于不相同行不相同列;④ 二阶行列式的元素在其张开式中出现了一次,而且每个元素出现的次数是相同的.)问题三,二阶行列式张开式就是:主对角线的元素乘积减去副对角线的元素的乘积.我a1b1c1们能够依照二阶行列式张开式的特色类比研究三阶行列式a2b c2按对角线张开后张开2a3b3c3式应该拥有的特色.那么三阶行列式的张开式中每一项有几个元素相乘?对这些能够相乘的元素有什么要求?(3 个.这 3 个能够相乘的元素应该位于不相同行不相同列.)问题四,三阶行列式的张开式的项中有哪些元素的乘积?二阶行列式的元素在其张开式中出现了一次,而且每个元素出现的次数是相同的.那么,请你猜想一下在三阶行列式的张开式中,每个元素应该出现几次呢?你猜想的依照是什么?[说明]二阶行列式与三阶行列式有必然的内在联系,上述各个问题的商议能够帮助学生学习三阶行列式的看法,并能意识到三阶行列式的张开式中必然会出现a1b2c3, a3b2 c1, a2b3c1,a3b1c2, a2b1c3, a1b3 c2.至于张开式中各项符号确实定,能够组织学生经过以下实验试一试解决.【实验研究】【工作 1】请你对a1, a2,a3, b1, b2, b3, c1, c2, c3分别赋值:a1______,a2______,a3______,b1______,b2______,b3______,c1______ ,c2______,c3______ ,a1b1c1利用计算器,计算得:a2b2c2____________.a3b3c3【工作 2】填写下表:各乘积a 1b 2c 3 a 2b 3c 1 =a 3b 1c 2 =a 3b 2c 1 =a 2b 1c 3 =a 1b 3c 2 ==各序 项符之和______________________________号号猜想 1猜想 2猜想 3⋯⋯【工作 3】由上述 算 果,能够 三 行列式按 角 张开后张开式 是:a 1b 1c 1a 2b 2c 2____________________________________ .a 3b 3c 3[ 明](1) 以上 主要由学生合作完成, 的目的主若是 学生 猜想 、 、 得新知的 程;(2) 了便于研究, 教 提示学生在完成工作(1) , a 1 , a 2 , a 3 , b 1 , b 2 , b 3 , c 1 ,c 2 , c 3 分 不相同的 ,而且不要0;(3) 教 能够将学生分成数个学 小 ,合作 研究,并交流研究 果,最后由教 ;(4) 通 上述研究,能够引 学生 :a 1b 1c 1a 2b 2c 2 a 1b 2c 3 a 2b 3c 1 a 3b 1c 2 a 3b 2c 1 a 2b 1c 3 a 1b 3c 2 ; a 3b 3c 3a 1 xb 1 yc 1 zd 1(5) 三元一次方程a 2 xb 2 yc 2 zd 2 消元后,得:a 3 xb 3 yc 3 zd 3( a 1b 2 c 3( a 1b 2 c 3( a 1b 2 c 3a 2b 3c 1 a 3b 1 c 2 a 3b 2 c 1 a 2b 1 c 3 a 1b 3 c 2 )x (d 1b 2 c 3 d 2 b 3c 1 d 3 b 1c 2 d 3 b 2 c 1 d 2 b 1 c 3 d 1 b 3 c 2 )a 2b 3c 1 a 3b 1 c 2 a 3b 2 c 1 a 2b 1 c 3 a 1b 3 c 2 ) y (a 1d 2 c 3 a 2 d 3 c 1 a 3 d 1 c 2 a 3 d 2 c 1 a 2 d 1c 3 a 1d 3c 2 )a 2b 3c 1 a 3b 1 c 2 a 3b 2 c 1 a 2b 1 c 3 a 1b 3 c 2 )z (a 1b 2d 3 a 2 b 3 d 1 a 3 b 1 d 2 a 3 b 2 d 1 a 2 b 1 d 3 a 1b 3 d 2 )所以 是吻合引入 号的 意 的。

高二数学教案:三阶行列式教案一、了解学生现状和班级实际水平。
在教学设计时,应该了解所教学生的现状和班级的实际水平,只有了解了学生对本课时有关的基本知识和技能、数学方法和数学思想的掌握程度,所需的知识、能力与以往经验之间的差异等。
才能通过恰当的处理教材内容,让学生顺利完成本节课的学习要求,同时使40分钟的教学效率较高。
我执教的高二(2)的学生对已有知识和能力的现状是:三阶行列式是学生学习了二阶行列式后紧接着学习的内容,他们对二阶行列式的学习是比较成功的,他们初步知道了二阶行列式的有关知识,知道如何利用二阶行列式解二元一次方程组和讨论二元一次方程组解的情况。
学生在能力和情感的现状是:对数学有一定的兴趣,有一定的类比推广能力,对化归的数学思想有所体会,也有部分学生具有初步的数学审美情趣。
二、了解所教内容的地位,确定教学目标。
了解所教内容在本章节、在高中数学乃至在整个数学中的地位,了解本节课内容在数学结构和学生知识结构中所处的地位和作用。
教材作为一个载体,分析是否具有在能力、情感态度价值观等方面有挖掘的方面。
以确定较全面、科学的教学目标。
课程标准对《三阶行列式》的学习要求是:掌握三阶行列式的对角线展开法则,以及三阶行列式按某一行(列)展开的方法;会用三阶行列式表示相应的特殊算式。
结合课程标准的学习要求,如果我们在设计时,重知识、轻能力,重结果、轻过程,重记忆、轻概念的形成过程,那么这节课的设计很可能显得平淡,学生可能会在大量的模仿、记忆和练习中,达到课程标准的学习要求,但长期这样下去,学生的能力得不到培养,学生可能会失去对数学的兴趣甚至厌学,更不要说对情感态度价值观的培养了。
我认为,尽管三阶行列式作为一个非高考内容,但它却是一个不可多得的让学生体验类比推广过程,体会化归思想,培养学生数学审美情趣的好教材。
基于以上原因,我把这节课的教学目标确定为:1。
让学生掌握三阶行列式的对角线展开法则,能把三阶行列式按某一行(列)化为二阶行列式;知道余子式和代数余子式的概念,并能把三阶行列式按某一行(列)化成二阶行列式,并求值。

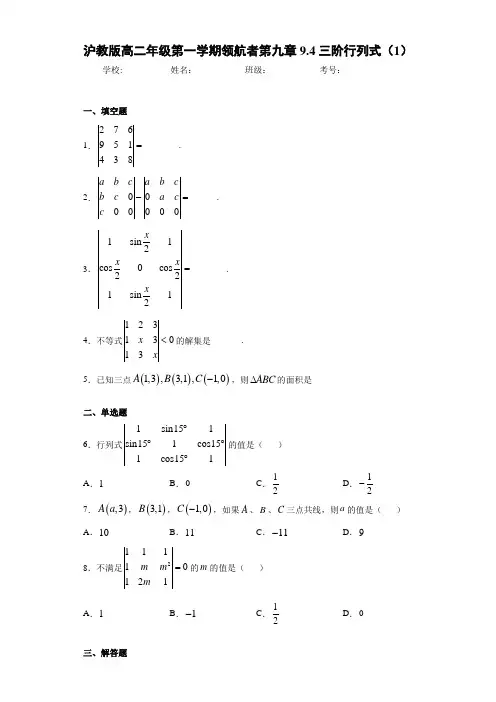
沪教版高二年级第一学期领航者第九章9.4三阶行列式(1)学校:___________姓名:___________班级:___________考号:___________一、填空题1.276951438=________.2.0000000a b ca b c bc a c c -=______.3.1sin 12cos0cos221sin12x x xx =________. 4.不等式12313013x x<的解集是_______.5.已知三点()()()1,3,3,1,1,0A B C -,则ABC ∆的面积是____________二、单选题6.行列式1sin151sin151cos151cos151︒︒︒︒的值是( )A .1B .0C .12D .12-7.(),3A a ,()3,1B ,()1,0C -,如果A 、B 、C 三点共线,则a 的值是( ) A .10B .11C .11-D .98.不满足211110121mm m =的m 的值是( )A .1B .1-C .12D .0三、解答题9.试将341413253522225---+写成一个三阶行列.10.解下列方程:(1)13450637xx--=-;(2)22613013xxx+=.11.不等式21101x xb ax a->-的解是12x<<,试求a,b的值.12.求证:sin cos1sin2cos21sin22sin sin3cos31x xx x x xx x=-.参考答案1.360- 【解析】 【分析】根据求行列式的方法化简即得. 【详解】276951438=2×5×8+7×1×4+9×3×6﹣4×5×6﹣3×1×2﹣9×7×8=﹣360, 故答案为:360- 【点睛】本题考查行列式的简单运算,属于基础题. 2.3c - 【分析】利用行列式的运算法则及性质化简求解即可 【详解】3000000000a b c a b cb cb c a c c c c c -=-=-.故答案为:3c - 【点睛】本题主要考查行列式的计算及性质,属于基础题. 3.0 【分析】由行列式的性质直接得解. 【详解】因为第一行与第三行完全相同,所以1sin 12cos 0cos221sin12x x xx =0, 故答案为:0 【点睛】本题考查了行列式的性质的应用,行列式的性质:若行列式中有两行完全相同,则这个行列式的值为零. 4.()2,3 【解析】 【分析】利用行列式的运算法则化简求解即可. 【详解】不等式12313013x x<, 即x 2+6+9﹣3x ﹣9﹣2x<0, 即x 2﹣5x+6<0,可得2<x <3.不等式的解集为:()23,. 故答案为()2,3 【点睛】本题考查行列式的运算法则的应用,不等式的解法,考查计算能力. 5.5 【详解】||||cos AB AC BC A ===∴==1sin 52A S ∴==⨯=6.D 【解析】 【分析】根据求行列式的方法化简即得. 【详解】三阶行列式221sin151sin151cos1512sin15cos151cos 15sin 151cos151︒︒︒=+︒︒--︒-︒︒=301sin ︒- =12-故选D . 【点睛】考查学生掌握行列式化简方法的能力,属于基础题. 7.B 【分析】构造方程组,利用方程组的解与行列式之间的关系求解a 即可. 【详解】∵A (2,2),B (a ,0),C (0,4)三点共线,∴l AB 与l AC 重合,又l AB :2x -(a -3)y +a -9=0,l AC :x -4y +1=0, 即2(3)941x a y ax y --=-⎧⎨-=-⎩有无数多个解,∴8329a a =-⎧⎨-=-⎩,解得a =11.故选:B . 【点睛】本题考查二元一次方程组的解与行列式之间的关系,考查了行列式的应用,属于中等题. 8.A 【分析】先利用三阶矩阵的计算方法,化简方程,再解方程即可.【详解】由题意,211110121mm m =,可化简为m +22m m +-321m m --=0,∴-2(1)m -=0,∴1m = 故选:A . 【点睛】本题的考点是三阶矩阵,主要考查利用三阶矩阵化简方程,属于基础题.9.253134252- 【分析】根据三阶行列式按某一行展开的系数可得到三阶矩阵的第一行,再根据行列式展开的运算法则可得结论. 【详解】341413253522225---+可得三阶矩阵的第一行为2,5,3,根据行列式展开的运算法则可得结果为:253134252-.【点睛】本题主要考查了三阶行列的定义,以及三阶行列式展开法则,属于基础题. 10.(1)2x =或117x =-;(2)3x =或2x =. 【分析】先利用三阶矩阵的计算方法,化简方程,再解方程即可. 【详解】(1)由题意,13450637xx--=-,可化简为131331456375454637x x x x x x----=++---=﹣30﹣18x+15x +36+27280x -=, ∴273220x x -+=,∴2x =或117x =-. (2)22613013x x x+=可化简为2263262613233313x x x x x x x x x+++=-+=222182183660x x x x x ---+++-=,∴2560x x -+=,∴3x =或2x =.【点睛】本题的考点是三阶矩阵,主要考查利用三阶矩阵化简方程,属于基础题. 11.12a =-,1b =-或1a =-,2b =- . 【解析】 【分析】将行列式展开,由行列式大于0,即ax 2+(1+ab )x +b >0,由1和2是方程ax 2+(1+ab )x +b =0的两个根,由韦达定理可知,列方程组即可求得a 和b 的值. 【详解】2111x xb a xa-=-x 2×(﹣a )×(﹣1)+x +abx ﹣x 2×(﹣a )﹣ax 2﹣(﹣1)×b =ax 2+(1+ab )x +b >0,∵不等式的解为1<x <2,∴a <0,且1,2为一元二次方程:ax 2+(1+ab )x +b =0的两个根,由韦达定理可知:11212ab ab a +⎧+=-⎪⎪⎨⎪⨯=⎪⎩,整理得:2a 2+3a +1=0,解得:12a b =-⎧⎨=-⎩或121a b ⎧=-⎪⎨⎪=-⎩,故a =﹣1,b =﹣2或a 12=-,b =﹣1. 【点睛】本题考查行列式的展开,考查一元二次不等式与一元二次方程的关系及韦达定理,考查计算能力,属于中档题. 12.证明见解析 【分析】先利用三阶矩阵的计算方法,化简等式的左边,再结合两角差的正弦公式化简即可证明. 【详解】sin cos 1sin 2cos 2sin cos sin cos sin 2cos 21sin 3cos3sin 3cos3sin 2cos 2sin 3cos31x x x x x x x xx x x x x x x xxx =-+=sin (-x )-sin(-2x )+sin (-x )=sin 2x -sin 2x . 【点睛】本题考查行列式的运算法则及性质的应用,变换的能力及数学分析能力,涉及两角和差的正弦公式,属于中档题.。

2019-2020年高二数学上册 9.3《二阶行列式》教案(2) 沪教版 教学目的:理解二阶行列式的定义;掌握用二阶行列式解二元一次方程组;用行列式判断二元一次方程组解的情况。
教学过程:一、 设问:什么叫二阶行列式?(一)定义:1、 我们用记号表示算式即 =其中记号叫做行列式,因为它只有两行、两列,所以把它叫做二阶行列式。
2、 叫做行列式的展开式,其计算结果叫做行列式的值。
3、 叫做行列式的元素。
(二)二阶行列式的展开满足:对角线法则1122a b a b 实线表示的对角线叫主对角线,虚线表示的对角线叫副对角线。
二阶行列式是这样两项的代数和:一个是从左上角到右下角的对角线(又叫行列式的主对角线)上两个元素的乘积,取正号;另一个是从右上角到左下角的对角线(又叫次对角线)上两个元素的乘积,取负号.(三)例和练习:例1、判断以下几项中哪些是二阶行列式?是的,求出值。
(1)(2)(3)123456(4)(5)1212343412242363--例2:将下列各式用行列式表示:——解唯一吗?(1)2214;(2)5;(3)422b ac x y x x ---+二、 用二阶行列式解二元一次方程组(四)设有二元一次方程组111222,(1)().(2)a xb yc A a x b y c +=⎧⎨+=⎩ 用加减消元法 得 1221122112211221();().a b a b x c b c b a b a b y a c a c -=--=- (1)当 时,有(A )有唯一解, (B) 122112211221122c b c b x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩求根公式。
(2)当 时,122112210c b c b a c a c -=-=无穷组解;(3)当 时122112210,0c b c b or a c a c -≠-≠无解。
(五)记,系数行列式 ,——类比,对照则(1)当D ≠0时,方程组(A) 的解(B)可以表示成X yD x D D y D⎧=⎪⎪⎨⎪=⎪⎩; (2)当D =0时, 无穷组解;(3) 当D =0时, 无解。
高二数学教课方案:三阶队列式教课方案一、认识学生现状和班级实质水平。
在教课方案时,应当认识所教课生的现状和班级的实质水平,只有认识了学生对本课时相关的基本知识和技术、数学方法和数学思想的掌握程度,所需的知识、能力与过去经验之间的差别等。
才能经过适合的办理教材内容,让学生顺利达成本节课的学习要求,同时使 40 分钟的教课效率较高。
我执教的高二 (2) 的学生对已有知识和能力的现状是:三阶队列式是学生学习了二阶队列式后紧接着学习的内容,他们对二阶队列式的学习是比较成功的,他们初步知道了二阶队列式的相关知识,知道如何利用二阶队列式解二元一次方程组和议论二元一次方程组解的状况。
学生在能力和感情的现状是:对数学有必定的兴趣,有必定的类比推行能力,对化归的数学思想有所领会,也有部分学生拥有初步的数学审美情味。
二、认识所教内容的地位,确立教课目的。
认识所教内容在本章节、在高中数学以致在整个数学中的地位,认识本节课内容在数学构造和学生知识构造中所处的地位和作用。
教材作为一个载体,剖析能否拥有在能力、感情态度价值观等方面有发掘的方面。
以确立较全面、科学的教课目的。
课程标准对《三阶队列式》的学习要求是:掌握三阶队列式的对角线睁开法例,以及三阶队列式按某一行(列 )睁开的方法;会用三阶队列式表示相应的特别算式。
联合课程标准的学习要求,假如我们在设计时,重知识、轻能力,重结果、轻过程,重记忆、轻观点的形成过程,那么这节课的设计很可能显得平庸,学生可能会在大批的模拟、记忆和练习中,达到课程标准的学习要求,但长久这样下去,学生的能力得不到培育,学生可能会失掉对数学的兴趣甚至厌学,更不要说对感情态度价值观的培育了。
我以为,只管三阶队列式作为一个非高考内容,但它倒是一个屈指可数的让学生体验类比推行过程,领会化归思想,培育学生数学审美情味的好教材。
鉴于以上原由,我把这节课的教课目的确立为:1。
让学生掌握三阶队列式的对角线睁开法例,能把三阶行列式按某一行 (列 ) 化为二阶队列式;知道余子式和代数余子式的观点,并能把三阶队列式按某一行(列 )化成二阶队列式,并求值。
2019-2020年高二数学上册 9.4《三阶行列式》教案(1)沪教版数学课堂教学是一个师生双方参与的动态的活动过程,学生是活动的主体,教师是这个过程的设计者和活动的指导者及合作者。
在一堂课中,如何体现学生学习的主体作用,激发学生学习的积极性,使学生在学习活动的过程中,在知识、能力、情感等诸方面得到发展,需要我们进行科学的设计。
下面就本人在06年9月执教的《三阶行列式》的教学设计过程为例,谈谈如何进行数学课堂教学设计。
一、了解学生现状和班级实际水平。
在教学设计时,应该了解所教学生的现状和班级的实际水平,只有了解了学生对本课时有关的基本知识和技能、数学方法和数学思想的掌握程度,所需的知识、能力与以往经验之间的差异等。
才能通过恰当的处理教材内容,让学生顺利完成本节课的学习要求,同时使40分钟的教学效率较高。
我执教的高二(2)的学生对已有知识和能力的现状是:三阶行列式是学生学习了二阶行列式后紧接着学习的内容,他们对二阶行列式的学习是比较成功的,他们初步知道了二阶行列式的有关知识,知道如何利用二阶行列式解二元一次方程组和讨论二元一次方程组解的情况。
学生在能力和情感的现状是:对数学有一定的兴趣,有一定的类比推广能力,对化归的数学思想有所体会,也有部分学生具有初步的数学审美情趣。
二、了解所教内容的地位,确定教学目标。
了解所教内容在本章节、在高中数学乃至在整个数学中的地位,了解本节课内容在数学结构和学生知识结构中所处的地位和作用。
教材作为一个载体,分析是否具有在能力、情感态度价值观等方面有挖掘的方面。
以确定较全面、科学的教学目标。
课程标准对《三阶行列式》的学习要求是:掌握三阶行列式的对角线展开法则,以及三阶行列式按某一行(列)展开的方法;会用三阶行列式表示相应的特殊算式。
结合课程标准的学习要求,如果我们在设计时,重知识、轻能力,重结果、轻过程,重记忆、轻概念的形成过程,那么这节课的设计很可能显得平淡,学生可能会在大量的模仿、记忆和练习中,达到课程标准的学习要求,但长期这样下去,学生的能力得不到培养,学生可能会失去对数学的兴趣甚至厌学,更不要说对情感态度价值观的培养了。
我认为,尽管三阶行列式作为一个非高考内容,但它却是一个不可多得的让学生体验类比推广过程,体会化归思想,培养学生数学审美情趣的好教材。
基于以上原因,我把这节课的教学目标确定为:1。
让学生掌握三阶行列式的对角线展开法则,能把三阶行列式按某一行(列)化为二阶行列式;知道余子式和代数余子式的概念,并能把三阶行列式按某一行(列)化成二阶行列式,并求值。
2。
在学习过程中,让学生体验类比推广的过程,体会化归思想。
让学生体会数学的思维方式。
3。
进一步让学生体会数学之美(高度的和谐、化归等),激发学生学习数学的积极性。
三、教学过程数学学习的意义在于通过数学学习而学习一种思维方式,进而培养学生的思维能力。
所以在教学过程的设计中,应该留出时间与空间,引导学生独立思考,自主探索,合作交流,重视概念、方法等的形成过程,使学生在理解和掌握数学知识的同时,既获得数学活动的经验,又得到美的熏陶。
对每一步的推导和变形,必须严密,以培养学生的理性精神。
在本节课的教学设计过程中,我通过学生类比二阶行列式的有关知识,让学生猜想三阶行列式的定义、对角线法则等内容,一方面是培养学生的类比能力,另一方面也让学生体会到这样定义三阶行列式的定义与对角线法则是合理的,进一步让学生体会到数学内部高度的和诣。
在引入余子式和代数余子式时,通过学生把式子改写为二阶行列式,探求二阶行列式中的元素在原行列式中位置,从而很自然地引进了余子式和代数余子式的概念,这样可让学生一方面体会到引入这些概念的必要性与过程(数学概念并不是凭空想象出来的,而是为数学本身的发展或社会发展服务的),也暗示学生数学内部无处不存在美。
本节课的教学过程简述如下: (一)概念的形成:(教师)我们学习了二阶行列式的概念、对角线展开法则和它的应用,请同学们思考:组成二阶行列式需要四个数(式),那么如果要组成一个三阶行列式,需要几个数(式)?他们应该如何排列?你能模仿二阶行列式的定义,给出三阶行列的定义吗?二阶行列式有对角线展开法则,请你注意主对角线和副对角线的方向,及主对角线和副对角上都是两个元素之积这个事实,你觉得三阶行列式是否有主、副对角线呢?如有,它们的方向是怎样的呢?应该是几个元素之积呢?你能给出三阶行列式的对角线展开法则吗?(二)按某一行(列)展开对三阶行列式的对角线展开法则,按第一行的元素进行整理得:a 1b 2c 3+a 2b 3c 1+a 3b 1c 2- a 3b 2c 1- a 2b 1c 3- a1b 3c 2=a 1(b 2c 3-b 3c 2)+b 1(a 3c 2-a 2c 3)+c 1(a 2b 3-a 3b 2),请学生观察,每一个括号都是二个数字积的差,它们能否用行列式表示?在这个过程中,对学生给出的各种形式的二阶行列式,与这些元素在原行列式中的位置对照,得出一个合理的行列式。
但中间的行列式,其元素与原位置不同,如何处理,才能使其位置与原位置一致,以达到高度的和谐?学生通过思考,有学生说:提出一个负号,这样元素与原位置一致了。
(让理想与现实产生冲突,激发学生的思维积极性)至此,学生受到了数学高度和谐美的冲击,有学生情不自禁地说:数学真美! 师:如果对其它行(列)进行整理,结果又会如何呢? 由此可以很自然地引进余子式和代数余子式的概念了。
(三)范例与练习例1.用对角线法则计算三阶行列式的值:132312203-- 。
学生练习:课本12页。
例2.按下列要求,对行列式111cbc aba ---进行展开,并化简。
(1)对角线法则。
(2)按第一行展开。
(3)按第一列展开。
学生练习:以上是本人对数学课堂教学设计的粗浅体会,以上管见,如有不当,恳请同行,不吝赐教。
2019-2020年高二数学上册 9.4《三阶行列式》教案(2)沪教版一、教学内容分析三阶行列式按一行(或一列)展开是三阶行列式计算的另外一种法则,学习这种法则有助于学生更好地理解二阶行列式、三阶行列式的内在联系,同时这个法则也是较复杂的行列式计算的常用方法,这个法则更是蕴涵了数学问题研究过程中将复杂问题转化为简单问题的研究方法.本节课的教学内容主要围绕代数余子式的符号的确定研究三阶行列式按一行(或一列)展开法则.二、教学目标设计⑴掌握余子式、代数余子式的概念;⑵经历实验、分析的数学探究,逐步归纳和掌握代数余子式的符号的确定方法和三阶行列式按一行(或一列)展开方法,体验研究数学的一般方法;(3)体会用简单(二阶行列式)刻画复杂(三阶行列式)、将复杂问题简单化的数学思想.三、教学重点及难点三阶行列式按一行(或一列)展开、代数余子式的符号的确定.四、教学过程设计一、情景引入(1)将下列行列式按对角线展开:_______________ ______________________________111222333a b ca b ca b c=_______________(2)对比、分析以上几个行列式的展开式,你能将三阶行列式111222333a b ca b ca b c表示成含有几个二阶行列式运算的式子吗?[说明](1)请学生展开几个行列式的主要目的是:巩固复习前面学习的知识;同时,有意识地设计这几个行列式的展开,有助于学生发现三阶行列式111222333a b ca b ca b c与相应的二阶行列式间的关系.(2)将三阶行列式111222333a b ca b ca b c表示成几个含有二阶行列式运算的式子,结果可能不唯一,可以有111222222222111333333333a b cb c a c a ba b c a b cb c a c a ba b c=-+等等.二、学习新课1.知识解析在刚才的实验中,将三阶行列式111222333a b c a b c a b c 表示成了含有三个二阶行列式运算的式子,主要有:111222222222111333333333a b c b c a c a b a b c a b c b c a c a b a b c =-+111221111222123333322333a b c b c b c b c a b c a a a b c a c b c a b c =-+ 111221111222123333322333a b c a c a c a c a b c b b b a c a c a c a b c =-+-等等. 请同学生选择其中的一个为例谈谈他们是如何发现这些等式的?事实上,以111222222222111333333333a b c b c a c a b a b c a b c b c a c a b a b c =-+为例,先将展开式111222123231312321213132333a b c a b c a b c a b c a b c a b c a b c a b c a b c =++---变形为: 111222123132312213231321333()()()a b c a b c a b c a b c a b c a b c a b c a b c a b c =-+-+-,然后分别提取公因式,可以得到111222123321322312332333()()()a b c a b c a b c b c b a c a c c a b a b a b c =-+-+- 再利用已有的展开式① ② ③ 从而很容易就得到结果了.其中二阶行列式①、②、③分别叫做元素,,的余子式...,添上相应的符号(正号省略),如, 、、分别叫做元素,,的代数余子式......于是三阶行列式可以表示为第一行的各个元素与其代数余子式的乘积之和:111222222222111333333333a b c b c a c a b a b c a b c b c a c a b a b c ⎛⎫=+-+ ⎪⎝⎭象这样的展开,我们称之为三阶行列式按第一行展开.类似的,我们可以将三阶行列式按第二行或按列展开.从上述研究,我们不难发现这种展开方法的关键是要找到三阶行列式某一行或某一列各个元素的代数余子式.不难发现,要确定某元素的代数余子式,我们可以先确定其余子式,然后确定代数余子式符号,而最主要的就是其符号的确定.为了让学生有较深刻的体会,教师可以组织学生完成 总结代数余子式的确定方法:_____________________________ _____________________________[说明](1)以上主要由学生合作完成,实验的目的主要是让学生经历实验、归纳、猜想、抽象并获得新知的过程;(2)教师可以将学生分成数个学习小组,合作实验研究,并交流研究结果,最后由教师总结.(3)通过上述研究,教师要引导学生发现:确定某个元素的余子式其实就是将这个元素所在的行和列划去,将剩下的元素按照原来的位置关系所组成的二阶行列式;而这个元素的代数余子式与该元素所在行列式的位置(即第行,第列)有关,其代数余子式的正负号是“”.一般地,三阶行列式可以按其任意一行(或一列)展开成该行(或该列)的各个元素与其代数余子式的乘积之和.其中,最关键的是确定三阶行列式某一行或某一列各个元素的代数余子式(尤其是其符号).2.例题解析例题1 按要求计算行列式:302213231-- (1)按第一行展开; (2)按第一列展开.[说明](1)一个三阶行列式可以按其任意一行(或一列)展开,其中,最关键的是确定三阶行列式某一行或某一列各个元素的代数余子式(尤其是其符号);(2)当一个三阶行列式的某一行(或某一列)元素中,0的个数较多,我们往往将行列式按照该行(或该列),这样计算往往比较方便.例题2.计算:222222222333333b c a c a b a b c b c a c a b -+〖参考答案〗描 述: 教学目标⑴掌握余子式、代数余子式的概念;⑵经历实验、对比、分析的数学探究,逐步归纳和掌握代数余子式的符号的确定方法和三阶行列式按一行(或一列)展开方法,体验研究数学的一般方法;(3)体会用简单(二阶行列式)刻画复杂(三阶行列式)、将复杂问题简单化的数学思想.教学重点及难点三阶行列式按一行(或一列)展开、代数余子式的符号的确定.四、课堂小结(1)余子式、代数余子式的概念;(2)三阶行列式按一行(或一列)展开方法.五、作业布置根据学生的具体情况,对习题册中的问题进行增减.五、教学设计说明本节课的教学内容是三阶行列式按一行(或一列)展开方法,从内容上看,这部分内容与上节课一样,同样概念性比较强,同样容易上成教师“一堂言”的枯燥无味的数学课,但是这部分内容却蕴涵了重要的数学思想方法.单纯的死记硬背不是好的学习方法,理解比记忆重要,能力比知识的本身重要.我把本节课的教学模式设计为通过实验探究、对比分析、大胆猜想、证实猜想,从而逐步获得新知,让学生体验数学学习的乐趣,感悟数学研究的一般方法.。