概率论与数理统计实验报告

概率论与数理统计上机实验报告实验一【实验目的】熟练掌握 MATLAB 软件的关于概率分布作图的基本操作会进行常用的概率密度函数和分布函数的作图绘画出分布律图形【实验要求】掌握 MATLAB 的画图命令 plot掌握常见分布的概率密度图像和分布函数图像的画法【实验容】2 、设X : U (−1,1)（1 ）求概率密度在 0 ，0.2 ，0.4 ，0.6 ，0.8，1 ，1.2 的函数值；（2 ）产生 18 个随机数（3 行 6 列）（3 ）又已知分布函数F ( x) = 0.45 ，求x（4 ）画出X 的分布密度和分布函数图形。

【实验方案】熟练运用基本的MATLAB指令【设计程序和结果】1.计算函数值Fx=unifcdf(0, -1,1)Fx=unifcdf(0.2, -1,1)Fx=unifcdf(0.4, -1,1)Fx=unifcdf(0.6, -1,1)Fx=unifcdf(0.8, -1,1)Fx=unifcdf(1.0, -1,1)Fx=unifcdf(1.2, -1,1)结果Fx =0.5000Fx =0.6000Fx =0.7000Fx =0.8000Fx =0.9000Fx =1Fx =12.产生随机数程序：X=unifrnd(-1,1,3,6)结果：X =0.6294 0.8268 -0.4430 0.9298 0.9143 -0.7162 0.8116 0.2647 0.0938 -0.6848 -0.0292 -0.1565 -0.7460 -0.8049 0.9150 0.9412 0.6006 0.83153.求x程序：x=unifinv(0.45, -1,1)结果：x =-0.10004.画图程序：x=-1:0.1:1;px=unifpdf(x, -1,1);fx=unifcdf(x, -1,1);plot(x,px,'+b');hold on;plot(x,fx,'*r');legend('均匀分布函数','均匀分布密度');结果：【小结】运用基本的MATLAB指令可以方便的解决概率论中的相关问题，使数学问题得到简化。

温州大学瓯江学院
概率论与数理统计实验报告
实验名称：实验2 圆周率的近似计算——蒲丰投针问题
实验目的：
1.加深理解几何概型的概率的概念和计算方法
2.掌握无理数的近似计算方法
3.了解Excel软件在模拟仿真中的应用
实验要求：
1.掌握Excel自带的随机数发生器产生随机数——（a,b）区间上均匀分布的随机数
2.理解等可能产生区间之内任一个随机数函数命令
3理解条件检测函数命令if
4.理解条件计数函数命令countif
实验内容：
1. 1777年,法国科学家蒲丰(Buffon)提出了投针试验问题.平面上画有等距离
为
(0)
a a>
的一些平行直线,现向此平面任意投掷一根长为
()
b b a
<
的针,取4
a=, 3
b=,试求针与某一平行直线相交的概率，并计算圆周率的近似值.
实验步骤（实验代码）:实验结果及分析、感想等：（将操作中打开的必要窗口界面抓图放到
R:
****************************************
谢翠华阅，2019年10月30日，成绩：90。

温州大学瓯江学院
概率论与数理统计实验报告
实验名称：实验3 随机变量的分布 实验目的：
1.加深理解随机变量的概率密度和分布函数的概念
2.掌握二项分布与泊松分布的近似关系
3.了解Excel 软件在模拟仿真中的应用
实验要求：
1.掌握二项分布计算概率函数binomdist 和泊松分布计算概率函数possion
2.掌握计算正态分布概率密度值和分布函数值的命令函数normdist 以及标准正态分布的计算概率密度值和分布函数值的命令函数norm.s.dist
实验内容：
1.画二项分布与泊松分布的近似关系图
其中二项分布中的参数25,n = 0.52,p = 泊松分布中的参数*13n p λ== 2.画正态分布的概率密度函数图和分布函数图 (1)在同一个坐标系中画出均值为3,3,5-，标准差为2的正态分布概率密度图形；
(2)在同一个坐标系中画出均值为6，标准差为1,2,3的正态分布概率密度图形.
实验步骤（实验代码）:实验结果及分析、感想等：（将操作中打开的必要窗口界面抓图放到
2：
R:
**************************************** 谢翠华阅，2019年10月30日，成绩：90 ****************************************。

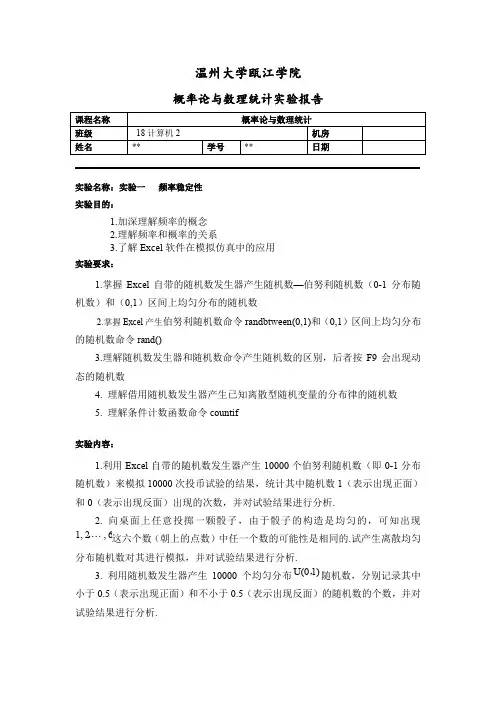
温州大学瓯江学院概率论与数理统计实验报告实验名称：实验一频率稳定性实验目的：1.加深理解频率的概念2.理解频率和概率的关系3.了解Excel软件在模拟仿真中的应用实验要求：1.掌握Excel自带的随机数发生器产生随机数—伯努利随机数（0-1分布随机数）和（0,1）区间上均匀分布的随机数2.掌握Excel产生伯努利随机数命令randbtween(0,1)和（0,1）区间上均匀分布的随机数命令rand()3.理解随机数发生器和随机数命令产生随机数的区别，后者按F9会出现动态的随机数4. 理解借用随机数发生器产生已知离散型随机变量的分布律的随机数5. 理解条件计数函数命令countif实验内容：1.利用Excel自带的随机数发生器产生10000个伯努利随机数（即0-1分布随机数）来模拟10000次投币试验的结果，统计其中随机数1（表示出现正面）和0（表示出现反面）出现的次数，并对试验结果进行分析.2. 向桌面上任意投掷一颗骰子，由于骰子的构造是均匀的，可知出现，这六个数（朝上的点数）中任一个数的可能性是相同的.试产生离散均匀1,2,6分布随机数对其进行模拟，并对试验结果进行分析.3. 利用随机数发生器产生10000个均匀分布U(01)，随机数，分别记录其中小于0.5（表示出现正面）和不小于0.5（表示出现反面）的随机数的个数，并对试验结果进行分析.实验步骤（实验代码）:实验结果及分析、感想等：（将操作中打开的必要窗口界面抓图放到2：评定成绩：R语言实现在R语言中，可以通过rbinom函数产生伯努利随机数，通过table函数来统计频数，具体的代码及运行结果如下：> a=table(rbinom(1000,1,0.5))> a0 1506 494> a/10000 10.506 0.494R语言实现下面用R语言sample函数进行随机抽样，具体代码及运行结果如下：> x=1:6> a=table(sample(x,1000,1/6))> a/10001 2 3 4 5 60.152 0.184 0.177 0.178 0.154 0.155。

概率论与数理统计实验报告实验名称： 区间估计姓名 学号 班级 实验日期一、实验名称：区间估计二、实验目的：1. 会用MATLAB 对一个正态总体的参数进行区间估计；2. 会对两个正态总体的均值差和方差比进行区间估计。

三、实验要求：1. 用MATLAB 查正态分布表、χ2分布表、t 分布表和F 分布表。

2. 利用MATLAB 进行区间估计。

四、实验内容：1. 计算α=0.1, 0.05, 0.025时，标准正态分布的上侧α分位数。

2. 计算α=0.1, 0.05, 0.025，n =5, 10, 15时，χ2(n )的上侧α分位数（注：α与n相应配对，即只需计算2220.10.050.025(5),(10),(15)χχχ的值，下同）。

3. 计算α=0.1, 0.05, 0.025，n =5, 10, 15时， t (n )的上侧α分位数。

4. 计算α=0.1, 0.05, 0.025时， F (8,15)的上侧α分位数； 验证：0.050.95(8,15)1(15,8)F F =；计算概率{}312P X ≤≤。

5. 验证例题6.28、例题6.29、例题6.30、习题6.27、习题6.30。

五、实验任务及结果：任务一：计算α=0.1, 0.05, 0.025时，标准正态分布的上侧α分位数。

源程序：%1-1x = norminv([0.05 0.95],0,1)%1-2y = norminv([0.025 0.975],0,1)%1-3z = norminv([0.0125 0.9875],0,1)结果：x =-1.6449 1.6449y =-1.9600 1.9600z =-2.2414 2.2414结论：α=0.1时的置信区间为[-1.6449，1.6449]，上侧α分位数为1.6449.α=0.05时的置信区间为[-1.9600，1.9600]，上侧α分位数为1.9600.α=0.025时的置信区间为[-2.2414，2.2414]，上侧α分位数为2.2414.任务二：计算α=0.1, 0.05, 0.025，n=5, 10, 15时，χ2(n)的上侧α分位数（注：α与n 相应配对，即只需计算2220.10.050.025(5),(10),(15)χχχ的值，下同）。

课程实习报告课程名称：概率论与数理统计实习题目：概率论与数理统计姓名：系：专业：年级：学号：指导教师：职称：年月日课程实习报告结果评定目录1.实习的目的和任务............................................. - 1 -2.实习要求..................................................... - 1 -3.实习地点..................................................... - 1 -4.主要仪器设备................................................. - 1 -5.实习内容..................................................... - 1 -5.1 MATLAB基础与统计工具箱初步............................. - 1 -5.2 概率分布及应用实例..................................... - 5 -5.3 统计描述及应用实例..................................... - 7 -5.4 区间估计及应用实例..................................... - 9 -5.5 假设检验及应用实例.................................... - 11 -5.6 方差分析及应用实例.................................... - 15 -5.7 回归分析及应用实例.................................... - 17 -5.8 数理统计综合应用实例.................................. - 22 -6.结束语...................................................... - 29 - 参考文献 ...................................................... - 29 -概率论与数理统计1.实习的目的和任务目的：通过课程实习达到让我们能够应用软件解决实际问题。

概率论与数理统计实验报告题目1：n个人中至少有两人生日相同的概率是多少？通过计算机模拟此结果。

问题分析：n个人生日的组合为a=n365，n个人中没有生日相同的组合为b=365*364*......*(365-n+1),则n个人中至少有两个人生日相同的概率为1-b/a。

编程：n=input('请输入总人数n=');a=365^n;m=n-1;b=1;for i=0:1:mb=b*(365-i);endf=1-b/a输出结果：（令n=50）结果分析：当人数为50人时，输出结果为0.9704，此即说明50人中至少有两人生日相同的概率为0.9704。

题目2：设x~N(μ,σ2)，（1）当μ=1.5，σ=0.5时，求p｛1.8<X<2.9｝;（2）当μ=1.5，σ=0.5时，若p{X<x}=0.95,求x;（3）分别绘制μ=1,2,3，σ=0.5时的概率密度函数图形。

问题分析：（1）、（2）题直接调用相应函数即可，（3）题需要调用绘图的相关函数。

编程：x1=[1.8,2.9];x2=-2.5;x3=[0.1,3.3];p1=cdf('Normal',x1,1.5,0.5);p2=cdf('Normal',x2,1.5,0.5);p3=cdf('Normal',x3,1.5,0.5);f1=p1(2)-p1(1)f2=1-p2f3=1-p3(2)+p3(1) %2(1)x=icdf('Normal',0.95,0,1) %2(2)x=[-4:0.05:10];y1=pdf('Normal',x,1,0.5);y2=pdf('Normal',x,2,0.5);y3=pdf('Normal',x,3,0.5);y4=pdf('Normal',x,4,0.5);plot(x,y1,'K-',x,y2,'K--',x,y3,'*',x,y4,'+')输出结果：f1 = 0.2717f2 = 1.0000f3 = 0.0027x = 1.6449（右图为概率密度函数图像）题目3：已知每百份报纸全部卖出可获利14元，卖不出去将赔8元，设报纸的需求量的分布律为试确定报纸的最佳购进量。

概率论与数理统计实验报告一、实验目的1.学会用matlab求密度函数与分布函数2.熟悉matlab中用于描述性统计的基本操作与命令3.学会matlab进行参数估计与假设检验的基本命令与操作二、实验步骤与结果概率论部分：实验名称：各种分布的密度函数与分布函数实验内容：1.选择三种常见随机变量的分布，计算它们的方差与期望<参数自己设定）。

2.向空中抛硬币100次，落下为正面的概率为0.5,。

记正面向上的次数为x，（1）计算x=45和x<45的概率，（2）给出随机数x的概率累积分布图像和概率密度图像。

3.比较t(10>分布和标准正态分布的图像<要求写出程序并作图）。

程序：1.计算三种随机变量分布的方差与期望[m0,v0]=binostat(10,0.3> %二项分布，取n=10,p=0.3[m1,v1]=poisstat(5> %泊松分布，取lambda=5[m2,v2]=normstat(1,0.12> %正态分布，取u=1,sigma=0.12计算结果：m0 =3 v0 =2.1000m1 =5 v1 =5m2 =1 v2 =0.01442.计算x=45和x<45的概率，并绘图Px=binopdf(45,100,0.5> %x=45的概率Fx=binocdf(45,100,0.5> %x<45的概率x=1:100。

p1=binopdf(x,100,0.5>。

p2=binocdf(x,100,0.5>。

subplot(2,1,1>plot(x,p1>title('概率密度图像'>subplot(2,1,2>plot(x,p2>title('概率累积分布图像'>结果：Px =0.0485 Fx =0.18413.t(10>分布与标准正态分布的图像subplot(2,1,1>ezplot('1/sqrt(2*pi>*exp(-1/2*x^2>',[-6,6]>title('标准正态分布概率密度曲线图'>subplot(2,1,2>ezplot('gamma((10+1>/2>/(sqrt(10*pi>*gamma(10/2>>*(1+x^2/10>^(-(10+1>/2>',[-6,6]>。

《概率论与数理统计》实验报告学生姓名学生班级学生学号指导教师学年学期实验报告实验内容实验过程（实验操作步骤）实验结果1 .某厂生产的化纤强度X 〜N( ,0.852)，现抽取一个容量为n 25的样本，测定其强度，得样本均值X 2.25，试求这批化纤平均强度的置信水平为0.95的置信区间. 第1步：打开【单个正太总体均值Z估计活动表】。

第2步：在单元格【B3】中输入0.95，在单元格【B4】中输入25,在单元格【B5】中输入2.25 ,显示结果。

单YE盍总臣均值出石计;騙洙由此可得，这批化纤平均强度的置信水平为0.95的置信区区间为(1.92 , 2.58).2 .已知某种材料的抗压2强度X ~ N（,），现随机抽取10个试件进行抗压试验，测得数据如下：482，493, 457, 471, 510，446， 435, 418, 394， 469 求平均抗压强度的置信水平为 0.95的置信区间；2（2）求的置信水平为0.95的置信区间. 第1步：打开【单个正太总体均值t估计活动表】•第2步：在D列输入原始数据.第3步：点击【工具（T）】-选择【数据分析（D）】一选择【描述统计】一点击【确定】按钮一在【描述统计】对话框输入相关内容—点击【确定】按钮，得到F列与G列结果。

第4步：在单元格【B3】中输入0.95，在单元格【B4】中输入10, 在【B5】中引用G3,在【B6】中引用G7,显示结果。

单个正击豆悴旳毡文洁id汚加置馆水平0.95禅本容呈10禅本均疽4E7. 5捽本掠性差35. 217b??68彳就误差11. 13677591I分应麹（軍）L. 333112^33十命惊數（双》 2.262157163单侧直订下限d37. 0S5C32至厕宣世丄限^77.^14563区可估计估i 下陨-132. 3063?26估计上限4S 2. 6^3137449?■J&7平均45T, 5裁上上椎代差11.丄3閃辭土51（1中也戲-I-.-446刪倍祈准年35.517^77^3H5方差124OLZT77YBjy^蛀度-0.僦希仙7・菟勺克飾¥04&9帽备眞坤11639Q总人值510㈣6LQM y J1ti)顼•£_唄w -由此可得，平均抗压强度的置信水平为0.95的置信区间（432.31 , 482.69）草不正蛊盘悴方茎卡方诂计^动B却計:平0.能畔多Fir1Q45T. 5祥車•方差1240. 2?7?78卡方下分G激 3. 325L12843卡方上分位厳f单了卡方下5K触（股）卡方上沁憨（敢）16. 91897762. 7GD3E9E19-022T67BC59. TCZOSSV二1“芒K7用匡is■估计3357, 02393?咕计EFU5B€. 7«S2S3'舌H丄哽4133.56324由此可得，2的置信水平为0.95的置信区间为（586.80 , 4133.66）3 .用一个仪表测量某一物理量9次，得样本均值x 56.32，样本标准差s 0.22.(1)测量标准差的大小反映了仪表的精度，试求的置信水平为 0.95 的置信区间；(2)求该物理量真值的置信水平为0.99的置信区间.(1)第1步：打开【单个正太总体方差卡方分布】第2步：在单元格【B3】中输入0.95 ,在单元格【B5】中输入56.32 ,在单元格【B6】中输入0.0484 ,显示结果。

概率论与数理统计实验报告概率论与数理统计实验报告引言：概率论与数理统计是数学的两个重要分支，它们在现代科学研究和实际应用中起着重要的作用。

本次实验旨在通过实际操作，加深对概率论与数理统计的理解，并探索其在实际问题中的应用。

实验一：掷硬币实验实验目的：通过掷硬币实验，验证硬币正反面出现的概率是否为1/2。

实验步骤：1. 准备一枚硬币，标记正反面。

2. 进行100次连续掷硬币实验。

3. 记录每次实验中正面朝上的次数。

实验结果与分析：经过100次掷硬币实验，记录到正面朝上的次数为47次。

根据概率论的知识，理论上硬币正反面出现的概率应为1/2。

然而，实验结果显示正面朝上的次数并未达到理论值。

这表明在实际操作中，概率与理论可能存在一定的差异。

实验二：骰子实验实验目的：通过骰子实验，验证骰子的点数分布是否符合均匀分布。

实验步骤：1. 准备一个六面骰子。

2. 进行100次连续投掷骰子实验。

3. 记录每次实验中骰子的点数。

实验结果与分析：经过100次投掷骰子实验，记录到骰子点数的分布如下：1出现了17次；2出现了14次；3出现了20次；4出现了19次；5出现了16次；6出现了14次。

根据概率论的知识，理论上骰子的点数分布应符合均匀分布，即每个点数出现的概率相等。

然而，实验结果显示骰子点数的分布并未完全符合均匀分布。

这可能是由于实际操作的不确定性导致的结果差异。

实验三：正态分布实验实验目的：通过测量人体身高数据，验证人体身高是否符合正态分布。

实验步骤：1. 随机选择一定数量的被试者。

2. 测量每个被试者的身高。

3. 统计并绘制身高数据的频率分布直方图。

实验结果与分析：通过测量100名被试者的身高数据，统计得到的频率分布直方图呈现出典型的钟形曲线，符合正态分布的特征。

这与概率论中对正态分布的描述相吻合。

结论：通过以上实验，我们对概率论与数理统计的一些基本概念和方法有了更深入的了解。

实验结果也向我们展示了概率与理论之间的差异以及实际操作的不确定性。

目录1.实习的目的和任务 (1)2.实习要求 (1)3.实习地点 (1)4.主要仪器设备 (1)5.实习内容 (1)5.1MATLAB基础与统计工具箱初步 (1)5.2概率分布及其应用实例 (3)5.3统计描述及应用实例 (9)5.4区间估计及应用实例 (12)5.5假设检验及应用实例 (13)5.6方差分析及应用实例 (15)5.7回归分析及应用实例 (187)5.8数理统计综合应用实例 (199)6.结束语 (233)7. 参考文献 (24)概率论与数理统计1.实习的目的和任务目的：通过课程实习达到能够熟练使用matlab数学软件，并用该软件解决实际问题。

任务：通过具体的案例描述，利用matlab软件来计算问题的结果，作出图形图象，并分析问题的结论。

2.实习要求要求：能够从案例的自然语言描述中，抽象出其中的数学模型，能够熟练应用所学的概率论与数理统计知识，能够熟练使用matlab软件。

3.实习地点：数学实验室4.主要仪器设备（实验用的软硬件环境）计算机、Microsoft Windows XP、Matlab 7.05.实习内容5.1 MATLAB基础与统计工具箱初步5.1.1目的：通过对MATLAB工作环境的操作，达到了解MATLAB的统计工具箱目的。

5.1.2任务：学会安装MATLAB软件，能进行简单的MATLAB编程，学会用MATLAB绘制简单的函数图像或检验5.1.3预期结果：样本数据在图中用“*”表示，如果数据来自于正态分布，则图形显示为直线，而其它分布在图中则会产生弯曲5.1.4：程序代码：在Matlab编辑器中输入如下:x=normrnd(10.05,0.36); (来自正态分布的数据)x=normrnd(8,12,60,2); (非来自正态分布的数据)normplot(x)得到图像如图5.1.1图5.1.1上图中直线部分由正态分布数据产生，非正态分布数据所产生的则为曲线5.1.5实习日记：实习时间：2008年6月10日星期二今天是初次接触matlab。

交通大学实验报告_______________________________________________________________________________ 课程：概率论与数理统计应用实验名称：概率论在实验中的应用实验日期：2021 年12 月15 日系别：电信专业班级：电信少41XX：星辰学号：2120406102_____________________________________________________________________一、实验目的：1. 了解matlab 在实现数学问题时如何应用；2. 加强对matlab 的操作能力；3. 对实际问题在概率论中的应用的理解有所加深；4. 将实际问题进展模拟，提高数学建模能力。

二、实验容：本次试验将解决下面4 个问题：1. 二项分布的泊松分布与正态分布的逼近；2. 正态分布的数值计算；3. 通过计算机模拟已有分布律进展模拟实验；4. 进展蒲丰投针实验模拟。

三、实验问题分析、解决与思考：1.二项分布的泊松分布与正态分布的逼近设X ~ B(n，p) ，其中np=21) 对n=101,…,104,讨论用泊松分布逼近二项分布的误差。

画处逼近的图形2) 对n=101,…,104, 计算)505(≤<X P ，)9020(≤<X P1〕用二项分布计算2〕用泊松分布计算3〕用正态分布计算比拟用泊松分布逼近与正态分布逼近二项分布的优劣。

解：〔1〕x = -10:0.1:10;y1 = binopdf(x,10,2/10); %此处仅列出n=10时的二项分布语句y2 = poisspdf(x,2); %泊松分布语句plot(x,y1,'r') %做出二项分布图像hold onplot(x,y2,'b') %做出泊松分布图像title('泊松分布逼近二项分布图像')(图中红线为二项分布，蓝线为泊松分布)n=10，很明显地看出拟合效果不太好，红线与蓝线没有完全重合：n=100，放大之后可以看出还是有一局部没有很好地拟合〔后为局部图〕：n=1000，仅仅只有一局部的拟合程度没有很完美〔后为局部图〕：n=10000可以看出，当n ≥100时拟合程度较好。