工程力学精品课程梁的应力及强度设计.ppt
- 格式:ppt
- 大小:807.50 KB
- 文档页数:32

《梁应力强度计算》课件一、梁的基本概念1.1 梁的定义梁是一种受弯和/或受剪的受力构件,常用于桥梁、建筑、机器结构等工程中。
1.2 梁的分类(1)按材料分类:钢梁、木梁、混凝土梁等。
(2)按截面形状分类:矩形梁、工字梁、T型梁、I型梁等。
(3)按受力状态分类:简支梁、悬臂梁、连续梁等。
二、梁应力强度计算的基本原理2.1 弹性理论弹性理论是研究弹性体在外力作用下的应力、应变及位移分布的数学理论。
对于梁的应力强度计算,主要应用弹性力学中的平面应变问题和平面应力问题。
2.2 截面应力梁截面上的应力分布不均匀,通常最大应力出现在截面中性轴上,称为截面应力。
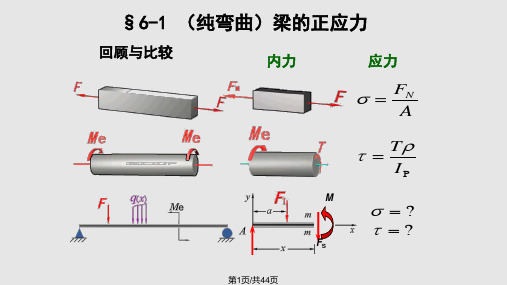
2.3 弯曲正应力弯曲正应力是梁截面上与中性轴垂直的应力,其计算公式为:σ= M·y / I,其中M为弯矩,y为截面上的点到中性轴的距离,I为截面的惯性矩。
2.4 剪切应力剪切应力是梁截面上与中性轴平行的应力,其计算公式为:τ= V·x / A,其中V为剪力,x为截面上的点到中性轴的距离,A为截面的面积。
三、梁应力强度计算的方法3.1 静力法静力法是通过对梁受力的分析,确定各部分的受力情况,根据力的平衡条件求解应力。
适用于简单梁结构。
3.2 弹性解析法弹性解析法是利用弹性力学的公式,通过计算梁的弯曲正应力和剪切应力,判断梁的应力强度。
适用于求解复杂梁结构的应力强度。
3.3 有限元法有限元法是利用计算机模拟梁的结构,将梁划分为若干个小的单元,通过对每个单元的应力分析,求解整个梁的应力强度。
适用于求解大型复杂梁结构的应力强度。
四、梁应力强度计算实例4.1 简支梁受集中载荷假设一根简支梁,跨度为L,截面惯性矩为I,截面面积为A,受集中载荷P作用。
求解梁的最大弯曲正应力和剪切应力。
(1)计算弯矩M:M = P·L / 2。
(2)计算截面应力σ:σ= M·y / I。
(3)计算剪切应力τ:τ= V·x / A,其中V为剪力,x为截面上的点到中性轴的距离。





《梁的应力强度计算》课件一、梁的概述1.梁的定义梁是一种受弯和剪力作用的横向受力构件,广泛应用于建筑、桥梁、机械等领域。
2.梁的材料梁的材料主要有钢梁和钢筋混凝土梁两种。
3.梁的分类根据截面形状,梁可以分为工字梁、T型梁、I型梁等;根据受力状态,梁可以分为简支梁、悬臂梁、连续梁等。
二、梁的应力计算1.基本概念(1)应力:单位面积上的内力,用σ表示,单位为Pa(帕斯卡)。
(2)应变:物体在受力作用下产生的形变与原长的比值,用ε表示。
(3)泊松比:材料在受力作用下横向应变与纵向应变的比值,用ν表示。
2.梁的应力分布(1)简支梁:在梁的截面上,剪应力分布均匀,正应力分布按三角形分布。
(2)悬臂梁:在梁的悬臂端截面,剪应力为零,正应力按二次曲线分布。
(3)连续梁:在梁的连续跨中截面,剪应力分布均匀,正应力分布按三角形分布。
3.梁的应力计算公式(1)简支梁:剪应力τ=V/I正应力σ=My/I其中,V为梁的剪力,M为梁的弯矩,I为梁的截面惯性矩,y为截面上距离中性轴的距离。
(2)悬臂梁:剪应力τ=0正应力σ=Ml/(2I)其中,l为悬臂梁的长度。
(3)连续梁:剪应力τ=V/I正应力σ=My/I其中,V为梁的剪力,M为梁的弯矩,I为梁的截面惯性矩,y为截面上距离中性轴的距离。
4.梁的强度校核(1)剪切强度校核:τ≤τ_max(2)弯曲强度校核:σ≤σ_max其中,τ_max为材料的剪切强度,σ_max为材料的弯曲强度。
三、梁的变形计算1.基本概念(1)挠度:梁在受力作用下产生的垂直于加载力的线位移。
(2)曲率:梁在受力作用下的弯曲程度,用κ表示。
2.梁的变形计算公式(1)简支梁:挠度f=VL^3/(3EI)其中,V为梁的剪力,L为梁的长度,E为材料的弹性模量,I为梁的截面惯性矩。
(2)悬臂梁:挠度f=VL^3/(3EI)其中,V为梁的剪力,L为悬臂梁的长度,E为材料的弹性模量,I 为梁的截面惯性矩。
(3)连续梁:挠度f=VL^3/(3EI)其中,V为梁的剪力,L为梁的长度,E为材料的弹性模量,I为梁的截面惯性矩。