当前位置：文档之家 › 第十三章结构的极限荷载(精)

第十三章结构的极限荷载(精)

  • 格式：doc
  • 大小：208.00 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

结构力学结构的极限荷载

结构力学结构的极限荷载

P
C
B
M u 5Pl / 32 Pl / 4
将P 代入，得
A
5Pl / 32
P
C
B
5 16 M u M u l Pl / 4 32 3l
P 2M u / 3l Pu P P 6 M u / l
P l / 4
逐渐加载法（增量法）
从受力情况，可判断出塑性铰发生的位置应为A、C。利用极限状态的 Pu 平衡可直接求出极限荷载。 Mu A B 1 l C Mu MA 0 RB ( Pu M u ) l 2 2 RB P l Pu l M u A MC 0 M u RB B 2 4 2 C
Ms s M A ydA A ydAe A s ydA p [3 ( )2 ] 2 Ms s M ——弯矩与曲率关系(非线性关系) M [3 ( )2 ] 或 s 3 2 2 Ms
e p
塑性极限状态： 截面上各点应力均达到屈服 s
§9-4
单跨超静定梁的极限荷载
超静定梁有多余约束，出现一个塑性铰后仍是几何不变体系。 A 截面先出现塑性铰，这时 M A 3Pl / 16 M u
A
P
C
B
P 16 M u / 3l
再增加荷载 l/2
3Pl / 16
A
l/2
M C 5Pl / 32 Pl / 4
令 MC Mu
只能出现一个塑性铰，所以
9M u Pu l
2 Pl 9
讨论： M C Pl / 9 1 Pl Mu Mu 9 Mu

M D 2 Pl / 9 1 Pl Mu 4M u 18 M u

结构力学极限荷载PPT课件

结构力学极限荷载PPT课件

i 1
上式中，n是塑性铰数目。
取任一可接受荷载 FP，相应的弯矩图称为 M 图。令
此荷载及内力在上述机构位移上作虚功，虚功方程为：
由实验可知理想刚塑性材料模型能较为准确反映结构极限状态的变形。
第9页/共63页
理想弹性状态下的变形（弹性变形）
强梁弱柱
理想刚塑性状态下的变形（塑性变形）
第10页/共63页
极限荷载
塑性铰
弯矩图
极限弯矩（P266）
杆件截面所能承受的最大弯矩。
塑性铰（P267）
当截面弯矩达到极限弯矩时，两个无限靠近的相邻截面可产生有限的相 对转角，产生局部弯曲变形，这种情况与带铰的截面相似，称为塑性铰。
对称截面的形心轴 与等面积轴重合， 皆为对称中心线。
矩形截面：
1.5
Mu Wu
M s Ws
圆形截面：
16 3
薄腹工字截面： 1.1
M
M
M
弹塑性变形发展阶段
Mu Ms
M s 屈服弯矩 M u 极限弯矩
弯矩与转角的关系曲线
第17页/共63页
弯矩M与曲率r的关系曲线例
h b
h strain
例 求单跨梁的极限荷载,截面极限弯矩为Mu（P269）
1）静力法(作弯矩图)：
FP
解： 结构在A、C截面出现塑性铰。 A
l/2 C
l/2
B
FPu
6M u l
Mu
FP
A
C
B
Mu
极限状态弯矩图
第29页/共63页
2）虚功法(作破坏机构图)
FP
红线为变形后的杆件，兰点为塑性铰
A
C
Mu
Mu Wu s

▲ 结构的极限荷载小结

▲ 结构的极限荷载小结

3.超静定结构极限荷载计算的特点 （1）先判断出超静定梁的破坏机构，即可直接利用机构的平衡 条件求FPu，不必考虑弹塑性变形过程。 （2）只需考虑平衡条件，不需考虑变形协调条件。因而计算比 弹性计算简单。 （3）超静定结构极限荷载，不受温度改变、支座移动等因素的 影响。（按最终的破坏机构计算，温度改变、支座移动等因素不再
2）第二跨破坏
ql q 1.5ql
ql ql l 17.6 1.2Mu 1.2Mu Mu 2 q2 2 Mu 2 2 2 l 3）第三跨破坏 q ql 1.5ql θ
1.2Mu θ M Δ u
θ
1.2Mu
1.2Mu
3ql 3ql 3l 1.2M u 2.4M u 2M u 2 2 2 4 6.4 M u 7.6Mu 8 Mu q3 2 6.756 2 破坏荷载为： qu 9 l l l2 （第一跨）
l
2.4Mu
ql 2 4
1.2Mu
1.2Mu
Mu
Mu
2Mu
ql 2 4
1.2Mu
ql 2 8
1.2Mu
9ql 2 16
2.4Mu
Mu
Mu
2Mu
第一跨单独破坏时： 第二跨单独破坏时： 第三跨单独破坏时：
q1l 2 M u 0.6M u 4
6.4M u q1 l2
17.6M u q2l 2 M u 1.2M u q2 8 l2 9q3l 2 6.76M u 2M u 1.8M u q3 16 l2
6 Mu FPu l
[例2] 图示各跨等截面连续梁，第一、二跨正极限弯矩为Mu， 第三跨正极限弯矩为2Mu，各跨负极限弯矩为正极限弯 矩的1.2倍，求qu 。

结构的极限荷载(13)

结构的极限荷载(13)
u
2
u
u
l
例12-1 试求图a所示两端固定的等截面梁的极限荷载。 解：此梁出现三个塑性铰即进入极限状态。 塑性铰出现在最大负弯矩A、B截面及 最大正弯矩C截面。 静力法：作极限状态弯矩图如图b。 由平衡条件有
Fu ab Mu Mu l
得极限荷载
Fu
2l Mu ab 2l Mu ab
机动法：作出机构的虚位移图如图c。
求得极限荷载为
Mu Fu l
§12-3 单跨超静定梁的极限荷载
超静定梁：具有多余联系，只有出现足够多的塑性铰，才能 使其成为破坏机构。 图(a)所示等截面梁，梁在弹性阶 段的弯矩图如图b，截面A的弯矩最大。 荷载增大到一定值时，A先出现塑 性铰。如图c，A端弯矩为Mu，变成静 定的问题。此时梁未破坏，承载能力未 达到极限。 荷载继续增大，跨中截面C的弯矩 达到Mu，C截面变成塑性铰。如图d， 此时梁成为几何可变的机构，达到极限 状态。
可破坏荷载：满足机构条件和平衡条件的荷载，用F +表示。 （不一定满足内力局限条件） 可接受荷载：满足内力局限条件和平衡条件的荷载，用F -表示。 （不一定满足机构条件） 1、极小定理：极限荷载是所有可破坏荷载中的极小者。 2、极大定理：极限荷载是所有可接受荷载中的极大者。 3、惟一性定理：极限荷载只有一个确定值。若某荷载既是可破 坏荷载，又是可接受荷载，则该荷载即为极限 荷载。
0.8Fa M u 2 M u
3.75 M u F a
第2跨机构如图c。
F 2a a M u M u 2 M u a 2 F 4M u a
第3跨机构如图d。
Fa F 2a M u 3M u 3
F
3.33M u a

结构力学 结构的极限荷载与弹性稳定图文

结构力学 结构的极限荷载与弹性稳定图文

A
B
D
C
l/3
l/3
l/3
解: AB段极限弯矩为 M u ，BC段极限弯矩为Mu。
塑性铰的可能位置：A、B、D。
A l/3
B
Mu B
l/3
FPu
DC Mu
D
l/3
§11-4 超静定结构的极限荷载计算
1）B、D截面出现塑性
FPu
铰，由弯矩图可知，只 有当 Mu 3Mu 时，此破
A l/3
B
Mu B
分析：(1) 图(a)表示截面处于弹性阶段。
该阶段的最大应力发生在截面最外纤维处，
称为屈服极限y，此时的弯矩Ms称为弹性 s a)
极限弯矩，或称为屈服弯矩。即：
s
MS
bh2 6
s
y0
（2）图(b）—截面处于弹塑性阶段，
y0
截面外边缘处成为塑性区，应力为常数， s b)
§11-2 基本概念
=s；在截面内部(|y|y0)则仍为弹性区，称为弹性
2
C l
2 4
B Mu
由We=Wi，可得 所以有1 4q源自l 24M uqu
16M l2
u
三次超静定 三个塑性铰
§11-4 超静定结构的极限荷载计算
例11-4-3 已知梁截面极限弯矩为Mu ，求极限荷载 。 解:塑性铰位置：A截面及梁上最大弯矩截面C。
q
qu
A
l
BA
Mu A
Mu C C B
l-x
x
例11-1-1 设有矩形截面简支梁在跨中承受集中荷载 作用(图a)，试求极限荷载FPu 。
解：由M图知跨中截面 弯矩最大，在极限荷载作用 下，塑性铰将在跨中截面形 成，弯矩达极限值Mu(图b)。

结构的极限荷载

结构的极限荷载
相邻跨联合破坏 不会出现
例：求图示连续梁的极限荷载。各跨分别是等截面的,AB、BC跨的极限 求图示连续梁的极限荷载。各跨分别是等截面的,AB、BC跨的极限 ,AB 弯矩为M CD跨的极限弯矩为 跨的极限弯矩为3 弯矩为 u ，CD跨的极限弯矩为3Mu 。 0.8P 解：先分别求出各跨独自破坏时的 q=P/ =P/a =P/ P P 破坏荷载. 破坏荷载. A D B C E F AB跨破坏时 （1）AB跨破坏时 a
（3）CD跨破坏时 CD跨破坏时
0.8P
q=P/ =P/a =P/
P
δθ
2δθ
P
P+ × aδθ + P+ ⋅ 2aδθ = Mu ⋅ δθ + 3Mu ⋅ 3δθ
2δθ
3δθ
P + = 3.33M u / a P = 3.33Mu / a u
§ 16-４ 比例加载时判定极限荷载的一般定理 161616-4-1 几个基本概念
求图示变截面梁的极限荷载.已知AB段的极限弯矩为2 AB段的极限弯矩为 例:求图示变截面梁的极限荷载.已知AB段的极限弯矩为2Mu,BC 段为M 段为 u 。 解:确定塑性铰的位置 确定塑性铰的位置 P A B C 1.若 出现塑性铰， 1.若B、D出现塑性铰，则B、D两截面的弯 D l/3 l/3 l/3 矩为M 这种情况不会出现。 矩为Mu，M A = 3M u 这种情况不会出现。 2.若A出现塑性铰，再加荷载时，B截面 2.若 出现塑性铰，再加荷载时， Mu 3M u 弯矩减少D截面弯矩增加， 弯矩减少D截面弯矩增加，故另一塑性 铰出现于D截面。 铰出现于D截面。 Mu
A = σ y × × 0.0633 = 27.36kN.m 2
20mm

结构的极限荷载和例题讲解

结构的极限荷载和例题讲解

简化计算： 假设材料为理想弹塑性材料，其应力～应变关系下图所示。
§12-2 极限弯矩和塑性铰 破坏机构 静定梁的计算
一、弹塑性阶段工作情况
理想弹塑性材料T形截面梁处于纯弯曲状态时
弹性状态：
图b：截面处于弹性阶段，σ<σs （屈服极限） 图c：截面最外边缘处σ＝σs （达到屈服极限） 屈服弯矩（弹性极限弯矩）MS = Wσs（W：弯曲截面系数） 图d：截面处于弹塑性阶段。 靠外部分形成塑性区，其应力为常数，σ＝σs ， 靠内部分仍为弹性区，称弹性核，其应力直线分布 图e：截面全部达到塑性——极限情形， 这时的弯矩是该截面所能承受的最大弯矩 ——极限弯矩，以Mu 表示。
等截面超静定梁（图a） （各截面Mu相同） 弹性——弹塑性阶段——极限状态过程:
（1）弹性阶段弯矩图：P≤Ps （2首）先弹在塑A性端阶形段成M并图扩：大荷，载然超后过CP截s，面塑也性形区成
塑性性铰区。。A端首先达到Mu并出现第一个塑
（3）极限状态M图：荷载再增加，A端弯矩 增量为零，当荷载增加到使跨中截面的弯矩达 到Mu时，在该截面形成第二个塑性铰，于是梁 即变为机构，而梁的承载力即达到极限值。此 时的荷载称为极限荷载Pu——极限状态（e）。
破坏机构——极限状态： 结构出现若干塑性铰而成为几何可变或瞬变体系时 ——结构丧失承载能力
三、静定梁的计算
静定梁由于没有多余联系，因此，出现一个塑性铰时，即 成为破坏机构。
对于等截面梁，在弯矩绝对值最大截面处达到极限弯矩， 该截面形成塑性铰。
由塑性铰处的弯矩等于极限弯矩和平衡条件，就可求出静 定梁的极限荷载。
结构的极限荷载和例题 讲解
§12－1 概述
结构设计方法：
1、容许应力法（弹性分析法）：

结构力学课件结构的极限荷载

结构力学课件结构的极限荷载

中性轴附近处于弹性状态，处于弹性的部分称为弹性核。
（3）塑性流动阶段
Mu
bh2 4
s
—— 塑性极限弯矩(简称为极限弯矩)
M u 1.5 —— 截面形状系数。圆形截面1.7，工字形
Ms
截面1.10-1.17，圆环截面1.27-1.40。
※塑性铰
当截面弯矩达到极限弯矩,这时的曲率记作 κ。u
s 3 2 Mu 0
（2）只需考虑平衡条件，无需考虑变形协调条件，比弹 性计算简单；
（3）超静定结构的极限荷载，不受温度变化、支座移动 等因素的影响。
例：求图示变截面梁的极限荷载。已知 AB 段的极限弯矩 为2Mu，BC 段为Mu 。
A
BP
2Mu
C
A
BD
3Mu
C
A
D
l/3 l/3 l/3
Mu
Mu D
C
B Mu
2Mu A
0.5Mu D
C
B
Mu
Pu min P1 , P2 , P3
7.5M u l
4Mu
P l 3 l
2l 3
1 3
2M
u
4M u ,
P1
21M u l
P l 3 l
2l 3
1 3
3M
u
Mu,
P2
9M u l
P l 3 l
2l 3
1 3 2M u
Mu,
P3
7.5M u l
例：求图示变截面梁的极限荷载。已知 AB 段的极限弯矩 为2Mu，BC 段为Mu 。
3. 连续梁的极限荷载
超静定结构有多余约束，必须出现足够多的塑性铰 才能成为机构，从而丧失承载能力。

第13章结构的极限荷载

第13章结构的极限荷载

塑性设计方法是为了消除弹性设计方法中的缺陷而 发展起来的.所谓的塑性设计是指首先 塑性设计是指首先确定结构破坏时 发展起来的.所谓的塑性设计是指首先确定结构破坏时 所能够承受的荷载即极限荷载 然后将极限荷载除以安 极限荷载, 所能够承受的荷载即极限荷载,然后将极限荷载除以安 全系数得到容许荷载, 全系数得到容许荷载,依次为依据来进行的结构设计称 为塑性设计. 为塑性设计.塑性设计的条件为
M M
随着弯矩M的不断增大, 随着弯矩 的不断增大,梁将 的不断增大 经历弹性阶段 弹塑性阶段→完全塑 弹性阶段→弹塑性阶段 经历弹性阶段 弹塑性阶段 完全塑 阶段的全过程.实验表明, 性阶段的全过程.实验表明,无论在 哪一个阶段,梁弯曲变形时的平面假 哪一个阶段,梁弯曲变形时的平面假 设都是成立的. 设都是成立的. (a) 弹性阶段
结构力学
第13章 结构的极限荷载
主要内容
1 基本概念 2 静定梁的弹塑性分析 3 超静定梁的极限荷载 4 比例加载时判定极限荷载的一般定理
§13.1引言 13.1引言 在以前各章中,主要讨论了结构的弹性设计问题. 在以前各章中,主要讨论了结构的弹性设计问题.在 计算过程中,假设应力~应变曲线是线性关系 应变曲线是线性关系, 计算过程中,假设应力 应变曲线是线性关系,且在荷载 全部卸除后.结构没有残余变形. 全部卸除后.结构没有残余变形.所谓的弹性设计是指利 用弹性理论的计算结果, 用弹性理论的计算结果,以许用应力为依据来确定结构的 尺寸或强度验算等, 尺寸或强度验算等,即设计条件为
bh2 M s = Wz σ s = σs 6
σs
弹塑性 阶段
(b) 弹塑性阶段 荷载继续增大,梁就进入了弹塑性阶段, 荷载继续增大,梁就进入了弹塑性阶段,此时靠近 下边缘区域形成了塑性区. 为常数, 上,下边缘区域形成了塑性区.其应力σ=σs为常数,在 截面内部( 为弹性区的高度)仍为弹性区, 截面内部(|y|<y0,y0为弹性区的高度)仍为弹性区,称 弹性核. 为弹性核.弹性区的应力为

结构力学 极限荷载讲解

结构力学 极限荷载讲解
q Байду номын сангаас1
qu 2
Mu Mu
M u Wu s
Mu
Mu
2、不同结构，只要材料、截面积、截面形状相同，塑性弯矩一定相同。
3、材料、截面积、截面形状相同的不同结构，qu不一定相同。
q u1
qu 2
Mu1
M u1 M u 2 qu1 qu 2
Mu2 Mu2
第15章
四、如何确定单跨梁的极限荷载 1、机理 q
s
y
第15章
3、截面形状系数：极限弯矩与屈服弯矩之比
M u Wu M s Ws

矩 形 截 面 ： 1.5 16 圆形截面： 3 工 字 形 截 面 ： 1.15
4、截面达到极限弯矩时的特点
极限状态时，无论截面形状如何，中性轴两侧的拉压面积相等。依 据这一特点可确定极限弯矩。
D
M u2
B A C
p
D
B
p
机构（一）A C M u2 D
M u2 M u1
M u2
B 情况（1）
M u1
C A B
p
D B
p
C D
机构（二）A
M u2
情况（2）
M u2
p
M u1
M u1
B C A
p
D
机构（三）A
C
M u2
D
B
M u2
不可能出现，为什么？ 情况（3）
第15章
试确定图示单跨梁的极限荷载
第15章
例题2 试用试算法求图示结构的极限荷载。 p 解 法2 ： 1.1 p
A D B E
C
试取机构（ 2） p2 a M u M u 2 Mu a 绘 出 与机 构 （ 2） 相应的 M图 ， p2 3

结构的极限荷载

结构的极限荷载

第11章 结构的极限荷载前面各章所讨论的结构计算均是以线弹性结构为基础的，即限定结构在弹性范围内工作。

当结构的最大应力达到材料的极限应力n σ时，结构将会破坏，故强度条件为[]max nKσσσ=≤ 式中，max σ为结构的最大工作应力；[]σ为材料的许用应力；n σ为材料的极限应力，对于脆性材料为其强度极限b σ，对于塑性材料为其屈服极限s σ；K 为安全系数。

基于这种假定的结构分析称为弹性分析。

从结构强度角度来看，弹性分析具有一定的缺点。

对于塑性材料的结构，尤其是超静定结构，在某一截面的最大应力达到屈服应力，某一局部已进入塑性阶段时，结构并不破坏，还能承受更大的荷载继续工作，因此按弹性分析设计是不够经济合理的。

另外，弹性分析无法考虑材料超过屈服极限以后，结构的这一部分的承载能力。

塑性分析方法就是为了弥补弹性分析的不足而提出和发展起来的。

它充分地考虑了材料的塑性性质，以结构完全丧失承载能力时的极限状态作为结构破坏的标志。

此时的荷载是结构所能承受荷载的极限，称为极限荷载，记为u F 。

结构的强度条件可表示为u F F K≤ 式中F 为结构工作荷载，K 为安全系数。

显然，塑性分析的强度条件比弹性分析更切合实际。

塑性分析方法只适用于延展性较好的塑性材料的结构，对于脆性材料的结构或对变形有较大限制的结构应慎用这种方法。

对结构进行塑性分析时，平衡条件和几何条件与弹性分析时相同，如平截面假设仍然成立，所不同的是物理条件。

为了简化计算，对于所用的材料，常用如图11.1所示的应力—应变曲线。

当应力达到屈服极限以前，材料处于弹性阶段，应力与应变成正比；当应力达到屈服极限s σ时，材料开始进入塑性变形阶段，应力保持不变，应变可无限增加；卸载时，材料恢复弹性但存在残余变形。

凡符合这种应力—应变关系的材料，称为理想弹塑性材料。

实际钢结构一般可视为理想弹塑性材料。

对于钢筋混凝土受弯构件，在混凝土受拉区出现裂缝后，拉力完全由钢筋承受，故也可采用这种简化的应力—应变曲线进行塑性分析。

第12章--结构的极限荷载

第12章--结构的极限荷载

计算静定梁极限荷载的步骤： 确定塑性铰的数量。静定梁出现1 个塑性铰即形成破坏机构； 确定塑性铰的位置。静定梁的塑 性铰总是出现在M/Mu取得最大值的 截面； 利用平衡条件求该截面的弯矩并 令其等于极限弯矩，就可以求得极 限荷载。
14.3 静定梁的极限荷载
破坏机构
Mu
M u0 2
(2
6)
=
14.2 极限弯矩和塑性铰
14.2.1极限弯矩
(1)
弹性阶段，如图(b)所示：
My I
中性轴与形心轴重合。
(2) 弹塑性阶段，如图(c)、(d)、(e)所示：
My
I y
ymax
W y
✓ 弯矩增加到屈服弯矩My后，上边缘开始屈服；
✓ 随着M继续增大，弹性区逐渐缩小，塑性区逐渐扩大；
✓ 在这一过程中，中性轴逐渐偏离形心轴而下移；
qu
M u0 6l 2
(27
11
6
)
8.990
M u0 l2
14.4 超静定梁的极限荷载
14.4.1 单跨超静定梁的极限荷载
梁端部的弯矩绝对值最大，因此最先达到屈服值My。
qy l 2 12
My
qu l 2 8
Mu
Mu
qy
1
2M l2
y
qu
16M u l2
qu 4M u 4
qy 3M y 3
工程中的连续梁大部分都满足 这两条假定。
各跨等截面、荷载方向相同条件下， 破坏机构只能在各跨内独立形成。
可能的破坏机构 单跨独立破坏 相邻跨联合破坏
14.4 超静定梁的极限荷载
12.4.2 连续梁的极限荷载
例14-3 试求图示
连续梁极限荷载(q
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第十三章 结构的极限荷载第一节 概述（先作三个图）1、 材料性质的简化模型：线弹性小变形、弹塑性、全塑性三种概念。

2容许应力法（弹性分析方法）:（1） 假定结构为理想弹性体，线弹性小变形，卸载变形可恢复，应力应变成正比 （2） 结构的最大应力达到材料的极限应力时结构将会破坏 （3） 强度条件：kuσσσ=≤][max（4） 缺点：a 塑性材料的结构，在最大应力到达屈服极限，甚至某一局部已进入塑性阶段时并不破坏b 以个别截面的局部应力来衡量整个结构的承载能力不经济合理c 安全系数k 也不能反映整个结构的强度储备2、 塑性分析方法：（不适用叠加原理）（1） 破坏标志：结构进入塑性阶段并最后丧失承载能力是的极限状态 （2） 极限荷载，结构的极限状态，考虑塑性；结构丧失承载能力，考虑安全系数。

r 0S ≤R（3）强度条件：KP Pu≤3、 理想弹塑性材料：应力应变关系4、 比例加载：荷载一次加于结构，且各荷载按同一比例增加 4、例子1） 一次超静定组合结构，不考虑横梁的弯曲影响和破坏（EI=∞） 2） 比例加载3） 弹性分析（力法）（线弹性小变形）：N AE =0.5P ，N BD =0.98P ，N CD =0.72P4） P 不断增大， N BD 先屈服（拉杆，应力均匀）：0.98P S =A σs ，P S =18.8KN 。

弹性极限状态，弹性极限荷载（卸载后，变形完全恢复）5） P 继续增加：（塑性分析）比例加载，BD 杆相当于一个常力：弹性塑性分两种颜色：P N AE∆=∆，P N CD ∆=∆245.18272.0==∆+s s A P P σ，ΔP=3.46KN ，P j =P s +ΔP=22.28KN 塑性极限荷载增量法：逐渐加载法（结构破坏，极限荷载），弹性极限荷载：线弹性小变形，变形恢复；塑性极限荷载：结构破坏。

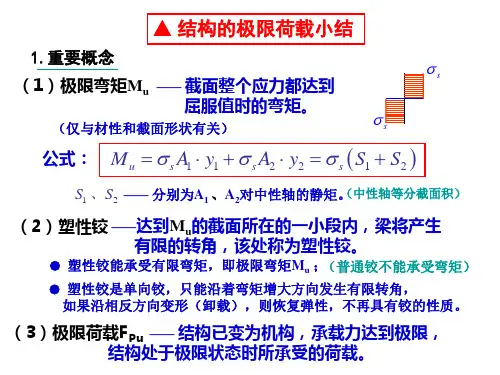
14-2极限弯距和塑性铰、破坏机构、静定梁的计算受拉、压杆件，应力均匀；受弯杆件：理想弹塑性材料，纯受弯，矩形截面梁。

一、矩形截面梁梁（纯弯曲塑性材料的矩形等截面梁，任一截面） 应力、应变、塑性区的分布图（先作三组图）1）弹性阶段弹性极限弯矩，屈服弯曲 σ=E ε，ε=k •y ，k EI ydA M A⋅=⋅=⎰σ，y y bh M σ62= 屈服弯距s s s bh W M σσ62==弹性抗弯截面系数62bh W =2）弹塑性阶段y y s ⋅=σσ，两部分组成。

3）塑性流动阶段s σσ=梁在竖向荷载下轴力为0021=-A A s s σσ2/21A A A ==)(212211S S a A a A M s s s u +=+=σσσ21S S W s += s s u W M σ=塑性极限弯矩：s u bh M σ⋅=4242bh W s =WW M M ss u ==αα=1.5截面形状系数 塑性铰：（1）单向铰一般铰：（2）承受弹性极限弯矩一般横向荷载，不考虑Q 、N 的影响，结论同样适用。

框架梁设计时，弯矩调幅，内力重分布。

二、具有一根对称轴的任意截面的梁 （σl =σy ） 1、静矩：220aA S ⋅=2、塑性截面模量（系数），形心轴、中性轴：W s =2S 03、系数，截面形状系数WW M M ssj ==α，s jW M0⋅=σ矩形 α=1.5 圆形 α=1.70薄壁圆环形 α=1.27—1.4(一般取 1.3) 工字形 α=1.1—1.2(一般取 1.15) 三、静定梁的极限荷载破坏机构：结构出现若干个塑性铰而成为几何可变或瞬变体系时，结构已丧失承载能力，达到了极限状态。

静定梁：只有一个塑性铰， 等截面：塑性铰出现于maxM处4lP M u u =lM P u u 4=变截面梁：塑性铰出现于maxuM M 处或minuM M 处1、平衡法2、虚功原理 结论相同（两个例子）第三节 单跨超静定梁的极限荷载一、单跨超静定梁极限荷载的方法 1）增量法 2）平衡法 3）虚功原理 1、 集中荷载，跨中间（图14-4） 静力法：利用平衡条件确定极限荷载24uu u M l P M -=lM P uu 6=机动法：利用虚功原理（机构沿荷载正方向产生任意微小的虚位移，外力虚功=变形虚功）确定极限荷载θθθ2*2u u u M M lP +=lM P u u 6=2、集中荷载，任意位移跨中 1）极限平衡法；弯矩调整法P j ×θ1×a=M j ×θ1+M j ×θ2+M j (θ1+θ2)=2M j (θ1+θ2)=2M j (1+a/b)θ1=2M j ·l ·θ1/b 2）虚功原理3、均匀分布荷载，两端固定1）弯矩调整法2）虚功原理（均布荷载虚功） 4、一端固定、一端铰支，均布q ： 先求x ，0=dxdM C，x=0.4142l ，M max 不在中间，先定位置。

三点结论：（1） 超静定结构极限荷载的计算无需考虑结构弹塑性变形的发展过程，只需考虑最后的破坏机构，需要确定真实的破坏机构才能求得其极限荷载值；（2） 超静定结构极限荷载的计算只需考虑静力平衡条件，无需考虑变形协调条件 （3） 超静定结构极限荷载不受温度变化、支座移动的影响 龙驭球书，P124。

先画几个图，先写几点结论。

第四节 比例加载时判定极限荷载的一般定理1、多种破坏形式（所有破坏形式中最小破坏荷载）2、荷载参数P j （比例加载）3、结构的极限状态满足如下三个条件： 1） 平衡（瞬时平衡）2） 2）屈服，自身截面的极限弯矩值。

3） 3）机构条件（足够塑性铰）。

（单向机构） 4、三个定理1）上限：P j ≤P k （可破坏）平衡+机构 2）下限：P s ≤P j （极大）平衡+屈服 3）单值定理（只有一个）5、方法：试算法。

比较法（机动法）步骤：列出各种可能的破坏机构，利用弯矩调整法或虚功原理求出各相应的破坏荷载，其中最小值 ⇒ P j 试算法：选一个破坏机构求出可破坏荷载，再验算在该荷载作用下的弯矩分布（结合超静定结构计算）是否满足屈服条件。

满足即P j例13-3，P135。

例题1、龙驭球P129，极小值定理dg/dx=0，x 2-4lx+2l 2=0l l l l l a ac b b x 2222416424222±=⨯-±=-±-=24232222l M q l l x uj -=⇒-=例13-2：两跨连续梁，例13-10a 图三跨连续梁（前面）虚功原理，注意中间跨 例4：P8，杨天祥书， 两种方法比较： 杨天祥P1014-5 计算极限荷载的穷举法和试算法一、 穷举法（机动法）：列出所有可能的各种破坏机构，由平衡条件或虚功原理求出相应的荷载，取其中最小者即为极限荷载二、 试算法：任选一种破坏机构，由平衡条件或虚功原理求出相应的荷载，并作出其弯距图，满足内力局限条件即是；不满足再试。

例14-3 试求图14-7a 所示变截面梁的极限荷载。

（1） 穷举法（3种可能的破坏机构） 机构1：A 、D 处出现塑性铰θθθ3*2*23u u M M lP +=lM P u21=机构2：A 、C 处出现塑性铰θθθ3**232u u M M lP+= l M P u 5.7=机构3：D 、C 处出现塑性铰θθθ2**3u u M M lP +=lM P u 9=取lM P uu5.7=（2） 试算法 机构1：lM P u21=，绘出弯距图如图，C 截面的弯距4M u > M u机构2:lM P u5.7=, 绘出弯距图如图，各截面的弯距均不大于M u14-6连续梁的极限荷载先决条件，每跨都可能局部破坏。

破坏机构的可能形式：1、比例加载；2、每跨内等截面，等材料；3、各跨截面可以不同，材料可以不同。

结合两跨连系梁。

（1） 某一跨出现三个塑性铰或铰支端跨出现两个塑性铰 （2） 相邻各跨联合形成破坏机构（不可能） 结论： 两个例子。

P j·1·3θ1=50×θ1+50θ1×2 ⇒ P j =50KN①② 0.2·P j12=16×70/64 ⇒ P j12=350/4=87.5（不对）θθθθ2707050412⨯+⨯+⨯=⋅⋅l q j260642.04112=⋅⨯j p ⇒ 3.2p j12=260KN③ 70×θ1+90θ2+90(θ1+θ2)=1.5P ·θ1×2+1.5P ·θ2×270×θ1+45θ1+90(θ1+0.5θ1)=3P ·θ1+1.5P ·θ1 70+45+90×1.5=4.5 P j·3 P=55.56KN ，显然P j =50KN弯矩调整法比较简单，两种方法各有优缺点：例14-4 试求图14-9a 所示连续梁的极限荷载。

第一跨机构：θθθ*2*8.0u u M M Pa += aM P u75.3=第二跨机构：θθθθ*2**22u u u M M M a aa P ++= a M P u 4= 第三跨机构：θθθθ3*3*2*u u M M a P Pa +=+ aM P u 33.3=第三跨首先破坏，极限荷载aM P uu 33.3=14-7 刚架的极限荷载1）手算方法（轴、剪力对塑性铰的影响可以忽略不计） 2）矩阵位移法（可视情况介绍）弯矩图轮廓，五个塑性铰的可能位置。

1）梁结构 2）侧移结构 3）组合结构 更多地采用试算法破坏形式：塑性铰可能出现位置：A 、B 、C 、D 、E 点4个塑性铰或一个杆上出现三个塑性铰 一、穷举法机构1：C 、D 、E 处出现塑性铰θθθθ*2*22u u u M M M Pa ++= aM P u 3=机构2：A 、C 、E 、B 处出现塑性铰θθu M a P 45.1*= aM P u67.2=机构3：A 、D 、E 、B 处出现塑性铰θθθθθθu u u u M M M M Pa a P +++=+2*2*225.1*aM P u29.2=机构4：A 、C 、D 、B 处出现塑性铰θθθθθθu u u u M M M M Pa a P +++=+-2*2*225.1* aM P u16=取aM P uu29.2=二、试算法选择机构2，得aM P u67.2=，作M 图u u u u D M M aP M M M 267.242*22>=+-=不满足内力平衡条件 选择机构2，得aM P u29.2=，作M 图u u C u M Pa aP M M M 29.242*222===+-u u C M M M <=42.0 满足内力局限条件，此机构为极限状态极限荷载aM P uu 29.2=。