2017年全国高考文科数学试题及答案-全国卷3
- 格式:doc
- 大小:36.00 KB
- 文档页数:11

2017 年普通高等学校招生全国统一考试文科数学 卷 3注意事项:1.答题前,考生务必将自己的、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动, 用橡皮擦干净后, 再选涂其他答案标号。
回答非选择题时, 将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一项是符合题目要求的。
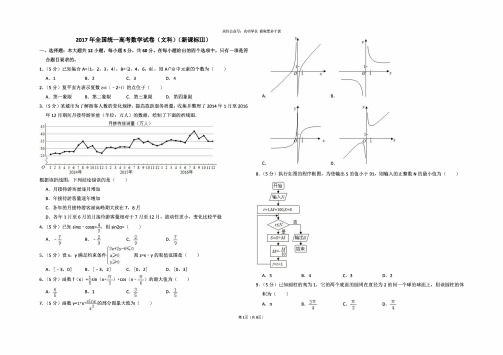
2016年 12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图根据该折线图,下列结论错误的是A .月接待游客逐月增加B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在 7,8 月D .各年 1 月至 6 月的月接待游客量相对于 7月至 12 月,波动性更小,变化比较平稳、选择题:本大题共 12小题,每小题 5 分,60 分。
在每小题给出的四个选项中,只有1.已知集合 A={1,2,3,4} , B={2,4,6,8} ,则 AI B 中元素的个数为2.3.A .1B .2C .D .4复平面表示复数 A .第一象限z i( 2 i) 的点位于 B .第二象限C . 第三象限D .第四象限 某城市为了解游客人数的变化规律,提高旅游服务质量, 收集并整理了 2014 年 1 月至4.已知 sincos434,则 sin2 =3x 2y 605.设x, y满足约束条件x0,则z x y 的取值围是y0A.[-3 ,0]B.[-3 ,2]C.[0 ,2]D.[0 ,3] 6.函数f(x)1 sin(x53)cos(x)的最大值为6631 A.B1C.D.5558.执行右面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A.5B.4C.3D.2 9.已知圆柱的高为1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的体积为A.C.7A.92B.92C.97D.9B.D.10.在正方体 ABCD A 1B 1C 1D 1 中, E 为棱 CD 的中点,则x 1,x 0,1x 则满足 f(x) f (x ) 1的 x 的取值围是 2x ,x 0, 2三、解答题:共 70 分。

–.学习资料收集于网络,仅供参考绝密★启用前2017年普通高等学校招生全国统一考试(新课标Ⅲ)文科数学注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A⋂B中元素的个数为A.1B.2C.3D.42.复平面内表示复数z=i(2+i)的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图根据该折线图,下列结论错误的是A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳44.已知sinα-cosα=,则sin2α=3A.-79C.29D.7x≥0学习资料收集于网络,仅供参考9B.-29⎧3x+2y-6≤0⎪5.设x,y满足约束条件⎨,则z=x-y的取值范围是⎪⎩y≥0A.[–3,0]B.[–3,2]C.[0,2]D.[0,3]1ππ6.函数f(x)=sin(x+)+cos(x−)的最大值为5366A.B.15sin x7.函数y=1+x+的部分图像大致为x2C.35D.15A.B.C.D.8.执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为A.5B.4C.3D.2A . πB . 3π= 1 ,(a >b >0)的左、右顶点分别为 A ,A ,且以线段 A A 为直3D . 12B . 1B b c b c 9.已知圆柱的高为 1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的体积为4 C . π 2 D .π 410.在正方体 ABCD - A B C D 中,E 为棱 CD 的中点,则1 1 1 1A . A E ⊥DC11B . A E ⊥BDC . A E ⊥BC1 1 1D . AE ⊥AC111.已知椭圆 C : x 2 y 2+a 2b 21 2 1 2径的圆与直线 b x - ay + 2ab = 0 相切,则 C 的离心率为A .63B .33C .2312.已知函数 f ( x ) = x 2 - 2 x + a(e x -1 + e - x +1 ) 有唯一零点,则 a =A . -13C .12 D .1二、填空题:本题共 4 小题,每小题 5 分,共 20 分。

2017年普通高等学校招生全国统一考试(新课标Ⅲ)文科数学注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A⋂B中元素的个数为A.1ﻩﻩﻩﻩB.2ﻩﻩﻩC.3 ﻩﻩﻩD.42.复平面内表示复数z=i(–2+i)的点位于A.第一象限ﻩB.第二象限ﻩﻩC.第三象限ﻩD.第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.已知4sin cos3αα-=,则sin2α=A.79-ﻩﻩﻩ B.29-ﻩﻩﻩC.29ﻩﻩD.795.设x,y满足约束条件3260x yxy+-≤⎧⎪≥⎨⎪≥⎩,则z=x-y的取值范围是A.[–3,0]ﻩﻩﻩB.[–3,2]ﻩﻩ C.[0,2] D.[0,3]6.函数f(x)=15sin(x+3π)+cos(x−6π)的最大值为A.65ﻩﻩB.1 ﻩﻩC.35ﻩﻩﻩD.157.函数y=1+x+2sin xx的部分图像大致为A.ﻩB.C.ﻩﻩD.8.执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为A.5 ﻩﻩﻩB.4ﻩﻩﻩ C.3ﻩﻩD.2。

2017年普通高等学校招生全国统一考试(全国Ⅲ)数学(文科)一、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要 求的.(1)【2017年全国Ⅲ,文1,5分】已知集合{}1,2,3,4A =,{}2,4,6,8B =,则A B 中的元素的个数为( )(A )1 (B )2 (C )3 (D )4【答案】B【解析】集合A 和集合B 有共同元素2,4,则{}2,4A B =I 所以元素个数为2,故选B .(2)【2017年全国Ⅲ,文2,5分】复平面内表示复数i(2i)z =-+的点位于( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限【答案】C【解析】化解i(2i)z =-+得22i i 2i 1z =-+=--,所以复数位于第三象限,故选C .(3)【2017年全国Ⅲ,文3,5分】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )(A )月接待游客量逐月增加 (B )年接待游客量逐年增加(C )各年的月接待游客量高峰期大致在7,8月(D )各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳【答案】A【解析】由折线图可知,每年月接待游客量从8月份后存在下降趋势,故选A .(4)【2017年全国Ⅲ,文4,5分】已知4sin cos ,3αα-=,则sin 2α=( ) (A )79- (B )29- (C )29(D )79 【答案】A【解析】()2167sin cos 12sin cos 1sin 2,sin 299αααααα-=-=-=∴=-,故选A . (5)【2017年全国Ⅲ,文5,5分】设,x y 满足约束条件3260,0,0,x y x y +-≤⎧⎪≥⎨⎪≥⎩则z x y =-的取值范围是( ) (A )[]3,0- (B )[]3,2- (C )[]0,2 (D )[]0,3【答案】B【解析】由题意,画出可行域,端点坐标()0,0O ,()0,3A ,()2,0B .在端点,A B 处分别取的最小值与最大值. 所以最大值为2,最小值为3-,故选B .(6)【2017年全国Ⅲ,文6,5分】函数1()sin()cos()536f x x x ππ=++-的最大值为( ) (A )65 (B )1 (C )35 (D )15【答案】A【解析】11113()sin()cos()(sin cos cos sin sin 5365225f x x x x x x x x x ππ=++-=⋅+++⋅=+6sin()53x π=+,故选A .(7)【2017年全国Ⅲ,文7,5分】函数2sin 1x y x x=++的部分图像大致为( )(A )(B )(C )(D )【答案】D【解析】当1x =时,()111sin12sin12f =++=+>,故排除A ,C ,当x →+∞时,1y x →+,故排除B ,满足条件的只有D ,故选D .(8)【2017年全国Ⅲ,文8,5分】执行右面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )(A )5 (B )4 (C )3 (D )2【答案】D【解析】若2N =,第一次进入循环,12≤成立,100100,1010S M ==-=-,2i =2≤成立,第二次进入循环,此时101001090,110S M -=-==-=,3i =2≤不成立,所以输出9091S =<成立,所以输入的正整数N 的最小值是2,故选D .(9)【2017年全国Ⅲ,文9,5分】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )(A )π (B )3π4(C )π2 (D )π4 【答案】B【解析】如果,画出圆柱的轴截面,11,2AC AB ==,所以r BC == 22314V r h πππ==⨯⨯=⎝⎭,故选B . (10)【2017年全国Ⅲ,文10,5分】在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则( ) (A )11A E DC ⊥ (B )1A E BD ⊥ (C )11A E BC ⊥ (D )1A E AC ⊥【答案】C【解析】11A B ⊥平面11BCC B 111A B BC ∴⊥,11BC B C ⊥又1111B C A B B =,1BC ∴⊥平面11A B CD ,又1A E ⊂平面11A B CD 11A E BC ∴⊥,故选C .(11)【2017年全国Ⅲ,文11,5分】已知椭圆()2222:10x y C a b a b+=>>的左、右顶点分别为1A ,2A ,且以线段12A A 为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为( )(A (B (C (D )13【答案】A【解析】以线段12A A 为直径的圆是222x y a +=,直线20bx ay ab -+=与圆相切,所以圆心到直线的距离d a ==,整理为223a b =,即()22222323a a c a c =-⇒=,即2223c a = ,c e a ==A . (12)【2017年全国Ⅲ,文12,5分】已知函数()()2112x x f x x x a e e --+=-++有唯一零点,则a =( )(A )12- (B )13 (C )12 (D )1【答案】C【解析】()()11220x x f x x a e e --+'=-+-=,得1x =,即1x =为函数的极值点,故()10f =,则1220a -+=,12a =,故选C . 二、填空题:本大题共4小题,每小题5分,共20分. (13)【2017年全国Ⅲ,文13,5分】已知向量()2,3a =-,()3,b m =,且a b ⊥,则m =______.【答案】2【解析】因为a b ⊥0a b ∴⋅=,得630m -+=,2m ∴=.(14)【2017年全国Ⅲ,文14,5分】双曲线2221(0)9x y a a -=>的一条渐近线方程为35y x =,则a =__ ____. 【答案】5 【解析】渐近线方程为b y x a=±,由题知3b =,所以5a =. (15)【2017年全国Ⅲ,文15,5分】ABC ∆内角C B A ,,的对边分别为c b a ,,,已知3,6,600===c b C ,则=A _______.【答案】075【解析】根据正弦定理有:03sin 60=sin B ∴=b c > 045=∴B 075=∴A . (16)【2017年全国Ⅲ,文16,5分】设函数1,0,()2,0,x x x f x x +≤⎧=⎨>⎩,则满足1()()12f x f x +->的x 的取值范围是_______. 【答案】1(,)4-+∞ 【解析】由题意得:当12x >时12221x x -+> 恒成立,即12x >;当102x <≤时12112x x +-+> 恒成立,即 102x <≤;当0x ≤时1111124x x x ++-+>⇒>-,即104x -<≤;综上x 的取值范围是1(,)4-+∞. 三、解答题:共70分。

2017年高考真题全国新课标三卷文科数学(解析版)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为几个?答案:2解析:A∩B={2,4},共2个元素。
选择B选项。
复平面内表示复数z=i(–2+i)的点位于哪个象限?答案:第二象限解析:z=-i(2-i)=-2i+i^2=-2i-1.所以z在第二象限。
选择B选项。
根据该折线图,下列结论错误的是?A。
月接待游客逐月增加B。
年接待游客量逐年增加C。
各年的月接待游客量高峰期大致在7,8月D。
各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳答案:A解析:由折线图,7月份后月接待游客量减少,所以A错误。
选择A选项。
已知sinα-cosα=4/9,则sin2α=?答案:-2/17解析:sin2α=2sinαcosα=2(sinα-cosα)cosα=2(4/9)cosα=-8/81.所以sin2α=-2/17.选择A选项。
设x,y满足约束条件{3x+2y-6≤0,x≥0,y≥0},则z=x-y 的取值范围是?A。
[-3,0]B。
[-3,2]C。
[0,2]D。
[0,3]答案:B解析:绘制不等式组表示的可行域,结合目标函数的几何意义可得函数在点A(0,3)处取得最小值z=-3,在点B(2,0)处取得最大值z=2.所以z的取值范围是[-3,2]。
选择B选项。
函数f(x)=sin(x+π/6)+cos(x-π/3)的最大值为多少?A。
5/6B。
1C。
1/5D。
5答案:A解析:由诱导公式可得:cos(x-π/3)=sin(π/2-(x-π/3))=sin(x-π/6),所以f(x)=sin(x+π/6)+sin(x-π/6)=2cos(π/6)sinx=√3sinx。
∵|sinx|≤1,∴f(x)的最大值为√3,即5/6.选择A选项。
函数y=1+x+sinx?(此处有格式错误,请删除)答案:无法判断解析:此题缺少函数的定义域和范围,无法判断。


2017高考全国3卷文科数学试题及答案D二、填空题:本题共4小题,每小题5分,共20分。
13.已知向量(2,3),(3,)a b m =-=,且a ⊥b ,则m = .14.双曲线22219x y a -=(a >0)的一条渐近线方程为35y x =,则a = .15.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c 。
已知C =60°,b 6,c =3,则A =_________。
16.设函数10()20xx x f x x +≤⎧=⎨>⎩,,,,则满足1()()12f x f x +->的x 的取值范围是__________。
三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)设数列{}n a 满足123(21)2n a a n a n +++-=.(1)求{}na 的通项公式; (2)求数列21na n ⎧⎫⎨⎬+⎩⎭的前n 项和. 18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数 2 16 36 25 7 4 以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y 大于零的概率.学#科@网19.(12分)如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.20.(12分)在直角坐标系xOy 中,曲线y =x 2+mx –2与x 轴交于A ,B 两点,点C 的坐标为(0,1).当m 变化时,解答下列问题:(1)能否出现AC ⊥BC 的情况?说明理由;(2)证明过A ,B ,C 三点的圆在y 轴上截得的弦长为定值.21.(12分)已知函数()f x =ln x +ax 2+(2a +1)x .(1)讨论()f x 的单调性;(2)当a ﹤0时,证明3()24f x a ≤--.(二)选考题:共10分。

2017年普通高等学校招生全国统一考试文科数学(适用地区:云南、贵州、广西、四川)第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.)1.已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )A.1 B.2 C.3 D.4[解析]由题意可得A∩B={2,4},故选B.答案:B2.复平面内表示复数z=i(–2+i)的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限[解析]由题意z=-1-2i,故选B.答案:B3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳[解析]由折线图,7月份后月接待游客量减少,A错误,故选A.答案:A4.已知sin α-cos α=错误!,则sin2α=( )A .-错误!B .-错误!C .错误!D .错误![解析] sin2α=2sin αcos α=错误!=-错误!,故选A .答案:A5.设x ,y 满足约束条件错误!,则z =x -y 的取值范围是( )A .[–3,0]B .[–3,2]C .[0,2]D .[0,3][解析] 绘制不等式组表示的可行域,结合目标函数的几何意义可得函数在点A (0,3) 处取得最小值z =0-3=-3.在点B (2,0) 处取得最大值z =2-0=2,故选A .答案:B6.函数f (x )=sin 错误!+cos 错误!的最大值为( )A .65B .1C .错误!D .错误![解析] 由诱导公式可得cos 错误!=cos 错误!=sin 错误!,则f (x )=错误!sin 错误!+sin 错误!=错误!sin 错误!,函数的最大值为错误!,故选A .答案:A7.函数y =1+x +错误!的部分图像大致为( )[解析] 当x =1时,f (1)=1+1+sin1=2+sin1〉2,故排除A ,C ,当x →+∞时,y →1+x ,故排除B,满足条件的只有D ,故选D .答案:D8.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A .5B .4C .3D .2[解析] 若N =2,第一次进入循环,1≤2成立,S =100,M =-10010=-10,i =2≤2成立;第二次进入循环,此时S =100-10=90,M =-错误!=1,i =3≤2不成立,∴输出S =90<91成立,∴输入的正整数N 的最小值是2,故选D .答案:D9.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB .错误!C .错误!D .错误![解析] 如果,画出圆柱的轴截面AC =1,AB =错误!,∴r =BC =错误!,那么圆柱的体积是V =πr 2h =π×错误!×1=错误!,故选B .答案:B10.在正方体ABCD -A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A .A 1E ⊥DC 1B .A 1E ⊥BDC .A 1E ⊥BC 1D .A 1E ⊥AC[解析] 根据三垂线逆定理,平面内的线垂直平面的斜线,那么也垂直斜线在平面内的射线.对于A ,若A 1E ⊥DC 1,那么D 1E ⊥DC 1,很显然不成立;对于B ,若A 1E ⊥BD ,那么BD ⊥AE ,显然不成立;对于C ,若A 1E ⊥BC 1,那么BC 1⊥B 1C ,成立,反过来BC 1⊥B 1C 时,也能推出BC 1⊥A 1E ,∴C 成立,对于D,若A1E⊥AC,则AE⊥AC,显然不成立,故选C.答案:C11.已知椭圆C:错误!+错误!=1(a>b>0)的左、右顶点分别为A1、A2,且以线段A1A2为直径的圆与直线bx-ay+2ab=0相切,则C的离心率为()A.错误!B.错误!C.错误!D.错误![解析]以线段A1A2为直径的圆是x2+y2=a2,直线bx-ay+2ab=0与圆相切,∴圆心到直线的距离d =错误!=a,整理为a2=3b2,即a2=3(a2-c2)⇒2a2=3c2,即错误!=错误!,e=错误!=错误!,故选A.答案:A12.已知函数f(x)=x2-2x+a(e x-1+e-x+1)有唯一零点,则a=( )A.-错误!B.错误!C.错误!D.1[解析] 方法一:由条件,f(x)=x2-2x+a(e x-1+e-x+1),得:f(2-x)=(2-x)2-2(2-x)+a(e2-x-1+e-(2-x)+1)=x2-4x+4-4+2x+a(e1-x+e x-1)=x2-2x+a(e x-1+e-x+1)∴f(2-x)=f(x),即x=1为f(x)的对称轴,由题意,f(x)有唯一零点,∴f(x)的零点只能为x=1,即f(1)=12-2·1+a(e1-1+e-1+1)=0,解得a=错误!.方法二:x2-2x=-a(e x-1+e-x+1),设g(x)=e x-1+e-x+1,g′(x)=e x-1-e-x+1=e x-1-错误!=错误!,当g′(x)=0时,x=1,当x〈1时,g′(x)〈0,函数单调递减,当x〉1时,g′(x)〉0,函数单调递增,当x=1时,函数取得最小值g(1)=2,设h(x)=x2-2x,当x=1时,函数取得最小值-1;若-a>0,函数h(x)和ag(x)没有交点,当-a〈0时,-ag(1)=h(1)时,此时函数h(x)和ag(x)有一个交点,即-a×2=-1⇒a =错误!,故选C.答案:C第Ⅱ卷(非选择题共90分)本试卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分.)13.已知向量错误!=(-2,3),错误!=(3,m),且错误!⊥错误!,则m=.[解析]由题意可得-2×3+3m=0,∴m=2.答案:214.双曲线错误!-错误!=1(a >0)的一条渐近线方程为y =错误!x ,则a = .[解析] 由双曲线的标准方程可得渐近线方程为y =±错误!x ,结合题意可得a =5.答案:515.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知C =60°,b =错误!,c =3,则A = . [解析] 由题意错误!=错误!,即sin B =错误!=错误!=错误!,结合b <c 可得B =45°,则A =180°-B -C =75°.答案:75°16.设函数f (x )=错误!则满足f (x )+f (x -错误!)〉1的x 的取值范围是 .[解析] 方法一:∵f (x )=错误!,f (x )+f 错误!〉1,即f 错误!>1-f (x ),由图象变换可画出y =f 错误!与y =1-f (x )的图象如下:1-1,)41)2-)由图可知,满足f 错误!〉1-f (x )的解为(-错误!,+∞).方法二:由题意得,当x >12时,2x +2x -错误!>1恒成立,即x >错误!;当0<x ≤错误!时,2x +x -错误!+1>1恒成立,即0<x ≤错误!;当x ≤0时x +1+x -错误!+1>1⇒x >-错误!,即-错误!<x ≤0;综上x 的取值范围是(-错误!,+∞).答案:(-14,+∞)三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(本小题满分12分)设数列{a n }满足a 1+3a 2+…+(2n -1)a n =2n .(1)求{a n }的通项公式;(2)求数列错误!的前n 项和.[解析] (1)∵a 1+3a 2+…+(2n -1)a n =2n ,①∴n ≥2时,a 1+3a 2+…+(2n -1)a n -1=2(n -1),②①-②得,(2n -1)a n =2,a n =错误!,又n =1时,a 1=2适合上式,∴a n =错误!;(2)由(1)a n 2n +1=错误!=错误!-错误!, ∴S n =错误!+错误!+…+错误!=(1-错误!)+(错误!-错误!)+…+(错误!-错误!)=1-错误!=错误!.18.(本小题满分12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15) [15,20) [20,25) [25,30) [30,35) [35,40) 天数 2 16 36 25 7 4以最高气温位于各区间的频率代替最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y (单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y 的所有可能值,并估计Y 大于零的概率.[解析] (1)需求量不超过300瓶,即最高气温不高于25℃,从表中可知有54天,∴所求概率为P =5490=35. (2)Y 的可能值列表如下:最高气温 [10,15)[15,20) [20,25) [25,30) [30,35) [35,40) Y -100 -100 300 900 900 900低于20℃:y =200×6+250×2-450×4=-100;[20,25):y =300×6+150×2-450×4=300;不低于25℃:y =450×(6-4)=900,∴Y 大于0的概率为P =290+错误!=错误!. 19.(本小题满分12分)如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE 与四面体ACDE的体积比.[解析] (1)证明:取AC中点O,连OD,OB,∵AD=CD,O为AC中点,∴AC⊥OD,又∵△ABC是等边三角形,∴AC⊥OB,又∵OB∩OD=O,∴AC⊥平面OBD,BD 平面OBD,∴AC⊥BD;(2)设AD=CD=2,∴AC=22,AB=CD=2错误!,又∵AB=BD,∴BD=2错误!,∴△ABD≌△CBD,∴AE=EC,又∵AE⊥EC,AC=2错误!,∴AE=EC=2,在△ABD中,设DE=x,根据余弦定理cos∠ADB=错误!=错误!=错误!=错误!,解得x=错误!,∴点E是BD的中点,则V D-ACE=V B-ACE,∴错误!=1.20.(本小题满分12分)在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:(1)能否出现AC⊥BC的情况?说明理由;(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.[解析] (1)设A(x1,0),B(x2,0),则x1,x2是方程x2+mx-2=0的根,∴x1+x2=-m,x1x2=-2,则错误!·错误!=(-x1,1)·(-x2,1)=x1x2+1=-2+1=-1≠0,∴不会能否出现AC⊥BC的情况.(2)解法一:过A,B,C三点的圆的圆心必在线段AB垂直平分线上,设圆心E(x0,y0),则x0=错误!=-错误!,由|EA|=|EC|得错误!+y02=错误!+(y0-1)2,化简得y0=错误!=-错误!,∴圆E的方程为错误!+错误!=错误!+错误!,令x=0得y1=1,y2=-2,∴过A,B,C三点的圆在y轴上截得的弦长为1-(-2)=3,∴过A,B,C三点的圆在y轴上截得的弦长为定值解法二:设过A,B,C三点的圆与y轴的另一个交点为D,由x1x2=-2可知原点O在圆内,由相交弦定理可得|OD||OC|=|OA||OB|=|x1||x2|=2,又|OC|=1,∴|OD|=2,∴过A ,B ,C 三点的圆在y 轴上截得的弦长为|OC |+|OD |=3,为定值.21.(本小题满分12分)已知函数f (x )=ln x +ax 2+(2a +1)x .(1)讨论f (x )的单调性;(2)当a 〈0时,证明f (x )≤-错误!-2.[解析] (1)f ′(x )=2ax 2+(2a +1)x +1x=错误!(x 〉0), 当a ≥0时,f ′(x )≥0,则f (x )在(0,+∞)单调递增,当a <0时,则f (x )在(0,-错误!)单调递增,在(-错误!,+∞)单调递减.(2)由(1)知,当a 〈0时,f (x )max =f (-错误!),f (-错误!)-(-错误!+2)=ln(-错误!)+错误!+1,令y =ln t +1-t (t =-错误!〉0),则y ′=1t-1=0,解得t =1, ∴y 在(0,1)单调递增,在(1,+∞)单调递减,∴y max =y (1)=0,∴y ≤0,即f (x )max ≤-(错误!+2),∴f (x )≤-错误!-2.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10分)选修4―4坐标系与参数方程:在直角坐标系xOy 中,直线l 1的参数方程为错误!(t 为参数),直线l 2的参数方程为错误!(m 为参数).设l 1与l 2的交点为P ,当k 变化时,P 的轨迹为曲线C .(1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l 3:ρ(cos θ+sin θ)-错误!=0,M 为l 3与C 的交点,求M 的极径.[解析] (1)将参数方程转化为普通方程l 1:y =k (x -2)……①;l 2:y =错误!(x +2)……②由①②消去k 可得:x 2-y 2=4,即P 的轨迹方程为x 2-y 2=4;(2)将参数方程转化为一般方程l 3:x +y -错误!=0……③联立l 3和曲线C 得错误!,解得错误!,由错误!,解得ρ=错误!,即M 的极半径是错误!.23.(本小题满分10分)选修4-5不等式选讲:已知函数f (x )=|x +1|–|x –2|.(1)求不等式f (x )≥1的解集;(2)若不等式f (x )≥x 2–x +m 的解集非空,求m 的取值范围.[解析] (1) f (x )=|x +1|–|x –2|可等价为f (x )=错误!.由f (x )≥1可得:①当x≤-1时显然不满足题意;②当-1〈x〈2时,2x-1≥1,解得x≥1;③当x≥2时,f(x)=3≥1恒成立.综上,f(x)≥1的解集为{x|x≥1}.(2)不等式f(x)≥x2-x+m等价为f(x)-x2+x≥m,令g(x)=f(x)-x2+x,则g(x)≥m解集非空只需要[g(x)]max≥m.而g(x)=错误!.①当x≤-1时,[g(x)]max=g(-1)=-3-1-1=-5;②当-1<x<2时,[g(x)]max=g(错误!)=-错误!+3·错误!-1=错误!;③当x≥2时,[g(x)]max=g(2)=-22+2+3=1.综上,[g(x)]max=错误!,故m≤错误!.∴m的取值范围为(-∞,错误!].。

2017 年全国 III 卷高考文科数学真题及答案注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动, 用橡皮擦干净后, 再选涂其他答案标号。
回答非选择题时, 将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
5 分,共 60 分。
在每小题给出的四个选项中,只 有一项是符合题目要求的。
2016 年 12 月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图根据该折线图,下列结论错误的是 A .月接待游客逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在 7,8 月D .各年 1 月至 6 月的月接待游客量相对于 7月至 12 月,波动性更小,变化比较平稳4.已知 sin cos4,则 sin 2 =37227A .B .C .D .99 9 9、选择题:本大题共 12 小题,每小题 1. 已知集合 A={1,2,3,4} , B={2,4,6,8} ,则 B 中元素的个数为 2. 3.A .1B .2C .D .4复平面内表示复数 z=i( –2+i) 的点位于 A .第一象限B .第二象限C . 第三象限D .第四象限 某城市为了解游客人数的变化规律,提高旅游服务质量, 收集并整理了 2014 年 1 月至3x 2y 5.设 x ,y 满足约束条件 x 0yB 1 D5A BCD .C .3D .2 B .4 A .5 B .1C .[0,2]D .[0,3]60C .35A .65 8.执行下面的程序框图,为使输出 S 的值小于 91,则输入的正整数N 的最小值为9.已知圆柱的高为 1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的[ – 3,2]16.函数 f (x )= sin( x + )+cos( x - ) 的最大值为 5 3 67.函数 y =1+x + sin 2 x 的部分图像大致为 x 20 ,则 z =x -y 的取值范围是A .[ –3,0]A . A 1E ⊥DC 1B . A 1E ⊥BDC . A 1E ⊥BC 1D . A 1E ⊥ AC2 y 2 1,( a >b >0)的左、右顶点分别为 b1(a >0)的一条渐近线方程为 y 3x , 95A ,B ,C 的对边分别为 a ,b ,c 。

绝密★启封并使用完毕前试题类型:新课标Ⅲ2017 年普通高等学校招生全国统一考试文科数学本试卷分第I卷(选择题)和第II 卷(非选择题)两部分,共24题,共150分,共4 页。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑字迹的签字笔书写,字体工整,笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破,不准使用涂改液、修正液、刮纸刀。
第I卷一、单选题(本大题共 12小题,每小题 5分,共 60分。
)1.已知集合A 1, 2, 3, 4 , B 2, 4, 6, 8 ,则A B 中的元素的个数为()A. 1B. 2C. 3D. 42.复平面内表示复数z i 2 i 的点位于()A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年 1 月至2016年 12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.7. 函数y 1 x sin 2xx的部分图像大致为( 根据该折线图,下列结论错误的是 ( )A. 月接待游客量逐月增加B. 年接待游客量逐年增加C. 各年的月接待游客量高峰期大致在 7,8月D. 各年 1 月至 6月的月接待游客量相对于 7 月至 12月,波动性更小,变化比较平稳44.已知 sin cos ,则 sin2 ( )7D2 C2B73x 2y 6 05. 设 x, y 满足约束条件 x 0 则 z x y 的取值范围是 ( ) y0A. 3, 0B. 3, 2C. 0, 2D. 0, 316. 函数 f x sin x cos x 的最大值为 ( )5 3 66 3 1 A. B. 1 C. D. 5 5 58.执行右面的程序框图,为使输出 S 的值小于 91,则输入的正整数 N 的最小值为 ( )第 II 卷本卷包括必考题和选考题两部分(22) 题、第 (23) 题为选考题,考生根据要求作答 二、填空题 (本大题共 4小A. 5B. 4C. 3D. 29. 已知圆柱的高为 1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的3A.B.C. D.42410. 在正方体 ABCDA 1B 1C 1D 1中,E 为棱 CD 的中点,则 ( ) A. A 1E DC 1B. A 1E BDC. A 1E BC 1D. A 1E ACx 2211. 已知椭圆 C: 2 y 2 1 a b 0 的左、右顶点分别为 A 1,A 2,且以线段 A 1A 2为直径的 ab圆与直线 bx ay 2ab 0 相切,则C 的离心率为 ( )A. 6 3B. 33C. 231 D.12. 已知函数 2x a e x 1 e x 1 有唯一零点,则 a=( )A. 12B. 13 C. 12D. 1.第(13)题 ~第(21)题为必考题,每个试题考生都必须作答 .第题,每小题 5分,共 20 分)13. 已知向量 a 2, 3 ,b 3, m ,且a b ,则 m = _____ 22 14. 双曲线 x 2y 1 a 0 的一条渐近线方程为15. ABC 内角 A, B, C 的对边分别为 a, b, c ,已知 C 60 , b 6, c 3 ,则 A三、简答题 (本大题共 6小题,共 70分。


2017年全国统一高考新课标版Ⅲ卷全国3卷文科数学试卷及参考答案与解析一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )A.1B.2C.3D.42.(5分)复平面内表示复数z=i(-2+i)的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.(5分)已知sinα-cosα=,则sin2α=( )A.-B.-C.D.5.(5分)设x,y满足约束条件则z=x-y的取值范围是( )A.[-3,0]B.[-3,2]C.[0,2]D.[0,3]6.(5分)函数f(x)=sin(x+)+cos(x-)的最大值为( )A. B.1 C. D.7.(5分)函数y=1+x+的部分图象大致为( )A. B.C. D.8.(5分)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )A.5B.4C.3D.29.(5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A.πB.C.D.10.(5分)在正方体ABCD-A1B1C1D1中,E为棱CD的中点,则( )A.A1E⊥DC1B.A1E⊥BD C.A1E⊥BC1D.A1E⊥AC11.(5分)已知椭圆C:=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx-ay+2ab=0相切,则C的离心率为( )A. B. C. D.12.(5分)已知函数f(x)=x2-2x+a(e x-1+e-x+1)有唯一零点,则a=( )A.-B.C.D.1二、填空题13.(5分)已知向量=(-2,3),=(3,m),且,则m=.14.(5分)双曲线(a>0)的一条渐近线方程为y=x,则a=.15.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知C=60°,b=,c=3,则A=.16.(5分)设函数f(x)=,则满足f(x)+f(x-)>1的x的取值范围是.三、解答题17.(12分)设数列{an }满足a1+3a2+…+(2n-1)an=2n.(1)求{an}的通项公式;(2)求数列{}的前n项和.18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.19.(12分)如图四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE 与四面体ACDE的体积比.20.(12分)在直角坐标系xOy中,曲线y=x2+mx-2与x轴交于A、B两点,点C的坐标为(0,1),当m变化时,解答下列问题:(1)能否出现AC⊥BC的情况?说明理由;(2)证明过A、B、C三点的圆在y轴上截得的弦长为定值.21.(12分)已知函数f(x)=lnx+ax2+(2a+1)x.(1)讨论f(x)的单调性;(2)当a<0时,证明f(x)≤--2.[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系xOy中,直线l1的参数方程为,(t为参数),直线l2的参数方程为,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)-=0,M为l3与C的交点,求M的极径.[选修4-5:不等式选讲]23.已知函数f(x)=|x+1|-|x-2|.(1)求不等式f(x)≥1的解集;(2)若不等式f(x)≥x2-x+m的解集非空,求m的取值范围.2017年全国统一高考数学试卷(文科)(新课标Ⅲ)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分。
2017年普通高等学校招生全国统一考试3juan
文科数学
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A B 中元素的个数为
A .1
B .2
C .3
D .4
2.复平面内表示复数(2)z i i =-+的点位于
A .第一象限
B .第二象限
C .第三象限
D .第四象限
3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图
.
根据该折线图,下列结论错误的是
A .月接待游客逐月增加
B .年接待游客量逐年增加
C .各年的月接待游客量高峰期大致在7,8月
D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
4.已知4sin cos 3
αα-=,则sin 2α= A .79- B .29- C . 29 D .79
5.设,x y 满足约束条件326000x y x y +-≤??≥??≥?
,则z x y =-的取值范围是
A .[-3,0]
B .[-3,2]
C .[0,2]
D .[0,3] 6.函数1()sin()cos()536
f x x x ππ=++-的最大值为 A .65 B .1 C .35
D .15 7.函数2sin 1x y x x =++的部分图像大致为
A .
B .
C .
D .
8.执行右面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值
为
A .5
B .4
C .3
D .2
9.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个
球的球面上,则该圆柱的体积为
A .π
B .34π
C .2π
D .4
π 10.在正方体1111ABCD A BC D -中,
E 为棱CD 的中点,则 A .11A E DC ⊥ B .1A E BD ⊥ C .11A E BC ⊥
D .1A
E AC ⊥
11.已知椭圆22
22:1(0)x y C a b a b
+=>>的左、右顶点分别为12,A A ,且以线段12A A 为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为
A B C .3 D .13 12.已知函数211()2()x x f x x x a e
e --+=-++有唯一零点,则a = A .12- B .1
3 C .12 D .1
二、填空题:本题共4小题,每小题5分,共20分。
13.已知向量(2,3),(3,)a b m =-=,且a b ⊥,则m = .
14.双曲线22
21(0)9
x y a a -=>的一条渐近线方程为35y x =,则a = .
15.ABC ?的内角,,A B C 的对边分别为,,a b c 。
已知60,3C b c === ,则A =_________。
16.设函数1,0,()2,0,
x x x f x x +≤?=?>?则满足1()()12f x f x +->的x 的取值范围是
__________。
三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)
设数列{}n a 满足123(21)2n a a n a n +++-= .
(1)求{}n a 的通项公式;(2)求数列{
}21
n a n +的前n 项和. 18.(12分)
某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y (单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y
的所有可能值,并估计Y 大于零的概率.
19.(12分)
如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .
(1)证明:AC ⊥BD ;
(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.
20.(12分)
在直角坐标系xOy 中,曲线22y x mx =+-与x 轴交于A ,B 两点,点C 的坐标为(0,1).当m 变化时,解答下列问题:
(1)能否出现AC ⊥BC 的情况?说明理由;
(2)证明过A ,B ,C 三点的圆在y 轴上截得的弦长为定值.
21.(12分)
已知函数()2(1)ln 2x ax a x f x =+++.
(1)讨论()f x 的单调性;(2)当0a <时,证明3()24f x a
≤--. (二)选考题:共10分。
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
22.[选修4―4:坐标系与参数方程](10分)
在直角坐标系xOy 中,直线1l 的参数方程为2,x t y kt =+??=?(t 为参数),直线2l 的参数方程为2,x m m y k =-+???=??
(m 为参数),设1l 与2l 的交点为P ,当k 变化时,P 的轨迹为曲线C .
(1)写出C 的普通方程:
(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设3l
:(cos sin )0ρθθ+=,M 为3l 与C 的交
点,求M 的极径.
23.[选修4—5:不等式选讲](10分)
已知函数()||||f x x x =+1--2.
(1)求不等式()f x ≥1的解集;
(2)若不等式()f x x x m 2≥-+的解集非空,求m 的取值范围.
2017年普通高等学校招生全国统一考试
文科数学参考答案
一、选择题
1.B
2.C
3.A
4.A
5.B
6.A
7.D
8.D 9.B 10.C 11.A 12.C 二、填空题
13.2
14.5 15.75° 16.1(,)4
-+∞ 三、解答题
17.解:
(1)因为123(21)2n a a n a n +++-= ,故当2n ≥时, 1213(23)2(1)n a a n
a n -+++-=- 两式相减得(21)2n n a -=所以2(2)21n a n n =
≥- 又由题设可得12a =从而{}n a 的通项公式为221n a n =
- (2)记{}21
n a n +的前n 项和为n S 由(1)知21121(21)(21)2121
n a n n n n n ==-++--+ 则1111112 (1335212121)
n n S n n n =-
+-++-=-++ 18.解: (1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,由表格数据知,最高气温低于25的频率为
216360.690
++=,所以这种酸奶一天的需求量不超过300瓶的概率的估计值为0.6 (2)当这种酸奶一天的进货量为450瓶时,
若最高气温不低于25,则64504450900Y =?-?=;
若最高气温位于区间[20,25),则63002(450300)4450300Y =?+--?=;
若最高气温低于20,则62002(450200)4450100Y =?+--?=-
所以,Y 的所有可能值为900,300,-100
Y 大于零当且仅当最高气温不低于20,
由表格数据知,最高气温不低于20的频率为3625740.890+++=,因此Y 大于零的概率的估计值为0.8
19.解:
(1)取AC 的中点O ,连结,DO BO ,
因为AD CD =,所以AC DO ⊥
又由于ABC ?是正三角形,故BO AC ⊥
O
D A B C E。