高一数学三角函数综合提升讲义

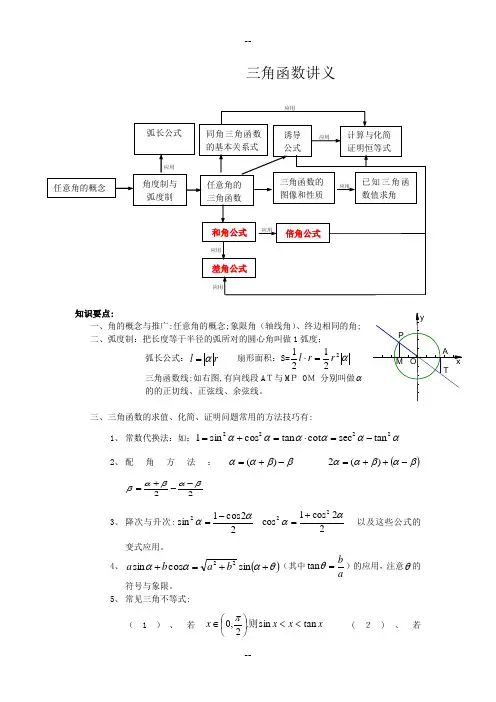
三角函数讲义知识要点:一、角的概念与推广:任意角的概念;象限角（轴线角）、终边相同的角;二、弧度制：把长度等于半径的弧所对的圆心角叫做1弧度；弧长公式：r l α=扇形面积：S=α22121r r l =⋅三角函数线:如右图,有向线段A Ｔ与M Ｐ O Ｍ 分别叫做α 的的正切线、正弦线、余弦线。

三、三角函数的求值、化简、证明问题常用的方法技巧有:1、 常数代换法：如：αααααα2222tan sec cot tan cos sin 1-=⋅=+=2、 配角方法：ββαα-+=)(()βαβαα-++=)(222βαβαβ--+=3、 降次与升次:22cos 1sin 2αα-= 22cos 1cos 22αα+= 以及这些公式的变式应用。

4、 ()θααα++=+sin cos sin 22b a b a （其中ab=θtan ）的应用，注意θ的符号与象限。

5、 常见三角不等式:（1）、若x x x x tan sin .2,0<<⎪⎭⎫⎝⎛∈则π (２)、若2cos sin 1.2,0≤+<⎪⎭⎫⎝⎛∈x x x 则π（３）、1cos sin ≥+x x 6、 常用的三角形面积公式：（1）、c b a ch bh ah S 212121===(2)、B ac A bcC ab S sin 21sin 21sin 21===（3）、S =四、三角函图象和性质:正弦函数图象的变换：()()αωαωω+=−−−→−+=−−−→−=−−−→−=x A y x y x y x y sin sin sin sin 振幅变换平移变换横伸缩变换万能公式:2tan 12tan2tan ,2tan 12tan 1cos ,2tan 12tan2sin 2222α-α=αα+α-=αα+α=α 证：2tan 12tan22cos 2sin 2cos 2sin 21sin sin 222α+α=α+ααα=α=α2tan 12tan 12cos 2sin 2sin 2cos 1cos cos 222222α+α-=α+αα-α=α=α2tan 12tan22sin 2cos 2cos 2sin 2cos sin tan 222α-α=α-ααα=αα=α例1 已知5cos 3sin cos sin 2-=θ-θθ+θ,求3c ｏｓ 2θ + 4ｓｉn 2θ 的值。

高一数学三角函数同步辅导讲义第1讲任意角的三角函数一、学习指导1．任意角的三角函数（1）任意角的三角函不能再用初中定义锐角三角函数的办法来定义，因此通过平面直角坐标系来定义任意角的三角函数.（2）对于任意角α的三角函数，由相似形的性质可知，α的三角函数值与P点在终边上的位置无关，仅与角的大小有关，即角的正弦、余弦、正切、余切、正割、余还要熟悉每个象限各个三角函数的符号.第Ⅰ象限：全正；第Ⅱ象限：仅αsin ，αcsc 为正，其余为负；第Ⅲ象限：仅αtan ，αcot 为正，其余为负；第Ⅳ象限：仅αcos ，αsec 为正，其余为负.4．终边相同角的三角函数值 公式一：ααsin )360sin(=⋅+k ， ααcos )360cos(=⋅+ k ，ααtan )360tan(=⋅+ k . )(Z k ∈也称为诱导公式一，利用公式一可以把任意角的三角函数化为0到360角的三角函数.二、典型例题分析例1 已知角α的终边上有一点)0()5,12(<a a a P ，求α的各三角函数值. 解 由已知，a x 12=，a y 5=. ∵0<a ，∴a a a a y x r 1313)5()12(2222-==+=+=.∴135sin -==r y α，1312cos -==r x α，125tan ==x y α， 512cot ==y x α，1213sec -==x r α，513csc -==y r α. 例2 已知角α的终边经过点)0()4,3(≠-a a a P ，求ααcos 2sin +的值. 分析 因a 的符号不确定，所以要对字母a 进行讨论.当0>a ，P 点在第四象限，当0<a ，P 点在第二象限.解 若0>a ，03>=a x ，04<-=a y ，P 点在第四象限. a a a a OP r 55)4()3(22==-+==.54sin -==r y α,53cos ==r x α. ∴5253254cos 2sin =⨯+-=+αα. 若0<a ，03<=a x ，04>-=a y ，P 点在第二象限. a a a a OP r 55)4()3(22-==-+==.54sin ==r y α，53cos -==r x α.∴5253254cos 2sin -=⎪⎭⎫⎝⎛-⨯+=+αα. 例3 若40πα<<，利用三角函数线证明：ααcos sin <，且1tan <α.① ααtan 21tan 12121=⋅⋅=⋅⋅=∆AT OA S TOA ， ∴αααtan 2121sin 21<<. αααtan sin <<. 例5 已知0sin >α，0cos <α，判断2tanα的符号.分析 首先应判断角α所在象限，然后再确定角2α所在象限及2tan α的符号. 解 ∵0sin >α，0cos <α， ∴α是第二象限角，)(222Z k k k ∈+<<+ππαππ.∴ππαππk k +<<+224.当)(2Z n n k ∈=，πππππn n 22224+<<+，2α是第一象限角，02tan >α. 当)(12Z n n k ∈+=，ππαππn n 2232245+<<+，2α是第三象限角，02tan >α. ∴2tanα必为正数.例6 求函数x x y tan cos -+=的定义域.解 由已知⎪⎩⎪⎨⎧≥-≥.0tan ,0cos x x由①，角x 的终边在y 轴上，或第一象限，或第四象限，或在x 轴的非负半轴上. 由②，0tan ≤x ，角α的终边在第二象限，或第四象限，或在x 轴上. ∴角x 的终边在第四象限或x 轴的非负半轴上. ∴函数的定义域为⎭⎬⎫⎩⎨⎧∈≤<+-Z k k x k x ,222πππ. 例7 求值：（1）)1020cot(1110tan )1380cos()1830sin(-⋅+-⋅； ②（2）⎪⎭⎫⎝⎛⋅⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-ππππ441cos 423sin 35cot 417cos 22.解 （1）)1020cot(1110tan )1380cos()1830sin(-⋅+-⋅]360)3(60cot[)360330tan(]360)4(60cos[)360530sin( ⨯-+⋅⨯++⨯-+⋅⨯+=60cot 30tan 60cos 30sin ⋅+⋅= 127314133332121=+=⨯+⨯=. （2）⎪⎭⎫⎝⎛⋅⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-ππππ441cos 423sin 35cot 417cos 22⎪⎭⎫⎝⎛+⋅⎥⎦⎤⎢⎣⎡⨯-++⎥⎦⎤⎢⎣⎡⨯-+⎪⎭⎫ ⎝⎛⨯+=ππππππππ104cos 2)3(4sin 2)1(3cot 224cos 22 532131214cos4sin3cot 4cos 22=+=⋅+=ππππ.巩固练习一、选择题1．已知角α是第四象限角，则下列各式中一定为正的是（ ）A ．ααcos sin +B ．ααcos sin ⋅C ．ααtan sin ⋅D ．ααcos sin -2．若点)0,4(-P 在角α的终边上，则下列函数中不存在的是（ ）A ．αsinB ．αcosC ．αtanD ．αcot3．下列四个命题：①若0cos <α，则α是第二象限角或第三象限角；②0cos sin >⋅αα且0cot cos <⋅αα是α为第三象限角的充要条件；③若βαcos cos =，则角α和角β的终边相同；④若βα>，则βαsin sin >.其中真命题有（ ）A ．1个B ．2个C ．3个D ．4个 二、解答题 1．求值：（1）405tan 780cos )690sin(2-+-； （2）πππππtan 5cot 49tan 527sin 223cos 3⋅+-+. .2．已知02sin <θ，且θθsin sin -=，判断点)cos ,(tan θθP 在第几象限.。

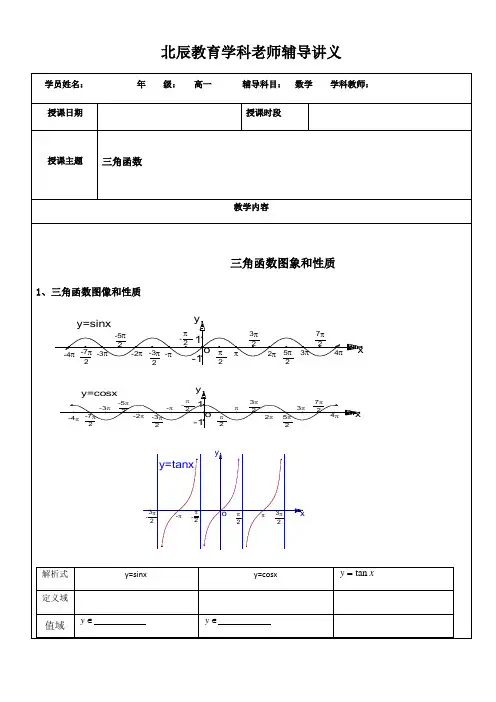
北辰教育学科老师辅导讲义(0)x>的周期与函数的周期相等，则等于（ (B)1 (2 在同一平面直角坐标系中，函数])20[)(232cos(ππ，∈+=x x y 的图象和直线21=y 的交点个数是（A ）0 （B ）1 （C ）2 （D ）43.已知函数y=2sin(ωx+φ)(ω>0)在区间[0，2π]的图像如下：那么ω=A. 1B. 2C. 1/2D. 1/34． 下列函数中，图象的一部分如右图所示的是 （ ） （A ）sin 6y x π⎛⎫=+⎪⎝⎭（B ）sin 26y x π⎛⎫=-⎪⎝⎭（C ）cos 43y x π⎛⎫=-⎪⎝⎭（D ）cos 26y x π⎛⎫=-⎪⎝⎭6． 为了得到函数y ＝sin ⎝⎛⎭⎫2x －π3的图象，只需把函数y ＝sin ⎝⎛⎭⎫2x ＋π6的图象 ( ) A ．向左平移π4个长度单位 B ．向右平移π4个长度单位 C ．向左平移π2个长度单位 D ．向右平移π2个长度单位7．已知函数y ＝sin ⎝⎛⎭⎫x －π12cos ⎝⎛⎭⎫x －π12，则下列判断正确的是 ( ) A ．此函数的最小正周期为2π，其图象的一个对称中心是⎝⎛⎭⎫π12，0 B ．此函数的最小正周期为π，其图象的一个对称中心是⎝⎛⎭⎫π12，0 C ．此函数的最小正周期为2π，其图象的一个对称中心是⎝⎛⎭⎫π6，07、已知函数()()sin ,f x A x x R ωϕ=+∈(其中0,0,22A ππωϕ>>-<<),其部分图象如图所示.(I)求()f x 的解析式;(II)求函数)4()4()(ππ-⋅+=x f x f x g 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值及相应的x 值.。

高中三角函数讲义概述及解释说明1. 引言1.1 概述在高中数学课程中，三角函数是一个重要的内容。

它是研究角度和三角形等几何图形性质的基础工具，并且在实际生活中有广泛的应用。

掌握三角函数的定义、性质以及其在解决实际问题中的应用是每位高中生数学学习的必备知识。

1.2 文章结构本文将围绕高中三角函数展开讲述。

首先，我们将介绍高中三角函数的基本概念，包括角度和弧度的概念以及正弦、余弦和正切的定义。

然后，我们将探讨三角函数之间的关系与公式推导，包括同一角度不同三角函数之间的关系与变化规律，倍角、半角以及相关角公式推导与应用，以及其他三角函数如割、减等的公式与性质说明。

接下来，我们将着重介绍高中三角函数在解决实际问题中的应用，例如测量和测绘领域、机械工程和建筑设计领域，以及物理学和天文学领域。

最后，在结论部分，我们将对主要内容进行总结与回顾，并提出对高中三角函数学习的建议以及进一步研究方向的展望。

1.3 目的本文的目的是为高中生提供一份全面且易懂的三角函数讲义，帮助他们掌握高中三角函数相关知识，并能够将其应用于实际问题解决中。

通过本文的学习，读者将能够理解三角函数在几何图形、物理和工程等领域的重要性，并从中获得启示，拓宽自己在数学领域的思维方式和解决问题的能力。

2. 高中三角函数的基本概念：2.1 角度和弧度的概念：在高中数学中，我们常常用角度来表示一个角的大小。

角度是以度（°）为单位来衡量的，一个圆共有360°。

但在三角函数的研究中，也经常使用弧度来表示角的大小。

弧度是单位圆上与它所对应的弧长相等的一段弧所对应的长度，常用符号“rad”表示。

一周对应的弧长为2π，即一个圆心角为360°或2π弧度。

2.2 正弦、余弦和正切的定义：在三角函数中，最基本的三个函数是正弦（sin）、余弦（cos）和正切（tan）。

这些函数可以通过单位圆上点的坐标来定义。

正弦函数(sin)：给定一个角θ，在单位圆上以θ作为终边所对应点(x, y)的y坐标即为该角θ的正弦值。

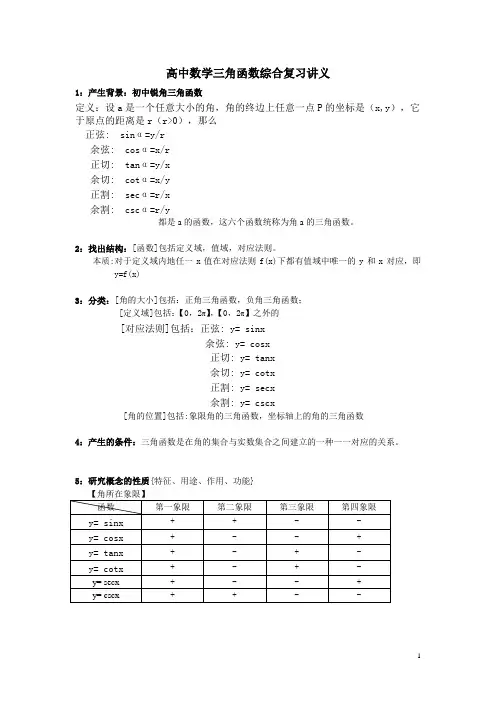
高中数学三角函数综合复习讲义1：产生背景：初中锐角三角函数定义：设a是一个任意大小的角，角的终边上任意一点P的坐标是（x,y），它于原点的距离是r（r>0），那么正弦: sinα=y/r余弦: cosα=x/r正切: tanα=y/x余切: cotα=x/y正割: secα=r/x余割: cscα=r/y都是a的函数，这六个函数统称为角a的三角函数。

2：找出结构：[函数]包括定义域，值域，对应法则。

本质:对于定义域内地任一x值在对应法则f(x)下都有值域中唯一的y和x对应，即y=f(x)3：分类：[角的大小]包括：正角三角函数，负角三角函数；[定义域]包括：【0，2π】，【0，2π】之外的[对应法则]包括：正弦: y= sinx余弦: y= cosx正切: y= tanx余切: y= cotx正割: y= secx余割: y= cscx[角的位置]包括:象限角的三角函数，坐标轴上的角的三角函数4：产生的条件：三角函数是在角的集合与实数集合之间建立的一种一一对应的关系。

5：研究概念的性质{特征、用途、作用、功能}基本三角函数的性质：同角的三角函数：倒数关系: 商的关系：平方关系： tanα ·cotα＝1 sinα ·cscα＝1 cosα ·secα＝1sinα/cosα＝tanα＝secα/cscα cosα/sinα＝cotα＝cscα/secαsin 2α＋cos 2α＝1 1＋tan 2α＝sec 2α 1＋cot 2α＝csc 2α诱导公式sin （－α）＝－sinα cos （－α）＝cosα tan （－α）＝－tanαcot （－α）＝－cotαsin （π/2－α）＝cos α cos （π/2－α）＝sin α tan （π/2－α）＝cot α cot （π/2－α）＝tan αsin （π/2＋α）＝cos αcos （π/2＋α）＝－sin α tan （π/2＋α）＝－cot α cot （π/2＋α）＝－tan α sin （π－α）＝sin α cos （π－α）＝－cos α tan （π－α）＝－tan α cot （π－α）＝－cot αsin （π＋α）＝－sin αcos （π＋α）＝－cos α tan （π＋α）＝tan α cot （π＋α）＝cot αsin （3π/2－α）＝－cos α cos （3π/2－α）＝－sin α tan （3π/2－α）＝cot α cot （3π/2－α）＝tan αsin （3π/2＋α）＝－cos α cos （3π/2＋α）＝sin α tan （3π/2＋α）＝－cot α cot （3π/2＋α）＝－tan α sin （2π－α）＝－sin α cos （2π－α）＝cos α tan （2π－α）＝－tan α cot （2π－α）＝－cot α sin （2k π＋α）＝sin αcos （2k π＋α）＝cos α tan （2k π＋α）＝tan α cot （2k π＋α）＝cot α(其中k∈Z)两角和与差的三角函数公式sin sin cos cos sin sin sin cos cos sin cos cos cos sin sin cos cos cos sin sin αβαβαβαβαβαβαβαβαβαβαβαβ（＋）＝＋（－）＝－（＋）＝－（－）＝＋ =1 ?tan tan tan tan tan αβαβαβ＋（＋）－1? ?tan tan tan tan tan αβαβαβ－（－）＝＋半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α＝2sinαcosαcos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α2tanαtan2α＝—————1－tan2αsin3α＝3sinα－4sin3αcos3α＝4cos3α－3cosα3tanα－tan3αtan3α＝——————1－3tan2α万能公式2tan(α/2) 1－tan2(α/2) 2tan(α/2) cosα＝—————— sinα＝—————— tanα＝——————1＋tan2(α/2) 1＋tan2(α/2) 1－tan2(α/2) 三角函数的和差化积公式三角函数的积化和差公式sinα＋sinβ＝2sin2βα+cos2βα-sinα－sinβ＝2cos2βα+sin2βα-cosα＋cosβ＝2cos2βα+·cos2βα-cosα－cosβ＝－2sin2βα+·sin2βα-sinα ·cosβ＝21[sin（α＋β）＋sin（α－β）]cosα ·sinβ＝-21[sin（α＋β）－sin（α－β）]cosα ·cosβ＝21[cos（α＋β）＋cos（α－β）]sinα ·sinβ＝－21[cos（α＋β）－cos（α－β）]【三角形边角关系】1.正弦定理：在△ABC 中，∠A , ∠B , ∠C 的对边分別为 a , b , c ，则其中R 为外接圆半径。

三角函数强化训练专项突破突破点一 三角函数的定义[例1] (1)如图所示，在平面直角坐标系xOy 中，角α的终边与单位圆交于点A ，点A 的纵坐标为45，则cos α＝________.(2)已知α是第二象限角，设点P (x ，5)是α终边上一点，且cos α＝24x ，求4cos ⎪⎭⎫ ⎝⎛+2πα－3tan α的值．(3)已知sin α＞0，cos α＜0，则12α所在的象限是( )A ．第一象限B ．第三象限C ．第一或第三象限D ．第二或第四象限跟踪训练：1．点P 从(1,0)出发，沿单位圆逆时针方向运动2π3弧长到达Q 点，则Q 点的坐标为( )A.⎪⎪⎭⎫⎝⎛-23,21B.⎪⎪⎭⎫⎝⎛--21,23 C.⎪⎪⎭⎫⎝⎛--23,21 D.⎪⎪⎭⎫ ⎝⎛-21,23 2．若α是第三象限角，则下列各式中不成立的是( ) A ．sin α＋cos α＜0 B ．tan α－sin α＜0 C ．cos α－tan α＜0 D ．tan αsin α＜03．已知角α的终边经过点(3a －9，a ＋2)，且cos α≤0，sin α＞0，则实数a 的取值范围是( ) A ．(－2,3] B ．(－2,3) C ．[－2,3) D ．[－2,3]4．如图所示，在直角坐标系xOy 中，射线OP 交单位圆O 于点P ，若∠AOP ＝θ，则点P 的坐标是( )A ．(cos θ，sin θ)B ．(－cos θ，sin θ)C ．(sin θ，cos θ)D ．(－sin θ，cos θ)5．已知角α的终边过点P (－8m ，－6sin 30°)，且cos α＝－45，则m 的值为( )A ．－12 B.12 C ．－32D.326．已知角α终边上一点P 的坐标是(2sin 2，－2cos 2)，则sin α等于( ) A ．sin 2 B ．－sin 2 C ．cos 2 D ．－cos 27．设α为第二象限角，其终边上一点为P (m ，5)，且cos α＝24m ，则sin α的值为________．[高考真题体验]1．（2018•新课标Ⅰ）已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点(1,)A a ，(2,)B b ，且2cos23α=，则||(a b -= ) A ．15B 5C 25D ．12．（2020新课标I ）若tan 0α>，则A ．sin 20α>B ． cos 0α>C ． sin 0α>D ． cos20α>3．（2018全国课标）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ= A ．45- B ．35- C ． 35 D ． 454．（2018浙江）已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边过点34(,)55P --． (1)求sin()απ+的值； (2)若角β满足5sin()13αβ+=，求cos β的值．5．(2016·高考)已知角θ的顶点为坐标原点，始边为x 轴的正半轴，若P (4，y )是角θ终边上一点，且sin θ＝－255，则y ＝________.突破点二 同角三角函数关系式的应用[例1] (1)若sin α＋cos α＝15，α∈(0，π)，则sin α－cos α的值为________．(2)已知tan θ＝2，则sin θcos θ＝________.跟踪训练：1．若本例(1)改为sin α＋cos α＝15，α∈⎪⎭⎫⎝⎛-0,2π求tan α.2．若本例(2)改为，tan θ＝2，求sin 2θ＋sin θcos θ－2cos 2θ的值．3．若sin θ·cos θ＝12，则tan θ＋cos θsin θ＝________.4．若cos θ＝35，sin θ＝－45，则角θ的终边所在的直线方程为( )A ．3x ＋4y ＝0B ．4x ＋3y ＝0C ．3x －4y ＝0D ．4x －3y ＝05．已知sin α＋cos α＝13，则sin 2⎪⎭⎫⎝⎛-απ4＝( )A.118 B.1718 C.89 D.296．若θ∈⎥⎦⎤⎢⎣⎡2,4ππ，sin 2θ＝378，则sin θ＝( ) A.35 B.45 C.74D.347．在△ABC 中，已知2cos 2A －3cos(B ＋C )＝2，则A ＝________.[高考真题体验]1．（2019•新课标Ⅱ）已知(0,)2πα∈，2sin2cos21αα=+，则sin (α= )A ．15B 5C 3D 252．（2016新课标卷3）若3tan 4α= ，则2cos 2sin 2αα+= A ．6425 B ． 4825 C ．1 D ．16253．（2018浙江）已知210cos 2sin ,=+∈αααR ，则=α2tan （ ） A ．34 B ．43 C ．43- D ．34-4．（2017新课标Ⅱ）若θ为第二象限角，1tan()42πθ+=，则sin cos θθ+= ．5．（2016•新课标Ⅰ）已知θ是第四象限角，且3sin()45πθ+=，则tan()4πθ-= ．突破点三 三角恒等变换[例1] (1)已知tan ⎪⎭⎫ ⎝⎛+4πα＝12，且－π2＜α＜0，则⎪⎭⎫ ⎝⎛-+4cos 2sin sin 22πααα等于( )A ．－255B ．－3510C ．－31010 D.255(2)已知α∈⎪⎭⎫ ⎝⎛2,0π，且2sin 2α－sin α·cos α－3cos 2α＝0，则12cos 2sin 4sin ++⎪⎭⎫ ⎝⎛+ααπα＝________.跟踪训练：1．已知cos ⎪⎭⎫ ⎝⎛-απ2＋sin ⎪⎭⎫ ⎝⎛-απ32＝235，则cos ⎪⎭⎫ ⎝⎛+32πα＝________.[例2] (1)已知cos α＝17，cos(α－β)＝1314，0＜β＜α＜π2，则β＝________.(2)已知α，β∈(0，π)，且tan(α－β)＝12，tan β＝－17，则2α－β的值为________．跟踪训练：1．设α，β为钝角，且sin α＝55，cos β＝－31010，则α＋β的值为( ) A.3π4 B.5π4 C.7π4D.5π4或7π42．已知tan α＝－13，cos β＝55，α∈⎪⎭⎫ ⎝⎛ππ,2，β∈⎪⎭⎫⎝⎛2,0π，求tan(α＋β)的值，并求出α＋β的值．3．tan 15°＋1tan 15°＝( )A ．2B ．2＋ 3C ．4D.4334. 2cos 10°－sin 20°sin 70°的值是( )A.12B.32C. 3D. 25．已知θ∈(0，π)，且sin ⎪⎭⎫⎝⎛-4πθ＝210，则tan 2θ＝( ) A.43B.34C ．－247D.2476．若点P (cos α，sin α)在直线y ＝－2x 上，则sin 2α＋2cos 2α＝________.7．设sin 2α＝－sin α，α∈⎪⎭⎫⎝⎛ππ,2，则tan 2α的值是________．8．已知α∈⎪⎭⎫⎝⎛ππ,2，且sin α2＋cos α2＝62. (1)求cos α的值；(2)若sin(α－β)＝－35，β∈⎪⎭⎫⎝⎛ππ,2，求cos β的值．9．已知sin α＋cos α＝22，则1－2sin2⎪⎭⎫ ⎝⎛-απ4＝( ) A.12 B.32C ．－12D ．－3210．已知sin α＝55，sin(α－β)＝－1010，α，β均为锐角，则角β等于( ) A.5π12 B.π3 C.π4 D.π611．若tan α＝lg(10a )，tan β＝lg 1a ，且α＋β＝π4，则实数a 的值为________．[高考真题体验]1. （2021全国甲）若cos 0,,tan 222sin παααα⎛⎫∈= ⎪-⎝⎭，则tan α=（ ）A.15D.32．（2020全国Ⅰ）已知() 0,πα∈，且3cos28cos 5αα-=，则sin α= （ ）A ．3B ．23C ．13D ．93．(2016·高考全国丙卷)若tan α＝34，则cos 2α＋2sin 2α＝( )A.6425B.4825 C ．1D.16254．（2020全国Ⅲ）已知2tan tan 74θθπ⎛⎫-+= ⎪⎝⎭，则tan θ= （ ）A ．2-B ．1-C ．1D ．25．（2019•新课标Ⅲ）函数()2sin sin 2f x x x =-在[0，2]π的零点个数为( ) A ．2 B ．3C ．4D ．56．(2017·高考四川卷)已知sin α＋2cos α＝0，则2sin αcos α－cos 2α的值是________．7．(2016·高考)cos 2π8－sin 2π8＝________.突破点四 三角函数值域问题[例1] (1)函数y ＝2sin ⎪⎭⎫⎝⎛-36ππx (0≤x ≤9)的最大值与最小值之和为( ) A ．2－3 B ．0 C ．－1 D ．－1－ 3(2)当x ∈⎥⎦⎤⎢⎣⎡67,6ππ时，函数y ＝3－sin x －2cos 2x 的最小值是________，最大值是________．跟踪训练：1．若在本例(1)中，x 的范围变为“－1≤x ≤9”，其它不变，如何选答案．2．若将本例(2)中的函数换为“y ＝sin x －cos x ＋sin x cos x ，x ∈[0，π]”，如何求解？3．函数f (x )＝3sin ⎪⎭⎫⎝⎛-62πx 在区间⎥⎦⎤⎢⎣⎡2,0π上的值域为( ) A.⎥⎦⎤⎢⎣⎡-23,23 B.⎥⎦⎤⎢⎣⎡-3,23C.⎥⎦⎤⎢⎣⎡-233,233 D.⎥⎦⎤⎢⎣⎡-3,233 4．(2020·山东烟台月考)函数y ＝sin x －cos x ＋sin x cos x 的值域为__________________.突破点五 三角函数的单调性和周期性[例1] (1)(2016·高考山东卷)函数f (x )＝(3sin x ＋cos x )(3cos x －sin x )的最小正周期是( ) A.π2 B ．π C.32π D ．2π(2)已知ω＞0，函数f (x )＝sin ⎪⎭⎫⎝⎛+4πωx 在⎪⎭⎫⎝⎛ππ,2上单调递减，则ω的取值范围是( ) A.⎥⎦⎤⎢⎣⎡45,21B.⎥⎦⎤⎢⎣⎡43,21C.⎥⎦⎤ ⎝⎛21,0D ．(0,2]跟踪训练：1．已知函数f (x )＝2sin ⎪⎭⎫⎝⎛-42πωx (ω＞0)的最大值与最小正周期相同，则函数f (x )在[]1,1-上的单调增区间为________．2．若将本例(2)改为f (x )＝sin ωx 在⎪⎭⎫⎝⎛ππ,2上为增函数(ω＞0)，如何求ω的范围？3．（2014新课标I ）在函数①|2|cos x y =，②|cos |x y = ，③)62cos(π+=x y ，④)42tan(π-=x y 中，最小正周期为π的所有函数为A ． ②④B ． ①③④C ． ①②③D ． ①③4．（2018•新课标Ⅱ）若()cos sin f x x x =-在[a -，]a 是减函数，则a 的最大值是( ) A ．4π B ．2π C ．34π D ．π5．（2018•新课标Ⅲ）函数2tan ()1xf x tan x=+的最小正周期为( )A ．4π B ．2π C ．π D ．2π6．（2019•新课标Ⅱ）下列函数中，以2π为周期且在区间(4π，)2π单调递增的是( ) A ．()|cos2|f x x = B ．()|sin 2|f x x =C ．()cos ||f x x =D ．()sin ||f x x =7．函数f (x )＝sin ⎪⎭⎫⎝⎛-42πx 在⎥⎦⎤⎢⎣⎡2,0π上的单调递增区间是________．8．已知f (x )＝sin ⎪⎭⎫⎝⎛+3πωx (ω＞0)，f ⎪⎭⎫ ⎝⎛6π＝f ⎪⎭⎫ ⎝⎛3π，且f (x )在区间⎪⎭⎫⎝⎛3,6ππ上有最小值，无最大值，则ω＝________.突破点六 三角函数的奇偶性、对称性[例1] (1)下列函数中，最小正周期为π，且为奇函数的是( ) A ．y ＝cos ⎪⎭⎫⎝⎛+22πx B ．y ＝sin ⎪⎭⎫⎝⎛+22πx C ．y ＝sin 2x ＋cos 2x D ．y ＝sin x ＋cos x(2)(2016·高考全国甲卷)若将函数y ＝2sin 2x 的图象向左平移π12个单位长度，则平移后图象的对称轴为( )A ．x ＝k π2－π6(k ∈Z )B ．x ＝k π2＋π6(k ∈Z )C ．x ＝k π2－π12(k ∈Z )D ．x ＝k π2＋π12(k ∈Z )(3)(2017·吉林长春模拟)函数f (x )＝sin(2x ＋φ)⎪⎭⎫⎝⎛<2πϕ向左平移π6个单位后是奇函数，则函数f (x )在⎥⎦⎤⎢⎣⎡2,0π上的最小值为________．跟踪训练：1．已知函数f (x )＝a sin x ＋b cos x (a ，b 为常数，a ≠0)在x ＝π4处取得最小值，则函数g (x )＝f ⎪⎭⎫⎝⎛-x 43π是( ) A ．偶函数且它的图象关于点(π，0)对称 B ．偶函数且它的图象关于点⎪⎭⎫⎝⎛0,23π对称 C ．奇函数且它的图象关于点⎪⎭⎫⎝⎛0,23π对称 D. 奇函数且它的图象关于点(π，0)对称2．已知f (x )＝cos(3x ＋φ)－3sin(3x ＋φ)为偶函数，则φ可以取的一个值为( ) A.π6 B.π3 C ．－π6D ．－π33．（2020全国Ⅲ）已知函数()1sin sin f x x x=+，则 ( )A ．()f x 的最小值为2B ．()f x 的图像关于y 轴对称C ．()f x 的图像关于直线x =π对称D ．()f x 的图像关于直线2x π=对称4．已知函数y ＝sin ⎪⎭⎫⎝⎛-x 23π，则函数在[－π，0]上的单调递减区间为________．5．与函数y ＝tan ⎪⎭⎫⎝⎛+42πx 的图象不相交的直线是( ) A ．x ＝π2 B ．y ＝π2 C ．x ＝π8 D ．y ＝π86．已知函数f (x )＝2cos(ωx ＋φ)＋b 对任意实数x 有f ⎪⎭⎫⎝⎛+4πx ＝f (－x )成立，且f ⎪⎭⎫⎝⎛8π＝1，则实数b 的值为( ) A ．－1 B ．3 C ．－1或3 D ．－37．设函数y ＝sin(ωx ＋φ)(ω＞0，φ∈⎪⎭⎫⎝⎛-2,2ππ)的最小正周期为π，且其图象关于直线x ＝π12对称，则在下面四个结论：①图象关于点⎪⎭⎫⎝⎛0,4π对称；②图象关于点⎪⎭⎫ ⎝⎛0,3π对称；③在⎥⎦⎤⎢⎣⎡6,0π上是增函数；④在⎥⎦⎤⎢⎣⎡-0,6π上是增函数中，所有正确结论的序号为________． 8．设函数f (x )＝3sin ⎪⎭⎫⎝⎛+42ππx ，若存在这样的实数x 1，x 2，对任意的x ∈R ，都有f (x 1)≤f (x )≤f (x 2)成立，则|x 1－x 2|的最小值为________．9．已知a ＞0，函数f (x )＝－2a sin ⎪⎭⎫⎝⎛+62πx ＋2a ＋b ，当x ∈⎥⎦⎤⎢⎣⎡2,0π时，－5≤f (x )≤1.求常数a ，b 的值；10．函数f (x )＝2sin(ωx ＋φ)对任意x 都有f ⎪⎭⎫ ⎝⎛+x 6π＝f ⎪⎭⎫ ⎝⎛-x 6π，则f ⎪⎭⎫⎝⎛6π等于( ) A ．2或0 B ．－2或2 C ．0D ．－2或0突破点七 由三角函数图象求解析式[例1] (1)如图是函数y ＝A sin(ωx ＋φ)＋2(A ＞0，ω＞0)的图象的一部分，它的振幅、周期、初相各是( )A ．A ＝3，T ＝4π3，φ＝－π6B ．A ＝1，T ＝4π3，φ＝3π4C ．A ＝1，T ＝4π3，φ＝－3π4D ．A ＝1，T ＝4π3，φ＝－π6(2)(2016·高考全国甲卷)函数y ＝A sin(ωx ＋φ)的部分图象如图所示，则( )A ．y ＝2sin ⎪⎭⎫ ⎝⎛-62πx B ．y ＝2sin ⎪⎭⎫⎝⎛-32πx C ．y ＝2sin ⎪⎭⎫⎝⎛+6πx D ．y ＝2sin ⎪⎭⎫⎝⎛+3πx 跟踪训练：1．已知函数f (x )＝2sin(ωx ＋φ)(ω＞0，且|φ|＜π2)的部分图象如图所示，则函数f (x )的一个单调递增区间是( )A.⎥⎦⎤⎢⎣⎡-125,127ππ B.⎥⎦⎤⎢⎣⎡--12,127ππC.⎥⎦⎤⎢⎣⎡-127,12ππ D.⎥⎦⎤⎢⎣⎡-125,12ππ 2．如图是函数y ＝A sin(ωx ＋φ)(A ＞0，ω＞0，|φ|＜π)的部分图象，则该函数的解析式为________．3．已知函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0,0＜φ＜π2)的部分图象如图所示．(1)求函数f (x )的解析式； (2)若f ⎪⎭⎫ ⎝⎛+θπ65＝－125，且0＜θ＜π3，求f ⎪⎭⎫ ⎝⎛-3πθ的值．4．已知函数f (x )＝A sin(ωx ＋φ)⎪⎭⎫⎝⎛<>>2,0,0πϕωA 的部分图象如图所示，则φ＝( )A ．－π6B.π6 C ．－π3D.π35．函数y ＝cos(2x ＋φ)(－π≤φ＜π)的图象向右平移π2个单位后，与函数y ＝sin ⎪⎭⎫ ⎝⎛+32πx 的图象重合，则φ＝________.6．（2020全国Ⅰ）设函数()cos π6f x x ω=+⎛⎫⎪⎝⎭在[],-ππ的图像大致如下图，则()f x 的最小正周期为（ ）A ．10π9 B ．7π6 C ．4π3 D ．3π27．（2020浙江 多选）函数cos sin y x x x =+在区间[],-ππ的图像大致为 （ ）A ．B ．C ．D ．8．（2020山东）右图是函数sin()y x ωϕ=+的部分图像，则sin()=x ωϕ+ （ ）A ．πsin()3x +B ．πsin(2)3x -C ．πcos(2)6x +D ．5πcos(2)6x -突破点八 图像平移问题1．要得到函数y ＝sin ⎪⎭⎫⎝⎛-34πx 的图象，只需将函数y ＝sin 4x 的图象( ) A ．向左平移π12个单位B ．向右平移π12个单位C ．向左平移π3个单位D ．向右平移π3个单位2．为得到函数y ＝cos ⎪⎭⎫⎝⎛+32πx 的图象，只需将函数y ＝sin 2x 的图象( ) A ．向左平移5π12个单位长度 B ．向右平移5π12个单位长度C ．向左平移5π6个单位长度D ．向右平移5π6个单位长度3．（2019天津）已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数，将()y f x =的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图像对应的函数为()g x ．若()g x 的最小正周期为2π，且π4g ⎛⎫= ⎪⎝⎭3π8f ⎛⎫= ⎪⎝⎭A ．2-B ．CD ．2 4．（2013福建）将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象，若)(),(x g x f 的图象都经过点)23,0(P ，则ϕ的值可以是 A ．35πB ．65πC ．2πD ．6π 5．（2020江苏）将函数3sin(2)4y x π=+的图象向右平移6π个单位长度，则平移后的图象中与y 轴最近的对称轴的方程是 ．6．（2016新课标卷3）函数sin y x x =的图像可由函数sin y x x =的图像至少向右平移_____________个单位长度得到．7．（2014重庆）将函数()()⎪⎭⎫⎝⎛<≤->+=220sin πϕπωϕω，x x f 图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移6π个单位长度得到x y sin =的图像，则=⎪⎭⎫⎝⎛6πf ______．三角函数综合演练1．已知角α的顶点在原点，始边为x 轴正半轴，终边与圆心在原点的单位圆交于点A (m ，3m )，则sin 2α＝( ) A ．±34B.34 C ．±32D.322.已知sin ⎪⎭⎫⎝⎛+απ2＝cos(π－α)，则α的取值范围是( ) A ．{α|α＝2k π＋π4，k ∈Z }B ．{α|α＝2k π－π4，k ∈Z }C ．{α|α＝k π＋π2，k ∈Z }D ．{α|α＝k π，k ∈Z }3．函数y ＝sin 24x 是( ) A ．最小正周期为π4的奇函数B ．最小正周期为π4的偶函数C ．最小正周期为π的奇函数D ．最小正周期为π的偶函数4．若函数f (x )＝sin(ωx ＋φ)(ω＞0，|φ|＜π2)的部分图象如图所示，则ω和φ的取值是( )A ．ω＝1，φ＝π3B ．ω＝1，φ＝－π3C ．ω＝12，φ＝π6D ．ω＝12，φ＝－π65．已知tan(α＋β)＝25，tan ⎪⎭⎫ ⎝⎛-4πβ＝14，则tan ⎪⎭⎫ ⎝⎛+4πα＝( )A.318 B.1318 C.322D.13226．已知函数f (x )＝3sin ωx (ω＞0)的周期是π，将函数f (x )的图象沿x 轴向右平移π8个单位，得到函数y ＝g (x )的图象，则函数g (x )的解析式为( )A ．g (x )＝3sin ⎪⎭⎫ ⎝⎛-82πx B ．g (x )＝3sin ⎪⎭⎫⎝⎛-42πx C ．g (x )＝－3sin ⎪⎭⎫⎝⎛+82πx D ．g (x )＝－3sin ⎪⎭⎫⎝⎛+42πx 7．函数y ＝sin 2x ＋2sin x cos x ＋3cos 2x 的最小正周期和最小值分别为( ) A ．π，2－ 2 B ．π，0 C ．2π，0D ．2π，2－ 28．已知函数f (x )＝sin ⎪⎭⎫⎝⎛+4πωx (ω＞0)在⎪⎭⎫⎝⎛ππ,2上单调递减，则ω的取值范围可以是( ) A.⎥⎦⎤⎢⎣⎡45,21B. ⎥⎦⎤⎢⎣⎡45,0C. ⎥⎦⎤ ⎝⎛21,0D.(]2,09．将函数y ＝3sin ⎪⎭⎫⎝⎛+32πx 的图象向右平移π2个单位长度，所得图象对应的函数( ) A ．在区间⎥⎦⎤⎢⎣⎡127,12ππ上单调递减 B ．在区间⎥⎦⎤⎢⎣⎡127,12ππ上单调递增 C ．在区间⎥⎦⎤⎢⎣⎡-3,6ππ上单调递减 D ．在区间⎥⎦⎤⎢⎣⎡-3,6ππ上单调递增 10．已知函数y ＝sin x ＋a cos x 的图象关于直线x ＝5π3对称，则函数y ＝a sin x ＋cos x 的图象关于直线( )A ．x ＝π3对称B ．x ＝2π3对称C ．x ＝11π6对称D ．x ＝π对称11．函数f (x )＝sin(x ＋2φ)－2sin φcos(x ＋φ)的最大值为________．12．在函数①y ＝cos|2x |，②y ＝|cos x |，③y ＝cos ⎪⎭⎫⎝⎛+62πx ，④y ＝tan ⎪⎭⎫ ⎝⎛-42πx 中，最小正周期为π的所有函数为________．13．(本小题满分10分)已知函数f (x )＝3cos 4x －2cos 2⎪⎭⎫ ⎝⎛+42πx ＋1.(1)求函数f (x )的最小正周期；(2)求函数f (x )在区间⎥⎦⎤⎢⎣⎡-4,6ππ上的取值范围．14. （2021浙江）设函数()sin cos (R)f x x x x =+∈.（1）求函数22y f x π⎡⎤⎛⎫=+ ⎪⎢⎥⎝⎭⎣⎦的最小正周期； （2）求函数()4y f x f x π⎛⎫=- ⎪⎝⎭在0,2π⎡⎤⎢⎥⎣⎦上的最大值.。

高一数学讲义 第六章 三角函数6.1 正弦函数和余弦函数的性质与图像每一个实数x 都有唯一确定的角与之对应，而这个角又可以与它的三角比sin x （或cos x ）对应，即每个实数x 都可以与唯一确定的值sin x （或cos x ）对应．按这样的对应法则建立起来的函数，表示为sin y x =（或cos y x =），叫做自变量为x 的正弦函数（或余弦函数）．sin y x =和cos y x =的定义域都是R ，值域都是[]11-，． ()()sin cos y x x y x x =∈=∈R R ，的性质：1．奇偶性根据诱导公式，对x ∀∈R ，有()sin sin x x -=-，()cos cos x x -=， ()sin y x x ∴=∈R 是奇函数，()cos y x x =∈R 是偶函数．2．周期性对于()()sin 2πsin k x x k +=∈Z ，当0k ≠时，2πk 是()sin f x x =的周期，2π是不是()sin f x x =的最小正周期呢？假设存在T ，满足02πT <<，且是函数()sin f x x =的周期，即()()f x T f x +=，令π2x =，得ππ1sinsin cos 22T T ⎛⎫==+= ⎪⎝⎭，与02πT <<时，cos 1T <矛盾． 3．函数图像 若把角x 的顶点置于坐标系uOv 的原点，角x 的始边与Ou 轴重合，终边与单位圆的交点为()P u v ，则sin cos x v x u ==，．当x 在区间[)02π，上连续变化的时候，都有单位圆上点()P u v ，与之对应．相应地在坐标系xOy 中，描绘出点()Q x v ，和点()R x u ，．点Q 便勾画出正弦函数sin y x =一个周期的图像（见图6－1），点R便勾画出余弦函数cos y x =一个周期的图像（见图6－2）．然后再利用函数的周期性将图像向左右延伸，便得到正弦函数和余弦函数的图像（见图6－3）．图6-34．单调性当ππ22x ⎡⎤∈-⎢⎥⎣⎦，时，角x 的始边与单位圆的交点的纵坐标随x 的递增而递增，∴函数sin y x =在ππ22⎡⎤-⎢⎥⎣⎦，上单调增．当π3π22x ⎡⎤∈⎢⎥⎣⎦，时，角x 的始边与单位圆的交点的纵坐标随x 的递增而递减，∴函数sin y x =在π3π22⎡⎤⎢⎥⎣⎦，上单调减．同理可得，函数cos y x =在[]0π，上单调减，在[]π2π，上单调增．拓展：函数sin y x =在ππ2ππ2π22k k ⎡⎤-+⎢⎥⎣⎦，上单调增，在π3π2π2π22k k ⎡⎤++⎢⎥⎣⎦，上单调减，其中k ∈Z ． 函数cos y x =在[]2π2ππk k +，上单调减，在[]2ππ2π2πk k ++，上单调增，其中k ∈Z ． 说明：若()y f x =是定义在实数集R 上的周期函数，最小正周期是T ，[]a b ，是()y f x =的单调区间，则对任意整数k ，[]kT a kT b ++，均是()y f x =的单调区间． 5．最值回顾：函数sin y x =在ππ2π2π22k k ⎡⎤-+⎢⎥⎣⎦，上单调增，在π3π2π2π22k k ⎡⎤++⎢⎥⎣⎦，上单调减，其中k ∈Z ． 函数cos y x =在[]2π2ππk k +，上单调减，在[]2ππ2π2πk k ++，上单调增，其中k ∈Z ． 结论：当()π2π2x k k =+∈Z 时，函数sin y x =取最大值1； 当()π2π2x k k =-∈Z 时，函数sin y x =取最小值1-； 当()2πx k k =∈Z 时，函数cos y x =取最大值1； 当()2ππx k k =+∈Z 时，函数cos y x =取最小值1-．例1．求证：()sin f x x =是偶函数．证明：对x ∀∈R ，有()()()sin sin f x x x f x -=-==， ()sin f x x ∴=是偶函数．例2．研究函数()sin cos f x x x =+的奇偶性． 解：πππsin cos 0444f ⎛⎫⎛⎫⎛⎫-=-+-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， πππsin cos 444f ⎛⎫⎛⎫⎛⎫=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()sin cos f x x x ∴=+既不是奇函数，也不是偶函数．另解：若()()f x f x -=，即()()sin cos sin cos x x x x -+-=+， 则sin 0x =，即πx k =，k ∈Z ．若()()f x f x -=-，即()()sin cos sin cos x x x x -+-=--， 则cos 0x =，即ππ2x k =+，k ∈Z ． ()sin cos f x x x ∴=+既不是奇函数，也不是偶函数．说明：对于()sin cos f x x x =+，虽然有无数多个实数x ，满足()()f x f x -=，但是()f x 并不是偶函数．同理()f x 也不是奇函数．函数的奇偶性是函数的整体性质．若()f x 是奇函数，则()()f x f x -=-对于定义域内的每一个x 恒成立； 若()f x 是偶函数，则()()f x f x -=对于定义域内的每一个x 恒成立．例3．已知A ωϕ、、都是常数，且0A >，ω>0，求证：函数()()sin f x A x ωϕ=+的最小正周期是2πω．解：对于任何实数x ，()2π2πsin sin 2πf x A x A x ωϕωϕωω⎡⎤⎛⎫⎛⎫+=++=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦()()sin A x f x ωϕ=+=，2πω∴是函数()()sin f x A x ωϕ=+的周期．可以证明2πω是函数()()sin f x A x ωϕ=+的最小正周期．例4．作出函数sin cos y x x =+在[]02π，上的图像．解：πsin cos 4y x x x ⎛⎫=+=+ ⎪⎝⎭．描点作图，见图6－4．图6-4例5．求函数sin cos y x x =+的单调增区间． 解：πsin cos 4y x x x ⎛⎫=+=+ ⎪⎝⎭．πππ2π2π242k x k k -++∈Z ，≤≤，3ππ2π2π44k x k k ∴-+∈Z ，≤≤． ∴函数sin cos y x x =+的单调增区间是()3ππ2π2π44k k k ⎡⎤-+∈⎢⎥⎣⎦Z ，．例6．求函数π2cos 33y x ⎛⎫=- ⎪⎝⎭的单调减区间．解：π2π32ππ3k xk k -+∈Z ，≤≤，2ππ2π4π3939k k x k ∴++∈Z ，≤≤．∴函数π2cos 33y x ⎛⎫=- ⎪⎝⎭的单调减区间是()2ππ2π4π3939k k k ⎡⎤++∈⎢⎥⎣⎦Z ，．例7．求函数()sin cos 0y a x b x ab =+≠的最值． 解：()sin cos y a x b x x ϕ=++，其中tan baϕ=， max min y y ∴==．例8．求下列函数的最值： （1）2sin 2cos y x x =+；（2）()22sin cos y a x b x a b =+≠； （3）()()3sin 2105sin 270y x x =+︒++︒；（4）66sin cos y x x =+．解：（1）()2111sin 2cos sin 2cos22222y x x x x x ϕ=+=++=++，max y ∴min y =． （2）()222sin cos sin y a x b x a b x b =+=-+，∴若a b >，则2sin 1x =时，max y a =；2sin 0x =时，min y b =．若a b <，则2sin 0x =时，max y b =；2sin 1x =时，min y a =． {}max max y a b ∴=，，{}min min y a b =，．另解：221cos21cos2sin cos cos22222x x b a a by a x b x ab x -+-+=+=+=+， ∴若a b >，则cos21x =-时，max y a =；cos21x =时，min y b =．若a b <，则cos21x =时，max y b =；cos21x =-时，min y a =． {}max max y a b ∴=，，{}min min y a b =，．（3）()()3sin 2105sin 270y x x =+︒++︒3cos10sin23sin10cos25cos70sin25sin70cos2x x x x =︒+︒+︒+︒()()3cos105cos70sin 23sin105sin 70cos2x x =︒+︒+︒+︒ ()7sin 2x ϕ=+，其中3sin105sin 70tan 3cos105cos70ϕ︒+︒=︒+︒，max 7y ∴=，min 7y =-．（4）664224sin cos sin sin cos cos y x x x x x x =+=-+()2222223sin cos 3sin cos 1sin 24x x x x x =+-=-，max 1y ∴=，min 14y =． 说明：在求函数的最值过程中，始终要贯彻“统一名称统一角”的观点． 基础练习1．判断下列函数的奇偶性，并求最小正周期： （1）()sin sin 2f x x x =+； （2）()sin f x x x =； （3）()πsin πf x x =；（4）()2sin sin 2f x x x =+；（5）()ππcos cos 33f x x x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭；（6）()22sin 2sin cos 3cos f x x x x x =++； （7）()66sin cos f x x x =+；（8）()()2222sin cos 0f x a x b x a b =++≠．2．用五点法分别作出下列各函数的图像，并说明这些函数的图像和sin y x =图像的区别．（1）2sin 1y x =-；（2）12sin 2y x =．3．观察正弦曲线和余弦曲线．写出满足下列条件的区间： （1）sin 0x >； （2）cos 0x <； （3）1sin 2x >； （4）cos x <． 4．求下列函数的单调区间：（1）πcos 27y x ⎛⎫=-- ⎪⎝⎭；（2）π2sin 34y x ⎛⎫=-- ⎪⎝⎭；（3）lg cos 13xy ⎛⎫= ⎪⎝⎭．5．求下列函数的最值，及取得相应最值的x 值．（1）π32sin 3y x ⎛⎫=-- ⎪⎝⎭； （2）23cos 4sin 2y x x =--；（3）22sin 3sin 1y x x =-+，π2π33x ⎡⎤∈⎢⎥⎣⎦，．6．确定函数131log 4y x ⎤⎛⎫=- ⎪⎥⎝⎭⎦的定义域、值域、单调区间、奇偶性、周期性．能力提高7．设π02αβγ⎛⎫∈ ⎪⎝⎭、、，，满足：()()cos cos sin sin cos ααββγγ===，，，则αβγ，，的大小关系为__________．8．求下列函数的周期： （1）sin3cos y x x =+；（2）1sin cos 1sin cos 1sin cos 1sin cos x x x xy x x x x+++-=++-++； （3）()2cos 325y x =-+．9．求5sin 2π2y x ⎛⎫=+ ⎪⎝⎭的图像的对称轴方程．10．（1）求函数()2sin sin f x a x x =-的最大值()g a ，并画出()g a 的图像．（2）若函数()2cos sin f x x a x b =-+的最大值为0，最小值为4-，实数0a >，求a b ，的值．6.2 正切函数的性质与图像定义：对于ππ2x x x k k ⎧⎫∀∈≠+∈⎨⎬⎩⎭Z ，都有唯一确定的值tan x 与之对应，按照此对应法则建立的函数tan y x =，叫做正切函数． 正切函数的性质：1．周期性ππ2x x x k k ⎧⎫∀∈≠+∈⎨⎬⎩⎭Z ，，有()tan πtan k x x k +=∈Z ，， tan t x ∴=是周期函数．可以证明函数tan y x =的最小正周期是π（见图6－5）．图6-52．奇偶性ππ2x x x k k ⎧⎫∀∈≠+∈⎨⎬⎩⎭Z ，，有()tan tan x x -=-，tan y x ∴=是奇函数． 3．单调性12π02x x ⎡⎫∀∈⎪⎢⎣⎭、，，且12x x <，()121212sin tan tan cos cos x x x x x x --=12π02x x -<-<， ()12sin 0x x ∴-<． 1cos 0x >，2cos 0x >，()121212sin tan tan 0cos cos x x x x x x -∴-=>，即tan y x =在π0,2⎡⎫⎪⎢⎣⎭上单调增．tan y x =是奇函数， tan y x =在ππ22⎛⎫- ⎪⎝⎭，上单调增．tan y x =是周期为π的函数，∴函数tan y x =的单调增区间是()ππππ22k k k ⎛⎫-+∈ ⎪⎝⎭Z ，．4．值域函数tan y x =的值域是R ．正切函数tan y x =在ππ22⎛⎫- ⎪⎝⎭，的图像如图6－6：图6-6利用正切函数的周期性，得到正切函数的图像． 例1．判断函数()tan 1lgtan 1x f x x +=-的奇偶性．解：函数的定义域应满足tan 10tan 1x x +>-，即tan 1x <-，或tan 1x >．于是定义域是()ππππππππ2442k k k k k ⎛⎫⎛⎫--++∈ ⎪ ⎪⎝⎭⎝⎭Z ，，，定义域是关于原点对称的． ()()()1tan 11tan 1tan lg lg lg tan 1tan 1tan 1x x x f x x x --+-+⎛⎫-=== ⎪-----⎝⎭()tan 1lgtan 1x f x x +=-=--．所以，tan 1lgtan 1x y x +=-是奇函数．例2．解不等式：tan21x -≤．解：在ππ22⎛⎫- ⎪⎝⎭，内，πtan 14⎛⎫-=- ⎪⎝⎭．∴不等式tan21x -≤的解集由不等式()πππ2π24k x k k -<-∈Z ≤确定，解得()ππππ22428k k x k -<-∈Z ≤， ∴不等式tan21x -≤的解集为ππππ22428k k x x k ⎧⎫-<-∈⎨⎬⎩⎭Z ，≤．基础练习 1．有人说：“正切函数在整个定义域内是单调递增的函数．”这句话对吗？为什么？ 2．求下列函数的周期： （1）()()tan 0y ax b a =+≠； （2）tan cot y x x =-． 3．求函数11tan 2y x=+五的定义域．4．求函数22tan tan 1tan tan 1x x y x x -+=++的最大值、最小值，并求函数取得最大值或最小值时自变量x 的集合．5．求下列函数的最大值和最小值：（1）sin 2sin 3x y x -=-；（2）sin 2cos 3x y x -=-．能力提高6．求函数sin cos π0,sin cos 2x x y x x x ⎛⎫⎡⎤=∈ ⎪⎢⎥+⎣⎦⎝⎭的最值．7．根据条件比较下列各组数的大小： （1）已知ππ32θ<<，比较sin θ，cot θ，cos θ的大小； （2）已知π04θ<<，比较sin θ，()sin sin θ，()sin tan θ的大小； （3）已知π02θ<<，比较cos θ，()cos sin θ，()sin cos θ的大小． 6.3 函数()sin y A x d ωϕ=++的图像与性质例1．对下列函数与函数()sin y x x =∈R 进行比较研究（最好利用几何画板进行动态的研究）： （1）()sin 01y A x x A A =∈>≠R ，，；（2）()sin 01y x x ωωω=∈>≠R ，，； （3）()()sin 0y x x ϕϕϕ=+∈∈≠R R ，，； （4）()sin 0y x d x d d =+∈∈≠R R ，，； （5）()()sin 01100y A x d x A A d d ωϕωωϕϕ=++∈>≠>0≠∈≠∈≠R R R ，，，，，，，，． 解：（1）函数sin y A x =与sin y x =都是奇函数，具有相同的周期和单调区间，但值域不同．当1A >时，函数sin y A x =的图像可以看成由函数sin y x =的图像纵向拉伸得到；当01A <<时，函数sin y A x =的图像可以看成由函数sin y x =的图像纵向压缩得到（见图6－7）．图6-7（2）函数sin y x ω=与sin y x =都是奇函数，值域相同，但函数sin y x ω=与sin y x =的周期和单调区间都不同．当ω>1时，函数sin y x ω=的图像可以看成由函数sin y x =的图像横向压缩得到；当0ω<<1时．函数sin y x ω=的图像可以看成由函数sin y x =的图像横向拉伸得到（见图6－8）．图6-8（3）当()πk k ϕ-+=∈Z Z 时，函数()sin y x ϕ=+是奇函数；当()ππ2k k ϕ=+∈Z ，函数()sin y x ϕ=+偶函数；函数()sin y x ϕ=+与sin y x =具有相同的周期和值域；当()2πk k ϕ-+=∈Z Z 时，函数()sin y x ϕ=+与sin y x =具有相同的单调区间．当ϕ>0时，函数()sin y x ϕ=+的图像可以看成由函数sin y x =的图像向左平移得到；当ϕ<0时，函数()sin y x ϕ=+的图像可以看成由函数sin y x =的图像向右平移得到（见图6－9）．图6-9（4）函数sin y x d =+既不是奇函数，也不是偶函数；函数sin y x d =+与sin y x =具有相同的周期和单调区间，但值域不同．当0d >时，函数sin y x d =+的图像可以看成由函数sin y x =的图像向上平移得到；当0d <时，函数sin y x d =+的图像可以看成由函数sin y x =的图像向下平移得到（见图6－10）．图6-10（5）函数()sin y A x d ωϕ=++的图像可以由函数sin y x =的图像经过一系列的变换得到．首先把函数sin y x =的图像进行纵向的变化，让函数sin y x =的图像上点的横坐标保持不变，让点的纵坐标变为原来的A 倍，得到函数sin y A x =的图像（见图6－11）．图6-11其次把函数sin y A x =的图像进行横向的变化，让函数sin y A x =的图像七点的纵坐标保持不变，让点的横坐标变为原来的1ω倍，得到函数sin y A x ω=。

P xy AOM T 高一数学三角函数综合提升讲义一．重难点整合：1.第一象限角的集合为{}36036090,k k k αα⋅<<⋅+∈Z第二象限角的集合为{}36090360180,k k k α⋅+<⋅+∈Z第三象限角的集合为{}360180360270,k k k αα⋅+<<⋅+∈Z第四象限角的集合为{}360270360360,k k k αα⋅+<<⋅+∈Z终边在x 轴上的角的集合为{}180,k k αα=⋅∈Z终边在y 轴上的角的集合为{}18090,k k αα=⋅+∈Z终边在坐标轴上的角的集合为{}90,k k αα=⋅∈Z与角α终边相同的角的集合为{}360,k k ββα=⋅+∈Z2.已知α是第几象限角，确定()*n nα∈N 所在象限的方法：先把各象限均分n 等份，再从x轴的正半轴的上方起，依次将各区域标上一、二、三、四，则α原来是第几象限对应的标号即为nα终边所落在的区域． 3.弧度制与角度制的换算公式：2360π=，1180π=，180157.3π⎛⎫=≈ ⎪⎝⎭．4.若扇形的圆心角为()αα为弧度制，半径为r ，弧长为l ，周长为C ，面积为S ，则l r α=，2C r l =+，21122S lr r α==．5.设α是一个任意大小的角，α的终边上任意一点P 的坐标是(),x y ，它与原点的距离是()220r r x y =+>，则sin y r α=，cos x r α=，()tan 0yx xα=≠．6.三角函数在各象限的符号：第一象限全为正，第二象限正弦为正，第三象限正切为正，第四象限余弦为正．7.三角函数线：sin α=MP ，cos α=OM ，tan α=AT ．7.同角三角函数的基本关系：()221sin cos 1αα+=()2222si n 1c o s ,c o sαααα=-=-； ()sin 2tan cos ααα=sin sin tan cos ,cos tan αααααα⎛⎫== ⎪⎝⎭．8.三角函数的诱导公式：()()1sin 2sin k παα+=，()cos 2cos k παα+=，()()tan 2tan k k παα+=∈Z ． ()()2sin sin παα+=-，()cos cos παα+=-，()tan tan παα+=． ()()3sin sin αα-=-，()cos cos αα-=，()tan tan αα-=-． ()()4sin sin παα-=，()cos cos παα-=-，()tan tan παα-=-．口诀：函数名称不变，符号看象限．()5sin cos 2παα⎛⎫-=⎪⎝⎭，cos sin 2παα⎛⎫-= ⎪⎝⎭． ()6sin cos 2παα⎛⎫+=⎪⎝⎭，cos sin 2παα⎛⎫+=- ⎪⎝⎭． 口诀：正弦与余弦互换，符号看象限．9.函数sin y x =的图象上所有点向左平移ϕ个单位长度，得到函数()sin y x ϕ=+的图象；再将函数()sin y x ϕ=+的图象上所有点的横坐标伸长（缩短）到原来的1ω倍（纵坐标不变），得到函数()sin y x ωϕ=+的图象；再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长（缩短）到原来的A 倍（横坐标不变），得到函数()sin y x ωϕ=A +的图象．函数sin y x =的图象上所有点的横坐标伸长（缩短）到原来的1ω倍（纵坐标不变），得到函数sin y x ω=的图象；再将函数sin y x ω=的图象上所有点向左（右）平移ϕω个单位长度，得到函数()sin y x ωϕ=+的图象；再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长（缩短）到原来的A 倍（横坐标不变），得到函数()sin y x ωϕ=A +的图象．10.正弦函数、余弦函数和正切函数的图象与性质： sin y x =cos y x = tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时，max 1y =；当22x k ππ=-()k ∈Z 时，min 1y =-．当()2x k k π=∈Z 时，max 1y =；当2x k ππ=+()k ∈Z 时，min 1y =-．既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数 奇函数单调性 在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z 上是增函数；在32,222k k ππππ⎡⎤++⎢⎥⎣⎦()k ∈Z 上是减函数．在[]()2,2k k k πππ-∈Z 上是增函数；在[]2,2k k πππ+()k ∈Z 上是减函数．在,22k k ππππ⎛⎫-+⎪⎝⎭()k ∈Z 上是增函数．对称性对称中心()(),0k k π∈Z 对称轴()2x k k ππ=+∈Z对称中心(),02k k ππ⎛⎫+∈Z⎪⎝⎭对称中心(),02k k π⎛⎫∈Z ⎪⎝⎭无对称轴函数 性质对称轴()x k k π=∈Z二．典例精析 基础题：1.若角α与β终边相同，则一定有（ ）．A ．180αβ+=B ．0αβ+=C ．360,k k Z αβ-=⋅∈D ．360,k k Z αβ+=⋅∈2.设角α、β满足180180αβ-<<<，则αβ-的范围是___________．(360,0)- ∵αβ<，∴0αβ-< ，又180180α-<< ，180180β-<-< ，∴360360αβ-<-<．综上可知αβ-的范围是3600αβ-<-<． 3.若α为第一象限角，那么sin2α，cos2α，sin α2，cos α2中必定为正值的有( )A ．0个B ．1个C ．2个D ．3个解析：由于α为第一象限角，所以2α为第一或二象限角，sin2α>0，cos2α符号不确定，α2为第一或三象限角，sin α2，cos α2的符号均不确定．故选B. 答案：B4.解答下列问题：(1)若θ在第四象限，试判断sin(cos θ)·cos(sin θ)的符号；(2)若tan(cos θ)·tan(sin θ)>0，试指出θ所在象限，并用图形表示出θ2所取的范围．解：(1)∵θ在第四象限， ∴0<cos θ<1<π2，－π2<－1<sin θ<0，∴sin(cos θ)>0，cos(sin θ)>0， ∴sin(cos θ)·cos(sin θ)>0.(2)由题知⎩⎪⎨⎪⎧ tan(cos θ)>0，tan(sin θ)>0或⎩⎪⎨⎪⎧tan(cos θ)<0，tan(sin θ)<0.∴⎩⎪⎨⎪⎧ 0<cos θ<1，0<sin θ<1或⎩⎪⎨⎪⎧－1<cos θ<0，－1<sin θ<0，即θ在第一或第三象限； 若θ在第一象限，则θ2的取值范围如图①所示；若θ在第三象限，则θ2的取值范围如图②所示(见阴影部分，不含边界)．5.已知tan 1tan 1αα=--，求下列各式的值：（1）sin 3cos sin cos αααα-+；（2）2sin sin cos 2ααα++．解：由已知，得1tan 2α=，则（1）sin 3cos sin cos αααα-+13tan 3521tan 1312αα--===-++； （2）2sin sin cos 2ααα++222sin sin cos 2(sin cos )ααααα=+++22223sin sin cos 2cos sin cos αααααα++=+ 223tan tan 2tan 1ααα++=+ 22113213225112⎛⎫⨯++ ⎪⎝⎭==⎛⎫+ ⎪⎝⎭． 6.已知1sin cos 5αα+=，(0π)θ∈，，求下列各式的值． （1）tan θ； （2）sin cos θθ-； （3）33sin cos θθ+．解：（1）1sin cos 5θθ+=∵，((0π))θ∈，， 21(sin cos )12sin cos 25θθθθ+=+=∴·． 12sin cos 025θθ=-<∴·．sin 0θ>∴，cos 0θ<．联合221sin cos 5sin cos 1θθθθ⎧+=⎪⎨⎪+=⎩，，整理可得225sin 5sin 120θθ--=．解得4sin 5θ=，或3sin 5θ=-（舍去）．4sin 5θ=∴，3cos 5θ=-．4tan 3θ=-∴． （2）2247sin cos (sin cos )12sin cos 1255θθθθθθ-=-=-=+=∵·． （3）3322sin cos (sin cos )(sin cos sin cos )θθθθθθθθ+=++-· 11213771525525125⎛⎫=+=⨯=⎪⎝⎭． 7.化简：︒+︒︒︒+790cos 250sin 430cos 290sin 21．解：︒+︒︒︒+790cos 250sin 430cos 290sin 21=)360270cos()70180sin()36070cos()36070sin(21︒⨯+︒+︒+︒︒+︒︒+︒-+=︒-︒︒︒-70sin 70cos 70cos 70sin 21=︒-︒︒-︒70sin 70cos )70cos 70(sin 2=︒-︒︒-︒70sin 70cos 70cos 70sin =－1．8.已知1cos(75)3α+=°，α是第三象限角，求cos(15)sin(15)αα-+-°°的值 ．解：cos(15)sin(75)αα-=+°°，又α是第三象限角，sin(75)0α+<∴°． 22sin(75)3α+=-∴°． 而1sin(15)cos(75)3αα-=-+=-°°．∴原式221221333+=--=-9.已知角α终边上一点P （－4，3），求)29sin()211cos()sin()2cos(απαπαπαπ+---+的值 【解】∵43tan -==x y α∴ 43tan cos sin sin sin )29sin()211cos()sin()2cos(-==⋅-⋅-=+---+ααααααπαπαπαπ已知cos α=31，cos （α+β）=1，求证：cos （2α+β）=31．证明：∵cos （α+β）=1，∴α+β=2k π．∴cos （2α+β）=cos （α+α+β）=cos （α+2k π）=cos α=31．10.是否存在一个实数k ，使方程286210x kx k +++=的两个根是一个直角三角形的两个锐角的正弦？解：设直角三角形两个锐角为αβ，，则sin sin αβ，是方程286210x kx k +++=的两个根． 90αβ+=∵°，sin cos βα=∴．由根与系数的关系，得3sin cos 421sin cos 8k k αααα⎧+=-⎪⎪⎨+⎪=⎪⎩①· ②2-⨯2①②，整理得298200k k --=，解得121029k k ==-，． 当2k =时，原方程变为281250x x ++=， 1441600∆=-<，∴原方程无解，2k =舍去． 将109k =-代入②，得11sin cos sin sin 72αααβ==-··， sin sin αβ，∴异号，应有sin 0α<或sin 0β<，实际上sin 0α>，sin 0β>， 109k =-∴不满足题意，k ∴值不存在．11.已知函数f (x )＝21log (sin x －cos x )（1）求它的定义域和值域；（2）求它的单调减区间； （3）判断它的奇偶性；（4）判断它的周期性，如果是周期函数，求出它的一个周期. 【分析】 研究复合函数的性质（定义域、值域、单调性、奇偶性、周期性）应同时考虑内层函数与外层函数各自的特性以及它们的相互制约关系.【解】 （1）由题意得sin x －cos x ＞0，即 2 sin(x －π4)＞0从而得2kπ＜x －π4 ＜2kπ＋π，所以函数的定义域为（2kπ＋π4 ，2kπ＋5π4 ）(k ∈Z )∵0＜sin(x －π4 )≤1，∴0＜sin x －cos x ≤ 2即有21log (sin x －cos x )≥21log 2 ＝－12 .故函数的值域是［－12，+∞).（2）∵sin x －cos x ＝ 2 sin （x －π4 )在f (x )的定义域上的单调递增区间为（2kπ＋π4 ，2kπ＋3π4 ）(k ∈Z )，函数f (x )的递减区间为（2kπ＋π4 ，2kπ＋3π4）(k ∈Z ). (3)∵f (x )的定义域在数轴上对应的点不关于原点对称， ∴函数f (x ）是非奇非偶函数.（4）f (x ＋2π)＝21log ［sin(x ＋2π)－cos(x ＋2π)］＝21log （sin x －cos x )＝f (x ).∴函数f (x )是周期函数，2π是它的一个周期.12.如下图为函数)0,0,0()sin(>>>++=ϕωϕωA c x A y 图像的一部分（1）求此函数的周期及最大值和最小值（2）求与这个函数图像关于直线2=x 对称的函数解析式【解】（1）由图可知，从4～12的的图像是函数)0,0,0()sin(>>>++=ϕωϕωA c x A y 的三分之二个周期的图像，所以1)24(213)24(21=-==+=c A ，故函数的最大值为3，最小值为－3∵8232=⋅ωπ∴ 6πω=∴ 12=T 把x=12,y=4代入上式，得2πϕ=所以，函数的解析式为：16cos3+=x y π（2）设所求函数的图像上任一点（x,y)关于直线2=x 的对称点为（y x '',），则y y x x ='-=',4代入16cos3+=x y π中得1)632cos(3+-=xy ππ ∴ 与函数16c o s 3+=x y π的图像关于直线2=x 对称的函数解析式为：1)632cos(3+-=xy ππ13.已知函数x x y 21cos 321sin +=，求：（1）函数y 的最大值，最小值及最小正周期；（2）函数y 的单调递增区间 【解】∵ )321sin(2π+=x y （1）∴ 函数y 的最大值为2，最小值为－2，最小正周期πωπ42==T（2）由Z k k x k ∈+≤+≤-,2232122πππππ，得函数y 的单调递增区间为：Z k k k ∈⎥⎦⎤⎢⎣⎡+-,34,354ππππ提高题：解：在单位圆中，作出锐角α在正弦线MP，如图2-9所示在△MPO中，MP+OM＞OP=1即MP+OM＞1∴sinα+cosα＞1于P1，P2两点，过P1，P2分别作P1M1⊥x轴，P2M2⊥x轴，垂足分k∈Z}【例3】求下列函数的定义域：解：(1)为使函数有意义，需满足2sin2x+cosx-1≥0由单位圆，如图2-12所示k∈Z}(4)为使函数有意义，需满足：取k=0和-1时，得交集为-4＜x≤-π或0≤x≤π∴函数的定义域为(-4，-π]∪[0，π]【例4】求下列函数的值域：∴此函数的值域为{y|0≤y＜1}∵1+sinx+cosx≠0 ∴t≠-1【例5】判断下列函数的奇偶性：【分析】先确定函数的定义域，然后根据奇函数成偶函数的定义判断函数的奇偶性．∵f(1-x)=-sin(-2x)=sin2x=-f(x)(2)函数的定义域为R，且f(-x)=sin[cos(-x))=sin(cosx)=f(x)∴函数f(x)=sin(cosx)是偶函数．(3)因1+sinx≠0，∴sinx≠-1，函数的定义域为{x|x∈R且x≠2k既不是奇函数，也不是偶函数．【例6】求下列函数的最小正周期：(2)y=cos4x+sin4x=(cos2x+sin2x)2-2sin2xcos2x=|cosx|+|sinx|=f(x)正周期．(x+T)|+|cos(x+T)|=|sinx|+|cosx|都成立．特别当x=0时，有|sinT|+|cosT|=sinT【例8】求下列各函数的最大值、最小值，并且求使函数取得最大值、最小值的x的集合．∴使y取得最大值的x的集合为{x|x=(2kπ+1)π，k∈Z}∴使y取得最小值的x的集合为{x|x=2kπ，k∈Z}当cosx=1，即x=2kπ(k∈Z)时，y取得最大值3．【说明】求三角函数的最值的类型与方法：1．形如y=asinx+b或y=acosx+b，可根据sinx，cosx的有界性来求最值；2．形如y=asin2x+bsinx+c或y=acos2x+bcosx+c看成是关于sinx或cosx的二次函数，变为y=a(sinx+m)2+k或y=a(cosx+m)2+k，但要注意它与二次函数求最值的区别，此时|sinx|≤1，|cosx|≤1【例9】求下列函数的单调区间：【分析】复杂三角函数的单调区间是运用基本函数的单调性及单调区间得出的．(2)函数y=sin2x-2sinx+2，是由y=u2-2u+2及u=sinx及复合而成，∴|u|≤1【例10】当a≥0，求函数f(x)=(sinx+a)(cosx+a)的最大值、最小值，及相应的x的取值．解：f(x)=(sinx+a)(cosx+a)=sinxcosx+a(sinx+cosx)+a2由于a是常数，故这里只要求y=(sinx+cosx+a)2的最大值、最小值．合物线的图象如图2-14所示两种可能．【例11】函数f(x)=Asin(ωx+ )的图象如图2-15，试依图指出(1)f(x)的最小正周期；(2)使f(x)=0的x的取值集合；(3)使f(x)＜0的x的取值集合；(4)f(x)的单调递增区间和递减区间；(5)求使f(x)取最小值的x的集合；(6)图象的对称轴方程；(7)图象的对称中心．注：得出函数f(x)的最小正周期之后，研究f(x)的其他性质，总是先在包含锐角在内的一个周期中研究，再延伸到整个定义域中．注：实际上f(x)图象的对称轴方程为x=x0，而其中x0使f(x0)=1或f(x0)=-1注：f(x)的图象的对称中心为(x0，0)，其中x0使f(x0)=0【例12】求如图2-16所示的函数解析式．(ω＞0，θ∈[0，2π])【例13】设y=Asin(ωx+ϕ)(A＞0，ω＞0，|ϕ|＜π)最高点D的标为(6，0)，(1)求A、ω、ϕ的值；(2)求出该函数的频率，初相和单调区间．y单调递增故递增区间为[16k-6，16k+2]，k∈Zy单调递减故递减区间为[16k+2，16k+10]，k∈ZA．sinθ＜cosθ＜ctgθB．cosθ＜sinθ＜ctgθC．sinθ＜ctgθ＜cosθD．cosθ＜ctgθ＜sinθ解一(直接法)：故选A．解二(图解法)：作出三角函数线，如图2-17MP=sinθ，OM=cosθ，BS=ctgθ通过观察和度量得MP＜OM＜BS 从而有sinθ＜cosθ＜ctgθ∴应选A∴cosθ＞sinθ从而可剔除B、D．再由sinθ＜ctgθ，故可剔除C故选A解四(特殊值法)：B、C、D，应选A．∴应选Dx轴交点中在原点右边最接近原点的交点，而在原点左边与x轴交点中最的图象．∴选D再把横坐标缩小到原来的一半，纵坐标扩大到原来的4倍，则所得的图象的解析式是 [ ]∴选A．【例17】方程sin2x=sinx在区间(0，2π)内解的个数是[ ]A．1 B．2 C．3 D．4在同一坐标系中作出函数y=sin2x和y=sinx的图象，如图2-18所示．它们在(0，2π)内交点个数，即为所求方程解的个数，从而应选C．【例18】设函数f(x)是定义在R上的周期为3的奇函数，且f(1)=2，则f(5)=____ 解：∵f(x)是奇函数，且f(1)=2，∴f(-1)=-2又∵f(x)是周期为3的函数．∴f(3+x)=f(x)∴f(-1+3)=f(-1)=-2 即f(2)=-2f(2+3)=f(2)=-2 即f(5)=-2【例19】有一块扇形铁板，半径为R，圆心角为60°，从这个扇形中切割下一个内接矩形，即矩形的各个顶点都在扇形的半径或弧上，求这个内接矩形的最大面积．解：如图2-19(1)设∠FOA=θ，则FG＝Rsinθ又设矩形EFGH的面积为S，那么又∵0°＜θ＜60°，故当cos(2θ－60°)＝1，即θ=30′时，如图2-19 (2)，设∠FOA＝θ，则EF＝2Rsin(30°-θ)，在△OFG中，∠OGF＝150°设矩形的面积为S．那么S＝EFFG＝4R2sinθsin(30°-θ)＝2R2［cos(2θ-30°)－cos30°]又∵0＜θ＜30°，故当cos(2θ-30°)＝1。

（word完整版）⾼中数学专题系列三⾓函数讲义§1.1.1、任意⾓1、正⾓、负⾓、零⾓、象限⾓的概念.2、与⾓α终边相同的⾓的集合：{}Z k k ∈+=,2παββ.§1.1.2、弧度制1、把长度等于半径长的弧所对的圆⼼⾓叫做1弧度的⾓.2、 rl =α. 3、弧长公式：R R n l απ==180. 4、扇形⾯积公式：lR R n S 213602==π. §1.2.1、任意⾓的三⾓函数1、设α是⼀个任意⾓，它的终边与单位圆交于点()y x P ,，那么：xyx y ===αααtan ,cos ,sin 2、设点(),A x y为⾓α终边上任意⼀点，那么：（设r =sin y r α=，cos x r α=，tan yxα=，cot x y α=3、αsin ，αcos ，αtan 在四个象限的符号和三⾓函数线的画法.正弦线：MP; 余弦线：OM; 正切线：AT5、特殊⾓0°，30°45°，60°，90°，180°，270等的三⾓函数值.§1.2.21、平⽅关系：1cos sin 22=+αα 2、商数关系：αααcos sin tan =. 3、倒数关系：tan cot 1αα=§1.3、三⾓函数的诱导公式（概括为Z k ∈）§1.4.1、正弦、余弦函数的图象和性质1、记住正弦、余弦函数图象：2、能够对照图象讲出正弦、余弦函数的相关性质：定义域、值域、最⼤最⼩值、对称轴、对称中⼼、奇偶性、单调性、周期性.3、会⽤五点法作图.sin y x =在[0,2]x π∈上的五个关键点为： 30010-12022ππππ（，）（，，）（，，）（，，）（，，）.y=tanx3π2ππ2-3π2-π-π2oyxy=cotx 3π2ππ22π-π-π2o yx图表归纳：正弦、余弦、正切函数的图像及其性质x y sin =x y cos =x y tan =图象定义域 RR},2|{Z k k x x ∈+≠ππ值域[-1,1][-1,1]R最值max min 2,122,12x k k Z y x k k Z y ππππ=+∈==-∈=-时，时，max min 2,12,1x k k Z y x k k Z y πππ=∈==+∈=-时，时，⽆周期性π2=T π2=Tπ=T奇偶性奇偶奇单调性Z k ∈在[2,2]22k k ππππ-+上单调递增在3[2,2]22k k ππππ++上单调递减在[2,2]k k πππ-上单调递增在[2,2]k k πππ+上单调递减在(,)22k k ππππ-+上单调递增对称性 Z k ∈对称轴⽅程：2x k ππ=+对称中⼼(,0)k π对称轴⽅程：x k π= 对称中⼼(,0)2k ππ+⽆对称轴对称中⼼,0)(2k π§1.4.3、正切函数的图象与性质1、记住正切函数的图象2、记住余切函数的图象：3、能够对照图象讲出正切函数的相关性质：定义域、值域、对称中⼼、奇偶性、单调性、周期性.§1.5、函数()?ω+=x A y sin 的图象 1、对于函数：()()sin 0,0y A x B A ωφω=++>>有：振幅A ，周期2T πω=，初相?，相位?ω+x ，频率πω21==Tf .2、能够讲出函数x y sin =的图象与()sin y A x B ω?=++的图象之间的平移伸缩变换关系.3、三⾓函数的周期，对称轴和对称中⼼函数sin()y x ω?=+，x ∈R 及函数cos()y x ω?=+，x ∈R(A,ω,?为常数，且A ≠0)的周期2|| T πω=；函数tan()y x ω?=+，,2x k k Z ππ≠+∈(A,ω,?为常数，且A ≠0)的周期||T πω=. 对于sin()y A x ω?=+和cos()y A x ω?=+来说，对称中⼼与零点相联系，对称轴与最值点联系. 求函数sin()y A x ω?=+图像的对称轴与对称中⼼，只需令()2x k k Z πω?π+=+∈与()x k k Z ω?π+=∈解出x 即可.余弦函数可与正弦函数类⽐可得.4、由图像确定三⾓函数的解析式利⽤图像特征：max min 2A =，max min2y y B +=. ω要根据周期来求,?要⽤图像的关键点来求.§1.6、三⾓函数模型的简单应⽤（要求熟悉课本例题.）§3.1.1、两⾓差的余弦公式§3.1.2、两⾓和与差的正弦、余弦、正切公式 1、()βαβαβαsin cos cos sin sin +=+ 2、()βαβαβαsin cos cos sin sin -=- 3、()βαβαβαsin sin cos cos cos -=+ 4、()βαβαβαsin sin cos cos cos +=- 5、()tan tan 1tan tan tan αβαβαβ+-+=.6、()tan tan 1tan tan tan αβαβαβ-+-=.§3.1.3、⼆倍⾓的正弦、余弦、正切公式1、αααcos sin 22sin =，2、ααα22sin cos 2cos -=变形： 12sin cos sin 2ααα=. 1cos 22-=αα2sin 21-=.升幂公式：221cos 22cos 1cos 22sin αααα+=-= 降幂公式：221cos (1cos 2)21sin (1cos 2)2αααα=+=-3、ααα2tan 1tan 22tan -=. 4、sin 21cos 2tan 1cos 2sin 2ααααα-==+ §3.2、简单的三⾓恒等变换1、注意正切化弦、平⽅降次.2、辅助⾓公式)sin(cos sin 22?++=+=x b a x b x a y （其中辅助⾓?所在象限由点(,)a b 的象限决定,tan b a=).解三⾓形1、正弦定理：R CcB A 2sin sin sin ===. （其中R 为ABC ?外接圆的半径） 2sin ,2sin ,2sin ;a R A b R B c R C ?===sin ,sin ,sin ;222a b c A B C R R R=== ::sin :sin :sin .a b c A B C ?=⽤途：⑴已知三⾓形两⾓和任⼀边，求其它元素；⑵已知三⾓形两边和其中⼀边的对⾓，求其它元素。

专题5.3 三角函数的概念-重难点题型精讲1．任意角的三角函数(1)利用单位圆定义任意角的三角函数设是一个任意角，∈R，它的终边OP与单位圆相交于点P(x,y).①把点P的纵坐标y叫做的正弦函数，记作，即y=；②把点P的横坐标x叫做的余弦函数，记作，即x=；③把点P叫做的正切，记作，即=(x≠0).我们将正弦函数、余弦函数和正切函数统称为三角函数，通常将它们记为：(2)用角的终边上的点的坐标表示三角函数如图，设是一个任意角，它的终边上任意一点P(不与原点O重合)的坐标为(x,y)，点P与原点的距离为r.则，=，=.2．三角函数的定义域和函数值的符号(1)三角函数的定义域(2)三角函数值在各象限的符号由于角的终边上任意一点P(x,y)到原点的距离r是正值，根据三角函数的定义，知①正弦函数值的符号取决于纵坐标y的符号；②余弦函数值的符号取决于横坐标x的符号；③正切函数值的符号是由x,y的符号共同决定的，即x,y同号为正，异号为负.因此，正弦函数()、余弦函数()、正切函数()的值在各个象限内的符号如图所示.3．诱导公式一由三角函数的定义，可以知道：终边相同的角的同一三角函数的值相等.由此得到一组公式(公式一)：4．同角三角函数的基本关系(1)同角三角函数的基本关系(2)基本关系式的变形公式【题型1 任意角的三角函数的定义及应用】【例3】（2022·湖南·高一课时练习）求值：√3cos420°+tan330°+sin(−60°)．【变式3-1】（2021·全国·高一课前预习）计算下列各式的值：(1)tan405°−sin450°+cos750°；(2)sin25π3+tan(−15π4).【变式3-2】（2021·全国·高一课时练习）化简下列各式：(1)sin760∘√1−cos240∘；(2)tanα√1sin2α−1（其中α是第二象限角）.【变式3-3】（2021·全国·高一课前预习）求下列各式的值：【例5】（2021·福建·高一阶段练习）（1）已知cosα+2sinα=0求1−2cos 2αsin 2α−sinαcosα的值；（2）已知sinβ+cosβ=23，且β为第四象限角，求sinβ−cosβ的值.【变式5-1】（2022·全国·高一课时练习）已知3sin 2α−4sinαcosα+1=0． (1)求tanα的值； (2)求sinαcosα1+cos 2α的值．【变式5-2】（2022·全国·高一课时练习）已知tan α=2，求下列各式的值. (1)1sin αcos α；(2)11−sin α+11+sin α.【变式5-3】（2022·天津·模拟预测）已知3π4<α<π， tan α＋1tana =−103. (1)求tanα的值； (2)求sinα+cosαsinα−cosα的值；(3)求2sin 2α−sin αco sα−3co s 2α .的值【例6】（2022·全国·高一课时练习）求证： (1)(1−cosαsinα+1sinα)(1−tanα+1cosα)=2；(2)sinα(1+tanα)+cosα(1+1tanα)=1sinα+1cosα.【变式6-1】（2021·全国·高一课时练习）求证： (1)1−2sinxcosx cos 2x−sinx 2=1−tanx 1+tanx(2)tan 2α−sin 2α=tan 2α⋅sin 2α【变式6-2】（2021·全国·高一专题练习）求证：sin 4α+cos 4α＝1﹣2sin 2αcos 2α【变式6-3】（2022·全国·高一课时练习）求证： (1)sinα−cosα+1sinα+cosα−1＝1+sinαcosα；(2)2(sin 6θ+cos 6θ)−3(sin 4θ+cos 4θ)+1=0。

精心整理专题四三角函数．基本知识点【1】角的基本概念 （1）正角负角零角（2终}36036090,k k α<<⋅+∈Z}36090360180,k k +<⋅+∈Z }360180360270,k k α+<<⋅+∈Z }360270360360,k k α+<<⋅+∈Z{}180,k ∈Z }}（3（4，18057.3≈【2设α是一个任意大小的角，α的终边上任意一点P 的坐标是(),x y ，它与原点的距离是()0r r =>，则sin y r α=，cos x r α=，()tan 0yx x α=≠．【3】三角函数的基本关系()sin 2tan cos ααα=sin sin tan cos ,cos tan αααααα⎛⎫== ⎪⎝⎭．【4】函数的诱导公式：奇变偶不变，符号看象限 【5】常用三角函数公式（1）两角和与差的三角函数关系 sin(α±β)=sin α·cos β±cos α·sin β cos(α±β)=cos α·cos β sin α·sin β （2（3sin2（4由a （5【6（1（2）正弦函数、余弦函数和正切函数的图象与性质：例1】变式1】变式2】变式3】（1）（2）变式4】（2012年江西）sin cos1sin cos2αα+=-，求tan2α的值变式4】（2012年全国卷）已知α为第二象限角，且sin cosαα+=，则cos2α= D变式5】（2012年重庆卷）设tan α，tan β是方程x2-3x+2=0的两个根，则tan （α+β）的值为（ ）-3B-1C1D3例2】已知1sin cos 8αα⋅=，02πα<<，求sin cos αα+的值. 变式1】已知3sin cos 8αα⋅=，且42ππα<<，求cos sin αα-的值.变式2】（2012例3】（2008）求sin 4x π⎛⎫-⎪⎝⎭）求x sin 的值；）求 ⎝⎛+32sin πx 变式1】已知函数Ⅰ）求函数()f x Ⅱ）若06(),5f x =例4】已知函数f ）求函数()f x 的周期、递增区间、递减区间）求函数()f x 取得最大值时x 的集合）求函数()f x 取得最小值时x 的集合变式1】已知函数()2sin(),f x x x R ωϕ=+∈，其中0,,()f x ωπϕπ>-<≤若的最小正周期为6π，且当2x π=时，()f x 得最大值，）求函数()f x的表达式）求函数()f x的递增区间和点减区间）求函数()f x取得最大值时x的集合变式2】（2011年和平区一模）知()cos3f x x π⎛⎫=+⎪⎝⎭，()()()g x f x f x=⋅-）求2fπ⎛⎫ ⎪⎝⎭）求函数()h x=变式3】（2012函数()f x）求()f x）求使得()f x ）若()20,πθ∈且例5】（2011Ⅰ）求()f xⅡ）求()f x变式1】（2007年天津理）已知函数()2cos(sin cos)1f x x x x x=-+∈R，．Ⅰ）求函数()f x的最小正周期；Ⅱ）求函数()f x在区间π3π84⎡⎤⎢⎥⎣⎦，上的最小值和最大值．变式2】（2012年和平区一模）()()22sin cosx x x x m m R=++∈）当x R∈时，求()f x的单调递增区间；）当0,2xπ⎡⎤∈⎢⎥⎣⎦时()f x的最大值是6，求实数m的值变式3】（2012河西一模）知平面内点A ⎛⎝2OCⅠ）求函数()f xⅡ）当[,xππ∈-变式4】（2012知函数()f x= )求函数()f x Ⅱ）求函数(f x 例6】（2011知函数()f x=Ⅰ）求()f xI）设0,4πα⎛⎫∈ ⎪⎝⎭变式1】求函数tan23y x=+⎪⎝⎭的定义域，周期和单调区间。

素诚教育高中数学素质、诚实SCE 金牌数学专题系列专题：三角函数§1.1.1、任意角1、正角、负角、零角、象限角的概念.2、与角终边相同的角的集合：2k , k Z .§1.1.2、弧度制1、把长度等于半径长的弧所对的圆心角叫做 1 弧度的角 .2、l. r3、弧长公式：l n R R . 4 、扇形面积公式：S n R21lR .180 360 2 § 1.2.1、任意角的三角函数1，那么：sin y, cos x, tany、设是一个任意角，它的终边与单位圆交于点P x, yx 2、设点A x , y 为角终边上任意一点，那么：（设 r x2 y2）sin y x y x ， cos ， tanx， cotr r y3、sin ， cos ， tan 在四个象限的符号和三角函数线的画法.y正弦线： MP; 余弦线： OM; 正切线： ATTPO M A x5、特殊角 0°， 30° 45°， 60°， 90°， 180°， 270 等的三角函数值 .0 6 4 3 2 2 3 323 4 2sincostan§ 1.2.2、同角三角函数的基本关系式1、平方关系：sin2 cos2 12、商数关系：tan sin .3、倒数关系：tan cot1cos§ 1.3 、三角函数的诱导公式（概括为 “奇变偶不变，符号看象限”k Z ）1、 诱导公式一 ：2、 诱导公式二 ：sin 2k sin ,sin sin , cos 2k cos , （其中： k Z ）cos cos ,tan2ktan .tantan .3、诱导公式三 ：4、诱导公式四 ：sin sin ,sin sin ,cos cos, cos cos,tantan .tantan .5、诱导公式五 ：6、诱导公式六 ：sin2cos ,sincos ,2cos2sin .cossin .2§ 1.4.1 、正弦、余弦函数的图象和性质y=sinxyy=cosxy3 73 7-5 -2 1-5-2 1222-3 2-23 2-4-7-3 -2 -3 -o 2 5 34x-4-7-2 -3o 2 54x22-1 2222 -1 221、记住正弦、余弦函数图象：2、能够对照图象讲出正弦、余弦函数的相关性质： 定义域、值域、最大最小值、对称轴、对称中心、奇偶性、单调性、周期性.3、会用 五点法作图 .y sin x 在 x [0, 2 ] 上的五个关键点为： （0，0）（，，1）（， ，0）（，3，-1）（，2 ，0）.2 2图表归纳：正弦、余弦、正切函数的图像及其性质y sin x y cosx y tan x 图象定义域R值域[-1,1]x 2k , k Z时， y max 1最值 2x 2k , k Z 时， y min 12周期性T 2奇偶性奇单调性在[2k , 2k ] 上单调递增2 2k Z 在 [2k,2k 3] 上单调递减2 2对称性对称轴方程：x kk Z 2对称中心 (k , 0)§ 1.4.3 、正切函数的图象与性质yy=cotx-- o 321、记住正 2 2 22、记住余3、能够对照偶性、单调性、周期性.R { x | x k , k Z }2[-1,1] Rx 2k , k Z时， y max 1无x 2k , k Z时， y min1T 2 T偶奇在 [2 k ,2 k ] 上单调递增在(k , k ) 上单调递2 2在[2 k ,2 k] 上单调递减增对称轴方程：x k 无对称轴对称中心 ( k , 0) 对称中心 (k,0)2 2yy=tanxx3 -- 2o 3x- 2 2 2图象切函数的切函数的图象：图象讲出正切函数的相关性质：定义域、值域、对称中心、奇§ 1.5 、函数 y A sin x 的图象1、对于函数：y Asin xB A 0,有：振幅 A2 ，初相 ，相位 x，频率 fT 2.，周期 T12、能够讲出函数 y sin x 的图象与y AsinxB 的图象之间的平移伸缩变换关系 .① 先平移后伸缩：② 先伸缩后平移：y sin x 平移 || 个单位（左加右减）横坐标不变纵坐标变为原来的 A 倍y sin xy sin x横坐标不变y A sin x纵坐标变为原来的 A 倍y Asin x纵坐标不变y Asin x横坐标变为原来的| 1| 倍纵坐标不变y Asin x横坐标变为原来的 | 1|倍平移 |B | 个单位y Asin x B平移个单位（左加右减）平移 |B| 个单位 y Asin xy Asin x B（上加下减）（上加下减）3、三角函数的周期，对称轴和对称中心函数 y sin( x) ，x ∈ R 及函数 y cos( x)， x ∈ R(A, , 为常数，且2 ；A ≠ 0) 的周期 T||函数 ytan( x) ， xk,kZ (A, ω , 为常数，且 A ≠ 0) 的周期 T.2| |对于 y A sin( x ) 和 y Acos( x ) 来说， 对称中心与零点相联系，对称轴与最值点联系.求 函 数 yAsin(x) 图 像 的 对 称 轴 与 对 称 中 心 ， 只 需 令 xk(k Z ) 与 x k (k Z )2解出 x 即可 . 余弦函数可与正弦函数类比可得 .4、由图像确定三角函数的解析式利用图像特征： Aymaxymin ，Bymaxymin.22要根据周期来求 ,要用图像的关键点来求 .§ 1.6 、三角函数模型的简单应用（要求熟悉课本例题 . ）§ 3.1.1 、两角差的余弦公式 记住 15°的三角函数值：sincostan6 26 2231244§3.1.2 、两角和与差的正弦、余弦、正切公式 1、 sin sin cos cos sin2、 sin sincoscos sin3、 cos cos cos sin sin4、 cos cos cossin sin5、 tantan tan .1 tan tan6、 tantan tan.1 tan tan§ 3.1.3 、二倍角的正弦、余弦、正切公式1、 sin 22 sin cos ，2、 cos2cos 2sin 2 变形 ： sincos1sin 2 .2 cos 2 121 2 sin 2.升幂公式：1 cos2 2cos 21cos22sin 2cos 21 (1 cos2 )降幂公式：2sin 21(1 cos 2 )23、 tan 22 tan . 4sin 21 cos2 1 tan2、 tan1 cos2sin 2§ 3.2 、简单的三角恒等变换 1、 注意 正切化弦、平方降次 . 2、辅助角公式y a sin x b cos xa 2b 2 sin( x ) （ 其 中 辅 助 角所 在 象 限 由 点 ( a, b) 的 象 限 决定 , tanb).a解三角形1、正弦定理：a b c 2R .sin A sin B sin C（其中 R 为 ABC 外接圆的半径）a2R sin A,b 2R sin B,c 2R sin C ; sin Aa ,sin B b,sin C c ;2R2R2Ra :b :c sin A :sin B :sin C.用途：⑴已知三角形两角和任一边，求其它元素；⑵已知三角形两边和其中一边的对角，求其它元素。

第１章三角函数[巩固层·知识整合][提升层·题型探究]三角函数的定义【例１】已知角θ终边上一点P（x，３）（x≠0），且cos θ＝错误!x，求sin θ，tan θ的值．[解] 因为r＝错误!，cos θ＝错误!，所以错误!x＝错误!＝错误!.又x≠0，所以x＝±１．又y＝３>0，所以θ是第一或第二象限角．当θ为第一象限角时，sin θ＝错误!，tan θ＝３；当θ为第二象限角时，sin θ＝错误!，tan θ＝—３．有关三角函数的概念主要有以下两个方面：（１）任意角和弧度制，理解任意角的概念，弧度的意义，能正确地进行弧度与角度的换算．（２）任意角的三角函数，掌握任意角的正弦、余弦、正切的定义及三角函数线，能够利用三角函数线判断三角函数的符号，借助三角函数线求三角函数的定义域．１．求函数f（x）＝错误!＋错误!的定义域．[解] 函数f（x）有意义，则错误!即错误!如图所示，结合三角函数线知错误!∴２kπ＋错误!≤x<２kπ＋错误!（k∈Z）.故f（x）的定义域为错误!（k∈Z）.三角函数的诱导公式【例２】已知f（α）＝错误!.（１）化简f（α）；（２）若α＝—错误!，求f（α）的值．[解] （１）f（α）＝错误!＝错误!＝—cos α.（２）f错误!＝—cos 错误!＝—cos 错误!＝—cos 错误!＝—错误!.正弦函数、余弦函数、正切函数的诱导公式是三角函数值的化简与求值的主要依据．利用诱导公式可以把任意角的三角函数转化为锐角三角函数，也可以实现正弦与余弦、正切与余切之间函数名称的变换．２kπ＋α，π±α，—α，２π±α，错误!±α的诱导公式可归纳为：k×错误!＋α（k∈Z）的三角函数值．当k为偶数时，得α的同名三角函数值；当k为奇数时，得α的余名三角函数值，然后在前面加上一个把α看成锐角时原函数值的符号，概括为“奇变偶不变，符号看象限”，这里的奇偶指整数k的奇偶．２．若sin 错误!＝错误!，求错误!＋错误!.[解] 因为sin 错误!＝错误!，所以cos θ＝—错误!.所以错误!＋错误!＝错误!＋错误!＝错误!—错误!＝错误!—错误!＝错误!—错误!＝错误!.三角函数的图像及其变换【例３】如图是函数y＝A sin （ωx＋φ）＋k（A>0，ω>0，|φ|<错误!）的一段图像．（１）求此函数的解析式；（２）分析一下该函数是如何通过y＝sin x变换得来的．[解] （１）由图像知，A＝错误!＝错误!，k＝错误!＝—１，T＝２×错误!＝π，∴ω＝错误!＝２，∴y＝错误!sin （２x＋φ）—１．当x＝错误!时，２×错误!＋φ＝错误!，∴φ＝错误!.∴所求函数解析式为y＝错误!sin 错误!—１．（２）把y＝sin x向左平移错误!个单位得到y＝sin 错误!，然后纵坐标保持不变，横坐标缩短为原来的错误!，得到y＝sin 错误!，再横坐标保持不变，纵坐标变为原来的错误!，得到y＝错误!sin 错误!，最后把函数y＝错误!sin 错误!的图像向下平移１个单位，得到y＝错误!sin 错误!—１的图像．三角函数的图像是研究三角函数性质的基础，又是三角函数性质的具体体现．在平时的考查中，主要体现在三角函数图像的变换和解析式的确定，以及通过对图像的描绘、观察来讨论函数的有关性质．３．若函数f（x）＝A sin （２x＋φ）（A>0，0<φ<π）在x＝错误!处取得最大值，且最大值为３，求函数f（x）的解析式，并说明怎样变换f（x）的图像能得到g（x）＝３sin 错误!的图像．[解] 因为函数f（x）最大值为３，所以A＝３，又当x＝错误!时函数f（x）取得最大值，所以sin 错误!＝１．因为0<φ<π，故φ＝错误!，故函数f（x）的解析式为f（x）＝３sin 错误!，将f（x）的图像向右平移错误!个单位，即得g（x）＝３sin 错误!＝３sin 错误!的图像．三角函数的性质[探究问题]１．如何求三角函数的值域问题？[提示] （１）利用sin x，cos x的有界性．（２）从y＝A sin （ωx＋φ）＋k的形式逐步分析ωx＋φ的范围，根据正弦函数单调性写出函数的值域．（３）换元法：把sin x或cos x看作一个整体，可化为求函数在区间上的值域（最值）问题．２．如何求三角函数的单调区间？[提示] 求形如y＝A sin （ωx＋φ）或y＝A cos （ωx＋φ）（A>0，ω>0）的函数的单调区间可以通过解不等式方法去解答，即把ωx＋φ视为一个“整体”，分别与正弦函数y＝sin x，余弦函数y＝cos x的单调递增（减）区间对应解出x，即得所求的单调递增（减）区间．【例４】已知函数f（x）＝２sin 错误!＋a＋１（其中a为常数）.（１）求f（x）的单调区间；（２）若x∈错误!时，f（x）的最大值为４，求a的值；（３）求f（x）取最大值时，x的取值集合．[思路探究] （１）将２x＋错误!看成一个整体，利用y＝sin x的单调区间求解；（２）先求x∈错误!时，２x＋错误!的范围，再根据最值求a的值；（３）先求f（x）取最大值时２x＋错误!的值，再求x的值．[解] （１）由—错误!＋２kπ≤２x＋错误!≤错误!＋２kπ（k∈Z），解得—错误!＋kπ≤x≤错误!＋kπ（k∈Z），∴函数f（x）的单调增区间为错误!（k∈Z），由错误!＋２kπ≤２x＋错误!≤错误!＋２kπ（k∈Z），解得错误!＋kπ≤x≤错误!＋kπ（k∈Z），∴函数f（x）的单调减区间为错误!（k∈Z）.（２）∵0≤x≤错误!，∴错误!≤２x＋错误!≤错误!，∴—错误!≤sin 错误!≤１，∴f（x）的最大值为２＋a＋１＝４，∴a＝１．（３）当f（x）取最大值时，２x＋错误!＝错误!＋２kπ（k∈Z）.∴x＝错误!＋kπ（k∈Z）.∴当f（x）取最大值时，x的取值集合是错误!.将例４中的函数变为“f（x）＝错误!sin 错误!（x∈R）”．（１）求函数f（x）的最小正周期；（２）求函数f（x）在区间错误!上的最大值和最小值．[解] （１）∵f（x）＝错误!sin 错误!，∴T＝错误!＝错误!＝π，故f（x）的最小正周期为π.（２）f（x）＝错误!sin 错误!在区间错误!上是增函数，在区间错误!上是减函数，∴函数f（x）在x＝错误!处取得最大值，在两端点之一处取得最小值．又f错误!＝0，f错误!＝错误!，f错误!＝—１．故函数f（x）在区间错误!上的最大值为错误!，最小值为—１．高考中三角函数的性质是必考内容之一，着重考查三角函数的定义域、值域、单调性、奇偶性、对称性等有关性质，特别是复合函数的周期性、单调性和最值（值域），应引起重视．。

专题四 三角函数一．基本知识点【1】角的基本概念（1）正角 负角 零角（2）角的顶点与原点重合，角的始边与轴的非负半轴重合，终边落在第几象限，则称为第几象限角． 第一象限角的集合为 第二象限角的集合为 第三象限角的集合 第四象限角的集合终边在轴上的角的集合为 终边在轴上的角的集合为 终边在坐标轴上的角的集合为 （3）与角终边相同的角的集合为 （4）弧度制与角度制的换算公式：，， 【2】三角函数的定义设是一个任意大小的角，的终边上任意一点的坐标是，它与原点的距离是，则，，．【3】三角函数的基本关系 ．【4】函数的诱导公式：奇变偶不变，符号看象限 【5】常用三角函数公式（1）两角和与差的三角函数关系sin(α±β)=sin α·cos β±cos α·sin β cos(α±β)=cos α·cos β sin α·sin β （2）倍角公式sin2α=2sin α·cos α ααα2tan 1tan 22tan -=cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α（3）半角公式sin 2α22cos 1α-=cos 2α22cos 1α+=（4）辅助角公式()()sin cos 0a x b x x a θ+=+> (其中θ角所在的象限由a , b 的符号确定，θ角的值由tan baθ=确定) （5）特殊角的三角函数 【6】三角函数的性质（1）函数的性质： ①振幅：；②周期：；③频率：； ④相位：；⑤初相：．二．例题分析【例1】已知角α的终边经过点()03,4P --，求角α的正弦值，余弦值，正切值.【变式1】已知3sin 5α=-，求cos α，tan α的值 【变式2】已知tan 2α=，求sin cos sin cos αααα+-的值【变式3】已知sin 2cos αα=，（1） 求sin 4cos 5sin 2cos αααα-+（2） 求2sin sin 2αα+【变式4】（2012年江西）sin cos 1sin cos 2αα+=-，求tan2α的值【变式4】（2012年全国卷）已知α为第二象限角，且sin cos 3αα+=，则cos2α=A D 【变式5】（2012年重庆卷）设tan α，tan β是方程x2-3x+2=0的两个根，则tan （α+β）的值为（ ） A ．-3 B-1 C 1 D3【例2】已知1sin cos 8αα⋅=，02πα<<，求sin cos αα+的值. 【变式1】已知3sin cos 8αα⋅=，且42ππα<<，求cos sin αα-的值.【变式2】（2012年辽宁）已知sin cos2αα-=(),o απ∈则tan α的值是 ；sin2α的值 .【例3】（2008年天津理）已知⎪⎭⎫ ⎝⎛3∈=⎪⎭⎫⎝⎛-4,2,1024cos πππx x . （1）求sin 4x π⎛⎫-⎪⎝⎭的值 （2）求x sin 的值； （3）求⎪⎭⎫⎝⎛+32sin πx 的值.【变式1】已知函数2()cos 2cos 1()f x x x x x R =+-∈（Ⅰ）求函数()f x 的最小正周期及在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值； （Ⅱ）若006(),,542f x x ππ⎡⎤=∈⎢⎥⎣⎦，求0cos 2x 的值。