物理光学第五章课后作业解答

一、选择题1．把凸透镜正对太阳光，可在距凸透镜15cm处得到一个最小最亮的光斑。

若将光屏放在距此透镜20cm处，可得到一个清晰的像。

这个像是（）A．倒立放大的实像B．倒立缩小的实像C．正立放大的实像D．正立放大的虚像2．如图所示，小明同学在“探究凸透镜成像规律”实验时，烛焰在光屏上成了一个清晰的像，下列说法正确的是（）A．投影仪就是利用这一成像原理制成的B．实验中烛焰在光屏上成的像是放大的C．为了从不同方向观察光屏上的像，光屏应选用较光滑的玻璃板D．将蜡烛向右移动靠近凸透镜，当放置在F和O之间时，光屏上将找不到像3．如图所示，AC为入射光线，CB为折射光线，且AO<OB。

已知OA=6cm，该凸透镜的焦距可能是（）A．f=2cm B．f=5cm C．f=7cm D．f=9cm4．每年6月6日是全国爱眼日。

如果不爱护眼睛容易患上近视眼，下列关于近视眼及其矫正的原理图正确的是（）A．甲乙B．丙乙C．甲丁D．丙丁5．小欢做“探究凸透镜成像的规律”的实验时，蜡烛、凸透镜、光屏在光具座上的位置如图所示，这时烛焰在光屏上成清晰的像（像未在图中画出来）。

下列说法正确的是（）A．光屏上形成的是烛焰倒立缩小的实像B．图中成像原理与照相机成像原理相同C．蜡烛和光屏的位置不动，凸透镜移到40cm刻度线处，光屏上能呈现清晰的烛焰像D．将蜡烛移到65cm刻度线处，凸透镜不动，光屏移到适当位置能呈现清晰的烛焰像6．如图是小明通过一块透镜观察物理课本的情况，此时他将这块透镜由图示位置慢慢远离课本，他在草稿纸上随手记录了成像情况如下：①倒立放大的像；②倒立缩小的像；③正立放大的像，那么，在这过程中像变化的正确顺序是（）A．①②③B．②③①C．③①②D．③②①7．如图所示，给凸透镜“戴”上远视眼镜，此时光屏上能成一清晰的像，若“取”下远视眼镜，光屏上的像变模糊。

为使光屏上的像清晰，某小组提出的做法如下：①将光屏远离透镜；②将光屏靠近透镜；③将蜡烛远离透镜；④将蜡烛靠近透镜，你认为可行的是（）A．①和④B．②和④C．①和③D．②和③8．照相机、投影仪和放大镜都是凸透镜成像原理的具体应用。

第五章光现象一、光的传播基础巩固1.（题型一）［甘肃天水甘谷期末］光在下列介质中一定沿直线传播的是( )A.玻璃B.水C.空气D.真空图5-1-1图5-1-23.（题型二）［福建三明中考］光在真空中的传播速度约为( )A.340 m/sB.340 km/sC.3×108 m/sD.3×108 km/s4.（题型二）［河北保定高阳期中］太阳光透过玻璃窗射进屋的过程中，光速将( )A.变大B.先变大后变小C.变小D.先变小后变大5.（题型一）《梦溪笔谈》中记载了这样一个现象：在纸窗上开一个小孔，窗外飞鸢的影子会呈现在室内的纸屏上.“鸢东则影西，鸢西则影东”.对此现象分析错误的是( )A.这是光的直线传播而形成的像B.纸屏上看到的是倒立的像C.纸屏上看到的“窗外飞鸢的影子”实际上是飞鸢的像6.（题型一）［云南西双版纳模拟］“一叶障目，不见泰山.”这句话说明了__________.图5-1-38.（题型二）［河南模拟］著名英国物理学家霍金2016年4月13日在纽约宣布，将与合作伙伴开发以激光推进的微型星际“飞船”，力争以光速五分之一的速度，在二三十年内就可以飞越4光年以上，即“突破摄星”计划，其中光在真空中的速度为______m/s，光年是______（填物理量）的单位.9.（题型一）［浙江宁波中考］在“制作小孔成像观察仪”活动中，需要把制作好的圆筒插入易拉罐中，如图5-1-4所示，圆筒的______（填“A”或“B”）端是用半透明薄纸制成的光屏.用制成的小孔成像观察仪观察静物时，移动圆筒位置，增大光屏与小孔之间距离，则光屏上像将______（填“变大”“变小”或“不变”）.图5-1-4能力提升10.（题型一）［新疆乌鲁木齐中考］大约两千四百年前，我国的学者墨翟和他的学生做了世界上第一个小孔成像的实验，解释了小孔成像的原理.小光同学将两个长度均为50 cm，直径为5 cm的直筒套在一起，做成如图5-1-5的仪器（M筒的直径稍大，可以在N筒上并能前后移动）.图5-1-5（1）小孔成的像是倒立的______像,可以用光的______解释,所成的像与小孔的形状______关.（2）若直筒M、N位置不动，让物体远离N筒，像距______，像的大小______.（均填“变大”“不变”或“变小”）（3）十五的夜晚，将小孔对准明月，测得月亮最大像的直径是9.1 mm，已知月球到地球的距离为380 000 km，月球的直径约为______km.答案基础巩固1. D 解析：光在同种均匀介质中沿直线传播，光在真空中一定是沿直线传播的，光在玻璃、水和空气中由于介质不一定均匀，所以不一定沿直线传播．2. A 解析：井外的物体发出或反射的光进入青蛙眼睛，才能被青蛙看到，由于光的直线传播，所以连接井口与青蛙的眼睛的范围即为青蛙的观察范围.3. C 解析：光在真空中的传播速度为3×108 m/s，在空气中的传播速度与在真空中相近.4. D 解析：太阳光在玻璃中的传播速度比在空气中的小，在太阳光透过玻璃窗射进屋的过程中，光先在玻璃中传播，后在空气中传播，传播速度先变小后变大．5. D 解析：题目中叙述的是小孔成像现象，小孔成像利用了光的直线传播，成倒立的像，故A、B、C说法正确；如果将纸窗全部打开，就没有小孔，也就无法成像，故D说法错误.6.光在空气中沿直线传播解析：由于光在空气中沿直线传播，光线不能绕到叶子后面，故能挡住泰山.7.直线解析：日晷上看到的是指针的影子，是由光的直线传播形成的.8. 3×108 长度解析：光在真空中的速度为3×108 m/s；光年是光在1年内通过的距离，是长度单位.9.A变大解析：小孔成像利用了光的直线传播的原理.半透明薄纸相当于光屏，应该在圆筒的A端.当增大光屏与小孔之间的距离时，光屏上的像将变大.能力提升10.（1）实 直线传播 无（2）不变变小（3）3.458×103 解析：（1）小孔所成的像是由于光的直线传播而形成的实像；小孔成的像是倒立的，是物体本身的像，与小孔的形状无关.（2）如图D5-1-1所示，若直筒M 、N 位置不动，让物体远离N 筒，像仍然成在M 筒的右侧，像距不变；让物体远离N 筒由几何知识可知，AB 大小不变，则像变小.（3）如图D5-1-1所示，要使月亮所成的像最大，则MN =OD =50cm+50 cm=100 cm=1 m,根据相似三角形的性质知，''OC AB OD A B =，则833.81019.110m AB m m -⨯=⨯,解得AB =3.458×106 m=3.458×103 km.图D5-1-1。

2021人教版八年级物理上册第五章第一节,透镜,课后练习及详解人教版八年级物理上册第五章第一节透镜课后练习及详解人教版八年级物理上册第五章第一节透镜课后练习及详解 - 1 - / 5 专题透镜题一：如图所示的各类用玻璃、树脂或水晶等透明材料做成的透镜中，属于凸透镜的是____________。

A B C D E F 题二：现将一个玻璃球分成A 、B 、C 、D 、E 五块，其截面如图所示，属于凸透镜的为____________；属于凹透镜的为___________（填字母符号）。

题三：如图所示透镜中，对光线有会聚作用的光学仪器有_________，对光线有发散作用的光学仪器有___________。

题四：永州阳明山国家森林公园风景秀丽，园内严禁游客随地丢弃饮料瓶，这不仅是为了保护环境，更重要的是因为透明圆饮料瓶装水后相当于一个________镜，它对太阳光具有________作用，可能引起森林火灾。

题五：某物理兴趣小组想制造一个平行光源，他们用硬纸做成圆纸筒，在圆纸筒一端 ___一个凸透镜，纸筒的另一端 ___一个可在筒内 ___的小灯泡，调整灯泡位于凸透镜_______位置时，筒内经凸透镜射出的灯光可以认为是平行的。

题六：某次实验时，在暗室中需要用平行光照亮一个物体。

可身边只有一个不知道焦距的凸透镜和一个可以发光的小灯泡，应该怎么办？题七：如图所示是德国设计师设计的一个球形透镜太阳能系统，通过透镜聚光之后再发电。

此透镜是一个（） A ．凸透镜，对光线具有会聚作用 B ．凸透镜，对光线具有发散作用 C ．凹透镜，对光线具有会聚作用 D ．凹透镜，对光线具有发散作用题八：关于透镜，下列说法中正确的是（）A ．光线通过凹透镜一定不会相交 B ．光线通过凸透镜一定能会聚于一点 C ．凸透镜只对平行光有会聚作用 D ．一个凸透镜有两个实焦点人教版八年级物理上册第五章第一节透镜课后练习及详解 - 2 - / 5 题九：小明同学利用太阳光测量凸透镜的焦距，方法如图所示．他注意到让凸透镜正对阳光，但没有仔细调节纸片与透镜的距离，在纸片上的光斑并不是最小时，就测出了光斑到凸透镜中心的距离L ，那么，凸透镜的实际焦距（）A ．一定小于L B ．一定大于L C ．可能等于L D ．可能小于L 、也可能大于L 题十：如图所示，当用眼睛去观察镜子时，光束似乎是从M 处发散开来的，则透镜的焦距是（）A ．0.1 m B ．0.2 m C ．0.3 m D ．0.5 m 题十一：如图所示，表示小欣同学用激光分别射向甲、乙两透镜后光的传播路径，由图可知甲透镜应是______透镜，乙透镜应是________透镜（两空选填“凹”或“凸”）。

（人教版）八年级物理第五章《透镜及其应用》专题透镜成像及应用同步练习1.如图所示,已知入射光线,画出通过透镜后的折射光线2.)请在下图甲、乙方框中画上合适的透镜3.如图S是S经凸透镜成的像,请作出S发出的两条入射光线经凸透镜折射后的光路4.图中S为烛焰s 的像,请通过作图画出透镜、标出一个焦点F的位置并完成光路图.5.如图所示,SA为水面上方的点光源S射向水面的一条光线,该光线射到水面的反射光线的方向刚好指向水面上方凹透镜右侧的焦点.请画出:(1)光线SA射入水中的折射光线(2)经过凹透镜的折射光线6.如图所示,凸透镜的主光轴与水面重合,F是凸透镜的焦点,S是水中的点光源,请画出由S发出的射向左侧焦点F并经过凸透镜的光路图.7.购物支付已进入“刷脸”时代,如图所示,消费者结账时只需面对摄像头(相当于一个凸透镜),经系统自动拍照、扫描等,确认相关信息后,即可迅速完成交易.下列有关说法正确的是( )A.光经过摄像头成像利用的是光的反射B.摄像头成像特点与投影仪相同C.“刷脸”时,面部应位于摄像头二倍焦距之外D.“刷脸”时,面部经摄像头成正立、缩小的实像8.如图所示,在A处点燃一支蜡烛,若在P处的方框内分别放入①平面镜、②凸透镜、③中央有小孔的纸板时,均能在方框右侧成清晰的像.现保持蜡烛在A的位置不变,若在方框内放入上述某一器材后,能在方框的右侧光屏上成像,而且随着光屏离开P的距离增大,所成清晰的像也逐渐变大对于方框内所放的器材,下列判断中正确的是( )A.一定是①B.一定是②C.一定是③D.②和③均有可能9.如图所示,虚线框内为透镜,MN为透镜的主光轴,O是透镜的光心,a(双箭头)和b(单箭头)是射向透镜的两条光线,已知光线a通过透镜之后与MN交于P点,光线b通过透镜之后与MN交于Q点,由图可知,下列说法中正确的是（）A.透镜是凸透镜,OP的距离小于焦距B.透镜是凹透镜,OQ的距离小于焦距C.透镜是凸透镜,OP的距离大于焦距D.透镜是凹透镜,OQ的距离大于焦距10.物体距离凸透镜8cm时,在凸透镜另一侧光屏上成一个清晰放大的实像,若保持物体与光屏的位置不变,把凸透镜向光屏方向移动2cm,则在光屏上又成一清晰的缩小的像则凸透镜的焦距为( )A f<2cm B. 2<cmf<4cm C 4cm<f<5cm D. 5cm<f<8cm11.昆虫观察盒的“盒盖”上嵌入一个凸透镜(如图所示),盒盖到盒底的距离为10cm,利用凸透镜能成正立、放大像的原理可以方便地观察小昆虫,现提供了焦距为4cm、8cm、10cm和12cm 的凸透镜各一个,他应该选择的是( )A.焦距为4cm的凸透镜B.焦距为8cm的凸透镜C.焦距为10cm的凸透镜D.焦距为12cm的凸透镜12.小明同学用数码相机(可调焦距)拍摄了同一花菜的两张照片,如图所示.结合图片分析,下面说法不正确的是( )A.照相机的镜头与老花镜属于一类透镜B.凸透镜能成缩小的实像是照相机的工作原理C.在物距相同的情况下,拍摄乙照片时,镜头焦距需调得小一些D.在物距相同的情况下,拍摄乙照片时,镜头焦距需调得大一些13.如图所示,站在对面的甲同学可以通过放大镜看到手拿放大镜的乙同学放大的眼睛.对此,下列说法正确的是( )A.乙通过放大镜看到甲是倒立、缩小的实像B.甲位于放大镜的焦距之内C.乙通过放大镜看不清甲D.甲距离放大镜一定在二倍焦距之内一倍焦距之外14.小明用焦距为10cm的凸透镜做“探究凸透镜成像规律”的实验时,某次实验时蜡烛、凸透镜和光屏的位置如图所示下列说法正确的是( )A.该成像原理与投影仪的成像原理相同B.保持凸透镜的位置不动,将蜡烛移到光具座42cm刻度处时,移动光屏,在光屏上呈现倒立、放大的像C.只将蜡烛移到光具座40cm刻度处时,移动光屏,可在光屏上呈现清晰的像D.若将蜡烛从光具座30cm刻度处向远离凸透镜方向移动时,烛焰所成的像将逐渐变大15.在探究“凸透镜成像规律”的实验中,将点燃的蜡烛放在距凸透镜32cm处,在透镜另一侧距透镜18cm处的光屏上得到烛焰清晰的像,则( )A.光屏上所成的是倒立、放大的实像B.该透镜的焦距∫小于9cmC.将点燃的蜡烛移至距透镜9cm处,不能观察到烛焰放大的虚像D.透镜位置不变,蜡烛和光屏位置互换,光屏上也得到烛焰清晰的像16.为了进一步研究凸透镜成像规律,小明同学进行了如下的探究(1)如图,将蜡烛放在A处时,此时光屏上成一个清晰的像.此时像的性质为_______(2)保持凸透镜的位置不变,将蜡烛从A移到B位置,要在光屏上仍得到清晰的像,则光屏应该往_______ (选填“左”或“右”)移动17.甲、乙一起探究“凸透镜成像规律”(1)甲、乙用相同规格的凸透镜做实验,分析数据时发现,他们实验时物距相同但像距不同,可能原因是______________(2)如图所示,线段AB为凸透镜成像的物距倒数和像距倒数的对应关系,则凸透镜焦距为_______cm;若用此凸透镜成像,当物距为0.3m时,可在光屏上看到______________的像答案7.C8.89.A10.C11.D12.C13.C14.A15.D16.倒立、缩小的实像左17.某次光屏上所成的像不是最清晰地像10。

1. 试确定下面两列光波E 1=A 0[e x cos （wt-kz ）+e y cos （wt-kz-π/2）] E 2=A 0[e x sin （wt-kz ）+e y sin （wt-kz-π/2）] 的偏振态。

解 ：E 1 =A 0[e x cos(wt-kz)+e y cos(wt-kz-π/2)]=A 0[e x cos(wt-kz)+e y sin(wt-kz)] 为左旋圆偏振光E 2 =A 0[e x sin(wt-kz)+e y sin(wt-kz-π/2)]=A 0[e x sin(wt-kz)+e y cos(wt-kz)] 为右旋圆偏振光2. 为了比较两个被自然光照射的表面的亮度，对其中一个表面直接进行观察，另一个表面通过两块偏振片来观察。

两偏振片透振方向的夹角为60°。

若观察到两表面的亮度相同，则两表面的亮度比是多少？已知光通过每一块偏振片后损失入射光能量的10%。

解∶∵亮度比 = 光强比设直接观察的光的光强为I 0,入射到偏振片上的光强为I ，则通过偏振片系统的光强为I'：I'=(1/2)I (1-10%)cos 2600∙(1-10%) 因此：∴ I 0/ I = 0.5×(1-10%)cos 2600∙(1-10%) = 10.125%.3. 两个尼科耳N 1和N 2的夹角为60°，在他们之间放置另一个尼科耳N 3，让平行的自然光通过这个系统。

假设各尼科耳对非常光均无吸收，试问N 3和N 1 的偏振方向的夹角为何值时，通过系统的光强最大？设入射光强为I 0，求此时所能通过的最大光强。

解：201I I()()()()有最大值时，亦可得令注：此时透过的最大光强为，须使欲使I I d d d dI I I II I I II I II I 20cos cos 2329434323060cos 30cos 2302602cos cos 2cos cos 2cos 2222max22232213θααθαααθααθααθαα==⎥⎦⎤⎢⎣⎡-==⋅⋅=-=====∴-=-===4. 在两个理想的偏振片之间有一个偏振片以匀角速度ω绕光的传播方向旋转（见题5.4图），若入射的自然光强为I 0，试证明透射光强为I =16πI 0（1-cos4ωt ）.解: I = 12I 0 cos 2ωt cos 2（2π-ωt ） = 12 I 0cos 2ωtsin 2 ωt = 18 I 0 1-cos4t2ω= I 0（1-cos4ωt ） `题5. 线偏振光入射到折射率为1.732的玻璃片上，入射角是60°，入射光的电失量与入射面成30°角。

人教版初二物理上册第五章透镜及其应用测带参考答案和解析选择题下列光学器件中，没有用到凸透镜的是( )A. B. C. D.【答案】C【解析】A. 照相机是利用凸透镜成倒立、缩小的实像工作的，故A不符合题意；B. 投影仪是利用凸透镜成倒立、放大的实像工作的，故B 不符合题意；C梳妆镜即平面镜是利用光的反射的原理，与凸透镜无关，故C符合题意；D. 放大镜实质就是一个凸透镜，即成正立、放大的虚像，故D不符合题意。

故选C.选择题图中画出了光线通过透镜（图中未画出）的情形。

其中凸透镜是A. aB. b.dC. cD.a.b.c.d【答案】C【解析】本题涉及的是透镜对光的作用，考查学生对会聚和发散的理解。

凸透镜和凹透镜都光路的改变都是遵循光的折射原理。

凸透镜是中心厚边缘薄，光路径透镜两次折射都是向靠近光轴方向（中心的方向）偏折，所以它有会聚作用。

凹透镜是中心薄边缘厚，光路径透镜两次折射都是向远离光轴方向（中心的方向）偏折，所以它有发散作用。

从a、b、c、d四个图可以看出对光有会聚作用的只有c。

选择题下列关于透镜的说法正确的是( )A. 凸透镜对光有发散作用，凹透镜对光有会聚作用B. 凸透镜的焦距越小，对光的会聚作用越强C. 任何光线经过凸透镜折射后都能会聚于一点D. 凹透镜只对平行于主光轴的光具有发散作用【答案】B【解析】A、凸透镜对光线有会聚作用，凹透镜对光线有发散作用，故A 错误；B、凸透镜的焦距越小，说明其对光的会聚作用越强，故B正确；C、发散光线经过凸透镜折射后可能成平行光线，故C错误；D、凹透镜可使任何光线发散，而不是只对平行于主光轴的光线具有发散作用，故D错误。

故选B。

选择题像的成因有三个：光的直线传播成像、反射成像和折射成像，所成的像有实像和虚像两种。

关于下面所列的成像实例：①针孔照相机内所成的像；②在潜望镜中看到的景物的像；③放大镜中看到的物体的像；④幻灯机屏幕上的像；⑤汽车观后镜中的像。

下列说法中正确的是( )A. 属于实像的是①④B. 属于虚像的是②③④C. 属于折射成像的是①③D. 属于反射成像的是①②⑤【答案】A【解析】①针孔照相机属于小孔成像原理，因此成的是实像，它是光的直线传播原理形成的；②从潜望镜中观察景物，观察到的是虚像，利用的是平面镜成像原理，属于光的反射现象；③用放大镜看物体，利用的是光的折射现象中成虚像的情况；④看幻灯机屏幕上的像，是光的折射现象，成的是倒立放大的实像；⑤汽车观后镜中的像是正立缩小的虚像。

【最新版】人教版八年级上册物理第五章《透镜及透镜成像作图》专项练习（含答案）类型一凸透镜、凹透镜三条特殊光线【方法技巧】1.凸透镜三条特殊光线：(1)过光心的光线，其传播方向不改变；(2)平行主光轴的光线折射后过焦点：(3)过焦点射向凸透镜的光线折射后将平行主光轴传播。

2.凹透镜三条特殊光线：（1）经过光心的光线传播方向不改变。

（2）与主光轴平行的光线折射后的反向延长线过虚焦点。

（3）射向虚焦点的光线折射后平行于主光轴。

【专项训练】1.在图1中完成凸透镜光路图，在图2中完成凹透镜光路图。

2.平行光经过凸透镜后会聚在主光轴上的一点，这个点叫凸透镜的焦点；平行光经过凹透镜后，光线发散，发散光线的反向延长线交在主光轴上的一点，这个点叫凹透镜的虚焦点。

如图，F 点既是图示凸透镜的焦点，也是图示凹透镜的虚焦点，请画出图中两条平行于主光轴的光线经过两个透镜的光路图。

3.如图所示，在平面镜与凸透镜之间放一物体AB，F为凸透镜的焦点，从B点发出的一条光线经平面镜反射后恰好通过凸透镜的焦点F，并射向凸透镜，经凸透镜发生折射。

请画出：(1)物体AB在平面镜中的像A′B′。

(2)B点发出的光线经平面镜反射后通过焦点F的光路。

(3)经凸透镜折射后的光线。

4.如图所示，一条光线经平面镜反射后，过凸透镜的焦点F射向凸透镜。

请在图中画出射向平面镜的入射光线和经凸透镜后的折射光线；5.如题所示，A光线是经平面镜反射后的反射光线。

请你画出：①A光线的入射光线：②A光线通过凹透镜的折射光线。

6.请完成图中，光线通过凸透镜折射，再经平面镜反射的光路图。

7.如图所示，ab为光线经平面镜反射后的光线，F为凹透镜的焦点请画出：①光线ab的入射光线；②光线ab经凹透镜后的折射光线；③标出入射角的度数。

8.请在虚线框内画出适当的透镜符号或面镜符号。

9.根据光的传播路径，在图中的虚线框内，填入符合要求的透镜。

10.小欣家收藏了一架老式照相机，如图所示是它内部结构的简图。

五、物体的颜色能力提升1.关于光现象,下列说法正确的是()。

A.用磨砂玻璃作教室的黑板是为了克服漫反射B.看到池子里的水深比实际的浅是由光的折射所致C.雨后天空出现彩虹是由光的反射形成的D.光的色散现象说明彩色光是由白光组成的2.在“人面桃花相映红”这句诗中,用光学知识解释桃花红的原因是()。

A.桃花自己能发出红光B.桃花吸收红光C.桃花反射红光D.以上说法都不对3.广告公司在拍摄水果广告时,为了追求某种艺术效果,在暗室里用红光照射装在白色瓷盘中的红色苹果及黄色香蕉。

站在旁边的摄影师将看到()。

A.苹果呈黑色,瓷盘呈白色,香蕉呈黑色B.苹果呈红色,瓷盘呈黑色,香蕉呈黑色C.苹果呈黑色,瓷盘呈红色,香蕉呈红色D.苹果呈红色,瓷盘呈红色,香蕉呈黑色4.如图5-5-3所示的现象中,属于光的色散现象的是()。

图5-5-35.太阳光经过三棱镜后分解为红、橙、黄、绿、蓝、靛、紫七色光,这种现象叫光的;红、、蓝叫色光的三原色。

6.在光学实验室内,将一辆玩具汽车放置在白色背景板前。

拉上窗帘,打开光源A,让一束白光照向汽车,发现汽车呈现黄色,这是由于汽车(选填“吸收”或“反射”)了黄色光。

若将另外一束红光照向汽车的影子,则影子区域此时呈现色。

图5-5-47.在商店里买布,特别是花布,为了看准颜色,往往把布拿到太阳光下观察,而不是在日光灯下看,这是为什么?探究创新8.小明设计了一个游戏,在一张白纸上画了四个动物的图案,每个动物的颜色如图5-5-5所示。

当小明分别透过红色玻璃纸、蓝色玻璃纸、绿色玻璃纸看白纸上图案时,三次分别看到的是甲、乙、丙三种在所看玻璃纸颜色中的黑色图案,请判断:透过红色玻璃纸看到的是图5-5-6中的图。

图5-5-5图5-5-6参考答案1.B解析:用磨砂玻璃作教室的黑板是为了克服镜面反射,雨后天空出现彩虹是由光的色散形成的,光的色散现象说明白光是由彩色光组成的。

2.C解析:不透明物体的颜色是由它反射的色光颜色决定的。

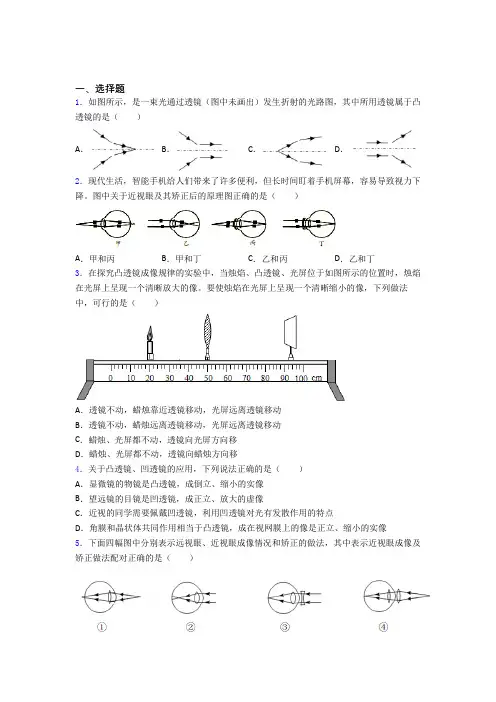
一、选择题1．如图所示，是一束光通过透镜（图中未画出）发生折射的光路图，其中所用透镜属于凸透镜的是（）A．B．C．D．2．现代生活，智能手机给人们带来了许多便利，但长时间盯着手机屏幕，容易导致视力下降。

图中关于近视眼及其矫正后的原理图正确的是（）A．甲和丙B．甲和丁C．乙和丙D．乙和丁3．在探究凸透镜成像规律的实验中，当烛焰、凸透镜、光屏位于如图所示的位置时，烛焰在光屏上呈现一个清晰放大的像。

要使烛焰在光屏上呈现一个清晰缩小的像，下列做法中，可行的是（）A．透镜不动，蜡烛靠近透镜移动，光屏远离透镜移动B．透镜不动，蜡烛远离透镜移动，光屏远离透镜移动C．蜡烛、光屏都不动，透镜向光屏方向移D．蜡烛、光屏都不动，透镜向蜡烛方向移4．关于凸透镜、凹透镜的应用，下列说法正确的是（）A．显微镜的物镜是凸透镜，成倒立、缩小的实像B．望远镜的目镜是凹透镜，成正立、放大的虚像C．近视的同学需要佩戴凹透镜，利用凹透镜对光有发散作用的特点D．角膜和晶状体共同作用相当于凸透镜，成在视网膜上的像是正立、缩小的实像5．下面四幅图中分别表示远视眼、近视眼成像情况和矫正的做法，其中表示近视眼成像及矫正做法配对正确的是（）A ．①③B ．②③C ．②④D ．①④6．关于生活中的光现象，下列说法正确的是（ ）A ．平面镜成像时，物体与平面镜的距离越远，所成的虚像越小B ．凸透镜成实像时对光线有会聚作用，成虚像时对光线有发散作用C ．因为光的折射，我们观察到日出的时刻会比实际日出的时间早D ．人站在河边看到自己在水中的倒影，是由于光的折射形成的虚像7．随着人们生活水平和文化水平的提高，望远镜已逐渐成为人们文化消费的必备品进入日常生活，如图所示，关于望远镜的知识，以下说法不正确的是（ ）A ．望远镜靠近眼睛的镜片叫目镜，利用目镜可以把景物的像放大，相当于放大镜B ．物镜的作用是使远处的物体在焦点附近成缩小的实像，这类似于照相机C ．第一个用天文望远镜观测天体的科学家是伽利略D ．望远镜都是由一个凸透镜和一个凹透镜构成的8．在探究凸透镜成像规律的实验中，当蜡烛、凸透镜、光屏位于如图所示的位置时，在光屏上呈现一个清晰的烛焰的像。

目录第五章透镜及其应用 (1)第1节透镜 (1)第2节生活中的透镜 (4)第3节凸透镜成像的规律 (7)第4节眼睛和眼镜 (11)第5节显微镜和望远镜 (13)第五章测评(A) (15)(时间:45分钟满分:100分) (15)第五章测评(B) (21)(时间:45分钟满分:100分) (21)第五章透镜及其应用第1节透镜1.如果把一个玻璃球分割成五块,其截面如图所示,再将这五块玻璃a、b、c、d、e 分别放在太阳光下,那么能使光线发散的是()A.aB.bC.cD.d2.下列关于透镜光学性质的说法正确的是()A.凡是过光心的光线,其传播方向都不变B.经透镜后其光线是发散的,该透镜肯定是凹透镜C.经透镜后其光线是会聚的,该透镜肯定是凸透镜D.以上说法都正确3.下列光路图中,正确的是()4.一种手电筒上所用的聚光电珠如图所示,其前端相当于一个玻璃制的凸透镜,为了使灯丝发出的光经凸透镜后变成平行光,应把灯珠放在()A.焦点处B.焦点以内C.焦点以外D.任意位置5.下图中画出了光线通过透镜(图中未画出)的情形。

其中凸透镜是()A.aB.b、dC.cD.a、b、c、d6.张家界因山而著名,吸引许多中外游客来旅游,有少数游客在山上游玩时将空纯净水瓶扔在山上,这样做既污染了环境,同时还可能引起山林火灾。

这是因为当下雨时纯净水瓶装入水后,就相当于一个透镜。

晴天强太阳光照射它时,它对光线会产生作用,可能会引起枯叶着火。

因此我们在山中游玩时一定要注意保护环境。

7.晴朗的夏日中午,往树或花的叶子上浇水,常会把叶子烧焦,其原因是这时叶面上的水珠相当于,它对光起作用,使透过它的光可能而将叶子烧焦。

8.给你一个透镜,不知道是凸透镜还是凹透镜,请你简要写出两种判断方法。

(1)。

(2)。

9.如图所示,SA、SB是光源S发出的两条光线。

其中SA平行于主光轴,SB过左焦点,请画出这两条光线通过凸透镜后的出射光线(注意标出箭头方向)。

教材习题答案第五章透镜及其应用第1节透镜1. 如图5.1－8，甲、乙两个凸透镜的焦距分别是3 cm和5 cm。

画出平行光经过它们之后的光线。

哪个凸透镜使光偏折得更显著些？图5.1－8[答案]如图所示，不同透镜的焦距是不同的，甲凸透镜使光偏折得更显著些。

2. 要想利用凸透镜使小灯泡发出的光变成平行光，应该把小灯泡放在凸透镜的什么位置？试试看。

在解决这个问题的时候，你利用了前面学过的什么知识？[答案]根据光路可逆原理，凸透镜可以将平行光会聚到焦点上，我们就应把小灯泡放在凸透镜的焦点上，小灯泡发出的光通过凸透镜后就可以变成平行光。

3. 一束光通过透镜的光路如图5.1－9所示，哪幅图是正确的？图5.1－9哪幅图是正确的？[答案]图甲是正确的[解析] 凸透镜对光线具有会聚作用，平行于主光轴的光会聚到焦点。

凹透镜对光线具有发散作用，平行光发散后的光线的反向延长线交于另一侧焦点。

4. 根据入射光线和折射光线，在图5.1－10中的虚线框内画出适当类型的透镜。

图5.1－10[答案]如图所示甲乙第2节生活中的透镜1. 如图5.2－1所示，照相机的镜头相当于一个凸透镜，像成在照相机的底片上。

判断图中的树所成像的正倒。

[答案]倒立[解析] 照相机成像的原理是成倒立、缩小的实像。

2. 凸透镜是许多光学仪器的重要元件，可以呈现不同的像。

应用凸透镜，在照相机中成________、________立的________像；通过投影仪成________、________立的________像；用凸透镜做放大镜时，成________、________立的________像。

[答案]缩小倒实放大倒实放大正虚3. 手持一个凸透镜，在室内的白墙和窗户之间移动(离墙近些)，在墙上能看到什么？这个现象启发我们，阴天怎样估测凸透镜的焦距？为使估测结果更准确，操作时应注意什么？[答案]手持凸透镜在窗户和室内的白墙之间移动(离墙近些)，移到某个位置时，窗户外的景物能在墙上形成一个清晰、倒立、缩小的实像。

初中物理人教版八年级上册第五章透镜及其应用透镜透镜对光的作用课后微练习 1参考答案：1．答案： A解析：玻璃瓶内有水，其截面中间厚，边缘薄，相当于凸透镜，对太阳光具有会聚作用，若在会聚处有干燥的易燃树枝树叶，会引发森林大火。

2．答案： D解析： A、光沿直线传播的条件：同种均匀介质中．B．根据光的反射定律的内容，特别是反射角与入射角的关系，其中必须搞清入射角与反射角的概念．C．凸透镜对光起会聚的作用，这里的光时泛指所有类型的光，包括发散的光、会聚的光和平行光．D．红外线是一种看不见的光，它也遵循光的直线传播和反射规律，在现实生活中有实际的应用．A．光在同种均匀介质中沿直线传播；当介质不均匀时，将发生折射；因地球周围的大气层密度不均匀；故说法A错误；B．因为入射光线垂直射到平面镜上，入射光线和法线重合，所以入射角等于0°，而反射角等于入射角，即反射角为0°，故B错误；C．凸透镜对所有的光线都有会聚的作用，所以此说法是片面的，故C错误．D．遥控器发出的红外线，它会以光波的性质直线传播，并且可以发生反射，有时遥控器并没有对准电视机的控制窗口，而是沿某一合适的方向对准墙壁按下按钮，也可以控制电视机，这是利用了光的反射．故D正确．3．答案： B解析：潜望镜是平面镜，用于改变光路；学过的光学元件有：凸透镜、凹透镜、平面镜、凸面镜、凹面镜．其中对光线会聚的光学元件有：凸透镜、凹面镜．平面镜对光学既不发散也不会聚．凹透镜和凸面镜对光学有发散作用．4．答案： D解析：对光有发散作用的由：凹透镜和凸面镜，对光有会聚作用的有：凸透镜和凹面镜，平面镜使光线发生镜面反射，既不会聚也不发散．故选D．5．答案： B解析：选B.水滴向外凸出相当于凸透镜，对光线有会聚作用，使车身局部产生高温.6．答案：光是沿直线传播的凸透镜对光有会聚作用解析：光在同种均匀物质中沿直线传播，太阳光穿过浓密的树叶孔隙，在地面上形成明亮的光斑，属于小孔成像，是光沿直线传播；太阳光正对凸透镜，有时也能看到一个明亮的光斑，凸透镜对光起到会聚的作用。