高一立体几何初步练习题

2023-2024学年高一数学《平面向量及立体几何初步》一．选择题（共12小题）
1．（2022春•鼓楼区校级期中）已知向量，，若∥，则实数m ＝（）
A．1B．﹣1C ．D
．﹣
2．（2022春•鼓楼区校级期中）已知向量，是单位向量，若|2﹣|＝，
则
与的夹角为（）
A ．
B ．
C ．
D ．
3．（2022春•鼓楼区校级期中）P是△ABC
所在平面内一点，若，则S△ABP：S
△ABC
＝（）
A．1：4B．1：3C．2：3D．2：1 4．（2022•福州模拟）已知向量，为单位向量，且⊥，则•（4﹣3）＝（）A．﹣3B．3C．﹣5D．5 5．（2022春•马尾区校级月考）已知△ABC的内角A，B，C对边分别为a，b，c，若2c sin C ＝（a+b）（sin B﹣sin A），则当角C取得最大值时，B＝（）
A ．
B ．
C ．
D ．
6．（2022春•福州期中）在四边形ABCD
中，若＝，且|﹣|＝|
+|，则该四边
形一定是（）
A．正方形B．菱形C．矩形D．等腰梯形7．（2022•鼓楼区校级三模）已知AB，CD分别是圆柱上、下底面圆的直径，且AB⊥CD．O1，O分别为上、下底面的圆心，若圆柱的底面圆半径与母线长相等，且三棱锥A﹣BCD的体积为18，则该圆柱的侧面积为（）
A．9πB．12πC．16πD．18π8．（2022•福州模拟）在底面半径为1的圆柱OO1中，过旋转轴OO1作圆柱的轴截面ABCD，其中母线AB＝2，E是BC的中点，F是AB的中点，则（）
A．AE＝CF，AC与EF是共面直线
第1页（共25页）。

高一数学必修第二册第八章《立体几何初步》单元练习题卷3（共22题）一、选择题（共10题）1.在空间四边形ABCD的边AB，BC，CD，DA上分别取E，F，G，H四点，若EF与HG交于点M，那么( )A．M一定在直线AC上B．M一定在直线BD上C．M可能在直线AC上，也可能在直线BD上D．M既不在直线AC上，也不在直线BD上2.关于“斜二测”画图法，下列说法不正确的是( )A．平行直线的斜二测图仍是平行直线B．斜二测图中，互相平行的任意两条线段的长度之比保持原比例不变C．正三角形的直观图一定为等腰三角形D．在画直观图时，由于坐标轴的选取不同，所得的直观图可能不同3.已知直线m，n与平面α，β，m⊥α，n⊥β，若α⊥β，则m，n的位置关系是( )A．平行B．垂直C．相交D．异面4.如图所示，正方体ABCD−A1B1C1D1的棱长为2，动点E，F在棱A1B1上，动点P，Q分别在棱AD，CD上，若EF=1，A1E=x，DQ=y，DP=z（x，y，z大于零），则四面体PQEF的体积( )A．与x，y，z都有关B．与x有关，与y，z无关C．与y有关，与x，z无关D．与z有关，与x，y无关5.在正方体中ABCD−A1B1C1D1中，E为棱CD的中点，则( )A．A1E⊥DC1B．A1E⊥BD C．A1E⊥BC1D．A1E⊥AC6.一个四面体的所有棱长都为√2，四个顶点在同一球面上，则此球的表面积为( )A．3πB．4πC．3√3πD．6π7.正方体的内切球与其外接球的体积之比为( )A．1:√3B．1:3C．1:3√3D．1:98.《九章算术》中，称底面为矩形且有一侧棱垂直于底面的四棱锥为阳马，如图，某阳马的三视图如图所示，则该阳马的最长棱的长度为( )A．√2B．√3C．2D．2√29.已知正六棱柱的12个顶点都在一个半径为3的球面上，当正六棱柱的体积取最大值时，其高的值为( )A．3√3B．√3C．2√6D．2√310.若一个圆锥的轴截面（过圆锥顶点和底面直径的截面）是等边三角形，其面积为√3，则这个圆锥的体积为( )A．3πB．√3π3C．√3πD．√3π2二、填空题（共6题）11.已知正方体ABCD−A1B1C1D1的棱长为1，除面ABCD外，该正方体其余各面的中心分别为点E，F，G，H，M（如图），则四棱锥M−EFGH的体积为．12.如图，在正三棱柱ABC−A1B1C1中，已知AB=AA1=3，点P在棱CC1上，则三棱锥P−ABA1的体积为．13.正六棱柱的底面边长为4，高为6，则它的外接球（正六棱柱的顶点都在此球面上）的表面积为．14.正△ABC的斜二测画法的水平放置图形的直观图，若△AʹBʹCʹ的面积为√3，那么△ABC的面积为．15.正方体ABCD−A1B1C1D1中，若过A，C，B1三点的平面与底面A1B1C1D1的交线为l，则l与A1C1的位置关系是．16.如图所示，长方形ABCD−A1B1C1D1的体积为24，E为线段B1C上的一点，则棱锥A−DED1的体积为．三、解答题（共6题）17.如图，在正方体ABCD−A1B1C1D1中，P，Q分别是平面AA1D1D，平面A1B1C1D1的中心，证明：(1) D1Q∥平面C1DB；(2) 平面D1PQ∥平面C1DB．18.如图，在四棱锥P−ABCD中，底面ABCD是菱形，PB=PD．(1) 求证：平面APC⊥底面BPD；(2) 若PB⊥PD，∠DAB=60∘，AP=AB=2，求二面角A−PD−C的余弦值．19.如图，在△AOB中，∠AOB=90∘，AO=2，OB=1．△AOC可以通过△AOB以直线AO为轴旋转得到，且OB⊥OC，动点D在斜边AB上．(1) 求证：平面COD⊥平面AOB；(2) 当D为AB的中点时，求二面角B−CD−O的余弦值；(3) 求CD与平面AOB所成的角中最大角的正弦值．20.如图，在三棱柱ABC−A1B1C1中，四边形A1C1CA为菱形，∠B1A1A=∠C1A1A=60∘，AC=4，AB=2，平面ACC1A1⊥平面ABB1A1，Q在线段AC上移动，P为棱AA1的中点．(1) 若Q为线段AC的中点，H为BQ的中点，延长AH交BC于D，求证：AD∥平面B1PQ；(2) 若二面角B1−PQ−C1的平面角的余弦值为√13，求点P到平面BQB1的距离．1321.如图，AE⊥面ABCD，ABCD是正方形，AE=AB=2，F为BE的中点．求证：DE∥面ACF．22.阅读下面题目及其证明过程，在横线处填写适当的内容．如图，长方体ABCD−A1B1C1D1的底面ABCD是边长为1的正方形，点E，F分别为线段BD1，CC1的中点．（Ⅰ）求证：EF∥平面ABCD；（Ⅰ）当DD1=√2时，求证：DE⊥平面BFD1；证明：（Ⅰ）如图，连接AC，BD，设AC∩BD=O，连接OE．因为长方体ABCD−A1B1C1D1的底面ABCD是边长为1的正方形，所以BO=OD，又因为BE=ED1，DD1，所以OE∥DD1，OE=12因为F为线段CC1中点，DD1，所以CF∥DD1，CF=12所以CF∥OE，CF=OE．所以四边形OCFE为平行四边形．所以EF∥OC．又因为EF⊄平面ABCD，OC⊂平面ABCD，所以EF∥平面ABCD．（Ⅰ）因为F为线段CC1中点，所以BF=D1F，所以△D1FB是等腰三角形．因为E为BD1的中点，所以EF⊥BD1．因为BD⊥OC，EF∥OC，所以EF⊥BD．因为BD∩BD1=B，所以①．因为DE⊂平面BDD1，所以②．因为DD1=√2，所以DD1=BD，所以③．因为EF∩D1B=E，所以DE⊥平面BFD1．在上述证明过程中，（Ⅰ）的证明思路是：先证明“④”，再证明“⑤”．答案一、选择题（共10题）1. 【答案】A【解析】如图，因为EF∩HG=M，所以M∈EF，M∈HG，又EF⊂平面ABC，HG⊂平面ADC，故M∈平面ABC，M∈平面ADC，又平面ABC∩平面ADC=AC，所以M∈AC．故选A．【知识点】平面的概念与基本性质2. 【答案】C【解析】对于A，平行直线的斜二测图仍是平行直线，A正确；对于B，斜二测图中，互相平行的任意两条线段的长度之比保持原比例不变，B正确；对于C，正三角形的直观图不一定为等腰三角形，如图所示，所以C错误；对于D，画直观图时，由于坐标轴的选取不同，所得的直观图可能不同，D正确．【知识点】直观图3. 【答案】B【解析】m，n有可能相交或异面，但必定垂直．故答案选B．【知识点】直线与直线的位置关系4. 【答案】D【解析】设P点到平面A1B1CD的距离为ℎ，因为A1B1∥DC，所以Q到EF的距离为定值2√2，又因为EF=1，所以S△QEF=12×1×2√2=√2，因为V四面体PQEF =V三棱锥P−QEF=13S△QEF⋅ℎ=√23ℎ，即四面体的体积只与点P到平面A1B1CD的距离无关，所以四面体的体积与z有关，与x，y无关．【知识点】棱锥的表面积与体积5. 【答案】C【解析】画出正方体ABCD−A1B1C1D1，如图所示．对于选项A，连D1E，若A1E⊥DC1，又DC1⊥A1D1，所以DC1平面A1ED1，所以可得DC1⊥D1E，显然不成立，所以A不正确．对于选项B，连AE，若A1E⊥BD，又BD⊥AA1，所以DB⊥平面A1AE，故得BD⊥AE，显然不成立，所以B不正确．对于选项C，连AD1，则AD1∥BC1．连A1D，则得AD1⊥A1D，AD1⊥ED，所以AD1⊥平面A1DE，从而得AD1⊥A1E，所以A1E⊥BC1．所以C正确．对于选项D，连AE，若A1E⊥AC，又AC⊥AA1，所以AC⊥平面A1AE，故得AC⊥AE，显然不成立，所以D不正确．【知识点】空间中直线与直线的垂直6. 【答案】A【解析】联想只有正方体中有这么多相等的线段，所以构造一个正方体，则正方体的面对角线即为四面体的棱长，求得正方体的棱长为1，体对角线为√3，从而外接球的直径也为√3，所以此球的表面积为3π．【知识点】组合体、球的表面积与体积7. 【答案】C【解析】设正方体的棱长为a，则其内切球的半径为a2，所以V内=43π(a2)3−πa36，正方体的外接球的半径为√32a，所以V外=43π(√32a)3=3√3πa36，所以V内:V外=1:3√3．【知识点】球的表面积与体积8. 【答案】B【解析】根据题设条件可知三视图还原成的几何体为四棱锥，如图所示，其中PD=1，底面ABCD是边长为1的正方形，易知PB=√3，PA=PC=√2，故最长棱的长度为√3．【知识点】三视图、棱锥的结构特征9. 【答案】D【知识点】棱柱的表面积与体积10. 【答案】B【解析】设圆锥底面圆的半径为r，圆锥的高为ℎ，体积为V，则ℎ=√3r．因为12×2r×√3r=√3r2=√3，所以r=1，所以V=13πr2h=√33πr3=√3π3．【知识点】圆锥的表面积与体积二、填空题（共6题）11. 【答案】112【解析】连接AD1，CD1，B1A，B1C，AC，因为E，H分别为AD1，CD1的中点，所以EH∥AC，EH=12AC，因为 F ，G 分别为 B 1A ，B 1C 的中点， 所以 FG ∥AC ，FG =12AC ，所以 EH ∥FG ，EH =FG ， 所以四边形 EHGF 为平行四边形， 又 EG =HF ，EH =HG ， 所以四边形 EHGF 为正方形， 又点 M 到平面 EHGF 的距离为 12， 所以四棱锥 M −EFGH 的体积为 13×(√22)2×12=112．【知识点】棱锥的表面积与体积12. 【答案】9√34【解析】因为在正三棱柱 ABC −A 1B 1C 1 中，AB =AA 1=3，点 P 在棱 CC 1 上， 所以点 P 到平面 ABA 1 的距离即为 △ABC 的高， 即为 ℎ=√32−(32)2=3√32，S △ABA 1=12×3×3=92，三棱锥 P −ABA 1 的体积为：V =13×S △ABA 1×ℎ=13×92×3√32=9√34．【知识点】棱锥的表面积与体积13. 【答案】 100π【解析】依题意，该正六棱柱的外接球的球心应是上、下底面中心连线的中点， 所以其半径等于 √42+(62)2=5，其表面积等于 4π×25=100π．【知识点】球的表面积与体积14. 【答案】 2√6【知识点】直观图15. 【答案】 A 1C 1∥l【解析】因为 平面ABCD ∥平面A 1B 1C 1D 1，AC ⊂平面ABCD ， 所以 AC ∥平面A 1B 1C 1D 1，又平面 ACB 1 经过直线 AC 与平面 A 1B 1C 1D 1 相交于直线 l ， 所以 AC ∥l ， 又因为 A 1C 1∥AC ， 所以 A 1C 1∥l ．【知识点】直线与平面平行关系的性质、直线与平面平行关系的判定16. 【答案】4【解析】设AB=a，AD=b，AA1=c，则长方体的体积V ABCD−A1B1C1D1=abc=24，三棱锥A−DED1的体积V A−DED1=V E−ADD1=13S△ADD1⋅AB=13×12×AD×DD1×AB=16×bc⋅a=16×24=4.【知识点】棱锥的表面积与体积三、解答题（共6题）17. 【答案】(1) 由题可知D1Q∥DB．因为D1Q⊄平面C1DB，DB⊂平面C1DB，所以D1Q∥平面C1DB．(2) 由题可知D1P∥C1B．因为D1P⊄平面C1DB，C1B⊂平面C1DB，所以D1P∥平面C1DB．由（1）知，D1Q∥平面C1DB，又D1Q∩D1P=D1，所以平面D1PQ∥平面C1DB．【知识点】平面与平面平行关系的判定、直线与平面平行关系的判定18. 【答案】(1) 记AC∩BD=O，连接PO，因为底面 ABCD 是菱形，所以 BD ⊥AC ，O 是 BD ，AC 的中点， 因为 PB =PD ， 所以 PO ⊥BD ， 因为 AC ∩PO =O ， 所以 BD ⊥平面APC ， 又因为 BD ⊂平面BPD ，所以 平面APC ⊥平面BPD ．(2) 如图，以 O 为原点，OA ，OB ，OP 所在直线分别为 x ，y ，z 轴建立如图所示的空间坐标系， 则 A(√3,0,0)，D (0,−1,0)，P (0,0,1)，C(−√3,0,0,)，所以 DA ⃗⃗⃗⃗⃗ =(√3,1,0)，DP ⃗⃗⃗⃗⃗ =(0,1,1)，DC ⃗⃗⃗⃗⃗ =(−√3,1,0)， 设 n 1⃗⃗⃗⃗ =(x 1,y 1,z 1) 是平面 APD 的法向量，则 {DA ⃗⃗⃗⃗⃗ ⋅n 1⃗⃗⃗⃗ =0,DP ⃗⃗⃗⃗⃗ ⋅n 1⃗⃗⃗⃗ =0⇒{√3x 1+y 1=0,y 1+z 1=0, 令 y 1=−√3，得 n 1⃗⃗⃗⃗ =(1,−√3,√3)，同理可得平面 PCD 的法向量 n 2⃗⃗⃗⃗ =(1,√3,−√3)，所以 cos ⟨n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ ⟩=n1⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗⃗ ∣∣n 1⃗⃗⃗⃗⃗ ∣∣⋅∣∣n2⃗⃗⃗⃗⃗ ∣∣=√3)×√3+(−√3)×√3√7×√7=−57，由图形可知二面角 A −PD −C 为钝二面角， 所以二面角 A −PD −C 的余弦值为 −57．【知识点】利用向量的坐标运算解决立体几何问题、平面与平面垂直关系的判定、二面角19. 【答案】(1) 在 △AOC 中，AO ⊥OC ， 因为 OB ⊥OC ，且 AO ∩OB =O ， 所以 OC ⊥平面AOB ， 又 OC ⊂平面COD ，所以 平面COD ⊥平面AOB ．(2) 如图建立空间直角坐标系 O −xyz ， 因为 D 为 AB 的中点，所以 O (0,0,0)，A (0,0,2)，B (0,1,0)，C (1,0,0)，D (0,12,1)，所以 OC ⃗⃗⃗⃗⃗ =(1,0,0)，OD ⃗⃗⃗⃗⃗⃗ =(0,12,1)，BC ⃗⃗⃗⃗⃗ =(1,−1,0)，BD⃗⃗⃗⃗⃗⃗ =(0,−12,1)， 设 n 1⃗⃗⃗⃗ =(x 1,y 1,z 1) 为平面 OCD 的法向量，所以 {n 1⃗⃗⃗⃗ ⋅OC ⃗⃗⃗⃗⃗ =0,n 1⃗⃗⃗⃗ ⋅OD ⃗⃗⃗⃗⃗⃗ =0, 即 {x 1=0,12y 1+z 1=0, 令 z 1=1，则 y 1=−2，所以 n 1⃗⃗⃗⃗ =(0,−2,1) 是平面 BCD 的一个法向量， 设 n 2⃗⃗⃗⃗ =(x 2,y 2,z 2) 为平面 OCD 的法向量， 所以 {n 2⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =0,n 2⃗⃗⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =0, 即 {x 2−y 2=0,−12y 2+z 2=0, 令 z 2=1，则 x 2=2，y 2=2，所以 n 2⃗⃗⃗⃗ =(2,2,1) 是平面 OCD 的一个法向量，所以 cos 〈n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ 〉=n 1⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗⃗ ∣∣n 1⃗⃗⃗⃗⃗ ∣∣⋅∣∣n 2⃗⃗⃗⃗⃗ ∣∣=√02+(−2)2+12⋅√22+22+12=−√55， 所以二面角 B −CD −O 的余弦值为 √55． (3) 解法一：因为 OC ⊥平面AOB ，所以 ∠CDO 为 CD 与平面 AOB 所成的角， 因为 OC =1，所以点 O 到直线 AB 的距离最小时，∠CDO 的正弦值最大， 即当 OD ⊥AB 时，∠CDO 的正弦值最大， 此时 OD =2√55， 所以 CD =3√55， 所以 sin∠CDO =√53． 解法二：设 AD⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ (λ∈[0,1])， 所以 D (0,λ,2−2λ)．CD ⃗⃗⃗⃗⃗ =(−1,λ,2−2λ)，平面 AOB 的法向量 n ⃗ =(1,0,0)，所以 sinθ=∣∣n ⃗ ⋅CD⃗⃗⃗⃗⃗ ∣∣∣∣n ⃗ ∣∣∣∣CD⃗⃗⃗⃗⃗ ∣∣=√5λ2−8λ+5=√5(λ−45)2+95，所以当 λ=45 时，CD 与平面 AOB 所成的角最大，sinθ=√53． 【知识点】二面角、平面与平面垂直关系的判定、线面角20. 【答案】(1) 如图，取 BB 1 的中点 E ，连接 AE ，EH ． 因为 H 为 BQ 的中点， 所以 EH ∥B 1Q ．在平行四边形 AA 1B 1B 中，P ，E 分别为 AA 1，BB 1 的中点， 所以 AE ∥PB 1．又 EH ∩AE =E ，PB 1∩B 1Q =B 1， 所以 平面EHA ∥平面B 1QP ． 因为 AD ⊂平面EHA ， 所以 AD ∥平面B 1PQ ．(2) 如图，连接 PC 1，AC 1，因为四边形 A 1C 1CA 为菱形，∠C 1A 1A =60∘， 所以 AA 1=AC 1=A 1C 1=4， 即 △AC 1A 1 为等边三角形． 因为 P 为 AA 1 的中点， 所以 PC 1⊥AA 1．因为 平面ACC 1A 1⊥平面ABB 1A 1，平面ACC 1A 1∩平面ABB 1A 1=AA 1，PC 1⊂平面ACC 1A 1， 所以 PC 1⊥平面ABB 1A 1．在平面 ABB 1A 1 内过点 P 作 PR ⊥AA 1 交 BB 1 于 R ．以 PR ，PA 1，PC 1 所在直线分别为 x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系 Pxyz ，则 P (0,0,0)，A 1(0,2,0)，A (0,−2,0)，C 1(0,0,2√3)，C(0,−4,2√3)．设 AQ ⃗⃗⃗⃗⃗ =λAC ⃗⃗⃗⃗⃗ =λ(0,−2,2√3)，λ∈(0,1]（当 λ=0 时，平面 B 1PQ 即平面 ABB 1A 1，不符合题意），所以 Q(0,−2(λ+1),2√3λ)． 所以 PQ⃗⃗⃗⃗⃗ =(0,−2(λ+1),2√3λ)． 因为 A 1B 1=AB =2，∠B 1A 1A =60∘， 所以 B 1(√3,1,0)， 所以 PB 1⃗⃗⃗⃗⃗⃗⃗ =(√3,1,0)．设平面 PQB 1 的法向量为 m ⃗⃗ =(x,y,z )，则 {m ⃗⃗ ⋅PQ⃗⃗⃗⃗⃗ =0⃗ ,m ⃗⃗ ⋅PB 1⃗⃗⃗⃗⃗⃗⃗ =0⃗ ,所以 {−2(λ+1)y +2√3λz =0,√3x +y =0,令 x =1， 则 y =−√3，z =−λ+1λ，所以平面 PQB 1 的一个法向量为 m ⃗⃗ =(1,−√3,−λ+1λ)．设平面 AA 1C 1C 的法向量为 n ⃗ =(1,0,0)， 二面角 B 1−PQ −C 1 的平面角为 θ， 则cosθ=∣m⃗⃗⃗ ⋅n ⃗ ∣∣m⃗⃗⃗ ∣∣n ⃗ ∣=√1+3+(−λ)2=√1313.所以 λ=12 或 λ=−14（舍）， 所以 AQ⃗⃗⃗⃗⃗ =12AC ⃗⃗⃗⃗⃗ ， 所以 Q(0,−3,√3)， 又 B(√3,−3,0)，所以 QB⃗⃗⃗⃗⃗ =(√3,0,−√3)， 所以 ∣QB ⃗⃗⃗⃗⃗ ∣=√3+3=√6． 又 ∣B 1Q ⃗⃗⃗⃗⃗⃗⃗ ∣=√22， 所以 BQ 2+BB 12=B 1Q 2， 所以 ∠QBB 1=90∘．连接 BP ，设点 P 到平面 BQB 1 的距离为 ℎ， 则 13×12×4×√3×√3=13×12×4×√6⋅ℎ．所以 ℎ=√62， 即点 P 到平面 BQB 1 的距离为√62． 【知识点】直线与平面平行关系的判定、利用向量的坐标运算解决立体几何问题、二面角21. 【答案】连接 BD 交 AC 于 G ，连接 FG ．因为 F ，G 分别为 BE ，BD 的中点， 所以 FG ∥DE ，因为 FG ⫋平面ACF ，DE ⊄面ACF ， 所以 DE ∥面ACF ．【知识点】直线与平面平行关系的判定22. 【答案】① EF ⊥平面BDD 1② EF ⊥DE③ DE ⊥BD 1 ④线线平行 ⑤线面平行【知识点】直线与平面垂直关系的判定、直线与直线的位置关系、直线与平面平行关系的判定、直线与平面垂直关系的性质。

高一数学立体几何初步试题答案及解析1.在空间直角坐标系中，已知点P（x，y，z），给出下列4条叙述：①点P关于x轴的对称点的坐标是（x，－y，z）②点P关于yOz平面的对称点的坐标是（x，－y，－z）③点P关于y轴的对称点的坐标是（x，－y，z）④点P关于原点的对称点的坐标是（－x，－y，－z）其中正确的个数是A．3B．2C．1D．0【答案】C【解析】其中正确的是④点P关于原点的对称点的坐标是（－x，－y，－z）故选C。

【考点】本题主要考查空间直角坐标系的概念。

点评：对于这类结论，应结合坐标系牢记。

2.在空间直角坐标系中，一定点到三个坐标轴的距离都是1，则该点到原点的距离是（）A．B．C．D．【答案】A【解析】依题意，构建正方体。

即求棱长为的正方体对角线长，计算得，故选A。

【考点】本题主要考查空间直角坐标系的概念及其应用。

点评：根据几何体的特征，认识点的坐标。

3.下面四个说法中，正确的个数为（）（1）如果两个平面有三个公共点，那么这两个平面重合（2）两条直线可以确定一个平面（3）若M∈α，M∈β，α∩β＝l，则M∈l（4）空间中，相交于同一点的三直线在同一平面内A．1B．2C．3D．4【答案】A【解析】如果两个平面有三个公共点，那么这两个平面重合或者是相交，故（1）不正确；两条异面直线不能确定一个平面，故（2）不正确；若M∈α，M∈β，α∩β=l，则M∈l，故（3）正确；空间中，相交于同一点的三直线不一定在同一平面内，故（4）不正确，综上所述只有一个说法是正确的，故选A．【考点】本题主要考查平面的基本性质及推论。

点评：理解并记忆，能结合身边的点线面关系加以说明。

4.圆锥的侧面展开图是直径为a的半圆面，那么此圆锥的轴截面是（）A．等边三角形B．等腰直角三角形C．顶角为30°的等腰三角形D．其他等腰三角形【解析】因为圆锥的侧面展开图是直径为a的半圆面，所以圆锥母线长为，圆锥底半径，所以此圆锥的轴截面是等边三角形，故选A。

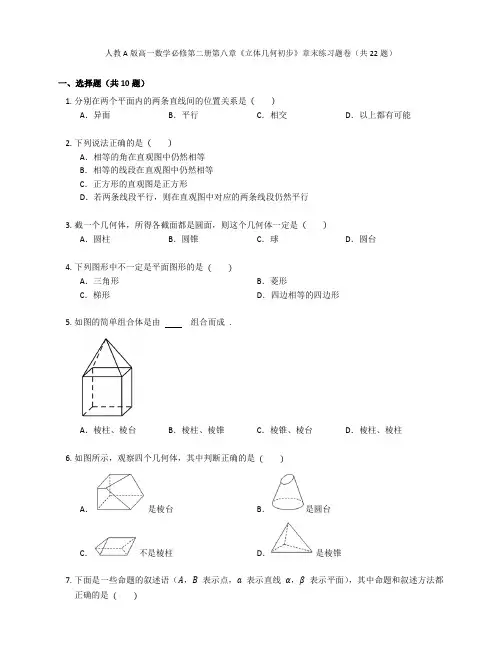
高一数学（必修二）立体几何初步单元测试卷及答案一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.如图所示，己知正方形O A B C ''''的边长为1，它是水平放置的一个平面图形的直观图，则其原图形的周长为( )A.8B.22C.4D.223+2.下列说法正确的是( ) A.三点确定一个平面B.圆心和圆上两个点确定一个平面C.如果两个平面相交有一个交点，则必有无数个公共点D.如果两条直线没有交点，则这两条直线平行3.正方体1111ABCD A B C D -中，P ，Q ，R 分别是AB ，AD ，11B C 的中点，那么正方体中过P ，Q ，R 的截面图形是( ) A.三角形B.四边形C.五边形D.六边形4.某圆柱的高为2，其正视图如图所示，圆柱上下底面圆周及侧面上的点A ，B ，D ，F ，C 在正视图中分别对应点A ，B ，E ，F ，C ，且3AE EF =，2BF BC =，异面直线AB ，CD 所成角的正弦值为45，则该圆柱的外接球的表面积为( )A.20πB.16πC.12πD.10π5.在《九章算术·商功》中将正四面形棱台体（棱台的上、下底面均为正方形）称为方亭.在方亭1111ABCD A B C D -中，1124AB A B ==，四个侧面均为全等的等腰梯形且面积之和为122( ) 282B.283142D.1436.异面直线是指( ) A.空间中两条不相交的直线B.分别位于两个不同平面内的两条直线C.平面内的一条直线与平面外的一条直线D.不同在任何一个平面内的两条直线7.如图，在正方体1111ABCD A B C D -中，E ，F 分别是11A D ，11B C 的中点，则与直线CF 互为异面直线的是( )A.1CCB.11B CC.DED.AE8.下列说法中正确的是( ) A.三点确定一个平面 B.四边形一定是平面图形 C.梯形一定是平面图形D.两个不同平面α和β有不在同一条直线上的三个公共点二、多选题（本题共4小题，每小题5分，共20分。

高一数学必修第二册第八章《立体几何初步》单元练习题卷6（共22题）一、选择题（共10题）1.下列命题中正确的有( )①一个棱柱至少有5个平面；②正棱锥的侧面都是全等的等腰三角形；③有两个面平行且相似，其他各面都是梯形的多面体是棱台；④正方形的直观图是正方形．A．1B．2C．3D．42.若a和b是异面直线，a和c是平行直线，则b和c的位置关系是( )A．平行B．异面C．异面或相交D．相交、平行或异面3.已知矩形ABCD的顶点都在球心为O，半径为R的球面上，AB=6，BC=2√3，且四棱锥O−ABCD的体积为8√3，则R等于( )A．4B．2√3C．4√79D．√134.已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A．πB．3π4C．π2D．π45.已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A．πB．3π4C．π2D．π46.一个三棱锥是正三棱锥的充要条件是( )A．底面是正三角形，三个侧面是全等的等腰三角形B．各个面都是正三角形C．三个侧面是全等的等腰三角形D．顶点在底面上的射影为重心7.某三棱锥的三视图如图所示，则该三棱锥的体积为( )A．43B．83C．4D．88.如图所示的平面中阴影部分绕中间轴旋转一周，形成的几何体形状为( )A．一个球体B．一个球体中间挖去一个圆柱C．一个圆柱D．一个球体中间挖去一个长方体9.若平面α∥平面β，点A,C∈α，B,D∈β，则直线AC∥BD的充要条件是( )A．AB∥CD B．AD∥CBC．AB与CD相交D．A，B，C，D共面10.一个几何体的三视图如图所示，则该几何体的体积为( )A．210B．208C．206D．204二、填空题（共6题）11.点A在平面α内，点B不在平面α内，点A，B都在直线l上，用集合的语言表述上述语句．12.在斜二测画法中，位于平面直角坐标系中的点M(4,4)在直观图中的对应点是Mʹ，则点Mʹ的坐标为．13.已知某球体的表面积为36π，则该球体的体积是．14.由斜二测画法得到以下结论：①三角形的直观图是三角形；②平行四边形的直观图是平行四边形；③正方形的直观图是正方形；④菱形的直观图是菱形．其中正确结论的序号是．15.立体图形直观图的画法步骤：（1）画轴：与平面图形的直观图画法相比多了一个轴，直观图中与之对应的是轴．（2）画底面：平面表示水平平面，平面和表示竖直平面，按照平面图形的画法，画底面的直观图．（3）画侧棱：已知图形中平行于z轴（或在z轴上）的线段，在其直观图中和都不变．（4）成图：去掉辅助线，将被遮挡的部分改为．16.思考辨析，判断正误．两个平面同时与第三个平面相交，若两交线平行，则这两个平面平行．三、解答题（共6题）17.如图，在正方体ABCD−A1B1C1D1中，设A1C∩平面ABC1D1=E．能否判断点E在平面A1BCD1内？并说明理由．18.已知三棱锥A−BCD的两条棱AB=CD=6，其余各棱长均为5，求三棱锥的内切球半径．19.简单组合体的结构特征请描述如图所示的几何体是如何形成的．20.圆台的母线长为2a，母线与轴的夹角为30∘，下底面半径是上底面半径的2倍，求两底面的半径及两底面面积之和．21.请回答下列问题：(1) 已知：l⫋α，D∈α，A∈l，B∈l，C∈l，D∉l．求证：直线AD，BD，CD共面于α．(2) 将一个苹果切3刀，最多可以切成x块，最少可切成y块，求x+y的值．22.已知P是平面ABC外一点，PA⊥平面ABC，AC⊥BC，求证：PC⊥BC．答案一、选择题（共10题）1. 【答案】B【解析】①因为底面最少为三角形，故3个侧面，2个底面，共5个面，故①正确；②正棱锥的底面是正多边形，顶点在底面上的射影是底面正多边形的中心，射影侧面都是全等的等腰三角形，故②正确；③不正确，因为不能保证各侧棱的延长线交与一点；④正方形的直观图是平行四边形，所以④不正确；正确的命题只有①②．故选：B．【知识点】直观图、棱台的结构特征、棱锥的结构特征、棱柱的结构特征2. 【答案】C【解析】考虑正方体ABCD−AʹBʹCʹDʹ中，直线AB看做直线a，直线BʹCʹ看做直线b，即直线a和直线b是异面直线，若直线CD看做直线c，可得a，c平行，则b，c异面；若直线AʹBʹ看做直线c，可得a，c平行，则b，c相交．若b，c平行，由a，c平行，可得a，b平行，这与a，b异面矛盾，故b，c不平行．故选：C．【知识点】直线与直线的位置关系3. 【答案】A【解析】设球心O到平面ABCD的距离为ℎ，由题意可知V O−ABCD=13S矩形ABCD⋅ℎ=13×6×2√3⋅ℎ=8√3，解得ℎ=2，又矩形ABCD所在的截面圆的半径为1 2√AB2+BC2=12√62+(2√3)2=2√3，从而球的半径R=√22+(2√3)2=4．【知识点】球的结构特征、棱锥的表面积与体积4. 【答案】B【解析】因为圆柱的高为 1，它的两个底面的圆周在直径为 2 的同一个球的球面上， 所以该圆柱底面圆周半径 r =√12−(12)2=√32， 所以该圆柱的体积：V =Sℎ=π×(√32)2×1=3π4．故选：B ．【知识点】圆柱的表面积与体积5. 【答案】B【解析】设圆柱的底面半径为 r ，则 r 2+(12)2=12，解得 r =√32， 所以 V 圆柱=π×(√32)2×1=3π4．【知识点】球的表面积与体积、圆柱的表面积与体积6. 【答案】A【解析】C 项，如图，橙色的 4 条棱相等，蓝色的 2 条棱相等，三个侧面是全等的等腰三角形，但不是正三棱锥．【知识点】充分条件与必要条件、棱锥的结构特征7. 【答案】A【知识点】棱锥的表面积与体积、由三视图还原空间几何体8. 【答案】B【知识点】圆柱的表面积与体积、球的表面积与体积9. 【答案】D【解析】当 AC ∥BD 时，A ，B ，C ，D 一定共面；当 A ，B ，C ，D 共面时，平面ABDC ∩α=AC ，平面ABDC ∩β=BD ，由 α∥β 得 AC ∥BD ．【知识点】直线与平面平行关系的判定、直线与平面平行关系的性质10. 【答案】D【解析】由已知中的三视图可得：该几何体是由一个正方体切去一个三棱锥所得的组合体，正方体的边长为6，切去一个三棱锥的底面是直角边长分别为6，6的等腰直角三角形，高为2，故该几何体的体积为V=63−13×12×6×6×2=204．【知识点】三视图、棱锥的表面积与体积、棱柱的表面积与体积二、填空题（共6题）11. 【答案】A∈α，B∉α，A∈l，B∈l【知识点】平面的概念与基本性质12. 【答案】(4,2)【解析】由直观图画法“横不变，纵折半”可得点Mʹ的坐标为(4,2)．【知识点】直观图13. 【答案】36π【解析】S=4πr2=36π⇒r=3，所以V=43πr3=36π．【知识点】球的表面积与体积14. 【答案】①②【知识点】直观图15. 【答案】z；zʹ；xʹOʹyʹ；yʹOʹzʹ；xʹOʹzʹ；平行性；长度；虚线【知识点】直观图16. 【答案】×【知识点】平面与平面平行关系的判定三、解答题（共6题）17. 【答案】可以判断点E在平面A1BCD1内．理由如下：如图，因为A1C∩平面ABC1D1=E，所以E∈A1C，E∈平面ABC1D1．因为 A 1C ⊂平面A 1BCD 1， 所以 E ∈平面A 1BCD 1．【知识点】平面的概念与基本性质18. 【答案】解法一：易知内切球球心 O 到各面的距离相等．设点 E ，F 为 CD ，AB 的中点，则点 O 在 EF 上且点 O 为 EF 的中点． 在 △ABE 中，AB =6，AE =BE =4， 所以 OH =3√78，即三棱锥的内切球半径为 3√78． 解法二：设球心 O 到各面的距离为 R ， 则 4×13S △BCD ×R =V A−BCD ．而 S △BCD =12×6×4=12，V A−BCD =2V C−ABE =6√7，所以 4×13×12R =6√7，即 R =3√78， 即三棱锥的内切球半径为 3√78．【知识点】棱锥的结构特征19. 【答案】 ① 是由一个圆锥和一个圆台拼接而成的组合体；② 是由一个长方体截去一个三棱锥后得到的几何体； ③ 是由一个圆柱挖去一个三棱锥后得到的几何体．【知识点】组合体20. 【答案】设圆台上底面半径为 r ，则下底面半径为 2r ．将圆台还原为圆锥，如图，则有 ∠ABO =30∘． 在 Rt △BOʹAʹ 中，r BAʹ=sin30∘=12，所以 BAʹ=2r ．在 Rt △BOA 中，2rBA =sin30∘=12， 所以 BA =4r ．又 BA −BAʹ=AAʹ，即 4r −2r =2a ， 所以 r =a ，所以两底面面积之和 S =πr 2+π(2r )2=5πr 2=5πa 2，所以圆台上底面半径为 a ，下底面半径为 2a ，两底面面积之和为 5πa 2． 【知识点】圆台的结构特征21. 【答案】(1) 因为l⫋α，A∈l，B∈l，C∈l，所以A,B,C∈α又D∈α，D∉l，所以AD⫋α，BD⫋α，CD⫋α，则直线AD，BD，CD共面．(2) x=8，y=3，x+y=11．【知识点】平面的概念与基本性质22. 【答案】如图，因为PA⊥平面ABC，PC是平面ABC的斜线，所以AC是PC在平面ABC上的射影，又BC⊂平面ABC，且AC⊥BC，所以由三垂线定理得PC⊥BC．【知识点】直线与平面垂直关系的性质。

高一数学必修第二册第八章《立体几何初步》单元练习题卷6（共22题）一、选择题（共10题） 1. 已知 4+(a−2)ii为纯虚数，则实数 a 的值为 ( )A ． 4B ． 2C ． 1D ． −22. 如图，在矩形 OACB 中，E 和 F 分别是边 AC 和 BC 上的点，且满足 AC =3AE ，BC =3BF ，若 OC⃗⃗⃗⃗⃗ =λOE ⃗⃗⃗⃗⃗ +μOF ⃗⃗⃗⃗⃗ ，其中 λ,μ∈R ，则 λ+μ 是A ．83B ．32C ．53D ．13. 棱锥的侧面和底面可以都是 ( ) A ．三角形B ．四边形C ．五边形D ．六边形4. 有下列三个说法：① 两个互相平行的面是正方形，其余各面都是四边形的几何体一定是棱台； ②有两个面平行且相似，其余各面都是梯形的多面体是棱台； ③有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台． 其中正确的有 ( ) A ． 0 个B ． 1 个C ． 2 个D ． 3 个5. 某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番．为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图： 则下面结论中不正确的是 ( )A．新农村建设后，种植收入减少B．新农村建设后，其他收入增加了一倍以上C．新农村建设后，养殖收入增加了一倍D．新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半6.根据下面给出的2004年至2013年我国二氧化硫年排放量（单位：万吨）柱形图，以下结论中不正确的是( )A．逐年比较，2008年减少二氧化硫排放量的效果最显著B．2007年我国治理二氧化硫排放显现成效C．2006年以来我国二氧化硫年排放量呈减少趋势D．2006年以来我国二氧化硫年排放量与年份正相关7.已知i为虚数单位，下列各式的运算结果为纯虚数的是( )A．i(1+i)B．i(1−i)2C．i2(1+i)2D．i+i2+i3+i48.在下列结论中，正确的是( )A．若两个向量相等，则它们的起点和终点分别重合B．模相等的两个平行向量是相等向量C．若a和b⃗都是单位向量，则a=b⃗D．两个相等向量的模相等9.某书店新进了一批书籍，如表是某月中连续6天的销售情况记录：日期6日7日8日9日10日11日根据上表估计该书店该月（按31天计当日销售量(本)304028443842算）的销售总量是 ( ) A ． 1147 本 B ． 1110 本 C ． 1340 本 D ． 1278 本10. 在 △ABC 中，内角 A ，B ，C 的对边分别为 a ，b ，c ，且 bsin (π−C )−√2ccos (π+B )=0，则tanB = ( ) A ．√22B ． √2C ． −√22D ． −√2二、填空题（共6题）11. A ，B 两种品牌各三种车型 2017 年 7 月的销量环比（与 2017 年 6 月比较）增长率如下表：A 品牌车型A 1A 2A 3环比增长率−7.29%10.47%14.70%B 品牌车型B 1B 2B 3环比增长率−8.49%−28.06%13.25%根据此表中的数据，有如下四个结论：① A 1 车型销量比 B 1 车型销量多；② A 品牌三种车型总销量环比增长率可能大于 14.70%； ③ B 品牌三种车型车总销量环比增长率可能为正；④ A 品牌三种车型总销量环比增长率可能小于B 品牌三种车型总销量环比增长率．其中正确的结论个数是 ．12. 设复数 z 1=x +2i ，z 2=3−yi （x,y ∈R ），若 z 1+z 2=5−6i ，则 z 1−z 2= ．13. 如果两个球的体积之比为 8:27，那么两个球的表面积之比为 ．14. 在复平面内，点 A (−2,1) 对应的复数 z ，则 ∣z +1∣= ．15. 已知点 A (−2,0)，设 B ，C 是圆 O ：x 2+y 2=1 上的两个不同的动点，且向量 OB⃗⃗⃗⃗⃗ =tOA ⃗⃗⃗⃗⃗ +(1−t )OC ⃗⃗⃗⃗⃗ （其中 t 为实数），则 AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ = ．16. 如图，在平面四边形 ABCD 中，AB ⊥BC ，AB =√3，BC =1，△ACD 是等边三角形，则 AC⃗⃗⃗⃗⃗ ⋅BD⃗⃗⃗⃗⃗⃗ 的值为 ．三、解答题（共6题）17. 某鱼苗实验场进行某种淡水鱼的人工孵化试验，按在同一条件下的试验结果，10000 个鱼卵能孵出 8520 尾鱼苗．(1) 求这种鱼卵孵化的频率（经验概率）；(2) 估计 30000 个这种鱼苗能孵化出多少尾鱼苗？ (3) 若要孵出 5000 尾鱼苗，估计需要准备多少个鱼卵？18. 在数学考试中，小明的成绩在 90 分以上的概率是 0.18，在 80∼89 分的概率是 0.51，在70∼79 分的概率是 0.15，在 60∼69 分的概率是 0.09，60 分以下的概率是 0.07，计算： (1) 小明在数学考试中取得 80 分以上成绩的概率； (2) 小明考试及格的概率．19. 从① B =π3，② a =2，③ bcosA +acosB =√3+1 这三个条件中任选一个，补充在下面问题中，并解决相应问题．已知在锐角 △ABC 中，角 A ，B ，C 的对边分别为 a ，b ，c ，△ABC 的面积为 S ，若 4S =b 2+c 2−a 2，b =√6，且 ，求 △ABC 的面积 S 的大小．20. 现有一个底面是菱形的直四棱柱，它的体对角线长为 9 和 15，高是 5，求该直四棱柱的侧面积、表面积．21. 某班抽取 20 名学生周测物理考试成绩（单位：分）的频率分布直方图如下．(1) 求频率分布直方图中 a 的值，并写出众数；(2) 分别求出成绩落在 [50,60) 与 [60,70) 中的学生人数；(3) 从成绩在 [50,70) 的学生中任选 2 人，求这 2 人的成绩都在 [60,70) 中的概率．22. 已知点 O (0,0)，A (1,2)，B (4,5)，且 OP ⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +tAB⃗⃗⃗⃗⃗ ． (1) t 为何值时，P 在 x 轴上？P 在 y 轴上？P 在第二象限？(2) 四边形 OABP 能否成为平行四边形？若能，求出相应的 t 值；若不能，说明理由．答案一、选择题（共10题）1. 【答案】B【解析】4+(a−2)ii =−i[4+(a−2)i]−i⋅i=a−2−4i为纯虚数，则实数a满足：a−2=0，解得a=2．【知识点】复数的乘除运算2. 【答案】B【解析】以O为原点，OA为x轴、OB为y轴建立平面直角坐标系．设OA=a，OB=b，则E(a,b3)，F(a3,b)，C(a,b)．由已知，得(a,b)=λ(a,b3)+μ(a3,b)，则有{a=λa+μa3,b=λb3+bμ,解得λ=μ=34，因此λ+μ=32．【知识点】平面向量的分解、平面向量的坐标运算3. 【答案】A【解析】三棱锥的侧面和底面都是三角形．故选A．【知识点】棱锥的结构特征4. 【答案】A【解析】当两个互相平行的正方形全等时，不是棱台，故①中说法错误；②③可用反例去检验，如图（1）（2）所示，故②③中说法错误．故选A．【知识点】棱台的结构特征5. 【答案】A【解析】设建设前经济收入为a，则建设后经济收入为2a，由题图可知：种植收入第三产业收入养殖收入其他收入建设前经济收入0.6a0.06a0.3a0.04a建设后经济收入0.74a0.56a0.6a0.1a据如表可知B，C，D中结论均正确，A中论不正确．【知识点】频率分布直方图6. 【答案】D【解析】由柱形图可知：A，B，C均正确，2006年以来我国二氧化硫年排放量在逐渐减少，所以排放量与年份负相关，所以D不正确．【知识点】频率分布直方图7. 【答案】C【解析】对于A，i(1+i)=i−1不是纯虚数；对于B，i(1−i)2=−2i2=2是实数；对于C，i2(1+i)2=−2i为纯虚数；对于D，i+i2+i3+i4=i−1−i+1=0不是纯虚数．【知识点】复数的乘除运算8. 【答案】D【解析】由平面向量的基本概念可得，D是正确的．【知识点】平面向量的概念与表示9. 【答案】A=37（本）,【解析】从表中6天的销售情况可得，一天的平均销售量为30+40+28+44+38+426该月共31天，故该月的销售总量约为37×31=1147（本）．【知识点】样本数据的数字特征10. 【答案】D【解析】由已知得bsinC+√2ccosB=0，即sinBsinC+√2sinCcosB=0，因为sinC≠0，所以sinB+√2cosB=0，故tanB=−√2．【知识点】正弦定理二、填空题（共6题）11. 【答案】2【知识点】概率的应用12. 【答案】 −1+10i【解析】因为 z 1+z 2=x +2i +(3−yi )=(x +3)+(2−y )i =5−6i (x,y ∈R )， 所以 x =2 且 y =8，所以 z 1−z 2=2+2i −(3−8i )=−1+10i ． 【知识点】复数的加减运算13. 【答案】 4:9【解析】因为 V 1:V 2=8:27=R 13:R 23，所以 R 1:R 2=2:3，所以 S 1:S 2=R 12:R 22=4:9．【知识点】球的表面积与体积14. 【答案】 √2【知识点】复数的几何意义15. 【答案】 3【解析】 OB⃗⃗⃗⃗⃗ =tOA ⃗⃗⃗⃗⃗ +(1−t )OC ⃗⃗⃗⃗⃗ ⇒CB ⃗⃗⃗⃗⃗ =tCA ⃗⃗⃗⃗⃗ ， 所以 A ，B ，C 三点共线，所以设直线 BC ：y =k (x +2)．{x 2+y 2=1,y =k (x +2)⇒(1+k 2)x 2+4k 2x +4k 2−1=0， 设 B (x 1,y 1)，C (x 2,y 2)， 所以 x 1+x 2=−4k 21+k 2，x 1x 2=4k 2−11+k 2．所以AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =(x 1+2,y 1)(x 2+2,y 2)=(x 1+2)(x 2+2)+k 2(x 1+2)(x 2+2)=(1+k 2)[x 1x 2+2(x 1+x 2)+4]=(1+k2)⋅(4k 2−11+k 2−8k 21+k 2+4)=3.【知识点】平面向量数量积的坐标运算16. 【答案】 −1【解析】 AB ⊥BC ，AB =√3，BC =1， 所以 AC =2，∠BCA =60∘； 又 △ACD 是等边三角形， 所以 AD =AC =2，AD ⊥AB ， 所以AC ⃗⃗⃗⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ =(AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )⋅(BA ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ )=AB ⃗⃗⃗⃗⃗ ⋅BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗ =−√3×√3+1×2=−1.【知识点】平面向量的数量积与垂直三、解答题（共6题） 17. 【答案】(1) 0.852．(2) 25560 尾．(3) 约 5869 个．【知识点】频率与概率18. 【答案】(1) 分别记小明的成绩“在 90 分以上”“在 80∼89 分”“在 70∼79 分”“在 60∼69 分”为事件 B ，C ，D ，E ，这四个事件彼此互斥．小明的成绩在 80 分以上的概率是 P (B ∪C )=P (B )+P (C )=0.18+0.51=0.69． (2) 法一：小明考试及格的概率是P (B ∪C ∪D ∪E )=P (B )+P (C )+P (D )+P (E )=0.18+0.51+0.15+0.09=0.93.法二：小明考试不及格的概率是 0.07，又小明考试不及格与及格互为对立事件，故小明考试及格的概率 P =1−0.07=0.93． 【知识点】事件的关系与运算19. 【答案】因为 4S =b 2+c 2−a 2，cosA =b 2+c 2−a 22bc，S =12bcsinA ，所以 2bcsinA =2bccosA ，显然 cosA ≠0， 所以 tanA =1， 又 A ∈(0,π)， 所以 A =π4．若选择① B =π3，由 asinA =bsinB ，得a=bsinAsinB =√6×√22√32=2．又sinC=sin[π−(A+B)]=sin(A+B)=sinAcosB+cosAsinB=√22×12+√22×√32=√6+√24,所以S=12absinC=3+√32．若选择② a=2，由asinA =bsinB，得sinB=bsinAa=√32，B∈(0,π2)，所以cosB=12．sinC=sin[π−(A+B)]=sin(A+B)=sinAcosB+cosAsinB=√6+√24.所以S=12absinC=3+√32．若选择③ bcosA+acosB=√3+1，所以acosB=1，即a⋅a 2+c2−62ac=1，所以a2=6+2c−c2，又a2=6+c2−2√6c⋅√22=6+c2−2√3c，所以6+2c−c2=6+c2−2√3c，解得c=√3+1，所以S=12bcsinA=3+√32．【知识点】正弦定理、余弦定理20. 【答案】如图，设底面对角线AC=a，BD=b，交点为O，体对角线A1C=15，B1D=9，所以a2+52=152，b2+52=92，所以a2=200，b2=56．因为该直四棱柱的底面是菱形，所以AB2=(AC2)2+(BD2)2=a2+b24=200+564=64，所以AB=8．所以直四棱柱的侧面积 S 侧=4×8×5=160． 所以直四棱柱的底面积 S 底=12AC ⋅BD =20√7．所以直四棱柱的表面积 S 表=160+2×20√7=160+40√7． 【知识点】棱柱的表面积与体积21. 【答案】(1) 据直方图知组距 =10，由 (2a +3a +6a +7a +2a )×10=1，解得 a =1200=0.005， 众数：75．(2) 成绩落在 [50,60) 中的学生人数为 2×0.005×10×20=2， 成绩落在 [60,70) 中的学生人数为 3×0.005×10×20=3．(3) 记成绩落在 [50,60) 中的 2 人为 A 1，A 2，成绩落在 [60,70) 中的 3 人为 B 1，B 2，B 3， 则从成绩在 [50,70) 的学生中任选 2 人的基本事件共有 10 个：(A 1,A 2)，(A 1,B 1)，(A 1,B 2)，(A 1,B 3)，(A 2,B 1)，(A 2,B 2)，(A 2,B 3)，(B 1,B 2)，(B 1,B 3)，(B 2,B 3)， 记“两人成绩都落在 [60,70)”为事件 C ，则事件 C 包含的基本事件有 3 个：(B 1,B 2)，(B 1,B 3)，(B 2,B 3)， P (C )=310．【知识点】样本数据的数字特征、频率分布直方图、古典概型22. 【答案】(1) OA⃗⃗⃗⃗⃗ =(1,2)，OB ⃗⃗⃗⃗⃗ =(4,5)，OP ⃗⃗⃗⃗⃗ =(1+3t,2+3t )． 若 P 在 x 轴上，则 t =−23． 若 P 在 y 轴上，则 t =−13． 若 P 在第二象限，则 −23<t <−13．(2) OA⃗⃗⃗⃗⃗ =(1,2)，PB ⃗⃗⃗⃗⃗ =(3−3t,3−3t )． 若 OABP 成平行四边形，则 OA ⃗⃗⃗⃗⃗ =PB⃗⃗⃗⃗⃗ ，即 {3−3t =1,3−3t =2, 此方程无解．故不能． 【知识点】平面向量的坐标运算、平面向量数乘的坐标运算。

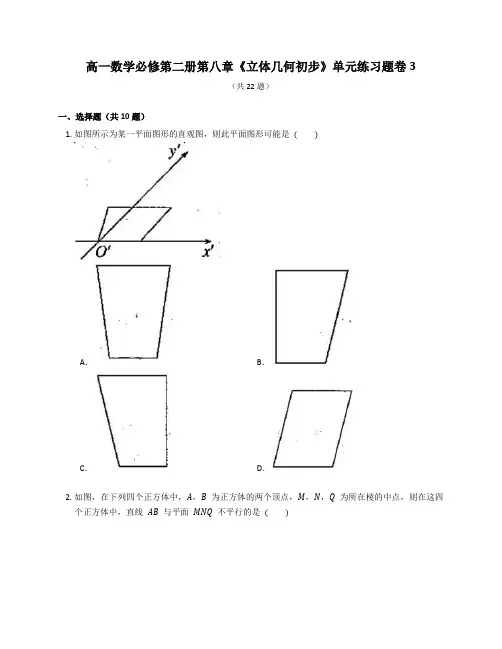
高一数学必修第二册第八章《立体几何初步》单元练习题卷3（共22题）一、选择题（共10题）1.如图所示为某一平面图形的直观图，则此平面图形可能是( )A．B．C．D．2.如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是( )A．B．C．D．3.如图所示，正方体ABCD−A1B1C1D1中，点E，F，G，P，Q分别为棱AB，C1D1，D1A1，D1D，C1C的中点．则下列叙述中正确的是( )A．直线BQ∥平面EFG B．直线A1B∥平面EFGC．平面APC∥平面EFG D．平面A1BQ∥平面EFG4.如图，若Ω是长方体ABCD−A1B1C1D1被平面EFGH截去几何体EB1FHC1G后得到的几何体，其中E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，且EH∥A1D1，则下列结论中不正确的是( )A．EH∥FG B．四边形EFGH是矩形C．Ω是棱柱D．Ω是棱台5.设α，β为两个平面，则α∥β的充要条件是( )A．α内有无数条直线与β平行B．α内有两条相交直线与β平行C．α，β平行于同一条直线D．α，β垂直于同一平面6.练习1．已知一个正三棱锥的高为3，如图是其底面用斜二测画法所画出的水平放置的直观图，其中OʹBʹ=OʹCʹ=1，则此三棱锥的体积为( )A．√3B．3√3C．√34D．3√347.如图，在正方体ABCD−A1B1C1D1中，E是棱CC1的中点，F是侧面BCC1B1内的动点，且A1F与平面D1AE的垂线垂直，则下列说法不正确的是( )A．A1F与D1E不可能平行B．A1F与BE是异面直线C．点F的轨迹是一条线段D．三棱锥F−ABD1的体积为定值8.如图，在各棱长均为1的正三棱柱ABC−A1B1C1中，M,N分别为线段A1B,B1C上的动点，且MN∥平面ACC1A1，则这样的MN有( )A．1条B．2条C．3条D．无数条9.有以下结论：①平面是处处平直的面；②平面是无限延展的；③平面的形状是平行四边形；④一个平面的厚度可以是0.001cm．其中正确结论的个数为A．1B．2C．3D．4．给10.如图，正方体ABCD−A1B1C1D1的棱长为1，线段AC1上有两个动点E，F，且EF=√33出下列四个结论：① CE⊥BD；② 三棱锥E−BCF的体积为定值；③ △BEF在底面ABCD内的正投影是面积为定值的三角形④ 在平面ABCD内存在无数条与平面DEA1平行的直线其中，正确结论的个数是( )A．1B．2C．3D．4二、填空题（共6题）11.已知l，m，n是互不相同的直线，α，β，γ是三个不同的平面，给出下列命题：①若l与m为异面直线，l⊂α，m⊂β，则α∥β;②若α∥β，l⊂α，m⊂β,则l∥m；③若α∩β= l,β∩γ=m,γ∩α=n,l∥γ,则加m∥n.其中所有真命题的序号为12.直线与平面垂直的性质定理．注意：一条直线与一个平面平行时，这条直线上任意一点到这个平面的距离，叫做这条直线到这个平面的距离，如果两个平面平行，那么其中一个平面内的任意一点到另一个平面的距离都相等，我们把它叫做这两个平行平面间的距离．13.判断下列结论是否正确（请在括号中打“√”或“×”）（1）若一条直线平行于一个平面内的一条直线，则这条直线平行于这个平面．( )（2）平行于同一条直线的两个平面平行．( )（3）如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行．( )（4）若α∥β，直线a∥α，则a∥β．( )14.直线与平面平行的判定定理15.对角线互相垂直的空间四边形ABCD各边的中点分别为M，N，P，Q，则四边形MNPQ是．16.如图，正方形BCDE的边长为a，已知AB=√3BC，将△ABE沿边BE折起，折起后A点在平面BCDE上的射影为D点，关于翻折后的几何体有如下描述：a3；④ 平面ABC⊥① AB与DE所成角的正切值是√2；② AB∥CE；③ V B−ACE=16平面ADC．其中正确的有．（填写你认为正确的序号）三、解答题（共6题）17.在正方体ABCD−A1B1C1D1中，如图．(1) 求证：平面AB1D1∥平面C1BD；(2) 试找出体对角线A1C与平面AB1D1和平面C1BD的交点E，F，并证明A1E=EF=FC．18.几何中的“平面”有边界吗？用什么图形表示平面？19.如图所示，正四棱台ABCD−A1B1C1D1的上底面是边长为2的正方形，下底面是边长为4的正方形，侧棱长为2，侧面是全等的等腰梯形，求四棱台的表面积．20.如图所示的几何体中，四边形AA1B1B是边长为3的正方形，CC1=2，CC1∥AA1，这个几何体是棱柱吗？若是，指出是几棱柱；若不是棱柱，请你试用一个平面截去一部分，使剩余部分是一个侧棱长为2的三棱柱，并指出截去的几何体的特征，在立体图中画出截面．⏜所在平面垂直，M是CD⏜上异于C，21.如图，边长为2的正方形ABCD所在的平面与半圆弧CDD的点．(1) 证明：平面AMD ⊥平面BMC ；(2) 当三棱锥 M −ABC 体积最大时，求面 MAB 与面 MCD 所成二面角的正弦值．22. 如图，在四棱锥 P −ABCD 中，底面 ABCD 为梯形，PD ⊥ 底面 ABCD ，AB ∥CD ，AD ⊥CD ，AD =AB =1，BC =√2．(1) 求证：平面PBD ⊥平面PBC ；(2) 设 H 为 CD 上一点，满足 CH ⃗⃗⃗⃗⃗ =2HD ⃗⃗⃗⃗⃗⃗ ，若直线 PC 与平面 PBD 所成的角的正切值为 √63，求二面角 H −PB −C 的余弦值．答案一、选择题（共10题）1. 【答案】C【知识点】直观图2. 【答案】A【解析】对于B，易知AB∥MQ，则直线AB∥平面MNQ；对于C，易知AB∥MQ，则直线AB∥平面MNQ；对于D，易知AB∥NQ，则直线AB∥平面MNQ．故排除B，C，D，选A．【知识点】直线与平面平行关系的判定3. 【答案】B【解析】过点E，F，G的截面如图所示（H，I分别为AA1，BC的中点），因为A1B∥HE，A1B⊄平面EFG，HE⊂平面EFG，所以A1B∥平面EFG．【知识点】平面与平面平行关系的判定4. 【答案】D【解析】因为EH∥A1D1，A1D1∥B1C1，所以EH∥B1C1，又EH⊄平面BCC1B1，所以EH∥平面BCC1B1，又EH⊂平面EFGH，平面EFGH∩平面BCC1B1=FG，所以EH∥FG，又EH∥B1C1，所以Ω是棱柱，所以A,C正确；因为A1D1⊥平面ABB1A1,EH∥A1D1，所以EH⊥平面ABB1A1，又EF⊂平面ABB1A1，故EH⊥EF，所以B正确．【知识点】棱柱的截面分析、直线与平面平行关系的性质、直线与平面垂直关系的性质5. 【答案】B【解析】对于A，α内有无数条直线与β平行，α∩β或α∥β；对于B，α内有两条相交直线与β平行，α∥β；对于C，α，β平行于同一条直线，α∩β或α∥β；对于D，α，β垂直于同一平面，α∩β或α∥β．【知识点】平面与平面平行关系的判定、充分条件与必要条件6. 【答案】A【解析】由直观图可知：正三棱锥的底面是边长为2的正三角形，所以底面面积为12×2×2×√3 2=√3，所以三棱锥的体积为：13×√3×3=√3．故选：A．【知识点】直观图、棱锥的表面积与体积7. 【答案】A【解析】设平面D1AE与直线BC交于G，连接AG，EG，则G为BC的中点，分别取B1B，B1C1的中点M，N，连接A1M，MN，A1N，如图，因为A1M∥D1E，A1M⊄平面D1AE，D1E⊂平面D1AE，所以A1M∥平面D1AE，同理可得MN∥平面D1AE，又A1M，MN是平面A1MN内的两条相交直线，所以平面A1MN∥平面D1AE，而A1F∥平面D1AE，所以A1F⊂平面A1MN，得点F的轨迹为一条线段，故C正确；并由此可知，当F与M重合时，A1F与D1E平行，故A错误；因为平面A1MN∥平面D1AE，BE和平面D1AE相交，所以A1F与BE是异面直线，故B正确；因为MN∥EG，则点F到平面D1AE的距离为定值，所以三棱锥F−ABD1的体积为定值，故D正确．【知识点】直线与直线的位置关系8. 【答案】D【解析】如图，过线段A1B上任一点M作MH∥AA1，交AB于点H，过点H作HG∥AC 交BC于点G，过点G作CC1的平行线，与CB1一定有交点N，且MN∥平面ACC1A1，则这样的MN有无数条．故选D．【知识点】直线与平面平行关系的判定9. 【答案】B【解析】平面处处平直，无限延展，但是没有大小、形状、厚薄等，因此①②两种说法是正确的，③④两种说法是错误的．【知识点】平面的概念与基本性质10. 【答案】D【解析】因为BD⊥平面ACC1，所以BD⊥CE，故① 正确；因为点C到直线EF的距离是定值，点B到平面CEF的距离也是定值，所以三棱锥B﹣CEF的体积为定值，故② 正确；线段EF在底面上的正投影是线段GH，所以△BEF在底面ABCD内的投影是△BGH．因为线段EF的长是定值，所以线段GH是定值，从而△BGH的面积是定值，故③ 正确；设平面ABCD与平面DEA1的交线为l，则在平面ABCD内与直线l平行的直线有无数条，故④ 对．【知识点】直线与平面垂直关系的性质二、填空题（共6题）11. 【答案】③【解析】① 中α还可能与β相交；②中直线l与m还可能异面；③中结合线面平行的性质可以证得m∥n．【知识点】空间的平行关系12. 【答案】平行【知识点】直线与平面垂直关系的性质13. 【答案】×；×；×；×【知识点】直线与平面平行关系的判定14. 【答案】此平面内一条直线平行【知识点】直线与平面平行关系的判定15. 【答案】矩形【解析】如图所示，因为点M，N，P，Q分别是四条边的中点，AC，所以MN∥AC，且MN=12AC，PQ∥AC，且PQ=12所以MN∥PQ，且MN=PQ，因为四边形MNPQ是平行四边形，又因为AC⊥BD，NP∥BD，所以PQ⊥NP，所以四边形MNPQ是矩形．【知识点】空间中直线与直线平行16. 【答案】①③④【解析】作出折叠后的几何体直观图如图所示：因为A点在平面BCDE上的射影为D点，所以AD⊥平面BCDE．因为BC⊂平面BCDE，所以AD⊥BC．因为四边形BCDE是正方形，所以BC⊥CD，又AD∩CD=D，所以BC⊥平面ADC．又BC⊂平面ABC，所以平面ABC⊥平面ADC，故④正确；因为DE∥BC，所以∠ABC为AB与DE所成的角或其补角，因为BC⊥平面ADC，AC⊂平面ADC，所以BC⊥AC，所以tan∠ABC=ACBC，因为AB=√3BC，BC=a，所以在Rt△ABC中，AC=√AB2−BC2=√2a，所以tan∠ABC=ACBC=√2，故①正确；连接BD，CE，则CE⊥BD，又AD⊥平面BCDE，CE⊂平面BCDE，所以CE⊥AD．又BD∩AD=D，所以CE⊥平面ABD，又AB⊂平面ABD，所以CE⊥AB．故②错误；在Rt△ABE中，AB=√3a，BE=a．所以AE=√2a，又DE=a，AD⊥DE，所以AD=a，所以三棱锥B−ACE的体积V B−ACE=V A−BCE=13S△BCE⋅AD=13×12×a2×a=a36，故③正确．【知识点】直线与平面的位置关系、直线与直线的位置关系三、解答题（共6题）17. 【答案】(1) 因为在正方体ABCD−A1B1C1D1中，AD∥B1C1，AD=B1C1，所以四边形AB1C1D是平行四边形，所以AB1∥C1D．又因为C1D⊂平面C1BD，AB1⊄平面C1BD，所以AB1∥平面C1BD．同理，B1D1∥平面C1BD．又因为AB1∩B1D1=B1，AB1⊂平面AB1D1，B1D1⊂平面AB1D1，所以平面AB1D1∥平面C1BD．(2) 如图，连接A1C1，交B1D1于点O1，连接AO1，与A1C交于点E．又因为AO1⊂平面AB1D1，所以点E也在平面AB1D1内，所以点E就是A1C与平面AB1D1的交点．连接AC，交BD于点O，连接C1O，与A1C交于点F，则点F就是A1C与平面C1BD的交点．下面证明A1E=EF=FC．因为平面A1C1C∩平面AB1D1=EO1，平面A1C1C∩平面C1BD=C1F，平面AB1D1∥平面C1BD，所以EO1∥C1F，在△A1C1F中，O1是A1C1的中点，所以E是A1F的中点，即A1E=EF．同理可证OF∥AE，所以F是CE的中点，即 FC =EF ，所以 A 1E =EF =FC ．【知识点】平面与平面平行关系的判定、平面与平面平行关系的性质18. 【答案】没有，平行四边形．【知识点】平面的概念与基本性质19. 【答案】因为正四棱台的上底面是边长为 2 的正方形，下底面是边长为 4 的正方形，所以上底面、下底面的面积分别是 4，16， 因为侧棱长为 2，侧面是全等的等腰梯形， 所以侧面等腰梯形的高为 √4−(4−22)2=√3，所以一个侧面等腰梯形的面积为 12×(2+4)×√3=3√3， 所以四棱台的表面积为 4+16+3√3×4=20+12√3． 【知识点】棱台的表面积与体积20. 【答案】这个几何体不是棱柱，截去的部分是一个四棱锥 C 1−EA 1B 1F ，如图所示．在四边形 ABB 1A 1 中，在 AA 1 上取点 E ，使 AE =2，在 BB 1 上取点 F 使 BF =2，连接 C 1E ，EF ，C 1F ，则过点 C 1，E ，F 的截面将几何体分成两部分，其中一部分是三棱柱 ABC −EFC 1，其侧棱长为 2．截去的部分是一个四棱锥 C 1−EA 1B 1F ，也可以从点 C 截． 【知识点】棱柱的结构特征21. 【答案】(1) 由题设知，平面CMD ⊥平面ABCD ，面CMD ∩面ABCD =CD ． 因为 BC ⊥CD ，BC ⊂平面ABCD ，所以 BC ⊥平面CMD ， 故 BC ⊥DM ．因为 M 为 CD ⏜ 上异于 C ，D 的点，且 DC 为直径， 所以 DM ⊥CM ，又 BC ∩CM =C ，BC ⊂面BCM ，CM ⊂面BCM ， 所以 DM ⊥平面BMC ，而 DM ⊂平面AMD ，故 平面AMD ⊥平面BMC ．(2) 以 D 为坐标原点，DA⃗⃗⃗⃗⃗ 的方向为 x 轴正方向，建立如图所示的空间直角坐标系 D −xyz ． 当三棱锥 M −ABC 体积最大时，M 为 CD⏜ 的中点． 由题设得 D (0,0,0)，A (2,0,0)，B (2,2,0)，C (0,2,0)，M (0,1,1)，AM ⃗⃗⃗⃗⃗⃗ =(−2,1,1)，AB⃗⃗⃗⃗⃗ =(0,2,0)，DA ⃗⃗⃗⃗⃗ =(2,0,0)，设 n ⃗ =(x,y,z ) 是平面 MAB 的法向量，则 {n ⃗ ⋅AM⃗⃗⃗⃗⃗⃗ =0,n ⃗ ⋅AB⃗⃗⃗⃗⃗ =0, 即 {−2x +y +z =0,2y =0.可取 n ⃗ =(1,0,2)．DA ⃗⃗⃗⃗⃗ 是平面 MCD 的法向量，所以 cos⟨n ⃗ ,DA ⃗⃗⃗⃗⃗ ⟩=n⃗ ⋅DA ⃗⃗⃗⃗⃗⃗ ∣∣n ⃗ ∣∣∣∣DA⃗⃗⃗⃗⃗⃗ ∣∣=√55，sin⟨n ⃗ ,DA ⃗⃗⃗⃗⃗ ⟩=2√55， 所以面 MAB 与面 MCD 所成二面角的正弦值是 2√55．【知识点】平面与平面垂直关系的判定、二面角、利用向量的坐标运算解决立体几何问题22. 【答案】(1) 因为 AD ⊥CD ，AB ∥CD ，AD =AB =1， 所以 BD =√2． 又 BC =√2，所以 CD =2， 所以 BC ⊥BD ． 因为 PD ⊥ 底面 ABCD ， 所以 PD ⊥BC ， 又 PD ∩BD =D ， 所以 BC ⊥平面PBD ． 又因为 BC ⊂平面PBC ，所以 平面PBD ⊥平面PBC ．(2) 由（Ⅰ）可知 ∠BPC 为 PC 与平面 PBD 所成的角， 所以 tan∠BPC =√63， 所以 PB =√3，PD =1．由 CH ⃗⃗⃗⃗⃗ =2HD ⃗⃗⃗⃗⃗⃗ 及 CD =2 得 CH =43，DH =23． 以点 D 为坐标原点，DA ，DC ，DP 所在的直线分别为 x 轴，y 轴，z 轴建立空间直角坐标系 D −xyz ，则 B (1,1,0)，P (0,0,1)，C (0,2,0)，H (0,23,0)． 设平面 HPB 的法向量为 n ⃗ =(x 1,y 1,z 1)， 则 {HP ⃗⃗⃗⃗⃗⃗ ⋅n ⃗ =0,HB ⃗⃗⃗⃗⃗⃗ ⋅n ⃗ =0,即 {−23y 1+z 1=0,x 1+13y 1=0.取 y 1=−3，则 n ⃗ =(1,−3,−2)． 设平面 PBC 的法向量为 m ⃗⃗ =(x 2,y 2,z 2)， 则 {PB ⃗⃗⃗⃗⃗ ⋅m ⃗⃗ =0,BC ⃗⃗⃗⃗⃗ ⋅m ⃗⃗ =0,即 {x 2+y 2−z 2=0,−x 2+y 2=0.取 x 2=1，则 m ⃗⃗ =(1,1,2)， 又 cos⟨m ⃗⃗ ,n ⃗ ⟩=m⃗⃗⃗ ⋅n ⃗ ∣∣m ⃗⃗⃗ ∣∣∣∣n ⃗ ∣∣=−√217， 所以二面角 H −PB −C 的余弦值为√217． 【知识点】平面与平面垂直关系的判定、二面角、利用向量的坐标运算解决立体几何问题。

立体几何训练题一、选择题：每题4分，共40分.1． 下列图形中，不是正方体的展开图的是----------------------------- （ ）A B C D2.已知直线//m α平面，直线n 在α内，则m n 与的关系为（ ）A 平行B 相交C 相交或异面D 平行或异面3．设A 1A 是正方体的一条棱，这个正方体中与A 1A 平行的棱共有（ ）A 1条B 2条C 3条D 4条4,,）A B C D5．如图，如果MC ⊥菱形ABCD 所在平面，那么MA 与BD 的位置关系是（ ） A 平行 B 垂直相交 C 异面 D 相交但不垂直CAB M6．下列条件中，能判断两个平面平行的是（ ）A 一个平面内的一条直线平行于另一个平面；B 一个平面内的两条直线平行于另一个平面；C 一个平面内有无数条直线平行于另一个平面；D 一个平面内任何一条直线都平行于另一个平面7.已知直线m ⊥平面α，直线n 平面β，下列说法正确的是()A 若a//β，则m ⊥n ；B 若α⊥β，则m//n；C 若m//n ，则α⊥β； D 若m ⊥n ，则α//β。

8．一个正三棱锥的底面边长为，高为4 ，则这个正三棱锥的侧面积是（ ）A B C D 9．如果轴截面为正方形的圆柱的侧面积是4π，那么圆柱的体积等于（ ）A 380cmB 3112cmC 356cmD 3336cm10．球面上有三个点A, B , C, 且AB= 3 , BC= 4 , AC= 5 ,球心到平面ABC 的距离为球的半径的12，那么这球的半径是（ ）A3 B 53 C3 D 103二、 填空题：每题4分，共16分11．已知圆锥的表面积为2acm ，且它的侧面展开图是一个半圆，则这个圆锥的底面直径为_____________.12.已知直线a ，b ，平面α，β，有下列命题：（1）若a//α，a//b ，则b//α；（2）若α//β，β//γ，则α//γ;(3) 若a ⊥α，b ⊥a ，则b//α； （4）若α⊥γ，β//γ,则α⊥β。

【必刷题】2024高一数学下册立体几何初步专项专题训练（含答案）试题部分一、选择题：1. 在空间直角坐标系中，点A(1,2,3)关于x轴的对称点的坐标是（）A. (1,2,3)B. (1,2,3)C. (1,2,3)D. (1,2,3)2. 下列关于直线l：x=1，y=2+t，z=32t的描述，正确的是（）A. 直线l平行于x轴B. 直线l平行于y轴C. 直线l平行于z轴D. 直线l垂直于x轴3. 一个正方体的对角线长度为6根号3，则其表面积为（）A. 216B. 54C. 108D. 1444. 若长方体的长、宽、高分别为2cm、3cm、4cm，则其对角线长度为（）A. 5cmB. 6cmC. 7cmD. 9cm5. 下列关于平面α：2x3y+z=6的描述，正确的是（）A. 平面α平行于x轴B. 平面α平行于y轴C. 平面α平行于z轴D. 平面α垂直于x轴6. 下列关于点P(2,3,4)到平面α：x+y+z=6的距离，正确的是（）A. 1B. 2C. 3D. 47. 若三棱锥的底面是边长为1的正三角形，侧棱长为根号3，则其体积为（）A. 1/3B. 1/6C. 1/9D. 1/128. 下列关于球体的描述，正确的是（）A. 球体的表面积与半径成正比B. 球体的体积与半径成正比C. 球体的表面积与半径的平方成正比D. 球体的体积与半径的平方成正比9. 若四面体的四个面均为等边三角形，边长为a，则其体积为（）A. a^3/6B. a^3/12C. a^3/18D. a^3/2710. 下列关于空间向量夹角的描述，正确的是（）A. 向量a与向量b的夹角为90°，则a·b=0B. 向量a与向量b的夹角为0°，则a·b=0C. 向量a与向量b的夹角为180°，则a·b=0D. 向量a与向量b的夹角为60°，则a·b=0二、判断题：1. 在空间直角坐标系中，点A(0,0,0)到点B(1,1,1)的距离等于根号3。

高一立体几何初步测试题答案参考答案及评分标准一、选择题 1 2 3 4 5 6 7 8 9 10 B B A B C A C D B B 二、填空题11. 2215()(5)252x y -+-=或2215()(5)252x y +++= 12. 3090α︒︒<<13. 20x -= 14. 22(1)1x y +-= 15. 2或-2 16. 240x y -+=; 25270x y -+= 三、解答题17. 解：解方程组2222(1)(3)20,10,x y x y ⎧-+-=⎪⎨+=⎪⎩得交点坐标为(3,1)-，(3,1)-. …5分 设所求圆的圆心坐标为(2,)a a -，=解得37a =-，r =， …5分因此，圆的方程为222610077x y x y +++-=. …2分 18. 解：设点P 的坐标为(,0)a (0)a >，点P 到直线AB 的距离为d . 由已知，得2211(31)(42)1022ABP S AB d d ∆==-+-=. …4分 解得d =…6分由已知易得，直线AB 的方程为10x y -+=. 所以d == …10分解得9a =，或11a =-(舍去). …12分 所以点P 的坐标为(9,0). …14分 19. 解：由已知得圆C 的圆心为(0,7)C ，半径为5r =. …3分如图所示，(25,18)M 关于x 轴的对称点为(25,18)M '-， …6分 所求反射光线过点M '，C ，所以所求直线方程为70187250y x --=---， 即70x y +-=. …9分 20. 设圆C 的方程为222()()x a y b r -+-=(0)r >，则圆心是(,)C a b ，半径是r . 因为圆C 截得y 轴所得的弦长为4，所以224r a =+. …4分 因为圆C 被x 轴分成两段圆弧，其弧长之比为3：1，所以2r b =. …8分 因为圆心(,)C a b 在直线y x =，所以b a =。

人教A版高一数学必修第二册第八章《立体几何初步》章末练习题卷（共22题）一、选择题（共10题）1.分别在两个平面内的两条直线间的位置关系是( )A．异面B．平行C．相交D．以上都有可能2.下列说法正确的是( )A．相等的角在直观图中仍然相等B．相等的线段在直观图中仍然相等C．正方形的直观图是正方形D．若两条线段平行，则在直观图中对应的两条线段仍然平行3.截一个几何体，所得各截面都是圆面，则这个几何体一定是( )A．圆柱B．圆锥C．球D．圆台4.下列图形中不一定是平面图形的是( )A．三角形B．菱形C．梯形D．四边相等的四边形5.如图的简单组合体是由组合而成.A．棱柱、棱台B．棱柱、棱锥C．棱锥、棱台D．棱柱、棱柱6.如图所示，观察四个几何体，其中判断正确的是( )A．是棱台B．是圆台C．不是棱柱D．是棱锥7.下面是一些命题的叙述语（A，B表示点，a表示直线α，β表示平面），其中命题和叙述方法都正确的是( )A．若A∈α，B∈α，则AB∈αB．若a∈α，a∈β，则α∩β=aC．若A∈α，a⫋α，则A∈αD．若A∉a，a⫋α，则A∉α8.下列四个命题中真命题是( )A．同垂直于一直线的两条直线互相平行B．底面各边相等，侧面都是矩形的四棱柱是正四棱柱C．过空间任一点与两条异面直线都垂直的直线有且只有一条D．过球面上任意两点的大圆有且只有一个9.两个球的表面积之差为48π，它们的大圆周长之和为12π，则这两个球的半径之差为( )A．1B．2C．3D．410.用符号表示“点A在直线l上，l在平面α内”，正确的是( )A．A∈l，l∉αB．A⊂l，l⊄αC．A⊂l，l∈αD．A∈l，l⊂α二、填空题（共6题）11.几何体体积说明棱柱V棱柱=SℎS为棱柱的 ,ℎ为棱柱的 棱锥V棱锥=13SℎS为棱锥的 ,ℎ为棱锥的 棱台V棱台=13(Sʹ+√SʹS+S)ℎSʹ,S分别为棱台的 ,ℎ为棱台的 12.如果两个球的体积之比为8:27，那么两个球的表面积之比为．13.思考辨析 判断正误棱锥的体积等于底面面积与高之积．14.已知正三棱柱ABC−A1B1C1的各条棱长都相等，M是侧棱BB1的中点，N是棱AB的中点，则∠NMC1的大小是．15.思考辨析，判断正误．如果两条直线同时平行于第三条直线，那么这两条直线互相平行．16.思考辨析，判断正误在斜二测画法中，各条线段的长度都发生了改变．( )三、解答题（共6题）17.如图所示，梯形ABCD中，AD∥BC，且AD<BC，当梯形ABCD绕AD所在直线旋转一周时，其他各边旋转围成了一个几何体，试描述该几何体的结构特征．18.如图是长方体的表面展开图，在这个长方体中：(1) 直线DM与平面ABQP的位置关系是怎样的？(2) 平面DCMN与平面ERFG的位置关系是怎样的？(3) 线段BC的长度是点C到平面APQB的距离吗？19.有4条长为2的线段和2条长为a的线段，用这6条线段作为棱，构成一个三棱锥．问a为何值时，可构成一个最大体积的三棱锥，最大值为多少？20.根据图形用符号表示下列点、直线、平面之间的位置关系．(1) 点P与直线AB；(2) 点C与直线AB；(3) 点M与平面AC；(4) 点A1与平面AC；(5) 直线AB与直线BC；(6) 直线AB与平面AC；(7) 平面A1B与平面AC．21.应用面面平行判断定理应具备哪些条件？22.观察（1），（2），（3）三个图形，说明它们的位置关系有什么不同，并用字母表示各个平面．答案一、选择题（共10题）1. 【答案】D【解析】分别在两个平面的两条直线平行、相交、异面都可能，可将两条直线放在长方体里进行研究．【知识点】直线与直线的位置关系2. 【答案】D【解析】等腰三角形的两底角相等，但在直观图中不相等，故A错误；正方形的直观图是平行四边形，正方形的两邻边相等，但在直观图中不相等，故B，C错误．【知识点】直观图3. 【答案】C【解析】由球的结构特征知该几何体是球．【知识点】球的结构特征4. 【答案】C【知识点】平面的概念与基本性质5. 【答案】B【解析】该简单组合体的上面是一个棱锥，下面是一个棱柱．【知识点】组合体6. 【答案】D【解析】对A，侧棱延长线不交于一点，不符合棱台的定义，所以A错误；对B，上下两个面不平行，不符合圆台的定义，所以B错误；对C，将几何体竖直起来看，符合棱柱的定义，所以C错误；对D，符合棱锥的定义，正确．【知识点】棱台的结构特征、棱锥的结构特征、棱柱的结构特征7. 【答案】C【知识点】平面的概念与基本性质8. 【答案】C【知识点】棱柱的结构特征、直线与直线的位置关系、球的结构特征9. 【答案】B【解析】设两球半径分别为R1，R2，且R1>R2，则4π(R12−R22)=48π，2π(R1+R2)=12π，所以R1−R2=2．【知识点】球的表面积与体积10. 【答案】D【解析】点A在直线l上，表示为A∈l，l在平面α内，表示为l⊂α．【知识点】平面的概念与基本性质二、填空题（共6题）11. 【答案】底面积；高；底面积；高；上、下底面面积；高【知识点】棱锥的表面积与体积、棱柱的表面积与体积、棱台的表面积与体积12. 【答案】4:9【解析】因为V1:V2=8:27=R13:R23，所以R1:R2=2:3，所以S1:S2=R12:R22=4:9．【知识点】球的表面积与体积13. 【答案】×【知识点】棱锥的表面积与体积14. 【答案】90°【解析】通过计算可知NC12=NM2+MC12，故∠NMC1=90∘．如图．【知识点】棱柱的结构特征15. 【答案】√【知识点】空间中直线与直线平行16. 【答案】×【知识点】直观图三、解答题（共6题）17. 【答案】如图所示，旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分构成的组合体．【知识点】组合体18. 【答案】(1) 根据展开图还原长方体，其示意图如图所示， 则 直线DM ∥平面ABQP ．(2) 平面 DCMN 垂直于平面 ERFG ．(3) 线段 BC 的长度是点 C 到平面 APQB 的距离．【知识点】平面与平面的位置关系、点面距离（线面距离、点线距离、面面距离）、直线与平面的位置关系19. 【答案】构成三棱锥，这 6 条线段作为棱有两种摆放方式．（1）2 条长为 a 的线段放在同一个三角形中．如图所示，不妨设底面 BCD 是一个边长为 2 的正三角形．欲使体积达到最大，必有 BA ⊥底面BCD ，且 BA =2，AC =AD =a =2√2， 此时 V =13×√34×22×2=23√3．（2）2 条长为 a 的线段不在同一个三角形中，此时长为 a 的两条线段必处在三棱锥的对棱，不妨设 AD =BC =a ，BD =CD =AB =AC =2． 取 BC 中点 E ，连接 AE ，DE （见下图）．则 AE ⊥BC,DE ⊥BC ⇒BC ⊥平面AED ，V =13S △AED ⋅BC ， 在 △AED 中，AE =DE =√4−a 24，AD =a ，S △AED =12a √4−a 24−a 24=12a √4−a 22，所以 V =16a 2√4−a 22=16√a 2a 2(16−2a 2)⋅14，由均值不等式 a 2a 2(16−2a 2)≤(163)3， 等号当且仅当 a 2=163时成立，即 a =43√3， 所以此时 V max =16√(163)3⋅14=1627√3．【知识点】棱锥的表面积与体积20. 【答案】(1) 点P∈直线AB．(2) 点C∉直线AB．(3) 点M∈平面AC．(4) 点A1∉平面AC．(5) 直线AB∩直线BC=点B．(6) 直线AB⊂平面AC．(7) 平面A1B∩平面AC=直线AB．【知识点】点、线、面的位置关系、直线与平面的位置关系、平面与平面的位置关系、直线与直线的位置关系21. 【答案】①平面α内两条相交直线a，b，即a⊂α，b⊂α，a∩b=P．②两条相交直线a，b都与β平行，即a∥β，b∥β．【知识点】平面与平面平行关系的判定22. 【答案】图（1）表示两个相交的半平面；图（2）表示开口向里的两个相交的半平面；图（3）表示开口向外的两个相交的半平面．【知识点】平面的概念与基本性质。

高一数学立体几何初步试题答案及解析1.已知平面α内有无数条直线都与平面β平行，那么A．α∥βB．α与β相交C．α与β重合D．α∥β或α与β相交【答案】D【解析】由题意当两个平面平行时符合平面α内有无数条直线都与平面β平行，当两平面相交时，在α平面内作与交线平行的直线，也有平面α内有无数条直线都与平面β平行．故为D。

【考点】本题主要考查平面与平面之间的位置关系。

点评：对两平面空间的位置要做出多种推测。

2.平面α∥平面β，AB、CD是夹在α和β间的两条线段，E、F分别为AB、CD的中点，则EF与α的关系是A．平行 B．相交 C．垂直 D．不能确定【答案】A【解析】若AB∥CD，易得EF与α、β均平行若AB与CD相交，则EF与α、β均平行若AB与CD异面，则设过AB和EF的平面交α，β分别于直线AG和BH，如下图所示：且使G，F，H在一直线上．因为平面α∥β，所以AG∥CH，连接CG和DH，则CGFDH在一个平面内，且CG∥DH，F为CD中点，所以三角形CFG和三角形DFH全等，即得FG=FH，因为AG∥CH，又E，F分别为AB，CD中点，且A，C，H，G在一个平面内，所以EF∥AG∥CH，CH在平面β内，故EF∥β．同理EF∥β故选A。

【考点】本题主要考查空间中直线与平面之间的位置关系。

点评：由于AB，CD的位置关系不确定，故要进行分类讨论。

将空间问题转化为平面问题的转化思想也是处理空间问题最常用的思路。

3.若三个平面把空间分成6个部分，那么这三个平面的位置关系是A．三个平面共线；B．有两个平面平行且都与第三个平面相交；C．三个平面共线，或两个平面平行且都与第三个平面相交；D．三个平面两两相交。

【答案】C【解析】①若三个平面两两平行，则把空间分成4部分；②若三个平面两两相交，且共线，则把空间分成6部分；③若三个平面两两相交，且有三条交线，则把空间分成7部分；④若三个平面其中两个平行和第三个相交，则把空间分成6部分；故选C．【考点】本题主要考查平面与平面之间的位置关系。

《立体几何、解析几何初步》训练题满分：100分考试时间：100分钟一、选择题：本大题共10小题，每小题4分，共40分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知直线α及平面、、n m l ，下列命题中的假命题是：A. 若n l n m m l //,//,//则B. 若n l n l ⊥⊥则,//,ααC. 若n l n m m l ⊥⊥则,//,D. 若n l n l //,//,//则αα2. 设D C B A 、、、是空间四个不同的点，在下列命题中，不正确．．．的是 A. 若BD AC 与共面，则BC AD 与共面; B. 若BD AC 与是异面直线，则BC AD 与是异面直线;C. 若BC AD DC DB AC AB ===则,,；D. 若BC AD DC DB AC AB ⊥==则,,3. “直线a 平行于直线b ”是“直线a 平行于过直线b 的平面”成立的：A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 如果正方体''''D C B A ABCD -的棱长为a ，那么四面体ABD A -'的体积是： A. 23a B. 33a C. 43a D. 63a 5. 一个梯形采用斜二测画法作出其直观图，则其直观图的面积是原来梯形面积的： A. 42倍 B. 21倍 C. 22倍 D. 2倍 6. 已知过点)4,(),2(m B m A 和-的直线与直线012=-+y x 平行，则m 的值为：A. 0B. 8-C. 2D. 107. 已知点)1,3()21(B A 和，，则线段AB 的垂直平分线的方程为： A. 0524=-+y x B. 0524=--y x C. 052=-+y x D. 052=--y x8. 已知点BC x A B xOy A C A 则轴对称关于与点点对称关于平面与点，点,,)1,2,1(-的长为： A. 52 B. 4 C. 22 D. 729. 若圆1)1()2(22=-++y x C 与圆关于原点对称，则圆C 的方程是：A. 1)1()2(22=++-y xB. 1)1()2(22=-+-y xC. 1)2()1(22=++-y xD. 1)2()1(22=-++y x10. 若直线的值为相切，则与圆a x y x y x a 0201)1(22=-+=+++：A. 1±B. 2±C. 1D. 1-二、 填空题：本大题共4小题，每小题5分，共20分. 把答案填在题中的横线上. 11. 已知点)0,1()01(B A 和，-. 若直线b x y +-=2与线段AB 相交，则b 的取值范围是_____________.12. 已知βα、是不同的直线、,n m 是不重合的平面，给出下列命题：①若,,//αβα⊂m n m n //,则β⊂；② 若βαββα//,//,//,,则n m n m ⊂；③若,//,,n m n m βα⊥⊥ 则 βα//；④ ,//,////αβαn m m n m 、是两条异面直线，若、βαβ//,//则n . 上面的命题中，真命题的序号是 ___________.( 写出所有真命题的序号)13. 设的方程为则直线的中点为的弦圆AB P AB x y x ),1,3(05422=--+___________.14. 在直四棱柱ABCD D C B A -1111中，当底面四边形ABCD 满足条件_________________时，有111D B C A ⊥.（填上你认为正确的一种条件即可，不必考虑所有可能的情形）OD 1C 1B 1A 1D CB A三、解答题：本大题共4小题，共50分. 解答应写出文字说明，证明过程或演算步骤.15.（本小题满分8分）已知两直线0120821=-+=++my x l n y mx l ：和：，试确定n m 、的值，使得： （1）)1,(21-m P l l 相交于点与；（2）21//l l ；（3）1121-⊥轴上的截距为在且y l l l .16.（本小题满分10分）如图，已知NM a AD a DC PD ABCD PD ABCD 、，，平面是矩形，2,===⊥分别是PB AD 、的中点. 求证：平面PBC MNC 平面⊥.N MP DCBA17.（本小题满分10分）已知O 为坐标原点，圆0320622=-+=+-++y x l c y x y x C ：与直线：的两个交点为Q P 、. OQ OP c ⊥为何值时，当？18.（本小题满分12分） 如图，PC AB N M ABCD PA 、分别是、所在的平面，矩形⊥的中点. （1）求证：PAD MN 平面//；（2）求证：CD MN ⊥；（3）若，ο45=∠PDA 求证：PCD MN 平面⊥.NM P D CBA参考答案一、选择题：1-5 DCDDA 6-10 BBBAD二、填空题：11. 22≤≤-b12. ③④13.04=-+y x14. 等或BD AC AD AB ⊥=三、解答题：15.（1）⎩⎨⎧==71n m ；（2）2424≠-=-≠=n m n m 时，，当时，当；（3）⎩⎨⎧==80n m .16. 提示：连接PB NC PB MN MB PM MB PM ⊥⊥=；再证，从而，证明、.17. 3=c .18. 提示：（1）取AE MN EN AE E PD //,,,证明连接的中点；（2）PAD AB 平面证明⊥；（3）.,,PCD MN CD MN PD MN 平面从而又证明⊥⊥⊥。

高一数学立体几何练习题及答案一、选择题1. 下列哪个图形不是立体图形？A. 立方体B. 圆锥C. 圆柱D. 正方形答案：D2. 已知一个立方体的边长为5cm，求它的表面积和体积分别是多少？A. 表面积：150cm²，体积：125cm³B. 表面积：100cm²，体积：125cm³C. 表面积：150cm²，体积：100cm³D. 表面积：100cm²，体积：100cm³答案：A3. 以下哪个选项可以形成一个正方体？A. 六个相等的长方体B. 一个正方形和一个长方体C. 六个相等的正方形D. 一个正方形和一个正方体答案：C4. 以下哪个图形可以形成一个圆柱？A. 一个正方形和一个长方体B. 一个圆和一个长方体C. 一个长方形和一个长方体D. 一个正方形和一个正方体答案：C5. 以下哪个选项可以形成一个圆锥？A. 一个圆和一个长方体B. 一个圆和一个正方体C. 一个正方形和一个长方体D. 一个正方形和一个正方体答案：B二、填空题1. 已知一个正方体的表面积为96cm²，求它的边长是多少？答案：4cm2. 已知一个圆柱的半径为3cm，高为10cm，求它的表面积和体积分别是多少？答案：表面积：198cm²，体积：90π cm³3. 以下哪个选项可以形成一个长方体？A. 六个相等的正方形B. 一个圆和一个长方形C. 六个相等的长方形D. 一个正方形和一个正方体答案：C三、解答题1. 某长方体的长、宽、高分别为3cm、4cm、5cm，请回答以下问题：（1）它的表面积是多少？（2）它的体积是多少？答案：（1）表面积 = 2(长×宽 + 长×高 + 宽×高)= 2(3×4 + 3×5 + 4×5)= 2(12 + 15 + 20)= 2(47)= 94cm²（2）体积 = 长×宽×高= 3×4×5= 60cm³2. 某圆锥的半径是5cm，高是12cm，请回答以下问题：（1）它的表面积是多少？（2）它的体积是多少？答案：（1）斜面积= π×半径×斜高= π×5×13≈ 204.2cm²（2）体积= (1/3)π×半径²×高= (1/3)π×5²×12≈ 314.2cm³四、解析题某正方体的表面积是96cm²，它的边长是多少？解答：设正方体的边长为x，由表面积的计算公式可得：表面积 = 6x²96 = 6x²16 = x²x = 4所以，该正方体的边长为4cm。

本章达标测评(总分:150分;时间:120分钟)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列说法中正确的是( )①三角形一定是平面图形;②若四边形的两条对角线相交于一点,则该四边形是平面图形;③圆心和圆上两点可确定一个平面;④三条平行线最多可确定三个平面.A.①③④B.②③④C.①②④D.①②③2.如下图所示,α∩β=l,A∈α,B∈α,AB∩l=D,C∈β,C∉l,则平面ABC与平面β的交线是( )A.直线ACB.直线ABC.直线CDD.直线BC3.一个圆锥的侧面积是其底面积的2倍,则该圆锥的母线与轴线所成的角为( )A.30°B.45°C.60°D.75°4.下面说法正确的是( )A.若直线l平行于平面α内的无数条直线,则l∥αB.若直线a在平面α外,则a∥αC.若直线a∥b,直线b⫋α,则a∥αD.与两条异面直线都平行的平面有无穷多个5.若平面α内不共线的三点到平面β的距离都相等,则平面α与平面β的位置关系是( )A.平行B.相交且不垂直C.垂直D.以上三种情况都有可能6.在正三棱锥P-ABC中,D,E分别是AB,BC的中点,有下列三个论断:①AC⊥PB;②AC∥平面PDE;③AB⊥平面PDE.其中正确的是( )A.①②③B.①③C.①②D.②③7.在长方体ABCD-A1B1C1D1中,AA1=2,AB=1,AD=4,则从A出发,沿长方体的表面到C1的最短距离是( ) A.5 B.7C.√29D.√378.在如下图所示的三棱锥A-BCD中,VA-BPQ =2,VC-APQ=6,VC-DPQ=12,则VA-BCD等于( )A.20B.24C.28D.569.如下图所示,在正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、CC1的中点,则在空间中与直线A1D1、EF、CD都相交的直线( )A.不存在B.有且只有两条C.有且只有三条D.有无数条10.如下图所示,在空间四边形ABCD中,E、F分别为AB、AD上的点,且AE∶EB=AF∶FD=1∶4,又H、G分别为BC、CD的中点,则( )A.BD∥平面EFGH,且四边形EFGH是矩形B.E F∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是菱形D.EH∥平面ADC,且四边形EFGH是平行四边形二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中横线上)11.若球的体积与其表面积的数值相等,则球的半径是.12.如下图所示,梯形A1B1C1D1是水平放置的平面图形ABCD的直观图,若A 1D1∥O'y',A1B1∥C1D1,A1B1=23C1D1=2,A1D1=1,则四边形ABCD的面积是.13.一个几何体的三视图(单位:cm)如下图所示,则该几何体的表面积是cm2.14.在△ABC中,∠BAC=90°,P为△ABC所在平面外一点,且PA=PB=PC,则平面PBC与平面ABC的位置关系是.15.在棱长为1的正方体ABCD-A1B1C1D1中,过体对角线BD1的一个平面交AA1于E,交CC1于F,得四边形BFD1E,给出下列结论:①四边形BFD1E有可能为梯形;②四边形BFD1E有可能为菱形;③四边形BFD1E在底面ABCD内的投影一定是正方形;④四边形BFD1E有可能垂直于平面BB1D1D.其中正确的是(请写出所有正确结论的序号).三、解答题(本大题共6小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤)16.(10分)一几何体按比例绘制的三视图如图(单位:m):(1)试画出它的直观图;(2)求它的表面积和体积.17.(12分)在三棱柱ABC-A1B1C1中,D是BC上一点,且A1B∥平面AC1D,D1是B1C1的中点,求证:平面A1BD1∥平面AC1D.18.(12分)一个多面体的直观图及三视图如图所示(其中M、N分别是AF、BC的中点).(1)求证:MN∥平面CDEF;(2)求多面体A-CDEF的体积.19.(13分)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC 的中点,PA=AD.(1)求证:MN∥平面PAD;(2)求证:平面PMC⊥平面PCD.20.(14分)已知正方体ABCD-A1B1C1D1中,O是底面ABCD的对角线的交点,求证:(1)C1O∥平面AB1D1;(2)A1C⊥平面AB1D1.21.(14分)如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E、F分别是棱CC1、BB1上的点,点M是线段AC上的动点,EC=2FB=2.问:当点M在什么位置时,BM∥平面AEF?附加题(2012上海理,14,4分,★★☆)如下图所示,AD与BC是四面体ABCD中互相垂直的棱,BC=2.若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是.一、选择题1.C 过不在同一条直线上的三点有且只有一个平面,所以三角形一定是平面图形,所以①对;两条对角线相交于一点的四边形一定是平面图形,所以②对;三条平行线可确定一个或三个平面,所以④对;可以有无数个平面经过圆的一条直径,③错.故选C.2.C D∈l,l⫋β,∴D∈β,又C∈β,∴CD⫋β.同理,CD⫋平面ABC,∴平面ABC∩平面β=直线CD.3.A 设圆锥的母线长为L,底面圆的半径为r,则由题意得πrL=2πr2,∴L=2r,∴圆锥的母线与轴线所成的角为30°.4.D 对于A,当l⫋α时,平面α内也有无数条直线与l平行;对于B,a在平面α外有a与α相交,a∥α两种情况;对于C,a∥b,b⫋α,则a⫋α或a∥α;对于D,平移异面直线中的一条,使之与另一条相交,两相交直线可确定一个平面α,则与平面α平行的无穷多个平面都与这两条异面直线平行.5.D 三点若在平面β的一侧,则α∥β,三点若在β的两侧,则α与β可能相交且不垂直,也有可能垂直.6.C 画图形(图略),可得①②正确.7.A 两点之间,线段最短,在长方体展开图中,由A到C1的路线有三条,如下图,三条路线长分别为l1=√12+(2+4)2=√37,l2=√42+(1+2)2=5,l3=√22+(1+4)2=√29,所以最短距离为5.8.B 由V A-BPQV C-APQ =26=13,得V P-BDQV P-CDQ=13,所以VP-BDQ=13VP-CDQ=4,所以VA-BCD=2+6+12+4=24.9.D 在EF上任意取一点M,直线A1D1与M确定一个平面,这个平面与CD有且仅有1个交点N,当M取不同的位置时就确定不同的平面,从而与CD有不同的交点N,而直线MN 与这三条异面直线都有交点,故选D.10.B 由AE∶EB=AF∶FD=1∶4知EF 15BD,∴EF∥平面BCD.又H 、G 分别为BC 、CD 的中点,∴HG12BD,∴EF∥HG 且EF≠HG,∴四边形EFGH 是梯形,故选B. 二、填空题 11.答案 3解析 设球的半径为R,由题意知4πR 2=43πR 3,∴R=3. 12.答案 5解析 还原图形,如下图所示.CD=C 1D 1=3,AD=2A 1D 1=2, AB=A 1B 1=2,∠ADC=90°, 所以S 梯形ABCD =12×(2+3)×2=5. 13.答案 (4π+12)解析 由三视图知该几何体为一个四棱柱、一个半圆柱和一个半球的组合体,其中四棱柱上底面与半球重合部分之外的面积为1×2-12×π×12=(2-π2)cm 2,四棱柱中不重合的表面积为2-π2+1×2×2+2×2+1×2=(12-π2)cm 2,半圆柱中不重合的表面积为12×2π×2+12π=52π cm 2,半球的表面积为12×4π×12=2π cm 2,所以该几何体的表面积为(4π+12)cm 2. 14.答案 垂直解析 如下图所示,取BC 的中点O,连接AO,PO.∵PB=PC,∴PO⊥BC.又△ABC 是以A 为直角顶点的直角三角形,∴OA=OB,又PA=PB, ∴△POA≌△POB,∴∠POA=∠POB=90°,即PO⊥OA, 而OA∩BC=O,∴PO⊥平面ABC,而PO ⫋平面PBC, ∴平面PBC⊥平面ABC. 15.答案 ②③④解析 因为正方体中对面互相平行,所以截面与对面的交线互相平行,所以一定是平行四边形,①不对;当E 、F 分别是所在棱的中点时,四边形BFD 1E 为菱形,②对;根据投影知识知③对;当E 、F 分别是所在棱中点时,EF⊥平面BB 1D 1D,④对. 三、解答题16.解析 (1)直观图如图①.(2)解法一:由三视图可知该几何体是由长方体截去一个角而得到的,且该几何体的体积是以A 1A,A 1D 1,A 1B 1为棱的长方体的体积的34,在直角梯形AA 1B 1B 中,作BE⊥A 1B 1于E,如图②,则四边形AA 1EB 是正方形, ∴AA 1=BE=1 m.在Rt△BEB 1中,BE=1 m,EB 1=1 m, ∴BB 1=√2 m.∴几何体的表面积S=S 正方形AA 1D 1D +2S 梯形AA 1B 1B +S 矩形BB 1C 1C +S正方形ABCD+S 矩形A 1B 1C 1D 1=1+2×12×(1+2)×1+1×√2+1+1×2=(7+√2)m 2,几何体的体积V=34×1×2×1=32 m 3.∴该几何体的表面积为(7+√2)m 2,体积为32 m 3.解法二:该几何体可看成以四边形AA 1B 1B 为底面的直四棱柱,其表面积求法同解法一, V 直四棱柱D 1C 1CD -A 1B 1BA =Sh=12×(1+2)×1×1=32 m 3. ∴该几何体的表面积为(7+√2)m 2,体积为32 m 3.17.证明 如图,连接AB 1交A 1B 于点E, 则E 为AB 1的中点,连接ED 1.∵E 为AB 1的中点,D 1是B 1C 1的中点, ∴ED 1为△B 1AC 1的中位线, ∴ED 1∥AC 1.∵ED 1⊈平面AC 1D,AC 1⫋平面AC 1D, ∴ED 1∥平面AC 1D,又∵A 1B∥平面AC 1D,且ED 1∩A 1B=E, ∴平面A 1BD 1∥平面AC 1D. 18.解析 由题图知该多面体是底面为直角三角形的直三棱柱ADE-BCF,AB=BC=BF=2,DE=CF=2√2,∠CBF=90°. (1)证明:取BF 的中点G,连接MG 、NG. 由M 、N 分别为AF 、BC 的中点,可得NG∥CF,MG∥AB∥EF,又MG∩NG=G,EF∩CF=F ⇒平面MNG∥平面CDEF ⇒MN∥平面CDEF.(2)取DE 的中点H,连接AH. 因为AD=AE,所以AH⊥DE. 在直三棱柱ADE-BCF 中, 平面ADE⊥平面CDEF, 平面ADE∩平面CDEF=DE, 所以AH⊥平面CDEF,所以多面体A-CDEF 是以AH 为高,矩形CDEF 为底面的棱锥. AH=√2,S 矩形CDEF =DE·EF=4√2,所以棱锥A-CDEF 的体积V=13S 矩形CDEF ·AH=83. 19.证明 (1)取PD 的中点E,连接EN,AE. ∵N 是PC 的中点,∴EN12DC.又∵AM12DC,∴EN AM,∴四边形AENM是平行四边形, ∴AE∥MN.又∵AE⫋平面PAD,MN⊈平面PAD, ∴MN∥平面PAD.(2)∵PA=AD,E是PD的中点,∴AE⊥PD.∵PA⊥平面ABCD,∴PA⊥CD.又AD⊥CD,PA∩AD=A,∴CD⊥平面PAD.∵AE⫋平面PAD,∴AE⊥CD.∵PD∩CD=D,∴AE⊥平面PCD. 又∵AE∥MN,∴MN⊥平面PCD.∵MN⫋平面PMC,∴平面PMC⊥平面PCD.20.证明(1)连接A1C1,设A1C1∩B1D1=O1,连接AO1.∵ABCD-A1B1C1D1是正方体,∴四边形A 1ACC 1是平行四边形, ∴A 1C 1∥AC,且A 1C 1=AC. 又O 1,O 分别是A 1C 1,AC 的中点, ∴O 1C 1∥AO,且O 1C 1=AO,∴AOC 1O 1是平行四边形,∴C 1O∥AO 1, 又AO 1⫋平面AB 1D 1, C 1O ⊈平面AB 1D 1, ∴C 1O∥平面AB 1D 1. (2)∵CC 1⊥平面A 1B 1C 1D 1, ∴CC 1⊥B 1D 1.又A 1C 1⊥B 1D 1,CC 1∩A 1C 1=C 1, ∴B 1D 1⊥平面A 1C 1C,∴A 1C⊥B 1D 1. 同理可证A 1C⊥AB 1, 又D 1B 1∩AB 1=B 1, ∴A 1C⊥平面AB 1D 1.21.解析 如图,取AE 的中点O,连接OF,过点O 作OM⊥AC 于点M,连接MB.因为侧棱A 1A⊥底面ABC,所以侧面A 1ACC 1⊥底面ABC,所以OM⊥底面ABC.则OM 12EC,又因为EC=2FB=2,所以OMFB,所以四边形OMBF 为矩形,所以BM∥OF. 又因为BM ⊈平面AEF,OF ⫋平面AEF, 故BM∥平面AEF,此时点M 为AC 的中点.附加题答案 23c √a 2-c 2-1解析 过点D 作DE⊥BC 于点E,连接AE,则BE⊥平面ADE.作△ADE 的边AD 上的高EF,则EF为最大值时,该几何体体积最大,则当BA=BD=CA=CD=a,且EF为AD和BC的公垂线段,F为AD的中点时,该几何体体积V最大,Vmax =13S△AED·BC=13×12AD·EF·BC=2c3√a2-c2-1.。

高一数学立体几何初步试题答案及解析1.点B是点A（1，2，3）在坐标平面内的射影，则OB等于（）A．B．C．D．【答案】B【解析】点A（1，2，3）在坐标平面内的射影为B（0,2,3），所以|OB|=，故选B。

【考点】本题主要考查空间直角坐标系的概念及两点间距离公式的应用。

点评：理解好射影的概念，用熟两点间距离公式。

2.两等角的一组对应边平行，则（）A．另一组对应边平行B．另一组对应边不平行C．另一组对应边也不可能垂直D．以上都不对【答案】D【解析】两等角的一组对应边平行，另一组对应边由多种情况，如平行、相交、异面等，关系D。

【考点】本题主要考查直线的位置关系。

点评：视野要开阔，考虑多种可能情况。

3.经过平面外两点与这个平面平行的平面（）A．只有一个B．至少有一个C．可能没有D．有无数个【答案】C【解析】经过平面外两点与这个平面平行的平面可能没有，如两点所在直线与平面相交时，关系C。

【考点】本题主要考查点线面的关系—--平行关系。

点评：考虑点与平面的多种可能情况思考，结合实物模型探究。

4.如图所示，平面M、N互相垂直，棱l上有两点A、B，AC M，BD N，且AC⊥l，AB＝8cm，AC＝6 cm，BD＝24 cm，则CD＝_________．【答案】26 cm；【解析】连接AD，∵平面M、N互相垂直，AC⊥l，∴AC⊥平面N∴AC⊥CD；∵AB=8cm，AC=6cm，∴BC=10cm，又∵BD=24cm，∴CD=26cm。

【考点】本题主要考查点、线、面间的距离计算、面面垂直。

点评：考查的知识点是空间点到点之间的距离，其中根据面面垂直及线面垂直的性质得到△ABC，△ACD均为直角三角形，是解答本题的关键。

5.下面的图形可以构成正方体的是（）【答案】C【解析】从选项出发，还原成正方体的只有C。

【考点】本题主要考查正方体的展开图。

点评：从选项出发，看能否还原成正方体。

6.下列命题中正确的是（）A．由五个平面围成的多面体只能是四棱锥B．棱锥的高线可能在几何体之外C．仅有一组对面平行的六面体是棱台D．有一个面是多边形，其余各面是三角形的几何体是棱锥【答案】B【解析】由五个平面围成的多面体除四棱锥外，还可以是三棱台；棱锥的高线应是其顶点向底面所作垂线段，斜棱锥的高即在几何体外，故选B。

《立体几何初步》全章训练一、选择题（每题5分，共60分）1、下列说法中正确的是（）A、由五个平面围成的多面体只能是四棱锥B、棱锥的高线可能在几何体之外C、仅有一组对面平行的六面体是棱台D、有一个面是多边形，其余各面是三角形的几何体是棱锥2、在一个正方体ABCD-A1B1C1D1中，若E是A1C1的中点，则直线CE垂直于（）A、直线ACB、直线BDC、直线A1DD、直线A1D13、中国古建筑借助榫卯将木构件连起来，构件的凸出部分叫榫头，凹进部分叫卯眼。

图中木构件右边的小长方体是榫头。

若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的左视图是（）。

4、已知圆台的轴截面为上底长为4，下底长为8的等腰梯形，且圆台的母线长为4，则圆台的高为（）。

2D、4A、3B、3C、35、在正方体ABCD-A1B1C1D1中，AB的中点为M，DD1的中点为N，则异面直线B1M与CN所成的角为（）。

A、30°B、45°C、60°D、90°6、圆锥的表面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为（）。

A、120°B、150°C、180°D、240°7、某数学小组进行“数学建模”社会实践调查，他们在调查过程中将一实际问题建立起数学模型，现展示如下：四个形状不同、内部高度相等、杯口半径相等的圆口容器，如图所示。

盛满液体后倒出一半，设剩余液体的高度从左到右依次为h1,h2,h3,h4，则它们的大小关系正确的是（）A、h2>h1>h4B、h1>h2>h3C、h3>h2>h4D、h2>h4>h18、如图所示（单位：cm ），直角梯形的左上角减去四分之一个圆，剩下的阴影部分绕AB 所在直线旋转一周形成的几何体的表面积为（ ）A 、260cm πB 、264cm πC 、268cm πD 、272cm π9、如图，在四面体ABCD 中，AB=1，AD=32，BC=3，CD=2，∠ABC=∠DCB=90°，则二面角A-BC-D 的大小为（ ）。

高一立体几何初步测试题及答案1.在空间四点中，无三点共线是四点共面的（充分不必要条件）。

2.若a∥b，b∩c=A，则a,c的位置关系是（相交直线或异面直线）。

3.圆锥的侧面展开图是直径为a的半圆面，那么此圆锥的轴截面是（等腰直角三角形）。

4.已知某几何体的俯视图是如图所示的矩形，正视图是一个底边长为8、高为4的等腰三角形，左视图是一个底边长为6、高为4的等腰三角形，则该几何体的体积为（64）。

5.长方体的一个顶点上三条棱长分别是3,4,5，且它的8个顶点都在同一球面上，则这个球的表面积是（50π）。

6.已知正方体外接球的体积是π，那么正方体的棱长等于（3）。

7.若l、m、n是互不相同的空间直线，α、β是不重合的平面，则下列命题中为真命题的是（若α⊥β,l∈α,n∈β，则l⊥n）。

8.如图，在正方体ABCD-A' B' C' D'中，E，F，G，H分别为AA'，AB，BB'，B'C'的中点，则异面直线EF与GH所成的角等于（90°）。

9.已知两个平面垂直，其中正确的命题数量是（2）。

10.平面α与平面β平行的条件可以是（直线a//α,a//β）。

三、简答题（本大题共4小题，每小题10分，共40分）1.如何确定一个圆锥的侧面展开图？答：将圆锥展开，使其侧面展开为一段扇形，然后将扇形展开成一个直角三角形，即可得到圆锥的侧面展开图。

2.如何确定一个几何体的三视图？答：俯视图是从正上方看几何体，可以看到几何体的顶面和底面；正视图是从正前方看几何体，可以看到几何体的前面和后面；左视图是从正左方看几何体，可以看到几何体的左面和右面。

通过这三个视图，可以确定一个几何体的形状和尺寸。

3.如何判断两个平面是否平行？答：如果两个平面的法向量平行，则这两个平面平行。

也可以通过判断它们的交线是否平行来确定两个平面是否平行。

4.如何判断两条直线是否相交？答：如果两条直线的方向向量不平行，则它们相交；如果两条直线的方向向量平行但不重合，则它们异面直线；如果两条直线的方向向量重合，则它们可能重合也可能平行。

高一数学（必修2）立体几何初步测试题一、选择题(本大题共10小题，每小题4分，共40分) 1、以下关于几何体的三视图的论述中，正确的是（ ）A 、球的三视图总为全等的圆B 、正方体的三个视图总是三个全等的正方形C 、水平放置的正四面体的三个视图都是正三角形D 、水平放置的圆台的俯视图是一个圆2、直线a 、b 、c 满足a ∥b ，b ⊥c,则a 与c 的关系是（ ） A 、异面直线 B 、平行直线 C 、垂直 D 、相交 3．下列说法正确的是A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点4、一个水平放置的平面图形的斜二测直观图是一个底角为 45，腰和上底边均为1的等腰梯形，则这个平面图形的面积是 （ ）A 、2221+ B 、 22+ C 、 21+ D 、 221+5、一个体积为38cm 的正方体的顶点都在球面上，则球的表面积是A 、28cm πB 、212cm πC 、216cm πD 、220cm π 6、垂直于同一条直线的两条直线一定A 、平行B 、相交C 、异面D 、以上都有可能 7、在正方体1111ABCD A BC D -中，下列几种说法正确的是A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45角 D 、11AC 与1BC成60 角8、将一个边长为a 的正方体，切成27个全等的小正方体，则表面积增加了 A 、26aB 、12a 2C 、18a 2D 、 24a 29、设γβα,,是三个不重合的平面，l 是直线，给出下列命题①若γββα⊥⊥,，则γα⊥；②若l 上两点到α的距离相等，则α//l ；B 1C 1A 1D 1BACD ③若βαβα⊥⊥则,//,l l ④若.//,//,,//βαββαl l l 则且⊄其中正确的命题是 （ ）A 、①②B 、②③C 、②④D 、③④10、圆柱的一个底面积为S ，侧面展开图是一个正方形，那么这个圆柱的侧面积是（ ）A 、S πB 、S π2C 、S π4D 、S π332 二、填空题: (本大题共4小题，每小题4分，共16分)11、等体积的球和正方体,它们的表面积的大小关系是S 球_____S 正方体(填”大于、小于或等于”).12、正方体1111ABCD A BC D -中，平面11AB D 和平面1BC D 的位置关系为 13、已知PA 垂直平行四边形ABCD 所在平面，若PC BD ⊥，平行则四边形ABCD 一定是 .14、如图，在直四棱柱A 1B 1C 1 D 1－ABCD 中，当底面四边形ABCD 满足条件_________时，有A 1 B ⊥B 1 D 1．(注：填上你认为正确的一种条件即可，不必考虑所有可能的情形.) 三、解答题:15、已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.16、已知ABC ∆中90ACB ∠=，SA ⊥面ABC ，AD SC ⊥，求证：AD ⊥面SBC ．SDB A17、如图，ABCD 是正方形，O 是正方形的中心，PO ⊥底面ABCD ，E 是PC 的中点。