计算方法上机作业

（完整版）数值计算⽅法上机实习题答案1．设?+=105dx xx I nn ，（1）由递推公式nI I n n 151+-=-，从0I 的⼏个近似值出发，计算20I ；解：易得：0I =ln6-ln5=0.1823, 程序为：I=0.182; for n=1:20I=(-5)*I+1/n; end I输出结果为：20I = -3.0666e+010 （2）粗糙估计20I ，⽤nI I n n 515111+-=--，计算0I ；因为 0095.056 0079.01020201020≈<<≈??dx x I dx x 所以取0087.0)0095.00079.0(2120=+=I 程序为：I=0.0087; for n=1:20I=(-1/5)*I+1/(5*n); end I0I = 0.0083（3）分析结果的可靠性及产⽣此现象的原因(重点分析原因)。

⾸先分析两种递推式的误差；设第⼀递推式中开始时的误差为000I I E '-=，递推过程的舍⼊误差不计。

并记nn n I I E '-=，则有01)5(5E E E n n n -==-=-Λ。

因为=20E 20020)5(I E >>-，所此递推式不可靠。

⽽在第⼆种递推式中n n E E E )51(5110-==-=Λ，误差在缩⼩，所以此递推式是可靠的。

出现以上运⾏结果的主要原因是在构造递推式过程中，考虑误差是否得到控制，即算法是否数值稳定。

2．求⽅程0210=-+x e x的近似根，要求41105-+?<-k k x x ，并⽐较计算量。

（1）在[0，1]上⽤⼆分法；程序：a=0;b=1.0;while abs(b-a)>5*1e-4 c=(b+a)/2;if exp(c)+10*c-2>0 b=c; else a=c; end end c结果：c =0.0903（2）取初值00=x ，并⽤迭代1021x k e x -=+；程序：x=0; a=1;while abs(x-a)>5*1e-4 a=x;x=(2-exp(x))/10; end x结果：x =0.0905（3）加速迭代的结果；程序：x=0; a=0;b=1;while abs(b-a)>5*1e-4 a=x;y=exp(x)+10*x-2; z=exp(y)+10*y-2;x=x-(y-x)^2/(z-2*y+x); b=x; end x结果：x =0.0995（4）取初值00=x ，并⽤⽜顿迭代法；程序：x=0; a=0;b=1;while abs(b-a)>5*1e-4 a=x;x=x-(exp(x)+10*x-2)/(exp(x)+10); b=x; end x结果： x =0.0905（5）分析绝对误差。

2.用下列方法求方程e^x+10x-2=0的近似根，要求误差不超过5*10的负4次方，并比较计算量（1）二分法（局部，大图不太看得清，故后面两小题都用局部截图）（2）迭代法（3）牛顿法顺序消元法#include<stdio.h>#include<stdlib.h>#include<math.h>int main(){ int N=4,i,j,p,q,k; double m;double a[4][5]; double x1,x2,x3,x4; for (i=0;i<N ;i++ )for (j=0;j<N+1; j++ )scanf("%lf",&a[i][j]);for(p=0;p<N-1;p++) {for(k=p+1;k<N;k++){m=a[k][p]/a[p][p];for(q=p;q<N+1;q++)a[k][q]=a[k][q]-m*a[p][q];}}x4=a[3][4]/a[3][3];x3=(a[2][4]-x4*a[2][3])/a[2][2];x2=(a[1][4]-x4*a[1][3]-x3*a[1][2])/a[1][1];x1=(a[0][4]-x4*a[0][3]-x3*a[0][2]-x2*a[0][1])/a[0][0];printf("%f,%f,%f,%f",x1,x2,x3,x4);scanf("%lf",&a[i][j]); （这一步只是为了看到运行的结果）}运行结果列主元消元法function[x,det,flag]=Gauss(A,b)[n,m]=size(A);nb=length(b);flag='OK';det=1;x=zeros(n,1);for k=1:n-1 max1=0;for i=k:nif abs(A(i,k))>max1max1=abs(A(i,k));r=i;endendif max1<1e-10flag='failure';return;endif r>kfor j=k:nz=A(k,j);A(k,j)=A(r,j);A(r,j)=z;endz=b(k);b(k)=b(r);b(r)=z;det=-det; endfor i=k+1:nm=A(i,k)/A(k,k);for j=k+1:nA(i,j)=A(i,j)-m*A(k,j);endb(i)=b(i)-m*b(k);enddet=det*A(k,k);enddet=det*A(n,n)if abs(A(n,n))<1e-10flag='failure';return;endx(n)=b(n)/A(n,n);for k=n-1:-1：1for j=k+1:nb(k)=b(k)-A(k,j)*x(j);endx(k)=b(k)/A(k,k);end运行结果：雅可比迭代法function y=jacobi(a,b,x0) D=diag(diag(a));U=-triu(a,1);L=-tril(a,-1);B=D\(L+U);f=D\b;y=B*x0+f;n=1;while norm(y-x0)>1e-4 x0=y;y=B*x0+f;n=n+1;endyn高斯赛德尔迭代法function y=seidel(a,b,x0) D=diag(diag(a));U=-triu(a,1);L=-tril(a,-1);G=(D-L)\U;f=(D-L)\b;y=G*x0+f;n=1;while norm(y-x0)>10^(-4) x0=y;y=G*x0+f;n=n+1;endynSOR迭代法function y=sor(a,b,w,x0)D=diag(diag(a));U=-triu(a,1);L=-tril(a,-1);lw=(D-w*L)\((1-w)*D+w*U); f=(D-w*L)\b*w;y=lw*x0+f;n=1;while norm(y-x0)>10^(-4) x0=y;y=lw*x0+f;n=n+1;endyn1.分段线性插值：function y=fdxx(x0,y0,x)p=length(y0);n=length(x0);m=length(x);for i=1:mz=x(i);for j=1:n-1if z<x0(j+1)break;endendy(i)= y0(j)*(z-x0(j+1))/(x0(j)-x0(j+1))+y0(j+1)*(z-x0(j))/(x0(j+1)-x0(j));fprintf('y(%d)=%f\nx1=%.3fy1=%.3f\nx2=%.3fy2=%.3f\n\n',i,y(i),x0(j),y0(j),x0(j+1),y0(j+1));endend结果0.39404 0.38007 0.356932.分段二次插值：function y=fdec(x0,y0,x)p=length(y0);n=length(x0);m=length(x);for i=1:mz=x(i);for j=1:n-1if z<x0(j+1)break;endendif j<2j=j+1;elseif (j<n-1)if (abs(x0(j)-z)>abs(x0(j+1)-z))j=j+1;elseif ((abs(x0(j)-z)==abs(x0(j+1)-z))&&(abs(x0(j-1)-z)>abs(x0(j+2)-z)))j=j+1;endendans=0.0;for t=j-1:j+1a=1.0;for k=j-1:j+1if t~=ka=a*(z-x0(k))/(x0(t)-x0(k));endendans=ans+a*y0(t);endy(i)=ans;fprintf('y(%d)=%f\n x1=%.3f y1=%.3f\n x2=%.3f y2=%.3f\n x3=%.3f y3=%.3f\n\n',i,y(i),x0(j-1),y0(j-1),x0(j),y0(j),x0(j+1),y0(j+1));endend结果为0.39447 0.38022 0.357253.拉格朗日全区间插值function y=lglr(x0,y0,x)p=length(y0);n=length(x0);m=length(x);for t=1:mans=0.0;z=x(t);for k=1:np=1.0;for q=1:nif q~=kp=p*(z-x0(q))/(x0(k)-x0(q));endendans=ans+p*y0(k);endy(t)=ans;fprintf('y(%d)=%f\n',t,y(t));endend结果为0.39447 0.38022 0.35722function [p,S,mu] = polyfit(x,y,n)if ~isequal(size(x),size(y))errorendx = x(:);y = y(:);if nargout > 2mu = [mean(x); std(x)];x = (x - mu(1))/mu(2);endV(:,n+1) = ones(length(x),1,class(x));for j = n:-1:1V(:,j) = x.*V(:,j+1);end[Q,R] = qr(V,0);ws = warning;p = R\(Q'*y); warning(ws);if size(R,2) > size(R,1)warning;elseif warnIfLargeConditionNumber(R)if nargout > 2warning;elsewarning;endendif nargout > 1r = y - V*p;S.R = R;S.df = max(0,length(y) - (n+1));S.normr = norm(r);endp = p.';function flag = warnIfLargeConditionNumber(R) if isa(R, 'double')flag = (condest(R) > 1e+10);elseflag = (condest(R) > 1e+05);endx=[1,3,4,5,6,7,8,9,10];y=[10,5,4,2,1,1,2,3,4];p=polyfit(x,y,2);y=poly2sym(p);a=-p(1)/p(2)*0.5;xa=-p(2)/(2*p(1));min=(4*p(1)*p(3)-p(2)^2)/(4*p(1)); yxamin运行截图运行结果function [I] = CombineTraprl(f,a,b,eps)if(nargin ==3)eps=1.0e-4;endn=1;h=(b-a)/2;I1=0;I2=(subs(sym(f),findsym(sym(f)),a)+subs(sym(f),findsym(sym(f)),b))/h; while abs(I2-I1)>epsn=n+1;h=(b-a)/n;I1=I2;I2=0;for i=0:n-1x=a+h*i;x1=x+h;I2=I2+(h/2)*(subs(sym(f),findsym(sym(f)),x)+subs(sym( f),findsym(sym(f)),x1));endendI=I2;程序：>> [q]=CombineTraprl('(1-exp(-x))^0.5/x'10^-12,1)结果：q =1.8521欧拉方法function [x,y]=euler(fun,x0,xfinal,y0,n);if nargin<5,n=50;endh=(xfinal-x0)/n;x(1)=x0;y(1)=y0;for i=1:nx(i+1)=x(i)+h;y(i+1)=y(i)+h*feval(fun,x(i),y(i));end程序：[x,y]=euler('doty',0,1,1,10)结果：改进欧拉方法function [x,y]=eulerpro(fun,x0,xfinal,y0,n); if nargin<5,n=50;endh=(xfinal-x0)/n;x(1)=x0;y(1)=y0;x(i+1)=x(i)+h;y1=y(i)+h*feval(fun,x(i),y(i));y2=y(i)+h*feval(fun,x(i+1),y1);y(i+1)=(y1+y2)/2;end程序：>> [x,y]=eulerpro('doty',0,1,1,10)结果：经典RK法function [x,y]=RungKutta4(dyfun,xspan,y0,h) x=xspan(1):h:xspan(2);y(1)=y0;for n=1:length(x)-1k1=feval(dyfun,x(n),y(n));k2=feval(dyfun,x(n)+h/2,y(n)+h/2*k1);k3=feval(dyfun,x(n)+h/2,y(n)+h/2*k2);k4=feval(dyfun,x(n+1),y(n)+h*k3);y(n+1)=y(n)+h*(k1+2*k2+2*k3+k4)/6; end程序：dyfun=inline('(2*x*y^-2)/3');[x,y]=RungKutta4(dyfun,[0,1],1,0.1)标准函数x(1)=0;h=0.1;for i=1:10y(i)=(1+x(i)^2)^(1/3); endxY结果：。

计算方法上机作业——龙格库塔法龙格库塔法（Runge-Kutta method）是一种常用于求解常微分方程（Ordinary Differential Equation，ODE）的数值解法。

它是由德国数学家卡尔·龙格（Carl Runge）和马丁·威尔海姆·库塔（Martin Wilhelm Kutta）在20世纪初提出的。

龙格库塔法的基本思想是通过数值逼近来计算微分方程的近似解。

在讲解龙格库塔法之前，我们先来简单回顾一下ODE的一阶常微分方程的基本形式：y′(y)=y(y,y)其中，y(y,y)是已知函数。

龙格库塔法的核心是使用差分逼近计算函数的斜率。

假设我们要求解的方程为：y′(y)=y(y,y),y(y)=y₀所需计算的点为y₀,y₁,...,yy，对应的函数值为y₀,y₁,...,yy，其中y是步长的个数。

龙格库塔法通过递推关系式来计算估计值，并不断更新当前点的函数值。

接下来以龙格库塔法的经典四阶形式为例进行说明。

该方法的基本方程如下：yy+1=yy+(y₁+2y₂+2y₃+y₄)/6y₁=ℎy(yy,yy)y₂=ℎy(yy+ℎ/2,yy+y₁/2)y₃=ℎy(yy+ℎ/2,yy+y₂/2)y₄=ℎy(yy+ℎ,yy+y₃)其中y表示当前步骤，ℎ表示步长，yy表示当前点的函数值，y₁,y₂,y₃和y₄则表示对应的斜率。

使用龙格库塔法，我们可以通过不断递归计算来求得指定区间（例如[y,y]）上的函数值。

具体步骤如下：1.确定求解区间[y,y]和初始点(y₀,y₀)以及步长ℎ。

2.初始化：设置yy=y₀，yy=y₀。

3.对所有y=0,...,y−1：计算y₁,y₂,y₃和y₄，根据上述递推关系式。

根据递推关系式计算yy+1更新当前点的函数值，即yy+1=y(yy+1)。

更新当前点的y值，即yy+1=yy+ℎ。

4.返回结果：最终求得的函数值。

需要注意的是，选择适当的步长对最终结果的精度和计算效率都有重要影响。

数值计算方法上机实验报告
一、实验目的
本次实验的主要目的是熟悉和掌握数值计算方法，学习梯度下降法的
原理和实际应用，熟悉Python语言的编程基础知识，掌握Python语言的
基本语法。

二、设计思路
本次实验主要使用的python语言，利用python下的numpy，matplotlib这两个工具，来实现数值计算和可视化的任务。

1. 首先了解numpy的基本使用方法，学习numpy的矩阵操作，以及numpy提供的常见算法，如矩阵分解、特征值分解等。

2. 在了解numpy的基本操作后，可以学习matplotlib库中的可视化
技术，掌握如何将生成的数据以图表的形式展示出来。

3. 接下来就是要学习梯度下降法，首先了解梯度下降法的主要原理，以及具体的实际应用，用python实现梯度下降法给出的算法框架，最终
可以达到所期望的优化结果。

三、实验步骤
1. 熟悉Python语言的基本语法。

首先是熟悉Python语言的基本语法，学习如何使用Python实现变量
定义，控制语句，函数定义，类使用，以及面向对象编程的基本概念。

2. 学习numpy库的使用方法。

其次是学习numpy库的使用方法，学习如何使用numpy库构建矩阵，学习numpy库的向量，矩阵操作，以及numpy库提供的常见算法，如矩阵分解，特征值分解等。

3. 学习matplotlib库的使用方法。

东南大学计算方法与实习实验报告学院：电子科学与工程学院学号：06A*****姓名：***指导老师：***实习题14、设S N=Σ(1)编制按从大到小的顺序计算S N的程序；(2)编制按从小到大的顺序计算S N的程序；(3)按两种顺序分别计算S1000，S10000，S30000，并指出有效位数。

解析：从大到小时，将S N分解成S N-1=S N-,在计算时根据想要得到的值取合适的最大的值作为首项；同理从小到大时，将S N=S N-1+ ，则取S2=1/3。

则所得式子即为该算法的通项公式。

(1)从大到小算法的C++程序如下：/*从大到小的算法*/#include<iostream>#include<iomanip>#include<cmath>using namespace std;const int max=34000; //根据第(3)问的问题，我选择了最大数为34000作为初值void main(){int num;char jus;double cor,sub;A: cout<<"请输入你想计算的值"<<'\t';cin>>num;double smax=1.0/2.0*(3.0/2.0-1.0/max-1.0/(max+1)),temps;double S[max];// cout<<"s["<<max<<"]="<<setprecision(20)<<smax<<'\n';for(int n=max;n>num;){temps=smax;S[n]=temps;n--;smax=smax-1.0/((n+1)*(n+1)-1.0);}cor=1.0/2.0*(3.0/2.0-1.0/num-1.0/(num+1.0)); //利用已知精确值公式计算精确值sub=fabs(cor-smax); //double型取误差的绝对值cout<<"用递推公式算出来的s["<<n<<"]="<<setprecision(20)<<smax<<'\n';cout<<"实际精确值为"<<setprecision(20)<<cor<<'\n';cout<<"则误差为"<<setprecision(20)<<sub<<'\n';cout<<"是否继续计算S[N],是请输入Y，否则输入N！"<<endl;cin>>jus;if ((int)jus==89||(int)jus==121) goto A;}(2)从小到大算法的C++程序如下：/*从小到大的算法*/#include<iostream>#include<iomanip>#include<cmath>using namespace std;void main(){int max;A: cout<<"请输入你想计算的数，注意不要小于2"<<'\t';cin>>max;double s2=1.0/3.0,temps,cor,sub;char jus;double S[100000];for(int j=2;j<max;){temps=s2;S[j]=temps;j++;s2+=1.0/(j*j-1.0);}cor=1.0/2.0*(3.0/2.0-1.0/j-1.0/(j+1.0)); //利用已知精确值公式计算精确值sub=fabs(cor-s2); //double型取误差的绝对值cout<<"用递推公式算出来的s["<<j<<"]="<<setprecision(20)<<s2<<'\n';cout<<"实际精确值为"<<setprecision(20)<<cor<<'\n';cout<<"则误差为"<<setprecision(20)<<sub<<'\n';cout<<"是否继续计算S[N],是请输入Y，否则输入N！"<<endl;cin>>jus;if ((int)jus==89||(int)jus==121) goto A;}(3)(注：因为程序中setprecision(20)表示输出数值小数位数20，则程序运行时所得到的有效数字在17位左右)ii.选择从小到大的顺序计算S1000、S10000、S30000的值需要计算的项S1000S10000S30000计算值0.74900049950049996 0.74966672220370571 0.74996666722220728实际精确值0.74900049950049952 0.74990000499950005 0.74996666722220373误差 4.4408920985006262*10-16 5.6621374255882984*10-15 3.5527136788005009*10-15有效数字17 17 17附上部分程序运行图：iii.实验分析通过C++程序进行计算验证采用从大到小或者从小到大的递推公式算法得到的数值基本稳定且误差不大。

计算方法上机报告姓名：学号：班级：上课班级：说明：本次上机实验使用的编程语言是Matlab 语言，编译环境为MATLAB 7.11.0，运行平台为Windows 7。

1. 对以下和式计算：∑∞⎪⎭⎫ ⎝⎛+-+-+-+=0681581482184161n n n n S n，要求：①若只需保留11个有效数字，该如何进行计算； ②若要保留30个有效数字，则又将如何进行计算； （1） 算法思想1、根据精度要求估计所加的项数，可以使用后验误差估计，通项为：142111416818485861681n n na n n n n n ε⎛⎫=---<< ⎪+++++⎝⎭；2、为了保证计算结果的准确性，写程序时，从后向前计算；3、使用Matlab 时，可以使用以下函数控制位数： digits(位数)或vpa(变量，精度为数)（2）算法结构1.;0=s⎪⎭⎫⎝⎛+-+-+-+=681581482184161n n n n t n ；2.for 0,1,2,,n i =⋅⋅⋅if 10mt -≤end;3.for ,1,2,,0n i i i =--⋅⋅⋅;s s t =+（3）Matlab 源程序clear; %清除工作空间变量 clc; %清除命令窗口命令m=input('请输入有效数字的位数m='); %输入有效数字的位数s=0;for n=0:50t=(1/16^n)*(4/(8*n+1)-2/(8*n+4)-1/(8*n+5)-1/(8*n+6));if t<=10^(-m) %判断通项与精度的关系break;endend;fprintf('需要将n值加到n=%d\n',n-1); %需要将n值加到的数值for i=n-1:-1:0t=(1/16^i)*(4/(8*i+1)-2/(8*i+4)-1/(8*i+5)-1/(8*i+6));s=s+t; %求和运算ends=vpa(s,m) %控制s的精度（4）结果与分析当保留11位有效数字时，需要将n值加到n=7，s =3.1415926536；当保留30位有效数字时，需要将n值加到n=22,s =3.14159265358979323846264338328。

#include "stdlib.h"#include "math.h"#include "stdio.h"#define N 4intagaus(double a[N][N],double b[N],int n);//高斯全主元法求deltaX，具体见程序中注释void GetFun(double x[N],double b[N]);//F(X),结果放在b里void GetJacobi(double x[N],double J[N][N]);//计算F'(X)，结果放在J里double GetDeltaX(double J[N][N],double b[N],double deltaX[N]);//求deltaX主程序，调用agaus voidUpdateX(double x[N],double deltaX[N]);//xk+1=xk+deltaXvoid SolveNonlinear(double x[N],double eps,int k);//非线性方程组主程序,迭代终止条件是最大迭代次数或者绝对值范数（街区距离）main(){inti,k;doubleeps;double x[4]={1,1.0,1.0,1.0};double b[N];eps=0.0000001; k=100;SolveNonlinear(x,eps,k);GetFun(x,b);printf("\n");printf("\n");for (i=0; i<N; i++)printf("x(%d)=%13.7e,F(x)=%13.7e\n",i,x[i],b[i]);printf("\n");getchar();return 0;}voidSolveNonlinear(double x0[N],double eps,int k){intnIter=0;double b[N],J[N][N],deltaX[N],NormDeltaX;while(1){nIter++;GetFun(x0,b);GetJacobi(x0,J);NormDeltaX=GetDeltaX(J,b,deltaX);UpdateX(x0,deltaX);if ((nIter>k)||(NormDeltaX<eps))break;}}void GetFun(x,y)//F(X),结果放在b里double x[],y[];{y[0]=x[0]*x[0]+x[1]*x[1]+x[2]*x[2]+x[3]*x[3]-1.0;y[1]=2.0*x[0]*x[0]+x[1]*x[1]-4.0*x[2]+2*x[3]*x[3];y[2]=3.0*x[0]*x[0]-4.0*x[1]+x[2]*x[2]+3*x[3]*x[3];y[3]=4.0*x[0]+x[1]*x[1]+2*x[2]*x[2]+5*x[3]*x[3]-3.0;return;}void GetJacobi(x,J)//计算F'(X)，结果放在J里double x[N],J[N][N];{J[0][0]=2*x[0];J[0][1]=2*x[1];J[0][2]=2*x[2];J[0][3]=2*x[3];J[1][0]=4*x[0];J[1][1]=2*x[1];J[1][2]=-4;J[1][3]=4*x[3];J[2][0]=6*x[0];J[2][1]=-4;J[2][2]=2*x[2];J[2][3]=6*x[3];J[3][0]=4;J[3][1]=2*x[1];J[3][2]=4*x[2];J[3][3]=10*x[3];return;}intagaus(a,b,n)//高斯全主元法解方程，结果放在b里int n;double a[N][N],b[N];{int *js,l,k,j,i,is;double d,t;js=malloc(n*sizeof(int));//记载列交换标号l=1;for (k=0;k<=n-2;k++){d=0.0;for (i=k;i<=n-1;i++)//求全主元{for (j=k;j<=n-1;j++){t=fabs(a[i][j]);if (t>d){d=t;js[k]=j;//记住列is=i;//记住行}}}if (d+1.0==1.0)l=0;else{/* if (js[k]!=k)//列交换{for (i=0;i<=n-1;i++){t=a[i][k]; a[i][k]=a[i][js[k]]; a[i][js[k]]=t;}}*/if (is!=k){for (j=k;j<=n-1;j++)//行交换{t=a[k][j]; a[k][j]=a[is][j]; a[is][j]=t;}t=b[k]; b[k]=b[is]; b[is]=t;//b交换}}if (l==0)//最大主元为零不能计算出正确结果{free(js);printf("fail\n");return(0);}//以下为消元过程d=a[k][k];a[k][k]=1;//这一步是否要无关紧要，只要在回代时不除以该项即可。

数值计算方法上机实验报告实验目的：复习和巩固数值计算方法的基本数学模型，全面掌握运用计算机进行数值计算的具体过程及相关问题。

利用计算机语言独立编写、调试数值计算方法程序，培养学生利用计算机和所学理论知识分析解决实际问题的能力。

上机练习任务：利用计算机基本C 语言编写并调试一系列数值方法计算通用程序，并能正确计算给定题目，掌握调试技能。

掌握文件使用编程技能，如文件的各类操作，数据格式设计、通用程序运行过程中文件输入输出运行方式设计等。

一、各算法的算法原理及计算机程序框图1. 列主元高斯消去法算法原理：高斯消去法是利用现行方程组初等变换中的一种变换，即用一个不为零的数乘一个方程后加只另一个方程，使方程组变成同解的上三角方程组，然后再自下而上对上三角方程组求解。

列选住院是当高斯消元到第k 步时，从k 列的kk a 以下（包括kk a ）的各元素中选出绝对值最大的，然后通过行交换将其交换到kk a 的位置上。

交换系数矩阵中的两行（包括常数项），只相当于两个方程的位置交换了，因此，列选主元不影响求解的结果。

●源程序：#define N 200#include "stdio.h"#include "math.h"FILE *fp1,*fp2;void LZ(){int n,i,j,k=0,l;double d,t,t1;static double x[N],a[N][N];fp1=fopen("a1.txt","r");fp2=fopen("b1.txt","w");fscanf(fp1,"%d",&n);for(i=0;i<n;++i)for(j=0;j<=n;++j){fscanf(fp1,"%lf",&a[i][j]);}{d=a[k][k];l=k;i=k+1;do{if(fabs(a[i][k])>fabs(d)) /*选主元*/{d=a[i][k];l=i;}i++;}while(i<n);if(d==0){printf("\n输入矩阵有误！\n");}else{ /*换行*/if(l!=k){for(j=k;j<=n;j++){t=a[l][j];a[l][j]=a[k][j];a[k][j]=t;}}}for(j=k+1;j<=n;j++) /*正消*/ a[k][j]/=a[k][k];for(i=k+1;i<n;i++)for(j=k+1;j<=n;j++)a[i][j]-=a[i][k]*a[k][j];k++;}while(k<n);if(k!=0){for(i=n-1;i>=0;i--) /*回代*/ {t1=0;for(j=i+1;j<n;j++)t1+=a[i][j]*x[j];x[i]=a[i][n]-t1;}for(i=0;i<n;i++)fprintf(fp2,"\n 方程组的根为x[%d]=%lf",i+1,x[i]); fclose(fp1); fclose(fp2); }main() { LZ(); }● 具体算例及求解结果：用列选主元法求解下列线性方程组⎪⎩⎪⎨⎧=++=++=-+28x x 23x 2232832321321321x x x x x x 输入3 输出结果：方程组的根为x[1]=6.0000001 2 -3 8 方程组的根为x[2]=4.000000 2 1 3 22 方程组的根为x[3]=2.000000 3 2 1 28● 输入变量、输出变量说明：输入变量：ij a 系数矩阵元素，i b 常向量元素 输出变量：12,,n b b b 解向量元素2. 杜里特尔分解法解线性方程● 算法原理：求解线性方程组Ax b =时，当对A 进行杜里特尔分解，则等价于求解LUx b =，这时可归结为利用递推计算相继求解两个三角形（系数矩阵为三角矩阵）方程组，用顺代，由Ly b =求出y ，再利用回带，由Ux y =求出x 。

计算方法上机作业作为一位学生，我经常需要完成各种数学计算。

无论是简单的加减乘除还是复杂的代数方程和数列求和，计算是我非常重要的一项能力。

然而，为了提高我的计算能力，我仍然需要不断的练习和实践。

下面是我在计算方法上机作业中遇到的一些题目，并附上了详细的解答过程。

1.求解方程组：{2x-3y=5{3x+4y=7解答：首先，我们可以通过消元法或代入法求解这个方程组。

这里我们选择代入法。

由第一个方程得：2x=3y+5将上式代入第二个方程中得：3(3y+5)+4y=7化简得：9y+15+4y=7继续化简：13y=-8得到：y=-8/13将y的值代入第一个方程得：2x-3(-8/13)=5化简得：2x=5+24/13继续化简：2x=65/13-24/13得到：2x=41/13最后，得到：x=(41/13)/2=41/26所以，方程组的解为：x=41/26，y=-8/132.求解不等式：2x+3>5x-1解答：首先，我们将不等式移项得：2>5x-2x-1继续化简：2>3x-1再次移项：3>3x继续化简：1>x所以，不等式的解集为：x<13.求函数f(x)=2x^2+3x-1的极值点。

解答：首先，我们利用求导的方法求解极值点。

对函数f(x)求导得：f'(x)=4x+3然后，令f'(x)=0化简得：4x=-3最后，得到：x=-3/4将极值点x=-3/4代入原函数得：f(-3/4)=2(-3/4)^2+3(-3/4)-1化简得：f(-3/4)=9/8-9/4-1最后，得到：f(-3/4)=-11/8所以，函数f(x)=2x^2+3x-1的极值点为x=-3/4，对应的函数值为f(-3/4)=-11/8通过这些题目的解答，我不仅巩固了计算方法的知识，也提高了我的计算能力和解题技巧。

我会继续努力学习和练习，以便更好地掌握计算方法。

1．设I n 1 x ndx ，0 5 x（ 1）由递推公式 I n 5I n 11，从 I 0的几个近似值出发，计算I 20；n解：易得： I 0 ln6-ln5=0.1823, 程序为：I=0.182;for n=1:20I=(-5)*I+1/n;endI输出结果为： I 20= -3.0666e+010（ 2）粗糙估计 I 20，用 I n 1 1I n 1 1 ，计算 I 0；5 5n0.0079 1 x 20 1 x 200.0095因为dx I 20dx 6 5所以取 I 20 1(0.0079 0.0095) 0.0087 2程序为： I=0.0087;for n=1:20I=(-1/5)*I+1/(5*n);endII 0= 0.0083（ 3）分析结果的可靠性及产生此现象的原因(重点分析原因 )。

首先分析两种递推式的误差；设第一递推式中开始时的误差为E0 I 0 I 0，递推过程的舍入误差不计。

并记 E n I n I n，则有 E n 5E n 1 ( 5) n E0。

因为 E20( 5) 20 E0 I 20，所此递推式不可靠。

而在第二种递推式中E0 1E1 (1)n E n，误差在缩小，5 5所以此递推式是可靠的。

出现以上运行结果的主要原因是在构造递推式过程中，考虑误差是否得到控制，即算法是否数值稳定。

2．求方程e x10x 2 0 的近似根，要求x k 1x k 5 10 4，并比较计算量。

（1）在 [0， 1]上用二分法；程序： a=0;b=1.0;while abs(b-a)>5*1e-4c=(b+a)/2;if exp(c)+10*c-2>0b=c;else a=c;endendc结果： c =0.0903（ 2）取初值x0 0，并用迭代 x k 1 2 e x ；10程序： x=0;a=1;while abs(x-a)>5*1e-4a=x;x=(2-exp(x))/10;endx结果： x =0.0905（3）加速迭代的结果；程序： x=0;a=0;b=1;while abs(b-a)>5*1e-4a=x;y=exp(x)+10*x-2;z=exp(y)+10*y-2;x=x-(y-x)^2/(z-2*y+x);b=x;endx结果： x =0.0995（ 4）取初值x00 ，并用牛顿迭代法；程序： x=0;a=0;b=1;while abs(b-a)>5*1e-4a=x;x=x-(exp(x)+10*x-2)/(exp(x)+10); b=x;end x 结果： x =0.0905（ 5） 分析绝对误差。

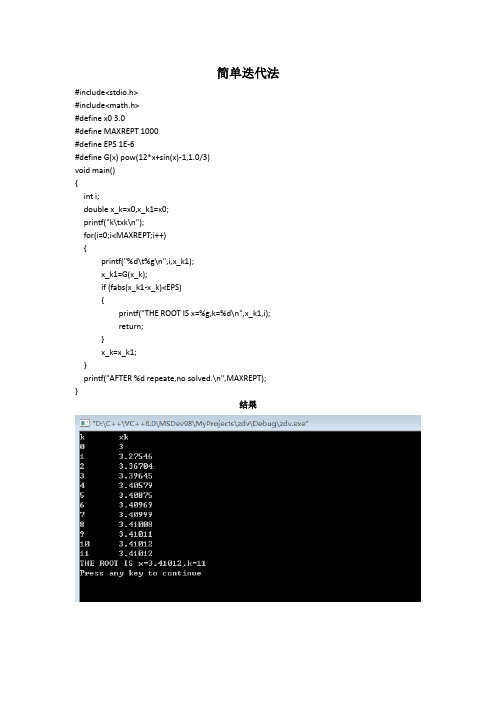
简单迭代法#include<stdio.h>#include<math.h>#define x0 3.0#define MAXREPT 1000#define EPS 1E-6#define G(x) pow(12*x+sin(x)-1,1.0/3)void main(){int i;double x_k=x0,x_k1=x0;printf("k\txk\n");for(i=0;i<MAXREPT;i++){printf("%d\t%g\n",i,x_k1);x_k1=G(x_k);if (fabs(x_k1-x_k)<EPS){printf("THE ROOT IS x=%g,k=%d\n",x_k1,i);return;}x_k=x_k1;}printf("AFTER %d repeate,no solved.\n",MAXREPT);}结果牛顿迭代法一#include<stdio.h>#include<math.h>#define x0 3.0#define MAXREPT 1000#define EPS 1E-6#define G(x) x-(pow(x,3)-sin(x)-12*x+1)/(3*pow(x,2)-cos(x)-12) void main(){int i;double x_k=x0,x_k1=x0;printf("k\txk\n");for(i=0;i<MAXREPT;i++){printf("%d\t%g\n",i,x_k1);x_k1=G(x_k);if (fabs(x_k1-x_k)<EPS){printf("THE ROOT IS x=%g,k=%d\n",x_k1,i);return;}x_k=x_k1;}printf("AFTER %d repeate,no solved.\n",MAXREPT);}结果埃特金加速法#include<stdio.h>#include<math.h>#define x0 3.0#define MAXREPT 1000#define EPS 1E-6#define G(x) (pow(x,3)-sin(x)+1)/12void main(){int i;double x1=x0,x2=x0;double z,y;printf("k\tx1\tx2\txk\n");for(i=0;i<MAXREPT;i++){if(i==0)printf("%d\t\t\t%g\n",i,x2);elseprintf("%d\t%g\t%g\t%g\n",i,y,z,x2);y=G(x1);z=G(y);x2=z-((z-y)*(z-y))/(z-2*y+x1);if (fabs(x2-x1)<EPS){printf("THE ROOT IS x=%g,k=%d\n",x2,i);return;}x1=x2;}printf("AFTER %d repeate,no solved.\n",MAXREPT);} 结果牛顿迭代法二#include<stdio.h>#include<math.h>#define x0 1.5#define MAXREPT 1000#define EPS 1E-6#define G(x) x-(pow(x,3)+pow(x,2)-3*x-3)/(3*pow(x,2)+2*x-3) void main(){int i;double x_k=x0,x_k1=x0;printf("k\txk\n");for(i=0;i<MAXREPT;i++){printf("%d\t%g\n",i,x_k1);x_k1=G(x_k);if (fabs(x_k1-x_k)<EPS){printf("THE ROOT IS x=%g,k=%d\n",x_k1,i);return;}x_k=x_k1;}printf("AFTER %d repeate,no solved.\n",MAXREPT);}结果弦截法#include<stdio.h>#include<math.h>#define x0 0#define x1 1.5#define MAXREPT 1000#define EPS 1E-6#define G(x) pow(x,3)+pow(x,2)-3*x-3void main(){int i;double x_k=x0,x_k1=x1,x_k2=0;double y,z;printf("k\txk\n");for(i=0;i<MAXREPT;i++){printf("%d\t%g\n",i,x_k2);y=G(x_k);z=G(x_k1);x_k2=x_k1-(z*(x_k1-x_k))/(z-y);if (fabs(x_k2-x_k1)<EPS){printf("THE ROOT IS x=%g,k=%d\n",x_k2,i);return;}x_k=x_k1;x_k1=x_k2;}printf("AFTER %d repeate,no solved.\n",MAXREPT); } 结果高斯顺序消元法#include<stdio.h>#include<math.h>#define N 4static double aa[N][N+1]={{2,4,0,1,1},{3,8,2,2,3},{1,3,3,0,6},{2,5,2,2,3}}; int gauss(double a[][N+2],double x[]);void putout(double a[][N+2]);void main(){int i,j,det;double a[N+1][N+2],x[N+1];for(i=1;i<=N;i++)for(j=1;j<=N+1;j++)a[i][j]=aa[i-1][j-1];det=gauss(a,x);if(det!=0)for(i=1;i<=N;i++)printf(" x[%d]=%g",i,x[i]);printf("\n");}int gauss(double a[][N+2],double x[]){int i,j,k;double c;putout(a);for(k=1;k<=N-1;k++){ if(fabs(a[k][k])<1e-17){printf("\n pivot element is 0.fail!\n");return 0;}for(i=k+1;i<=N;i++){c=a[i][k]/a[k][k];for(j=k;j<=N+1;j++){a[i][j]=a[i][j]-c*a[k][j];}}putout(a);}if(fabs(a[N][N])<1e-17){printf("\n pivot element is 0.fail!\n");return 0;}for(k=N;k>=1;k--){x[k]=a[k][N+1];for(j=k+1;j<=N;j++){x[k]=x[k]-a[k][j]*x[j];}x[k]=x[k]/a[k][k];}return(1);}void putout(double a[][N+2]){for(int i=1;i<=N;i++){for(int j=1;j<=N+1;j++)printf("%-15g",a[i][j]);printf("\n");}printf("\n");}结果雅克比迭代法#include<stdio.h>#include<math.h>#define N 5#define EPS 0.5e-4static double aa[N][N]={{4,-1,0,-1,0},{-1,4,-1,0,-1},{0,-1,4,-1,0},{-1,0,-1,4,-1},{0,-1,0,-1,4}}; static double bb[N]={2,1,2,1,2};void main(){int i,j,k,NO;double a[N+1][N+1],b[N+1],x[N+1],y[N+1];double d,sum,max;for(i=1;i<=N;i++){for(j=1;j<=N;j++)a[i][j]=aa[i-1][j-1];b[i]=bb[i-1];}printf("\n 请输入最大迭代次数（尽量取大值！）NO:");scanf("%d",&NO);printf("\n");for(i=1;i<=N;i++)x[i]=0;k=0;printf(" k",' ');for(i=1;i<=N;i++)printf("%8cx[%d]",' ',i);printf("\n 0");for(i=1;i<=N;i++)printf("%12.8g",x[i]);printf("\n");do{for(i=1;i<=N;i++){sum=0.0;for(j=1;j<=N;j++)if(j!=i) sum=sum+a[i][j]*x[j];y[i]=(-sum+b[i])/a[i][i];}max=0.0;for(i=0;i<=N;i++){d=fabs(y[i]-x[i]);if(max<d) max=d;x[i]=y[i];}printf("%6d",k+1);for(i=1;i<=N;i++)printf("%12.8g",x[i]);printf("\n");k++;}while((max>=EPS)&&(k<NO));printf("\nk=%d\n",k);if(k>=NO) printf("\nfail!\n");elsefor(i=1;i<=N;i++)printf("x[%d]=%g\t",i,x[i]);}结果拉格朗日插值多项式#include<stdio.h>#include<math.h>#define N 4doublex[N]={0.56160,0.56280,0.56401,0.56521},y[N]={0.82741,0.82659,0.82577,0.82495}; void main(){double x=0.5635;double L(double xx);double lagBasis(int k,double xx);void output();output();printf("\n近似值L(%g)=%g\n",x,L(x));}double lagBasis(int k,double xx){double lb=1;int i;for(i=0;i<N;i++)if(i!=k) lb*=(xx-x[i])/(x[k]-x[i]);return lb;}double L(double xx){double s=0;int i;for(i=0;i<=N;i++)s+=lagBasis(i,xx)*y[i];return s;}void output(){int i;printf("\n各节点信息:\nxi:");for(i=0;i<N;i++)printf("\t%g",x[i]);printf("\nyi:");for(i=0;i<N;i++)printf("\t%g",y[i]);}结果牛顿插值多项式#include <math.h>#include <stdio.h>int a;#define M 4double x[M+1]={0.4,0.55,0.65,0.8,0.9},y[M+1]={0.41075,0.57815,0.69675,0.88811,1.02652}; void main(){double x;printf("输入x=");scanf("%lf",&x);printf("次数：");scanf("%d",&a);double N(double xx,int a);void output();output();printf("\n%d次牛顿插值多项式N(%g)=%g\n",a,x,N(x,a));}double N(double xx,int a){double s=y[0],d=1;int i,j;double df[M+1][M+1];for(i=0;i<=M;i++)df[i][0]=y[i];for(j=1;j<=a;j++)for(i=j;i<=a;i++)df[i][j]=(df[i][j-1]-df[i-1][j-1])/(x[i]-x[i-j]);printf("\nx\tf(x)\t");for(j=1;j<=a;j++) printf("%5d阶",j);for(i=0;i<=a;i++){printf("\n%g\t%g",x[i],y[i]);for(j=1;j<=i;j++)printf("\t%7.5g",df[i][j]);}for(i=1;i<=a;i++){d*=(xx-x[i-1]);s+=df[i][i]*d;}return s;}void output(){int i;printf("\n各节点信息:\nxi:");for(i=0;i<=M;i++)printf("\t%7g",x[i]);printf("\nyi:");for(i=0;i<=M;i++)printf("\t%7g",y[i]);}结果复合梯形公式#include<stdio.h>#include<math.h>#define f(x) 1/(x*x+1)#define Pi 3.1415926void main(){double a=0,b=1;double T,h,x;int n,i;printf("please input n:");scanf("%d",&n);h=(b-a)/n;x=a;T=0;for(i=1;i<n;i++){x+=h;T+=f(x);}T=(f(a)+2*T+f(b))*h/2;printf("T(%d)=%g\n",n,T);printf("The exact value is %g\n",Pi/4);}复合辛普森公式#include<stdio.h>#include<math.h>#define f(x) 1/(1+x*x)#define Pi 3.1415926void main(){double a=0,b=1;double S,h,x;int n,i;printf("please input Even n:");scanf("%d",&n);h=(b-a)/n;x=a; S=0;for(i=1;i<n;i++){x+=h;if(i%2==0) S+=2*f(x);else S+=4*f(x);}S=(f(a)+S+f(b))*h/3;printf("S(%d)=%g\n",n,S);printf("The exact value is %g\n",Pi/4);}龙贝格公式加速#include<stdio.h>#include<math.h>#define f(x) sin(x)/(1+x)#define M 3void main(){double a=0,b=1;double Long(double a,double b);printf("近似值I=%g\n",Long(a,b));}double Long(double a,double b){int n=1,i=1,j=1;double T[M+1][M+1],h,x,sum;h=b-a;T[0][0]=(f(a)+f(b))/2;for(j=1;j<=3;j++){x=a;h/=2;n*=2;sum=0;for(i=1;i<=n;i+=2){x=a+i*h;sum+=f(x);}T[j][0]=T[j-1][0]/2+h*sum;}for(i=1;i<=M;i++)for(j=1;j<=i;j++){T[i][j]=(pow(4,j)*T[i][j-1]-T[i-1][j-1])/(pow(4,j)-1);}printf("k\tT0\tT1\tT2\tT3\n");for(i=0;i<=M;i++){printf("%d",i);for(j=0;j<=i;j++)printf(" %g",T[i][j]);printf("\n");}return T[M][M];}。

应用计算方法学院：自动化学院班级：硕1104班姓名：陈兆辉计算方法2班教师：张晓丹目录上机作业1 (3)上机作业2 (6)上机作业3 (10)上机作业4 (12)上机作业5 (17)上机作业6 (18)上机作业7 (19)上机作业11.分别用不动带你迭代法与Newton 法求解方程2x- ex +3=0的正根和负根解：（1）用不动点迭代法求方程的正根1）迭代公式：()231ln k P k P ++=，初值p0=1.02）程序：k=1;Tol=0.00001;p0=1.0;N=100;while k<=Np=log(2*p0+3);if abs(p-p0)<Tolbreak;endk=k+1;p0=p;enddisp(p);disp(k)3)显示结果：P= 1.9239K=11（2） 用不动点迭代法求解方程的负根1）迭代公式： 1(3)/2k p k p e +=-，初值p0=-1.02）程序：k=1;Tol=0.00001;p0=-1.0;N=100;while k<=Np=(exp(p0)-3)/2;if abs(p-p0)<Tolbreak;endk=k+1;p0=p;enddisp(p);disp(k)3）显示结果：P= -1.3734k=7(3)用牛顿法求方程的正根1）迭代公式：()1232k k p k k k p p e p p e +-+=--，初值p0=1.02）程序：k=1;Tol=0.00001;p0=1.0;N=100;while k<=Np=p0-(2*p0-exp(p0)+3)/(2-exp(p0));if abs(p-p0)<Tolbreak;endk=k+1;p0=p;enddisp(p);disp(k)3）显示结果：P=1.9239K=8（4）用牛顿法求解方程的负根1）迭代公式：()1232k k p k k k p p e p p e +-+=--，初值p0=-1.02）程序：k=1;Tol=0.00001;p0=-1.0;N=100;while k<=Np=p0-(2*p0-exp(p0)+3)/(2-exp(p0));if abs(p-p0)<Tolbreak;endk=k+1;p0=p;enddisp(p);disp(k)3）显示结果：P= -1.3734K= 44）结果分析：不动点迭代法是求解非线性方程的主要方法，其中牛顿法应用最广泛，它求解方程的单根时具有二阶收敛性，但是它要求较好的初始近似值，牛顿法比普通的迭代法收敛速度快，能较少的迭代达到理想的值。

计算⽅法上机作业请注意! Pay attention!计算⽅法作业要求1.上机内容：只要求完成《计算⽅法》实验报告那⼀部分的内容。

2.试验报告要求：（1）要求写出解题的程序代码和结果，以及必要的⽂字说明。

（2）报告要求打印，封⾯上写清班级、学号和姓名。

（3）提交报告时间：2013年6⽉13号（16周周四）。

⽬录第⼀部分基本操作 (1)§1.Matlab的使⽤ (1)1-1.直接输⼊命令 (1)1-2.⽤M⽂件开发程序 (1)§2.M⽂件程序的主要语句和主要函数 (2)2-1.Matlab的数字特征 (2)2-2.主要语句 (3)2-3.常⽤函数 (4)2-4.⼏个常⽤的命令 (5)§3.矩阵的有关计算 (5)3-1.矩阵的输⼊ (5)3-2.矩阵/向量的运算 (6)3-3.矩阵的范数 (6)3-4.向量的范数 (7)3-5.矩阵的条件数 (7)3-6.矩阵的特征值和特征向量 (8)§4.Matlab绘图 (9)4-1.绘图的基本命令 (9)4-2.图形的交互编辑 (11)第⼆部分数值计算 (12)§1.⽅程求根 (12)1-1.⽜顿迭代法 (12)1-2.图解法确定迭代的初始点 (13)§2.线性⽅程组 (13)2-1.迭代法的收敛性 (13)2-2.线性⽅程组的病态问题 (14)2-3.求解线性⽅程组 (15)§3.插值和拟合 (16)/doc/b4c2d2dfc850ad02de8041fc.html grange插值 (16)3-2.代数多项式插值 (17)3-3.插值误差 (17)3-4.分段线性插值 (18)3-5.数据的曲线拟合 (18)§4.数值积分 (20)4-1.复合梯形求积公式 (20)4-2.复合Simpson求积公式 (20)§5.常微分⽅程的数值解法 (21)5-1.Euler⽅法 (21)5-2.改进的Euler⽅法 (23)5-3.四阶龙格-库塔⽅法 (24)习题 (27)⼀、⽅程求根 (27)⼆、线性⽅程组 (27)三、插值与拟合 (28)四、数值积分 (29)五、常微分⽅程 (30)《计算⽅法》实验报告 (31)⼀、⽅程求根 (31)⼆、线性⽅程组 (31)三、插值与拟合 (32)四、数值积分 (32)五、常微分⽅程 (33)第⼀部分基本操作§1.1.MatlabMatlab 的使⽤Matlab 的使⽤⽅法有两种：（1）在Matlab 的命令窗⼝（Matlab Command Windows ）中直接输⼊命令，即可得到结果；（2）在Matlab 的编辑窗⼝（Matlab Editor ）内编写M ⽂件，然后在命令窗⼝执⾏该⽂件，得到所需的结果。