叠前深度偏移培训汇报

第四章波动方程法叠前深度偏移前面我们讨论了基于射线追踪或有限差分走时计算的Kirchhoff积分法叠前深度偏移。

可以说，在过去的十几年间，Kirchhoff积分法叠前深度偏移在地下地质构造的地震成像中发挥了巨大作用，并且在将来还会继续发挥作用。

这主要取决于Kirchhoff积分法的高效率、易于实现、适应性强和能满足大多数条件下地质构造地震成像要求的特点和优势。

近年来，对Kirchhoff保幅型叠前深度偏移的大量研究和部分应用也充分说明了Kirchhoff积分法在叠前深度域构造成像和岩性成像中的巨大潜力。

但是，该类方法本身存在明显的缺陷。

例如射线追踪前需要对速度场进行平滑，在速度分布过于复杂的区域，会出现焦散或阴影区，这时计算出来的旅行时场也就不准确。

后来，为提高旅行时场的精度，发展起来的有限差分法直接求解程函方程的Kirchhoff积分偏移方法，一般也仅能计算初至旅行时，无法处理在复杂速度场中存在的多值走时现象，从而影响了Kirchhoff积分偏移在复杂地质体（如盐丘、推覆体和逆掩断层等）的成像效果。

从近十年Kirchhoff积分偏移的实际应用可以证明这一点。

如果应用完全射线理论的Green函数，在计算时求解所有的到达时和相应的振幅值，可以改善该方法的成像质量，但其计算效率又会大打折扣。

由于Kirchhoff积分偏移采用了高频近似地震射线理论,导致了波场动力学信息受到严重畸变,这显然不能满足岩性油藏勘探中需要进行深度域保持振幅偏移的要求。

由于波动方程偏移方法基本不存在Kirchhoff积分偏移的这些困难，因此，近年来人们对波动方程法叠前深度偏移进行了大量的研究并做了部分应用。

向量并行巨型机和高性能多节点微机集群的出现以及它们在地震数据处理中的应用为波动方程法叠前深度偏移提供了硬件条件和高的计算效率。

从目前的研究成果、应用效果以及可行性和实用性上看，波动方程法叠前深度偏移有很好的发展前景。

§4.1 概述波动方程叠前深度偏移成像解决的是强横向变速条件下复杂地质体的地震波成像问题。

叠前时间偏移与叠前深度偏移1、叠前偏移从实现方法上可分为叠前时间偏移和叠前深度偏移。

从理论上讲，叠前时间偏移只能解决共反射点叠加的问题，不能解决成像点与地下绕射点位置不重合的问题，因此叠前时间偏移主要应用于地下横向速度变化不太复杂的地区。

当速度存在剧烈的横向变化、速度分界面不是水平层状时，只有叠前深度偏移能够实现共反射点的叠加和绕射点的归位，叠前深度偏移是一种真正的全三维叠前成像技术，但它的成像效果必须依赖于准确的速度-深度模型，而模型的迭代和修改是一个非常复杂和费时的过程，周期长，花费也相当昂贵。

1．1 叠前时间偏移叠前时间偏移是复杂构造成像和速度分析的重要手段，它可以有效地克服常规NMO、DMO和叠后偏移的缺点，实现真正的共反射点叠加。

叠前时间偏移产生的共反射点（CRP）道集，消除了不同倾角和位置的反射带来的影响，不仅可以用来优化速度分析，而且也是进行AVO地震反演的前提。

Kirchhoff叠前时间偏移方法的基础是计算地下散射点的时距曲面。

根据Kirchhoff绕射积分理论，时距曲面上的所有样点相加就得到该绕射点的偏移结果。

具体的实现过程就是沿非零炮检距的绕射曲线旅行时轨迹对振幅求和，速度场决定求和路径的曲率，对每个共炮检距剖面单独成像，然后将所有结果叠加起来形成偏移剖面。

1．2 叠前深度偏移实际上，叠前时间偏移可认为是一种能适应各种倾斜地层的广义NMO叠加，其目的是使各种绕射能量聚焦，而不是把绕射能量归位到其相应的绕射点上去，它基于的速度模型是均匀的，或者仅允许有垂直变化，因此，叠前时间偏移仅能实现真正的共反射点叠加，当地下地层倾角较大，或者上覆地层横向速度变化剧烈，速度分界面不是水平层状的条件下，叠前时间偏移并不能解决成像点与地下绕射点位置不重合的问题。

为了校正这种现象，我们可以在时间剖面的基础上，再做一次校正，使成像点与绕射点位置重合，这就是做叠后深度偏移的目的，但叠后深度偏移有缺点，主要是无法避免NMO校正叠加所产生的畸变，而且在实现过程中缺少模型叠代修正的手段，因此叠后深度偏移一般作为叠前深度偏移流程的一部分，用于深度域模型层位的解释。

Omega 培训报告地震资料处理包括预处理、常规处理和特殊处理三个基本阶段。

其中预处理是把野外采集数据转换成计算机处理的格式；常规处理是针对地震数据做基本处理运算；特殊处理，即目标处理，是针对不同目的采取不同处理手段，如叠前深度偏移、子波处理、属性分析和反演等。

针对现场处理的要求，我们学习了预处理和常规处理。

1．预处理预处理包括数据解编、道编辑、野外静校正、建立野外观测系统、置道头、线性动校正、分频扫描以及能量谱等。

1）数据解编及格式转换把按时分道的数据记录方式变换成按道分时的数据记录方式，即共炮点记录。

在这个阶段数据要转换成本机格式，全部处理过程都用这个格式。

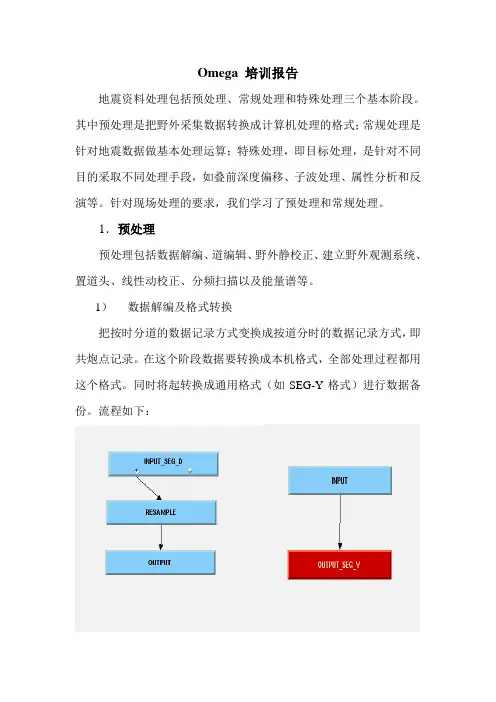
同时将起转换成通用格式（如SEG-Y格式）进行数据备份。

流程如下：2）道编辑将噪音道、带有瞬变噪音道、单频信号以及极性反转的道删除。

用手工剔除坏炮并且利用Omega处理软件特有的道头值识别法技术自动剔除某一范围值内的坏道和工业电干扰。

3）野外静校正对陆上资料，把所有道的炮点和接收点位置均校正到一个公共基准面上，以消除高程、低降速带和井深对旅行时间的影响。

单炮记录上初至不光滑，有效反射波同相轴不连续，存在严重的静校正问题。

实际处理过程中采用高程静校正，最大限度地解决静校正问题，提高资料的信噪比以及丰富高频信息，为后续处理打好基础，提高叠加质量。

静校正是利用高程或提供的静校正量，直接进行高频分量野外静校正。

4）建立野外观测系统把所有道的炮点和接收点位置坐标等测量信息都存储于道头中，以保证各道的正确叠加。

观测系统调整是通过线性动校正，对位置不准单炮的坐标进行反复调整，在调整中，先分别对横纵方向试出偏移量，而后通过自编程序将其投影到大地坐标系中，同时加入坐标库中，完成单炮坐标重新定位编辑观测系统示意图5）置道头、线性动校正。

置道头是把单炮记录加上道头字。

线性动校正是进行炮偏校正。

二者在一个模块中实现，在EDDI中检查线性动校正是否有偏点，如果有用START_TIME测出偏移量，并返回到观测系统中在炮偏文件OFF中输入偏移量，执行上述操作到无偏点为止。

叠前时间偏移与叠前深度偏移摘要：偏移使倾斜反射归位到它们真正的地下界面位置，并使绕射波收敛，即可以提高空间分辨率。

按所处理的地震资料是否做过水平叠加划分为叠后偏移和叠前偏移两大类。

这里主要讨论叠前偏移。

偏移方法分为时间域和深度域两类，时间偏移技术是基于横向速度变化弱的水平层状介质模型产生的，而深度偏移技术是基于横向变速的真实地质深度模型发展而来的。

这里主要介绍克希霍夫积分法叠前时间偏移、有限差分法叠前时间偏移、Fourier变换法叠前时间偏移三种叠前时间偏移方法。

在叠前深度偏移上面，主要根据其技术的发展历史，现状，及未来趋势进行叙述，并进行了不同偏移技术的成像对比。

关键字：叠前时间偏移叠前深度偏移克希霍夫积分法正文：一、引言偏移使倾斜反射归位到它们真正的地下界面位置，并使绕射波收敛，即可以提高空间分辨率。

按所处理的地震资料是否做过水平叠加划分为叠后偏移和叠前偏移两大类。

偏移方法分为时间域和深度域两类。

时间偏移技术是基于横向速度变化弱的水平层状介质模型产生的，而深度偏移技术是基于横向变速的真实地质深度模型发展而来的。

从当前技术发展的状况看，目前国内应用的叠前偏移技术基本上可以概括为以下两类。

一种是基于波动方程积分解的克希霍夫积分法叠前偏移。

这种技术，在20世纪90年代以前就在研究，目前，随着多年来持续不断地改进和完善，已经成为一种高效实用的叠前偏移方法，它具有高角度成像、无频散、占用资源少和实现效率高的特点，能适应不均匀的空间采样和起伏地表，比较适合复杂构造的成像。

目前国际上有多种较为成熟的积分法叠前成像软件，是当前实际生产中使用的主要叠前深度偏移方法。

一种是基于波动方程微分解的波动方程叠前偏移。

这种技术目前在国内的应用还处于试验阶段。

叠前时间偏移与叠后时间偏移和叠前深度偏移一样，都是基于三大数学工具，即克希霍夫积分、有限差分和Fourier变换。

二、叠前时间偏移技术叠前时间偏移的可行性分为下面三个方面：①实现这种技术所需的软硬件成本合理。

叠前深度偏移技术一、技术原理及主要技术内容叠前深度偏移技术已由克希霍夫积分法发展到波动方程法，同时还发展了其它的偏移方法，如：高斯束（Beam）偏移、相移屏偏移技术、转换波叠前深度偏移、各向异性叠前深度偏移等，现把上述各种方法分述如下：（1）克希霍夫积分法叠前深度偏移：该偏移方法一般由两部分组成：一部分是旅行时计算，另外一部分是克希霍夫积分处理。

偏移的精度主要取决于旅行时的精度。

旅行时计算建立在费马原理的基础上，即地下两点间的一切可能路径中实际路径对应于最小旅行时间。

它遵循倒转射线追踪机制，大多数情况下使用对应于体波而不是首波的射线，这样减少了偏移成像的畸变，且输出轨迹是灵活的。

新方法主要改进了原方法中单波至、不保幅的缺点，现在是计算多波至旅行时，并且具有振幅与相位保持特性，最具代表性的方法是由以色列PARADIGM公司发展的共反射角克希霍夫积分法，其原理与方法是：由成像点到地面采用照明式射线追踪；在每个射线均计算旅行时、观测位置、相位旋转因子、慢度；在特定倾角每对射线均是潜在反射；求和某成像点同一层的所有反射形成共反射成像道集；所有到达时的振幅与相位都是保持的。

高斯射线束（Gaussian Beam）偏移方法有别于常规的克希霍夫积分法深度偏移方法，目前只有Chevron公司使用它，它分多组射线束进行研究，采用Gaussian法振幅衰减与相位抛物线近似等。

具体讲它是将震源和接受点波场局部分解成“束”，并利用精确的射线追踪将这些束返回地下。

一个地面位置能发出几个束，不同的束对应不同的初始传播方向，每个束独立于其他束传播，且受单个射线管引导。

射线管可以重叠，所以能量能在成像位置、震源位置及接受点位置间以多个路径传播，因此高斯射线束偏移可处理多路径。

该种方法部分解决了常规克希霍夫积分法精度不高的问题。

（2）波动方程法叠前深度偏移：该种方法研究多波至，易振幅与相位保持，精度高，但费机时，主要方法有有限差分法（FD）与相移校正法（PSPC），它们均基于单程波动方程、平方根算子向下延拓，并使用多个参考速度。

地震叠前深度偏移技术进展及应用问题与对策王延光【摘要】地震叠前深度偏移技术是目前油气勘探、开发、科研和生产中应用的关键技术.结合胜利油区在叠前深度偏移技术方面的研究、应用成果及经验,首先介绍面向研究区块地表和地下地质情况的特色化实用叠前深度偏移与建模技术,在不同区块和地质任务的应用中,这些技术可以根据需求配套使用.其次,从采集—处理—解释一体化的思路出发,分析了叠前深度偏移技术的影响因素,并提出了针对性的解决对策.最后,通过几个典型区块的工业化应用实例验证了胜利油区叠前深度偏移技术一体化解决方案的效果,总结出一套“深度域+”的叠前深度偏移技术研究思路,进一步推动深度域地震技术的发展,更好地为油气田勘探和开发服务.%Seismic prestack depth migration is a key technology in hydrocarbon exploration,development,research and production.Based on study on prestack depth migration technology research and its application achievement and experience in Shengli oilfield,characteristics and practical prestack depth migration and modeling techniques were introduced firstly according to surface and subsurface geologic conditions of the study area,which could be used together in application to different study area and different geologic task according to the actual need.And secondly,effects on the prestack migration technique were analyzed based on the idea of integration of acquisition,processing and interpretation,and then the corresponding countermeasures were put forward.Finally,several industrial applications of the technique to typical examples in Shengli oilfield were used to verify effectiveness of integration solution of prestackdepth migration technology for hydrocarbon exploration.A set of "depth domain+" prestack depth migration technology has been summarized to promote further development of the seismic technique in domain of depth and to provide better service for oilfield exploration and development.【期刊名称】《油气地质与采收率》【年(卷),期】2017(024)004【总页数】8页(P1-7,29)【关键词】叠前深度偏移;速度建模;影响因素;应用实践;各向异性【作者】王延光【作者单位】中国石化胜利油田分公司物探研究院,山东东营257022【正文语种】中文【中图分类】P631.443近年来，随着油气勘探开发研究与实践的不断深入以及计算机运算能力的提升，地震叠前深度偏移技术成为广泛应用的常规技术，胜利油区的生产和科研实践充分验证了这一点。

叠前时间偏移与叠前深度偏移1、叠前偏移从实现方法上可分为叠前时间偏移和叠前深度偏移。

从理论上讲，叠前时间偏移只能解决共反射点叠加的问题，不能解决成像点与地下绕射点位置不重合的问题，因此叠前时间偏移主要应用于地下横向速度变化不太复杂的地区。

当速度存在剧烈的横向变化、速度分界面不是水平层状时，只有叠前深度偏移能够实现共反射点的叠加和绕射点的归位，叠前深度偏移是一种真正的全三维叠前成像技术，但它的成像效果必须依赖于准确的速度-深度模型，而模型的迭代和修改是一个非常复杂和费时的过程，周期长，花费也相当昂贵。

1．1 叠前时间偏移叠前时间偏移是复杂构造成像和速度分析的重要手段，它可以有效地克服常规NMO、DMO和叠后偏移的缺点，实现真正的共反射点叠加。

叠前时间偏移产生的共反射点（CRP）道集，消除了不同倾角和位置的反射带来的影响，不仅可以用来优化速度分析，而且也是进行AVO地震反演的前提。

Kirchhoff叠前时间偏移方法的基础是计算地下散射点的时距曲面。

根据Kirchhoff绕射积分理论，时距曲面上的所有样点相加就得到该绕射点的偏移结果。

具体的实现过程就是沿非零炮检距的绕射曲线旅行时轨迹对振幅求和，速度场决定求和路径的曲率，对每个共炮检距剖面单独成像，然后将所有结果叠加起来形成偏移剖面。

1．2 叠前深度偏移实际上，叠前时间偏移可认为是一种能适应各种倾斜地层的广义NMO叠加，其目的是使各种绕射能量聚焦，而不是把绕射能量归位到其相应的绕射点上去，它基于的速度模型是均匀的，或者仅允许有垂直变化，因此，叠前时间偏移仅能实现真正的共反射点叠加，当地下地层倾角较大，或者上覆地层横向速度变化剧烈，速度分界面不是水平层状的条件下，叠前时间偏移并不能解决成像点与地下绕射点位置不重合的问题。

为了校正这种现象，我们可以在时间剖面的基础上，再做一次校正，使成像点与绕射点位置重合，这就是做叠后深度偏移的目的，但叠后深度偏移有缺点，主要是无法避免NMO校正叠加所产生的畸变，而且在实现过程中缺少模型叠代修正的手段，因此叠后深度偏移一般作为叠前深度偏移流程的一部分，用于深度域模型层位的解释。

叠前时间偏移与叠前深度偏移摘要：偏移使倾斜反射归位到它们真正的地下界面位置，并使绕射波收敛，即可以提高空间分辨率。

按所处理的地震资料是否做过水平叠加划分为叠后偏移和叠前偏移两大类。

这里主要讨论叠前偏移。

偏移方法分为时间域和深度域两类，时间偏移技术是基于横向速度变化弱的水平层状介质模型产生的，而深度偏移技术是基于横向变速的真实地质深度模型发展而来的。

这里主要介绍克希霍夫积分法叠前时间偏移、有限差分法叠前时间偏移、Fourier变换法叠前时间偏移三种叠前时间偏移方法。

在叠前深度偏移上面，主要根据其技术的发展历史，现状，及未来趋势进行叙述，并进行了不同偏移技术的成像对比。

关键字：叠前时间偏移叠前深度偏移克希霍夫积分法正文：一、引言偏移使倾斜反射归位到它们真正的地下界面位置，并使绕射波收敛，即可以提高空间分辨率。

按所处理的地震资料是否做过水平叠加划分为叠后偏移和叠前偏移两大类。

偏移方法分为时间域和深度域两类。

时间偏移技术是基于横向速度变化弱的水平层状介质模型产生的，而深度偏移技术是基于横向变速的真实地质深度模型发展而来的。

从当前技术发展的状况看，目前国内应用的叠前偏移技术基本上可以概括为以下两类。

一种是基于波动方程积分解的克希霍夫积分法叠前偏移。

这种技术，在20世纪90年代以前就在研究，目前，随着多年来持续不断地改进和完善，已经成为一种高效实用的叠前偏移方法，它具有高角度成像、无频散、占用资源少和实现效率高的特点，能适应不均匀的空间采样和起伏地表，比较适合复杂构造的成像。

目前国际上有多种较为成熟的积分法叠前成像软件，是当前实际生产中使用的主要叠前深度偏移方法。

一种是基于波动方程微分解的波动方程叠前偏移。

这种技术目前在国内的应用还处于试验阶段。

叠前时间偏移与叠后时间偏移和叠前深度偏移一样，都是基于三大数学工具，即克希霍夫积分、有限差分和Fourier变换。

二、叠前时间偏移技术叠前时间偏移的可行性分为下面三个方面：①实现这种技术所需的软硬件成本合理。

§4.6 广义屏法波动方程叠前深度偏移本节基于波的散射理论，首先从波动方程Green函数解出发，借助Born近似等一系列数学手段，导出广义屏（GS）偏移算子。

然后在小角度近似条件下，得到相屏（PS）偏移算子（分步Fourier算子）。

为了克服广义屏算子在计算中遇到奇点，特采用Taylor展开方法得到扩展的局部Born近似的广义屏算子。

接着我们对相屏算子和扩展的局部Born近似的广义屏（ELBF）算子在数值上做了脉冲测试，并用于凹陷模型的叠后深度偏移处理和复杂模型叠前深度偏移处理。

一．概述三维叠前深度偏移广泛地应用于地下复杂地质体成像。

对当前工作量较大的三维成像问题一般采用基于射线追踪或有限差分走时计算的Kirchhoff积分方法，但该方法在处理复杂构造（如盐丘或陡倾地层）时总存在困难（Hu & McMechan, 1986）。

虽然基于有限差分方法的全方程逆时偏移对存在剧烈横向速度变化的非均匀介质也具有非常好的成像精度，但是，把该方法应用于三维叠前深度偏移需要花费较多的机时和占用巨大的计算机内存容量，这些要求在目前是不太现实的。

于是从20世纪80年代后期直至目前，地球物理学家们一直在寻求一种既方便快捷又准确可靠的叠前深度偏移方法。

要研究波动方程偏移问题，搞清楚波的传播问题是非常必要和有帮助的。

在80年代中后期，Knepp与de Hoop等人为了研究波在随机介质中的传播问题，在地震波场的叠加原理基础上，基于速度场分解、波的散射理论以及波动方程的Green函数解法来求解Helmholtz 方程，提出了一种在频率-波数域和频率-空间域（双域）交替进行的波动方程解法。

这可以说是屏方法的雏形。

20世纪90年代初，Wu R.S.与de Hoop等在屏的雏形理论基础上，通过一系列近似处理手段，发展成了较实用的广义屏算法。

这类算法既可用于研究波（声波或弹性波）的传播问题，又可用于地震波场成像。

该类方法认为速度场可分解为层内常速背景和层内变速扰动。

正文：在2023年3月至4月期间，我有幸参加了由我国知名企业举办的叠穿培训课程。

此次培训旨在提升我们的专业技能，增强团队协作能力，以适应企业发展的需求。

经过这段时间的学习和实践，我收获颇丰，现将培训总结如下：一、培训内容丰富，实用性高此次叠穿培训课程内容丰富，涵盖了叠穿的基本概念、技术要点、搭配技巧以及行业应用等多个方面。

通过学习，我对叠穿有了更深入的了解，掌握了叠穿的基本方法和技巧。

同时，培训中穿插的实际案例分析，使我能够将理论知识与实际工作相结合，提高了解决问题的能力。

二、师资力量雄厚，教学方法先进本次培训由行业资深专家担任主讲，他们具备丰富的实践经验，授课内容深入浅出，使我们在短时间内掌握了叠穿的核心技能。

此外，培训采用理论与实践相结合的教学方法，通过互动式教学、案例分析、现场演示等形式，使我们在轻松愉快的氛围中学习到了知识。

三、团队协作，共同进步在培训过程中，我们来自不同部门的学员共同学习、共同进步。

通过分组讨论、小组竞赛等活动，我们加强了团队协作能力，学会了如何与他人沟通、协调，共同完成培训任务。

这种团队精神将有助于我们在今后的工作中更好地发挥团队力量，提高工作效率。

四、培训成果显著，应用前景广阔通过本次叠穿培训，我们不仅掌握了叠穿的基本技能，还对行业发展趋势有了更清晰的了解。

在今后的工作中，我们将充分发挥所学知识，为企业创造更多价值。

同时，叠穿技术在各个领域都有广泛的应用前景，相信我们的技能将为企业带来更多商机。

总结：此次叠穿培训使我受益匪浅，不仅提升了我的专业技能，还增强了团队协作能力。

在今后的工作中，我将继续努力学习，将所学知识运用到实际工作中，为企业的发展贡献自己的力量。

同时，我也将珍惜这次学习机会，不断拓展自己的知识面，为我国叠穿行业的发展贡献自己的一份力量。