期末模拟试题4及参考答案

北师大版2020七年级数学下册期末模拟测试题4（培优 附答案） 1．下列长度的三条线段能组成三角形的是（ ） A ．3, 4, 6B ．6， 9，17C ．5， 12， 18D ．2， 2， 42．如图，将一副直角三角板摆放，点C 在EF 上，AC 经过点D ，已知∠A =∠EDF =90°，AB =AC ，∠E =30°，∠BCE =40°，则∠CDF =（ ）A ．20oB ．25oC ．30oD ．35o3．如图，直线AB 、CD 相交于点O ，OE CD ⊥，垂足为O ，若射线OF 在AOE ∠的内部，EOF 25∠=︒，2AOF BOD 3∠∠=，则BOC ∠的度数为（ ）A ．120︒B ．135︒C ．141︒D ．145︒4．如图，AB CD ∥ ，点E 在CA 的延长线上若50BAE ∠=︒，则ACD ∠的大小为( )A ．100°B ．120°C ．130°D ．110°5．如图，把一块含有45°角的直角三角板的两个顶点分别放在直尺的一组对边上.如果∠1=22°，那么∠2的度数是（ ）A ．21°B ．22°C ．23°D ．25°6．泰勒斯是古希腊哲学家，相传他利用三角形全等的方法求出岸上一点到海中一艘船的距离．如图，B 是观察点，船A 在B 的正前方，过B 作AB 的垂线，在垂线上截取任意长BD ，C 是BD 的中点，观察者从点D 沿垂直于BD 的DE 方向走，直到点E 、船A 和点C 在一条直线上，那么△ABC ≌△EDC ，从而量出DE 的距离即为船离岸的距离AB ，这里判定△ABC ≌△EDC 的方法是（ ）A ．SASB ．ASAC ．AASD ．SSS7．下列四个算式中，可以直接用平方差公式进行计算的是（ ） A ．（﹣a +b ）（﹣a ﹣b ） B ．（2a +b ）（a ﹣2b ） C ．（a ﹣b ）（b ﹣a ）D ．（a +b ）（﹣a ﹣b ）8．如图，点E, F 在直线AC 上，DF=BE ， ∠AFD=∠CEB,下列条件中不能判断△ADF ≌△CBE 的是( )A ．∠D=∠B B ．AD=CBC ．AE=CFD ．AD// BC9．如图，把△ABC 纸片沿DE 折叠，当A 落在四边形BCDE 内时，则∠A 与∠1+∠2之间有始终不变的关系是（ ）A ．∠A =∠1+∠2B ．2∠A =∠1+∠2C ．3A =∠1+∠2D ．3∠A =2（∠1+∠2）10．下列运算正确的是（ ） A ．3a 2b 5ab +=B ．325a a a ⋅=C ．824a a a ⋅=D ．236(2a )6a =-11．如图，直线a ，b 被直线c 所截，若a ∥b ，∠1=40°，∠2=60°，则∠3=____.12．用简便方法计算：20192－2019×38＋361＝________．13．在Rt ABC ∆中，90C ∠=°，10AC cm =，5BC cm =，某线段PQ AB =， P ，Q 两点分别在AC 和AC 的垂线AX 上移动，则当AP =__________.时，才能使ABC∆和APQ ∆全等.14．如图，AD 是△ABC 的中线，E ，F 分别是AD 和AD 延长线上的点，且DE=DF ，连接BF ，CE ．下列说法：①△BDF ≌△CDE ；②CE=BF ； ③BF ∥CE ；④△ABD 和△ACD 周长相等．其中正确的有___________（只填序号）15．计算：()20202019133⎛⎫-⋅-= ⎪⎝⎭_____.16．已知|x-2|+y 2+2y+1=0，则x y 的值为__________________17．“国际半程马拉松”的赛事共有三项：A ．“半程马拉松”、B ．“10公里”、C ．“迷你马拉松”．小明和小刚参与了该项赛事的志愿者服务工作，组委会随机将志愿者分配到三个项目组．小明和小刚被分配到不同项目组的概率______；18．如图，已知△ABC ≌△DEC ，∠E ＝40°，∠ACB=110°，则∠D 的度数为________．19．如图所示，是一块三角形木板，量的100A ∠=o ，40B ∠=o 则这块三角形木板的另外一个角的度数是___.20．若a m ＝4，a n ＝8，则a m +n ＝_____．21．已知ABC V 中，90BAC ∠=o ，AB AC =，点D 为直线BC 上的一动点(点D 不与点B 、C 重合)，以AD 为边作ADE V ，使90DAE ∠=o ，AD AE =，连接CE ． 发现问题：如图1，当点D 在边BC 上时，()1请写出BD 和CE 之间的位置关系为______，并猜想BC 和CE 、CD 之间的数量关系：______． 尝试探究：()2如图2，当点D 在边BC 的延长线上且其他条件不变时，()1中BD 和CE 之间的位置关系、BC 和CE 、CD 之间的数量关系是否成立？若成立，请证明；若不成立，请写出新的数量关系，说明理由； 拓展延伸：()3如图3，当点D 在边CB 的延长线上且其他条件不变时，若6BC =，2CE =，求线段ED 的长．22．已知，点D 和三角形ABC 在同一平面内.（1）如图1，点D 在BC 边上，DE BA P 交AC 于E ，DF CA ∥交AB 于F .若o（2）如图2，点D 在BC 的延长线上，DF CA ∥，EDF A ∠=∠，证明：DE BA P . （3）点D 是三角形ABC 外部的任意一点，过D 作DE BA P 交直线AC 于E ，DF CA ∥交直线AB 于F ，直接写出EDF ∠与A ∠的数量关系（不需证明）.23．（1）操作思考：如图1，在平面直角坐标系中，等腰Rt △ACB 的直角顶点C 在原点，将其绕着点O 旋转，若顶点A 恰好落在点（1，2）处．则①OA 的长为 ；②点B 的坐标为 （直接写结果）；（2）感悟应用：如图2，在平面直角坐标系中，将等腰R t △ACB 如图放置，直角顶点 C (-1,0)，点A (0，4)，试求直线AB 的函数表达式；（3）拓展研究：如图3，在平面直角坐标系中，点B （4；3），过点B 作BA ⊥y 轴，垂足为点A ；作BC ⊥x 轴，垂足为点C ，P 是线段BC 上的一个动点，点Q 是直线26y x =-上一动点．问是否存在以点P 为直角顶点的等腰R t △APQ ，若存在，请求出此时P 的坐标，若不存在，请说明理由．24．如图，长方形ABCD 表示一块草地，点E ，F 分别在边AB 、CD 上，BF ∥DE ，四边形EBFD 是一条水泥小路，若AD ＝12米，AB ＝7米，且AE ∶EB ＝5∶2，求草地的面积．25．已知：如图，AC ∥DF ，直线AF 分别直线BD 、CE 相交于点G 、H ，∠1=∠2，求证：∠C=∠D ．解：∵∠1=∠2（已知）∠1=∠DGH （_________________） ∴∠2=__________（______________） ∴BD ∥CE （________________） ∴∠C= ________（_______________） 又∵AC ∥DF∴∠D=∠ABG （________________） ∴∠C=∠D （________________）26．已知△ABC 三边长分别为4，2a +1，7，求a 的取值范围． 27．（1）02201820181( 3.14)(0.5)()(3)3π---+⨯-； （2）（﹣3a ）2•（a 2）3÷a 3．28．先化简再求值：x²（x-1）- x （x²+x-1），其中x=1参考答案1．A【解析】【分析】根据三角形的三边关系：三角形任意两边的和大于第三边进行分析判断．【详解】A、3+4=7＞6，能组成三角形；B、9+6＜17，不能组成三角形；C、5+12＜18，不能够组成三角形；D、2+2=4，不能组成三角形．故选A．【点睛】本题考查了三角形的三边关系，在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．2．B【解析】【分析】由AB=AC，∠A=90°，根据等腰直角三角形的性质可得∠ACB=45°，即可求得∠ACE=85°，又因∠ACE=∠F+∠CDF，∠F=60°，由此可得∠CDF=25°.【详解】∵AB=AC，∠A=90°，∴∠ACB=45°，∵∠BCE=40°，∴∠ACE=85°，∵∠ACE=∠F+∠CDF，∠F=60°，∴∠CDF=25°，故选B．【点睛】本题考查了三角形内角和定理，三角形的外角的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．3．C【解析】【分析】由ED⊥CD可得∠EOC=∠EOD=90°，根据对顶角的定义可得∠AOC=∠BOD，根据∠AOC+∠AOF+∠EOF=∠EOC=90°，即可求出∠AOC的度数，利用邻补角的定义即可求出∠BOC的度数.【详解】∵ED⊥CD，∴∠EOC=∠EOD=90°，∵∠AOC=∠BOD，∠AOF=23∠BOD，∠EOF=25°，∴∠AOC+∠AOF+∠EOF=∠EOC=90°∴∠AOC+23∠AOC+25°=90°，∴∠AOC=39°，∴∠BOC=180°-∠AOC=180°-39°=141°，故选C.【点睛】本题考查了垂直的定义、对顶角的性质及角的和差运算，认真观察图形是解题关键. 4．C【解析】【分析】本题先运用邻补角定义，得到∠BAC的度数，然后根据平行得到结果.【详解】解：∵∠BAE=50°,∴∠BAC=180°-50°=130°,∵AB CD∥,∴∠ACD=∠BAC=130°.故选择：C.【点睛】本题考查了平行线的性质和邻补角的定义，解题的关键是熟练运用平行线的性质.5．C【解析】【分析】直接利用平行线的性质，求得∠AFE的度数，进而结合等腰直角三角形的性质得出答案．【详解】如图，∵AB∥CD，∴∠AFE=∠2，∵∠GFE=45°，∠1=22°，∴∠AFE=23°，∴∠2=23°，故选：C．【点睛】此题考查平行线的性质，等腰直角三角形的性质，正确运用平行线的性质是解题关键．6．B【解析】【分析】根据题目确定出△ABC和△EDC全等的条件，然后根据全等三角形的判定方法解答即可；【详解】∵C是BD的中点，∴BC＝DC，∵AB⊥BD，DE⊥BD，∴∠ABC＝∠EDC＝90°，∵在△ABC和△EDC中，90ABC EDC BC DCACB ECD ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩， ∴△ABC ≌△EDC （ASA ）， ∴DE ＝AB ． 故选：B ． 【点睛】本题主要考查了全等三角形的应用，掌握全等三角形的应用是解题的关键. 7．A 【解析】 【分析】根据平方差公式的结构特点“两数之和与两数之差的乘积等于这两数的平方差”，对各项分析判断即可. 【详解】解：A 、（﹣a +b ）（﹣a ﹣b ）＝（﹣a ）2﹣b 2＝a 2﹣b 2，符合平方差公式的结构特点，正确； B 、（2a +b ）（a ﹣2b ），不是相同的两个数的和与差的积，不符合平方差公式的结构特点，错误；C 、（a ﹣b ）（b ﹣a ），两项互为相反数，不符合平方差公式的结构特点，错误；D 、（a +b ）（﹣a ﹣b ），两项互为相反数，不符合平方差公式的结构特点，错误； 故选：A ． 【点睛】本题考查的是平方差公式的结构特点，熟记公式的结构是解题的关键. 8．B 【解析】 【分析】已知条件有一角和一边，可采用ASA 、AAS 或SAS 判定全等，据此逐项判断即可. 【详解】A. ∠D=∠B ，与已知条件组合可用ASA 判定△ADF ≌△CBE ，不符合题意；B. AD=CB ，与已知条件组合为“SSA ”，不能判定△ADF ≌△CBE ，符合题意；C. 由AE=CF 可得AF=CE ，与已知条件组合可用SAS 判定△ADF ≌△CBE ，不符合题意；D. 由AD// BC可得∠A=∠C，与已知条件组合可用AAS判定△ADF≌△CBE，不符合题意；故选B.【点睛】本题考查全等三角形的判定，熟练掌握判定定理是关键.9．B【解析】【分析】本题问的是关于角的问题，当然与折叠中的角是有关系的，∠1与∠AED的2倍和∠2与∠ADE的2倍都组成平角，结合△AED的内角和为180°可求出答案．【详解】∵△ABC纸片沿DE折叠，∴∠1+2∠AED=180°,∠2+2∠ADE=180°，∴∠AED=12(180°−∠1),∠ADE=12(180°−∠2)，∴∠AED+∠ADE=12(180°−∠1)+12(180°−∠2)=180°−12(∠1+∠2)在△ADE中,∠A=180°−(∠AED+∠ADE)=180°−[180°−12(∠1+∠2)]=12(∠1+∠2)则2∠A=∠1+∠2，故选择B项.【点睛】本题考查折叠和三角形内角和的性质，解题的关键是掌握折叠的性质.10．B【解析】【分析】根据合并同类项，系数相加字母和字母的指数不变；同底数幂的乘法，底数不变指数相加；幂的乘方，底数不变指数相乘，对各选项计算后利用排除法求解．【详解】A、不是同类项，不能合并，选项错误；B、正确；C、a8•a2=a10，选项错误；D、（2a2）3=8a6，选项错误．故选B．考查合并同类项，同底数幂的乘法和幂的乘方，解题关键是熟记运算法则．11．100°【解析】【分析】根据两直线平行，内错角相等求出∠4，再根据对顶角相等解答．【详解】如图所示：∵a∥b，∠1=40°，∴∠4=∠1=40°，∴∠3=∠2+∠4=60°+40°=100°．故答案是：100°.【点睛】考查了平行线的性质，对顶角相等的性质，是基础题，熟记性质是解题的关键．12．4000000【解析】【分析】运用完全平方公式进行计算即可.【详解】20192－2019×38＋361＝20192－2×2019×19＋192＝（2019-19）2=4000000.故答案为：4000000.【点睛】本题考查了完全平方公式.13．5㎝或10㎝【解析】本题要分情况讨论：①Rt△ABC≌Rt△QPA，此时AP=BC=5cm，可据此求出P点的位置；②Rt△ABC≌Rt△PQA，此时AP=AC，P、C重合．【详解】解：∵PQ=AB，∴根据三角形全等的判定方法HL可知，当P运动到AP=BC时，在Rt△ABC和Rt△QPA中PQ AB AP BC=⎧⎨=⎩，∴Rt△ABC≌Rt△QPA（HL），即AP=BC=5cm；当P运动到与C点重合时，在Rt△ABC和Rt△QPA中PQ AB AP AC=⎧⎨=⎩，∴Rt△ABC≌Rt△PQA（HL），即AP=AC=10cm．故答案为：5㎝或10㎝．【点睛】本题考查三角形全等的判定方法和全等三角形的性质，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．由于本题没有说明全等三角形的对应边和对应角，因此要分类讨论，以免漏解．14．①②③【解析】【分析】根据AD是中线可知BD=CD，结合题意从而可证△BDF≌△CDE，继而可知CE=BF，BF∥CE，由于△ABC的两边AB与AC不一定相等，可判断△ABD和△ACD周长相等的对错，进而可以得出答案.【详解】∵AD 是△ABC 的中线，∴BD=CD在△BDF 和△CDE 中BD CD BDF CDE DF DE =⎧⎪∠=∠⎨⎪=⎩∴△BDF ≌△CDE （SAS ）故①正确；∵△BDF ≌△CDE∴BF=CE ，∠FBD=∠ECD故②正确；∵∠FBD=∠ECD∴BF ∥CE （内错角相等两直线平行）故③正确；∵△ABC 中AB 和AC 不一定相等∴△ABD 和△ACD 周长不一定相等故④错误；综上，答案为①②③.【点睛】本题考查的是中线的性质，三角形全等的判定与性质和平行线的判定，能够根据中线得出BD=CD 证得△BDF ≌△CDE 是解题的关键.15．1.3-【解析】【分析】先根据同底数幂的乘法逆运算化简，再根据积的乘方逆运算计算.【详解】解：()20202019133⎛⎫-⋅- ⎪⎝⎭()2019201911333⎛⎫⎛⎫=-⋅-⨯- ⎪ ⎪⎝⎭⎝⎭()201911333⎡⎤⎛⎫⎛⎫=-⨯-⨯- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 1.3=- 故答案为1.3-【点睛】 此题重点考察学生对同底数幂的乘法和积的乘方的理解，掌握其计算方法是解题的关键. 16．12． 【解析】【分析】根据非负数的性质列出算式，求出x 、y 的值，计算即可．【详解】解：由题意得，|x-2|+（y+1）2=0，则x-2=0，y+1=0，解得，x=2，y=-1， 则y 1x 2= 故答案为：12 . 【点睛】本题考查的是非负数的性质，掌握当几个非负数相加和为0时，则其中的每一项都必须等于0是解题的关键．17．23； 【解析】【分析】利用树状图法列出所有的分配情况，再看小明和小刚被分配到不同项目组的情况，根据概率公式求解即可．【详解】解：画树状图如图所示：由图可知，共有9种情况，其中小明和小刚被分配到不同项目组有6种情况，根据概率公式，则可知小明和小刚被分配到不同项目组的概率是：61 =93．【点睛】本题考查了求概率的方法，熟练应用树状图法或列表法求出所求情况数和总情况数是解题的关键．18．30°【解析】【分析】根据全等三角形的性质得到∠DCE=∠ACB=110°，然后利用三角形内角和定理求∠D即可. 【详解】解：∵△ABC≌△DEC，∠E＝40°，∴∠DCE=∠ACB=110°，∴∠D=180°-∠E-∠DCE=180°-40°-110°=30°，故答案为：30°.【点睛】本题考查了全等三角形的性质和三角形内角和定理，熟知三角形内角和为180°是解题关键. 19．40【解析】【分析】直接根据三角形内角和定理解答即可．【详解】∵△ABC中，∠A=100°，∠B=40°，∴∠C=180°−∠A−∠B=180°−100°−40°=40°故答案为：40°【点睛】此题考查三角形内角和定理，难度不大20．32【解析】【分析】根据同底数幂的乘法，底数不变指数相加计算．【详解】解：∵a m ＝4，a n ＝8，∴a m +n ＝a m ×a n ＝4×8＝32． 故答案为：32【点睛】题考查同底数幂的乘法，一定要记准法则才能做题．21．（1）BD CE ⊥；BC CD CE =+；（2）BD CE ⊥成立，数量关系不成立，关系为BC=CE-CD ；（3）DE =【解析】【分析】()1根据条件AB AC =，BAC 90∠=o ，AD AE =，DAE 90∠=o ，判定ABD V ≌()ACE SAS V ，即可得出BD 和CE 之间的关系，根据全等三角形的性质，即可得到CE CD BC +=；()2根据已知条件，判定ABD V ≌()ACE SAS V，得出BD CE =，再根据BD BC CD =+，即可得到CE BC CD =+；()3根据条件判定ABD V ≌()ACE SAS V ，得出BD CE =，在Rt DCE V 中，由勾股定理得22222DE DC CE 8268=+=+=，即可解决问题.【详解】()1如图1，BAC DAE 90∠∠==o Q ，BAD CAE ∠∠∴=，在ABD V 和ACE V中， AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，ABD ∴V ≌()ACE SAS V， BD CE ∴=，B ACE 45∠∠==o ，BCE 454590∠∴=+=o o o ，即BD CE ⊥；由①可得，ABD V ≌ACE V， BD CE ∴=，BC BD CD CE CD ∴=+=+，故答案为BD CE ⊥，BC CD CE =+；()2BD CE ⊥成立，数量关系不成立，关系为BC CE CD =-．理由：如图2中，由()1同理可得，BAC DAE 90∠∠==o Q ，∴BAC CAD DAE CAD ∠∠∠∠+=+即BAD CA ∠∠=E ，∴在ABD V 和ACE V中， AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，ABD ∴V ≌()ACE SAS V， BD CE ∴=，ACE ABC ∠∠=，AB AC =Q ，ABC ACB 45∠∠∴==o ，BD BC CD ∴=+，即CE BC CD =+，ACE ACB 90∠∠+=o ，BC CE CD ∴=-；BD CE ⊥；()3如图3中，由()1同理可得，BAC DAE 90∠∠==o Q ，BAC BAE DAE BAE ∠∠∠∠∴-=-，即BAD EAC ∠∠=，易证ABD V ≌()ACE SAS V， BD CE 2∴==，ACE ABD 135∠∠==o ，CD BC BD BC CE 8∴=+=+=，∵ACB 45∠=oDCE 90∠∴=o ，在Rt DCE V 中，由勾股定理得22222DE DC CE 8268=+=+=，DE ∴=【点睛】本题属于三角形综合题，主要考查了全等三角形的判定与性质以及等腰直角三角形的性质的运用，等腰直角三角形是一种特殊的三角形，具有所有三角形的性质，还具备等腰三角形和直角三角形的所有性质.解决问题的关键是掌握：两边及其夹角分别对应相等的两个三角形全等.解题时注意：全等三角形的对应边相等．22．（1）85o ；（2）见解析；（3）EDF A ∠=∠或180EDF A ∠+∠=o【解析】【分析】根据题意可知:（1）通过DE BA P 得到两同位角A DEC ∠=∠，DF CA ∥得到两内错角DEC EDF ∠=∠，然后等量代换.（2）通过延长BA ，构造出新的角BGD ∠，再用等量代换找到内错角EDF BGD ∠=∠，从而证明直线平行.（3）直线BA 与直线AC 相交分成四部分，分别考虑这四部分且在三角形ABC 外部的点，可知只有EDF A ∠=∠或180EDF A ∠+∠=o 这两种情况.【详解】（1）∵DE BA P ，DF CA ∥，∴A DEC ∠=∠，DEC EDF ∠=∠，∵85EDF ∠=o ，∴85A EDF ∠=∠=o ；（2）证明：如图1，延长BA 交DF 于G ．∵DF AC P ，∴BAC BGD ∠=∠．又∵EDF BAC ∠=∠，∴EDF BGD ∠=∠．∴DE BA P ．（3）EDF A ∠=∠或180EDF A ∠+∠=o证明如下：①按题意画出图形如上所示：因为DF AE ∥,DE AF P所以四边形AEDF 是平行四边形（两组对边平行的四边形是平行四边形） 所以EDF A ∠=∠（平行四边形对角相等）②按题意画出图形如上所示：因为DF AE ∥,DE AF P所以四边形AEDF 是平行四边形（两组对边平行的四边形是平行四边形）所以 EDF FAE ∠=∠（平行四边形对角相等）又因为180FAE BAC ∠+∠=o所以180EDF BAC ∠+∠=o BAC ∠即为原图中的A ∠BAC ∠即为原图中的A ∠，即180EDF A ∠+∠=o故答案为EDF A ∠=∠或180EDF A ∠+∠=o【点睛】本题运用到两直线平行内错角相等，内错角相等两直线平行的知识点。

小学三年级下学期期末数学模拟模拟试题（含答案）一、填空题1．在括号里填上合适的单位名称。

(1)课桌的高度约是7( )。

(2)一元硬币的厚度约是2( )。

(3)飞机每小时飞行约是900( )。

(4)卡车的载重量是5( )。

(5)一袋面粉的重量是25( )。

(6)小明刷牙的时间大约需要3( )。

2．小明乘车去奶奶家，路上用了45分钟，在上午9：55到达。

他是从上午（____：____）出发的。

3．一盒彩笔18元，王老师买了9盒，大约需要( )元。

4．填上合适的单位。

（1）小学生大约每天睡9_____。

（2）犍为距离乐山大约60_____。

（3）一袋大米的质量25_____。

（4）做眼保健操大约需要5_____。

5．红红在计算126加一个数时，不小心把126抄成了216，得数是835，正确的结果是( )。

6．一捆绳子长60米，第一次用去23米，第二次用去了20米，这捆绳子比原来少了( )米。

7．0和任何数相乘都得( )，250×8的积的末尾有( )个0。

8．□324的积是三位数，□内最大可以填( )；要使积是四位数，□内最小可以填( )。

二、选择题9．一张长方形纸对折1次，得到的图形大小是整张纸的( )；如果连续对折4次，得到的图形大小是整张纸的( )。

10．一本书厚约6毫米，5本同样的书摞在一起厚约3（）。

A．毫米B．厘米C．分米11．三位同学参加400米跑步比赛，李强用了65秒，周斌用了1分15秒，刘磊用了70秒，他们三人中，跑得最快的是（）。

A．李强B．周斌C．刘磊12．同学们参加兴趣小组，参加航模组的有25人，参加手工组的有40人，两个组都参加的有8人。

（1）请将上图填写完整。

（2）两个组一共有（ ）人。

13．学校操场跑道一圈长400米，丁丁跑了2圈，再跑（ ）米就是1千米。

A ．600B ．400C ．200D ．10014．下面各图的涂色部分不能用14表示的是（ ）。

A ．B ．C ．D ．15．学校开展了“制作宣传画”和“变废为宝作品展”两项垃圾分类的宣传活动。

《国际法》模拟题一．单项选择题1．现代国际法不承认国家有（A）。

A域外庇护权B领土庇护权C领水庇护权D领域庇护权2．（D）不能行使紧追权。

A军舰 B 军用飞机C政府船舶D民用商船3．所谓“最惠国待遇”是指（D）的待遇。

A高于本国国民 B 等于本国国民C高于第三国国民 D 等于第三国国民4．外交团是（A）方面的团体。

A外交礼仪B外交使团C领事D私人5．现行的国际海底开发制度实行（C）A单一开发制 B 协商开发制C平行开发制 D 自由开发制6．联合国安理会“五大国一致”原则是在（D）确定的。

A 1941年“大西洋宪章”B 1942年“联合国家宣言”C 1944年华盛顿“橡树园会议”D 1945年“雅尔塔会议”7．过境通行制度适用于（C）A内海B历史性海湾C国际航行的海峡 D 群岛水域8．将争端提交由一个若干人组成的委员会。

并由其查明事实。

提出报告和建议促使当事国达成协议。

解决争端的方法称为（D）A 斡旋B 调停C 调查D 和解9．在国际法历史上，最古老的国际法渊源是：（A）A 国际习惯B 国际条约C 一般法律原则D 国际法院判例10．当国家参加的国际条约与《联合国宪章》规定的会员国义务发生冲突时, ( B)A 国际条约的义务应优先履行B 《联合国宪章》的义务应优先履行C 适用“后法优于先法”的原则D 适用“先法优于后法”的原则11．国际法上的承认在承认国和被承认国之间引起一系列法律效果,因此( D)A 承认仅仅是单方面的行为B 承认意味着建交C 承认不具有溯及力D 承认只表明了建交的愿望,并不等于建交12．根据国际实践,排除行为不法性主要有以下几种情形: ( A)A 事先同意B 报复措施C 平时封锁D 武装干涉13．中国和印度之间的边界属于( A)A 传统习惯边界线B 自然边界线C 确定边界线D 条约边界线14．按照《海洋法公约》的规定,群岛国群岛直线基线最长不得超过（C）A 24海里B 100海里C 125海里D 200海里15．庇护权在国际法上（B）A. 是个人的权利；B. 是国家的权利；C. 是个人根据国际法得到的权利；D. 是国家的义务。

2022-2023学年八年级数学上册期末模拟测试题（附答案）一、选择题（共计24分）1．点P（1，2）关于y轴对称点的坐标是（）A．（﹣1，2）B．（1，﹣2）C．（1，2）D．（﹣1，﹣2）2．将下列长度的三根木棒首尾顺次连接，能组成直角三角形的是（）A．1、2、3B．2、3、4C．3、4、5D．4、5、63．如图，点D为△ABC的边BC延长线上一点，关于∠B与∠ACD的大小关系，下列说法正确的是（）A．∠B＞∠ACD B．∠B＝∠ACD C．∠B＜∠ACD D．无法确定4．明明在对一组数据：9，1■，25，25，进行统计分析，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（）A．众数B．中位数C．平均数D．方差5．代入法解方程组时，代入正确的是（）A．x﹣2﹣x＝7B．x﹣2﹣2x＝7C．x﹣2+2x＝7D．x﹣2+x＝7 6．下列计算不正确的是（）A．3﹣＝2B．×＝C．+＝＝3D．÷＝＝27．中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两（我国古代货币单位）；马三匹、牛五头，共价三十八两．问马、牛各价几何？”设马每匹价值x两，牛每头y两，根据题意可列方程组为（）A．B．C．D．8．下表中列出的是一个一次函数的自变量x与函数y的几组对应值：x…﹣2﹣11…y…﹣128…若将该一次函数的图象向下平移2个单位，得到一个新一次函数，下列关于新一次函数的说法中，正确的是（）A．函数值y随自变量x的增大而减小B．函数图象不经过第四象限C．函数图象经过原点D．当x＝2时，y的值为7二、填空题（共计15分）9．请写出一个大于3的无理数．10．命题“同位角相等”是命题（填“真”或“假”）．11．甲，乙两人进行射击比赛，每人射击5次，所得平均环数相等，其中甲所得环数的方差为 2.1，乙所得环数分别为：8，7，9，7，9，那么成绩较稳定的是（填“甲”或“乙”）．12．如图，点P（m+n，4m﹣n）为平面直角坐标系中第一象限内一点，PM⊥x轴于点M，PN⊥y轴于点N，若四边形OMPN是边长为5的正方形，则mn的值为．13．如图，长方体的高为9dm，底面是边长为6dm的正方形，一只蚂蚁从顶点A开始爬向顶点B，那么它爬行的最短路程为dm．三、解答题（计81分）14．计算：（π﹣3）0﹣×+|﹣1|．15．解方程组：16．如图，求图中x的值．17．若是二元一次方程4x﹣3y＝10的一个解，求m的值．18．某校招聘一名数学老师，对应聘者分别进行了教学能力、教研能力和组织能力三项测试，并按教学能力占70%，教研能力占20%，组织能力占10%，计算加权平均数，作为最后评定的总成绩．王伟和李婷都应聘了该岗位，经计算，王伟的最后评定总成绩为87.8分，已知李婷的教学能力、教研能力和组织能力三项成绩依次为88分、84分、86分．若该校要在李婷和王伟两人中录用一人，谁将被录用？19．已知a+b是25的算术平方根，2a﹣b是﹣8的立方根，c是的整数部分，求a+bc的平方根．20．已知：如图：∠BEC＝∠B+∠C．求证：AB∥CD．21．2021年12月12日是西安事变85周年纪念日，西安事变及其和平解决在中国社会发展中占有重要的历史地位，为中国社会的发展起到了无可替代的作用．为此，某社区开展了系列纪念活动，如图，有一块三角形空地ABC，社区计划将其布置成展区，△BCD区域摆放花草，阴影部分陈列有关西安事变的历史图片，现测得AB＝20米，AC＝10米，BD＝6米，CD＝8米，且∠BDC＝90°．（1）求BC的长；（2）求阴影部分的面积．22．为巩固“精准扶贫”成果，市农科院专家指导李大爷种植某种优质水果喜获丰收，上市20天全部销售完，专家对销售情况进行了跟踪记录，并将记录情况绘制成如图所示的函数图象，其中x（天）表示上市时间，y（千克）表示日销售量．（1）当12≤x≤20时，求日销售量y与上市时间x的函数关系式；（2）求出第15天的日销售量．23．如图，在平面直角坐标系中，已知四边形ABCD的四个顶点都在网格的格点上．（1）在图中画出四边形ABCD关于x轴对称的四边形A'B'C'D'；（2）在（1）的条件下，分别写出点A、B、D的对应点A'、B'、D'的坐标．24．某公司对消费者进行了随机问卷调查，共发放1000份调查问卷，并全部收回，根据调查问卷，将消费者年收入情况整理后，制成如下表格（被调查的消费者年收入情况）：年收入/万元38102050被调查的消费者数/人1005003005050（1）根据表中数据，被调查的消费者平均年收入为多少万元？（2）被调查的消费者年收入的中位数和众数分别是和万元．（3）在平均数、中位数这两个数据中，谁更能反映被调查的消费者的收入水平？请说明理由．25．某山区有23名中、小学生因贫困失学需要捐助．资助一名中学生的学习费用需要a元，一名小学生的学习费用需要b元．某校学生积极捐助，初中各年级学生捐款数额与用其恰好捐助贫困中学生和小学生人数的部分情况如下表：年级捐款数额（元）捐助贫困中学生人数（名）捐助贫困小学生人数（名）初一年级400024初二年级420033初三年级7400（1）求a、b的值；（2）初三年级学生的捐款解决了其余贫困中小学生的学习费用，求初三年级学生可捐助的贫困中小学生人数．26．如图，已知直线AB经过点（1，﹣2），且与x轴交于点A（2，0），与y轴交于点B，作直线AB关于y轴对称的直线BC交x轴于点C，点P为OC的中点．（1）求直线AB的函数表达式和点B的坐标；（2）若经过点P的直线l将△ABC的面积分为1：3的两部分，求所有符合条件的直线l的函数表达式．参考答案一、选择题（共计24分）1．解：∵点P（1，2）关于y轴对称，∴点P（1，2）关于y轴对称的点的坐标是（﹣1，2）．故选：A．2．解：A、∵12+22≠32，∴不能组成直角三角形，故A选项错误；B、∵22+32≠42，∴不能组成直角三角形，故B选项错误；C、∵32+42＝52，∴组成直角三角形，故C选项正确；D、∵42+52≠62，∴不能组成直角三角形，故D选项错误．故选：C．3．解：∵∠ACD是△ABC的外角，∴∠ACD＝∠B+∠A，∴∠B＜∠ACD．故选：C．4．解：这组数据的平均数、方差和中位数都与被涂污数字有关，而这组数据的众数为25，与被涂污数字无关．故选：A．5．解：把②代入①得，x﹣2（1﹣x）＝7，去括号得，x﹣2+2x＝7．故选：C．6．解：A．3﹣＝2，故此选项不合题意；B．×＝，故此选项不合题意；C．+无法合并计算，故此选项符合题意；D．÷＝＝2，故此选项不合题意．故选：C．7．解：设马每匹x两，牛每头y两，根据题意可列方程组为：．故选：A．8．解：设原来的一次函数解析式为y＝kx+b（k≠0），代入（﹣2，﹣1），（﹣1，2），得，解得，∴原来的一次函数解析式为y＝3x+5，将该一次函数图象向下平移2个单位，得到新的一次函数的解析式为y＝3x+3，∵k＝3＞0，∴函数值y随自变量x的增大而增大，故A选项不符合题意；∵函数y＝3x+3经过第一、二、三象限，不经过第四象限，故B选项符合题意；∵函数y＝3x+3不是正比例函数，不经过原点，故C选项不符合题意；当x＝2时，y＝3×2+3＝9，故D选项不符合题意，故选：B．二、填空题（共计15分）9．解：由题意可得，＞3，并且是无理数．故答案为：．10．解：两直线平行，同位角相等，命题“同位角相等”是假命题，因为没有说明前提条件．故答案为：假．11．解：∵乙的平均环数为＝8，∴乙射击成绩的方差为×[2×（7﹣8）2+（8﹣8）2+2×（9﹣8）2]＝0.8，∵甲所得环数的方差为2.1，0.8＜2.1，∴成绩比较稳定的是乙，故答案为：乙．12．解：∵P（m+n，4m﹣n）为平面直角坐标系中第一象限内一点，PM⊥x轴于点M，PN⊥y轴于点N，∴PN＝m+n，PM＝4m﹣n，∵四边形OMPN是边长为5的正方形，∴PM＝PN＝5，，∴，则mn的值为6．故答案为：6．13．解：如图，（1）AB＝＝＝3；（2）AB＝＝15，由于15＜3；则蚂蚁爬行的最短路程为15dm．故答案为：15．三、解答题（共计81分）14．解：（π﹣3）0﹣×+|﹣1|＝1﹣3+﹣1＝﹣2．15．解：①×2得：4x+6y＝16③，③﹣②得：11y＝22，解得：y＝2，把y＝2代入②，得4x﹣10＝﹣6，解得：x＝1，故原方程组的解为：．16．解：由题意得：x°+（x+10）°＝（x+70）°，解得：x＝60．即x的值为60．17．解：把代入方程4x﹣3y＝10，可得：12m+4﹣6m+6＝10，解得：m＝0．18．解：李婷的最后评定总成绩为：88×70%+84×20%+86×10%＝87（分），∵王伟的最后评定总成绩为87.8分，87＜87.8，∴王伟将被录用．19．解：∵a+b是25的算术平方根，2a﹣b是﹣8的立方根，∴，解得：，∵4＜5＜9，∴2＜＜3，∴的整数部分是2，∴c＝2，∴a+bc＝1+4×2＝1+8＝9，∴a+bc的平方根为±3．20．证明：如图，过点E作EM∥AB，∴∠B＝∠BEM，∵∠BEC＝∠B+∠C，∠BEC＝∠BEM+∠CEM，∴∠C＝∠CEM，∴EM∥CD，∴AB∥CD．21．解：（1）∵BD＝6米，CD＝8米，∠BDC＝90°，∴BC＝＝＝10（米），答：BC的长为10米；（2）∵AB＝20米，AC＝10米，BC＝10米，∴AB2+BC2＝202+102＝（10）2＝AC2，∴△ABC是直角三角形，且∠ABC＝90，∴S阴影＝S△ABC﹣S△BCD＝AB•BC﹣BD•CD＝×20×10﹣×6×8＝76（平方米）．22．解：（1）当12≤x≤20时，设y与x的函数关系式为y＝kx+b，由题意得：，解得：，∴当12≤x≤20时，y与x的函数关系式为：y＝﹣120x+2 400；（2）当x＝15时，y＝﹣120×15+2 400＝600，所以第15天的日销售量为600千克．23．解：（1）如图所示：四边形A'B'C'D'即为所求；（2）点A、B、D的对应点：A'（﹣5，﹣6），B'（﹣5，﹣2），D'（3，﹣7）．24．解：（1）＝＝10.8（万元），答：被调查的消费者平均年收入约为10.8万元；（2）这组数据从小到大排列后，处在中间位置的两个数都是8万元，因此中位数为8万元；这组数据中出现次数最多的是8万元，因此众数为8万元；故答案为：8，8；（3）中位数更能反映被调查的消费者的收入水平，理由：虽然平均数，中位数均能反映一组数据的集中程度，但平均数易受极端数值影响，所以中位数更能反映被调查的消费者的收入水平．25．解：（1）依题意得：，解得：．答：a的值为800，b的值为600．（2）设初三年级学生可捐助贫困中学生x人，小学生y人，依题意得：，解得：．答：初三年级学生可捐助贫困中学生4人，小学生7人．26．解：（1）设直线AB的函数表达式为y＝kx+b（h≠0）．把点（1，﹣2），（2，0）代入得，解得，∴直线AB为y＝2x﹣4．当x＝0时，y＝2x﹣4＝﹣4，∴B（0，﹣4）．（2）①当直线l经过点B时，如图1．∵直线AB关于y轴对称的直线BC交x轴于点C，∴OA＝OC＝2，∴C（﹣2，0）．∵P为OC的中点，∴P（﹣1，0），∴AP＝3CP，∴S△BCP：S△BAP＝1：3．设此时直线l的表达式为y＝mx+n（m≠0）．将点P（﹣1，0）、B（0，﹣4）代入得，解得，∴此时直线l的表达式为y＝﹣4x﹣4；②当直线l与AB的交点D在第四象限时，如图2．∵A（2，0），C（﹣2，0），B（0，﹣4），∴AC＝4，OB＝4，∴S△ABC＝AC•OB＝×4×4＝8．∵直线l将△ABC的面积分为1：3的两部分，∴S△APD＝S△ABC＝2，∴•AP•|y D|＝2，即×3×|y D|＝2，解得|y D|＝，将y＝﹣代入y＝2x﹣4，得x＝，∴D（，﹣）．设此时直线l的函数表达式为y＝m2x+n2（m2≠0）．将点D（，﹣）、P（﹣1，0）代入得，解得，∴此时直线l的函数表达式为y＝﹣．综上所述，所有符合条件的直线l的函数表达式为y＝﹣4x﹣4或y＝﹣x﹣．。

试卷精选期末达标模拟测试题（4）含答案期末达标检测模拟试题（4）一、积累与运用。

1.选择每小题中加点字读音正确的一项，画"V"。

(1) A.鸟巢(cháo) B.劈开(bì) C.鲍鱼(bāo)(2) A.挑衅(xì) B.笨拙(zhuō) C.琵琶(pí)(3) A.签收(qiān) B.赖账(lǎn) C.昔日(qī)2. 读拼音，写词语。

(1)你别fā lèng（）了，快帮我把cōng huā（）放进锅里。

(2)师长命令我们马上撒退到安全地带，不得wéi kàng（）命令。

(3)由于长时间没有lián xì（）,我们的关系越来越shēng shū（）在战友们的yǎn hù（）下，他终于冲出了敌人的包围圈。

3.按查字典的要求填空。

“据”用音序查字法先查音序再查音节用部首查字法先查部再查画。

“据”在字典中的解释有:①占据;②凭借、依靠;③按照、依据;④可以用作证明的事物。

下列词语中的“据”是什么意思? 请选择。

据理力争（）据为已有（）查无实据（）据险固守（）4. 下列句子中加点词语运用正确的一项是（）A.她有一个独生女儿，身体非常脆弱．．，躺在床上一整年了。

B. 飞机是怎么做到安全飞行的呢?原来是人们从蝙蝠身上得到了启事．．。

C. 不要瞧不起那些灰色的脚，那些脚巴在墙上相当牢固．．。

D. 盘古用他的整个身体建造．．了美丽的世界。

二、在下面括号中填上恰当的词语。

（）的愿望（）的巨人（）地问道一（）大雨一（）豌豆一（）滚珠三、把下面成语补充完整,并选填到句子中。

（）（）不息（）七（）八（）（）不平无可（）（）（）（）会神（）心（）胆（）,谬以千里机不可失, （）1.在一间屋子里（）地拉了许多绳子,绳子上系着许多铃铛。

2.我顺着林荫路望去，看见一只小麻雀呆呆地站在地上，（）地拍打着小翅膀。

2024年天津市数学小学五年级上学期期末模拟试题(答案在后面)一、选择题（本大题有6小题，每小题2分，共12分）1、下列数中，哪个数既是偶数又是质数？A. 2B. 4C. 6D. 82、如果一个正方形的边长是5厘米，那么它的面积是多少平方厘米？A. 10B. 15C. 20D. 253、一个长方形的长是8厘米，宽是4厘米，这个长方形的面积是多少平方厘米？选项：A. 12B. 16C. 24D. 324、小华有一些铅笔，如果他每天用掉3支，那么这些铅笔可以用10天。

如果小华每天用掉5支，那么这些铅笔可以用几天？选项：A. 6天B. 7天C. 8天D. 9天5、一个正方形的周长是20厘米，它的面积是多少？A. 25平方厘米B. 20平方厘米C. 16平方厘米D. 30平方厘米6、如果一个数除以7后余数是2，那么这个数最小是多少？A. 9B. 14C. 20D. 23二、填空题（本大题有6小题，每小题4分，共24分）1、1个苹果的重量是200克，那么4个苹果的总重量是____ 克。

2、一个长方形的长是8厘米，宽是5厘米，这个长方形的周长是 ____ 厘米。

3、一个长方形的长是12厘米，宽是长的一半，那么这个长方形的面积是 ____ 平方厘米。

4、一个三位数，百位和十位上的数字相同，个位上的数字是百位和十位数字的和，这个数最大是 ____ 。

5、一个长方形的长是宽的3倍，如果宽是8厘米，则这个长方形的面积是 ______ 平方厘米。

6、小明有5本书，小华比小明多3本，小红有书的数量是小明的两倍减去2本，那么小华和小红一共有 ______ 本书。

三、计算题（本大题有5小题，每小题4分，共20分）1、计算下列各题。

（1）(325×7+432)（2）(567−234−56)（3）(845÷5×3)（4）(1256÷8−63)2、计算下列各题。

（1）(246×6−378)（2）(765+398−543)（3）(789÷3+252)（4）(1125÷15−432)3、计算以下各题：（1）123 × 45 + 678 ÷ 214、计算以下各题：（1）256 ÷ (4 - 2) + 3 × 85、计算下列各题。

《统计学》模拟试题（第4套）一、单项选择题（每小题1分，共20分）1、为了了解城乡居民家庭收支基本情况，以作为研究城乡居民生活水平的依据，需要进行一次专门调查，最为合适的调查组织形式是（）。

①普查②抽样调查③重点调查④典型调查2、对于一个统计总体（）。

①只能有一个标志②只能有一个统计指标③可以有多个标志④可以有多个统计指标3、统计工作各环节中处于基础环节的工作阶段是（）。

①统计设计②统计调查③统计整理④统计分析4、标准差指标的表现形式属于（）。

①平均指标②比较相对指标③总量指标④强度相对指标5、对统计分组结果表述正确的是（）。

①组内同质性，组间同质性②组内差异性，组间差异性③组内同质性，组间差异性④组内差异性，组间同质性6、某公司2009年四季度主营业务利润计划比上年同期提高6.5%，实际执行结果：超额完成计划3.3%，2009年四季度主营业务利润实际比上年同期增长（）。

① 10% ② 6.5% ③ 3.2% ④ 3.0%7、通过调查几个主要汽车制造企业的汽车生产情况，就可以判断全国汽车生产的基本情况。

这种调查属于（）。

①抽样调查②重点调查③典型调查④普查8、对加权算术平均数的影响起根本作用的是（）。

①权数所在组标志值水平的高低②权数的绝对量大小③各组单位数占总体单位数的比重大小④总体单位数多少9、若按连续变量进行统计分组，其中第一组是200以下，第二组是200—400，第三组是400—600，第四组是600以上，则下列表述正确的是（）。

① 200在第一组② 400在第二组③ 600在第四组④ 600可以在第三组，也可以在第四组10、若时间数列的逐期增长量大体相同，宜拟合（）。

①直线趋势方程②二次曲线方程③指数曲线方程④抛物线趋势方程11、标志变异指标的数值越小，表明（）。

①总体分布越集中，平均指标的代表性越大②总体分布越集中，平均指标的代表性越小③总体分布越分散，平均指标的代表性越大④总体分布越分散，平均指标的代表性越小12、统计误差中的登记性误差（）。

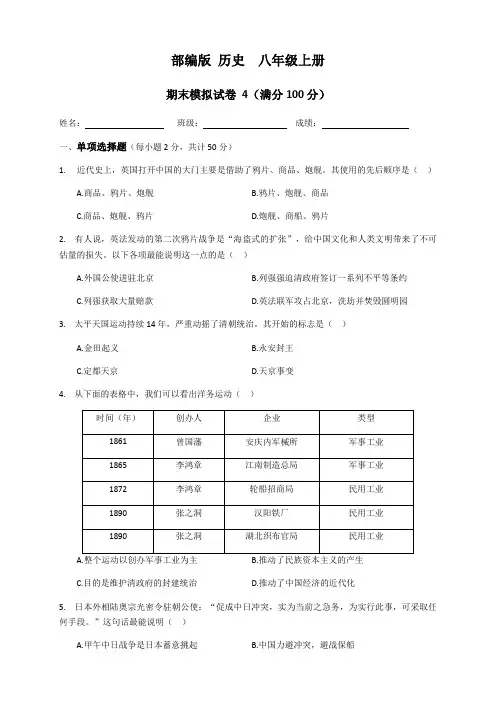
部编版历史八年级上册期末模拟试卷4（满分100分）姓名：班级：成绩：一、单项选择题（每小题2分，共计50分）1.近代史上，英国打开中国的大门主要是借助了鸦片、商品、炮舰。

其使用的先后顺序是（）A.商品、鸦片、炮舰B.鸦片、炮舰、商品C.商品、炮舰、鸦片D.炮舰、商船、鸦片2. 有人说，英法发动的第二次鸦片战争是“海盗式的扩张”，给中国文化和人类文明带来了不可估量的损失。

以下各项最能说明这一点的是（）A.外国公使进驻北京B.列强强迫清政府签订一系列不平等条约C.列强获取大量赔款D.英法联军攻占北京，洗劫并焚毁圆明园3. 太平天国运动持续14年，严重动摇了清朝统治。

其开始的标志是（）A.金田起义B.永安封王C.定都天京D.天京事变4. 从下面的表格中，我们可以看出洋务运动（）A.整个运动以创办军事工业为主B.推动了民族资本主义的产生C.目的是维护清政府的封建统治D.推动了中国经济的近代化5. 日本外相陆奥宗光密令驻朝公使：“促成中日冲突，实为当前之急务，为实行此事，可采取任何手段。

”这句话最能说明（）A.甲午中日战争是日本蓄意挑起B.中国力避冲突，避战保船C.中国是日本占领朝鲜的障碍D.日本独吞朝鲜后入侵中国6. 戊戌变法在中国历史上第一次提出了由传统走向近代的系统方案，倡导博爱、平等、自由、人权。

这些思想观念并没有因变法失败而消失，相反更加深入人心，体现在变法（）A.对中国社会起到了思想启蒙的作用B.推翻了以慈禧为首的顽固派的统治C.使中国走上了发展资本主义的道路D.虽最终失败但挽救了中华民族危机7. “北地终招八国兵，金城坐被联军毁，拳民思想一朝熄，又换奴颜事洋鬼。

”诗句中涉及的历史事件发生在（）A.鸦片战争时期B.第二次鸦片战争时期C.甲午中日战争时期D.八国联军侵华战争时期8. 孙中山认为：“（太平天国失败）最大的原因是，他们那一班人到了南京之后，就互争皇帝，闭起城来自相残杀。

”“那种失败，完全是由于大家想做皇帝。

期末模拟试题卷（四）一、选择题A1型题(最佳选择题肯定型)1．男，40岁，上腹胀痛2年，有呃气，无返酸，血清胃泌素14pg ／ml，胃镜见胃窦部萎缩性胃炎，病理结果为慢性粘膜炎症，伴重度不典型增生。

最理想的治疗方法为：A．手术治疗B．H2-受体阻滞剂C．抗多巴胺受体阻滞剂D．胰酶制剂E．肾上腺皮质激素2．烧伤病人发生多器官系统功能衰竭的最主要原因是：A．呼吸道烧伤B．烧伤休克C．创面感染D．抗生素损害E．肺部感染3．适于手术削痂治疗的烧伤创面是：A．局部红斑，轻度肿胀，有疼痛和灼感B．水泡，剧痛，皮温高，创底肿胀发红C．小水泡，感觉迟钝，皮温稍低，创底红白相间D．无水泡，蜡白或焦黄，感觉消失，皮温低E．焦痂，可见树枝状栓塞血管，无感觉4．对污染较重的伤口清创后暂不予缝合，观察2～3天后如无明显感染，再行缝合，这种缝合称：A．一期缝合B．二期缝合C．延期缝合D．减张缝合E．以上都不是5．战伤救护中，遇肠管脱出体外，转运前下列处理哪项最恰当? A．立即送回腹腔，包扎伤口B．缝线缝扎固定肠管与腹壁再行包扎C．直接用急救包覆盖包扎固定D．敷料覆盖再以钟形器皿(如碗)盖住再包扎E．以生理盐水冲洗后常规包扎保护6．慢性感染是指病程超过：A．1周B．2周C．3周D．1个月E．2个月7．深部脓肿的特点是：A．局部红、肿、热、痛明显B．局部波动感明显C．全身中毒症状不明显D．局部仅有水肿现象，但无压痛E．局部水肿，压痛明显，穿刺可抽到脓液8．下列哪项是血液透析的禁忌证?A．BUN＞30mmol／LB．血清钾＞6.5mmol／LC．血清肌酐＞908μmol／LD．严重酸中毒E．休克9．患者误输异型血后无尿6天，无休克，最有效的治疗应是：A．输注地塞米松B．输注碳酸氢钠C．输注甘露醇D．输注速尿E．血液透析10．二氧化碳蓄积后，如迅速排出可能出现：A．血压下降、呼吸变快B．血压上升、呼吸变快C．血压下降、呼吸暂停D．血压、呼吸均无变化E．血压上升、呼吸变慢11．局麻药中毒早期表现为肌肉颤动，其常见部位是：A．颈部肌肉B．腹部肌肉C．颜面部肌肉D．肩部和胸部肌群E．躯干肌肉12．诊断急性呼吸窘迫综合征最重要的措施是：A．X线胸片有广泛性点、片状阴影B．心电图C．肺部听诊有罗音D．血气分析为低氧血症E．一般吸氧疗法无效13．ARDS的最突出表现为：A．呼吸增快，吸氧后减慢B．紫绀，吸氧后减轻C．动脉血氧分压降低，吸氧后改善D．动脉血氧分压降低，大量给氧也不能改善E．严重胸痛，止痛剂无效14．低阻力型休克最常见于哪种休克? A．失血性休克B．损伤性休克C．感染性休克D．心原性休克E．过敏性休克15．纠正休克所并发的酸中毒的关键在于：A．及时应用大量碱性药物B．过度通气C．改善组织灌注D．利尿排酸E．提高血压16．慢性肠梗阻患者，10天来每天呕吐大量胃肠液，每天给输液为：10％葡萄糖溶液3000ml，5％葡萄糖盐水500ml。

药物化学期末考试模拟试题四一、单项选择题（每小题1分，共1×20=20分)1。

药物的解离度与生物活性的关系是( ）A。

增加解离度，有利于吸收，活性增加 B. 合适的解离度，有最大的活性C. 增加解离度，离子浓度上升活性增强D. 增加解离度，离子浓度下降，活性增强2. 与前药设计的目的不符的是（)A.提高药物的稳定性B. 提高药物的生物利用度C. 提高药物的活性D. 延长药物的作用时间3. 先导化合物是指( ）A。

很理想的临床用药 B. 新化合物C。

不具有生物活性的化合物D. 具有某种生物活性的化学结构，可作为结构修饰和化学改造的化合物4. 从植物中发现的先导物的是（）A.扑热息痛B。

青蒿素C。

红霉素D。

卡托普利5. 下列常用作抗溃疡药的是（)A。

钙拮抗剂B。

β受体阻断剂 C. H2受体拮抗剂D。

H1受体拮抗剂6. 两个非极性区的键合形式是（）A。

电荷转移复合物B。

共价键C。

疏水键D。

氢键7。

经典的Ｈ1受体拮抗剂的通式为（）A。

Ar-X-（CH2)n-NR1R2B。

Ar1Ar2X-（CH2)n— NR1R2C. Ar1Ar2X-（CH2)n- N(CH3)2D。

Ar-X-（CH2)n- N(CH3）28. 由于药物与特定受体相互作用而产生某种药效的药物是( )A. 结构特异性药物B。

前药 C. 软药D。

结构非特异性药物9. 巴比妥类药物的pKa值如下，显效最快的是（)A.苯巴比妥，pKa7。

9(未解离率50％）B。

己锁巴比妥,pKa8。

4（未解离率90%）C。

异戊巴比妥，pKa7.9（未解离率75%）D。

戊巴比妥，pKa8.0（未解离率75%) 10。

吡唑酮类药物具有的药理作用是（）A.催眠镇静B.解热镇痛抗炎C。

抗病毒 D.降血脂11。

奥沙西泮的化学名为（)A.7—氯—1,3-二氢—3—羟基—5—苯基-2H—1，4-苯并二氮卓—2—酮B.7—氯-1,3—二氢-1-甲基-5—苯基-2H-1，4—苯并二氮卓-2-酮C.8-氯—1,3-二氢-3-羟基-5—苯基—2H-1,4-苯并二氮卓—2—酮D.8—氯—1，3—二氢—1-甲基-5—苯基—2H-1，4—苯并二氮卓-2—酮12. 与苯妥英钠的性质不符的是（）A。

2022-2023学年第一学期九年级数学期末模拟测试题（附答案）一、选择题（共计24分）1．已知sinα＝，若α是锐角，则α的度数为（）A．30°B．45°C．60°D．90°2．如图所示几何体的主视图是（）A．B．C．D．3．圆形物体在阳光下的投影可能是（）A．三角形B．圆形C．矩形D．梯形4．如图，l1∥l2∥l3，直线AC和DE分别交l1、l2、l3于点A、B、C和点D、B、E，AB＝4，BC＝8，DB＝3，则DE的长为（）A．4B．5C．6D．95．反比例函数y＝﹣图象上的两点为（x1，y1），（x2，y2），且x1＜x2＜0，则y1与y2的大小关系是（）A．y1＞y2B．y1＜y2C．y1＝y2D．不能确定6．如图，图形甲与图形乙是位似图形，点O是位似中心，点A、B的对应点分别为点A′、B′，若OA'＝2OA，则图形乙的面积是图形甲的面积的（）A．2倍B．3倍C．4倍D．5倍7．如图，四边形ABCD为菱形，若CE为边AB的垂直平分线，则∠ADB的度数为（）A．20°B．25°C．30°D．40°8．已知反比例函数的图象在每个象限内y随x的增大而增大，则关于x的一元二次方程的根的情况是（）A．没有实数根B．有两个相等的实数根C．有两个不相等的实数根D．无法确定二、填空题（共计15分）9．若关于x的方程ax2﹣2ax+1＝0的一个根是﹣1，则a的值是．10．如图，在正方形网格中，△AOC的顶点均在格点上，则tan∠CAO的值为．11．在一个不透明的盒子中装有黑球和白球共200个，这些球除颜色外其余均相同，将球搅匀后任意摸出一个球，记下颜色后放回，通过大量重复摸球试验后，发现摸到白球的频率稳定在0.2，则盒子中白球有个．12．如图，点A为反比例函数的图象上一点，连接AO并延长交反比例函数的图象于另一点B，过点A、B分别作x轴、y轴的平行线，两平行线交于点C，则△ABC的面积为．13．如图，将矩形ABCD放置在平面直角坐标系的第一象限内，使顶点A，B分别在x轴、y轴上滑动，矩形的形状保持不变，若AB＝2，BC＝1，则顶点C到坐标原点O的最大距离为．三、解答题（计81分）14．解方程：（2x﹣9）2＝5（2x﹣9）．15．如图，AD是△ABC的高，cos B＝，sin C＝，AC＝10，求AD及AB的长．16．如图，在四边形ABCD中，AD∥BC，点E在BC上，∠C＝∠DEA．（1）求证：△DEC∽△ADE；（2）若CE＝2，DE＝4，求△DEC与△ADE的周长之比．17．已知反比例函数y＝（k为常数）．（1）若函数图象在第二、四象限，求k的取值范围；（2）若x＞0时，y随x的增大而减小，求k的取值范围．18．如图，在正方形ABCD中，E，F分别为AB，AD上的点，且AE＝AF，点M是EF的中，点，连接CM、CF、CE．求证：CM⊥EF．19．《城镇污水处理厂污染物排放标准》中硫化物的排放标准为1.0mg/L．某污水处理厂在自查中发现，所排污水中硫化物浓度超标，因此立即整改，并开始实时监测．据监测，整改开始第60小时时，所排污水中硫化物的浓度为5mg/L；从第60小时开始，所排污水中硫化物的浓度y（mg/L）是监测时间x（小时）的反比例函数，其图象如图所示．（1）求y与x之间的函数关系式；（2）按规定所排污水中硫化物的浓度不超过0.8mg/L时，才能解除实时监测，此次整改实时监测的时间至少要多少小时？20．如图，▱ABCD的对角线AC、BD交于点O，点E在边CB的延长线上，连接AE，且∠EAC＝90°，AE2＝EB•EC．求证：四边形ABCD是矩形．21．2021年是中国共产党建党100周年，全国各地积极开展以“弘扬红色文化，重走长征路”为主题的教育学习活动，郑州市“二七纪念堂“成为重要的活动基地．据了解，今年3月份该基地接待参观人数10万，5月份接待参观人数增加到12.1万．求这两个月参观人数的月平均增长率．22．一个阳光明媚的午后，王婷和李力两个人去公园游玩，看见公园里有一棵古老的大树，于是，他们想运用所学知识测量这棵树的高度，如图，李力站在大树AB的影子BC的末端C处，同一时刻，王婷在李力的影子CE的末端E处做上标记，随后两人找来米尺测得BC＝10米，CE＝2米．已知李力的身高CD＝1.6米，B、C、E在一条直线上，DC⊥BE，AB⊥BE，请你运用所学知识，帮助王婷和李力求出这棵树的高度AB．23．随着信息技术的迅猛发展，移动支付已成为一种常见的支付方式．在一次购物中，陈老师和陆老师都随机从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付．（1）陆老师选择用“微信”支付的概率是；（2）请用画树状图或列表的方法表示所有结果，并求出两位老师恰好一人用“微信”支付，一人用“银行卡”支付的概率．24．晓琳想用所学知识测量塔CD的高度．她找到一栋与塔CD在同一水平面上的楼房，在楼房的A处测得塔CD底部D的俯角为26.6°，测得塔CD顶部C的仰角为45°，AB ⊥BD，CD⊥BD，BD＝30m，求塔CD的高度．（参考数据：sin26.6°≈0.45，c0s26.6°≈0.89，tan26.6°≈0.50）25．如图，一次函数y＝k1x+b的图象与反比例函数y＝的图象相交于A、B两点，其中点A的坐标为（﹣1，4），点B的坐标为（4，n）．（1）求这两个函数的表达式；（2）一次函数y＝k1x+b的图象交y轴于点C，若点P在反比例函数y＝的图象上，使得S△COP＝9，求点P的坐标．26．如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC＝∠EDF＝90°，△DEF 的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．（1）当点Q在线段CA上时，如图1，求证：△BPE∽△CEQ；（2）当点Q在线段CA的延长线上时，如图2，△BPE和△CEQ是否相似？说明理由；（3）在（2）的条件下，若BP＝1，CQ＝，求PQ的长．参考答案一、选择题（共计24分）1．解：∵sinα＝，α是锐角，∴α的度数为：45°．故选：B．2．解：由题意知，几何体的主视图为，故选：D．3．解：∵同一物体的影子的方向和大小可能不同，不同时刻物体在太阳光下的影子的大小在变．∴圆形物体在阳光下的投影可能是圆形、线段和椭圆形，故选：B．4．解：∵l1∥l2∥l3，∴，∵AB＝4，BC＝8，DB＝3，∴，∴BE＝6，∴DE＝DB+BE＝3+6＝9，故选：D．5．解：∵反比例函数y＝﹣中，k＝﹣6＜0，∴此函数的图象在二、四象限，在每一象限内y随x的增大而增大，∵x1＜x2＜0，∴（x1，y1）、（x2，y2）两点均位于第二象限，∴y1＜y2．故选：B．6．解：由题意可得，甲乙两图形相似，且相似比为，根据相似图形的面积比是相似比的平方可得，图形乙的面积是图形甲的面积的4倍，故选：C．7．解：如图，连接AC，∵四边形ABCD为菱形，∴AB＝BC＝AD，∵CE为边AB的垂直平分线，∴AC＝BC，∴AB＝AC＝BC，∴△ABC是等边三角形，∴∠ABC＝60°，∴∠ABD＝30°，∵AB＝AD，∴∠ADB＝∠ABD＝30°，故选：C．8．解：∵在每一个象限内y随着x增大而增大，∴k＜0，∴一元二次方程的判别式Δ＝b2﹣4ac＝（2k−1）2−4（k2+14）＝﹣4k＞0，∴方程有两个不相等的实数根，故选：C．二、填空题（共计15分）9．解：∵关于x的方程ax2﹣2ax+1＝0的一个根是﹣1，∴a+2a+1＝0，∴3a+1＝0，解得a＝﹣，故答案为：﹣．10．解：∵正方形网格中，△AOC的顶点均在格点上，∴∠ACO＝90°，∴，故答案为：．11．解：因为通过大量重复摸球试验后，发现摸到白球的频率稳定在0.2，所以摸到白球的概率约为0.2，所以白球有200×0.2＝40，故答案为：40．12．解：设点A的坐标为（﹣a，），根据中心对称的性质知点B的坐标为（a，﹣），∴点C的坐标为（a，），∴AC＝2a，BC＝，则△ABC的面积为：×2a×＝12．故答案为：12．13．解：如图，取AB的中点E，连接CE，OE，∵∠AOB＝90°，在Rt△AOB中，OE＝AB＝1，∵∠ABC＝90°，AE＝BE＝CB＝1，∴在Rt△CBE中，CE＝＝，∵OC≤CE+OE＝1+，∴OC的最大值为1+，即点C到原点O距离的最大值是1+，故答案为：1+．三、解答题（共计81分）14．解：方程移项得：（2x﹣9）2﹣5（2x﹣9）＝0，分解因式得：（2x﹣9）（2x﹣9﹣5）＝0，所以2x﹣9＝0或2x﹣14＝0，解得：x1＝4.5，x2＝7．15．解：在Rt△ACD中，，∵，∴，∴AD＝6．在Rt△ABD中，，∴∠B＝60°，∴∠BAD＝90°﹣∠B＝30°．∴，∴，∴．16．证明：（1）∵AD∥BC，∴∠DEC＝∠ADE．又∵∠C＝∠DEA，∴△DEC∽△ADE．解：（2）∵△DEC∽△ADE，∴△DEC与△ADE的周长之比＝＝＝．17．解：（1）∵函数图象在第二、四象限，∴k﹣5＜0，解得：k＜5，∴k的取值范围是k＜5；（2）∵若x＞0时，y随x的增大而减小，∴k﹣5＞0，解得：k＞5，∴k的取值范围是k＞5．18．证明：∵四边形ABCD是正方形∴AB＝AD＝BC＝CD，∠B＝∠D＝90°∵AE＝AF，∴BE＝DF．在△BCE和△DCF中，，∴△BCE≌△DCF（SAS），∴CE＝CF，∵点M是EF的中点，∴CM⊥EF．19．解：（1）设y与x之间的函数关系式为，根据题意，得：k＝xy＝60×5＝300，∴y与x之间的函数关系式为．（2）当y＝0.8时，．20．证明：∵AE2＝EB•EC，∴，又∵∠AEB＝∠CEA，∴△AEB∽△CEA，∴∠EBA＝∠EAC而∠EAC＝90°，∴∠EBA＝∠EAC＝90°，又∵∠EBA+∠CBA＝180°，∴∠CBA＝90°，而四边形ABCD是平行四边形，∴四边形ABCD是矩形．21．解：设这两个月参观人数的月平均增长率为x，根据题意，得：10（1+x）2＝12.1，解得：x1＝0.1＝10%，x2＝﹣2.1（舍去），答：这两个月参观人数的月平均增长率为10%．22．解：根据题意可得，AC∥DE，∴∠DEC＝∠ACB．又∵DC⊥BE，AB⊥BE，即∠DCE＝∠ABC＝90°，∴△ABC∽△DCE，∴．∵BC＝10米，CE＝2米，CD＝1.6米．∴，∴AB＝8米，即这棵树的高度AB为8米．23．解：（1）陆老师选择用“微信”支付的概率是，故答案为：；（2）将“微信”、“支付宝”、“银行卡”三种支付方式分别记为：A、B、C，画树状图如下：共有9种等可能的结果，其中两位老师恰好一人用“微信”支付，一人用“银行卡”支付的结果有2种，∴两位老师恰好一人用“微信”支付，一人用“银行卡”支付的概率为．24．解：过A点作AE⊥CD于E点，由题意得，四边形ABDE为矩形，∵∠DAE＝26.6°，BD＝30m，∴，∴DE＝tan26.6°⋅AE≈0.50×30＝15m，∵∠CAE＝45°，∴∠ACE＝45°，∴AE＝EC＝30m，∴CD＝CE+ED＝30+15＝45（m），∴塔CD的高度是45m．25．解：（1）把点A（﹣1，4）代入反比例函数得，，∴k2＝﹣4，∴反比例函数的表达式为，将点B（4，n）代入得，，∴B（4，﹣1），将A、B的坐标代入y＝k1x+b得，解得∴一次函数的表达式为y＝﹣x+3．（2）在y＝﹣x+3中，令x＝0，则y＝3，∴直线AB与y轴的交点C为（0，3），设P（x，y），由题意得，∴|x|＝6，∴x＝6或x＝﹣6，当x＝6时，，此时点P的坐标为；当x＝﹣6时，，此时点P的坐标为．∴点P的坐标或．26．（1）证明：如图1中，∵△ABC和△DEF是两个全等的等腰直角三角形，∴∠B＝∠C＝∠DEF＝45°，∵∠BEQ＝∠BEP+∠DEF＝∠EQC+∠C，∴∠BEP+45°＝∠EQC+45°，∴∠BEP＝∠EQC，∵∠B＝∠C，∴△BPE∽△CEQ；（2）解：结论：△BPE∽△CEQ．理由：如图2中，∵∠BEQ＝∠EQC+∠C，即∠BEP+∠DEF＝∠EQC+∠C，∴∠BEP+45°＝∠EQC+45°，∴∠BEP＝∠EQC，又∵∠B＝∠C，∴△BPE∽△CEQ；（3）解：∵△BPE∽△CEQ，∴，∵BE＝CE，∴，解得：BE＝CE＝，∴BC＝，∴AB＝AC＝，∴AQ＝CQ﹣AC＝，AP＝AB﹣BP＝3﹣1＝2，在Rt△APQ中，PQ＝．。

部编版四年级上语文期末模拟试题及答案（4）积累运用一、看拼音写词语。

（10分）mào shèng nèn lǜcāng ying yăn hùlǒng zhàoxùn chìwán píhúdiéyíhuòbódòu二、选择正确的读音。

（6分）茅．屋（máo mào) 即．使（ jì jí)淮．安（wéi huái) 轰隆．（lōng lóng)剂．量（jí jì) 芦苇．（wéi wěi)三、选择正确的读音用“√”标出来。

（8分）1.敌人的飞机降（xiáng jiàng)落到这片土地时，人们奋起抵抗，坚决不投降（xiáng jiàng)。

2.课间，王老师像哄小孩似的话，引起了同学们哄（hōng h óng)堂大笑，大家一哄（hōng hóng)而散。

3.梅兰芳宁（nīng nìng)可卖房度日，也决不登台演出。

4.两只旋（xuàn xuán)转（zhuàn zhuăn)的陀螺奋勇搏斗，旋（xuàn xuán)风般撞向对手，刚一接触，又各自闪向一边，然后重整旗鼓再战。

四、根据要求完成下面各题。

（11分）1.把下列词语补充完整，并从中选择合适的词语填空。

（9分）( )大（ )圆（ )七（ )八腾（ )驾（ ) ( )( )无声手（ )足（ ) 铁（ )无（ )①孙悟空不仅能（ ),还能要风得风，要雨得雨。

②包青天是个（ )的清官，所以百姓非常敬重他。

③虽然老师不在，教室里仍然（ ),同学们都在认真练字。

2.仿写句子。

（2分）例：那时没有电灯，没有电视，没有收音机，也没有汽车。

浙江省杭州余杭区2023-2024学年八年级数学第一学期期末考试模拟试题学校_______ 年级_______ 姓名_______注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

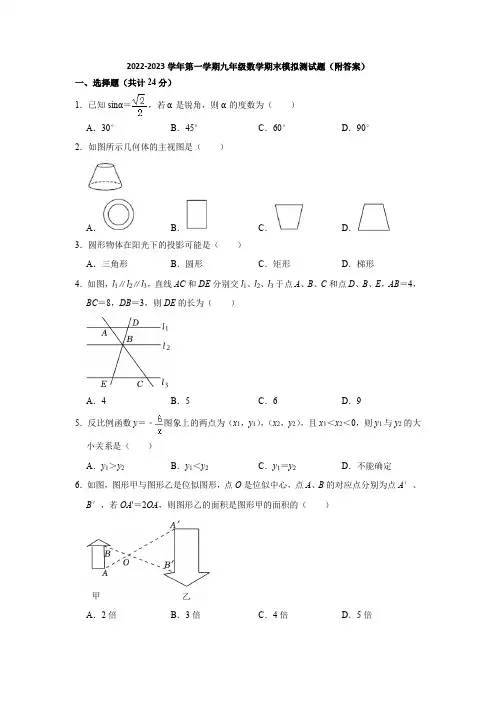
一、选择题（每题4分，共48分）1．小李家装修地面，已有正三角形形状的地砖，现打算购买不同形状的另一种正多边形地砖，与正三角形地砖一起铺设地面，则小李不应购买的地砖形状是( )A．正方形B．正六边形C．正八边形D．正十二边形2．下列各数中，无理数是（）A．0.101001B．0C．5D．2 3 -3．下列条件中，能确定三角形的形状和大小的是（）A．AB＝4，BC＝5，CA＝10 B．AB＝5，BC＝4，∠A＝40°C．∠A＝90°，AB＝8 D．∠A＝60°，∠B＝50°，AB＝54．下列各式中，能用完全平方公式进行因式分解的是() ．A．2x4x4-+B．2x1+C．2x2x2--D．2x4x1++5．如图，以△ABC的顶点B为圆心，BA长为半径画弧，交BC边于点D，连接AD．若∠B＝40°，∠C＝36°，则∠DAC 的大小为（）A．30°B．34°C．36°D．40°6．如图为某居民小区中随机调查的10户家庭一年的月平均用水量（单位：t）的条形统计图，则这10户家庭月均用水量的众数和中位数分别是（）．A．6.5，7B．6.5，6.5C．7，7D．7，6.57．二班学生某次测试成绩统计如下表：则得分的众数和中位数分别是（）得分（分）60 70 80 90 100人数（人）7 12 10 8 3A．70分，70分B．80分，80分C．70分，80分D．80分，70分8．在平面直角坐标系中，点（－1，2）在（）A．第一象限B．第二象限C．第三象限D．第四象限9．在下列交通标识图案中，不是轴对称图形的是（）A．B．C．D．+⨯的值应在（）10．估计5210A．5和6之间B．6和7之间C．7和8之间D．8和9之间11．如图，已知∠ACB＝∠DBC，添加以下条件，不能判定△ABC≌△DCB的是（）A．∠ABC＝∠DCB B．∠ABD＝∠DCAC．AC＝DB D．AB＝DC12．已知：如图，点P在线段AB外，且PA=PB，求证：点P在线段AB的垂直平分线上，在证明该结论时，需添加辅助线，则作法不正确的是（）A ．作∠APB 的平分线PC 交AB 于点C B ．过点P 作PC ⊥AB 于点C 且AC=BC C ．取AB 中点C ，连接PCD ．过点P 作PC ⊥AB ，垂足为C 二、填空题（每题4分，共24分） 13．若112x y+=，则分式22x xy y x xy y -+++的值为__________．14．一个样本的40个数据分别落在4个组内，第1、2、3组数据的个数分别是7、8、15，则第4组数据的频率分别为_______．15．已知点A （x ，2），B （﹣3，y ），若A ，B 关于x 轴对称，则x +y 等于_____． 16．分解因式：3x 2-6x+3=__．17．如图，在ABC ∆中，90BAC ∠=︒，点D 、E 分别在AB 、BC 上，连接DE 并延长交AC 的延长线于点F ，若AF AB BE =+，2BCA BED ∠=∠，5AB =，3CE =，则BD 的长为_________．18．如图，ABC ∆和EBD ∆都是等腰三角形，且100ABC EBD ∠=∠=︒，当点D 在AC 边上时，BAE ∠=_________________度．三、解答题（共78分）19．（8分）已知，如图，在△ABC 中，AD ，AE 分别是△ABC 的高和角平分线，若∠B ＝20°，∠C ＝60°．求∠DAE 的度数．20．（8分）已知：∠AOB 和两点C 、D ，求作一点P ，使PC=PD ，且点P 到∠AOB 的两边的距离相等．（要求：用尺规作图，保留作图痕迹，不写作法，不要求证明）21．（8分）如图，已知△ABC 中，AB=AC=10cm ，BC=8cm ，点D 为AB 的中点．如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动．（1）若点Q 的运动速度与点P 的运动速度相等，经过1s 后，BP= cm ，CQ= cm ．（2）若点Q 的运动速度与点P 的运动速度相等，经过1s 后，△BPD 与△CQP 是否全等，请说明理由； （3）若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使△BPD 与△CQP 全等？ （4）若点Q 以（3）中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿△ABC 三边运动，求经过多长时间点P 与点Q 第一次相遇？22．（10分）在Rt ABC △中，90BAC ∠=︒，2AB AC ==，AD BC ⊥于点D .（1）如图1所示，点,M N 分别在线段,AD AB 上，且90BMN ∠=︒，当30AMN =︒∠时，求线段AM 的长；（2）如图2，点M在线段AD的延长线上，点N在线段AC上，（1）中其他条件不变.①线段AM 的长为；②求线段AN的长.23．（10分）用消元法解方程组35,43 2.x yx y-=⎧⎨-=⎩①②时，两位同学的解法如下：（1）反思：上述两个解题过程中有无计算错误？若有误，请在错误处打“×”.（2）请选择一种你喜欢的方法，完成解答.24．（10分）某电器公司计划装运甲、乙两种家电到农村销售（规定每辆汽车按规定满载，且每辆汽车只能装同一种家电），已知每辆汽车可装运甲种家电20台，乙种家电30台．（1）若用8辆汽车装运甲、乙两种家电共190台到A地销售，问装运甲、乙两种家电的汽车各有多少辆？（2）如果每台甲种家电的利润是180元，每台乙种家电的利润是300元，那么该公司售完这190台家电后的总利润是多少？25．（12分）龙人文教用品商店欲购进A、B两种笔记本，用160元购进的A种笔记本与用240元购进的B种笔记本数量相同，每本B种笔记本的进价比每本A种笔记本的进价贵10元．(1)求A、B两种笔记本每本的进价分别为多少元？(2)若该商店准备购进A、B两种笔记本共100本，且购买这两种笔记本的总价不超过2650元，则至少购进A种笔记本多少本26．（12分）如图1，在平面直角坐标系中，直线AB分别交y轴、x轴于点A（1，a），点B（b，1），且a、b满足a2-4a+4+22b ＝1．（1）求a，b的值；（2）以AB为边作Rt△ABC，点C在直线AB的右侧，且∠ACB＝45°，求点C的坐标；（3）若（2）的点C在第四象限（如图2），AC与x轴交于点D，BC与y轴交于点E，连接DE，过点C作CF⊥BC 交x轴于点F．①求证：CF=12 BC；②直接写出点C到DE的距离．参考答案一、选择题（每题4分，共48分）1、C2、C3、D4、A5、B6、B7、C8、B9、D10、B11、D12、B二、填空题（每题4分，共24分）13、114、0.115、﹣1．16、3(x-1)217、118、1三、解答题（共78分）19、20°20、见详解.21、（1）BP=3cm，CQ=3cm；（2）全等，理由详见解析；（3）154；（4）经过803s点P与点Q第一次相遇．22、（13；（223、（1）解法一中的计算有误；（2）原方程组的解是12 xy=-⎧⎨=-⎩.24、（1）装运甲种家电的汽车有5辆，装运乙种家电的汽车有3辆；（2）该公司售完这190台家电后的总利润是45000元．25、（1）A、B两种笔记本每本的进价分别为20 元、30 元；（2）至少购进A种笔记本35 本26、（2）a＝2，b＝-2；（2）满足条件的点C（2，2）或（2，-2）；（3）①证明见解析；②2．。

2024年江苏省苏州市语文小学四年级上学期期末模拟试题(答案在后面)一、基础知识与积累（本大题有9小题，每小题4分，共36分）1、题目：请根据拼音写出下列汉字。

（1）jiān chī （）（2）lǚxíng （）（3）sèshū （）2、题目：请根据意思写出下列词语。

（1）表示行动迟缓，慢吞吞的样子。

（）（2）表示对别人的关心和爱护。

（）（3）表示用言语或文字表达出来。

（）3、选择正确的读音，把正确选项的字母填在括号里。

（每小题2分，共4分）A. 鲜(xiān)花B. 鲜(xiǎn)见4、根据句子的意思，选择合适的词语填空。

（每小题2分，共4分）•( )的阳光洒在了大地上，一切都变得明亮起来。

A. 温暖B. 炎热5、下列加点字注音完全正确的一项是（）A. 惊叹（jīng zhàn）B. 跌倒（diē dǎo）C. 搬运（bān yùn）D. 拍打（pāi d ǎ）6、下列词语中，字形、字音完全正确的一项是（）A. 梦寐以求（mèng mèi yǐ qiú）B. 眼疾手快（yǎn jí shǒu kuài）C. 奇珍异宝（qízhēn yì bǎo）D. 一丝不苟（yīsī bù gǒu）7、选出下列词语中加点字的正确读音，并解释该字在词中的意思。

（2分）A. 漂亮(piào) “漂亮”在这里读作“piào”，意思是外观好看，美观。

B. 漂亮(piāo) “漂亮”如果读作“piāo”，则意为停留在液体表面不下沉，但此选项不符合本词意。

9、题目：下列词语中，字形、字音完全相同的一组是：A. 漫步、漫步、漫天、漫延B. 跃进、跃然、跃然纸上、跃然心动C. 捐献、捐躯、捐赠、捐助D. 翻译、翻译、翻山越岭、翻箱倒柜二、阅读理解（本部分有2大题，每大题15分，共30分）第一题阅读文章题目：《秋天的礼物》秋天，是一个收获的季节。