第八届奥林匹克全国数学大赛初二的题
- 格式:docx
- 大小:37.22 KB
- 文档页数:3

初二数学竞赛试题7套整理版(含答案)初二数学竞赛试题7套整理版(含答案)第一套试题1. 某数与它的四分之一之和的和是28,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/4)x + x = 28,化简得9/4x = 28,解得 x = 44.2. 有一个矩形,长是宽的3倍,如果长再加上宽再加上1的和等于50,求矩形的长和宽各是多少?解:设矩形的宽为x,则长为3x,根据题意可得方程 3x + x + 1 = 50,化简得 4x + 1 = 50,解得 x = 12,所以长为3 * 12 = 36,宽为12.3. 某个数的三次方减去它自身等于608,求这个数是多少?解:设这个数为x,根据题意可得方程 x^3 - x = 608,化简得 x^3 - x - 608 = 0,因此需求解该方程的解x.4. 甲数和乙数之和是300,甲数比乙数大30,求甲数和乙数各是多少?解:设甲数为x,乙数为y,根据题意可得方程 x + y = 300,x - y = 30,联立这两个方程可以解得甲数x和乙数y.5. 家长购买某品牌的饮料,每瓶售价为5元,如果购买10瓶,优惠50%,那么需要支付的价格是多少?解:购买10瓶优惠50%,相当于购买5瓶的价格,所以需要支付 5 * 10 * (1 - 50%) = 25元.第二套试题1. 学校图书馆购买300本新书,若图书馆中已有书籍500本,现将这些书按每排放10本的方式摆放,共需要多少排?解:新书300本加上原有书籍500本,共计800本书,每排放10本,所以需要 800 / 10 = 80排.2. 小明每天早上跑步30分钟,下午骑自行车25分钟,晚上游泳40分钟,求他一天中运动的总时长是多少分钟?解:小明一天早上跑步30分钟,下午骑自行车25分钟,晚上游泳40分钟,总时长为 30 + 25 + 40 = 95分钟.3. 甲、乙两人开始一起钓鱼,甲每分钟能钓2条鱼,乙每分钟能钓1条鱼,如果他们一起钓了45分钟,那么他们一共钓到了多少条鱼?解:甲每分钟能钓2条鱼,乙每分钟能钓1条鱼,他们一起钓了45分钟,所以甲和乙一共钓到了 2 * 45 + 1 * 45 = 135 条鱼.4. 某商品原价100元,现在打8折,过了一段时间后再降价,降到原价的85%,现在这个商品的售价是多少?解:原价100元,打8折后为 100 * (1 - 80%) = 80元,再降到原价的85%为 80 * 85% = 68元.5. 某人的年收入为12000元,每月生活费占月收入的1/5,那么这个人每月的生活费用是多少元?解:年收入12000元,月收入为 12000 / 12 = 1000元,生活费占收入的1/5,所以生活费用为 1000 * 1/5 = 200元.第三套试题1. 甲、乙两个人合作修一个房子,甲一个人修需要8天,乙一个人修需要12天,问他们一起修需要多少天?解:甲一个人修需要8天,乙一个人修需要12天,他们一起修需要的时间为 1/(1/8 + 1/12) = 4.8天.2. 甲购买一本书花费了原价的3/4,折后价格为60元,问这本书的原价是多少?解:折后价格为60元,花费原价的3/4,所以原价为 60 / (3/4) = 80元.3. 甲、乙两人比赛,甲第一轮跑步用时1分钟,第二轮用时50秒,第三轮用时40秒;乙第一轮跑步用时55秒,第二轮用时45秒,第三轮用时35秒,问谁的平均速度更快?解:甲第一轮跑步用时1分钟,第二轮用时50秒,第三轮用时40秒,平均速度为 (60 + 50 + 40) / 3 = 50 秒/轮;乙第一轮跑步用时55秒,第二轮用时45秒,第三轮用时35秒,平均速度为 (55 + 45 + 35) / 3 = 45 秒/轮;所以甲的平均速度更快.4. 一只小狗每小时能跑5公里,一只小猫每小时能跑8公里,如果它们从同一地点同时出发并分别向东和西跑,4小时后它们相距了多少公里?解:小狗每小时能跑5公里,4小时后跑了5 * 4 = 20公里,小猫每小时能跑8公里,4小时后跑了8 * 4 = 32公里,所以它们相距了 32 -20 = 12 公里.5. 三个连续的偶数相加的和是60,求这三个数分别是多少?解:设第一个偶数为x,那么第二个偶数为x + 2,第三个偶数为x+ 4,根据题意可得方程 x + (x + 2) + (x + 4) = 60,求解该方程可得x及其对应的三个连续偶数.第四套试题1. 一个数的2倍加上5等于13,求这个数是多少?解:设这个数为x,根据题意可得方程 2x + 5 = 13,解得 x = 4.2. 甲乙两数相差22,乙数的2倍与甲数的3倍之和等于70,求甲、乙两数各是多少?解:设甲数为x,乙数为y,根据题意可得方程 y - x = 22,2y + 3x= 70,联立这两个方程可以解得甲数x和乙数y.3. 一辆汽车以每小时80千米的速度行驶,行驶了1小时20分钟后停下来休息,求这段时间内汽车行驶的路程?解:汽车以每小时80千米的速度行驶,1小时20分钟共1.33 小时,所以汽车行驶的路程为 80 * 1.33 = 106.4 千米.4. 甲、乙两个人一起做一件工作,甲单独完成需要4小时,乙单独完成需要6小时,他们一起完成这件工作需要多少小时?解:甲单独完成需要4小时,乙单独完成需要6小时,他们一起完成需要的时间为 1/(1/4 + 1/6) = 2.4小时.5. 一个数加上它的四分之一之和的和是28,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/4)x + x = 28,化简得9/4x = 28,解得 x = 44.第五套试题1. 一条宽10米的路,两边分别种植了向阳向每排7棵树或9棵树,每棵树之间距离相等,而且与路两边相邻树之间距离也相等,问道路中间最宽的地方有多宽?解:分别种植7棵树和9棵树,每棵树之间距离相等,所以道路中间最宽的地方为两排树之间的距离.2. 一个数与4的乘积减去2等于18,求这个数是多少?解:设这个数为x,根据题意可得方程 4x - 2 = 18,解得 x = 5.3. 甲、乙、丙三人合作种田,甲一个人种地需要10天,乙一个人种地需要12天,丙一个人种地需要15天,问他们三个人一起种地需要多少天?解:甲一个人种地需要10天,乙一个人种地需要12天,丙一个人种地需要15天,他们一起种地需要的时间为 1/(1/10 + 1/12 + 1/15) =4.8天.4. 某人共有100元,买了一本书花掉了原价的3/5,剩下的钱还能买另一本原价为80元的书吗?解:100元买了一本书花掉了原价的3/5,剩下的钱为 100 * (1 - 3/5) = 40元,剩下的钱不足以购买另一本80元的书.5. 一团面粉重800克,其中水分为15%,求这团面粉中水分的重量是多少克?解:面粉重800克,其中水分为15%,所以水分的重量为800 * 15% = 120克.第六套试题1. 一个数与它的五分之一之和的和是40,求这个数是多少?解:设这个数为x,根据题意可得方程 x + (1/5)x + x = 40,化简得7/5x = 40,解得 x = 28.57.2. 甲、乙两个人分别完成一项工作需要的时间比为2:5,如果他们一起完成这项工作需要3小时,求乙单独完成这项工作需要多少时间?解:甲、乙两个人分别完成一项工作需要的时间比为2:5,设甲单独完成需要的时间为x,乙单独完成需要的时间为y,根据题意可得方程 2x + 5x = 3,解得 y = 7.5.3. 有两个相交的圆,圆心之间的距离为8,两圆的半径分别为5和3,求两圆相交的弦的长度是多少?解:两个圆的半径分别为5和3,圆心之间的距离为8,利用勾股定理可以求得两圆相交的弦的长度.4. 甲乙两个人一起做一件工作,甲单独完成需要10小时,乙单独完成需要15小时,他们一起完成这件工作需要多少小时?解:甲单独完成需要10小时,乙单独完成需要15小时,他们一起完成需要的时间为 1/(1/10 + 1/15) = 6小时.5. 甲给乙20元,乙给丙30元,丙给甲10元,这三个人一共交易了多少元?解:甲给乙20元,乙给丙30元,丙给甲10元,所以一共交易了20 + 30 + 10 = 60元.第七套试题1. 某数比它的2/3小12,求这个数是多少?解:设这个数为x,根据题意可得方程 x - (2/3)x = 12,化简得 1/3x = 12,解得 x = 36.2. 甲、乙两个人一起修一条路,甲单独修需要8小时,乙单独修需要12小时,也有可能甲的速度是乙的倍数,问他们一起修需要多少小时?解:甲单独修需要8小时,乙单独修需要12小时,他们一起修需要的时间为 1/(1/8 + 1/12) = 4.8小时.3. 某品牌的衣服原价为200元,现在打折8折,过了一段时间后再降价,降到原价的85%,现在这件衣服的售价是多少?解:原价200元,打8折后为 200 * (1 - 80%) = 160元,再降到原价的85%为 160 * 85% = 136元.4. 甲、乙两个人一起做工,甲一个小时能做1/3的工作量,乙一个小时能做1/4的工作量,问他们一起做一份工作需要多少时间?解:甲一个小时能做1/3的工作量,乙一个小时能做1/4的工作量,他们一起做一份工作需要的时间为 1/(1/3 + 1/4) = 12/7小时.5. 某人的年收入为12000元,每月花销占收入的1/4,那么这个人每月的花销是多少元?解:年收入12000元,。

全国奥林匹克数学初二竞赛题
全国奥林匹克数学初二竞赛题
一、数学逻辑
1、已知函数f(x)的定义域为[a,b],若f(a)=8,f(b)=15,求f(c)的值。
2、若函数f(x)的定义域为[a,b],其图像对称轴的方程若为y=kx-k,求a,b的值。
3、已知椭圆的两个焦点F1,F2在x轴上,以及它们到圆心的距离为a,求椭圆方程。
二、不等式
4、设a,b,c分别为正实数,求使a,b,c满足不等式x^2+2ax+2bx+c=0
的有界解集。
5、若x^2+2ax+2bx+c>0,其中a,b,c均为正实数,求对应的x的取值范围。
6、已知x,y,a,b均为正实数,求使x^2+2ax+2bx+y^2+2ay+2by=c的有
界解集。
三、函数
7、已知f(x)的定义域为[2,30],求f(x)的最大值以及f(x)的最小值。
8、已知直线上有m,n两点,求m到n的最短距离以及对应的方程(以
y=mx+b的形式表示)。
9、已知椭圆上有m,n两点,求m到n的最短距离以及对应的方程(以ax^2+by^2+cx+dy+k=0的形式表示)。
四、应用题
10、已知某商品的销售总额为50万,还知该商品的单位成本为100元,求该商品的最大利润。
11、若有两段距离分别为a,b共需要t小时,若要同时全程行驶,求所
需的最大时间。
12、已知f(x)的定义域为[1,50],求f(x)的单调递增区间及它们的
端点值。

初二数学竞赛试题及答案一、选择题(每题4分,共40分)1. 下列哪个数是无理数?A. 0.5B. √2C. 0.33333…D. 3答案:B2. 一个等腰三角形的底边长为6,腰长为5,那么这个三角形的面积是多少?A. 12B. 15C. 18D. 20答案:B3. 如果一个数的平方等于它本身,那么这个数可能是:A. 0B. 1C. -1D. 以上都是答案:D4. 一个两位数,十位上的数字比个位上的数字大3,这个两位数可能是:A. 23B. 47C. 52D. 69答案:B5. 下列哪个分数是最简分数?A. 3/6B. 4/8C. 5/10D. 7/14答案:A6. 一个圆的直径是10厘米,那么这个圆的面积是多少平方厘米?A. 25πB. 50πC. 100πD. 200π答案:C7. 一个数的相反数是-5,那么这个数是:A. 5C. 0D. 10答案:A8. 一个数的绝对值是5,那么这个数可能是:A. 5B. -5C. 0D. 以上都是答案:D9. 一个等差数列的前三项分别是2,5,8,那么这个数列的第五项是多少?A. 11B. 12C. 13答案:A10. 下列哪个图形是轴对称图形?A. 平行四边形B. 梯形C. 等腰三角形D. 不规则多边形答案:C二、填空题(每题4分,共20分)11. 一个等腰直角三角形的斜边长为10厘米,那么这个三角形的面积是______平方厘米。
答案:2512. 如果一个数的立方等于8,那么这个数是______。
答案:213. 一个数的平方根是3,那么这个数是______。
答案:914. 一个数的倒数是1/4,那么这个数是______。
答案:415. 一个圆的周长是31.4厘米,那么这个圆的半径是______厘米。
答案:5三、解答题(每题10分,共40分)16. 已知一个等腰三角形的底边长为8,腰长为10,求这个三角形的高。
解:根据勾股定理,设高为h,则有:h^2 + (8/2)^2 = 10^2h^2 + 16 = 100h^2 = 84h = √84 = 2√21答:这个三角形的高是2√21。

数学竞赛8年级真题试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若函数f(x) = x² 2x + 1,则f(1)的值为?A. 0B. 1C. 2D. 32. 下列哪个数是无理数?A. √9B. √16C. √3D. √13. 若a > b,则下列哪个选项是正确的?A. a c > b cB. a + c < b + cC. ac < bcD. a/c > b/c (c ≠ 0)4. 下列哪个方程的解集是实数集?A. x² + 1 = 0B. x² 2x + 1 = 0C. x² + x + 1 = 0D. x² x + 1 = 05. 若一组数据的平均数为10,则这组数据的和为?A. 5B. 10C. 20D. 50二、判断题(每题1分,共5分)1. 若a > b,则a² > b²。
()2. 两个负数相乘的结果是正数。
()3. 任何实数的平方都是非负数。
()4. 若a、b、c是等差数列,则a²、b²、c²也是等差数列。
()5. 两个无理数的和一定是无理数。
()三、填空题(每题1分,共5分)1. 若a + b = 5,a b = 3,则a = ______,b = ______。
2. 若x² 5x + 6 = 0,则x = ______或x = ______。
3. 若一组数据的方差为4,则这组数据的平均数为______。
4. 若等差数列{an}的前n项和为Sn = 2n² + 3n,则a1 = ______,d = ______。
5. 若函数f(x) = 2x + 3,则f(2) = ______。
四、简答题(每题2分,共10分)1. 解释什么是无理数。
2. 什么是等差数列?给出一个等差数列的例子。
3. 解释函数的定义。

初二数学奥林匹克竞赛题及答案,连结ECEF=交BC于点F,,AD∥BCDE=EC,EF∥AB1、如图,梯形ABCD中,。
DF 是等腰梯形;试说明梯形ABCD(1)2 DCFDC=的形状;,试判断△=(2)若AD=1,BC3,是等腰三角形,若存在,,使△PCD下,射线BC上是否存在一点P(3)在条件(2) PB的长;若不存在,请说明理由。
请直接写出DAECBFCAABCABCDM运动,出发,沿→中,动点→从点2、在边长为6的菱形向终点NDMAC. 交连接于点BNMAB.)如图25-1,当点边上时,连接在1(ADNABN≌①求证:△△;ADABC AM M°,到= 4,求点②若∠的距离;= 60xMxABC )运动所经过的路程为≤(6(2)如图25-2,若∠≤= 90°,记点12ADNx. 试问:为等腰三角形为何值时,△ONOMMOONOMM,的方向运动到左转弯继续运动到,点=沿,使3、对于点、OMOMON ⊥.,这一过程称为且点完成一次“左转弯运动”点关于PPBABCDPPAPP,左转弯运动到正方形左转弯运动到和点,,点关于关于2211PDCPPPPA左转弯运动到,,关于左转弯运动到关于左转弯运动到…….,关于53344P 1)请你在图中用直尺和圆规在图中确定点的位置;(1ADP之间有怎样的关系?并说明理由。
BPA、P,判断△ABP与△2()连接111ABDAD y、在第二象限,为轴建立直角坐标系,并且已知点(3)以为原点、直线AB PPPP三点的坐标.)1,请你推断:、、,(),两点的坐标为(04、1201020094O1PNMCD1图2图4、如图1和2,在20×20的等个距网格(每格的宽和高均是1AABC与单位长)中,Rt△从点M1重合的位置开始,以每秒点当个单位长的速度先向下平移,BC边与网的底部重合时,继续C 同样的速度向右平移,当点ABCP停止△重合时,Rt与点x秒,△设运动时间为移动.yQAC.的面积为CABABC的位置时,请你在网格中画出Rt1,当Rt△△向下平移到(1)如图111QNCAB Rt△关于直线成轴对称的图形;111xyABC的函数关系式,向下平移的过程中,请你求出2,在Rt△与(2)如图yx取得最大值和最小值?最大值和最小值分别是多并说明当分别取何值时,少?yxABC取得最大值和)在Rt△取何值时,向右平移的过程中,请你说明当(3 最小值?最大值和最值分别是多少?为什么?BCEF点作∥的平分线交于O点,过O5、如图①,△ABC中,AB=AC,∠B、∠C F.AC 于E、交AB、之间有怎样的关系,并说、CF EF与BE猜想:(1)图中有几个等腰三角形? 明理由.如果有,AB≠AC,其他条件不变,图中还有等腰三角形吗?(2)如图②,若?间的关系还存在吗BE、CF问中分别指出它们.在第(1)EF与,过O与三角形外角平分线CO交于ABC中∠B的平分线BO(3)如图③,若△CFBE、F于.这时图中还有等腰三角形吗?EF与BC点作OE∥交AB于E,交ACO理你的?说明系关又如何由。

22008年初中数学联赛(初二组)试卷一、选择题(本大题满分56分,每小题8分)1、已知a 、b 、c 是三角形的三边,则a 4+b 4c 4 -2 a 2c 2-2 b 2c 2-2 a 2c 2的值是( )A.恒正 B. 恒负 C.可正可负 D.非负 2、已知a +b +c =0, a1+b1+c1=-4,那么,(a1)2+(b1)2+(c1)2的值是( ) A.3 B. 8 C. 16 D.203、已知:a 1-│a │=1,那么代数式a1+│a │的值是( )A.25B.-25C.-5D. 54、已知│a │=5,b 2=9时,且ab >0则a +b 的值为( ),A. 8B.-2C.-8或8D.-2或25、已知a 、b 、c 是正整数,a >b ,且a 2-a b -a c +bc =7,则a -c 的值为( )A.-1B.-1或-7C.1D.1或7 6、已知△ABC 的一个角是400,且∠A =∠B ,那么∠C 的外角的大小是( )A. 1400B. 800或1000C. 1000或 1400D. 800 或14007、如图,已知FA =FB,FC =FD,下列结论中:①∠A ②DE =CE ;③连接FE ,则FE 平分∠F ,正确的是( ) A. ①② B.②③ C.①③ D.①②③二、填空题(本大题满分40分,每小题8分)1、若x 2+x y +y =14,y 2+x y +x =28,则 x +y 的值为 .2、(3+1)2001-2(3+1)2000-2(3+1)1999+2008= .3、已知x 、y 是实数,43+x +y 2-6y+9=0,若axy-3x=y ,则a= . 4、a 、b 、c 为△ABC 的三边,且3a 3+6a 2b-3a 2c-6abc=0,则△ABC 的形状为 .5、已知x1+y1=5,则yxy x yxy x +++-2252= .1 2三、计算(本大题满分20分,)要求写出必要的步骤.(1)2115141021151410+++--+2) 18612⨯+(1+3)(1-3)四、(本大题满分12分,)如图,在△ABC 中,AD 若AB=5,AC=3,求AD五、(本大题满分12分)如图,在△ABC 中,AB=AC ∠BAC=80°O 为△ABC 内一点,且∠OBC=10°,∠OCA=20°,求∠BAO 的度数.。

F EA DC B 初二数学奥林匹克竞赛题及答案1、如图,梯形ABCD 中,AD ∥BC,DE =EC ,EF ∥AB 交BC 于点F,EF =EC ,连结DF 。
(1)试说明梯形ABCD 是等腰梯形;(2)若AD =1,BC =3,DC 2DCF 的形状;(3)在条件(2)下,射线BC 上是否存在一点P ,使△PCD 是等腰三角形,若存在,请直接写出PB 的长;若不存在,请说明理由。
2、在边长为6的菱形ABCD 中,动点M 从点A 出发,沿A →B →C 向终点C 运动,连接DM 交AC 于点N .(1)如图25-1,当点M 在AB 边上时,连接BN 。
①求证:△ABN ≌△ADN ; ②若∠ABC = 60°,AM = 4,求点M 到AD 的距离; (2)如图25-2,若∠ABC = 90°,记点M 运动所经过的路程为x (6≤x ≤12)试问:x 为何值时,△ADN 为等腰三角形。
3、对于点O 、M ,点M 沿MO 的方向运动到O 左转弯继续运动到N ,使OM =ON ,且OM ⊥ON ,这一过程称为M 点关于O 点完成一次“左转弯运动”.正方形ABCD 和点P ,P 点关于A 左转弯运动到P 1,P 1关于B 左转弯运动到P 2,P 2关于C 左转弯运动到P 3,P 3关于D 左转弯运动到P 4,P 4关于A 左转弯运动到P 5,……. (1)请你在图中用直尺和圆规在图中确定点P 1的位置;(2)连接P 1A 、P 1B ,判断 △ABP 1与△ADP 之间有怎样的关系?并说明理由。
(3)以D 为原点、直线AD 为y 轴建立直角坐标系,并且已知点B 在第二象限,A 、P 两点的坐标为(0,4)、(1,1),请你推断:P 4、P 2009、P 2010三点的坐标.4、如图1和2,在20×20的等PBAON距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网的底部重合时,继续同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动。

第八届 全国数学大赛初二试题(时间:120分钟 满分:140分)题号 一 二三总分 1718 19 20 得分一、选择 题(每小题5分,共40分)1、已知a ,b ,c 为△ABC 三边,且满足a 2c 2-b 2c 2=a 4-b 4,则它的形状为( )A .直角三角形B .等腰三角形C .等腰直角三角形D .等腰三角形或直角三角形2、已知方程组⎩⎨⎧=+=+4535y ax y x 与⎩⎨⎧=-=+5235y x by x 有相同的解,则b a ,的值为( )A .⎩⎨⎧==21b aB .⎩⎨⎧-=-=64b aC .⎩⎨⎧=-=26b aD .⎩⎨⎧==114b a3、甲是乙现在的年龄时,乙l0岁;乙是甲现在的年龄时,甲25岁,那么( ). A .甲比乙大5岁 B .甲比乙大10岁 C .乙比甲大10岁 D .乙比甲大5岁4、化简)2(2)2(2234++-n n n 得( ). A .8121-+n B .12+-n C .87 D .475、如果式子aa ---11)1( 根号外的因式移入根号内,化简的结果为( )A .a -1B .1-aC .1--aD .a --1 6、如图,已知△ABC 中,AB =AC ,∠BAC =90°,直角EPF 的 顶点P 是BC 中点,两边PE 、PF 分别交AB 、AC 于点C 、F , 给出以下四个结论:①AE =CF ; ②△EPF 是等腰直角三角形; ③S 四边形AEPF =21S △ABC ;④EF =AP .当∠EPF 在△ABC 内绕顶点P 旋转时(点E 不与A 、B 重合),上述结论中始终正确的有( )A .1个B .2个C .3个D .4个.7、在实验课上,小明用弹簧称将铁块A 悬于盛有水的水槽中,然后匀速向上提起(不考虑水的阻力),直至铁块完全露出水面一定高度,则下图能反映弹簧称的读数y (单位N )与铁块被提起的高度x (单位cm )之间的函数关系的大致图象是( )A .B .C .D .8、若p 为质数,35p +仍为质数,则57p +为( ).A.质数B.可为质数也可为合数C.合数D.既不是质数也不是合数二、填空题(每小题5分,共40分)9、若关于x 的方程)2(2015)1(--=-x n x m 有无数个解,则m 2015+n 2015= . 10、已知3=xy ,那么yx y xy x +的值为 .11、某数的平方根是22b a +和1364+-b a ,那么这个数是 . 12、设43239-的整数部分为a ,小数部分为b ,则ba b a -+++41111= . 13、直角三角形有一条直角边为11,另外两条边长是自然数,则周长为__________.14、如图,已知直线l :y =33x ,过点A (0,1)作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;……按此作法继续下去,则点A 2015的坐标为 .15.如上图,在四边形ABCD 中,∠A =60°,∠B =∠D =90°,BC =2, CD =3,则AB =16、小明、小强、小华三人参加奥林匹克杯数学大赛,他们是来自北京、上海、成都的选手,并分别获得一、二、三等奖。

八年级奥林匹克数学竞赛题八年级的奥林匹克数学竞赛题相对于一般数学题而言,更侧重考查学生对知识的综合运用能力和解题思维能力,题目相对偏难一些。
接下来是店铺为大家带来的八年级奥林匹克的数学竞赛题,供大家参考。
八年级奥林匹克数学竞赛题目一填空题1、观察下列各式1× 3=3而3=22-1,3×5=15而15=42-1,5×7=35而35=62-1,……,11×13=143而143=122-1;你猜想到的规律用只含一个字母n的式子表示出来是 __ 。
2、a=2005x+2004,b=2005x+2005,c=2005x+2006,代数式a2+b2+c2-ab-bc-ca= 。
3、一个多边形的对角线的条数等于边数的5倍,则这个多边形是_____边形.4、现有铁矿石73吨,计划用载重量分别为7吨和5吨的两种卡车一次运走,已知载重量7吨的卡车每台车的运费为65元,载重量5吨的卡车每台车运费为50元,则最省的运费是元。
5、100个数据分成5组,其中第一、二小组的频率之和等于0.11,第四、五小组的频率之和等于0.27,则第三小组的频数等于_______________。
6、甲、乙、丙三人进行智力抢答活动,规定:第一个问题由乙提出,由甲、丙抢答.以后在抢答过程中若甲答对1题,就可提6个问题,乙答对1题就可提5个问题,丙答对1题就可提4个问题,供另两人抢答.抢答结束后,总共有16个问题没有任何人答对,则甲、乙、丙答对的题数分别是________。
7、在四边形ABCD中,如果要使对角线AC⊥BD,可添加条件(只需填写一个你认为适当的条件即可)。
8、有3堆硬币,每枚硬币的面值相同.小李从第1堆取出和第2堆一样多的硬币放入第2堆;又从第2堆中取出和第3堆一样多的硬币放人第3堆;最后从第3堆中取出和现存的第1堆一样多的硬币放人第1堆,这样每堆有16枚硬币,则原来第1堆有硬币___枚,第2堆有硬币____枚,第3堆有硬币_____枚.9、盒子里有10个球,每个球上写有1~10中的1个数字,不同的球上数字不同,其中两个球上的数的和可能是3,4,…,19.现从盒中随意取两个球,这两个球上的数的和,最有可能出现的是_______。

一,选择题。
1、已知a 、b 都是正整数,那么以a 、b 和8为边组成的三角形有(D )A 、3个B 、4个C 、5个D 、无数个2、将一长方形切去一角后得一边长分别为13、19、20、25和31的五边形(顺序不一定按此),则此五边形的面积为(C )A 、680 B 、720 C 、745 D 、760 3、已知四边形ABCD 为任意凸四边形,E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点,用S 、P 分别表示四边形ABCD 的面积和周长;S 1、P 1分别表示四边形EFGH 的面积和周长.设K = S S 1,K 1 = PP 1,则下面关于K 、K 1的说法正确的是(A ).A .K 、K 1均为常值B .K 为常值,K 1不为常值C .K 不为常值,K 1为常值D .K 、K 1均不为常值二,填空题。
1、如图,△ABC 是一个等边三角形,它绕着点P 旋转,可以与等边△ABD重合,则这样的点P 有__3_____个。
2、如图,现有棱长为a 的8个正方体堆成一个棱长为2a 的正方体,它的主视图、俯视图、左视图均为一个边长为2a 的正方形,现如果要求从图中上面4个正方体中拿去2个,而三个视图的形状仍不改变,那么拿去的2个正方体的编号应为____A 、C 或B 、D______。
3、如图、如图,G ,G 是边长为4的正方形ABCD 的边BC 上一点上一点,,矩形DEFG 的边EF 过点A,GD=5,A,GD=5,则则FG 的长为的长为_____3,2_____. _____3,2_____.4、如图,P 为平行四边形ABCD 内一点,内一点,过点过点P 分别作AB 、AD 的平行线交平行四边形E 、F 、G 、H 四点,若S AHPE =3, S PFCG =5,则S△PBD= 1 5、如图,边长分别为1、2、3、4、……2007、2008的正方形叠放在一起,则图中阴影部分D CBAABCDF AEHBP DGC BCDFGE A的面积和为的面积和为 20170362017036 。

数学奥林匹克竞赛试卷(八年级)一、选择题1、已知三点A(2,3),B(5,4),C(-4,1)依次连接这三点,则( )A、构成等边三角形B、构成直角三角形C、构成锐角三角形D、三点在同一直线上2、边长为整数,周长为20的三角形个数是()A、4个B、6个C、8个D、123、N=31001+71002+131003,则N的个位数字是()A、3B、6C、9D、04、P为正方形ABCD内一点,若PA:PB:PC=1:2:3,则∠APB的度数为()A、120°B、135°C、150°D、以上都不对6、已知a+b+c≠0,且a+bc=b+ca=a+cb=p,则直线y=px+p不经过()A、第一象限B、第二象限C、第三象限D、第四象限7、计算(1252011)(2462010)的结果是()A.1004 B.1006 C.1008 D.10108、如果有四个不同的正整数m、n、p、q满足(7-m)(7-n)(7-p)(7-q)=4,那么m+n+p+q等于()A.21 B.24 C.26 D.289、如图2,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,AD的延长线交BF于E,且E为垂足,则结论①AD=BF,②CF=CD,③AC+CD=AB,④BE=CF,⑤BF=2BE,其中正确的结论的个数是()A.4 B.3 C.2 D.110、如果实数8181m n mm n m nn m n,且,则()A.7 B.8 C.9 D.10 二、填空题11、如果a是方程x2-3x+1=0的根,那么分式2a5-6a4+2a3-a2-13aF( 图2 )EDCBA的值是;12、甲乙两个机器人同时按匀速进行100米速度测试,自动记录仪表明:当甲距离终点差1米,乙距离终点2米;当甲到达终点时,乙距离终点 1.01米,经过计算,这条跑道长度不标准,这这条跑道比100米多;13、根据图中所标的数据,图中的阴影部分的面积是;14、有三个含有30°角的直角三角形,它们的大小互不相同,但彼此有一条边相等,这三个三角形按照从大到小的顺序,其斜边的比为;15.若(20114149aQ a ,)是第三象限内的点,且a 为整数,则a =.16.若实数22222313-2x y x y S x y,满足,,则S 的取值范围是.17.在△ABC 中,三个内角的度数均为整数,且∠A<∠B<∠C ,5∠C=9∠A ,则∠B 的度数是.18.已知22302010 672010xyxy,,则.三、解答题(本大题共有3小题,第11小题20分,第12、13小题各25分,满分70分)19、已知△ABC 是等边三角形,E 是AC 延长线上一点,选择一点D ,使得△CDE是等边三角形,如果M 是线段AD 的中点,N 是线段BE 的中点,求证:△CMN 是等边三角形20、已知n是大于1的整数求证:n3可以写出两个正整数的平方差21、已知正整数x、y满足条件:2x+1y=a,(其中,a是正整数,且x<y)求x和y。

一、选择题(每题5分,共20分)1. 下列数中,不是有理数的是()A. 2/3B. -1/4C. √2D. 3.142. 已知a=2,b=-3,那么a²+b²的值是()A. 1B. 5C. 13D. 173. 下列图形中,不是轴对称图形的是()A. 正方形B. 等边三角形C. 等腰梯形D. 长方形4. 下列等式中,不成立的是()A. a²+b²=c²(c为直角三角形斜边)B. (a+b)²=a²+2ab+b²C. (a-b)²=a²-2ab+b²D. (a+b)(a-b)=a²-b²5. 已知函数f(x)=3x²-4x+1,当x=2时,f(x)的值是()A. 5B. 7C. 9D. 11二、填空题(每题5分,共20分)6. 分数4/5的倒数是__________。
7. 下列数中,最小的负整数是__________。
8. 一个等腰三角形的底边长为6cm,腰长为8cm,那么这个三角形的周长是__________cm。
9. 若a、b、c为三角形的三边,且满足a+b>c,b+c>a,a+c>b,那么这个三角形一定是__________三角形。
10. 在平面直角坐标系中,点A(2,3),点B(-1,-2),那么线段AB的中点坐标是__________。
三、解答题(每题20分,共80分)11. (10分)已知一元二次方程x²-5x+6=0,求它的两个根。
12. (10分)已知函数f(x)=2x+1,求函数f(x)的值域。
13. (10分)已知等差数列{an}的首项为2,公差为3,求第10项an的值。
14. (10分)已知直角三角形ABC中,∠C=90°,AB=10cm,BC=6cm,求AC的长度。
15. (10分)已知函数f(x)=ax²+bx+c(a≠0),若f(1)=2,f(2)=5,f(3)=10,求a、b、c的值。

初二数竞赛试题及答案初二数学竞赛试题一、选择题(每题3分,共15分)1. 下列哪个数不是有理数?A. πB. √2C. 0.33333(无限循环)D. 1/32. 如果一个数的平方等于81,那么这个数是:A. 9B. -9C. 9 或 -9D. 813. 一个直角三角形的两条直角边分别为3和4,那么它的斜边长是:A. 5B. 6C. 7D. 84. 一个数列的前三项为2, 4, 6,这个数列是:A. 等差数列B. 等比数列C. 既不是等差数列也不是等比数列D. 无法判断5. 以下哪个是二次方程的解:A. x = 1/2B. x = 2C. x = -3D. x = 0二、填空题(每题2分,共10分)6. 一个数的立方等于-27,这个数是_________。
7. 如果一个数的绝对值是5,那么这个数可以是_________。
8. 一个数的倒数是1/4,那么这个数是_________。
9. 一个数的平方根是4,那么这个数是_________。
10. 一个数的平方根是-4,那么这个数是_________。
三、解答题(每题5分,共20分)11. 解方程:2x + 3 = 11。
12. 证明:如果一个三角形的两边分别为a和b,且a < b,那么这个三角形的周长不可能是偶数。
13. 计算:(2x + 3)(x - 4)。
14. 一个圆的半径是5厘米,求它的面积。
四、证明题(每题5分,共10分)15. 证明:直角三角形的斜边的平方等于两直角边的平方和。
16. 证明:如果一个数的平方是正数,那么这个数本身是正数或负数。
五、综合题(每题10分,共10分)17. 一个班级有40名学生,其中20名男生和20名女生。
如果随机抽取一名学生,求以下概率:A. 抽到男生的概率。
B. 抽到女生的概率。
C. 如果已经知道抽到的是男生,那么这名男生是班长的概率。
答案:一、选择题1. A2. C3. A4. A5. D二、填空题6. -37. ±58. 49. 1610. 无实数解三、解答题11. 解:2x + 3 = 11,2x = 8,x = 4。
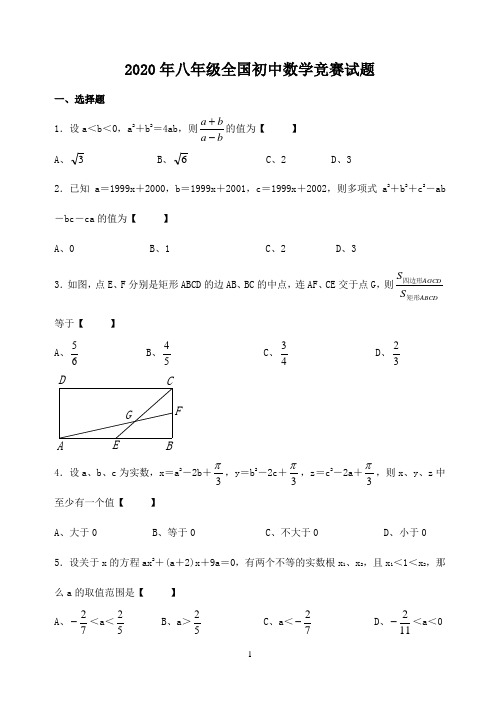
2020年八年级全国初中数学竞赛试题一、选择题1.设a <b <0,a 2+b 2=4ab ,则ba ba -+的值为【 】 A 、3 B 、6 C 、2 D 、32.已知a =1999x +2000,b =1999x +2001,c =1999x +2002,则多项式a 2+b 2+c 2-ab -bc -ca 的值为【 】A 、0B 、1C 、2D 、33.如图,点E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连AF 、CE 交于点G ,则ABCDAGCD S S 矩形四边形等于【 】 A 、65 B 、54 C 、43 D 、32ABC DEF G4.设a 、b 、c 为实数,x =a 2-2b +3π,y =b 2-2c +3π,z =c 2-2a +3π,则x 、y 、z 中至少有一个值【 】A 、大于0B 、等于0C 、不大于0D 、小于0 5.设关于x 的方程ax 2+(a +2)x +9a =0,有两个不等的实数根x 1、x 2,且x 1<1<x 2,那么a 的取值范围是【 】 A 、72-<a <52 B 、a >52 C 、a <72- D 、112-<a <06.A 1A 2A 3…A 9是一个正九边形,A 1A 2=a ,A 1A 3=b ,则A 1A 5等于【 】 A 、22b a + B 、22b ab a ++ C 、()b a +21D 、a +b 二、填空题7.设x 1、x 2是关于x 的一元二次方程x 2+ax +a =2的两个实数根,则(x 1-2x 2)(x 2-2x 1)的最大值为 。
8.已知a 、b 为抛物线y =(x -c)(x -c -d)-2与x 轴交点的横坐标,a <b ,则b c c a -+-的值为 。
9.如图,在△ABC 中,∠ABC =600,点P 是△ABC 内的一点,使得∠APB =∠BPC =∠CPA ,且PA =8,PC =6,则PB = 。


八年级数学竞赛练习题一、选择题:1.如果a >b ,则2a -b 一定是( )A.负数B.正数C.非负数D.非正数2.n 是某一正整数,由四位学生分别代入代数式n 3-n 算出的结果如下,其中正确的结果是( )A.337414B.337415C.337404D.3374033.三进位制数201可表示为十进位制数21023031319⨯+⨯+⨯=,二进位制数1011可表示为十进位制数32101202121211⨯+⨯+⨯+⨯=,现有三进位制数a=221,二进位制数b=10111,则a ,b 的大小关系是( )A.a >bB.a=bC.a <bD.不能比较4.若2x+5y+4z=6,3x+y-7z=-4,则x+y-z 的值为( )A.-1B.0C.1D.45.过点P (-1,3)作直线,使它与两坐标轴围成的三角形面积为5,这样的直线可以作( )A.1条B.2 条C.3条D.4条6.已知731-的整数部分是a ,小数部分是b ,则a 2+(1+7)ab=( )A.12B.11C.10D.97.某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘,根据需要,单片软件至少买3片,盒装磁盘至少买2盒,则不同的选购方式共有( )A.5种B.6种C.7种D.8种8.如图,是一个边长为2的正方体,现有一只蚂蚁要从一条棱的中点A 处沿正方体的表面到C 处,则它爬行的最短线路长是( )A.5B.4C.13D. 17二、填空题:9.如果整数a(a ≠2)使得关于x 的一元一次方程ax+5=a 2+2a+2x 的解是整数,则满足条件的所有整数a 的和是__________.10. 对于所有的正整数k,设直线kx+(k+1)y-1=0与两坐标轴所围成的直角三角形的面积为Sk ,则 S1+S2+S3+…+S2006= .11. 一只猴子爬一个8级的梯子,每次可爬一级或上跃二级,最多上跃三级。

初二的数学竞赛试题及答案初二数学竞赛试题一、选择题(每题3分,共15分)1. 下列哪个数是无理数?A. -3.14B. √2C. 0.33333(无限循环)D. 1/32. 如果一个直角三角形的两条直角边分别为3和4,那么斜边的长度是?A. 5B. 6C. 7D. 83. 一个数的平方根是它本身,这个数是?A. 0B. 1C. -1D. 24. 以下哪个不是二次根式?A. √3B. 2√2C. √(-1)D. √45. 一个多项式P(x) = x^2 - 5x + 6可以分解为?A. (x - 1)(x - 6)B. (x - 2)(x - 3)C. (x - 3)(x - 2)D. (x + 1)(x + 6)二、填空题(每题3分,共15分)6. 如果一个数的立方根是2,那么这个数是______。
7. 一个数的相反数是-5,那么这个数是______。
8. 如果一个数的绝对值是7,那么这个数可以是______或______。
9. 一个二次方程x^2 + ax + b = 0的判别式是______。
10. 如果一个分数的分子是3,分母是6,那么这个分数化简后的结果是______。
三、解答题(每题10分,共70分)11. 解方程:2x + 5 = 3x - 2。
12. 证明:如果一个三角形的两边和这两边之间的夹角相等,那么这个三角形是等腰三角形。
13. 计算:(2a + 3b)(2a - 3b)。
14. 化简:(3x^2 - 2x + 1) / (x + 1)。
15. 解不等式:3x - 5 > 2x + 4。
答案一、选择题1. B2. A3. A4. C5. C二、填空题6. 87. 58. 7, -79. a^2 - 4b10. 1/2三、解答题11. 解:2x + 5 = 3x - 2x = 712. 证明:设三角形ABC中,AB = AC,∠BAC = ∠BAC,根据SAS(边角边)相似,△ABC ∽ △BAC,所以AB = AC,故△ABC是等腰三角形。

初中二年级数学奥林匹克竞赛训练题目录本内容适合八年级学生竞赛拔高使用。
注重中考与竞赛的有机结合,重点落实在中考中难以上题、奥赛方面的基础知识和基本技能培训和提高。
本内容难度适中,讲练结合,由浅入深,讲解与练习同步,重在提高学生的数学分析能力与解题能力。
另外在本次培训中,内容的编排大多大于120分钟的容量,因此在实际教学过程中可以根据学生的具体状况和层次,由任课教师适当的调整顺序和选择内容(如专题复习可以提前上)。
注:有(*) 标注的为选做内容。
本次培训具体计划如下,以供参考:第一讲如何做几何证明题第二讲平行四边形(一)第三讲平行四边形(二)第四讲梯形第五讲中位线及其应用第六讲一元二次方程的解法第七讲一元二次方程的判别式第八讲一元二次方程的根与系数的关系第九讲一元二次方程的应用第十讲专题复习一:因式分解、二次根式、分式第十一讲专题复习二:代数式的恒等变形第十二讲专题复习三:相似三角形第十三讲结业考试(未装订在内,另发)第十四讲试卷讲评第一讲:如何做几何证明题【知识梳理】1、几何证明是平面几何中的一个重要问题,它对培养学生逻辑思维能力有着很大作用。
几何证明有两种基本类型:一是平面图形的数量关系;二是有关平面图形的位置关系。
这两类问题常常可以相互转化,如证明平行关系可转化为证明角等或角互补的问题。
2、掌握分析、证明几何问题的常用方法:(1)综合法(由因导果),从已知条件出发,通过有关定义、定理、公理的应用,逐步向前推进,直到问题的解决;(2)分析法(执果索因)从命题的结论考虑,推敲使其成立需要具备的条件,然后再把所需的条件看成要证的结论继续推敲,如此逐步往上逆求,直到已知事实为止;(3)两头凑法:将分析与综合法合并使用,比较起来,分析法利于思考,综合法易于表达,因此,在实际思考问题时,可合并使用,灵活处理,以利于缩短题设与结论的距离,最后达到证明目的。
3、掌握构造基本图形的方法:复杂的图形都是由基本图形组成的,因此要善于将复杂图形分解成基本图形。
第八届奥林匹克全国数学大赛初二的题题目一:第八届奥林匹克全国数学大赛初二组
一、选择题(共20题,每题4分,共80分)
1. 在一个等差数列中,首项为3,公差为5,第5项为23,则这个等差
数列的前n项和Sn为__________。
2. 已知一组数的平均值是18,如果将其中一个数3改成2,则新的平
均值为____。
3. 若一个正整数除以8余2,除以10余6,求这个数除以40的余数是
多少?
4. 若直线y=3x+2与圆的方程为$x^2+y^2-2x-4y-11=0$,求这个圆与y
轴的交点坐标。
5. 若正方形的边长为a,则其对角线的长度为______。
6. 若两条直线的斜率之和为5,斜率之积为-6,则这两条直线的方程分
别是______。
7. 若甲乙两个数的和是100,乙丙两个数的和是80,乙数比丙数多10,求甲数是多少?
8. 若一个正整数除以5余3,除以6余4,求这个数除以30的余数是多少?
9. 设A、B、C三个整数满足A<B<C,如果A、B、C是一个等差数列,则这个等差数列的公差为______。
10. 若集合A={1, 2, 3},集合B={2, 3, 4},则集合A与集合B的并集为______。
二、填空题(共5题,每题6分,共30分)
1. 在一个等差数列中,首项为2,公差为4,若前n项的和为56,则这个等差数列的第n项为______。
2. 设矩形的长是宽的3倍,周长为72,这个矩形的长和宽的分别是
______。
3. 若$ax^2+bx+c$的图像与x轴两交点均为负数,则a、b、c的关系式为______。
4. 若直线y=2x-7与直线y=kx-2平行,则k的值为______。
5. 设一个正整数的个、十位数字和为12,将该数字的个、十位数字对调后,新数字比原数字增大36,该正整数为______。
三、解答题(共5题,每题10分,共50分)
1. 设$\log_5{x}=a,\log_3{x}=b$,求$\log_{75}{x}$的值。
2. 若正方体三个相邻顶点上的数字之和为15,求该正方体的体积。
3. 判断函数$y=2x^2-3x+1$的单调性,并画出该函数的图像。
4. 已知$\frac{1}{a}+\frac{1}{b}=\frac{2}{5}$,求$\frac{2a+3b}{5a}$的值。
5. 一条长为12米的绳子上有7只蚂蚁在爬行,每只蚂蚁匀速爬行,蚂蚁每次都随机选择一方向爬行的距离,每次爬行的距离在0到12米之间,已知蚂蚁爬行的总距离是有限的,求蚂蚁爬行的总距离可能的最小值和最大值。
四、证明题(共2题,每题15分,共30分)
1. 证明:如果两个整数互质,那么它们的乘积也是它们的最小公倍数。
2. 设由0、1两个数字组成的6位数有多少个?请按照正确的计算步骤
给出计算过程。