重庆大学工程力学作业解答

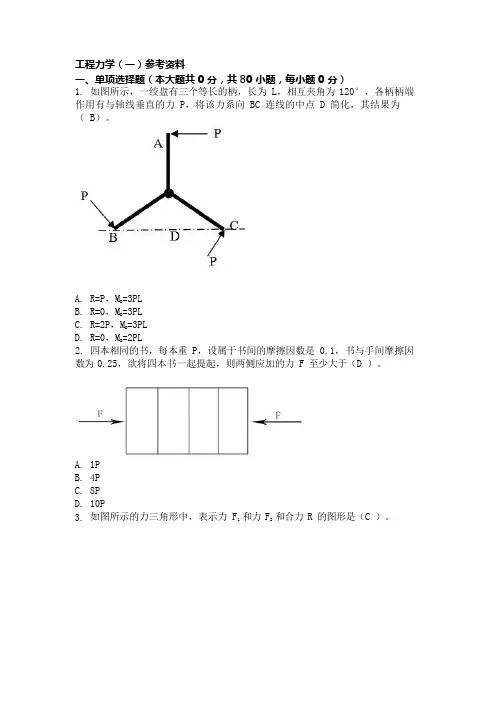
工程力学（一）参考资料一、单项选择题（本大题共 0 分，共 80 小题，每小题 0 分）1.如图所示，一绞盘有三个等长的柄，长为 L，相互夹角为120°，各柄柄端作用有与轴线垂直的力 P，将该力系向 BC 连线的中点 D 简化，其结果为（ B）。

=3PLA.R=P，MDB.R=0，M=3PLD=3PLC.R=2P，MDD.R=0，M=2PLD2.四本相同的书，每本重 P，设属于书间的摩擦因数是 0.1，书与手间摩擦因数为 0.25，欲将四本书一起提起，则两侧应加的力 F 至少大于（D ）。

A.1PB.4PC.8PD.10P3.如图所示的力三角形中，表示力 F1 和力 F2 和合力 R 的图形是（C ）。

A.图1B.图2C.图3D.图44.如图所示某种材料的σ-ε曲线，若在 k 点时将荷载慢慢卸掉，则σ-ε曲线将沿着与 Oa 平行的直线 kA 回落到 A 点，从图可以看出（ B）。

A.OA 段是弹性变形，AB 段是塑性变形B.OA 段是塑性变形，AB 段是弹性变形C.如果在重新加载，σ-ε曲线将沿着 Oa 上升到 k 点D.如果在重新加载，σ-ε曲线将沿着 Bk 上升到 k 点5.图示简支梁，已知 C 点的挠度为 y，在其他条件不变的情况下，若将荷载 F 增大一倍，则 C 点的挠度为（ C）。

A. 0.5y；B.y；C.2y；D.4y。

6.简支梁受力如图，下列说法正确的是（B ）。

A.1-1 截面的弯矩为零，3-3 截面的弯矩为零；B.1-1 截面的弯矩为-12kN.m，3-3 截面的弯矩为零；C.1-1 截面的弯矩为 12kN.m，3-3 截面的弯矩为零；D.3-3 截面的弯矩不为零；7.图示悬臂梁拟用(a)(b)两种方式搁置，则两种情况下的最大应力（σmax）ａ／(σmax）b 为之比为（A ）。

A. 1/4B. 1/16C. 1/64D. 48. 冲床如图所示，若要在厚度为δ的钢板上冲出直径为 d 的圆孔，则冲头的冲压力 F 必须不小于（D ）。

工程力学课后解答5、9 题图5、9所示中段开槽得杆件,两端受轴向载荷P 得作用,试计算截面1-1与2-2上得应力。

已知:P = 140kN,b = 200mm,b 0 = 100mm,t = 4mm 。

题图5、9解:(1) 计算杆得轴力 kN 14021===P N N (2) 计算横截面得面积21m m 8004200=⨯=⨯=t b A202mm 4004)100200()(=⨯-=⨯-=t b b A (3) 计算正应力MPa 1758001000140111=⨯==A N σ MPa 3504001000140222=⨯==A N σ (注:本题得目得就是说明在一段轴力相同得杆件内,横截面面积小得截面为该段得危险截面)5、10 横截面面积A=2cm 2得杆受轴向拉伸,力P=10kN,求其法线与轴向成30°得及45°斜截面上得应力ασ及ατ,并问m ax τ发生在哪一个截面？ 解:(1) 计算杆得轴力kN 10==P N(2) 计算横截面上得正应力MPa 501002100010=⨯⨯==A N σ(3) 计算斜截面上得应力MPa 5.37235030cos 2230=⎪⎪⎭⎫ ⎝⎛⨯==σσMPa 6.2123250)302sin(230=⨯=⨯=στ MPa 25225045cos 2245=⎪⎪⎭⎫⎝⎛⨯==σσMPa 251250)452sin(245=⨯=⨯=στ (4) m ax τ发生得截面 ∵0)2cos(==ασαταd d 取得极值 ∴ 0)2cos(=α 因此:22πα=, 454==πα故:m ax τ发生在其法线与轴向成45°得截面上。

(注:本题得结果告诉我们,如果拉压杆处横截面得正应力,就可以计算该处任意方向截面得正应力与剪应力。

对于拉压杆而言,最大剪应力发生在其法线与轴向成45°得截面上,最大正应力发生在横截面上,横截面上剪应力为零) 5、17 题图2、17所示阶梯直杆AC ,P =10kN,l 1=l 2=400mm,A 1=2A 2=100mm 2,E =200GPa 。

答案+我名字2020年春季学期课程作业工程力学（一）第1次工程力学（一）题号一二合计已做/题量20 / 2020 / 2040 / 40得分/分值48 / 6030 / 4078 / 100一、单项选择题(共20 题、48 / 60 分)1、有主次之分的物体系统，关于其荷载传递规律的论述不正确的是（）正确!收藏该题展开该题2、如果梁上某段承受梯形分布荷载，那么该梁段的挠曲线是（）。

正确!收藏该题展开该题3、关于铰链约束，以下说法不正确的是（）。

正确!收藏该题展开该题4、图示四根细长压杆，其材料、截面相同，它们在纸平面内失稳的先后次序正确的是（）。

正确!收藏该题展开该题5、如图所示，插销穿过水平位置的平板上的圆孔，在其下端受有一拉力F，该插销的剪切面面积和挤压面面积分别等于（）。

正确!收藏该题展开该题6、图示梁，弯矩图发生突变的截面是：正确!收藏该题展开该题7、铸铁试件压缩时沿与轴线约为45o的斜截面断裂，产生破坏的主要原因是（）。

正确!收藏该题展开该题8、如图所示等直杆，抗拉刚度为EA，则杆段AB的轴向线变形为（）。

正确!收藏该题展开该题9、如图所示，结构在D点作用一水平力F，大小为F=2kN，不计杆ABC的自重，则支座B 的约束反力为（）。

A、RB＜2kNB、RB=2kNC、RB＞2kND、RB=0收藏该题10、边长为a的正方形截面对其对称轴的回转半径为（）正确!收藏该题展开该题11、图示T字形截面，要使y、z轴始终为该截面的主惯性轴，则下述正确的是（）正确!收藏该题展开该题12、矩形截面细长压杆如题11.4图所示，其两端约束情况为：在纸平面内为两端铰支，在出平面内一端固定、一端夹支（不能水平移动与转动）。

其横截面高度b和宽度a的合理比值为（）。

正确!收藏该题展开该题13、梁的转角出现极值的截面为（）正确!收藏该题展开该题14、图示矩形截面梁采用两种放置方式, 从弯曲正应力强度观点, (b)的承载能力是(a)的多少倍?（）。

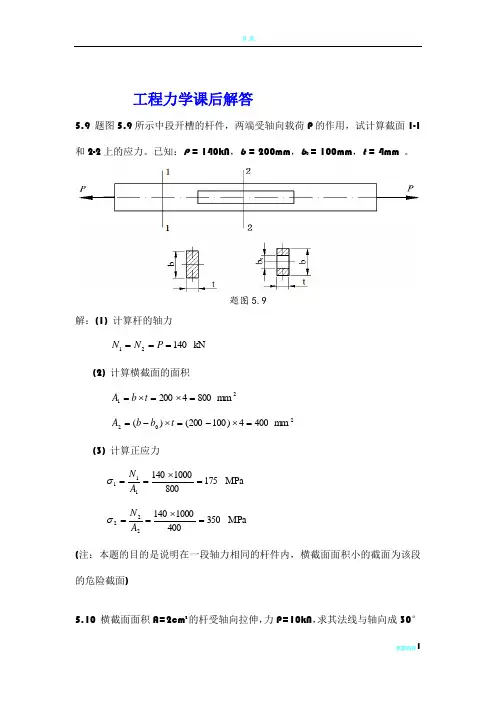
工程力学课后解答5.9 题图5.9所示中段开槽的杆件，两端受轴向载荷P 的作用，试计算截面1-1和2-2上的应力。

已知：P = 140kN ，b = 200mm ，b 0 = 100mm ，t = 4mm 。

题图5.9解：(1) 计算杆的轴力 kN 14021===P N N (2) 计算横截面的面积21m m 8004200=⨯=⨯=t b A202mm 4004)100200()(=⨯-=⨯-=t b b A (3) 计算正应力MPa 1758001000140111=⨯==A N σ MPa 3504001000140222=⨯==A N σ (注：本题的目的是说明在一段轴力相同的杆件内，横截面面积小的截面为该段的危险截面)5.10 横截面面积A=2cm 2的杆受轴向拉伸，力P=10kN ，求其法线与轴向成30°的及45°斜截面上的应力ασ及ατ，并问m ax τ发生在哪一个截面？ 解：(1) 计算杆的轴力kN 10==P N(2) 计算横截面上的正应力MPa 501002100010=⨯⨯==A N σ (3) 计算斜截面上的应力MPa 5.37235030cos 2230=⎪⎪⎭⎫⎝⎛⨯==σσMPa 6.2123250)302sin(230=⨯=⨯=στ MPa 25225045cos 2245=⎪⎪⎭⎫⎝⎛⨯==σσMPa 251250)452sin(245=⨯=⨯=στ (4) m ax τ发生的截面 ∵0)2cos(==ασαταd d 取得极值 ∴ 0)2cos(=α 因此：22πα=， 454==πα故：m ax τ发生在其法线与轴向成45°的截面上。

（注：本题的结果告诉我们，如果拉压杆处横截面的正应力，就可以计算该处任意方向截面的正应力和剪应力。

对于拉压杆而言，最大剪应力发生在其法线与轴向成45°的截面上，最大正应力发生在横截面上，横截面上剪应力为零）5.17 题图2.17所示阶梯直杆AC ，P =10kN ，l 1=l 2=400mm ，A 1=2A 2=100mm 2，E =200GPa 。

工程力学课后习题答案工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC 或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。

（a）（b）（c）（d）（e）（f）（g）1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）1-3 画出图中指定物体的受力图。

所有摩擦均不计，各物自重除图中已画出的外均不计。

（a）（b）（c）（d）（e）（f）（g）第一章静力学基础 9第二章平面力系2-1 电动机重P=5000N，放在水平梁AC 的中央，如图所示。

梁的A端以铰链固定，另一端以撑杆BC支持，撑杆与水平梁的夹角为30 0。

如忽略撑杆与梁的重量，求绞支座A、B处的约束反力。

题2-1图∑∑=︒+︒==︒-︒=PF F F F F FB A y A B x 30sin 30sin ,0030cos 30cos ,0 解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如图所示。

转动绞车，物体便能升起。

设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C三处均为铰链连接。

当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。

题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F F P F F FBC y BC AB x解得:P F P F AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。

电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。

题2-3图以AC 段电线为研究对象，三力汇交N F NF F F F F F FC A GA y C A x 200020110/1tan sin ,0,cos ,0=======∑∑解得：ααα2-4 图示为一拔桩装置。

答案+名字2019年秋季学期课程作业工程力学（一）第1次工程力学（一）题号一二三四五合计已做/题量0 / 10 0 / 10 0 / 6 0 / 2 0 / 2 0 / 30得分/分值0 / 30 0 / 20 0 / 18 0 / 16 0 / 16 0 / 100一、单项选择题(共10 题、0 / 30 分)1、简支梁受力如图，下列说法正确的是（）。

A、1-1截面的弯矩为零，3-3截面的弯矩为零；B、1-1截面的弯矩为-12kN.m，3-3截面的弯矩为零；C、1-1截面的弯矩为12kN.m，3-3截面的弯矩为零；D、3-3截面的弯矩不为零；收藏该题2、冲床如图所示，若要在厚度为δ的钢板上冲出直径为d的圆孔，则冲头的冲压力F必须不小于（）。

已知钢板的屈服应力τs和强度极限应力τb。

B、C、D、收藏该题3、以下说法错误的是（）。

A、对形心轴的静矩一定为零B、对形心轴的静矩不一定为零C、静矩为零的轴一定是形心轴D、静矩可能为正、可能为负、可能为零收藏该题4、平面一般力系的最后可能简化结果情形有（）A、1种；2种；C、3种；D、4种。

收藏该题5、直径为d的实心圆截面等直梁的抗弯截面模量是（）。

A、；B、；C、；D、。

收藏该题6、图示四根细长压杆，其材料、截面相同，它们在纸平面内失稳的先后次序正确的是（）。

A、（a）（b）（c）（d）；B、（d）（a）（b）（c）；C、（c）（d）（a）（b）；D、（b）（c）（d）（a）。

收藏该题7、图示梁，弯矩图发生突变的截面是：A、B截面B、C截面C、D截面D、C截面和D截面收藏该题8、直径为d的圆形截面对其形心轴的回转半径为（）A、B、C、D、收藏该题9、均质杆AB重P=6KN，A端置于粗糙地面上，静滑动摩擦因数fs=0.3，B端靠在光滑墙上，杆在图示位置保持平衡，则杆在A端所受的摩擦力Fs为（）。

A、Fs = 2kNB、Fs = 1.8kNC、D、Fs=1.5kN收藏该题10、作用在一个刚体上的两力，满足的条件，则该二力可能是（）A、作用力和反作用力或一对平衡的力；B、一对平衡的力或一个力偶；C、一对平衡的力或一个力或一个力偶；D、作用力和反作用力或一个力偶。

一、判断题（共20题、共40分）1.使用单位荷载法计算计算位移时,是适用了虚力原理。

正确错误2.两端同支等截面直杆的转角位移方程表达的是三个独立的杆端位移和三个杆端力之间的函数变换关系。

正确错误3.力法基本方程实质是静力平衡方程。

正确错误4.频率方程，为关于w的一元n次方程（n为体系的动力自由度）。

正确错误5.图示体系中的I、II两部分为较结三角形。

正确荷载作用下的梁和刚架中,位移的主要贡献是弯曲变形，通常剪切变形和轴向变形可以忽略不i+o正确错误7.平面一般力系的平衡方程一定可以求解出三个未知量。

正确错误8.两个弯矩图都是非直线图形时,图形相乘法无法直接适用。

正确错误9.图示两弯矩图（对应日为常数），图乘结果为。

正确错误10.力法基本方程中，主系数可能等于零。

正确钱结点可以承受和传递所有类型的内力。

正确错误12.构件抗侧刚度系数越大，其承受的剪力值也就相对越大。

正确错误13.虚位移原理等价于体系的真实平衡条件。

正确错误14.刚体或刚片也可以写作钢体或钢片，是指用钢材制成的物体。

正确错误15.若已知体系运动的初速度（初位移为零），质点的运动规则应表达为正弦函数。

正确错误16.几何瞬变体系不能用作结构的原因是，这类体系在有限的外力作用下可能产生极大的内力。

错误17.钢筋混凝土现浇结点在计算简图中一定都简化成刚结点。

正确错误18.虚功互等定理表明：一个线弹性结构，第一状态的外力在第二状态的位移上所做的外力虚功（W12）,等于第二状态的外力在第一状态的位移上所做的外力虚功（W21）。

正确错误19.若解耦成功，在每一广义自由度上，体系作单频振动。

正确错误20.位移计算公式5.4.1-1只适用于小变形状态。

正确错误二、单项选择题（共20题、共60分）1.下列关于三钱拱或相当简支梁说法中，正确的是（）。

A、任意荷载作用下，三钱拱的弯矩都等于相当简支梁对应截面弯矩减去水平反力与该截面高之三钱拱与相当简支梁相比，具有弯矩和剪力减小，而轴力增大的特点c、三钱拱的内力与相当简支梁的轴力相关D、三较拱的水平推力与其自身（或相当简支梁）的跨度成反比2.国家大剧院（北京）属于（）结构。

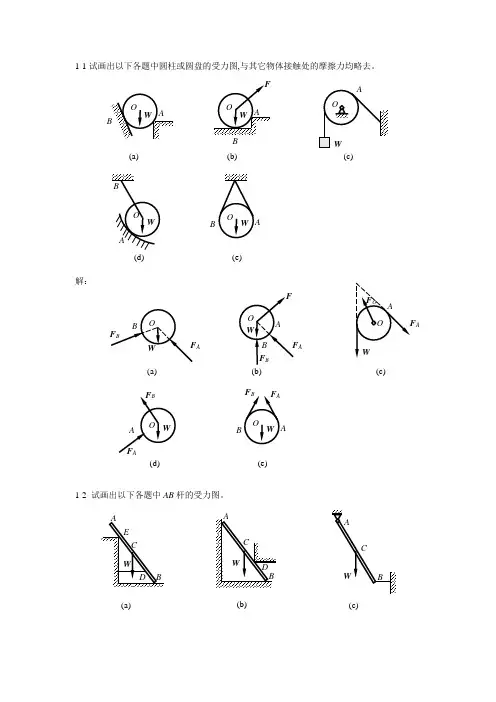
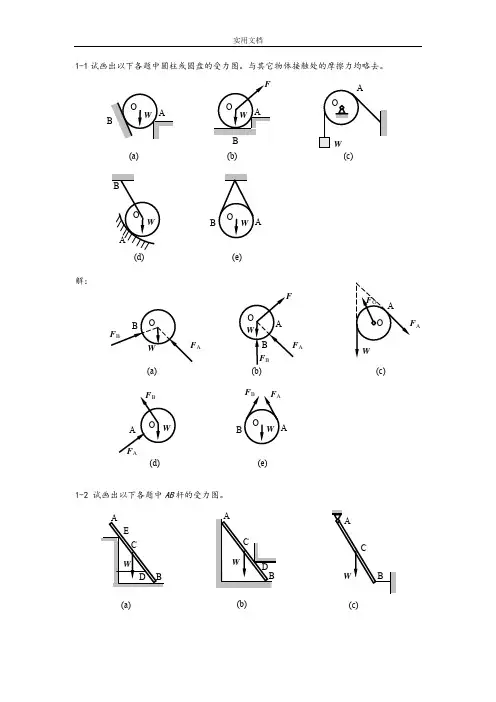
1-1试画出以下各题中圆柱或圆盘的受力图,与其它物体接触处的摩擦力均略去。

解：1-2 试画出以下各题中AB 杆的受力图。

(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。

(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。

解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b) CB(c)BF D1-5 试画出以下各题中指定物体的受力图。

(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

解：(a)(d) FC(e)WB (f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-3 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.1222D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。

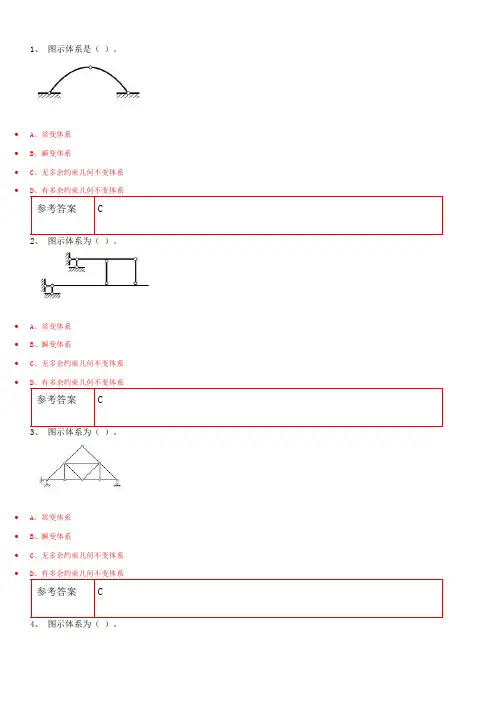
1、图示体系是（）。

•A、常变体系
•B、瞬变体系
•C、无多余约束几何不变体系•
2、图示体系为（）。

•A、常变体系
•B、瞬变体系
•C、无多余约束几何不变体系•
•A、常变体系
•B、瞬变体系
•C、无多余约束几何不变体系•
4、图示体系为（）。

•A、常变体系
•B、瞬变体系
•C、无多余约束几何不变体系
•
5、
图示结构的超静定次数为（）。

•A、1
•B、2
•C、3
•
6、
设水平简支梁跨度为l，横截面C位于距左支座l/3处，则M C和F QC影响线在跨中的值分别为（）。

•A、
l/9，1/3
•B、
l/6，1/2
•C、
l/9，1/2
•
7、（），都相当于解除了结构中的1个约束。

•A、去掉一根支杆或将固定支座变成活动铰支座
•B、断开一根链杆或去掉一个单铰结点
•C、将固定支座变成固定铰支座或者将固定支座变成定向支座
•
8、
力法步骤前四步的顺序是（）。

设①代表步骤“列写基本方程”、②代表“确定基本体系”、③代表“确定超静定次数”、④代表“求解系数和自由项”。

•A、
①④②③
•B、
②①③④
•C、
③②①④
•
9、一个体系的计算自由度为-3，已知其有3个多余约束。

（）
•A、该体系为几何可变体系
•B、该体系为无多余约束的几何不变体系
•C、该体系为有3个多余约束的几何不变体系
•
•A、常变体系。

实用文档1-1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去。

解：1-2 试画出以下各题中AB 杆的受力图。

(a) B(b)(c)(d)A(e) A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。

(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。

解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D1-5 试画出以下各题中指定物体的受力图。

(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

解：(a)(d)FC(e)WB(f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDC ’B2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC ox BC ACAC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-3 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o的力F ，力的大小等于20KN ，如图所示。

《工程力学》作业1参考答案说明：本次作业对应于文字教材第0—3章，应按相应教学进度完成。

一、单项选择题（每小题2分，共30分）在每小题的四个备选答案中选出一个正确答案，并将其代号填在题干后面的括号内。

不选、错选或多选者，该题无分。

1．三刚片组成几何不变体系的规则是（ B ）A三链杆相连，不平行也不相交于一点B三铰两两相连，三铰不在一直线上C三铰三链杆相连，杆不通过铰D一铰一链杆相连，杆不通过铰2．在无多余约束的几何不变体系上增加二元体后构成（C ）A可变体系B瞬变体系B瞬变C不变且无多余联系三、填空题（每空2分，共20分）1．定向支座的反力分量是一个力和一个反力偶。

2．连接两个刚片的单铰相当于两个约束。

= 5kN （ 拉力 ）。

10．位移计算公式ds GAF F ds EA F F ds EI M M QP Q NP N PiP ⎰⎰⎰++=∆μ是由变形体虚功原理推出来的。

解：（1）.求支座反力：F A= F P/2 , F B= 3F P/2 . （2）.作刚架的弯矩图FL3FL/4M图解：（1）求支座反力：F A= F B= lm/；（2）作刚架的弯矩图.L/2L/24解：（1）求支座反力：F Ax=20kN ，F A y=F B=10kN 。

方向如图kN⋅(内侧受拉) （2）作刚架的弯矩图：M EA=M EB= M BE= M BC=40m（3）作刚架的剪力图：AE段：Q=20kNEB段：Q=0BC段：Q=-10kNCD段：Q=040 10 kN_4040+M图20 kN Q图kN⋅)(mB《工程力学》作业2参考答案说明：本次作业对应于文字教材第4章，应按相应教学进度完成。

一、单项选择题（每小题2分，共30分）在每小题的四个备选答案中选出一个正确答案，并将其代号填在题干后面的括号内。

不选、错选或多选者，该题无分。

1．力法计算的基本未知量为（ D ）A杆端弯矩B结点角位移C结点线位移D多余未知力2．超静定结构在荷载作用下产生的内力与刚度（B ）A无关B相对值有关C绝对值有关345．在力法方程的系数和自由项中（ B ）C绝对值有关D相对值绝对值都有关8．力法典型方程中的自由项iP∆是基本体系在荷载作用下产生的（C ）C结点数D杆件数11．力法的基本体系是（D ）A一组单跨度超静定梁B瞬变体系C可变体系D几何不变体系12．撤去一单铰相当于去掉了多少个约束（C ）A1个B3个C2个D4个）1．超静定次数一般不等于多余约束的个数。

4日1-1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去。

解：1-2 试画出以下各题中AB 杆的受力图。

(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)98 解：1-3 试画出以下各题中AB 梁的受力图。

(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。

解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D1-5 试画出以下各题中指定物体的受力图。

(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

解：(a)(d)FC(e)WB(f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-3 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。

【最新整理，下载后即可编辑】工程力学课后解答2.9 题图2.9所示中段开槽的杆件，两端受轴向载荷P 的作用，试计算截面1-1和2-2上的应力。

已知：P = 140kN ，b = 200mm ，b 0 = 100mm ，t = 4mm 。

题图2.9解：(1) 计算杆的轴力 kN 14021===P N N (2) 计算横截面的面积21m m 8004200=⨯=⨯=t b A202mm 4004)100200()(=⨯-=⨯-=t b b A(3) 计算正应力MPa 1758001000140111=⨯==A N σ MPa 3504001000140222=⨯==A N σ(注：本题的目的是说明在一段轴力相同的杆件内，横截面面积小的截面为该段的危险截面)2.10 横截面面积A=2cm 2的杆受轴向拉伸，力P=10kN ，求其法线与轴向成30°的及45°斜截面上的应力ασ及ατ，并问m ax τ发生在哪一个截面？解：(1) 计算杆的轴力kN 10==P N(2) 计算横截面上的正应力MPa 501002100010=⨯⨯==A N σ(3) 计算斜截面上的应力MPa 5.37235030cos 2230=⎪⎪⎭⎫ ⎝⎛⨯==σσMPa 6.2123250)302sin(230=⨯=⨯=στ MPa 25225045cos 2245=⎪⎪⎭⎫⎝⎛⨯== σσMPa 251250)452sin(245=⨯=⨯= στ(4) m ax τ发生的截面∵ 0)2cos(==ασαταd d 取得极值∴0)2cos(=α因此：22πα=， 454==πα故：m ax τ发生在其法线与轴向成45°的截面上。

（注：本题的结果告诉我们，如果拉压杆处横截面的正应力，就可以计算该处任意方向截面的正应力和剪应力。

对于拉压杆而言，最大剪应力发生在其法线与轴向成45°的截面上，最大正应力发生在横截面上，横截面上剪应力为零）2.17 题图2.17所示阶梯直杆AC ，P =10kN ，l 1=l 2=400mm ，A 1=2A 2=100mm 2，E =200GPa 。

第一章测试1.变形固体的基本假设是（）。

A:连续、均匀性假设和线性弹性假设；B:各向同性假设、小变形假设和线性弹性假设。

C:线性弹性假设和小变形假设；D:连续、均匀性假设和各向同性假设；答案:D2.要使构件安全、正常地工作，必须满足（）。

A:强度要求B:稳定性要求C:强度要求、刚度要求、稳定性要求D:强度要求和稳定性要求答案:C第二章测试1.平衡是指物体相对于惯性参考系保持静止或作匀速转动的状态。

（）A:对B:错答案:B2.根据力的平行四边形法，作用于同一物体上的两个力都可以合成为一个合力。

（）A:错B:对答案:A3.变形体在两个大小相等、方向相反、作用线沿同一直线的力作用下不一定能维持平衡。

（）A:对B:错答案:A4.受力图中各约束反力的作用线方位及指向（除柔索和光滑接触面约束外）一般自己假定。

（）A:错B:对答案:B5.下列关于刚体的描述，不正确的是（）。

A:刚体是工程力学的一种抽象化的力学模型B:刚体中任意两点间的距离始终保持不变C:变形极小的物体就可视为刚体D:刚体在自然界中不存在答案:C6.下列关于约束反力的表述中，不正确的是（）。

A:约束反力的方向与约束能够阻止的位移方向相反B:约束反力的大小和方向由约束构造特点确定C:约束反力是一种被动力D:约束反力的大小和方向一般随主动力的改变而改变答案:B7.如题图所示体系，构件自重不计，则支座A处约束反力作用线方位正确的是（）。

A:沿ABB:沿ADC:沿AID:沿AE答案:D8.如题图所示体系，构件自重不计，则受力分析图不正确的是（）。

A:B:C:D:答案:C第三章测试1.在任何坐标系中，力都可以用其在坐标轴上的投影解析表示。

（）A:错B:对答案:A2.力对某轴之矩等于力对轴上任一点之矩在该轴上的投影。

（）A:对B:错答案:A3.只要保持力偶矩不变，力偶可在其作用面内任意移动和转动，都不会改变原力偶对物体的作用效应。

（）A:错B:对答案:A4.力系向某点简化，其主矢和主矩都不为零，且主矢和主矩正交，则该力系可以继续简化为一合力。

第一章静力学的基本概念受力图第二章 平面汇交力系2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故：22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+= 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ） 由平衡方程有：0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=（拉力）1.155AC F W=（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=（拉力）0.364AC F W=（压力）（c ） 由平衡方程有：0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=（压力）（d ） 由平衡方程有：0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解：（a ）受力分析如图所示：由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解：受力分析如图所示：由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式，得：22.410RA RB F KN F KN==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力）列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得： 5RD F Q =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。

工程力学（一）参考资料一、单项选择题（本大题共 0 分，共 80 小题，每小题 0 分）1.如图所示，一绞盘有三个等长的柄，长为 L，相互夹角为120°，各柄柄端作用有与轴线垂直的力 P，将该力系向 BC 连线的中点 D 简化，其结果为=3PLA.R=P，MDB.R=0，M=3PLD=3PLC.R=2P，MDD.R=0，M=2PLD2.四本相同的书，每本重 P，设属于书间的摩擦因数是 0.1，书与手间摩擦因数为 0.25，欲将四本书一起提起，则两侧应加的力 F 至少大于（D ）。

A.1PB.4PC.8PD.10P3.如图所示的力三角形中，表示力 F1 和力 F2 和合力 R 的图形是（C ）。

A.图1B.图2C.图3D.图44.如图所示某种材料的σ-ε曲线，若在 k 点时将荷载慢慢卸掉，则σ-ε曲线将沿着与 Oa 平行的直线 kA 回落到 A 点，从图可以看出（ B）。

A.OA 段是弹性变形，AB 段是塑性变形B.OA 段是塑性变形，AB 段是弹性变形C.如果在重新加载，σ-ε曲线将沿着 Oa 上升到 k 点D.如果在重新加载，σ-ε曲线将沿着 Bk 上升到 k 点5.图示简支梁，已知 C 点的挠度为 y，在其他条件不变的情况下，若将荷载 F 增大一倍，则 C 点的挠度为（ C）。

A. 0.5y；B.y；C.2y；D.4y。

6.简支梁受力如图，下列说确的是（B ）。

A.1-1 截面的弯矩为零，3-3 截面的弯矩为零；B.1-1 截面的弯矩为-12kN.m，3-3 截面的弯矩为零；C.1-1 截面的弯矩为 12kN.m，3-3 截面的弯矩为零；D.3-3 截面的弯矩不为零；7.图示悬臂梁拟用(a)(b)两种方式搁置，则两种情况下的最大应力（σmax）ａ／(σmax）b 为之比为（A ）。

A. 1/4B. 1/16C. 1/64D. 48. 冲床如图所示，若要在厚度为δ的钢板上冲出直径为 d 的圆孔，则冲头的冲压力 F 必须不小于（D ）。

重庆大学网络教育学院-2020年春季学期课程作业工程力学（一）第2次-参考资料请认真阅读一下说明然后下载：题库有可能会换，不保证全部都有！请仔细核对是不是您需要的题目再下载！！！！本文档的说明：如果题目顺序和你的试卷不一样，按CTRL+F在题库中逐一搜索每一道题的答案，预祝您取得好成绩百！一、单项选择题 (共 20 题、0 / 60 分 )1、简支梁受力如图，列弯矩方程时（）。

A、不需要分段；B、需要分两段，分别为AB段和BD段；C、需要分两段，分别为AB段和CD段；D、需要分三段；参考答案是：D2、等直杆受力如图，其上端截面的轴力为（）。

A、F；B、F+ql；C、-F+ql；D、ql。

参考答案是：C3、已知F1，F2，F3，F4为作用在一刚体上的平面汇交力系，其力矢之间的关系有如图所示的关系，所以有：（）A、其力系的合力为R=F4B、其力系的合力为R=0C、其力系的合力为R=2F4D、其力系的合力为R=﹣F4参考答案是：C4、图示四根细长压杆，其材料、截面相同，它们在纸平面内失稳的先后次序正确的是（）。

A、（a）（b）（c）（d）；B、（d）（a）（b）（c）；C、（c）（d）（a）（b）；D、（b）（c）（d）（a）。

参考答案是：A5、直径为d的实心圆轴的抗扭截面模量是（）。

A、；B、；C、；D、。

参考答案是：B6、如图所示，插销穿过水平位置的平板上的圆孔，在其下端受有一拉力F，该插销的剪切面面积和挤压面面积分别等于（）。

A、πd h，B、πd h，C、πD h，D、πD h，参考答案是：B7、如图所示平面图形的形心坐标正确的是（）。

A、（，）B、（，）C、（，）D、（，）参考答案是：C8、如图所示等直杆，抗拉刚度为EA，则杆段BC的轴向线变形为（）。

A、；B、；C、；D、参考答案是：B9、如图所示等直杆，抗拉刚度为EA，则杆段AB的轴向线变形为（）。

A、；B、；C、；D、参考答案是：A10、如图（a）、（b）所示面积相同的矩形截面和正方形截面，则下列选项中正确的是（）A、，B、，C、，参考答案是：B11、均质杆AB重P=6KN，A端置于粗糙地面上，静滑动摩擦因数fs=0.3，B端靠在光滑墙上，杆在图示位置保持平衡，则杆在A端所受的摩擦力Fs为（）。