第三讲__拉姆齐模型
- 格式：ppt
- 大小：347.50 KB
- 文档页数：34
下载文档原格式
合集下载
中级宏观经济学第章拉姆齐模型
第一节 拉姆齐问题
家庭行为－效用最大化
B
et c
t 1 dt
0
1
k 0
eRtengt w t dt-
0
0
eRt
en
g
t
c
t
dt
（ 5-16）
在每个时点家庭选择c，这样就会形成无限多个c(t)。对每一单 个c(t)，其一阶条件是对于任意的t：
第一节 拉姆齐问题
厂商行为
厂商行为相对简单。在每个时点上，他们租用劳动与资本进行生
产，并按这些要素各自的边际产品支付报酬，并出售所生产的产出。
由于生产函数具有不变的规模报酬，经济是竞争性的，厂商因此获得
正常利润。我们知道，资本的边际产品F为K, AL =f ' k
K
。由于市场是
竞争性的，资本只能获得其边际产品。由于不存在折旧，资本的真实
C
t
Lt
H
dt
(可以是负值)；
eRsRt 则表明从t时刻到s时刻该储蓄值的变动状况。
式(5-9)表达式是 eRs 与式(5-8)的大括号中的表达式的乘
积，预算约束写成下式：
第一节 拉姆齐问题
家庭行为－预算约束（续）
lim eRs K s 0（ 5-10）
报酬率等于其每单位时间的收入，因此，在t时刻，真实利率为：
r t f ' k t（ 5-3）
第一节 拉姆齐问题
厂商行为（续）
劳动的边际产品为 F K, AL ，它也等于 AF K, AL 。根据
L
AL
上述生产函数的紧凑形式，它可写成A f k kf ' k 。因此在c
2.拉姆齐-卡斯-库普曼模型
高级经济学Ⅰ（宏观部分）
2.1 模型的假设条件
2.1.1基本假设 完全竞争市场结构； 长生不老的不断扩展 的家庭（有限寿命的 个人和基于利他主义 的代际转让）； 家庭和个人完全同质； 忽略资本的折旧。
租让资本，获取利息 提供劳动，赚取工资 购买产品，进行消费
家庭
相互拥有
厂商
销售产品，获得利润 雇佣劳动，支付工资 租用资本，支付利息
2.2.2 家庭的行为 家庭的行为是去选择各个时刻t的消费，以使家庭在服 从预算约束的条件下获得最大的终生效用，即 ：
L(t ) max : U e u[C (t )] dt t o H L(t ) K (0) L(t ) R (t ) R (t ) s.t.: e C (t ) dt e A(t ) w(t ) dt 0 0 H H H
高级经济学Ⅰ（宏观部分）
2.2 家庭与厂商的行为
2.2.2 家庭的行为 对于家庭部门来说，每个家庭都把实际利率和实际工 资率的运动路径 r（t）和 w（t）视为既定。家庭只能 接受它们，而无法影响它们，因为要素市场是完全竞 争的。 家庭的目标是实现终生效用最大化。在追求这一目标 的过程中，家庭的经济活动要受到预算约束的限制， 也就是说，家庭终生消费的现值不能超过家庭初始拥 有的财富与家庭终生劳动收入的现值之和。
t
高级经济学Ⅰ（宏观部分）
2.2 家庭与厂商的行为
2.2.2 家庭的行为 求解此效用最大化问题，可得描述C(t)调整路径的 “欧拉方程” ：
C (t ) r (t ) C (t )
和每单位有效劳动消费的“欧拉方程” ：
高级经济学Ⅰ（宏观部分）
2.1 模型的假设条件
2.拉姆齐-卡斯-库普曼模型
高级经济学Ⅰ（宏观部分）
2.2 家庭与厂商的行为
2.2.2 家庭的行为 这样家庭的预算约束可以写作：
0
e
R (t )
L(t ) K (0) C(t ) dt H H
0
e R(t ) A(t )w(t )
L(t ) dt H
高级经济学Ⅰ（宏观部分）
2.2 家庭与厂商的行为
n (1 ) g 0
f ' (k gold ) < f ' (k * (t ))
因此 k * k gold
。
高级经济学Ⅰ（宏观部分）
2.3 经济的动态学
2.3.4 初始值与经济运行路径
c
0 c
A
0 k
B
C
F D
O
k (0)
k*
k
高级经济学Ⅰ（宏观部分）
2.3 经济的动态学
2.3.5 鞍点路径
c
0 c
k 0
如果我们引入消费 者预算约束和资本 存量为正的条件， 鞍点路径是一个经 济唯一可能运行的 路径。
O
k*
k
高级经济学Ⅰ（宏观部分）
2.4 平衡增长路径
变量 绝 对 量 K L A AL Y C 相 对 量 k K/L y Y/L c C/L K/Y s 资本存量 含义 平衡增长速度 n+g n g n+g n+g n+g 0 g 0 g 0 g 0 0 c=c* y=f(k)=Y/AL F(cK,cAL)=cF(K,AL) C=ALc k=k* k=K/AL 备注证明
高2.3.2 k的动态学
高级经济学Ⅰ（宏观部分）
(高级宏观经济学课件)拉姆齐—卡斯—库普曼斯模型
• 由此得出结论：拉姆齐模型表明，索洛模型中 关于经济增长的驱动力的中心含义并不依赖于 储蓄率为常数的假定。即使储蓄率内生，劳动 的有效性仍然是增长的唯一可能源泉。
4 平衡增长路径
• 2、索洛模型与拉姆齐－凯斯－库普曼斯模型的 平衡增长路径之间的惟一显著的差异是，在后 者不可能出现动态无效率(k<k黄金)。
k t f k t c t n g k t 5
当 k 0时 ,c f k n g k. 根 据
稻 田 条 件 lim f ' k , lim f ' k 0,
k 0
k
f k 与 n g k必 有 两 个 交 点 .
故 我 们 可 将 c和 k的 关 系 描 述 如 右 图 . 消费等于实际产量线与
AL)； • ②生产函数的性质与索洛模型相同(如:规模报酬
不变,稻田条件,等等)； • ③要素市场和产品市场均为竞争性市场； • ④ A给定，并以外生速率g增长； • ⑤厂商为家庭拥有，因此，厂商所得的全部利润
均归家庭。
1 模型的假设
• 3、家庭： • ①有大量的家庭，每一家庭的规模以速率n增长； • ②家庭每一成员在每一时点供给一单位劳动； • ③家庭将所拥有的资本均租给厂商； • ④家庭的最初资本持有量为K(0)/H； • ⑤不存在折旧； • ⑥家庭将每一时点上的收入用于消费和储蓄，以
以 最 大 化 一 生 效 用. 我 们 用 目 标 函 数 1 和
预算约束 2来构建拉格朗日函数:
L B e t c t 1 d t +
t0
1
k
0
t eRtw
t0
t
en g tdt
eRtc
t0
t
e
4 平衡增长路径
• 2、索洛模型与拉姆齐－凯斯－库普曼斯模型的 平衡增长路径之间的惟一显著的差异是，在后 者不可能出现动态无效率(k<k黄金)。
k t f k t c t n g k t 5
当 k 0时 ,c f k n g k. 根 据
稻 田 条 件 lim f ' k , lim f ' k 0,
k 0
k
f k 与 n g k必 有 两 个 交 点 .
故 我 们 可 将 c和 k的 关 系 描 述 如 右 图 . 消费等于实际产量线与
AL)； • ②生产函数的性质与索洛模型相同(如:规模报酬
不变,稻田条件,等等)； • ③要素市场和产品市场均为竞争性市场； • ④ A给定，并以外生速率g增长； • ⑤厂商为家庭拥有，因此，厂商所得的全部利润
均归家庭。
1 模型的假设
• 3、家庭： • ①有大量的家庭，每一家庭的规模以速率n增长； • ②家庭每一成员在每一时点供给一单位劳动； • ③家庭将所拥有的资本均租给厂商； • ④家庭的最初资本持有量为K(0)/H； • ⑤不存在折旧； • ⑥家庭将每一时点上的收入用于消费和储蓄，以
以 最 大 化 一 生 效 用. 我 们 用 目 标 函 数 1 和
预算约束 2来构建拉格朗日函数:
L B e t c t 1 d t +
t0
1
k
0
t eRtw
t0
t
en g tdt
eRtc
t0
t
e
拉姆齐模型1-2
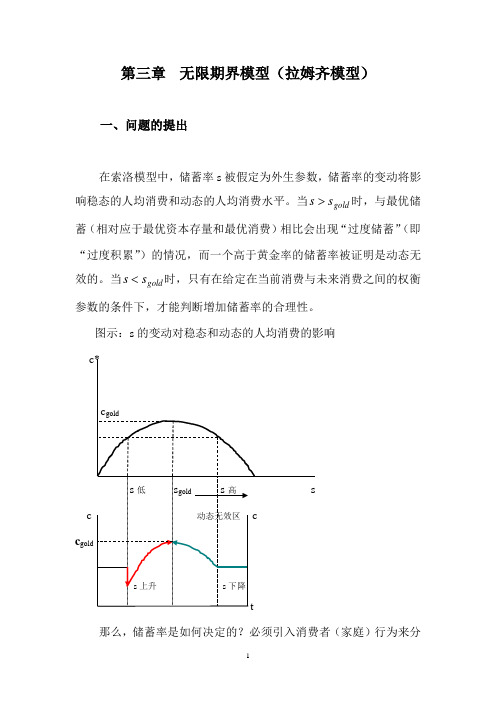
第三章 无限期界模型（拉姆齐模型）一、问题的提出在索洛模型中，储蓄率s 被假定为外生参数，储蓄率的变动将影响稳态的人均消费和动态的人均消费水平。
当gold s s >时，与最优储蓄（相对应于最优资本存量和最优消费）相比会出现“过度储蓄”（即“过度积累”）的情况，而一个高于黄金率的储蓄率被证明是动态无效的。
当gold s s <时，只有在给定在当前消费与未来消费之间的权衡参数的条件下，才能判断增加储蓄率的合理性。
图示：s 的变动对稳态和动态的人均消费的影响c c gold 那么，储蓄率是如何决定的？必须引入消费者（家庭）行为来分析跨期预算约束条件下的消费和储蓄选择，即储蓄率的“内生化”。
二、模型假定1．完全竞争市场结构2．长生不老的不断扩展的家庭（有限寿命的个人和基于利他主义的代际转让）3．家庭和个人完全同质4．忽略资本的折旧5．暂不考虑政府行为在简单经济中，家庭与厂商之间的关系：三、厂商行为沿用新古典生产函数),(AL K F Y = 根据欧拉定理，AL AL Y K K Y Y )(∂∂+∂∂=其中，资本的边际产品为：r k f KY==∂∂)('（真实利率） 有效劳动的边际产品为：w k kf k f AL Y=-=∂∂)(')()(（工资率）四、家庭行为1.一些假定和符号总人口为L ，以速率n 增长，e L t L nt )0()(=； 家庭的个数为H ，每个家庭有L/H 个人； 每个家庭成员在每一时点上提供1单位劳动；资本最初存量为K(0)，每个家庭初始资本存量为K(0)/H 。
2. 家庭效用函数和即期效用函数定义家庭效用函数（也称作“幸福函数”）为：dt HL t C u dt H t L t C u U o t tn o t te e )0()]([)()]([)(⎰⎰∞=--∞=-==ρρ 其中，C(t)为每个家庭成员的消费，)(∙u 为即期效用函数，ρ为贴现率（ρ越大表明与现期消费相比远期消费的价值就越低）。
2-拉姆齐模型
七、修正的黄金资本存量
定理1：在拉姆齐模型中，人均资本存量k收敛于k*，且低于索洛模
型中的黄金资本存量k*, 因此k*被称作“修正的黄金资本存量”。
定理2：拉姆齐模型表明在索洛模型中高于黄金资本存量的平衡增
长路径是不可能的。
【证明】通过相位图可以证明当k(0)>k(gold)时，追求跨期最优化的
家庭将降低储蓄，使k收敛于k*，且k*<k(gold)。
定理3：经济不收敛于产生最大c（即c(gold)）的平衡增长路径，而
是收敛于一个较低的水平c*。
【证明】c*<c(gold)的前提是，它表明贴现率较高，家庭和个人更
重视现期消费，而不是未来消费。
图示（在索洛模型中当s低于s(gold)时提高s的影响）：
c(gold)
c*
c0
c0
t
t
s较大的提高
s较小的提高
思考：在动态转移过程中ρ、ln(Y/L)、c、k、s的轨迹是什么？ 此外，贴现率下降将可以使人均消费达到黄金律水平的平衡增长。
九、基本结论
1．拉姆齐模型没有改变索洛模型关于经济增长平衡路径的基本结 论。
2．索洛模型可以被看作是拉姆齐模型的一个特例，它必须对应于 后者特殊的参数和稳态。
3．拉姆齐模型的特点在于从家庭和个人的跨期消费行为的微观基 础出发决定稳态的消费（储蓄），从厂商的微观基础出发决定稳态的资 本存量，因此c和k是同时决定的。在这样的过程中，储蓄的决定被内生 化了。
六、平衡增长路径
均衡点E(c*,k*)的解为： 因此模型中的各个变量的长期变动如下：
变量
含义
平衡增长速度
K
资本存量
n+g
绝 对
拉姆齐模型
拉姆齐模型家庭行为：总人口：L 人口增长率：n 家庭数量：H 家庭初始资本量：K （0）/H家庭效用函数：()[]()dt Ht L t C u eU t t⎰∞=-=0ρ （1）C （t ）：t 时刻家庭每个成员的消费 u ：瞬时效用函数，L （t ）/H ：家庭成员数 ρ：贴现率瞬时效用函数（相对风险厌恶不变的函数（CRRA ））：()()()θθ-=-11t C t C u θ＞0，ρ-n-（1-θ）g ＞0 （2） 相对风险厌恶的系数：()()θ=-C u C Cu '/''厂商行为：厂商生产函数：Y=F （K ，AL ） A 以速率g 外生的增长资本的边际产品：)(/),('k f K AL K F =∂∂，()∙f 是生产函数的紧致形式 市场竞争性的，不存在折旧，资本的真实报酬率等于其每单位时间的收入，即真实利率为：()()()t k f t r '=有效劳动的边际产品：()AL AL K F ∂∂/,=()()()())('t k f t k t k f -，即等于每单位有效劳动的工资：w(t)=()()()())('t k f t k t k f - （3）家庭预算约束：家庭的终生消费的贴现值不能超过其初始财富与其终生劳动收入的现值之和 考虑r 可随时间变化，定义()()τττd r t R t⎰==(4)在0时刻投资一单位产出品，在t 时刻获得产品()t R e在t 时刻的一单位产品的价值用0时刻的产出表示为()t R e-每个家庭成员数：L （t ）/Ht 时刻的劳动总收入是W （t ）L （t ）/H t 时刻的消费支出是C （t ）L （t ）/H 家庭初始资本：K （0）/H家庭预算约束：()()()()()()()⎰⎰∞=-∞=-+≤00t t R t t R dt H t L t W e H K dt H t L t C e(5) 我们可以用家庭的资本持有量的极限形式表示预算约束将（5）式各项移到右边，化简得：()()()()[]()⎰∞=-≥-+000t t R dt H t L t C t W e H K （6）我们可以写出从t=0到t=∞的及积分形式作为一种极限，（6）式等价于：()()()()[]()00lim 0≥⎥⎦⎤⎢⎣⎡-+⎰=-∞→st t R s dt H t L t C t W e H K （7）家庭最大化问题：考虑到技术进步，c （t ）为有效劳动的消费()()gt e A t A 0=，()()()t c t A t C =,()()()()H L A k K /0000=由（2）式：()()()()()[]()[]()()()()θθθθθθθθθθθ-=-=-=-=-------1010111111111t c e A t c e A t c t A t C t C u gt gt （8）将（8）式代入（1）得： a ．家庭效用函数：()()()()()()()()()()()dt t c e Bdt t c e e H L A dt H e L t c e A edt Ht L t C eU t tt gt t nt t gt tt t⎰⎰⎰⎰∞=--∞=----∞=----∞=---=-=⎥⎦⎤⎢⎣⎡-=-=1011101110111000101θθθθθβθθρθθθθρθρ （9）其中，()()H L A B /001θ-=，()g n θρβ---=1b ．家庭预算约束()()()()()()()()()()()⎰⎰∞=-∞=-+≤00000t t R t t R dt H t L t A t w e H L A k dt H t L t A t c e （10）其中，家庭的有效劳动数量是A （t ）L （t ）/H ，A （t ）L （t ）等于()()()t g n e L A +00 （11）将（11）代入（10）得到：()()()()()()()⎰⎰∞=+-∞=+-+≤000t tg n t R t t g n t R dt e t w e k dt e t c e （12） 求家庭最大化，由（9）和（12）式构造拉格朗日函数：()()()()()()()()⎥⎦⎤⎢⎣⎡-++-=Φ⎰⎰⎰∞=∞=+-+-∞=--000101t t tg n t R t g n t R t t dt t c e e dt t w e e k dt t c e B λθθβ （13）其中，()g n θρβ---=1在时刻t ，家庭消费c （t ），对于每一个c （t ），一阶条件是：()()()t g n t R te e t c Be+---=λθβ （14）对（14）式两边取对数：()()()()()t g n d r t g n t R t c t B t++-=++-=--⎰=0ln ln ln ln τττλλθβ （15）利用了()()τττd r t R t⎰==两边求关于t 的导数：()()()()g n t r t c t c ++-=--∙θβ （16） 由（16）式得到：()()()()θθρθβgt r g n t r t c t c --=---=∙（17）利用了()g n θρβ---=1的定义。
拉姆齐定价模型
公用事业大都是自然垄断的行业，其定价受到政府主管机关的管制。
公用事业的定价与补贴机制是公用事业良性发展问题的核心。
由于公用事业的边际成本递减，边际成本定价法会导致企业的亏损，而平均成本定价法则会导致社会福利的净损失。
拉姆塞定价实际上是一种价格歧视，但它与获得垄断利润最大化为目的的第三级价格歧视不同，其价格的差别是以回收成本为目的，因此是一种管制上容许的价格歧视。
在盈亏平衡约束下,次优的定价方法是实现消费者剩余的最大化。
引用拉姆塞定价模型，令公用事业企业对n个不同市场（用户群）的需求逆函数：pi=p(qi)第i市场上的消费者剩余为:St=pi（qi）dqi−pi(qi)∗qiqi引入拉格朗日乘数⋋：π=pi qi dqi−pi qi∗qi−⋋(pi qi∗q−c(qi)nt−1)qi0经计算得：pi−mcpi ∗ε=⋋+1⋋整合有：p1−mc1p1p2−mc2p2=ε2式中:pi表示第I 时段的价格水平；mci表示第I 时段的边际成本；qi表示第I 个时段的客流量；εi表示pi对应的价格弹性。
图4-4 拉姆塞定价模型图示客流时间分布不均衡有3种情况，季节性或短期性客流不均衡（如旅游的旺淡季）；全日客流不均衡（不同线路工作日和双休日的客流变化）；不同时段客流不均衡（随人们的生活节奏和出行特点而变化）。
由于第1种情况规律性差，变化随机性大（如城市主办某一项重大活动），所以轨道交通余能利用的分时段票价主要针对后两种情况。
客流的空间分布不均衡也有3种情况:各条线路客流的不均衡，由于城市经济功能区、生活功能区与生态功能区的布局之间关系的差异而形成；上下行方向客流不均衡；各个车站乘降人数不均衡（与车站周边土地开发强度有关）。
而拉姆塞模型的含义为：需求弹性越小的市场，定价可以超出其边际成本的比例就越大，即越是在高峰时间，地铁票价越可以涨价可以凭此在最大化乘客满意度的情况下，根据弹性大小适当调整，设定最为适当的价格。
宏观经济学(袁强)-北京师范大学 第四章__拉姆齐模型[1]
![宏观经济学(袁强)-北京师范大学 第四章__拉姆齐模型[1]](https://img.taocdn.com/s1/m/0cdb94797fd5360cba1adb87.png)
第四章 拉姆齐模型（Ramsey Model ）一、问题的提出和模型的建立Solow 模型和内生增长模型实际上是考虑和讨论经济增长的总供给方面，或生产函数的总供给方面，主要讲的是资本循环的流转的故事。
本章转向对总需求的考虑，总需求C 和I 是宏观经济的另一个重要方面，但在solow 和新增长模型中，我们明显把它们简单化了，这实际是一种强制计划经济的特征，在市场经济系统中，消费投资是非常易变的因素，本章我们放松消费仅是产出的一个比例的限制，从社会福利函数的观点，在宏观意义上对消费行为进行深入探讨。
[][][][][]成员数，是平均家庭位的，故统计是以家庭为核算单美国的是家庭数，均量，即时刻的瞬时消费，是人是抽象个人在这里，太一般，进一步简化为的累积效用所有时刻的消费的效用现在看在是一个积分值，含义是注：是时间偏好率是瞬时社会效用函数，是总消费，其中，为也称社会福利函数）考虑现实总效用函数（化的技术路线。
）关于全社会总消费优（据时段作整体的把握。
依费应当在一个动态演化的过程，故消意义不大，由于宏观是时点考虑消费，宏观上有关，在一个的是，因为消费与时间，求和不准确，更重要简单的求和不行，因为到宏观呢观个体的消费行为推广是效用函数，如何把微个人可支配收入，是相应的商品价格是商品量，其中，，种商品，个人，设系统有）的消费行为表述为（微观理论中，关于个体Ht L GDP H t L t C t c t t c Ht L t c U t c U t c U J dtet c U J J U y P P X X y X P X P X X U tT i i n n i n n n i X X n)()()()()()()()()(T 0U C )(1938Ramsy .........l......2.1i )...(max n l iagent 2000011111...1 =⋅==≤++=⎰⋅-ρρ][][][][][][][][][][]θνννθθθθθθθθ--=⋅'''-=∴⋅'''-='''-=→''''-=''-===-∴=+=⇒=>--=⎪⎩⎪⎨⎧=≠>-=⋅∴---11)()()()()()(/,)/(////,)/()/(///)/(/)/(0),(),(0,,0111)()(1),(1,01)()()()()(1111112221211212121212211212121212121212122121121221221121212111t c t c U t c t c U t c U t t c U t c c U c U c U c c U t t t c c d c U c U d c c c U c U c U c U c c X XX X d U U d X X U U U U U U d X X X X d X X X X U U U U dXdX dXU dX U X X dU rX X U rXX U T t c t c U t Inc t c t c U t c U Ht L t c U t t t t t t t t t t t t t t t t t t 再由性的消费关于替代率的弹在任意时点效用的任意性，再由令现在任意固定的弹性就是关于替代率和点，消费由定义，再任意两个时负号表示取正的增长率的影响即替代率的增长率对的替代率的弹性相对于商品进一步，定义商品的替代率相对于商品为商品称，确定无差异曲线任给若有效用函数我们知道时间上是均匀状我态，消费的影响在）认为替代率的变化对（下两点考虑：取这个效用函数是由以或者统一成，取如下形式：消费，是抽象意义上的家庭的[][][][][][][][]数称为常相对风险效用函于是，数险和常相对风险厌恶系为常数时，称常绝对风或特别当成为相对风险厌恶系数称为绝对风险厌恶系数恶的程度，继续规定为了反映消费者对风厌对风险的偏好态度数的符号决定了消费者即，效用函数的二阶导风险中性的线形函数时，消费者是当，消费者风险偏好严格凸时，当，消费者风险厌恶严格凹时，当的态度，称消费者为风险中性若的态度，称消费者为风险偏好若的态度，称消费者为风险厌恶若定义：的效用就是则消费期望值中，平均消费设想，在，那么效用的期望就是和，概率为和时刻消费为和设消费者在者对风险的偏好程度影响时，需要考虑消费在考虑有不确定性因素，，从而存在着消费风险段的消费存在不确定性，时刻看未来）因为现时在（还有另外一层含义，这个，边际效用减少弹性，消费每增加即边际效用关于消费的：用是一致的，也就是说的改变对边际效用的作上，时点是怎样消费的，在任何的经济意义是：不论是未知的，该效用函数由于函数”成为“不变弹性的效用时相等。
(高级宏观经济学课件)拉姆齐—卡斯—库普曼斯模型
2.2
1 定义R t
t
家庭的最大化问题
先看家庭的预算约束
0
r t d ,
Rt
含义 : 在0期投资的1单位产品在t期产生e 反之, t期1单位产品在0期的价值为:e 家庭的预算约束为 :
Rt Rt
单位的产品,
.
L t K 0 t Rt L t t 0 e C t H dt H t 0 e A t w t H dt 对上式用有效劳动进行正规化,并化简 :
e dt
nt
2.2
家庭的最大化问题
1
U A 0 B 其中 : B A 0
1
L 0 n 1 g t c t e dt H t 0 1 c t dt 1
1
t 0
e
t
2
1
L 0 , n 1 g 0 H
家庭的问题是, 在预算约束下选择c t 的路径 以最大化一生效用.
1
2.3
家庭行为
我们用目标函数 1 和
预算约束 2 来构建拉格朗日函数: L B e
t 0 t
c t dt + 1
t R t R t n g t n g t k 0 e w t e dt e c t e dt t 0 t 0 家庭选择每一时点上的c,对单个c t 的一阶条件是 :
第三章
拉姆齐—卡斯—库普曼斯模型
这一堂课的内容安排
• • • • • • 1 2 3 4 5 6 模型的假设； 家庭与厂商的行为； 经济动态学； 平衡增长路径； 贴现率下降的影响； 调整速度与鞍点路径的斜率。
拉姆齐模型的主要结论
拉姆齐模型的主要结论
拉姆齐模型，又称拉姆齐-拉米哈模型，是当代生物信息学领域中一种非常重要且被广泛使用的基因表达预测模型。
该模型的核心思想是利用RNA结合蛋白（RBP）相互作用来预测基因表达。
拉姆齐模型由多个步骤组成，包括：1）基因筛选2）RP结合3）RP解离4）基因表达5）蛋白质检测。
拉姆齐模型的主要优点在于其高度的预测准确性。
与传统的基因表达预测方法相比，拉姆齐模型在预测基因表达方面具有更好的表现。
此外，该模型还具有较好的可扩展性，可以处理大规模数据。
除此之外，拉姆齐模型还具有其他优点，如易于计算，并且可以与其他生物信息学方法相结合。
然而，拉姆齐模型也存在一些局限性。
首先，该模型主要适用于预测编码蛋白质的基因表达。
对于其他类型的基因表达，如RNA预测、代谢网络预测等，拉姆齐模型可能无法获得同样的预测准确。
其次，拉姆齐模型的预测结果可能受到RP结合物的选择性影响。
因
此，在进行基因表达预测时，需要进行严格的实验验证，以确保结果的可靠性。
尽管如此，拉姆齐模型在基因表达预测中仍然具有广泛的应用。
该模型可以用于研究基因功能、基因表达调控、基因敲除等研究领域。
此外，随着生物信息学技术的不断发展，拉姆齐模型也在不断更新，以更好地满足新的研究需求。
总之，拉姆齐模型是一种非常有价值的基因表达预测工具。
它的主要优点在于高度的预测准确性和较好的可扩展性。
然而，也存在一些局限性，需要根据具体需求进行选择。
(高级宏观经济学课件)拉姆齐卡斯库普曼斯模型(2024)
2024/1/27
5
跨期选择与最优化原理
跨期选择
消费者需要在不同时间点之间进行权衡，以最大化 其一生中的总效用。这涉及到对当前消费和未来消 费的权衡取舍。
最优化原理
在给定约束条件下，消费者通过选择最优的消费和 储蓄路径来实现效用最大化。这要求消费者在每一 时点上根据边际效用和预期未来收益进行决策。
(高级宏观经济学课件)拉姆齐卡斯 库普曼斯模型
2024/1/27
1
目录
2024/1/27
• 模型背景与基本概念 • 模型构建与假设条件 • 动态规划与最优控制方法 • 模型拓展与应用举例 • 模型评价与现实意义 • 相关研究领域前沿动态
2
01
模型背景与基本概念
Chapter
2024/1/27
3
拉姆齐-卡斯-库普曼斯模型简介
2024/1/27
17
应用举例：经济增长、社会福利等
经济增长
通过技术进步、人力资本积累等途径提高潜在增长率
社会福利
优化收入分配、提高公共服务水平等提升社会福利水 平
政策评估
分析政策效果及可持续性，为政策制定提供理论依据
2024/1/27
18
05
模型评价与现实意义
Chapter
2024/1/27
19
对投资决策的影响
预防性储蓄动机增强，消 费平滑化
对消费行为的影响
未来生产率、政策变动、 市场需求等
不确定性来源
2024/1/27
16
考虑政府行为的拓展模型
01
政府支出与税收
直接影响总需求与资源配置
02
社会保障制度
改变居民预期，影响消费与储蓄 行为
拉姆齐模型
4
模型说明
索洛模型主要从生产角度研究平衡增长路径， 空间是一维的；
R-C-K模型从生产者、家庭两个角度研究 增长路径，空间是二维的。
5
循环图
家庭
租让资本，获取利息 提供劳动，赚取工资 购买产品，进行消费
相互拥有
厂商
销售产品，获得利润
雇佣劳动，支付工资
租用资本，支付利息
6
模型所描述的经济体： 厂商租用资本雇佣劳动用以生产并销售产品， 而数量固定的长生不老家庭供给劳动、持有 资本、消费并储蓄。这回避了所有的市场不 完美性，以及由异质家庭和代际联系造成的 所有问题，因此提供了一个理论上的参照系。
16
如果趋近于零，则效用几乎是C的线性函数：
经济含义：因此家庭也就愿意消费的大的波动
以利用贴现率与储蓄报酬率之间小的差异。
具体而言，可以证明任意两时点的消费之间
的替代弹性为1 / 。
17
注释（1）：为什么效用函数要除以 1
18
注释（2）： 1的特殊情况
根据罗必塔 法则
19
根据：（ax）' ax ln a
的生产函数Y=F(K,AL) ；
✓ 要素市场、产品市场都是完全竞争的； ✓ A外生以速率g增长； ✓ 厂商追求最大化利润。
9
一、模型的基本假定
家庭
✓ 大量相同家庭（数量H），每一家庭规模 以速率n增长（长生不老且没有新家庭加 入）。
✓ 家庭每一成员在每一时点上供给1单位劳动， 将所拥有资本均租给厂商，家庭拥有企业， 因此，企业产生的利润归于家庭。
是时间偏好率，表示获得效用越晚价值 越低，越大，则相对于现期消费，家庭对
未来的消费估价越小
12
关于家庭效用函数的说明：
模型说明
索洛模型主要从生产角度研究平衡增长路径， 空间是一维的；
R-C-K模型从生产者、家庭两个角度研究 增长路径，空间是二维的。
5
循环图
家庭
租让资本，获取利息 提供劳动，赚取工资 购买产品，进行消费
相互拥有
厂商
销售产品，获得利润
雇佣劳动，支付工资
租用资本，支付利息
6
模型所描述的经济体： 厂商租用资本雇佣劳动用以生产并销售产品， 而数量固定的长生不老家庭供给劳动、持有 资本、消费并储蓄。这回避了所有的市场不 完美性，以及由异质家庭和代际联系造成的 所有问题，因此提供了一个理论上的参照系。
16
如果趋近于零，则效用几乎是C的线性函数：
经济含义：因此家庭也就愿意消费的大的波动
以利用贴现率与储蓄报酬率之间小的差异。
具体而言，可以证明任意两时点的消费之间
的替代弹性为1 / 。
17
注释（1）：为什么效用函数要除以 1
18
注释（2）： 1的特殊情况
根据罗必塔 法则
19
根据：（ax）' ax ln a
的生产函数Y=F(K,AL) ；
✓ 要素市场、产品市场都是完全竞争的； ✓ A外生以速率g增长； ✓ 厂商追求最大化利润。
9
一、模型的基本假定
家庭
✓ 大量相同家庭（数量H），每一家庭规模 以速率n增长（长生不老且没有新家庭加 入）。
✓ 家庭每一成员在每一时点上供给1单位劳动， 将所拥有资本均租给厂商，家庭拥有企业， 因此，企业产生的利润归于家庭。
是时间偏好率，表示获得效用越晚价值 越低，越大，则相对于现期消费，家庭对
未来的消费估价越小
12
关于家庭效用函数的说明：
高等宏观经济学-第三章拉姆齐模型
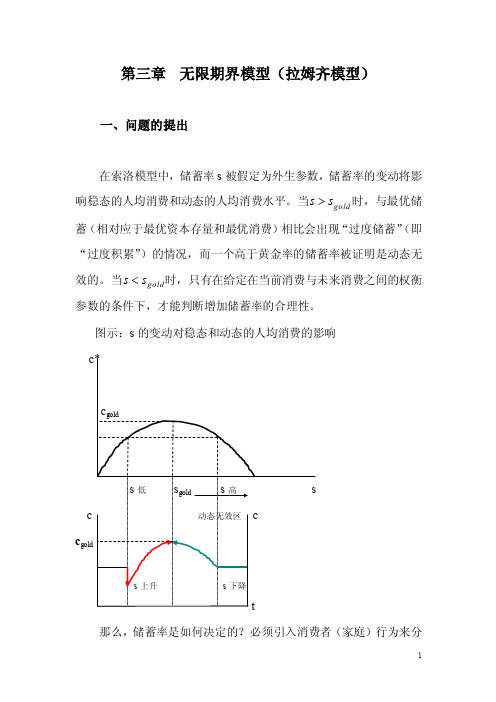
第三章 无限期界模型（拉姆齐模型）一、问题的提出在索洛模型中，储蓄率s 被假定为外生参数，储蓄率的变动将影响稳态的人均消费和动态的人均消费水平。
当gold s s >时，与最优储蓄（相对应于最优资本存量和最优消费）相比会出现“过度储蓄”（即“过度积累”）的情况，而一个高于黄金率的储蓄率被证明是动态无效的。
当gold s s <时，只有在给定在当前消费与未来消费之间的权衡参数的条件下，才能判断增加储蓄率的合理性。
图示：s 的变动对稳态和动态的人均消费的影响c gold 那么，储蓄率是如何决定的？必须引入消费者（家庭）行为来分析跨期预算约束条件下的消费和储蓄选择，即储蓄率的“内生化”。
二、模型假定1．完全竞争市场结构2．长生不老的不断扩展的家庭（有限寿命的个人和基于利他主义的代际转让）3．家庭和个人完全同质4．忽略资本的折旧5．暂不考虑政府行为在简单经济中，家庭与厂商之间的关系：三、厂商行为沿用新古典生产函数),(AL K F Y = 根据欧拉定理，AL AL Y K K Y Y )(∂∂+∂∂=其中，资本的边际产品为：r k f KY==∂∂)('（真实利率） 有效劳动的边际产品为：w k kf k f AL Y=-=∂∂)(')()(（工资率）四、家庭行为1.一些假定和符号总人口为L ，以速率n 增长，e L t L nt )0()(=； 家庭的个数为H ，每个家庭有L/H 个人； 每个家庭成员在每一时点上提供1单位劳动；资本最初存量为K(0)，每个家庭初始资本存量为K(0)/H 。
2. 家庭效用函数和即期效用函数定义家庭效用函数（也称作“幸福函数”）为：dt HL t C u dt H t L t C u U o t tn o t te e)0()]([)()]([)(⎰⎰∞=--∞=-==ρρ其中，C(t)为每个家庭成员的消费，)(∙u 为即期效用函数，ρ为贴现率（ρ越大表明与现期消费相比远期消费的价值就越低）。
拉姆齐卡斯库普曼模型
劳动力
知识或技术 有效劳动 总产出 总消费 有效劳动的平均资本
人均资本
有效劳动的人均产出 人均产出 有效劳动的人均消费 人均消费 资本产出比
储蓄率
s=(y-c)/y
高级经济学Ⅰ（宏观部分）
2.4 平衡增长路径
结论： 将储蓄率内生化并没有改变索洛模型中关于平衡增长路 径的描述。即使储蓄率是内生的，外生的技术进步依 然是人均产出持续增长的唯一根源。
高级经济学Ⅰ（宏观部分）
2.2 家庭与厂商的行为
2.2.2 家庭的行为 对于家庭部门来说，每个家庭都把实际利率和实际工 资率的运动路径 r（t）和 w（t）视为既定。家庭只能 接受它们，而无法影响它们，因为要素市场是完全竞 争的。 家庭的目标是实现终生效用最大化。在追求这一目标 的过程中，家庭的经济活动要受到预算约束的限制， 也就是说，家庭终生消费的现值不能超过家庭初始拥 有的财富与家庭终生劳动收入的现值之和。
高级经济学Ⅰ（宏观部分）
2.2 家庭与厂商的行为
2.2.2 家庭的行为 贴现率：按连续复利计算，从时刻0到时刻t这一时间 区间上单位资本的(连续复利)利率为：
R(t )
r( ) d
0
t
这意味着时刻0的1单位资本，在到达时刻t时变成为 e R(t ) 个单位的资本。等价地说，未来t时刻的一元钱的价值(即 R (t ) 现值)是 e 。所以R(t)就是未来价值向当前的贴现率。
0
*
f k f k *
c
c0 c0
*
0
高级经济学Ⅰ（宏观部分） k
当 k k 时， f k f k c 0 当 k k 时， f k f k c 0
第三讲 拉姆齐模型
2.家庭的资产和债务
记t时刻家庭拥有的总资产为A(t)。这里A(t) 可以为正的，也可以为负的。当A(t)为正时表明 此时家庭拥有正的资产;反之，A(t)表示家庭的负 债。假设在完全竞争条件下，市场上的资本回报 率(即利率)为r(t)。这样家庭所拥有的资产在t时 刻可以带来的收益为A(t)r(t) 。如果A(t)为负， A(t)r(t) 表示此时家庭必须付的债务利息。同时， 假设家庭可以为社会提供劳动力，得到工资回报。 假设在t时刻的工资率（人均工资）为w(t)，家庭 提供的劳动力为L(t)。这样，家庭通过劳动得到 的收益为w(t)L(t)。因此，在t时刻家庭的总收入 为r(t)A(t)+w(t)L(t)。
t
该横截性条件表明,当时间趋向于无穷远时,家庭人均 资产的效用 t a t 必须趋向于0, 即无穷远时间的资产 在现在看来毫无价值.
H r n / r n , 方程两边对时间 : 0 t积分, a
得:(t)= 0 exp r v n dv , v 0 是一常数,v 0 u c(0) . 0
t
将上式代入 lim t a (t ) 0, 则横截性条件变为: t r v n dv 0该式意味着:长期人均资产a不能 lim a t exp 0 t 以r-n那么快的速度增长,否则家庭不能实现效用最大化.如a的增长 速度超过r-n,那么多出来的那一部分用于消费,家庭人均福利能够提高. 消费函数 : 上述方程中的 : exp r v dv 项是将时刻t的一单位收入转化为0时刻的
第二个限制条件是 :
t r v n dv 0 lim a t exp 0 t 即时间的无限推移,人均净资产的"贴现值"渐进非负, 这说明人均净资产的净贴现值 由r t n决定 不能为负, 否则,在未来远期的某一时刻,家庭将会停止投资. 也可反过来说,一个家庭的长期人均债务的增长速度不能 超过r t n, 否则收益将为负. 现在, 家庭的最优消费问题变为,在预算约束: t r v n dv 0和 lim a t exp 0 t a w t r t a t c t na t 下 求解 : U
拉姆齐模型(RCK)与世代交替模型的异同
拉姆齐模型与世代交替模型的异同一、拉姆齐模型与世代交替模型的相同点拉姆齐模型(又称RCK 模型）与世代交替模型（又称Diamond 模型)都是现代经济增长理论的基准分析模型.两个模型的主要相同点在于：第一，在这两种基准模型的一般均衡分析框架下,宏观层面的经济增长都具备了各个经济主体追求利益最大化的微观基础，这就使得经济学家能够在动态时间视角以及资源跨期最优配置的设定下对宏观经济增长进行更为深入的研究。
第二，两个模型均放弃了储蓄率外生给定的假设而通过家庭的效用最大化行为，将储蓄率表示为资本存量的函数,以便分析储蓄率的变动情况。
第三，两个模型在求解经济体一般均衡的结果时，都从市场竞争以及中央计划者配置（社会性最优）两个角度审视相应最优化结果是否具有一致性，从而比较并分析市场机制与计划手段的社会福利情况。
第四,两个模型的一般均衡结果中，人均资本存量以及人均消费量（以效率劳动的角度衡量)在长期内的增长率均为零，不存在持续性的增长机制。
二、拉姆齐模型与世代交替模型的区别从两个模型形式上的区别来看,经典的拉姆齐模型假设经济体中个人的寿命是无限的，因此对于家庭效用函数的构建以及效用最大化问题的讨论便从数理角度转化为了无限期连续型最优控制问题；而经典的世代交替模型假设经济体中个人的寿命是有限的，将人的一生简单划分为青年和老年两个阶段，青年阶段通过投入自身要素禀赋获得相应收入并消费,老年阶段则消费青年阶段的储蓄量，经济体每一期都存在着青年人出生、老年人死亡、上一期青年人变成老年人的迭代，因此对于消费者效用最大化行为的刻划便从数理角度转化为了跨期的非线性规划问题。
除了这种形式上的区别之外,两类模型还存在如下两点本质性的差异： 第一，竞争性均衡与社会性最优的关系。
在经典的拉姆齐模型中，竞争性均衡与社会性最优的结果是一致的。
首先考虑社会性最优的情形（计划增长模型），假设存在一个代表经济体中全部民众的善意计划者（中央政府）在既定资源约束下选择最优消费与资本增长路径使得家庭消费效用最大化，则最优选择问题可以表示为如下最优控制问题：0(,)0max :(())..:(),(0)t c k U c t e dt s t k f k c nk k k θ∞-=--=⎰解该最优控制问题,得到家庭最优消费路径为： (())c k cc U c f k n c U cθ=--- 接下来考虑竞争性均衡（分散化决策）的情形。
拉姆齐（Ramsey）模型的详细推导
拉姆齐（Ramsey）模型的详细推导弗兰克·拉姆齐(英国著名科学家）弗兰克·拉姆齐（Frank Plumpton Ramsey)，1903年2月22日—1930年1月19日），英国科学家、数学家、哲学家、逻辑学家、经济学家，在他短促的一生中对许多领域做出开拓性的贡献。
弗兰克·拉姆齐（Frank Plumpton Ramsey,1903.2.22 - 1930.1.19）生于剑桥，其父亲是麦格达伦学院的校长，其弟弟迈克尔·拉姆齐是第100任坎特伯里大主教。
拉姆齐于温切斯特公学学习，后来进入剑桥大学三一学院学习数学。
他涉猎了很多领域。
在政治上，他有左翼的倾向；宗教上，其妻指他是个态度坚定的无神论者。
他和查尔斯·凯·奥格顿聊天时，说他想学德语。
奥格顿便给他一本文法书、字典和一篇深奥的心理学论文并告诉他：使用那本文法书和字典，告诉我们你的想法。
约一星期后，他不止学会了德语，还对语法书中一些理论提出了反对意见。
他阅读了维根斯坦的Tractatus Logico-Philosophicus。
这本书深深影响了他，1923年他去奥地利跟维根斯坦讨论。
1924年21岁的他成为国王学院的研究员。
拉姆齐为治疗慢性肝疾而接受腹部手术，但术后并发黄疸，于1930年1月19日病逝于伦敦盖氏医院（Guy's Hospital），得年仅26岁又11个月。
有些哲学家将他视为可能比维根斯坦更伟大的哲学家。
一些重要贡献：哲学：真理的多余理论组合数学：拉姆齐定理经济学：拉姆齐定价拉姆齐(Ramsey)模型为现代宏观经济分析最有力的工具之一。
弗兰克·拉姆齐是英国剑桥大学的数学家和逻辑学家，1928年12月，他在[经济学杂志]上发表了[储蓄的数学原理]一文，建立了拉姆齐模型。
该模型在确定性的条件下，分析最优经济增长，推导满足最优路径的跨时条件，阐述了动态非货币均衡模型中的消费和资本积累原理。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
•
At wt Lt r t At C t代入得 :
•
a wt r tat ct nat na t 表示人口按n速率增长时使家庭人均资产保持原有水平必须追加的投资或储蓄.
•
方程a wt r tat ct nat表明:人均资产随着人均收入wt r ta t的增长而增长,
随着人均消费ct和人口扩张率n 的上升而下降.这是家庭消费最大化的第一个限制条件.
ln C1/ ln P1/
C2 P2
得 u '(C) .同理我们可证明一个两期效用函数 :
u ''(C)C
U C11 1 C21 的 u '(C) .
1 1 1
u ''(C)C
•
将u
'(C)
C
,
u
''(C
)
C
1代入r
u c gc uc
gcc
•
得 : c 1/ r ,该式表明,r大于,等于,还是小于
首先建立这种家庭最优消费选择模型的是拉 姆赛(Rmsey,1928) ，凯斯(Cass)和科普曼斯 (Koopmans)在1965年又分别对它作了改进，我 们把这种类型的增长模型称为"拉姆赛模型"。
回顾：黄金分割律、最优消费和黄金率 资本存量水平
在索洛模型中，储蓄率s被假定为外生参数， 储蓄率的变动将影响稳态的人均消费和动态的人 均消费水平。当 s sgold 时，与最优储蓄（相对应 于最优资本存量和最优消费）相比会出现“过度 储蓄”（即“过度积累”）的情况，而一个高于 黄金率的储蓄率被证明是动态无效的s 。s当gold 时，只有在给定在当前消费与未来消费之间的权 衡参数的条件下，才能判断增加储蓄率的合理性。
2 跨期替代弹性不变，为1/，表示相对风险回避系数不变。
1，2表示两期的消费，定义跨期替代弹性为：
(C1/ C2) (C1/ C2)
/ /
(P1/ P2) (P1/ P2)
ln C1/ C2 ln P1/ P2
针对:
Max u[C(t)] C(t)1
1
s.t. P1C1 P2C2 W
应用L求极值法,求出C1和C2,代入
式中第一项是时刻t消费c的效用的贴现值.为Hamilton乘子,
表示在t时刻一个单位的资本存量的增加所带来效用增加量
的现值,也有将其称为效用的影子价格.这样,第二项表示:
t时收益的效用以0时刻的收益效用来表示.
一阶最优条件为:
H u c ent 0
1
c
•
H
r n
2
a
横截性条件(Transversality condition-TVC,
本讲的主要工作是将储蓄率作为内生变量引
入模型，做到这一点的办法是考察家庭的消费行 为，因为储蓄率是由家庭的消费行为决定的。
考察家庭费行为的办 法是利用消费的效用函
数，家庭消费决策的原则是使长期内家庭整体消 费效用最大化。 有了家庭的消费效用函数，我门 可以分析家庭在各种资本和产出水平(相当于当前 和长期的消费约束)，如何选择消费量(或储蓄率) 的规律，从而使储蓄率成为模型的内生变量。
c
决定了家庭的最佳消费模式是人均消费不断上升, 保持
不变,还是逐步下降.
我们讨论一下横截性条件
TVC
:
lim
t
t
ga
t
0,
该横截性条件表明,当时间趋向于无穷远时,家庭人均
资产的效用 t ga t 必须趋向于0,即无穷远时间的资产
在现在看来毫无价值.
•
H
r n
•
/
r
n,方程两边对时间: 0 t积分,
家庭收入除用来消费外，其余的用来储蓄以增加资产。记t时刻家庭的总的消费水平为C t ，
这样家庭的预算约束可以表示为:
•
At wtLtrt AtCt 定义at At / Lt为t时刻家庭拥有的人均资产,ct C t / Lt为和t时刻家庭的人均消费, 并且L的增长率为n,这样方程:at At / Lt两边对t求导,并将
A Contribution to the Theory of Taxation,1927
A Mathematical Theory of Saving,1928
一、问题的提出
前面各种增长模型之所以都将储蓄率看作外 生常数，主要是为了简化模型的分析，另一方面 是因为在许多经济中其相对比较稳定，在一定时 期内变化不大。但是，增长理论研究的是长期的 动态经济增长，长期间储蓄率是变化的，将其作 为外生常数排除了经济增长与其的相互作用。从 前面的讨论可知，一个经济是否有稳定状态，是 否收敛，收敛速度多快以及是否存在内生经济增 长等都与储蓄率的变化有关，因此排除经济增长 对储蓄率的反作用必然使经济增长的关键特征都 由模型的外生参数决定，使模型无法解释经济增 长真正的内在规律和机制，这是造成哈罗德一多 马模型、索洛（及其基础之上的衍生）模型解释 经济增长能力局限性的根本原因。
现在, 家庭的最优消费问题变为,在预算约束:
lim
t
a t gexp
t 0
r
v
n
dv
0和
•
a wt r t a t c t na t 下
e 求解 :U (n)tu[c(t)]dt的最大值. t o
利用Hamilton系统来求解上述优化问题.对于上面的优化问题
定义Hamilton方程 : H u c ent w r n a c
当前人均消费c的变化而引起效用的变化率之和,这个和表明了
当前消费的回报率,它应等于当前投资的回报率r.这就是通常所讲
的市场无套利原则在宏观经济学中的体现.
效用函数的形式为：u[C(t)] C(t)1 , 0, n (1 )g 0 保证效用u不发散
1
该函数具有以下三个特点：
1边际效用弹性不变: du ' C u ''C ; u '(C) C ,u ''(C) C 1 dC u ' u '
第二个限制条件是 :
lim
t
a t gexp
t 0
r
v
n
dv
0
即时间的无限推移,人均净资产的"贴现值"渐进非负,
这说明人均净资产的净贴现值 由r t n决定不能为负,
否则,在未来远期的某一时刻,家庭将会停止投资.
也可反过来说,一个家庭的长期人均债务的增长速度不能
超过r t n,否则收益将为负.
0 0
对给定的财富量, 平均利率r t 的提高对方程 1 e dt rt1 / / ngt
0 0
中的边际财富消费倾向有两方面的影响:
1较高的利率提高当前消费相对于将来消费的机会成本, 跨时期消费的
替代效应会刺激人们把当前消费改为将来消费,即当前少消费,多储蓄(投资).
2较高的利率又有收入效应, 会提高所有时间的消费水平,包括当前的消费 水平.因此平均利率r t 的提高对 0的净影响取决于上述哪种效应更强. 分析 : 1如果 1( 0), 越小,随r t 的上升, 0 将下降, c 0也将下降,意味着
速度超过r-n,那么多出来的那一部分用于消费,家庭人均福利能够提高.
消费函数 :
上述方程中的: exp
t
0
r
v
dv
项是将时刻t的一单位收入转化为0时刻的
等价单位的贴现因子.如果r v等于常数r,则贴现因子简化为ert .
如果定义:r
t
1
/
t
t
0
r
v
dv为时间0至t之间的平均利息率,
则贴现因子为ertgt .
第三讲 无限期界模型（拉姆齐模型）
Frank Ramsey
Frank Ramsey (1903-1930), Britishmathe matician and philosopher, best known for his work on the foundations of mathematics. But Ramsey also made remarkable contributions to epistemology, semantics, logic, philosophy of science, mathematics, statistics, probability and decision theory, economics and metaphysics.
e e e
U
tu[c(t)] ntdt
( n)tu[c(t)]dt
t o
t o
n说明子女越多，父母对每个子女福利的重视程度就会越小，
即父母会加速对不断增多子女的"轻视"程度.
2.家庭的资产和债务
记t时刻家庭拥有的总资产为A(t)。这里A(t) 可以为正的，也可以为负的。当A(t)为正时表明 此时家庭拥有正的资产;反之，A(t)表示家庭的负 债。假设在完全竞争条件下，市场上的资本回报 率(即利率)为r(t)。这样家庭所拥有的资产在t时 刻可以带来的收益为A(t)r(t) 。如果A(t)为负， A(t)r(t) 表示此时家庭必须付的债务利息。同时， 假设家庭可以为社会提供劳动力，得到工资回报。 假设在t时刻的工资率（人均工资）为w(t)，家庭 提供的劳动力为L(t)。这样，家庭通过劳动得到 的收益为w(t)L(t)。因此，在t时刻家庭的总收入 为r(t)A(t)+w(t)L(t)。
当前少消费,多储蓄(投资).说明替代效应强.
2如果 1, 越大,随r t 的上升, 0也会上升, c 0上升,说明替代效应强逐渐
将
•
c/
c
1
/
r
At wt Lt r t At C t代入得 :
•
a wt r tat ct nat na t 表示人口按n速率增长时使家庭人均资产保持原有水平必须追加的投资或储蓄.
•
方程a wt r tat ct nat表明:人均资产随着人均收入wt r ta t的增长而增长,
随着人均消费ct和人口扩张率n 的上升而下降.这是家庭消费最大化的第一个限制条件.
ln C1/ ln P1/
C2 P2
得 u '(C) .同理我们可证明一个两期效用函数 :
u ''(C)C
U C11 1 C21 的 u '(C) .
1 1 1
u ''(C)C
•
将u
'(C)
C
,
u
''(C
)
C
1代入r
u c gc uc
gcc
•
得 : c 1/ r ,该式表明,r大于,等于,还是小于
首先建立这种家庭最优消费选择模型的是拉 姆赛(Rmsey,1928) ，凯斯(Cass)和科普曼斯 (Koopmans)在1965年又分别对它作了改进，我 们把这种类型的增长模型称为"拉姆赛模型"。
回顾：黄金分割律、最优消费和黄金率 资本存量水平
在索洛模型中，储蓄率s被假定为外生参数， 储蓄率的变动将影响稳态的人均消费和动态的人 均消费水平。当 s sgold 时，与最优储蓄（相对应 于最优资本存量和最优消费）相比会出现“过度 储蓄”（即“过度积累”）的情况，而一个高于 黄金率的储蓄率被证明是动态无效的s 。s当gold 时，只有在给定在当前消费与未来消费之间的权 衡参数的条件下，才能判断增加储蓄率的合理性。
2 跨期替代弹性不变，为1/，表示相对风险回避系数不变。
1，2表示两期的消费，定义跨期替代弹性为：
(C1/ C2) (C1/ C2)
/ /
(P1/ P2) (P1/ P2)
ln C1/ C2 ln P1/ P2
针对:
Max u[C(t)] C(t)1
1
s.t. P1C1 P2C2 W
应用L求极值法,求出C1和C2,代入
式中第一项是时刻t消费c的效用的贴现值.为Hamilton乘子,
表示在t时刻一个单位的资本存量的增加所带来效用增加量
的现值,也有将其称为效用的影子价格.这样,第二项表示:
t时收益的效用以0时刻的收益效用来表示.
一阶最优条件为:
H u c ent 0
1
c
•
H
r n
2
a
横截性条件(Transversality condition-TVC,
本讲的主要工作是将储蓄率作为内生变量引
入模型，做到这一点的办法是考察家庭的消费行 为，因为储蓄率是由家庭的消费行为决定的。
考察家庭费行为的办 法是利用消费的效用函
数，家庭消费决策的原则是使长期内家庭整体消 费效用最大化。 有了家庭的消费效用函数，我门 可以分析家庭在各种资本和产出水平(相当于当前 和长期的消费约束)，如何选择消费量(或储蓄率) 的规律，从而使储蓄率成为模型的内生变量。
c
决定了家庭的最佳消费模式是人均消费不断上升, 保持
不变,还是逐步下降.
我们讨论一下横截性条件
TVC
:
lim
t
t
ga
t
0,
该横截性条件表明,当时间趋向于无穷远时,家庭人均
资产的效用 t ga t 必须趋向于0,即无穷远时间的资产
在现在看来毫无价值.
•
H
r n
•
/
r
n,方程两边对时间: 0 t积分,
家庭收入除用来消费外，其余的用来储蓄以增加资产。记t时刻家庭的总的消费水平为C t ，
这样家庭的预算约束可以表示为:
•
At wtLtrt AtCt 定义at At / Lt为t时刻家庭拥有的人均资产,ct C t / Lt为和t时刻家庭的人均消费, 并且L的增长率为n,这样方程:at At / Lt两边对t求导,并将
A Contribution to the Theory of Taxation,1927
A Mathematical Theory of Saving,1928
一、问题的提出
前面各种增长模型之所以都将储蓄率看作外 生常数，主要是为了简化模型的分析，另一方面 是因为在许多经济中其相对比较稳定，在一定时 期内变化不大。但是，增长理论研究的是长期的 动态经济增长，长期间储蓄率是变化的，将其作 为外生常数排除了经济增长与其的相互作用。从 前面的讨论可知，一个经济是否有稳定状态，是 否收敛，收敛速度多快以及是否存在内生经济增 长等都与储蓄率的变化有关，因此排除经济增长 对储蓄率的反作用必然使经济增长的关键特征都 由模型的外生参数决定，使模型无法解释经济增 长真正的内在规律和机制，这是造成哈罗德一多 马模型、索洛（及其基础之上的衍生）模型解释 经济增长能力局限性的根本原因。
现在, 家庭的最优消费问题变为,在预算约束:
lim
t
a t gexp
t 0
r
v
n
dv
0和
•
a wt r t a t c t na t 下
e 求解 :U (n)tu[c(t)]dt的最大值. t o
利用Hamilton系统来求解上述优化问题.对于上面的优化问题
定义Hamilton方程 : H u c ent w r n a c
当前人均消费c的变化而引起效用的变化率之和,这个和表明了
当前消费的回报率,它应等于当前投资的回报率r.这就是通常所讲
的市场无套利原则在宏观经济学中的体现.
效用函数的形式为：u[C(t)] C(t)1 , 0, n (1 )g 0 保证效用u不发散
1
该函数具有以下三个特点：
1边际效用弹性不变: du ' C u ''C ; u '(C) C ,u ''(C) C 1 dC u ' u '
第二个限制条件是 :
lim
t
a t gexp
t 0
r
v
n
dv
0
即时间的无限推移,人均净资产的"贴现值"渐进非负,
这说明人均净资产的净贴现值 由r t n决定不能为负,
否则,在未来远期的某一时刻,家庭将会停止投资.
也可反过来说,一个家庭的长期人均债务的增长速度不能
超过r t n,否则收益将为负.
0 0
对给定的财富量, 平均利率r t 的提高对方程 1 e dt rt1 / / ngt
0 0
中的边际财富消费倾向有两方面的影响:
1较高的利率提高当前消费相对于将来消费的机会成本, 跨时期消费的
替代效应会刺激人们把当前消费改为将来消费,即当前少消费,多储蓄(投资).
2较高的利率又有收入效应, 会提高所有时间的消费水平,包括当前的消费 水平.因此平均利率r t 的提高对 0的净影响取决于上述哪种效应更强. 分析 : 1如果 1( 0), 越小,随r t 的上升, 0 将下降, c 0也将下降,意味着
速度超过r-n,那么多出来的那一部分用于消费,家庭人均福利能够提高.
消费函数 :
上述方程中的: exp
t
0
r
v
dv
项是将时刻t的一单位收入转化为0时刻的
等价单位的贴现因子.如果r v等于常数r,则贴现因子简化为ert .
如果定义:r
t
1
/
t
t
0
r
v
dv为时间0至t之间的平均利息率,
则贴现因子为ertgt .
第三讲 无限期界模型（拉姆齐模型）
Frank Ramsey
Frank Ramsey (1903-1930), Britishmathe matician and philosopher, best known for his work on the foundations of mathematics. But Ramsey also made remarkable contributions to epistemology, semantics, logic, philosophy of science, mathematics, statistics, probability and decision theory, economics and metaphysics.
e e e
U
tu[c(t)] ntdt
( n)tu[c(t)]dt
t o
t o
n说明子女越多，父母对每个子女福利的重视程度就会越小，
即父母会加速对不断增多子女的"轻视"程度.
2.家庭的资产和债务
记t时刻家庭拥有的总资产为A(t)。这里A(t) 可以为正的，也可以为负的。当A(t)为正时表明 此时家庭拥有正的资产;反之，A(t)表示家庭的负 债。假设在完全竞争条件下，市场上的资本回报 率(即利率)为r(t)。这样家庭所拥有的资产在t时 刻可以带来的收益为A(t)r(t) 。如果A(t)为负， A(t)r(t) 表示此时家庭必须付的债务利息。同时， 假设家庭可以为社会提供劳动力，得到工资回报。 假设在t时刻的工资率（人均工资）为w(t)，家庭 提供的劳动力为L(t)。这样，家庭通过劳动得到 的收益为w(t)L(t)。因此，在t时刻家庭的总收入 为r(t)A(t)+w(t)L(t)。
当前少消费,多储蓄(投资).说明替代效应强.
2如果 1, 越大,随r t 的上升, 0也会上升, c 0上升,说明替代效应强逐渐
将
•
c/
c
1
/
r