磁性物理-2
- 格式:pdf
- 大小:829.92 KB
- 文档页数:47


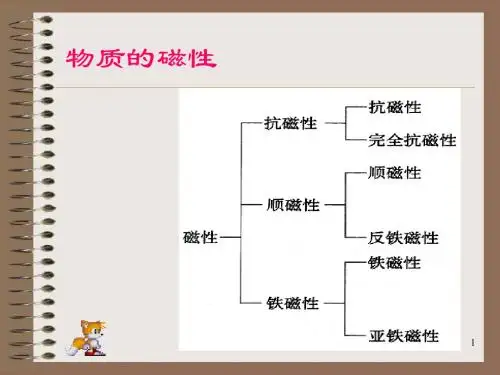
物质的磁性(抗磁性)铁磁性材料特性一、磁化曲线铁磁性物质的磁化曲线(M -H 或B -H )是非线性的。
随磁化场的增加,磁化强度M 或磁感强度B 开始时缓慢增加,然后迅速增加,再转而缓慢增加,最后磁化饱和。
B/Hμ=磁化曲线上任何点B 和H 的比值称为磁导率。
(1)起始磁导率:i H 0H 0B H lim →∆→∆μ=∆i H 0dB dHlim →μ=磁化曲线起始部分斜率或(2)最大磁导率:磁化曲线红箭头所指拐点处的斜率。
μ二、磁滞回线磁化饱和后,慢慢减少H ,则M 亦减小,此过程为退磁。
退磁过程中M 的变化落后于H 的变化,称为磁滞现象。
Q HdB =⎰【J/m 3】磁滞回线所包围的面积表征磁化一周时所消耗的功,称为磁滞损耗Q 。
CD 段:退磁曲线M S :饱和磁化强度B S :饱和磁感强度M r :剩余磁化强度B r :剩余磁感强度H C :矫顽力三、磁晶各向异性和各向异性能在单晶体的不同晶体学方向上,其光学、电学、热膨胀、力学和磁学等性能都不同,这种特性称为晶体的各向异性。
单晶体的磁性各向异性称为磁晶各向异性。
铁磁体在磁化时,外磁场对铁磁体所做的功称为磁化功。
其数值上相当于图中的阴影部分的面积。
1M 00W HdM=μ⎰磁晶各向异性的起源与晶格场对电子轨道的束缚作用有关。
一方面电子轨道平面受晶格场的作用;另一方面电子的轨道运动与电子的自旋运动存在耦合作用。
磁化功小的方向称为易磁化方向;磁化功大的方向称为难磁化方向。
不同晶向的磁化功不同,反映了磁化强度矢量(Ms )在不同方向取向时的能量不同。
Fe Ni Co磁化矢量沿不同晶轴方向的磁化功之差称为磁晶各向异性能,E K 。
磁晶各向异性能是磁化矢量方向的函数。
立方晶体:E K =W [uvw]-W [001]K 222222222K 12E f (,,)E K ()K =αβγ=αβ+βγ+γα+αβγα、β、γ:磁化强度与三个晶轴的方向余弦K 1、K 2为磁晶各向异性常数,与物质结构有关。




第一章磁性物理学(Lisa Tauxe著,刘青松译)建议补充读物关于基础知识,可以参考Butler (1992),1-4页;以及大学物理教科书中关于磁学基础的有关章节。
更多信息可参看:Jiles (1992) 和Cullity (1972) 的第一章。
本章中,我们将了解磁学的基本物理基础,我们主要使用基于“米-千克-秒”制的国际单位(SI)系统。
在磁学中,还有另外一些单位系统也是很重要的,其中,最常用的基于cgs系统的电磁单位系统页也将在本章后面介绍。
1.1 什么是磁场?和重力场一样,磁场既看不见也摸不着。
对于地球重力场来说,我们可以通过引力直接感知其存在。
而对于磁场,只有它作用于一些磁性物体时(例如某些被磁化的金属,天然磁石,或者通电的线圈),我们才能确定其存在。
例如,如果我们把一个磁化的针头放在漂于水面的软木塞上,它会缓慢地指向其周围的磁场方向。
再比如,通电的线圈会产生磁场,从而引起其附近的磁针转动。
磁场的概念正是根据这些现象建立起来的。
电流能够产生磁场,因此我们可以借助于电场来定义由其产生的磁场。
图1.1a展示了当导线通以电流i时,其四周铁屑分布的情形。
根据右手法则,右手的大拇指指向电流方向(即正方向,与电子流动方向相反),其它成环状的四指则指示了相应的磁场方向(图1.1b)。
磁场H同时垂直于电流方向和径向单位矢量r(图1.1b),其强度与电流强度i成正比。
如图1.1所示,磁场强度H可以由安培定律给出:因此,磁场强度H的单位为Am-1。
安培定律的最普遍形式服从麦克斯韦电磁方程。
在稳定电场情况下,∇⨯H = J f, 其中J f 是电流密度。
也就是说,磁场的旋度等效于电流场的密度。
1.2 磁矩我们已知电流在其四周产生环绕的磁场。
如果把通电导线圈成一个面积为πr2的圆环(图1.2a),其周围的铁屑则展示了其产生的磁场的形态。
这个磁场等效于一个磁矩为m的磁铁产生的磁场(图1.2b)。
由电流i产生的磁场,其强度和圆环的面积相关(圆环越大,磁矩就越大),即m = iπr2。




磁性物理与性能摘要:物质的磁性是指能激发磁场、并在外磁场中受到作用力的性质,是物质的一种固有属性,几乎所有物质或多或少都具有磁性。
磁性是很重要的一种物理性能,在现代科学技术中应用得非常广泛。
磁化率、磁导率以及矫顽力等参量对组织、结构很敏感,而饱和磁化强度和居里点等则只与合金相的数量和成分有关。
因此,可根据磁化率和矫顽力的变化分析组织的变化规律,而根据饱和磁化强度和居里点对合金进行相分析,研究组织转变的动力学。
关键字:磁性、磁场、物理、性能。
一、磁性物理(magnetic physics)1、磁性物理的起源19世纪法国物理学家A.-M.安培首先利用分子电流的假设解释了物质磁性的起因。
安培认为物质分子中存在分子电流,并把物质的磁性归因于分子电流的磁效应。
无磁性的分子具有对称的分子电流分布,不显示磁性。
在外磁场作用下分子电流的分布失去对称性,宏观上表现出磁性。
安培的分子电流观点最初只是一种假设,但近代原子物理的发展表明,物质的磁性来源于分子内部的电流这一观点是正确的。
按近代理论,原子或分子内部的每个电子绕原子核作轨道运动,等效于一个电流环,具有一定的磁矩;电子和原子核的自旋运动也相当于一个电流环,也具有一定的磁矩。
这些磁矩能激发磁场,在外磁场中也要受到磁力矩的作用。
无外磁场时各磁矩的取向由于热运动而作无规分布,其磁效应互相抵消,宏观上不显示磁性;有外磁场作用时,各磁矩趋向于一致的排列,单位宏观体积中的总磁矩不等于零,宏观上显示磁性,此现象称为物质的磁化。
2、磁性物理的发展根据物质磁性的强弱或被磁化的程度大小可分为弱磁物质和强磁物质两大类。
弱磁物质又可分为抗磁体和顺磁体两种。
强磁物质主要是由铁族元素及它们的合金组成的铁磁体。
铁磁体由于其很强的磁性和独特的磁化性质而得到广泛应用。
铁磁学已成为磁性物理学中的一个重要分支。
铁磁学除研究典型的铁磁性外,还要研究反铁磁性和亚铁磁性等性质。
铁氧体是属半导体性质的非金属磁性材料,其很高的电阻率使涡流损失很小,广泛应用于微波领域,是继金属磁性材料后的新一代磁性材料。