角平分线的性质与判定学案

11.1.2三角形的高，中线，角平分线导学案主备人：张伟班级：________ 使用人：________ 时间8月26日【学习目标】1.认识并会画出三角形的高线、三角形的角平分线、三角形的中线、并利用其解决相关问题；2、认识三角形的稳定性，并会用其解决一些实际问题【重点】1、认识三角形的高线、中线与角平分线。

并会画出图形。

2、三角形的稳定性【难点】1、画出三角形的高线、中线与角平分线．2、三角形的稳定性的理解一、【温故而知新】下列长度的三个线段能否组成三角形？（1）3，6，8 （2）1，2，3 （3）6，8，2二、【预习检测】知识点1：认识并会画三角形的高线，利用其解决相关问题自学课本4页三角形的高并完成下列各题：1、作出下列三角形三边上的高：2、上面第1图中，AD是△ABC的边BC上的高，则∠ADC=∠ = °3、由作图可得出如下结论：（1）三角形的三条高线所在的直线相交于点；（2）锐角三角形的三条高相交于三角形的；（3）钝角三角形的三条高所在直线相交于三角形的；（4）直角三角形的三条高相交三角形的；练习一：如图所示，画△ABC的一边上的高，下列画法正确的是（）．知识点二：认识并会画三角形的中线，利用其解决相关问题自学课本4页下方三角形的中线并完成下列各题：1、作出下列三角形三边上的中线2、AD是△ABC的边BC上的中线，则有BD = =21，3、由作图可得出如下结论：（1）三角形的三条中线相交于点,这个交点叫做三角形的（2）锐角三角形的三条中线相交于三角形的；（3）钝角三角形的三条中线相交于三角形的；（4）直角三角形的三条中线相交于三角形的；练习二：如图，D、E是边AC的三等分点，图中有个三角形，BD是三角形中边上的中线，BE是三角形中________上的中线；知识点三：认识并会画三角形的角平分线，利用其解决相关问题自学课本5页三角形的角平分线并完成下列各题：1、作出下列三角形三角的角平分线：2、AD是△ABC中∠BAC的角平分线，则∠BAD=∠ =3、由作图可得出如下结论：（1）三角形的三条角平分线相交于点；（2）锐角三角形的三条角平分线相交三角形的；（3）钝角三角形的三条角平分线相交三角形的；（4）直角三角形的三条角平分线相交三角形的 .练习三：如图，已知∠1=21∠BAC，∠2 =∠3，则∠BAC的平分线为，∠ABC的平分线为 .总结：三角形的高、中线、角平分线都是一条线段。

专题06 角的平分线的性质1、如图，把两根钢条AA′，BB′的中点连在一起，可以做成一个测量内槽宽的卡钳，卡钳的工作原理利用了三角形全等判定定理．【答案】SAS．2.王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90∘)，点C在DE上，点A和B分别与木墙的顶端重合，求两堵木墙之间的距离．【答案】解：由题意得：AC=BC，∠ACB=90∘，AD⊥DE，BE⊥DE，∴∠ADC=∠CEB=90∘，∴∠ACD+∠BCE=90∘，∠ACD+∠DAC=90∘，∴∠BCE=∠DAC，在ΔADC和ΔCEB中，{∠ADC=∠CEB ∠DAC=∠BCEAC=BC，∴ΔADC≅ΔCEB(AAS)；由题意得：AD=EC=6cm，DC=BE=14cm，∴DE=DC+CE=20(cm)，答：两堵木墙之间的距离为20cm．知识梳理知识点一：角的平分线的性质角的平分线的性质：角的平分线上的点到角两边的距离相等.要点诠释：用符号语言表示角的平分线的性质定理：若CD平分∠ADB，点P是CD上一点，且PE⊥AD于点E，PF⊥BD于点F，则PE＝PF.例题精讲例1、已知：如图，AD是△ABC的角平分线，且，则△ABD与△ACD的面积之比为（）A．3：2 B． C．2：3 D.【答案】B；提示：∵AD是△ABC的角平分线，∴点D到AB的距离等于点D到AC的距离，又∵，则△ABD与△ACD的面积之比为例2、已知：如图，在ABC∆中，AD平分∠BAC，DE⊥AB于E，DF⊥AC于F.求证：AE＝AF．:3:2AB AC=3:22:3:3:2AB AC=3:2【答案】 证明：∵AD 平分∠BAC ，DE ⊥AB 于E ，DF ⊥AC 于F.∴DE ＝DF （角平分线上的点到角两边的距离相等）90AED AFD ∠=∠=︒（垂直定义）在Rt AED ∆和Rt AFD ∆中 DE DF AD AD =⎧⎨=⎩∴Rt AED ∆≌Rt AFD ∆（HL ）∴AE AF =巩固练习1、如图，AD 是△ABC 的角平分线，DF ⊥AB ，垂足为F ，DE ＝DG ，△ADG 和△AED 的面积分别为50和39，则△EDF 的面积为：（ ）A.11B.5.5C.7D.3.5【答案】解： 过D 点作DH ⊥AC 于H ，∵AD 是△ABC 的角平分线，DF ⊥AB ，DH ⊥AC∴DF ＝DH在Rt △EDF 和Rt △GDH 中DE ＝DG ，DF ＝DH∴Rt △EDF ≌Rt △GDH同理可证Rt △ADF 和Rt △ADH∴AED EDF ADG GDH S =S S S +-△△△△∴EDF ADG AED 2=S S S -△△△＝50－39＝11，∴△EDF 的面积为5.52、如图，AD 是∠BAC 的平分线，DE ⊥AB ，交AB 的延长线于点E ，DF ⊥AC 于点F ，且DB ＝DC. 求证：BE ＝CF.【答案】证明：∵DE ⊥AE ，DF ⊥AC ，AD 是∠BAC 的平分线，∴DE ＝DF ，∠BED ＝∠DFC ＝90°在Rt △BDE 与Rt △CDF 中，DB DCDE DF =⎧⎨=⎩，∴Rt △BDE ≌Rt △CDF （HL ）∴BE ＝CF知识点二：角的平分线的判定角平分线的判定：角的内部到角两边距离相等的点在角的平分线上.要点诠释：用符号语言表示角的平分线的判定：若PE ⊥AD 于点E ，PF ⊥BD 于点F ，PE ＝PF ，则PD 平分∠ADB例题精讲例3、如图，AC=DB ，△PAC 与△PBD 的面积相等．求证：OP 平分∠AOB ．【答案】证明：作PM ⊥OA 于M ，PN ⊥OB 于N12PAC S AC PM =△∵，12PBD S BD PN =△，且PAC S =△PBD S △∴ 12AC PM 12BD PN =又∵AC ＝BD∴PM ＝PN又∵PM ⊥OA ，PN ⊥OB∴OP 平分∠AOB巩固练习1、已知：如图，CD ⊥AB 于D ，BE ⊥AC 于E ，CD 、BE 交于O ，∠1＝∠2．求证：OB ＝OC.【答案】证明：∵CD ⊥AB ，BE ⊥AC ，∠1＝∠2．∴OD ＝OE在Rt △ADO 与Rt △AEO 中，OD OEAO AO =⎧⎨=⎩∴Rt △ADO ≌Rt △AEO （HL ）∴AD ＝AE在Rt △ADC 与Rt △AEB 中，DAC EABAD AEADC AEB ∠=∠⎧⎪=⎨⎪∠=∠⎩∴Rt △ADC ≌Rt △AEB （ASA ）∴CD ＝BE∴CD －OD ＝BE －OE ，即OC ＝OB.知识点三：角的平分线的尺规作图角平分线的尺规作图（1）以O为圆心，适当长为半径画弧，交OA于D，交OB于E.（2）分别以D、E为圆心，大于12DE的长为半径画弧，两弧在∠AOB内部交于点C.（3）画射线OC.射线OC即为所求.例题精讲1、如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC 于点D，若CD=4，AB=15，则△ABD的面积是（）A．15 B．30 C．45 D．60【答案】B；【解析】由题意得AP是∠BAC的平分线，过点D作DE⊥AB于E，又∵∠C=90°，∴DE=CD，∴△ABD的面积=AB•DE=×15×4=30．知识点四：三角形角平分线的性质三角形三条角平分线交于三角形内部一点，此点叫做三角形的内心且这一点到三角形三边的距离相等.三角形的一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三角形的旁心.三角形有三个旁心.所以到三角形三边所在直线距离相等的点共有4个.如图所示：△ABC 的内心为1P ，旁心为234,,P P P ，这四个点到△ABC 三边所在直线距离相等.知识点五：角的平分线的性质综合应用例4、如图，四边形ABDC 中，∠D=∠ABD=90゜，点O 为BD 的中点，且OA 平分∠BAC ．（1）求证：OC 平分∠ACD ；（2）求证：OA ⊥OC ；（3）求证：AB+CD=AC ．【答案】证明：（1）过点O 作OE ⊥AC 于E ，∵∠ABD=90゜，OA 平分∠BAC ，∴OB=OE ，∵点O 为BD 的中点，∴OB=OD ，∴OE=OD，∴OC平分∠ACD；（2）在Rt△ABO和Rt△AEO中，，∴Rt△ABO≌Rt△AEO（HL），∴∠AOB=∠AOE，同理求出∠COD=∠COE，∴∠AOC=∠AOE+∠COE=×180°=90°，∴OA⊥OC；（3）∵Rt△ABO≌Rt△AEO，∴AB=AE，同理可得CD=CE，∵AC=AE+CE，∴AB+CD=AC．巩固练习已知：如图，在ΔABC中，AD是△ABC的角平分线，E、F分别是AB、AC上一点，并且有∠EDF＋∠EAF＝180°．试判断DE和DF的大小关系并说明理由．【答案】证明：过点D 作DM ⊥AB 于M ，DN ⊥AC 于N ，∵AD 是△ABC 的角平分线，∴DM ＝DN∵∠EDF ＋∠EAF ＝180°，即∠2＋∠3＋∠4＋∠EAF ＝180°又∵∠1＋∠2＋∠3＋∠EAF ＝180°∴∠1＝∠4在Rt △DEM 与Rt △DFN 中14DM DNEMD FND ∠=∠⎧⎪=⎨⎪∠=∠⎩∴Rt △DEM ≌Rt △DFN （ASA ）∴DE ＝DF1．如图，已知∠AOB =30∘，P 是∠AOB 平分线上一点，CP//OB ，交OA 于点C ，PD ⊥OB ，垂足为点D ，且PC =4，则PD 等于_______．【解答】解：作PE ⊥OA 于E ，∵CP//OB，∴∠OPC=∠POD，∵P是∠AOB平分线上一点，∴∠POA=∠POD=15∘，∴∠ACP=∠OPC+∠POA=30∘，∴PE=1PC=2，2∵P是∠AOB平分线上一点，PD⊥OB，PE⊥OA，∴PD=PE=2，2．如图，AD是ΔABC的角平分线，∠C=90∘，CD=3cm，点P在AB上，连接DP，则DP的最小值为________cm．【解答】解：作DP′⊥AB于P′，∵AD是ΔABC的角平分线，∠C=90∘，DP′⊥AB∴DP′=DC=3cm，则DP的最小值为3cm，3．如图，ΔABC中，∠C=90∘，AD平分∠CAB，交BC于点D，DE⊥AB于点E，若CD=√3，则DE的长为()A. 2B. 3C. √3D. 2√3【解答】解：∵AD平分∠CAB，DE⊥AB，∠C=90∘，∴CD=DE=√3，4．如图，ΔABC，用尺规作图作角平分线CD．（保留作图痕迹，不要求写作法）【解答】解：如图所示：DC即为所求．5．如图，已知DE∥BC，BE是∠ABC的平分线，∠C=70∘，∠ABC=50∘．求∠DEB和∠BEC的度数．【解答】解：∵BE是∠ABC的平分线，∠ABC=50∘，∴∠1=∠2=25°∵DE∥BC，∴∠DEB=∠2=25∘，在△BEC中，∠C=70∘，∴∠BEC=180∘−∠C−∠2=180∘−70∘−25∘=85∘．6．如图，OC 是∠AOB 的角平分线，点P 、F 在OC 上，PD ⊥AO 于点D ，PE ⊥BO 于点E ，连接DF 、EF ．求证：DF =EF ．【解答】证明：∵OC 是∠AOB 的平分线，PD ⊥OA ，PE ⊥BO ，∴PD =PE ，在Rt△OPD 和Rt△OPE 中，{OP =OP PD =PE ，∴Rt△OPD ≌Rt△OPE （HL ），∴OD =OE ，∵OC 是∠AOB 的平分线，∴∠DOF =∠EOF ，在△ODF 和△OEF 中，{OD =OE∠DOF =∠EOF OF =OF，△ODF ≌△OEF （SAS ），∴DF =EF ．课后巩固1.请将本次课错题组卷，进行二次练习，培养错题管理习惯；2.学霸笔记复习，培养复习习惯。

12.3 《角的平分线的性质》教案台前县吴坝镇中学李桂香一、教学背景的分析1、教学内容本节课是在七年级学习了角平分线的概念和前面刚学完证明直角三角形全等的基础上进行教学的。

内容包括角平分线的作法、角平分线的性质及初步应用。

作角的平分线是基本作图，角平分线的性质为证明线段或角相等开辟了新的途径，体现了数学的简洁美，同时也是全等三角形知识的延续，又为后面角平分线的判定定理的学习奠定了基础。

因此，本节内容在数学知识体系中起到了承上启下的作用。

同时教材的安排由浅入深、由易到难、知识结构合理，符合学生的心理特点和认知规律。

2、学生刚进入八年级的学生观察、操作、猜想能力较强，但归纳、运用数学意识的思想比较薄弱，思维的广阔性、敏捷性、灵活性比较欠缺，需要在课堂教学中进一步加强引导。

根据学生的认知特点和接受水平，我把第一课时的教学任务定为：掌握角平分线的画法及会用角平分线的性质定理解题，同时为下节判定定理的学习打好基础。

3、教学环境利用多媒体技术可以方便地创设、改变和探索某种数学情境，在这种情境下，通过思考和操作活动，研究数学现象的本质和发现数学规律。

4、教学重点、难点本节课的教学重点为：掌握角平分线的尺规作图，理解角的平分线的性质并能初步运用。

教学难点是：1、对角平分线性质定理中点到角两边的距离的正确理解；2、对于性质定理的运用。

教学难点突破方法：（1）利用多媒体动态显示角平分线性质的本质内容，在学生脑海中加深印象，从而对性质定理正确使用；（2）通过对比教学让学生选择简单的方法解决问题；（3）通过多媒体创设具有启发性的问题情境，使学生在积极的思维状态中进行学习。

二、教学目标的确定1、知识与技能：（1）掌握用尺规作已知角的平分线的方法（2）理解角的平分线的性质并能初步运用。

2、数学思考：通过让学生经历观察演示，动手操作，合作交流，自主探究等过程，培养学生用数学知识解决问题的能力。

3、解决问题：（1）初步了解角的平分线的性质在生产、生活中的应用。

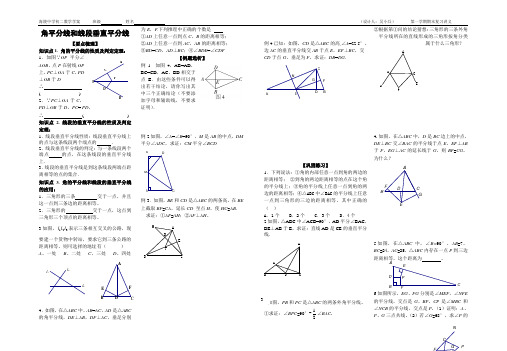
E D C A G NCF B D E A角平分线和线段垂直平分线【要点梳理】知识点1. 角的平分线的性质及判定定理： 1．如图∵OP 平分∠AOB ，点P 在射线OP上，PC ⊥OA 于C ，PD⊥OB 于D ∴ ( )2．∵PC ⊥OA 于C ，PD ⊥OB 于D ，PC = PD ，∴ ( ) 知识点 2. 线段的垂直平分线的性质及判定定理：1．线段垂直平分线性质：线段垂直平分线上的点与这条线段两个端点的 ．2．线段垂直平分线的判定：与一条线段两个端点 的点，在这条线段的垂直平分线上． 3．线段的垂直平分线是到这条线段两端点距离相等的点的集合．知识点 3. 角的平分线和线段的垂直平分线的应用：1．三角形的三条 交于一点，并且这一点到三条边的距离相等。

2．三角形的 交于一点，这点到三角形三个顶点的距离相等。

3.如图，321l l l 表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可选择的地址有（ ） A 、一处 B 、二处 C 、三处 D 、四处4．如图，在△ABC 中，AB =AC ，AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，垂足分别为E ，F .下列推理中正确的个数是 . ①AD 上任意一点到点C ，B 的距离相等； ②AD 上任意一点到AC ，AB 的距离相等； ③BD =CD ，AD ⊥BC ；④∠BDE =∠CDF【例题选析】例1 如图4，AB=AD ，BC=CD ，AC 、BD 相交于点E ．由这些条件可以得出若干结论，请你写出其中三个正确结论（不要添加字母和辅助线，不要求证明）．例2.如图，∠A =∠B =90°，M 是AB 的中点，DM 平分∠ADC ，求证：CM 平分∠BCDMDBCA例3．如图，BE 和CD 是△ABC 的两条高，在BE 上截取BF =CA ，延长CD •至点H ，使HC =AB ． 求证：①AF =AH ；②AF ⊥AH 。

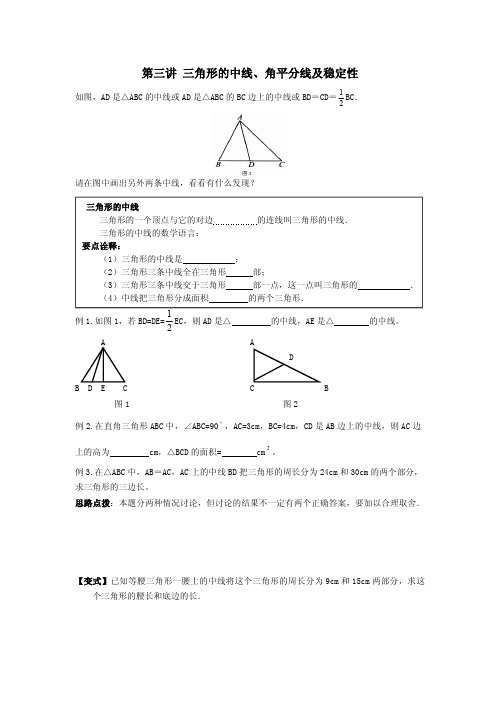
角平分线模型授课日期时间主题教学内容1．熟练掌握与角平分线相关的性质；2．会根据角平分线模型分析证明．1．角平分线的性质定理：角平分线上的点到这个角的两边的距离相等（作用：证明两条线段相等）；2．角平分线的性质定理逆定理：在一个角的内部（包括顶点）且到角的两边距离相等的点在这个角的角平分线上。

（作用：证明两角相等或一条射线是一个角的角平分线）．3．还有哪些性质或定理与角平分线有关？角平分线+平行线→等腰三角形：如图，已知BP平分ABC∠，//PA BC，则AB AP=；如图，已知BP平分ABC∠，//EF PB，则BE BF=．NBMPCABPCAFE三线合一（利用角平分线+垂线→等腰三角形）：如图，已知AD平分BAC∠，且AD BC⊥，则AB AC=，BD CD=．CDAB【例1】如图：已知在ABC∆中，ABC∠的平分线与ACB∠的外角平分线交于点D，DE∥BC，交AB于点E，交AC于点F，求证：FCBEEF-=．FE DAB C M 【例2】如图，已知在ABC∆中，60=∠B，ABC∆的两条角平分线AD CE、相交于点O，求证：ACCDAE=+．DEOB CA【例3】如图，已知ABC ∆中CD AC AB BAC ,,90==∠垂直于ABC ∠的平分线BD 于D ，BD 交AC 于E ，求证：CD BE 2=．ED CAB【例4】已知如图在△ABC 中，∠ACB =90°，CD ⊥AB 于D ，∠A 的平分线交CD 于F ，BC 于E ，过点E 作EH ⊥AB 于H ．求证：（1）CF =EH ． （2）四边形CEHF 是菱形．1．已知：如图，平行四边形ABCD各角的平分线分别相交于点E，F，G，H，求证：四边形EFGH是矩形．2．已知：如图，ADCDACABCADBAD⊥>∠=∠,,于点HD,是BC中点，求证：()ACABDH-=21．HD CAB3．如图，已知∠BAC =90°，AD ⊥BC 于点D ，∠1=∠2，EF ∥BC 交AC 于点F ．试说明AE =CF ．21FE DABC。

《12.3 角的平分线的性质》教案李爽2013-9-24一、内容和内容解析1、内容：角的平分线的性质2、内容解析：角的平分线的性质反映了角的平分线的基本特征，也是证明两条线段相等的常用方法。

角的平分线的性质的研究过程为以后学习线段的垂直平分线的性质提供了思路和方法。

.本节内容是全等三角形知识的运用和延续，用尺规作一个角的平分线，其作法原理是三角形全等的“边边边”判定方法和全等三角形的性质；角的平分线的性质证明，运用了三角形全等的“角角边”判定方法和全等三角形的性质。

角的平分线的性质证明提供了使用角的平分线的一种重要模式------利用角的平分线构造两个全等的直角三角形，进而证明相关元素对应相等。

基于以上分析，确定本节课的教学重点：探索并证明角的平分线的性质。

二、目标和目标解析1、目标（1）会用尺规作一个角的平分线，知道作法的合理性；（2）探索并证明角的平分线的性质；（3）能用角的平分线的性质解决简单问题。

2、目标解析达成目标（1）的标志是：学生明确尺规作图的基本要求，知道用尺规作图作角的平分线的方法与原理，能在教师的引导下用尺规作出一个已知角的平分线。

达成目标（2）的标志是：学生能在教师的引导下通过观察、测量等方法，发现角的平分线的性质，能准确表达性质的内容，能正确地写出已知、求证，能运用三角形全等的“AAS”判定方法和全等三角形的性质证明角的平分线的性质。

达成目标（3）的标志是：学生能利用角的平分线的性质构造全等三角形，证明与线段相等有关的简单问题。

三、教学问题诊断分析本节课的学习中，学生在分清角的平分线的性质的条件和结论，并进行严格的逻辑证明的过程中常常感到困难。

例如，在用符号语言表述性质的条件和结论时，不知“距离”应为“条件”还是“结论”。

其重要原因是角的平分线的性质是以文字命题的形式给出的，其条件和结论具有一定的隐蔽性。

教学时，教师要引导学生分析性质中的条件和结论（必要时可让学生将性质改写成“如果······那么······”的形式），找出结论中的隐含条件（垂直），正确写出已知和求证，并归纳出证明命题的一般步骤。

导学案格式科目/教材数学年级：七课题:角平分线的性质（1）学习目标1、能用三角形全等的知识，解释角平分线的原理；2、会用尺规作已知角的平分线．学习重点能用三角形全等的知识，解释角平分线的原理。

学习难点会用尺规作已知角的平分线。

学习方法：自主学习与小组合作探究教学内容提要（描述主要教学环节与教学要点）时间教学操作流程所需资源设计意图听课记录评价学生学习事项——学生用什么教学组织形式（个人、双人或小组、全班）和方法去完成学习事项（问题、任务、活动、作业），用什么方式表达呈现。

教师导控事项——需要教师做什么以支持学生学习(讲授、提问、举例、演示、布置、板书……)；——怎样检测学生学习效果并反馈。

环节（任务）一新课导入环节（任务）一新课导入根据问题回答（在学习案上完成）环节（任务）二知识点探究1、（两人合作完成）应怎样平分一个角呢？2、讨论结论是否仍然成立呢？3、师友制作一个如图2所示的平分角的仪器 , 说明它的道理探究（二）师友合作完成：1.如何作出一个角的平分线呢？跟老师动手画2.议一议(根据自已所画说一说)（环节（任务）一温故知新1．（Ⅰ．想一想，填一填：(学习案内容)环节（任务）二知识点探究探究（一）1、依据上题我们应怎样平分一个角呢？2、完成学习案中思考:讨论结论是否仍然成立呢？3、我们可以制作一个如图2所示的平分角的仪器：其中AB=AD，BC=DC．将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线AE，AE就是角平分线．你能说明它的道理吗？探究（二）1.思考：如何作出一个角的平分线呢？师示范并讲解,要求学生跟动2.议一议： (1)、在上面作法的第二步中，去掉“大于12MN的长”这个条件行吗？环节（任务）二知识点探究环节（任务）三讨论交流环节（四、反思总结：环节五：作业探究（三）按学习案探究三内容完成并体验知识点的形成过程。

完成学习案检测练习一2、展示学习情况3、口述三角形三边的关系环节（任务）三讨论交流1.在研读的过程中，你认为有哪些不懂的问题？2.学习案双基检测环节（四、反思总结：1、叙述本节课知识点（多人复述）2、多人复述3、完成学习案达标检测环节五：作业强化训练(2)、第二步中所作的两弧交点一定在∠AOB的内部吗？探究（三）学生完成学案内容.观察测量结果，猜想线段OD与OE的大小关系，写出结论：下面用我们学过的知识证明发现：已知：如图4，AO平分∠BAC，OE⊥AB，OD⊥AC。

第2课时角的平分线的判定1．掌握角平分线的判定．2．熟练运用角的平分线的判定及性质解决问题．阅读教材P50，完成预习内容．知识探究1．到角的两边距离相等的点在________________．所以，如果点P到∠AOB两边的距离相等，那么射线OP是________________．2．完成下列各命题，注意它们之间的区别与联系．(1)如果一个点在角的平分线上，那么________________________；(2)如果一个点到角的两边的距离相等，那么________________________；(3)综上所述，角的平分线是____________________的集合．3．(1)三角形的三条角平分线相交于______点，它到______________．(2)三角形内，到三边距离相等的点是____________．利用角平分线的判定证角平分线比证全等要简便得多．自学反馈如图，AD⊥DC，AB⊥BC，若AB＝AD，∠DAB＝120°，则∠ACB的度数为( )A．60°B．45°C．30°D．75°活动1小组讨论例1已知：如图，△ABC.求作：点P，使得点P在△ABC内，且到三边AB、BC、CA的距离相等．作法：(提示)作三个内角平分线交于一点P，点P即为所求作的点．例2如图，在△ABC中，外角∠CBD和∠BCE的平分线BF、CF相交于点F.求证：点F也在∠BAC的平分线上．证明：过点F作FM⊥BC于点M，FG⊥AB于点G，FH⊥AC于点H，∵BF、CF是∠CBD和∠BCE的平分线，∴FG＝FM，FH＝FM.∴FG＝FH.∴点F也在∠BAC的平分线上．过点F作AD、BC、AE的垂线段FG、FM、FH，然后证FG＝FH.活动2跟踪训练1．已知：如图，CD⊥AB于D，BE⊥AC于E，CD、BE交于O，∠1＝∠2.求证：OB＝OC.2．已知：如图，OD平分∠POQ，在OP、OQ边上取OA＝OB，点C在OD上，CM⊥AD于M，CN⊥BD于N.求证：CM＝CN.角平分线的性质与判定通常是交叉使用．活动3课堂小结角平分线的性质是证线段相等的常用方法之一，角平分线的性质与判定通常是交叉使用，作角的平分线或过角的平分线上一点作角两边的垂线段是常用辅助线之一．【预习导学】知识探究1．这个角的平分线上∠AOB的平分线 2.(1)这个点到角两边的距离相等(2)这个点在这个角的平分线上(3)到角两边距离相等的点 3.(1)一三边的距离相等(2)三条角平分线的交点自学反馈1．C【合作探究】活动2跟踪训练1．证明：∵∠1＝∠2，OD⊥AB，OE⊥AC，∴OD＝OE.在△BDO与△CEO中，∵∠BDO＝∠CEO＝90°，OD＝OE，∠BOD＝∠COE，∴△BDO≌△CEO.∴OB＝OC. 2.证明：∵OD平分∠POQ，∴∠AOD＝∠BOD.在△AOD与△BOD中，∵OA ＝OB，∠AOD＝∠BOD，OD＝OD，∴△AOD≌△BOD.∴∠ADO＝∠BDC.∵CM⊥AD，CN⊥BD，∴CM＝CN.。

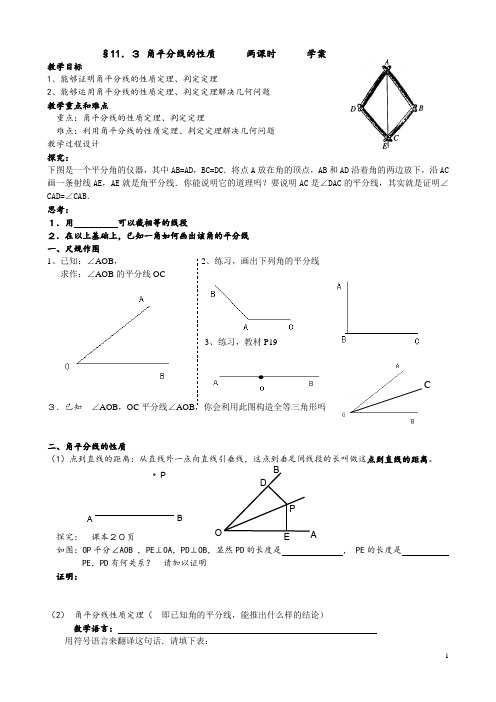
§11．３ 角平分线的性质 两课时 学案教学目标1、能够证明角平分线的性质定理、判定定理2、能够运用角平分线的性质定理、判定定理解决几何问题教学重点和难点重点：角平分线的性质定理、判定定理难点：利用角平分线的性质定理、判定定理解决几何问题教学过程设计探究：下图是一个平分角的仪器，其中AB=AD ，BC=DC ．将点A 放在角的顶点，AB 和AD 沿着角的两边放下，沿AC 画一条射线AE ，AE 就是角平分线．你能说明它的道理吗？要说明AC 是∠DAC 的平分线，其实就是证明∠CAD=∠CAB ．思考：１．用 可以截相等的线段２．在以上基础上，已知一角如何画出该角的平分线一、尺规作图1、已知：∠AOB ，2、练习，画出下列角的平分线求作：∠AOB 的平分线OC3、练习，教材P19３．已知 ∠AOB ，OC 平分线∠AOB ，你会利用此图构造全等三角形吗二、角平分线的性质（1）点到直线的距离：从直线外一点向直线引垂线，这点到垂足间线段的长叫做这点到直线的距离。

探究： 课本２０页如图：OP 平分∠AOB ，PE ⊥OA ，PD ⊥OB ，显然PD 的长度是 ， PE 的长度是 PE ，PD 有何关系？ 请加以证明证明：（2） 角平分线性质定理（ 即已知角的平分线，能推出什么样的结论）数学语言：用符号语言来翻译这句话．请填下表：B A P O D A BP C（老师在此补充命题证明的步骤）1）符号语言∵或∴思考：那么在角的内部，到角的两边距离相等的点是否在角的平分线上呢？根据下表中的图形写出已知事项，猜想由已知事项可推出的事项，并加以证明：证明:由此得角平分线的判定三、角平分线的判定定理定理：符号语言∵∴或思考：角平分线的判定和性质之间有什么联系？四、应用：如图所示，要在S区建一个集贸市场，使它到公路、铁路距离相等，•离公路与铁路交叉处500m，这个集贸市场应建于何处（在图上标出它的位置，比例尺为1：20000）？1．集贸市场建于何处，和本节学的角平分线性质和判定有关吗？用哪一个解决这个问题？2．比例尺为1：20000是什么意思？结论：1．应该用．•集贸市场应该建在公路与铁路形成的角的平分线上，并且要求离角的顶点500米处．2．在纸上画图时，常用厘米为单位，而题中距离又是以米为单位，•这就涉及一个单位换算问题．1m=100cm，所以比例尺为1：20000，其实就是图中表示实际距离的意思．作图如下：第一步：第二步：总结：应用角平分线的性质和判定，可以省去证明三角形全等的步骤，•使问题简单化．所以若遇到有关角平分线，又要证线段相等的问题，•可以直接利用性质解决问题．五、练习1、如图，△ABC 的角平分线BM 、CN 相交于点P ．求证：点P 到三边AB 、BC 、CA 的距离相等．思考：点P 在∠A 的平分线上吗？为什么？２、如图，△ABC 的∠B 的外角平分线BD 与∠C 的外角的平分组CE 相交于P,求证点P 到三边AB ，BC ，CA 所在直线的距离相等。

结论：DE=DF方法1在BC上截取BG=BE,连接GD请小组派代表讲解不同思路截取构造全等因为BD是N B的平分线，N EBD二N GBD,在4DBE和4DBG中BG=BEZ EBD=Z GBD,PE=PD所以△DBE/Rt A DBG(SAS),所以DE=DG。

Z DEB=Z DGB,Z EBG=Z EDF=90°Z DEB+Z DFB=180°Z DGB+Z DGF=180°Z DGF=Z DFG,DG=DFDE=DF方法2在BA上截取BG，使BG=BF，连接GD方法3过D点作DG L AB于G,DH±BC于H截取构造全等此题用到四边形内角和以及，其中一组对角互补另一组对角也互补作垂线构造全等环节五如果有时间画思维导图，谈自己收你的收获获作业超市：A同学们根据自己兴趣挑环节六1.如图，已知直角三角形ABC中，选至少2个自己喜欢的试作业N C=90°,CA=CB,AD平分/ 题布置BAC,DE±AB于E点，求证：CD=BE2已知：如图，中，N=N,N=N,求证：=。

巩固所学知识提升学生能力D C学生活动的说明（200字内）学生活动的设计目的在于，鼓励学生积极思考勇于发言，处于青春期的学生，逻辑思维、创造性思维迅速发展，他们能够从不同的角度、多维的、立体的考虑问题，并且通过综合、分析、推理找出本质和规律鼓励创新，并利用已有知识解决问题。

明确已知角平分线求线段长度的基本解题思路，掌握多题一解方法，并训练学生学会读题，理解题意，综合运用所学知识解题能力。

教学设计的说明（200字内）―本节课的教学设计围绕教学目标，运用全等判定及性质相关知识，角平分线性质综合应用的重点，运用类比联想，激发学生的积极性主动探究知识解决问题。

学会添加辅助线。

同时渗透爱家、爱国的教育，同时渗透青春期教育，让同学们友好相处，让他们树立远大志向，共同度过快乐时光。

板书设计例1如图，四边形ABCD中，N A+N C=180°，变式训练：BD平分/ABC，求证：AD=CD已知Rt^ABC中，N B=90°,BD是N B的平分线，将三角板的直角顶点放在D点，三角板的两角边与AB交于E与直角边BC交于F，你能判断DE与DF的数量关系吗？你是如何证明？。

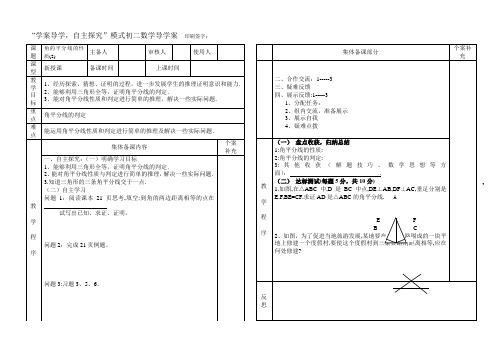
§12.3.2 角的平分线的性质（2）教材：义务教育教科书实八年级上册第十二章全等的三角形第11课时课程标准探索并证明角平分线的性质定理：角平分线上的点到角两边的距离相等；反之，角的内部到角两边距离相等的点在角的平分线上。

教学目标知识与技能1．掌握角平分线的判定定理。

2.会证明角的平分线的判定定理能用角平分线的判定解决有关问题。

过程与方法使学生经历观察—实验—猜想—验证—推理—交流分享的过程探索出角平分线的判定，会运用HL证明三角形全等从而证明角平分线的判定。

情感态度与价值观通过探究角平分线的判定活动，逐步培养学生合作交流的意识和大胆猜想、乐于探究的良好学习品质以及发现问题的能力。

教学重点难点1．学习重点：角平分线的判定定理。

2．学习难点：应用角平分线的判定以及应用时和性质的区别。

教法学法教学方法：“互助导学——四步.六环”教学模式，辅助以自学辅导法，练习法、谈话法等。

学法指导：以导学案为载体，指导学生学会阅读教材和自主探究的方法。

运用师友互助和小组合作，体会合作学习的方法。

鼓励学生梳理知识，指导学生小结的方法。

教学准备1.教具：多媒体课件ppt，三角板等。

2.学具：画图工具、练习本、教材、学习指南等。

3.教学环境：交互式电子白板多媒体系统。

问题情境师生互动设计意图媒体运用活动一：情境导入、明晰目标（时间：2分钟）问题1：（1）结合图形叙述角平分线的性质定理。

（2）如图要在两条公路的夹角S区建一个离相交地100米且到两公路的距离相等的长途货运站，应建在什么位置?（比例尺1：5000）【教师活动】1.向学生发放“学习指南”，指导学生阅读学习目标。

2.教师提出问题，并用ppt出示问题1，引发学生思考。

3.在学生思考并回答的基础上引出并板书节课题。

【学生活动】1.阅读“学习指南”，明确学习目标，思考并回答问题1，同学互评、补充纠正。

2.回答老师提出的问题，参与对同伴表现情况的评价。

【设计意图】通过问题1，回顾角平分线的性质定理，对问题（2）进行思考。

（1）教师引导学生分析，寻找证明方法。

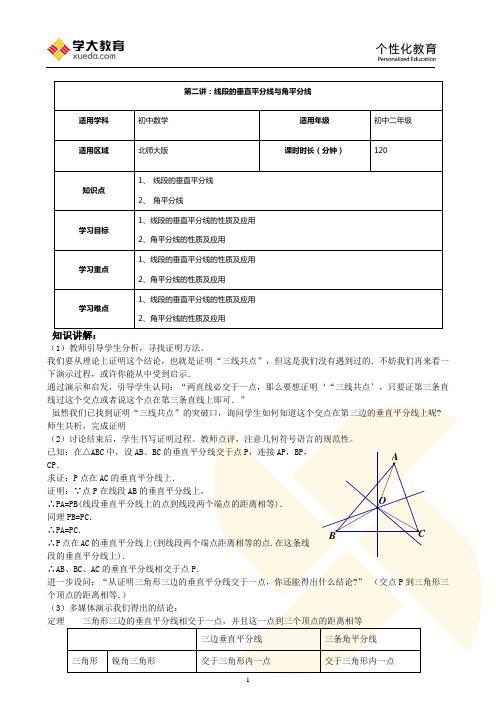
我们要从理论上证明这个结论，也就是证明“三线共点”，但这是我们没有遇到过的．不妨我们再来看一下演示过程，或许你能从中受到启示．通过演示和启发，引导学生认同：“两直线必交于一点，那么要想证明‘“三线共点’，只要证第三条直线过这个交点或者说这个点在第三条直线上即可．”虽然我们已找到证明“三线共点”的突破口，询问学生如何知道这个交点在第三边的垂直平分线上呢? 师生共析，完成证明（2）讨论结束后，学生书写证明过程。

教师点评，注意几何符号语言的规范性。

已知：在△ABC 中，设AB 、BC 的垂直平分线交于点P ，连接AP ，BP ，CP ．求证：P 点在AC 的垂直平分线上．证明：∵点P 在线段AB 的垂直平分线上， ∴PA=PB(线段垂直平分线上的点到线段两个端点的距离相等)．同理PB=PC ．∴PA=PC． ∴P 点在AC 的垂直平分线上(到线段两个端点距离相等的点.在这条线段的垂直平分线上)．∴AB、BC 、AC 的垂直平分线相交于点P ．进一步设问：“从证明三角形三边的垂直平分线交于一点，你还能得出什么结论?” （交点P 到三角形三个顶点的距离相等．）（3）多媒体演示我们得出的结论：定理三边垂直平分线 三条角平分线 三角形锐角三角形 交于三角形内一点 交于三角形内一点第二讲：线段的垂直平分线与角平分线适用学科 初中数学 适用年级 初中二年级适用区域 北师大版 课时时长（分钟） 120知识点 1、 线段的垂直平分线2、 角平分线学习目标 1、线段的垂直平分线的性质及应用2、角平分线的性质及应用学习重点 1、线段的垂直平分线的性质及应用2、角平分线的性质及应用学习难点1、线段的垂直平分线的性质及应用2、角平分线的性质及应用 C B A O钝角三角形交于三角形外一点直角三角形交于斜边的中点交点性质到三角形三个顶点的距离相等到三角形三边的距离相等课堂练习：考点一：线段的垂直平分线【例题】1．（2014春•宜宾校级期末）如图，在△ABC中，AD为∠BAC的平分线，FE垂直平分AD，交AD于E，交BC的延长线于F，那么∠B与∠CAF相等吗？为什么？2（2014秋•定陶县期中）如图，AB=AC，AB的垂直平分线DE交BC的延长线于点E，交AC于点F，∠A=50°，AB+BC=6．求：（1）△BCF的周长；（2）∠E的度数．3．（2014秋•芜湖校级期末）作图题：（不写作法，但必须保留作图痕迹）如图：某地有两所大学和两条相交叉的公路，（点M，N表示大学，AO，BO表示公路）．现计划修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等．你能确定仓库P应该建在什么位置吗？在所给的图形中画出你的设计方案．4．（2014秋•江阴市校级期中）已知直线l及其两侧两点A、B，如图．（1）在直线l上求一点P，使PA=PB；（2）在直线l上求一点Q，使l平分∠AQB．（以上两小题保留作图痕迹，标出必要的字母，不要求写作法）【习题】1．（2014秋•江津区月考）如图，已知AD是∠BAC的角平分线，AD的垂直平分线EF交AB于点E，交BC 延长线于F．求证：（1）∠B=∠FAC；（2）DE∥AC．2．（2013春•莘县期末）如图，在△ABC中，AB=AC，P、Q、R分别在AB、AC上，且BP=CQ，BQ=CR．求证：点Q在PR的垂直平分线上．3．（2013春•锦江区校级期末）如图，已知：AB∥CD，∠BAE=∠DCF，AC，EF相交于点M，有AM=CM．（1）求证：AE∥CF；（2）若AM平分∠FAE，求证：FE垂直平分AC．4．（海南）如图所示，正方形ABCD的边长为1，G为CD边上的一个动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于H．（1）求证：①△BCG≌△DCE；②BH⊥DE．（2）试问当点G运动到什么位置时，BH垂直平分DE？请说明理由．5．（2013秋•房山区期末）（1）已知：图1中，点M、N在直线l的同侧，在l上求作一点P，使得PM+PN 的值最小．（不写作法，保留作图痕迹）（2）图2中，联结M、N与直线l相交于点O，当两直线的夹角等于45°，且OM=6，MN=2时，PM+PN的最小值是．6．（2013秋•厦门期末）已知直线l的同侧有A，B两点（图1），要在直线l上确定一点P，使PA+PB的值最小．小明同学的做法如图2：①作点A关于直线l的对称点A′，连接A′B交l于点P，则PA+PB=A′P+PB=A′B，由“两点之间，线段最短”可知，点P即为所求的点．请问小明同学的做法是否正确？说明理由．7．（2013秋•临沭县校级期末）在学习轴对称的时候，老师让同学们思考课本中的探究题．如图（1），要在燃气管道l上修建一个泵站，分别向A、B两镇供气．泵站修在管道的什么地方，可使所用的输气管线最短？请你参考小华的做法解决下列问题．如图3，在△ABC中，点D、E分别是AB、AC边的中点，请你在BC边上确定一点P，使△PDE得周长最小．在图中作出点P（保留作图痕迹，不写作法）．8．（2014秋•广丰县校级期中）如图：PA、PC分别是△ABC外角∠MAC与∠NCA的平分线，并交于点P，PD⊥BM 于点D，PF⊥BN于点F．（1）求证：BP是∠MBN的平分线；（2）请你在BM、BN上分别找出点G、H，使得△PGH的周长最小．（温馨提示：不要求尺规作图，但必须保留作图痕迹，不用证明）9．（2014秋•姜堰市校级月考）作图：（1）如图：已知∠AOB和C、D两点，求作一点P，使PC=PD，且P到∠AOB两边的距离相等．（2）如图：已知直线m是一条小河，有一牧马人准备从A处牵马去河边饮水，然后返回B处，马在何处饮水才能使所走路程最短，请在图中作出该点Q的位置．10．（2014秋•天长市校级月考）公路l同侧的A、B两村，共同出资在公路边修建一个客车停靠站C，并使停靠站到A、B两村的距离相等，你如何确定停靠站C的位置．利用尺规作图作出点C，写出作法，并保留作图痕迹．11．（2013春•霍邱县期中）解答题①已知：如图，在△ABC中，∠CAB=120°，AB=4，AC=2，AD⊥BC，D是垂足．求：AD的长．②如图，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km处，他想把他的马牵到小河边去饮水，然后回家．他要完成这件事情所走的最短路程是多少？考点二：角平分线【例题】1．（2015秋•北京校级期中）如图，在四边形ABCD中，BC＞BA，AD=CD，BD平分∠ABC，求证：∠A+∠C=180°．2．（2014秋•新洲区期末）如图，在△ABC中，∠ABC的平分线与∠ACB的外角的平分线相交于点P，连接AP．（1）求证：PA平分∠BAC的外角∠CAM；（2）过点C作CE⊥AP，E是垂足，并延长CE交BM于点D．求证：CE=ED．【习题】1．（2011秋•横峰县期末）如图所示，△ABC为直角三角形，∠ACB=90°，BF平分∠ABC，CD⊥AB于D，CD 交BF于点G，GE∥CA，求证：CE与FG互相垂直平分．2．（2014秋•肥东县期末）已知：如图，P是OC上一点，PD⊥OA于D，PE⊥OB于E，F、G分别是OA、OB 上的点，且PF=PG，DF=EG．求证：OC是∠AOB的平分线．3．（2004•青海）（1）如图，E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别是C、D，求证：OC=OD；（2）已知，点A和B．求作：经过A、B两点且半径最小的圆．（用直尺和圆规作图，保留作图痕迹不写作法）4．（2012秋•云阳县校级期中）如图，△ABC中，若AD平分∠BAC，过D点作DE⊥AB，DF⊥AC，分别交AB、AC于E、F两点．求证：AD⊥EF．5．（2015•株洲）如图，在Rt△ABC中，∠C=90°，BD是△ABC的一条角平分线．点O、E、F分别在BD、BC、AC上，且四边形OECF是正方形．（1）求证：点O在∠BAC的平分线上；（2）若AC=5，BC=12，求OE的长．6．（2014秋•江阴市校级期中）如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD，（1）求证：△BCE≌△DCF；（2）若AB=21，AD=9，AC=17，求CF的长．7．（2013秋•涉县校级月考）如图所示，已知∠EAF，FB⊥AE于点B，PC⊥AF于点C，M，N分别是射线AE，AF上的点，∠PNC=∠PMB，PM=PN．求证：AP平分∠EAF．8．如图，△ABC中，∠ABC的外角平分线BD与∠ACB外角平分线CE相交于点P，求证：点P到三边AB、BC、CA所在直线的距离相等．。