下载文档原格式
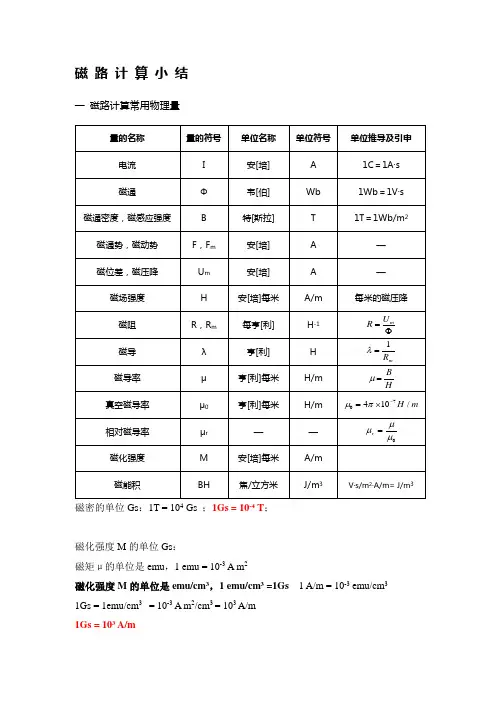
磁路计算小结一磁路计算常用物理量磁密的单位Gs：1T = 104 Gs ；1Gs = 10-4 T；磁化强度M的单位Gs：磁矩μ的单位是emu，1 emu = 10-3 A m2磁化强度M的单位是emu/cm3，1 emu/cm3 =1Gs 1 A/m = 10-3 emu/cm3 1Gs = 1emu/cm3 = 10-3 A m2/cm3 = 103 A/m1Gs = 103 A/m二磁路基本定律1．安培环路定律H恰好等由麦克斯韦方程可知，沿着任何一条闭合回线L，磁场强度H的线积分值⎰⋅L dl于该闭合回路所包围的总电流值∑i（代数和），即∑⎰=Hdl⋅iL式中，若电流的正方向与闭合回线的环行方向符合右手螺旋关系，i取正号，否则i取负号。
若沿着回线L，磁场强度H的方向总是切线方向、大小处处相等，且闭合回线所包围的总电流是由通有电流i的N匝线圈提供，则上式将简化为HL=Ni（1）安培定则也叫右手螺旋定则，是表示电流和电流激发磁场的磁感线方向间关系的定则。
●通电直导线中的安培定则（安培定则一）用右手握住通电直导线，让大拇指指向电流的方向，那么四指的指向就是磁感线的环绕方向；●通电螺线管中的安培定则（安培定则二）用右手握住通电螺线管，让四指指向电流的方向，那么大拇指所指的那一端是通电螺线管的N极。
2．磁路的欧姆定律设环形螺线管铁心的截面积为A，磁通量密度为B，总磁通量为Φ，则有=Φ（2.1）BAμ=HA设线圈匝数为N，螺线管平均长度为l，给线圈通电流I，根据安培环路定律，则有HL NI =所以l NI H /=代入式（2.1），则有l NIA /μ=Φ 整理得Al NI⋅=Φμ1 或RNI=Φ （2.2） 式中AlR ⋅=μ （2.3） 在电路中，设电动势（电压）为E ，电阻为R ，电流为I ，则有电路的欧姆定律RE I =设导体电阻率为σ，长度为l ，截面积为S ，则回路的电阻为Sl R ⋅=σ 由于式(2.2)与电路中的欧姆定律非常相似，所以称之为磁路的欧姆定律。
书山有路勤为径，学海无涯苦作舟
磁性流体密封能力的数值计算分析
磁场和磁性流体的饱和磁化强度对磁性流体的密封有着直接的影响。
磁性流体密封间隙的变化、转轴偏心、磁性流体的量、转轴直径、离心力等对磁性流体密封间隙处的磁场产生影响，同时也对磁性流体的密封压差也产生影响。
本文定量的分析了密封间隙、转轴偏心、转轴直径、离心力对磁性流体密封能力的影响。
影响磁性流体旋转轴密封能力的因素很多，其中磁性流体的材料特性，磁场的强度对轴密封有着直接的影响，对于材料相同和结构相似的密封装置而言，转轴的偏心、密封间隙的变化以及在转轴的直径、离心力的作用都会对密封能力产生影响。
分析这些因素的影响对磁性流体密封的设计和使用是十分重要的。
本文采用数值计算方法分析了设计与制造因素对密封能力的影响。
1、磁流体密封的理论基础通常而言，外加磁场较强，磁性流体处于饱和状态，其磁化强度近似等于其饱和磁化强度Ms，不考虑旋转时离心力的作用，磁性流体单级密封内任一点处的压强为:
式中h 沿重力方向自参考点至磁性流体微团的距离，C 积分常数，由边界条件确定。
当磁性流体较多时，可以认为在极限状态下，此时流体低压侧的磁感应强度为0，忽略重力作用，单级轴密封的极限密封压强差近似为：当转轴以角速度w0 旋转时，此时磁性流体还会受到离心力的作用。
假设转轴半径为R1，磁极内径为R2，则旋转密封磁性流体内的压强为：式中：
2、外加磁场强度及磁性流体磁化强度对密封压差的影响从式(2)可以看。
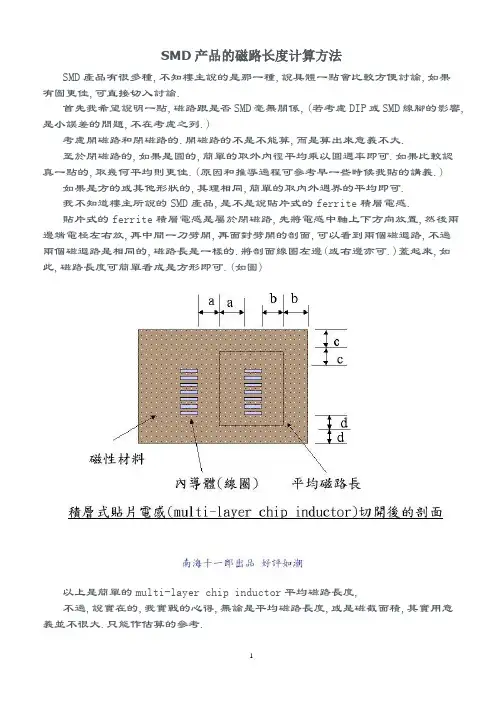
SMD产品的磁路长度计算方法SMD產品有很多種,不知樓主說的是那一種,說具體一點會比較方便討論,如果有圖更佳,可直接切入討論.首先我希望說明一點,磁路跟是否SMD毫無關係,(若考慮DIP或SMD線腳的影響,是小誤差的問題,不在考慮之列.)考慮開磁路和閉磁路的.開磁路的不是不能算,而是算出來意義不大.至於閉磁路的,如果是圓的,簡單的取外內徑平均乘以圓週率即可.如果比較認真一點的,取幾何平均則更佳.(原因和推導過程可參考早一些時候我貼的講義.) 如果是方的或其他形狀的,其理相同,簡單的取內外週界的平均即可.我不知道樓主所說的SMD產品,是不是說貼片式的ferrite積層電感.貼片式的ferrite積層電感是屬於閉磁路,先將電感中軸上下方向放置,然後兩邊端電極左右放,再中間一刀劈開,再面對劈開的剖面,可以看到兩個磁迴路,不過兩個磁迴路是相同的,磁路長是一樣的.將剖面線圈左邊(或右邊亦可.)蓋起來,如此,磁路長度可簡單看成是方形即可.(如圖)以上是簡單的multi-layer chip inductor平均磁路長度,不過,說實在的,我實戰的心得,無論是平均磁路長度,或是磁截面積,其實用意義並不很大.只能作估算的參考.更重要一點,我實戰的結果,一般來說,multi-layer chip inductor的感值,感值並不是跟圈數的平方成正比,而是跟圈數成正比.這是我多年來做multi-layer chip inductor很重要的心得.這實戰的結論以後可以進教課書喔!當然,這結論也告訴我們一個很重要的訊息,我們做的multi-layer chip inductor還有很大很大的改進空間!我們肯定尚沒有將所有條件做到最佳化!很可惜,我已經沒有做研發,現在也沒有機台做研究,如果有人有這方面的資源(機台)作研究,我是可以提供他很多很多心得的,同時,我更可以確定,只要肯用心,單這方面的專利就可以拿不完,而且,在市場上,肯定是可以打遍全球無敵手.唉! 沒有戰場的將軍是很痛苦的啊!闭合磁路中，如果漏磁可忽略的话，可以用有效磁导率来表征磁芯的性能：u e= L/ u o N2 *( Le/ Ae)L为装有磁芯的线圈的电感量（H），N为线圈匝数，Le为有效磁路长度（m），Ae为有效截面积（m2）。
永磁体磁链计算公式
永磁体的磁链计算公式可以通过磁通量和磁场强度之间的关系来表示。
磁链（Φ）是指通过一个闭合线圈或磁路的磁通量，通常用韦伯（Wb）作为单位。
磁场强度（H）是指单位长度内通过导体的磁通量，通常用安培每米（A/m）作为单位。
根据安培环路定理，磁通量Φ与磁场强度H之间的关系可以用以下公式表示：
Φ = B A.
其中，B为磁感应强度（单位为特斯拉，T），A为磁路截面积（单位为平方米，m^2）。
磁感应强度B与磁场强度H之间的关系可以用以下公式表示：
B = μ0 μr H.
其中，μ0为真空中的磁导率（约为4π×10^-7 H/m），μr 为相对磁导率，H为磁场强度。
因此，永磁体的磁链计算公式可以表示为：
Φ = μ0 μr H A.
这个公式可以用来计算在给定磁场强度下永磁体的磁链，进而帮助分析永磁体的磁性能和应用特性。
需要注意的是，实际应用中永磁体的磁链计算可能会受到多种因素的影响，如温度、材料特性等，因此在具体问题中需要综合考虑这些因素进行计算。
磁路计算是用于计算磁场中磁路参数的过程，它是磁场分析和电磁设备设计中的重要步骤之一。
磁路计算可以帮助确定磁路的磁通量、磁势、磁阻和磁感应强度等参数。
下面是进行磁路计算的一般步骤：
⚫确定磁路几何形状：首先需要确定磁路的几何形状，包括磁心、线圈和气隙等部分。
这些部分的形状和尺寸对磁路参数的计算有重要影响。
⚫材料特性和参数：确定各个磁路部分的材料特性和参数，包括磁性材料的磁导率、导磁率以及其他相关参数。
这些参数是进行磁路计算的基础。
⚫磁路分析方程：根据磁路的几何形状和材料特性，建立磁路分析方程。
这些方程可以是基于法拉第电磁感应定律或安培环路定理等。
⚫边界条件和约束：根据具体情况，确定磁路中的边界条件和约束。
这些条件可以是给定的电流、磁通量或磁势值等。
⚫解方程和计算：使用数值方法或解析方法，求解磁路分析方程，
得到磁路中各个部分的磁通量、磁势和磁感应强度等参数。
⚫结果分析和优化：分析计算结果，评估磁路的性能，并根据需要进行优化调整。
这可以包括改变磁路的几何形状、材料选型或改变线圈的绕组方式等。
需要注意的是，磁路计算是一个复杂的过程，涉及到电磁学、数学和工程等知识领域。
在实际应用中，通常会借助电磁场仿真软件或计算工具来辅助进行磁路计算，以提高计算的准确性和效率。
永磁体的模型、工作点以及永磁磁路目录永磁体的磁偶极子模型 (1)退磁曲线与内禀退磁曲线 (1)孤立永磁体的磁场、工作点 (3)永磁磁路 (4)永磁体的磁偶极子模型永磁体的基本组成单位是磁偶极子。
从磁荷的观点看，磁偶极子是一对距离为1的正负点磁荷，点磁荷的单位是Wb（类似于电荷的单位为库仑C）。
所以磁偶极子的磁偶极矩Pm的单位是Wb ∙ m。
电磁学中，定义单位体积内磁偶极矩的矢量和为磁极化强度J,即J=Σpm∕AV,这样磁极化强度J的单位是Wb ∙ m∕m3=T o有时磁极化强度J 也被称作内禀磁感应强度Bi o从分子电流的观点看，磁偶极子可以用微小的电流回路表达，它的磁矩m 分子定义为平面回路中电流和回路面积的乘积，即m分子二i∙S,单位为A∙m2. 电磁学中，定义单位体积内包含磁偶极子磁矩的矢量和为磁化强度M,即M= ∑m分子/ A V,磁化强度M的单位为A∕m o磁荷观点和分子电流观点在宏观上是等效的，磁极化强度J与磁化强度M 的关系为J=UOM。
一块永磁体可以看作为一个大的磁偶极子，它的磁偶极矩等于它包含的磁偶极子磁偶极矩的矢量和。
若永磁体的体积为V,即其磁偶极矩j=JV。
当永磁体材料确定后，充磁越饱和，磁偶极子的排列越整齐，永磁体的磁极化强度越大, 磁偶极矩也越大。
永磁体的磁矩m=MV,也符合本段论述。
退磁曲线与内禀退磁曲线描述外磁场的物理量通常是磁场强度H,在外磁场的作用下，永磁体的磁感应强度B= μ 0（H+M]= μ 0H+ μ OM= μ OH+J（公式一）。
即永磁体内部的磁感应强度等于磁极化强度J与H在真空中的作用之和。
当然理论上，因为外磁场H 与永磁体的磁化强度M都是矢量，它们之间的角度可以是随机的；不过通常它们是平行的，同向时H取正，反向时H取负，反向时的外磁场称为退磁场。
永磁体在外磁场的磁化作用下饱和充磁后，再撤消外磁场时，永磁体的磁极化强度J（内禀磁感应强度Bi）并不会因外磁场H的消失而消失，而会保持一定大小的数值，习惯上称为剩余磁感应强度Br。
磁路计算小结磁路计算常用物理量磁密的单位Gs：仃=104 Gs ; 1Gs = 10'4T ；磁化强度M的单位Gs：磁矩卩的单位是emu, 1 emu = 103 A m2、 3 3 3 3 磁化强度M 的单位是emu/cm , 1 emu/cm =1Gs 1 A/m = 10" emu/cm1Gs = lemu/cm3 = 10"3 A m2/cm3 = 103 A/m31Gs = 10 A/m二磁路基本定律1.安培环路定律由麦克斯韦方程可知，沿着任何一条闭合回线L,磁场强度H的线积分值j L H・dl恰好等于该闭合回路所包围的总电流值v i （代数和），即■L H dl 二i式中，若电流的正方向与闭合回线的环行方向符合右手螺旋关系，i取正号，否则i取负号。
若沿着回线L,磁场强度H的方向总是切线方向、大小处处相等，且闭合回线所包围的总电流是由通有电流i的N匝线圈提供，则上式将简化为HL 二Ni（1）安培定则也叫右手螺旋定则，是表示电流和电流激发磁场的磁感线方向间关系的定则。
通电直导线中的安培定则（安培定则一）用右手握住通电直导线，让大拇指指向电流的方向，那么四指的指向就是磁感线的环绕方向；通电螺线管中的安培定则（安培定则二）用右手握住通电螺线管，让四指指向电流的方向，那么大拇指所指的那一端是通电螺线管的N极。
2.磁路的欧姆定律. ____________ ___________________蜡铁心烧域■话通电.在铁出中产生■晉设环形螺线管铁心的截面积为A，磁通量密度为B，总磁通量为①，则有(2.1)设线圈匝数为N，螺线管平均长度为l，给线圈通电流I，根据安培环路定律，则有所以代入式(2.1),则有整理得式中NI 二HL H 二NI /I-'NIA/INI1 INIR(2.2)I^"A (2.3) 在电路中，设电动势(电压)为E,电阻为R,电流为I，则有电路的欧姆定律R设导体电阻率为b，长度为I，截面积为S,则回路的电阻为由于式(2.2)与电路中的欧姆定律非常相似，所以称之为磁路的欧姆定律。
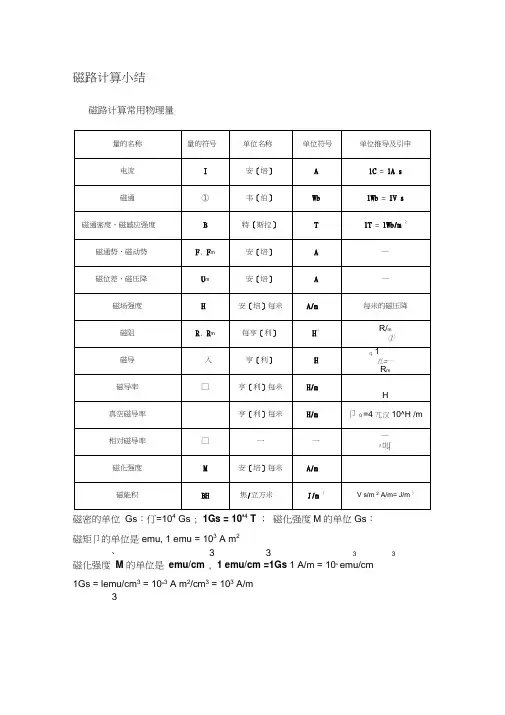
磁路计算小结一磁路计算常用物理量磁密的单位Gs：1T = 104 Gs ；1Gs = 10-4 T；磁化强度M的单位Gs：磁矩μ的单位是emu，1 emu = 10-3 A m2磁化强度M的单位是emu/cm3，1 emu/cm3 =1Gs 1 A/m = 10-3 emu/cm3 1Gs = 1emu/cm3 = 10-3 A m2/cm3 = 103 A/m1Gs = 103 A/m二磁路基本定律1．安培环路定律H恰好等由麦克斯韦方程可知，沿着任何一条闭合回线L，磁场强度H的线积分值⎰⋅L dl于该闭合回路所包围的总电流值∑i（代数和），即∑⎰=H⋅idlL式中，若电流的正方向与闭合回线的环行方向符合右手螺旋关系，i取正号，否则i取负号。
若沿着回线L，磁场强度H的方向总是切线方向、大小处处相等，且闭合回线所包围的总电流是由通有电流i的N匝线圈提供，则上式将简化为HL=Ni（1）安培定则也叫右手螺旋定则，是表示电流和电流激发磁场的磁感线方向间关系的定则。
通电直导线中的安培定则（安培定则一）用右手握住通电直导线，让大拇指指向电流的方向，那么四指的指向就是磁感线的环绕方向；通电螺线管中的安培定则（安培定则二）用右手握住通电螺线管，让四指指向电流的方向，那么大拇指所指的那一端是通电螺线管的N极。
2．磁路的欧姆定律设环形螺线管铁心的截面积为A，磁通量密度为B，总磁通量为Φ，则有=Φ（）BAμHA=设线圈匝数为N ，螺线管平均长度为l ，给线圈通电流I ，根据安培环路定律，则有HL NI =所以l NI H /=代入式（），则有l NIA /μ=Φ 整理得Al NI⋅=Φμ1 或RNI=Φ （） 式中AlR ⋅=μ （） 在电路中，设电动势（电压）为E ，电阻为R ，电流为I ，则有电路的欧姆定律RE I =设导体电阻率为σ，长度为l ，截面积为S ，则回路的电阻为Sl R ⋅=σ 由于式与电路中的欧姆定律非常相似，所以称之为磁路的欧姆定律。
如上图，两个欧姆定律的相似点有（1） 电动势E → 磁动势NI （2）电流I → 磁通量Φ （3） 电阻R → 磁阻R （4）电导率σ → 磁导率μ另外， 磁通密度B → 电流密度 磁场强度H → 每米的磁压降 应用磁路欧姆定律必须注意：磁阻必须是磁通量所通过闭合回路内的全部阻抗。
由于没有磁绝缘体，所以必须考虑漏磁的存在。
磁导率随电场和温度变化，以及磁饱和。
3．串联磁路上图所示为串联磁路的典型例子，环行磁路中有一定的空气隙，相当于电路中的串联电路。
磁路由铁心和空气隙构成，合成磁阻由下式表示：222111A lA l R ⋅+⋅=μμ 设在上图中线圈匝数为N ，电流为I ，则磁路中的磁通量为222111A lA l I N ⋅+⋅⋅=Φμμ变换上式，则2211222111μμμμl A l A A l A l NI Φ+Φ=⋅Φ+⋅Φ= ⎪⎪⎭⎫⎝⎛+=2211μμl l B 2211l H l H += 4．并联磁路上图所示为并联磁路的典型例子，相当于电路中的并联电路。
磁路的处理仿效电路的方法，如下进行。
首先求各支路的磁阻R1、R2、R31111A l R ⋅=μ， 2222A l R ⋅=μ， 3333A l R ⋅=μ 合成磁阻R 0为⎪⎪⎭⎫ ⎝⎛+⋅+⋅=+⋅+=2332321113232101A L A l l l A l R R R R R R μμ 根据磁路的欧姆定律，磁通量为⎪⎪⎭⎫ ⎝⎛+⋅+⋅==Φ233232111011A L A l l l A l NIR NIμμ两个支路磁通量为 32312R R R +⨯Φ=Φ32213R R R +⨯Φ=Φ磁动势NI 为⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⋅+Φ=Φ=23323211011A L A l l l A l R NI μ总结：磁路中各要素遵循如下关系5．磁路的基尔霍夫第一定律（对应磁路并联）穿出（或进入）任一闭合面的总磁通恒等于零。
如图示：0321=Φ+Φ+Φ-6．磁路的基尔霍夫第二定律（对应串联磁路）k k k k kk k k R R R l H l H l H l H Ni ⋅Φ++⋅Φ+⋅Φ=⋅++⋅+⋅=⋅=∑=ΛΛ221122111k H 可理解为单位长度上的磁位降，k k l H ⋅是某一段磁路的磁位降， Ni 是作用于该磁路的总磁动势，上式表明，作用在任何封闭磁路的总磁动势恒等于各段磁路磁位降的代数和。
三 永磁磁路的计算永磁体的特点是：剩余磁通密度r B 较大，矫顽力c H 很大。
所谓剩余磁通密度是指永磁体所构成的闭合磁路在外加励磁磁动势下降为0时，磁路内剩余的磁通密度。
实用的永磁磁路中都有工作气隙，如图（a ）所示。
此时气隙中的磁场是由永磁体所形成的磁动势产生。
当磁路为闭合（没有气隙）时，磁路内的磁通密度为r B ，如图（b ）中的R 点所示。
当磁路中具有气隙时，由于磁阻增大，磁路内的磁通量和磁通密度将要减小，磁路的工作点将从R 点沿永磁体的去磁曲线（磁滞回线在第二象限内的部分）下移到A 点。
下面说明工作点是如何确定的。
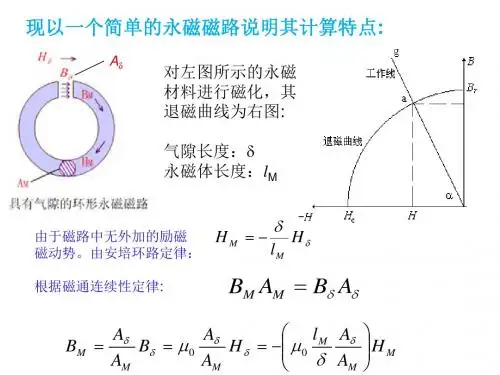
图（a ）表示一个具有气隙的环形永磁回路。
设永磁体中的磁通密度为m B ，磁场强度为m H ；气隙中的磁通密度为δB ，磁场强度为δH ；图中的箭头表示B 和H 的正方向。
由于磁路中没有外加磁动势，所以由安培环路定律可知0=+=∑δδH l H F m m ， 即 δδH l H mm -= 或 m H lmH δδ-= （3-1）式中，m l 和δ分别为永磁体和气隙的长度。
另外，根据磁通连续性定律可知δδA B A B m m = ， 即 δδB A A B mm =（3-2） 式中，m A 和δA 分别为永磁体和气隙的截面积（涉及边缘效应时，δA 略大于m A ）。
将式（3-1）代入（3-2），可得m m m m m H A A l H A A B ⎪⎪⎭⎫ ⎝⎛-==δδδδμμ00 （3-3） 式（3-3）表示m B 与m H 为一直线关系，此直线称为工作线。
不难看出，工作线OG 与负横轴的夹角α （图b ）为⎪⎪⎭⎫⎝⎛=m m A A l δδμα0arctan （3-4） 由于工作点一方面应在永磁体的去磁曲线RC 上，另一方面又应在工作线OG 上，所以去磁曲线RC 与工作线OG 的交点就是工作点A ，如图（b ）所示，永磁磁路的工作点由永磁体的去磁曲线和工作线两者来确定，这是永磁磁路的特点。
从式（3-3）可见，当气隙磁导δμδA 0改变时，工作点以及永磁体内的m B 和m H 将随之改变；换言之，作为一个磁动势源，永磁体对外磁路所提供的磁动势不是一个恒值，而是与外磁路的磁阻有关。
另外，从式（3-3）和图（b ）可知，当磁路的尺寸不变，采用不同材料的永磁体时，永磁体的矫顽力越大，工作点的位置就越高，气隙磁通密度就越大。
所以矫顽力也是该永磁体能够产生多大气隙磁通密度的一个度量。
从式（3-1）和式（3-2）可以导出气隙磁密的平方为()m m m m m m m B H V V B A Al H B H B -=⎪⎭⎫ ⎝⎛-==δδδδδμδμμ0002)( （3-5）式中，m V 为永磁体的体积，m m m l A V =；δV 为气隙的体积，δδδA V =；m m B H -通常称为磁能积（实质上是磁能密度），负号是由于工作点在永磁体的去磁曲线上m H 为负值所引起。
由式（3-5）可知()m m m B H V B V -=02μδδ （3-6） 式（3-6）表示，为得到所需的气隙磁密δB ，应可能把工作点选在去磁曲线上磁能积()m m B H -为最大的这一点，以使永磁体的体积最小。
另一方面，对于不同的永磁体，最大磁能积()m m B H -越大，产生同样气隙磁密所需的永磁材料就越少，所以磁能积是永磁体的三个主要性能指标之一。
四 磁性液体密封的磁路模型单级与多级密封的磁力线分布如下图4-1所示。
由于磁场是以轴线为对称线对称分布的，所以只分析其轴线上部分即可。
这样，单级与多级密封的等效磁路即可用图4-2来表示。
其中考虑到形状和尺寸的不同，将磁极分为极身与极尖或齿两部分，分别用磁阻p R 和t R 表示。
图4-1 磁性液体密封中的磁场分布图4-2 磁性液体密封中的等效磁路c F —永磁体的磁动势；m R —永磁体的磁阻；1p R 、2p R —极身磁阻，单级密封中2p R 为磁回路磁阻；s R —转轴磁阻；1σR 、2σR —磁铁外部和极间漏磁阻；1t R 、2t R —齿部磁阻，单级密封中以t R 表示；1g R 、2g R —密封间隙磁阻图4-2的磁路图包括了所有磁通及其对应的磁阻。
在实际应用中，可以根据磁通和磁阻的大小进行简化。
因为极身和转轴的磁导率很高，而且截面积大，这部分磁路一般不饱和，因而磁阻很小，可以忽略。
相应的，等效磁路图简化为图4-3所示的形式。
如果极尖和齿部也不饱和，相应的磁阻也可以忽略，等效磁路图又可以简化为图4-4所示的形式。
这时，单级密封和多级密封的等效磁路相同。
图4-3 忽略极身及转轴磁阻时的等效磁路图4-4 忽略极尖及齿部磁阻时的等效磁路五磁性液体密封磁路的磁导计算1.密封间隙磁导1）单级密封如图5-1为单级密封磁极的形状及参数。
对于矩形磁极D g Db g 0036.11μπμλ+=（5-1）对于单侧斜角磁极()⎪⎪⎭⎫ ⎝⎛-+++=g b a g D D g Dbg ββπμμπμλln 68.5000 （5-2） 对于双侧斜角磁极()⎪⎪⎭⎫ ⎝⎛-++=g b a g D g Db g ββπμπμλln 200 （5-3）图5-1 单级密封磁极形状2）多级密封多级密封的磁极呈齿槽形状，如图5-2所示，各级的齿槽尺寸相同。
齿下的磁导、磁极侧面的磁导的求法与单级密封中矩形磁极磁导的求法相同，所不同的是槽下磁导的求法。
图5-2 多级密封的磁极形状为增加磁场梯度，磁极的槽深度通常设计得较深，槽内磁力线的分布如图5-3（a ）所示。
假如用圆弧和直线代替磁力线，则磁力线的分布如图5-3（b ）所示，相当于减小了磁路的截面积。
为了补偿这一误差，用一条斜角为β的直线来代替实际槽的侧面边界，如图5-3（c ）所示，相当于在缩小磁路面积的同时，也人为缩短了磁路长度。
槽较深时，可取1.1~1=β，这种方法叫代角法。
图5-3 用代角法求槽下磁导按照代角法，半个槽距下的磁导为⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎪⎪⎭⎫ ⎝⎛+=+=⎰g s D g s g D x g Ddx s gs 21ln 2ln 2100200ββπμββπμβπμλ （5-4） 以gt λ和ge λ分别表示齿下磁导和磁极侧面磁导，对于密封级数为N 的多级密封，密封间隙的总磁导为()ge gs gt g N N λλλλ21+-+= （5-5） 式中g Dtgt πμλ0= （5-6） D ge 068.5μλ= （5-7） 式中，t 为齿宽；s 为槽宽；D 为转轴直径。
