第4章 t检验和Z检验

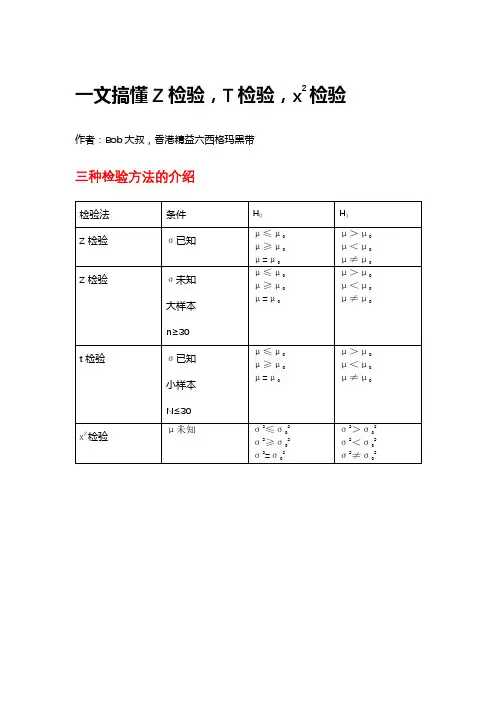
一文搞懂Z检验，T检验，x2检验作者：Bob大叔，香港精益六西格玛黑带
三种检验方法的介绍
Z检验举例：
某产品，其装量服从N（2.1，0.012），即均值2.1，标准差0.01。

抽取15个样品，其测量值如下：
2.08 2.10 2.10
2.09 2.10 2.10
2.09 2.09 2.11
2.09 2.12 2.10
2.10 2.10 2.10
建立假设H0:μ=2.1，H1 μ≠2.1，由于σ已知，故选择Z检验
操作如下：
P=0.36>0.05，无法拒绝原假设H0, 所以认为取样的平均装量没有变化。

t检验举例：
某设备的OEE目标为70%，连续15天的OEE如下，请判断OEE是否已达到70%目标？
由于σ（标准差）未知，且为小样本，故而选择，t检验
建立假设：HO: μ=70%, H1>70%,
操作如下：
P=0.252>0.05，无法拒绝原假设，说明0EE并未大于70%。

X2检验举例：
已知某产品装量，符合N（μ，σ2）分布，μ未知，但是要求标准差不能超过0.01，随机抽取30个样品，请问标准差是否有变化？
由于μ未知，故而选择X2检验，
建立假设：H0:σ=0.01, H1:σ≠0.01
操作如下：
（weixin gongzhonghao: HK_BobUncle）
P=0.303>0.05, 无法拒绝原假设，说明标准差无变化。

教育科研中的统计方法——Z检验和t检验乌海市海勃湾区教研室王根运通常我们用平均分比较两个班的成绩的优劣是不妥的。

即某次考试中初二、二班数学成绩平均分低于初二、五班的平均分，不一定说明初二、二班数学真实成绩比初二、五班的差。

这是因为一个班的的平均成绩具有统计意义，存在抽样误差，其平均成绩在一定范围内波动，假如再进行一次考试也许初二、二班数学成绩平均分高于初二、五班的平均分。

所以比较成绩时应用平均数差异的显著性检验更科学。

统计学中平均数差异的显著性检验时规定一个显著性水平，经过检验所得差异超过这个显著性水平，表明这个差异不属于抽样误差，确实存在差异，反之属于抽样误差。

这个平均数差异的显著性检验在教育科研统计中总结为Z检验或t 检验。

一般地样本容量大于30时，用Z检验；样本容量小于30时，用t检验。

当问题所给的条件用t检验方便时，样本容量虽然大于30，也可以用t检验。

下面是样本容量大于30时的Z检验和样本容量小于30时的t检验案例。

一、样本容量大于30时的Z检验案例：比较初三第一学期期末实验班和对比班的化学成绩表1、初三、八班（实验班）第一学期期末化学成绩表表2、初三、七7班（对比班）第一学期期末化学成绩表时间：2010年1月实验班和对比班学生人数均为52，样本容量大于30，用Z 检验看实验班和对比班成绩有无显著性差异（用计算机处理）。

实验班：初三、八班,据表1,样本容量：n 1=52,平均分：1X =11n X∑=69.84每个学生分数与平均分离差的平方和：∑21d ==-∑211)(X X 13243.86 标准差：S 1=121n d ∑=15.96对比班：初三、七班，据表2，样本容量：n 2=52, 平均分 ：2X =22n X ∑=66.92每个学生分数与平均分离差的平方和：∑22d ==-∑222)(X X 7967.19标准差：S 2=222n d ∑=12.38, Z=22212121n S n S X X +-=1.043Z 检验的判断方法： 0＜Z ＜1.96时，两个班的成绩无显著性差异；1.96＜Z ＜2.58时，两个班的成绩成绩有显著性差异。

z检验和t检验的区别
卡方检验是对两个或两个以上样本率（构成比）进行差别比较的统计方法。

t检验，主要是用于小样本（样本容量小于30）的两个平均值差异程度的检验方法。

它是用t分布理论来推断差异发生的概率，从而判定两个平均数的差异是否显著。

t检验的适用条件：正态分布资料。

1、卡方检验是用途非常广的一种假设检验方法，它在分类资料统计推断中的应用，
包括：两个率或两个构成比比较的卡方检验；多个率或多个构成比比较的卡仿检验以及分
类资料的相关分析等。

2、t检验，亦称student t检验( student's ttest) ，主要用作样本含量较小(比
如n大于30) ，总体标准差o未明的正态分布。

t检验就是用t原产理论去推断差异出现
的概率，从而比较两个平均数的差异与否明显。

t检验
3、t检验共分成三种方法，分别就是单一制样本t检验，接合样本t检验和单样本t
检验。

单一制样本t检验和单因素方差分析功能上基本一致，但是单一制样本t检验就可
以比较两组选项的差异，比如说男性和女性。

相对来讲，独立样本t检验在实验比较时使用频率更高，尤其是生物、医学相关领域。

针对问卷研究，如果比较的类别为两组，独立样本t检验和单因素方差分析均可实现，研
究者自行选择使用即可。

4、卡方分析：卡方检验用作分析定类数据与定类数据之间的关系情况。

比如研究人
员想要晓得两组学生对于手机品牌的偏好差异情况，则必须采用卡方分析。

卡方就是通过
分析相同类别数据的相对挑选频数和比重情况，进而展开差异推论，单选题或多选题均可
以采用卡方分析展开对照差异分析。

统计学检验方法比较统计学检验方法是在统计学中用来判断研究假设是否成立的一种方法。

它通过分析样本数据来推断总体参数，并根据结果得出判断。

在进行统计学检验之前，我们首先需要明确研究问题和研究假设。

接下来，我将介绍一些常见的统计学检验方法的比较。

1.T检验和Z检验T检验和Z检验都是用来推断一个样本的均值是否与总体均值有显著差异。

T检验主要用于小样本，而Z检验适用于大样本。

相较于Z检验，T检验考虑到了样本的自由度，因此对于小样本的推断更加准确。

2.单样本检验和双样本检验单样本检验用于比较一个样本的均值是否与一个已知的总体均值有显著差异。

双样本检验则用于比较两个样本的均值是否存在显著差异。

双样本检验可以进一步分为独立样本检验和配对样本检验。

独立样本检验适用于两个独立的样本，而配对样本检验适用于同一组个体在不同时间或不同处理下的两次测量。

3.卡方检验和F检验卡方检验主要用于判断两个分类变量之间是否存在相关性。

它将观察频数与期望频数进行比较，以确定差异的显著性。

F检验则用于比较两个或更多个总体方差是否相等。

它将组间离散度与组内离散度进行比较，从而推断总体方差是否存在显著差异。

4.非参数检验和参数检验非参数检验不依赖于总体的特定分布，而是对总体的分布进行较少的假设。

它通过对数据的排序和秩次转换来进行推断。

非参数检验一般适用于数据不服从正态分布或样本量较小的情况。

参数检验则建立在对总体参数分布的假设上，通常假设数据服从正态分布。

参数检验的推断结果相对较为准确，但对数据的假设要求较高。

综上所述，不同的统计学检验方法适用于不同的研究问题和数据类型。

选择合适的统计学检验方法可以提高推断结果的准确性。

因此，在进行统计学检验之前，我们需要充分理解研究问题的背景，研究假设的特点以及数据的类型和分布，从而选择适当的检验方法。

同时，还需要注意检验过程中的假设和限制，以及结果的解释和推断的合理性。

t检验和z检验的比较
检验类型单样本资料的t检验配对设计资料的t检验两独立样本资料的t检验两独立样本资料的z检验
应用条件当样本例数n较小，样本来自正态总体，总体标准差未知。

在作两个样本均数比较时，还要求两样本
相应的两总体方差相等。

（用于定量资料）
两个样本含量n较大（均大于50）
的情况
举例已知一个样本的指标的真值，现
在重复测定15次，问此法测得的
均数与真值有无差别（P296例）
用某药治疗8例高血压患者，观
察治疗前后舒张压的变化情况，
问该药是否对高血压患者治疗前
后舒张压变化有影响（P297例）
两组雄性大鼠（n1=12，n2=12）
分别用高蛋白和低蛋白饲料喂
养，问体重的增加有无差别
（P299例）
某医院用120名2型糖尿病患者
分成两组，用不同降血糖药，比
较两种降糖药的降血糖效果是否
不同（P299例）
假设（注意单侧和双侧假设区别）H 0:μ=μ0
H 1:μ≠μ0 α= 0.05
H 0:μd=0
H 1:μd≠0 α= 0.05
H 0:μ1=μ2
H 1:μ1≠μ2 α= 0.05
H 0:μ1=μ2
H 1:μ1≠μ2 α= 0.05
计算公式
比较，结论t>t界值（z>z界值），p≤0.05，拒绝Ho，接受H1，差异有统计学意义，可以认为······
t<t界值（z<z界值），p>0.05，不拒绝Ho，差异无统计学意义，尚不能认为······（根据题目下结论）。

实验八：t检验、z检验【目的要求】1.熟悉假设检验的基本步骤2.掌握t检验、z检验的应用条件及分析过程3.熟悉假设检验的基本思想【案例分析】案例1：某医生研究脑缺氧对脑组织中生化指标的影响，将乳猪按出生体重配成7对，一组为对照组，一组为脑缺氧模型组。

两组乳猪脑组织钙泵的含量差值（对照组减脑缺氧模型组）均数为0.0441ug/g，标准差为0.05716ug/g，经配对t检验（双侧），得t=2.0412，P>0.05，按a=0.05的水准，不拒绝H0，差别无统计学意义，尚不能认为脑缺氧可造成钙泵含量的变化。

（1）本例结论是否正确？为什么？（2）该结论可能犯几型错误？案例2：7名接种卡介苗的儿童，8周后用两批不同的结核菌素，一批是标准结核菌素，一批是新制结核菌素，分别注射在儿童的左右前臂。

以皮肤浸润直径（mm）为指标。

数据如下表所示。

某医生计算标准品与新制品的差值，均数为3.19mm，故认为新制结核菌素的皮肤浸润直径比标准结核菌素小。

两种结核菌素皮肤浸润直径比较（mm）编号1234567标准品12.014.515.513.012.010.57.5新制品10.010.012.210.0 5.58.5 6.5该医师对资料的统计分析是否正确？为什么？若不正确，应该怎么做？案例3：2005年某县疾病预防控制中心为评价该县小学生卡介苗抗体效价，随机抽取了30名小学生，测定结果如表2。

经完全随机设计两样本均数比较的t检验（方差齐，F=0.05，P>0.05），t=0.014，P>0.05，故认为该县小学生卡介苗抗体效价无性别差异。

2005年某县30名小学生卡介苗抗体滴度测定结果分组卡介苗抗体滴度（倒数）男生40201604032080402040801604080404040女生80201604040160402040160160408040该案例中资料的统计分析是否正确？为什么？若不正确，应该怎么做？【SPSS操作】1.单样本t检验Analyze → Compare Means →one-sample T Test…→ Test Variable(s):变量→ Test Value：总体水平→OK2.配对t检验Analyze → Compare Means → Paired-Samples T Test …→ Paired Variables:x1-x2（同时选中）→OK3.两样本均数比较的t 检验Analyze → Compare Means →Independent-samples T Test …→ Test Variable(s):x → Grouping Variable:group →OK【练习题】一、填空题1.假设检验中的Ⅰ型错误指 。

T检验与Z检验中态性的理解
统计书上说当样本足够大时，无论X服从什么分布，只要各X间相互独立，且Xi同分布，期望、方差有界（这一条件大多数情况都是成立的），根据中心极限定理即可得X服从正态分布。

现在问题来了，为什么书上又说无论什么情况下采用Z检验都得进行正态性检验呢，即使样本已经很大了？（注意Xi的分布和X的是不同的）
首先得明确我们的目的是什么，我们是检验总体的平均数，当该总体不服从正态分布时，所得的X（算数平均数）用来表示平均数是不恰当的，而Z检验和T检验都是检验的算数平均数与目标数的差异，所以必须在做Z、T检验前需正态性检验。

仍Z检验和T检验有一点不同的是，在X分布为非正态，n很大时，
σ/n
服从正态分布，而
就不一定服从T分布了。

所以理论上当不服从
s/n
正态分布的X的算数平均数（一定要是算数平均数）做Z检验是可以的，而做T检验是不行的。

另外有同学可能对σx 不好理解，觉得既然都是总体的均数了，那还来的标准误。

确实σx 是总体均数的标准误，但是他是把每一个Xi看成一个随机变量，而我们样本中的每一个值只是某一个Xi的一次实现(Xi 应该有无穷多个值，我们只能得到其中的一个值)。

就例如有一个总体，进行两次普查，得到两个x ，而这两个值有可能不一样，也就存在标准误了。