第5章-1 曲线拟合(线性最小二乘法)讲解

曲线拟合最小二乘法
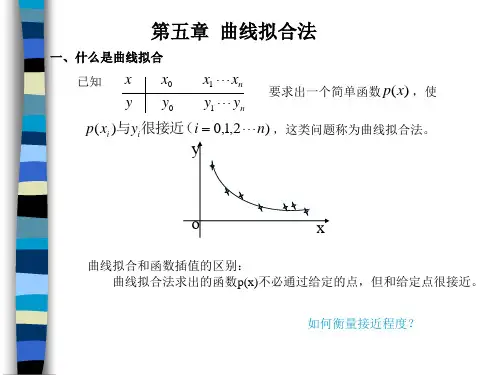
曲线拟合是指通过已知数据点来推导出一条函数曲线，使得该曲线尽
可能地贴近这些数据点。

而最小二乘法（Least Squares Method）是求解
这种拟合问题的一种常用方法。

最小二乘法的核心思想是尽量减小误差平方和。

假设已知的数据点为$(x_i, y_i)$，曲线函数为 $y=f(x)$，我们希望找到一组参数 $\theta$，使得 $f(x_i;\theta)$ 与 $y_i$ 的差距最小，即：
$$\min_{\theta}\sum_{i=1}^n [y_i - f(x_i;\theta)]^2$$。

这个式子被称为目标函数，也叫做残差平方和（RSS）。

通过对目标
函数进行求导，可以得到最优参数 $\theta^*$ 的解析解：
$$\theta^* = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T
\mathbf{y}$$。

其中，$\mathbf{X}$ 是一个 $n \times p$ 的矩阵，每一行代表一
个数据点的特征向量，$p$ 是曲线函数的参数个数。

$\mathbf{y}$ 是一
个 $n \times 1$ 的列向量，代表数据点的真实输出值。

最小二乘法在实际应用中有很广泛的应用。

例如，可以用它来构建多
项式回归模型、高斯过程回归模型等。

此外，在机器学习领域，最小二乘
法也被用于求解线性回归模型、岭回归模型等。

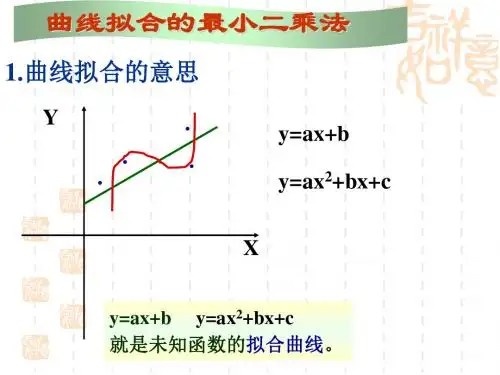
曲线拟合问题最常用的解法——线性最小二乘法的基本思路第一步:先选定一组函数 r 1(x), r 2(x), …r m (x), m<n, 令f(x)=a 1r 1(x)+a 2r 2(x)+ …+a m r m (x) （1） 其中 a 1,a 2, …a m 为待定系数。

第二步: 确定a 1,a 2, …a m 的准则（最小二乘准则）： 使n 个点（x i ,y i ) 与曲线 y=f(x) 的距离δi 的平方和最小 。

记221211211(,,)[()][()](2)n nm i i i i i nmk k i i i k J a a a f x y a r x y δ======-=-∑∑∑∑问题归结为，求 a 1,a 2, …a m 使 J(a 1,a 2, …a m ) 最小。

线性最小二乘法的求解：预备知识超定方程组：方程个数大于未知量个数的方程组111122111122 ()m m n n nm m nr a r a r a y n m r a r a r a y +++=⎧⎪>⎨⎪+++=⎩ 即 Ra=y其中111112112,,m n n nm m n a y r r r R a y r r r a y ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦超定方程一般是不存在解的矛盾方程组。

如果有向量a 使得211221()ni i im m i i r ar a r a y =+++-∑ 达到最小，则称a 为上述超定方程的最小二乘解。

线性最小二乘法的求解所以，曲线拟合的最小二乘法要解决的问题，实际上就是求以下超定方程组的最小二乘解的问题。

Ra=y （3）其中111111()(),,()()m n m n m n r x r x a y R a y r x r x a y ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦定理：当R T R 可逆时，超定方程组（3）存在最小二乘解，且即为方程组 R T Ra=R T y的解：a=(R T R)-1R T y线性最小二乘拟合f(x)=a1r1(x)+ …+a m r m(x)中函数{r1(x), …r m(x)}的选取1. 通过机理分析建立数学模型来确定f(x)；2. 将数据(x i,y i) i=1, …n 作图，通过直观判断确定f(x)：用MATLAB作线性最小二乘拟合1. 作多项式f(x)=a1x m+ …+a m x+a m+1拟合,可利用已有程序:例对下面一组数据作二次多项式拟合xi 0.1 0.2 0.4 0.5 0.6 0.7 0.8 0.9 1 yi 1.978 3.28 6.16 7.34 7.66 9.58 9.48 9.30 11.22123()f x a x a x a =++中 的123(,,)A a a a =使得:1121[()] iii f x y =-∑最小解法1．用解超定方程的方法211211111 1x x R x x ⎛⎫⎪=⎪ ⎪⎝⎭此时 1）输入以下命令：x=0:0.1:1;y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2]; R=[(x.^2)' x' ones(11,1)]； A=R\y'2）计算结果： Ａ = -9.8108 20.1293 -0.03172()9.810820.12930.0317f x x x =-+-解法2．用多项式拟合的命令 1）输入以下命令： x=0:0.1:1;y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2]; A=polyfit(x,y,2) z=polyval(A,x);plot(x,y,'k+',x,z,'r') %作出数据点和拟合曲线的图形 2）计算结果： Ａ = -9.8108 20.1293 -0.03172()9.810820.12930.0317f x x x =-+-用MATLAB 作非线性最小二乘拟合Matlab 的提供了两个求非线性最小二乘拟合的函数：lsqcurvefit 和lsqnonlin 。

---------------------------------------------------------------最新资料推荐------------------------------------------------------ 数值分析论文--曲线拟合的最小二乘法曲线拟合的最小二乘法姓名：徐志超学号：2019730059 专业：材料工程学院：材料科学与工程学院科目：数值分析曲线拟合的最小二乘法一、目的和意义在物理实验中经常要观测两个有函数关系的物理量。

根据两个量的许多组观测数据来确定它们的函数曲线，这就是实验数据处理中的曲线拟合问题。

这类问题通常有两种情况：一种是两个观测量 x 与 y 之间的函数形式已知，但一些参数未知，需要确定未知参数的最佳估计值；另一种是 x 与 y 之间的函数形式还不知道，需要找出它们之间的经验公式。

后一种情况常假设 x 与 y 之间的关系是一个待定的多项式，多项式系数就是待定的未知参数，从而可采用类似于前一种情况的处理方法。

在两个观测量中，往往总有一个量精度比另一个高得多，为简单起见把精度较高的观测量看作没有误差，并把这个观测量选作x，而把所有的误差只认为是y 的误差。

设 x 和 y 的函数关系由理论公式 y＝f（x； c1， c2， cm）1 / 13（0-0-1）给出，其中 c1， c2， cm 是 m 个要通过实验确定的参数。

对于每组观测数据（xi， yi） i＝1， 2，， N。

都对应于 xy 平面上一个点。

若不存在测量误差，则这些数据点都准确落在理论曲线上。

只要选取m 组测量值代入式（0-0-1），便得到方程组yi＝f （x；c1，c2，cm）（0-0-2）式中 i＝1，2，， m.求 m 个方程的联立解即得 m 个参数的数值。

显然Nm 时，参数不能确定。

在 Nm 的情况下，式（0-0-2）成为矛盾方程组，不能直接用解方程的方法求得 m 个参数值，只能用曲线拟合的方法来处理。

实验三函数逼近与曲线拟合、问题的提出：函数逼近是指“对函数类A中给定的函数f(x),记作f(x)・A,要求在另一类简的便于计算的函数类B中求函数p(x)・A,使p(x)与f (x)的误差在某中度量意义下最小”函数类A通常是区间[a,b]上的连续函数，记作C[a,b],称为连续函数空间，而函数类B通常为n次多项式，有理函数或分段低次多项式等，函数逼近是数值分析的基础。

主要内容有：(1)最佳一致逼近多项式(2)最佳平方逼近多项式(3 )曲线拟合的最小二乘法实验要求:1、构造正交多项式；2、构造最佳一致逼近；3、构造最佳平方逼近多项式；4、构造最小二乘法进行曲线拟合；5、求出近似解析表达式，打印出逼近曲线与拟合曲线，且打印出其在数据点上的偏差;6、探讨新的方法比较结果。

三、实验目的和意义:1、学习并掌握正交多项式的MATLAB编程；2、学习并掌握最佳一致逼近的MATLAB实验及精度比较;3、学习并掌握最佳平方逼近多项式的MATLAB实验及精度比较;4、掌握曲线拟合的最小二乘法；5、最小二乘法也可用于求解超定线形代数方程组；6、探索拟合函数的选择与拟合精度之间的关系；四、算法步骤：1、正交多项式序列的生成{ \ ( X)}o •:设\ ( X)是［a,b］上首项系数数，如果多项式序列{ \ ( X)}o：满足关系式则称多项式序列{ \(X)}o：为在［a,b］上带权的n次正交多项式。

1 )输入函数「(x)和数据a,b;2) 分别求(x n, j(x)),C j (x), j(x))的内积；. . n 2 (X n,®j(X)), ,3) 按公式①；：o(X)=1, -(X) =X n j j(X)计算；：n(X)，生成正交多项式;j鼻Wj(x),W j(x))流程图：开始a n=0的n次多项式，r(x)为［a,b］上权函；Q j秋A 0, jb(j, k)」(x) j(x) k(x)d(X> =a「(x)正交，称;:n (x)为［a,b］上带权「(x)cz>结束2、最佳一致逼近多项式f(x) C[a,b]，若存在 R*(x) H n 使得.：(f,P ；^E n ，则称 P ； (x)是 f (x)在[a,b]上的最佳一致逼近多项式或最小偏差逼近多项式，简称最佳逼近多项式。

一、曲线拟合是什么？曲线拟合也就是求一条曲线,使数据点均在离此曲线的上方或下方不远处, 它既能反映数据的总体分布,又不至于出现局部较大的波动, 能反映被逼近函数的特性,使求得的逼近函数与已知函数从总体上来说其偏差按某种方法度量达到最小。

设函数y=f(x)在m个互异点的观测数据为求一个简单的近似函数φ(x)，使之“最好”地逼近f(x),而不必满足插值原则。

这时没必要取φ(xi) = yi, 而要使i=φ(xi)yi 总体上尽可能地小。

这种构造近似函数的方法称为曲线拟合,称函数y=φ(x)为经验公式或拟合曲线。

如下为一个曲线拟合示意图。

清楚什么是曲线拟合之后，我们还需要了解一个概念——残差。

曲线拟合不要求近似曲线严格过所有的数据点，但使求得的逼近函数与已知函数从总体上来说其偏差按某种方法度量达到总体上尽可能地小。

若令（1-1）则为残向量（残差）。

“使（1-1）尽可能地小”有不同的准则（1）残差最大值最小（2）残差绝对值和最小（绝对值的计算比较麻烦）（3）残差平方和最小（即最小二乘原则。

计算比较方便，对异常值非常敏感，并且得到的估计量具有优良特性。

）二、最小二乘法是什么？个人粗俗理解：按照最小二乘原则选取拟合曲线的方法,称为最小二乘法。

百度百科：最小二乘法（又称最小平方法）是一种数学优化技术。

它通过最小化误差的平方和寻找数据的最佳函数匹配。

利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

最小二乘法还可用于曲线拟合。

其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

三、求解最小二乘法（包含数学推导过程）我们以最简单的线性模型来解释最小二乘法。

什么是线性模型呢？监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。

回归分析中，n个自变量，且因变量和自变量之间是线性关系，则称为一/多元线性回归分析。

曲线拟合--最小二乘法1：已知平面上四个点：（0，1）、（1，2.1）、（2，2.9）和（3，3.2），求出一条直线拟合这四个点，使得偏差平方和变为极小。

解：设直线方程为：0 1 0 01 2.1 1 2.12 2.9 4 5.83 3.2 9 9.6Sum=6 Sum=9.2 Sum=14 Sum=17.5 代入正规方程：，编程求解上方程组：>> eq1='14*A+6*B=17.5';>>eq2='6*A+4*B=9.2';>> [A,B]=solve(eq1,eq2,'A,B');>> disp(A)0.74>> disp(B)1.19所以直线方程为：2：已知数据如下表所示1 2 4 610 5 2 1试求（1）用抛物线拟合这些数据使得偏差平方和最小；（2）用型如的函数来拟合这些数据使得偏差平方和最小。

（3）比较这两种拟合结果。

解：（1）设抛物线方程为：1 10 1 1 1 10 102 5 4 8 16 10 20 4 2 16 64 256 8 326 1 36 216 1296 6 36 Sum=13 Sum=18 Sum=57 Sum=289 Sum=1569 Sum=34 Sum=98代入正规方程：得到系数A，B，C的方程组：编程求解上方程组：>>eq1='1569*A+289*B+57*C=98';>>eq2='289*A+57*B+13*C=34';>>eq3='57*A+13*B+4*C=18';>> [A,B,C]=solve(eq1,eq2,eq3,'A,B,C');>> disp(A); disp(B); disp(C)102/199-1048/1992848/199>> A=102/199; disp(A) 0.5126>> B=-1048/199; disp(B) -5.2663>> C=2848/199; disp(C) 14.3116所以得到抛物线的方程为：（2）设函数1 10 1 1 102 5 1/2 1/4 5/24 2 1/4 1/16 1/26 1 1/6 1/36 1/6Sum=13 Sum=18 Sum=23/12 Sum=193/144 Sum=79/6 得到系数A，B的方程组：编程求解上方程组：>> eq1='4*A+23*B/12=18';>>eq2='23*A/12+193*B/144=79/6';>> [A,B]=solve(eq1,eq2,'A,B');>> disp(A); disp(B)-160/243872/81>> A=-160/243; disp(A)-0.6584>> B=827/81; disp(B)10.2099所以得到的函数为：（3）比较（1）和（2）两种方法拟合的方程：编程画出抛物线的图像为：>> x=-2:0.1:12;>> y=0.5126*x.^2-5.2663*x+14.3116;plot(x,y);grid on（a）再编程画出的图像为：>> x=-2:0.1:12;>> y=-0.6584+10.2099*(x.^(-1));>> plot(x,y);grid on>> x=-1:0.01:1;>> y=-0.6584+10.2099*(x.^(-1));plot(x,y);grid on(b)比较两图像可知，图像（b）在点（0，0）处不连续。

线性最⼩⼆乘法①前置知识：曲线拟合问题：已知⼀组⼆维数据，寻求⼀个函数（曲线）\(y=f(x)\)使\(f(x)\)在某种准则下与所有数据点最为接近，即曲线拟合得最好。

②线性最⼩⼆乘法：\(1.1\) 定义线性最⼩⼆乘法是解决曲线拟合最常⽤的⽅法，基本思路是，令：\[f(x)=a_1r_1(x)+a_2r_2(x)+...+a_mr_m(x), \]式中：\(r_k(x)\)为事先选定的⼀组线性⽆关的函数;\(a_k\)为待定系数。

\(1.2\) 拟合准则使\(y_i\)与\(f(x_i)\)的距离\(\delta_i\)的平⽅和最⼩\(1.3\) 系数确认记\[J(a_1,...,a_m)=\sum_{i=1}^n \delta_i^2=\sum_{i=1}^n [f(x_i)-y_i]^2, \]要使J最⼩，即令\(\frac{\partial J}{\partial a_j}=0(j=1,...,m)\),即：\[\sum_{i=1}^nr_j(x_i)[\sum_{k=1}^ma_kr_k(x_i)-y_i]=0,j=1,...,m, \]即：\[\sum_{k=1}^ma_k[\sum_{i=1}^n r_j(x_i)r_k(x_i)]=\sum_{i=1}^nr_j(x_i)y_i,j=1,...,m, \]记：\[R=\begin{bmatrix} r_1(x_1)& \cdots & r_m(x_1) \\ \vdots &\vdots& \vdots \\ r_1(x_n)& \cdots & r_m(x_n) \end{bmatrix} ,\]\[A=[a_1,\cdots,a_m]^T,Y=[y_1,\cdots,y_n]^T, \]则⽅程式可表⽰为：\[R^TRA=R^TY。

\]当\({r_1(x),\cdots,r_m(x)}\)线性⽆关时，R满秩，\(R^TR\)可逆，此时有唯⼀解：\[A=(R^TR)^{-1}R^TY \]1.4 实际意义在空间内，任意两个向量都可以组合成新的向量，我们不妨如下表⽰：\[a_1 x_1+a_2 x_2=b \Leftrightarrow A X=B \]对于拟合的向量\(y_i\)，要使其与⽬标向量\(f(x_i)\)距离最⼩，即满⾜：\[\exists k\in N,\forall i \in N,|\vec {f(x_i)}-\vec y_i|\geq |\vec {f(x_k)}-\vec y_k| \]在此处，\(y_i=b\),\(f(x_i)\)对应的矩阵为\(AX\)，故要满⾜距离最⼩，即使得\(\vec{b-AX}\)与\(\vec b\)所在平⾯正交，也就是使\(\vec{b-AX}\)与\(\vec b\)和\(\vec a\)都正交。

曲线拟合的最小二乘法原理及实现
最小二乘法是一种用于拟合数据的常用方法，特别是在需要找到一条曲线或函数来最好地描述数据时。

它的基本思想是找到一条最适合数据的曲线，使得数据点与曲线之间的偏差最小。

具体来说，最小二乘法的原理是在给定一些数据点的情况下，通过最小化每个数据点到一条曲线或函数之间的垂直距离或水平距离来找到最适合这些数据的曲线或函数。

在实际应用中，可以使用最小二乘法来拟合各种类型的曲线，如线性、二次、三次、指数等。

下面是最小二乘法的基本步骤：
1.收集数据并确定要拟合的函数类型。

2.确定函数中的待定系数，例如线性函数中的截距和斜率，二次
函数中的二次项系数、一次项系数和截距等。

3.计算每个数据点到拟合曲线的垂直距离或水平距离。

4.通过最小化距离平方和来确定待定系数，例如线性函数中可以
使用公式(b-x)² + (c-y)² = 最小值，其中b和c是待定的截距和斜率。

5.求解方程组来确定待定系数，例如在线性函数中可以使用公式
b = ∑xiyi / ∑xi，
c = ∑xi² / ∑xi来计算截距和斜率。

6.使用确定的函数系数来绘制拟合曲线。

需要注意的是，最小二乘法可能不适用于所有类型的数据，并且可能需要使用其他曲线拟合方法来获得更好的结果。

在实际应用中，还需要考虑数据的准确性和可靠性，以及选择最适合数据类型的拟合方法。

曲线拟合的最小二乘法原理及实现任务名称简介在数据处理和统计分析中，曲线拟合是一种常见的技术，旨在通过数学函数找到最佳拟合曲线，以尽可能准确地描述给定数据集的变化趋势。

在曲线拟合的过程中，最小二乘法是一种常用的数学方法，用于选择最佳拟合曲线。

本文将详细介绍最小二乘法的原理和实现方法。

最小二乘法原理最小二乘法是一种通过最小化误差平方和来拟合数据的方法。

其基本原理是将数据集中的每个数据点与拟合曲线上对应点的差值进行平方，然后将所有差值的平方相加，得到误差平方和。

最小二乘法的目标是通过调整拟合曲线的参数，使得误差平方和达到最小值。

假设我们有一个包含n个数据点的数据集，每个数据点的横坐标为x，纵坐标为y。

我们希望找到一个拟合曲线，可以通过曲线上的点与数据点的差值来评估拟合效果。

拟合曲线的一般形式可以表示为：y = f(x, β)其中，β为拟合曲线的参数，f为拟合曲线的函数。

最小二乘法的基本思想是选择适当的参数β，使得误差平方和最小化。

误差平方和可以表示为：S(β) = Σ(y - f(x, β))^2其中，Σ表示求和操作，拟合曲线上的点的横坐标为x，纵坐标为f(x, β)。

为了找到误差平方和的最小值，我们需要对参数β进行求解。

最常用的方法是对参数β求导数，令导数为0，从而得到参数的估计值。

求解得到的参数估计值就是使得误差平方和最小化的参数。

最小二乘法实现步骤最小二乘法的实现可以分为以下几个步骤：1.确定拟合曲线的函数形式。

根据数据的特点和拟合的需求，选择合适的拟合曲线函数，例如线性函数、多项式函数等。

2.建立误差函数。

根据选择的拟合曲线函数，建立误差函数，即每个数据点与拟合曲线上对应点的差值的平方。

3.求解参数估计值。

对误差函数求导数，并令导数为0，求解得到参数的估计值。

4.进行拟合曲线的评估。

通过计算误差平方和等指标来评估拟合曲线的质量，可以使用残差平方和、R方值等指标。

5.优化拟合结果（可选）。

根据评估的结果，如有必要可以调整拟合曲线的参数或选择其他拟合曲线函数，以得到更好的拟合效果。

曲线拟合的线性最小二乘法拟合是已知有限个数据点，求近似函数，不要求过已知数据点，只要求在某种意义下它在这些点上的总偏差最小。

线性最小二乘法曲线拟合问题的提法是，已知一组（二维）数据，即平面上的n 个点(,),i i x y 1,2,,i n =⋅⋅⋅，i x 互不相同，寻求一个函数（曲线）()y f x =，使()f x 在某种准则下与所有数据点最为接近，即曲线拟合的最好。

线性最小二乘法是解决曲线拟合最常用的方法，基本思路是，令1122()()()(),m m f x a r x a r x a r x =++⋅⋅⋅+其中：()k r x 是事先选定的一组线性无关的函数；k a 是待定系数(1,2,,;k m =⋅⋅⋅)m n <。

拟合准则是使(1,2,,)i y i n =⋅⋅⋅与()i f x 的距离i δ的平方和最小，称为最小二乘准则。

1.系数k a 的确定 记[]221211(,,,)()nnm i i i i i J a a a f x y δ====-∑∑为求12,,,m a a a ⋅⋅⋅使J 达到最小，只需利用极值的必要条件0jJa ∂=∂(1,2,,)j m =⋅⋅⋅，得到关于12,,,m a a a ⋅⋅⋅的线性方程组11()[()]0,1,2,,n mjik kiii k r x a r x y j m ==-==∑∑，即111[()()](),1,2,,.m n nkjikijiik i i a r x r x r x y j m =====∑∑∑ （1.1）记1111()()()()m n m n n mr x r x R r x r x ⨯⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ [][]TT1212,,,,,,,m n A a a a Y y y y =⋅⋅⋅=⋅⋅⋅方程（1.1）可表为T T .R RA R Y = （1.2） 当{}12(),(),,()m r x r x r x ⋅⋅⋅线性无关时，R 列满秩，T R R 可逆，于是方程组（1.2）有唯一解()1TT .A R R R Y -=2.函数()k r x 的选取面对一组数据(,),1,2,,i i x y i n =⋅⋅⋅，用线性最小二乘法作曲线拟合时，首要的也是关键的一步是恰当地选取12(),(),,()m r x r x r x ⋅⋅⋅。