湖北省武汉市蔡甸区实验高级中学2020-2021学年高二数学10月联考试题【含答案】

姓名，年级：时间：2020年高二联合考试高二数学试卷考试时间：2020年 10 月 9日上午 试卷满分：150分一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1。

已知直线6x-3y+2=0的倾斜角为 ，则 （ ）A. B 。

C. D。

522.已知向量 与 的夹角为， ，当 时，实数 为（ )A. 1B. 2 C 。

D.3。

若圆C ： 上恰有3个点到直线l ： 的距离为2,，则与 间的距离为( ) A 。

1B 。

C 。

3D 。

24. 已知椭圆 的左右焦点为,点P 在椭圆上，则 的最大值是（ )A 。

9 B.16 C 。

25 D.275. 已知 ，则 （ )A. B 。

C 。

D 。

6.已知半径为2的圆经过点（4，3），则其圆心到原点的距离的最小值为( )A. 3B. 4C 。

5D 。

6452,2==b a 9191-323sin =⎪⎭⎫ ⎝⎛+απ=⎪⎭⎫ ⎝⎛+απ26sin 91±98-=∆∆ABCOBCS S α=-αα2cos 22sin 52-54-512-21F F ，21PF PF ⋅922=+y x 023:1=+-y x l 192522=+yx a 2()0b 0b y -x >=+λ()b a b λ-⊥221-211l l7.已知o 为三角形ABC 所在平面内一点, ,则 ( )31.A8.如图，要测量电视塔AB 的高度，在C 点测得塔顶A 的仰角是 ，在D 点测得塔顶A 的仰角是 ，水平面上的 ，CD=40m ，则电视塔AB 的高度为（ ）mA 。

20 Ｂ．30 Ｃ．40 Ｄ．50二、选择题：本题共4小题，每小题5分，共20分。

在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分,部分选对的得3分。

9。

下列说法正确的是（ ）A 。

平面内到两个定点 的距离之和等于常数的点的轨迹为椭圆；B 。

高二年级10月联考数学试卷(理科)考试时间： 试卷满分：150分一､选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1下列说法正确的是( )A.方程k x x y y =--11表示过点()111,y x P 且斜率为的直线 B.直线b kx y +=与轴的交点为()b B ,0,其中截距OB b = C.在轴、轴上的截距分别为、的直线方程为1=+bya x D.方程()()()()112112x x y y y y x x --=--表示过任意不同两点()111,y x P ,()222,y x P 的直线2．直线x cos α＋3y ＋2＝0的倾斜角的范围是 ( )A.⎣⎢⎡⎭⎪⎫π6，π2∪⎝ ⎛⎦⎥⎤π2，5π6B.⎣⎢⎡⎦⎥⎤0，π6∪⎣⎢⎡⎭⎪⎫5π6，πC.⎣⎢⎡⎦⎥⎤0，5π6D.⎣⎢⎡⎦⎥⎤π6，5π63．直线2x －my ＋1－3m ＝0，当m 变动时，所有直线都通过定点 ( ) A.⎝ ⎛⎭⎪⎫－12，3 B.⎝ ⎛⎭⎪⎫12，3 C.⎝ ⎛⎭⎪⎫12，－3 D.⎝ ⎛⎭⎪⎫－12，－34.已知集合A ＝{(x ，y )|x ，y 为实数，且x 2＋y 2＝1}，B ＝{(x ，y )|x ，y 为实数，且x ＋y ＝1}，则A ∩B 的元素个数为( )．A．4 B．3 C．2 D．15. 设集合{}(,)|,,1A x y x y x y --＝是三角形的三边长，则A 所表示的平面区域(不含边界的阴影部分)是( )6. 在坐标平面内,与点A(1,2)的距离为1,且与点B(3,1)的距离为2的直线共有( )A.1条B.2条C.3条D.4条7.若圆(x －3)2＋(y ＋5)2＝r 2上有且只有两个点到直线4x －3y －2＝0距离等于1，则半径r 的取值范围是( )．A ．(4,6)B ．[4,6)C ．(4,6]D ．[4,6]8. 如图所示,已知两点()()4,0,0,4B A ,从点()0,2P 射出的光线经直线反射后再射到直线OB 上,最后经直线OB 反射后又回到P 点,则光线所经过的路程是( )A. 102B. 6C. 33D. 529.设1m >，在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下，目标函数z x my =+的最大值小于2,则m 的取值范围为（ ）A ．(1,3)B ．(12,)++∞C ．(1,12)+D ．(3,)+∞10. 已知圆()()221:231C x y -+-=,圆()()222:349C x y -+-=,,M N 分别是圆12,C C 上的动点,P 为x 轴上的动点,则PM PN +的最小值为( )A ．524-B ．171-C ．622-D ．1711.若圆C 1：x 2＋y 2＋2ax ＋a 2－4＝0(a ∈R )与圆C 2：x 2＋y 2－2by －1＋b 2＝0 (b ∈R )恰有三条切线，则a ＋b 的最大值为 ( )． A ．－3 2 B ．－3 C ．3 D ．3 212. 已知圆()()22:1C x a y b -+-=，设平面区域()70,300x y x y x y y ⎧⎫+-≤⎧⎪⎪⎪Ω=-+≥⎨⎨⎬⎪⎪⎪≥⎩⎩⎭，若圆心C ∈Ω,且圆C 与x 轴相切，则22a b +的最大值为（ ）A.5B.29C.37D.49二､填空题：本大题共4小题，每小题5分，满分20分．13. 已知直线l 过点()1,2,且在两坐标轴上的截距互为相反数,则直线l 的方程为14.已知圆C ：(x －3)2＋(y －4)2＝1，点A (0，－1)，B (0,1)．P 是圆C 上的动点，当|P A |2＋|PB |2取最大值时，点P 的坐标是________．15. 若直线1+=kx y 与圆0422=-+++my kx y x 交于N M ,两点,且N M ,关于直线0=-y x 对称,动点()b a P ,在不等式组⎪⎩⎪⎨⎧≥≤-≥+-0002y my kx y kx 表示的平面区域内部及边界上运动,则12--=a bω的取值范围是16．设有一组圆224*:(1)(3)2()k C x k y k k k -++-=∈N ．下列四个命题： ①．存在一条定直线与所有的圆均相切 ②．存在一条定直线与所有的圆均相交 ③．存在一条定直线与所有的圆均不．相交 ④．所有的圆均不．经过原点 其中真命题的代号是 ．（写出所有真命题的代号）三､解答题：本大题共6个小题，满分70分．解答应写出文字说明､证明过程或推演步骤．17．（本题满分10分）已知△ABC 的顶点A (5,1)，AB 边上的中线CM 所在直线方程为2x －y －5＝0，AC 边上的高BH 所在直线方程为x －2y －5＝0，求直线BC 的方程. 18．（本题满分12分）如图，射线OA 、OB 分别与x 轴正半轴成45°和30°角，过点P (1,0)作直线AB 分别交直线y ＝12xOA 、OB 于A 、B 两点，当AB 的中点C 恰好落在上时，求直线AB 的方程. 19．（本题满分12分）某客运公司用A 、B 两种型号的车辆承担甲、乙两地间的长途客运业务，每车每天往返一次．A 、B 两种车辆的载客量分别为36人和60人，从甲地去乙地的营运成本分别为1600元/辆和2400元/辆，公司拟组建一个不超过21辆车的客运车队，并要求B 型车不多于A 型车7辆．若每天运送人数不少于900，且使公司从甲地去乙地的营运成本最小，那么应配备A 型车、B 型车各多少辆？20．（本题满分12分）在平面直角坐标系xOy 中,点)3,0(A ,直线42:-=x y l ,设圆C 的半径为1,圆心在l 上.(1)若圆心C 也在直线1-=x y 上,过点A 作圆C 的切线,求切线的方程; (2)若圆C 上存在点M ,使MO MA 2=,求圆心C 的横坐标a 的取值范围.21．（本题满分12分）已知与圆0122:22=+--+y x y x C 相切的直线l 交x 轴，y 轴于B A ,两点，a OA =,()2,2>>=b a b OB (1)求证：()()222=--b a (2)求线段AB 中点的轨迹方程； (3)求△AOB 面积的最小值．22．（本小题满分12分） 已知圆C 的方程为22(4)4x y +-=,点O 是坐标原点.直线:l y kx =与圆C 交于,M N 两点. (Ⅰ)求k 的取值范围;(Ⅱ) 求,M N 的中点P 的轨迹;(Ⅲ)设(,)Q m n 是线段MN 上的点,且222211||||||OQ OM ON =+.请将n 表示为m 的函数.高二年级10月联考数学试卷(理科)答案一､选择题：1．D 2．B 3．D 4. C 5. A 6. B 7. A 8. A 9.C 10. A 11. D 12．C二､填空题：13．或 14．⎝ ⎛⎭⎪⎫185，24515． 16．②④三､解答题：17．（本题满分10分 ）解 依题意知：k AC ＝－2，A (5,1)， ∴l AC 为2x ＋y －11＝0，联立l AC 、l CM 得⎩⎨⎧2x ＋y －11＝0，2x －y －5＝0，∴C (4,3). ...........................4分设B (x 0，y 0)，AB 的中点M 为(x 0＋52，y 0＋12)， 代入2x －y －5＝0，得2x 0－y 0－1＝0，∴⎩⎨⎧2x 0－y 0－1＝0，x 0－2y 0－5＝0，∴B (－1，－3)，...........................4分 ∴k BC ＝65，∴直线BC 的方程为y －3＝65(x －4)， 即6x －5y －9＝0. ...........................4分18．（本小题满分12分）解 由题意可得k OA ＝tan 45°＝1，k OB ＝tan(180°－30°)＝－33，所以直线l OA ：y ＝x ，l OB ：y ＝－33x , 设A (m ，m )，B (－3n ，n )，所以AB 的中点C ⎝ ⎛⎭⎪⎫m －3n 2，m ＋n 2，由点C 在y ＝12x 上，且A 、P 、B 三点共线得⎩⎪⎨⎪⎧m ＋n 2＝12·m －3n 2，m －0m －1＝n －0－3n －1，解得m ＝3，所以A (3，3). ...........................8分又P (1,0)，所以k AB ＝k AP ＝33－1＝3＋32，所以l AB ：y ＝3＋32(x －1)，即直线AB 的方程为(3＋3)x －2y －3－3＝0. ...........................4分19．（本小题满分12分）解 设A 型、B 型车辆分别为x 、y 辆，相应营运成本为z 元，则z ＝1600x ＋2400y .由题意，得x ，y 满足约束条件⎩⎨⎧x ＋y ≤21，y ≤x ＋7，36x ＋60y ≥900，x ，y ≥0，x ，y ∈N ............................4分作可行域如图所示，可行域的三个顶点坐标分别为P (5，12)，Q (7,14)，R (15,6)．...........................2分由图可知，当直线z ＝1600x ＋2400y 经过可行域的点P 时，直线z ＝1600x ＋2400y 在y 轴上的截距z2400最小，即z 取得最小值．...........................3分故应配备A 型车5辆、B 型车12辆，可以满足公司从甲地去乙地的营运成本最小．...........................1分20．【答案】解:(1)由⎩⎨⎧-=-=142x y x y 得圆心C 为(3,2),∵圆C 的半径为1∴圆C 的方程为:1)2()3(22=-+-y x显然切线的斜率一定存在,设所求圆C 的切线方程为3+=kx y ,即03=+-y kx∴113232=++-k k ∴1132+=+k k ∴0)34(2=+k k ∴0=k 或者43-=k∴所求圆C 的切线方程为:3=y 或者343+-=x y 即3=y 或者01243=-+y x ...........................6分(2)解:∵圆C 的圆心在在直线42:-=x y l 上,所以,设圆心C 为(a,2a-4) 则圆C 的方程为:[]1)42()(22=--+-a y a x又∵MO MA 2=∴设M 为(x,y)则22222)3(y x y x +=-+整理得:4)1(22=++y x 设为圆D ∴点M 应该既在圆C 上又在圆D 上 即:圆C 和圆D 有交点∴[]12)1()42(1222+≤---+≤-a a由08852≥+-a a 得R x ∈ 由01252≤-a a 得5120≤≤x 终上所述,a 的取值范围为:⎥⎦⎤⎢⎣⎡512,0 ...........................6分21．解 (1)证明：圆的标准方程是(x －1)2＋(y －1)2＝1，设直线方程为x a ＋yb ＝1，即bx ＋ay －ab ＝0，圆心到该直线的距离d ＝|a ＋b －ab |a 2＋b 2＝1，即a 2＋b 2＋a 2b 2＋2ab －2a 2b －2ab 2＝a 2＋b 2，即a 2b 2＋2ab －2a 2b －2ab 2＝0， 即ab ＋2－2a －2b ＝0，即(a －2)(b －2)＝2. ...........................4分 (2)设AB 中点M (x ，y )，则a ＝2x ，b ＝2y ，代入(a －2)(b －2)＝2， 得(x －1)(y －1)＝12(x >1，y >1)．...........................4分 (3)由(a －2)(b －2)＝2得ab ＋2＝2(a ＋b )≥4ab ， 解得ab ≥2＋2(舍去ab ≤2－2)，当且仅当a ＝b 时，ab 取最小值6＋42，...........................4分22．（本小题满分12分）解:(Ⅰ)将x k y =代入22(4)4x y +-=得 则 0128)1(22=+-+x k x k ,(*)由012)1(4)8(22>⨯+--=∆k k 得32>k .所以k 的取值范围是),3()3,(+∞--∞ ...........................3分(Ⅱ) P 的轨迹方程22(2)433,0)x y x x +-=<<≠（-且,P 的轨迹是以(0，2)为圆心,2为半径的圆在圆22(4)4x y +-=内的一段圆弧,去掉点(0，4). ...........................3分(Ⅲ)因为M 、N 在直线l 上,可设点M 、N 的坐标分别为),(11kx x ,),(22kx x ,则2122)1(x k OM+=,2222)1(x k ON +=,又22222)1(m k n m OQ +=+=,由222112ONOMOQ+=得,22221222)1(1)1(1)1(2x k x k m k +++=+, 所以222121221222122)(112x x x x x x x x m -+=+=由(*)知 22118k k x x +=+,221112k x x +=, 所以 353622-=k m , 因为点Q 在直线l 上,所以m n k =,代入353622-=k m 可得363522=-m n , 由353622-=k m 及32>k 得 302<<m ,即 )3,0()0,3( -∈m . 依题意,点Q 在圆C 内,则0>n ,所以 518015533622+=+=m m n , 于是, n 与m 的函数关系为5180152+=m n ()3,0()0,3( -∈m )...........................6分。

学2020-2021学年高二数学上学期10月联考试题一、单选题1．设集合，集合，则（）A． B． C． D．2．数列，，，，，，的一个通项公式为（）A．B．C．D．3．椭圆的两个焦点是F1(－1, 0), F2(1, 0)，P为椭圆上一点，且|F1F2|是|PF1|与|PF2|的等差中项，则该椭圆方程是（）A． B． C． D．4．已知命题且为假命题，则可以肯定（）A．为真命题B．为假命题C．都是假命题D．中至少有一个是假命题5．把函数图象上所有点的横坐标缩短到原来的倍（纵坐标不变），再把所得曲线向右平移个单位长度，最后所得曲线的一条对称轴是（）A．B．C．D．6．若, 则“”是“方程表示双曲线”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件7．命题“”的否定为（）A．B．C．D．8．如图所示，将若干个点摆成三角形图案，每条边（包括两个端点）有个点，相应的图案中总的点数记为，则等于（）A．B．C．D．9．已知的内角所对的边分别是，且，若边上的中线，则的外接圆面积为（）A．B．C．D．10．在中，内角A，B，C的对边分别为a，b，c，.若对于任意实数x，不等式恒成立，则实数t的取值范围为（）A．B．C．D．11．（多选题）下列命题正确的是（）A． B．，使得C．是的充要条件 D．若，则12．（多选题）数列的前项和为，若，，则有（）A．B．为等比数列C．D．二、填空题13．如果方程的两根为和3且，那么不等式的解集为____________．14．已知的一个内角为，并且三边长构成公差为4的等差数列，则的面积为_______________.15．正项等比数列满足，且2，，成等差数列，设，则取得最小值时的值为_________．16．已知椭圆的左焦点为，右焦点为．若椭圆上存在一点，线段与圆相切于点，且为线段中点，则该椭圆的离心率为_____．三、解答题17．焦点在轴上的椭圆的方程为，点在椭圆上.（1）求的值.（2）依次求出这个椭圆的长轴长、短轴长、焦距、离心率.18．如图，在中，已知，是边上的一点，，，.（1）求的面积；（2）求边的长.19．已知数列是等比数列，且，其中成等差数列．（1）数列的通项公式；（2）记，则数列的前项和．20．已知函数，且的解集为.（1）求函数的解析式；（2）解关于x的不等式，；（3）设，若对于任意的都有，求M的最小值.21．设数列的前项和为，已知.（1）令，求数列的通项公式；（2）若数列满足：.①求数列的通项公式；②是否存在正整数，使得成立？若存在，求出所有的值；若不存在，请说明理由.22.设O为坐标原点,椭圆的左焦点为F,离心率为.直线与C交于两点, 的中点为M,（1）求椭圆C的方程（2）设点,求证:直线l过定点,并求出定点的坐标.高二年级10月联考数学试题答案一、单选题1．设集合，集合，则（）A．B．C．D．【答案】A【解析】【分析】解一元二次不等式得集合，利用并集的概念即可.【详解】由题意可得，，所以，故选：A．2．数列，，，，，，的一个通项公式为（）A．B．C．D．【答案】C【解析】【分析】首先注意到数列的奇数项为负，偶数项为正，其次数列各项绝对值构成一个以1为首项，以2为公差的等差数列，从而易求出其通项公式．【详解】∵数列{an}各项值为，，，，，，∴各项绝对值构成一个以1为首项，以2为公差的等差数列，∴|an|＝2n﹣1又∵数列的奇数项为负，偶数项为正，∴an＝（﹣1）n（2n﹣1）．故选C．3．椭圆的两个焦点是F1(－1, 0), F2(1, 0)，P为椭圆上一点，且|F1F2|是|PF1|与|PF2|的等差中项，则该椭圆方程是（）A．B．C．D．【答案】B【解析】【分析】【详解】试题分析：由题意可得：|PF1|+|PF2|=2|F1F2|=4,而结合椭圆的定义可知，|PF1|+|PF2|=2a,∴2a=4，2c=2，由a2=b2+c2，∴b2=3∴椭圆的方程为，选B.4．已知命题且为假命题，则可以肯定（）A．为真命题B．为假命题C．都是假命题D．中至少有一个是假命题【答案】D【解析】本题考察的是复合命题．由条件可知，只有当都是真命题时“”才为真命题．所以应选D．5．把函数图象上所有点的横坐标缩短到原来的倍（纵坐标不变），再把所得曲线向右平移个单位长度，最后所得曲线的一条对称轴是（）A．B．C．D．【答案】A【解析】【分析】先求出图像变换最后得到的解析式，再求函数图像的对称轴方程.【详解】由题得图像变换最后得到的解析式为，令，令k=-1,所以.故选A6．若, 则“”是“方程表示双曲线”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】【分析】当时，可验证方程满足双曲线的要求，充分性得证；根据，可求得当方程表示双曲线时的取值范围，得到必要性不成立，从而得到结果.【详解】当时，，则方程表示双曲线，充分条件成立；若方程表示双曲线，则，解得：或必要条件不成立综上所述：“”是“方程表示双曲线”的充分而不必要条件故选7．命题“”的否定为（）A．B．C．D．【答案】B【解析】【分析】根据全称命题的否定是特称命题，直接进行判断可得答案.【详解】解：根据全称命题的否定是特称命题，将全称量词换为存在量词，不等号换为＞，可得命题“”的否定为“”，故选：B.8．如图所示，将若干个点摆成三角形图案，每条边（包括两个端点）有个点，相应的图案中总的点数记为，则等于（）A．B．C．D．【答案】D【解析】【分析】求出数列的通项公式，然后利用裂项求和法可求得所求代数式的值.【详解】，，，，则，所以，，其中且，因此，.故选：D.9．已知的内角所对的边分别是，且，若边上的中线，则的外接圆面积为（）A．B．C．D．【答案】A【解析】【分析】由余弦定理求出，由平方后可求得即，再由已知求得，结合正弦定理可求得外接圆半径，从而得外接圆面积.【详解】∵，∴，．又是中点，∴，∴，即，解得，∴，，∴，，∴．故选：A．10．在中，内角A，B，C的对边分别为a，b，c，.若对于任意实数x，不等式恒成立，则实数t的取值范围为（）A．B．C．D．【答案】A【解析】【分析】化角为边，由余弦定理求出角的取值范围，设，则，并确定的取值范围，再由关于的一元二次不等式恒成立，，求出间的不等量关系，利用的取值范围，即可求出结果.【详解】在中，由正弦定理及，得，由余弦定理，得，又因为，所以，记，则.因为，所以，从而，所以可化为，即，恒成立，所以依题有，化简得，即得恒成立，又由，得或.故选:A.11．（多选题）下列命题正确的是（）A．B．，使得C．是的充要条件D．若，则【答案】AD【解析】【分析】对四个选项逐一分析，由此得出正确选项.【详解】对于A选项，时，，故A选项正确.对于B选项，当时，不成立，故B选项错误.对于C选项，当“”时，“”成立；当“”时，如，此时，故“”不成立，也即“”是“”的充分不必要条件.故C选项错误.对于D选项，当时，，，由于，故，所以D选项正确.故填：AD.12．（多选题）数列的前项和为，若，，则有（）A．B．为等比数列C．D．【答案】ABD【解析】【分析】由数列中和的关系式，求得数列的通项公式，可判定D正确；再利用题设条件，求得的表达式，可判定A正确，最后结合等比数列的定义，可判定B正确.【详解】由题意，数列的前项和满足，当时，，两式相减，可得，可得，即，又由，当时，，所以，所以数列的通项公式为；当时，，又由时，，适合上式，所以数列的的前项和为；又由，所以数列为公比为3的等比数列，综上可得选项是正确的.故选：ABD.二、填空题13．如果方程的两根为和3且，那么不等式的解集为____________．【答案】或【解析】【分析】由韦达定理可得出，，代入不等式，消去得出，再解该不等式即可.【详解】由韦达定理得，，代入不等式，得，，消去得，解该不等式得，因此，不等式的解集为或，故答案为或.14．已知的一个内角为，并且三边长构成公差为4的等差数列，则的面积为_______________.【答案】【解析】【分析】【详解】试题分析：设三角形的三边长为a-4,b=a,c=a+4,(a<b<c),根据题意可知三边长构成公差为4的等差数列，可知a+c=2b ,C=120,，则由余弦定理，c= a+ b-2abcosC，,三边长为6,10,14，,b= a+ c-2accosB,即（a+c）=a+c-2accosB, cosB=，sinB=可知S== .15．正项等比数列满足，且2，，成等差数列，设，则取得最小值时的值为_________．【答案】【解析】【分析】先由题意列关于的方程组，求得的通项公式，再表示出，即可求得答案.【详解】设等比数列的公比为.由，，成等差数列，可得，则，所以，解得(舍去)或.因为，所以.所以.所以.所以，当时，取得最小值，取得最小值.故答案为：.16．已知椭圆的左焦点为，右焦点为．若椭圆上存在一点，线段与圆相切于点，且为线段中点，则该椭圆的离心率为_____．【答案】.【解析】【分析】连接，．利用切线的性质可得．利用三角形中位线定理可得：，．再利用勾股定理与离心率计算公式即可得出．【详解】解：如图所示，连接线段与圆相切于点，．又为的中点，化为：解得．故答案为：．三、解答题17．焦点在轴上的椭圆的方程为，点在椭圆上.（1）求的值.（2）依次求出这个椭圆的长轴长、短轴长、焦距、离心率.【答案】（1）2（2）长轴长4、短轴长、焦距、离心率【解析】【分析】（1）根据题意，代入点，即可求解.（2）由（1），写出椭圆方程，求解，根据椭圆长轴长、短轴长、焦距、离心率定义，即可求解.【详解】（1）由题意，点在椭圆上，代入，得，解得（2）由（1）知，椭圆方程为，则椭圆的长轴长；’短轴长；焦距；离心率.18．如图，在中，已知，是边上的一点，，，.（1）求的面积；（2）求边的长.【答案】（1）；（2）分析：（1）在中，根据余弦定理求得，然后根据三角形的面积公式可得所求．（2）在中由正弦定理可得的长．详解：（1）在中，由余弦定理得，∵为三角形的内角，，，．（2）在中，，由正弦定理得：∴．19．已知数列是等比数列，且，其中成等差数列．（1）数列的通项公式；（2）记，则数列的前项和．【答案】（1）；（2）【分析】(1)设数列是公比为的等比数列,运用等差数列的中项性质和等比数列的通项公式,解方程可得公比,进而得到所求通项公式;(2)求得,运用数列的分组求和法,结合等差数列和等比数列的求和公式,计算可得所求和.【详解】(1)设数列的公比为,因为,,成等差数列,所以,又因为,所以,即,所以或(舍去),所以;(2)由(1)知,,所以.20．已知函数，且的解集为.（1）求函数的解析式；（2）解关于x的不等式，；（3）设，若对于任意的都有，求M的最小值.【答案】（1）（2）答案不唯一，具体见解析（3）【解析】【分析】（1）根据韦达定理直接求解即可.（2）转化为，然后分别对，，，进行讨论即可.（3）因为对于任意的都有，转化为，进而得到，然后分别求出，即可.【详解】解：（1）因为的解集为，所以的根为，2，所以，，即，；所以；（2），化简有，整理，所以当时，不等式的解集为，当时，不等式的解集为，当时，不等式的解集为，当时，不等式的解集为，（3）因为时，根据二次函数的图像性质，有，则有，所以，，因为对于任意的都有，即求，转化为，而，，所以，此时可得，所以M的最小值为.21．设数列的前项和为，已知.（1）令，求数列的通项公式；（2）若数列满足：.①求数列的通项公式；②是否存在正整数，使得成立？若存在，求出所有的值；若不存在，请说明理由.【答案】（1）；（2）①；②存在，【解析】【分析】（1）由题，得，即可得到本题答案；（2）①由，得，所以，恒等变形得，，由此即可得到本题答案；②由错位相减求和公式，得的前n项和，然后通过求的解，即可得到本题答案.【详解】（1）因为，所以，即，又因为，所以，即，所以数列是以2为公比和首项的等比数列，所以；（2）①由（1）知，，当时，，又因为也满足上式，所以数列的通项公式为，因为，所以，所以，即，因为，所以数列是以1为首项和公差的等差数列，所以，故；②设，则，所以，两式相减得，所以，∵，∴，即：，即.令，则，即，所以，数列单调递减，，因此，存在唯一正整数，使得成立.22.设O为坐标原点,椭圆的左焦点为F,离心率为.直线与C交于两点, 的中点为M,（1）求椭圆C的方程（2）设点,求证:直线l过定点,并求出定点的坐标解：（1）设椭圆的右焦点为,则为的中位线,所以,所以因为,所以,所以,所以椭圆C的方程为:（2）设联立,消去y整理得:所以,,所以因为所以所以整理得: 解得: 或 (舍去)所以直线l过定点.学2020-2021学年高二数学上学期10月联考试题一、单选题1．设集合，集合，则（）A． B． C． D．2．数列，，，，，，的一个通项公式为（）A．B．C．D．3．椭圆的两个焦点是F1(－1, 0), F2(1, 0)，P为椭圆上一点，且|F1F2|是|PF1|与|PF2|的等差中项，则该椭圆方程是（）A． B． C． D．4．已知命题且为假命题，则可以肯定（）A．为真命题B．为假命题C．都是假命题D．中至少有一个是假命题5．把函数图象上所有点的横坐标缩短到原来的倍（纵坐标不变），再把所得曲线向右平移个单位长度，最后所得曲线的一条对称轴是（）A．B．C．D．6．若, 则“”是“方程表示双曲线”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件7．命题“”的否定为（）A．B．C．D．8．如图所示，将若干个点摆成三角形图案，每条边（包括两个端点）有个点，相应的图案中总的点数记为，则等于（）A．B．C．D．9．已知的内角所对的边分别是，且，若边上的中线，则的外接圆面积为（）A．B．C．D．10．在中，内角A，B，C的对边分别为a，b，c，.若对于任意实数x，不等式恒成立，则实数t的取值范围为（）A．B．C．D．11．（多选题）下列命题正确的是（）A． B．，使得C．是的充要条件 D．若，则12．（多选题）数列的前项和为，若，，则有（）A．B．为等比数列C．D．二、填空题13．如果方程的两根为和3且，那么不等式的解集为____________．14．已知的一个内角为，并且三边长构成公差为4的等差数列，则的面积为_______________.15．正项等比数列满足，且2，，成等差数列，设，则取得最小值时的值为_________．16．已知椭圆的左焦点为，右焦点为．若椭圆上存在一点，线段与圆相切于点，且为线段中点，则该椭圆的离心率为_____．三、解答题17．焦点在轴上的椭圆的方程为，点在椭圆上.（1）求的值.（2）依次求出这个椭圆的长轴长、短轴长、焦距、离心率.18．如图，在中，已知，是边上的一点，，，.（1）求的面积；（2）求边的长.19．已知数列是等比数列，且，其中成等差数列．（1）数列的通项公式；（2）记，则数列的前项和．20．已知函数，且的解集为.（1）求函数的解析式；（2）解关于x的不等式，；（3）设，若对于任意的都有，求M的最小值.21．设数列的前项和为，已知.（1）令，求数列的通项公式；（2）若数列满足：.①求数列的通项公式；②是否存在正整数，使得成立？若存在，求出所有的值；若不存在，请说明理由.22.设O为坐标原点,椭圆的左焦点为F,离心率为.直线与C交于两点, 的中点为M,（1）求椭圆C的方程（2）设点,求证:直线l过定点,并求出定点的坐标.高二年级10月联考数学试题答案一、单选题1．设集合，集合，则（）A．B．C．D．【答案】A【解析】【分析】解一元二次不等式得集合，利用并集的概念即可.【详解】由题意可得，，所以，故选：A．2．数列，，，，，，的一个通项公式为（）A．B．C．D．【答案】C【解析】【分析】首先注意到数列的奇数项为负，偶数项为正，其次数列各项绝对值构成一个以1为首项，以2为公差的等差数列，从而易求出其通项公式．【详解】∵数列{an}各项值为，，，，，，∴各项绝对值构成一个以1为首项，以2为公差的等差数列，∴|an|＝2n﹣1又∵数列的奇数项为负，偶数项为正，∴an＝（﹣1）n（2n﹣1）．故选C．3．椭圆的两个焦点是F1(－1, 0), F2(1, 0)，P为椭圆上一点，且|F1F2|是|PF1|与|PF2|的等差中项，则该椭圆方程是（）A．B．C．D．【答案】B【解析】【分析】【详解】试题分析：由题意可得：|PF1|+|PF2|=2|F1F2|=4,而结合椭圆的定义可知，|PF1|+|PF2|=2a,∴2a=4，2c=2，由a2=b2+c2，∴b2=3∴椭圆的方程为，选B.4．已知命题且为假命题，则可以肯定（）A．为真命题B．为假命题C．都是假命题D．中至少有一个是假命题【答案】D【解析】本题考察的是复合命题．由条件可知，只有当都是真命题时“”才为真命题．所以应选D．5．把函数图象上所有点的横坐标缩短到原来的倍（纵坐标不变），再把所得曲线向右平移个单位长度，最后所得曲线的一条对称轴是（）A．B．C．D．【答案】A【解析】【分析】先求出图像变换最后得到的解析式，再求函数图像的对称轴方程.【详解】由题得图像变换最后得到的解析式为，令，令k=-1,所以.故选A6．若, 则“”是“方程表示双曲线”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】【分析】当时，可验证方程满足双曲线的要求，充分性得证；根据，可求得当方程表示双曲线时的取值范围，得到必要性不成立，从而得到结果.【详解】当时，，则方程表示双曲线，充分条件成立；若方程表示双曲线，则，解得：或必要条件不成立综上所述：“”是“方程表示双曲线”的充分而不必要条件故选7．命题“”的否定为（）A．B．C．D．【答案】B【解析】【分析】根据全称命题的否定是特称命题，直接进行判断可得答案.【详解】解：根据全称命题的否定是特称命题，将全称量词换为存在量词，不等号换为＞，可得命题“”的否定为“”，故选：B.8．如图所示，将若干个点摆成三角形图案，每条边（包括两个端点）有个点，相应的图案中总的点数记为，则等于（）A．B．C．D．【答案】D【解析】【分析】求出数列的通项公式，然后利用裂项求和法可求得所求代数式的值.【详解】，，，，则，所以，，其中且，因此，.故选：D.9．已知的内角所对的边分别是，且，若边上的中线，则的外接圆面积为（）A．B．C．D．【答案】A【解析】【分析】由余弦定理求出，由平方后可求得即，再由已知求得，结合正弦定理可求得外接圆半径，从而得外接圆面积.【详解】∵，∴，．又是中点，∴，∴，即，解得，∴，，∴，，∴．故选：A．10．在中，内角A，B，C的对边分别为a，b，c，.若对于任意实数x，不等式恒成立，则实数t的取值范围为（）A．B．C．D．【答案】A【解析】【分析】化角为边，由余弦定理求出角的取值范围，设，则，并确定的取值范围，再由关于的一元二次不等式恒成立，，求出间的不等量关系，利用的取值范围，即可求出结果.【详解】在中，由正弦定理及，得，由余弦定理，得，又因为，所以，记，则.因为，所以，从而，所以可化为，即，恒成立，所以依题有，化简得，即得恒成立，又由，得或.故选:A.11．（多选题）下列命题正确的是（）A．B．，使得C．是的充要条件D．若，则【答案】AD【解析】【分析】对四个选项逐一分析，由此得出正确选项.【详解】对于A选项，时，，故A选项正确.对于B选项，当时，不成立，故B选项错误.对于C选项，当“”时，“”成立；当“”时，如，此时，故“”不成立，也即“”是“”的充分不必要条件.故C选项错误.对于D选项，当时，，，由于，故，所以D选项正确.故填：AD.12．（多选题）数列的前项和为，若，，则有（）A．B．为等比数列C．D．【答案】ABD【解析】【分析】由数列中和的关系式，求得数列的通项公式，可判定D正确；再利用题设条件，求得的表达式，可判定A正确，最后结合等比数列的定义，可判定B正确.【详解】由题意，数列的前项和满足，当时，，两式相减，可得，可得，即，又由，当时，，所以，所以数列的通项公式为；当时，，又由时，，适合上式，所以数列的的前项和为；又由，所以数列为公比为3的等比数列，综上可得选项是正确的.故选：ABD.二、填空题13．如果方程的两根为和3且，那么不等式的解集为____________．【答案】或【解析】【分析】由韦达定理可得出，，代入不等式，消去得出，再解该不等式即可.【详解】由韦达定理得，，代入不等式，得，，消去得，解该不等式得，因此，不等式的解集为或，故答案为或.14．已知的一个内角为，并且三边长构成公差为4的等差数列，则的面积为_______________.【答案】【解析】【分析】【详解】试题分析：设三角形的三边长为a-4,b=a,c=a+4,(a<b<c),根据题意可知三边长构成公差为4的等差数列，可知a+c=2b ,C=120,，则由余弦定理，c= a+ b-2abcosC，,三边长为6,10,14，,b= a+ c-2accosB,即（a+c）=a+c-2accosB, cosB=，sinB=可知S==.15．正项等比数列满足，且2，，成等差数列，设，则取得最小值时的值为_________．【答案】【解析】【分析】先由题意列关于的方程组，求得的通项公式，再表示出，即可求得答案.【详解】设等比数列的公比为.由，，成等差数列，可得，则，所以，解得(舍去)或.因为，所以.所以.所以.所以，当时，取得最小值，取得最小值.故答案为：.16．已知椭圆的左焦点为，右焦点为．若椭圆上存在一点，线段与圆相切于点，且为线段中点，则该椭圆的离心率为_____．【答案】.【解析】【分析】连接，．利用切线的性质可得．利用三角形中位线定理可得：，．再利用勾股定理与离心率计算公式即可得出．【详解】解：如图所示，连接线段与圆相切于点，．又为的中点，化为：解得．故答案为：．三、解答题17．焦点在轴上的椭圆的方程为，点在椭圆上.（1）求的值.（2）依次求出这个椭圆的长轴长、短轴长、焦距、离心率.【答案】（1）2（2）长轴长4、短轴长、焦距、离心率【解析】【分析】（1）根据题意，代入点，即可求解.（2）由（1），写出椭圆方程，求解，根据椭圆长轴长、短轴长、焦距、离心率定义，即可求解.【详解】（1）由题意，点在椭圆上，代入，得，解得（2）由（1）知，椭圆方程为，则椭圆的长轴长；’短轴长；焦距；离心率.18．如图，在中，已知，是边上的一点，，，.（1）求的面积；（2）求边的长.【答案】（1）；（2）【解析】分析：（1）在中，根据余弦定理求得，然后根据三角形的面积公式可得所求．（2）在中由正弦定理可得的长．详解：（1）在中，由余弦定理得，∵为三角形的内角，，，．（2）在中，，由正弦定理得：∴．19．已知数列是等比数列，且，其中成等差数列．（1）数列的通项公式；（2）记，则数列的前项和．【答案】（1）；（2）【解析】【分析】(1)设数列是公比为的等比数列,运用等差数列的中项性质和等比数列的通项公式,解方程可得公比,进而得到所求通项公式;(2)求得,运用数列的分组求和法,结合等差数列和等比数列的求和公式,计算可得所求和.【详解】(1)设数列的公比为,因为,,成等差数列,所以,又因为,所以,即,所以或(舍去),所以;(2)由(1)知,,所以.20．已知函数，且的解集为.（1）求函数的解析式；（2）解关于x的不等式，；（3）设，若对于任意的都有，求M的最小值.【答案】（1）（2）答案不唯一，具体见解析（3）【解析】【分析】（1）根据韦达定理直接求解即可.（2）转化为，然后分别对，，，进行讨论即可.（3）因为对于任意的都有，转化为，进而得到，然后分别求出，即可.【详解】解：（1）因为的解集为，所以的根为，2，所以，，即，；所以；（2），化简有，整理，所以当时，不等式的解集为，当时，不等式的解集为，当时，不等式的解集为，当时，不等式的解集为，（3）因为时，根据二次函数的图像性质，有，则有，所以，，因为对于任意的都有，即求，转化为，而，，所以，此时可得，所以M的最小值为.21．设数列的前项和为，已知.（1）令，求数列的通项公式；（2）若数列满足：.①求数列的通项公式；②是否存在正整数，使得成立？若存在，求出所有的值；若不存在，请说明理由.【答案】（1）；（2）①；②存在，【解析】【分析】（1）由题，得，即可得到本题答案；（2）①由，得，所以，恒等变形得，，由此即可得到本题答案；②由错位相减求和公式，得的前n项和，然后通过求的解，即可得到本题答案.【详解】（1）因为，所以，即，又因为，所以，即，所以数列是以2为公比和首项的等比数列，所以；（2）①由（1）知，，当时，，又因为也满足上式，所以数列的通项公式为，因为，所以，所以，即，因为，所以数列是以1为首项和公差的等差数列，所以，故；②设，则，所以，两式相减得，所以，∵，∴，即：，即.令，则，即，所以，数列单调递减，，因此，存在唯一正整数，使得成立.22.设O为坐标原点,椭圆的左焦点为F,离心率为.直线与C交于两点, 的中点为M,（1）求椭圆C的方程（2）设点,求证:直线l过定点,并求出定点的坐标解：（1）设椭圆的右焦点为,则为的中位线,所以,所以因为,所以,所以,所以椭圆C的方程为:（2）设联立,消去y整理得:所以,,所以因为所以所以整理得: 解得: 或 (舍去)所以直线l过定点.。

湖北省武汉市蔡甸区实验高级中学2020-2021学年高二第一学期10月联合考试数学试卷含答案数学本卷考试时间：120分钟 总分：150分一、选择题:(本题共8小题，每小题5分,共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的） 1。

sin 20cos10cos160sin10-= （ ） A ．32- B ．32C ．12- D 。

122.ABC的内角,,A B C的对边分别为,,a b c.已知355,2, ,10a c cos B ===则b =（ ) A 。

B 。

C 。

2 D 。

33. 双曲线方程为2221x y -=，则它的右焦点坐标为( ） A 。

62 B. 5(2 C. 22D 。

(3,0) 4。

已知两条直线,m n ,两平面,αβ,给出下面四个命题,其中正确的命题是（ ) A. //,////m n m n αα⇒ B. //,,//m n m n αβαβ⊂⊂⇒ C 。

//,m n m n αα⊥⇒⊥D. ,//,m n m n αβαβ⊥⊥⇒⊥5。

直三棱柱111ABC A B C -中，若90BAC ∠=︒,1AB AC AA == ，则异面直线1BA 与1AC 所成的角等于( )A.30︒ B 。

45︒ C.60︒ D.90︒6。

已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ，且以线段12F F 为直径的圆与直线0bx cy -+=相切，则C 的离心率为( )A C 。

12D 。

27. 已知圆22:680C x y x y +--=,则：22x y +的最大值与最小值的和为（ ）A.5 B 。

10 C.25 D.1008。

点O 和点F 分别为椭圆2212x y +=的中心和右焦点，点P 为椭圆上的任意一点，则OP FP 的最小值为( ）A.2 B.12C 。

2 D.1二、多项选择题：（本题共4小题,每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求。

数学试卷第I 卷（选择题)一、单选题1．已知集合1{|1},{||1|1}M x N x x x=<=+<，则M ∩N =（ ） A ．∅B ．{x |-2<x <0}C ．{x |-2<x <1}D ．{x |0<x <1}2.下列命题中是假命题的是（ ）A.0log ,020=∈∃x R xB.1cos ,00=∈∃x R xC.02,>∈∀x R xD.0,2>∈∀x R x3．“0m ≥”是“220x x m ++≥对任意x R ∈恒成立”的( ) A ．充分不必要条件 B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件4．已知()f x 是定义在R 上的偶函数，且(5)(3)f x f x +=-，如果当[0,4)x ∈时，2()log (2)f x x =+，则(766)f =（ ）A ．3B ．-3C ．2D ．-25．已知x>0，y>0,x+2y+2xy=8，则x+2y 的最小值是（ ） A ．3B ．4C ．92D ．1126．函数()21cos 1xf x x e ⎛⎫=-⎪+⎝⎭图象的大致形状是（ ） A ． B ．C ．D ．7．已知双曲线221(0,0)x y m n m n -=>>和椭圆22152x y +=有相同的焦点，则41m n +的最小值为（ ） A ．2B ．3C ．4D ．58．已知函数()y f x =在区间(),0-∞内单调递增，且()()f x f x -=，若12log 3a f ⎛⎫= ⎪⎝⎭，()1.22b f -=，12c f ⎛⎫= ⎪⎝⎭，则a 、b 、c 的大小关系为（ ）A ．a c b >>B ．b c a >>C ．b a c >>D ．a b c >>9．若函数()sin 2x x f x e e x -=-+，则满足2(21)()0f x f x -+>的x 的取值范围为（ ） A ．1(1,)2- B ．1(,1)(,)2-∞-+∞ C ．1(,1)2-D ．1(,)(1,)2-∞-⋃+∞10．已知()f x 为偶函数，对任意x ∈R ，()(2)f x f x =-恒成立，且当01x ≤≤时，2()22f x x =-.设函数3()()log g x f x x =-，则()g x 的零点的个数为（ ）A ．6B ．7C ．8D ．911．已知函数()ln ,011,1x x f x x x-<≤⎧⎪=⎨>⎪⎩ ，若0a b << 且满足()()f a f b =，则()()af b bf a +的取值范围是（ ) A ．(11,1)e+B ．1(,1]e-∞+ C ．1(1,1]e+D ．1(0,1)e+ 12．已知22,0()ln(1),0x x f x x x ⎧≤=⎨+>⎩，对于[1,)x ∀∈-+∞，均有()2(1)f x m x -≤+，则实数m的取值范围是（ ） A ．21[,)e +∞ B ．31[,)e +∞ C ．1[,)e+∞ D ．211[,)e e第II 卷（非选择题)二、填空题13．函数y=log 3（x 2﹣2x ）的单调减区间是 ．14．若函数()()3212f x a x ax x =++-为奇函数，则曲线()y f x =在点()()1,1f 处的切线方程为______________．15．若函数2()1ln f x x x a x =-++在(0,)+∞上单调递增，则实数a 的最小值是__________．16．定义函数{}()max ,f x x x λλ=-，x ∈R ，其中0λ>，符号max{,}a b 表示数,a b 中的较大者，给出以下命题： ①()f x 是奇函数；②若不等式(1)(2)1f x f x -+-≥对一切实数x 恒成立，则1λ≥ ③=1λ时，()()(1)(2)(100)F x f x f x f x f x =+-+-++-最小值是2450④“0xy >”是“()()()f x f y f x y +≥+”成立的充要条件以上正确命题是__________．（写出所有正确命题的序号）三、解答题17．（10分）已知p ：x 2≤5x －4，q ：x 2－(a ＋2)x ＋2a ≤0. (1)若p 是真命题，求对应x 的取值范围； (2)若p 是q 的必要不充分条件，求a 的取值范围．18．（12分）设函数()()2228f x log x x =--的定义域为A ,集合()(){|10}B x x x a =--≤.(1)若4a =-,求A B ⋂;(2)若集合A B ⋂中恰有一个整数,求实数a 的取值范围. 19．（12分）已知函数()231x af x =+-为奇函数. （1）求实数a 的值；（2）求不等式()3log 1f x x <+的解集.20．（12分）某厂家举行大型的促销活动，经测算某产品当促销费用为x 万元时，销售量t 万件满足，为正常数其中),0(3125a a x x t ≤≤+-= 现假定生产量与销售量相等，已知生产该产品t 万件还需投入成本)210(t +万元（不含促销费用），产品的销售价格定为)205(t+万元/万件。

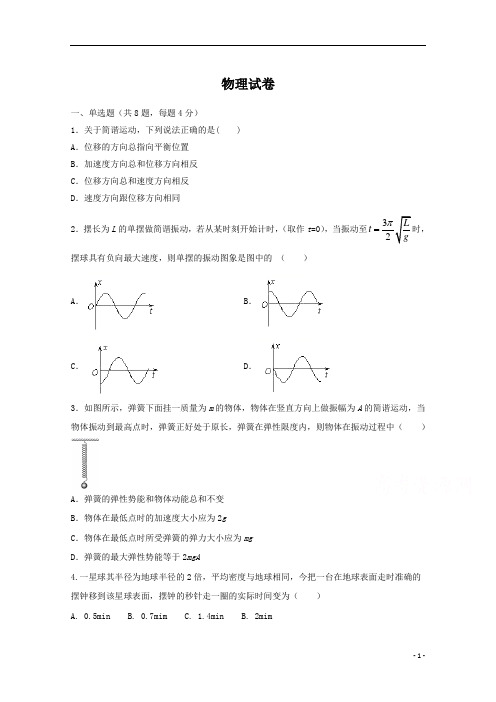
物理试卷一、单选题（共8题，每题4分）1．关于简谐运动，下列说法正确的是( )A．位移的方向总指向平衡位置B．加速度方向总和位移方向相反C．位移方向总和速度方向相反D．速度方向跟位移方向相同2．摆长为L的单摆做简谐振动，若从某时刻开始计时，（取作t=0），当振动至32Ltgπ=时，摆球具有负向最大速度，则单摆的振动图象是图中的（）A．B．C．D．3．如图所示，弹簧下面挂一质量为m的物体，物体在竖直方向上做振幅为A的简谐运动，当物体振动到最高点时，弹簧正好处于原长，弹簧在弹性限度内，则物体在振动过程中（）A．弹簧的弹性势能和物体动能总和不变B．物体在最低点时的加速度大小应为2gC．物体在最低点时所受弹簧的弹力大小应为mgD．弹簧的最大弹性势能等于2mgA4.一星球其半径为地球半径的2倍，平均密度与地球相同，今把一台在地球表面走时准确的摆钟移到该星球表面，摆钟的秒针走一圈的实际时间变为（）A. 0.5minB. 0.7mimC. 1.4min B. 2mim5．汽车无人驾驶技术已逐渐成熟，最常用的是ACC 自适应巡航控制，它可以控制无人车在前车减速时自动减速、前车加速时自动跟上去。

汽车使用的传感器主要是毫米波雷达，该雷达会发射和接收调制过的无线电波，再通过因波的时间差和多普勒效应造成的频率变化来测量目标的相对距离和相对速度。

若该雷达发射的无线电波的频率为f，接收到的回波的频率为f '，则（）A．当f '=f 时，表明前车一定做匀速直线运动B．当f '=f 时，表明前车一定处于静止状态C．当f '>f 时，表明前车正在减速行驶D．当f '<f 时，表明前车正在减速行驶6．关于波的叠加和干涉，下列说法中正确的是（）A．两列频率不相同的波相遇时，因为没有稳定的干涉图样，所以波没有叠加B．两列频率相同的波相遇时，振动加强的点只是波峰与波峰相遇的点C．两列频率相同的波相遇时，如果介质中的某点振动是加强的，某时刻该质点的位移可能是零D．两列频率相同的波相遇时，振动加强点的位移总是比振动减弱点的位移大7．如图所示，水面上有一个半径4.5m的圆圆心O与圆周上的a点各放一个振源，两振源的振动情况相同，产生波长为2m的水波，c，d为Oa连线的中垂线与圆周的交点，则（）A. 圆周上b点的振幅为0B. c, d两点的位移始终最大C. 圆周上振动加强的点共有12个D. 圆周上振动减弱的点共有8个8. 如图所示为波源开始振动后经过一个周期的波形图，设介质中质点振动周期为T，下列说法正确的是()A ．若M 质点为波源，则M 质点开始振动时方向向下B ．若M 质点为波源，则P 质点已经振动了34TC ．若N 质点为波源，则P 质点已经振动了34TD ．若N 质点为波源，则该时刻P 质点动能最大二、多选题（共4题，每题4分，漏选得2分，错选不得分）9．如图所示是一弹簧振子做受迫振动时的振幅与驱动力频率的关系，由图可知( )A ．驱动力的频率为f 2时，振子处于共振状态B ．驱动力的频率为f 3时，振子的振动频率为f 3C ．假如让振子自由振动，它的频率为f 2D ．振子做自由振动时，频率可以为f 1、f 2和f 310. 一列沿x 轴正方向传播的简谐横波在t 时刻的波形如图所示，已知该波的周期为T ，a 、b 、c 、d 为沿波传播方向上的四个质点。

2020-2021学年度第一学期新高考五校联合体期中考试高二数学试题答案一、选择题（本大题共12题，每小题5分，共60分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DCCCCBBDABCBCBCACD二、填空题（本大题共4小题，每小题5分，共20分）13、 22+ 14、 3715、1316、 ①②④三、解答题（本大题共6小题，共70分）17、（10分）（1）4883ππ+；(5分)（2）4033π.（5分） 【详解】所求旋转体的表面积由三部分组成：圆锥的底面、侧面，圆柱的侧面. 圆锥的底面积为16π，圆锥的侧面积为8432ππ⨯⨯=， ······2分 圆柱的侧面积为222383ππ⨯⨯=，·······4分故所求几何体的表面积为1632834883πππππ++=+.·······5分 阴影部分形成的几何体的体积为2214034432233ππ⨯⨯⨯⨯=.······10分（圆锥体积2分，圆柱体积2分，结果1分） 18、（12分）（1）证明见解析；（6分）（2）3（6分） 【详解】（1）证明：如图，C 为圆O 上的一点，AB 为圆O 的直径，BC AC ∴⊥，又P A 垂直圆O 所在的平面，PA BC ∴⊥，·······4分 又因为PA AC A PA ⋂=⊂，平面P AC ，AC ⊂平面P AC ， 则BC ⊥平面P AC ；········6分 （2）23AB BC AC ==，，∴在Rt ABC 中，可得13AC BC ==，，·······8分又2PA AB ==，点M 为PC 的中点，∴点M 到平面ABC 的距离等于点P 到平面ABC 的距离的12，·······10分 1113113322B MOC M BOC V V --∴==⨯⨯⨯⨯⨯=．······12分19、（12分）（1）证明见解析；（6分）（2）63（6分） 【详解】（1）证明：∵正方体1111ABCD A B C D -中E ，F 分别为11A D ，11B C 的中点， ∴1D E ∥1B F ，1D E =1B F ∴四边形11B FD E 是平行四边形. ∴11//B E D F .又1B E ⊄平面1BD F ，1D F ⊂平1BD F ，∴1//B E 平面1BD F .· ·······2分 ∵EF ∥AB ，EF =AB∴四边形ABFE 是平行四边形.∴//AE BF .又AE ⊄平向1BD F ，BF ⊂平面1BD F ， ∴AE ∥平面1BD F . ········4分 又∵1AE B E E ⋂=，∴平面1//AB E 平面1BD F . ···········6分（2）平面1AB E 与平面1BD F 之间的距离也就是点B 到面1AB E 的距离，设为h ， ∵正方体1111ABCD A B C D -的棱长为2，∴1AE B E ==1AB =∴1AB E △的面积112AB E S =⨯=△∴三棱锥1B AB E -的体积11133B AB E AB E V S h h -=⋅=△， ·········8分 又三棱锥1E ABB -的体积11111122213323E ABB ABB V S A E -=⋅=⨯⨯⨯⨯=△.········10分由11B AB E A E BB V V --=可得，233h =解得3h =.··········11分∴平面1AB E 与平面1BD F .·········12分20（12分） 【详解】 (1)证明:因为侧面BCC 1B 1是菱形，所以B 1C ⊥BC 1·······2分 又B 1C ⊥A 1B ，且A 1B ∩BC 1＝B 所以B 1C ⊥平面A 1BC 1．········4分 又B 1C ⊂平面AB 1C所以平面AB 1C ⊥平面A 1BC 1．········6分 (2)解：设BC 1交B 1C 于点E ，连接DE ，则DE 是平面A 1BC 1与平面B 1CD 的交线．······8分因为A 1B ∥平面B 1CD ，所以A 1B ∥DE ．·······10分 又E 是BC 1的中点，所以D 为A 1C 1的中点，即11DC DA =1 ．········12分21（12分） 法一： (1)证明：由已知BC ⊥AC ，BC ⊥CC 1，得BC ⊥平面ACC 1A 1． 连接AC 1，则BC ⊥AC 1．·········2分由已知，可知侧面ACC 1A 1是正方形，所以A 1C ⊥AC 1． 又BC ∩A 1C ＝C ，所以AC 1⊥平面A 1BC ．··········4分因为侧面ABB 1A 1是正方形，M 是A 1B 的中点， 连接AB 1，则点M 是AB 1的中点．又点N 是B 1C 1的中点，则MN 是△AB 1C 1的中位线 所以MN ∥AC 1．故MN ⊥平面A 1BC ．········6分 (2)解：因为AC 1⊥平面A 1BC ，设AC 1与A 1C 相交于点D ，连接BD ，则∠C 1BD 为直线BC 1和平面A 1BC 所成的角．········8分 设AC ＝BC ＝CC 1＝a ，则C 1D ＝22a ，BC 1＝2a ． 在Rt △BDC 1中，sin ∠C 1BD ＝11BC D C ＝12， 所以∠C 1BD ＝30°，·········11分故直线BC 1和平面A 1BC 所成的角为30°．·········12分 法二：（向量法）（1） 据题意CA 、CB 、CC 1两两垂直，以C 为原点，CA 、CB 、CC 1所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系，如图 设AC=BC=CC 1=a ，则B （0，a,0），B 1（0,a,a ），A （a,0,0），C （0,0,0），C 1（0,0,a ），A 1（a,0,a ），M （2a ,2a ,2a ），N （0,2a ,a ）········1分 所以)2,0,2(),,0,(),,,(11a a MN a a CA a a a BA -==-=，········2分 于是01=⋅,01=⋅,即MN ⊥BA 1，MN ⊥CA 1 ·····4分又111A CA BA =⋂，故MN ⊥平面A 1BC ·······6分 （2）因为MN ⊥平面A 1BC ，则MN 为平面A 1BC 的法向量 又),,0(1a a BC -=，·······2分则2122222=⨯==a a a ········4分所以60=·······5分故直线BC 1和平面A 1BC 所成的角为30°.·······6分22、（12分） （1）证明见解析；（4分）（2）存在，AE ＝2（8分） 【详解】如下图，以D 为坐标原点，DA ，DC ，DD 1所在直线分别为x 轴，y 轴，z 轴， 建立如图所示的空间直角坐标系，则D (0，0，0)，C (0，2，0)，A 1(1，0，1)， D 1(0，0，1)，设E (1，y 0，0)(0≤y 0≤2)，（1）证明：因为1D E ＝(1，y 0，-1)，1A D ＝(－1，0，－1)，·······1分 则1D E ·1A D ＝(1，y 0，-1)·(－1，0，－1)＝0，········3分 所以11D E A D ⊥，即D 1E ⊥A 1D ；·········4分 （2）假设在棱AB 上存在点E ，使二面角D 1-EC -D 的平面角为30°. 因为EC ＝(－1，2－y 0，0)，1D C ＝(0，2，－1)，·········5分 设平面D 1EC 的一个法向量为1n ＝(x ，y ，z )，则11100n EC n D C ⎧⋅=⎪⎨⋅=⎪⎩即0(2)020x y y y z -+-=⎧⎨-=⎩，取y ＝1，则1n ＝(2－y 0，1，2)是平面D 1EC 的一个法向量，易知平面ECD 的一个法向量为2n ＝1DD ＝(0，0，1)，········8分 要使二面角D 1-EC -D 的平面角为30°，则1212cos30n n n n ⋅︒=＝2220(212)y -++＝3，·······10分 解得y 0＝2－33或y 0＝2＋33 (不合题意，舍去)，········11分所以当AE ＝2－3时，二面角D 1-EC -D 的平面角为30°.········12分。

数学本卷考试时间：120分钟总分：150分一、选择题：(本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的)1. (2015新课标全国Ⅰ理科)=A. B.C. D.【答案】D【解析】原式===，故选D.考点：本题主要考查诱导公式与两角和与差的正余弦公式.2. 的内角的对边分别为.已知则（）A. B. C. 2 D. 3【答案】B【解析】【分析】直接利用余弦定理求解即可．【详解】因为由余弦定理可得，所以故选：B．【点睛】本题主要考查了余弦定理在解三角形中的应用，属于基础题．3. 双曲线方程为，则它的右焦点坐标为（）．A. B. C. D.【答案】C【解析】试题分析：双曲线方程变形为焦点为考点：双曲线方程及性质4. 已知两条直线，两平面，给出下面四个命题，其中正确的命题是（）A. B.C. D.【答案】C【解析】【分析】由线线、线面的位置关系，逐项判断即可得解.【详解】对于A，若，则或，故A错误；对于B，若，则或与异面，故B错误；对于C，若，则，故C正确；对于D，若，则或，故D错误.故选：C.【点睛】本题考查了线线、线面位置关系的判断，考查了空间思维能力，属于基础题.5. 直三棱柱中，若，，则异面直线与所成的角等于A. 30°B. 45°C. 60°D. 90°【答案】C【解析】【详解】本试题主要考查异面直线所成的角问题，考查空间想象与计算能力．延长B1A1到E，使A1E=A1B1，连结AE，EC1，则AE∥A1B，∠EAC1或其补角即为所求，由已知条件可得△AEC1为正三角形，∴∠EC1B为，故选C．6. 已知椭圆的左、右焦点分别为，且以线段为直径的圆与直线相切，则的离心率为（）A. B. C. D.【答案】D【解析】【分析】求出圆心与半径，利用圆心到直线的距离等于半径，可得，结合以及离心率的定义，即可得结果.【详解】由题知圆心坐标为，半径为，又圆与直线相切，得，得，又，联立可得，故离心率为.故选：D【点睛】本题主要考查椭圆的离心率的求解.离心率的求解在圆锥曲线的考查中是一个重点也是难点，一般求离心率有以下几种情况：①直接求出，从而求出；②构造的齐次式，求出；③采用离心率的定义以及圆锥曲线的定义来求解．7. 已知圆，则：的最大值与最小值的和为（）A. B. C. D.【答案】D【解析】【分析】设，，代入化简，利用辅助角公式以及三角函数的有界性可得答案. 【详解】把已知圆的一般方程化为标准方程得，可设，．，因为，所以，，即的最大值为100，最小值为0，的最大值与最小值的和为100，故选：D.【点睛】本题主要考查圆的方程与性质，考查了辅助角公式以及三角函数的有界性，属于中档题．8. 若点和点分别为椭圆的中心和右焦点，点为椭圆上的任意一点，则的最小值为A. B. C. D. 1【答案】B【解析】【详解】试题分析：设点，所以，由此可得，，所以的最小值为.考点：向量数量积以及二次函数最值．二、多项选择题：(本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得3分)9. 已知椭圆的中心在原点，焦点，在轴上，且短轴长为2，离心率为，过焦点作轴的垂线，交椭圆于，两点，则下列说法正确的是（）A. 椭圆方程为B. 椭圆方程为C. D. 的周长为【答案】ACD【解析】【分析】由已知求得b，再由离心率结合隐含条件求得a，可得椭圆方程，进一步求得通径及的周长判断得答案．【详解】由已知得，2b=2，b=1，，又，解得，∴椭圆方程为，如图：∴，的周长为．故选：ACD．【点睛】本题考查椭圆简单性质，考查数形结合的解题思想方法，是中档题．10. 已知圆和两点.若圆上存在点，使得，则实数的取值可以为（）A. B. C. D.【答案】ABC【解析】【分析】的圆心，半径，设在圆上，则，，由已知得，的最值即为的最值，从而可得结论．【详解】圆的圆心，半径，设在圆上，则，，若，则，，，的最大值即为的最大值，等于．最小值为，的取值范围是．故选：ABC．【点睛】本题考查圆的方程与性质、垂直关系的向量表示，考查点与圆的位置关系，是中档题．11. ，是不在平面内的任意两点，则（）A. 在内存在直线与直线异面B. 在内存在直线与直线相交C. 存在过直线的平面与垂直D. 在内存在直线与直线平行【答案】AC【解析】【分析】根据异面直线的定义，以及线面位置的判定及性质，逐项判定，即可求解.【详解】由题意知，点，是不在平面内的任意两点，对于A 中，根据异面直线定义，可得平面内存在直线与直线异面，所以是正确的；对于B中，若直线平行于平面时，可得在内不存在直线与直线相交，所以不正确；对于C中，过作平面的垂线，则由直线和直线确定的平面垂直与平面，所以是正确的；对于D中，当直线与平面相交时，在内不存在直线与直线平行，所以不正确.故选：AC【点睛】本题主要考查了异面直线的定义，线面位置关系的判定及应用，其中解答中熟记线面位置的判定及性质是解答的关键，着重考查推理与论证能力.12. 在中，角所对的边分别为，给出下列四个命题中，其中正确的命题为（）A. 若，则；B. 若，则；C. 若，则这个三角形有两解；D. 当是钝角三角形.则.【答案】BCD【解析】【分析】A，求出，即可由正弦定理求出；B，由得出，即得，由正弦定理即可判断；C，由正弦定理解三角形即可判断；D，由和的正切个数化简可判断.【详解】对于A，若，，，由正弦定理可得，故A错误；对于B，，且在单调递减，若，则，由三角形中大边对大角得，再由正弦定理得，故B正确；对于C，由正弦定理得，则，因为，故有两解，故C正确；对于D，在中，，则，当是钝角三角形，若或为钝角，则，满足；若为钝角，则，即，满足，故D正确.故选：BCD.【点睛】本题考查正弦定理的应用，考查和的正切公式的应用，属于基础题.三、填空题(本题共4小题，每小题5分，共20分)13. 长方体长、宽、高分别为4，2，1，其顶点都在球的球面上，则球的表面积为__.【答案】【解析】【分析】根据长方体的对角线长等于它的外接球的直径，可得外接球的半径，然后利用球的表面积公式可求结果.【详解】因为长方体的长、宽、高分别为4，2，1，所以其对角线长为，所以外接球的半径为，球的表面积为.故答案为：.【点睛】本题主要考查长方体的外接球问题，明确对角线的长等于外接球的直径是解题关键，侧重考查数学运算的核心素养.14. 如果方程表示双曲线，则实数的取值范围是_______.【答案】【解析】【分析】根据方程表示是双曲线，得到，由此求解出的取值范围.【详解】因为方程表示双曲线，所以，所以，所以，故答案为：.【点睛】本题考查根据双曲线方程特点求解参数范围，难度较易.形如的方程如果表示双曲线，则有.15. 已知k∈R，过定点A的动直线和过定点B的动直线交于点P，则的值为__________.【答案】13【解析】【分析】由两直线方程可得定点，，再联立两直线方程解出的坐标，然后由两点间距离公式可得，，进而可以求解．【详解】动直线过定点动直线过定点联立方程，解得，，则由两点间距离公式可得：，，故答案为：13．【点睛】本题考查了直线中定点问题以及两点间距离公式，考查了学生的运算能力，属于基础题．16. 在∆ABC中，，点为边上的点，AD是∠BAC的角平分线，则AD的取值范围是________________.【答案】【解析】【分析】由角分线定理知，，设，，然后根据，化简后可推出，再求出的取值范围．【详解】由角分线定理知，，设，，，，，，，．故答案为：．【点睛】本题考查解三角形在几何中的应用，主要涉及正弦的面积公式、二倍角公式，运用角分线定理是解题的突破口，考查学生的逻辑推理能力和运算能力，属于中档题．四、解答题(本题共6小题，共70分.解答题应写出文字说明、证明过程或演算步骤)17. 如图，在四棱锥中，⊥平面，（1）求证：平面；（2）设平面平面，求证：.【答案】（1）证明见解析；（2）证明见解析.【解析】【分析】（1）推导出，，由此能证明平面，结合即可得结论．（2）由可证明平面，再由线面平行的性质定理可得结论.【详解】（1）在四棱锥中，平面，平面，，，，平面．又，所以平面；（2）平面平面平面又平面，平面平面【点睛】本题主要考查线面垂直的判定定理，考查了线面平行的判定定理与性质定理的应用，属于中档题.18. 在△ABC中，，再从条件①、条件②这两个条件中选择一个作为已知，求：（1）的大小；（2）的面积.条件①：；条件②：.【答案】选择见解析；（1）；（2）.【解析】【分析】（1）若选择条件①时根据余弦定理，求得的值，即可求得的大小；若选择条件条件②时，由正弦定理，求得，得到，即可求得的大小；（2）由正弦定理求得，结合两角和的公式，求得的值，利用三角形的面积公式，即可求解. 【详解】若选择条件①：（1）因为，由余弦定理，可得，因为，所以.（2）由正弦定理，可得，又由，所以.若选择条件②：（1）因为，由正弦定理，可得，因为，则，所以，即，因为，所以.（2）由正弦定理，可得，又由，所以.【点睛】本题主要考查了正弦定理、余弦定理和三角形的面积公式的应用，其中在解有关三角形的题目时，要抓住题设条件和利用某个定理的信息，合理应用正弦定理和余弦定理求解是解答的关键，着重考查了运算与求解能力，属于基础题．19. 已知抛物线与直线交于两点．（1）求弦的长度;（2）若点在抛物线上,且的面积为,求点的坐标．【答案】（1）（2）或.【解析】【分析】（1）联立抛物线与直线方程,根据弦长公式,即可求得答案;（2）设点,求得到的距离,结合已知,即可求得答案.【详解】（1）设,,由消掉,可得,,由韦达定理可得,,,弦的长度为.（2）设点,设点到的距离为,,,即,,解得或,点为或.【点睛】本题主要考查了抛物线的弦长和抛物线中三角形面积问题,解题关键是掌握抛物线的基础知识和在求圆锥曲线与直线交点问题时,通常用直线和圆锥曲线联立方程组,通过韦达定理建立起直线的斜率与交点坐标的关系式,考查了分析能力和计算能力,属于难题.20. 已知点及圆：.(1)若直线过点且与圆心的距离为，求直线的方程．(2)设直线与圆交于，两点，是否存在实数，使得过点的直线垂直平分弦？若存在，求出实数的值；若不存在，请说明理由．【答案】（1）或；（2）见解析【解析】试题分析:(1)当直线斜率存在时,设出直线方程,利用圆心到直线的距离等于建立方程,解出子线的斜率,由此求得直线方程.当直线斜率不存在时,直线方程为,经验证可知也符合.(2)将直线方程代入圆的方程,利用判别式大于零求得的取值范围,利用”圆的弦的垂直平分线经过圆心”,求出直线的斜率,进而求得的值,由此判断不存在.试题解析:(1)设直线l的斜率为k(k存在)，则方程为y－0＝k(x－2)，即kx－y－2k＝0.又圆C的圆心为(3，－2)，半径r＝3，由＝1，解得k＝－.所以直线方程为，即3x＋4y－6＝0.当l的斜率不存在时，l的方程为x＝2，经验证x＝2也满足条件(2)把直线y＝ax＋1代入圆C的方程，消去y，整理得(a2＋1)x2＋6(a－1)x＋9＝0.由于直线ax－y＋1＝0交圆C于A，B两点，故Δ＝36(a－1)2－36(a2＋1)>0，解得a<0.则实数a的取值范围是(－∞，0)．设符合条件的实数a存在．由于l2垂直平分弦AB，故圆心C(3，－2)必在l2上．所以l2的斜率k PC＝－2.而k AB＝a＝－，所以a＝.由于，故不存在实数a，使得过点P(2,0)的直线l2垂直平分弦AB【点睛】本小题主要考查直线和圆的位置关系,考查直线和圆相交时的代数表示方法.第一问由于题目给出圆心到直线的距离,故可利用点到直线的距离公式,建立方程,求的直线的斜率.由于直线的斜率可能不存在,故必须对直线斜率不存在的情况进行验证.直线和圆相交,那么直线和圆方程联立所得一元二次不等式的判别式要大于零.21. 已知四棱锥，底面为矩形，，，，为中点，．（1）求证：平面平面；（2）若，求二面角的余弦值．【答案】（1）见解析；（2）【解析】【分析】(1)方法一:由推出,结合可推出,又,所以平面,进而得证;方法二:由推出,从而有,结合可推出,又,所以平面,进而得证;(2)由勾股定理逆定理推出,结合可得平面,故以为原点,､､方向为､､轴正方向建立空间直角坐标系,再利用向量法求出二面角的余弦值.【详解】(1)方法一:因为,,为中点,所以在中,,在中,,所以,所以,又因为,所以,所以,又因为,,所以平面,又平面,所以平面平面.方法二:由题意可知:在中,,在中,,即,所以,所以,又因为,所以,所以,又因为,,所以平面,又平面,所以平面平面.(2)因为,又,,所以,所以,又因为,且与相交,所以平面,故以为原点,､､方向为､､轴正方向建立如图所示的空间直角坐标系,则,,,,所以,,,设平面的一个法向量为,由可得,令,则,所以,设平面的一个法向量为,由可得令,则,所以,所以,由题意可知二面角为锐二面角,所以二面角的余弦值为.【点睛】本题考查了空间中的垂直证明,考查了向量法求二面角的余弦值,需要学生具备一定的空间思维及计算能力,属于中档题.22. 已知：交轴于，两点，过以为长轴，离心率为的椭圆的左焦点的直线交椭圆于，，分别交轴和圆于，.（1）求椭圆的标准方程；（2）若，.求证：为定值；（3）过原点作直线的垂线交直线于点.试探究：当点在圆上运动时（不与，重合），直线与圆是否保持相切？若是，请证明；若不是，请说明理由.【答案】（1）；（2）；（3）故直线与圆相切，证明见详解.【解析】【分析】（1）由题意可得，再根据离心率可得，由，可得椭圆的标准方程.（2）设直线的方程为：，将直线与椭圆方程联立，求出两根之和、两根之积，再根据向量的坐标运算可得，求出即可证出.（3）设，则，只要证出即可.【详解】（1）由，解得，又因为，所以，所以，所以椭圆的标准方程为.（2）证明，如图，由题设知直线的斜率存在，设直线的方程为：，则点，将直线代入椭圆方程可得，设，，，，由，，知，故.（3）点在圆上运动时，直线与圆相切，证明：设，则，，，直线的方程为，即点，，，，即，故直线与圆相切.【点睛】本题考查了由离心率求椭圆的标准方程、直线与椭圆的位置关系中的定值问题，此题对计算能力要求比较高，属于难题.登录组卷网可对本试卷进行单题组卷、细目表分析、布置作业、举一反三等操作。

2021年高二上学期10月份测试数学试题 含答案（本试卷考试时间120分钟，满分160分，请将答案做在答题卡上）一、填空题（本大题共14小题，每小题5分，共70分）1.直线的倾斜角为 ▲ ．2. 焦点在轴上的椭圆m x2＋4y2＝1的焦距是2，则m 的值是____▲____．3.若直线与直线关于点对称，则直线恒过定点____▲___．4. 从点引圆的切线，则切线长是 ▲ ．5. 若P 是以F 1，F 2为焦点的椭圆25x2＋9y2＝1上一点，则三角形PF 1F 2的周长等于 ▲ ．6. 圆，圆，则这两圆公切线的条数为 ▲ ．7. 经过点且在两坐标轴上的截距互为相反数的直线方程是 ▲ ．8. 圆关于直线对称的圆的标准方程是 ▲ .9. 已知是由不等式组所确定的平面区域，则圆在区域内的弧长为 ▲ ．10. 圆，则圆上到直线距离为3的点共有▲ 个．11. 在平面直角坐标系中，若直线与圆心为的圆相交于，两点，且为直角三角形，则实数的值是 ▲ ．12. 已知椭圆，点依次为其左顶点、下顶点、上顶点和右焦点，若直线 与直线 的交点恰在椭圆的右准线上，则椭圆的离心率为____▲ __.13. 已知圆，点在直线上，为坐标原点.若圆上存在点使得，则的取值范围为 ▲ ．14. 若对于给定的负实数，函数的图象上总存在点C ，使得以C 为圆心，1为半径的圆上有两个不同的点到原点的距离为2，则的取值范围为 ▲ .二、解答题（本大题共6小题，共90分）15.（本小题满分14分）已知直线和．问：m 为何值时，有：（1）；（2）．16.（本小题满分14分）已知椭圆818x2＋36y2＝1上一点，且，．（1）求的值；（2）求过点M 且与椭圆9x2＋4y2＝1共焦点的椭圆的方程．17.（本小题满分15分）在平面直角坐标系中，己知点，，、分别为线段，上的动点，且满足.（1）若，求直线的方程;（2）证明：的外接圆恒过定点（异于原点）.18.（本小题满分15分）在一个特定时段内，以点为中心的7海里以内海域被设为警戒水域.点正北55海里处有一个雷达观测站.某时刻测得一艘匀速直线行驶的船只位于点北偏东且与点相距海里的位置，经过40分钟又测得该船已行驶到点北偏东(其中，)且与点相距海里的位置.（1）求该船的行驶速度（单位：海里/小时）;（2）若该船不改变航行方向继续行驶.判断它是否会进入警戒水域，并说明理由.19.（本小题满分16分）在平面直角坐标系中，已知圆经过，，三点，是线段上的动点，、是过点且互相垂直的两条直线，其中交轴于点，交圆于、两点．（I）若，求直线的方程；（II）若是使恒成立的最小正整数，求三角形的面积的最小值．20.（本小题满分16分）已知函数,．（1）当时，求的最小值；（2）若函数图象上的点都在不等式组表示的平面区域内，求实数的取值范围；（3）若函数在上有零点，求的最小值.10月份测试数学参考答案1. 2.5 3. (0,2) 4.3 5.18 6.2 7.或8.9.10.3 11. －1 12.13.14.15.解：（1）∵，∴，得或；当m＝4时，l1：6x＋7y－5＝0，l2：6x＋7y＝5,即l1与l2重合，故舍去．当时，即∴当时，．（2）由得或；∴当或时，．16.解：(1)把M的纵坐标代入8x281＋y236＝1，得8x281＋436＝1，即x2＝9.∴x＝±3.故M的横坐标.(2)对于椭圆x29＋y24＝1，焦点在x轴上且c2＝9－4＝5，故设所求椭圆的方程为x2a2＋y2a2－5＝1(a2>5)，把M点坐标代入得9a2＋4a2－5＝1，解得a2＝15(a2＝3舍去)．故所求椭圆的方程为x215＋y210＝1.17. 解：（1）因为，所以，又因为，所以，所以，由，得，所以直线的斜率，所以直线的方程为，即．（2）设，则．则，因为，所以，所以点的坐标为又设的外接圆的方程为，则有解之得,,所以的外接圆的方程为，整理得，令，所以（舍）或所以△的外接圆恒过定点为．18.解：（I）如图，AB=40，AC=10，由于0<<,所以cos=由余弦定理得BC=所以船的行驶速度为（海里/小时）.（II）如图所示，以A为原点建立平面直角坐标系，设点B、C的坐标分别是B（x1，y2）, C（x1，y2）,BC与x轴的交点为D.由题设有，x1=y1=AB=40, x2=AC cos,y2=AC sin.所以过点B、C的直线l的斜率k=,直线l的方程为y=2x-40.又点E（0，-55）到直线l的距离d=所以船会进入警戒水域.19.解：（I）由题意可知，圆C的直径为A D，所以，圆C方程为：．当直线垂直于轴时，方程为，不合题意；当直线不垂直于轴时，设方程为：，则，解得，，当时，直线与y轴无交点，不合，舍去．所以，此时直线的方程为．（II）设，由点M在线段A D上，得，即．由AM≤2ＢM，得．依题意知，线段A D与圆至多有一个公共点，故，解得或．因为t是使AM≤2BM恒成立的最小正整数，所以，t=4．所以，圆C方程为：（1）当直线：时，直线的方程为，此时，；（2）当直线的斜率存在时，设的方程为：（），则的方程为：，点．所以，．又圆心Ｃ到的距离为，所以，PQ==故12EPQS BE PQ=⋅==．因为所以，．20.解：（1）（2）由题意可知，在上恒成立，把根式换元之后容易计算出；（3）422()()(1)1h x x f x x bx⎡=++++⎣=0，即，令,方程为，设，，当，即时，只需，此时，；当，即时，只需，即，此时．故的最小值为．20466 4FF2 俲Y22614 5856 塖 25824 64E0 擠NPy36818 8FD2 迒Xr21190 52C6 勆27888 6CF0 泰31013 7925 礥。