(完整版)2018年北京市高考理科数学试题及答案.docx

2018年普通高等学校招生全国统一考试数 学（理）（北京卷）注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合A{x ||x |<2},B{-2,0,1,2},则AB（A ）{0,1} （B ）{-1,0,1}（C ）{-2,0,1,2} （D ）{-1,0,1,2} （2）在复平面内，复数的共轭复数对应的点位于（A ）第一象限 （B ）第二象限（C ）第三象限 （D ）第四象限（3）执行如图所示的程序框图，输出的S 值为 （A ） （B ）（C ）（D ）（4）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献，十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它前一个单音的频率的比都等于，若第一个单音的频率为，则第八个单音的频率为（A ） （B ） （C ）（D ）（5）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（A ） 1 （B ） 2（C ） 3（D ） 4 此卷只装订不密封班级 姓名 准考证号 考场号 座位号（6）设a,b 均为单位向量，则“”是“a”的（A）充分而不必要条件（B）必要而不充分条件（C）充分必要条件（D）既不充分也不必要条件（7）在平面直角坐标系中，记d 为点到直线x 的距离，当m变化时，d的最大值为（A）1（B）2（C）3（D）4(8)设集合A，则（A）对任意实数a ，（B）对任意实数a ，（C）当且仅当a 时，（D）当且仅当a 时，第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分。

2018年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

学科：网第一部分(选择题共40 分)8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

在复平面内，复数丄的共轭复数对应的点位于1 —i5 (B )-67(D )—12(4) “十二平均律”是通用的音律体系，明代朱载埴最早用数学方法计算出半音比例，为这个理论的发展绝密★启用前(1) 已知集合 A={x|| x|<2} , B={E , 0, 1 , 2},则 A B= (A ) {0, 1} (B ) { - , 0, 1}(C )1, 2}(D ) { - , 0, 1, 2}、选择题共 (2) (A ) 第一象限 (B )第二象限 (C ) 第三象限(D )第四象限(3) 执行如图所示的程序框图，输出的s 值为(A ) (C )2 做出了重要贡献•十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每第二部分(非选择题共110 分)一个单音的频率与它的前一个单音的频率的比都等于122 •若第一个单音的频率为 f ，则第八个单音的频率(A )32f(B ) 3 22 f(5)(C )(6) 设a , b 均为单位向量，则“a -3b 二3a b ”是“ a 丄b ”的 充分而不必要条件(B )必要而不(C ) 充分必要条件(D )既不充分也不必要条件(7) 在平面直角坐标系中，记 d 为点P (cos B, si n B)到直线x-my-2=0的距离，当0, m 变化时，d 的 最大值为 (A )(B ) 2 (D ) 4(8) 设集合 A ={( x, y) |x —y 丄1, ax y 4,x —ay 込2},则(A ) 对任意实数 a , (2,1) • A(B )对任意实数a , ( 2, 1)-' A当且仅当a<0时，(2, 1 A3(D )当且仅当^1-时，(2, 1 A(D ) 12 27 f某四棱锥的三视图如图所示,(D ) 4、填空题共6小题，每小题5分，共30分。

绝密★启用前2018年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1. 已知集合A={x||x|<2}，B={–2，0，1，2}，则A B=A. {0，1}B. {–1，0，1}C. {–2，0，1，2}D. {–1，0，1，2}【答案】A【解析】分析：先解含绝对值不等式得集合A，再根据数轴求集合交集.详解：因此A B=，选A.点睛：认清元素的属性，解决集合问题时，认清集合中元素的属性(是点集、数集或其他情形)和化简集合是正确求解的两个先决条件.2. 在复平面内，复数的共轭复数对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】D【解析】分析：将复数化为最简形式，求其共轭复数，找到共轭复数在复平面的对应点，判断其所在象限.详解：的共轭复数为对应点为，在第四象限，故选D.点睛：此题考查复数的四则运算，属于送分题，解题时注意审清题意，切勿不可因简单导致马虎丢分.3. 执行如图所示的程序框图，输出的s值为A. B.C. D.【答案】B【解析】分析：初始化数值，执行循环结构，判断条件是否成立，详解：初始化数值循环结果执行如下：第一次：不成立；第二次：成立，循环结束，输出，故选B.点睛：此题考查循环结构型程序框图，解决此类问题的关键在于：第一，要确定是利用当型还是直到型循环结构；第二，要准确表示累计变量；第三，要注意从哪一步开始循环，弄清进入或终止的循环条件、循环次数.4. “十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于．若第一个单音的频率为f，则第八个单音的频率为A. B.C. D.【答案】D【解析】分析：根据等比数列的定义可知每一个单音的频率成等比数列，利用等比数列的相关性质可解. 详解：因为每一个单音与前一个单音频率比为，所以，又，则故选D.点睛：此题考查等比数列的实际应用，解决本题的关键是能够判断单音成等比数列. 等比数列的判断方法主要有如下两种：（1）定义法，若（）或（），数列是等比数列；（2）等比中项公式法，若数列中，且（），则数列是等比数列.5. 某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为A. 1B. 2C. 3D. 4【答案】C【解析】分析：根据三视图还原几何体，利用勾股定理求出棱长，再利用勾股定理逆定理判断直角三角形的个数.详解：由三视图可得四棱锥，在四棱锥中，，由勾股定理可知：，则在四棱锥中，直角三角形有：共三个，故选C.点睛：此题考查三视图相关知识，解题时可将简单几何体放在正方体或长方体中进行还原，分析线面、线线垂直关系，利用勾股定理求出每条棱长，进而可进行棱长、表面积、体积等相关问题的求解.6. 设a，b均为单位向量，则“”是“a⊥b”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】C【解析】分析：先对模平方，将等价转化为0，再根据向量垂直时数量积为零得充要关系.详解：，因为a，b均为单位向量，所以a⊥b，即“”是“a⊥b”的充分必要条件.选C.点睛：充分、必要条件的三种判断方法．1．定义法：直接判断“若则”、“若则”的真假．并注意和图示相结合，例如“⇒”为真，则是的充分条件．2．等价法：利用⇒与非⇒非，⇒与非⇒非，⇔与非⇔非的等价关系，对于条件或结论是否定式的命题，一般运用等价法．3．集合法：若⊆，则是的充分条件或是的必要条件；若＝，则是的充要条件．7. 在平面直角坐标系中，记d为点P（cosθ，sinθ）到直线的距离，当θ，m变化时，d的最大值为A. 1B. 2C. 3D. 4【答案】C【解析】分析：P为单位圆上一点，而直线过点A（2，0），则根据几何意义得d的最大值为OA+1.详解：P为单位圆上一点，而直线过点A（2，0），所以d的最大值为OA+1=2+1=3,选C.点睛：与圆有关的最值问题主要表现在求几何图形的长度、面积的最值，求点到直线的距离的最值，求相关参数的最值等方面．解决此类问题的主要思路是利用圆的几何性质将问题转化．8. 设集合则A. 对任意实数a，B. 对任意实数a，（2，1）C. 当且仅当a<0时，（2，1）D. 当且仅当时，（2，1）【答案】D【解析】分析：求出及所对应的集合，利用集合之间的包含关系进行求解.详解：若，则且，即若，则，此命题的逆否命题为：若，则有，故选D.点睛：此题主要结合充分与必要条件考查线性规划的应用，集合法是判断充分条件与必要条件的一种非常有效的方法，根据成立时对应的集合之间的包含关系进行判断. 设，若，则；若，则，当一个问题从正面思考很难入手时，可以考虑其逆否命题形式.第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分。

2018年北京市高考数学试卷（理科）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1．（5分）已知集合A={x||x|＜2}，B={﹣2，0，1，2}，则A∩B=（）A．{0，1}B．{﹣1，0，1}C．{﹣2，0，1，2} D．{﹣1，0，1，2} 2．（5分）在复平面内，复数的共轭复数对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限3．（5分）执行如图所示的程序框图，输出的s值为（）A．B．C．D．4．（5分）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献，十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于．若第一个单音的频率为f，则第八个单音的频率为（）A． f B． f C． f D．f5．（5分）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（）A．1 B．2 C．3 D．46．（5分）设，均为单位向量，则“|﹣3|=|3+|”是“⊥”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件7．（5分）在平面直角坐标系中，记d为点P（cosθ，sinθ）到直线x﹣my﹣2=0的距离．当θ、m变化时，d的最大值为（）A．1 B．2 C．3 D．48．（5分）设集合A={（x，y）|x﹣y≥1，ax+y＞4，x﹣ay≤2}，则（）A．对任意实数a，（2，1）∈A B．对任意实数a，（2，1）∉AC．当且仅当a＜0时，（2，1）∉A D．当且仅当a≤时，（2，1）∉A二、填空题共6小题，每小题5分，共30分。

9．（5分）设{a n}是等差数列，且a1=3，a2+a5=36，则{a n}的通项公式为．10．（5分）在极坐标系中，直线ρcosθ+ρsinθ=a（a＞0）与圆ρ=2cosθ相切，则a=．11．（5分）设函数f（x）=cos（ωx﹣）（ω＞0），若f（x）≤f（）对任意的实数x都成立，则ω的最小值为．12．（5分）若x，y满足x+1≤y≤2x，则2y﹣x的最小值是．13．（5分）能说明“若f（x）＞f（0）对任意的x∈（0，2]都成立，则f（x）在[0，2]上是增函数”为假命题的一个函数是．14．（5分）已知椭圆M：+=1（a＞b＞0），双曲线N：﹣=1．若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，则椭圆M的离心率为；双曲线N的离心率为．三、解答题共6小题，共80分。

绝密★启用前2018年普通高等学校招生全国统一考试数学(理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效.考试结束后，将本试卷和答题卡一并交回。

学科：网第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中,选出符合题目要求的一项。

（1）已知集合A={x|｜x｜〈2｝，B=｛–2，0，1，2｝，则A B=（A）｛0,1} (B)｛–1，0，1｝（C）｛–2，0,1,2｝（D）{–1，0，1，2｝（2）在复平面内,复数11i的共轭复数对应的点位于（A）第一象限（B)第二象限（C)第三象限（D）第四象限（3）执行如图所示的程序框图，输出的s值为（A）12（B）56（C)76（D）712(4）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于122．若第一个单音的频率为f ，则第八个单音的频率为 （A)32f （B ）322f （C ）1252f（D ）1272f（5）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（A ）1 （B ）2 （C ）3（D ）4（6）设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的 （A)充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件(D ）既不充分也不必要条件（7）在平面直角坐标系中,记d 为点P （cos θ，sin θ)到直线20x my --=的距离，当θ，m 变化时，d 的最大值为 （A)1 （B)2 （C ）3（D ）4（8）设集合{(,)|1,4,2},A x y x y ax y x ay =-≥+>-≤则 （A)对任意实数a ,(2,1)A ∈（B ）对任意实数a ,（2，1）A ∉（C ）当且仅当a <0时，（2,1）A ∉ （D ）当且仅当32a ≤时，（2，1)A ∉ 第二部分(非选择题 共110分）二、填空题共6小题,每小题5分，共30分。

2018年普通高等学校招生全国统一考试数 学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回.第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分.1. 已知集合，，则 ( ){}2|<=x x A {}2,1,0,2-=B =⋂B A .A {}1,0.B {}1,0,1-.C {}2,1,0,2-.D {}2,1,0,1-2. 在复平面内，复数的共轭复数对应的点位于( )i-11第一象限第二象限 第三象限第四象限.A .B .C .D 3. 执行如图所示的程序框图，输出的值为()s.A 21.B 65.C 67.D 127s4.“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于．若第一个单音的频率为，则第八个单音的频率122f 为( ).A f 32.B f 322.C f 1252.D f12725. 某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为()12 34.A .B .C .D 6. 设a ，b 均为单位向量，则“”是“a ⊥b ”的()33-=+a b a b充分而不必要条件 必要而不充分条件 充分必要条件既不充分也不必要条件.A .B .C .D 7. 在平面直角坐标系中，记为点到直线的距离，当变化时，的最d ()θθsin ,cos P 02=--my x m ,θd 大值为()1234.A .B .C .D 8. 设集合，则( )(){}2,4,1|,≤->+≥-=ay x y ax y x y x A 对任意实数，对任意实数，.A a ()A∈1,2.B a ()A∉1,2当且仅当时，当且仅当时，.C 0<a ()A∉1,2.D 23≤a ()A ∉1,2第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分.9. 设是等差数列，且，，则的通项公式为__________．{}n a 31=a 3652=+a a {}n a 10.在极坐标系中，直线与圆相切，则_________．()0sin cos >=+a a θρθρθρcos 2==a 11. 设函数，若对任意的实数都成立，则的最小值为()()06cos >⎪⎭⎫⎝⎛-=ωπωx x f ()⎪⎭⎫⎝⎛≤4πf x f x ω__________．12.若，满足，则的最小值是__________．x y x y x 21≤≤+x y -213.能说明“若对任意的都成立，则在上是增函数”为假命题的一个函数()()0f x f >]2,0(∈x ()x f []2,0是__________．14. 已知椭圆，双曲线，若双曲线的两条渐近线与椭圆()01:2222>>=+b a b y a x M 1:2222=-ny m x N N 的四个交点及椭圆的两个焦点恰为一个正六边形的顶点，则椭圆的离心率为__________；双曲M M M 线的离心率为__________．N 3、解答题共6小题，共80分。

2018年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

学科：网第一部分（选择题共40 分）、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一 项。

已知集合 A={x||x|<2}, B={ -, 0, 1 , 2}，则 A B={乞，0, 1, 2}1在复平面内，复数——的共轭复数对应的点位于1 —i（D ）第四象限(A)绝密★启用前(3) 执行如图所示的程序框图，输出的s 值为(C )(D)7 12(A) {0 , 1} (B) { -, 0, 1}(1) (2)(D) { - , 0, 1, 2} (A) 第一象限（B ）第二象限第三象限(B)(4) “十二平均律”是通用的音律体系，明代朱载埴最早用数学方法计算出半音比例，为这个理论 的发展做出了重要贡献•十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二 个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122 •若第一个单音的频率为 f ,则第八个单音的频率为(B) 3 22 f(14)已知椭圆M :冷 爲 -1(a b 0)，双曲线N:二-笃=1 .若双曲线N 的两条渐近线与椭圆(A) 32f(A)(5)(D) 12 27 f左〉视圏2(C ) 3(6)设a , b 均为单位向量，则“ a -3b = 3a b ”是“ a 丄b ”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件(7)在平面直角坐标系中，记 d 为点P (cos B, si n B)到直线x —my —2=0的距离，当9, m 变化时,(B) 2(D)4设集合 A 二{( x, y) |x-y 亠1,ax y 4,x-ay 二2},则a b m nM 的四个交点及椭圆 M 的两个焦点恰为一个正六边形的顶点，则椭圆 M 的离心率为 ___________________ 双曲线N 的离心率为 _____________ .三、解答题共6小题，共80分。

绝密★启用前2018年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

学科：网第一部分(选择题共40分)一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

(1 )已知集合A={x|X|<2} , B={ -, 0, 1, 2}，则A p|B=(A ) {0 , 1} ( B) { -, 0, 1}(C) { 2 0, 1 , 2} ( D) { -1, 0, 1 , 2}(2)在复平面内，复数丄的共轭复数对应的点位于1 —i(A)第一象限(B)第二象限(C)第三象限(D)第四象限(3)执行如图所示的程序框图，输出的s值为(A) (C) (B) (D)7_125(4)“十二平均律”是通用的音律体系，明代朱载埴最早用数学方法计算出半音比例，为这个理论的发展、填空题共6小题，每小题5分，共30分。

做出了重要贡献•十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每 一个单音的频率与它的前一个单音的频率的比都等于 122 •若第一个单音的频率为 f ，则第八个单音的频率为 (A ) 32f( B ) 32^f(C ) 12.25f( D ) 1227f(5) 某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为(B) 2(D) 4(6) 设a , b 均为单位向量，则“ a -3b = 3a b ”是“ a 丄b ”的 (A )充分而不必要条件 (B )必要而不充分条件(C) 充分必要条件(D )既不充分也不必要条件(7)在平面直角坐标系中，记 d 为点P (cos 0, sin 0)到直线x —my —2=0的距离，当9, m变化时，d 的 最大值为 (A ) 1 (B ) 2 (C ) 3(D ) 4(8)设集合 A 二{(x,y)|x — y _1,ax y 4, x — ay 込2},则(A )对任意实数 a , (2,1) • A (B )对任意实数a , (2, 1 )■' A(C )当且仅当a<0时，(2, 1A(D )当且仅当a J 时，(2, 1) A2(A) 1(C ) 3正(主)视图 ffi (左〉视圏第二部分(非选择题共110分)、填空题共6小题，每小题5分，共30分。

绝密★启用前2018年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合A={x||x|<2}，B={–2，0，1，2}，则A B=（A）{0，1} （B）{–1，0，1}（C）{–2，0，1，2} （D）{–1，0，1，2}（2）在复平面内，复数11i的共轭复数对应的点位于（A）第一象限（B）第二象限（C）第三象限（D）第四象限（3）执行如图所示的程序框图，输出的s值为（A）12（B）56（C）76（D）712（4）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122．若第一个单音的频率为f ，则第八个单音的频率为 学&科网 （A ）32f （B ）322f （C ）1252f（D ）1272f（5）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（A ）1 （B ）2 （C ）3（D ）4（6）设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件（7）在平面直角坐标系中，记d 为点P （cos θ，sin θ）到直线20x my --=的距离，当θ，m 变化时，d 的最大值为 （A ）1 （B ）2 （C ）3（D ）4（8）设集合{(,)|1,4,2},A x y x y ax y x ay =-≥+>-≤则（A ）对任意实数a ，(2,1)A ∈（B ）对任意实数a ，（2，1）A ∉ （C ）当且仅当a <0时，（2，1）A ∉（D ）当且仅当32a ≤时，（2，1）A ∉ 第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

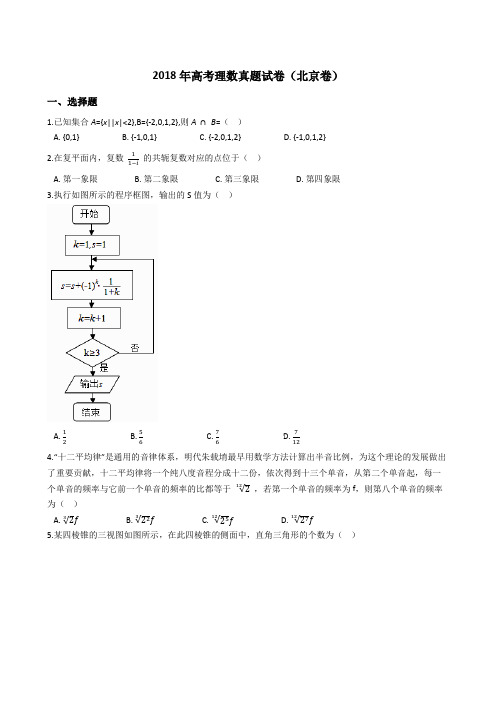
2018年高考理数真题试卷（北京卷）一、选择题1.已知集合A ={x ||x |<2},B={-2,0,1,2},则A ∩ B =（ ） A. {0,1} B. {-1,0,1} C. {-2,0,1,2} D. {-1,0,1,2}2.在复平面内，复数 11−i 的共轭复数对应的点位于（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3.执行如图所示的程序框图，输出的S 值为（ ）A. 12B. 56C. 76D. 7124.“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献，十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它前一个单音的频率的比都等于 √212 ，若第一个单音的频率为f ，则第八个单音的频率为（ ）A. √23fB. √223fC. √2512fD. √2712f5.某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（ ）A. 1B. 2C. 3D. 46.设a,b均为单位向量，则“ |a−3b|=|3a+b|”是“a⊥b”的（）A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件7.在平面直角坐标系中，记d为点ρ(cosθ,sinθ)到直线x-my-2=0的距离，当θ，m变化时，d的最大值为（）A. 1B. 2C. 3D. 48.设集合A= {(x,y)|x−y≥1,ax+y>4,x−ay≤2}，则（）A. 对任意实数a，(2,1)∈AB. 对任意实数a，(2,1)∉AC. 当且仅当a<0时，(2,1)∉AD. 当且仅当a ≤32时，(2,1)∉A二、填空题9.设{a n}是等差数列，且a1=3, a2+a5= 36，则{a n}的通项公式为________10.在极坐标系中，直线ρcosθ+ρsinθ=a(a>0)与圆ρ=2 cosθ相切，则a=________11.设函数f(x)= cos(ωx−π6)(ω>0)，若f(x)≤f(π4)对任意的实数x都成立，则ω的最小值为________12.若x,y满足x+1 ≤y≤2x,则2y - x的最小值是________13.能说明“若f(x)>f(0)对任意的x ∈(0,2]都成立，则f(x)在[0,2]上是增函数”为假命题的一个函数是________14.已知椭圆M:x2a2+y2b2=1(a>b>0),双曲线N:x2m2−y2n2=1. 若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，则椭圆M的离心率为________；双曲线N的离心率为________三、解答题15.在△ABC中，a=7,b=8,cos B=- 17，（Ⅰ）求∠A ：（Ⅱ）求AC 边上的高。

绝密★启用前2018年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40 分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

A. {0 , 1} B. { -1, 0, 1}C. { 2 0, 1, 2}D. { -1 , 0, 1 , 2} 【答案】A【解析】分析：先解含绝对值不等式得集合 详解：■■-二因此 A B-二 二一,::，选 A.点睛：认清元素的属性，解决集合问题时，认清集合中元素的属性 （是点集、数集或其他情形）和化简集合是正确求解的两个先决条件 •12.在复平面内，复数——的共轭复数对应的点位于1-1A.第一象限B. 第二象限C.第三象限D.第四象限【答案】D【解析】分析：将复数化为最简形式，求其共轭复数，找到共轭复数在复平面的对应点，判断其所在象限D. 点睛：此题考查复数的四则运算，属于送分题，解题时注意审清题意，切勿不可因简单导致马虎丢分A ，再根据数轴求集合交集2弓的共轭复数为详解:1 I i在第四象限，故选3.执行如图所示的程序框图，输出的s值为C.【答案】B【解析】分析：初始化数值：，.「：，执行循环结构，判断条件是否成立， 详解：初始化数值-1.1-1循环结果执行如下：.I I、第一次：•「：-「，.…-•不成立;12 15第二次：• '- •成立，236循环结束，输出=- 6故选B.点睛：此题考查循环结构型程序框图，解决此类问题的关键在于：第一，要确定是利用当型还是直到 型循环结构；第二，要准确表示累计变量；第三，要注意从哪一步开始循环，弄清进入或终止的循环 条件、循环次数• 4•“十二平均律”是通用的音律体系 ，明代朱载埴最早用数学方法计算出半音比例 ，为这个理论的发展做 出了重要贡献•十二平均律将一个纯八度音程分成十二份 ,依次得到十三个单音，从第二个单音起，每- 个单音的频率与它的前一A.B.开始7个单音的频率的比都等于：.若第一个单音的频率为f,则第八个单音的频率为A. .B.C. D.【答案】D【解析】分析：根据等比数列的定义可知每一个单音的频率成等比数列，利用等比数列的相关性质可解.详解：因为每一个单音与前一个单音频率比为：，所以?, - ■,•; i：'.■.I l 八:..又，则•：.：； =十：：.■:, - i故选D.点睛：此题考查等比数列的实际应用，解决本题的关键是能够判断单音成等比数列.等比数列的判断方法主要有如下两种：" ] 日（1）定义法，若•（、“匚、.）或Ci .1二.1 ：-，.），数列是等比数列；a ll 斗】-1（2）等比中项公式法，若数列中，且.,| 则数列是等比数列•5.某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为1 I ■adj N ）詞正（主）视图侧（左）规图A. 1B. 2C. 3D. 4【答案】C【解析】分析：根据三视图还原几何体，利用勾股定理求出棱长，再利用勾股定理逆定理判断直角三角形的个数•详解：由三视图可得四棱锥m在四棱锥厂⑴：门中n = • • 2由勾股定理可知：u' 、「、则在四棱锥中，直角三角形有:共三个,故选C.ft点睛：此题考查三视图相关知识，解题时可将简单几何体放在正方体或长方体中进行还原，分析线面、线线垂直关系，利用勾股定理求出每条棱长，进而可进行棱长、表面积、体积等相关问题的求解6•设a, b均为单位向量，则“b-闷- ”是“ a丄b”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】C【解析】分析：先对模平方，将b-砌-等价转化为0，再根据向量垂直时数量积为零得充要关系.详解：■ .：、；.i ■'. ；•，，.| 卜，—■- |■.- |-- - -, | ■- ■',因为a, b均为单位向量，所以/ -.I- - - ■.■ ■. ■ ■■ •- 卜，一a] b,即“ …'、”是“ a丄b”的充分必要条件.选C.点睛：充分、必要条件的三种判断方法.1.定义法：直接判断“若.•则”、“若•.则"的真假.并注意和图示相结合，例如“ ？为真，则是的充分条件.2•等价法：利用？•.与非•.?非」，? .•与非」?非?与非？非的等价关系，对于条件或结论是否定式的命题，一般运用等价法.3 .集合法：若？，则是的充分条件或是的必要条件；若 =，则是的充要条件.7. 在平面直角坐标系中，记d为点P (cos 0 sin )到直线5厂2=0的距离,当0, m变化时，d的最大值为A. 1B. 2C. 3D. 4【答案】C【解析】分析：P为单位圆上一点，而直线二-叱一―：过点A（2, 0）,则根据几何意义得d的最大值为OA+1. 详解：｛「、、'、..「P为单位圆上一点，而直线〉“过点A （2，0），所以d的最大值为OA+仁2+仁3,选C.点睛：与圆有关的最值问题主要表现在求几何图形的长度、面积的最值，求点到直线的距离的最值，求相关参数的最值等方面•解决此类问题的主要思路是利用圆的几何性质将问题转化.8. 设集合•■- •■- -:则A.对任意实数a, ；B. 对任意实数a,（2, 1）-C.当且仅当a<0时，（2, 1）D. 当且仅当时，（2, 1）-2【答案】D【解析】分析：求出：及；所对应的集合，利用集合之间的包含关系进行求解详解：若，，则•且，即若，，则 ,2 23此命题的逆否命题为：若，则有、，故选D.2点睛：此题主要结合充分与必要条件考查线性规划的应用，集合法是判断充分条件与必要条件的一种非常有效的方法，根据|・|成立时对应的集合之间的包含关系进行判断•设\ : x :"' x：：. I ■■ : \ '..I1|:，若■ L 1\则I- :-1；若&-三，则| .1,当一个问题从正面思考很难入手时，可以考虑其逆否命题形式•第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分。

绝密★启用前2018年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合A={x||x|<2}，B={–2，0，1，2}，则A B=（A）{0，1} （B）{–1，0，1}（C）{–2，0，1，2} （D）{–1，0，1，2}（2）在复平面内，复数11i的共轭复数对应的点位于（A）第一象限（B）第二象限（C）第三象限（D）第四象限（3）执行如图所示的程序框图，输出的s值为（A）12（B）56（C）76（D）712（4）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122．若第一个单音的频率为f ，则第八个单音的频率为 （A ）32f （B ）322f （C ）1252f（D ）1272f（5）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（A ）1 （B ）2 （C ）3（D ）4（6）设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件（7）在平面直角坐标系中，记d 为点P （cos θ，sin θ）到直线20x my --=的距离，当θ，m 变化时，d 的最大值为 （A ）1 （B ）2 （C ）3（D ）4（8）设集合{(,)|1,4,2},A x y x y ax y x ay =-≥+>-≤则（A ）对任意实数a ，(2,1)A ∈（B ）对任意实数a ，（2，1）A ∉ （C ）当且仅当a <0时，（2，1）A ∉（D ）当且仅当32a ≤时，（2，1）A ∉ 第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

绝密★启用前2018年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试 结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40 分）、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

已知集合 A={x|X|<2} , B={ -, 0, 1, 2}，则 A p|B=(2) (3) (A) {0 , 1}(C ) { z 0, 1,在复平面内，复数 （A ）第一象限 （C ）第三象限2} 丄的共轭复数对应的点位于1 —i执行如图所示s 值为(B ) (D) (B ) (D) { -1, 0, 1}{ - , 0, 1 , 2}第二象限第四象限1(A) 丄2(B )(C) 7(D)7 12(1)(4)“十二平均律”是通用的音律体系，明代朱载埴最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于122 •若第一个单音的频率为的频率为(A) 32f ( B) 3.2^f最大值为(A) 1 ( B) 2(C) 3 ( D) 4(8)设集合 A ={( x, y) |x—y 亠1,ax y 4,x—ay 込2},则(A)对任意实数a, (2,1)，A ( B)对任意实数a, (2, 1) A3(C)当且仅当a<0时，(2, 1)-' A ( D )当且仅当a乞3时，(2, 1) A 2第二部分(非选择题共110分) f,则第八个单(5)(C) 1225 f(A) 1(B)(C) 3 (D)(6)设a, b均为单位向量，则a - 3b = 3a b ”是“ a 丄b” 的(A)充分而不必要条件(B) 必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件(7)在平面直角坐标系中，记d为点P (cos 0, si n B)到直线x—my—2=0的距离，当0:m变化时，d的(D) 12 27 f某四棱锥的三视图如图所示,恻(左〉现圏正(主)视團、填空题共6小题，每小题5分，共30分。

绝密★启用前2018年普通高等学校招生全国统一考试数 学（理）（北京卷）第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合A ={x ||x |<2}，B ={–2，0，1，2}，则AB =（A ）{0，1}（B ）{–1，0，1} （C ）{–2，0，1，2}（D ）{–1，0，1，2}（2）在复平面内，复数11i-的共轭复数对应的点位于 （A ）第一象限（B ）第二象限 （C ）第三象限（D ）第四象限（3）执行如图所示的程序框图，输出的s 值为（A ）12（B ）56 （C ）76（D ）712（4）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122．若第一个单音的频率为f ，则第八个单音的频率为 学&科网 （A ）32f（B ）322f （C ）1252f （D ）1272f（5）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（A ）1（B ）2 （C ）3（D ）4（6）设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件（7）在平面直角坐标系中，记d 为点P （cos θ，sin θ）到直线20x my --=的距离，当θ，m 变化时，d 的最大值为 （A ）1（B ）2 （C ）3（D ）4（8）设集合{(,)|1,4,2},A x y x y ax y x ay =-≥+>-≤则（A ）对任意实数a ，(2,1)A ∈（B ）对任意实数a ，（2，1）A ∉ （C ）当且仅当a <0时，（2，1）A ∉（D ）当且仅当32a ≤时，（2，1）A ∉ 第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。