最新七年级数学下册《相交线与平行线》证明题

人教版七年级数学下册第五章相交线与平行线：几何计算和证明综合练习试题1、如图，已知∠2＝∠3，∠C＝∠D，求证：∠A＝∠F.证明：∵∠2＝∠3，∠1＝∠2，∴∠1＝∠3.∴DB∥CE.∴∠DBA＝∠C.∵∠D＝∠C，∴∠D＝∠DBA.∴DF∥AC.∴∠A＝∠F.2、如图，已知EF∥AD，∠1＝∠2，∠BAC＝80°，求∠AGD的度数．解：∵EF∥AD，∴∠2＝∠3(两直线平行，同位角相等)．∵∠1＝∠2，∴∠1＝∠3(等量代换)．∴AB∥DG(内错角相等，两直线平行)．∴∠BAC＋∠AGD＝180°(两直线平行，同旁内角互补)．3、如图，∠1＝115°，∠2＝50°，∠3＝65°，EG为∠NEF的平分线．求证：AB∥CD，EG∥FH.证明：∵∠1＝115°，∴∠FCD＝180°－∠1＝180°－115°＝65°.∵∠3＝65°，∴∠FCD＝∠3.∴AB∥CD.∵∠2＝50°，∴∠NEF＝180°－∠2＝180°－50°＝130°.∵EG为∠NEF的平分线，∴∠GEF＝12∠NEF＝65°.∴∠GEF＝∠3.∴EG∥FH.4、如图，已知∠B＝∠D，∠E＝∠F，判断BC与AD的位置关系，并说明理由．解：BC∥AD，理由：∴BE∥FD.∴∠B＝∠BCF.又∵∠B＝∠D，∴∠BCF＝∠D.∴BC∥AD.5、如图，AD⊥BC于点D，EG⊥BC于点G，∠E＝∠1.求证：AD平分∠BAC.证明：∵AD⊥BC，EG⊥BC，∴∠ADC＝∠EGC＝90°.∴AD∥EG.∴∠1＝∠2，∠E＝∠3.∵∠E＝∠1，∴∠2＝∠3.∴AD平分∠BAC.6、如图，B，C，E三点在一条直线上，A，F，E三点在一条直线上，AB∥CD，∠1＝∠2，∠3＝∠4.求证：AD∥BE.证明：∵AB∥CD，∴∠4＝∠BAE.∴∠3＝∠BAE.∵∠1＝∠2，∴∠1＋∠CAF＝∠2＋∠CAF，即∠BAE＝∠CAD.∴∠3＝∠CAD.∴AD∥BE.7、如图，已知AB∥CD，试判断∠B，∠BED和∠D之间的关系，并说明理由．解：∠BED＝∠B＋∠D.理由如下：过点E作EF∥AB，则∠B＝∠BEF.∵AB∥CD，∴EF∥CD.∴∠DEF＝∠D.∵∠BED＝∠BEF＋∠DEF，∴∠BED＝∠B＋∠D.8、如图，∠AEF＋∠CFE＝180°，∠1＝∠2，EG与HF平行吗？为什么？解：平行．理由：∵∠AEF＋∠CFE＝180°，∴AB∥CD.∴∠AEF＝∠EFD.∴∠AEF －∠1＝∠EFD －∠2，即∠GEF ＝∠HFE.∴EG ∥HF.9、如图，A ，B ，C 三点在同一直线上，∠1＝∠2，∠3＝∠D ，试判断BD 与CF 的位置关系，并说明理由．解：BD ∥CF.理由如下：∵∠1＝∠2，∴AD ∥BF.∴∠D ＝∠DBF.∵∠3＝∠D ，∴∠3＝∠DBF.∴BD ∥CF.10、如图，∠ABC ＝∠ADC ，BF ，DE 分别是∠ABC ，∠ADC 的平分线，∠1＝∠2，试说明：DC ∥AB.解：∵BF ，DE 分别是∠ABC ，∠ADC 的平分线，∴∠3＝12∠ADC ，∠2＝12∠ABC. ∵∠ABC ＝∠ADC ，∴∠3＝∠2.∵∠1＝∠2，∴∠1＝∠3.∴DC∥AB.11、如图，AD平分∠BAC，AD⊥BC于D，点E，A，C共线，∠DAC＝∠EFA，延长EF 交BC于点G.求证：EG⊥BC.证明：∵AD平分∠BAC，∴∠DAC＝∠DAB.又∵∠DAC＝∠EFA，∴∠DAB＝∠EFA.∴AD∥EG.∴∠ADC＝∠EGD.∵AD⊥BC，∴∠ADC＝90°.∴∠EGD＝90°.∴EG⊥BC.12、已知AB∥CD，点E为AB，CD之外任意一点．(1)如图1，探究∠BED与∠B，∠D的数量关系，并说明理由；(2)如图2，探究∠CDE与∠B，∠BED的数量关系，并说明理由．解：(1)∠B＝∠BED＋∠D.理由如下：过点E作EF∥AB.又∵AB∥CD，∴EF∥AB∥CD.∴∠BEF＝∠B，∠D＝∠DEF.∵∠BEF＝∠BED＋∠DEF，∴∠B＝∠BED＋∠D.(2)∠CDE＝∠B＋∠BED.理由如下：过点E作EF∥AB.又∵AB∥CD，∴EF∥AB∥CD.∴∠B＋∠BEF＝180°，∠CDE＋∠DEF＝180°.又∵∠DEF＝∠BEF－∠BED，∴∠CDE＋∠BEF－∠BED＝∠B＋∠BEF，即∠CDE＝∠B＋∠BED.13、如图，把一张长方形纸片ABCD沿EF折叠后，D，C分别落在D′和C′的位置上，ED′与BC的交点为G.若∠EFG＝50°，求∠1，∠2，∠3的度数．解：根据折叠的性质可知，∠DEF＝∠D′EF，∠EFC＝∠EFC′.∵∠EFG＝50°，∴∠EFC＝180°－50°＝130°.∴∠EFC′＝∠EFC＝130°.∴∠3＝∠EFC′－∠EFG＝130°－50°＝80°.∵AD∥BC，∴∠DEF＝∠EFG＝50°.∴∠DED′＝2∠DEF＝100°.∴∠1＝180°－∠DED′＝180°－100°＝80°.∵AD∥BC，∴∠1＋∠2＝180°.∴∠2＝180°－∠1＝100°.故∠1＝80°，∠2＝100°，∠3＝80°.14、如图，AE⊥BC，FG⊥BC，∠1＝∠2，∠D＝∠3＋60°，∠CBD＝70°.(1)求证：AB∥CD；(2)求∠C的度数．解：(1)证明：∵AE⊥BC，FG⊥BC，∴AE∥GF.∴∠2＝∠A.∵∠1＝∠2，∴∠1＝∠A.∴AB∥CD.(2)∵AB∥CD，∴∠D＋∠CBD＋∠3＝180°.∵∠D ＝∠3＋60°，∠CBD ＝70°，∴∠3＝25°.∵AB ∥CD ，∴∠C ＝∠3＝25°.15、(1)如图1，AB ∥CD ，则∠E ＋∠G 与∠B ＋∠F ＋∠D 有何关系？(2)如图2，若AB ∥CD ，又能得到什么结论？请直接写出结论．解：(1)过点E 作EM ∥AB ，过点F 作FN ∥AB ，过点G 作GH ∥CD. ∵AB ∥CD ，∴AB ∥EM ∥FN ∥GH ∥CD.∴∠1＝∠B ，∠2＝∠3，∠4＝∠5，∠6＝∠D.∴∠1＋∠2＋∠5＋∠6＝∠B ＋∠3＋∠4＋∠D ，即∠BEF ＋∠FGD ＝∠B ＋∠EFG ＋∠D.(2)∠B ＋∠F 1＋∠F 2＋…＋∠F n －1＋∠D ＝∠E 1＋∠E 2＋…＋∠E n .16、已知E ，F 分别是AB ，CD 上的动点，P 也为一动点．(1)如图1，若AB ∥CD ，求证：∠P ＝∠BEP ＋∠PFD ；(2)如图2，若∠P ＝∠PFD －∠BEP ，求证：AB ∥CD ；(3)如图3，AB ∥CD ，移动E ，F ，使∠EPF ＝90°，作∠PEG ＝∠BEP ，则∠AEG∠PFD ＝2．证明：(1)过点P作PG∥AB，则∠EPG＝∠BEP.∵AB∥CD，∴PG∥CD.∴∠GPF＝∠PFD.∴∠EPF＝∠EPG＋∠FPG＝∠BEP＋∠PFD.(2)过点P作PQ∥AB，则∠QPE＝∠BEP.∵∠EPF＝∠PFD－∠BEP，∴∠PFD＝∠EPF＋∠BEP＝∠EPF＋∠QPE＝∠FPQ. ∴DC∥PQ.∴AB∥CD.。

B CD 4FECD) ) )z Ez )A B z DCz )))))又) 180°)( )又)())ABA BFE和zABC BE DE// 2-82 ))())试说明 z C= z D )) )) 求证AB//EF ))AFD) )BCE)AB// CF ) )z Fz DOF= z CFB EFC 求证CFB= z EDO CF // DO()) ))BD //CE. 匸仁z 2,z_ （ （已知）, 等量代换）)即 z ABC= z BCD z (z 1=z CDE // BO ( z EDO= z DOF ( (求证：BD// CE 5•如图，已知：z BCF= z B+ z F 证明：经过点C 作CD//AB••• BD// CE (3.已知z B =z 证明：•••/ • AB// CD •••/ DGF=z • CD// EF •/ AB// EF • z B + zBC, z ADE=z z BCD= z B 。

(z BCF= z B+ z F ,(已知))=z F o ( 8、已知：如图 z 1 = z 2 证明：••• DE // • z ADE= _ •••/ ADE=z \G D-------- D分别平分z ) ) ) ) )4.已知：如图、BE//CF BCD 求证：AB//CD证明：••• BE 、平分z ABC （已CD//EF o ( AB//EF (证明：••• DE 丄AO , BO 丄AO (已知)z DEA= z BOA=90 0(( 又•••/ C= z D(已知) • z 1 = z C(等量代换)• BD // CE(）F 求证z B +已知） BGD z DGF=z B =z BGD(F ;(已知 ((F = 180 °z 2= - z2 —BE//CF (已知)z 1 = z 2 ( z 仁-z _________2CF 平分z BCD ( 1 1z ABC= z BCD ( 2 2 AB//CD (• DB// EF ( • z 1 = z 2 (9、如图，已知z A= z F 证明：•••/ A= z F(已知)• AC // DF( • z D= z 北师大版七年级下第二章平行线与相交线1.如图，已知直线 EF 与AB CD 都相交，且 AB// CD 说 明z 仁z 2的理由.理由：••• EF 与AB 相交（已知）• z 仁 z 3（ ）•/ AB// CD （已知）• z 2=z 3（ • z 仁z 2（AC// DF (z D=z洞z A =z F ,z C =z D, A =z F (已知)• z 3=z ______ (• AD// BE (7、已知：DE 丄 AO 于 E , BO 丄 AO ，/ CFB= z EDO 试 说明：CF // DO1 2 :B6.已知，如图，BCE AFE 是直线 3=z 4 o 求证：AD// BE= 证明：••• AB// CD (已知)• z 4=z ______ ( 3=z 4 (已知) 3=z _____ ( 1 = z 2 (已知) 1 + z CAF=/ 2+z CAF ( 即z = z BC( —( EFC( ____ (10、如图，已知/ B+ / BCD=180 °,/ B= / D.求证：/ E= / DFE.证明：T/ B+ / BCD=180 ° (已知),• AB // CD().• / B= / DCE ( ).又•••/ B= / D （已知），• / DCE= / D ().• AD // BE().• / E= / DFE ( ).11、如图，已知：/ 1 = / 2，当DE// FH时，（1）证明/ EDA= / HFB ( 2) CD 与FG 有何关系？证明：(1)v DE // FH (已知)，•••/ EDF= / DFH ( ),•••/ EDA= / HFB ( ). (2) I / EDF= / DFH ( ),且/ CDF= / EDF- / 1，/ DFG= / DFH- / 2 , 又•••/仁/ 2 (已知)• CD // FG( 14、如图所示，已知直线EF和, AB,CD 分别相交于K,H,且EG 丄AB, / CHF=60 0,/E=30。

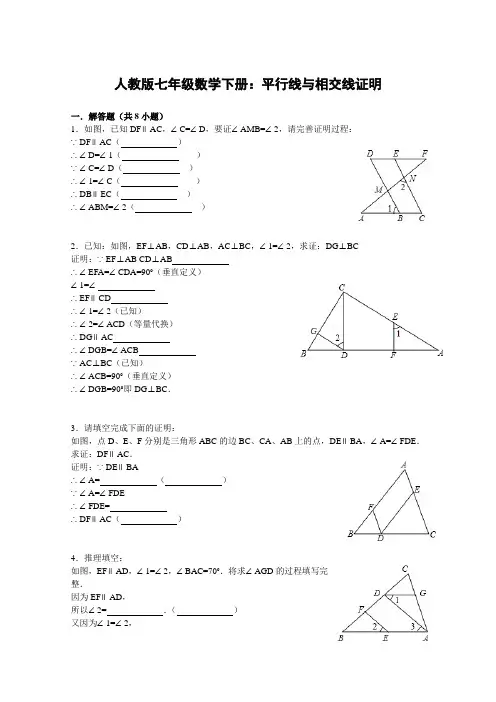
人教版七年级数学下册：平行线与相交线证明一．解答题（共8小题）1．如图，已知DF∥AC，∠C=∠D，要证∠AMB=∠2，请完善证明过程：∵DF∥AC（_________）∴∠D=∠1（_________）∵∠C=∠D（_________）∴∠1=∠C（_________）∴DB∥EC（_________）∴∠ABM=∠2（_________）2．已知：如图，EF⊥AB，CD⊥AB，AC⊥BC，∠1=∠2，求证：DG⊥BC证明：∵EF⊥AB CD⊥AB_________∴∠EFA=∠CDA=90°（垂直定义）∠1=∠_________∴EF∥CD_________∴∠1=∠2（已知）∴∠2=∠ACD（等量代换）∴DG∥AC_________∴∠DGB=∠ACB_________∵AC⊥BC（已知）∴∠ACB=90°（垂直定义）∴∠DGB=90°即DG⊥BC．3．请填空完成下面的证明：如图，点D、E、F分别是三角形ABC的边BC、CA、AB上的点，DE∥BA，∠A=∠FDE．求证：DF∥AC．证明：∵DE∥BA∴∠A=_________（_________）∵∠A=∠FDE∴∠FDE=_________∴DF∥AC（_________）4．推理填空：如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．因为EF∥AD，所以∠2=_________．（_________）又因为∠1=∠2，所以∠1=∠3．（_________）所以AB∥_________．（_________）所以∠BAC+_________=180°（_________）又因为∠BAC=70°，所以∠AGD=_________．5．如图：∠ABC=∠ACB，BD平分∠ABC，CE平分∠ACB，∠DBF=∠F，那么EC与DF平行吗？为什么？请完成下面的解题过程解：∵BD平分∠ABC，CE平分∠ACB （已知）∴∠DBC=∠_________，∠ECB=∠_________∵∠ABC=∠ACB （已知）∴∠_________=∠_________．∠_________=∠_________（已知）∴∠F=∠_________∴EF∥AD_________．6．补全下列推理过程：如图，EF∥AD，∠1=∠2，∠BAC=80°．求∠AGD的度数．因为EF∥AD （已知）所以∠2=_________（_________）又因为∠1=∠2 （已知）所以∠1=∠3（等量代换）所以AB∥_________（_________）所以∠BAC+_________=180°（两直线平行，同旁内角互补）因为∠BAC=80°（已知）所以∠AGD=_________（等量代换）7．完成下面的证明：（1）如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA．求证：∠FDE=∠A．证明：∵DE∥BA，∴∠FDE=_________（_________），∵DF∥CA，∴∠A=_________（_________），∴∠FDE=∠A；（2）如图2，AB和CD相交于点O，∠C=∠COA，∠D=∠BOD，求证：AC∥BD；证明：∵∠C=∠COA，∠D=∠BOD，∵∠COA=∠BOD（_________），∴∠C=_________，∴AC∥BD（_________）．参考答案与试题解析一．解答题（共8小题）1．如图，已知DF∥AC，∠C=∠D，要证∠AMB=∠2，请完善证明过程：∵DF∥AC（已知）∴∠D=∠1（两直线平行，内错角相等）∵∠C=∠D（已知）∴∠1=∠C（等量代换）∴DB∥EC（同位角相等，两直线平行）∴∠ABM=∠2（两直线平行，同位角相等）考点：平行线的判定与性质．专题：推理填空题．分析：先根据平行线的性质由DF∥AC得到∠D=∠1，再根据等量代换得到∠1=∠C，于是可根据平行线的判定方法得到DB∥EC，然后根据平行线的性质得到∠AMB=∠2．解答：证明：∵DF∥AC（已知），∴∠D=∠1（两直线平行，内错角相等），∵∠C=∠D（已知），∴∠1=∠C（等量代换），∴DB∥EC（同位角相等，两直线平行），∴∠AMB=∠2（两直线平行，同位角相等）．故答案为：已知，两直线平行，内错角相等，已知，等量代换，同位角相等，两直线平行，两直线平行，同位角相等．点评：本题考查了平行线的判定与性质：同位角相等，两直线平行；内错角相等，两直线平行；两直线平行，同位角相等；两直线平行，内错角相等．2．已知：如图，EF⊥AB，CD⊥AB，AC⊥BC，∠1=∠2，求证：DG⊥BC 证明：∵EF⊥AB CD⊥AB已知∴∠EFA=∠CDA=90°（垂直定义）∠1=∠ACD∴EF∥CD（两直线平行，同位角相等）∴∠1=∠2（已知）∴∠2=∠ACD（等量代换）∴DG∥AC（内错角相等，两直线平行）∴∠DGB=∠ACB（两直线平行，同位角相等）∵AC⊥BC（已知）∴∠ACB=90°（垂直定义）∴∠DGB=90°即DG⊥BC．考点：平行线的判定与性质；垂线．专题：推理填空题．分析：根据垂直定义求出∠EFA=∠CDA=90°，求出∠1=∠ACD，推出EF∥CD，根据平行线的性质得出∠2=∠ACD，推出DG∥AC，根据平行线的性质推出∠ACB=∠DGB即可．解答：证明：∵EF⊥AB，CD⊥AB（已知），∴∠EFA=∠CDA=90°（垂直定义），∴EF∥CD（同位角相等，两直线平行），∴∠1=∠ACD（两直线平行，同位角相等），∵∠1=∠2（已知），∴∠2=∠ACD（等量代换），∴DG∥AC（内错角相等，两直线平行），∴∠DGB=∠ACB（两直线平行，同位角相等），∵AC⊥CB，∴∠ACB=90°，∴∠DGB=90°，即DG⊥BC，故答案为：已知，ACD，（两直线平行，同位角相等），（内错角相等，两直线平行），（两直线平行，同位角相等）．点评：本题考查了平行线的判定和性质，三角形内角和定理，垂直定义的应用，主要考查学生的推理能力．3．请填空完成下面的证明：如图，点D、E、F分别是三角形ABC的边BC、CA、AB上的点，DE∥BA，∠A=∠FDE．求证：DF∥AC．证明：∵DE∥BA∴∠A=∠DEC（两直线平行，同位角相等）∵∠A=∠FDE∴∠FDE=∠DEC∴DF∥AC（内错角相等，两直线平行）考点：平行线的判定与性质．专题：推理填空题．分析：根据平行线的性质得出∠A=∠DEC，求出∠FDE=∠DEC，根据平行线的判定推出即可．解答：证明：∵DE∥BA，∴∠A=∠DEC（两直线平行，同位角相等），∵∠A=∠FDE（已知），∴∠FDE=∠DEC（等量代换），∴DF∥AC（内错角相等，两直线平行），故答案为：∠DEC，两直线平行，同位角相等；∠DEC，内错角相等，两直线平行．点评：本题考查了平行线的性质和判定的应用，注意：①两直线平行，同位角相等，②内错角相等，两直线平行．4．推理填空：如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．因为EF∥AD，所以∠2=∠3．（两直线平行，同位角相等）又因为∠1=∠2，所以∠1=∠3．（等量代换）所以AB∥DG．（内错角相等，两直线平行）所以∠BAC+∠AGD=180°（两直线平行，同旁内角互补）又因为∠BAC=70°，所以∠AGD=110°．考点：平行线的判定与性质．专题：推理填空题．分析：根据平行线的性质推出∠1=∠2=∠3，推出AB∥DG，根据平行线的性质得出∠BAC+∠DGA=180°，代入求出即可．解答：解：∵EF∥AD，∴∠2=∠3（两直线平行，同位角相等），∵∠1=∠2，∴∠1=∠3（等量代换），∴AB∥DG（内错角相等，两直线平行），∴∠BAC+∠DGA=180°（两直线平行，同旁内角互补），∵∠BAC=70°，∴∠AGD=110°，故答案为：∠3，两直线平行，同位角相等，等量代换，DG，内错角相等，两直线平行，∠AGD，两直线平行，同旁内角互补，110°．点评：本题考查了平行线的性质和判定的应用，注意：平行线的性质是①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．5．如图：∠ABC=∠ACB，BD平分∠ABC，CE平分∠ACB，∠DBF=∠F，那么EC与DF 平行吗？为什么？请完成下面的解题过程解：∵BD平分∠ABC，CE平分∠ACB （已知）∴∠DBC=∠ABC，∠ECB=∠ACB∵∠ABC=∠ACB （已知）∴∠DBC=∠ECB．∠F=∠DBF（已知）∴∠F=∠ECB∴EF∥AD（同位角相等，两直线平行）．考点：平行线的判定．专题：推理填空题．分析：利用角平分线的性质得出∠DBC=∠ABC，∠ECB=∠ACB，进而求出∠F=∠ECB，得出答案即可．解答：解：∵BD平分∠ABC，CE平分∠ACB（已知）∴∠DBC=∠ABC，∠ECB=∠ACB，∵∠ABC=∠ACB （已知）∴∠DBC=∠ECB．∵∠DBF=∠F，（已知）∴∠F=∠ECB，∴EF∥AD（同位角相等，两直线平行）．点评：此题主要考查了平行线的判定以及角平分线的性质，得出∠F=∠ECB是解题关键．6．补全下列推理过程：如图，EF∥AD，∠1=∠2，∠BAC=80°．求∠AGD的度数．因为EF∥AD （已知）所以∠2=∠3（两直线平行，同位角相等）又因为∠1=∠2 （已知）所以∠1=∠3（等量代换）所以AB∥DG（内错角相等，两直线平行）所以∠BAC+∠AGD=180°（两直线平行，同旁内角互补）因为∠BAC=80°（已知）所以∠AGD=100°（等量代换）考点：平行线的判定与性质．专题：推理填空题．分析：根据平行线性质推出∠2=∠3，推出∠1=∠3，根据平行线的判定推出AB∥DG，根据平行线的性质得出∠BAC+∠AGD=180°，代入求出即可．解答：解：∵EF∥AD，∴∠2=∠3（两直线平行，同位角相等），∵∠1=∠2，∴∠1=∠3，∴AB∥DG（内错角相等，两直线平行），∴∠BAC+∠AGD=180°，∵∠BAC=80°，∴∠AGD=100°，故答案为：∠3，两直线平行，同位角相等，DG，内错角相等，两直线平行，∠AGD，100°．点评：本题考查了平行线的性质和判定的应用，注意：平行线的性质是：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．7．完成下面的证明：（1）如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA．求证：∠FDE=∠A．证明：∵DE∥BA，∴∠FDE=∠BFD（两直线平行，内错角相等），∵DF∥CA，∴∠A=∠BFD（两直线平行，同位角相等），∴∠FDE=∠A；（2）如图2，AB和CD相交于点O，∠C=∠COA，∠D=∠BOD，求证：AC∥BD；证明：∵∠C=∠COA，∠D=∠BOD，∵∠COA=∠BOD（对顶角相等），∴∠C=∠D，∴AC∥BD（内错角相等，两直线平行）．考点：平行线的判定与性质．专题：推理填空题．分析：（1）根据平行线的性质得出∠FDE=∠BFD，∠A=∠BFD，推出即可；（2）根据对顶角相等和已知求出∠C=∠D，根据平行线的判定推出即可．解答：（1）证明：∵DE∥BA，∴∠FDE=∠BFD（两直线平行，内错角相等），∵DF∥CA，∴∠A=∠BFD（两直线平行，同位角相等），∴∠FDE=∠A，故答案为：∠BFD，两直线平行，内错角相等，∠BFD，两直线平行，同位角相等；（2）证明：∵∠C=∠COA，∠D=∠BOD，又∵∠COA=∠BOD（对顶角相等），∴∠C=∠D，∴AC∥BD（内错角相等，两直线平行），故答案为：对顶角相等，∠D，内错角相等，两直线平行．点评：本题考查了平行线的性质和判定的应用，注意：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然，题目比较好，难度适中．8．如图，在△ABC中，DE∥BC，连结DC，点F是边BC上一点，GF⊥AB，垂足为G，∠1=∠2，求证：CD⊥AB．考点：平行线的判定与性质；垂线．专题：证明题．分析：求出∠BGF=90°，根据平行线的性质和已知求出∠2=∠BCD，推出FG∥CD，根据平行线的性质得出∠CDB=∠BGF=90°即可．解答：证明：∵FG⊥AB，∴∠BGF=90°，∵DE∥BC，∴∠1=∠BCD，∵∠1=∠2，∴∠2=∠BCD，∴FG∥CD，∴∠CDB=∠BGF=90°，∴CD⊥AB．点评：本题考查了平行线的性质和判定，垂直的定义的应用，主要考查学生的推理能力．。

B CD 4FECD) ) )z Ez )A B z DCz )))))又) 180°)( )又)())ABA BFE和zABC BE DE// 2-82 ))())试说明 z C= z D )) )) 求证AB//EF ))AFD) )BCE)AB// CF ) )z Fz DOF= z CFB EFC 求证CFB= z EDO CF // DO()) ))BD //CE. 匸仁z 2,z_ （ （已知）, 等量代换）)即 z ABC= z BCD z (z 1=z CDE // BO ( z EDO= z DOF ( (求证：BD// CE 5•如图，已知：z BCF= z B+ z F 证明：经过点C 作CD//AB••• BD// CE (3.已知z B =z 证明：•••/ • AB// CD •••/ DGF=z • CD// EF •/ AB// EF • z B + zBC, z ADE=z z BCD= z B 。

(z BCF= z B+ z F ,(已知))=z F o ( 8、已知：如图 z 1 = z 2 证明：••• DE // • z ADE= _ •••/ ADE=z \G D-------- D分别平分z ) ) ) ) )4.已知：如图、BE//CF BCD 求证：AB//CD证明：••• BE 、平分z ABC （已CD//EF o ( AB//EF (证明：••• DE 丄AO , BO 丄AO (已知)z DEA= z BOA=90 0(( 又•••/ C= z D(已知) • z 1 = z C(等量代换)• BD // CE(）F 求证z B +已知） BGD z DGF=z B =z BGD(F ;(已知 ((F = 180 °z 2= - z2 —BE//CF (已知)z 1 = z 2 ( z 仁-z _________2CF 平分z BCD ( 1 1z ABC= z BCD ( 2 2 AB//CD (• DB// EF ( • z 1 = z 2 (9、如图，已知z A= z F 证明：•••/ A= z F(已知)• AC // DF( • z D= z 北师大版七年级下第二章平行线与相交线1.如图，已知直线 EF 与AB CD 都相交，且 AB// CD 说 明z 仁z 2的理由.理由：••• EF 与AB 相交（已知）• z 仁 z 3（ ）•/ AB// CD （已知）• z 2=z 3（ • z 仁z 2（AC// DF (z D=z洞z A =z F ,z C =z D, A =z F (已知)• z 3=z ______ (• AD// BE (7、已知：DE 丄 AO 于 E , BO 丄 AO ，/ CFB= z EDO 试 说明：CF // DO1 2 :B6.已知，如图，BCE AFE 是直线 3=z 4 o 求证：AD// BE= 证明：••• AB// CD (已知)• z 4=z ______ ( 3=z 4 (已知) 3=z _____ ( 1 = z 2 (已知) 1 + z CAF=/ 2+z CAF ( 即z = z BC( —( EFC( ____ (10、如图，已知/ B+ / BCD=180 °,/ B= / D.求证：/ E= / DFE.证明：T/ B+ / BCD=180 ° (已知),• AB // CD().• / B= / DCE ( ).又•••/ B= / D （已知），• / DCE= / D ().• AD // BE().• / E= / DFE ( ).11、如图，已知：/ 1 = / 2，当DE// FH时，（1）证明/ EDA= / HFB ( 2) CD 与FG 有何关系？证明：(1)v DE // FH (已知)，•••/ EDF= / DFH ( ),•••/ EDA= / HFB ( ). (2) I / EDF= / DFH ( ),且/ CDF= / EDF- / 1，/ DFG= / DFH- / 2 , 又•••/仁/ 2 (已知)• CD // FG( 14、如图所示，已知直线EF和, AB,CD 分别相交于K,H,且EG 丄AB, / CHF=60 0,/E=30。

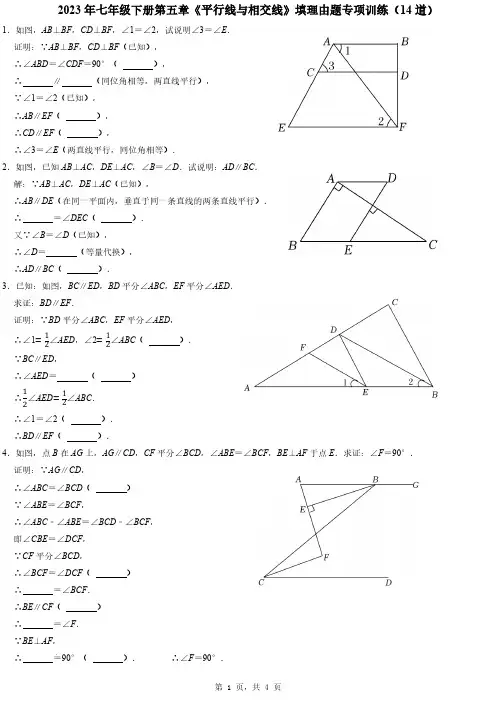
2023年七年级下册第五章《平行线与相交线》填理由题专项训练（14道）1．如图，AB⊥BF，CD⊥BF，∠1＝∠2，试说明∠3＝∠E．证明：∵AB⊥BF，CD⊥BF（已知），∴∠ABD＝∠CDF＝90°（），∴∥（同位角相等，两直线平行），∵∠1＝∠2（已知），∴AB∥EF（），∴CD∥EF（），∴∠3＝∠E（两直线平行，同位角相等）．2．如图，已知AB⊥AC，DE⊥AC，∠B＝∠D．试说明：AD∥BC．解：∵AB⊥AC，DE⊥AC（已知），∴AB∥DE（在同一平面内，垂直于同一条直线的两条直线平行）．∴＝∠DEC（）．又∵∠B＝∠D（已知），∴∠D＝（等量代换），∴AD∥BC（）．3．已知：如图，BC∥ED，BD平分∠ABC，EF平分∠AED．求证：BD∥EF．证明：∵BD平分∠ABC，EF平分∠AED，∴∠1=12∠AED，∠2=12∠ABC（）．∵BC∥ED，∴∠AED＝（）∴12∠AED=12∠ABC．∴∠1＝∠2（）．∴BD∥EF（）．4．如图，点B在AG上，AG∥CD，CF平分∠BCD，∠ABE＝∠BCF，BE⊥AF于点E．求证：∠F＝90°．证明：∵AG∥CD，∴∠ABC＝∠BCD（）∵∠ABE＝∠BCF，∴∠ABC﹣∠ABE＝∠BCD﹣∠BCF，即∠CBE＝∠DCF，∵CF平分∠BCD，∴∠BCF＝∠DCF（）∴＝∠BCF．∴BE∥CF（）∴＝∠F．∵BE⊥AF，5．（2023秋•海口期末）如图，AB∥CD，∠1＝∠A．（1）试说明：AC∥ED；（2）若∠2＝∠3，FC与BD的位置关系如何？为什么？解：（1）∵AB∥CD，（已知）∴∠1＝∠BED，（）又∵∠1＝∠A，（已知）∴∠BED＝∠，（等量代换）∴∥．（）（2）FC与BD的位置关系是：．理由如下：∵AC∥ED，（已知）∴∠2＝∠．（）又∵∠2＝∠3，（已知）∴∠＝∠．（等量代换）∴∥．（）6．已知：如图，在△ABC中，FG∥CD，∠1＝∠3．求证：∠B+∠BDC＝180°．解：因为FG∥CD（已知），所以∠1＝．又因为∠1＝∠3（已知），所以∠2＝（等量代换）．所以BC∥（），所以∠B+∠BDE＝180°（）．7．如图，已知∠D＝108°，∠BAD＝72°，AC⊥BC于C，EF⊥BC于F．求证：∠1＝∠2．证明：∵∠D＝108°，∠BAD＝72°（已知）∴∠D+∠BAD＝180°∴AB∥CD（）∴∠1＝（）又∵AC⊥BC于C，EF⊥BC于F（已知）∴EF∥（）∴∠2＝（）∴∠1＝∠2（）8．如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3＝180°．试说明：∠GDC＝∠B．解：∵AD⊥BC，EF⊥BC（已知）∴∠ADB＝∠EFB＝90°（）∴EF∥AD（）∴+∠2＝180°（）又∵∠2+∠3＝180°（已知）∴∠1＝（）∴∥（）9．（2023秋•丹江口市期末）如图，E、F分别在AB和CD上，∠1＝∠D，∠2与∠C互余，AF⊥CE于G，求证：AB∥CD．证明：∵AF⊥CE（已知），∴∠CGF＝90°（垂直的定义），∵∠1＝∠D（已知），∴AF∥（），∴∠4＝＝90°（），又∵∠2+∠3+∠4＝180°，∴∠2+∠3＝90°，∵∠2与∠C互余（已知），∴∠2+∠C＝90°，∴∠C＝，∴AB∥．（）10．（2023秋•青神县期末）如图，AB与EF交于点B，CD与EF交于点D，根据图形，请补全下面这道题的解答过程．（1）∵∠1＝∠2（已知）∴∥CD（）∴∠ABD+∠CDB＝（）（2）∵∠BAC＝65°，∠ACD＝115°，（已知）∴∠BAC+∠ACD＝180°（等式性质）∴AB∥CD（）（3）∵CD⊥AB于D，EF⊥AB于F，∠BAC＝55°，（已知）∴∠ABD＝∠CDF＝90°（垂直的定义）∴∥（同位角相等，两直线平行）又∵∠BAC＝55°，（已知）∴∠ACD＝．（）11．如图所示，已知∠1+∠2＝180°，∠3＝∠B，试判断∠AED与∠C的大小关系，并说明理由．证明：∵∠1+∠2＝180°（）∠1＝∠DFH（）∴（）∴EH∥AB（）∴∠3＝∠ADE（）∵∠3＝∠B∴∠B＝∠ADE（）∴DE∥BC∴∠AED＝∠C（）12．如图，已知AB∥CD，BE平分∠ABC，DB平分∠CDF，且∠ABC+∠CDF＝180°．求证：BE⊥DB．证明：∵AB∥CD∴∠ABC＝∠BCD（）∵∠ABC+∠CDF＝180°（）∴∠BCD+∠CDF＝180°（）∴BC∥DF（）于是∠DBC＝∠BDF（）∵BE平分∠ABC，DB平分∠CDF∴∠EBC=12∠ABC，∠BDF＝（）∵∠EBC+∠DBC＝∠EBC+∠BDF=12（∠ABC+∠CDF）即∠EBD＝∴BE⊥DB（）13．如图，EF⊥BC，∠1＝∠C，∠2+∠3＝180°，试说明∠ADC＝90°．请完善解答过程，并在括号内填写相应的理论依据．解：∵∠1＝∠C，（已知）∴GD∥．（）∴∠2＝∠DAC．（）∵∠2+∠3＝180°，（已知）∴∠DAC+∠3＝180°．（等量代换）∴AD∥EF．（）∴∠ADC＝∠．（）∵EF⊥BC，（已知）∴∠EFC＝90°．（）∴∠ADC＝90°．（等量代换）14．（2023秋•南关区期末）如图，已知AB∥DC，AC⊥BC，AC平分∠DAB，∠B＝50°，求∠D的大小．阅读下面的解答过程，并填括号里的空白（理由或数学式）．解：∵AB∥DC（），∴∠B+∠DCB＝180°（）．∵∠B＝（已知），∴∠DCB＝180°﹣∠B＝180°﹣50°＝130°．∵AC⊥BC（已知），∴∠ACB＝（垂直的定义）．∴∠2＝．∵AB∥DC（已知），∴∠1＝（）．∵AC平分∠DAB（已知），∴∠DAB＝2∠1＝（角平分线的定义）．∵AB∥DC（已知），∴+∠DAB＝180°（两条直线平行，同旁内角互补）．。

（完整）七年级下数学平行线相交线必背证明题这一部分习题会了，就可以有很大提高了！-------董老师一、（完整）七年级下数学平行线相交线必背证明题二、三、四、编辑整理：五、 六、 七、 八、九、尊敬的读者朋友们：十、这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）七年级下数学平行线相交线必背证明题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

十一、本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快 业绩进步，以下为（完整）七年级下数学平行线相交线必背证明题的全部内容。

十二、十三、平行线之间的基本图1、如图已知，AB∥CD。

,AF CF分别是EAB∠、ECD∠的角平分线，F是两条角平分线的交点；求证：12F AEC∠=∠.2、已知AB//CD,此时A∠、AEF∠、EFC∠和C∠的关系又如何？你能找出其中的规律吗？ED3、将题变为如下图：AB//CDEFD∠和D∠的关系又如何？你能找出其中的规律吗？4、如图，AB//CD，那么AECCA∠∠∠与、有什么关系?D DEC十四、两组平行线的证明题【找出连接两组平行线的角】这一部分习题会了，就可以有很大提高了！-------董老师1。

已知：如图，CD平分∠ACB，AC∥DE，∠DCE=∠FEB,求证：EF平分∠DEB．3、已知：如图2—96，DE⊥AO于E,BO⊥AO，FC⊥AB于C，∠1=∠2，求证：DO⊥AB.3、如图,已知EF⊥AB，∠3=∠B，∠1=∠2，求证：CD⊥AB。

4、已知AD⊥BC，FG⊥BC,垂足分别为D、G，且∠1=∠2，猜想∠BDE与∠C有怎样的大小关系？试说明理由。

三、两组平行线构造平行四边形1．已知：如图，AB是一条直线,∠C= ∠1，∠2和∠D互余,BE⊥FD于G．求证:AB∥CD．ADFBEC这一部分习题会了，就可以有很大提高了！-------董老师这一部分习题会了，就可以有很大提高了！-------董老师2、如图，E 点为DF 上的点,B 为AC 上的点，∠1=∠2，∠C =∠D ，求证DF ∥AC ．3、如图，M 、N 、T 和A 、B 、C 分别在同一直线上,且∠1=∠3，∠P=∠T ，求证:∠M=∠R.四、证特殊角1、AB ∥CD ，∠BAC 的平分线和∠ACD 的平分线交于点E ，则∠AEC 的度数是 ．2、AB CD ∥，直线EF 与AB 、CD 分别相交于E 、F 两点，EP 平分∠AEF ,过点F 作PF EP 垂足为P ，若∠PEF ＝300，则∠PFC ＝_____．ABCDEF1 4 23 (第22题) 图7 图8这一部分习题会了，就可以有很大提高了！-------董老师MN A DBCb21a E 3．已知：如图,AB ∥DE ,CM 平分∠BCE ，CN ⊥CM ．求证：∠B＝2∠DCN ．4.如图已知直线a ∥b ，AB 平分∠MAD ，AC 平分∠NAD ，DE ⊥AC于E ，求证：∠1=∠2．五、寻找角之间的关系1、如图2-97，已知：∠1=∠2，∠3=∠4,∠5=∠6。

平行线与相交线几何证明题专项训练及答案证明题1：平行线与等角线的性质问题描述在平面内给出一组平行线和一条相交线，证明以下性质：如果该相交线与任意一条平行线均成相等角，则该相交线与其它平行线也成相等角。

证明过程已知条件设给出的平行线为l1 和 l2，给出的相交线为l3。

根据已知条件，相交线l3与平行线l1成相等角，即∠A = ∠D（角度A在l1上，角度D在l3上）。

证明目标要证明相交线l3与平行线l2成相等角，即∠B = ∠E（角度B在l2上，角度E在l3上）。

证明过程1.假设相交线l3与平行线l2不成相等角，即∠B ≠ ∠E。

2.在l2上取一点F，并作垂线FG与l1相交于G点。

3.连接点E和G，并延长线段EG与l1和l2相交于H 点。

4.根据平行线的性质，得到∠D = ∠F（对应角相等）和∠A = ∠G（同旁内角相等）。

5.在△DGF和△AEG中，根据三角形内角和定理，得到∠D + ∠F + ∠G = 180°和∠A + ∠E + ∠G = 180°。

6.结合前述结果，得到∠D + ∠F = ∠A + ∠E。

7.根据已知条件，得到∠A = ∠D。

8.结合步骤6和7的结果，得到∠F = ∠E。

9.根据角度相等的定义，得到∠B = ∠E，即相交线l3与平行线l2也成相等角，证明完毕。

答案根据以上证明过程，可以得出结论：如果相交线与一组平行线成等角，那么相交线与其它平行线也成等角。

证明题2：平行线的封闭性问题描述在平面内给出一组平行线，证明以下性质：如果两条平行线的一个夹角与另外一条平行线的一个角相等，则这两条平行线也相等。

证明过程已知条件设给出的平行线为l1 和 l2，给出的夹角为∠A（角度A在l1和l2之间）。

根据已知条件，∠A = ∠B（角度B在l1和另外一条平行线l3之间）。

证明目标要证明l1 = l2，即两条平行线相等。

证明过程1.假设l1 ≠ l2，即l1和l2不相等。

证明题七年级下册一、相交线与平行线证明题。

1. 如图，已知直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，∠2 : ∠1 = 4:1，求∠AOF的度数。

证明：设∠1 = x，因为∠2:∠1 = 4:1，则∠2 = 4x。

因为OE平分∠BOD，所以∠DOE=∠1 = x。

又因为∠2+∠DOE = 180°（邻补角之和为180°），即4x + x=180°，5x = 180°，解得x = 36°。

所以∠COE=180° - ∠1=180° - 36° = 144°。

因为OF平分∠COE，所以∠COF=(1)/(2)∠COE=(1)/(2)×144° = 72°。

∠AOC = ∠1 = 36°（对顶角相等）所以∠AOF=∠AOC + ∠COF = 36°+72° = 108°。

2. 已知：如图，AB∥CD，∠1 = ∠2，求证：AM∥CN。

证明：因为AB∥CD，所以∠EAB = ∠ACD（两直线平行，同位角相等）。

又因为∠1 = ∠2，所以∠EAB - ∠1=∠ACD - ∠2，即∠MAC = ∠NCA。

所以AM∥CN（内错角相等，两直线平行）3. 如图，已知∠1 = ∠2，∠C = ∠D，求证：∠A = ∠F。

证明：因为∠1 = ∠2，∠1 = ∠3（对顶角相等），所以∠2 = ∠3。

所以DB∥EC（同位角相等，两直线平行）。

所以∠D = ∠4（两直线平行，同位角相等）。

又因为∠C = ∠D，所以∠C = ∠4。

所以DF∥AC（内错角相等，两直线平行）。

所以∠A = ∠F（两直线平行，内错角相等）二、三角形证明题。

4. 在△ABC中，AD是BC边上的中线，E是AD的中点，BE的延长线交AC于F。

求证：AF=(1)/(3)AC。

证明：过点D作DG∥BF交AC于G。

七年级下册相交线与平行线练习题及答案第五章相交线与平行线一、典型例题例1.如图1，直线a与b平行，∠1=(3x+70)°，∠2=(5x+22)°，求∠3的度数。

图1例2.已知：如图2，AB∥EF∥CD，EG平分∠XXX，∠B+∠BED+∠D=192°，求∠EGD的度数。

图2例3.如图3，已知AB∥CD，且∠B=40°，∠D=70°，求∠DEB的度数。

图3例4.平面上n条直线两两相交且无3条或3条以上直线共点，有多少个不同交点？例5.6个不同的点，其中只有3点在同一条直线上，2点确定一条直线，问能确定多少条直线？例6.10条直线两两相交，最多将平面分成多少块不同的区域？例7.两条直线相交于一点，所形成的角中有2对对顶角，4对邻补角，那么，三条直线相交于一点时，有多少对对顶角，多少对邻补角？四条直线相交于一点时，有多少对对顶角，多少对邻补角？n条直线相交于一点时，有多少对对顶角，多少对邻补角？二、巩固练1.平面上有5个点，其中仅有3点在同一直线上，过每2点作一条直线，一共可以作直线（）条。

A。

6B。

7C。

8D。

92.平面上三条直线相互间的交点个数是（）。

A。

3B。

1或3C。

1或2或3D。

不一定是1，2，33.平面上6条直线两两相交，其中仅有3条直线过一点，则截得不重叠线段共有（）。

A。

36条B。

33条C。

24条D。

21条4.已知平面中有n个点，A、B、C三个点在一条直线上，A、D、F、E四个点也在一条直线上，除这些之外，再没有三点共线或四点共线，以这n个点作一条直线，一共可以画出38条不同的直线，这时n等于（）。

A。

9B。

10C。

11D。

125.若平行直线AB、CD与相交直线EF、GH相交成如图所示的图形，则共得同旁内角（）。

A。

4对B。

8对C。

12对D。

16对6.如图，已知FD∥BE，则∠1+∠2-∠3=()。

图4A。

90°B。

135°C。

北师大版七年级下第二章平行线与相交线 1.如图，已知直线EF 与AB 、CD 都相交，且AB ∥CD ，说明∠1=∠2的理由. 理由：∵EF 与AB 相交(已知) ∴∠1=∠3( ) ∵AB ∥CD(已知) ∴∠2=∠3( )∴∠1=∠2( )2.如图：已知∠A ＝∠F ，∠C ＝∠D ，求证：BD ∥CE 。

证明：∵∠A ＝∠F （ 已知 ）∴AC ∥DF （ ） ∴∠D＝∠（ ） 又∵∠C ＝∠D （ 已知 ），∴∠1＝∠C （ 等量代换 ） ∴BD∥CE（ ）。

3.已知∠B ＝∠BGD ∠DGF ＝∠F 求证∠B ＋ ∠F ＝180°证明：∵∠B ＝∠BGD （ 已知 ） ∴AB ∥CD（ ）∵∠DGF ＝∠F ；（ 已知 ） ∴CD ∥EF（ ）∵AB ∥EF（）∴∠ B ＋ ∠ F ＝180°（ ）。

4.已知：如图、BE21212121图，已知：∠BCF=∠B+∠F 。

求证：AB 知，如图，BCE 、AFE 是直线，AB ∥CD ，∠1=∠2，∠3=∠4。

求证：AD ∥BE 。

证明：∵AB ∥CD （已知）∴∠4=∠ （ ）321FE DC B A∵∠3=∠4（已知）∴∠3=∠（）∵∠1=∠2（已知）∴∠1+∠CAF=∠2+∠CAF （）即∠ =∠∴∠3=∠（）∴AD∥BE（）7、已知：DE⊥AO于E， BO⊥AO，∠CFB=∠EDO试说明：CF∥DO证明：∵DE⊥AO， BO⊥AO（已知）∴∠DEA=∠BOA=900（）∵DE∥BO （））∴∠EDO=∠DOF （）又∵∠CFB=∠EDO（）∴∠DOF=∠CFB（）∴CF∥DO （））8、已知：如图2-82，DE∥BC，∠ADE＝∠EFC，求证：∠1＝∠2证明：∵ DE∥BC（）∴∠ADE＝______（）∵∠ADE＝∠EFC（）∴______＝______（）∴DB∥EF（）∴∠1＝∠2（）9、如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE.证明：∵∠A=∠F(已知)∴AC∥DF( )∴∠D=∠( )又∵∠C=∠D(已知)∴∠1=∠C(等量代换)∴BD∥CE( )10、如图，已知∠B+∠BCD=180°，∠B=∠D.求证：∠E=∠DFE.证明：∵∠B+∠BCD=180°(已知 ),∴AB∥CD( ).∴∠B=∠DCE（）.又∵∠B=∠D（已知）,∴∠DCE=∠D ( ).∴AD∥BE( ).∴∠E=∠DFE （）.11、如图，已知：∠1=∠2，当DE∥FH时，（1）证明：∠EDA=∠HFB （2）CD与FG 有何关系证明：（1）∵DE∥FH (已知),∴∠EDF=∠DFH ( ),∴∠EDA=∠HFB ( ).(2) ∵∠EDF=∠DFH ( ),且∠CDF=∠EDF-∠1 ,∠DFG=∠DFH-∠2 ,又∵∠1=∠2（已知）,∴CD∥FG( ).12、如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.证明：∵AD⊥BC,EF⊥BC ( ) ∴∠EFB=∠ADB=90° ( )∴EF∥AD( )∴∠1=∠BAD( )DABFGHKF EDC B A 又∵∠1=∠ 2( )∴ （等量代换）∴DG ∥BA.( )13、如图：已知：AD ⊥BC 于D ，EF ⊥BC 于F ，∠1=∠3， 求证 ：AD 平分∠BAC 。

北师大版七年级下第二章平行线与相交线 1.如图，已知直线EF 与AB 、CD 都相交，且AB ∥CD ，说明∠1=∠2的理由. 理由：∵EF 与AB 相交(已知) ∴∠1=∠3( ) ∵AB ∥CD(已知) ∴∠2=∠3( ) ∴∠1=∠2( ) 2.如图：已知∠A ＝∠F ，∠C ＝∠D ，求证：BD ∥CE 。

证明：∵∠A ＝∠F （ 已知 ） ∴AC ∥DF （ ） ∴∠D ＝∠ （ ） 又∵∠C ＝∠D （ 已知 ）， ∴∠1＝∠C （ 等量代换 ） ∴BD ∥CE （ ）。

3.已知∠B ＝∠BGD ∠DGF ＝∠F 求证∠B ＋ ∠F ＝180° 证明：∵∠B ＝∠BGD （ 已知 ） ∴AB ∥CD （ ） ∵∠DGF ＝∠F ；（ 已知 ）∴CD ∥EF （ ）∵AB ∥EF （ ）∴∠B ＋ ∠F ＝180°（ ）。

4.已知：如图、BE//CF ，BE 、CF 分别平分∠ABC 和∠BCD 求证：AB//CD证明：∵BE 、平分∠ABC （已知） ∴∠1=21∠∵CF 平分∠BCD （ ）∴∠2=21∠ （ ） ∵BE//CF （已知）∴∠1=∠2（ ） ∴21∠ABC=21∠BCD （ ）即∠ABC=∠BCD∴AB//CD （ ）5.如图，已知：∠BCF=∠B+∠F 。

求证：AB//EF证明：经过点C 作CD//AB∴∠BCD=∠B 。

（ ）∵∠BCF=∠B+∠F ，（已知） ∴∠ （ ）=∠F 。

（ ） ∴CD//EF 。

（ ） ∴AB//EF （ ）6.已知，如图，BCE 、AFE 是直线，AB ∥CD ，∠1=∠2，∠3=∠4。

求证：AD ∥BE 。

证明：∵AB ∥CD （已知）∴∠4=∠ （ ）∵∠3=∠4（已知） ∴∠3=∠ （ ） ∵∠1=∠2（已知） ∴∠1+∠CAF=∠2+∠CAF （ ） 即∠ =∠ ∴∠3=∠ （ ） ∴AD ∥BE （ ） 7、已知：DE ⊥AO 于E ， BO ⊥AO ，∠CFB=∠EDO 试说明：CF ∥DO 证明：∵DE ⊥AO ， BO ⊥AO （已知） ∴∠DEA=∠BOA=900 （ ）∵DE ∥BO （ ） ） ∴∠EDO=∠DOF （ ） 又∵∠CFB=∠EDO （ ） ∴∠DOF=∠CFB （ ） ∴CF ∥DO （ ） ）8、已知：如图2-82，DE ∥BC ，∠ADE ＝∠EFC ，求证： ∠1＝∠2 证明：∵ DE ∥BC （ ）∴∠ADE ＝______（ ）∵∠ADE ＝∠EFC （ ）∴______＝______（ ） ∴DB ∥EF （ ） ∴∠1＝∠2（ ） 9、如图，已知∠A=∠F ，∠C=∠D ，试说明BD ∥CE. 证明：∵∠A=∠F(已知) ∴AC ∥DF( ) ∴∠D=∠ ( ) A C DFB E 1 2 A D BC E F1 2 34321FED C B AGHKF E DC B A 又∵∠C=∠D(已知) ∴∠1=∠C(等量代换)∴BD ∥CE( )10、如图，已知∠B+∠BCD=180°，∠B=∠D.求证： ∠E=∠DFE.证明：∵∠B+∠BCD=180°(已知 ),∴AB ∥CD( ). ∴∠B=∠DCE （ ）. 又∵∠B=∠D （已知 ）, ∴∠DCE=∠D ( ).∴AD ∥BE( ). ∴∠E=∠DFE （ ）. 11、如图，已知：∠1=∠2，当DE ∥FH 时，（1）证明：∠EDA=∠HFB （2）CD 与FG 有何关系? 证明：（1）∵DE ∥FH (已知),∴∠EDF=∠DFH ( ),∴∠EDA=∠HFB ( ). (2) ∵∠EDF=∠DFH ( ), 且∠CDF=∠EDF-∠1 ,∠DFG=∠DFH-∠2 , 又∵∠1=∠2（已知 ）,∴CD ∥FG( ).12、如图,已知AD ⊥BC,EF ⊥BC,∠1=∠2.求证:DG ∥BA. 证明：∵AD ⊥BC,EF ⊥BC ( ) ∴∠EFB=∠ADB=90° ( ) ∴EF ∥AD( ) ∴∠1=∠BAD( ) 又∵∠1=∠2 ( ) ∴ （等量代换）∴DG ∥BA.( )13、如图：已知：AD ⊥BC 于D ，EF ⊥BC 于F ，∠1=∠3， 求证 ：AD 平分∠BAC 。

北师大版七年级下第二章平行线与相交线1.如图，已知直线EF 与AB 、CD 都相交，且AB ∥CD ，说明∠1=∠2的理由.理由：∵EF 与AB 相交(已知)∴∠1=∠3( )∵AB ∥CD(已知)∴∠2=∠3( )∴∠1=∠2( )2.如图：已知∠A ＝∠F ，∠C ＝∠D ，求证：BD ∥CE 。

证明：∵∠A ＝∠F （ 已知 ）∴AC ∥DF （ ）∴∠D ＝∠ （ ）又∵∠C ＝∠D （ 已知 ），∴∠1＝∠C （ 等量代换 ）∴BD ∥CE （ ）。

∠B ＝∠BGD ∠DGF ＝∠F 求证∠B ＋ ∠F ＝180°证明：∵∠B ＝∠BGD （ 已知 ）∴AB ∥CD （ ）∵∠DGF ＝∠F ；（ 已知 ）∴CD ∥EF （ ）∵AB ∥EF （ ）∴∠B ＋ ∠F ＝180°（ ）。

4.已知：如图、BE//CF ，BE 、CF 分别平分∠ABC 和∠BCD 求证：AB//CD证明：∵BE 、平分∠ABC （已知）∴∠1=21∠ ∵CF 平分∠BCD （ ） ∴∠2=21∠ （ ） ∵BE//CF （已知）∴∠1=∠2（ ） ∴21∠ABC=21∠BCD （ ）即∠ABC=∠BCD ∴AB//CD （ ）5.如图，已知：∠BCF=∠B+∠F 。

求证：AB//EF证明：经过点C 作CD//AB∴∠BCD=∠B 。

（ ）∵∠BCF=∠B+∠F ，（已知）A C DF B E 1 2 321F ED C B A∴∠ （）=∠F 。

（ ）∴CD//EF 。

（ ）∴AB//EF （ ）6.已知，如图，BCE 、AFE 是直线，AB ∥CD ，∠1=∠2，∠3=∠4。

求证：AD ∥BE 。

证明：∵AB ∥CD （已知）∴∠4=∠ （ ）∵∠3=∠4（已知）∴∠3=∠ （ ）∵∠1=∠2（已知）∴∠1+∠CAF=∠2+∠CAF （ ）即∠ =∠∴∠3=∠ （ ）∴AD ∥BE （ ）7、已知：DE ⊥AO 于E ， BO ⊥AO ，∠CFB=∠EDO 试说明：CF ∥DO证明：∵DE ⊥AO ， BO ⊥AO （已知）∴∠DEA=∠BOA=900 （ ）∵DE ∥BO （ ） ）∴∠EDO=∠DOF （ ）又∵∠CFB=∠EDO （ ）∴∠DOF=∠CFB （ ）∴CF ∥DO （ ） ）8、已知：如图2-82，DE ∥BC ，∠ADE ＝∠EFC ，求证：∠1＝∠2证明：∵ DE ∥BC （ ）∴∠ADE ＝______（ ）∵∠ADE ＝∠EFC （ ）∴______＝______（ ）∴DB ∥EF （ ）∴∠1＝∠2（ ）9、如图，已知∠A=∠F ，∠C=∠D ，试说明BD ∥CE.证明：∵∠A=∠F(已知)∴AC ∥DF( )∴∠D=∠ ( )又∵∠C=∠D(已知)∴∠1=∠C(等量代换)A DBC E F 1 2 3 4G H K F E D C BA ∴BD ∥CE( )10、如图，已知∠B+∠BCD=180°，∠B=∠D.求证：∠E=∠DFE.证明：∵∠B+∠BCD=180°(已知 ),∴AB ∥CD( ).∴∠B=∠DCE （ ）.又∵∠B=∠D （已知 ）,∴∠DCE=∠D ( ).∴AD ∥BE( ).∴∠E=∠DFE （ ）.11、如图，已知：∠1=∠2，当DE ∥FH 时，（1）证明：∠EDA=∠HFB （2）CD 与FG 有何关系? 证明：（1）∵DE ∥FH (已知),∴∠EDF=∠DFH ( ),∴∠EDA=∠HFB ( ).(2) ∵∠EDF=∠DFH ( ),且∠CDF=∠EDF-∠1 ,∠DFG=∠DFH-∠2 ,又∵∠1=∠2（已知 ）,∴CD ∥FG( ).12、如图,已知AD ⊥BC,EF ⊥BC,∠1=∠2.求证:DG ∥BA.证明：∵AD ⊥BC,EF ⊥BC ( )∴∠EFB=∠ADB=90° ( )∴EF ∥AD( )∴∠1=∠BAD( )又∵∠1=∠2 ( )∴ （等量代换）∴DG ∥BA.( )13、如图：已知：AD ⊥BC 于D ，EF ⊥BC 于F ，∠1=∠3， 求证 ：AD 平分∠BAC 。

平行线与相交线证明题专项（最终五篇）第一篇：平行线与相交线证明题专项证明题专练二、两组平行线的证明题【找出连接两组平行线的角】1.已知：如图，CD平分∠ACB，AC∥DE，∠DCE=∠FEB，求证：EF平分∠DEB．1、如图已知，AB∥CD.AF,CF分别是∠EAB、∠ECD的角平分线，F是两条角平分线的一、平行线之间的基本图交点；求证：∠F= 1B2∠AEC.E FCDB2、已知AB//CD，此时∠A、∠AEF、∠EFC和∠C的关系又如何？你能找出其中的规律吗？ ED3、将题变为如下图：AB//CD此时∠A、∠AEF、∠EFD和∠D的关系又如何？你能找出其中的规律吗？CD4、如图，AB//CD，那么∠A、∠C与∠AEC有什么关系？ ECDEC E B3、已知：如图2-96,DE⊥AO于E,BO⊥AO,FC⊥AB于C，∠1=∠2,求证：DO⊥AB.三、两组平行线构造平行四边形1．已知：如图，AB是一条直线，∠C = ∠1，∠2和∠D互余，BE⊥FD于G．求证：AB∥CD ．2、如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，求证DF∥AC．DF42A(第22B 题)C五、寻找角之间的关系1、如图2-97,已知：∠1=∠2，∠3=∠4，∠5=∠6.求证:AD∥BC.2、已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4。

求证：AD∥BE。

D3．如图12，∠ABD和∠BDC的平分线交于E，BE交CD于点F，∠1 +∠2 = 90°．求证：（1）AB∥CD；（2）∠2 +∠3 = 90°．六、翻折图103、如图，M、N、T和A、B、C分别在同一直线上，且∠1=∠3，∠P=∠T，求证：∠M=∠R。

四、证特殊角1、AB∥CD，∠BAC的平分线和∠ACD的平分线交于点E，则∠AEC的度数是．图7 图82、AB∥CD，直线EF与AB、CD分别相交于E、F两点，EP平分∠AEF，过点F作PF⊥EP垂足为P，若∠PEF＝30，则∠PFC＝_____．3、如图，已知：DE∥AC，CD平分∠ACB，EF平分∠DEC，∠1与∠2互余，求证：DG∥EF.A1、如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为．2、如图（1），已知矩形ABCD，将△BCD沿对角线BD折叠，记点C的对应点为C′，若D5.如图已知直线a∥b，AB平分∠MAD，AC平分∠NAD，DE⊥AC 于E，求证：∠1=∠2．∠ADC′=20°，则∠DBC=的度数为。

人教版七年级下册数学第5章相交线与平行线证明题专题训练1．如图，直线CD ，AB 相交于点O ，∠BOM ＝90°，∠DON ＝90°.(1)若∠COM ＝∠AOC ，求∠AOD 的度数；(2)若∠COM ＝14∠BOC ，求∠BOD 的度数．2．已知：如图，∠1＝∠2，∠3＝∠4，∠5＝∠C ．DE 与BF 平行吗？请说明理由．3．如图，已知：12∠=∠，50D ︒∠=，求B 的度数4．如图，已知AB//CD ，AE//CF ，求证：∠BAE=∠DCF.5．如图//AB CD ，AE 平分BAD ∠，CD 与AE 相交于F ，CFE E ∠=∠，求证：//AD BC ．6．如图，已知//AB CD ，40B ∠=，CN 是BCE ∠的平分线，CM CN ⊥，求BCM ∠的度数．7．如图，已知EA∠AB 于A ，CD∠DF 于D ，AB∠CD ，请判断：EA 与DF 平行吗？为什么？8．如图，AB∠CD ，BN ，DN 分别平分∠ABM ，∠MDC ，试问∠M 与∠N 之间的数量关系如何？请说明理由．9．如图，已知∠B=∠C ．（1）若AD∠BC ，则AD 平分∠EAC 吗？请说明理由．（2）若∠B+∠C+∠BAC=180°，AD 平分∠EAC ，则AD∠BC 吗？请说明理由．10．如图，AB∠DE ，C 为BD 上一点，∠A ＝∠BCA ，∠E ＝∠ECD ，求证：CE∠CA ．11．如图所示，已知∠1＝∠2，AC 平分∠DAB ，试说明DC∠AB ．12．如图，AB∠DE∠GF ，∠1：∠D ：∠B ＝2：3：4，求∠1的度数．13．如图，四边形ABCD中，∠A＝∠C＝90°，BE，DF分别是∠ABC，∠ADC的平分线．(1)∠1与∠2有什么关系，为什么？(2)BE与DF有什么关系？请说明理由．14．如图，AD是∠EAC的平分线，AD∠BC，∠B=30o，∠EAD、∠DAC、∠C的度数．15．已知：如图，∠BAP+∠APD =180°，∠1 =∠2.求证：AE∠PF．16．如图，∠1＝∠2，∠3＝∠4，∠5＝∠6，求证：CE//BF．17．如图，AD∠BC，垂足为D，∠ADE=∠CFG，∠C+∠CFG=90°.试说明DE∠AC18．如图，AD∠BC，BE平分∠ABC交AD于点E，BD平分∠EBC．(1)若∠DBC＝30°，求∠A的度数；(2)若点F在线段AE上，且7∠DBC－2∠ABF＝180°，请问图中是否存在与∠DFB相等的角？若存在，请写出这个角，并说明理由；若不存在，请说明理由．19．如图，已知∠BEF+∠EFD=180°，EM平分∠BEF，FN平分∠EFC，求证：∠M=∠N.20．已知：如图，AB∠CD，∠1=∠2，∠3=∠4．（1）求证：AD∠BE；（2）若∠B=∠3=2∠2，求∠D的度数．。