西方经济学模型整理

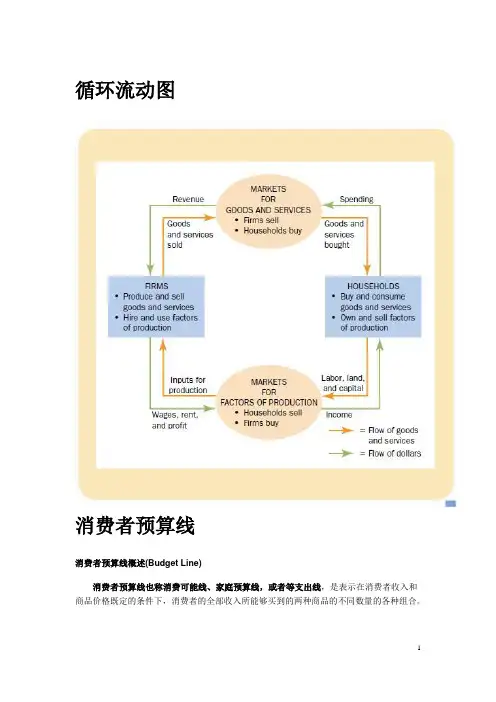
循环流动图消费者预算线消费者预算线概述(Budget Line)消费者预算线也称消费可能线、家庭预算线，或者等支出线，是表示在消费者收入和商品价格既定的条件下，消费者的全部收入所能够买到的两种商品的不同数量的各种组合。

如上图，预算线AB把平面坐标图分为三个区域：预算线AB以外的区域中的任何一点，如C点，是消费者利用全部收入不可能实现的商品购买组合点。

预算线AB以内的区域中的任何一点，比如D点，表示消费者的全部收入购买该点的商品组合以后还有剩余。

唯有预算线AB上的任何一点，才是消费者的全部收入刚好花完所能购买到的商品组合点。

消费者预算线的方程如果以I表示消费者的既定收入，以P1和P2分别表示已知的商品1和商品2的价格，以X1和X2分别表示商品1和商品2的数量，那么，预算线的方程为:I = P1X1 + P2X2该式表示，消费者的全部收入等于他购买商品1的支出和购买商品2的支出的总和。

消费者预算线的变动1、当两种商品的价格不变、消费者收入发生变化时；2、当消费者的收入不变、两种商品的价格同比例变化时；3、当消费者的收入不变、一种商品的价格不变而另一种商品的价格发生变化时；4、当消费者的收入和两种商品的价格都同比例同方向变化时。

变动情况如下图:两种商品价格不变，消费者的收入变化时，会引起预算线的截距变化，使预算线发生平移。

两种商品价格和消费者的收入同比例同方向变化时，预算线不变。

消费者的收入不变，一种商品价格不变而另一种商品价格变化时，会引起预算线的斜率及相应截距变化。

偏好公理偏好公理在西方消费需求理论中，被认为可以检验消费者行为的理论。

包括：完备性公理；传递性公理；选择性公理；优势公理；连续性公理和偏好的凸性公理。

[编辑]偏好公理的具体内涵偏好公理的具体内涵：1.完备性公理。

指消费者对于某些商品所有可能的组合能够按照他的偏好程度大小，有顺序地排列出完整的、可供选择的商品组合。

2.传递性公理。

消费者对A商品组合的偏好，大于B商品组合，而对B商品组合的偏好又大于C组合的商品，则消费者对于A组合的商品的偏好必然大于对C组合的商品的偏好。

西方经济学中的经济增长模型经济增长一直是西方经济学研究的核心内容之一。

为了更好地理解和解释经济增长，西方经济学家们发展了多种经济增长模型。

本文将介绍几种经济增长模型，并探讨它们的特点和应用。

1. 扩展的哈罗德-多马模型扩展的哈罗德-多马模型是经济学家罗伯特·哈罗德和埃弗里特·多马在20世纪50年代提出的。

该模型主要着眼于资本形成和资本积累对经济增长的影响。

在这个模型中，经济增长取决于储蓄率、有效资本边际产出和人口增长率等因素。

它强调了投资在经济增长中的作用，并提出了有效资本边际产出递减的观点。

2. 新古典增长理论新古典增长理论是20世纪80年代后期由罗伯特·索洛经提出的。

该理论主要关注资本积累和技术进步对经济增长的影响。

在这个模型中，经济增长取决于储蓄率、资本边际产出和技术进步率等因素。

新古典增长理论强调了技术进步在经济增长中的重要性，并认为长期经济增长取决于技术进步的速度和效率。

3. 内生增长模型内生增长模型是20世纪90年代由保罗·罗默和罗伯特·卢卡斯等经济学家提出的。

该模型以经济中人力资本和知识的积累为核心要素，强调创新、技术进步和知识产权保护对经济增长的重要性。

内生增长模型认为经济增长是自我推动的，并提出了增加研发和教育投资的建议。

4. 新凯恩斯主义增长模型新凯恩斯主义增长模型是近年来发展起来的一种经济增长模型。

该模型主张政府在经济中发挥积极作用，通过财政政策和货币政策来稳定经济，并促进经济增长。

新凯恩斯主义增长模型强调需求驱动的经济增长，并提出了通过提高消费和投资来刺激经济增长的建议。

以上所述的经济增长模型是西方经济学中常见且具有较大影响力的模型。

每个模型都从不同的角度出发，解释和分析经济增长的机制。

通过研究这些模型，我们能更好地了解经济增长的本质，并为经济政策制定提供理论基础。

总结起来，西方经济学中的经济增长模型包括扩展的哈罗德-多马模型、新古典增长理论、内生增长模型和新凯恩斯主义增长模型等。

1、哈罗德—多马模型哈罗德多马模型是在一系列严格的假设条件下得到的。

这些假设条件主要有：（1）全社会只生产一种产品，这种产品既可以作为消费品，也可以作为资本品；（2）生产过程中只使用两种生产要素，即劳动L和资本K，这两种生产要素之间相互不能替代，每单位产量所需要的生产要素数量保持不变；（3）生产规模收益不变；（4）储蓄在国民收入中所占的份额保持不变；（5）劳动力按照一个固定不变的比率增长；（6）不存在技术进步，也不存在资本折旧问题。

哈罗德-多马模型的基本公式可以表示为：公式它表明，当经济处于均衡时，国民收入增长率等于该社会的储蓄率除以资本–产出比。

哈罗德–多马模型反映了经济增长率与储蓄率和资本产出比之间的关系。

在资本–产量比既定的条件下，如果要获得一定的增长率，就必须维持一定的能为投资所吸收的储蓄率；反之，若将一定的储蓄率形成的储蓄全部为投资所吸收，经济就必须保持一定的增长率。

在资本产出比不变的条件下，储蓄率越高，经济的增长率越高，反之，储蓄率越低，经济增长率也就越低。

2、哈罗德-多马模型稳定增长的条件经济增长率，等于人口增长率，即GA = GW = Gn。

首先考察实际增长率等于人口增长率，即GA = Gn。

由于生产过程中资本与劳动不能相互替代，因而当实际增长率超过人口增长率，即GA＞Gn时劳动力就会构成经济增长的制约因素，经济就不可能长期稳定增长；反之，当实际增长率小于人口增长率，即GA＜Gn时，劳动力出现过剩，从而经济中出现失业。

因此，只有当实际经济增长率与人口增长率相等时，经济才可能在充分就业状态下运行。

其次考察实际增长率等于有保证的经济增长率，即GA = GW。

如果实际经济增长率大于有保证的增长率，即GA＞GW，在储蓄率s既定的条件下，实际的资本产出比小于资本家意愿的资本产出比，即，从而投资者会增加投资。

增加投资的结果是国民收入增加，实际增长率进一步提高。

反之，若实际经济增长率小于有保证的增长率，即GA＜GW，则实际的资本–产出比大于投资者意愿的资本–产出比，即，投资者将根据意愿的资本存量进一步减少投资，国民收入减少，从而实际增长率更趋于下降，经济将继续收缩。

循环流动图消费者预算线消费者预算线概述(Bｕｄget Liｎe)消费者预算线也称消费可能线、家庭预算线,或者等支出线，就是表示在消费者收入与商品价格既定得条件下,消费者得全部收入所能够买到得两种商品得不同数量得各种组合。

如上图，预算线ＡB把平面坐标图分为三个区域：预算线AB以外得区域中得任何一点，如C点，就是消费者利用全部收入不可能实现得商品购买组合点.预算线AB以内得区域中得任何一点，比如D点，表示消费者得全部收入购买该点得商品组合以后还有剩余。

唯有预算线ＡB上得任何一点，才就是消费者得全部收入刚好花完所能购买到得商品组合点。

消费者预算线得方程如果以I表示消费者得既定收入,以P1与P2分别表示已知得商品1与商品2得价格，以Ｘ与X2分别表示商品１与商品２得数量，那么,预算线得方程为：1I＝P1X1 +Ｐ２X２该式表示,消费者得全部收入等于她购买商品1得支出与购买商品２得支出得总与.消费者预算线得变动１、当两种商品得价格不变、消费者收入发生变化时；2、当消费者得收入不变、两种商品得价格同比例变化时；3、当消费者得收入不变、一种商品得价格不变而另一种商品得价格发生变化时;4、当消费者得收入与两种商品得价格都同比例同方向变化时。

变动情况如下图:两种商品价格不变，消费者得收入变化时，会引起预算线得截距变化，使预算线发生平移.两种商品价格与消费者得收入同比例同方向变化时，预算线不变.消费者得收入不变，一种商品价格不变而另一种商品价格变化时，会引起预算线得斜率及相应截距变化。

偏好公理偏好公理在西方消费需求理论中,被认为可以检验消费者行为得理论。

包括：完备性公理;传递性公理；选择性公理；优势公理;连续性公理与偏好得凸性公理。

[编辑]偏好公理得具体内涵偏好公理得具体内涵：1、完备性公理。

指消费者对于某些商品所有可能得组合能够按照她得偏好程度大小，有顺序地排列出完整得、可供选择得商品组合。

2、传递性公理。

消费者对A商品组合得偏好，大于Ｂ商品组合，而对Ｂ商品组合得偏好又大于C组合得商品,则消费者对于A组合得商品得偏好必然大于对C组合得商品得偏好.3、选择性公理.消费者在购买或消费行为中总就是力图使其偏好达到最大与最佳状态。

西方经济学知识点总结一、判断分析1.寡头垄断（1）市场存在多个企业，但又很有限，不构成完全竞争市场。

（2）每个企业的价格和产量决策都会对市场价格以及其他企业的收益产生影响。

（3）市场均衡就取决于各个企业之间的相互作用2.伯特兰德模型古诺模型讨论的是：厂商如何决定产量，而让市场决定价格。

伯特兰德模型讨论的是：厂商如何决定价格，而让市场决定销售量。

前提条件：生产同质产品，成本相同假设市场上只有两家企业：企业1和企业2，双方同时定价，它们生产的产品完全相同（同质），寡头企业的成本函数也完全相同：生产的边际成本等于单位成本c，且假设不存在固定成本。

市场需求函数D（p）是线性函数，相互之间没有任何正式的串谋行为。

由于两个寡头垄断企业生产的产品同质，因而定价高者将失去整个市场；如果两个企业定价相同，则它们将平分市场。

Bertrand均衡的含义:如果同业中的两家企业经营同样的产品，且成本一样，则价格战必定使每家企业按p=边际成本的原则来经营，即只获得正常利润。

但是，如果两家企业的成本不同，则从长期看，成本低的企业必定挤走成本高的企业Bertrand悖论：伯特兰德均衡说明，只要市场上有两个或两个以上生产同样产品的企业，则没有一个企业可以控制市场价格，获取垄断利润；超过边际成本的价格不是均衡价格。

而在现实市场上，企业间的价格竞争往往没有使均衡价格降低到等于边际成本的水平上，而是高于边际成本。

对于大多数产业而言，即使只有两个竞争者，它们也能获得超额利润。

三种解释：Edgeworth解释：现实生活中企业生产能力是有限的。

生产能力约束解。

博弈时序解：企业很可能勾结，以避免价格战。

产品差异解：企业产品有差异，服务上也有可能有差异。

3.无限次重复博弈：当博弈重复无穷次而不是有限次时，存在着完全不同于一次博弈的子博弈纳什均衡考虑囚徒困境冷酷战略：1、开始选择沉默2、选择沉默知道一方选择坦白，然后永远选择坦白如果要达到（沉默，沉默）的均衡，囚徒要考虑无限次后的结果是否好于一次博弈的结果存在贴现因子δ，当其中一个没有选择坦白，另一个将不会选择坦白，于是有0+δ（-6）+δ2（-6）+……≤ 0+δ（-1）+δ2（-1）+……δδδδ所以，无限次重复博弈是有可能出现不同于单词博弈的结果，但需要保证的前提是：1、参与人均采取冷酷战略2、贴现因子足够大双方都采用“冷酷的战略”，即（1）从选择“合作”（高价）开始；（2）只要对方一直选择合作，便合作下去；直到有一天发现多方偷偷实行了不合作，便因此采取不合作到永远；（3）贴现因子足够的大，即将来在收益贴现之后还比较值钱。