高中奥林匹克物理竞赛 微元法

高中物理竞赛方法集锦微元法针对训练例18：如图3—17所示，电源的电动热为E ，电容器的电容为C ，S 是单刀双掷开关，MN 、PQ 是两根位于同一水平面上的平行光滑长导轨，它们的电阻能够忽略不计，两导轨间距为L ，导轨处在磁感应强度为B 的平均磁场中，磁场方向垂直于两导轨所在的平面并指向图中纸面向里的方向.L 1和L 2是两根横放在导轨上的导体小棒，质量分不为m 1和m 2，且21m m <.它们在导轨上滑动时与导轨保持垂直并接触良好，不计摩擦，两小棒的电阻相同，开始时两根小棒均静止在导轨上.现将开关S 先合向1，然后合向2.求：〔1〕两根小棒最终速度的大小；〔2〕在整个过程中的焦耳热损耗.〔当回路中有电流时，该电流所产生的磁场可忽略不计〕 解析：当开关S 先合上1时，电源给电容器充电，当开关S 再合上2时，电容器通过导体小棒放电，在放电过程中，导体小棒受到安培力作用，在安培力作用下，两小棒开始运动，运动速度最后均达到最大.〔1〕设两小棒最终的速度的大小为v ，那么分不为L 1、L 2为研究对象得： 1111v m v m t F i i -'=∆ ∑=∆v m t F i i 111 ① 同理得： ∑=∆v m t F i i 222 ② 由①、②得：v m m t F t F i i i i )(212211+=∆+∆∑∑又因为 11Bli F i = 21i i t t ∆=∆ 22Bli F i = i i i =+21因此 ∑∑∑∑∆=∆+=∆+∆i i i i t i BL t i i BL t BLi t BLi )(212211v m m q Q BL )()(21+=-=而Q=CE q=CU ′=CBL v因此解得小棒的最终速度 2221)(L CB m m BLCE v ++= 〔2〕因为总能量守恒，因此热Q v m m C q CE +++=22122)(212121 即产生的热量 22122)(212121v m m C q CE Q +--=热)(2)()()]([2121)(21)(12121222122122212122222122C L B m m CE m m L CB m m BLCE m m L CB CE v m m CBLv C CE +++=+++--=+--=针对训练1．某地强风的风速为v ，设空气的密度为ρ，假如将通过横截面积为S 的风的动能全部转化为电能，那么其电功率为多少？2．如图3—19所示，山高为H ，山顶A 和水平面上B 点的水平距离为s.现在修一条冰道ACB ，其中AC 为斜面，冰道光滑，物体从A 点由静止开释，用最短时刻经C 到B ，不计过C 点的能量缺失.咨询AC 和水平方向的夹角θ多大？最短时刻为多少？3．如图3—21所示，在绳的C 端以速度v 匀速收绳从而拉动低处的物体M 水平前进，当绳AO 段也水平恰成α角时，物体M 的速度多大？4，如图3—22所示，质量相等的两个小球A 和B 通过轻绳绕过两个光滑的定滑轮带动C 球上升，某时刻连接C 球的两绳的夹角为θ，设A 、B 两球现在下落的速度为v ，那么C 球上升的速度多大？5．质量为M 的平板小车在光滑的水平面上以v 0向左匀速运动，一质量为m 的小球从高h 处自由下落，与小车碰撞后反弹上升的高度仍为h.设M>>m ，碰撞弹力N>>g ，球与车之间的动摩擦因数为μ，那么小球弹起后的水平速度可能是〔 〕 A ．gh 2 B ．0 C ．gh 22μ D ．v 0 6．半径为R 的刚性球固定在水平桌面上.有一质量为M 的圆环状平均弹性细绳圈，原长 2πa ，a =R/2，绳圈的弹性系数为k 〔绳伸长s 时，绳中弹性张力为ks 〕.将绳圈从球的正 上方轻放到球上，并用手扶着绳圈使其保持水平，并最后停留在某个静力平稳位置.考 虑重力，忽略摩擦.〔1〕设平稳时弹性绳圈长2πb ，b=a 2，求弹性系数k ；〔用M 、R 、g 表示，g 为重力加速度〕〔2〕设k=Mg/2π2R ，求绳圈的最后平稳位置及长度.7．一截面呈圆形的细管被弯成大圆环，并固定在竖直平面内，在环内的环底A处有一质量为m、直径比管径略小的小球，小球上连有一根穿过环顶B处管口的轻绳，在外力F作用下小球以恒定速度v沿管壁做半径为R的匀速圆周运动，如图3—23所示.小球与管内壁中位于大环外侧部分的动摩擦因数为μ，而大环内侧部分的管内壁是光滑的.忽略大环内、外侧半径的差不，认为均为R.试求小球从A点运动到B点过程中F做的功W F.8．如图3—24，来自质子源的质子〔初速度为零〕，经一加速电压为800kV的直线加速器加速，形成电流为1.0mA 的细柱形质子流.质子电荷e=1.60×10－19C.这束质子流每秒打到靶上的质子数为.假设分布在质子源到靶之间的加速电场是平均的，在质子束中与质子源相距l 和4l的两处，各取一段极短的相等长度的质子流，其中质子数分不为n1和n2，那么n1: n2.9．如图3—25所示，电量Q平均分布在一个半径为R的细圆环上，求圆环轴上与环心相距为x的点电荷q所受的力的大小.10．如图3—26所示，一根平均带电细线，总电量为Q，弯成半径为R的缺口圆环，在细线的两端处留有专门小的长为△L的间隙，求圆环中心处的场强.11．如图3—27所示，两根平均带电的半无穷长平行直导线〔它们的电荷线密度为η〕，端点联线LN垂直于这两直导线，如下图.LN的长度为2R.试求在LN的中点O处的电场强度.12．如图3—28所示，有一平均带电的无穷长直导线，其电荷线密度为η.试求空间任意一点的电场强度.该点与直导线间垂直距离为r.13．如图3—29所示，半径为R的平均带电半球面，电荷面密度为δ，求球心O处的电场强度.14．如图3—30所示，在光滑的水平面上，有一垂直向下的匀强磁场分布在宽度为L 的区域内，现有一个边长为a 〔a <L 〕，质量为m 的正方形闭合线框以初速v 0垂直磁场边界滑过磁场后，速度变为v 〔v <v 0〕，求：〔1〕线框在这过程中产生的热量Q ；〔2〕线框完全进入磁场后的速度v ′.15．如图3—31所示，在离水平地面h 高的平台上有一相距L 的光滑轨道，左端接有已充电的电容器，电容为C ，充电后两端电压为U 1.轨道平面处于垂直向上的磁感应强度为B 的匀强磁场中.在轨道右端放一质量为m 的金属棒，当闭合S ，棒离开轨道后电容器的两极电压变为U 2，求棒落在离平台多远的位置.16．如图3—32所示，空间有一水平方向的匀强磁场，大小为B ，一光滑导轨竖直放置，导轨上接有一电容为C 的电容器，并套一可自由滑动的金属棒，质量为m ，开释后，求金属棒的加速度a .答案：1．321v S ρ 2．θ=60°)223(2hs g h + 3．)cos 1/(x v + 4．2cos /θv 5．CD 6．〔1〕R Mg 22)12(π+ 〔2〕绳圈掉地上，长度为原长 7．22v m mgR πμ+ 8．6.25×1015,2:1 9．2322)(x R QqxK + 10．32R l Q K ρ∆ 11．R k λ2 12．rk λ2 13．σπR 2 14．2),(210220v v v v v m +='- 15．gh m u u CBL 2)(21- 16．22L CB m mg a +=。

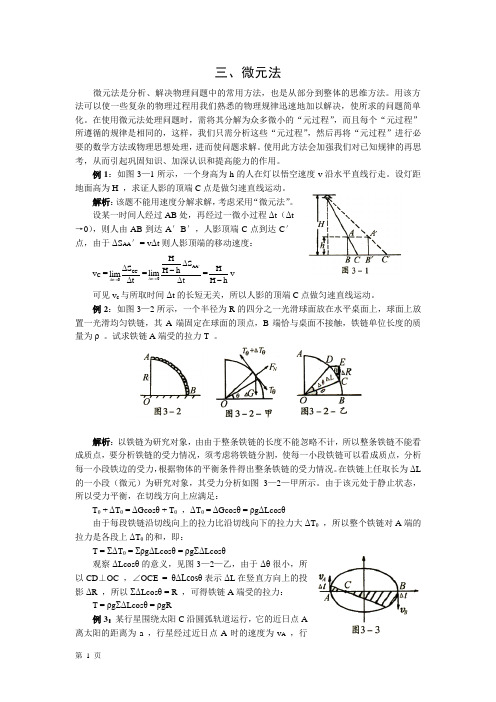
三、微元法微元法是分析、解决物理问题中的常用方法，也是从部分到整体的思维方法。

用该方法可以使一些复杂的物理过程用我们熟悉的物理规律迅速地加以解决，使所求的问题简单化。

在使用微元法处理问题时，需将其分解为众多微小的“元过程”，而且每个“元过程”所遵循的规律是相同的，这样，我们只需分析这些“元过程”，然后再将“元过程”进行必要的数学方法或物理思想处理，进而使问题求解。

使用此方法会加强我们对已知规律的再思考，从而引起巩固知识、加深认识和提高能力的作用。

例1：如图3—1所示，一个身高为h 的人在灯以悟空速度v 沿水平直线行走。

设灯距地面高为H ，求证人影的顶端C 点是做匀速直线运动。

解析：该题不能用速度分解求解，考虑采用“微元法”。

设某一时间人经过AB 处，再经过一微小过程Δt （Δt→0），则人由AB 到达A ′B ′，人影顶端C 点到达C ′点，由于ΔS AA ′= v Δt 则人影顶端的移动速度：v C =CC t 0S lim t '∆→∆∆=AA t 0H S H h lim t '∆→∆-∆=H H h -v 可见v c 与所取时间Δt 的长短无关，所以人影的顶端C 点做匀速直线运动。

例2：如图3—2所示，一个半径为R 的四分之一光滑球面放在水平桌面上，球面上放置一光滑均匀铁链，其A 端固定在球面的顶点，B 端恰与桌面不接触，铁链单位长度的质量为ρ 。

试求铁链A 端受的拉力T 。

解析：以铁链为研究对象，由由于整条铁链的长度不能忽略不计，所以整条铁链不能看成质点，要分析铁链的受力情况，须考虑将铁链分割，使每一小段铁链可以看成质点，分析每一小段铁边的受力，根据物体的平衡条件得出整条铁链的受力情况。

在铁链上任取长为ΔL 的一小段（微元）为研究对象，其受力分析如图3—2—甲所示。

由于该元处于静止状态，所以受力平衡，在切线方向上应满足：T θ + ΔT θ = ΔGcos θ + T θ ，ΔT θ = ΔGcos θ = ρg ΔLcos θ由于每段铁链沿切线向上的拉力比沿切线向下的拉力大ΔT θ ，所以整个铁链对A 端的拉力是各段上ΔT θ的和，即：T = ΣΔT θ = Σρg ΔLcos θ = ρg ΣΔLcos θ观察ΔLcos θ的意义，见图3—2—乙，由于Δθ很小，所以CD ⊥OC ，∠OCE = θΔLcosθ表示ΔL 在竖直方向上的投影ΔR ，所以ΣΔLcos θ = R ，可得铁链A 端受的拉力：T = ρg ΣΔLcos θ = ρgR例3：某行星围绕太阳C 沿圆弧轨道运行，它的近日点A离太阳的距离为a ，行星经过近日点A 时的速度为v A，行星的远日点B 离开太阳的距离为b ，如图3—3所示，求它经过远日点B 时的速度v B 的大小。

省前中物理奥赛讲座一、微元法知识方法微元法是分析、解决物理问题中的常用方法，也是从部分到整体的思维方法。

用该方法可以使一些复杂的物理过程用我们熟悉的物理规律迅速地加以解决，使所求的问题简单化。

在使用微元法处理问题时，需将其分解为众多微小的“元过程”，而且每个“元过程”所遵循的规律是相同的，这样，我们只需分析这些“元过程”，然后再将“元过程”进行必要的数学方法或物理思想处理，进而使问题求解。

使用此方法会加强我们对已知规律的再思考，从而引起巩固知识、加深认识和提高能力的作用。

题型讲解例1：如图所示，一个半径为R 的四分之一光滑球面放在水平桌面上，球面上放置一光滑均匀铁链，其A 端固定在球面的顶点，B 端恰与桌面不接触，铁链单位长度的质量为ρ.试求铁链A 端受的拉力T.解析：以铁链为研究对象，由由于整条铁链的长度不能忽略不计，所以整条铁链不能看成质点，要分析铁链的受力情况，须考虑将铁链分割，使每一小段铁链可以看成质点，分析每一小段铁边的受力，根据物体的平衡条件得出整条铁链的受力情况.在铁链上任取长为△L 的一小段（微元）为研究对象，其受力分析如图甲所示.由于该元处于静止状态，所以受力平衡，在切线方向上应满足：θθθθT G T T +∆=∆+cos θρθθc o s c o s Lg G T ∆=∆=∆由于每段铁链沿切线向上的拉力比沿切线向下的拉力大△T θ，所以整个铁链对A 端的拉力是各段上△T θ的和，即∑∑∑∆=∆=∆=θρθρθc o s c o s L g Lg T T观察 θcos L ∆的意义，见图乙，由于△θ很小，所以CD ⊥OC ，∠OCE=θ△Lcos θ表示△L 在竖直方向上的投影△R ，所以∑=∆R L θc o s 可得铁链A 端受的拉力 ∑=∆=gR L gT ρθρcos例2：半径为R 的光滑球固定在水平桌面上，有一质量为M 的圆环状均匀弹性绳圈，原长为πR ，且弹性绳圈的劲度系数为k ，将弹性绳圈从球的正上方轻放到球上，使弹性绳圈水平停留在平衡位置上，如图所示，若平衡时弹性绳圈长为R π2，求弹性绳圈的劲度系数k.解析：由于整个弹性绳圈的大小不能忽略不计，弹性绳圈不能看成质点，所以应将弹性绳圈分割成许多小段，其中每一小段△m 两端受的拉力就是弹性绳圈内部的弹力F.在弹性绳圈上任取一小段质量为△m 作为研究对象，进行受力分析.但是△m 受的力不在同一平面内，可以从一个合适的角度观察.选取一个合适的平面进行受力分析，这样可以看清楚各个力之间的关系.从正面和上面观察，分别画出正视图的俯视图，如图甲和乙.先看俯视图甲，设在弹性绳圈的平面上，△m 所对的圆心角是△θ，则每一小段的质量 M m πθ2∆=∆△m 在该平面上受拉力F 的作用，合力为2sin 2)2cos(2θθπ∆=∆-=F F T 因为当θ很小时，θθ≈sin 所以θθ∆=∆=F F T 22 再看正视图乙，△m 受重力△mg ，支持力N ，二力的合力与T 平衡.即 θt a n ⋅∆=mg T现在弹性绳圈的半径为 R R r 2222==ππ 所以 ︒===4522sin θθR r 1t a n=θ 因此T=Mg mg πθ2∆=∆ ①、②联立，θπθ∆=∆F Mg 2， 解得弹性绳圈的张力为： π2Mg F = 设弹性绳圈的伸长量为x 则 R R R x πππ)12(2-=-=所以绳圈的劲度系数为：RMg R Mg x F k 222)12()12(2ππ+=-==例3：一质量为M 、均匀分布的圆环，其半径为r ，几何轴与水平面垂直，若它能经受的最大张力为T ，求此圆环可以绕几何轴旋转的最大角速度.解析：因为向心力F=mr ω2，当ω一定时，r 越大，向心力越大，所以要想求最大张力T 所对应的角速度ω，r 应取最大值.如图所示，在圆环上取一小段△L ，对应的圆心角为△θ，其质量可表示为M m πθ2∆=∆，受圆环对它的张力为T ，则同上例分析可得 22sin 2ωθmr T ∆=∆因为△θ很小，所以22sin θθ∆≈∆，即 2222ωπθθMr T ∆=∆⋅解得最大角速度 MrT πω2= 例4：中，半径为R 的圆盘固定不可转动，细绳不可伸长但质量可忽略，绳下悬挂的两物体质量分别为M 、m.设圆盘与绳间光滑接触，试求盘对绳的法向支持力线密度.解析：求盘对绳的法向支持力线密度也就是求盘对绳的法向单位长度所受的支持力.因为盘与绳间光滑接触，则任取一小段绳，其两端受的张力大小相等，又因为绳上各点受的支持力方向不同，故不能以整条绳为研究对象，只能以一小段绳为研究对象分析求解.在与圆盘接触的半圆形中取一小段绳元△L ，△L 所对应的圆心角为△θ，如图甲所示，绳元△L 两端的张力均为T ，绳元所受圆盘法向支持力为△N ，因细绳质量可忽略，法向合力为零，则由平衡条件得：2sin 22sin 2sinθθθ∆=∆+∆=∆T T T N 当△θ很小时，22sin θθ∆≈∆ ∴△N=T △θ 又因为 △L=R △θ则绳所受法向支持力线密度为 RT R T L N n =∆∆=∆∆=θθ ① 以M 、m 分别为研究对象，根据牛顿定律有 Mg －T=Ma ②T －mg=m a ③ 由②、③解得： m M Mmg T +=2 将④式代入①式得：R m M Mmg n )(2+=例5：电量Q 均匀分布在半径为R 的圆环上（如图所示），求在圆环轴线上距圆心O 点为x 处的P 点的电场强度.解析：带电圆环产生的电场不能看做点电荷产生的电场，故采用微元法，用点电荷形成的电场结合对称性求解.选电荷元 ,2RQ R q πθ∆=∆它在P 点产生的电场的场强的x 分量为： 22222)(2cos xR x x R R Q R k r q k E x ++∆=∆=∆πθα 根据对称性 322322322)(2)(2)(2x R kQx x R kQxx R kQxE E x +=+=∆+=∆=∑∑ππθπ由此可见，此带电圆环在轴线P 点产生的场强大小相当于带电圆环带电量集中在圆环的某一点时在轴线P 点产生的场强大小，方向是沿轴线的方向.例6：如图所示，一质量均匀分布的细圆环，其半径为R ，质量为m.令此环均匀带正电，总电量为Q.现将此环平放在绝缘的光滑水平桌面上，并处于磁感应强度为B 的均匀磁场中，磁场方向竖直向下.当此环绕通过其中心的竖直轴以匀角速度ω沿图示方向旋转时，环中的张力等于多少？（设圆环的带电量不减少，不考虑环上电荷之间的作用）解析：当环静止时，因环上没有电流，在磁场中不受力，则环中也就没有因磁场力引起的张力.当环匀速转动时，环上电荷也随环一起转动，形成电流，电流在磁场中受力导致环中存在张力，显然此张力一定与电流在磁场中受到的安培力有关.由题意可知环上各点所受安培力方向均不同，张力方向也不同，因而只能在环上取一小段作为研究对象，从而求出环中张力的大小.在圆环上取△L=R △θ圆弧元，受力情况如图甲所示.因转动角速度ω而形成的电流 πω2Q I =，电流元I △L 所受的安培力θπω∆=∆=∆QB R LB I F 2 因圆环法线方向合力为圆弧元做匀速圆周运动所需的向心力，R m F T 22sin 2ωθ∆=∆-∆当△θ很小时，R m QB R T 2222sin ωθπωθθθ∆=∆-∆∆≈∆ θπωθπωθθπ∆=∆-∆∴∆=∆2222R m QB R T m m 解得圆环中张力为 )(2ωπωm QB R T +=。

三、微元法方法简介微元法是分析、解决物理问题中的常用方法，也是从部分到整体的思维方法。

用该方法可以使一些复杂的物理过程用我们熟悉的物理规律迅速地加以解决，使所求的问题简单化。

在使用微元法处理问题时，需将其分解为众多微小的“元过程”，而且每个“元过程”所遵循的规律是相同的，这样，我们只需分析这些“元过程”，然后再将“元过程”进行必要的数学方法或物理思想处理，进而使问题求解。

使用此方法会加强我们对已知规律的再思考，从而引起巩固知识、加深认识和提高能力的作用。

赛题精讲例1：如图3—1所示，一个身高为h 的人在灯以悟空速度v 沿水平直线行走。

设灯距地面高为H ，求证人影的顶端C 点是做匀速直线运动。

解析：该题不能用速度分解求解，考虑采用“微元法”。

设某一时间人经过AB 处，再经过一微小过程△t （△t →0），则人由AB 到达A ′B ′，人影顶端C 点到达C ′点，由于△S AA ′=v △t 则人影顶端的 移动速度h H Hv t S h H H t S v A A t C C t C -=∆∆-=∆∆='→∆'→∆00lim lim可见v c 与所取时间△t 的长短无关，所以人影的顶端C 点做匀速直线运动.例2：如图3—2所示，一个半径为R 的四分之一光滑球面放在水平桌面上，球面上放置一光滑均匀铁链，其A端固定在球面的顶点，B 端恰与桌面不接触，铁链单位长度的质量为ρ.试求铁链A 端受的拉力T.解析：以铁链为研究对象，由由于整条铁链的长度不能忽略不计，所以整条铁链不能看成质点，要分析铁链的受 力情况，须考虑将铁链分割，使每一小段铁链可以看成质 点，分析每一小段铁边的受力，根据物体的平衡条件得出 整条铁链的受力情况.在铁链上任取长为△L 的一小段（微元）为研究对象，其受力分析如图3—2—甲所示.由于该元处于静止状态，所以受力平衡，在切线方向上应满足：θθθθT G T T +∆=∆+cos θρθθcos cos Lg G T ∆=∆=∆由于每段铁链沿切线向上的拉力比沿切线向下的拉力大△T θ，所以整个铁链对A 端的拉力是各段上△T θ的和，即 ∑∑∑∆=∆=∆=θρθρθcos cos L g Lg T T观察 θcos L ∆的意义，见图3—2—乙，由于△θ很小，所以CD ⊥OC ，∠OCE=θ△Lcos θ表示△L 在竖直方向上的投影△R ， 所以 ∑=∆R L θcos 可得铁链A 端受的拉力 ∑=∆=gR L g T ρθρcos例3：某行星围绕太阳C 沿圆弧轨道运行，它的近日点A 离太阳的距离为a ，行星经过近日点A 时的速度为A v ，行星的远日点B 离开太阳的距离为b ，如图3—3所示，求它经过远日点B 时的速度B v 的大小.解析：此题可根据万有引力提供行星的向心力求解.也可根据开普勒第二定律，用微元法求解.设行星在近日点A 时又向前运动了极短的时间△t ，由于时间极短可以认为行星在△t 时间内做匀速圆周运动，线速度为A v ，半径为a ，可以得到行星在△t 时间内扫过的面积 a t v S A a ⋅∆=21 同理，设行星在经过远日点B 时也运动了相同的极短时间△t ，则也有 b t v S B b ⋅∆=21 由开普勒第二定律可知：S a =S b 即得 A B v b a v = 此题也可用对称法求解.例4：如图3—4所示，长为L 的船静止在平静的水面上， 立于船头的人质量为m ，船的质量为M ，不计水的阻力， 人从船头走到船尾的过程中，问：船的位移为多大？解析：取人和船整体作为研究系统，人在走动过程中，系统所受合外力为零，可知系统动量守恒.设人在走动过程中的△t 时间内为匀速运动，则可计算出船的位移.设v 1、v 2分别是人和船在任何一时刻的速率，则有21Mv mv = ① 两边同时乘以一个极短的时间△t ， 有 t Mv t mv ∆=∆21 ②由于时间极短，可以认为在这极短的时间内人和船的速率是不变的， 所以人和船位移大小分别为t v s ∆=∆11，t v s ∆=∆22由此将②式化为 21s M s m ∆=∆ ③把所有的元位移分别相加有 ∑∑∆=∆21s M s m ④即 ms 1=Ms 2 ⑤ 此式即为质心不变原理. 其中s 1、s 2分别为全过程中人和船对地位移的大小， 又因为 L=s 1+s 2 ⑥由⑤、⑥两式得船的位移 L m M m s +=2 例5：半径为R 的光滑球固定在水平桌面上，有一质量为M 的圆环状均匀弹性绳圈，原长为πR ，且弹性绳圈的劲度系数为k ，将弹性绳圈从球的正上方轻放到球上，使弹性绳圈水平停留在平衡位置上，如图3—5所示，若平衡时弹性绳圈长为R π2，求弹性绳圈的劲度系数k.解析：由于整个弹性绳圈的大小不能忽略不计，弹性绳圈 不能看成质点，所以应将弹性绳圈分割成许多小段，其中 每一小段△m 两端受的拉力就是弹性绳圈内部的弹力F.在弹性绳圈上任取一小段质量为△m 作为研究对象，进行受力分析.但是△m 受的力不在同一平面内，可以从一个合适的角度观察.选取一个合适的平面进行受力分析，这样可以看清楚各个力之间的关系.从正面和上面观察，分别画出正视图的俯视图，如图3—5—甲和2—3—5—乙.先看俯视图3—5—甲，设在弹性绳圈的平面上，△m 所对的圆心角是△θ，则每一小段的质量 M m πθ2∆=∆ △m 在该平面上受拉力F 的作用，合力为 2sin 2)2cos(2θθπ∆=∆-=F F T 因为当θ很小时，θθ≈sin 所以θθ∆=∆=F F T 22 再看正视图3—5—乙，△m 受重力△mg ，支持力N ，二力的合力与T 平衡.即 θtan ⋅∆=mg T现在弹性绳圈的半径为 R R r 2222==ππ 所以 ︒===4522sin θθR r 1tan =θ因此T=Mg mg πθ2∆=∆ ①、②联立，θπθ∆=∆F Mg 2， 解得弹性绳圈的张力为： π2Mg F = 设弹性绳圈的伸长量为x 则 R R R x πππ)12(2-=-=所以绳圈的劲度系数为：RMg R Mg x F k 222)12()12(2ππ+=-== 例6：一质量为M 、均匀分布的圆环，其半径为r ，几何轴与水平面垂直，若它能经受的最大张力为T ，求此圆环可以绕几何轴旋转的最大角速度.解析：因为向心力F=mr ω2，当ω一定时，r 越大，向心力越大，所以要想求最大张力T 所对应的角速度ω，r 应取最大值.如图3—6所示，在圆环上取一小段△L ，对应的圆心角为△θ，其质量可表示为M m πθ2∆=∆，受圆环对它的张 力为T ，则同上例分析可得 22sin 2ωθmr T ∆=∆ 因为△θ很小，所以22sin θθ∆≈∆，即2222ωπθθMr T ∆=∆⋅ 解得最大角速度 MrT πω2= 例7：一根质量为M ，长度为L 的铁链条，被竖直地悬挂起来，其最低端刚好与水平接触，今将链条由静止释放，让它落到地面上，如图3—7所示，求链条下落了长度x 时，链条对地面的压力为多大？ 解析：在下落过程中链条作用于地面的压力实质就是链条对地面的“冲力”加上落在地面上那部分链条的重力.根据牛顿第三定律，这个冲力也就等于同一时刻地面对链条的反作用力，这个力的冲量，使得链条落至地面时的动量发生变化.由于各质元原来的高度不同，落到地面的速度不同，动量改变也不相同.我们取某一时刻一小段链条（微元）作为研究对象，就可以将变速冲击变为恒速冲击.设开始下落的时刻t=0，在t 时刻落在地面上的链条长为x ，未到达地面部分链条的速度为v ，并设链条的线密度为ρ.由题意可知，链条落至地面后，速度立即变为零.从t 时刻起取很小一段时间△t ，在△t 内又有△M=ρ△x 落到地面上静止.地面对△M 作用的冲量为I t Mg F ∆=∆∆-)( 因为 0≈∆⋅∆t Mg所以 x v v M t F ∆=-⋅∆=∆ρ0 解得冲力：t x v F ∆∆=ρ，其中tx ∆∆就是t 时刻链条的速度v ， 故 2v F ρ= 链条在t 时刻的速度v 即为链条下落长为x 时的即时速度，即v 2=2g x ，代入F 的表达式中，得 gx F ρ2= 此即t 时刻链对地面的作用力，也就是t 时刻链条对地面的冲力.所以在t 时刻链条对地面的总压力为.332L Mgx gx gx gx N ==+=ρρρ 例8：一根均匀柔软的绳长为L ，质量为m ，对折后两端固定在一个钉子上，其中一端突然从钉子上滑落，试求滑落的绳端点离钉子的距离为x 时，钉子对绳子另一端的作用力是多大？解析：钉子对绳子另一端的作用力随滑落绳的长短而变化， 由此可用微元法求解.如图3—8所示，当左边绳端离钉子的距离为x 时，左边绳长为)(21x l -，速度 gx v 2=，右边绳长为).(21x l + 又经过一段很短的时间△t 以后，左边绳子又有长度t V ∆21的一小段转移到右边去了，我们就分 析这一小段绳子，这一小段绳子受到两力：上面绳子对它的拉 力T 和它本身的重力l m g t v /(21=∆λλ为绳子的线密度），根据动量定理，设向上方向为正 )21(0)21(v t v t g t v T ⋅∆--=∆∆-λλ由于△t 取得很小，因此这一小段绳子的重力相对于T 来说是很小的，可以忽略，所以有 λλgx v T ==221 因此钉子对右边绳端的作用力为 )31(21)(21l x mg T g x l F +=++=λ 例9：图3—9中，半径为R 的圆盘固定不可转动，细绳不可伸长 但质量可忽略，绳下悬挂的两物体质量分别为M 、m.设圆盘与 绳间光滑接触，试求盘对绳的法向支持力线密度.解析：求盘对绳的法向支持力线密度也就是求盘对绳的法向单位 长度所受的支持力.因为盘与绳间光滑接触，则任取一小段绳， 其两端受的张力大小相等，又因为绳上各点受的支持力方向不同，故不能以整条绳为研究对象，只能以一小段绳为研究对象分析求 解.在与圆盘接触的半圆形中取一小段绳元△L ，△L 所对应的 圆心角为△θ，如图3—9—甲所示，绳元△L 两端的张力均为T ， 绳元所受圆盘法向支持力为△N ，因细绳质量可忽略，法向合力为 零，则由平衡条件得： 2sin 22sin 2sin θθθ∆=∆+∆=∆T T T N 当△θ很小时，22sin θθ∆≈∆ ∴△N=T △θ 又因为 △L=R △θ则绳所受法向支持力线密度为 R T R T L N n =∆∆=∆∆=θθ ① 以M 、m 分别为研究对象，根据牛顿定律有 Mg －T=Ma ② T －mg=m a ③ 由②、③解得： mM Mmg T +=2 将④式代入①式得：R m M Mmg n )(2+= 例10：粗细均匀质量分布也均匀的半径为分别为R 和r 的两圆环相切.若在切点放一质点m ，恰使两边圆环对m 的万有引力的合力为零，则大小圆环的线密度必须满足什么条件？解析：若要直接求整个圆对质点m 的万有引力比较难，当若要用到圆的对称性及要求所受合力为零的条件，考虑大、小圆环上关于切点对称的微元与质量m 的相互作用，然后推及整个圆环即可求解. 如图3—10所示，过切点作直线交大小圆分别于P 、Q 两点，并设与水平线夹角为α，当α有微小增量时，则大小圆环上对应微小线元 αα∆⋅=∆∆⋅=∆2221r L R L其对应的质量分别为 αρρ∆⋅=∆=∆21111R l mαρρ∆⋅=∆=∆22222r l m 由于△α很小，故△m 1、△m 2与m 的距离可以认为分别是 ααcos 2cos 221r r R r ==所以△m 1、△m 2与m 的万有引力分别为 222222212111)cos 2(2,)cos 2(2ααρααρr m R G r m Gm F R m R G r m Gm F ∆⋅=∆=∆∆⋅=∆=∆ 由于α具有任意性，若△F 1与△F 2的合力为零，则两圆环对m 的引力的合力也为零， 即2221)cos 2(2)cos 2(2ααρααρr m r G R m R G ∆⋅=∆⋅ 解得大小圆环的线密度之比为：r R =21ρρ 例11：一枚质量为M 的火箭，依靠向正下方喷气在空中保持静止，如果喷出气体的速度为v ，那么火箭发动机的功率是多少？解析：火箭喷气时，要对气体做功，取一个很短的时间，求出此时间内，火箭对气体做的功，再代入功率的定义式即可求出火箭发动机的功率.选取在△t 时间内喷出的气体为研究对象，设火箭推气体的力为F ，根据动量定理，有F △t=△m ·v 因为火箭静止在空中，所以根据牛顿第三定律和平衡条件有F=Mg即 Mg ·△t=△m ·v △t=△m ·v/Mg对同样这一部分气体用动能定理，火箭对它做的功为： 221mv W ∆=所以发动机的功率 MgV Mg mV mv t W P 21)/(212=∆∆=∆=例12：如图3—11所示，小环O 和O ′分别套在不动的竖直 杆AB 和A ′B ′上，一根不可伸长的绳子穿过环O ′，绳的两端分别系在A ′点和O 环上，设环O ′以恒定速度v 向下运动，求当∠AOO ′=α时，环O 的速度.解析：O 、O ′之间的速度关系与O 、O ′的位置有关，即与α 角有关，因此要用微元法找它们之间的速度关系.设经历一段极短时间△t ，O ′环移到C ′，O 环移到C ，自C ′ 与C 分别作为O ′O 的垂线C ′D ′和CD ，从图中看出. ααcos ,cos D O C O OD OC ''=''= 因此OC+O ′C ′=αcos D O OD ''+ ① 因△α极小，所以EC ′≈ED ′，EC ≈ED ，从而OD+O ′D ′≈OO ′－CC ′ ②由于绳子总长度不变，故 OO ′－CC ′=O ′C ′ ③由以上三式可得：OC+O ′C ′=αcos C O '' 即)1cos 1(-''=αC O OC 等式两边同除以△t 得环O 的速度为 )1cos 1(0-=αv v 例13： 在水平位置的洁净的平玻璃板上倒一些水银，由于重力和 表面张力的影响，水银近似呈现圆饼形状（侧面向外凸出），过圆 饼轴线的竖直截面如图3—12所示，为了计算方便，水银和玻璃的 接触角可按180°计算.已知水银密度33/106.13m kg ⨯=ρ，水 银的表面张力系数./49.0m N =σ当圆饼的半径很大时，试估算其厚度h 的数值大约为多少？（取1位有效数字即可）解析：若以整个圆饼状水银为研究对象，只受重力和玻璃板的支持力，在平衡方程中，液体的体积不是h 的简单函数，而且支持力N 和重力mg 都是未知量，方程中又不可能出现表面张力系数，因此不可能用整体分析列方程求解h.现用微元法求解.在圆饼的侧面取一个宽度为△x ，高为h 的体积元，，如图 3—12—甲所示，该体积元受重力G 、液体内部作用在面 积△x ·h 上的压力F ，x gh xh hg S P F ∆⋅=∆⋅==22121ρρ， 还有上表面分界线上的张力F 1=σ△x 和下表面分界线上的 张力F 2=σ△x .作用在前、后两个侧面上的液体压力互相平衡，作用在体积元表面两个弯曲分界上的表面张力的合力，当体积元的宽度较小时，这两个力也是平衡的，图中都未画出.由力的平衡条件有：0cos 21=--F F F θ即 0cos 212=∆-∆-∆x x x gh σθσρ 解得：θρθσcos 1107.2)cos 1(23+⨯=+=-gh 由于 ,2cos 11,20<+<<<θπθ所以 故2.7×10－3m<h<3.8×10－3m 题目要求只取1位有效数字，所以水银层厚度h 的估算值为3×10－3m 或4×10－3m.例14：把一个容器内的空气抽出一些，压强降为p ，容器 上有一小孔，上有塞子，现把塞子拔掉，如图3—13所示. 问空气最初以多大初速度冲进容器？（外界空气压强为p 0、密度为ρ）解析：该题由于不知开始时进入容器内分有多少，不知它 们在容器外如何分布，也不知空气分子进入容器后压强如 何变化，使我们难以找到解题途径.注意到题目中“最初”二字，可以这样考虑：设小孔的面积为S ，取开始时位于小孔外一薄层气体为研究对象，令薄层厚度为△L ，因△L 很小，所以其质量△m 进入容器过程中，不改变容器压强，故此薄层所受外力是恒力，该问题就可以解决了.由以上分析，得：F=(p 0－p)S ① 对进入的△m 气体， 由动能定理得：221mv L F ∆=∆ ② 而 △m=ρS △L联立①、②、③式可得：最初中进容器的空气速度 ρ)(20p p v -=例15：电量Q 均匀分布在半径为R 的圆环上（如图3—14 所示），求在圆环轴线上距圆心O 点为x 处的P 点的电场 强度.解析：带电圆环产生的电场不能看做点电荷产生的电场， 故采用微元法，用点电荷形成的电场结合对称性求解.选电荷元 ,2R Q R q πθ∆=∆它在P 点产生的电场的场强的x 分量为： 22222)(2cos x R xx R R Q R k r q k E x ++∆=∆=∆πθα 根据对称性 322322322)(2)(2)(2x R kQx x R kQxx R kQx E E x +=+=∆+=∆=∑∑ππθπ由此可见，此带电圆环在轴线P 点产生的场强大小相当于带电圆环带电量集中在圆环的某一点时在轴线P 点产生的场强大小，方向是沿轴线的方向.例16：如图3—15所示，一质量均匀分布的细圆环，其半径为R ，质量为m.令此环均匀带正电，总电量为Q.现将此环平放在绝缘的光滑水平桌面上，并处于磁感应强度为B 的均匀磁场中，磁场方向竖直向下. 当此环绕通过其中心的竖直轴以匀角速度ω沿图示方向旋转时，环中的张力等于多少？（设圆环的带电量不减少，不考虑环上电荷之间的作用）解析：当环静止时，因环上没有电流，在磁场中不受力，则 环中也就没有因磁场力引起的张力.当环匀速转动时，环上电 荷也随环一起转动，形成电流，电流在磁场中受力导致环中存 在张力，显然此张力一定与电流在磁场中受到的安培力有关. 由题意可知环上各点所受安培力方向均不同，张力方向也不同， 因而只能在环上取一小段作为研究对象，从而求出环中张力的 大小.在圆环上取△L=R △θ圆弧元，受力情况如图3—15—甲所示.因转动角速度ω而形成的电流 πω2Q I =，电流元I △L 所受的安培力θπω∆=∆=∆QB R LB I F 2 因圆环法线方向合力为圆弧元做匀速圆周运动所需的向心力，R m F T 22sin2ωθ∆=∆-∆ 当△θ很小时，R m QB R T 2222sin ωθπωθθθ∆=∆-∆∆≈∆ θπωθπωθθπ∆=∆-∆∴∆=∆2222R m QB R T m m Θ解得圆环中张力为 )(2ωπωm QB R T += 例17：如图3—16所示，一水平放置的光滑平行导轨上放一质量 为m 的金属杆，导轨间距为L ，导轨的一端连接一阻值为R 的电 阻，其他电阻不计，磁感应强度为B 的匀强磁场垂直于导轨平面. 现给金属杆一个水平向右的初速度v 0，然后任其运动，导轨足够 长，试求金属杆在导轨上向右移动的最大距离是多少？ 解析：水平地从a 向b 看，杆在运动过程中的受力分析 如图3—16—甲所示，这是一个典型的在变力作用下求位移的题，用我们已学过的知识好像无法解决，其实只要 采用的方法得当仍然可以求解.设杆在减速中的某一时刻速度为v ，取一极短时间△t ，发 生了一段极小的位移△x ，在△t 时间内，磁通量的变化为 △φ △φ=BL △x tRx BL tR R I ∆∆=∆∆Φ==ε金属杆受到安培力为tRx L B ILB F ∆∆==22安 由于时间极短，可以认为F 安为恒力，选向右为正方向，在△t 时间内， 安培力F 安的冲量为：Rx L B t F I ∆-=∆⋅-=∆22安 对所有的位移求和，可得安培力的总冲量为x R L B R x L B I 2222)(-=∆-=∑ ① 其中x 为杆运动的最大距离，对金属杆用动量定理可得 I=0－mV 0 ②由①、②两式得：220L B R mV x =。

高中奥林匹克物理竞赛解题方法三、微元法针对训练1．某地强风的风速为v ，设空气的密度为ρ，如果将通过横截面积为S 的风的动能全部转化为电能，则其电功率为多少？2．如图3—19所示，山高为H ，山顶A 和水平面上B 点的水平距离为s.现在修一条冰道ACB ，其中AC 为斜面，冰道光滑，物体从A 点由静止释放，用最短时间经C 到B ，不计过C 点的能量损失.问AC 和水平方向的夹角θ多大？最短时间为多少？3．如图3—21所示，在绳的C 端以速度v 匀速收绳从而拉动低处的物体M 水平前进，当绳AO 段也水平恰成α角时，物体M 的速度多大？4，如图3—22所示，质量相等的两个小球A 和B 通过轻绳绕过两个光滑的定滑轮带动C 球上升，某时刻连接C 球的两绳的夹角为θ，设A 、B 两球此时下落的速度为v ，则C 球上升的速度多大？5．质量为M 的平板小车在光滑的水平面上以v 0向左匀速运动，一质量为m 的小球从高h 处自由下落，与小车碰撞后反弹上升的高度仍为h.设M>>m ，碰撞弹力N>>g ，球与车之间的动摩擦因数为μ，则小球弹起后的水平速度可能是（ ） A ．gh 2 B ．0 C ．gh 22 D ．v 0 6．半径为R 的刚性球固定在水平桌面上.有一质量为M 的圆环状均匀弹性细绳圈，原长 2πa ，a =R/2，绳圈的弹性系数为k （绳伸长s 时，绳中弹性张力为ks ）.将绳圈从球的正 上方轻放到球上，并用手扶着绳圈使其保持水平，并最后停留在某个静力平衡位置.考 虑重力，忽略摩擦.（1）设平衡时弹性绳圈长2πb，b=a2，求弹性系数k；（用M、R、g表示，g为重力加速度）（2）设k=Mg/2π2R，求绳圈的最后平衡位置及长度.7．一截面呈圆形的细管被弯成大圆环，并固定在竖直平面内，在环内的环底A处有一质量为m、直径比管径略小的小球，小球上连有一根穿过环顶B处管口的轻绳，在外力F作用下小球以恒定速度v沿管壁做半径为R的匀速圆周运动，如图3—23所示.已知小球与管内壁中位于大环外侧部分的动摩擦因数为μ，而大环内侧部分的管内壁是光滑的.忽略大环内、外侧半径的差别，认为均为R.试求小球从A点运动到B点过程中F做的功W F.8．如图3—24，来自质子源的质子（初速度为零），经一加速电压为800kV的直线加速器加速，形成电流为1.0mA 的细柱形质子流.已知质子电荷e=1.60×10－19C.这束质子流每秒打到靶上的质子数为.假设分布在质子源到靶之间的加速电场是均匀的，在质子束中与质子源相距l 和4l的两处，各取一段极短的相等长度的质子流，其中质子数分别为n1和n2，则n1: n2.9．如图3—25所示，电量Q均匀分布在一个半径为R的细圆环上，求圆环轴上与环心相距为x的点电荷q所受的力的大小.10．如图3—26所示，一根均匀带电细线，总电量为Q，弯成半径为R的缺口圆环，在细线的两端处留有很小的长为△L的空隙，求圆环中心处的场强.11．如图3—27所示，两根均匀带电的半无穷长平行直导线（它们的电荷线密度为η），端点联线LN 垂直于这两直导线，如图所示.LN 的长度为2R.试求在LN 的中点O 处的电场强度.12．如图3—28所示，有一均匀带电的无穷长直导线，其电荷线密度为η.试求空间任意一点的电场强度.该点与直导线间垂直距离为r.13．如图3—29所示，半径为R 的均匀带电半球面，电荷面密度为δ，求球心O 处的电场强度.14．如图3—30所示，在光滑的水平面上，有一垂直向下的匀强磁场分布在宽度为L 的区域内，现有一个边长为a （a <L ），质量为m 的正方形闭合线框以初速v 0垂直磁场边界滑过磁场后，速度变为v （v <v 0），求：（1）线框在这过程中产生的热量Q ；（2）线框完全进入磁场后的速度v ′.15．如图3—31所示，在离水平地面h 高的平台上有一相距L 的光滑轨道，左端接有已充电的电容器，电容为C ，充电后两端电压为U 1.轨道平面处于垂直向上的磁感应强度为B 的匀强磁场中.在轨道右端放一质量为m 的金属棒，当闭合S ，棒离开轨道后电容器的两极电压变为U 2，求棒落在离平台多远的位置.16．如图3—32所示，空间有一水平方向的匀强磁场，大小为B ，一光滑导轨竖直放置，导轨上接有一电容为C 的电容器，并套一可自由滑动的金属棒，质量为m ，释放后，求金属棒的加速度a .答案1．321v S ρ 2．θ=60°)223(2hs g h + 3．)cos 1/(x v + 4．2cos /θv 5．CD 6．（1）R Mg 22)12(π+ （2）绳圈掉地上，长度为原长 7．22v m mgR πμ+ 8．6.25×1015,2:1 9．2322)(x R QqxK + 10．32R l Q K ρ∆ 11．Rk λ2 12．r k λ2 13．σπR 2 14．2),(210220v v v v v m +='- 15．g hm u u CBL 2)(21- 16．22L CB m mga +=。

运用微元思维方法解物理竞赛试题吕贤年袁孝金所谓微元思维方法一是指从整体中取某个特定的微小部分作为研究对彖，从而达到解决事物整体问题的一种思维方式。

这种思维方法是基于宏观事物的普遍性（即共性）不仅存在于事物发展的全过程屮，而且也包含在每微元的特殊性（即个性）之中这一基木属性的基础上，而产牛的一种创造性思维方式。

因此，我们在研究物理问题时，对于某一具体的研究对象，当从整体或宏观上无法求解时，运用微元思维方法，往往会收到化难为易，化繁为简的意想不到的效果。

木文试通过近年来的冇关全国屮学牛物理竞赛试题为例，导析微元思维方法解题的一般思路，供同学们参考。

一、长度微元△/对长度进行微小分割，称为线分割，分割出來的长度单元，称之为长度微元，用A/表示。

例1 -根无限长的均匀带电细线，弯成图1所示的平面图形。

其中AB是半径为R的半圆弧，AA，〃BB，。

试求圆心0处的电场强度。

（1988年全国中学生物理竞赛试题）解析因为电荷均匀布在整条曲线上，所以不能把它当作点电荷处理。

因此，无法直接应用初等方法求出它在0点所形成的电场强度。

如果将曲线分成无数小线元，可看作点电荷，则弯曲的带电细线在0处所产牛的电场，就是各小段线元在0处的电场强度，就能按矢量合成法求得曲线整体在O处的电场强度。

在半圆弧AB上取任一小段线元ab = A/,则线元ab对应的圆心角为△（）,对应于直导线线元为当厶。

-*。

时，a 图1 逼近于b, 逼近于b‘。

此时，我们可以认为ab所帯电荷△（）集中于一点（如b点）, Yb，所带的电荷集中于对应的另一点（如b‘点）。

这样，对于M张角所包含的区域在O点所形成的场强，我们认为是由两个点电荷形成的。

设细线上单位长度所带的正电荷为则ab线元所带的电荷为Aq= HRA0, Aq在O点所形成的场强为：回，其中AE的方向指向Ob，。

Ra zb z线元所带电荷为Aq= na^b^,距离圆心0的距离用I•表示（△&越小，以上考虑越准确），作aa"垂直于OW,贝!]Za"ah= Zb r OB=0 + A0 因而a'b'= a'a"/cos 0 =aa" r/R,又因为aa" = r0,故得：a r b r =r2A0/R.o因此，点电荷在O点产生的电场强度的大小为：AE =k^=k^=AE,方r2 R向与AE方向相反。

高中奥林匹克物理竞赛解题方法微元法方法简介微元法就就是分析、解决物理问题中得常用方法,也就就是从部分到整体得思维方法。

用该方法可以使一些复杂得物理过程用我们熟悉得物理规律迅速地加以解决,使所求得问题简单化。

在使用微元法处理问题时,需将其分解为众多微小得“元过程”,而且每个“元过程”所遵循得规律就就是相同得，这样,我们只需分析这些“元过程”,然后再将“元过程”进行必要得数学方法或物理思想处理,进而使问题求解。

使用此方法会加强我们对已知规律得再思考,从而引起巩固知识、加深认识与提高能力得作用。

赛题精讲例1:如图3—1所示,一个身高为h得人在灯以悟空速度v沿水平直线行走。

设灯距地面高为H,求证人影得顶端C点就就是做匀速直线运动。

解析:该题不能用速度分解求解,考虑采用“微元法”。

设某一时间人经过AB处,再经过一微小过程△ｔ(△ｔ→０）,则人由AＢ到达Ａ′Ｂ′，人影顶端C点到达C′点,由于△SＡA′=v△t则人影顶端得移动速度可见ｖc与所取时间△t得长短无关，所以人影得顶端C点做匀速直线运动、例2:如图3—2所示,一个半径为Ｒ得四分之一光滑球面放在水平桌面上,球面上放置一光滑均匀铁链,其A端固定在球面得顶点,B端恰与桌面不接触,铁链单位长度得质量为ρ、试求铁链A端受得拉力T、解析:以铁链为研究对象，由由于整条铁链得长度不能忽略不计,所以整条铁链不能瞧成质点,要分析铁链得受力情况,须考虑将铁链分割,使每一小段铁链可以瞧成质点,分析每一小段铁边得受力，根据物体得平衡条件得出整条铁链得受力情况、在铁链上任取长为△Ｌ得一小段(微元)为研究对象,其受力分析如图３—2—甲所示、由于该元处于静止状态，所以受力平衡，在切线方向上应满足:由于每段铁链沿切线向上得拉力比沿切线向下得拉力大△Tθ,所以整个铁链对A端得拉力就就是各段上△Tθ得与,即观察得意义，见图3—２—乙,由于△θ很小,所以ＣD⊥OＣ，∠OCE＝θ△Lcosθ表示△L在竖直方向上得投影△R,所以可得铁链A端受得拉力例3:某行星围绕太阳C沿圆弧轨道运行,它得近日点A离太阳得距离为a,行星经过近日点Ａ时得速度为，行星得远日点B离开太阳得距离为b,如图3—3所示,求它经过远日点Ｂ时得速度得大小、解析：此题可根据万有引力提供行星得向心力求解、也可根据开普勒第二定律,用微元法求解、设行星在近日点Ａ时又向前运动了极短得时间△t,由于时间极短可以认为行星在△ｔ时间内做匀速圆周运动，线速度为,半径为a,可以得到行星在△ｔ时间内扫过得面积同理,设行星在经过远日点B时也运动了相同得极短时间△t，则也有由开普勒第二定律可知:Sａ＝S b即得此题也可用对称法求解、例4:如图３—4所示,长为L得船静止在平静得水面上,立于船头得人质量为m,船得质量为Ｍ,不计水得阻力，人从船头走到船尾得过程中,问:船得位移为多大？解析:取人与船整体作为研究系统,人在走动过程中,系统所受合外力为零，可知系统动量守恒、设人在走动过程中得△t时间内为匀速运动,则可计算出船得位移、设v1、v2分别就就是人与船在任何一时刻得速率,则有①两边同时乘以一个极短得时间△ｔ, 有②由于时间极短,可以认为在这极短得时间内人与船得速率就就是不变得,所以人与船位移大小分别为,由此将②式化为③把所有得元位移分别相加有④即ms1=Ms2⑤此式即为质心不变原理、其中ｓ1、s2分别为全过程中人与船对地位移得大小, 又因为L＝s1+s2⑥由⑤、⑥两式得船得位移例5:半径为R得光滑球固定在水平桌面上,有一质量为M得圆环状均匀弹性绳圈,原长为πR,且弹性绳圈得劲度系数为k,将弹性绳圈从球得正上方轻放到球上，使弹性绳圈水平停留在平衡位置上,如图３—5所示,若平衡时弹性绳圈长为，求弹性绳圈得劲度系数k、解析:由于整个弹性绳圈得大小不能忽略不计,弹性绳圈不能瞧成质点,所以应将弹性绳圈分割成许多小段,其中每一小段△m两端受得拉力就就就是弹性绳圈内部得弹力F、在弹性绳圈上任取一小段质量为△m作为研究对象,进行受力分析、但就就是△m受得力不在同一平面内,可以从一个合适得角度观察、选取一个合适得平面进行受力分析，这样可以瞧清楚各个力之间得关系、从正面与上面观察,分别画出正视图得俯视图,如图3—5—甲与2—３—５—乙、先瞧俯视图3—5—甲,设在弹性绳圈得平面上,△m所对得圆心角就就是△θ,则每一小段得质量△m在该平面上受拉力F得作用,合力为因为当θ很小时, 所以再瞧正视图3—5—乙,△m受重力△mg,支持力Ｎ,二力得合力与T平衡、即现在弹性绳圈得半径为所以因此T= ①、②联立，,解得弹性绳圈得张力为：设弹性绳圈得伸长量为ｘ则所以绳圈得劲度系数为:例6：一质量为M、均匀分布得圆环,其半径为r,几何轴与水平面垂直,若它能经受得最大张力为T,求此圆环可以绕几何轴旋转得最大角速度、解析：因为向心力F=mrω2,当ω一定时,r越大,向心力越大,所以要想求最大张力Ｔ所对应得角速度ω,r应取最大值、如图3—6所示,在圆环上取一小段△L,对应得圆心角为△θ,其质量可表示为,受圆环对它得张力为Ｔ，则同上例分析可得因为△θ很小，所以,即解得最大角速度例7:一根质量为M，长度为L得铁链条，被竖直地悬挂起来,其最低端刚好与水平接触,今将链条由静止释放,让它落到地面上,如图3—7所示,求链条下落了长度x时,链条对地面得压力为多大？解析:在下落过程中链条作用于地面得压力实质就就就是链条对地面得“冲力”加上落在地面上那部分链条得重力、根据牛顿第三定律,这个冲力也就等于同一时刻地面对链条得反作用力,这个力得冲量,使得链条落至地面时得动量发生变化、由于各质元原来得高度不同,落到地面得速度不同,动量改变也不相同、我们取某一时刻一小段链条(微元）作为研究对象,就可以将变速冲击变为恒速冲击、设开始下落得时刻ｔ＝０，在ｔ时刻落在地面上得链条长为ｘ，未到达地面部分链条得速度为ｖ，并设链条得线密度为ρ、由题意可知,链条落至地面后,速度立即变为零、从t时刻起取很小一段时间△ｔ,在△t内又有△M=ρ△ｘ落到地面上静止、地面对△Ｍ作用得冲量为因为所以解得冲力:,其中就就就是ｔ时刻链条得速度v，故链条在t时刻得速度v即为链条下落长为ｘ时得即时速度,即ｖ２=2gｘ,代入Ｆ得表达式中,得此即t时刻链对地面得作用力，也就就就是ｔ时刻链条对地面得冲力、所以在t时刻链条对地面得总压力为例８:一根均匀柔软得绳长为L,质量为m，对折后两端固定在一个钉子上,其中一端突然从钉子上滑落,试求滑落得绳端点离钉子得距离为x时,钉子对绳子另一端得作用力就就是多大? 解析：钉子对绳子另一端得作用力随滑落绳得长短而变化,由此可用微元法求解、如图3—8所示，当左边绳端离钉子得距离为ｘ时,左边绳长为,速度，右边绳长为又经过一段很短得时间△t以后,左边绳子又有长度得一小段转移到右边去了,我们就分析这一小段绳子,这一小段绳子受到两力:上面绳子对它得拉力T与它本身得重力为绳子得线密度),根据动量定理,设向上方向为正由于△ｔ取得很小,因此这一小段绳子得重力相对于T来说就就是很小得,可以忽略，所以有因此钉子对右边绳端得作用力为例9:图３—9中,半径为Ｒ得圆盘固定不可转动，细绳不可伸长但质量可忽略,绳下悬挂得两物体质量分别为Ｍ、m、设圆盘与绳间光滑接触,试求盘对绳得法向支持力线密度、解析:求盘对绳得法向支持力线密度也就就就是求盘对绳得法向单位长度所受得支持力、因为盘与绳间光滑接触，则任取一小段绳,其两端受得张力大小相等,又因为绳上各点受得支持力方向不同,故不能以整条绳为研究对象,只能以一小段绳为研究对象分析求解、在与圆盘接触得半圆形中取一小段绳元△L,△L所对应得圆心角为△θ,如图3—9—甲所示,绳元△L两端得张力均为T,绳元所受圆盘法向支持力为△N，因细绳质量可忽略,法向合力为零,则由平衡条件得：当△θ很小时, ∴△N=Ｔ△θ又因为△Ｌ=Ｒ△θ则绳所受法向支持力线密度为①以M、m分别为研究对象,根据牛顿定律有Mg－T=Mａ②T-mｇ=m a③由②、③解得:将④式代入①式得:例10：粗细均匀质量分布也均匀得半径为分别为R与r得两圆环相切、若在切点放一质点ｍ,恰使两边圆环对m得万有引力得合力为零,则大小圆环得线密度必须满足什么条件？解析:若要直接求整个圆对质点m得万有引力比较难,当若要用到圆得对称性及要求所受合力为零得条件,考虑大、小圆环上关于切点对称得微元与质量m得相互作用,然后推及整个圆环即可求解、如图3—10所示,过切点作直线交大小圆分别于P、Q两点,并设与水平线夹角为α,当α有微小增量时,则大小圆环上对应微小线元其对应得质量分别为由于△α很小，故△m 1、△m 2与m 得距离可以认为分别就就是所以△m 1、△m 2与m 得万有引力分别为 222222212111)cos 2(2,)cos 2(2ααρααρr m R G r m Gm F R m R G r m Gm F ∆⋅=∆=∆∆⋅=∆=∆ 由于α具有任意性,若△F １与△F ２得合力为零,则两圆环对m 得引力得合力也为零， 即解得大小圆环得线密度之比为:例11:一枚质量为M 得火箭，依靠向正下方喷气在空中保持静止,如果喷出气体得速度为v,那么火箭发动机得功率就就是多少?解析:火箭喷气时，要对气体做功，取一个很短得时间,求出此时间内,火箭对气体做得功，再代入功率得定义式即可求出火箭发动机得功率、选取在△t 时间内喷出得气体为研究对象,设火箭推气体得力为F ，根据动量定理,有F △ｔ=△m ·ｖ 因为火箭静止在空中,所以根据牛顿第三定律与平衡条件有F=M ｇ 即 Mg ·△t=△m ·v △t=△m ·ｖ/M ｇ对同样这一部分气体用动能定理，火箭对它做得功为:所以发动机得功率例1２:如图3—１１所示,小环Ｏ与O ′分别套在不动得竖直杆AB 与A ′B ′上,一根不可伸长得绳子穿过环O ′,绳得两端分别系在A ′点与Ｏ环上，设环O ′以恒定速度ｖ向下运动,求当∠AOO ′=α时，环O 得速度、解析：O 、O ′之间得速度关系与O 、O ′得位置有关,即与α角有关,因此要用微元法找它们之间得速度关系、设经历一段极短时间△ｔ,O ′环移到C ′,Ｏ环移到Ｃ，自C ′与C 分别作为O ′O 得垂线C ′D ′与CD,从图中瞧出、因此OC+O ′C ′= ①因△α极小，所以ＥＣ′≈ＥD ′,E Ｃ≈ＥD,从而ＯD+O ′D ′≈OO ′－CC ′ ②由于绳子总长度不变,故 OO ′-CC ′=O ′Ｃ′ ③由以上三式可得:ＯC+Ｏ′Ｃ′= 即等式两边同除以△t 得环O 得速度为例１3： 在水平位置得洁净得平玻璃板上倒一些水银,由于重力与表面张力得影响,水银近似呈现圆饼形状(侧面向外凸出),过圆饼轴线得竖直截面如图3—1２所示，为了计算方便,水银与玻璃得接触角可按180°计算、已知水银密度,水银得表面张力系数当圆饼得半径很大时,试估算其厚度h 得数值大约为多少？（取1位有效数字即可)解析：若以整个圆饼状水银为研究对象,只受重力与玻璃板得支持力，在平衡方程中,液体得体积不就就是h 得简单函数，而且支持力Ｎ与重力mg 都就就是未知量,方程中又不可能出现表面张力系数，因此不可能用整体分析列方程求解h 、现用微元法求解、在圆饼得侧面取一个宽度为△x ,高为h 得体积元,,如图3—１２—甲所示,该体积元受重力G 、液体内部作用在面积△x ·h 上得压力F ，,还有上表面分界线上得张力F 1=σ△x 与下表面分界线上得张力Ｆ2=σ△x 、作用在前、后两个侧面上得液体压力互相平衡，作用在体积元表面两个弯曲 分界上得表面张力得合力，当体积元得宽度较小时,这两个力也就就是平衡得,图中都未画出、 由力得平衡条件有：即解得:由于 故2、7×10-3m ＜h<3、８×1０－3ｍ题目要求只取１位有效数字,所以水银层厚度ｈ得估算值为3×10－３ｍ或４×10－3m 、 例14:把一个容器内得空气抽出一些，压强降为p,容器上有一小孔,上有塞子,现把塞子拔掉，如图３—1３所示、问空气最初以多大初速度冲进容器?(外界空气压强为p 0、密度为ρ)解析：该题由于不知开始时进入容器内分有多少,不知它们在容器外如何分布，也不知空气分子进入容器后压强如何变化,使我们难以找到解题途径、注意到题目中“最初”二字,可以这样考虑:设小孔得面积为Ｓ,取开始时位于小孔外一薄层气体为研究对象，令薄层厚度为△L ，因△L 很小,所以其质量△m 进入容器过程中,不改变容器压强,故此薄层所受外力就就是恒力,该问题就可以解决了、由以上分析,得:F ＝(ｐ0-p)S ① 对进入得△m 气体,由动能定理得: ② 而 △m ＝ρS △L联立①、②、③式可得:最初中进容器得空气速度例15:电量Q 均匀分布在半径为R 得圆环上(如图３—１4所示)，求在圆环轴线上距圆心O 点为x 处得Ｐ点得电场强度、解析:带电圆环产生得电场不能瞧做点电荷产生得电场,故采用微元法,用点电荷形成得电场结合对称性求解、选电荷元 它在P 点产生得电场得场强得x 分量为:根据对称性 322322322)(2)(2)(2x R kQx x R kQx x R kQxE E x +=+=∆+=∆=∑∑ππθπ由此可见,此带电圆环在轴线P 点产生得场强大小相当于带电圆环带电量集中在圆环得某一点时在轴线P点产生得场强大小,方向就就是沿轴线得方向、例16:如图3—１5所示,一质量均匀分布得细圆环,其半径为R,质量为m、令此环均匀带正电,总电量为Ｑ、现将此环平放在绝缘得光滑水平桌面上,并处于磁感应强度为Ｂ得均匀磁场中，磁场方向竖直向下、当此环绕通过其中心得竖直轴以匀角速度ω沿图示方向旋转时，环中得张力等于多少？(设圆环得带电量不减少,不考虑环上电荷之间得作用)解析:当环静止时，因环上没有电流，在磁场中不受力,则环中也就没有因磁场力引起得张力、当环匀速转动时,环上电荷也随环一起转动，形成电流,电流在磁场中受力导致环中存在张力,显然此张力一定与电流在磁场中受到得安培力有关、由题意可知环上各点所受安培力方向均不同,张力方向也不同,因而只能在环上取一小段作为研究对象,从而求出环中张力得大小、在圆环上取△Ｌ＝Ｒ△θ圆弧元,受力情况如图3—15—甲所示、因转动角速度ω而形成得电流,电流元I△L所受得安培力因圆环法线方向合力为圆弧元做匀速圆周运动所需得向心力,当△θ很小时,解得圆环中张力为例17:如图3—1６所示,一水平放置得光滑平行导轨上放一质量为m得金属杆,导轨间距为L,导轨得一端连接一阻值为Ｒ得电阻,其她电阻不计,磁感应强度为B得匀强磁场垂直于导轨平面、现给金属杆一个水平向右得初速度v０,然后任其运动,导轨足够长,试求金属杆在导轨上向右移动得最大距离就就是多少?解析:水平地从a向ｂ瞧,杆在运动过程中得受力分析如图3—16—甲所示,这就就是一个典型得在变力作用下求位移得题,用我们已学过得知识好像无法解决，其实只要采用得方法得当仍然可以求解、设杆在减速中得某一时刻速度为v，取一极短时间△ｔ，发生了一段极小得位移△ｘ,在△t时间内,磁通量得变化为△φ△φ=BL△x金属杆受到安培力为由于时间极短,可以认为F安为恒力,选向右为正方向,在△t时间内,安培力F安得冲量为:对所有得位移求与，可得安培力得总冲量为①其中x为杆运动得最大距离,对金属杆用动量定理可得I=0－mV0②由①、②两式得:例１8:如图3—１7所示,电源得电动热为E,电容器得电容为C,Ｓ就就是单刀双掷开关，MN、PQ就就是两根位于同一水平面上得平行光滑长导轨,它们得电阻可以忽略不计,两导轨间距为L,导轨处在磁感应强度为B得均匀磁场中,磁场方向垂直于两导轨所在得平面并指向图中纸面向里得方向、L1与L２就就是两根横放在导轨上得导体小棒,质量分别为m１与m2,且、它们在导轨上滑动时与导轨保持垂直并接触良好,不计摩擦,两小棒得电阻相同，开始时两根小棒均静止在导轨上、现将开关Ｓ先合向1,然后合向２、求:(1)两根小棒最终速度得大小;（2)在整个过程中得焦耳热损耗、(当回路中有电流时,该电流所产生得磁场可忽略不计)解析:当开关S先合上１时，电源给电容器充电,当开关S再合上２时，电容器通过导体小棒放电，在放电过程中,导体小棒受到安培力作用,在安培力作用下,两小棒开始运动，运动速度最后均达到最大、（１)设两小棒最终得速度得大小为v,则分别为L1、Ｌ2为研究对象得：①同理得: ②由①、②得:又因为所以而Ｑ=CＥq=CU′＝CBL v所以解得小棒得最终速度(２)因为总能量守恒,所以即产生得热量针对训练１、某地强风得风速为ｖ，设空气得密度为ρ,如果将通过横截面积为S得风得动能全部转化为电能,则其电功率为多少?２、如图3—19所示,山高为H，山顶A与水平面上B点得水平距离为ｓ、现在修一条冰道ＡCB,其中AＣ为斜面,冰道光滑,物体从Ａ点由静止释放，用最短时间经Ｃ到B,不计过C点得能量损失、问AC与水平方向得夹角θ多大？最短时间为多少?３、如图３—21所示,在绳得C端以速度v匀速收绳从而拉动低处得物体M水平前进,当绳AO段也水平恰成α角时，物体M得速度多大？4,如图３—22所示，质量相等得两个小球A与Ｂ通过轻绳绕过两个光滑得定滑轮带动C 球上升,某时刻连接C球得两绳得夹角为θ,设A、B两球此时下落得速度为ｖ,则C球上升得速度多大？5、质量为M得平板小车在光滑得水平面上以v0向左匀速运动,一质量为m得小球从高ｈ处自由下落,与小车碰撞后反弹上升得高度仍为h、设M>>m，碰撞弹力Ｎ>>g，球与车之间得动摩擦因数为μ,则小球弹起后得水平速度可能就就是（)A、B、０C、D、v０6、半径为R得刚性球固定在水平桌面上、有一质量为M得圆环状均匀弹性细绳圈,原长2πa,a=R/2,绳圈得弹性系数为ｋ(绳伸长s时,绳中弹性张力为kｓ）、将绳圈从球得正上方轻放到球上,并用手扶着绳圈使其保持水平，并最后停留在某个静力平衡位置、考虑重力，忽略摩擦、（１）设平衡时弹性绳圈长2πｂ,b=，求弹性系数k；(用M、R、g表示,g为重力加速度) (2)设k＝Ｍｇ/2π2R,求绳圈得最后平衡位置及长度、7、一截面呈圆形得细管被弯成大圆环,并固定在竖直平面内,在环内得环底A处有一质量为ｍ、直径比管径略小得小球,小球上连有一根穿过环顶B处管口得轻绳,在外力Ｆ作用下小球以恒定速度v沿管壁做半径为Ｒ得匀速圆周运动,如图3—23所示、已知小球与管内壁中位于大环外侧部分得动摩擦因数为μ,而大环内侧部分得管内壁就就是光滑得、忽略大环内、外侧半径得差别，认为均为Ｒ、试求小球从Ａ点运动到B点过程中F做得功W F、8、如图3—２4,来自质子源得质子(初速度为零）,经一加速电压为800kV得直线加速器加速，形成电流为1、０mA得细柱形质子流、已知质子电荷ｅ=1、6０×１0－19C、这束质子流每秒打到靶上得质子数为、假设分布在质子源到靶之间得加速电场就就是均匀得,在质子束中与质子源相距l与4l得两处,各取一段极短得相等长度得质子流,其中质子数分别为n1与n2,则ｎ1: n2、9、如图3—25所示,电量Q均匀分布在一个半径为R得细圆环上,求圆环轴上与环心相距为ｘ得点电荷q所受得力得大小、1０、如图３—26所示,一根均匀带电细线，总电量为Q,弯成半径为R得缺口圆环,在细线得两端处留有很小得长为△Ｌ得空隙，求圆环中心处得场强、11、如图3—27所示,两根均匀带电得半无穷长平行直导线(它们得电荷线密度为η),端点联线LN垂直于这两直导线,如图所示、LＮ得长度为２Ｒ、试求在ＬN得中点Ｏ处得电场强度、12、如图3—2８所示，有一均匀带电得无穷长直导线,其电荷线密度为η、试求空间任意一点得电场强度、该点与直导线间垂直距离为r、13、如图3—２9所示,半径为R得均匀带电半球面,电荷面密度为δ，求球心Ｏ处得电场强度、14、如图3—３０所示，在光滑得水平面上,有一垂直向下得匀强磁场分布在宽度为L得区域内,现有一个边长为a(a＜L),质量为m得正方形闭合线框以初速v0垂直磁场边界滑过磁场后,速度变为v（v<v0)，求：（1）线框在这过程中产生得热量Ｑ;（2)线框完全进入磁场后得速度v′、15、如图3—３1所示，在离水平地面h高得平台上有一相距Ｌ得光滑轨道，左端接有已充电得电容器,电容为C,充电后两端电压为U1、轨道平面处于垂直向上得磁感应强度为B得匀强磁场中、在轨道右端放一质量为m得金属棒,当闭合S,棒离开轨道后电容器得两极电压变为U2, 求棒落在离平台多远得位置、１6、如图3—3２所示，空间有一水平方向得匀强磁场，大小为B,一光滑导轨竖直放置，导轨上接有一电容为C得电容器,并套一可自由滑动得金属棒，质量为m,释放后，求金属棒得加速度a、答案:１、2、θ＝60°3、４、5、CD6、(1) (2)绳圈掉地上，长度为原长7、８、6、２5×1015，2:１9、１0、１１、12、１３、１4、15、1６、。

微元法简介
----高中物理竞赛讲义（一）一、微元法的应用范围：
一、何时使用微元法
二、微元法处理的可靠性
三、一些经典模型中的微元法
二、微元法处理的关键步骤：
一、微对象的选取
二、微过程处理
三、微小量的选取与近似处理
三、常用的微元法技巧及微元法遵循的一些一般原则：
一、化曲为直
二、尝试选取
三、近似的原则
四、一些微元法应用中的关键细节：
一、特征
二、微元使用的暗示性语言
三、定量的与定性的描述
一、何时使用微元法
微元法常用于处理非均匀变化的问题，对于均匀变化问题（例如最简单的匀速直线运动00x t v x +⋅=）其过程相对简单
因而无需使用微元法。

而对于比较复杂的非均匀变化的过程以及非均匀的对象（例如将试探电荷从点电荷形成的电场某一点处移到无穷远处的做功问题；大气层整体的气体密度分布的分析等）不能直接得到所研究量的关系，但是通过选取整个对象中的一小部分或者整个过程中的一小段（即微元），具体分析所取微元遵循的规律并由此推广到研究对象整体就可以使问题迎刃而解。

微元法的基本思路也就是如此。

二、微元法处理的可靠性
了解了微元法处理的一般对象及基本思路之后自然会有这样的疑问，从微元到整体的处理方法是否具有可靠性呢？
答案是肯定的，我们在选取微元的时候关注于所选微元的一般性质或特点（例如求解单个天体万有引力对质点的做功问题时，其做功的形式及表达式在引力场中任何一处都是相同的即x x GM
W ∆⋅=∆2）而这种性质在整体上也是成立的，这自然
保证了处理的可靠性。

三、一些经典模型中的微元法
A 、有心力场的做功问题
B 、悬链线等绳子问题。

作者： 余建刚
作者机构： 广东省佛山市南海区石门中学,广东佛山528248
出版物刊名： 物理教师：高中版
页码： 63-66页
主题词： 微元法 物理 思维方法 变化量 高中 竞赛题 例题解析
摘要：微元法，又称元素法，是指从整体中取某一特定的微小部分作为研究对象。

从而达到解决事物整体的一种思维方法，微元法是物理学中研究连续变化量的一种常用方法，即把整个复杂、变化的物理过程分解为许多短暂的小过程或把研究对象整体分割成大量的微小的单元来考察。

然后通过对这些小过程或微小局部的研究从而归纳出适用于全过程或整体的结论。

受力情况ꎬ进而引申到弹力知识的学习上.学生对于最近发生的重大事件非常感兴趣ꎬ非常关注奥运会ꎬ再加上教师的精心引导ꎬ也会对弹力知识的学习非常感兴趣.在激发学生的学习兴趣之后ꎬ教师也要注意引导学生进行创新ꎬ培养学生的创新习惯.比如教师在引导学生学习弹力知识之后ꎬ应引导学生去发现生活中更多的弹力现象ꎬ让学生去熟悉弹力知识ꎬ有些学生也会提出错误的例子ꎬ然后教师带领学生分析ꎬ发现新的力学知识.㊀㊀三㊁倡导合作学习ꎬ提升创新能力在高中物理学习中ꎬ教师也要倡导合作学习ꎬ引导学生通过合作学习物理知识的方式来进行创新学习ꎬ并培养学生的创新能力.教师可以通过小组学习的方式来培养学生合作学习的习惯ꎬ将学生分成数个小组ꎬ让学生以小组形式完成学习任务.比如教师可以让小组学生进行课前预习㊁解决物理习题㊁上台讲解物理知识ꎬ通过小组完成综合型任务ꎬ学生可以获得物理知识㊁综合能力的全面提升.另外ꎬ教师还可以鼓励学生进行自主合作学习ꎬ让学生自由组合完成课外物理知识的学习ꎬ比如学生在参加奥林匹克物理竞赛时ꎬ教师可以鼓励学生在赛前准备时进行合作ꎬ在练习时互相帮助ꎬ互相激励ꎬ从而提升学生的学习效率.通过长期的合作学习ꎬ学生的合作意识也会得到稳固ꎬ其合作能力也会大幅提升.在高中物理教学中ꎬ教师应重视培养学生创新能力.广大教师可以参考本文方案ꎬ更新师生理念ꎬ建立创新意识ꎬ激发其创新兴趣ꎬ培养创新习惯ꎬ并通过合作学习逐步提升其创新能力㊁合作能力㊁交流能力㊁表达能力.㊀㊀参考文献:[１]陈方.高中物理教学中创新能力的培养研究[Ｊ].高中生学习:师者ꎬ２０１３(１０):２８－２８.[２]黄春生ꎬ李娜.如何在高中物理教学中培养学生的创新能力[Ｊ].现代交际ꎬ２０１５(５):１９５－１９５.[责任编辑:闫久毅]高中物理学习中应用微元法进行解题的实践分析姜凯元(山东省青岛格兰德中学㊀２６６０３５)摘㊀要: 微元法 是高中物理解题一种经典的解题方法.这种解题方法能够将复杂的物理问题尽量简单化ꎬ将问题分解成为小问题ꎬ然后从局部出发解决整体问题ꎬ最终达到快速准确解题的目的.将 微元法 应用在高中物理解题当中ꎬ可以有效的提高解题速度ꎬ同时锻炼学生的解题能力.本文将结合具体实例ꎬ探讨 微元法 在高中物理解题中的应用.关键词:微元法ꎻ高中物理ꎻ解题中图分类号:Ｇ６３２㊀㊀㊀㊀㊀㊀文献标识码:Ａ㊀㊀㊀㊀㊀㊀文章编号:１００８－０３３３(２０１８)１２－００６１－０２收稿日期:２０１８－０１－２０作者简介:姜凯元(２００１.１－)ꎬ男ꎬ高中在读.㊀㊀ 微元法 指的是在局部具有相同物理规律的前提下ꎬ将一个复杂的大问题分解为多个小问题ꎬ即多个 元 ꎬ然后选择其中最具有代表性的局部进行分析ꎬ从而解决整体问题. 微元法 的使用可以把变化的物理过程转变为不变的物理过程ꎬ从而简化了物理问题ꎬ是高中生必须要掌握好的物理方法之一.㊀㊀一㊁ 微元法 解决变力做功问题将一个复杂的问题进行分割ꎬ即可以让原来问题变得简单化.在力学问题当中ꎬ常见的 元 有: 线元 ㊁ 面积元 ㊁ 质量元 以及 时间元 等.在解决实际问题时ꎬ首先需要分析研究对象ꎬ选取最为合适的 微元 ꎬ然后运用所学物理规律分析 微元 的运动过程ꎬ最后叠加求解整个过程.例１㊀现使用一个大小为１０Ｎꎬ方向沿圆周切线方向的力作用于小滚珠ꎬ让其沿着半径为Ｒ的圆周运动ꎬ请思考:当滚珠回到起点时ꎬ力Ｆ做功的大小.解析㊀在本题中ꎬ由于力的方向时刻在变化ꎬ不能从整个过程考虑ꎬ使用恒力做功的公式ꎬ但是力的方向始终与物体的运动方向相同.选择 线元 来解决此题ꎬ即将整个圆周分为若干个小部分ꎬ观察每个 线元 ꎬ我们可以认为是恒力做功ꎬ使用公式Ｗ＝Ｆ ΔＬꎬ所有的小部分之和１６Copyright©博看网 . All Rights Reserved.为整个圆周的周长ꎬ因此可以得到Ｗ＝ðＦ ΔＬ＝ＦðΔＬ＝Ｆ ２πＲ＝２πＲＦ.例２㊀将一木块水平放置在光滑的水平面上ꎬ左端使用弹簧与竖直墙壁链接ꎬ右端有一水平方向的力作用于木块ꎬ使物体缓慢前进ꎬ已知弹簧的劲度系数为ｋꎬ求拉力对木块做的功?解析㊀分析整个过程ꎬ可以得到拉力始终是变化的ꎬ但是由于物体是匀速运动ꎬ因此拉力始终等于弹簧的弹力ꎬ弹簧的弹力与伸长量成正比.此题当中ꎬ我们仍然使用 线元 ꎬ将弹簧的伸长量划分为ｎ段ꎬ则在每一段上可以将拉力近似看作恒力ꎬ在第ｍ段上拉力做功为Ｗｍ＝ｋ ｍｘｎ ｘｎ＝ｋｍｘ２ｎ２ꎬ在拉伸ｘ的过程中ꎬ所做功之和为ðｗｍ＝ðｎｍ＝１ｋｍｘ２ｎ２＝ｋｘ２ｎ２ ｎ(ｎ＋１)２.假设ｎ趋向于无穷大ꎬ则可以得到拉力所做的功ꎬ即ｗ＝１２ｋｘ２.㊀㊀二㊁ 微元法 解决运动问题高中物理当中诸多的运动学概念都使用了微元法进行定义ꎬ在人教版的教材上ꎬ微元法已经有所体现.例如在阐述瞬时速度时ꎬ教材考虑的时运动对象从ｔ到ｔ＋Δｔ这段时间内速度的变化ꎬ将Δｔ趋于零即可以认为这段时间内的平均速度即为瞬时速度.实际的解题过程当中ꎬ运动的合成与分解等问题上使用到 微元法 ꎬ可以让解题效率得到显著提高.例３㊀在距离水平面ｈ高的平台上ꎬ现使用定滑轮匀速拉动水平面上的一木箱ꎬ现假设水平面与木箱之间不存在摩擦力ꎬ若人匀速拉动绳子的速度大小为ｖꎬ则当绳子与水平面夹角为α时ꎬ求木箱运动的速度.解析㊀绳子在人的拉动下所做的运动为匀速运动ꎬ由于木箱与绳子的夹角一直在改变ꎬ因此木箱所做的运动是非匀变速直线运动.题目要求我们求解的是木箱在某个位置时的瞬时速率ꎬ则我们可以选择 时间元 ꎬ从该时刻起经过某个 时间元 之后ꎬ这个时间段的平均速度.当这个时间元趋近于零时ꎬ这个平均速度即是所求的瞬时速度.假设木箱在ɖ角度时ꎬ经过Δｔ时间之后前进了Δｘ的距离ꎬ则绳长变化为ΔＬ＝Δｘｃｏｓαꎬ则有ΔＬΔｔ＝ΔｘΔｔｃｏｓαꎬ即ｖ＝ｖ０ｃｏｓαꎬｖ０＝ｖｃｏｓα.㊀㊀三㊁ 微元法 解决综合性问题上述的三个例题都是 微元法 的简单应用ꎬ但是实际的考试当中ꎬ综合类的题目仍然占很大比重.综合类的问题往往会结合力学㊁电磁学㊁运动学等各个知识点进行综合性命题ꎬ这类题目往往难度较大ꎬ对学生物理的综合能力要求较高.解决综合性问题时ꎬ首先要求学生能够熟练掌握题目中涉及到的相关物理概念以及规律ꎬ然后找到使用 微元法 的研究对象ꎬ借助数学知识ꎬ解决问题.下面结合具体的题目进行分析:例４㊀有两条间距为Ｌ的平行导轨.导轨的上方有一个平行板电容器.现将导轨放置于匀强磁场当中ꎬ方向垂直于导轨所在的平面.将一个金属棒放置于导轨上ꎬ金属棒沿着导轨由静止开始下滑ꎬ且始终接触良好.现已知导轨与水平地面之间的夹角为αꎬ电容器的电容为Ｃꎬ磁感应强度大小为Ｂꎬ金属棒质量为ｍꎬ与导轨之间的动摩擦因子为μ.求:金属棒的速度大小与时间的关系.分析㊀此题综合性较强ꎬ考察了电学㊁电磁感应以及运动学等多方面的知识.拿到题目以后ꎬ首先需要对问题进行分析:在一个时间段流经金属棒的电荷量等于平行电容器极板在该时间间隔内增加的电荷量.从而建立起一个与时间相关的等式.因此此题中选择 时间元 进行解答.解㊀根据定义可以求得电容器积累的电荷量为Ｑ＝Ｃ Ｕ＝ＣＢＬｖ.在Δｔ时间内增加的电荷量为ΔＱ＝ＣＢＬΔｖ.根据运动学知识可以得到ａ＝ΔｖΔｔ.下面重点在于求加速度ａꎬ因此需要对金属棒进行受力分析.金属棒受到磁场沿导轨向上的力ꎬ斜向上的摩擦力以及重力.根据牛顿第二定律可以得到:ｍｇｓｉｎα－ＢＬｉ－μｍｇｃｏｓα＝ｍａꎬ可以得到ａ＝ｍ(ｓｉｎα－μα)ｍ＋Ｂ２Ｌ２Ｃｇ.金属棒做初速度为零的匀加速运动ꎬ则ｖ＝ｍ(ｓｉｎα－μα)ｍ＋Ｂ２Ｌ２Ｃｇｔ.经过上述例题ꎬ可以发现使用 微元法 进行解题时ꎬ思路是将一个整体的物理问题分解成为多个局部的问题ꎬ进行分析思考之后ꎬ将结论放回到整体中.关键在于找到最具代表性的 元 .常见的解题步骤:１)判定研究对象２)分析局部的过程和规律３)叠加到整体进行求解.随着物理改革的不断深入ꎬ高中生面临的物理问题越来越复杂ꎬ综合性更强.对高中物理的学习造成了更多的困难. 微元法 是处理复杂物理问题常用的一种思维ꎬ教师在授课过程中ꎬ要让学生明白 微元法 思想的核心并且学会根据具体的题目进行应用.教师要把重心放在方法和技巧的教学上ꎬ让学生的综合物理素养得到提高.㊀㊀参考文献:[１]崔利花.分析高中物理解题中 微元法 的应用探析[Ｊ].数理化解题研究ꎬ２０１５(１５):５６－５６.[２]曹志扬.微元法在高中物理解题过程中的应用分析[Ｊ].中学生数理化:学习研版ꎬ２０１７(９):８４－８４.[责任编辑:闫久毅]２６Copyright©博看网 . All Rights Reserved.。

微元法和微积分在物理竞赛培优中的运用摘要：在物理竞赛培优教学过程中采用微元法和微积分法拓宽学生的分析、表达和演算；提高学生创造性思维能力。

本文针对几个典型例题采用微元法和微积分法进行分析、讨论、演算和点评，从而认识到微元法和微积分法解题的关键点及数学运算的难易程度，有助于学生根据自己的数学知识采用适当的解题方法快速准确解题。

关键词：微元法；微积分；物理竞赛；培优Application OfInfinitesimal Method and Calculus In PhysicsCompetition Excellent TrainingAbstract: Infinitesimal method and calculus method are notonly applied to expand students’ ability in analysis, expression and calculation duringphysics competition excellent training, but also applied to improve students' creative thinking ability.This paper aims at adopting infinitesimal method and calculus method to analyze, discuss, calculate and comment on several typical problems, so as to realize the key points of solving problems by infinitesimal method and calculus method and the difficulty degree of mathematical operation. This is also helpful for students to solve problems quickly and accurately by using appropriate method according to their own mathematical knowledge.Key Words:Infinitesimal Method；Calculus；Physics competition；Excellent training引言物理学是一切自然学科的基础，它被公认为科学技术发展中最重要的带头学科，物理学对各种工科专业有直接或间接的支撑。

高中奥林匹克物理竞赛解题方法三三、微元法方法简介微元法是分析、解决物理问题中的常用方法，也是从部分到整体的思维方法。

用该方法可以使一些复杂的物理过程用我们熟悉的物理规律迅速地加以解决，使所求的问题简单化。

在使用微元法处理问题时，需将其分解为众多微小的“元过程”，而且每个“元过程”所遵循的规律是相同的，这样，我们只需分析这些“元过程”，然后再将“元过程”进行必要的数学方法或物理思想处理，进而使问题求解。

使用此方法会加强我们对已知规律的再思考，从而引起巩固知识、加深认识和提高能力的作用。

赛题精讲例1：如图3—1所示，一个身高为h 的人在灯以悟空速度v 沿水平直线行走。

设灯距地面高为H ，求证人影的顶端C 点是做匀速直线运动。

解析：该题不能用速度分解求解，考虑采用“微元法”。

设某一时间人经过AB 处，再经过一微小过程△t （△t →0），则人由AB 到达A ′B ′，人影顶端C 点到达C ′点，由于△S AA ′=v △t 则人影顶端的 移动速度hH Hv t S h H H t S v A A t C C t C -=∆∆-=∆∆='→∆'→∆00lim lim 可见v c 与所取时间△t 的长短无关，所以人影的顶端C 点做匀速直线运动.例2：如图3—2所示，一个半径为R 的四分之一光滑球面放在水平桌面上，球面上放置一光滑均匀铁链，其A端固定在球面的顶点，B 端恰与桌面不接触，铁链单位长度的质量为ρ.试求铁链A 端受的拉力T.解析：以铁链为研究对象，由由于整条铁链的长度不能忽略不计，所以整条铁链不能看成质点，要分析铁链的受力情况，须考虑将铁链分割，使每一小段铁链可以看成质点，分析每一小段铁边的受力，根据物体的平衡条件得出整条铁链的受力情况.在铁链上任取长为△L 的一小段（微元）为研究对象，其受力分析如图3—2—甲所示.由于该元处于静止状态，所以受力平衡，在切线方向上应满足：θθθθT G T T +∆=∆+cos θρθθcos cos Lg G T ∆=∆=∆由于每段铁链沿切线向上的拉力比沿切线向下的拉力大△T θ，所以整个铁链对A 端的拉力是各段上△T θ的和，即 ∑∑∑∆=∆=∆=θρθρθcos cos L g Lg T T观察 θcos L ∆的意义，见图3—2—乙，由于△θ很小，所以CD ⊥OC ，∠OCE=θ△Lcos θ表示△L 在竖直方向上的投影△R ，所以 ∑=∆R L θcos 可得铁链A 端受的拉力 ∑=∆=gR L g T ρθρcos例3：某行星围绕太阳C 沿圆弧轨道运行，它的近日点A 离太阳的距离为a ，行星经过近日点A 时的速度为A v ，行星的远日点B 离开太阳的距离为b ，如图3—3所示，求它经过远日点B 时的速度B v 的大小.解析：此题可根据万有引力提供行星的向心力求解.也可根据开普勒第二定律，用微元法求解.设行星在近日点A 时又向前运动了极短的时间△t ，由于时间极短可以认为行星在△t 时间内做匀速圆周运动，线速度为A v ，半径为a ，可以得到行星在△t 时间内扫过的面积 a t v S A a ⋅∆=21 同理，设行星在经过远日点B 时也运动了相同的极短时间△t ， 则也有 b t v S B b ⋅∆=21 由开普勒第二定律可知：S a =S b 即得 A B v b a v = 此题也可用对称法求解. 例4：如图3—4所示，长为L 的船静止在平静的水面上，立于船头的人质量为m ，船的质量为M ，不计水的阻力，人从船头走到船尾的过程中，问：船的位移为多大？解析：取人和船整体作为研究系统，人在走动过程中，系统所受合外力为零，可知系统动量守恒.设人在走动过程中的△t 时间内为匀速运动，则可计算出船的位移.设v 1、v 2分别是人和船在任何一时刻的速率，则有21Mv mv = ① 两边同时乘以一个极短的时间△t ， 有 t Mv t mv ∆=∆21 ②由于时间极短，可以认为在这极短的时间内人和船的速率是不变的，所以人和船位移大小分别为t v s ∆=∆11，t v s ∆=∆22由此将②式化为 21s M s m ∆=∆ ③把所有的元位移分别相加有 ∑∑∆=∆21s M s m④ 即 ms 1=Ms 2 ⑤ 此式即为质心不变原理. 其中s 1、s 2分别为全过程中人和船对地位移的大小， 又因为 L=s 1+s 2 ⑥由⑤、⑥两式得船的位移 L mM m s +=2 例5：半径为R 的光滑球固定在水平桌面上，有一质量为M 的圆环状均匀弹性绳圈，原长为πR ，且弹性绳圈的劲度系数为k ，将弹性绳圈从球的正上方轻放到球上，使弹性绳圈水平停留在平衡位置上，如图3—5所示，若 平衡时弹性绳圈长为R π2，求弹性绳圈的劲度系数k.解析：由于整个弹性绳圈的大小不能忽略不计，弹性绳圈不能看成质点，所以应将弹性绳圈分割成许多小段，其中每一小段△m 两端受的拉力就是弹性绳圈内部的弹力F.在弹性绳圈上任取一小段质量为△m 作为研究对象，进行受力分析.但是△m 受的力不在同一平面内，可以从一个合适的角度观察.选取一个合适的平面进行受力分析，这样可以看清楚各个力之间的关系.从正面和上面观察，分别画出正视图的俯视图，如图3—5—甲和2—3—5—乙. 先看俯视图3—5—甲，设在弹性绳圈的平面上，△m 所对的圆心角是△θ，则每一小段的质量 M m πθ2∆=∆ △m 在该平面上受拉力F 的作用，合力为 2sin 2)2cos(2θθπ∆=∆-=F F T 因为当θ很小时，θθ≈sin 所以θθ∆=∆=F F T 22再看正视图3—5—乙，△m 受重力△mg ，支持力N ，二力的合力与T 平衡.即 θtan ⋅∆=mg T现在弹性绳圈的半径为 R R r 2222==ππ 所以 ︒===4522sin θθR r 1tan =θ因此T=Mg mg πθ2∆=∆ ①、②联立，θπθ∆=∆F Mg 2， 解得弹性绳圈的张力为： π2Mg F = 设弹性绳圈的伸长量为x 则 R R R x πππ)12(2-=-=所以绳圈的劲度系数为：RMg R Mg x F k 222)12()12(2ππ+=-== 例6：一质量为M 、均匀分布的圆环，其半径为r ，几何轴与水平面垂直，若它能经受的最大张力为T ，求此圆环可以绕几何轴旋转的最大角速度.解析：因为向心力F=mr ω2，当ω一定时，r 越大，向心力越大，所以要想求最大张力T 所对应的角速度ω，r 应取最大值.如图3—6所示，在圆环上取一小段△L ，对应的圆心角为△θ，其质量可表示为M m πθ2∆=∆，受圆环对它的张 力为T ，则同上例分析可得 22sin 2ωθmr T ∆=∆ 因为△θ很小，所以22sin θθ∆≈∆，即 2222ωπθθMr T ∆=∆⋅ 解得最大角速度 MrT πω2= 例7：一根质量为M ，长度为L 的铁链条，被竖直地悬挂起来，其最低端刚好与水平接触，今将链条由静止释放，让它落到地面上，如图3—7所示，求链条下落了长度x 时，链条对地面的压力为多大？解析：在下落过程中链条作用于地面的压力实质就是链条对地面的“冲力”加上落在地面上那部分链条的重力.根据牛顿第三定律，这个冲力也就等于同一时刻地面对链条的反作用力，这个力的冲量，使得链条落至地面时的动量发生变化.由于各质元原来的高度不同，落到地面的速度不同，动量改变也不相同.我们取某一时刻一小段链条（微元）作为研究对象，就可以将变速冲击变为恒速冲击.设开始下落的时刻t=0，在t 时刻落在地面上的链条长为x ，未到达地面部分链条的速度为v ，并设链条的线密度为ρ.由题意可知，链条落至地面后，速度立即变为零.从t 时刻起取很小一段时间△t ，在△t 内又有△M=ρ△x 落到地面上静止.地面对△M 作用的冲量为I t Mg F ∆=∆∆-)( 因为 0≈∆⋅∆t Mg所以 x v v M t F ∆=-⋅∆=∆ρ0 解得冲力：t x v F ∆∆=ρ，其中tx ∆∆就是t 时刻链条的速度v ， 故 2v F ρ= 链条在t 时刻的速度v 即为链条下落长为x 时的即时速度，即v 2=2g x ，代入F 的表达式中，得 gx F ρ2=此即t 时刻链对地面的作用力，也就是t 时刻链条对地面的冲力.所以在t 时刻链条对地面的总压力为 .332LMgx gx gx gx N ==+=ρρρ 例8：一根均匀柔软的绳长为L ，质量为m ，对折后两端固定在一个钉子上，其中一端突然从钉子上滑落，试求滑落的绳端点离钉子的距离为x 时，钉子对绳子另一端的作用力是多大？ 解析：钉子对绳子另一端的作用力随滑落绳的长短而变化，由此可用微元法求解.如图3—8所示，当左边绳端离钉子的距离为x 时，左边绳长为)(21x l -，速度 gx v 2=， 右边绳长为).(21x l + 又经过一段很短的时间△t 以后， 左边绳子又有长度t V ∆21的一小段转移到右边去了，我们就分 析这一小段绳子，这一小段绳子受到两力：上面绳子对它的拉 力T 和它本身的重力l m g t v /(21=∆λλ为绳子的线密度）， 根据动量定理，设向上方向为正 )21(0)21(v t v t g t v T ⋅∆--=∆∆-λλ由于△t 取得很小，因此这一小段绳子的重力相对于T 来说是很小的，可以忽略，所以有 λλgx v T ==221 因此钉子对右边绳端的作用力为 )31(21)(21lx mg T g x l F +=++=λ 例9：图3—9中，半径为R 的圆盘固定不可转动，细绳不可伸长但质量可忽略，绳下悬挂的两物体质量分别为M 、m.设圆盘与绳间光滑接触，试求盘对绳的法向支持力线密度.解析：求盘对绳的法向支持力线密度也就是求盘对绳的法向单位长度所受的支持力.因为盘与绳间光滑接触，则任取一小段绳，其两端受的张力大小相等，又因为绳上各点受的支持力方向不同，故不能以整条绳为研究对象，只能以一小段绳为研究对象分析求解.在与圆盘接触的半圆形中取一小段绳元△L ，△L 所对应的圆心角为△θ，如图3—9—甲所示，绳元△L 两端的张力均为T ，绳元所受圆盘法向支持力为△N ，因细绳质量可忽略，法向合力为零，则由平衡条件得： 2sin 22sin 2sinθθθ∆=∆+∆=∆T T T N 当△θ很小时，22sin θθ∆≈∆ ∴△N=T △θ 又因为 △L=R △θ则绳所受法向支持力线密度为 RT R T L N n =∆∆=∆∆=θθ ① 以M 、m 分别为研究对象，根据牛顿定律有 Mg －T=Ma ② T －mg=m a ③ 由②、③解得： m M Mmg T +=2 将④式代入①式得：Rm M Mmg n )(2+= 例10：粗细均匀质量分布也均匀的半径为分别为R 和r 的两圆环相切.若在切点放一质点m ，恰使两边圆环对m 的万有引力的合力为零，则大小圆环的线密度必须满足什么条件？解析：若要直接求整个圆对质点m 的万有引力比较难，当若要用到圆的对称性及要求所受合力为零的条件，考虑大、小圆环上关于切点对称的微元与质量m 的相互作用，然后推及整个圆环即可求解.如图3—10所示，过切点作直线交大小圆分别于P 、Q 两点，并设与水平线夹角为α，当α有微小增量时，则大小圆环上对应微小线元αα∆⋅=∆∆⋅=∆2221r L R L其对应的质量分别为 αρρ∆⋅=∆=∆21111R l mαρρ∆⋅=∆=∆22222r l m 由于△α很小，故△m 1、△m 2与m 的距离可以认为分别是 ααcos 2cos 221r r R r ==所以△m 1、△m 2与m 的万有引力分别为 222222212111)cos 2(2,)cos 2(2ααρααρr m R G r m Gm F R m R G r m Gm F ∆⋅=∆=∆∆⋅=∆=∆ 由于α具有任意性，若△F 1与△F 2的合力为零， 则两圆环对m 的引力的合力也为零， 即2221)cos 2(2)cos 2(2ααρααρr m r G R m R G ∆⋅=∆⋅ 解得大小圆环的线密度之比为：rR =21ρρ 例11：一枚质量为M 的火箭，依靠向正下方喷气在空中保持静止，如果喷出气体的速度为v ，那么火箭发动机的功率是多少？解析：火箭喷气时，要对气体做功，取一个很短的时间，求出此时间内，火箭对气体做的功，再代入功率的定义式即可求出火箭发动机的功率.选取在△t 时间内喷出的气体为研究对象，设火箭推气体的力为F ，根据动量定理，有F △t=△m ·v 因为火箭静止在空中，所以根据牛顿第三定律和平衡条件有F=Mg即 Mg ·△t=△m ·v △t=△m ·v/Mg对同样这一部分气体用动能定理，火箭对它做的功为： 221mv W ∆= 所以发动机的功率 MgV Mg mV mv t W P 21)/(212=∆∆=∆= 例12：如图3—11所示，小环O 和O ′分别套在不动的竖直杆AB 和A ′B ′上，一根不可伸长的绳子穿过环O ′，绳的两端分别系在A ′点和O 环上，设环O ′以恒定速度v 向下运动，求当∠AOO ′=α时，环O 的速度.解析：O 、O ′之间的速度关系与O 、O ′的位置有关，即与α角有关，因此要用微元法找它们之间的速度关系.设经历一段极短时间△t ，O ′环移到C ′，O 环移到C ，自C ′与C 分别作为O ′O 的垂线C ′D ′和CD ，从图中看出.ααcos ,cos D O C O OD OC ''=''= 因此OC+O ′C ′=αcos D O OD ''+ ① 因△α极小，所以EC ′≈ED ′，EC ≈ED ，从而OD+O ′D ′≈OO ′－CC ′ ②由于绳子总长度不变，故 OO ′－CC ′=O ′C ′ ③由以上三式可得：OC+O ′C ′=αcos C O '' 即)1cos 1(-''=αC O OC 等式两边同除以△t 得环O 的速度为 )1cos 1(0-=αv v 例13： 在水平位置的洁净的平玻璃板上倒一些水银，由于重力和表面张力的影响，水银近似呈现圆饼形状（侧面向外凸出），过圆饼轴线的竖直截面如图3—12所示，为了计算方便，水银和玻璃的接触角可按180°计算.已知水银密度33/106.13m kg ⨯=ρ，水 银的表面张力系数./49.0m N =σ当圆饼的半径很大时，试估算其厚度h 的数值大约为多少？（取1位有效数字即可）解析：若以整个圆饼状水银为研究对象，只受重力和玻璃板的支持力，在平衡方程中，液体的体积不是h 的简单函数，而且支持力N 和重力mg 都是未知量，方程中又不可能出现表面张力系数，因此不可能用整体分析列方程求解h.现用微元法求解.在圆饼的侧面取一个宽度为△x ，高为h 的体积元，，如图3—12—甲所示，该体积元受重力G 、液体内部作用在面积△x ·h 上的压力F ，x gh xh hg S P F ∆⋅=∆⋅==22121ρρ， 还有上表面分界线上的张力F 1=σ△x 和下表面分界线上的 张力F 2=σ△x .作用在前、后两个侧面上的液体压力互相平衡，作用在体积元表面两个弯曲 分界上的表面张力的合力，当体积元的宽度较小时，这两个力也是平衡的，图中都未画出. 由力的平衡条件有：0cos 21=--F F F θ即 0cos 212=∆-∆-∆x x x gh σθσρ由于 ,2cos 11,20<+<<<θπθ所以 故2.7×10－3m<h<3.8×10－3m题目要求只取1位有效数字，所以水银层厚度h 的估算值为3×10－3m 或4×10－3m.例14：把一个容器内的空气抽出一些，压强降为p ，容器上有一小孔，上有塞子，现把塞子拔掉，如图3—13所示.问空气最初以多大初速度冲进容器？（外界空气压强为p 0、密度为ρ）解析：该题由于不知开始时进入容器内分有多少，不知它们在容器外如何分布，也不知空气分子进入容器后压强如何变化，使我们难以找到解题途径.注意到题目中“最初”二字，可以这样考虑：设小孔的面积为S ，取开始时位于小孔外一薄层气体为研究对象，令薄层厚度为△L ，因△L 很小，所以其质量△m 进入容器过程中，不改变容器压强，故此薄层所受外力是恒力，该问题就可以解决了.由以上分析，得：F=(p 0－p)S ① 对进入的△m 气体，由动能定理得：221mv L F ∆=∆ ② 而 △m=ρS △L 联立①、②、③式可得：最初中进容器的空气速度 ρ)(20p p v -=例15：电量Q 均匀分布在半径为R 的圆环上（如图3—14所示），求在圆环轴线上距圆心O 点为x 处的P 点的电场强度.解析：带电圆环产生的电场不能看做点电荷产生的电场，故采用微元法，用点电荷形成的电场结合对称性求解.选电荷元 ,2R Q R q πθ∆=∆它在P 点产生的电场的场强的x 分量为： 22222)(2cos x R x x R R Q R k r q k E x ++∆=∆=∆πθα 根据对称性 322322322)(2)(2)(2x R kQx x R kQxx R kQxE E x +=+=∆+=∆=∑∑ππθπ由此可见，此带电圆环在轴线P 点产生的场强大小相当于带电圆环带电量集中在圆环的某一点时在轴线P 点产生的场强大小，方向是沿轴线的方向.例16：如图3—15所示，一质量均匀分布的细圆环，其半径为R ，质量为m.令此环均匀带正电，总电量为Q.现将此环平放在绝缘的光滑水平桌面上，并处于磁感应强度为B 的均匀磁场中，磁场方向竖直向下.当此环绕通过其中心的竖直轴以匀角速度ω沿图示方向旋转时，环中的张力等于多少？（设圆环的带电量不减少，不考虑环上电荷之间的作用）解析：当环静止时，因环上没有电流，在磁场中不受力，则环中也就没有因磁场力引起的张力.当环匀速转动时，环上电荷也随环一起转动，形成电流，电流在磁场中受力导致环中存在张力，显然此张力一定与电流在磁场中受到的安培力有关.由题意可知环上各点所受安培力方向均不同，张力方向也不同，因而只能在环上取一小段作为研究对象，从而求出环中张力的大小.在圆环上取△L=R △θ圆弧元，受力情况如图3—15—甲所示.因转动角速度ω而形成的电流 πω2Q I =，电流元I △L 所受的安培力θπω∆=∆=∆QB R LB I F 2 因圆环法线方向合力为圆弧元做匀速圆周运动所需的向心力，R m F T 22sin 2ωθ∆=∆-∆ 当△θ很小时，R m QB R T 2222sin ωθπωθθθ∆=∆-∆∆≈∆ θπωθπωθθπ∆=∆-∆∴∆=∆2222R m QB R T m m 解得圆环中张力为 )(2ωπωm QB R T +=例17：如图3—16所示，一水平放置的光滑平行导轨上放一质量为m 的金属杆，导轨间距为L ，导轨的一端连接一阻值为R 的电阻，其他电阻不计，磁感应强度为B 的匀强磁场垂直于导轨平面.现给金属杆一个水平向右的初速度v 0，然后任其运动，导轨足够长，试求金属杆在导轨上向右移动的最大距离是多少？解析：水平地从a 向b 看，杆在运动过程中的受力分析如图3—16—甲所示，这是一个典型的在变力作用下求位移的题，用我们已学过的知识好像无法解决，其实只要采用的方法得当仍然可以求解.设杆在减速中的某一时刻速度为v ，取一极短时间△t ，发生了一段极小的位移△x ，在△t 时间内，磁通量的变化为△φ △φ=BL △x tRx BL tR R I ∆∆=∆∆Φ==ε金属杆受到安培力为tRx L B ILB F ∆∆==22安 由于时间极短，可以认为F 安为恒力，选向右为正方向，在△t 时间内，安培力F 安的冲量为：Rx L B t F I ∆-=∆⋅-=∆22安 对所有的位移求和，可得安培力的总冲量为x RL B R x L B I 2222)(-=∆-=∑ ① 其中x 为杆运动的最大距离， 对金属杆用动量定理可得 I=0－mV 0 ② 由①、②两式得：220LB R mV x = 例18：如图3—17所示，电源的电动热为E ，电容器的电容为C ，S 是单刀双掷开关，MN 、PQ 是两根位于同一水平面上的平行光滑长导轨，它们的电阻可以忽略不计，两导轨间距为L ，导轨处在磁感应强度为B 的均匀磁场中，磁场方向垂直于两导轨所在的平面并指向图中纸面向里的方向.L 1和L 2是两根横放在导轨上的导体小棒，质量分别为m 1和m 2，且21m m <.它们在导轨上滑动时与导轨保持垂直并接触良好，不计摩擦，两小棒的电阻相同，开始时两根小棒均静止在导轨上.现将开关S 先合向1，然后合向2.求：（1）两根小棒最终速度的大小；（2）在整个过程中的焦耳热损耗.（当回路中有电流时，该电流所产生的磁场可忽略不计） 解析：当开关S 先合上1时，电源给电容器充电，当开关S 再合上2时，电容器通过导体小棒放电，在放电过程中，导体小棒受到安培力作用，在安培力作用下，两小棒开始运动，运动速度最后均达到最大.（1）设两小棒最终的速度的大小为v ，则分别为L 1、L 2为研究对象得：1111v m v m t F i i -'=∆ ∑=∆v m t F i i 111 ① 同理得： ∑=∆v m t F i i 222 ② 由①、②得：v m m t F t F i i i i )(212211+=∆+∆∑∑又因为 11Bli F i = 21i i t t ∆=∆ 22Bli F i = i i i =+21所以 ∑∑∑∑∆=∆+=∆+∆i i i i t i BL t i i BL t BLi t BLi )(212211v m m q Q BL )()(21+=-=而Q=CE q=CU ′=CBL v所以解得小棒的最终速度 2221)(LCB m m BLCE v ++= （2）因为总能量守恒，所以热Q v m m C q CE +++=22122)(212121 即产生的热量 22122)(212121v m m C q CE Q +--=热 )(2)()()]([2121)(21)(12121222122122212122222122C L B m m CE m m L CB m m BLCE m m L CB CE v m m CBLv C CE +++=+++--=+--=针对训练1．某地强风的风速为v ，设空气的密度为ρ，如果将通过横截面积为S 的风的动能全部转化为电能，则其电功率为多少？2．如图3—19所示，山高为H ，山顶A 和水平面上B 点的水平距离为s.现在修一条冰道ACB ，其中AC 为斜面，冰道光滑，物体从A 点由静止释放，用最短时间经C 到B ，不计过C 点的能量损失.问AC 和水平方向的夹角θ多大？最短时间为多少？3．如图3—21所示，在绳的C 端以速度v 匀速收绳从而拉动低处的物体M 水平前进，当绳AO 段也水平恰成α角时，物体M 的速度多大？4，如图3—22所示，质量相等的两个小球A 和B 通过轻绳绕过两个光滑的定滑轮带动C 球上升，某时刻连接C 球的两绳的夹角为θ，设A 、B 两球此时下落的速度为v ，则C 球上升的速度多大？5．质量为M 的平板小车在光滑的水平面上以v 0向左匀速运动，一质量为m 的小球从高h处自由下落，与小车碰撞后反弹上升的高度仍为h.设M>>m ，碰撞弹力N>>g ，球与车之间的动摩擦因数为μ，则小球弹起后的水平速度可能是（ ） A ．gh 2 B ．0 C ．gh 22 D ．v 0 6．半径为R 的刚性球固定在水平桌面上.有一质量为M 的圆环状均匀弹性细绳圈，原长 2πa ，a =R/2，绳圈的弹性系数为k （绳伸长s 时，绳中弹性张力为ks ）.将绳圈从球的正 上方轻放到球上，并用手扶着绳圈使其保持水平，并最后停留在某个静力平衡位置.考 虑重力，忽略摩擦.（1）设平衡时弹性绳圈长2πb ，b=a 2，求弹性系数k ；（用M 、R 、g 表示，g 为重力加速度）（2）设k=Mg/2π2R ，求绳圈的最后平衡位置及长度.7．一截面呈圆形的细管被弯成大圆环，并固定在竖直平面内，在环内的环底A 处有一质量为m 、直径比管径略小的小球，小球上连有一根穿过环顶B 处管口的轻绳，在外力F 作用下小球以恒定速度v 沿管壁做半径为R 的匀速圆周运动，如图3—23所示.已知小球与管内壁中位于大环外侧部分的动摩擦因数为μ，而大环内侧部分的管内壁是光滑的.忽略大环内、外侧半径的差别，认为均为R.试求小球从A 点运动到B 点过程中F 做的功W F .8．如图3—24，来自质子源的质子（初速度为零），经一加速电压为800kV 的直线加速器加速，形成电流为1.0mA的细柱形质子流.已知质子电荷e=1.60×10－19C.这束质子流每秒打到靶上的质子数为.假设分布在质子源到靶之间的加速电场是均匀的，在质子束中与质子源相距l 和4l的两处，各取一段极短的相等长度的质子流，其中质子数分别为n1和n2，则n1: n2.9．如图3—25所示，电量Q均匀分布在一个半径为R的细圆环上，求圆环轴上与环心相距为x的点电荷q所受的力的大小.10．如图3—26所示，一根均匀带电细线，总电量为Q，弯成半径为R的缺口圆环，在细线的两端处留有很小的长为△L的空隙，求圆环中心处的场强.11．如图3—27所示，两根均匀带电的半无穷长平行直导线（它们的电荷线密度为η），端点联线LN垂直于这两直导线，如图所示.LN的长度为2R.试求在LN的中点O处的电场强度.12．如图3—28所示，有一均匀带电的无穷长直导线，其电荷线密度为η.试求空间任意一点的电场强度.该点与直导线间垂直距离为r.13．如图3—29所示，半径为R的均匀带电半球面，电荷面密度为δ，求球心O处的电场强度.14．如图3—30所示，在光滑的水平面上，有一垂直向下的匀强磁场分布在宽度为L的区域内，现有一个边长为a（a<L），质量为m的正方形闭合线框以初速v0垂直磁场边界滑过磁场后，速度变为v（v<v0），求：（1）线框在这过程中产生的热量Q；（2）线框完全进入磁场后的速度v ′.15．如图3—31所示，在离水平地面h 高的平台上有一相距L 的光滑轨道，左端接有已充电的电容器，电容为C ，充电后两端电压为U 1.轨道平面处于垂直向上的磁感应强度为B 的匀强磁场中.在轨道右端放一质量为m 的金属棒，当闭合S ，棒离开轨道后电容器的两极电压变为U 2，求棒落在离平台多远的位置.16．如图3—32所示，空间有一水平方向的匀强磁场，大小为B ，一光滑导轨竖直放置，导轨上接有一电容为C 的电容器，并套一可自由滑动的金属棒，质量为m ，释放后，求金属棒的加速度a .答案：1．321v S ρ 2．θ=60°)223(2hs g h + 3．)cos 1/(x v + 4．2cos /θv 5．CD 6．（1）R Mg 22)12(π+ （2）绳圈掉地上，长度为原长 7．22v m mgR πμ+ 8．6.25×1015,2:1 9．2322)(x R QqxK + 10．32Rl Q K ρ∆ 11．R k λ2 12．r k λ2 13．σπR 2 14．2),(210220v v v v v m +='- 15．gh m u u CBL 2)(21- 16．22L CB m mg a +=。

高中物理竞赛专题一：微元法求速度微元法是分析、解决物理问题中的常用方法，也是从部分到整体的思维方法。

用该方法可以使一些复杂的物理过程用我们熟悉的物理规律迅速地加以解决，使所求的问题简单化。

在使用微元法处理问题时，需将其分解为众多微小的“元过程”，而且每个“元过程”所遵循的规律是相同的，这样，我们只需分析这些“元过程”，然后再将“元过程”进行必要的数学方法或物理思想处理，进而使问题求解。

使用此方法会加强我们对已知规律的再思考，从而引起巩固知识、加深认识和提高能力的作用。

1.如图所示，当小车B 以恒定的速度v 向下运动时，求当绳子与水平方向成θ时，A 的速度为多少？3.如图3—1所示，一个身高为h 的人在灯以悟空速度v 沿水平直线行走。

设灯距地面高为H ，求人影的顶端C 点速度。

4..如图所示，一平面内有两根细杆 l 1 和 l 2 ，夹角为 θ，各自以垂直于自己的速度 v 1 和 v 2在该平面内运动，试求交点相对于纸平面的速率及交点相对于每根杆的速率。

5.如图3—11所示，小环O 和O ′分别套在不动的竖直杆AB 和A ′B ′上，一根不可伸长的绳子穿过环O ′，绳的两端分别系在A ′点和O 环上，设环O ′以恒定速度v 向下运动，求当∠AOO ′= α时，环O 的速度。

6.某行星围绕太阳C 沿圆弧轨道运行，它的近日点A 离太阳的距离为a ，行星经过近日点A 时的速度为v A ，行星的远日点B 离开太阳的距离为b ，如图3—3所示，求它经过远日点B 时的速度v B 的大小。

2二.微元法在动力学中的应用1.某游乐园入口旁有一喷泉，喷出的水柱将一质量为M的卡通玩具稳定地悬停在空中．为计算方便起见，假设水柱从横截面积为S的喷口持续以速度v0竖直向上喷出；玩具底部为平板（面积略大于S）；水柱冲击到玩具底板后，在竖直方向水的速度变为零，在水平方向朝四周均匀散开．忽略空气阻力．已知水的密度为ρ，重力加速度大小为g．求：（i）喷泉单位时间内喷出的水的质量；（ii）玩具在空中悬停时，其底面相对于喷口的高度．2.激光束可以看作是粒子流，其中的粒子以相同的动量沿光传播方向运动．激光照射到物体上，在发生反射、折射和吸收现象的同时，也会对物体产生作用．光镊效应就是一个实例，激光束可以像镊子一样抓住细胞等微小颗粒．一束激光经S点后被分成若干细光束，若不考虑光的反射和吸收，其中光束①和②穿过介质小球的光路如图②所示，图中O点是介质小球的球心，入射时光束①和②与SO的夹角均为θ，出射时光束均与SO平行．请在下面两种情况下，分析说明两光束因折射对小球产生的合力的方向．a．光束①和②强度相同；b．光束①比②强度大．3.半径为R的光滑球固定在水平桌面上，有一质量为M的圆环状均匀弹性绳圈，原长为πR ，且弹性绳圈的劲度系数为k ，将弹性绳圈从球的正上方轻放到球上，使弹性绳圈水平停留在平衡位置上，如图3—5R ，求弹性绳圈的劲度系数k 。