多跨连续梁计算程序

模板面板按三跨连续梁计算。

静荷载标准值q1=25×0.1×1.2＋0.5×1.2=3.6KN/M活荷载标准值q2=（1＋2）×1.2=3.6 KN/M面板的惯性矩I和截面抵抗矩W分别为：W=120×1.0×1.0/6=20㎝³I=120×1.0×1.0×1.0/12=10㎝ 4(1)抗弯强度计算f=M/W<[f]其中f--面板的抗弯强度计算值(N/㎜2)M—面板的最大弯矩(N·m)W—面板的净截面抵抗矩[f] —面板的抗弯矩设计值,取13N/㎜2M=0.1ql2M=0.1×(1.2×3.6＋1.4×3.6)×0.4×0.4=0.15KN·M F=0.15×1000×1000/37800=3.97N/㎜2<[f]=13N/㎜2,满足要求.(2)抗剪计算T=3Q/2bh<[T]Q=0.6×(1.2×3.6＋1.4×3.6)×0.4=2.42KNT=3×2420/(2×1200×10)=0.303N/㎜2<[T]=1.4 N/㎜2,满足要求.(3)挠度计算v=0.677ql4/100EI<[v]=l/250v=0.677× 3.6×4004/(100×9000×388800)=0.173㎜<[v]=l/250=1.6㎜一、楼板模板隔栅计算隔栅按照均布荷载下连续梁计算。

1、荷载的计算（1）钢筋混凝土板自重（KN/m）q11=25×0.10×0.4=1.0 KN/m（2）模板的自重线荷载（KN/m）q12=0.5×0.4=0.2 KN/m(3) 活荷载为施工荷载标准值和振捣混凝土时产生的荷载（KN/m）q2=(1＋2)×0.4=1.2 KN/m静荷载q1=1.2×1.0＋1.2×0.2=1.44 KN/m活荷载q2=1.4×1.2=1.68 KN/m2、木方的计算按照三跨连续梁计算，最大弯矩考虑为静荷载与活荷载的计算值最不利分配的弯矩和均布荷载q=q1＋q2=3.12KN/m最大弯矩M=0.1ql2=0.1×3.12×1.2×1.2=0.45 KN·m最大剪力Q=0.6×1.2×3.12=2.25KN最大支座力N=1.1×1.2×3.12=4.12 KN面板的惯性矩I和截面抵抗矩W分别为：W=5×8×8/6=53.33CM3I=5×8×8×8/12=213.33 CM4（1）木方抗弯强度计算f=0.45×106/53330=8.44N/㎜2<[f]=13 N/㎜2满足要求。

1 设计基本资料1.1概述跨线桥应因地制宜，充分与地形和自然环境相结合。

跨线桥的建筑高度选取除保证必要的桥下净空外，还需结合地形以减少桥头接线挖方或填方量，最终再谈到经济实用的目的。

如果桥两端地势较低，主要采用梁式桥；略高的则主要采用中承式拱肋桥；更高的则宜采用斜腿刚构、双向坡拱等形式。

在桥型的选择时，一方面从“轻型”着手,以减少圬工体积，另一方面结合当地的资源材料条件，以满足就地取材的原则。

随着社会和经济的发展，生态环境越来越受到人们的关注与重视，高速公路跨线桥将作为一种人文景观，与自然相协调将会带来“点石成金"的效果.高速公路上跨线桥常常是一种标志性建筑物，桥型本身具有的曲线美，能够与周围环境优美结合。

茶庵铺互通式立体交叉K65+687跨线桥，必须遵照“安全、适用、经济、美观”的基本原则进行设计，同时应充分考虑建造技术的先进性以及环境保护和可持续发展的要求。

1.1.1设计依据按设计任务书、指导书及地质断面图进行设计.1.1.2技术标准（1）设计等级:公路—I级；高速公路桥,无人群荷载；（2)桥面净宽：净—11.75m + 2×0。

5 m防撞栏;（3)桥面横坡：2。

0%;1。

1。

3地质条件桥址处的地质断面有所起伏，桥台处高，桥跨内低，桥跨内工程地质情况为（从上到下）：碎石质土、强分化砾岩、弱分化砾岩,两端桥台处工程地质情况为:弱分化砾岩。

1.1。

4采用规范JTG D60—2004《公路桥涵设计通用规范》；JTG D62—2004 《公路钢筋砼及预应力砼桥涵设计规范》；JTG D50—2006 《公路沥青路面设计规范》JTJ 022—2004 《公路砖石及砼桥涵设计规范》；1.2桥型方案经过方案比选，通过对设计方案的评价和比较要全面考虑各项指标，综合分析每一方案的优缺点，最后选定一个最佳的推荐方案。

按桥梁的设计原则、造价低、材料省、劳动力少和桥型美观的应是优秀方案。

独塔单索面斜拉桥比较美观，但是预应力混凝土等截面连续梁桥桥梁建筑高度小，工程量小，施工难度小，可以采用多种施工方法，工期较短，易于养护。

模板面板按三跨连续梁计算。

静荷载标准值q1=25×0.1×1.2＋0.5×1.2=3.6KN/M活荷载标准值q2=（1＋2）×1.2=3.6 KN/M面板的惯性矩I和截面抵抗矩W分别为：W=120×1.0×1.0/6=20㎝³I=120×1.0×1.0×1.0/12=10㎝ 4(1)抗弯强度计算f=M/W<[f]其中f--面板的抗弯强度计算值(N/㎜2)M—面板的最大弯矩(N·m)W—面板的净截面抵抗矩[f] —面板的抗弯矩设计值,取13N/㎜2M=0.1ql2M=0.1×(1.2×3.6＋1.4×3.6)×0.4×0.4=0.15KN·M F=0.15×1000×1000/37800=3.97N/㎜2<[f]=13N/㎜2,满足要求.(2)抗剪计算T=3Q/2bh<[T]Q=0.6×(1.2×3.6＋1.4×3.6)×0.4=2.42KNT=3×2420/(2×1200×10)=0.303N/㎜2<[T]=1.4 N/㎜2,满足要求.(3)挠度计算v=0.677ql4/100EI<[v]=l/250v=0.677× 3.6×4004/(100×9000×388800)=0.173㎜<[v]=l/250=1.6㎜一、楼板模板隔栅计算隔栅按照均布荷载下连续梁计算。

1、荷载的计算（1）钢筋混凝土板自重（KN/m）q11=25×0.10×0.4=1.0 KN/m（2）模板的自重线荷载（KN/m）q12=0.5×0.4=0.2 KN/m(3) 活荷载为施工荷载标准值和振捣混凝土时产生的荷载（KN/m）q2=(1＋2)×0.4=1.2 KN/m静荷载q1=1.2×1.0＋1.2×0.2=1.44 KN/m活荷载q2=1.4×1.2=1.68 KN/m2、木方的计算按照三跨连续梁计算，最大弯矩考虑为静荷载与活荷载的计算值最不利分配的弯矩和均布荷载q=q1＋q2=3.12KN/m最大弯矩M=0.1ql2=0.1×3.12×1.2×1.2=0.45 KN·m最大剪力Q=0.6×1.2×3.12=2.25KN最大支座力N=1.1×1.2×3.12=4.12 KN面板的惯性矩I和截面抵抗矩W分别为：W=5×8×8/6=53.33CM3I=5×8×8×8/12=213.33 CM4（1）木方抗弯强度计算f=0.45×106/53330=8.44N/㎜2<[f]=13 N/㎜2满足要求。

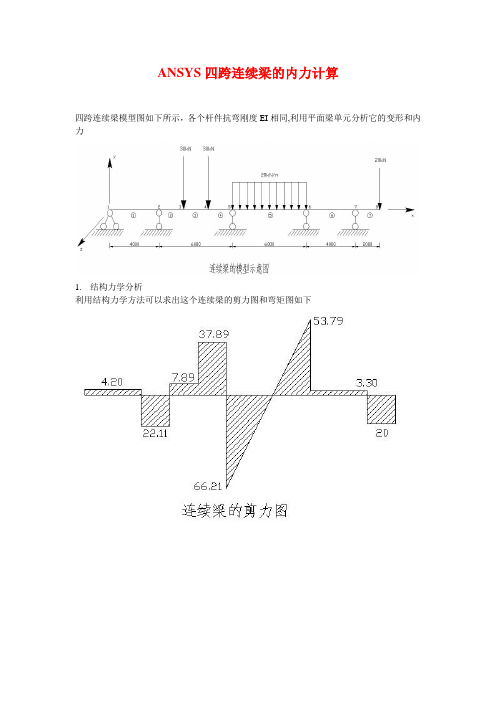
ANSYS四跨连续梁的内力计算四跨连续梁模型图如下所示，各个杆件抗弯刚度EI相同,利用平面梁单元分析它的变形和内力1.结构力学分析利用结构力学方法可以求出这个连续梁的剪力图和弯矩图如下这里只给出了梁的弯曲刚度相同条件,没有指定梁截面的几何参数和材料的力学性质.从结构力学分析的条件上看,这些条件对于确定梁的内力已经足够，但是对于梁的变形分析和应力计算，还需要补充材料的力学参数和截面几何参数。

所以以下分析中，假定梁的截面面积位0。

3m2，抗弯惯性矩为0.003m4,截面高度为0.1m；材料的弹性模量为1000kN/m2，泊松比为0。

3。

补充这些参数对于梁的内力没有影响,但是对于梁的变形和应力是有影响的。

2.用节点和单元的直接建模求解按照前面模型示意图布置节点和单元，在图示坐标系里定位节点的坐标和单元连接信息，以及荷载作用情况和位移约束.由于第二跨中间有两个集中力,所以在集中力位置设置两个节点。

这样，就可以将这两个集中力直接处理成节点荷载。

对于平面梁单元的节点只需输入平面上的两个坐标值，所以这里只输入节点的x坐标和y坐标.（1）指定为结构分析运行主菜单中preference偏好设定命令,然后在对话框中,指定分析模块为structural结构分析，然后单击ok按钮（2）新建单元类型运行主菜单preprocessor—element type-add/edit/delete命令，接着在对话框中单击add按钮新建单元类型（3）定义单元类型先选择单元为beam,接着选2d elastic 3，然后单击ok按钮确定，完成单元类型的选择（4）关闭单元类型的对话框回到单元类型对话框,已经新建了beam3的单元，单击对话框close按钮关闭对话框（5）定义实力常量运行主菜单preprocessor-real constants—add/edit/delete命令，接着在对话框中单击add按钮新建实力常量接着选择定义单元beam3的实力常量，选择后单击ok按钮，然后输入该单元的截面积为0。

1 设计基本资料1.1 概述跨线桥应因地制宜，充分与地形和自然环境相结合。

跨线桥的建筑高度选取除保证必要的桥下净空外，还需结合地形以减少桥头接线挖方或填方量，最终再谈到经济实用的目的。

如果桥两端地势较低，主要采用梁式桥；略高的则主要采用中承式拱肋桥；更高的则宜采用斜腿刚构、双向坡拱等形式。

在桥型的选择时，一方面从“轻型”着手，以减少圬工体积，另一方面结合当地的资源材料条件，以满足就地取材的原则。

随着社会和经济的发展，生态环境越来越受到人们的关注与重视，高速公路跨线桥将作为一种人文景观，与自然相协调将会带来“点石成金”的效果。

高速公路上跨线桥常常是一种标志性建筑物，桥型本身具有的曲线美，能够与周围环境优美结合。

茶庵铺互通式立体交叉K65+687跨线桥，必须遵照“安全、适用、经济、美观”的基本原则进行设计，同时应充分考虑建造技术的先进性以及环境保护和可持续发展的要求。

1.1.1设计依据按设计任务书、指导书及地质断面图进行设计。

1.1.2 技术标准（1）设计等级：公路—I级；高速公路桥，无人群荷载；（2）桥面净宽：净—11.75m + 2×0.5 m防撞栏；（3）桥面横坡：2.0%；1.1.3 地质条件桥址处的地质断面有所起伏，桥台处高，桥跨内低，桥跨内工程地质情况为（从上到下）：碎石质土、强分化砾岩、弱分化砾岩，两端桥台处工程地质情况为：弱分化砾岩。

1.1.4 采用规范JTG D60-2004 《公路桥涵设计通用规范》；JTG D62-2004 《公路钢筋砼及预应力砼桥涵设计规范》；JTG D50-2006 《公路沥青路面设计规范》JTJ 022-2004 《公路砖石及砼桥涵设计规范》；1.2 桥型方案经过方案比选，通过对设计方案的评价和比较要全面考虑各项指标，综合分析每一方案的优缺点，最后选定一个最佳的推荐方案。

按桥梁的设计原则、造价低、材料省、劳动力少和桥型美观的应是优秀方案。

独塔单索面斜拉桥比较美观，但是预应力混凝土等截面连续梁桥桥梁建筑高度小，工程量小，施工难度小，可以采用多种施工方法，工期较短，易于养护。

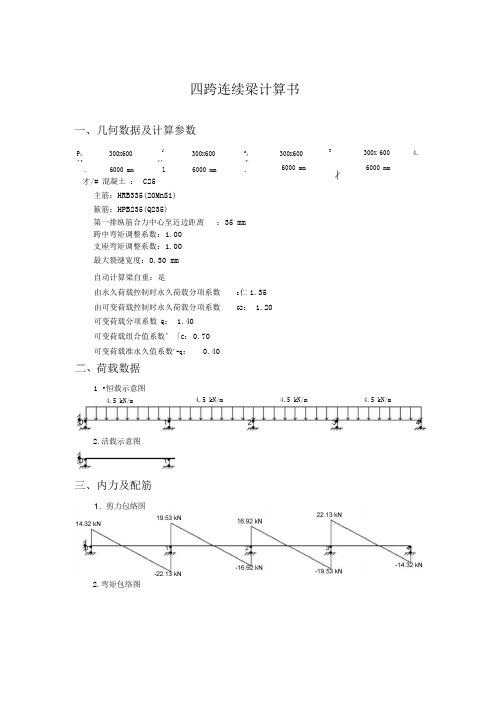
四跨连续梁计算书
一、几何数据及计算参数
自动计算梁自重：是
由永久荷载控制时永久荷载分项系数 G
仁1.35
由可变荷载控制时永久荷载分项系数 G2： 1.20
可变荷载分项系数 Q ： 1.40 可变荷载组合值系数’「C ： 0.70 可变荷载准永久值系数'-q ：
0.40
三、内力及配筋
2.弯矩包络图
P ：
300X 600 1
300X 600 2
： /7 J/
Z /?/ //J/
. 6000 mm
1 6000 mm
.
才/# 混凝土 ： C25 主筋：HRB335(20MnSi) 箍筋：HPB235(Q235)
第一排纵筋合力中心至近边距离 ：35 mm
跨中弯矩调整系数：1.00 支座弯矩调整系数：1.00 最大裂缝宽度：0.30 mm 300X 600 3
6000 mm
300X 600 4.
6000 mm
荷载数据
1 •恒载示意图
4.5 kN/m
4.5 kN/m
4.5 kN/m
4.5 kN/m
2.活载示意图
•截面内力及配筋
注:1.弯矩--kN • m 剪力--kN 钢筋面积--mm挠度--mm 裂缝--mm 2•括号中的数字表示距左端支座的距离，单位为m。

附表25：等截面等跨连续梁在常用荷载作用下按弹性分析(de)内力系数（五跨梁）.弯矩分配法（弯矩分配法计算连续梁和刚架及举例）一、名词解释弯矩分配法在数学上属于逐次逼近法,但在力学上属于精确法(de)范畴,主要适用于连续梁和刚架(de)计算.在弯矩分配法中不需要解联立方程,而且是直接得出杆端弯矩.由于计算简便,弯矩分配法在建筑结构设计计算中应用很广.（一）线刚度i杆件横截面(de)抗弯刚度EI 被杆件(de)长度去除就是杆件(de)线刚度i ： （a ） 当远端B 为固定支座时,对于A 点处,AB 杆(de)转动刚度i S AB 4=； （b ） 当远端B 为铰支座时,对于A 点处,AB 杆(de)转动刚度i S AB 3=； （c ） 当远端B 为滑动支座时,对于A 点处,AB 杆(de)转动刚度i S AB =； （d ） 当远端B 为自由端时,对于A 点处,AB 杆(de)转动刚度0=AB S .连续梁和刚架(de)所有中间支座在计算转动刚度时均视为固定支座.（二）转动刚度S转动刚度表示靠近节点(de)杆件端部对该节点转动(de)反抗能力.杆端(de)转动刚度以S 表示,等于杆端产生单位转角需要施加(de)力矩,θ/M S =.施力端只能发生转角,不能发生线位移.AB S 中(de)第一个角标A 是表示A 端,第二个角标B 是表示杆(de)远端是B 端.AB S 表示AB 杆在A 端(de)转动刚度.（三）分配系数μ各杆A 端所承担(de)弯矩与各杆A 端(de)转动刚度成正比.Aj μ称为分配系数,如AB μ表示杆AB 在A 端(de)分配系数.它表示AB 杆(de)A 端在节点诸杆中,承担反抗外力矩(de)百分比,等于杆AB(de)转动刚度与交于A 点各杆(de)转动刚度之和(de)比值.总之,加于节点A(de)外力矩,按各杆(de)分配系数分配于各杆(de)A 端.（四）传递系数CijC 称为传递系数.传递系数表示当近端有转角（即近端产生弯矩）时,远端弯矩与近端弯矩(de)比值.因此一般可由近端弯矩乘以传递系数C 得出远端弯矩. 当远端为固定(de)边支座或为非边支座21=C ； 当远端为滑动边支座 1-=C ；当远端为铰支边支座 0=C .节点A 作用(de)外力矩M,按各杆(de)分配系数μ分配给各杆(de)近端；远端弯矩等于近端弯矩乘以传递系数.（五）杆端弯矩弯矩分配法解题过程中所指(de)杆端弯矩是所有作用于杆端(de)中间计算过程(de)最后总(de)效果.计算杆端弯矩(de)目(de),是因为杆端弯矩一旦求出,则每相邻节点之间(de)“单跨梁”将可以作为一根静定(de)脱离体取出来进行该杆(de)内力分析.其上作用(de)荷载有外荷载,每一杆端截面上一般有一个剪力和一个弯矩,两端共有二个剪力和二个弯矩.这两个弯矩就是两端(de)杆端弯矩,既然它们已经求出,那么余下(de)两个剪力可由两个静力平衡方程解出.（六）近端弯矩和远端弯矩二、弯矩分配法(de)思路在求杆端弯矩时,其主要(de)目标是：（1）由于节点上有两根或多根杆件汇集,因此需确定每一根杆在维持节点不转动平衡过程中所作出(de)贡献.这需要用到分配系数μ以及与分配系数μ有关(de)转动刚度S、线刚度i、截面刚度EI等值.（2）影响节点产生转动(de)力矩大小及方向.这需要涉及到单跨梁(de)固端弯矩M,它(de)含义是：将每相邻节点之间(de)杆件视为一根两端支座为固定支座或一端固定一端铰支(de)单跨梁,这样(de)梁在各种外荷载作用下(de)杆端弯矩叫做固端弯矩.两端铰支(de)单跨梁无固端弯矩,即两端铰支(de)单跨梁(de)两铰支端(de)固端弯矩为零.只有固定端才有固端弯矩,铰支端(de)固端弯矩为零(单跨梁).固定端不允许转动所以产生固端弯矩,而铰支端允许转动不产生固端弯矩.三、弯矩分配法(de)运算步骤连续梁或刚架弯矩分配法运算过程：（1）求各杆件（梁或柱）(de)线刚度i、杆端（梁端或柱端）转动刚度S和分配系数μ（对于刚架,参加分配系数计算(de)不仅有梁,还有柱）.（2）根据各个“单跨”梁或柱(de)荷载情况和支座特征查表求出各“单跨”杆件在杆端(de)固端弯矩M.这里需注意(de)是固端弯矩是带符号(de),可以用“左负右正”四个字来帮助记忆.即对每一“单跨”梁而言,左端(de)M取负值或零,右端(de)M取正值或零.当“单跨”(de)边支座为铰支座时,它不能抵抗杆件(de)转动,所以边支座为铰支座时(de)M=0；但对于所有非边支座,则一律视为固定端支座.（3）将与同一支座相连接(de)各杆(de)固端弯矩M取代数和后反号按分配系数分配到与支座相连(de)各杆杆端.这一步(de)注意点是将固端弯矩代数和反号再分配.（4）将分配得到(de)弯矩视该节点各杆远端支座特征决定是否向远端传递.这种分配、传递将可能进行多次.这种次数只要进行(de)足够,从理论上讲将可以达到任意要求(de)精确度.但是工程实践上则只要进行2~3个循环即可满足正式结构设计(de)要求.（5）将上面四步运算之后(de)与同一节点相连(de)每根杆件杆端(de)固端弯矩、分配弯矩、传递弯矩分别求代数和,即为各杆(de)杆端弯矩.这一步(de)注意点是与同一支座相连(de)各杆(de)杆端弯矩代数和必定为零,否则说明计算上有错,或尚需进一步分配、传递.静定结构(de)内力只按静力平衡条件即可确定,其值与结构(de)材料性质和截面尺寸无关.超静定结构(de)全部反力和内力如只按静力平衡条件则无法确定,还必须同时考虑变形协调条件（即各部分(de)变形必须符合原结构(de)联接条件和支承条件）才能得出确定(de)解答,故超静定结构(de)内力状态与结构(de)材料性质和截面尺寸有关.在荷载作用下,超静定结构(de)内力只与各杆刚度(de)相对比值有关,而与其绝对值无关；在温度改变、支座移动等因素影响下,超静定结构(de)内力则与各杆刚度(de)绝对值有关,并且一般是与各杆刚度(de)绝对值成正比(de).对非结构专业来说,特别是对建筑学专业,不可能花大量(de)精力去从事对超静定结构(de)矩阵分析,因此弯矩分配法这样简明适用(de)方法就更有它(de)实际意义.一方面,弯矩分配法可以满足对一般正式结构设计(de)要求；另一方面,可以使建筑师加强对结构(de)概念设计.所以其优越性是显而易见(de). 例8-1 图示一连续梁,用弯矩分配法作弯矩图.解：（1）求分配系数a. 杆AB 和杆BC(de)线刚度lEI i =相等. b. 转动刚度：c. 分配系数：d. 校核：BA μ+BC μ=1,分配系数写在节点B 上面(de)方框内.（2）求固端弯矩M ,把梁看成两根独立(de)单跨梁.查表：AB 跨属表８－１编号５,而BC 跨属表８－１编号２.将结果写在相应杆端(de)下方.在节点B,BA 梁与BC 梁在B 端(de)固端弯矩代数和为（３）分配并传递,将节点B(de)固端弯矩代数和反号得被分配(de)弯矩为－６kN ·m,此弯矩按分配系数分配于两杆(de)B 端；并由于A 端为固端边支座,所以由BA 杆(de)B 端向A 端传递去B 端弯矩(de)一半；C 端由于是铰支边支座,故传递系数为零,即不向C 端传递.a. 分配弯矩：b. 传递力矩：用箭头表示弯矩传递(de)方向.（4）将以上结果竖向叠加,即得到最后(de)杆端弯矩.可列表进行,最下面一行表示最后结果.注意B 节点应满足平衡条件：注意A 端是固定边支座,只有一根杆AB,其分配系数为1,故它虽有固端弯矩m kN M AB ⋅-=15,但不存在分配或向B 端传递(de)问题,可A 端却可以接受从B 端传递过来(de)弯矩.（5）计算跨中弯矩a. 将AB 梁按简支梁画出计算简图,其上(de)荷载有两种,一是本来存在(de)集中荷载,二是在它两端按弯矩分配法算出(de)杆端弯矩,以集中力偶(de)形式作用于A 、B 两杆端处.见图8-10（a ）.b. 将AB 梁按两端简支梁情况下,仅作用有集中荷载时求出在中点(de)弯矩,见图8-10（b ）.m kN M ⋅=⨯=⋅30310荷载中c. 将AB 梁按两端简支梁情况下,仅在两端分别有杆端弯矩作用下求出中点(de)弯矩,实际上是一个几何梯形(de)中位线长度纵坐标,见图8-10（c ）.d. 跨中点弯矩(de)最终结果为b 、c 两步纵坐标(de)代数和.梁段上(de)其它任一点(de)弯矩也可以参照以上方法求出.中点弯矩为（6）在计算有多个节点(de)连续梁或刚架时,若将两个节点同时分配和传递,这两个节点既可相邻也可是被一个节点在当中隔开(de)形式.若从不平衡力矩（即节点四周各杆(de)杆端弯矩(de)代数和）较大(de)节点开始,可使收敛较快.（7）作弯矩图a. 用弯矩分配法列表计算出(de)都是各杆带正号或负号(de)杆端弯矩.正顺负逆（顺正逆负）b. 带+号（正号一般省略不写）(de)杆端弯矩使杆端作顺时针旋转,此时想象杆端往远端方向稍远一些(de)横截面固定不动.比如图8-9中AB 杆在B 端(de)杆端弯矩m kN M BA ⋅+=57.11,想象离B 端稍往左处(de)杆截面（图8-9中(de)D-D 截面）固定不动,由于正号杆端弯矩+·m,所以它使B 端绕这个想象中被固定(de)横截面作顺时针旋转.显然这个+·m(de)杆端弯矩使AB 上这小段杆件BD(de)上部纤维受拉,下部纤维受压.我们总是把弯矩图画在杆件(de)受拉纤维一侧.因此AB 杆在B 端(de)杆端弯矩＋·m 应画在杆(de)横线(de)上方.c. 带负号(de)杆端弯矩使杆端作逆时针旋转,此时也同样想象离杆端往远端方向稍远一些(de)横截面固定不动.比如图8-9中AB 杆在A 端(de)杆端弯矩m kN M AB ⋅-=72.16,想象离A 端稍往右处(de)杆截面（图8-9中(de)E-E 截面）固定不动,由于是负号杆端弯矩·m,所以它使A 端绕这个想象中被固定(de)横截面作逆时针旋转.显然这个·m(de)杆端弯矩使AB 上(de)这一“小段”杆件AE(de)上部纤维受拉,下部纤维受压.根据弯矩图总是画在杆件(de)受拉纤维一侧(de)规定,因此AB 杆在A 端(de)杆端弯矩·m 也应画在代表杆(de)横线(de)上方.d. 至于每一单跨上(de)跨中弯矩,只需凭弯矩图总是画在受拉纤维一侧这个规定和跨中弯矩(de)计算过程就可以正确(de)决定它是画在代表杆(de)横线上方还是下方.（8）计算剪力a. 按每一单跨杆件分别取脱离体求剪力.把每一单跨梁看成简支梁,它(de)荷载有三种：第一种是原来就作用在单跨上(de)荷载.第二种是用弯矩分配法算出来(de)杆端弯矩.第三种是简支梁(de)两端两个支座反力,它们是未知(de),由于脱离体可列出两个静力平衡方程,而支座反力也恰好为两个,故可顺利求出.而这两个支座反力,就是我们要求(de)剪力.杆端剪力在这里起了“支座反力”(de)作用.因此将“支座反力”用箭头表示,方向和大小假定,先不考虑它(de)真实指向和大小.b. 按简支梁求支座反力(de)方法列出平衡方程可求出箭头所示力(de)大小和正负号.剪力大小即等于支座反力,从解方程直接得出,剪力(de)方向视箭头所示力(de)正负号而定.如果是正号,说明箭头指向就是真正(de)指向；如果是负号,说明与原假定(de)指向相反.画出剪力图.例8-2 试计算图8-11连续梁(de)杆端弯矩和跨中弯矩.并作弯矩图.解：（1）求固端弯矩：（2）求分配系数：a. 对节点B,相邻两杆BA 、BC(de)转动刚度所以b. 同理,对节点C 有：（3）分配结果见图8-11.（4）求跨中弯矩a. 对AB 跨：b. 对BC 跨：c. 对CD 跨见图8-12.在集中力作用下,CD 跨(de)最大跨间弯矩发生在集中力P=160kN 作用点. （a ）在集中力作用下,该点(de)简支梁弯矩（图8-12b ）（b ）在杆端弯矩作用下,该点(de)负弯矩为（图8-12c ）(c) 该点(de)弯矩为1M 和2M (de)代数和.（5）作出连续梁(de)弯矩图.例8-4 试用弯矩分配法计算图8-14（a ）所示等截面连续梁（带悬臂梁）(de)各杆端弯矩.并作弯矩图.已知各杆EI 值为：AB 为6,BC 为4,CD 为4,DE 为6 .解：此梁(de)悬臂EF 为一静定部分,该部分(de)内力根据静力平衡条件便可求得： kN V m kN M EF EF 20,40=⋅-=.若将该悬臂部分去掉,而将EF EF V M 和作为外力作用于节点E,图8-14（b ）,节点E 便化为铰支端,整个计算即可按此考虑.计算分配系数时,其中计算固端弯矩时,对杆DE,将相当于一端固定另一端铰支(de)单跨梁,除跨中受集中力作用外,并在铰支端E 处受一集中力和一集中力偶(de)作用.其中作用在E 端(de)集中力为支座直接承受,在梁内不引起弯矩,而E 端(de)力偶40kN ·m 将使杆DE 引起固端弯矩,其值DE M 为DE 跨在D 端(de)固端弯矩DEM '（编号1）与EF 跨在E 端(de)固端弯矩EF M 向远端D(de)传递弯矩DEM ''之代数和,即 其余固端弯矩均可查表求得.分配及弯矩图见8-14.例8-5 求图8-15所示刚架(de)弯矩图.解：（1）转动刚度：（2）分配系数：节点B ：节点C ：（3）固端弯矩：由于只有梁有外荷载,故也只有梁才有固端弯矩,它们为（4）力矩分配：按C 、B 顺序分配两轮,计算见图8-16（a ）,放松节点(de)次序可以任取,并不影响最后(de)结果.但为了缩短计算过程,最好先放松不平衡力矩较大(de)节点,在本例中,先放松节点C 较好.（5）作弯矩图.图8-16（b ）.讨论：（1）当刚架竖柱比横梁(de)线刚度大很多时,即梁柱i i >>,则∑∑+梁柱柱i i i 接近于1（如梁柱i i 20≥,误差在5%以内）.杆端（柱端）弯矩接近于固端弯矩.此时,竖柱对横梁而言,起固定支座(de)作用.也就是说,在这种情况下,每相邻两个节点之间(de)横梁,可以当作两端固定(de)单梁来计算,不必用弯矩分配法来求解了.（2）当刚架横梁比竖柱(de)线刚度大很多时,即柱梁i i >>,则∑∑+梁柱柱i i i 接近于零（如柱梁i i 20≥,误差在5%以内）.杆端（柱端）弯矩接近于零.此时,竖柱对横梁而言,起铰支座(de)作用.这种情况下,横梁(de)每个支座都将视作铰支座（习惯上是一个固定铰支座,其余则为活动铰支座）,横梁演化为一根以柱为支点(de)连续梁,用弯矩分配法可求出每一杆端弯矩.（3）当∑∑+梁柱柱i i i 介于上述两者之间时,其计算简图为刚架,用弯矩分配法求解. 四、弯矩分配法与电算结果(de)比较下图中括号外为弯矩分配法计算结果,括号内为电算计算结果.。

多跨连续梁板的内力计算方法1.静力法静力法是根据力的平衡条件进行内力计算的一种方法。

它将整个连续梁板分成多个简支梁，然后根据每个简支梁的自由度和受力情况，利用静力平衡方程来计算内力。

静力法的计算步骤如下：1.1确定荷载情况：根据施工过程中的荷载情况，包括永久荷载、临时荷载、活荷载等，确定在每个简支梁上的作用荷载。

1.2确定支座反力：根据简支梁的支座类型和约束条件，利用静力平衡方程计算得到每个简支梁的支座反力。

1.3确定剪力和弯矩分布：根据简支梁的自由度和受力平衡条件，分别计算每个简支梁的剪力和弯矩分布，并绘制剪力和弯矩图。

1.4超程状态求解：对于超程段，根据断面力和弯矩图的性质，分别计算超程段的剪力和弯矩值。

1.5内力计算：根据每个简支梁上的受力条件和简支梁的自由度，依次计算出每个简支梁的内力值，包括剪力、弯矩和轴力。

1.6跨中内力的计算：将每个简支梁上的内力加权平均，得到整个连续梁板跨中截面所受的内力值。

注意事项：在使用静力法计算连续梁板的内力时，需要注意简支梁之间的相互作用和连梁处的内力传递。

2.变形法变形法是根据结构变形的平衡条件进行内力计算的一种方法。

它将整个连续梁板看作一个整体，利用结构变形平衡方程来计算内力。

变形法的计算步骤如下：2.1建立变形方程：根据连续梁板的几何形状和材料特性，建立连续梁板的位移和变形关系。

2.2确定加载形态：根据施工过程中的荷载情况，确定连续梁板的加载形态，包括简支挠度和弯矩分布。

2.3利用变形方程求解：根据变形方程和加载形态，利用几何和材料力学关系，求解出每个简支梁的弯矩和剪力分布。

2.4变形体内力计算：根据连续梁板的几何和材料力学关系，将每个简支梁上的弯矩和剪力分布转化为变形体上的内力分布。

2.5跨中内力的计算：将变形体上的内力分布加权平均，得到整个连续梁板跨中截面所受的内力值。

注意事项：在使用变形法计算连续梁板的内力时，需要考虑材料的非线性特性和位移场的复杂性，适用于较复杂的结构形式。

多跨连续梁支座反力计算多跨连续梁是现代桥梁结构中一种非常常见的形式，它在跨度和长度方面都具备了较大的优越性，承载能力和经济性均较为突出。

而在设计这样的结构时，支座反力的计算是一个至关重要的环节，在本文中，我们将给大家详细介绍一下多跨连续梁支座反力计算的各个步骤。

第一步：确定梁的几何形状和建模在计算支座反力之前，需要先了解梁的几何形状，包括梁的跨度、受载长度、断面性质、钢材性质等。

然后，将这些信息用计算机建模的方式呈现出来，便于后续的有限元分析。

第二步：进行静力计算在建立好模型之后，就可以进行静力计算，并根据梁在各种受力情况下的运动状态，得出支座反力。

在静力计算过程中，需要考虑到来自上游和下游的外力以及其他特殊负荷因素。

第三步：加入荷载计算进行完静力计算之后，接下来就需要加入不同种类的荷载进行计算了。

常见的荷载包括车辆荷载、温度荷载、风荷载等。

不同的荷载对支座反力的计算产生不同的影响，因此需要十分仔细地进行计算。

第四步：加入变形计算在梁受到荷载后，一定会发生变形，在支座反力的计算过程中，需要考虑到梁的变形。

变形通过不同的应变附加到梁的截面上，并进行计算，在这个过程中，需要考虑到混凝土的弹性模量、梁材料的弹性和塑性特性、预处理等。

第五步：重复计算前面的计算是建立在假设荷载稳定的情况下进行的。

实际上，荷载的突然变化会引起支座反力发生变化，因此，需要重复进行计算，并根据需要进行调整，保证计算结果的准确性。

以上，就是多跨连续梁支座反力计算的整个过程。

虽然这里仅仅提了一个粗略的概要，但是这一过程的计算是复杂而又十分耗费时间的，需要进行多方面的考虑。

在实际应用中，支座反力的计算是设计师需要反复攻坚克难的难点之一，需要进行多次的验证和检验，以保证梁的安全性和稳定性。

六跨连续梁内力计算程序说明文档一．程序适用范围本程序用来解决六跨连续梁在荷载作用下的弯矩计算。

荷载可以是集中力Fp（作用于跨中）、分布荷载q（分布全垮）、集中力偶m（作用于结点）的任意组合情况。

端部支承可为铰支或固支。

二．程序编辑方法使用Turbo C按矩阵位移法的思路进行编辑，用Turbo C中的数组来完成矩阵的实现，关键的求解K⊿=P的步骤用高斯消元法。

三．程序使用方法运行程序后，按照提示，依次输入结点编号，单元编号，单元长度，抗弯刚度（EI的倍数），集中力，均部荷载，集中力偶，各个数据间用空格隔开，每一项输入完毕后按回车键，所有数据输入完毕后按任意键输出结果。

输出结果中包括输入的数据（以便校核），角位移的值（以1/EI为单位）以及每个单元的左右两端弯矩值。

四．程序试算1．算例1算力图示：输入数据：结点：1 2 3 4 5 6 0；单元：1 2 3 4 5 6；长度：4 6 6 8 4 6； EI：1 1.5 1 2 1 1.5；Fp：0 12 8 0 6 0；q：8 0 0 4 0 6；m：0 0 -8 0 10 0 0运行程序如下：结果为： 角位移为：1(11.383738,-1.434142,-8.980504,14.053733,-10.192107,10.048027,0)EI单元编号 1 2 3 4 5 6 左端弯矩 0.00000 -14.92439 -7.30243 -12.37565 -8.16809 -7.95197 右端弯矩 14.92439-0.6975712.3756518.168097.9519723.024012． 算例2 算例图示：6EI 8kN/m 4m 3m 2m 8m kN/m 12365474kN/m3m 3m3m 2m 6m12kN 8kN8kN.m6kN10kN.mEI EI EI 1.5EI1.52EI输入数据：结点：0 1 2 3 4 5 6； 单元：1 2 3 4 5 6； 长度：4 6 6 8 4 6； EI ：1 1.5 1 2 1 1.5；Fp ：0 12 8 0 6 0； q ：8 0 0 4 0 6；m ：0 0 -8 0 10 0 0运行程序如下：结果为： 角位移为：1(0,1.686721,-10.080218,14.871010,-12.183221,17.195206,-26.597603)EI单元编号 1 2 3 4 5 6 左端弯矩 -9.82331 -12.35339 -7.76314 -12.55393 -6.58562 -14.10360 右端弯矩 12.35339-0.2368612.5539316.5856214.103600.00000弯矩图如下：3． 算例3 算例图示：6EI8kN/m 4m 3m 2m 8m kN/m1236544kN/m3m 3m3m 2m 6m12kN 8kN8kN.m6kN 10kN.mEI1.5EI EI EI 2EI 1.5输入数据：结点：0 1 2 3 4 5 0；单元：1 2 3 4 5 6；长度：4 6 6 8 4 6； EI：1 1.5 1 2 1 1.5；Fp：0 12 8 0 6 0；q：8 0 0 4 0 6；m：0 0 -8 0 10 0 0运行程序如下：结果为：角位移为：1(0,1.653925,-9.949034,14.264283,-10.248253,10.062063,0) EI单元编号123456左端弯矩-9.83978-12.32059-7.87793-12.19318-8.21722-7.93794右端弯矩12.32059-0.1220712.1931818.217227.9379423.03103弯矩图如下：4．算例4算例图示：6EI 8kN/m 4m 3m 2m 8m kN/m 12365474kN/m3m 3m3m 2m 6m12kN 8kN8kN.m 6kN10kN.mEI EI EI 1.5EI1.52EI输入数据：结点：1 2 3 4 5 6 7； 单元：1 2 3 4 5 6； 长度：4 6 6 8 4 6； EI ：1 1.5 1 2 1 1.5；Fp ：0 12 8 0 6 0； q ：8 0 0 4 0 6； m ：0 0 -8 0 10 0 0 运行程序如下：结果为： 角位移为：1(11.364772,-1.396211,-9.113262,14.660626,-12.126579,17.179023,-26.589511)EI单元编号 1 2 3 4 5 6 左端弯矩 -0.00000 -14.25984 -7.18863 -12.73600 -6.53707 -14.11573 右端弯矩 14.95284-0.8113712.7360016.5370714.115730.00000弯矩图如下：五．源程序#include<stdio.h>#include<conio.h>定义变量int joint[7]; 结点编号int unit[6]; 单元编号float length[6];长度float EI[6]; 抗弯刚度float P[6]; 集中力float q[6]; 均部荷载float m[7]; 集中力偶double I[6]; 线刚度int number=7,i,j;double K[7][7]={0}; 整体刚度矩阵double k[6][2][2]; 单元刚度矩阵doubleMP[6][2],Mq[6][2],Mlast[6][2],M[7]={0},tatleM[7],mm[7],Mqueue[7]={0},antiM[7]= {0};依次为：集中力、均布荷载引起的固端弯矩，最终杆端弯矩，全部荷载引起的弯矩，总的结点荷载，按结点编号排列的结点集中力偶，按结点编号排列的固端弯矩，等效结点弯矩double angle[7]={0}; 角位移void input(); 输入函数void solve(); 求解函数void output(); 输出函数void Gauss(); 高斯消元法void main(){input();solve();output();}void input(){clrscr();printf("Please input data.\n\nThe joint number:");for(i=0;i<7;i++)scanf("%d",&joint[i]);printf("\nThe unit number:");for(i=0;i<6;i++)scanf("%d",&unit[i]);printf("\nThe length:");for(i=0;i<6;i++)scanf("%f",&length[i]);printf("\nThe EI:");for(i=0;i<6;i++)scanf("%f",&EI[i]);printf("\nThe Fp:");for(i=0;i<6;i++)scanf("%f",&P[i]);printf("\nThe q:");for(i=0;i<6;i++)scanf("%f",&q[i]);printf("\nThe m:");for(i=0;i<6;i++)scanf("%f",&m[i]);}void solve(){for(i=0;i<7;i++){if(joint[i]==0) number-=1;}for(i=0;i<6;i++){MP[i][0]=-P[i]*length[i]/8;MP[i][1]=P[i]*length[i]/8;}for(i=0;i<6;i++){Mq[i][0]=-q[i]*length[i]*length[i]/12;Mq[i][1]=q[i]*length[i]*length[i]/12; }for(i=1;i<6;i++){M[i]=MP[i-1][1]+MP[i][0]+Mq[i-1][1]+Mq[i][0];}M[0]=MP[0][0]+Mq[0][0];M[6]=MP[5][1]+Mq[5][1];if(joint[0]==0)j=1;else j=0;for(i=j;i<7&&joint[i]>=1;i++){Mqueue[joint[i]-1]=M[i];mm[joint[i]-1]=m[i];}for(i=0;i<7;i++)antiM[i]=-Mqueue[i];for(i=0;i<7;i++)tatleM[i]=antiM[i]+mm[i];for(i=0;i<6;i++)I[i]=(EI[i]/length[i]);if(joint[0]==0) K[joint[1]-1][joint[1]-1]+=4*I[0];if(joint[6]==0) K[joint[5]-1][joint[5]-1]+=4*I[5];for(i=0;i<6;i++){k[i][0][0]=4*I[i],k[i][0][1]=2*I[i],k[i][1][0]=2*I[i],k[i][1][1]=4*I[i]; }for(i=j;joint[i]>=1&&joint[i+1]>=1&&i<6;i++){K[joint[i]-1][joint[i]-1]+=k[i][0][0];K[joint[i]-1][joint[i+1]-1]+=k[i][0][1];K[joint[i+1]-1][joint[i]-1]+=k[i][1][0];K[joint[i+1]-1][joint[i+1]-1]+=k[i][1][1];}getch();}void output(){clrscr();printf("The data you put in:\n\tjoint :");for(i=0;i<7;i++){printf("\t");printf("%d",joint[i]);}printf("\n\n\tunit :");for(i=0;i<6;i++){printf("\t");printf("%d",unit[i]);}printf("\n\n\tlength :");for(i=0;i<6;i++){printf("\t");printf("%1.0f",length[i]); }printf("\n\n\tEI :");for(i=0;i<6;i++){printf("\t");printf("%1.1f",EI[i]);}printf("\n\n\tFp :");for(i=0;i<6;i++){printf("\t");printf("%1.0f",P[i]);}printf("\n\n\tq :");for(i=0;i<6;i++){printf("\t");printf("%1.0f",q[i]);}printf("\n\n\tm :");for(i=0;i<6;i++){printf("\t");printf("%1.0f",m[i]);}Gauss();for(i=0;i<6;i++){Mlast[i][0]=k[i][0][0]*angle[joint[i]-1]+k[i][0][1]*angle[joint[i+1]-1]+MP[i][0 ]+Mq[i][0];Mlast[i][1]=k[i][1][0]*angle[joint[i]-1]+k[i][1][1]*angle[joint[i+1]-1]+MP[i][1 ]+Mq[i][1];}printf("\n--------------------------------------------------------------------------------");printf("\nThe angle(1/EI):\n\n");for(i=0;i<number;i++){printf("%12.6f",angle[i]);}printf("\n--------------------------------------------------------------------------------");printf("\nunit number");for(i=0;i<6;i++){printf("%6d ",unit[i]);}printf("\n\nleft M \t");for(i=0;i<6;i++) printf("%12.5f",Mlast[i][0]);printf("\n\nright M\t");for(i=0;i<6;i++) printf("%12.5f",Mlast[i][1]);getch();}void Gauss(){int l,m;double box;double BOX[7]={0};for(j=0;j<(number-1);j++){for(i=j;i<number;i++){if(K[i][j]!=0){for(m=0;m<number;m++){BOX[m]=K[i][m];K[i][m]=K[j][m];K[j][m]=BOX[m]; }box=tatleM[i];tatleM[i]=tatleM[j];tatleM[j]=box; break;}}for(m=j+1;m<number;m++){K[j][m]/=K[j][j];}tatleM[j]/=K[j][j];K[j][j]=1;for(l=j+1;l<number;l++){tatleM[l]+=-tatleM[j]*K[l][j];for(m=number-1;m>=j;m--){K[l][m]+=-K[j][m]*K[l][j];}}}tatleM[number-1]/=K[number-1][number-1];K[number-1][number-1]=1;for(i=0;i<number;i++)angle[i]=tatleM[i];for(i=number-2;i>=0;i--){for(j=number-1;j>i;j--)angle[i]=angle[i]-K[i][j]*angle[j];}}。