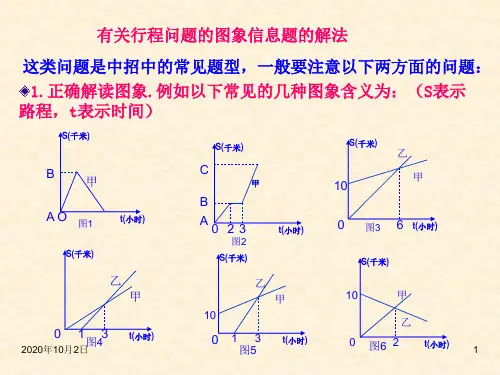
y(千米)
20
10
O
12
44
x(分)
11
6.在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发, 沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离 分别为y(km)y与x的函数关系如图所示. (1)填空:A、C两港口间的距离为 km, ; (2)求图中点P的坐标,并解释该点坐标所表示的实际意义; (3)若两船的距离不超过10 km时能够相互望见,求甲乙两船可以相互望见时x 的取值范围.
一次函数“图象应用题”专项训 练(中考第25题) 初三数学组 集体备课
1
考点链接:
一次函数“图象应用题” 联系实际,贴近生活,备受命题 者的青睐.试题不仅考察函数的基础知识,同时考察综合 运用所学知识,解决实际问题的能力,探索创新能力以及 实践能力.
解题技巧: 1.观察图象,学会识图,读图,并从中获取信息. 2.由折线特征结合生活实际造应用背景. 3.弄清起点,终点,转折点的含义,以及对应用背景的影响. 4.进行“数”与 “形”之间的互换: a.将图象转化为解析式; b.将图象中的信息转化为数据,进而转化为方程; c.几何图形的线段转化为距离.
2
一.知识准备:
甲、乙两同学从A地出发,骑自行车,骑自行车在同一 条路上行驶到B地,他们离出发地的距离S(千米)和行驶 时间t(小时)之间的函数关系的图象如图所示,你能从图 象中获得哪些信息?甲乙(t/小时)012S/千米2.50.518
S/千米
18
乙
甲
(t/小时)
0 0.5 1
2 2.5
3
二.经典考题:
y千米
120
()
0
()
3
![行程问题中的函数图象[下学期] 华师大版 (PPT)4-4](https://uimg.taocdn.com/fb19ff8590c69ec3d4bb7521.webp)