三角函数公式大全及推导过程

三角函数公式大全及推导过程一、任意角的三角函数在角α的终边上任取．．一点),(y x P ，记：22y x r +=， 正弦：r y =αsin 余弦：r x =αcos 正切：xy =αtan 二、同角三角函数的基本关系式 商数关系：αααcos sin tan =，平方关系：1cos sin 22=+αα，221cos 1tan αα=+ 三、诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）= sinα cos（2kπ＋α）= cosα tan（2kπ＋α）= tanα 公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin （π＋α）= -sinα cos（π＋α）= -cosα tan（π＋α）= tanα 公式三：任意角α与 -α的三角函数值之间的关系：sin （-α）= -sinα cos（-α）= cosα tan（-α）= -tanα 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系： sin （π-α）= sinα cos（π-α）= -cosα tan（π-α）= -tanα 公式五： 利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系： sin （2π-α）= -sinα cos（2π-α）= cosα tan（2π-α）= -tanα 公式六：2π±α及23π±α与α的三角函数值之间的关系： sin （2π-α）= cosα cos（2π-α）= sinα sin （2π+α）= cosα cos（2π+α）= -sinα sin （23π-α）= -cosα cos（23π-α）= -sinα sin （23π+α）= -cosα cos（23π+α）= sinα 三、两角和差公式βαβαβαsin cos cos sin )sin(⋅+⋅=+βαβαβαsin cos cos sin )sin(⋅-⋅=-βαβαβαsin sin cos cos )cos(⋅-⋅=+βαβαβαsin sin cos cos )cos(⋅+⋅=-βαβαβαtan tan 1tan tan )tan(⋅-+=+ βαβαβαtan tan 1tan tan )tan(⋅+-=- 四、二倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=…)(*ααα2tan 1tan 22tan -= 二倍角的余弦公式)(*有以下常用变形：（规律：降幂扩角，升幂缩角） αα2cos 22cos 1=+ αα2sin 22cos 1=-2)cos (sin 2sin 1ααα+=+ 2)cos (sin 2sin 1ααα-=-其它公式 五、辅助角公式：)sin(cos sin 22ϕ++=+x b a x b x a （其中ab =ϕtan ） 其中：角ϕ的终边所在的象限与点),(b a 所在的象限相同，(以上k ∈Z)六、其它公式：1、正弦定理：R Cc B b A a 2sin sin sin ===（R 为ABC ∆外接圆半径） 2、余弦定理 A bc c b a cos 2222⋅-+=B ac c a b cos 2222⋅-+=C ab b a c cos 2222⋅-+=3、三角形的面积公式 高底⨯⨯=∆21ABC S B ca A bc C ab S ABC sin 21sin 21sin 21===∆（两边一夹角）万能公式推导sin2α=2sinαcosα=2sinαcosα/(cos^2(α)+sin^2(α))......*，（因为cos^2(α)+sin^2(α)=1）再把*分式上下同除cos^2(α)，可得sin2α=2tanα/(1+tan^2(α))然后用α/2代替α即可。

一、两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotA cotB 1cotAcotB -+推导：1、应用三角函数线推导差角公式的方法设角α的终边与单位圆的交点为P 1，∠POP 1＝β，则∠POx ＝α－β．过点P 作PM ⊥x 轴，垂足为M ，那么OM 即为α－β角的余弦线，这里要用表示α，β的正弦、余弦的线段来表示OM ．过点P 作PA ⊥OP 1，垂足为A ，过点A 作AB ⊥x 轴，垂足为B ，再过点P 作PC ⊥AB ，垂足为C ，那么cos β＝OA ，sin β＝AP ，并且∠PAC ＝∠P 1Ox ＝α，于是OM ＝OB ＋BM ＝OB ＋CP ＝OA cos α＋AP sin α＝cos βcos α＋sin βsin α．综上所述，.说明：应用三角函数线推导差角公式这一方法简单明了，构思巧妙，容易理解. 但这种推导方法对于如何能够得到解题思路，存在一定的困难. 此种证明方法的另一个问题是公式是在均为锐角的情况下进行的证明，因此还要考虑的角度从锐角向任意角的推广问题.2、设α、β是两个任意角，把α、β两个角的一条边拼在一起，顶点为O，过B点作OB的垂线，交α另一边于A，交β另一边于C，则有S△OAC=S△OAB+S△OBC..根据三角形面积公式，有，∴.∵，，，∴，∵，∴sin(α+β)=sinαcosβ+sinβcosα.或者：sin(a+b)=cos[(π/2)-(a+b)]=cos[(π/2-a)-b]=cos(π/2-a)cosb-sin(π/2-a)sinb=sinacosb-cosasinb（就是利用π/2的诱导公式）3、tan(a+b)=sin(a+b)/cos(a+b)=(sinacosb+cosasinb)/(cosacosb-sinasinb) 分子分母同除以cosacosb 得(tana+tanb)/【1-tanatanb 】 二、倍角公式tan2A =Atan 12tanA2Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A1、公式sin2α=2sinα·cosα推导过程sin2α=sin(α+α)=sinα·cosα+cosα·sinα=2sinα·cosα2、公式余弦二倍角公式有三组表示形式，三组形式等价： cos2α=2cos²α-1 cos2α=1-2sin²α cos2α=cos²α-sin²α推导过程cos2α=cos(α+α)=cosα·cosα-sinα·sinα=cos²α-sin²α=2(cos²α)-1 =1-2(sin²α)3、正切二倍角公式tan2α=2tanα/[1-tan²α] 推导过程：tan2α=sin2α/cos2α=2sinα·cosα/cos²α-sin²α=[2sinα·cosα/cos²α]/[cos²α-sin²α/cos²α]=2tanα/[1-tan²α]三、半角公式（正负由所在的象限决定）（正负由所在的象限决定）（正负由所在的象限决定）推导过程：……①sin由等式①，整理得： 将 代入α，整理得：开方，得cos在等式①两边加上1，整理得：将代入 ，整理得：开方，得tansina=cos （π/2-a ）注：四、三倍角公式（常用）四、五、六、七、八、九、十、N 倍角公式(不常用)sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)推导： sin3a =sin(2a+a)=sin2acosa+cos2asina =2sina(1-sin ²a)+(1-2sin ²a)sina =3sina-4sin ³a cos3a =cos(2a+a)=cos2acosa-sin2asina=(2cos ²a-1)cosa-2(1-cos ²a)cosa =4cos ³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)四倍角公式sin4A=-4*(cosA*sinA*(2*sinA^2-1)) cos4A=1+(-8*cosA^2+8*cosA^4)tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式sin5A=16sinA^5-20sinA^3+5sinA cos5A=16cosA^5-20cosA^3+5cosAtan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)六倍角公式sin6A=2*(cosA*sinA*(2*sinA+1)*(2*sinA-1)*(-3+4*sinA^2))cos6A=((-1+2*cosA^2)*(16*cosA^4-16*cosA^2+1))tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)七倍角公式sin7A=-(sinA*(56*sinA^2-112*sinA^4-7+64*sinA^6))cos7A=(cosA*(56*cosA^2-112*cosA^4+64*cosA^6-7))tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tanA^6) 八倍角公式sin8A=-8*(cosA*sinA*(2*sinA^2-1)*(-8*sinA^2+8*sinA^4+1))cos8A=1+(160*cosA^4-256*cosA^6+128*cosA^8-32*cosA^2)tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8) 九倍角公式sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4+36*sinA^2-3))cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4+36*cosA^2-3))tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*tanA^4-84*tan A^6+9*tanA^8)十倍角公式sin10A=2*(cosA*sinA*(4*sinA^2+2*sinA-1)*(4*sinA^2-2*sinA-1)*(-20*sinA^2+5+16*sinA^4)) cos10A=((-1+2*cosA^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*cosA^2+1))tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tanA^ 4+210*tanA^6-45*tanA^8+tanA^10)N倍角公式根据棣美弗定理，(cosθ+ i sinθ)^n = cos(nθ)+ i sin(nθ) 为方便描述，令sinθ=s，cosθ=c 考虑n为正整数的情形：cos(nθ)+ i sin(nθ) = (c+ i s)^n = C(n,0)*c^n + C(n,2)*c^(n-2)*(i s)^2 +C(n,4)*c^(n-4)*(i s)^4 + ... +C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 + C(n,5)*c^(n-5)*(i s)^5 + ... =>比较两边的实部与虚部实部：cos(nθ)=C(n,0)*c^n + C(n,2)*c^(n-2)*(i s)^2 +C(n,4)*c^(n-4)*(i s)^4 + ... i*(虚部)：i*sin(nθ)=C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 + C(n,5)*c^(n-5)*(i s)^5 + ... 对所有的自然数n，1. cos(nθ)：公式中出现的s都是偶次方，而s^2=1-c^2(平方关系)，因此全部都可以改成以c(也就是cosθ)表示。

锐角三角函数锐角三角函数三角关系倒数关系：tanα·α=1sinα·α=1cosα·α=1商的关系：平方关系：三角函数公式公式相关两角和公式cos（α+β）=cosαcosβ-αsinβcos（α-β）=cosαcosβ+sinαsinβsin（α+β）=sinαcosβ+cosαsinβsin（α-β）=sinαcosβ -cosαsinβ（α+β）=(tanα+tanβ）/（1-tanαtanβ）tan（α-β）=(tanα-tanβ）/（1+tanαtanβ）cot(A+B) = (cotAcotB-1）/(cotB+cotA)cot(A-B) = (cotAcotB+1）/(cotB-cotA)三角和公式sin（α+β+γ）=sinα·cosβ·cosγ+cosα·sinβ·cos γ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos（α+β+γ）=cosα·cosβ·cosγ-cosα·sinβ·sin γ-sinα·cosβ·sinγ-sinα·sinβ·cosγ诱导公式的诱导公式（六公式）公式一：sin(α+k*2π)=sinαcos(α+k*2π)=cosαtan(α+k*π)=tanα公式二：sin(π+α) = -sinαcos(π+α) = -cosαtan(π+α）=tanα公式三：sin(-α) = -sinαcos(-α) = cosαtan (-α)=-tanα公式四：sin(π-α) = sinαcos(π-α) = -cosαtan(π-α) =-tanα公式五：sin(π/2-α) = cosαcos(π/2-α) =sinα由于π/2+α=π-（π/2-α），由公式四和公式五可得公式六：sin(π/2+α) = cosαcos(π/2+α) = -sinα诱导公式记背诀窍：奇变偶不变，符号看。

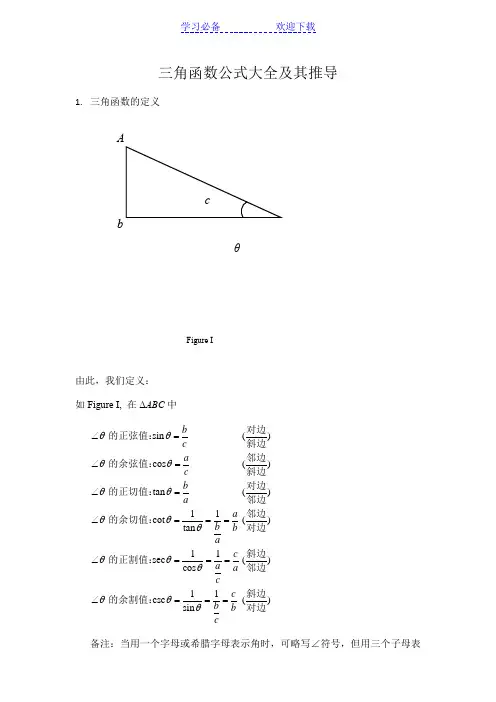
三角函数公式大全及其推导1. 三角函数的定义由此，我们定义：如Figure I, 在ΔABC 中sin () cos () tan ()11 cot ()tan 11 sec ()cos 11 csc ()sin bca cb a a b b ac a a c c b b c θθθθθθθθθθθθθθθ∠=∠=∠=∠===∠===∠===对边的正弦值：斜边邻边的余弦值：斜边对边的正切值：邻边邻边的余切值：对边斜边的正割值：邻边斜边的余割值：对边备注：当用一个字母或希腊字母表示角时，可略写∠符号，但用三个子母表A c b θ Figure I示时，不能省略。

在本文中，我们只研究sin 、cos 、tan 。

2. 额外的定义222222sin (sin )cos (cos )tan (tan )θθθθθθ===3. 简便计算公式22sin cos cos(90)cos sin sin(90)111tan tan tan(90)sin cos 1b A cc A b b a a A bθθθθθθθθ===-∠===-∠====-∠+= 证明： 2222222222901sin sin 1sin cos 1ABC ABC a b c a b c cB A θθ∆∠=∴+=∴+=∴+=∴+=在中,证完222222sin tan cos sin cos 1tan 1cos cos cos bb c a a cθθθθθθθθθ===+=+= 4. 任意三角形的面积公式如Figure II , C a b hFigure II121sin 21sin ()2ABC S ah ab C ac B ∆===两边和其夹角正弦的乘积 5. 余弦定理：任意三角形一角的余弦等于两邻边的平方和减对边的平方之差与两邻边积的两倍之比。

证明：如Figure II, 2222222222222222222222(cos )(sin )2cos cos sin =2cos (cos sin )2cos cos 22b d h a c B c B a ac B c B c Ba ac B c B B a c ac Bb ac a c b B ac ac=+=-+=-++-++=+---+-⇒==-证完6. 海伦公式证明：如Figure II ,1sin 212121212ABC S ab C∆=========2ABC a b cs S ∆===++=设： 7. 正弦定理如 Figure III ,c 为ΔABC 外接圆的直径,sin 2 sin a A c ac r r ABC A =∴==∆（为的外接圆半径）同理：, sin sin 2sin sin sin b c c c B C a b c r A B C ==∴===8. 加法定理(1) 两角差的余弦如 Figure IV , AOC BOC AOB αβαβ∠=∠∠=∠∠=∠-∠令AO=BO=r点A 的横坐标为cos A x r α=点A 的纵坐标为sin A y r α=点B 的横坐标为cos B x r β=Figure IV点B 的纵坐标为sin B y r β=()()()()()()22222222222222222222222222sin sin cos cos sin sin 2sin sin cos cos 2cos cos sin sin 2sin sin cos cos 2cos cos sin cos sin cos 2sin sin 2cos cos 112s A B A B AB y y x x r r r r r r r r r r r r r αββααβαβαβαβαβαβαβαβααββαβαβ=-+-=-+-=+-++-=+-++-=+++--=+-()()()22in sin cos cos 22sin sin cos cos 21sin sin cos cos r r αβαβαβαβαβαβ+⎡⎤⎣⎦=-+⎡⎤⎣⎦=-+⎡⎤⎣⎦由余弦公式可得：()()()()2222222222cos 2cos 22cos 22cos 21cos AB AC BC AC BC ACBr r r r r r r r αβαβαβαβ=+-⋅∠=++⋅-=+-=--⎡⎤⎣⎦=--⎡⎤⎣⎦综上得：()cos sin sin cos cos αβαβαβ-=+(2) 两角和的余弦()()()()cos cos sin sin cos cos sin sin cos cos cos cos sin sin αβαβαβαβαβαβαβαβ+=--⎡⎤⎣⎦=-+-=-+=-(3) 两角和的正弦()()()()()sin cos 90cos 90sin 90sin cos 90cos cos sin sin cos αβαβαβαβαβαβαβ+=︒-+⎡⎤⎣⎦=︒--⎡⎤⎣⎦=︒-+︒-=+(4) 两角差的正弦()()()()sin sin cos sin sin cos cos sin sin cos sin cos cos sin αβαβαβαβαβαβαβαβ-=+-⎡⎤⎣⎦=-+-=-+=-(5) 两角和的正切()()()sin tan cos cos sin sin cos cos cos sin sin cos sin sin cos cos cos cos cos sin sin cos cos sin sin cos cos sin sin 1cos cos tan tan 1tan tan αβαβαβαβαβαβαβαβαβαβαβαβαββαβααβαβαβαβ++=++=-+=-+=-+=-(6) 两角差的正切()()()()tan tan tan tan 1tan tan tan tan 1tan tan αβαβαβαβαβαβ-=+-⎡⎤⎣⎦+-=---=+ 9. 两倍角公式()()()()()()()222222222222sin 2sin sin cos sin cos 2sin cos cos 2cos cos cos sin sin cos sin 12sin 2cos 1sin 2tan 2cos 22sin cos cos sin 2sin cos cos cos sin cos 2sin cos sin 1cos 2tan 1ta αααααααααααααααααααααααααααααααααααααα=+=+==+=-=-=-=-==-=-=-=-2n α10. 积化和差公式()()()()1sin cos 2sin cos 21sin cos sin cos cos sin cos sin 21sin sin 2αβαβαβαβαβαβαβαβ==++-=++-⎡⎤⎣⎦()()()()()()()()1cos cos 2cos cos 21cos cos cos cos sin sin sin sin 21cos cos 21sin sin 2sin sin 21sin sin sin sin cos cos cos cos 21cos cos 2αβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβ==++-=++-⎡⎤⎣⎦==++-=+--⎡⎤⎣⎦ 11. 和差化积公式 (1)设：A=α+β, B=α-β,()()()()sin sin sin sin sin cos cos sin sin cos cos sin 2sin cos 2sin cos 222sin cos 22sin sin sin sin sin cos cos sin sin cos cos sin 2cos si A B A B A B A B αβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβα+=++-=++-=++-+--⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭+-⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭-=+--=+-+=n 2cos sin 222cos sin 22A B A B βαβαβαβαβ++-+-+⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭+-⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭(2)设：cos sin αα==∵22cos sin 1αα+=()()sin sin coscos sin sin cossinsin baθθθθαθαθαθ+=+=+=+12.其他常用公式()()()()()()()()()()()()()()000sin 360sin cos 360cos tan 360tan sin 90cos cos 90sin 1tan 90tan sin 90cos cos 90sin 1tan 90tan sin 90cos cos 90sin 1tan 90tan sin 180sin cos 180cos n n n θθθθθθθθθθθθθθθθθθθθθθθθθθθ+⨯=+⨯=+⨯=︒-=︒-=︒-=︒+=︒+=-︒+=--︒=--︒=-︒=-︒-=︒-=-()()()()()()()()tan 180tan sin 180sin cos 180cos tan 180tan sin sin cos cos tan tan tan 2190 1cos 1cos 11sin 1sin 1n θθθθθθθθθθθθθθθθθθθ︒-=-±︒=-±︒=-±︒=-=--=-=-+⨯︒⎡⎤⎣⎦-≤≤⇒≤-≤≤⇒≤不存在13. 特殊的三角函数值14. 关于机器算法在计算机中，三角函数的算法是这样的，其中x 用弧度计算()()1357210246sin 1!3!5!7!21!cos 0!2!4!6!2!n n nn x x x x x x n x x x x x x n +=∞=∞=-+-+=+=-+-+=∑∑推导公式：(a+b+c)/(sinA+sinB+sinC)=2R(其中，R为外接圆半径) 由正弦定理有a/sinA=b/sinB=c/sinC=2R所以a=2R*sinAb=2R*sinBc=2R*sinC加起来a+b+c=2R*(sinA+sinB+sinC)带入(a+b+c)/(sinA+sinB+sinC)=2R*(sinA+sinB+sinC)/(sinA+sinB+sinC)=2R 两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cosAsinBcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)cot(A+B)=(cotAcotB-1)/(cotB+cotA)cot(A-B)=(cotAcotB+1)/(cotB-cotA)倍角公式Sin2A=2SinA?CosA对数的性质及推导用^表示乘方，用log(a)(b)表示以a为底，b的对数*表示乘号，/表示除号定义式：若a^n=b(a>0且a≠1)则n=log(a)(b)基本性质：1.a^(log(a)(b))=b2.log(a)(MN)=log(a)(M)+log(a)(N);3.log(a)(M/N)=log(a)(M)-log(a)(N);4.log(a)(M^n)=nlog(a)(M)推导1.这个就不用推了吧，直接由定义式可得(把定义式中的[n=log(a)(b)]带入a^n=b)2.MN=M*N由基本性质1(换掉M和N)a^[log(a)(MN)]=a^[log(a)(M)]*a^[log(a)(N)] 由指数的性质a^[log(a)(MN)]=a^{[log(a)(M)]+[log(a)(N)]} 又因为指数函数是单调函数，所以log(a)(MN)=log(a)(M)+log(a)(N)3.与2类似处理MN=M/N由基本性质1(换掉M和N)a^[log(a)(M/N)]=a^[log(a)(M)]/a^[log(a)(N)] 由指数的性质a^[log(a)(M/N)]=a^{[log(a)(M)]-[log(a)(N)]} 又因为指数函数是单调函数，所以log(a)(M/N)=log(a)(M)-log(a)(N)4.与2类似处理M^n=M^n由基本性质1(换掉M)a^[log(a)(M^n)]={a^[log(a)(M)]}^n由指数的性质a^[log(a)(M^n)]=a^{[log(a)(M)]*n}又因为指数函数是单调函数，所以log(a)(M^n)=nlog(a)(M)其他性质：性质一：换底公式log(a)(N)=log(b)(N)/log(b)(a)推导如下N=a^[log(a)(N)]a=b^[log(b)(a)]综合两式可得N={b^[log(b)(a)]}^[log(a)(N)]=b^{[log(a)(N)]*[log(b)(a)]}又因为N=b^[log(b)(N)]所以b^[log(b)(N)]=b^{[log(a)(N)]*[log(b)(a)]}所以log(b)(N)=[log(a)(N)]*[log(b)(a)]{这步不明白或有疑问看上面的} 所以log(a)(N)=log(b)(N)/log(b)(a)性质二：（不知道什么名字）log(a^n)(b^m)=m/n*[log(a)(b)]推导如下由换底公式[lnx是log(e)(x),e称作自然对数的底]log(a^n)(b^m)=ln(a^n)/ln(b^n)由基本性质4可得log(a^n)(b^m)=[n*ln(a)]/[m*ln(b)]=(m/n)*{[ln(a)]/[ln(b)]}再由换底公式log(a^n)(b^m)=m/n*[log(a)(b)]--------------------------------------------（性质及推导完）公式三:log(a)(b)=1/log(b)(a)证明如下:由换底公式log(a)(b)=log(b)(b)/log(b)(a)----取以b为底的对数,log(b)(b)=1=1/log(b)(a)还可变形得:log(a)(b)*log(b)(a)=1平方关系：sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·商的关系：tanα=sinα/cosαcotα=cosα/sinα·倒数关系：tanα·cotα=1sinα·cscα=1cosα·secα=1万能公式：sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]常用的诱导公式有以下几组：公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)一般的最常用公式有:Sin(A+B)=SinA*CosB+SinB*CosASin(A-B)=SinA*CosB-SinB*CosACos(A+B)=CosA*CosB-SinA*SinBCos(A-B)=CosA*CosB+SinA*SinBTan(A+B)=(TanA+TanB)/(1-TanA*TanB) Tan(A-B)=(TanA-TanB)/(1+TanA*TanB) 平方关系：sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系：sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*cscαsecα=tanα*cscαcscα=secα*cotα·倒数关系：tanα·cotα=1sinα·cscα=1cosα·secα=1直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,三角函数恒等变形公式·两角和与差的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ) tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ) ·辅助角公式：Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]·三倍角公式：sin(3α)=3sinα-4sin^3(α)cos(3α)=4cos^3(α)-3cosα·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=vercos(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·其他：sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*( n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*( n-1)/n]=0以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0部分高等内容·高等代数中三角函数的指数表示(由泰勒级数易得)：sinx=[e^(ix)-e^(-ix)]/(2i)cosx=[e^(ix)+e^(-ix)]/2tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]泰勒展开有无穷级数，e^z=exp(z)＝1＋z/1！＋z^2/2！＋z^3/3！＋z^4/4！＋…＋z^n/n！＋…此时三角函数定义域已推广至整个复数集。

三角函数公式及推导
三角函数是数学中常见的函数之一，常用于解决与角度相关的问题。

三角函数公式是三角函数的基本知识点之一，掌握了三角函数公式，就能更好的理解和应用三角函数。

三角函数公式主要包括正弦、余弦、正切、余切、正割、余割等六种函数的公式。

这些公式可以通过三角函数的定义和性质来推导得到。

正弦函数公式：sin(a+b)=sinacosb+cosasinb
余弦函数公式：cos(a+b)=cosacosb-sinasinb
正切函数公式：tan(a+b)= (tana + tanb)/ (1 - tana*tanb) 余切函数公式：cot(a+b)= (cota*cotb - 1) / (cota + cotb) 正割函数公式：sec(a+b)= (secacosb+sinasectanb) / (secb) 余割函数公式：csc(a+b)= (cscacosc+b) / (sincosb)
以上公式都可以通过三角函数的定义和一些基本的代数运算及恒等式推导出来。

了解这些公式，可以在解决复杂三角函数问题时更灵活应用。

除了以上推导的公式，还有许多其它的三角函数公式，比如二倍角公式、半角公式、余角公式等等，这些公式也是非常重要的。

在学习三角函数时，需要重点掌握这些公式，才能更好地理解和运用三角函数。

三角函数公式的推导并不是一件容易的事情，需要对三角函数的性质和一些基本的代数运算非常熟练才能够推导得出。

因此，在学习
三角函数时，需要认真掌握每一个知识点，努力理解和应用三角函数公式，才能在以后的学习和工作中发挥更大的作用。

三角函数诱导公式公式一:设α为任意角，终边相同的角的同一三角函数的值相等sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)公式二:设α为任意角，π+α的三角函数值与α的三角函数值之间的关系sin(π+α)=－sinαcos(π+α)=－cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系sin(－α)=－sinαcos(－α)=cosαtan(－α)=－tanαcot(－α)=－cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系sin(π－α)=sinαcos(π－α)=－cosαtan(π－α)=－tanαcot(π－α)=－cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系sin(2π－α)=－sinαcos(2π－α)=cosαtan(2π－α)=－tanαcot(2π－α)=－cotα公式六:π/2±α与α的三角函数值之间的关系sin(π/2+α)=cosαsin(π/2－α)=cosαcos(π/2+α)=－sinαcos(π/2－α)=sinαtan(π/2+α)=－cotαtan(π/2－α)=cotαcot(π/2+α)=－tanαcot(π/2－α)=tanα诱导公式记忆口诀：“奇变偶不变，符号看象限”。

“奇、偶”指的是π/2的倍数的奇偶，“变与不变”指的是三角函数的名称的变化：“变”是指正弦变余弦，正切变余切。

（反之亦然成立）“符号看象限”的含义是：把角α看做锐角，不考虑α角所在象限，看n·(π/2)±α是第几象限角，从而得到等式右边是正号还是负号。

以cos（π/2+α）=－sinα为例，等式左边cos（π/2+α）中n=1，所以右边符号为sinα，把α看成锐角，所以π/2<（π/2+α）<π，y=cosx在区间（π/2，π）上小于零，所以右边符号为负，所以右边为－sinα。

三角函数诱导公式万能公式和差化积公式倍角公式等公式总结及其推导一、三角函数诱导公式1、万能公式a sin(A+B) = a sinAcosB + a cosAsinBa cos(A+B) = a cosAcosB - a sinAsinB2、差化积公式sinAcosB - cosAsinB = sin(A-B)cosAcosB + sinAsinB = cos(A-B)3、倍角公式sin2A = 2sinAcosAcos2A = cos2A - sin2A = 2cos2A - 1 = 1 - 2sin2A4、和差公式sin(A±B) = sinAcosB±cosAsinBcos(A±B) = cosAcosB∓sinAsinB二、推导1、万能公式推导过程设定A+B=C，则有：a sin(A + B)= a sinC左右两侧同时乘以cosB:a sin(A + B)cosB = a sinCcosB左右两侧同时乘以sinB:a sin(A + B)sinB = a sinCsinB将上式整合即可得：a sin(A + B)= a sinAcosB + a cosAsinB同理，可推导出：a cos(A + B) = a cosAcosB - a sinAsinB2、差化积公式推导过程设定A=B，则有：sinAcosB - cosAsinB = sinAcosA - cosAcosA 经过整合可得：sinAcosB - cosAsinB = sinA -cosA将A=B替换为A-B,即可得sinAcosB - cosAsinB = sin(A-B)同理：cosAcosB + sinAsinB = cosAcosA + sinAsinA 经过整合可得：cosAcosB +sinAsinB = cosA +sinA将A=B替换为A-B,即可得cosAcosB +sinAsinB = cos(A-B)3、倍角公式的推导过程由于A为任意角度，对其两侧两边可以分别进行乘以cosA及sinA，得到：sinAcosA + sinAcosA = cosA*sinA + cosA*sinA经过整合可得：sin2A = 2sinAcosAcos2A = cosAcosA - sinAcosA经过整合可得：cos2A = 2cos2A - 1再把上式中的cos2A代入：2cos2A - 1 = 1 - 2sin2A4、和差公式推导过程设定A+B=C，则有：sin(A + B)= sinC将左右两侧分别乘以cosB及sinB：。

锐角三角函数公式sin α=∠α的对边/ 斜边cos α=∠α的邻边/ 斜边tan α=∠α的对边/ ∠α的邻边cot α=∠α的邻边/ ∠α的对边倍角公式sin2A=2sinA•cosAcos2A=cosA;方-sinA方;A=1-2sin&sup2;A=2cos&sup2;A-1 tan2A=（2tanA）÷（1-tan^2A）三倍角公式sin3α=4sinα²sin(π/3+α)sin(π/3-α)cos3α=4cosα²cos(π/3+α)cos(π/3-α)tan3a = tan a ²tan(π/3+a)²tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin&sup2;a)+(1-2sin&sup2;a)sina=3sina-4sin&sup3;acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos&sup2;a-1)cosa-2(1-cos&sup2;a)cosa=4cos&sup3;a-3cosasin3a=3sina-4sin&sup3;a=4sina(3/4-sin&sup2;a)=4sina[(√3/2)&sup2;-sin&sup2;a]=4sina(sin&sup2;60°-sin&sup2;a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos&sup3;a-3cosa=4cosa(cos&sup2;a-3/4)=4cosa[cos&sup2;a-(√3/2)&sup2;]=4cosa(cos&sup2;a-cos&sup2;30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))和差化积sinθ+sinφ= 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ= 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ= -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)积化和差sinαsinβ= [cos(α-β)-cos(α+β)] /2cosαcosβ= [cos(α+β)+cos(α-β)]/2sinαcosβ= [sin(α+β)+sin(α-β)]/2cosαsinβ= [sin(α+β)-sin(α-β)]/2双曲函数sinh(a) = [e^a-e^(-a)]/2cosh(a) = [e^a+e^(-a)]/2tanh(a) = sin h(a)/cos h(a)公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）= sinαcos（2kπ＋α）= cosαtan（2kπ＋α）= tanαcot（2kπ＋α）= cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）= -sinαcos（π＋α）= -cosαtan（π＋α）= tanαcot（π＋α）= cotα公式三：任意角α与-α的三角函数值之间的关系：sin（-α）= -sinαcos（-α）= cosαtan（-α）= -tanαcot（-α）= -cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π-α）= sinαcos（π-α）= -cosαtan（π-α）= -tanαcot（π-α）= -cotα公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π-α）= -sinαcos（2π-α）= cosαtan（2π-α）= -tanαcot（2π-α）= -cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2+α）= cosαcos（π/2+α）= -sinαtan（π/2+α）= -cotαcot（π/2+α）= -tanαsin（π/2-α）= cosαcos（π/2-α）= sinαtan（π/2-α）= cotαcot（π/2-α）= tanαsin（3π/2+α）= -cosαcos（3π/2+α）= sinαtan（3π/2+α）= -cotαcot（3π/2+α）= -tanαsin（3π/2-α）= -cosαcos（3π/2-α）= -sinαtan（3π/2-α）= cotαcot（3π/2-α）= tanα(以上k∈Z)A²sin(ωt+θ)+ B²sin(ωt+φ) =√{(A^2 +B^2 +2ABcos(θ-φ)} •sin{ ωt + arcsin[ (A•sinθ+B•sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} }√表示根号,包括{……}中的内容诱导公式sin(-α) = -sinαcos(-α) = cosαtan (-α)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan（π/2＋α）＝－cotαtan（π/2－α）＝cotαtan（π－α）＝－tanαtan（π＋α）＝tanα诱导公式记背诀窍：奇变偶不变，符号看象限万能公式其它公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA）^2+(cosB）^2+(cosC）^2=1-2cosAcosBcosC(8)（sinA）^2+（sinB）^2+（sinC）^2=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)[编辑本段]内容规律三角函数看似很多，很复杂，但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。

三角恒等变换的所有公式及其推导公式三角恒等变换是指对于任意角度x，存在一系列等价的三角函数表达式。

这些等价的表达式可以通过一些特定的关系来推导出来。

下面将介绍一些常见的三角恒等变换公式及其推导过程。

1. 倍角公式：sin(2x) = 2sin(x)cos(x)cos(2x) = cos^2(x) - sin^2(x) = 2cos^2(x) - 1 = 1 - 2sin^2(x)tan(2x) = 2tan(x) / (1 - tan^2(x))推导过程：对于sin(2x)，可以利用三角函数的加法公式sin(A+B)=sinAcosB+cosAsinB，将A=B=x代入得到：sin(2x) = sin(x+x) = sin(x)cos(x) + cos(x)sin(x) = 2sin(x)cos(x)对于cos(2x)，可以利用cos(2x)=cos^2(x) - sin^2(x)得到：cos(2x) = cos^2(x) - sin^2(x) = 2cos^2(x) - 1 = 1 - 2sin^2(x)对于tan(2x)，可以利用tan(2x) = sin(2x) / cos(2x)得到：tan(2x) = 2sin(x)cos(x) / (1 - 2sin^2(x)) = 2tan(x) / (1 - tan^2(x))2. 和差公式：sin(A+B) = sinAcosB + cosAsinBsin(A-B) = sinAcosB - cosAsinBcos(A+B) = cosAcosB - sinAsinBcos(A-B) = cosAcosB + sinAsinB推导过程：对于sin(A+B)，可以利用sin(A+B)=sinAcosB+cosAsinB得到：sin(A+B) = sinAcosB + cosAsinB对于sin(A-B)，可以利用sin(A-B)=sinAcosB-cosAsinB得到：sin(A-B) = sinAcosB - cosAsinB对于cos(A+B)，可以利用cos(A+B)=cosAcosB-sinAsinB得到：cos(A+B) = cosAcosB - sinAsinB对于cos(A-B)，可以利用cos(A-B)=cosAcosB+sinAsinB得到：cos(A-B) = cosAcosB + sinAsinB3. 万能公式：sin^2(x) + cos^2(x) = 11 + tan^2(x) = sec^2(x)1 + cot^2(x) = csc^2(x)推导过程：对于sin^2(x) + cos^2(x)，可以利用三角函数的平方和公式sin^2(x) + cos^2(x) = 1得到：sin^2(x) + cos^2(x) = 1对于1 + tan^2(x)，可以利用tan^2(x) + 1 = sec^2(x)得到：1 + tan^2(x) = sec^2(x)对于1 + cot^2(x)，可以利用cot^2(x) + 1 = csc^2(x)得到：1 + cot^2(x) = csc^2(x)通过以上的公式及其推导过程，我们可以在三角函数的计算中灵活运用，简化计算过程，提高计算的准确性和效率。

三角函数公式及推导公式三角函数是解析几何中的重要内容，它研究的是角度和三角形的关系。

三角函数包括正弦函数、余弦函数、正切函数等，它们常用于求解角度、测量距离和角度的相关问题。

一、正弦函数正弦函数是三角函数中最基本的函数之一，它表示的是一个锐角的对边与斜边之间的比值。

正弦函数可以用如下公式表示：sinθ = 对边 / 斜边其中，θ是一个锐角，对边是与该锐角相对的边，斜边是与该锐角相邻的边。

二、余弦函数余弦函数是三角函数中的另一个基本函数，它表示的是锐角的邻边与斜边之间的比值。

余弦函数可以用如下公式表示：cosθ = 邻边 / 斜边其中，θ是一个锐角，邻边是与该锐角相邻的边，斜边是与该锐角相对的边。

三、正切函数正切函数是三角函数中的第三个基本函数，它表示的是锐角的对边与邻边之间的比值。

正切函数可以用如下公式表示：tanθ = 对边 / 邻边其中，θ是一个锐角，对边是与该锐角相对的边，邻边是与该锐角相邻的边。

四、推导公式1.和差公式sin(α + β) = sinαcosβ + cosαsinβsin(α - β) = sinαcosβ - cosαsinβcos(α + β) = cosαcosβ - sinαsinβcos(α - β) = cosαcosβ + sinαsinβtan(α + β) = (tanα + tanβ) / (1 - tanαtanβ)tan(α - β) = (tanα - tanβ) / (1 + tanαtanβ)2.积化和差公式sin2θ = (1 - cos2θ) / 2cos2θ = (1 + cos2θ) / 2tan2θ = (1 - cos2θ) / (1 + cos2θ)3.和差化积公式sinα + sinβ = 2sin((α + β) / 2)cos((α - β) / 2)sinα - sinβ = 2cos((α + β) / 2)sin((α - β) / 2)cosα + cosβ = 2cos((α + β) / 2)cos((α - β) / 2)cosα - cosβ = -2sin((α + β) / 2)sin((α - β) / 2)四、推导下面以正弦函数的推导为例进行详细说明。

一、推导公式：(a+b+c)/(sinA+sinB+sinC)=2R(其中，R为外接圆半径) 由正弦定理有a/sinA=b/sinB=c/sinC=2R 所以a=2R*sinA b=2R*sinB c=2R*sinC加起来a+b+c=2R*(sinA+sinB+sinC) 带入(a+b+c)/(sinA+sinB+sinC)=2R*(sinA+sinB+sinC) /(sinA+sinB+sinC)=2R 两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cosAsinBcos(A+B)=cosAcos B-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)cot(A+B)=(cotAcotB-1)/(cotB+cotA)cot(A-B)=(cotAcotB+1)/(cotB-cotA)二．倍角公式Sin2A=2SinA?CosA 对数的性质及推导用^表示乘方，用log(a)(b)表示以a为底，b的对数*表示乘号，/表示除号定义式：若a^n=b(a>0且a≠1) 则n=log(a)(b)三．基本性质：1.a^(log(a)(b))=b2.log(a)(MN)=log(a)(M)+log(a)(N);3.log(a)(M/N)=log(a)(M)-log(a)(N);4.log(a)(M^n)=nlog(a)(M)四．推导1.这个就不用推了吧，直接由定义式可得(把定义式中的[n=log(a)(b)]带入a^n=b) 2. MN=M*N 由基本性质1(换掉M和N)a^[log(a)(MN)]=a^[log(a)(M)]*a^[log(a)(N)]由指数的性质a^[log(a)(MN)]=a^{[log(a)(M)]+[log(a)(N)]}又因为指数函数是单调函数，所以log(a)(MN)=log(a)(M)+log(a)(N) 3.与2类似处理MN=M/N 由基本性质1(换掉M和N)a^[log(a)(M/N)]=a^[log(a)(M)]/a^[log(a)(N)] 由指数的性质a^[log(a)(M/N)]=a^{[log(a)(M)]-[log(a)(N)]}又因为指数函数是单调函数，所以log(a)(M/N)=log(a)(M)-log(a)(N) 4.与2类似处理M^n=M^n由基本性质1(换掉M) a^[log(a)(M^n)]={a^[log(a)(M)]}^n 由指数的性质a^[log(a)(M^n)]=a^{[log(a)(M)]*n} 又因为指数函数是单调函数，所以log(a)(M^n)=nlog(a)(M) 5．其他性质：性质一：换底公式log(a)(N)=log(b)(N)/log(b)(a) 推导如下N=a^[log(a)(N)] a=b^[log(b)(a)] 综合两式可得N={b^[log(b)(a)]}^[log(a)(N)]=b^{[log(a)(N)]*[l og(b)(a)]} 又因为N=b^[log(b)(N)] 所以b^[log(b)(N)]=b^{[log(a)(N)]*[log(b)(a)]} 所以log(b)(N)=[log(a)(N)]*[log(b)(a)]{ 这步不明白或有疑问看上面的} 所以log(a)(N)=log(b)(N)/log(b)(a)。

三角函数万能公式推导过程在数学中，三角函数是研究角的函数关系的重要工具。

而三角函数万能公式是指一组公式，可以将角上的正弦、余弦、正切等三角函数相互转换。

这组公式的推导从欧拉公式开始。

1.欧拉公式的推导：exp(z) = e^z = 1 + z/1! + z^2/2! + z^3/3! + ...将e^ix展开，其中i是虚数单位，i^2 = -1：e^ix = 1 + (ix)/1! + (ix)^2/2! + (ix)^3/3! + ...= 1 + ix - x^2/2! - ix^3/3! + ...将e^ix拆分为实部和虚部：e^ix = cos(x) + i*sin(x)这就是欧拉公式。

2.指数公式的推导：我们利用欧拉公式推导指数公式。

先考虑e^x的导数。

由定义得：d(e^x)/dx = d(1 + x/1! + x^2/2! + x^3/3! + ...)/dx=0+1/1!+2x/2!+3x^2/3!+...=1+x/1!+x^2/2!+x^3/3!+...这就是指数函数e^x的导数，也就是自身。

同理，我们可以推导出指数函数e^(-x)的导数等于自身。

现在考虑复数指数函数e^(ix)的导数：d(e^(ix))/dx = d(cos(x) + i*sin(x))/dx= -sin(x) + i*cos(x)= i*(cos(x) + i*sin(x))= i*e^(ix)这个结果告诉我们，e^(ix)的导数等于i*e^(ix)。

3.正弦函数和余弦函数的推导：利用欧拉公式，我们可以推导出正弦函数和余弦函数。

首先，我们将欧拉公式中的x替换为-ix，并利用e^(-ix) = cos(x) - i*sin(x)：e^(-ix) = cos(x) - i*sin(x)现在我们将上述等式两边同时乘以i：i*e^(-ix) = i*cos(x) - i*i*sin(x)利用前面推导的e^(ix)的导数等于i*e^(ix)：i*e^(-ix) = i*cos(x) + sin(x)这样，我们就得到了sin(x)和cos(x)的表达式：sin(x) = (1/i)*(e^(-ix) - e^(ix))/2cos(x) = (e^(-ix) + e^(ix))/24.正切函数的推导：利用sin(x)和cos(x)的表达式，我们可以推导出正切函数。

锐角三角函数锐角三角函数三角关系倒数关系：tanα·cotα=1sinα·cscα=1cosα·secα=1商的关系：平方关系：三角函数公式2公式相关编辑两角和公式cos〔α+β〕=cosαcosβ-sinαsinβcos〔α-β〕=cosαcosβ+sinαsinβsin〔α+β〕=sinαcosβ+cosαsinβsin〔α-β〕=sinαcosβ -cosαsinβtan〔α+β〕=(tanα+tanβ〕/〔1-tanαtanβ〕tan〔α-β〕=(tanα-tanβ〕/〔1+tanαtanβ〕cot(A+B) = (cotAcotB-1〕/(cotB+cotA)cot(A-B) = (cotAcotB+1〕/(cotB-cotA)三角和公式sin〔α+β+γ〕=sinα·cosβ·cosγ+cosα·sinβ·cos γ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos〔α+β+γ〕=cosα·cosβ·cosγ-cosα·sinβ·sin γ-sinα·cosβ·sinγ-sinα·sinβ·cosγ诱导公式三角函数的诱导公式〔六公式〕[1]公式一：sin(α+k*2π)=sinαcos(α+k*2π)=cosαtan(α+k*π)=tanα公式二：sin(π+α) = -sinαcos(π+α) = -cosαtan(π+α〕=tanα公式三：sin(-α) = -sinαcos(-α) = cosαtan (-α)=-tanα公式四：sin(π-α) = sinαcos(π-α) = -cosαtan(π-α) =-tanα公式五：sin(π/2-α) = cosαcos(π/2-α) =sinα由于π/2+α=π-〔π/2-α〕，由公式四和公式五可得公式六：sin(π/2+α) = cosαcos(π/2+α) = -sinα诱导公式记背诀窍：奇变偶不变，符号看象限。