整式的乘除整章练习题(完整)
- 格式:doc
- 大小:1.57 MB
- 文档页数:33
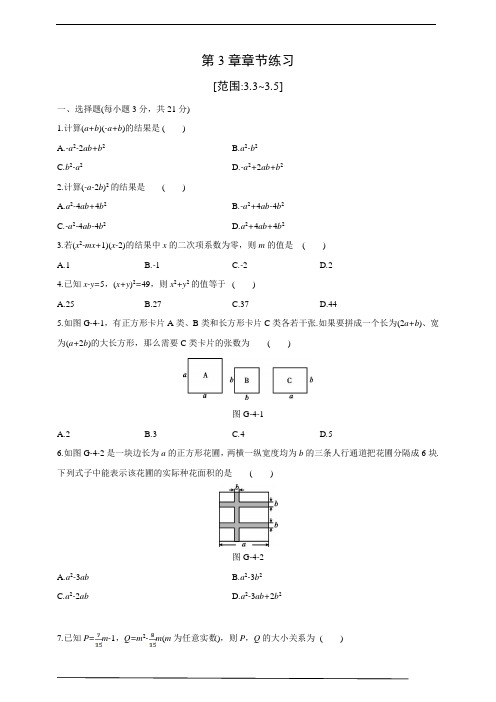
第3章章节练习[范围:3.3~3.5]一、选择题(每小题3分,共21分)1.计算(a+b)(-a+b)的结果是 ()A.-a2-2ab+b2B.a2-b2C.b2-a2D.-a2+2ab+b22.计算(-a-2b)2的结果是()A.a2-4ab+4b2B.-a2+4ab-4b2C.-a2-4ab-4b2D.a2+4ab+4b23.若(x2-mx+1)(x-2)的结果中x的二次项系数为零,则m的值是()A.1B.-1C.-2D.24.已知x-y=5,(x+y)2=49,则x2+y2的值等于()A.25B.27C.37D.445.如图G-4-1,有正方形卡片A类、B类和长方形卡片C类各若干张.如果要拼成一个长为(2a+b)、宽为(a+2b)的大长方形,那么需要C类卡片的张数为()图G-4-1A.2B.3C.4D.56.如图G-4-2是一块边长为a的正方形花圃,两横一纵宽度均为b的三条人行通道把花圃分隔成6块.下列式子中能表示该花圃的实际种花面积的是()图G-4-2A.a2-3abB.a2-3b2C.a2-2abD.a2-3ab+2b27.已知P=m-1,Q=m2-m(m为任意实数),则P,Q的大小关系为()A.P<QB.P=QC.P>QD.由m的值确定二、填空题(每小题3分,共21分)8.整式A与m2-2mn+n2的和是(m+n)2,则A=.9.已知ab=5,(a-b)2=5,则(a+b)2=.10.若(x+2)(x-a)=x2+bx-10,则ab的值为.11.若(a+b-3)2+|a-b+5|=0,则a2-b2=.12.已知a+b=,ab=1,则(a-2)(b-2)的值为.13.已知ab=a+b+1,则(a-1)(b-1)=.14.一组数:2,1,3,x,7,y,23,…满足“从第三个数起,若前面两个数依次为a,b,则紧随其后的数就是2a-b”,例如:这组数中的第三个数“3”是由“2×2-1”得到的,那么这组数中的y表示的数为.三、解答题(共58分)15.(8分)计算:(1)(a+b)2-b(2a+b);(2)(x+1)(x-1)+x(3-x).16.(8分)解方程:(1)(2a-3)(a+1)=2a2-2;(2)3(2x+1)2-12(x+1)(x-1)=0.17.(10分)先化简,再求值:(a+b)(a-b)+(a+b)2-2a2,其中ab=-1.18.(10分)王老师家买了一套新房,其结构如图G-4-3所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.(1)木地板和地砖分别需要多少平方米?(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?图G-4-319.(10分)观察下列等式:32-4×12=5,①52-4×22=9,②72-4×32=13,③…根据上述规律解决下列问题:(1)完成第四个等式:92-4×()2=;(2)写出你猜想的第n(n为正整数)个等式(用含n的式子表示),并验证.20.(12分)把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.(1)图G-4-4①是将几个面积不完全相等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论?请写出来;(2)图②是将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连结BD和BF.若两个正方形的边长满足a+b=10,ab=20,请你求出阴影部分的面积.图G-4-4详解详析1.C2.D3.C4.C[解析] x2+y2=[(x+y)2+(x-y)2]=×(49+25)=37.5.D[解析] 大长方形的面积=(2a+b)·(a+2b)=2a2+5ab+2b2,所以大长方形是由2张A类正方形卡片、5张C类长方形卡片、2张B类正方形卡片组成的.故选D.6.D[解析] ∵正方形花圃的边长为a,人行通道的宽为b,∴经过平移后,实际种花部分是一个长为(a-b),宽为(a-2b)的长方形,其面积=(a-2b)(a-b)=a2-3ab+2b2.故选D.7.A8.4mn9.25[解析] ∵ab=5,(a-b)2=5,∴(a+b)2=(a-b)2+4ab=5+20=25.10.-15[解析] (x+2)(x-a)=x2+(2-a)x-2a=x2+bx-10,可得2-a=b,-2a=-10,解得a=5,b=-3,则ab=-15.故答案为-15.11.-15[解析] 由题意,得a+b-3=0且a-b+5=0,∴a=-1,b=4,∴a2-b2=(-1)2-42=1-16=-15.12.2[解析] (a-2)(b-2)=ab-2(a+b)+4=2.13.2[解析] (a-1)(b-1)=ab-a-b+1.当ab=a+b+1时,原式=a+b+1-a-b+1=2.故答案为2.14.-915.解:(1)原式=a2+2ab+b2-2ab-b2=a2.(2)原式=x2-1+3x-x2=3x-1.16.解:(1)(2a-3)(a+1)=2a2-2,2a2-a-3=2a2-2,-a=1,a=-1.(2)3(2x+1)2-12(x+1)(x-1)=0,3(4x2+4x+1)-12(x2-1)=0,12x2+12x+3-12x2+12=0,12x+15=0,x=-.17.解:原式=a2-b2+a2+2ab+b2-2a2=2ab.当ab=-1时,原式=-2.18.解:(1)卧室的面积是2b(4a-2a)=4ab(m2),厨房、卫生间、客厅的面积和是b·(4a-2a-a)+a·(4b-2b)+2a·4b=ab+2ab+8ab=11ab(m2),即木地板需要4ab m2,地砖需要11ab m2.(2)11ab·x+4ab·3x=11abx+12abx=23abx(元),即王老师需要花23abx元.19.解:(1)417(2)(2n+1)2-4n2=4n+1.验证:∵左边=(2n+1)2-4n2=4n2+4n+1-4n2=4n+1=右边,∴等式成立.20.[解析] (1)此题根据面积的不同求解方法,可得到不同的表示方法.一种是3个正方形的面积和6个长方形的面积和,一种是大正方形的面积,可得等式(a+b+c)2=a2+b2+c2+2ab+2bc+2ac.(2)利用S阴影=正方形ABCD的面积+正方形ECGF的面积-三角形BGF的面积-三角形ABD的面积求解.解:(1)S=(a+b+c)2或S=a2+b2+c2+2ab+2bc+2ac.结论:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac.(2)∵a+b=10,ab=20,∴S阴影=a2+b2-(a+b)•b-a2=a2+b2-ab=(a+b)2-ab=×102-×20=50-30=20.。

整式乘除单元测试题及答案一、选择题:1. 已知 \( a^2 - 4 \) 可以分解为 \( (a+2)(a-2) \),那么下列哪个表达式不能被 \( a^2 - 4 \) 整除?A. \( a^3 - 4a \)B. \( a^3 - 8 \)C. \( a^3 - 4a + 4 \)D. 提供的选项都是错误的2. 如果 \( x - 1 \) 是多项式 \( x^3 - 2x^2 + x - 2 \) 的一个因子,那么 \( x \) 的值是多少?A. 1B. 2C. 0D. 3二、填空题:1. 计算 \( (3x^2 - 2x + 1) \div (x - 1) \) 的结果为__________。
2. 将多项式 \( 2x^3 - 5x^2 + 3x - 6 \) 除以 \( x - 2 \) 的商是 __________。
三、简答题:1. 证明 \( (x - 1)^3 = x^3 - 3x^2 + 3x - 1 \)。
2. 给定多项式 \( P(x) = x^4 - 2x^3 + x^2 - 2x + 1 \),求\( P(1) \) 的值。
四、解答题:1. 已知 \( (x + y)^2 = 9 \) 和 \( (x - y)^2 = 1 \),求 \( x^2 + y^2 \) 的值。
2. 计算 \( \frac{2x^3 - 8x^2 + 6x}{2x - 4} \) 的简化形式。
五、应用题:1. 一个长方形的长是宽的两倍,如果长和宽的乘积是 24,求长方形的长和宽。
2. 某工厂生产一种零件,每个零件的成本是 \( c \) 元,售价是\( 2c \) 元。
如果工厂卖出了 \( n \) 个零件,求工厂的总利润。
答案:一、选择题:1. 答案:D. 提供的选项都是错误的。
2. 答案:A. 1二、填空题:1. 答案:\( 3x - 1 \)2. 答案:\( 2x^2 - 7x + 3 \)三、简答题:1. 证明:\( (x - 1)^3 = x^3 - 3x^2 + 3x - 1 \) 可以通过展开\( (x - 1) \) 的三次幂来验证。

整式的乘除练习题(8套)含答案整式的乘除测试题练习一一、精心选一选(每小题3分,共30分) 1、下面的计算正确的是( )A 、1234a a a =⋅B 、222b a )b a (+=+C 、22y 4x )y 2x )(y 2x (-=--+-D 、2573a a a a =÷⋅ 2、在n m 1n x )(x +-=⋅中,括号内应填的代数式是( )A 、1n m x ++B 、2m x +C 、1m x +D 、2n m x ++ 3、下列算式中,不正确的是( )A 、xy 21y x y x 21)xy 21)(1x2x (n 1n 1n n -+-=-+-+-B 、1n 21n n x )x (--= C 、y x x 2x31)y x 2x 31(x n 1n n 2nn --=--+D 、当n 为正整数时,n 4n 22a )a (=- 4、下列运算中,正确的是( )A 、222ac 6c b 10)c 3b 5(ac 2+=+B 、232)a b ()b a ()1b a ()b a (---=+--C 、c b a )c b a (y )a c b (x )1y x )(a c b (-+-----+=++-+D 、2)a b 2(5)b a 3)(b 2a ()a 2b 11)(b 2a (--+-=-- 5、下列各式中,运算结果为422y x xy 21+-的是( )A 、22)xy 1(+-B 、22)xy 1(--C 、222)y x 1(+-D 、222)y x 1(-- 6、已知5x 3x 2++的值为3,则代数式1x 9x 32-+的值为( ) A 、0 B 、-7 C 、-9 D 、3 7、当m=( )时,25x )3m (2x 2+-+是完全平方式 A 、5± B 、8 C 、-2 D 、8或-28、某城市一年漏掉的水,相当于建一个自来水厂,据不完全统计,全市至少有5106⨯个水龙头,5102⨯个抽水马桶漏水。


☆☆☆ 北师大版数学七年级【下册】第一章 整式的乘除一、 同底数幂的乘法同底数幂的乘法法则: n m n ma a a +=⋅(m,n 都是正数)是幂的运算中最基本的法则,在应用法则运算时,要注意以下几点:①法则使用的前提条件是:幂的底数相同而且是相乘时,底数a 可以是一个具体的数字式字母,也可以是 一个单项或多项式;②指数是1时,不要误以为没有指数;③不要将同底数幂的乘法与整式的加法相混淆,对乘法,只要底数相同指数就可以相加;而对于加法,不仅底数相同,还要求指数相同才能相加;④当三个或三个以上同底数幂相乘时,法则可推广为p n m p n ma a a a ++=⋅⋅(其中m 、n 、p 均为正数);⑤公式还可以逆用:n m nm a a a⋅=+(m 、n 均为正整数)二.幂的乘方与积的乘方1。
幂的乘方法则:mnnm a a =)((m ,n 都是正数)是幂的乘法法则为基础推导出来的,但两者不能混淆.2. ),()()(都为正数n m a a a mn mn nm ==.3。
底数有负号时,运算时要注意,底数是a 与(-a )时不是同底,但可以利用乘方法则化成同底,如将(-a )3化成—a 3⎩⎨⎧-=-).(),()(,为奇数时当为偶数时当一般地n a n a a n n n4.底数有时形式不同,但可以化成相同。
5.要注意区别(ab )n与(a+b)n意义是不同的,不要误以为(a+b )n=a n+b n(a 、b 均不为零).6.积的乘方法则:积的乘方,等于把积每一个因式分别乘方,再把所得的幂相乘,即nnnb a ab =)((n 为正整数)。
7.幂的乘方与积乘方法则均可逆向运用。
三. 同底数幂的除法1。
同底数幂的除法法则:同底数幂相除,底数不变,指数相减,即n m n ma a a -=÷ (a ≠0,m 、n 都是正数,且m 〉n ).2。
在应用时需要注意以下几点:①法则使用的前提条件是“同底数幂相除"而且0不能做除数,所以法则中a ≠0。

欢迎您选择新活力教育用心学习教案2017 学年七年级数学下册第一章整式的乘除综合一.选择题。
1.下列运算正确的是()A. x+x=x 2 2 2 2C . 3x3 2 5 8 2 4B .( x+y) =x +y ?2x =6a D . x ÷x=x2.如( x+m)与( x+ 3)的乘积中不含 x 的一次项,则m的值为().A.- 3 B . 3C.0 D.13.计算( ab2)3的结果是()A、 ab5B、ab6C、a3b5D、a3b64.下列运算正确的是()A.3x 2+2x3=5x6B.50=0C.2﹣3=D.(x3)2=x65.下列运算正确的是().A. a·a2=a2 B . (a5 ) 3 =a8C.(ab)3=a3b3 D . a6 ÷ a2 =a36.a 1 ( 1) 2 0, 则 ab 的值是()2 bA. 1 B . 1 C .3D.12 2 4 27.下面的计算正确的是()A. 3x2?4x 2=12x2 B . x3?x5=x15 C . x4÷x=x 3 D .( x5)2=x 7 8.下列计算,正确的是()A. 2x2 3 8x6 B . a6 a2 a3.1 0C.3a22a2 6a2 D 3 039、设a m 3 , a n 6 ,则 a2m n ()A 、 12B 、 15C 、 54D 、 2410、H7N9是一种新型禽流感,其病毒颗粒呈多形性,其中球形病毒的最大直径为0.00000012米,这一直径用科学记数法表示为()A、1.2 ×10 -9米 B 、1.2 ×10 -7米 C 、1.2 ×10 -8米D、12×10-8米1二、填空题。
1.已知实数a、b 满足: a+b= 2,a- b= 5,则( a+ b)3·( a-b)3的值是 ___________ .2.若x2 kx 1 是一个完全平方式,则k=163.若x y 4 ( xy 3)2 0 ,则x2 y 2 .4.已知P 7 m 1, Q m 2 8m (m为任意实数),则P、Q的大小关系为15 15P Q .(填“>”“<”或“=” )13 .计算: 2a3 a 4 =___________.5. 若 a2﹣ 4a+b2﹣10b+29=0,则 a= , b= .6、若x22x 3 ,则代数式2x 2 4 x 3 的值为。

完整版)整式的乘除综合练习题欢迎您选择新活力教育的数学教案,本教案是2017学年七年级数学下册第一章整式的乘除综合。
一.选择题:1.正确的运算是(B)x+y=x+y。
2.如果(x+m)与(x+3)的乘积中不含x的一次项,那么m的值是(A)-3.3.计算(ab)的结果是(B)ab。
4.正确的运算是(A)3x+2x=5x。
5.正确的运算是(C)(ab)=ab。
6.如果a1(b1)22,那么ab的值是(A)3111.7.正确的计算是(B)x•x=x2.8.正确的计算是(C)3a•2a=6a。
9.如果a=3,a=6,则a2的值是(C)54.10.0.xxxxxxxx米用科学记数法表示为(B)1.2×10-7米。
11.填空题:1.(a+b)·(a-b)的值是(-21)。
2.如果x2kx1是一个完全平方式,那么k的值是(-8)。
3.如果x+y-4+(xy-3)=0,那么x+y的值是(4)。
4.如果P=15/78,则P<Q。
5.2a3a4的值是(2a-1)。
6.如果x22x3,那么2x24x3的值是(7)。
二.解答题:(1)略。
1.计算题:a-b)(a-b)15xy-12xy-3x)/(-3x)a^2*a^5-(-a)*a^3-(2a^2)^2*a^264x^4y^3)/(-2xy)^332(1)-23+(π-3.14)-(1-2)(2x-y)/(2)化简后的式子为:4-a^2-4a,代入a=-2,得到答案为10 阴影部分的面积为1/22.改写:求(a-b)的平方化简(15xy-12xy-3x)/(-3x),得到-2化简a^2*a^5-(-a)*a^3-(2a^2)^2*a^2,得到a^8+2a^6-4a^5 化简(-64x^4y^3)/(-2xy)^33,得到-2^31*x^3*y^30化简2(1)-23+(π-3.14)-(1-2)(2x-y)/(2),得到-2a^2-4a+4化简4-a^2-4a,代入a=-2,得到答案为10阴影部分的面积为1/23.删除段落:文章中没有明显有问题的段落,因此不需要删除。

华师大版八年级数学上册《整式的乘除》单元试卷检测练习及答案解析一、选择题1、下列运算正确的是()A.(a3)2=a6B.2a+3a=5a2C.a8÷a4=a2D.a2·a3=a62、若、、是正整数,则=()A.B.C.D.3、若,,则等于()A.B.C.2 D.4、计算的结果是()A.B.C.D.5、若,,则代数式的值等于()A.B.C.D.26、若(x2+px+q)(x2+7)的计算结果中,不含x2项,则q的值是()A.0 B.7 C.-7 D.±77、已知x+y=-5,x-y=2,则x2-y2=()A.. B.C.D.8、如果是一个完全平方式,那么的值是().A.B.C.D.9、计算(36x6-16x2)÷4x2的结果为()A.9x3﹣4x2B.9x4+4 C.9x3+4x D.9x4﹣4 10、某同学粗心大意,因式分解时,把等式x4-■=(x2+4)(x+2)(x-▲)中的两个数字弄污了,则式子中的■,▲对应的一组数字可以是( )A.8,1 B.16,2C.24,3 D.64,8二、填空题11、分解因式:3a3-3a=______.12、已知x a=3,x b=4,则x3a﹣2b的值是_____.13、计算:=_______.14、若的结果中不含x的一次项,则=________.15、已知x﹣y=4,则代数式x2﹣2xy+y2﹣25的值为_____.16、已知一个三角形的面积为8x3y2-4x2y3,一条边长为8x2y2,则这条边上的高为___________.17、计算:(﹣a)2÷(﹣a)= ,0.252007×(﹣4)2008= .18、已知,则=______.19、计算的结果是_______.20、若=7,则___________.三、计算题21、计算:(1)(2)(3)(4)22、因式分解:⑴⑵⑶⑷四、解答题23、一个三角形的底边长为,高为,该三角形面积为S,试用含的代数式表示S,并求当时,S的值.24、先化简,再求值:,其中x =-1,y =.25、计算:(1)已知a+b=-3,ab=5,求多项式4a2b+4ab2-4a-4b的值;(2)已知x2-3x-1=0,求代数式3-3 x2+9x的值?26、已知(x2+px+8)与(x2﹣3x+q)的乘积中不含x3和x2项,求p、q的值.27、阅读:将代数式转化为的形式,(期中为常数),则其中.(1)仿照此法将代数式化为的形式,并指出的值.(2)若代数式可化为的形式,求的值.参考答案1、A2、C3、A4、B5、B6、C7、D8、D9、D10、B11、3a(a+1)(a-1)12、13、214、-815、-916、2x-y17、﹣a,﹣4.18、-219、.20、±321、(1)1;(2);(3);(4)2.22、⑴==⑵==⑶===4⑷=== 23、.24、原式==025、(1)-48;(2)026、p=3,q=1.27、①;②答案详细解析【解析】1、分析:结合选项分别进行幂的乘方、合并同类项、同底数幂的乘除法等运算,然后选择计算正确选项即可.详解:A、(a3)2=a6,原式计算正确,故本选项正确;B、2a+3a=5a,原式计算错误,故本选项错误;C、a8÷a4=a4,原式计算错误,故本选项错误;D、a2·a3=a5,原式计算错误,故本选项错误.故选A.点睛:本题考查了幂的乘方乘方,合并同类项,同底数幂的乘除法. 熟练掌握它们的计算法则是计算正确的关键.2、分析:首先根据同底数幂的乘法将括号里面的进行计算,然后根据积的乘方计算法则得出答案.详解:原式=,故选C.点睛:本题主要考查的是同底数幂的乘法以及幂的乘方计算,属于基础题型.解决这个问题的关键就是明确幂的计算法则.3、分析:先把23m﹣2n化为(2m)3÷(2n)2,再求解.详解:∵2m=3,2n=5,∴23m﹣2n=(2m)3÷(2n)2=27÷25=.故选A.点睛:本题主要考查了同底数幂的除法及幂的乘方与积的乘方,解题的关键是把23m﹣2n化为(2m)3÷(2n)2.4、试题解析:故选B.5、∵,,∴(x-1)(y+1)=xy+x-y-1=.故选B.6、(x2+px+q)(x2+7)=x4+7x2+px3+7px+qx2+7q=x4+px3+(7+q)x2+7px+7q,因为计算结果中不含x2项,所以7+q=0,所以q=-7;故选C.7、本题考查平方差公式进行因式分解,因为x2-y2=(x+y)(x-y),将x+y=-5,x-y=2,代入得: -5×2=-10,因此,正确选项是D.8、∵形如的式子叫完全平方式,而,∴若是完全平方式,则,∴,故选D.9、多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.所以(36x6-16x2)÷4x2= 9x4﹣4考点:整式的除法.10、由(x2+4)(x+2)(x-▲)得出▲=2,则(x2+4)(x+2)(x-2)=(x2+4)(x2-4)=x4-16,则■=16.故选B.【点睛】此题考查了学生用平方差公式分解因式的掌握情况,灵活性比较强.11、分析:提取公因式法和公式法相结合进行因式分解即可.详解:原式故答案为:点睛:考查因数分解,提取公因式法和公式法相结合进行因式分解.注意分解一定要彻底.12、分析:直接利用同底数幂的除法运算法则计算得出答案.详解:∵x a=3,x b=4,∴x3a﹣2b=(x a)3÷(x b)2=33÷42=.故答案为:.点睛:本题主要考查了同底数幂的乘除运算,正确将原式变形是解题的关键.13、分析:先把改写成2100=,然后逆用积的乘方公式(ab)m=a m·b m,即a m·b m=(ab)m解答.详解:====2.点睛:本题考查了偶次幂的性质和积的乘方运算,解答本题的关键是逆用乘方运算公式.14、试题解析:结果中不含的一次项.故答案为:15、解: x2﹣2xy+y2﹣25=(x﹣y)2﹣25 =42﹣25=﹣9,故答案为:﹣9.16、∵三角形的面积为8x3y2-4x2y3,一条边长为8x2y2,∴这条边上的高为2(8x3y2-4x2y3) ÷8x2y2=16x3y2÷8x2y2-8x2y3÷8x2y2=2x-y,故答案为:2x-y.17、试题分析:根据同底数幂的除法底数不变指数相减,可得答案;根据同底数幂的乘法底数不变指数相加,可得积的乘方,根据积的乘方,可得答案.解:(﹣a)2÷(﹣a)=﹣a,0.252007×(﹣4)2008=[0.25×(﹣4)]2007×(﹣4)=﹣4,故答案为:﹣a,﹣4.18、本题利用拆常数项凑完全平方的方法进行求解,,可变形为:,即,根据非负数的非负性可得:解得: :,所以19、原式===12017=-.故答案为-.点睛:积的乘方公式:(ab)n=a n b n(n为正整数)的逆运算:a n b n = (ab)n(n为正整数)也成立.20、(x+)2=x2+2+=7+2=9,x+=±3.故答案为±3.点睛:(1)(x+)2=x2+2+;(x-)2=x2-2+.21、试题分析:(1)原式=;(2)原式=;(3)原式=;(4)原式=.考点:整式的混合运算.22、试题解析:点睛:因式分解:把一个多项式分解成几个整式的积的形式.因式分解的主要方法:提公因式法,公式法,十字相乘法,分组分解法.23、分析:利用三角形的面积公式得到三角形的面积S=(4a+2)(2a-1),然后利用平方差公式计算可得用含a的代数式表示S;再将a=2代入计算即可求解.详解:,当时,.点睛:本题考查了多项式乘多项式,平方差公式的知识,解决此类问题的关键是牢记平方差公式.24、分析:首先根据乘法公式将括号去掉,然后进行合并同类项,最后根据多项式除以单项式的法则得出答案,将x和y的值代入化简后的式子进行计算得出答案.详解:原式===,将x =,y =代入上式,原式=0.点睛:本题主要考查的是多项式的乘法和除法的计算法则,属于基础题型.在解决这个问题的时候,公式的应用是非常关键的.25、分析:(1)、首先进行分组分解,然后提取公因式,最后利用整体代入的思想进行求解;(2)、首先提取公因式-3,然后整体代入进行求解.详解:(1)、解:原式 ="4" ab(a+b)-4(a+b)="(4" ab-4)(a+b)=4(ab-1)(a +b)当a+b=-3,ab=5时,原式=4×(5-1)×(-3)=4×4×(-3)=-48(2)、原式=-3(x2-3x-1),当x2-3x-1="0," 原式=-3×0=0.点睛:本题主要考查的是利用因式分解进行简便计算,属于基础题型.解决这个问题的关键就是将所求的代数式进行因式分解.26、试题分析:根据整式的乘法,化简完成后,根据不含项的系数为0求解即可.试题解析:∵(x2+px+8)(x2﹣3x+q)=x4﹣3x3+qx2+px3﹣3px2+pqx+8x2﹣24x+8q=x4+(p﹣3)x3+(q﹣3p+8)x2+(pq﹣24)x+8q.∵乘积中不含x2与x3项,∴p﹣3=0,q﹣3p+8=0,∴p=3,q=1.27、试题分析:根据完全平方公式的结构,按照要求即可得出答案.试题解析:①则②则.。

第4课 整式的乘除 目的:复习幂的运算法则,整式的乘除运算.中考基础知识1. 幂的运算法则:a m ·a n=______(m ,n 都是正整数),(a m )n =_______(m ,n 都是正整数).a m ÷a n =_______(m ,n 都是正整数,且m>n ,a ≠0),(ab )n =______(n 为正整数).2.整式的乘除(1)单项式×单项式:4a 2x 5·(-3a 3bx )=_________,(2)单项式×多项式:m (a+b+c )=__________,(3)多项式×多项式:(a+b )(m+n-d )=_______.(4)单项式÷单项式:-12a 5b 3x 2÷4a 3x 2=________.3.乘法公式(1)平方差公式:(a+b )(a-b )=________.(2)完全平方公式:(a+b )2=_______,(a-b )2=_________.(3)立方和、立方差公式:(a+b )(a 2-ab+b 2)=________,__________=a 3-b3 4.在做整式乘除时,严格按照运算法则进行,做每一步都应有计算依据,•充分利用乘法公式简化计算. 备考例题指导例1.下列计算正确的是( )(A )x 5+x 5=x 10 (B )(3ab 2)3=9a 3b6 (C )a 2·a 3=a 6 (D )(-c )6÷(-c )5=-c (c ≠0)选(D )例2.(2005,金华市)如图,沿正方形的对角线对折,•把对折后重合的两个小正方形内的单项式相乘,乘积是___________(只要写出一个结论)a2a b-2b 答案:2a 2或-2b 2任写一个.例3.化简(a-b )3·(b-a )2÷(b-a )3.分析:底数不同,不能直接乘除,但注意到a-b 与b-a 是互为相反数,而且(a-b )3=-(b-a )3 解:原式=-(b-a )3·(b-a )2÷(b-a )3 =-(b-a )3+2-3 (注意乘除在一起要依次运算)=-(b-a )2 例4.计算(1)(-2b-5)(2b-5);(2)(a+b-1)(a-b+1).分析:在(a+b )(a-b )=a 2-b 2中,其左边的两个多项式有两项(a 与a )相同,有两项b 与-b 是互为相反数.这里平方差公式的使用条件.解:(1)原式=(-5)2-(2b)2=25-4b2.(2)原式=[a+(b-1)][a-(b-1)]=a2-(b-1)2=a2-(b2-2b+1)=a2-b2+2b-1备考巩固练习1.填空题(1)-x3·(-x)5=________;[(-x)3]2·(-x)3=________;(-2x2y3)2·(-12xy)3=________.(2)-6x(x-2y)=_______;(x-6)(x+7)=________;(x-2)(x-y)=________.(3)(2x-3y)2=________;(3a+b)2=________.(4)(x+1)(x2-x+1)=_______;(_______-2b)(_______)=a3-(________).(5)若4m·8m-1÷2m=32,则m=________.2.选择题(1)下列各式中,计算正确的是()(A)a2·a3=a6(B)a3÷a2=a2 (C)(a2)3=a6(D)(3a2)4=9a8(2)(2005,黄冈)下列计算中正确的是()(A)x5+x5=2x10(B)-(-x)3·(-x)5=-x8(C)(-2x2y)3·4x-3=-24x3y3(D)(12x-3y)(-12x+3y)=14x2-9y23.(2004,太原市)某公园一块草坪的形状如图所示(阴影部分),用代数式表示它的面积为__________.4.化简求值:(a+2b)(a2+4b2)(a-2b),其中a=2,b=-12.5.解答下列各题:(1)若a-1a=3,求a2+21a的值.(2)若3x2-mxy+6y2是一个完全平方式,求m的值.(3)已知x+y=2,xy=12,求x3+y3的值.(4)计算(8x2m-3-6x m+2-4x m)÷(-2x m-3).6.(2003,四川)观察下面的式子:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,39=19683,……它们的个位数字的变化有一定规律,用你发现的规律直接写出910的个位数字是几?7.(2005,苗城)先化简后求值:[(x-y)2+(x+y)(x-y)]÷2x,其中x=3,y=1.5 答案:1.(1)x8;-x9;-12x7y9(2)-6x2+12xy;x2+x-42;x2-xy-2x+2y(3)4x2-12xy+9y2,9a2+6ab+b2(4)x3+1;(a-2b)(a2+2ab+b2)=a3-8b3(5)22m·23m-3÷2m=25,m=22.(1)D (2)C 3.22a24.原式=(a2-4b2)(a2+4b2)=a4-16b4,当a=2,b=-1 2原式=24-16×(-12)4=16-1=155.(1)由a-1a=3得(a-1a)2=9∴a 2-2+21a =9 ∴a 2+21=11(2)∵3x 2-mxy+6y 2=x )2-mxy+y )2∴m=±=± 或用△=0,求m .(3)x 3+y 3=(x+y )(x 2-xy+y 2)=(x+y )[(x+y )2-3xy] =2(22-3×12)=2×52=5 (4)原式=-4x m +3x 5+2x 36.17.原式=1.5。

第一章整式的乘除单元测试卷(一)一、精心选一选(每小题3分,共21分)43 31•多项式xy 2x y 9xy 8的次数是A. 3B. 4C. 5D. 62•下列计算正确的是 ()A. 2x 26x 412x 84 mB . y3mmyy C .x y 2 x 22 , 2y D. 4a 2a33.计算a ba b 的结果是()A. b 2 a 2B.2 ,2a bC. a 22ab b 2D.a 2 2ab b 224. 3a 5a1与 2a 2 3a 4的和为()A. 5a 22a 3 2小B. a 8a3 C.2a3a 52小D. a 8a55.下列结果正确的是()21 A.-1 B. 9 50C.53.7 01D. 2 31398m^n26.右 a b8 6a b,那么m 22n 的值是()A. 10B. 52C. 20D. 327•要使式子9x 225y 2成为一个完全平方式,则需加上( )二、耐心填一填(第1~4题每空1分,第5、6题每空2分,共28分)班级 ____ 姓名 ______ 学号 ________ 得分 ________A. 15xyB. 15xyC. 30xyD. 30xy1•在代数式3xy 2 ,个,多项式有一2m ,6a个。
2a 3 , 12 , 4x yz1 2xy 2 , 中,单项式有 5 3ab2•单项式 5x 2y 4z 的系数是,次数是 。
,413•多项式3ab ab 有项,它们分别是。
54•⑴ x 2 x 5。
34⑵y 3。
23⑶2a b。
⑷x 5y24。
93⑸a a。
⑹ 10 5 2 40z 1 2 635.⑴ mnmn。
⑵x 5 x 5。
3 5⑶(2a b )25 。
⑷ 12x 3小 2y3xy 。
/、m32m6•⑴ aa a。
⑵ 22a 8a242…。
20062 220051 ⑶ x y x y x y。
⑷3。
3三、精心做一做(每题5分,共15分)1. 4x 2 y 5xy 7x5x 2 y 4xy x2 2 32. 2a 23a 2 2a 1 4a 32 ^343.2x y 6x y 8xy 2xy1. X 1 2x 1 x 22. 2x 3y 5 2x 3y 5四、计算题(每题6分,共12分)1五、化简再求值:XX 2y x 12 2x,其中X -,y 25。

2022-2023学年华东师大版八年级数学上册《第12章整式的乘除》同步练习题(附答案)一.选择题1.利用乘法公式计算正确的是()A.(4x﹣3)2=8x2+12x﹣9B.(2m+5)(2m﹣5)=4m2﹣5C.(a+b)(a+b)=a2+b2D.(4x+1)2=16x2+8x+12.下列多项式能直接用完全平方公式进行因式分解的是()A.4x2﹣4x+1B.x2+2x﹣1C.x2+xy+2y2D.9+x2﹣4x3.已知关于x的二次三项式2x2+bx+a分解因式的结果是(x+1)(2x﹣3),则代数式a b的值为()A.﹣3B.﹣1C.﹣D.4.已知a,b满足(3﹣9b)(a+b)+9ab=4a﹣a2,且a≠3b,则关于a与b的数量关系,下列说法中正确的是()①a2﹣a=9b2﹣3b;②(a﹣3b)2=a﹣3b;③a﹣3b=1;④a+3b=1.A.①②B.②③C.①④D.③④5.用4个长为a,宽为b的长方形拼成如图所示的大正方形,则用这个图形可以验证的恒等式是()A.(a+b)2=a2+2ab+b2B.(a﹣b)2=a2﹣2ab+b2C.(a+b)(a﹣b)=a2﹣b2D.(a+b)2﹣(a﹣b)2=4ab6.下列各式能用完全平方公式进行分解因式的是()A.x2+1B.x2+2x﹣1C.x2+3x+9D.7.下列运算正确的是()A.(a+b)2=a2+b2B.(﹣)﹣2=C.4a6+2a2=2a3D.(﹣3x3)2=9x68.计算(1﹣3x)(3x+1)的结果为()A.1﹣9x2B.9x2﹣1C.﹣1+6x﹣9x2D.1﹣6x+9x29.下列运算正确的是()A.2a2b•3a3b2=6a6b2B.(a2)3=a5C.a3b3=(ab)6D.(a+2b)(a﹣2b)=a2﹣4b210.下列运算正确的是()A.a2•a3=a6B.(2a)3=2a3C.(a2)3=a6D.(a+1)2=a2+2a二.填空题11.若xy=﹣3,x+y=5,则2x2y+2xy2=.12.计算:2021×512﹣2021×492的结果是.13.杨辉三角形,又称贾宪三角形,帕斯卡三角形,是二项式系数在三角形中的一种几何排列.在我国南宋数学家杨超所著的《详解九章算术》(1261年)一书中用如图的三角形解释二项和的乘方规律,观察下列各式及其展开式:请你猜想(a+b)9展开式的第三项的系数是.14.若多项式4x2+kx+25是完全平方式,则k的值是.15.已知(m﹣n)2=16,(m+n)2=24,m2+n2=.16.若a﹣b=5,a2+b2=13,则ab=.三.解答题17.一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和等数”.例如:4563,x=4+5=9,y=6+3=9,因为x =y,所以4563是“和等数”.(1)请判断3975、5648是否是“和等数”;(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的所有满足条件的“和等数”.18.发现与探索(1)根据小明的解答将下式因式分解:a2﹣12a+20.小明的解答:a2﹣6a+5=a2﹣6a+9﹣9+5=(a﹣3)2﹣4=(a﹣5)(a﹣1).(2)根据小丽的思考解决下列问题:小丽的思考:代数式(a﹣3)2+4无论a取何值,(a﹣3)2≥0,则(a﹣3)2+4≥4,所以(a﹣3)2+4有最小值为4.请仿照小丽的思考解释代数式﹣(a+1)2+8的最大值为8.19.如图1所示的正方形,我们可以利用两种不同的方法计算它的面积,从而得到完全平方公式:(a+b)2=a2+2ab+b2.请你结合以上知识,解答下列问题:(1)写出图2所示的长方形所表示的数学等式.(2)根据图3得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=38,求代数式a2+b2+c2的值.(3)小华同学用图4中x张边长为a的正方形纸片,y张边长为b的正方形纸片,z张边长分别为a,b的长方形纸片拼出一个面积为(2a+3b)(6a+5b)的长方形,求代数式x+y+z的值.20.利用因式分解计算:(1)9002﹣894×906;(2)2.68×15.7﹣31.4+15.7×1.32.21.数学课上,在计算(x+a)(x+b)时,琪琪把b看成6,得到的结果是x2+8x+12,莹莹把a看成7,得到的结果是x2+12x+35.根据以上提供的信息:(1)请直接写出a、b的值.(2)请你写出原算式并计算正确的结果.22.材料1:对于一个四位自然数M,如果M满足各数位上的数字均不为0,它的百位上的数字比千位上的数字大1,个位上的数字比十位上的数字大1,则称M为“满天星数”.对于一个“满天星数”M,同时将M的个位数字交换到十位、十位数字交换到百位、百位数字交换到个位,得到一个新的四位数N,规定:F(M)=.例如:M=2378,因为3﹣2=1,8﹣7=1,所以2378是“满天星数”;将M的个位数字8交换到十位,将十位数字7交换到百位,将百位数字3交换到个位,得到N=2783,F (2378)==﹣45.材料2:对于任意四位自然数=1000a+100b+10c+d(a、b、c、d是整数且1≤a≤9,0≤b,c,d≤9),规定:G()=c•d﹣a•b.根据以上材料,解决下列问题:(1)请判断2467、3489是不是“满天星数”,请说明理由;如果是,请求出对应的F(M)的值;(2)已知P、Q是“满天星数”,其中P的千位数字为m(m是整数且1≤m≤7),个位数字为7;Q的百位数字为5,十位数字为s(s是整数且2≤s≤8).若G(P)+G(Q)能被11整除且s>m,求F(P)的值.23.我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙的解决一些图形问题.比如:用图1所示的正方形与长方形纸片,可以拼成一个图2所示的正方形.请你解决下列问题:(1)利用不同的代数式表示:图2中阴影部分的面积S,写出你从中获得的等式,并加以证明;(2)已知(2022﹣m)(2019﹣m)=3505,请用(1)中的结论,求(2022﹣m)2+(2019﹣m)2的值.24.阅读材料:利用公式法,可以将一些形如ax2+bx+c(a≠0)的多项式变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项式ax2+bx+c(a≠0)的配方法,运用多项式的配方法及平方差公式能对一些多项式进行因式分解.例如x2+4x﹣5=x2+4x+()2﹣()2﹣5=(x+2)2﹣9=(x+2+3)(x+2﹣3)=(x+5)(x﹣1).根据以上材料,解答下列问题.(1)分解因式:x2+2x﹣8;(2)求多项式x2+4x﹣3的最小值;(3)已知a,b,c是△ABC的三边长,且满足a2+b2+c2+50=6a+8b+10c,求△ABC的周长.25.如果一个自然数M能分解成A×B,其中A和B都是两位数,且A与B的十位数字之和为10,个位数字之和为9,则称M为“十全九美数”,把M分解成A×B的过程称为“全美分解”,例如:∵2838=43×66,4+6=10,3+6=9,∴2838是“十全九美数“;∵391=23×17,2+1≠10,∴391不是“十全九美数”.(1)判断2100和168是否是“十全九美数”?并说明理由;(2)若自然数M是“十全九美数“,“全美分解”为A×B,将A的十位数字与个位数字的差,与B的十位数字与个位数字的和求和记为S(M);将A的十位数字与个位数字的和,与B的十位数字与个位数字的差求差记为T(M).当能被5整除时,求出所有满足条件的自然数M.参考答案一.选择题1.解:A.(4x﹣3)2=16x2﹣24x+9,故本选项不合题意;B.(2m+5)(2m﹣5)=4m2﹣25,故本选项不合题意;C.(a+b)(a+b)=a2+2ab+b2,故本选项不合题意;D.(4x+1)2=16x2+8x+1,故本选项符合题意;故选:D.2.解:A、4x2﹣4x+1=(2x﹣1)2,故A符合题意;B、x2+2x+1=(x+1)2,故B不符合题意;C、x2+xy+y2=(x+y)2,故C不符合题意;D、9+x2﹣6x=(x﹣3)2,故D不符合题意;故选:A.3.解:由题意得:2x2+bx+a=(x+1)(2x﹣3),2x2+bx+a=2x2﹣3x+2x﹣3,2x2+bx+a=2x2﹣x﹣3,∴b=﹣1,a=﹣3,∴a b=(﹣3)﹣1=﹣,故选:C.4.解:∵(3﹣9b)(a+b)+9ab=4a﹣a2,∴3a+3b﹣9ab﹣9b2+9ab=4a﹣a2a2﹣a=9b2﹣3ba2﹣9b2=a﹣3b(a+3b)(a﹣3b)=a﹣3b,∵a≠3b,∴a﹣3b≠0,∴a+3b=1.故选:C.5.解:∵此题阴影部分面积可表示为:(a+b)2﹣(a﹣b)2和4ab,∴可得等式(a+b)2﹣(a﹣b)2=4ab,故选:D.6.解:A.x2+1,不能用完全平方公式进行分解因式,故A不符合题意;B.x2+2x﹣1,不能用完全平方公式进行分解因式,故B不符合题意;C.x2+3x+9,不能用完全平方公式进行分解因式,故C不符合题意;D.x2﹣x+=(x﹣)2,故D符合题意;故选:D.7.解:A、原式=a2+2ab+b2,∴不符合题意;B、原式=4,∴不符合题意;C、原式=4a6+2a2,∴不符合题意;D、原式=9x6,∴符合题意;故选:D.8.解:原式=1﹣(3x)2=1﹣9x2;故选:A.9.解:A、原始=6a5b3,∴不符合题意;B、原始=a6,∴不符合题意;C、原始=(ab)3,∴不符合题意;D、原始=a2﹣4b2,∴符合题意;故选:D.10.解:A、a2•a3=a5,原计算错误,故此选项不符合题意;B、(2a)3=8a3,原计算错误,故此选项不符合题意;C、(a2)3=a6,原计算正确,故此选项符合题意;D、(a+1)2=a2+2a+1,原计算错误,故此选项不符合题意;故选:C.二.填空题11.解:2x2y+2xy2=2xy(x+y).∵xy=﹣3,x+y=5.∴原式=2×(﹣3)×5,=﹣30.12.解:2021×512﹣2021×492=2021×(512﹣492)=2021×(51+49)×(51﹣49)=2021×100×2=404200,故答案为:404200.13.解:依据规律可得到:(a+n)9的展开式的系数是杨辉三角第10行的数,第3行第三个数为1,第4行第三个数为3=1+2,第5行第三个数为6=1+2+3,…第10行第三个数为:1+2+3+…+8==36.故答案为:36.14.解:∵4x2+kx+25是一个完全平方式,∴4x2+kx+25=(2x)2+kx+52=(2x±5)2,∵(2x±5)2=4x2±20x+25,∴kx=±20x,解得k=±20.故答案为:±20.15.解:∵(m+n)2=24,(m﹣n)2=16,∴m2+2mn+n2=24①,m2﹣2mn+n2=16②,①+②得:2(m2+n2)=40,∴m2+n2=20.故答案为:20.16.解:将a﹣b=5两边平方得:(a﹣b)2=a2+b2﹣2ab=25,把a2+b2=13代入得:13﹣2ab=25,解得:ab=﹣6.故答案为:﹣6.三.解答题17.解:(1)3975是“和等数”;5648不是“和等数”;理由如下:3975,x=3+9=12;y=7+5=12,∵x=y,∴3975是“和等数”;∴5648,x=5+6=11;y=4+8=12,∵x≠y,∴5648不是“和等数”.(2)设这个“和等数”千位、百位、十位、个位上数字分别为a、b、c、d,根据题意得:d=2a,a+b=c+d,b+c=12,∴2c+a=12,即a=2,4,6,8,d=4,8,12(舍去),16(舍去),①当a=2,d=4时,2(c+1)=12,可知c+1=6且a+b=c+d,∴c=5,b=7,②当a=4,d=8时,2(c+2)=12,可知c+2=6且a+b=c+d,∴c=4,b=8,综上所述,这个数为2754和4848.18.解:(1)a2﹣12a+20=a2﹣12a+36﹣36+20=(a﹣6)2﹣42=(a﹣10)(a﹣2).(2)无论a取何值时,﹣(a+1)2≤0,则﹣(a+1)2+8≤8,所以﹣(a+1)2+8的最大值为8.19.(1)拼成的大矩形面积之和=(a+b)(a+2b),各个小图形面积之和=a2+3ab+2b2,∴图2所表示的数学等式是(a+b)(a+2b)=a2+3ab+2b2.故答案为:(a+b)(a+2b)=a2+3ab+2b2.(2)图(3)中大正方形的面积=(a+b+c)2,各个小图形面积之和=a2+b2+c2+2ab+2ac+2bc,∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.∵a+b+c=10,ab+ac+bc=38.∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=102,即a2+b2+c2+2(ab+ac+bc)=100,∴a2+b2+c2=100﹣2×38=24.(3)大长方形的面积为(2a+3b)(6a+5b)=12a2+10ab+18ab+15b2=12a2+28ab+15b2,小图形的面积分别为a2,b2,ab,∴x=12,y=15,z=28.∴x+y+z=12+15+28=55.20.(1)9002﹣894×906=9002﹣(900﹣6)(900+6)=9002﹣(9002﹣62)=9002﹣9002+62=36.(2)2.68×15.7﹣31.4+15.7×1.32=15.7×(2.68+1.32)﹣31.4=15.7×4﹣31.4=31.4×2﹣31.4=31.4.21.解:(1)a=2,b=5;(2)(x+a)(x+b)=(x+2)(x+5)=x2+5x+2x+10=x2+7x+10.22.解:(1)2467不是“满天星数”,3489是“满天星数”,理由如下:∵2467的百位数字为4,千位数字为2,∴4﹣2=2≠1,∴2467不是“满天星数”.∵3489的千位数字为3,百位数字为4,十位数字为8,个位数字为9,∴4﹣3=1,9﹣8=1,∴M=3489是“满天星数”,∴N=3894,∴F(3489)==﹣45.(2)由题意可得:P=,Q=,则P=1000m+100(m+1)+60+7=1100m+167,Q=4000+500+10s+s+1=4501+11s.∴G(P)=6×7﹣m(m+1)=42﹣m2﹣m,G(Q)=s(s+1)﹣20=s2+s﹣20,∴G(P)+G(Q)=42﹣m2﹣m+s2+s﹣20=s2+s﹣m2﹣m+22.∵G(P)+G(Q)能被11整除且s>m,∴只要s2+s﹣m2﹣m=(s+m)(s﹣m)+s﹣m=(s﹣m)(s+m+1)能被11整除.∵2≤s≤8,1≤m≤7,s、m均为整数,s>m,∴4≤s+m+1≤16,∴s+m+1=11即s+m=10.∴.∴P=2367或3467或4567.∴F(2367)=,F(3467)==﹣23,F(4567)==﹣12.23.解:(1)图②中,S阴影=a2+b2,还可以表示为:S阴影=(a+b)2﹣2ab.∴a2+b2=(a+b)2﹣2ab.(2)设a=2022﹣m,b=2019﹣m,则ab=3505,a﹣b=3.∴(2022﹣m)2+(2019﹣m)2=a2+b2=(a﹣b)2+2ab=9+7010=7019.24.解:(1)x2+2x﹣8=x2+2x+1﹣1﹣8=(x+1)2﹣9=(x+1﹣3)(x+1+3)=(x﹣2)(x+4);(2),∵(x+2)2≥0,∴(x+2)2﹣7≥﹣7,∴多项式x2+4x﹣3的最小值为﹣7;(3)∵a2+b2+c2+50=6a+8b+10c,∴a2+b2+c2+50﹣6a﹣8b﹣10c=0,a2﹣6a+9+b2﹣8b+16+c2﹣10c+25﹣9﹣16﹣25+50=0,(a﹣3)2+(b﹣4)2+(c﹣5)2=0,∴a﹣3=0,b﹣4=0,c﹣5=0,∴a=3,b=4,c=5,∴△ABC的周长=3+4+5=12.25.解:(1)2100是“十全九美数”,168不是“十全九美数”,理由如下:∵2100=25×84,2+8=10,5+4=9,∴2100是“十全九美数”;∵168=14×12,l+l≠10,∴168不是“十全九美数“;(2)设A的十位数字为m,个位数字为n,则A=10m+n,∵M是“十全九美数”,M=A×B,∴B的十位数字为10﹣m,个位数字为9﹣n,则B=10(10﹣m)+9﹣n=109﹣10m﹣n,由题知:S(M)=m﹣n+10﹣m+9﹣n=19﹣2n,T(M)=m+n﹣[10﹣m﹣(9﹣n)]=2m﹣1,根据题意,令==5k(k为整数),由题意知:1≤m≤9,0≤n≤9,且都为整数,∴1≤19﹣2n≤19,1≤2m﹣1≤17,当k=l时,=5,∴或或,解得或(舍去)或;∴M=A×B=17×92=1564或M=A×B=22×87=1914;当k=2时,=10,∴,解得(舍去);当k=3时,=15,∴,解得;∴M=A×B=12×97=1164,综上,满足“十全九美数”条件的M有:1564或1914或1164.。

整式的乘除(习题)➢ 例题示范例1:计算328322(2)(2)(84)(2)x y y x y x x ⋅-+-+÷-.【操作步骤】(1)观察结构划部分:328322(2)(2)(84)(2)x y y x y x x ⋅-+-+÷-① ②(2)有序操作依法则:辨识运算类型,依据对应的法则运算.第一部分:先算积的乘方,然后是单项式相乘;第二部分:多项式除以单项式的运算.(3)每步推进一点点.【过程书写】解:原式62634(2)(42)x y y x y =⋅-+-6363842x y x y =-+-6342x y =--➢ 巩固练习1. ①3225()a b ab -⋅-=________________;②322()(2)m m n -⋅-=________________;③2332(2)(3)x x y -⋅-; ④323(2)(2)b ac ab ⋅-⋅-.2. ①2223(23)xy xz x y ⋅+=_____________________; ②31422xy y ⎛⎫-⋅-= ⎪⎝⎭_______________________; ③2241334ab c a b abc ⎛⎫-⋅= ⎪⎝⎭___________________; ④222(2)(2)ab a b ⋅-=________________________;⑤32(3231)a a a a -⋅+--=____________________.3. ①(3)(3)x y x y +-;②(2)(21)a b a b -++;③(23)(24)m n m n ---; ④2(2)x y +;⑤()()a b c a b c -+++.4. 若长方形的长为2(421)a a -+,宽为(21)a +,则这个长方形的面积为()A .328421a a a -+-B .381a -C .328421a a a +--D .381a +5. 若圆形的半径为(21)a +,则这个圆形的面积为( )A .42a π+πB .2441a a π+π+C .244a a π+π+πD .2441a a ++6. ①32223x yz xy ⎛⎫÷= ⎪⎝⎭__________________;②3232()(2)a b a b -÷-=________________;③232(2)()x y xy ÷=___________;④2332(2)(__________)2x y x y -÷=;⑤23632()(6)(12)m n m n mn -÷⋅-=_________.7. ①32(32)(3)x yz x y xy -÷-=____________; ②233242112322a b a b a b a b ⎛⎫⎛⎫-+÷-= ⎪ ⎪⎝⎭⎝⎭_______________;③24422(48)(2)m n m n mn --÷=_______________;④()221___________________32m mn n ÷=-+-. 8. 计算:①322322(4)(4)()(2)a c a c a c ac -÷--⋅-;②224(2)(21)a a a -+--;③33(2)(2)(2)()a b a b a b ab ab +-+-÷-.➢ 思考小结1. 老师出了一道题,让学生计算()()a b p q ++的值.小聪发现这是一道“多×多”的问题,直接利用握手原则展开即可. ()()a b p q ++=小明观察这个式子后,发现可以把这个式子看成长为(a +b ),宽为(p +q )的长方形,式子的结果就是长方形的面积;于是通过分割就可以表达这个长方形的面积为_________________.∴()()a b p q ++=请你类比上面的做法,利用两种方法计算(a +b )(a +2b ).【参考答案】➢ 巩固练习1. ①445a b ②522m n③12272x y - ④3524a b c -2. ①222336+9x y z x y ②428xy xy -+ ③232321334a b c a b c - ④442584a b a b - ⑤432323a a a a --++3. ①229x y - ②2242a b a b -+-③224212m mn n -++④2244x xy y ++ ⑤2222a b c ac -++4. D5. C6. ①223x z②12 ③48x y④34x y - ⑤22mn7. ①223x z x -+ ②2246b ab a -+-③222n m --④3222132m n m n m -+- 8. ①322a c②7 ③23a ab + ➢ 思考小结()()a b p q ap aq bp bq ++=+++ 22()(2)32a b a b a ab b ++=++。


第一章 整式的乘除第1节同底数幂的乘法知识点:n m n m a a a +=⋅( m 、n 都是正整数) 同底数幂相乘,底数不变,指数相加。
练习题1、填空(1)m a 叫做a 的m 次幂,其中a 叫幂的________,m 叫幂的________;(2)写出一个以幂的形式表示的数,使它的底数为c ,指数为3,这个数为________; (3)例题:43表示有_ 个 相乘。
可以写成43=3×3×3×3=81;43()7表示有_ 个 相乘。
可以写成43()7= ; 43()7-表示有_ 个 相乘。
可以写成43()7-= ; 42表示有_ 个 相乘。
可以写成42= ;4)2(-表示有_____个 相乘。
可以写成4)2(-= ;42-表示有____个 相乘的 数。
可以写成42-= ;412⎛⎫ ⎪⎝⎭表示有_____个 相乘。
可以写成412⎛⎫ ⎪⎝⎭= ; 412⎛⎫- ⎪⎝⎭表示有_____个 相乘。
可以写成412⎛⎫- ⎪⎝⎭= ; 412⎛⎫- ⎪⎝⎭表示有___个 相乘的 数。
可以写成412⎛⎫- ⎪⎝⎭= ;-412⎛⎫- ⎪⎝⎭表示有___个 相乘的 数。
可以写成-412⎛⎫- ⎪⎝⎭= ; 412表示有___个 相乘的 数。
可以写成412= ; 41(2)-表示有___个 相乘的 数。
可以写成41(2)-= ; 41(2)-表示有___个 相乘的 数。
可以写成41(2)-= ; 412-表示有___个 相乘的 数。
可以写成412-= ;2、根据乘方的意义,例题:3a =a ·a ·a ,4a =a ·a ·a ·a 7a (1)102= ,103= ,因此102×103= = 。
(2)105= ,108= ,因此105×108= = 。
(3)x 5= ,x 3= ,因此x 5·x 3= = 。
![《整式乘除100题》[大全]](https://img.taocdn.com/s1/m/3a51d638bb1aa8114431b90d6c85ec3a87c28be8.png)
《整式乘除100题》[大全]第一篇:《整式乘除100题》[大全]整式乘除计算 100 题使用说明:本专题的制作目的是提高学生在整式乘除这一部分的计算能力。
大致分了三个模块:①单项式与单项式(34题);②单项式与多项式(33题);③多项式与多项式(33题);共题。
建议先仔细研究方法总结、易错总结和例题解析,再进行巩固练习。
模块一单项式与单项式方法总结:单项式乘单项式:单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式中含有的字母,则连同它的指数作为积的一个因式.单项式相除,把系数、同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.易错总结:相同字母相乘,注意是字母不变,指数相加;注意单项式相乘,他们的系数也是分别相乘,不是相加;系数里的负号要注意不要忘掉单独出现的字母最后要作为积的一个因式,不要遗漏例题解析:—ꅘy 2 · 2ꅘ2 y 2 .解:—ꅘy 2 · 2ꅘ2 y 2 =—ꅘ y 2· 4ꅘ4 y 2=— 4ꅘ5 y 4 .……【系数、相同字母分别相乘】巩固练习:1.计算:— 8a⺁·a 2 ⺁. 422ꅘ3 · —져ꅘ y 3 . 4.计算:a 4 ·—a 3÷ — a 2. 5.计算:——ꅘ2 3 · —ꅘ 2 2 —ꅘ· —ꅘ 3 3 . 6.计算:—ꅘ6—— 3ꅘ 3 2 — [ — 2ꅘ 2 ] 3 . 7.计算:—a 2 ·— a 3·— a+— a 2—— a 3. 8.计算:a —2 ⺁2 · a 2 ⺁—2 —3 . 9.计算:— 2ꅘ2 ·(ꅘ2)3 · —ꅘ 2 . 10.计算:— 21ꅘ2 y 4 ÷ — 3ꅘ 2 y 3 . 11.计算:2a 3 ⺁ 3— 8a⺁ 2÷ — 4a 4 ⺁ 3. 12—a 2 · a 4 ÷ a 3 . 13.计算:12a⺁ 2a⺁c 4 ÷ — 3a 2 ⺁3 c ÷ 2 a⺁c 3 . 17—a 3·— a 218.计算:(2a)3 —a · a 2 + 3a 6 ÷ a 3 . 19.(a 5)2·(a 2)2—(a 2)4·(a 3)2 . 20.ꅘ + 2ꅘ + 3ꅘ + ꅘ· ꅘ2 · ꅘ 3 + ꅘ 3 2 . 21.计算:ꅘm · ꅘn 3 ÷ ꅘ m—1 · 2ꅘ n—1 . 22.计算:— 2ꅘ2 y · 5ꅘy 3 ·— 3ꅘ 3 y 2. 523.ꅘ5 · ꅘ져 + ꅘ6 ·(—ꅘ 3)2 + 2(ꅘ 3)4 . 24.计算:— 1a⺁ 2·— 2a 3 ⺁c . 425.计算:— 2ꅘ— 3ꅘ2 y 2 3 · 1y 2 + t ꅘ져 y 8 . 32 3 4 14.计算:a 3 · a 5 · a 2 +a 5—a 2· a 2 . 15.化简:(4ꅘ2 y)2 ÷ 8y 2 . / 服务内核部-初数教研10.计算:6ꅘy ·ꅘ y — 1y+ 3ꅘ y2 . 211.计算:8a 2 ⺁— 4a⺁ 2÷ — 1a⺁ 2服务内核部-初数教研/ 28.— 2ꅘ2 y 2 3 · 3ꅘ y 4 . 29.计算:— 1a 3 · — 6a⺁ 2 . 330.计算:2ꅘ3 y — 2ꅘ y + — 2ꅘ 2 y 2 . 312a 2 ⺁·— 3⺁2 c ÷ 4a⺁ 3. 32.计算:— 3ꅘ2 y 3·— 2 ꅘ y 233.计算:—3a 2·a 2 ÷ — 1 a 22. 3 2 34.计算:(— 2ꅘm y n)2 ·(—ꅘ2 y n)3 ·(— 3ꅘ y 2).模块二单项式与多项式方法总结:单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加.多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.易错总结:巩固练习:1.化简:—져ꅘ2 y 2ꅘ 2 y — 3ꅘ y 3 + ꅘ y . 22ꅘ y 5ꅘ y 2 + 3ꅘ y —1 . 3.计算:— a 2 ⺁c + 2a⺁ 2 — 3 ac·— 2 ac 2 . 5 3 4.计算:— 2ꅘ2 y — 3ꅘ y + 3ꅘ 2 y 3 — 6ꅘ 3 . 3 2 5.计算:ꅘn+1 · ꅘ 2n —ꅘ n+1 + ꅘ 2 . 6.计算:2 2 3a 2 2— 1 . 7.计算:a⺁2 · 2a 2 ⺁— 3a⺁2 . 282a 23a⺁ 2 — 5a⺁ 3. 9.计算:— 4 a⺁2 ·— ta 2 ⺁— 12a⺁ + 3⺁ 2. 3 2 4 12.化简3a 5 ⺁ 3 — a 4 ⺁ 2÷ — a 2 ⺁ 213.计算:2져ꅘ3 — 18ꅘ 2 + 3ꅘ÷ — 3ꅘ. 14.计算:45a 3 — 1a 2 ⺁ + 3a÷ — 1a . 6 3 15.计算:6m 2 n — 6m 2 n 2 — 3m 2÷ — 3m 2. 16.计算:—ꅘ2 3 — 3ꅘ 2 ꅘ 4 + 2ꅘ— 2 . 17.计算:— 1ꅘ y 2 3 — 2ꅘ y ꅘ y —ꅘ2 y 5 . 318.计算:a⺁ 2 — 2a⺁ + 4⺁· 1a⺁—a⺁ 2 . 3 3 2 2 19.计算:— 2a ⺁(6a ⺁— 3a + 3 ⺁).2 20.计算:2a a — 2a 3—— 3a 2. 21.化简 1单项式乘多项式中的每一项时,注意不要漏掉前面的符号注意多项式中的每一项都要和单项式相乘,不要漏项例题解析:计算:— 2ꅘy 2 2 ·y 2 — 1ꅘ2 — 3ꅘ y . 4 2 2 解:原式= 4ꅘ2 y 4 · 1y 2 — 1ꅘ 2 — 3ꅘ y 4 2 2 = ꅘ2 y 6 — 2 ꅘ 4 y 4 — 6 ꅘ 3 y 5 .……【用单项式去乘多项式的每一项】/ 服务内核部-初数教研3ꅘ2 — y — 22ꅘ2 + y . 24.计算:(— 2ꅘy 2)2 · 1y 2 — 1ꅘ2 — 3ꅘ y . 4 2 2 25.计算:(3ꅘ y)2(ꅘ2 — y 2)—(4ꅘ2 y 2)2 ÷ 8y 2 + t ꅘ 2 y 4 . 26.计算:4a ⺁(2a 2 ⺁ 2 — a ⺁+ 3)27.计算:2ꅘ—ꅘ2 + 3ꅘ— 4 — 3ꅘ 2ꅘ + 1 . 228.计算:ꅘꅘ2 —ꅘ— 1 + 3 ꅘ 2 + ꅘ— 1ꅘ 3ꅘ 2 + 6ꅘ. 329.化简:ꅘ 1ꅘ + 1— 3ꅘ 3ꅘ— 2 . 2 2 30.求值:ꅘ2 3ꅘ— 5 — 3ꅘꅘ 2 + ꅘ— 3,其中ꅘ= 1 . 231.先化简,再求值:ꅘꅘ2 —ꅘ— 1+ 2 ꅘ2 + 2 — 1ꅘ 3ꅘ 2 + 6ꅘ— 1,其中ꅘ =— 3. 333.先化简,再求值:ꅘ— 2 1 — 3ꅘ— 2ꅘ 2 —ꅘ,其中ꅘ = 4. 2 3 2 模块三多项式乘多项式方法总结:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.易错总结:在不引起歧义的情况下,单项式和其它单项式或多项式作运算时本身可以不加括号;计算时注意符号变化,不要丢掉单独的字母或数字;多项式与多项式相乘后如果出现同类项必须合并.合并同类项时,可以在同类项下边标上相同的符号,避免引起错误.例题解析:计算:ꅘ— aꅘ2 + aꅘ + a 2解:ꅘ— aꅘ2 + aꅘ + a 2= ꅘ3 + aꅘ 2 + a 2 ꅘ— aꅘ 2 — a 2 ꅘ—a 3 ……【用一个多项式的每一项乘另一个多项式的每一项】= ꅘ3 — a 3 .巩固练习:12ꅘ + 5y3ꅘ— 2y . 2a — 2⺁(a + ⺁). 332ꅘ— 1 . 6ꅘ + yꅘ— 2y . 72ꅘ + 3y3ꅘ— 2y . 8— 1ꅘ + — 3ꅘꅘ + 3 . 9.计算:ꅘ 1ꅘ— 2 . 10a + 32a + 5. 11m + 22m — 3 . 12ꅘ— 32ꅘ + 5 . 13.计算:4ꅘ2 y — 5ꅘ y 2· 져ꅘ 2 y — 4ꅘ y 2 . 14.计算:ꅘm — 2y n3ꅘ m + y n. 15.计算:ꅘ— 1ꅘ2 + ꅘ + 1 . 18.计算:ꅘ— aꅘ2 + aꅘ + a 2.19.计算:ꅘ + yꅘ2 —ꅘ y + y 2. 203ꅘ + 1ꅘ— 3 . 21ꅘ + y — 2ꅘ— y . 22.计算:2a —⺁ + c2a —⺁— c . 23.—ꅘ3 + 2ꅘ 2 — 5 2ꅘ 2 — 3ꅘ + 1 . 24.计算:ꅘ + 52ꅘ— 3 — 2ꅘꅘ2 — 2ꅘ + 3 . 25.计算:ꅘ2 — 2ꅘ + 3ꅘ— 1ꅘ + 1 . 26ꅘ 4ꅘ— 3 — 2 ꅘ— 3ꅘ + 1 . 272ꅘ— 3ꅘ + 4—ꅘ— 1ꅘ + 1 . 30— 1ꅘ + 2ꅘꅘ + 3 . 31ꅘ + 3ꅘ— 5— 3 ꅘ— 1ꅘ + 6 . 325ꅘ + 3y3y — 5ꅘ—4ꅘ— y4y + ꅘ. 33.计算:a⺁ a + ⺁—a —⺁a 2 + ⺁ 2. 4.计算:2ꅘ + 3yꅘ— 2y . 5.计算:(ꅘ2 y 3 —ꅘ3 y 2)·(ꅘ 2 — y 2). / 服务内核部-初数教研2 3 4 16.计算:(2m + n 2)(4m 2 — 2mn 2 + n 4). 17.化简:3ꅘ2 + 2ꅘ + 13ꅘ— 1 .服务内核部-初数教研/ 服务内核部-初数教研/第二篇:第一章整式的乘除单元测试第一章整式的乘除单元测试(时间120分钟,满分150分)A卷(100分)一、选择题:本大题共10小题,每小题3分,共30分;在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列各题中计算错误的是()2.化简x(y-x)-y(x-y)得()A、x2-y2B、y2-x2C、2xyD、-2xy3.计算的结果是()A.B.-C.D.-4.是一个完全平方式,则a的值为()A.4B.8C.4或—4D.8或—85.三个数中,最大的是()A.B.C.D.不能确定6.化简(a+b+c)-(a-b+c)的结果为()A.4ab+4bcB.4acC.2acD.4ab-4bc7.已知,,则、、的大小关系是()A.>>B.>>C.<<D.>>8.若,则等于()A.-5B.-3C.-1D.19.边长为a的正方形,边长减少b以后所得较小正方形的面积比原来正方形的面积减少了()A.B.+2abC.2abD.b(2a—b)10.多项式的最小值为()A.4B.5C.16D.25二、填空题:本大题共6小题,每小题3分,共18分,把答案填写在题中横线上.11.是_____次_____项式,常数项是_____,最高次项是_____.12.(1)(2)13.(1)(2)14.已知是关于的完全平方式,则=;15.若m2+n2-6n+4m+13=0,m2-n2=;16、如果时,代数式的值为2008,则当时,代数式的值是三、计算题:本大题共5小题,每小题4分,共20分,解答应写出必要的计算过程.17.;18.19.20.21.四、综合题:本大题共5小题,共32分,解答应写出必要的计算过程.22.(5分)已知,求的值[来23.(6分)简便计算:(1)(2)3.76542+0.4692×3.7654+0.23462.24.(5分)已知,,求代数式的值;25.(6分)若4m2+n2-6n+4m+10=0,求的值;26.(8分)若的积中不含与项,(1)求、的值;(2)求代数式的值;B卷(50分)1.若,则=;2.有理数a,b,满足,=;3.=;4.若那么=;5.观察下列各式:1×3=12+2×1,2×4=22+2×2,3×5=32+2×3,…,请你将猜想到的规律用自然数n(n≥1)表示出来:__________.6.(6分)计算:.7.(7分)已知:,求-的值.8.(8分)已知a2-3a-1=0.求、的值;9.(9分)一元二次方程指:含有一个未知数,且未知数的最高次数为2的等式,求一元二次方程解的方法如下:第一步:先将等式左边关于x的项进行配方,第二步:配出的平方式保留在等式左边,其余部分移到等式右边,;第三步:根据平方的逆运算,求出;第四步:求出.类比上述求一元二次方程根的方法,(1)解一元二次方程:;(2)求代数式的最小值;答案:1-5.CBBCA;6-10.AABDC;11.12.(1)(2);13.(1)(2);14.;15.-5;16、-2006;17.;18.2;19.;20.;21.22.15;23.(1)1;(2)16;24.3;25.-8;26.;B卷:1.-2;2.6;3.;4.6;5.;6.2;7.30;8.3,13;9.(1);(2)2;第三篇:初中数学复习整式的乘除专题01整式的乘除阅读与思考指数运算律是整式乘除的基础,有以下5个公式:,,,.学习指数运算律应注意:1.运算律成立的条件;2.运算律中字母的意义:既可以表示一个数,也可以表示一个单项式或者多项式;3.运算律的正向运用、逆向运用、综合运用.多项式除以多项式是整式除法的延拓与发展,方法与多位数除以多位数的演算方法相似,基本步骤是:1.将被除式和除式按照某字母的降幂排列,如有缺项,要留空位;2.确定商式,竖式演算式,同类项上下对齐;3.演算到余式为零或余式的次数小于除式的次数为止.例题与求解【例1】(1)若为不等式的解,则的最小正整数的值为.(“华罗庚杯”香港中学竞赛试题)(2)已知,那么.(“华杯赛”试题)(3)把展开后得,则.(“祖冲之杯”邀请赛试题)(4)若则.(创新杯训练试题)解题思路:对于(1),从幂的乘方逆用入手;对于(2),目前无法求值,可考虑高次多项式用低次多项式表示;对于(3),它是一个恒等式,即在允许取值范围内取任何一个值代入计算,故可考虑赋值法;对于(4),可考虑比较系数法.【例2】已知,则等于()A.2B.1C.D.(“希望杯”邀请赛试题)解题思路:为指数,我们无法求出的值,而,所以只需求出的值或它们的关系,于是自然想到指数运算律.【例3】设都是正整数,并且,求的值.(江苏省竞赛试题)解题思路:设,这样可用的式子表示,可用的式子表示,通过减少字母个数降低问题的难度.【例4】已知多项式,求的值.解题思路:等号左右两边的式子是恒等的,它们的对应系数对应相等,从而可考虑用比较系数法.【例5】是否存在常数使得能被整除?如果存在,求出的值,否则请说明理由.解题思路:由条件可推知商式是一个二次三项式(含待定系数),根据“被除式=除式×商式”,运用待定系数法求出的值,所谓是否存在,其实就是关于待定系数的方程组是否有解.【例6】已知多项式能被整除,求的值.(北京市竞赛试题)解题思路:本题主要考查了待定系数法在因式分解中的应用.本题关键是能够通过分析得出当和时,原多项式的值均为0,从而求出的值.当然本题也有其他解法.能力训练A级1.(1).(福州市中考试题)(2)若,则.(广东省竞赛试题)2.若,则.3.满足的的最小正整数为.(武汉市选拔赛试题)4.都是正数,且,则中,最大的一个是.(“英才杯”竞赛试题)5.探索规律:,个位数是3;,个位数是9;,个位数是7;,个位数是1;,个位数是3;,个位数是9;…那么的个位数字是,的个位数字是.(长沙市中考试题)6.已知,则的大小关系是()A.B.C.D.7.已知,那么从小到大的顺序是()A.B.C.D.(北京市“迎春杯”竞赛试题)8.若,其中为整数,则与的数量关系为()A.B.C.D.(江苏省竞赛试题)9.已知则的关系是()A.B.C.D.(河北省竞赛试题)10.化简得()A.C.D.11.已知,试求的值.12.已知.试确定的值.13.已知除以,其余数较被除所得的余数少2,求的值.(香港中学竞赛试题)B级1.已知则=.2.(1)计算:=.(第16届“希望杯”邀请竞赛试题)(2)如果,那么.(青少年数学周“宗沪杯”竞赛试题)3.(1)与的大小关系是(填“>”“<”“=”).(2)与的大小关系是:(填“>”“<”“=”).4.如果则=.(“希望杯”邀请赛试题)5.已知,则.(“五羊杯”竞赛试题)6.已知均为不等于1的正数,且则的值为()A.3B.2C.1(“CASIO杯”武汉市竞赛试题)7.若,则的值是()A.1B.0C.—1D.28.如果有两个因式和,则()A.7B.8C.15D.21(奥赛培训试题)9.已知均为正数,又,则与的大小关系是()A.B.C.D.关系不确定10.满足的整数有()个A.1B.2C.3D.411.设满足求的值.12.若为整数,且,求的值.(美国犹他州竞赛试题)13.已知为有理数,且多项式能够被整除.(1)求的值;(2)求的值;(3)若为整数,且.试比较的大小.(四川省竞赛试题)第四篇:整式乘除与因式分解复习教案整式的乘除与因式分解复习菱湖五中教学内容复习整式乘除的基本运算规律和法则,因式分解的概念、方法以及两者之间的关系。

整式的乘除计算练习题及答案一.解答题1.计算:①③④?[﹣4]?÷32;②[]÷[]?y233522.计算:222①﹣8y;②﹣;③;④;⑤;⑥[+﹣2x]÷2x.⑦222⑧.3.计算:564233336abc÷÷.﹣.[]?3xy. +﹣2m.2234224.计算:?x÷x﹣2x?÷x.ab÷a+b?.﹣.+﹣2.5.因式分解:3322①6ab﹣24ab;②﹣2a+4a﹣2;③4n﹣6;④2xy﹣8xy+8y;⑤a+4b;⑥4mn﹣;⑦22222222222841053232222;⑧﹣4a;⑨3x222n+1﹣6x+3xnn﹣1⑩x﹣y+2y﹣1;4a﹣b﹣4a+1;4﹣4x+4y+1;3ax﹣6ax﹣9a;x﹣6x﹣27;﹣2﹣3.242222222226.因式分解:4x﹣4xy+xy. a﹣4.7.给出三个多项式:x+2x﹣1,x+4x+1,x﹣2x.请选择你最喜欢的两个多项式进行加法运算,并把结果因式分解.8.先化简,再求值:+b﹣4ab÷b,其中a=﹣,b=2. 9.当x=﹣1,y=﹣2时,求代数式[2x﹣][+2y]的值. 10.解下列方程或不等式组:①﹣=0;②2﹣≤4.11.先化简,再求值:﹣,其中,.2222232222若x﹣y=1,xy=2,求xy﹣2xy+xy.12.解方程或不等式:222+2=3x+13.+>13.2223223整式的乘除因式分解习题精选参考答案与试题解析一.解答题1.计算:①②[]÷[]?y ③632523352;;④?[﹣4]?÷2.计算:22①﹣8y;2②﹣;③;④;⑤;2⑥[+﹣2x]÷2x.22⑦⑧.2一.计算题19、已知a?b?,a?b?11,求0、已知x?3,x?2,求x 3334221、m??22、 3、?22ab2a?b34、235、?432324、?x8x4x425、?2?226、xy2327、?28、2229、2006200530、231、32、22?4x33、??4xy?6xy??第1页、共6页36、?2xy7、解方程?2x2?2?2x?6x38、已知xm4,xn?3,求x2mx3n的值39、已知x2?xy?21 ,y2?xy?28,求20、已知x3a27,求x4a的值41、2??342、?3?243、?2244、6245、?46、11?222m4m47、?8?48、x?x122259、已知m?3,m?4,求m ab3a?2b的值.0、已知a?115,求a4?4的值. aa 23323261、25?2?62、23?349、4m651、253、55、257、第2页、共6页 50、2、29254、、2258、63、2?365、5667、??47369、199264、a6a2a2a366、255?33?2118、3?4?270、72、28273、74、23232375、??ab6、?77、8、?5x?79、先化简再求值x?,当x??的值80、已知:2?2?5,求2第3页、共6页ab3a?2b?33422322222221时,求此代数式4的值。

整式的乘除》单元考试题及答案第五章:整式的乘除单元测验数学试卷班级:______ 姓名:______ 得分:______一、填空题:(每小题3分,共30分)1.(-a)×(-a)×a = ________;-x²⁵³ ÷ (-x)³²² = ________2.-2x²y³3.2c³ × 3(-8x²) × (-x) × (-y)² = ________;abc² × (-2ac) =________4.(2²)² ÷ 2x = ________;5.-x²y × (x²-2xy+1/5) = ________;6.(-1/2) × (-4xy) = 12xy;-2 + (π-3.14) - (-2) = ________7.(a-10a+7) = ________;若x-3x+1=2,则x+(2/2)¹ =________8.若x²n=2,则2x³n = ________;若642 × 83 = 2ⁿ,则n = ________9.(-8)²⁰⁰⁴ = ________10.已知ab=-3,则-abab-ab-b = ________二、选择题:(每小题3分,共30分)11.下列各式计算正确的是()A、a² = a×a;B、3×5x² = 10x⁶;C、(-c)÷(-c) = -1;D、ab³ = a³b³12.下列各式计算正确的是()A、(x+2y)² = x²+4y²;B、(x+5)(x-2) = x²+3x-10;C、(-x+y)² = x²+y²;D、(x+2y)(x-2y) = x²-4y²13.用科学记数法表示的各数正确的是()A、 = 3.45×10⁴;B、0. = 4.3×10⁻⁵;C、-0. = -4.8×10⁻⁴;D、- = 3.4×10⁵14.当a=1/3时,代数式(a-4)(a-3)-(a-1)(a-3)的值为()A、3/4;B、-6;C、0;D、815.已知a+b=2,ab=-3,则a²-ab+b²的值为()A、11;B、12;C、13;D、1416.已知28a²bm÷4anb²=7b²,那么m、n的值为()A、m=4,n=2;B、m=4,n=1;17、设正方形边长为x,则面积为x^2,根据题意可得(x+3)^2-x^2=39,化简得x=6,答案为C。
第13章 整式的乘除第1课时 幂的运算(一)1.计算:(1)791010⨯=_________; (2)34111222⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭g g _____________. 2.计算:(1)23x x =g ___________; (2)74m m =g ______________.3.计算:(1)()43aa -=g ________; (2)()()42x x x ---=g g ____________.4.计算:()()()234m n n m n m ---=g g ____________.5.计算:(1)322d d d d +=g g __________; (2)5462m m m m m -=g g g __________.6.(1)若710maa a =g ,则m=_________; (2)若8m m a a a =g ,则m=_________.7.一长方体的长、宽、高分别是710cm 、610cm 、310cm ,则它的体积是_________3cm . 8.下列运算正确的是 ( )A . 339x x x =gB . 336x x x =gC . 3332x x x =gD .3262xx x =g9.下列计算正确的是 ( )A .()()235a a a --=-g B .()()()264a a a --=-gC .()()374aa a --=-g D .4312a a a -=-g10.下列各式计算结果为7x 的是 ( )A . ()()25x x --g B .()25x x -g -C .()()43x x --g D . 34x x +11.已知2,5abx x ==,则a bx+等于 ( )A .7B .10C .20D .5012.已知311a a a χχ+=g,则χ的值为 ( )A .2B .3C .4D .5 13.计算.(1) ()()2322x y y x --g ; (2) 131n n yy y y -++g g ;(3);()()334433x x x x x x x ++--g g (4)52342n n x x x x x x --g g g g14.一台电子计算机每秒可作1010次计算,它工作3510⨯秒可作多少次运算?15.已知12km 的土地上,一年内从太阳得到的能量相当于燃烧1.3810⨯kg 煤所产生的能量,那么我国6210km ⨯的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤?16.我们约定1010ab a b ⊗=⨯,如25231010⊗==.(1)试求123⊗和48⊗的值; (2)想一想:()a b c ⊗⊗是否与()a b c ⊗⊗的值相等?验证你的结论.第13章 整式的乘除第2课时 幂的运算(二)1.计算:(1)()320.3⎡⎤-=⎣⎦_________; (2) ()7102=_________.2.计算:(1)()43a =__________; (2) ()2x m =________.3.计算:(1)()43χ-=___________; (2)()35a -=__________.4.计算:(1)()54a b ⎡⎤-=⎣⎦___________; (2)()32m n --=⎡⎤⎣⎦________________. 5.计算:(1)()()2334m m --=g ________; (2)()()3221m m b b +=g ____________.6.下列计算正确的是 ( ) A .()257a a = B .()3327a a = C .()236a a = D .()2121n n a a ++=7.下列各式中错误的是 ( ) A .()()2510n n x y x y ⎡⎤-=-⎣⎦B .()()nm mn a b a b ⎡⎤+=+⎣⎦C .()()236a b a b ⎡⎤-=-⎣⎦ D .()()3131m m x y x y --⎡⎤-=-⎣⎦8.计算()()8424xx g 的结果为 ( )A .18x B .24x C .28x D .32x 9.计算1001000mn g 的结果为 ( )A .100000m n+ B .2310m n+ C .100m D .1000mn10.若5544332,3,4a b c ===,则a 、b 、c 的大小关系是 ( )A .b >c >aB .a >b >cC .c >a >bD .a <b <c 11.计算. (1)()532y y y g g ; (2)()()3122n n n x x x -g g ;(3)()()3511m m b b +-g ; (4)()()235a b b a ⎡⎤--⎣⎦g ;(5)()()()332x y x y x y ⎡⎤---⎣⎦gg ; (6)()()2122nn x x x +-g .12.已知正方体的棱长为()23a b cm +,试分别求出这个正方体的表面积和体积.13.(1)已知182482mm m =g g ,求m 的值;(2)已知22ma =,求()32m a 的值.14.求1007和2003的末位数字.15.求满足()()23320nnn n ----=的正整数n 的值.第13章 整式的乘除第3课时 幂的运算(三)1.计算:(1)()32x =_________; (2)()23mx y =____________.2.计算:(1)212ab ⎛⎫-= ⎪⎝⎭__________; (2)()322xy -=__________.3.计算:(1)()32310-⨯=__________; (2)()34410-⨯=______________.4.计算:(1)()()223222a a a +=g ____________;(2)()()()428236x y x y +-=g _______.5.已知2,3nnx y ==,则()nxy =____________.6.计算:(1)200820083553⎛⎫⎛⎫-= ⎪⎪⎝⎭⎝⎭g ______________. (2)741497⎛⎫-⨯= ⎪⎝⎭____________.7.下列计算正确的是 ( ) A .()326ab ab = B .()22236xy x y = C .()22424aa -=- D .()2323mm m a ba b =8.下列计算正确的个数为 ( ) (1)()224ab ab = (2)()333412ab a b = (3)()428216x x -=- (4)()2234524m n m n =A .0个B .1个C .2个D .3个 9.若()3915mn xyx y =,则m 、n 的值为 ( )A .m=9,n=5B .m=3,n=5C .m=5,n=3D .m=6,n=1210.计算: 6640.753⎛⎫⨯- ⎪⎝⎭的结果为 ( )A .0B .1C .-5D .16411.计算:(1)()4233xy z -; (2)()()25332a b ⎡⎤-⎢⎥⎣⎦g ;(3)()()4225243a a a aa +--g g ; (4)()()()2323337235x x x x x-+g g12.先化简再求值.()3233212a bab ⎛⎫-+- ⎪⎝⎭g ,其中1,44a b ==.13.若25nx =,求()()223234nn x x -的值.14.太阳可以近似地看作是球体,如果用V 、r 分别代表球的体积和半径,那么343V r π=. 太阳的半径约为6×610千米,它的体积大约是多少立方千米?15.你能确定510256625⨯的位数吗?请大胆试一试.第13章 整式的乘除第5课时 整式的乘法(一)1.计算:(1)232xy x y -=g___________;(2)24342535x y x y z ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭g __________. 2.计算:(1)221323ab abc abc =g g _____________;(2)2352231343a bc c abc ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭g g _____________. 3.计算. (1)()()()35210310510⨯⨯⨯=g g ________________,(2)()()()345310410510⨯⨯⨯=g g ________________.4.计算.(1)()2122xyz xy ⎛⎫-= ⎪⎝⎭g __________;(2)()221322m mn mn ⎛⎫--=⎪⎝⎭g g __________. 5.卫星脱离地球进入太阳系的速度是1.12⨯410米/秒,则3.6310⨯秒卫星行走________米.6.计算()24334x y x y ⎛⎫-⎪⎝⎭g 的结果为 ( ) A .6253x y B .84x y - C .624x y - D .62x y 7.下列计算正确的是 ( )A .23639x xy x y =gB .()()22323ab ab a b -=-C .()()2233mn m n m n -=-g D .()232339x y xy x y --=g8.若()()()6571051021010na ⨯⨯⨯=⨯,则a 、n 的值分别为 ( )A .7,11a n ==B .a = 5,n = 12C .a =7,n =13D .a =2,n =13 9.计算()()()232341.210510210-⨯⨯⨯⨯⨯的结果为 ( )A .205.7610⨯ B .195.7610⨯ C .202.8810⨯ D .192.8810⨯ 10.计算. (1)()2332310.534x y x y z xyz ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭g g ; (2)()()()2330.30.27ay bx a by g g11.计算.(1)()()22233ab a b a b ab +-g ;(2) ()()()23222222x y xy xy xy --+.12.先化简再求值. ()()()()222335364a b b ab ab ab a -+----,其中a =12,b=0.5.13.光的速度大约是3510⨯千米/秒,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要4年时间才能到达地球,一年以3710⨯秒计算,求这颗恒星与地球的距离.14.已知1292nm n a b a b +-的积与435a b 是同类项,求m 、n 的值.15.已知435,477m n ==. 求代数式()()()()321322m n m n m n m n ⎡⎤-+--+-⎡⎤⎣⎦⎢⎥⎣⎦g g 的值.第6课时 整式的乘法(二)1.计算:(1) a (2a 2一3a +1)=________;(2)(42x 一3x+6)g 12x =____________.2.计算:(1)3a b(2a 2b--a b+1) =_____________;(2)(34a b 2+3a b 一23b )(12a b)=_____________. 3.计算:(1)(一22x )(2x -12x 一1) =____________;(2) 322213342x y x y x ⎛⎫+-⎪⎝⎭(一12xy) =______________.4.计算:(1)3x(5x -2)一5x(1+3x)=____________; (2)32x (1--2x)+2x(32x -x+1)=___________.5.若A 表示一个单项式,B 表示一个三项式,则AB 是__________项式.6.下列各式中,计算正确的是 ( )A .(a -3b+1)(一6a )=一6a 2+18a b+6aB .()232191313x y xy x y ⎛⎫--+=+ ⎪⎝⎭C .6mn(2m+3n -1) =12m 2n+18mn 2-6mnD .一a b(a2一a -b) =-a 3b -a2b--a b 27.计算(62x -4xy+3y 2)·213x y ⎛⎫-⎪⎝⎭的结果为 ( ) A .一2x 4y+43x 2y 2+x 2y 3 B .一2x 4y -43x 2y 2-x 2y 3C .一2x 4y+43x 3y 2一x 2y 3 D .一2x 4y 一43x 3y 2+x 2y 3 8.计算a2(a +1) -a (a2-2a -1)的结果为 ( )A .一a2一a B .2a2+a +1 C .3a2+a D .3a2-a9.一个长方体的长、宽、高分别是2x 一3、3x 和x ,则它的体积等于 ( ) A .22x —32x B .6x -3 C .62x -9x D .62x -92x10.计算.(1)(2x 3一32x +4x -1)(一3x); (2)()22213632xy y x xy ⎛⎫-+-- ⎪⎝⎭.11.计算. (1)2a 2-a (2a -5b)-b(5a -b);(2)22249312324ab a b ab b ⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭.12.先化简,再求值.(1)m 2(m+3)+2m(m 2—3)一3m(m 2+m -1),其中m 52=; (2)4a b(a 2b -a b 2+a 6)一2a b 2(2a2—3a b+2a ),其中a =3,b=2.13.(1)解方程:x(x2+3)+ 2x(2x-3)--3x(2x-x-1)=12;(2)解不等式:2x(x一1)一3(2x+5x一6)>l+4x(1一14 x).14.若n为自然数,则n(2n+1) -2n(n-3)的值是7的倍数吗?试说明理由.15.若(3x+2y) 2+2x+3y+5=0.化简(一122x y)(xy2+42x y-6x3)+2xy(x3y-2x4)+xy2,并求它的值.第7课时整式的乘法(三)1.计算:(1)(y—12)(y+13)=___________;(2)(x+20)(x+10) =__________.2.计算:(1)(2x一5)(x+4)=___________;(2)(2y—1)(2y+3) =__________.3.计算:(1)(x+3y)(3x-4y)=__________;(2)(2a一b)(3a+b) =___________.4.计算:(1)(22x+3y2)(22x-5y2)=__________;(2)52x一(2x-1)(3x+ 1) =__________.5.计算:(1)(3m+2n)(3m-2n-1) =____________;(2)(2x+3)( 2x一5x-1) =___________.6.下列计算中,错误的是( ) A.(x+1)(x+4) =2x+5x+4 B.(m一2)(m+3) =m2+m一6C.(y+4)(y一5) =y2+9y一20 D.(x一3)(x一6) =2x一9x+187.计算结果为2m2-7mn+6n2的是( )A.(2m—n)(m 6n) B.(2m-3n)(m-2n)C.(2m一3n)(m+2n) D.(2m+3n)(m+2n)8.计算t2一(t+1)(t-5)的结果为( ) A.4t-5 B.一4t一5 C.一4t+5 D.4t+59.若(x-2)(x+3) =2x+px+q,贝p、q的值是( )A.p=5,q=6 B.p=l,q=-6 C.p=1,q=6 D.p=5,q=一6 10.计算.(1)(12x+3)(22x一4x+1);(2)(3x3一2x+1))2-x)(3)3(x一2)(x+1)一2(x一5)(x-3);(4)x(2x一4)一(x+3)( 2x一3x+2) .11.先化简,再求值.(1)3(x+5)(x一3) -5(x一2)(x+3),其中32x=:(2)(3x-2)(x-3)一2(x+6)(x-5)+3(2x-7x+13),其中132x=.12.计算下图中阴影部分的面积.13.把一个长方形的长增加2 cm,宽减少l cm,它的面积不变;把它的长减少3 cm,宽增加4 cm,面积也不变,求这个长方形原来的面积.14.已知:如图,现有a ×a 、b ×b 的正方形纸片和a ×b 的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次)在下面的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),使拼出的矩形面积为2a2+5a b+2b 2,并标出此矩形的长和宽.15.你能求(x 一1)(99x +98x +97x +…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形人手,分别计算下列各式的值. (1)(x -1)(x+1) =_____________; (2)(x —1)( 2x +x+1) =_____________; (3)(x -1)(3x + 2x +x+1) =____________; …由此我们可以得到:(x 一1)( 99x +98x +97x +…+x+1) =___________, 请你利用上面的结论,完成下列两题的计算: (4)992+982+972+…+2+1; (5)()()()504948222-+-+-+…+(一2)+1.第8课时 乘法公式(一)1.计算:(1)(1--2y)(1+2y)=___________; (2)(2x+3)(3—2x)=____________.2.计算:(1)(一2y 一3x)(3x 一2y)=__________; (2)(一2y 2-3x)(3x 一2y 2)=_________. 3.计算:(1)( a2b —c 3)(a2b+c 3)=_________; (2)(-3a b+c)(3a b+c)=___________.4.计算:(1)(2x+1)(2x 一1)(4x 2+1)=__________; (2)2111242x x x ⎛⎫⎛⎫⎛⎫-++ ⎪⎪⎪⎝⎭⎝⎭⎝⎭=_______________. 5.计算:(1)(x+5)2一(x 一5)2=_____________;(2)(m+t)(m 一t)一(3m+2t)(3m--2t)=____________. 6.利用平方差公式计算.(1)1.02 ×0.98=___________; (2)12151433⨯=______________. 7.下列运算中,正确的是 ( ) A .(a 一2b)( a -2b)= a2-4b 2B .(-a +2b)( a 一2b)= -a2一2b 2C .(a +2b)( a 一2b)= -a2-2b 2D .(一a 一2b)(一a +2b)= a2-4b 28.在下列各式中,运算结果为36y 2+49x 2的是 ( ) A .(一6y+7x)(一6y 一7x) B .(一6y+7x)(6y 一7x) C .(7x 一4y)(7x+9y) D .(一6y 一7x)(6y 一7x) 9.在①(一3x -y)(3x+y);②(一3x —y)(3x -y);③(一3x+y)(3x 一y);④(一3x+y)(3x+y)这四个式子中,能利用平方差公式计算的是 ( ) A .①② B .②③ C .③④ D .②④10.利用平方差公式计算(x 一1)(x+1)(x 2+1),正确的结果是 ( ) A .x 4-1 B .x 4+1 C .(x 一1) 4D .(x+1)411.利用平方差公式计算.(1)59.8×60.2; (2)99×101×10 001. 12.计算.(1)x 2(x -2y)(x+2y)一(x 2+y)(x 2-y);(2)( a +1)( a 一1)( a 2+1)( a4+1)(8a +1).13.先化简,再求值.(1)2(3a +1)(1--3a )+(a -2)(2+a ),其中a =2;(2)(2x -y)(y+2x)一(2y+x)(2y -),其中x=1,y=2.14.利用平方差公式计算.(1)1002一992+982-972+962-952+…+22一12;(2)222111111234⎛⎫⎛⎫⎛⎫--- ⎪⎪⎪⎝⎭⎝⎭⎝⎭…22111199100⎛⎫⎛⎫--⎪⎪⎝⎭⎝⎭.15.计算图中阴影部分的面积,其中R=7.22 cm ,r=1.39 cm .(π取3.14,结果保留整塑)16.已知962-1可以被在60至70之间的两个整数整除,求这两个整数.13.3 乘法公式(1)一、基础训练1.下列运算中,正确的是()A.(a+3)(a-3)=a2-3 B.(3b+2)(3b-2)=3b2-4 C.(3m-2n)(-2n-3m)=4n2-9m2 D.(x+2)(x-3)=x2-6 2.在下列多项式的乘法中,可以用平方差公式计算的是()A.(x+1)(1+x)B.(12a+b)(b-12a)C.(-a+b)(a-b)D.(x2-y)(x+y2)3.对于任意的正整数n,能整除代数式(3n+1)(3n-1)-(3-n)(3+n)的整数是()A.3 B.6 C.10 D.94.若(x-5)2=x2+kx+25,则k=()A.5 B.-5 C.10 D.-105.9.8×10.2=________; 6.a2+b2=(a+b)2+______=(a-b)2+________.7.(x-y+z)(x+y+z)=________; 8.(a+b+c)2=_______.9.(12x+3)2-(12x-3)2=________.10.(1)(2a-3b)(2a+3b);(2)(-p2+q)(-p2-q);(3)(x-2y)2;(4)(-2x-12y)2.11.(1)(2a-b)(2a+b)(4a2+b2);(2)(x+y-z)(x-y+z)-(x+y+z)(x-y-z).12.有一块边长为m的正方形空地,想在中间位置修一条“十”字型小路,•小路的宽为n,试求剩余的空地面积;用两种方法表示出来,比较这两种表示方法,•验证了什么公式?二、能力训练13.如果x2+4x+k2恰好是另一个整式的平方,那么常数k的值为()A.4 B.2 C.-2 D.±214.已知a+1a=3,则a2+21a,则a+的值是()A.1 B.7 C.9 D.1115.若a-b=2,a-c=1,则(2a-b-c)2+(c-a)2的值为()A.10 B.9 C.2 D.116.│5x-2y│·│2y-5x│的结果是()A.25x2-4y2B.25x2-20xy+4y2C.25x2+20xy+4y2D.-25x2+20xy-4y2 17.若a2+2a=1,则(a+1)2=_________.三、综合训练18.(1)已知a+b=3,ab=2,求a2+b2;(2)若已知a+b=10,a2+b2=4,ab的值呢?19.解不等式(3x-4)2>(-4+3x)(3x+4).20.观察下列各式的规律.12+(1×2)2+22=(1×2+1)2;22+(2×3)2+32=(2×3+1)2;32+(3×4)2+42=(3×4+1)2;…(1)写出第2007行的式子;(2)写出第n行的式子,并说明你的结论是正确的.13.3 乘法公式(2)1.计算:(1)(2x2+13)(2x2-13);(2)(3a+b)(b-3a);(3)(-2x-3y)(2x-3y).2.判断下列各式能否用平方差公式计算,若能,请把结果计算出来.(1)(2x-13y)(-13x-2y);(2)(-2m+3n)(2n+3m);(3)(-3m+2)(3m-2);(4)(13a-b)(-b-13a).3.判断:(1)(b-4a)2=b2-16a2.()(2)(12a+b)2=14a2+ab+b2.()(3)(4m-n)2=16m2-4mn+n2.()(4)(-a-b)2=a2-2ab+b2.()4.计算:(1)(2a-3)2;(2)(-2a-13)2.5.运用乘法公式计算:(1)1997×2003;(2)10.32;(3)(9923)2;(4)1523×1613.6.如图,老张家有一块L形菜地,要把L形菜地按图那样分成面积相等的梯形,种上不同的蔬菜,这两个梯形的上底都是a米,下底都是b米,高都是(b-a)米,请你算一下,这块菜地面积共有多少?当a=10,b=30时,面积是多少?7.计算(a+b-c)2.8.计算(a+4b-3c)2.9.计算(3x+y-2)2.10.计算(x+y+z)(x-y-z).11.计算(a+4b-3c)(a-4b-3c).12.计算(3x+y-2)(3x-y+2).13.已知:a+b=9,a2+b2=21,求ab.14.已知a+1a=10,求a2+21a的值.15.若已知a-1a=3,且a>1a,求a2+21a的值.13.5 因式分解(1)一、基础训练1.若多项式-6ab+18abx+24aby 的一个因式是-6ab ,那么其余的因式是( )A .-1-3x+4yB .1+3x-4yC .-1-3x-4yD .1-3x-4y2.多项式-6ab 2+18a 2b 2-12a 3b 2c 的公因式是( )A .-6ab 2cB .-ab 2C .-6ab 2D .-6a 3b 2c3.下列用提公因式法分解因式正确的是( )A .12abc-9a 2b 2=3abc (4-3ab )B .3x 2y-3xy+6y=3y (x 2-x+2y )C .-a 2+ab-ac=-a (a-b+c )D .x 2y+5xy-y=y (x 2+5x )4.下列等式从左到右的变形是因式分解的是( )A .-6a 3b 2=2a 2b ·(-3ab 2)B .9a 2-4b 2=(3a+2b )(3a-2b )C .ma-mb+c=m (a-b )+cD .(a+b )2=a 2+2ab+b 25.下列各式从左到右的变形错误的是( )A .(y-x )2=(x-y )2B .-a-b=-(a+b )C .(m-n )3=-(n-m )3D .-m+n=-(m+n )6.若多项式x 2-5x+m 可分解为(x-3)(x-2),则m 的值为( )A .-14B .-6C .6D .47.(1)分解因式:x 3-4x=_______;(2)因式分解:ax 2y+axy 2=________.8.因式分解:(1)3x 2-6xy+x ; (2)-25x+x 3;(3)9x 2(a-b )+4y 2(b-a ); (4)(x-2)(x-4)+1.二、能力训练9.计算54×99+45×99+99=________.10.若a 与b 都是有理数,且满足a 2+b 2+5=4a-2b ,则(a+b )2006=_______.11.若x 2-x+k 是一个多项式的平方,则k 的值为( )A .14 B .-14 C .12 D .-1212.若m 2+2mn+2n 2-6n+9=0,求2m n 的值.13.利用整式的乘法容易知道(m+n)(a+b)=ma+mb+na+nb,现在的问题是:如何将多项式ma+mb+na+nb因式分解呢?用你发现的规律将m3-m2n+mn2-n3因式分解.14.由一个边长为a的小正方形和两个长为a,宽为b的小矩形拼成如图的矩形ABCD,则整个图形可表达出一些有关多项式分解因式的等式,请你写出其中任意三个等式.15.说明817-299-913能被15整除.13.5 因式分解(2)1.3a4b2与-12a3b5的公因式是_________.2.把下列多项式进行因式分解(1)9x2-6xy+3x;(2)-10x2y-5xy2+15xy;(3)a(m-n)-b(n-m).3.因式分解:(1)16-125m2;(2)(a+b)2-1;(3)a2-6a+9;(4)12x2+2xy+2y2.4.下列由左边到右边的变形,属于因式分解的是()A.(x+2)(x-2)=x2-4 B.x2-2x+1=x(x-2)+1C.a2-b2=(a+b)(a-b)D.ma+mb+na+nb=m(a+b)+n(a+b)5.因式分解:(1)3mx2+6mxy+3my2;(2)x4-18x2y2+81y4;(3)a4-16;(4)4m2-3n(4m-3n).6.因式分解:(1)(x+y)2-14(x+y)+49;(2)x(x-y)-y(y-x);(3)4m2-3n(4m-3n).7.用另一种方法解案例1中第(2)题.8.分解因式:(1)4a2-b2+6a-3b;(2)x2-y2-z2-2yz.9.已知:a-b=3,b+c=-5,求代数式ac-bc+a2-ab的值.第12课时因式分解1.(1)多项式8x3y2一18xy2z的公因式是_____________;(2)多项式2x2y+6xy-10y的公因式是_____________.2.(1)多项式4x3-12x2-18x的公因式是2x,则另一个因式是______________;(2)多项式-7a b-14a bx+49a by的公因式是-7a b,则另一个因式是_____________.3.分解因式.(1) a(2x-y)一b(y一2x)=_____________:(2)3((a一b)2一4(b一a)=_____________.4.分解因式.(1)5x(a+b一c) -l0y(a+b一c)=_____________;(2)5m2(a一b)一l0m(a-b)2=_____________.5.分解因式.(1)x4-x2=____________________:(2)b2 (a一4)+(4一a)=_________________.6.分解因式.(1)一12x2+xy一12y2=_________________;(2)2m3一28m2n2+98mn4=__________________.7.下列等式从左到右的变形属于因式分解的是( ) A.(x+1)(x-1)=x2一1 B.(2x)2一y2=(2x+y)(2x—y)C.a x+a y—a=a(x+y)一a D.5a2y-10a y+20y=5y(a2—2a)+20y8.把多项式9a2b2-18a b2+45a2b分解因式时,公因式是( )A.9a2b B.45a2b2 C .9a b D.18a b2 9.下列各式中,分解因式正确的是( ) A.6(x一2)+x(2一x)=(x一2)(6+x) B.x3+2x2+x=x(x2+2x)C.a(a一b) 2+a b(a一b)= a2(a-b) D.3x2+6x=3x(x+6) 10.下列各式中,分解结果为2a(x-3) 2的是( )A .2a x 2-6x+9B .2a x 2-18aC .2a x 2+12a x+18aD .2a x 2—12a x+18a11.下列多项式①10a m 一15a ;②4xm 2一9x ;③4a m 2一12a m+9a ;④一4m 2—9中,含有因式2m -3的有 ( )A .1个B .2个C .3个D .4个12.分解因式.(1)16a2b -25bc 2; (2)( a -b) 4一(b -a )2:(3)()()2293x y x y --+; (4)()()()322x y x y x y -+--13.分解因式(1)-a2-4a b -4b 2; (2)4a 2x 2-8a 2x ;(3)3a (b 2+9)2-108a b 2; (4)9a b 2(x -y)+6a2b(x -y) -a 3(y -x) .14.(1)已知m+n=3,mn=23,求m 3n 一m 2n 2+mn 3的值;(2)已知a (a 一1)一(a2-b)=3,求a b 一12(a 2+b 2)的值.15.试说明四个连续自然数的积加上1是一个完全平方数.16.有两个孩子的年龄分别为x 、y ,且满足x 2+xy=99,你能求出这两个孩子的年龄吗?因式分解姓名1.下列因式分解中,正确的是()(A) 1- 14x2=14(x + 2) (x- 2) (B)4x –2 x2– 2 = - 2(x- 1)2(C) ( x- y )3–(y- x) = (x – y) (x – y + 1) ( x –y – 1)(D) x2–y2– x + y = ( x + y) (x – y – 1)2.下列各等式(1) a2-b2 = (a + b) (a–b ),(2) x2–3x +2 = x(x–3) + 2(3 )1x2–y2=1( x + y) (x – y ) ,(4 )x2 +1x2=-(x -1x)2从左到是因式分解的个数为()(A) 1 个(B) 2 个(C) 3 个(D) 4个3.若x2+mx+25 是一个完全平方式,则m的值是()(A)20 (B) 10 (C) ±20 (D) ±104.若x2+mx+n能分解成( x+2 ) (x – 5),则m= ,n= ; 5.若二次三项式2x2+x+5m在实数范围内能因式分解,则m= ; 6.若x2+kx-6有一个因式是(x-2),则k的值是;7.把下列因式因式分解:(1)a3-a2-2a (2)4m2-9n2-4m+1(3)3a2+bc-3ac-ab (4)9-x2+2xy-y28.在实数范围内因式分解:(1)2x2-3x-1 (2)-2x2+5xy+2y29.分解下列因式:(1).10a(x-y)2-5b(y-x) (2).a n+1-4a n+4a n-1(3).x3(2x-y)-2x+y (4).x(6x-1)-1(5).2ax-10ay+5by+6x (6).1-a2-ab-14b2*(7) 3X2-7X+2 (8).(x2+x)(x2+x-3)+2(9).x5y-9xy5(10).-4x2+3xy+2y2(11).4a-a5(12).2x2-4x+1(13).4y2+4y-510.多项式x2-y2, x2-2xy+y2, x3-y3的公因式是。